
Pytania na egzamin
1. Sprawdź metodą zero-jedynkową czy następujące wyrażenie jest tezą rachunku zdań
(wyrażenie z trzema zmiennymi).
2. Alternatywnie jedno z czterech
a) Dokończ następujące zdania tak, aby stały się egzemplifikacjami (przykład,
potwierdzenie) znanych ci praw logiki. 3 połówki zdań: pierwsza ma podpadać pod tezę
rachunku zdań (ale żadna z pierwszych czterech), druga tak, żeby podpadała pod tezę z
rachunku predykatów, trzecia z twierdzeń rachunku zbiorów.
b) Wykaż, że poniższa sekwencja jest wyrażeniem rachunku zdań.
c) Wykaż, że poniższa sekwencja jest formułą zdaniową rachunku predykatów.
d) W poniższej formule zdaniowej rachunku predykatów wskaż zasięgi poszczególnych
kwantyfikatorów oraz ustal, która zmienna, na jakim miejscu występuje jako zmienna
wolna, a na jakim miejscu jako zmienna związana i przez który kwantyfikator.
3. Pojęciówka z czterech pierwszych rozdziałów (będą kumulatywne podpunkty a, b, c)
określenia tłustym drukiem.
4. Zapisz symbolicznie (będą 3 kumulatywne podpunkty zapisów formalnych z pierwszych
czterech rozdziałów).
5.
a) Na jednym rysunku zawierającym 3 koła zaznacz (tak ustawić 3 koła, żeby ilustrowały
związki między określonymi zbiorami). Objaśnij rysunek.
b) Mając na uwadze znane ci rodzaje relacji zakwalifikuj następującą relację. Uzasadnij
swoje ustalenia (trzeba odnotować tylko pozytywne kwalifikacje, tzn. wskazać jaka ta
relacja jest, nie ma potrzeby wskazywać jaka ta relacja nie jest). Wymienić jak najwięcej
kwalifikacji.
6. Alternatywnie jedno z dwóch
a) Jedno z 8 pytań dotyczących wynikania lub wynikania logicznego.
1) Ze zdania A wynika w języku J zdanie B. Zdanie A jest prawdziwe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania B? Uzasadnij swoją odpowiedź.
2) Ze zdania A wynika w języku J zdanie B. Zdanie A jest fałszywe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania B? Uzasadnij swoją odpowiedź.
3) Ze zdania A wynika w języku J zdanie B. Zdanie B jest prawdziwe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania A? Uzasadnij swoją odpowiedź.
4) Ze zdania A wynika w języku J zdanie B. Zdanie B jest fałszywe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania A? Uzasadnij swoją odpowiedź.
5) Ze zdania A wynika logicznie zdanie B. Zdanie A jest prawdziwe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania B? Uzasadnij swoją odpowiedź.
6) Ze zdania A wynika logicznie zdanie B. Zdanie A jest fałszywe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania B? Uzasadnij swoją odpowiedź.

7) Ze zdania A wynika logicznie zdanie B. Zdanie B jest prawdziwe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania A? Uzasadnij swoją odpowiedź.
8) Ze zdania A wynika logicznie zdanie B. Zdanie B jest fałszywe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania A? Uzasadnij swoją odpowiedź.
b) Jedno z 9 pytań dotyczących definicji
1) Omów budowę definicji równościowej.
2) Omów budowę definicji przez abstrakcję.
3) Omów budowę definicji indukcyjnej.
4) Przedstaw wszystkie znane ci schematy definicji cząstkowych.
5) Omów funkcjonowanie definicji przez postulaty.
6) Omów rodzaje definicji ze względu na zadania.
7) Omów błędy w definiowaniu za wyjątkiem błędu nieadekwatności.
8) Omów błąd nieadekwatności w definiowaniu (podać wszystkie możliwości- wzory
symboliczne).
7. Pojęciówka z rozdziałów od 4 do 7 (będą kumulatywne 3 podpunkty).
8. Alternatywnie jedno z czterech
a) Zilustruj i omów związki między rodzajami reguł językowych (str. 142 przedstawić i
omówić).
b) Przedstaw ogólny schemat wnioskowania przez indukcję enumeracyjną niezupełną i
podaj jeden nieksiążkowy przykład takiego wnioskowania.
c) Przedstaw schemat wnioskowania przez analogię pierwszego typu i podaj jeden
nieksiążkowy przykład takiego wnioskowania.
d) Przedstaw schemat wnioskowania przez analogię drugiego typu i podaj jeden
nieksiążkowy przykład takiego wnioskowania.

Odpowiedzi ad. 3. i ad. 7.
1. Rachunek zdań
Wartość logiczna zdania jest jego właściwością obiektywną. Nie zależy ona od tego, czy trafnie
rozpoznają ją ci, którzy używają danego zdania.
Zdanie w sensie logicznym jest to takie wyrażenie, które jest prawdziwe albo fałszywe. Wyrażenie
jest prawdziwe, gdy opisuje rzeczywistość tak, jak się ona ma. Natomiast wyrażenie jest fałszywe, gdy
opisuje rzeczywistość nie tak, jak się ona ma. Ponieważ prawdę oraz fałsz nazywamy wartościami
logicznymi, dlatego możemy powiedzieć, że zdaniem w sensie logicznym jest takie wyrażenie, które
ma wartość logiczną.
Zmienna zdaniowa to takie wyrażenie, za które wolno wstawić dowolne zdanie.
Spójnik jednoargumentowy jest to takie wyrażenie, które po dołączeniu do niego jednego zdania
jako argumentu daje nowe zdanie o wartości logicznej wyznaczonej – w szczególny sposób – przez
wartość logiczną zdania dołączonego.
Spójnik negacji oznaczamy symbolem „~”. Określa go następująca matryca [tu
matryca]. Matryca tego spójnika wskazuje, że gdy argument jest zdaniem
prawdziwym, to zdanie powstałe przez poprzedzenie go tym spójnikiem jest
fałszywe. Gdy natomiast argument jest fałszywy, to zdanie powstałe przez
poprzedzenie go spójnikiem negacji jest prawdziwe. Odpowiednikiem tak pojętego
spójnika negacji jest w języku polskim wyrażenie „nie jest tak, że”. Do pewnego
stopnia jest odpowiednikiem jest także wyrażenie „nieprawda, że”, a również i samo
słowo „nie”. Zdanie dołączone do spójnika negacji jako argument nazywamy zdaniem
zanegowanym, zaś zdanie powstałe przez zanegowanie określonego zdania
nazywamy negacją. Zdanie zanegowane oraz powstała z niego negacja stanowią parę
zdań wzajem sprzecznych.
Spójnik dwuargumentowy jest to takie wyrażenie, które po dołączeniu do niego dwóch zdań jako
argumentów daje nowe zdanie o wartości logicznej wyznaczonej – w szczególny sposób – przez
wartości logiczne dołączonych zdań.
Spójnik koniunkcji jest spójnikiem dwuargumentowym oznaczanym symbolem „^”.
Określa go następująca matryca [tu matryca]. Spójnik koniunkcji tym się
charakteryzuje, że powstałe z niego zdanie jest prawdziwe tylko wtedy, gdy oba jego
argumenty są prawdziwe. Gdy zaś choć jeden z argumentów jest fałszywy, to zdanie
zbudowane za pomocą spójnika koniunkcji też jest fałszywe. Zdania dołączone jako
argumenty do spójnika koniunkcji nazywa się czynnikami. Zdanie zbudowane z tego
spójnika i jego argumentów nazywa się koniunkcją. Spójnikowi koniunkcji odpowiada
w języku polskim słowo „i”, a do pewnego stopnia także słowa „oraz” tudzież „a”.

Spójnik alternatywy jest spójnikiem dwuargumentowym oznaczanym symbolem „v”.
Określa go następująca matryca [tu matryca]. Spójnik alternatywy tym się
charakteryzuje, że powstałe z niego zdanie jest prawdziwe już wtedy, gdy chociaż
jeden z jego argumentów jest prawdziwy. Gdy zaś oba argumenty są fałszywe, to
zdanie zbudowane za pomocą spójnika alternatywy też jest fałszywe. Zdania
dołączone do spójnika alternatywy jako argumenty nazywa się składnikami. Zdanie
zbudowane z tego spójnika i jego argumentów nazywa się alternatywą. Spójnikowi
alternatywy odpowiada w języku polskim słowo „lub”.
Spójnik implikacji jest spójnikiem dwuargumentowym oznaczanym symbolem „→”.
Określa go następująca matryca [tu matryca]. Spójnik implikacji tym się
charakteryzuje, że powstałe z niego zdanie jest fałszywe tylko wtedy, gdy argument
poprzedzający spójnik jest prawdziwy a argument występujący po spójniku jest
fałszywy. Ponieważ pierwszy z argumentów nazywa się poprzednikiem, zaś drugi
nazywa się następnikiem, dlatego możemy powiedzieć, że zdanie powstałe ze
spójnika implikacji jest fałszywe tylko wtedy, gdy poprzednik jest prawdziwy, a
następnik fałszywy. Zdanie zbudowane z tego spójnika i jego argumentów nazywa się
implikacją. Spójnikowi implikacji odpowiadają w języku polskim takie wyrażenia jak
„jeśli, to”, „jeżeli, to”, a do pewnego stopnia także wyrażenie „gdyby, to”.
Spójnik równoważności jest spójnikiem dwuargumentowym oznaczanym symbolem
„≡”. Określa go następująca matryca [tu matryca]. Jak widać, spójnik równoważności
tym się charakteryzuje, że powstałe z niego zdanie jest prawdziwe wtedy, gdy oba
argumenty mają taką samą wartość logiczną, a więc oba są prawdziwe albo oba są
fałszywe. Zdania dołączone do spójnika równoważności jako argumenty nazywa się
członami. Zdanie zbudowane z tego spójnika i jego argumentów nazywa się
równoważnością. Spójnikowi równoważności odpowiada w języku polskim wyrażenie
„wtedy i tylko wtedy, gdy”.
Spójnik n-argumentowy jest to takie wyrażenie, które z n-tką zdań jako argumentów daje nowe
zdanie o wartości logicznej wyznaczonej – w szczególny sposób – przez wartość logiczną dołączonych
zdań.
Zdanie proste to takie zdanie, w którym nie występuje żaden spójnik.
Zdanie złożone to takie zdanie, w który występuje co najmniej jeden spójnik.

Wyrażenie rachunku zdań:
1) Każda zmienna zdaniowa jest wyrażeniem rachunku zdań
2) Jeżeli sekwencja postaci A jest wyrażeniem rachunku zdań, to także sekwencja postaci ~(A)
jest wyrażeniem rachunku zdań.
3) Jeżeli sekwencje postaci A oraz B są wyrażeniami rachunku zdań, to także sekwencje postaci
(A) ^ (B), (A) v (B), (A) → (B), (A) ≡ (B) są wyrażeniami rachunku zdań.
Tezy rachunku zdań są to wyrażenia rachunku zdań, które przy wszelkich wstawieniach za
występujące w nich zmienne przekształcają się w zdania prawdziwe. Wyrażenia te nazywa się także
schematami tautologicznymi rachunku zdań albo (rachunkowozdaniowymi) prawami logiki.
Formalizacja rachunku zdań to operacja, która polega na wyborze pewnych tez rachunku zdań jako
aksjomatów i podaniu reguł wprowadzania z jednych tez innych tez.
Pierwszy etap nazywa się aksjomatyzacją rachunku zdań. Przeprowadza się go, dobierając określony
zestaw tez jako zestaw aksjomatów.
(A1) (p→q) → [(q→r) → (p→r)]
(A2) (~p→p) → p
(A3) p→(~p→q)
Drugi etap formalizacji polega na sprecyzowaniu reguł wyprowadzania z jednych tez innych tez
rachunku zdań. Przy tym aksjomaty i reguły musza być tak dobrane, aby spełniały dwa warunki. Po
pierwsze, z aksjomatów za pomocą reguł winny być wyprowadzane wszystkie tezy rachunku zdań. Po
drugie, z aksjomatów za pomocą reguł winny być wyprowadzane tylko tezy rachunku zdań. Innymi
słowy, reguły winny umożliwiać wyprowadzenie z aksjomatów wszystkich i tylko tez rachunku zdań.
Jedną z reguł jest reguła podstawienia, która brzmi następująco: jeżeli wyrażenie postaci A jest tezą
rachunku zdań, to tezą rachunku zdań jest też wyrażenie postaci B powstałe z A przez konsekwentne
podstawienie za występującą w nim zmienną zdaniową dowolnego wyrażenia rachunku zdań.
Drugą regułą jest reguła odrywania, która brzmi następująco: jeżeli wyrażenie postaci A → B jest
tezą rachunku zdań i wyrażenie postaci A jest tezą rachunku zdań, to także wyrażenie postaci B jest
tezą rachunku zdań.
Trzecią regułą jest reguła zastępowania, która brzmi następująco: jeżeli wyrażenie postaci A jest tezą
rachunku zdań, to tezą rachunku zdań jest także wyrażenie postaci B powstałe z A przez zastąpienie
występujące w A wyrażenia rachunku zdań innym wyrażeniem rachunku zdań odpowiadającym mu
na podstawie następujących definicji:
(D1) C ^ D = ~(C → ~D)
(D2) C v D = ~C → D
(D3) C ≡ D = ~[(C → D) → ~ (D → C)]
Aby wykazać, że dane wyrażenie jest tezą rachunku zdań należy przeprowadzić dowód tego
wyrażenia. Dowodem wyrażenia W, na gruncie aksjomatów 1, 2 i 3, w oparciu o reguły
podstawiania, odrywania i zastępowania jest ciąg wyrażeń rachunku zdań, taki że każde wyrażenie

tego ciągu albo jest jednym z aksjomatów 1-3, albo powstaje z wcześniejszego wyrażenia ciągu przez
zastosowanie reguły podstawiania, albo powstaje z wcześniejszego wyrażenia ciągu przez
zastosowanie reguły odrywania, albo powstaje z wcześniejszego wyrażenia ciągu przez zastosowanie
reguły zastępowania, a przy tym ostatnim wyrażeniem tego ciągu jest wyrażenie W. Zabieg
konstruowania danego wyrażenia nazywamy jego dowodzeniem.
Dowód wyrażenia W, na gruncie aksjomatów tworzących zbiór A, w oparciu o reguły tworzące
zbiór R, jest taki ciąg wyrażeń, że każde wyrażenie tego ciągu albo jest jednym z aksjomatów zbioru
A, albo powstaje z wcześniejszych wyrażeń tego ciągu przez zastosowanie którejś z reguł zbioru R, a
przy tym ostatnim wyrażeniem tego ciągu jest wyrażenie W.
2. Wprowadzenie do rachunku predykatów
Imię własne jest to wyrażenie, które znamionuje to, że ma ono za zadanie oznaczać jakieś
indywiduum, w celu wyróżnienia go spośród innych obiektów. Stąd też każde z nich oznacza tylko
jakiś jeden obiekt.
Deskrypcja jest to wyrażenie będące charakterystyką odnoszącą się do co najwyżej jednego obiektu,
które przeto oznacza co najwyżej jeden obiekt.
Imiona własne oraz deskrypcje nazywa się ogólnie terminami jednostkowymi.
Funktor jednoargumentowy to takie wyrażenie, które z jednym terminem jednostkowym daje
termin jednostkowy. Termin jednostkowy, z którym dany funktor tworzy nowy termin jednostkowy,
nazywamy argumentem owego funktora.
Funktor dwuargumentowy to takie wyrażenie, które z dwoma terminami jednostkowymi daje termin
jednostkowy. Terminy jednostkowe dołączone do takiego funktora są jego argumentami.
Funktor n-argumentowy to takie wyrażenie, które z n-tką terminów jednostkowych daje termin
jednostkowy.
Zmienna indywiduowa to takie wyrażenie, za które wolno wstawiać dowolny termin jednostkowy.
Term
1) każda zmienna indywiduowa jest termem i każde imię własne jest termem,
2) jeżeli wyrażenia w
1
, …, w
n
są termami, to termem jest także wyrażenie f
n
k
(w
1
, …, w
n
) (dla
każdego k).
Zatem w rachunku predykatów termami są wszystkie zmienne indywiduowe i wszystkie imiona
własne. Termami są również wyrażenia f(a), f(b), f(c), f(x), f(y), f(z), g[f(a)] itd.
Predykat jednoargumentowy to takie wyrażenie, które z jednym terminem jednostkowym daje
zdanie.

Predykat dwuargumentowy to takie wyrażenie, które z dwoma terminami jednostkowymi daje
zdanie.
Predykatem n-argumentowy to takie wyrażenie, które z n-tką terminów jednostkowych daje zdanie.
Formuła zdaniowa atomowa to wyrażenie powstałe przez stosowne dołączenie do n-
argumentowego predykatu n-tki termów.
Zdanie atomowe to wyrażenie powstałe prze stosowne dołączenie do n-argumentowego predykatu
n-tki terminów jednostkowych. Zdaniami atomowymi są więc te formuły zdaniowe atomowe, w
których nie występują zmienne indywiduowe.
Zdanie molekularne to zdanie zbudowane z jednego lub więcej zdań atomowych i co najmniej
jednego spójnika.
Duży kwantyfikator zwany także kwantyfikatorem ogólnym albo generalnym, oznaczymy symbolem
" ⋀ " Jego odpowiednikiem w języku polskim są takie wyrażenia jak „dla każdego”, „każdy”, a do
pewnego stopnia także wyrażenie „wszyscy”.
Mały kwantyfikator zwany również kwantyfikatorem szczególnym albo egzystencjalnym oznaczamy
symbolem "
⋁ " Jego odpowiednikami w języku polskim są takie wyrażenia, jak „dla pewnego”,
„pewien”, „istnieje” bądź „egzystuje”.
Zasięg dużego kwantyfikatora to wyrażenie występujące w nawiasach bezpośrednio po dużym
kwantyfikatorze.
Zasięg małego kwantyfikatora to wyrażenie występujące w nawiasach bezpośrednio po małym
kwantyfikatorze.
Zmienna związana jest to zmienna występująca w zasięgu odnoszącego się do niej kwantyfikatora.
Zmienna wolna jest to zmienna, która występuje w danym miejscu wyrażenia, nie będąc tam
zmienną związaną.
Formuła zdaniowa rachunku predykatów
1) każda formuła zdaniowa atomowa rachunku predykatów jest formułą zdaniową rachunku
predykatów,
2) jeżeli wyrażenie postaci A jest formułą zdaniową rachunku predykatów, to jest też formułą
zdaniową rachunku predykatów ~(A),
3) jeżeli wyrażenia postaci A i B są formułami zdaniowymi rachunku predykatów, to są też
formułami rachunku predykatów wyrażenia postaci (A) ^(B), (A) v (B), (A) → (B) oraz (A) ≡ (B),
4) jeżeli wyrażenie postaci A jest formułą zdaniową rachunku predykatów, to formułami
zdaniowymi rachunku predykatów są też wyrażenia postaci
⋀ (𝐴)
𝑥𝑖
oraz
⋁ (𝐴)
𝑥𝑖
(dla
dowolnego i).
Określenie to wyznacza zbiór wszystkich formuł atomowych rachunku predykatów. Innymi słowy,
określenie to wskazuje, jak należy budować wyrażenie, aby było ono formułą zdaniową rachunku
predykatów.
Zdanie rachunku predykatów jest to formuła zdaniowa nie zawierająca zmiennym wolnych.

3. Zbiory
Zbiór w sensie kolektywnym jest to pewna całość składająca się z przedmiotów będących jej
częściami.
Zbiór w sensie dystrybutywnym jest to zespół pewnych obiektów wyróżnionych w określony sposób.
Obiekty należące do danego zbioru w sensie dystrybutywnym nazywamy jego elementami.
Dział szeroko pojętej logiki zajmujący się badaniem zbiorów nazywamy teorią zbiorów albo – częściej
– teorią mnogości. Dla oznaczenia poszczególnych zbiorów używa się dużych liter „Z”, „X”, „Y”, „Z
1
”,
„Z’” itd.
Zbiór pusty jest to zbiór nie posiadający żadnego elementu. Jest tylko jeden zbiór pusty.
Zbiór jednoelementowy to taki zbiór, który ma tylko jeden element.
Zbiór dwuelementowy to taki zbiór, który ma tylko dwa elementy.
Zbiór skończony to zbiór posiadający skończoną ilość elementów. Zbiór pusty, wszystkie zbiory
jedno-, dwu-, trój-, czteroelementowe są zbiorami skończonymi.
Zbiór pełny danej nauki albo też jej uniwersum to zbiór wszystkich przedmiotów badanych przez tę
naukę. Zbiór ten oznaczamy symbolami „1” lub „U”.
Obiekty nie będące zbiorami są pewnymi przedmiotami indywidualnymi.
Rodzina zbiorów to zbiór, którego wszystkie elementy są zbiorami.
Stosunki między zbiorami:
Dwa zbiory są identyczne wtedy, gdy mają te same elementy.
Innymi słowy, dwa dowolne zbiory Z i Y są identyczne wtedy i tylko wtedy, gdy mają te same
elementy. Dwa zbiory są więc identyczne, gdy wszystkie elementy pierwszego z nich są
elementami drugiego, a wszystkie elementy drugiego z nich są elementami pierwszego.
Stosunek identyczności zbiorów ilustruje następujący rysunek:
Z Y
Między niektórymi zbiorami zachodzi stosunek zawierania się jednego z nich w drugim.
Stosunek ten nazywamy też inkluzją i oznaczamy symbolem „ ”. Otóż:
Innymi słowy, jeden zbiór zawiera się w drugim wtedy i tylko wtedy, gdy każdy element
pierwszego jest też elementem drugiego. Zbiór Z nazywa się wówczas podzbiorem zbioru Y,
zaś zbiór Y nazywa się nadzbiorem zbioru Z. Warto zauważyć, że dwa zbiory identyczne także
zawierają się w sobie.
Od tak szeroko pojętego stosunku zawierania się zbiorów odróżniamy stosunek właściwego
zawierania się zbiorów nazywany też inkluzją właściwą i oznaczany symbolem „ ”. Otóż:
Innymi słowy, jeden zbiór właściwie zawiera się w drugim wtedy i tylko wtedy, gdy
spełnione są łącznie dwa warunki: 1) każdy element pierwszego zbioru jest też elementem
drugiego zbioru i 2) istnieje taki obiekt, który nie jest elementem pierwszego zbioru, ale jest
elementem drugiego. Pierwszy zbiór nazywa się wtedy właściwym podzbiorem drugiego z
nich, a drugi nazywa się właściwym nadzbiorem pierwszego. Stosunek właściwego
zawierania się zbioru Z w zbiorze Y ilustruje następujący rysunek:
Y
Z
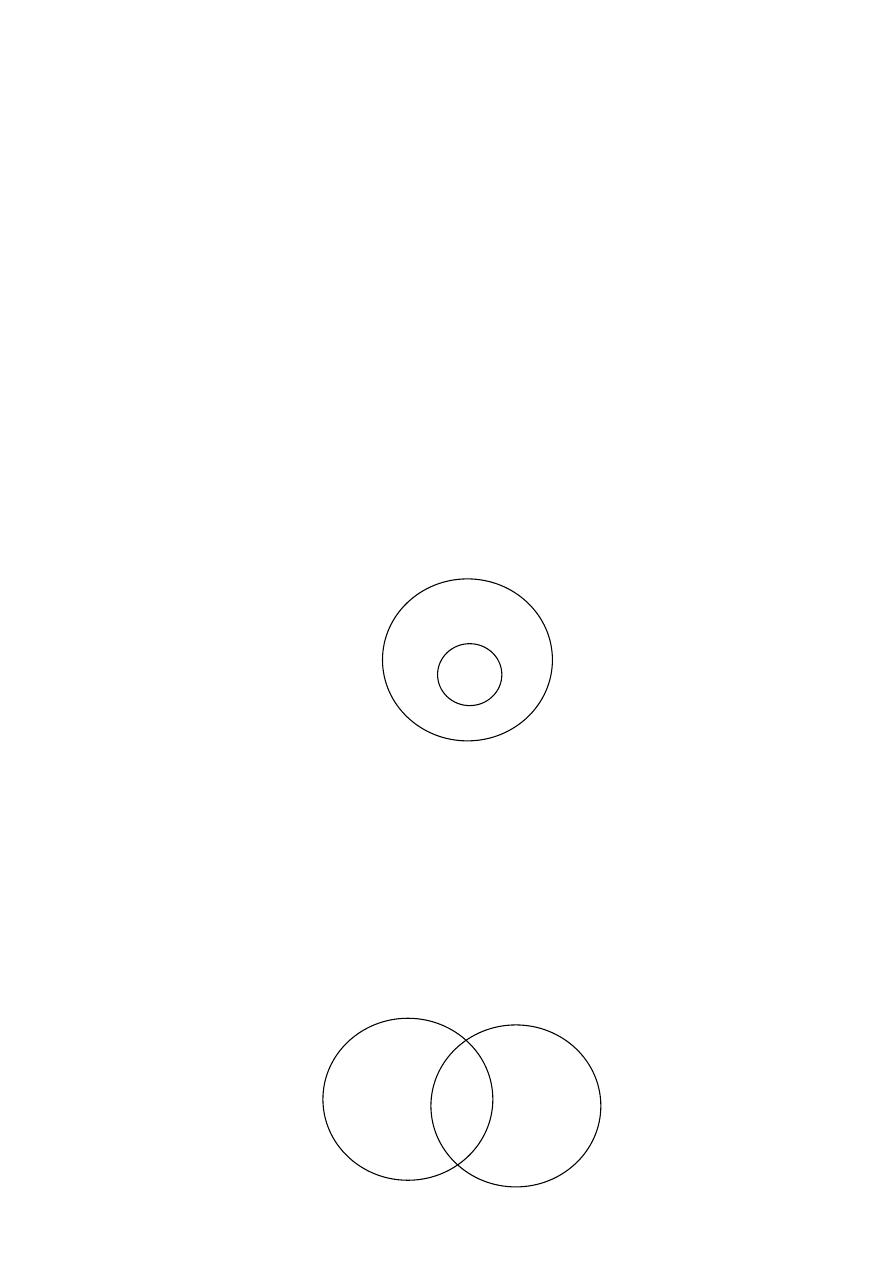
Między niektórymi zbiorami zachodzi stosunek krzyżowania się. Otóż:
Innymi słowy, dwa zbiory krzyżują się wtedy i tylko wtedy, gdy istnieje taki obiekt, który jest
elementem każdego z tych zbiorów i istnieje taki obiekt, który jest elementem pierwszego, a
nie jest elementem drugiego i istnieje taki obiekt, który nie jest elementem pierwszego, ale
jest elementem drugiego zbioru. Stosunek krzyżowania się dwóch zbiorów ilustruje
następujący rysunek:
Z Y
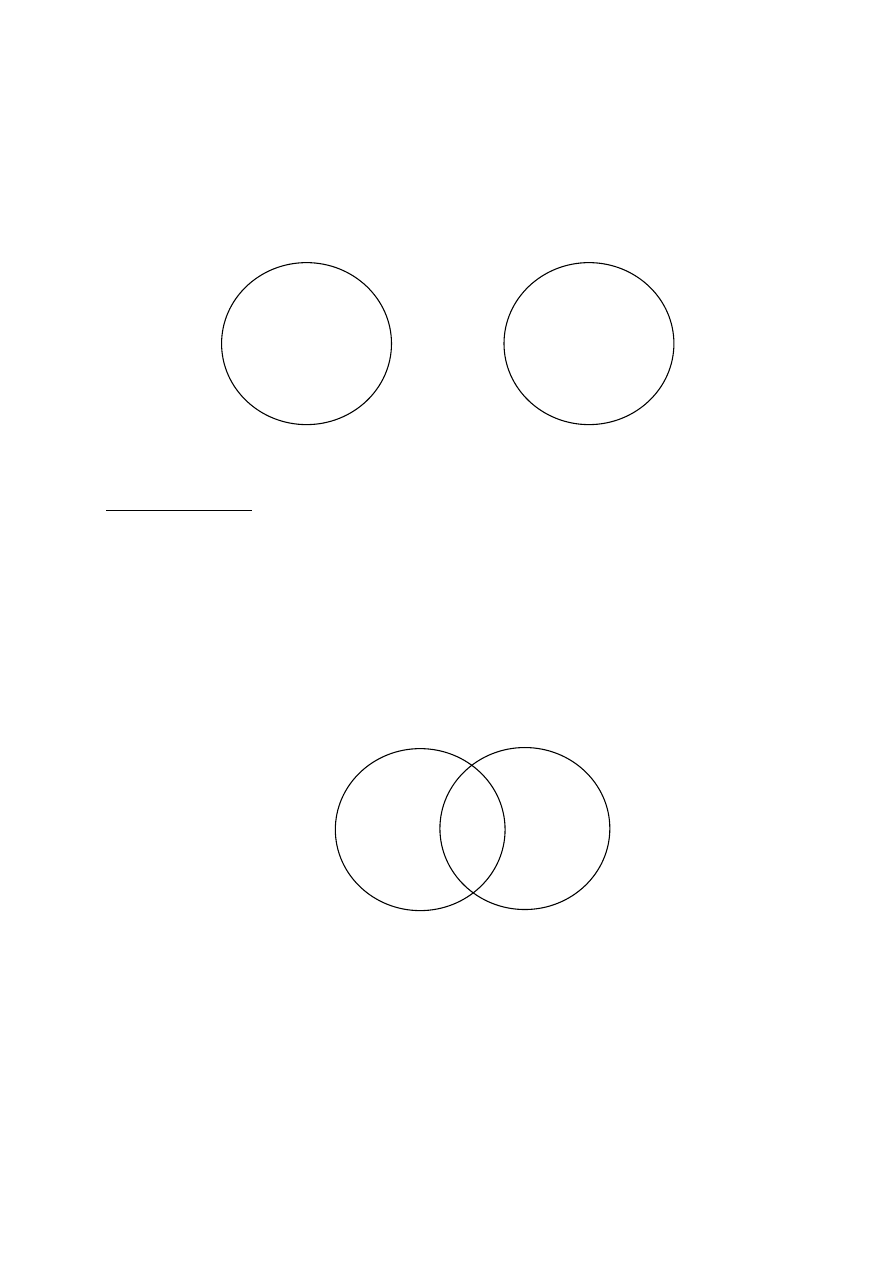
Wreszcie są i takie zbiory, które wykluczają się. Otóż:
Innymi słowy, dwa zbiory wykluczają się wtedy i tylko wtedy, gdy nie mają one wspólnych
elementów. Stosunek wykluczania się dwóch zbiorów ilustruje następujący rysunek:
Z Y
Działania na zbiorach
Na zbiorach dają się przeprowadzić pewne działania. Jednym z nich jest tworzenie sumy
dwóch zbiorów oznaczanej symbolem „∪”. Otóż:
Innymi słowy, dany obiekt jest elementem sumy dwóch zbiorów wtedy, gdy jest elementem
chociaż jednego tych zbiorów. Zatem suma dwóch zbiorów też jest zbiorem, a jej
elementami są elementy zbiorów sumę te tworzących. Tworzenie sumy zbiorów Z i Y ilustruje
następujący rysunek:
Z Y
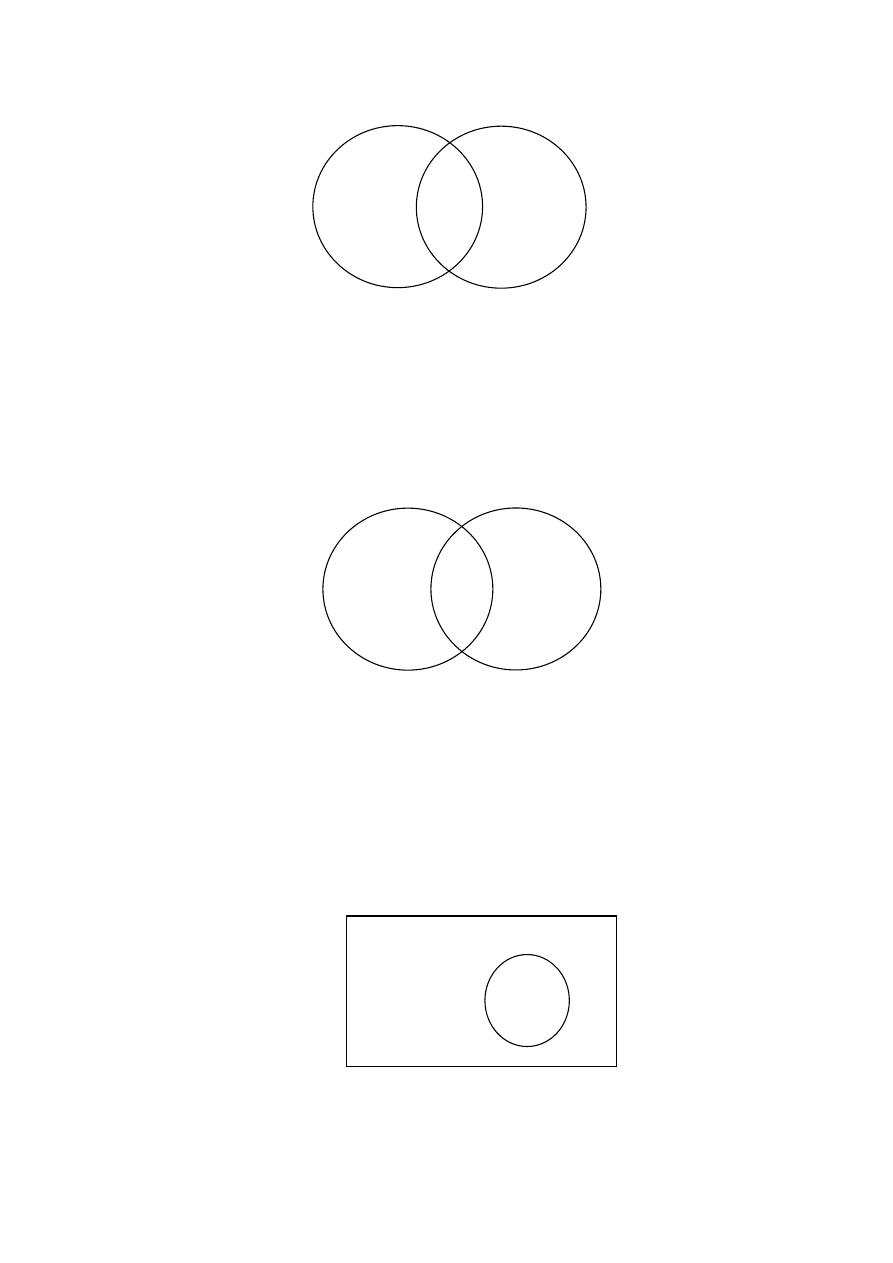
Tworzy się także iloczyn dwóch zbiorów oznaczany symbolem „∩”. Otóż:
Innymi słowy, dany obiekt jest elementem iloczynu dwóch zbiorów wtedy, gdy jest
elementem każdego z tych zbiorów. Tedy iloczyn dwóch zbiorów też jest zbiorem, a jego
elementami są obiekty będące elementami jednocześnie obu zbiorów iloczyn ten
tworzących. Tworzenie iloczynu zbiorów Z i Y ilustruje następujący rysunek:
Z
Y
Tworzy się również różnicę dwóch zbiorów oznaczaną symbolem „-”. Otóż:
Innymi słowy obiekt jest elementem różnicy między jednym zbiorem a drugim wtedy, gdy
jest elementem pierwszego zbioru, a nie jest elementem drugiego zbioru. Przeto różnica
zbiorów też jest zbiorem, a jej elementami są te elementy pierwszego zbioru, które nie są
elementami drugiego z nich. Tworzenie różnicy zbiorów Z i Y pokazuje następujący rysunek:
Z Y
Mając dany zbiór pełny, oznaczany symbolem „U”, możemy tworzyć dopełnienie zbioru,
który jest w nim zawarty. Dopełnienie zbioru Z oznacza się symbolem „Z’”. Otóż:
Innymi słowy, dany obiekt jest elementem dopełnienia zbioru Z wtedy, gdy jest on
elementem zbioru pełnego U, a nie jest elementem zbioru Z. Tedy dopełnienie zbioru też jest
zbiorem, a jego elementami są te elementy zbioru pełnego, które nie są elementami zbioru
wyjściowego. Tworzenie dopełnienia zbioru ilustruje następujący rysunek:
U Z

Podzbiorem zbioru nazywamy tylko taki zabieg wyróżniania jego podzbiorów, który spełnia dwa
wymogi, a mianowicie wymóg rozłączności i wymóg adekwatności. Zabieg wyróżniania podzbiorów
danego zbioru spełnia wymóg rozłączności wtedy, gdy dowolne dwa wyróżnione podzbiory są
wzajem rozłączone, to znaczy, wzajemnie wykluczają się. Z kolei zabieg wyróżniania podzbiorów
danego zbioru spełnia wymóg adekwatności, zwany również wymogiem zupełności, wtedy, gdy
suma wszystkich wyróżnionych podzbiorów jest identyczna ze zbiorem, z którego wyróżniono owe
podzbiory.
Zbiór dzielony to zbiór, z którego wyróżnia się podzbiory, dokonując jego podziału . Wyróżnione z
niego podzbiory nazywamy członami podziału.
Podział nieskończony to podział danego zbioru na nieskończenie wiele członów.
Podział skończony to podział danego zbioru na skończenie wiele członów. Podział skończony
możemy zawsze przedstawić jako podział n-członowy.
Ze względu na sposób przeprowadzania podziału odróżniamy podziały wedle pewnej zasady i
podziały dychotomiczne.
Podział wedle pewnej zasady polega na wyróżnieniu w zbiorze dzielonym członów zawierających
elementy posiadające tę samą odmianę cechy będącej zasadą podziału.
Człony podziału przeprowadzonego wedle pewnej zasady nazywają się zbiorami współrzędnymi ze
względu na tę zasadę.
Podział wedle pewnej zasady zostaje przeprowadzony, gdy spełnione są łącznie trzy następujące
warunki:
1) cecha stanowiąca zasadę podziału przysługuje wszystkim elementom zbioru dzielonego,
2) uwzględnione zostały wszystkie odmiany cechy będącej podstawą podziału,
3) żaden element zbioru dzielonego nie posiada dwóch odmian cechy będącej zasadą podziału.
Podział dychotomiczny polega na wyróżnieniu w zbiorze dzielonym członu składającego się z
elementów posiadających określoną cechę i członu składającego się z pozostałych elementów, nie
mających owej cechy. Podział dychotomiczny jest więc zawsze 2-członowym.
Podział uchodzi za naturalny z danego punktu widzenia, gdy w poszczególnych jego członach
znajdują się obiekty z tego punktu widzenia bardziej do siebie podobne, niż obiekty należące do
różnych członów.
Podział uchodzi za sztuczny, z danego punktu widzenia, gdy w poszczególnych jego członach znajdują
się obiekty z tego punktu widzenia mniej do siebie podobne, niż obiekty należące do różnych
członów.
Każdy podział zbioru stanowi jego jednostopniową klasyfikację. Stąd też zbiór dzielony nazywa się
także zbiorem klasyfikowanym, zaś człony podziału nazywa się członami klasyfikacji. Jeżeli każdy z
członów jednostopniowej klasyfikacji poddamy podziałowi, to otrzymamy klasyfikacje
dwustopniową. Jeżeli każdy z członów dwustopniowej klasyfikacji poddamy podziałowi, to
otrzymamy klasyfikację trójstopniową. W podobny sposób można przeprowadzić klasyfikację
czwartego stopnia, piątego stopnia itd.

4. Relacje
Człony relacji są to obiekty, między którymi dana relacja zachodzi.
Cechy są to relacje jednoczłonowe.
W odróżnieniu od cech wszystkie pozostałe relacje są relacjami wieloczłonowymi.
Relacje dwuczłonowe to takie relacje wieloczłonowe, które zachodzą zawsze między dwoma
obiektami.
Relacje trójczłonowe to takie relacje wieloczłonowe, które zachodzą zawsze między trzema
obiektami.
Łatwo zauważyć, że z każdą cechą wiąże się określony predykat jednoargumentowy. Podobnie, z
każda relacją dwuczłonową wiąże się określony predykat dwuargumentowy. Dla podkreślenia, że
chodzi tu o relacje będziemy dalej w roli predykatów używać wyrażeń „R”, „R
1
” itd. Relacje
dwuczłonowe przyjęło się zapisywać w szczególny sposób, a mianowicie „aRb”, „xRy” itp.
Dziedzina relacji R to zbiór wszystkich tych obiektów, które pozostają w relacji R do pewnych
obiektów. Dziedzinę relacji R oznaczamy symbolem „D”. Zatem:
Dziedziną relacji bycia mężem jest więc zbiór wszystkich żonatych mężczyzn.
Przeciwdziedzina relacji R to zbiór wszystkich tych obiektów, do których pewne obiekty pozostają w
relacji R. Przeciwdziedzinę relacji R oznaczamy symbolem „D(R)”. Zatem:
Przeciwdziedziną relacji bycia mężem jest tedy zbiór wszystkich zamężnych kobiet.
Pole relacji R jest to suma dziedziny i przeciwdziedziny relacji R. Zbiór ten oznaczamy symbolem
„P(R)”. Zatem:
Relacja jest zwrotna, gdy każdy obiekt pozostaje w niej do samego siebie. A więc:
Relacja R jest zwrotna w zbiorze Z, gdy każdy element tego zbioru pozostaje w niej do samego siebie.
A więc relacja R jest zwrotna w zbiorze Z
Każda relacja, która nie jest zwrotna w danym zbiorze jest w tym zbiorze relacją niezwrotną. Zatem:

Innymi słowy, relacja R jest niezwrotna w zbiorze Z wtedy, gdy nie jest tak, że każdy element tego
zbioru pozostaje w niej do samego siebie. A więc relacja jest niezwrotna w danym zbiorze, gdy
przynajmniej jeden element tego zbioru nie pozostaje w niej do samego siebie. Oczywiście relacja
jest niezwrotna w danym zbiorze także i wtedy, gdy żaden jego element nie pozostaje w niej do
samego siebie.
Szczególną odmianę relacji niezwrotnych stanowią relacje przeciwzwrotne. Otóż
Innymi słowy, relacja R jest przeciwzwrotna w zbiorze Z wtedy, gdy żaden element tego zbioru nie
pozostaje w niej do samego siebie.
Patrząc na relacje z nieco innego punktu widzenia, możemy wyróżnić wśród nich relacje symetryczne
w danych zbiorach. Otóż:
Innymi słowy, relacja R jest symetryczna w zbiorze Z wtedy, gdy zachodząc między dwoma
dowolnymi elementami x oraz y tego zbioru, zachodzi też między elementem y oraz elementem x.
Swobodnie mówiąc, relacja jest symetryczna w danym zbiorze, gdy zachodzenie jej w jednym
kierunku przesądza o zachodzeniu jej w drugim kierunku.
Każda relacja, która nie jest symetryczna w danym zbiorze, jest w tym zbiorze relacją
niesymetryczną. A więc:
Innymi słowy, relacja R jest niesymetryczna w zbiorze Z wtedy, gdy nie jest tak, że zachodząc między
dwoma dowolnymi elementami x oraz y tego zbioru zachodzi też między elementem y oraz
elementem x. Swobodnie mówiąc, relacja jest niesymetryczna w danym zbiorze, gdy nie jest tak, że
jej zachodzenie w jednym kierunku przesądza o zachodzeniu jej w odwrotnych kierunku.
Szczególną odmianę relacji niesymetrycznych stanowią relacje przeciwsymetryczne, zwane też
relacjami asymetrycznymi. Otóż:
Innymi słowy, relacja R jest przeciwsymetryczna w zbiorze Z wtedy, gdy zachodząc między dwoma
dowolnymi elementami x oraz y tego zbioru nie zachodzi między elementem y oraz elementem x.
Zatem relacja jest przeciwsymetryczna w danym zbiorze, gdy – swobodnie mówiąc – zachodzenie jej
w jednym kierunku wyklucza zachodzenie jej w odwrotnym kierunku.
Patrząc na relacje z jeszcze innego punktu widzenia możemy wyróżnić wśród nich relacje przechodnie
w określonych zbiorach. Otóż:
Innymi słowy, relacja R jest przechodnia w zbiorze Z wtedy, gdy dla wszelkich jego trzech
elementów, ilekroć zachodzi ona między pierwszym a drugim z nich i zachodzi między drugim a

trzecim z nich, to zachodzi też między pierwszym a trzecim z nich. Trzeba podkreślić, że relacje
przechodnie w danych zbiorach są relacjami dwuczłonowymi, bo w każdym wypadku zachodzą
między dwoma obiektami. Relacje przechodnie nazywa się też relacjami tranzytywnymi.
Każda relacja, która nie jest przechodnia w danym zbiorze jest w tym zbiorze relacją nieprzechodnią,
czyli nontranzytywną. Zatem:
Innymi słowy, relacja R jest nieprzechodnia w zbiorze Z wtedy, gdy nie jest tak, że ilekroć zachodzi
ona między dowolnymi dwoma elementami i zachodzi między tymże drugim a dowolnym trzecim
elementem, to zachodzi ona też między owym pierwszym a tym trzecim jego elementem. Relacja
jest więc nieprzechodnia w danym zbiorze, gdy są w nim przynajmniej trzy takie elementy, z których
pierwszy pozostaje w tej relacji do drugiego, drugi do trzeciego, ale pierwszy nie pozostaje w niej do
trzeciego.
Szczególną odmianę relacji nieprzechodnich stanowią relacje przeciwprzechodnie, zwane też
relacjami tranzytywnymi. Otóż:
Innymi słowy, relacja R jest przeciwprzechodnia w zbiorze Z wtedy, gdy dla wszystkich jego trzech
elementów, ile ktoś zachodzi ona między pierwszym a drugim z nich i zachodzi między drugim a
trzecim z nich, to nie zachodzi między pierwszym a trzecim z nich.
Między pewnymi relacjami zachodzą szczególne związki. Mianowicie:
Innymi słowy, relacja R
1
jest konwersem relacji R
2
wtedy, gdy dla dowolnych dwóch elementów
relacja R
1
zachodzi między pierwszym a drugim z nich i wtedy i tylko wtedy, gdy relacja R
2
zachodzi
między drugim a pierwszym z nich. Swobodnie mówiąc, konwersem danej relacji jest taka relacja,
która zachodzi między dwoma dowolnymi obiektami w jednym kierunku wtedy tylko, gdy relacja
wyjściowa zachodzi między tymi obiektami w odwrotnym kierunku. Relację Stanowiącą konwers
relacji R oznaczamy symbolem „R”.
Swoiście powiązane są też relacje tworzące iloczyn względny. Otóż:
Innymi słowy, relacja R
1
jest iloczynem względnym relacji R
2
i R
3
wtedy, gdy zachodzi ona między
jednym a drugim obiektem tylko, gdy istnieje taki przedmiot, że pierwszy obiekt pozostaje w relacji R
2
do tego przedmiotu, a przedmiot ten pozostaje w relacji R
3
do drugiego obiektu. Swobodnie mówiąc,
relacja będąca iloczynem względnym dwóch innych relacji łączy bezpośrednio dwa obiekty wtedy,
gdy tamte relacji łączą je pośrednio, przez przedmiot występujący jednocześnie jako człon każdej z
nich.
Relacja równościowa w zbiorze to taka relacja, która jest w tym zbiorze jednocześnie zwrotna,
symetryczna i przechodnia. Relacja równościowa w określonym zbirze zachodzi między tymi jego
elementami, które są pod pewnym względem sobie równe.

Przyjmijmy, że relacja R jest równościowa w zbiorze Z, do którego należy element x. Zbiór wszystkich
tych elementów zbioru Z, które pozostają w relacji R do x-a nazywamy klasą abstrakcji od x-a w
zbiorze Z, ze względu na relację R i oznaczamy symbolem „ ”.
Wyróżnimy jeszcze pewną odmianę relacji, mianowicie relacje spójne w określonych zbiorach. Otóż:
Innymi słowy, relacja R jest spójna w zbiorze Z wtedy, gdy zachodzi ona między wszelkimi dwoma
różnymi jego elementami. Swobodnie mówiąc, relacja jest spójna w danym zbiorze wtedy, gdy z
wszelkich dwóch różnych jego elementów pierwszy pozostaje w niej do drugiego lub też drugi
pozostaje w niej do pierwszego.
Relacja liniowo porządkująca zbiór jest to relacja, która jest w tym zbiorze jednocześnie spójna,
przechodnia i przeciwsymetryczna. Często też nazywa się ją po prostu relacją porządkującą ów zbiór.
Pozwala ona bowiem ustawić wszystkie elementy tego zbioru w jeden szereg tak, że na każdym
miejscu tego szeregu znajduje się tylko jeden jego element.
Dwuczłonowa relacja R jest funkcją jednoargumentową
Innymi słowy, dwuczłonowa relacja R jest funkcją jednoargumentową, gdy każdy element jej
dziedziny pozostaje w niej do jednego tylko elementu przeciwdziedziny. Jeśli bowiem jakikolwiek
element jej dziedziny pozostaje w tej relacji do dwóch elementów przeciwdziedziny, to owe dwa
elementy okazują się identyczne.
5. Język
Reguły ustalające słownik danego języka są to reguły, które w pierwszym rzędzie konstytuują język
wyznaczając jego podstawowe wyrażenia zwane słowami. Ogół słów języka stanowi jego słownik.
Reguły gramatyczne są to reguły interweniujące przy budowie wyrażeń języka. Dzielą się one na
reguły ustalające kategorie gramatyczne i reguły ustalające sposób budowania wyrażeń złożonych z
wyrażeń o określonych kategoriach gramatycznych/
Kategoria gramatyczna danego języka jest to zbiór tych wszystkich wyrażeń określonego języka,
które pozwalają się wzajemnie zastępować w dowolnym zdaniu owego języka, dając w efekcie zdanie
tego języka.
Reguły ustalające kategorie gramatyczne to takie reguły gramatyczne, które kwalifikują
poszczególne słowa oraz złożone wyrażenia danego języka jako elementy określonych jego kategorii
gramatycznych.

Reguły ustalające sposób budowania wyrażeń złożonych z wyrażeń o określonych kategoriach
gramatycznych są to reguły gramatyczne, które ustalają sposób łączenia wyrażeń prostszych w
wyrażenia bardziej złożone.
Reguły gramatyczne i reguły ustalające słownik tworzą łącznie reguły formowania.
Reguły dedukcyjne są to reguły składniowe, które wyróżniają pewne zdania określonego języka jako
zdania prawdziwe. Reguły dedukcyjne danego języka dzielą się na reguły aksjomatyczne i reguły
inferencyjne.
Tezy danego języka są to zdania wyróżnione jako prawdziwe przez reguły dedukcyjne.
Reguły aksjomatyczne są to reguły dedukcyjne, które wyróżniają pewne zdania jako prawdziwe
niezależnie od wartości logicznej jakichkolwiek innych zdań.
Aksjomaty danego języka są to zdania wyróżnione jako tezy przez reguły aksjomatyczne.
Reguły inferencyjne są to reguły dedukcyjne, które wyróżniają pewne zdania jako prawdziwe pod
warunkiem, że wyróżnione są jako prawdziwe określone inne zdania danego języka.
Bezpośrednia konsekwencja inferencyjna danej tezy jest to zdanie zakwalifikowane jako teza w
wyniku jednokrotnego zastosowania jednej reguły inferencyjnej do określonej tezy.
Pośrednia konsekwencja inferencyjna danej tezy jest to zdanie zakwalifikowane jako teza w wyniku
wielokrotnego zastosowanie jednej reguły inferencyjnej lub zastosowania wielu reguł inferencyjnych
do określonej tezy.
Tautologie są to zdania powstałe z tez rachunku zdań oraz tez rachunku predykatów.
Aksjomaty danego języka wespół z ich konsekwencjami inferencyjnymi tworzą ogół tez tego języka.
Wyznaczające te tezy reguły dedukcyjne wraz z regułami formowania stanowią reguły składniowe
danego języka.
Kontrtezy danego języka są to zaprzeczenie tez danego języka. Oczywiście jako zaprzeczenia zdań
prawdziwych wszystkie kontrtezy danego języka są zdaniami fałszywymi.
Kontrtautologie są to zaprzeczenia tautologii.
Język ukonstytuowany jedynie przez reguły składniowe stanowi tak zwany czysty rachunek, który
wymaga dopiero stosownego interpretowania. Dokonują tego konstytuujące go reguły semantyczne,
które dzielą się na reguły odniesienia przedmiotowego i reguły prawdziwościowe.
Reguły odniesienia przedmiotowego dzielą się z kolei na reguły ustające uniwersum danego języka
oraz reguły denotowania.
Uniwersum danego języka jest to zbiór obiektów, do którego odnosi się każdy język i których
właściwości oraz wzajemne powiązania opisuje.
Reguły ustalające uniwersum danego języka są to reguły, które wyznaczają uniwersum tego języka.

Reguły denotowania to takie reguły odniesienia przedmiotowego, które przyporządkowują
poszczególnym wyrażeniom danego uniwersum języka określone obiekty, czyli wskazują, co
poszczególne wyrażenia oznaczają.
Reguły prawdziwościowe są to reguły odniesienia przedmiotowego, które określają warunki, pod
jakimi poszczególne zdania danego języka są zdaniami prawdziwymi.
Zdanie Z
1
danego języka jest równoznaczne ze zdaniem Z
2
tego języka wtedy, gdy tezą owego języka
jest implikacja, której poprzednik stanowi Z
1
, a następnik stanowi Z
2
, oraz tezą owego języka jest
implikacja, której poprzednik stanowi zdania Z
2
, a następnik stanowi zdanie Z
1
. Innymi słowy, dwa
zdania Z
1
i Z
2
danego języka są równoznaczne, gdy zdania postaci „Z
1
->Z
2
”
oraz „Z
2
-> Z
1
” są tezami
tego języka.
Niezdaniowe wyrażenie W
1
jest równoznaczne w danym języku z niezdaniowym wyrażeniem W
2
wtedy, gdy wszelkie dwa zdania tego języka tym tylko się różniące, że w jednym z nich występuje
wyrażenie W
1
, a w drugim wyrażenie W
2
, są równoznaczne.
Ze zdań Z
1
, Z
2
, …, Z
k
wynika w danym języku zdanie Z
n
wtedy i tylko wtedy, gdy implikacja, której
poprzednik tworzy koniunkcja zdań Z
1
, Z
2
, …, Z
k
, a następnik stanowi zdanie Z
n
, jest tezą tego języka.
Racja jest to koniunkcja zdań, z których w określonym języku wynika dane zdanie.
Następstwo jest to zdanie, które wynika z racji.
Ze zdań Z
1
, Z
2
, …, Z
k
wynika logicznie zdanie Z
n
wtedy i tylko wtedy, gdy implikacja, której poprzednik
tworzy koniunkcję zdań Z
1
, Z
2
, …, Z
k
, a następnik stanowi zdanie Z
n
, jest tautologią.
Racja logiczna jest to koniunkcja zdań, z których wynika logicznie dane zdanie.
Następstwo logiczne jest to zdanie które wynika logicznie z racji logicznej.
Język J jest fragmentem języka J’ wtedy gdy
1) zbiór reguł słownikowych języka J jest [podzbiorem właściwym zbioru reguł słownikowych
języka J’, zaś
2) zbiory reguł gramatycznych, dedukcyjnych i semantycznych języka J są podzbiorami zbiorów
reguł- odpowiednio- gramatycznych, dedukcyjnych i semantycznych języka J’.
Język J jest jednorodny gramatycznie z językiem J’ wtedy, gdy
1) zbiór reguł formowania języka J jest identyczny ze zbiorem reguł formowania języka J’, zaś
2) zbiór reguł dedukcyjnych języka J różni się od zbioru reguł dedukcyjnych języka J’.
Język J jest metajęzykiem języka J’ wtedy, gdy
1) dla każdego wyrażenia języka J’ występuje w języku J termin jednostkowy oznaczający to
wyrażenie oraz
2) dla każdego wyrażenia języka J’ występuje w języku J wyrażenie stanowiące jego przykład.

6. Definicje
Definicja metajęzykowa to taka definicja, która jest sformułowana w języku, który jest metajęzykiem
języka, dla którego sformułowana jest ta definicja.
Definicja przedmiotowa to taka definicja, która jest sformułowana w tym samym języku, dla którego
jest ona sformułowana.
Definicja równościowa jest to definicja o postaci równoważności albo identyczności. Każda definicja
równościowa zbudowana jest z trzech części. Jedną z nich tworzy zwrot zawierający wyrażenie
definiowane zwany definiendum. Drugą część definicji równościowej tworzy zwrot definiujący zwany
definiensem. Wreszcie trzecią część definicji równościowej tworzy zwrot łączący definiendum z
definiensem zwany spójką definicyjną.
Definicja wyraźna jest to definicja równościowa, w której wyrażenie definiowane jest identyczne z
definiendum. Innymi słowy, definicja wyraźna to taka definicja równościowa, w której definiendum
znajduje się wyłącznie wyrażenie definiowane.
Definicja kontekstowa jest to definicja równościowa, w której wyrażenie definiowane nie jest
identyczne z definiendum. Innymi słowy, definicja kontekstowa to taka definicja równościowa, w
której definiendum stanowi kontekst zawierający w sobie wyrażenie definiowane.
Definicja cząstkowa stanowi jedną z odmian definicji nierównościowych. Każda definicja cząstkowa
jest zdaniem o postaci implikacji albo sekwencją dwóch zdań o postaci implikacji. W definicji
cząstkowej wyrażeniem definiowanym jest zawsze predykat. Podaje ona warunek wystarczający albo
warunek konieczny, albo też warunek wystarczający i warunek konieczny stosowalności
definiowanego wyrażenia.
Definicja indukcyjna, zwana też definicją rekurencyjną, stanowi jedną z odmian definicji
nierównościowych. Każda definicja indukcyjna zbudowana jest z dwóch części, a mianowicie z
warunku wstępnego i z warunku indukcyjnego. W zdaniu stanowiącym warunek wstępny podaje się
najprostszy kontekst, w którym występuje wyrażenie definiowane. Z kolei w zdaniu stanowiącym
warunek indukcyjny zawarta jest zasada przekształcania bardziej złożonych kontekstów
zawierających wyrażenia definiowane w konteksty prostsze.
Definicja przez postulaty, zwana definicją aksjomatyczną, stanowi jedną z odmian definicji
nierównościowych. Definicja przez postulaty składa się z dwóch lub więcej zdań zawierających
definiowane wyrażenie. Każde z tych zdań uznaje się za zdanie prawdziwe. Zdania tworzące definicję
przez postulaty muszą więc być tak dobrane, aby ich łączna prawdziwość wyznaczała tylko jedno
znaczenie zawartego w nich wyrażenia definiowanego.
Definicja sprawozdawcza, zwana też definicją analityczną, danego wyrażenia dla określonego,
zastanego języka jest taka definicja, która informuje o znaczeniu, jakie definiowane wyrażenie ma już
w tym języku.
Definicja projektująca, zwana też definicją syntetyczną, danego wyrażenia dla określonego,
budowanego właśnie języka to taka definicja, która informuje o znaczeniu, jakie definiowane

wyrażenie będzie mieć w tym języku. Projektuje ona znaczenie wyrażeń, a więc wyznacza znaczenie
definiowanych wyrażeń na przyszłość.
Definicja konstrukcyjna to taka definicja projektująca danego wyrażenia dla określonego,
budowanego właśnie języka, która nie liczy się ze znaczeniem, jakie wyraz definiowany ma-
ewentualnie- w języku, na bazie którego powstaje budowany język.
Definicja regulująca to taka definicja projektująca danego wyrażenia dla określonego, budowanego
właśnie języka, która liczy się ze znaczeniem, jakie wyraz definiowany ma w języku, na bazie którego
powstaje budowany język.
Eksplikacje stanowią szczególną odmianę definicji projektujących. Pierwszy etap eksplikowania
polega na sformułowanie definiowanego wyrażenia. Drugi etap eksplikowania polega na podaniu tak
zwanych kryteriów adekwatności eksplikacji. Trzeci etap eksplikowania polega na sformułowaniu
oczekiwanej definicji. Wreszcie czwarty etap eksplikowania polega na wykazaniu trafności podanej
definicji przez wykazanie, iż zapewnia ona prawdziwość zdań stanowiących kryteria jej adekwatności.
Wyrażenie poddane eksplikacji nazywa się eksplikandum. Wyrażenie definiowane w eksplikacji
nazywa się eksplikatum.
Definicja ostensywna, zwana też definicją deiktyczną, stanowi jedną z odmian definicji
nierównościowych. Definicja ostensywna to taka, która składa się z wyrażeń oraz towarzyszących ich
wypowiadaniu gestów pokazywania. Wyrażenia te zawierają wyrażenie definiowane w postaci
niezaprzeczonej oraz zaprzeczonej.
Definicja perswazyjna jest to taka definicja, której zadanie polega na zmienianiu określonej postawy
ocennej jej odbiorcy.
Błąd nieznane przez nieznane, czyli po łacinie ignotum per ignotum jest jednym z błędów
popełnianych przy definiowaniu. W definicji objaśnia się bowiem nieznane przez nieznane.
Zauważmy, że kwalifikacja definicji jako błędnej uzależniona jest od ustalenia, do kogo definicja ta
jest skierowana.
Błędne koło jest błędem popełnianym przy definiowani. Błąd polega tu na tym, że wyrażenie
definiowane występuje nie tylko w definiendum, gdzie jest jego miejsce, ale także w definiensie,
gdzie nie powinna się pojawić.
Błędne koło bezpośrednie, albo po łacinie idem per idem, czyli to przez to samo, stanowi szczególną
odmianę błędnego koła. Błąd w definiowaniu polega tu na tym, że wyrażenie definiowane występuje
nie tylko w definiendum, gdzie jest jego miejsce, ale także w definiensie, gdzie nie powinna się
pojawić.
Błędne koło pośrednie stanowi skomplikowaną odmianę błędu błędnego koła. Błąd obarczający tu
nie tyle jedną definicję, ile ich zestaw, polega na tym, że wyrażenie pierwotnie definiowane zostaje
użyte dla zdefiniowania wyrażenia je definiującego. Pośrednio powstaje tu swoiste błędne koło, stąd i
nazwa tego błędu.

Błąd sprzeczności jest to błąd popełniany przy definiowaniu. Jeżeli wśród tez języka wyjściowego nie
ma zdań wzajem sprzecznych, a wśród tez języka nowego są zdania wzajem sprzeczne, to
współtworząca go definicja dotknięta jest błędem sprzeczności.
Błąd nieadekwatności to błąd, którym dotknięte mogą być tylko definicje sprawozdawcze. Definicja
sprawozdawcza winna należycie zdawać sprawę ze znaczenia, jakie ma w danym języku definiowane
w niej wyrażenie, czyli winna być definicją adekwatną. Jeżeli definicja sprawozdawcza nienależycie
informuje o znaczeniu definiowanego w niej wyrażenia, to obarczona jest błędem nieadekwatności.
7. Wnioskowania
Wnioskowanie jest to rozumowanie, w którym na podstawie pewnych przekonań dochodzi się do
jakiegoś przekonania. Zdolne do wnioskowania są tylko, które przeprowadzają operacje myślowe.
Przekonanie, do którego dochodzi się w danym wnioskowaniu, następuje pod wpływem przekonań
wyjściowych i nieco później od nich. Zatem każde wnioskowanie jest wnioskowaniem określonego
podmiotu z określonego odcinka czasu.
Przesłanka danego wnioskowania jest to zdanie wyrażające jedno z jego przekonań wyjściowych.
Wniosek danego wnioskowania jest to zdanie wyrażające przekonanie, do którego dochodzi się w
tym wnioskowaniu.
Przesłanka entymematyczna jest to domyślna, nieodtworzona przesłanka zrekonstruowanego
wnioskowania. Nazwa ta pochodzi od greckiego wyrażenia „en thymo”, co znaczy zatrzymana „w
umyśle”.
Wnioskowanie entymematyczne jest to zrekonstruowane wnioskowanie zawierające choć jedną
przesłankę entymematyczną.
Wnioskowanie dedukcyjne jest to takie wnioskowanie, z którego przesłanek wynika logicznie
wniosek. Wnioskowanie jest dedukcyjne wtedy, gdy implikacja, której poprzednik stanowi koniunkcja
wszystkich przesłanek tego wnioskowania, a następnik stanowi wniosek tego wnioskowania, jest
tautologią.
Wnioskowanie dedukcyjne entymematyczne to takie wnioskowanie, w którym wniosek wynika
logicznie z jego przesłanek zrekonstruowanych i przesłanek entymematycznych.
Wnioskowanie niededukcyjne to takie wnioskowanie, z którego przesłanek nie wynika logicznie
wniosek.
Wnioskowanie redukcyjne to takie wnioskowanie niededukcyjne, którego przesłanki wynikają
logicznie z wniosku albo też którego pewne przesłanki wynikają logicznie z koniunkcji wniosku i
innych jego przesłanek.

Wnioskowanie przez indukcję enumeracyjną niezupełną jest to wnioskowanie niededukcyjne, w
którym dochodzi się do wniosku opisującego jakąś ogólną prawidłowość, wychodząc od przesłanek
opisujących pewne jednostkowe przypadki tej prawidłowości.
Wnioskowanie przez indukcję to wnioskowanie polegające, potocznie mówiąc, na przechodzeniu od
szczegółu (od przekonań o jednostkowych przypadkach prawidłowości) do ogółu (do przekonań o
ogólnej prawidłowości).
2 typy wnioskowania przez analogię:
1) Po pierwsze, wnioskowanie przez analogię jest to wnioskowanie niededukcyjne, w którym od
przesłanek przypisujących wskazanym obiektom jakiegoś rodzaju pewną cechę dochodzi się
do wniosku, przypisującego tę cechę kolejnemu obiektowi tego rodzaju.
2) Po drugie, wnioskowanie przez analogię jest to wnioskowanie niededukcyjne, w którym od
przesłanek konstatujących podobieństwo pod względem pewnych cech dwóch wskazanych
obiektów dochodzi się do wniosku konstatującego podobieństwo tych obiektów pod
względem jeszcze jednej cechy.
Wnioskowanie jest obarczone błędem materialnym wtedy, gdy choć jedna z jego przesłanek jest
zdaniem fałszywym.
Wnioskowanie obarczone jest błędem bezpodstawności (petitio principii, czyli „żądanie
podstawy”)wtedy, gdy choć jedna z jego przesłanek jest zdaniem bezpodstawnym. Zdanie
bezpodstawne to takie, które wyraża przekonanie nabywane przez podmiot pomimo, że nie
dysponuje on żadnymi ku temu danymi.
Wnioskowanie jest obarczone błędem formalnym (non sequitur, czyli „nie wynika”), gdy wedle
wnioskującego jest ono wnioskowaniem dedukcyjnym, a w rzeczywistości z przesłanek tego
wnioskowania nie wynika logicznie jego wniosek.
Wnioskowanie jest obarczone błędnym kołem (w jego najprostszej postaci) wtedy, gdy wniosek tego
wnioskowania jest identyczny z którąś z jego przesłanek.

Odpowiedzi ad. 6.
a) Jedno z 8 pytań dotyczących wynikania lub wynikania logicznego.
1) Ze zdania A wynika w języku J zdanie B. Zdanie A jest prawdziwe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania B? Uzasadnij swoją odpowiedź.
Skoro ze zdania A wynika w języku J zdanie B, to implikacja A implikuje B (A->B), jest
tezą tego języka. Jako teza implikacja ta jest więc w owym języku zdaniem
prawdziwym. Gdy nadto prawdziwym jest jej poprzednik, czyli zdanie A, to na
podstawie modus ponendo ponens przesądza to o prawdziwości następnika tej
implikacji, czyli zdania B.
Reasumując, w tym przypadku zdanie B okazuje się prawdziwe.
2) Ze zdania A wynika w języku J zdanie B. Zdanie A jest fałszywe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania B? Uzasadnij swoją odpowiedź.
Skoro ze zdania A wynika w języku J zdanie B, to implikacja A implikuje B (A->B), jest
tezą tego języka. Jako teza implikacja ta jest więc w owym języku zdaniem
prawdziwym. Gdy przy tym fałszywy jest jej poprzednik, czyli zdanie A, to, na
podstawie matrycy spójnika implikacji prawdziwość tej implikacji jest
zagwarantowana zarówno wtedy, gdy jej następnik, czyli zdanie B, jest prawdziwe,
jak i wtedy, gdy zdanie te jest fałszywe.
Reasumując, w tym przypadku można powiedzieć tylko tyle, że zdanie B jest
prawdziwe albo fałszywe.
3) Ze zdania A wynika w języku J zdanie B. Zdanie B jest prawdziwe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania A? Uzasadnij swoją odpowiedź.
Skoro ze zdania A wynika w języku J zdanie B, to implikacja A implikuje B (A->B), jest
tezą tego języka. Jako teza implikacja ta jest więc w owym języku zdaniem
prawdziwym. Gdy nadto prawdziwy jest jej następnik, czyli zdanie B, to na podstawie
matrycy spójnika implikacji, prawdziwość tej implikacji jest zagwarantowana zarówno
wtedy, gdy jej poprzednik, czyli zdanie A, jest prawdziwe jak i wtedy, gdy zdanie te
jest fałszywe.
Reasumując, w tym przypadku można powiedzieć tylko tyle, że zdanie a jest
prawdziwe albo fałszywe.
4) Ze zdania A wynika w języku J zdanie B. Zdanie B jest fałszywe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania A? Uzasadnij swoją odpowiedź.
Skoro ze zdania A wynika w języku J zdanie B, to implikacja A implikuje B (A->B), jest tezą
tego języka. Jako teza implikacja ta jest więc w owym języku zdaniem prawdziwym. Gdy
przy tym fałszywy jest jej następnik, czyli zdanie B, to na podstawie modus tollendo
tollens przesądza to o fałszywości poprzednika tej implikacji, czyli zdania A.

Reasumując, w tym przypadku zdanie A okazuje się fałszywe.
5) Ze zdania A wynika logicznie zdanie B. Zdanie A jest prawdziwe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania B? Uzasadnij swoją odpowiedź.
Skoro ze zdania A wynika logicznie zdanie B, to implikacja A implikuje B (A->B) jest
tautologią. Jako tautologia implikacja ta jest więc zdaniem prawdziwym. Gdy nadto
prawdziwy jest jej poprzednik, czyli zdanie A, to na podstawie modus ponendo
ponens przesądza to o prawdziwości następnika tej implikacji, czyli zdania B.
Reasumując, w tym przypadku zdanie B okazuje się prawdziwe.
6) Ze zdania A wynika logicznie zdanie B. Zdanie A jest fałszywe. Co na tej podstawie można
powiedzieć o wartości logicznej zdania B? Uzasadnij swoją odpowiedź.
Skoro ze zdania A wynika logicznie zdanie B, to implikacja A implikuje B (A->B) jest
tautologią. Jako tautologia implikacja ta jest więc zdaniem prawdziwym. Gdy przy
tym fałszywy jest jej poprzednik, czyli zdanie A, to na podstawie matrycy spójnika
implikacji, prawdziwość tej implikacji jest zagwarantowana zarówno, gdy jej
następnik, czyli zdanie B jest prawdziwe, jak i wtedy, gdy zdanie te jest fałszywe.
Reasumując, w tym przypadku można powiedzieć tylko tyle, że zdanie B jest
prawdziwe albo fałszywe.
7) Ze zdania A wynika logicznie zdanie B. Zdanie B jest prawdziwe. Co na tej podstawie
można powiedzieć o wartości logicznej zdania A? Uzasadnij swoją odpowiedź.
Skoro ze zdania A wynika logicznie zdanie B, to implikacja A implikuje B (A->B) jest
tautologią. Jako tautologia implikacja ta jest więc zdaniem prawdziwym. Gdy nadto
prawdziwy jest jej następnik, czyli zdanie B, to na podstawie matrycy spójnika
implikacji, prawdziwość tej implikacji jest zagwarantowana zarówno wtedy, gdy jej
poprzednik, czyli zdanie A, jest prawdziwe jak i wtedy, gdy zdanie te jest fałszywe.
Reasumując, w tym przypadku można powiedzieć tylko tyle, że zdanie A jest
prawdziwe albo fałszywe.
8) Ze zdania A wynika logicznie zdanie B. Zdanie B jest fałszywe. Co na tej podstawie można
powiedzieć o wartości logicznej zdania A? Uzasadnij swoją odpowiedź.
Skoro ze zdania A wynika logicznie zdanie B, to implikacja A implikuje B (A->B) jest
tautologią. Jako tautologia implikacja ta jest więc zdaniem prawdziwym. Gdy przy
tym fałszywy jest jej następnik, czyli zdanie B, to na podstawie modus tollendo
tollens przesądza to o fałszywości poprzednika tej implikacji, czyli zdania A.
Reasumując, w tym przypadku zdanie A okazuje się fałszywe.

b) Jedno z 9 pytań dotyczących definicji
1) Omów budowę definicji równościowej
Definicja równościowa jest to definicja o postaci równoważności albo identyczności.
Każda definicja równościowa zbudowana jest z trzech części. Jedną z nich tworzy zwrot
zawierający wyrażenie definiowane zwany definiendum. Drugą część definicji
równościowej tworzy zwrot definiujący zwany definiensem. Wreszcie trzecią część
definicji równościowej tworzy zwrot łączący definiendum z definiensem zwany spójką
definicyjną. Jako spójki definicyjne używa się zwrotów wyrażających równoważność albo
identyczność, takich jak: „wtedy i tylko wtedy, gdy”, „zawsze i tylko wtedy, gdy”, „≡”, „=”,
„jest identyczny z”, „to samo, co”, itp.
2) Omów budowę definicji przez abstrakcję.
Definicja przez abstrakcję jest to szczególna odmiana definicji kontekstowej. Ponieważ
definicje kontekstowe są definicjami równościowymi, przeto definicje przez abstrakcję
też należą do definicji równościowych. A więc jak wszystkie definicje równościowe
składają się z definiendum, definiensa i spójki definicyjnej. W definiensie definicji przez
abstrakcję występuje predykat denotujący określoną relację równościową w danym
zbiorze, czyli taką relację, która w tym zbiorze jest jednocześnie zwrotna, symetryczna i
przechodnia. Wyrażeniem definiowanym w definicji przez abstrakcję jest zaś funktor
jednoargumentowy denotujący określoną funkcję jednoargumentową. Przy tym funkcja
ta przyporządkowuje dwóm różnym argumentom tę samą wartość wtedy i tylko wtedy,
gdy między tymi argumentami zachodzi relacja denotowana przez predykat występujący
w definiensie owej definicji.
3) Omów budowę definicji indukcyjnej.
Definicja indukcyjna, zwana też definicją rekurencyjną, jest to szczególna odmiana
definicji nierównościowej. Każda definicja indukcyjna zbudowana jest z dwóch części, a
mianowicie z warunku wstępnego i z warunku indukcyjnego. W zdaniu stanowiącym
warunek wstępny podaje się najprostszy kontekst, w którym występuje wyrażenie
definiowane. Z kolei w zdaniu stanowiącym warunek indukcyjny zawarta jest zasada
przekształcania bardziej złożonych kontekstów zawierających wyrażenia definiowane w
konteksty prostsze.
4) Przedstaw wszystkie znane ci schematy definicji cząstkowych.
Definicje cząstkowe stanowią jedną z odmian definicji nierównościowych. Każda definicja
cząstkowa jest zdaniem o postaci implikacji albo sekwencją dwóch zdań o postaci
implikacji. W definicji cząstkowej wyrażeniem definiowanym jest zawsze predykat.
Podaje ona warunek wystarczający albo warunek konieczny, albo też warunek
wystarczający i warunek konieczny stosowalności definiowanego wyrażenia.
Schematy:

5) Omów funkcjonowanie definicji przez postulaty.
Definicje przez postulaty stanowią odmianę definicji nierównościowych. Definicja przez
postulaty składa się z dwóch lub więcej zdań zawierających definiowane wyrażenie.
Każde z tych zdań uznaje się za zdanie prawdziwe. Oczywiście, prawdziwość zdania
zawierającego wyrażenie definiowane nakłada pewne restrykcje na pojmowanie tego
wyrażenia. Tylko bowiem przy pewnym rozumieniu wyrażenia definiowanego
zawierające je zdanie jest prawdziwe. Zdania tworzące definicję przez postulaty muszą
więc być tak dobrane, aby ich łączna prawdziwość wyznaczała tylko jedno znaczenie
zawartego w nich wyrażenia definiowanego.
6) Omów rodzaje definicji ze względu na zadania
Definicje, ze względu na realizowane przez nie zadania, dzielą się na definicje
sprawozdawcze i definicje projektujące.
Definicją sprawozdawczą danego wyrażenia dla określonego, zastanego języka jest taka
definicja, która informuje o znaczeniu, jakie definiowane wyrażenie ma już w tym języku.
Definicje sprawozdawcze nazywa się też definicjami analitycznymi.
W odróżnieniu od definicji sprawozdawczych informujących o zastanych,
dotychczasowych znaczeniach
wyrażeń,
definicje
projektujące
informują
o
projektowanych dopiero znaczeniach wyrażeń. Definicją projektująca danego wyrażenia
dla określonego, budowanego właśnie języka jest taka definicja, która informuje o
znaczeniu, jakie definiowane wyrażenie będzie mieć w tym języku. Definicje projektujące
nazywa się też definicjami syntetycznymi. Projektują one znaczenia wyrażeń, a więc
wyznaczają znaczenia definiowanych wyrażeń na przyszłość.
Nowy, projektowany język powstaje zazwyczaj na bazie jakiegoś już istniejącego języka.
Ze względu na stosunek definicji do znaczeń wyrażeń definiowanych w tych już
istniejących językach, stanowiących bazy dla języków projektowanych, dzielimy definicje
projektujące na definicje konstrukcyjne i definicje regulujące. Definicja projektująca
danego wyrażenia dla określonego, budowanego właśnie języka jest definicją
konstrukcyjną, jeżeli nie liczy się ze znaczeniem, jakie wyraz definiowany ma –
ewentualnie – w języku, na bazie którego powstaje budowany język. Definicja
projektująca danego wyrażenia dla określonego, budowanego właśnie języka jest
definicją regulującą, jeżeli liczy się ze znaczeniem, jakie wyraz definiowany ma w języku,
na bazie którego powstaje budowany język.
7) Omów błędy w definiowaniu za wyjątkiem błędu nieadekwatności.

Jednym z błędów przy definiowaniu jest błąd zwany nieznane przez nieznane, czyli po
łacinie ignotum per ignotum. W definicji tej objaśnia się bowiem nieznane przez
nieznane, bo właśnie stanowi błąd omawianego tu rodzaju. Zauważmy, że kwalifikacja
owej definicji jako błędnej uzależniona jest od ustalenia, do kogo definicja ta jest
skierowana. Innym błędem popełnianym przy definiowaniu jest tak zwane błędne koło.
Błąd polega tu na tym, że wyrażenie definiowane występuje nie tylko w definiendum,
gdzie jest jego miejsce, ale także w definiensie, gdzie nie powinna się pojawić. Stanowi to
szczególną odmianę błędnego koła zwaną błędnym kołem bezpośrednim, albo po łacinie
idem per idem, czyli to przez to samo. Inną, o wiele bardziej skomplikowaną odmianę
błędu omawianego tu rodzaju stanowi błędne koło pośrednie. Błąd obarczający tu nie
tyle jedną definicję, ile ich zestaw, polega na tym, że wyrażenie pierwotnie definiowane
zostaje użyte dla zdefiniowania wyrażenia je definiującego. Pośrednio powstaje tu
swoiste błędne koło, stąd i nazwa tego błędu. Jeszcze innym błędem przy definiowaniu
jest błąd sprzeczności. Jeżeli wśród tez języka wyjściowego nie ma zdań wzajem
sprzecznych, a wśród tez języka nowego są zdania wzajem sprzeczne, to współtworząca
go definicja dotknięta jest błędem sprzeczności.
8) Omów błąd nieadekwatności w definiowaniu (podać wszystkie możliwości- wzory
symboliczne).
Błąd nieadekwatności to błąd, którym dotknięte mogą być tylko definicje
sprawozdawcze. Definicja sprawozdawcza winna należycie zdawać sprawę ze znaczenia,
jakie ma w danym języku definiowane w niej wyrażenie, czyli winna być definicją
adekwatną. Jeżeli definicja sprawozdawcza nienależycie informuje o znaczeniu
definiowanego w niej wyrażenia, to obarczona jest błędem nieadekwatności.
Nieadekwatność definicji sprawozdawczej przejawia się na kilka sposobów. Omówimy tu
trzy z nich. Po pierwsze, definicja sprawozdawcza jest nieadekwatna, gdy jest definicją za
szeroką. Przypuśćmy, że podano następującą definicję n-argumentowego predykatu „P”
sprawozdawczą w danym języku: P (x
1
, …, x
n
) ≡ R (x
1
, …, x
n
). Otóż definicja ta jest za
szeroka, jeżeli tezą tego języka jest zdanie:
ale nie jest tezą tego języka zdanie
Po drugie, definicja sprawozdawcza jest nieadekwatna, gdy jest definicją za wąską.
Podana wyżej definicja predykatu „P” jest za wąska, jeżeli tezą rzeczonego języka jest
zdanie
ale nie jest tezą tego języka zdanie
Po trzecie, definicja sprawozdawcza jest nieadekwatna, gdy jest definicją krzyżującą.
Podana wyżej definicja predykatu „P” jest krzyżująca, jeżeli nie jest tezą rzeczonego
języka zdanie
ani nie jest jego tezą zdanie
ale jego tezą jest zdanie
Odpowiedzi ad. 8.
Alternatywnie jedno z czterech
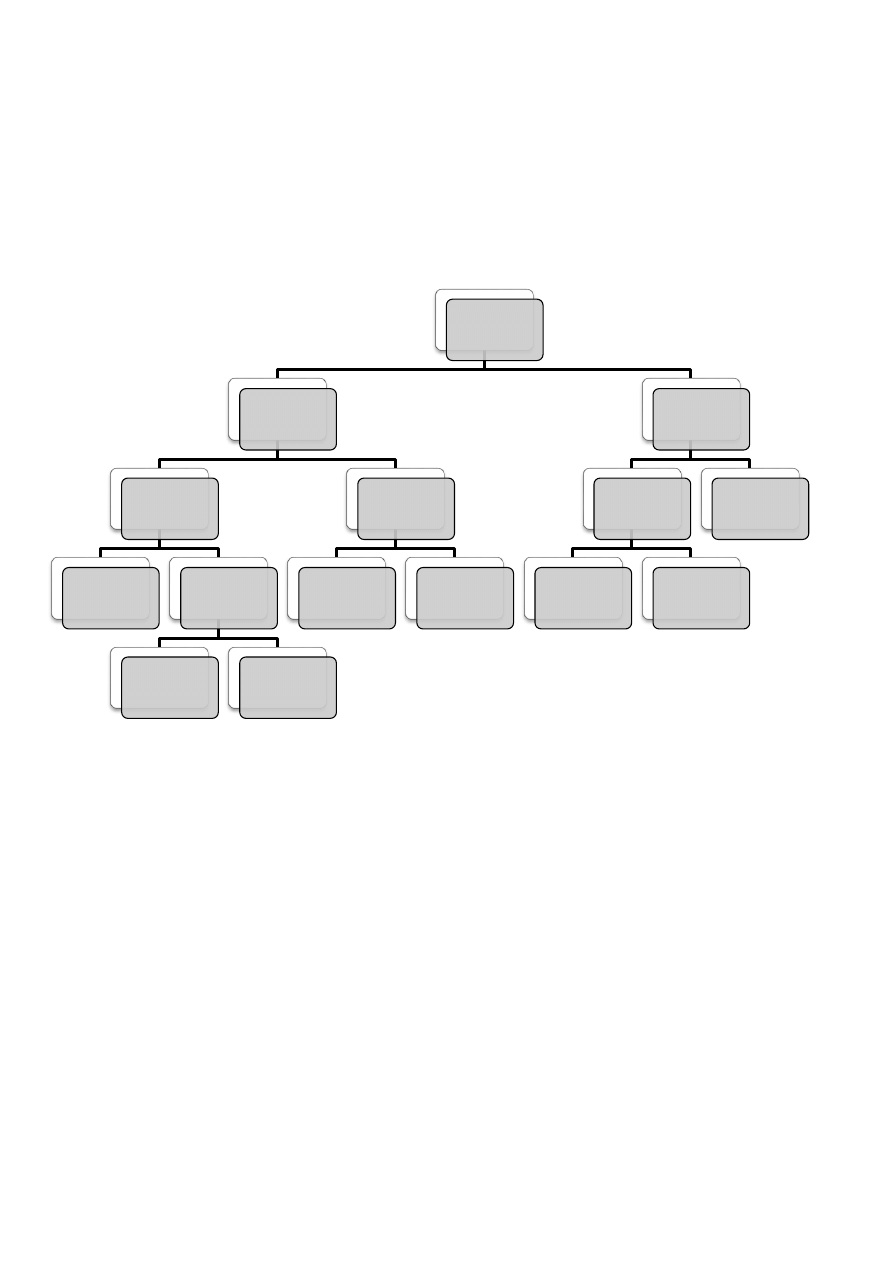
a) Zilustruj i omów związki między rodzajami reguł językowych (str. 142 przedstawić i
omówić).
Jak widać, każdy język konstytuuje wiele różnych rodzajów reguł. Ujmuje je następujące zestawienie:
Każdy język w pierwszym rzędzie konstytuują reguły wyznaczające jego podstawowe wyrażenia
zwane słowami. Ponieważ ogół słów danego języka stanowi jego słownik, dlatego reguły te
nazywamy regułami ustalającymi słownik danego języka. Oprócz reguł ustalających słownik danego
języka inne jeszcze reguły interweniują przy budowie jego wyrażeń. Nazywamy je regułami
gramatycznymi. Dzielą się one na reguły ustalające kategorie gramatyczne i reguły ustalające
sposób budowania wyrażeń złożonych z wyrażeń o określonych kategoriach gramatycznych. Z kolei
reguły gramatyczne oraz reguły ustalające słownik tworzą łącznie reguły formowania. Reguły
wyróżniające pewne zdania określonego języka jako zdania prawdzie nazywamy regułami
dedukcyjnymi. Reguły dedukcyjne dzielą się na reguły aksjomatyczne i reguły inferencyjne. Reguły
dedukcyjne wraz z regułami formowania stanowią reguły składniowe danego języka. Język
ukonstytuowany jedynie przez reguły składniowe stanowi tak zwany czysty rachunek, który wymaga
dopiero stosownego interpretowania. Dokonują tego konstytuujące go reguły semantyczne, które
dzielą się na reguły odniesienia przedmiotowego i reguły prawdziwościowe. Reguły odniesienia
przedmiotowego dzielą się z kolei na reguły ustające uniwersum danego języka oraz reguły
denotowania.
reguły
językowe
reguły
składniowe
reguły
formowania
reguły
ustalające
słownik
reguły
gramatyczne
reguły ustające
kategorie
gramatyczne
reguły ustające
sposób
budowania
wyrażeń
złożonych
reguły
dedukcyjne
reguły
aksjomatyczne
reguły
inferencyjne
reguły
semantyczne
reguły
odniesienia
przedmiotowego
reguły
ustalające
uniwersum
reguły
denotowania
reguły
prawdziwościo
we

b) Przedstaw ogólny schemat wnioskowania przez indukcję enumeracyjną niezupełną i
podaj jeden nieksiążkowy przykład takiego wnioskowania.
Wnioskowanie przez indukcję enumeracyjną niezupełną jest to wnioskowanie
niededukcyjne, w którym dochodzi się do wniosku opisującego jakąś ogólną
prawidłowość, wychodząc od przesłanek opisujących pewne jednostkowe przypadki tej
prawidłowości.
/P1’/, /P1’’/ R(a
1
, …, a
n
), S(a
1
, …, a
n
)
/P2’/, /P2’’/ R(b
1
, …, b
n
), S(b
1
, …, b
n
)
/P3’/, /P3’’/ R(c
1
, …, c
n
), S(c
1
, …, c
n
)
……………………………………
/Pk’/, /Pk’’/ R(m
1
, …, m
n
), S(m
1
, …, m
n
)
_______
/W/ [R(x
1
, …x
n
) S(x
1
, …x
n
)]
Pierwsze przesłanki z poszczególnych par nazywa się niekiedy przesłankami
klasyfikującymi. Wówczas drugie przesłanki z tych par nazywa się przesłankami
kwalifikującymi.
Łatwo zauważyć, że we wnioskowaniu przez indukcję enumeracyjną niezupełną z samego
wniosku nie wynikają logicznie jego przesłanki. Natomiast z wniosku i dowolnej
przesłanki klasyfikującej wynika logicznie stosowna przesłanka kwalifikująca.
Przykład:
/P1’/, /P1’’/
/P2’/, /P2’’/
/P3’/, /P3’’/
/P4’/, /P4’’/
/P5’/, /P5’’/
__________________________________________
/W/
c) Przedstaw schemat wnioskowania przez analogię pierwszego typu i podaj jeden
nieksiążkowy przykład takiego wnioskowania.
Wnioskowanie przez analogię pierwszego typu jest to wnioskowanie niededukcyjne, w
którym od przesłanek przypisujących wskazanym obiektom jakiegoś rodzaju pewną cechę
dochodzi się do wniosku, przypisującego tę cechę kolejnemu obiektowi tego rodzaju.
/P1’/, /P1’’/ R(a
1
), S(a
1
)
/P2’/, /P2’’/ R(a
2
), S(a
2
)
……………….
/Pn’/, /Pn’’/ R(a
n
), S(a
n
)

/Pn+1/ R(a
n+1
)
________
/W/ S(a
n+1
)
W powyższym schemacie wnioskowania pary przesłanek przypisują wskazanym obiektom
jakiegoś rodzaju pewną cechę. Ostatnia przesłanka wskazuje kolejny obiekt tego rodzaju.
Wniosek przypisuje i temu obiektowi ową cechę.
Przykład:
/P1’/, /P1’’/
/P2’/, /P2’’/
/P3’/, /P3’’/
/P4’/, /P4’’/
/P5’/
_______________________________________
/W/
d) Przedstaw schemat wnioskowania przez analogię drugiego typu i podaj jeden
nieksiążkowy przykład takiego wnioskowania.
Wnioskowanie przez analogię drugiego typu jest to wnioskowanie niededukcyjne, w
którym od przesłanek konstatujących podobieństwo pod względem pewnych cech dwóch
wskazanych obiektów dochodzi się do wniosku konstatującego podobieństwo tych
obiektów pod względem jeszcze jednej cechy.
/P1’/, /P1’’/ S
1
(a), S
1
(b)
/P2’/, /P2’’/ S
2
(a), S
2
(b)
……………….
/Pn’/, /Pn’’/ S
n
(a), S
n
(b)
/Pn+1/ S
n+1
(a)
________
/W/ S
n+1
(b)
W powyższym schemacie wnioskowania pary przesłanek konstatują podobieństwo
wskazanych obiektów pod względem pewnej cechy. Ostatnia przesłanka przypisuje
jednemu z tych obiektów jeszcze jedną cechę. Wniosek przypisuje tę cechę drugiemu z
owych obiektów, upodabniając go tym samym i pod tym względem do pierwszego
obiektu.

Przykład:
/P1’/, /P1’’/
/P2’/, /P2’’/
/P3’/, /P3’’/
/P4/
__________________________________________
/W/
Wyszukiwarka
Podobne podstrony:
Nasze opracowanie pytań 1 40
Opracowanie pytań z anatomii
opracowanie pytań z optyki
Maszyny Elektryczne Opracowanie Pytań Na Egzamin
opracowanie pytan id 338374 Nieznany
opracowanie pytan karafiata
Opracowanie pytań 2 kolokwium
cw 3 broma opracowanie pytan 810
Nhip opracowanie pytan id 31802 Nieznany
filozofia opracowanie pytań
opracowanie pytan Automatyka
pytania egz ekonimak II, OPRACOWANIE PYTAŃ NA EGZAMIN
Zestaw 88 Kasia Goszczyńska, materiały farmacja, Materiały 3 rok, Od Ani, biochemia, biochemia, opra
opracowane zestawy, OPRACOWANIE PYTAŃ NA EGZAMIN
Opracowanie pytań MAMET METALE
egzamin z sorbentów opracowanie pytań 1 2 JM
Opracowanie pytań na zaliczenie Opto
więcej podobnych podstron