Kolokwium Wariant

A

Maszyny Elektryczne i Transformatory

sem. III 2008/2009

Transformatory

Transformator trójfazowy ma następujące dane znamionowe:

S

N

= 1600 kVA

f

N

= 50 Hz

U

1N

/U

2N

= 6300 ±5% / 400 V

P

kN

= 13,8 kW

poł. - Dy

u

k%N

= 5 %

Ponadto wiadomo, że:
napięcie zwojowe wynosi u

phN

≈ 21 V/zwój

przekrój kolumny netto wynosi A

1

= 0,059 m

2

znamionowe,

względne parametry gałęzi poprzecznej schematu zastępczego

wynoszą: r

FeN

= 384 j.w. oraz x

mN

= 66,9 j.w.

Obliczyć:

1. znamionowy prąd fazowy i przewodowy strony GN
2. liczbę zwojów strony GN oraz znamionową wartość indukcji w kolumnie
3. znamionowe straty stanu jałowego
4. napięcie po stronie DN transformatora pracującego na jałowo, zasilanego po

stronie GN na zaczepie „+5%” napięciem U = 6,5 kV o znamionowej częstotliwości

5. napięcie po stronie DN transformatora, zasilanego po stronie GN na zaczepie „0”

napięciem U

1

= U

1N

o znamionowej częstotliwości a obciążonego odbiornikiem o

cos

ϕ= 0,8

ind.

i prądem I

2

= 0,8·I

2N

Maszyny Prądu Stałego

Prądnica bocznikowa prądu stałego o znamionach:

P

N

= 220 kW

n

N

= 1500 obr/min

U

N

= 220 V

jest wyposażona w uzwojenie kompensacyjne i można przyjąć, że reakcja poprzeczna
twornika jest w pełni skompensowana.
Dana jest charakterystyka biegu jałowego E

0

= E

a(I

a

=I

aN

)

= E’

(I

a

=I

aN

)

= f(I

f

) zmierzona dla n = n

N

oraz wartości rezystancji obwodu twornika

ΣR

a

= 0,006

Ω

i uzwojenia wzbudzenia

R

E1E2

= 13

Ω

.

Obliczyć:

6. rezystancję krytyczną obwodu wzbudzenia przy n = n

N

7. rezystancję dodatkową w obwodzie wzbudzenia przy pracy znamionowej. Narysuj

układ połączeń

8. napięcie na zaciskach prądnicy przy prędkości n = 0,8·n

N

, oraz prądzie

wzbudzenia I

f

= 14 A, obciążonej prądem I

a

= I

aN

9. znamionowy prąd wzbudzenia tej maszyny dla pracy silnikowej, zakładając, że

będzie pracować w sieci o napięciu U = 220 V

10. wartość maksymalną prądu pobieranego z sieci, przy pracy silnikowej, dla

rozruchu bezpośredniego przy napięciu U = 110 V

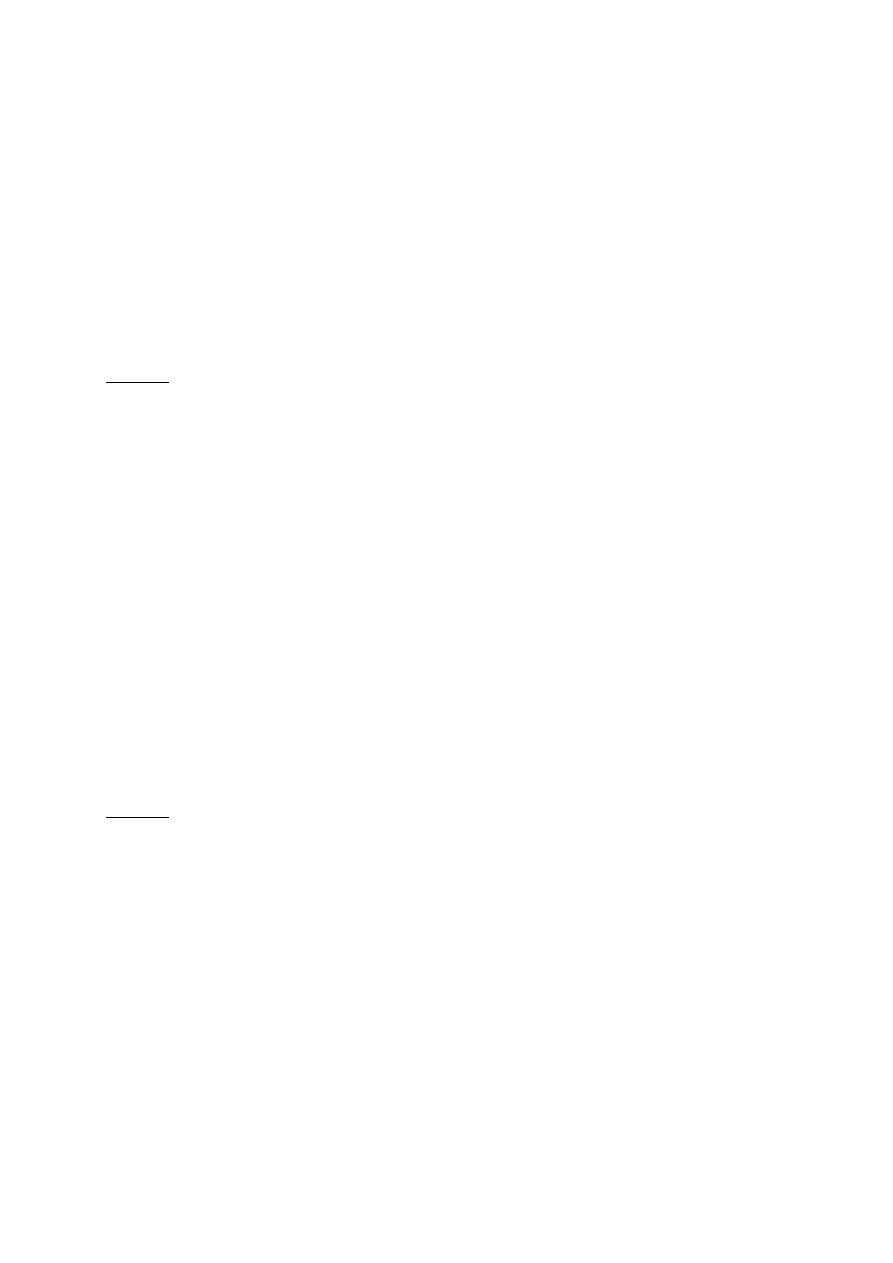
Kolokwium Wariant

B

Maszyny Elektryczne i Transformatory

sem. III 2008/2009

Transformatory

Transformator trójfazowy ma następujące dane znamionowe:

S

N

= 1600 kVA

f

N

= 50 Hz

U

1N

/U

2N

= 6300 ±5% / 400 V

P

kN

= 13,8 kW

poł. - Dy

u

k%N

= 5 %

Ponadto wiadomo, że:
napięcie zwojowe wynosi u

phN

≈ 21 V/zwój

przekrój kolumny netto wynosi A

1

= 0,059 m

2

Obliczyć:

1. znamionowy prąd fazowy oraz przewodowy strony DN
2. liczbę zwojów strony DN oraz znamionową wartość indukcji w kolumnie
3. znamionową, względną wartość rezystancji gałęzi podłużnej schematu

zastępczego typu gamma (

Γ)

4. napięcie po stronie DN transformatora pracującego na jałowo, zasilanego po

stronie GN na zaczepie „-5%” napięciem U = 6,1 kV o znamionowej częstotliwości

5. napięcie po stronie DN transformatora, zasilanego po stronie GN na zaczepie „0”

napięciem U

1

= U

1N

o znamionowej częstotliwości a obciążonego odbiornikiem o

cos

ϕ= 0,6

ind.

i prądem I

2

= 0,6·I

2N

Maszyny Prądu Stałego

Prądnica bocznikowa prądu stałego o znamionach:

P

N

= 220 kW

n

N

= 1500 obr/min

U

N

= 220 V

jest wyposażona w uzwojenie kompensacyjne i można przyjąć, że reakcja poprzeczna
twornika jest w pełni skompensowana.
Dana jest charakterystyka biegu jałowego E

0

= E

a(I

a

=I

aN

)

= E’

(I

a

=I

aN

)

= f(I

f

) zmierzona dla n = n

N

oraz wartości rezystancji obwodu twornika

ΣR

a

= 0,006

Ω

i uzwojenia wzbudzenia

R

E1E2

= 13

Ω

.

Obliczyć:

6. prędkość krytyczną przy R

f

= R

E1E2

7. znamionowy prąd wzbudzenia
8. maksymalne napięcie na zaciskach prądnicy w stanie jałowym, przy prędkości

n = n

N

, gdy w obwodzie wzbudzenia dołączono szeregowo dodatkową rezystancję

o wartości R

ad

= 3

Ω

9. znamionowy prąd tej maszyny dla pracy silnikowej, jeżeli ma pracować w sieci

o napięciu U = 220 V

10. wartość opornika dodatkowego, który ograniczy prąd twornika do wartości

znamionowej, przy pracy silnikowej, dla rozruchu z sieci o napięciu U = 220 V.
Narysuj układ połączeń

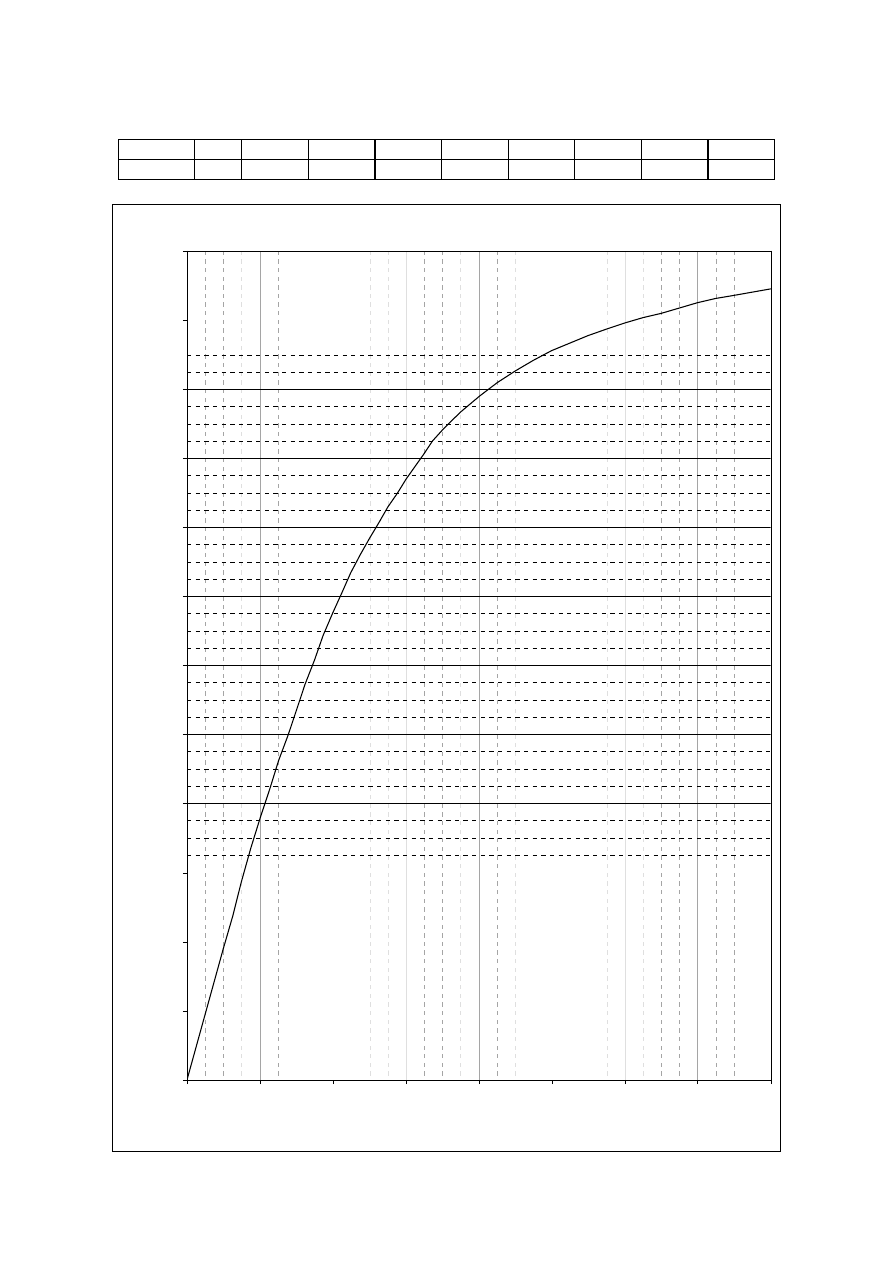
Maszyna Prądu Stałego

I

f

A

2 4 6 8 10 12 14 16

E

0

=E

a

V 76 135 174 198 211 219 225 229

E

0

=E

a

=f(I

f

) dla n=n

N

0

20

40

60

80

100

120

140

160

180

200

220

240

0

2

4

6

8

10

12

14

1

I

f

[A]

E

0

, E

a

[V

]

6

Rozwiązanie Wariant

A

Transformatory

Ad. 1 znamionowy prąd przewodowy strony GN

6

,

146

10

3

,

6

3

10

1600

U

3

S

I

3

3

N

1

N

N

1

=

⋅

⋅

⋅

=

⋅

=

A

połączenie

Δ, więc:

66

,

84

10

3

,

6

3

10

1600

U

3

S

3

I

I

3

3

N

1

N

N

1

phN

1

=

⋅

⋅

⋅

=

⋅

=

=

A

Ad. 2 połączenie

Δ, więc:

N

1

phN

1

U

U

=

stąd:

300

21

6300

u

U

u

U

N

phN

N

1

phN

phN

1

N

1

=

=

=

=

zw.

znamionowa indukcja w kolumnie

603

,

1

50

059

,

0

44

,

4

21

f

A

44

,

4

u

N

f

A

44

,

4

U

B

N

1

phN

N

1

N

1

phN

1

mN

=

⋅

⋅

=

⋅

⋅

=

⋅

⋅

⋅

=

T

Ad. 3 bezwzględna wartość rezystancji gałęzi poprzecznej liczona od strony GN

58

,

28

10

1600

6300

3

384

S

U

3

r

I

U

r

Z

r

R

3

2

N

2

N

1

FeN

phN

1

phN

1

FeN

phN

1

FeN

FeN

=

⋅

⋅

⋅

=

⋅

⋅

=

⋅

=

⋅

=

k

Ω

znamionowe straty stanu jałowego

4167

384

10

1600

r

S

R

U

3

P

3

FeN

N

FeN

2

phN

1

N

0

=

⋅

=

=

⋅

=

W

Ad. 4 przekładnia napięciowa przy zasilaniu na zaczepie „+5%”

N

2

N

1

2

1

U

05

,

1

U

U

U

⋅

=

stąd:

393

05

,

1

10

3

,

6

10

5

,

6

400

05

,

1

U

U

U

U

3

3

N

1

1

N

2

2

=

⋅

⋅

⋅

⋅

=

⋅

⋅

=

V

Ad. 5 znamionowy procentowy czynny spadek napięcia (składowa czynna napięcia

zwarcia)

%

100

S

P

%

100

U

3

S

3

U

P

%

100

U

I

3

P

%

100

U

U

u

N

kN

N

1

N

N

1

kN

N

1

N

1

kN

N

1

kRN

N

%

kR

⋅

=

⋅

⋅

⋅

⋅

=

⋅

⋅

=

⋅

=

863

,

0

%

100

10

1600

10

8

,

13

u

3

3

N

%

kR

=

⋅

⋅

⋅

=

%

znamionowy procentowy bierny spadek napięcia (składowa bierna napięcia zwarcia)

92

,

4

863

,

0

5

u

u

u

2

2

2

N

%

kR

2

N

%

k

N

%

kX

=

−

=

−

=

%

procentowa zmiana napięcia przy obciążeniu indukcyjnym,
przyjmujemy wzór uproszczony

(

)

(

)

91

,

2

6

,

0

92

,

4

8

,

0

863

,

0

8

,

0

sin

u

cos

u

u

2

N

%

kX

2

N

%

kR

%

=

⋅

+

⋅

⋅

=

ϕ

⋅

+

ϕ

⋅

⋅

β

=

Δ

%

gdzie:

N

I

I

2

2

=

β

i

- współczynnik mocy obciążenia

2

ϕ

cos

napięcie po stronie wtórnej

4

,

388

100

91

,

2

1

400

%

100

u

1

U

U

%

N

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛ −

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛

Δ

−

⋅

=

V

Maszyny Prądu Stałego

Ad. 6 rezystancja krytyczna wynika z nachylenia charakterystyki stanu jałowego E

0

= f(I

f

)

w jej początkowym, prostoliniowym odcinku

38

2

76

I

E

R

.)

pocz

(

f

.)

pocz

(

0

cr

=

=

=

Ω

Ad. 7 I iteracja, przyjmujemy

N

a

I

I

=

1000

220

10

220

U

P

I

3

N

N

N

=

⋅

=

=

A

228

2

006

,

0

1000

220

u

2

R

I

U

E

E

tc

a

a

N

a

=

+

⋅

+

=

Δ

+

⋅

+

=

′

=

∑

V

z charakterystyki odczytujemy dla

228

E

a

=

V prąd wzbudzenia

15,5

I

f

=

A

II

iteracja

1016

5

,

15

1000

I

I

I

f

N

aN

≅

+

=

+

=

A

228

1

,

228

2

006

,

0

1016

220

u

2

R

I

U

E

E

tc

a

aN

N

N

aN

≈

=

+

⋅

+

=

Δ

+

⋅

+

=

′

=

∑

V

stąd:

5

,

15

I

fN

=

A

znamionowa rezystancja obwodu wzbudzenia

19

,

14

5

,

15

220

I

U

R

R

R

fN

N

ad

2

E

1

E

fN

=

=

=

+

=

Ω

stąd:

19

,

1

13

19

,

14

R

R

R

2

E

1

E

fN

ad

=

−

=

−

=

Ω

Ad. 8 przy wzbudzeniu

A i znamionowej prędkości

14

I

f

=

N

n

n

=

siła elektromotoryczna

V

225

E

)

n

(

a

N

=

przy tych samych warunkach wzbudzenia oraz obciążenia i zmianie prędkości siła

elektromotoryczna jest proporcjonalna do prędkości obrotowej

180

225

8

,

0

E

8

,

0

n

n

8

,

0

E

n

n

E

E

)

n

(

a

N

N

)

n

(

a

N

)

n

(

a

)

n

(

a

N

N

N

=

⋅

=

⋅

=

⋅

=

=

V

napięcie na zaciskach prądnicy

172

9

,

171

2

006

,

0

1016

180

u

2

R

I

E

U

tc

a

aN

)

n

8

,

0

(

a

≈

=

−

⋅

−

=

Δ

−

⋅

−

=

∑

V

Ad. 9 przy pracy silnikowej musi być zachowana ta sama znamionowa prędkość obrotowa

oraz ten sam znamionowy prąd twornika, stąd siła elektromotoryczna przy pracy
silnikowej:

9

,

211

2

006

,

0

1016

220

u

2

R

I

U

E

E

tc

a

aN

M

aM

=

−

⋅

−

=

Δ

−

⋅

−

=

′

=

∑

V

z charakterystyki odczytujemy dla

212

E

a

≅

V prąd wzbudzenia

10,2

I

f

=

A, stąd:

10,2

I

fMN

=

A

Ad. 10 przy pracy silnikowej, przy rozruchu

0

n

=

czyli

0

n

c

E

=

⋅

Φ

⋅

=

, stąd:

tc

a

max

as

u

2

R

I

U

Δ

+

⋅

=

∑

maksymalny prąd twornika

18

006

,

0

2

110

R

u

2

U

I

a

tc

max

as

=

−

=

Δ

−

=

∑

kA

maksymalny prąd wzbudzenia

46

,

8

13

110

R

U

I

2

E

1

E

max

f

=

=

=

A

maksymalny prąd pobierany z sieci

18008

46

,

8

18000

I

I

I

max

f

max

as

max

s

=

+

=

+

=

A

Rozwiązanie Wariant

B

Transformatory

Ad. 1 znamionowy prąd przewodowy strony DN, połączenie Y, więc:

2309

400

3

10

1600

U

3

S

I

I

3

N

2

N

phN

2

N

2

=

⋅

⋅

=

⋅

=

=

A

Ad. 2 połączenie Y, więc:

3

U

U

N

2

phN

2

=

stąd:

11

21

3

400

u

3

U

u

U

N

phN

N

2

phN

phN

2

N

2

=

⋅

=

⋅

=

=

zw. (zaokr. do liczby całk.)

znamionowa indukcja w kolumnie

603

,

1

50

059

,

0

44

,

4

21

f

A

44

,

4

u

N

f

A

44

,

4

U

B

N

1

phN

N

2

N

1

phN

2

mN

=

⋅

⋅

=

⋅

⋅

=

⋅

⋅

⋅

=

T

Ad. 3 bezwzględna, znamionowa wartość rezystancji gałęzi podłużnej liczona od strony DN

863

,

0

10

1600

400

10

8

,

13

S

U

P

U

3

S

3

P

I

3

P

R

2

3

3

2

N

N

2

kN

2

N

2

2
N

kN

2

phN

2

kN

kN

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⋅

⋅

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

⋅

⋅

=

⋅

=

m

Ω

znamionowa, względna wartość gałęzi podłużnej

00863

,

0

10

1600

10

8

,

13

S

P

U

I

I

3

P

Z

R

r

3

3

N

kN

phN

2

phN

2

2

phN

2

kN

phN

2

kN

kN

=

⋅

⋅

=

=

⋅

⋅

=

=

j.w.

Ad. 4 przekładnia napięciowa przy zasilaniu na zaczepie „-5%”

N

2

N

1

2

1

U

95

,

0

U

U

U

⋅

=

stąd:

7

,

407

95

,

0

10

3

,

6

10

1

,

6

400

95

,

0

U

U

U

U

3

3

N

1

1

N

2

2

=

⋅

⋅

⋅

⋅

=

⋅

⋅

=

V

Ad. 5 znamionowy procentowy czynny spadek napięcia (składowa czynna napięcia

zwarcia)

%

100

S

P

%

100

U

3

S

3

U

P

%

100

U

I

3

P

%

100

U

U

u

N

kN

N

1

N

N

1

kN

N

1

N

1

kN

N

1

kRN

N

%

kR

⋅

=

⋅

⋅

⋅

⋅

=

⋅

⋅

=

⋅

=

863

,

0

%

100

10

1600

10

8

,

13

u

3

3

N

%

kR

=

⋅

⋅

⋅

=

%

znamionowy procentowy bierny spadek napięcia (składowa bierna napięcia zwarcia)

92

,

4

863

,

0

5

u

u

u

2

2

2

N

%

kR

2

N

%

k

N

%

kX

=

−

=

−

=

%

procentowa zmiana napięcia przy obciążeniu indukcyjnym,
przyjmujemy wzór uproszczony

(

)

(

)

67

,

2

8

,

0

92

,

4

6

,

0

863

,

0

6

,

0

sin

u

cos

u

u

2

N

%

kX

2

N

%

kR

%

=

⋅

+

⋅

⋅

=

ϕ

⋅

+

ϕ

⋅

⋅

β

=

Δ

%

gdzie:

N

I

I

2

2

=

β

i

- współczynnik mocy obciążenia

2

ϕ

cos

napięcie po stronie wtórnej

3

,

389

100

67

,

2

1

400

%

100

u

1

U

U

%

N

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛ −

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛

Δ

−

⋅

=

V

Maszyny Prądu Stałego

Ad. 6 prędkość krytyczna to taka, przy której charakterystyka stanu jałowego E

0

= f(I

f

) jest

styczna, w jej początkowym, prostoliniowym odcinku, do prostej obrazującej spadek
napięcia na rezystancji obwodu wzbudzenia, dla

2

I

.)

pocz

(

f

=

A

26

13

2

R

I

E

2

E

1

E

.)

pocz

(

f

)

n

(

0

=

⋅

=

⋅

=

V

z charakterystyki odczytujemy dla

2

I

.)

pocz

(

f

=

A siła elektromotoryczna

V

76

E

)

n

(

0

N

=

ponieważ te same warunki wzbudzenia, to:

N

)

n

(

0

)

n

(

0

n

c

n

c

E

E

N

⋅

Φ

⋅

⋅

Φ

⋅

=

stąd:

2

,

513

76

26

1500

E

E

n

n

)

n

(

0

)

n

(

0

N

N

=

⋅

=

⋅

=

obr/min

Ad. 7 I iteracja, przyjmujemy

N

a

I

I

=

1000

220

10

220

U

P

I

3

N

N

N

=

⋅

=

=

A

228

2

006

,

0

1000

220

u

2

R

I

U

E

E

tc

a

a

N

a

=

+

⋅

+

=

Δ

+

⋅

+

=

′

=

∑

V

z charakterystyki odczytujemy dla

228

E

a

=

V prąd wzbudzenia

15,5

I

f

=

A

II

iteracja

1016

5

,

15

1000

I

I

I

f

N

aN

≅

+

=

+

=

A

228

1

,

228

2

006

,

0

1016

220

u

2

R

I

U

E

E

tc

a

aN

N

N

aN

≈

=

+

⋅

+

=

Δ

+

⋅

+

=

′

=

∑

V

stąd:

5

,

15

I

fN

=

A

Ad. 8 napięcie w stanie jałowym będzie równe SEM w punkcie przecięcia charakterystyki

E

0

= f(I

f

) z prostą obrazującą spadek napięcia na rezystancji obwodu wzbudzenia

16

3

13

R

R

R

ad

2

E

1

E

f

=

+

=

+

=

Ω

przecięcie występuje przy prądzie wzbudzenia

14

I

f

≅

A, stąd:

224

16

14

R

I

E

U

f

f

0

0

=

⋅

=

⋅

≅

=

V

Ad. 9 przy pracy silnikowej musi być zachowana ta sama znamionowa prędkość obrotowa

oraz ten sam znamionowy prąd twornika, stąd siła elektromotoryczna przy pracy
silnikowej:

9

,

211

2

006

,

0

1016

220

u

2

R

I

U

E

E

tc

a

aN

M

aM

=

−

⋅

−

=

Δ

−

⋅

−

=

′

=

∑

V

z charakterystyki odczytujemy dla

212

E

a

≅

V prąd wzbudzenia

10,2

I

f

=

A, stąd

znamionowy prąd przy pracy silnikowej:

1026

2

,

10

1016

I

I

I

fMN

aN

MN

≅

+

=

+

=

A

Ad. 10 przy pracy silnikowej, przy rozruchu

0

n

=

czyli

0

n

c

E

=

⋅

Φ

⋅

=

, stąd:

(

)

tc

s

a

aN

u

2

R

R

I

U

Δ

+

+

⋅

=

∑

dodatkowy opornik włączony szeregowo w obwód twornika

209

,

0

006

,

0

1016

2

220

R

I

u

2

U

R

a

aN

tc

s

=

−

−

=

−

Δ

−

=

∑

Ω

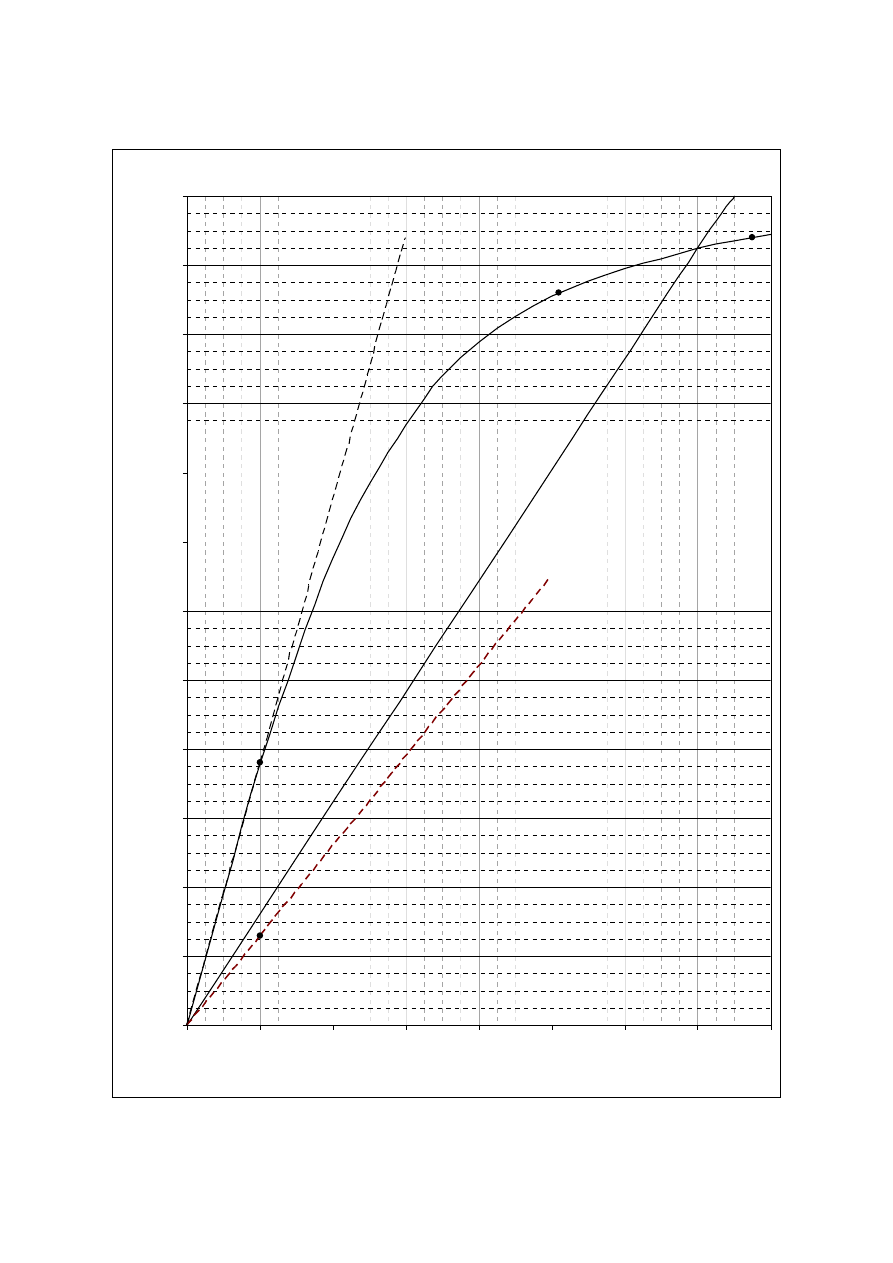
Rozwiązania wykreślne dla maszyny prądu stałego

E

0

=E

a

=f(I

f

) dla n=n

N

0

20

40

60

80

100

120

140

160

180

200

220

240

0

2

4

6

8

10

12

14

1

I

f

[A]

E

0

, E

a

[V

]

6

P8

P7

P9

P6

P6