Cel ćwiczenia:

Celem ćwiczenia jest wyznaczenie charakterystyki Ms=f(ϕ) zależności momentu skręcającego od
odpowiadającego mu kąta skręcenia próbki o przekroju kołowym, oraz znalezienie modułu
sprężystości postaciowej G materiału tej próbki, poprzez pomiar jej kąta skręcenia.

Wstęp:

Momenty skręcające Ms- momenty sił działających w dwóch oddalonych od siebie płaszczyznach,
prostopadłych do osi pręta.

Skręcanie- powstaje na skutek działania dwóch par wyżej wymienionych sił, które powodują
występowanie naprężeń ścinających w płaszczyźnie równoległej do płaszczyzny działania
momentu. Skręcanie występuje najczęściej w prętach.

Skręcanie czyste- stan naprężenia oraz odkształcenia powstały w pręcie pryzmatycznym,
obciążonym dwiema parami sił o jednakowych wartościach momentów i przeciwnych zwrotach,
działającymi w dwóch płaszczyznach prostopadłych do osi pręta.

Opis zjawiska:

Przy skręcaniu uproszczonego modelu gumowego pręta o przekroju osiowym, z naniesioną

na jego powierzchnię wyobrażalną siatką przestrzenną, złożoną z tworzących i okręgów kół,
prostopadłych do osi pręta możemy zauważyć, że:
- tworzące odchylą się od początkowego położenia o pewien kąt γ, (kąt odkształcenia
postaciowego) zmieniając swój kształt.
- powierzchnia końcowa obróci się względem powierzchni początkowej o kąt skręcenia ϕ
- oś pręta pozostanie mimo skręcania linią prostą
- okręgi siatki pozostaną okręgami, a przekroje końcowe nadal będą płaskie
- promienie powierzchni czołowych pozostaną liniami prostymi

Tak więc promienie przekrojów poprzecznych pręta o przekroju kołowym pozostaną w

trakcie skręcania liniami prostymi, natomiast same przekroje pozostaną płaskie.

Aby znaleźć kąt odkształcenia postaciowego na powierzchni zewnętrznej, wycina się

elementarny walec o wysokości dx (za pomocą dwóch płaszczyzn prostopadłych do osi pręta),
następnie używając zależności geometrycznych wyznacza się:

γ =

rd

ϕ

dx

Co dla dowolnego promienia ma postać:

γ

ρ

=

ρ

d

ϕ

dx

Stan odkształcenia wyciętego ze skręcanego pręta elementu, jest identyczny jak przy czystym
ścinaniu. Można więc skorzystać z prawa Hooke'a dla ścinania:

γ

ρ

=

τ

ρ

G

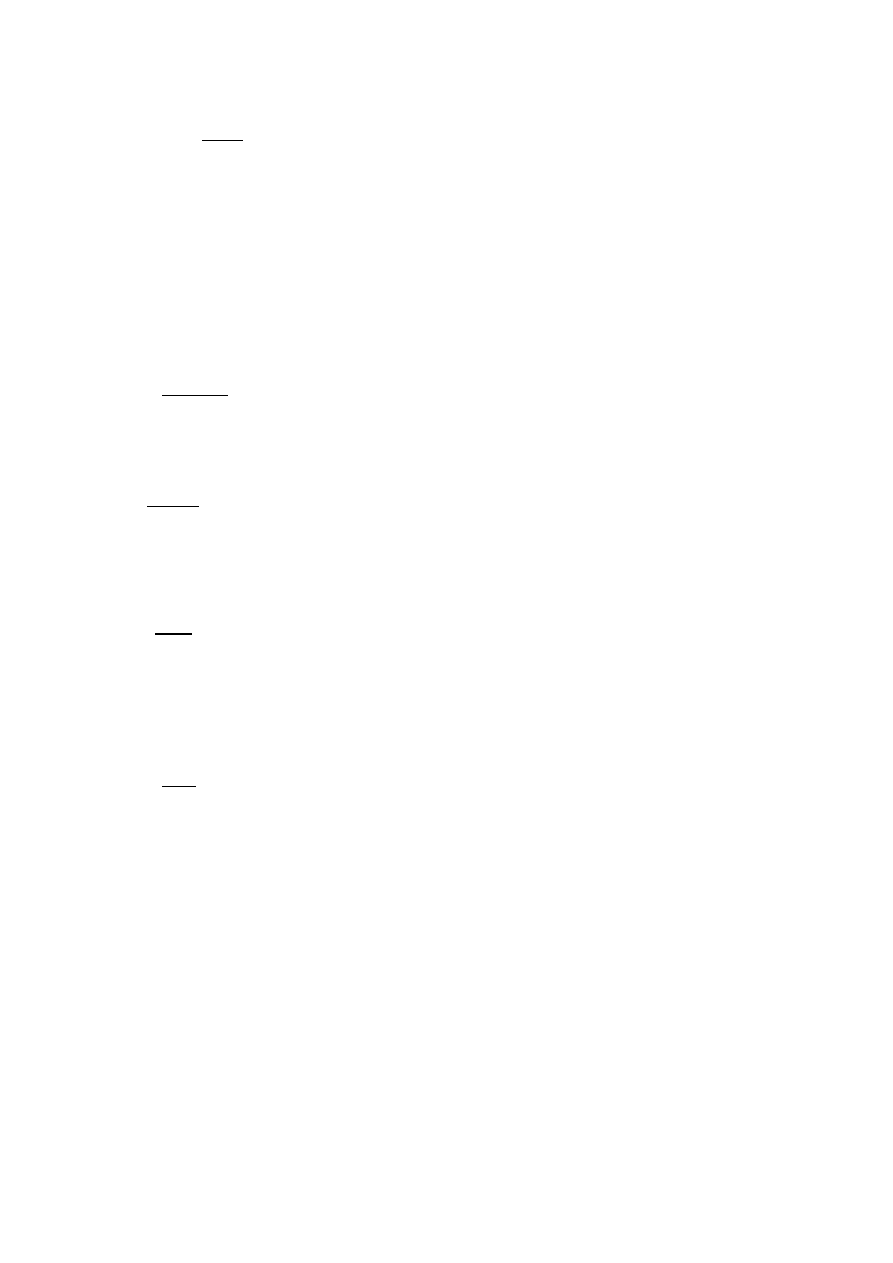
Łącząc dwie powyższe zależności w jedno równanie otrzymuje się:

τ

ρ

=

G

ρ

d

ϕ

dx

(1)

Moment skręcający Ms można wyznaczyć z warunku równowagi pręta skręcanego:

M

s

=

∫

τ

ρ

ρ

d F

(2)

Zależność określającą kąt skręcenia odcinka pręta kołowego w wysokości dx i promieniu r
otrzymuje się podstawiając (po dokonaniu przekształceń) zależność (1) do wzoru (2).

d

ϕ

=

M

s

dx

G J

0

Natomiast na całej długości pomiarowej, kąt skręcenia ϕ pręta obciążonego momentem Ms wynosi:

ϕ

=

M

s

l

G J

0

Naprężenia styczne powstające w przekrojach prostopadłych do osi pręta skręcanego (o kierunku
prostopadłym do promienia) wyznacza się z zależności:

τ

ρ

=

M

s

J

0

ρ

(Wyżej wymienione naprężenia zmieniają się liniowo w zakresie od τρ=0 = 0 do τρ=r = τmax.)

Przy wytrzymałościowym obliczaniu prętów skręcanych korzystamy z zależności:

τ

max

=

M

s

W

0

⩽

k

s

Objaśnienie symboli:
M

s

[Nm] – moment skręcający

l [m] – długość pręta
r= d/2 – promień pręta
ρ [m] – promień
G [MPa] – moduł sprężystość postaciowej
k

s

[MPa] – naprężenie dopuszczalne przy skręcaniu

J

0

[m

4

] – biegunowy moment bezwładności

W

0

[m

3

] – wskaźnik wytrzymałości przekroju na skręcanie

Podczas skręcania rozkłady naprężeń w przekrojach poprzecznych pręta nie są stałe.

Zachodzące zmiany powstają na skutek przejścia zewnętrznych warstw przekroju pręta poza
granicę plastyczności, podczas gdy warstwy położone w bliższym otoczeniu osi nadal pozostają w
zakresie odkształceń sprężystych. Dzieje się tak do momentu w którym wszystkie punkty przekroju
pręta przekroczą granicę plastyczności.