1

Maciej St

ę

pi

ń

ski

1

Etapy badania statystycznego

1.Programowanie badania statystycznego

1.1. Okre

ś

lenie celów badania statystycznego

Celem badania statystycznego jest poznanie rzeczywisto

ś

ci:

a) teoretyczno-naukowe, czyli „dobrze jest, gdy wie si

ę

”;

b) w celu praktycznym, głównie by na postawie wyników bada

ń

diagnozuj

ą

cych rzeczywisto

ść

podejmowa

ć

okre

ś

lone, odpowiednie decyzje.

1.2. Okre

ś

lenie przedmiotu badania

Przedmiotem badania statystycznego s

ą

zbiorowo

ś

ci osób, rzeczy lub zjawisk. Zbiorowo

ść

jest

zdeterminowana celem badania. Składa si

ę

z jednostek statystycznych. Podstaw

ą

wyodr

ę

bnienia zbiorowo

ś

ci

statystycznej s

ą

cechy rzeczowe, czasowe i przestrzenne. S

ą

to tzw. cechy stałe. Dana jednostka, aby

została obj

ę

ta badaniem, musi zatem spełnia

ć

wszystkie kryteria sformułowane dla badanej zbiorowo

ś

ci

statystycznej (musi posiada

ć

wszystkie cechy stałe).

1.3. Okre

ś

lenie zakresu badania

Cechy stałe nie podlegaj

ą

badaniu, słu

żą

jedynie wyodr

ę

bnieniu zbiorowo

ś

ci. Cechy, które podlegaj

ą

badaniu

nazywa si

ę

cechami zmiennymi. One ró

ż

ni

ą

jednostki zbiorowo

ś

ci statystycznej.

Maciej St

ę

pi

ń

ski

2

Etapy badania statystycznego cd.

Cechy zmienne mo

ż

emy podzieli

ć

na:

a) cechy ilo

ś

ciowe, czyli takie, które mo

ż

na zmierzy

ć

i które wyst

ę

puj

ą

z okre

ś

lonym nat

ęż

eniem u ka

ż

dej

jednostki zbiorowo

ś

ci statystycznej; przykłady: liczba mieszka

ń

ców gminy, wzrost osoby,

ś

rednie

wynagrodzenie w przedsi

ę

biorstwie, liczba posiadanych odbiorników telewizyjnych w gospodarstwie domowym,

wielko

ść

ogródka działkowego itd. Wa

ż

ne ze wzgl

ę

dów analitycznych jest rozró

ż

nienie na:

•

cechy ilo

ś

ciowe skokowe, czyli takie, które przyjmuj

ą ś

ci

ś

le okre

ś

lone warto

ś

ci na danej skali

liczbowej; przykład: liczba mieszka

ń

ców gminy, liczba posiadanych odbiorników telewizyjnych w

gospodarstwie domowym;

Oznaczaj

ą

c cech

ę

ilo

ś

ciow

ą

przez X, a jej warto

ść

przez x

i

, dla i = 1, 2, …, N, gdzie N jest liczebno

ś

ci

ą

zbiorowo

ś

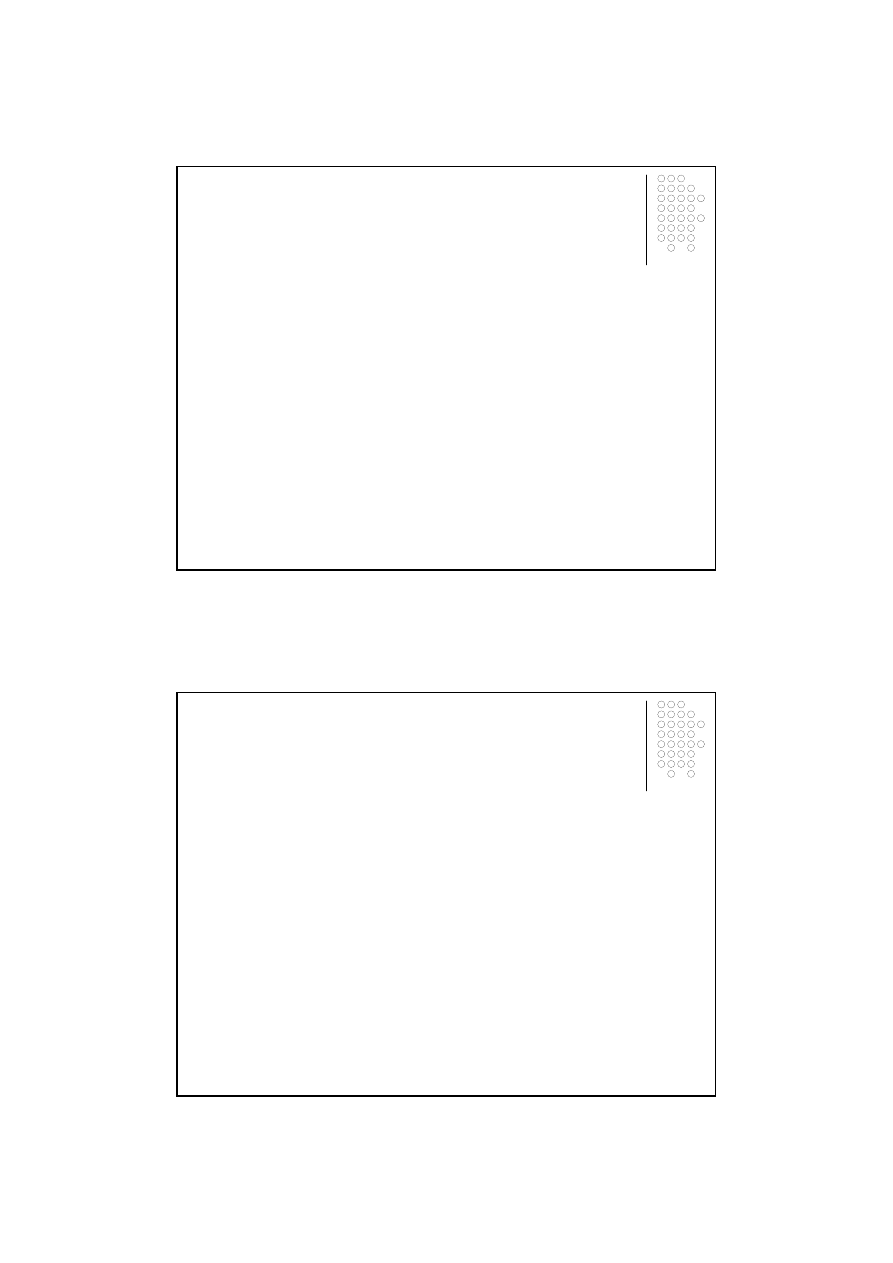
ci, mo

ż

na to graficznie przedstawi

ć

w nast

ę

puj

ą

cy sposób:

•

cechy ilo

ś

ciowe ci

ą

głe, czyli takie, które mog

ą

przyj

ąć

ka

ż

d

ą

z warto

ś

ci z okre

ś

lonego przedziału

liczbowego; przykład: wzrost osoby,

ś

rednie wynagrodzenie w przedsi

ę

biorstwie, wielko

ść

ogródka

działkowego. Cech

ę

ilo

ś

ciow

ą

ci

ą

gł

ą

równie

ż

oznaczymy przez X, z tym

ż

e dla zbiorowo

ś

ci licz

ą

cej

N jednostek, poszczególne warto

ś

ci x

i

(warto

ś

ci i-tej jednostki) mog

ą

si

ę

mie

ś

ci

ć

w dowolnym

punkcie danego przedziału zmienno

ś

ci <a,b>

W szczególnym przypadku mog

ą

to by

ć

warto

ś

ci od -

∞

do +

∞

.

x

1

x

2

x

3

x

4

x

5

…

x

N-1

x

N

x

a b x

2

Maciej St

ę

pi

ń

ski

3

Etapy badania statystycznego cd.

b) cechy jako

ś

ciowe (niemierzalne), czyli takie, które maja okre

ś

lon

ą

liczb

ę

wariantów. Jednostka mo

ż

e

posiada

ć

, lub nie, okre

ś

lony wariant badanej cechy. Podział zbiorowo

ś

ci wg cechy jako

ś

ciowej mo

ż

e mie

ć

charakter dychotomiczny (gdy badana cecha ma tylko dwa warianty, np. płe

ć

) lub wielodzielny (gdy wariantów

jest wi

ę

cej, np. podział populacji osób w wieku produkcyjnym w Polsce na osoby bierne zawodowo, bezrobotne

b

ą

d

ź

poszukuj

ą

ce zatrudnienia (mamy zatem trzy warianty cech);

c) cechy quazi-ilo

ś

ciowe, czyli takie, które ł

ą

cz

ą

charakter ilo

ś

ciowy z jako

ś

ciowym (przykład miast, które

podzielono by ze wzgl

ę

du na wielko

ść

, u

ż

ywaj

ą

c nast

ę

puj

ą

cych wariantów: bardzo du

ż

e, du

ż

e,

ś

rednie, małe i

podkre

ś

laj

ą

c w ten sposób ich charakter społeczno-ekonomiczno-kulturowy. Kryterium przedzielaj

ą

cym byłoby

jednak nat

ęż

enie cechy ilo

ś

ciowej, jak

ą

jest liczba mieszka

ń

ców.

ZADANIE DOMOWE:

Podaj przykładowy cel badania statystycznego, okre

ś

laj

ą

c jego przedmiot i zakres – po jednym przykładzie dla

cechy ilo

ś

ciowej skokowej, ilo

ś

ciowej ci

ą

głej, cechy jako

ś

ciowej i cechy quazi-ilo

ś

ciowej.

1.4. Wybór metody badania

a) badanie całkowite (pełne) s

ą

takimi, w których badaniu podlegaj

ą

wszystkie jednostki zbiorowo

ś

ci

statystycznej. Bada si

ę

zatem cał

ą

populacj

ę

generaln

ą

. Tego typu badania b

ę

d

ą

tez przedmiotem analizy na

naszych spotkaniach;

b) badania cz

ęś

ciowe, czyli takie, w których badaniu podlega tylko cz

ęść

jednostek zbiorowo

ś

ci statystycznej

(reprezentatywna próba wylosowana z populacji generalnej).

Maciej St

ę

pi

ń

ski

4

Etapy badania statystycznego cd.

2. Obserwacja statystyczna

2.1. Wybór

ź

ródeł danych statystycznych

a)

ź

ródła pierwotne, a wi

ę

c takie, które tworzone s

ą

specjalnie dla potrzeb okre

ś

lonego badania;

b)

ź

ródła wtórne, czyli takie, które nie były tworzone dla potrzeb danego badania.

Najcz

ęś

ciej wykorzystywane

ź

ródła wtórne, to:

•

Powszechne Spisy Ludno

ś

ci;

•

Powszechne Spisy Rolne;

•

Wydawnictwa GUS: Roczniki Statystyczne RP, roczniki specjalistyczne, itp.;

•

Bank Danych Lokalnych;

•

rejestracja bie

żą

ca – bazy danych ró

ż

nych podmiotów gospodarczych i instytucji;

•

sprawozdawczo

ść

statystyczna;

•

publikacje w czasopismach.

2.2. Kontrola materiału statystycznego

Czynno

ść

ta jest szczególnie istotna w przypadku

ź

ródeł pierwotnych. Zebrany materiał pierwotny (najcz

ęś

ciej

w postaci kwestionariuszy) powinien podlega

ć

kontroli:

a) formalnej, czyli identyfikacji formularzy i pyta

ń

, na które nie udzielono odpowiedzi. Zostaj

ą

one automatycznie

wyeliminowane z badania;

b) merytorycznej, która polega na ocenie przy u

ż

yciu posiadanej wiedzy, i zdrowego rozs

ą

dku,

prawdopodobie

ń

stwa realno

ś

ci odpowiedzi.

3

Maciej St

ę

pi

ń

ski

5

Etapy badania statystycznego cd.

2.3. Klasyfikacja i grupowanie statystyczne

Informacje zgromadzone w wyniku badania statystycznego nazywamy surowym materiałem statystycznym.
Przykład 2.1.
Załó

ż

my,

ż

e na osiedlu Z w miejscowo

ś

ci „Sło

ń

ce” badano zbiorowo

ść

wynajmowanych mieszka

ń

pod

wzgl

ę

dem ich powierzchni u

ż

ytkowej i liczby zamieszkuj

ą

cych w nim osób wg stanu z dnia 30 IV 2011 r.

Otrzymano nast

ę

puj

ą

ce wyniki:

Powierzchnia u

ż

ytkowa mieszkania [m

2

]

37,8 72,4 35,6 46,8 54,2 62,4

44 39,8 85,7 62,3

Liczba mieszkaj

ą

cych osób

2

3

1

4

6

5

3

3

7

6

Powierzchnia u

ż

ytkowa mieszkania [m

2

]

74,7 46,8 34,7 56,2 95,4 67,8 54,7 72,1 46,7 87,6

Liczba mieszkaj

ą

cych osób

6

0

3

2

9

5

5

8

3

12

Powierzchnia u

ż

ytkowa mieszkania [m

2

]

43,7 76,6 55,7 44,2 97,3 43,7 72,1 39,9 57,9

40

Liczba mieszkaj

ą

cych osób

0

2

4

4

10

3

0

4

8

5

Dane podane w postaci surowego materiału statystycznego s

ą

nieuporz

ą

dkowane i trudno jest przeprowadzi

ć

ich analiz

ę

. Pierwszy krok polega na ich uporz

ą

dkowaniu, najcz

ęś

ciej wg rosn

ą

cych warto

ś

ci zmiennej i

przedstawieniu w postaci szeregu szczegółowego. Omawiane szeregi miałyby posta

ć

:

Powierzchnia mieszkania [m2]:

34,7; 35,6; 37,8; 39,8; 39,9; 40,0; 43,7; 43,7; 44,0; 44,2; 46,7; 46,8; 46,8; 54,2; 54,7; 55,7; 56,2; 57,9; 62,3;

62,4; 67,8; 72,1; 72,1; 72,4; 74,7; 76,6; 85,7; 87,6; 95,4; 97,3.
Liczba mieszkaj

ą

cych osób:

0; 0; 0; 1; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 7; 8; 8; 9; 10; 12.
Uporz

ą

dkowanie zatem to tworzenie ładu wg przyj

ę

tego kryterium (najcz

ęś

ciej rosn

ą

cej warto

ś

ci zmiennej,

czyli uporz

ą

dkowany szereg szczegółowy ma posta

ć

:

x

1

≤

x

2

≤

x

3

≤

…

≤

x

N-1

≤

x

N

Maciej St

ę

pi

ń

ski

6

Etapy badania statystycznego cd.

Mimo,

ż

e materiał statystyczny został uporz

ą

dkowany, to nadal prezentuje si

ę

mało czytelnie

(nieczytelno

ść

ro

ś

nie wraz z rosn

ą

c

ą

liczb

ą

zbiorowo

ś

ci), dlatego przeprowadza si

ę

grupowanie

statystyczne.
Grupowanie statystyczne polega na wyodr

ę

bnieniu z rozpatrywanej populacji generalnej jednorodnych, lub

wzgl

ę

dnie jednorodnych grup, wg przyj

ę

tych kryteriów.

Grupy te b

ę

dziemy nazywa

ć

subpopulacjami. Kryterium grupowania jest najcz

ęś

ciej jedna z cech zmiennych.

Grupowanie mo

ż

emy podzieli

ć

na:

a) grupowanie wariancyjne, które oparte jest na cesze ilo

ś

ciowej (skokowej b

ą

d

ź

ci

ą

głej);

b) grupowanie typologiczne oparte na cesze jako

ś

ciowej, czyli wg wariantu badanej cechy.

Gdy cecha jest quasi-ilo

ś

ciowa, grupowanie odbywa si

ę

na podstawie cechy jako

ś

ciowej, która jest

ś

ci

ś

le

zwi

ą

zana z nat

ęż

eniem cechy ilo

ś

ciowej.

3. Prezentacja wyników obserwacji statystycznej

3.1. Szeregi statystyczne

Szeregiem

statystycznym

nazywamy

ci

ą

g

wielko

ś

ci

statystycznych

rosn

ą

cych

lub

malej

ą

cych,

uporz

ą

dkowanych według okre

ś

lonego kryterium.

Jest on ograniczony z góry i z dołu, zatem jego wyrazy przyjmuj

ą

warto

ś

ci tylko z okre

ś

lonego przedziału.

a) szereg szczegółowy obejmuje wszystkie uporz

ą

dkowane warto

ś

ci zmiennej;

b) szeregi rozdzielcze stanowi

ą

form

ę

prezentacji wyników grupowania statystycznego. Otrzymujemy je wi

ę

c

dziel

ą

c populacje na okre

ś

lone subpopulacje wg okre

ś

lonej cechy i podajemy liczebno

ś

ci ka

ż

dej z nich. Szereg

rozdzielczy składa si

ę

z dwóch kolumn. W pierwszej z nich podajemy warto

ś

ci badanej zmiennej lub wariant

cechy, które umo

ż

liwiaj

ą

wyodr

ę

bnienie populacji. W drugiej kolumnie podaje si

ę

liczebno

ś

ci subpopulacji. Przy

budowaniu szeregu rozdzielczego nale

ż

y przestrzega

ć

dwóch zasad:

4

Maciej St

ę

pi

ń

ski

7

Etapy badania statystycznego cd.

• rozł

ą

czno

ś

ci, która polega na tym,

ż

e dana jednostka – o okre

ś

lonej warto

ś

ci zmiennej lub okre

ś

lonym

wariancie zmiennej mo

ż

e by

ć

przydzielona tylko do jednej subpopulacji;

• zupełno

ś

ci, polegaj

ą

cej na tym,

ż

e rozdzielaj

ą

c jednostki populacji na klasy (subpopulacje), musimy nimi

obj

ąć

wszystkie jednostki zbiorowo

ś

ci statystycznej.

Szereg rozdzielczy w przypadku cechy ilo

ś

ciowej skokowej

Cz

ę

sto

ś

ci, z jak

ą

okre

ś

lona warto

ść

zmiennej wyst

ę

powała w populacji generalnej nazywamy

liczebno

ś

ciami i oznaczamy symbolem n

i

. Czyli n

i

to cz

ę

sto

ść

, z jak

ą

wyst

ą

piła i-ta warto

ść

zmiennej. To

inaczej liczebno

ść

i-tej klasy (subpopulacji).

Szereg rozdzielczy powstały w oparciu o dane z przykładu 2.1 miałby nast

ę

puj

ą

c

ą

posta

ć

:

Tablica 3.1

Liczba

zamieszkuj

ą

cych

osób x

i

Liczba

mieszka

ń

n

i

0

3

1

1

2

3

3

6

4

4

5

4

6

3

7

1

8

2

9

1

10

1

12

1

Razem

30

Maciej St

ę

pi

ń

ski

8

Etapy badania statystycznego cd.

Szereg rozdzielczy w przypadku cechy ilo

ś

ciowej ci

ą

głej

Chc

ą

c zbudowa

ć

szereg rozdzielczy oparty na cesze ilo

ś

ciowej ci

ą

głej, nale

ż

y wyznaczy

ć

minimaln

ą

warto

ść

zmiennej x

min

i maksymaln

ą

warto

ść

zmiennej. Ró

ż

nic

ę

x

max

- x

min

nazywa si

ę

rozst

ę

pem lub przedziałem

zmienno

ś

ci badanej zmiennej.

Przedział zmienno

ś

ci dzieli si

ę

nast

ę

pnie na klasy (subpopulcje). Klasy musz

ą

obj

ąć

wszystkie warto

ś

ci

badanej zmiennej. Klasy mo

ż

na równie

ż

nazwa

ć

przedziałami klasowymi lub przedziałami. (przedział o

równej b

ą

d

ź

ró

ż

nej rozpi

ę

to

ś

ci)

W pierwszej kolumnie umieszcza si

ę

rozpi

ę

to

ś

ci poszczególnych klas (przedziałów), natomiast w drugiej

liczebno

ś

ci poszczególnych klas, czyli liczby jednostek przyjmuj

ą

cych warto

ś

ci badanej zmiennej z danego

przedziału klasowego.
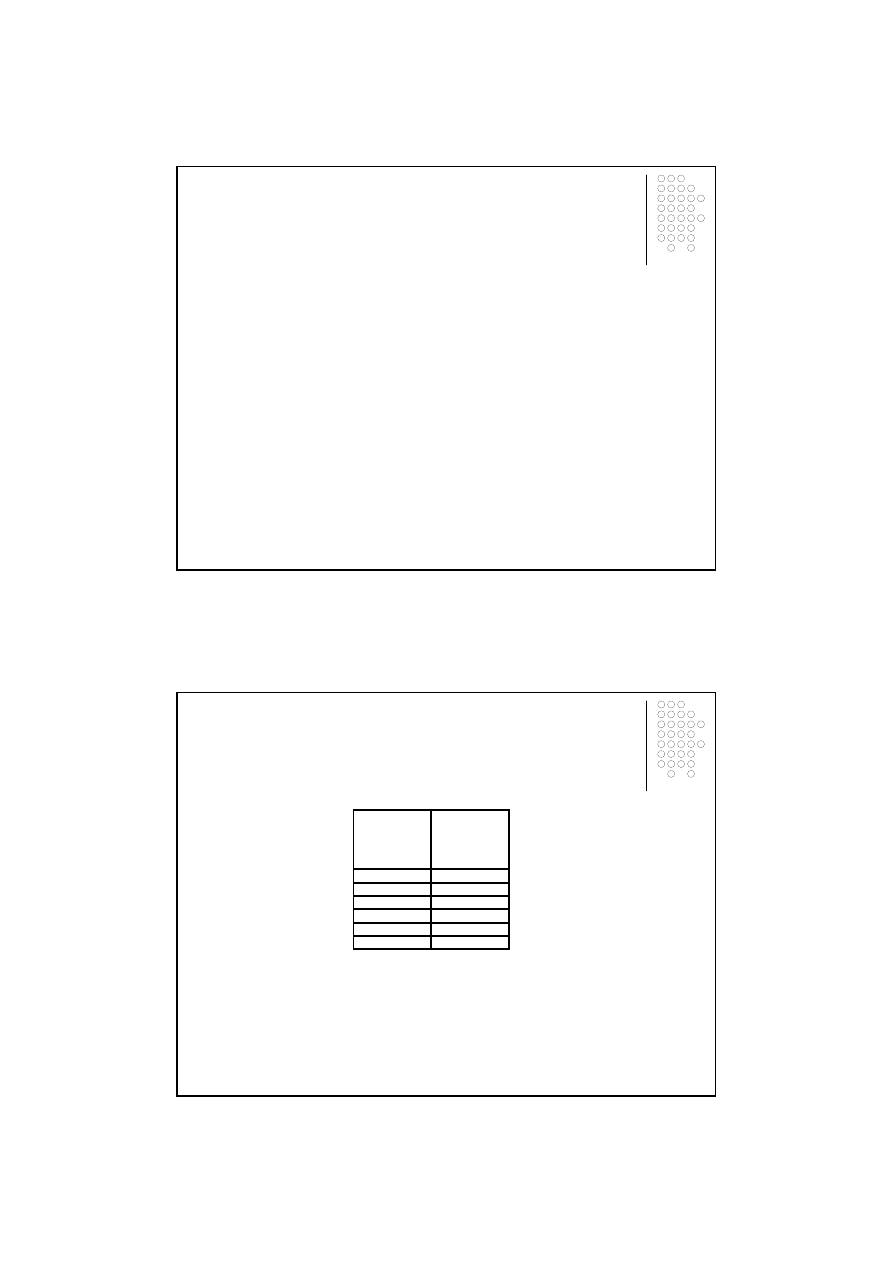
Szereg rozdzielczy powstały w oparciu o dane z przykładu 2.1 ma posta

ć

:

Tablica 3.2

Powierzchnia

mieszkania [m

2

]

x

i

min

- x

i

max

Liczba mieszka

ń

n

i

30-40

6

40-50

7

50-60

5

60-70

3

70-80

5

80-90

2

90-100

2

Razem

30

5

Maciej St

ę

pi

ń

ski

9

Etapy badania statystycznego cd.

Szeregi o ró

ż

nej rozpi

ę

to

ś

ci stosujemy w trzech przypadkach:

a) gdy w jednym z przedziałów szeregu o równej rozpi

ę

to

ś

ci wyst

ą

piła wyra

ź

nie przewa

ż

aj

ą

ca koncentracja

jednostek zbiorowo

ś

ci – wtedy warto rozbi

ć

ten przedział na kilka klas o mniejszych rozpi

ę

to

ś

ciach; umo

ż

liwia

to lepsze, bardziej dogł

ę

bne poznanie struktury badanej zbiorowo

ś

ci;

b) gdy w kilku przedziałach liczebno

ś

ci s

ą

relatywnie małe na tle pozostałych – wówczas zasadne jest ich

poł

ą

czenie, gdy

ż

taka koncentracja nie wypacza obrazu struktury zbiorowo

ś

ci; co wi

ę

cej, czyni go bardziej

przejrzystym;

c) w przypadku cechy quazi-ilo

ś

ciowej, kiedy nat

ęż

enie cechy ilo

ś

ciowej przes

ą

dza o wariancie jako

ś

ciowym na

podstawie kryteriów przyjmowanych w ró

ż

nych dziedzinach nauki.

ZADANIE DOMOWE:

W oparciu o wymy

ś

lone przez siebie dane, zapisane w formie surowego materiału statystycznego, dokonaj

grupowania, a nast

ę

pnie zbuduj szereg rozdzielczy (patrz tablica 3.1 i 3.2). Zadanie powinno zawiera

ć

po

jednym przykładzie dla cechy ilo

ś

ciowej skokowej i cechy ilo

ś

ciowej ci

ą

głej.

Szeregi o otwartych przedziałach klasowych

Korzystaj

ą

c ze

ź

ródeł wtórnych cz

ę

sto spotyka si

ę

szeregi rozdzielcze, w których nieznana jest dolna granica

pierwszego przedziału klasowego i/lub górna granica ostatniego przedziału klasowego. Takie szeregi nazywa
si

ę

szeregami o otwartych przedziałach klasowych. Identyfikacja otwartego charakteru przedziału ma istotny

wpływ na analiz

ę

struktury populacji, gdy

ż

determinuje zestaw mo

ż

liwych do obliczenia parametrów

Maciej St

ę

pi

ń

ski

10

Etapy badania statystycznego cd.

Przykład 3.1
W tablicy 3.3 przedstawiono wydajno

ść

wodoci

ą

gów miejskich w Polsce na podstawie ewidencji z dnia 31

grudnia 2008 r.

Tablica 3.3

Wydajno

ść

w

m

3

/dzie

ń

Liczba

wodoci

ą

gów

poni

ż

ej 100

818

100-1000

706

1001-10000

534

10001-100000

56

powy

ż

ej 100000

5

Razem

2119

Ź

ródło: Mały rocznik statystyczny Polski 2009, GUS, Warszawa 2009, s. 46.

Gdy materiał statystyczny pochodzi ze

ź

ródeł pierwotnych i badacz zna wszystkie warto

ś

ci zmiennej, mo

ż

e

równie

ż

stosowa

ć

szeregi o otwartych przedziałach klasowych. Jest to wskazane wtedy, kiedy liczebno

ś

ci

kilku pierwszych lub kilku ostatnich klas s

ą

zdecydowanie mniejsze od pozostałych. Wówczas badacz ł

ą

czy

je, tworz

ą

c otwarty przedział.

Szeregi rozdzielcze otwarte mo

ż

na równie

ż

stosowa

ć

wtedy, gdy badana zmienna ma charakter skokowy.

6

Maciej St

ę

pi

ń

ski

11

Etapy badania statystycznego cd.

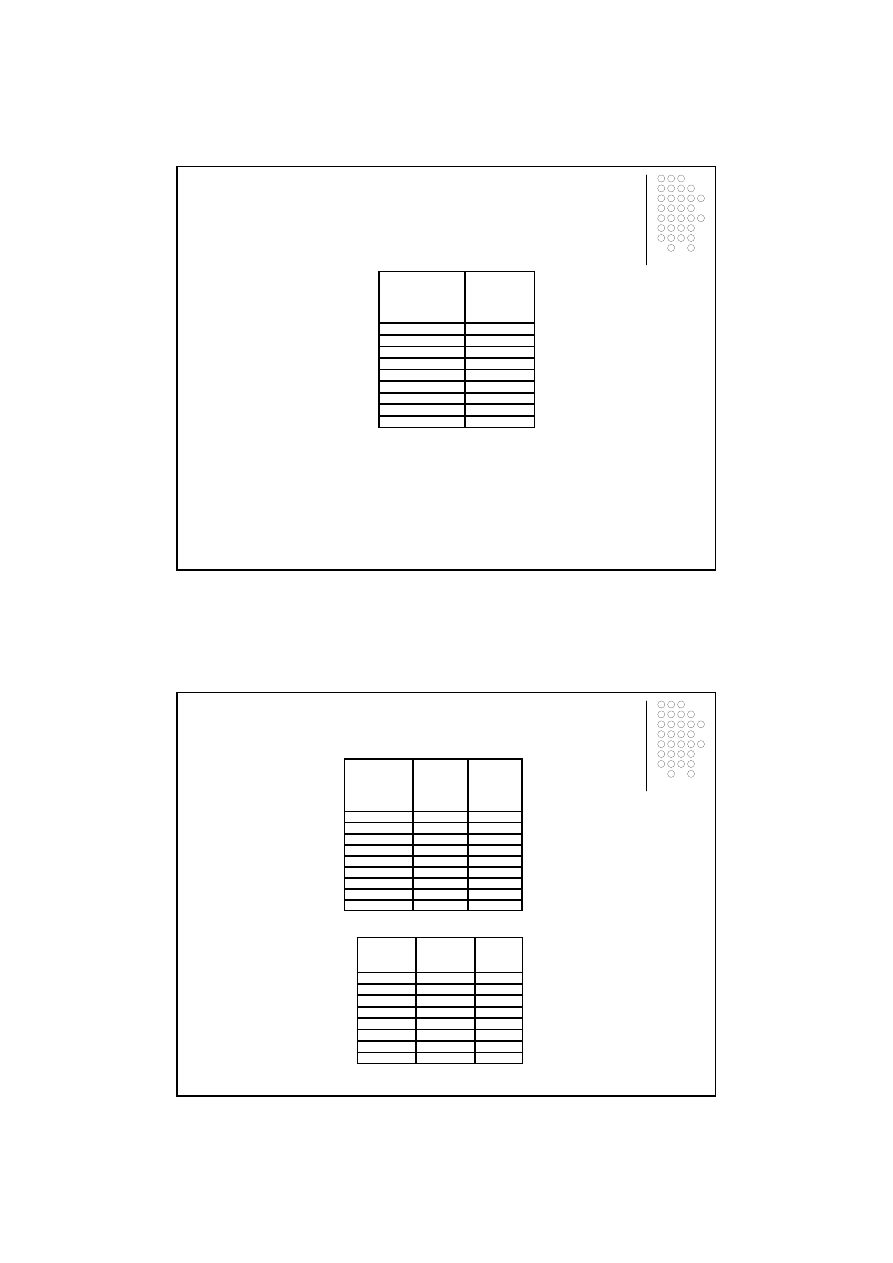
Przykład 3.2
W tablicy 3.4 przedstawiono liczb

ę

prywatnych telefonów komórkowych przypadaj

ą

cych na jedno

gospodarstwo domowe w miejscowo

ś

ci X według spisu z roku 2009:

Tablica 3.4

Liczba

prywatnych

telefonów kom. w

gospodarstwie

domowym

Liczba

gospodarstw

[tys.]

0

1000,2

1

1548,4

2

2341,7

3

5632,1

4

4567,9

5

2567,1

6

1728,9

7 i wi

ę

cej

1567,2

Razem

20953,5

Ź

ródło: dane fikcyjne

.

Szeregi kumulacyjne

Szeregi rozdzielcze pozwalały odpowiedzie

ć

na pytanie, ile jednostek zbiorowo

ś

ci statystycznej charakteryzuje

si

ę

okre

ś

lon

ą

warto

ś

ci

ą

zmiennej (szeregi oparte na cesze skokowej) lub warto

ś

ciami z okre

ś

lonego przedziału

(najcz

ęś

ciej szeregi oparte na cesze ci

ą

głej). Wyst

ę

puj

ą

jednak przypadki, gdy chcemy odpowiedzie

ć

na

pytanie, ile jednostek zbiorowo

ś

ci ma warto

ś

ci zmiennej mniejsze lub równe danej warto

ś

ci (w przypadku cechy

skokowej) lub ile jednostek zbiorowo

ś

ci statystycznej ma warto

ś

ci zmiennej mniejsze od górnej granicy danych

przedziałów (lub nie wi

ę

ksze, w zale

ż

no

ś

ci od tego, jak przebiegał podział na przedziały). Buduje si

ę

wówczas

tzw. liczebno

ś

ci kumulacyjne.

Maciej St

ę

pi

ń

ski

12

Etapy badania statystycznego cd.

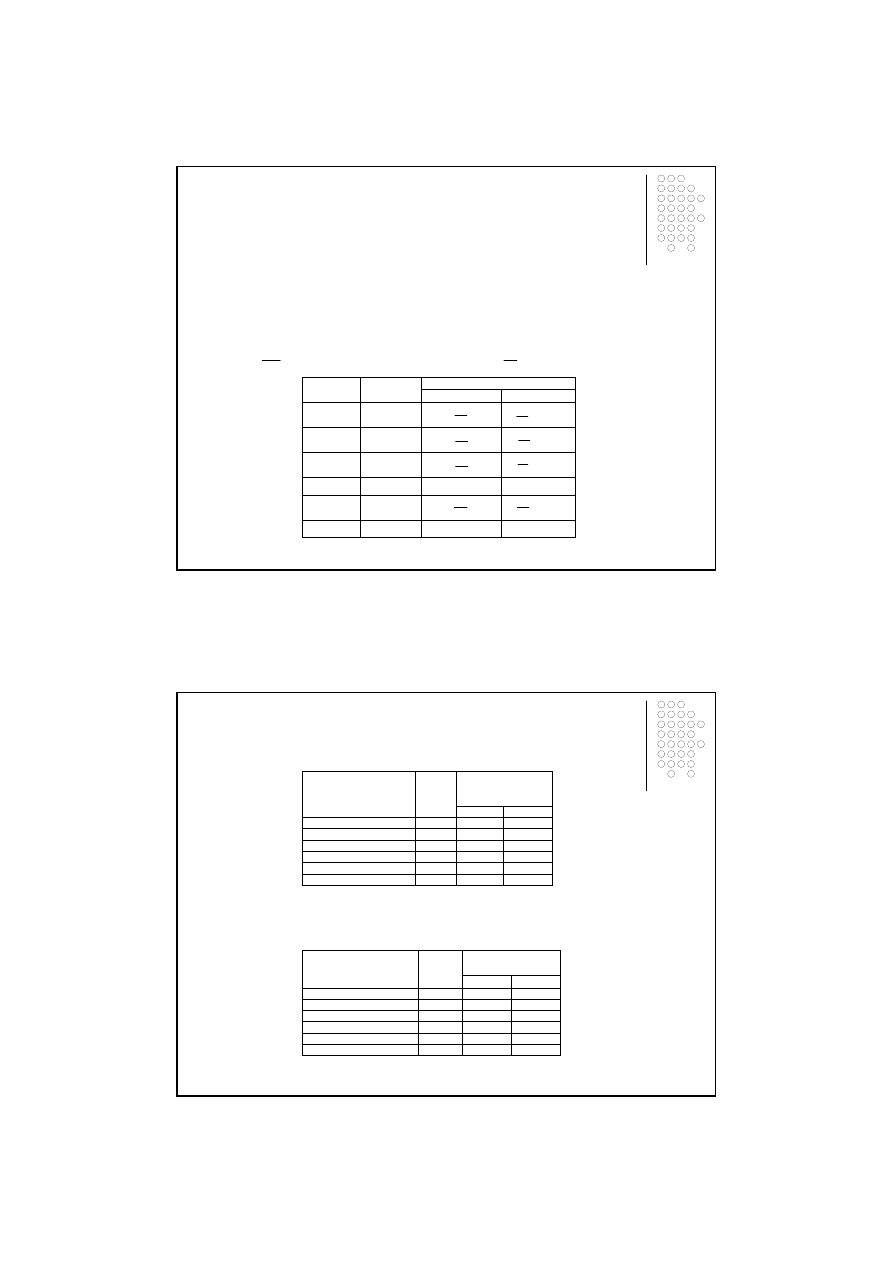
Przykład 3.3
Na podstawie danych z przykładu 3.2 zbudowano szereg kumulacyjny:

Tablica 3.5

Liczba

prywatnych

telefonów kom. w

gospodarstwie

domowym

Liczba

gospodarstw

[tys.]

Liczebno

ś

ci

kumulacyjne

n

p,cum

0

1000,2

1000,2

1

1548,4

2548,6

2

2341,7

4890,3

3

5632,1

10522,4

4

4567,9

15090,3

5

2567,1

17657,4

6

1728,9

19386,3

7 i wi

ę

cej

1567,2

20953,5

Razem

20953,5

Przykład 3.4
Na podstawie danych z przykładu 2.1 zbudowano nast

ę

puj

ą

cy szereg kumulacyjny:

Tablica 3.6

Powierzchnia

mieszkania [m

2

]

x

i

min

- x

i

max

Liczba mieszka

ń

n

i

Liczebno

ść

kumulacyjna

n

p,cum

30-40

6

6

40-50

7

13

50-60

5

18

60-70

3

21

70-80

5

26

80-90

2

28

90-100

2

30

Razem

30

7

Maciej St

ę

pi

ń

ski

13

Etapy badania statystycznego cd.

Szeregi strukturalne

Gdy podstaw

ą

grupowania jednostek populacji o liczebno

ś

ci N jest cecha jako

ś

ciowa, wyniki badania

przedstawiamy w postaci szeregu strukturalnego. Składa si

ę

on z dwóch kolumn: w pierwszej podajemy

warianty badanej cechy, powiedzmy warianty A, B, C,…K, natomiast w drugiej wstawiamy liczb

ę

jednostek,

które maj

ą

okre

ś

lony wariant badanej cechy – n

i

, dla i= A, B, C,…K.

∑

=

=

K

A

i

N

n

Liczebno

ś

ci proste (n

i

) mo

ż

na przedstawi

ć

równie

ż

za pomoc

ą

liczb wzgl

ę

dnych, czyli jako udziały wzgl

ę

dne:

• ułamkowe

N

n

i

dla i = A, B,…, K;

• procentowe

%

100

∗

N

n

i

dla i = A, B,…, K;

ułamkowy

procentowy

A

n

A

B

n

B

C

n

C

.

.

.

.

.

.

.

.

.

.

.

.

K

n

K

N

1

100%

Wariant cechy

Liczebno

ść

bezwzgl

ę

dna

Liczebno

ść

wzgl

ę

dna - udział wzgl

ę

dny

N

n

A

N

n

B

N

n

C

N

n

K

%

100

*

N

n

A

%

100

*

N

n

B

%

100

*

N

n

B

%

100

*

N

n

K

Maciej St

ę

pi

ń

ski

14

Etapy badania statystycznego cd.

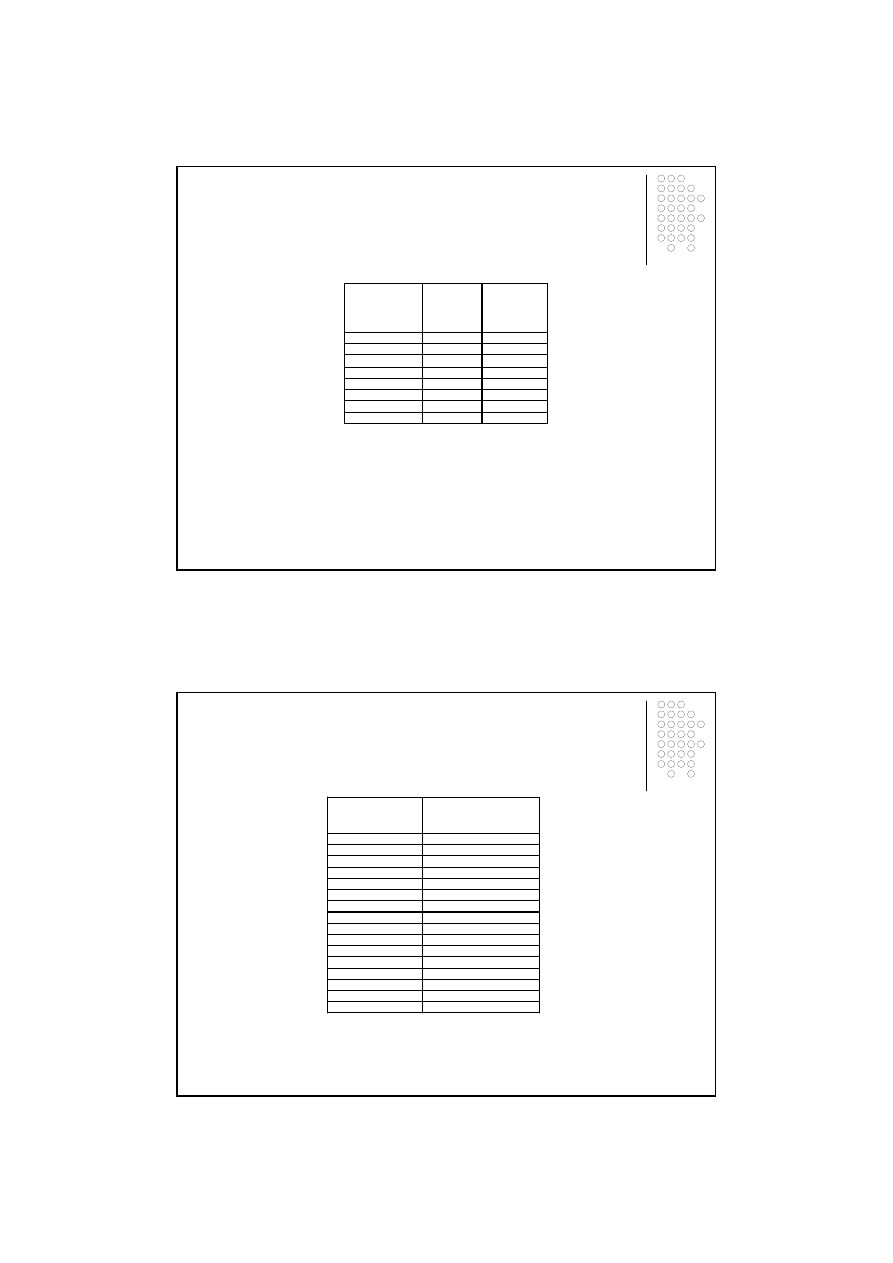
Przykład 3.4
W tablicy 3.7 przedstawiono liczb

ę

zarejestrowanych bezrobotnych w Wielkopolsce według

poziomu wykształcenia zgodnie ze stanem z dnia 31 XII 2009 roku.

Tablica 3.7

ułamkowy

procentowy

Wy

ż

sze

12 837

0,096

9,6%

Policealne,

ś

rednie zawodowe

30 679

0,230

23,0%

Ś

rednie ogólnokształc

ą

ce

13 405

0,100

10,0%

Zasadnicze zawodowe

42 453

0,318

31,8%

Gimnazjalne i poni

ż

ej

34 189

0,256

25,6%

Ogółem

133 563

1,000

100,0%

Liczba

osób

n

i

Liczebo

ść

wzgl

ę

dna -

udział wzgl

ę

dny

Wykształcenie

Ź

ródło: opracowanie własne na podstawie zasobów Banku Danych Regionalnych [online, dost

ę

p 23 IX 2010 r.]. Dost

ę

pne w

Internecie: http://www.stat.gov.pl/bdr_n/app/dane_podgrup.nowe_okno?p_zest_id=737365&p_typ=HTML

Przykład 3.5
W tablicy 3.8 przedstawiono

ś

rednioroczn

ą

liczb

ę

ludno

ś

ci w wieku produkcyjnym w Wielkopolsce według

poziomu wykształcenia w roku 2009

Tablica 3.8

ułamkowy

procentowy

Wy

ż

sze

336

0,134

13,4%

Policealne,

ś

rednie zawodowe

550

0,220

22,0%

Ś

rednie ogólnokształc

ą

ce

244

0,098

9,8%

Zasadnicze zawodowe

784

0,314

31,4%

Gimnazjalne i poni

ż

ej

586

0,234

23,4%

Ogółem

2 500

1,000

100,0%

Wykształcenie

Liczba

osób [tys.]

n

i

Liczebo

ść

wzgl

ę

dna -

udział wzgl

ę

dny

Ź

ródło: opracowanie własne na podstawie zasobów Banku Danych Regionalnych [online, dost

ę

p 23 IX 2010 r.]. Dost

ę

pne w

Internecie: http://www.stat.gov.pl/bdr_n/app/dane_podgrup.nowe_okno?p_zest_id=737768&p_typ=HTML

8

Maciej St

ę

pi

ń

ski

15

Etapy badania statystycznego cd.

Liczebno

ś

ci wzgl

ę

dne stosuje si

ę

cz

ę

sto równie

ż

w szeregach rozdzielczych opartych na cesze

ilo

ś

ciowej. Dotyczy to zarówno liczebno

ś

ci prostych, jak i kumulacyjnych.

Przykład 3.6
Szereg rozdzielczy z przykładu 3.4 mo

ż

na przedstawi

ć

w uj

ę

ciu wzgl

ę

dnym. B

ę

dzie miał on wówczas posta

ć

:

Tablica 3.9

Powierzchnia

mieszkania [m

2

]

x

i

min

- x

i

max

Liczebno

ść

wzgl

ę

dna

[%]

Liczebno

ść

kumulacyjna

wzgl

ę

dna

30-40

20,00

0,20

40-50

23,33

0,43

50-60

16,67

0,60

60-70

10,00

0,70

70-80

16,67

0,87

80-90

6,67

0,93

90-100

6,67

1,00

Razem

100,00

Ź

ródło: parz tablica 3.6

ZADANIE DOMOWE:

W oparciu o faktycznie istniej

ą

ce

ź

ródła wtórne zbuduj tablic

ę

, w której obok liczebno

ś

ci prostych i liczebno

ś

ci

kumulacyjnych znajd

ą

si

ę

kolumny z ich odpowiednikami w warto

ś

ciach wzgl

ę

dnych.

Maciej St

ę

pi

ń

ski

16

Etapy badania statystycznego cd.

Szeregi geograficzne

Szereg geograficzny przedstawia nat

ęż

enie badanej zmiennej w jednostkach terytorialnych.

Przykład 3.7

Tablica 3.10

Województwo

Wydatki bud

ż

etów województw

na jednego mieszka

ń

ca [zł]

Dolno

ś

l

ą

skie

552,85

Kujawsko-Pomorskie

471,07

Lubelskie

441,83

Lubuskie

769,95

Łódzkie

559,95

Małopolskie

455,07

Mazowieckie

622,24

Opolskie

670,78

Podkarpackie

547,56

Podlaskie

517,64

Pomorskie

573,79

Ś

l

ą

skie

372,47

Ś

wi

ę

tokrzyskie

593,40

Warmi

ń

sko-Mazurskie

568,15

Wielkopolskie

553,15

Zachodniopomorskie

644,56

9

Maciej St

ę

pi

ń

ski

17

Etapy badania statystycznego cd.

Szeregi dynamiczne

Szereg dynamiczny prezentuje poziom badanej zmiennej w kolejnych momentach lub okresach.

Przykład 3.8

W poni

ż

szych tablicach przedstawiono w dwóch wariantach liczb

ę

pracuj

ą

cych w gospodarce narodowej

w Polsce w latach 1998-2008 (obja

ś

nienie ró

ż

nic pomi

ę

dzy wariantami – w trakcie zaj

ęć

):

Tablica 3.11

Tablica 3.12

Lata

Pracuj

ą

cy w

gospodarce narodowej

ogółem (Wariant A)

1998

15 921 084

1999

15 691 724

2000

15 159 228

2001

14 670 553

2002

14 607 128

2003

14 452 852

2004

12 413 284

2005

12 576 281

2006

12 905 398

2007

13 456 973

2008

13 711 043

Lata

Pracuj

ą

cy w

gospodarce narodowej

ogółem (Wariant B)

1998

15 921 084

1999

15 691 724

2000

15 159 228

2001

14 670 553

2002

12 486 682

2003

12 332 406

2004

12 413 284

2005

12 576 281

2006

12 905 398

2007

13 456 973

2008

13 711 043

Ź

ródło: opracowanie własne na podstawie zasobów Banku Danych Regionalnych [online, dost

ę

p 24 IX 2010 r.]. Dost

ę

pne w

Internecie: http://www.stat.gov.pl/bdr_n/app/dane_podgrup.nowe_okno?p_zest_id=739919&p_typ=HTML

Maciej St

ę

pi

ń

ski

18

Etapy badania statystycznego cd.

3.2. Tablice statystyczne

Tablice statystyczne s

ą

zbiorem szeregów statystycznych. Szereg statystyczny mo

ż

na zatem uzna

ć

za

najprostsz

ą

tablic

ę

. Je

ż

eli w tablicy znajduj

ą

si

ę

przynajmniej dwa szeregi, to musz

ą

by

ć

one ze sob

ą

merytorycznie powi

ą

zane i dotyczy

ć

jednej zbiorowo

ś

ci statystycznej.

Modelowa tablica składa si

ę

z trzech cz

ęś

ci: tytułu, tablicy wła

ś

ciwej i informacji na temat

ź

ródeł oraz

ewentualnych uwag. Tytuł tablicy powinien zawiera

ć

okre

ś

lenie zbiorowo

ś

ci statystycznej w wymiarze

rzeczowym, czasowym i przestrzennym (kto? co? kiedy? gdzie?), a tak

ż

e zmienne, w oparciu o które

budowano szeregi wchodz

ą

ce w skład tablicy.

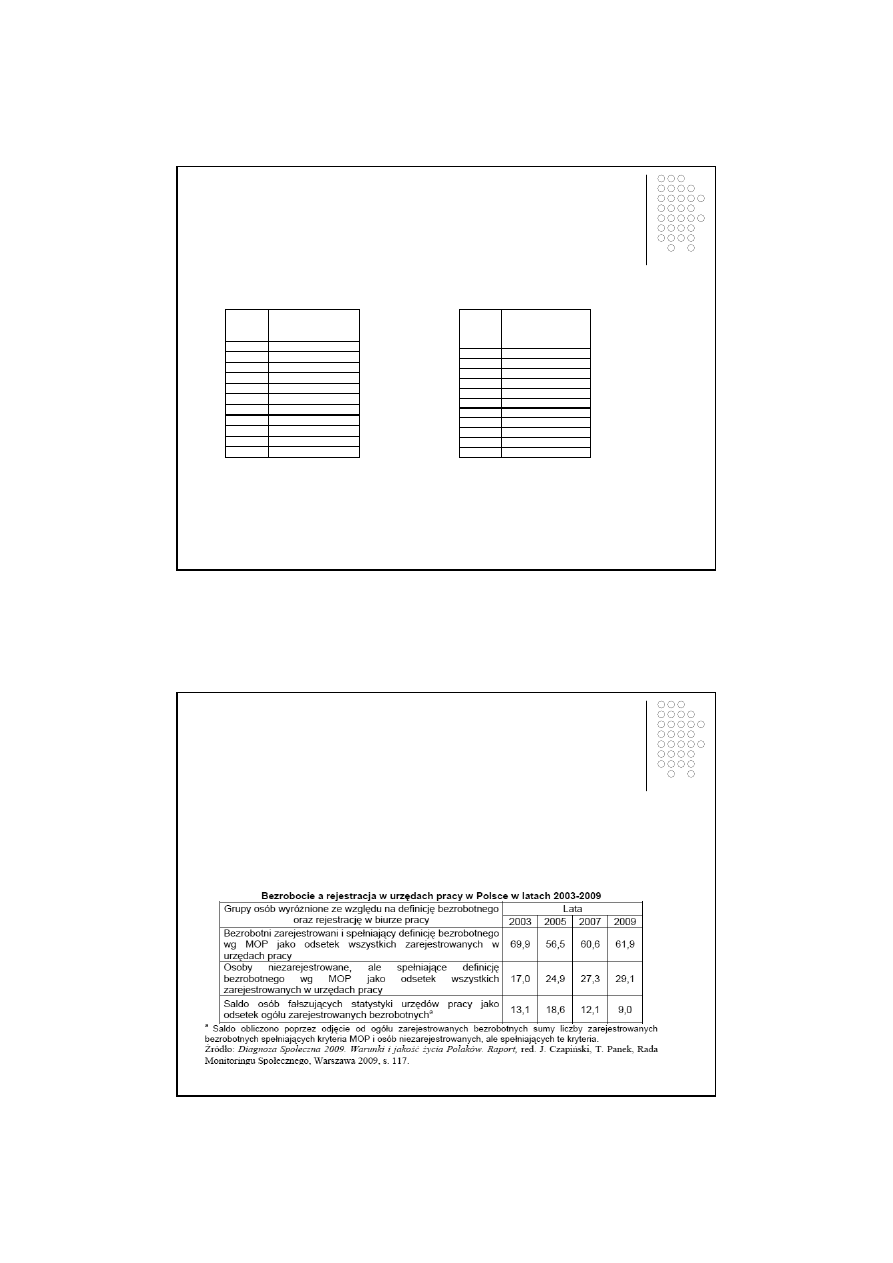
Przykład 3.9

W tablicy 3.13 przedstawiono wielko

ść

zło

ż

onego zjawiska jakim jest rozbie

ż

no

ść

pomi

ę

dzy wielko

ś

ci

ą

bezrobocia rejestrowanego w urz

ę

dach pracy a wielko

ś

ci

ą

bezrobocie faktycznego w Polsce w latach

2003-2009.

Tablica 3.13

10

Maciej St

ę

pi

ń

ski

19

Etapy badania statystycznego cd.

3.3. Wykresy statystyczne

Wykres statystyczny jest graficznym sposobem prezentacji informacji zawartych w szeregach statystycznych.
Składa si

ę

z cz

ęś

ci tekstowej i pola wykresu. Cz

ęść

tekstowa zawiera (podobnie jak tablica) cz

ęść

tekstow

ą

(z

tytułem i informacj

ą

o

ź

ródle i ewentualnymi uwagami) oraz pole wykresu. Mo

ż

liwo

ś

ci konfiguracji pola wykresu

i doboru okre

ś

lonych form graficznych wykresu s

ą

praktycznie nieograniczone. Poni

ż

ej przykłady najbardziej

podstawowe.
Wykresy szeregów rozdzielczych
Wykres punktowy słu

ż

y do graficznego przedstawiania szeregu opartego na cesze ilo

ś

ciowej skokowej. Na osi

OX (odci

ę

tych) zaznacza si

ę

warto

ś

ci zmiennych, a na osi rz

ę

dnych (OY) cz

ę

sto

ś

ci ich wyst

ę

powania

(liczebno

ś

ci proste).

Przykład 3.10
Na poni

ż

szym wykresie punktowym przedstawiono graficznie informacj

ę

zawart

ą

w tablicy 3.1.

Wykres 3.1

Liczba osób zam ieszkuj

ą

cych w w ynajm ow anym m ieszkaniu na

osiedlu Z w m iejscow o

ś

ci Sło

ń

ce w dniu 30 IV 2009 r. (na podstaw ie

tablicy 3.1)

0

1

2

3

4

5

6

7

0

2

4

6

8

10

12

14

x

i

n

i

Ź

ródło: przykład 2.1, tablica 3.1.

Maciej St

ę

pi

ń

ski

20

Etapy badania statystycznego cd.

Wykres słupkowy (histogram) przedstawia graficznie dane tworz

ą

ce szereg rozdzielczy z przedziałami

klasowymi. Na osi OX zaznacza si

ę

przedziały klasowe, które staj

ą

si

ę

podstaw

ą

słupków, natomiast na

osi rz

ę

dnych zaznaczamy liczebno

ś

ci tych

ż

e przedziałów. Wysoko

ść

słupka zale

ż

y wi

ę

c od liczebno

ś

ci

przedziałów klasowych.

Przykład 3.11

Dane zawarte w tablicy 3.6 (szeregu rozdzielczego opartego na cesze ci

ą

głej) wyra

ż

ono za pomoc

ą

histogramu (wykres 3.2). Szereg mo

ż

na przedstawi

ć

równie

ż

w postaci wieloboku liczebno

ś

ci, który

buduje si

ę

ł

ą

cz

ą

c odcinkami

ś

rodki górnych boków wszystkich prostok

ą

tów histogramu (rysunek 3.1). Je

ś

li

natomiast linie wieloboku zostan

ą

wygładzone, wówczas mamy do czynienia z krzyw

ą

liczebno

ś

ci.

Wykres 3.2

Rysunek 3.1

Powierzchnia mieszka

ń

wynajmowanych na osiedlu

Z w miejscowo

ś

ci Sło

ń

ce w dniu 30 IV 2009 r.

0

2

4

6

8

0-30

30-40

40-50

50-60

60-70

70-80

80-90

90-100

powierzchnia mieszkania [m2]

li

c

z

b

a

m

ie

s

z

k

a

ń

0

1

2

3

4

5

6

7

8

0-30

30-40

40-50

50-60

60-70

70-80

80-90

90-100

Ź

ródło: przykład 2.1, tablica 3.2.

11

Maciej St

ę

pi

ń

ski

21

Etapy badania statystycznego cd.

Wykresy szeregów strukturalnych

Najcz

ę

stsz

ą

form

ą

prezentacji wykresów strukturalnych s

ą

wykresy kołowe, (rysunek na zaj

ę

ciach) ale

równie

ż

liniowe.

Wykresy szeregów dynamicznych maj

ą

najcz

ęś

ciej form

ę

liniow

ą

lub słupkow

ą

.