1

Maciej St

ę

pi

ń

ski

1

Analiza struktury zbiorowo

ś

ci statystycznej

1.Analiza tendencji centralnej

1.1

Ś

rednie klasyczne

Ś

rednia arytmetyczna jest parametrem abstrakcyjnym. Wyra

ż

a przeci

ę

tny poziom badanej zmiennej (cechy)

w populacji generalnej

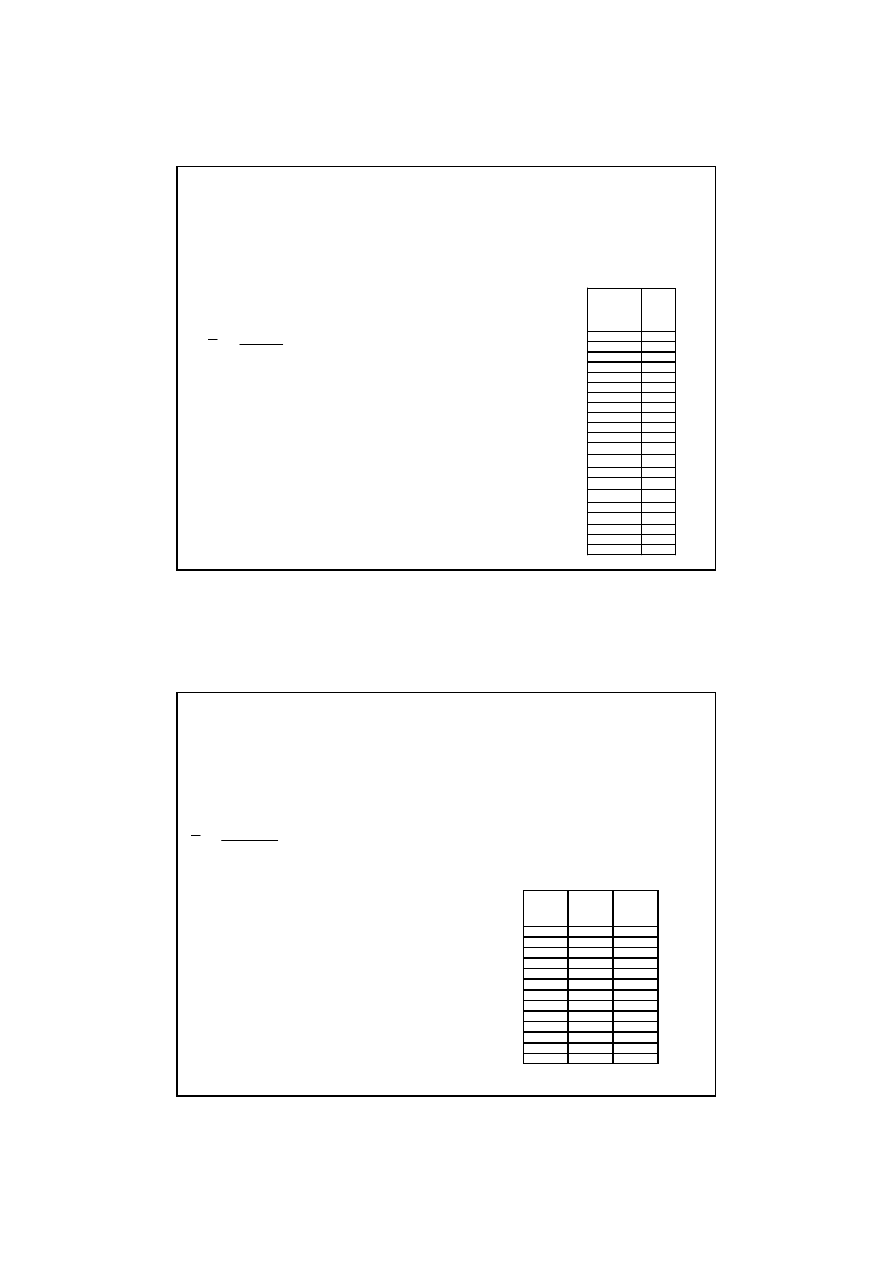
Tablica 1.1

a) szereg szczegółowy

N

x

x

N

i

i

∑

=

=

1

x

i

– i-ta warto

ść

zmiennej (warto

ść

zmiennej, któr

ą

ma i-ta jednostka statystyczna),

N – liczebno

ść

populacji generalnej.

Wielko

ść

ogródka

działkowego

[ar] x

i

i

2,1

1

2,7

2

3,1

3

4,4

4

5,0

5

5,7

6

6,3

7

6,3

8

6,4

9

7,8

10

7,9

11

8,2

12

8,2

13

9,0

14

10,3

15

11,4

16

11,5

17

12,8

18

13,0

19

13,5

20

Razem

155,6

Przykład 1.1

W tablicy 1.1 zamieszczono szereg szczegółowy
obrazuj

ą

cy powierzchni

ę

ogródków działkowych

spółdzielni „Pod miastem” wg stanu pod koniec
2009 r. Oblicz przeci

ę

tn

ą

powierzchni

ę

ogródka

w tej spółdzielni.

Maciej St

ę

pi

ń

ski

2

Analiza struktury zbiorowo

ś

ci statystycznej cd.

b) szereg rozdzielczy oparty na cesze zmiennej

skokowej

N

n

x

x

k

i

i

i

∑

=

=

1

(

ś

rednia arytmetyczna wa

ż

ona)

x

i

– i-ta warto

ść

badanej zmiennej,

n

i

– cz

ę

sto

ść

, z jak

ą

wyst

ę

puje i-ta warto

ść

zmiennej,

k – liczba warto

ś

ci (wariantów) badanej zmiennej (cechy),

N – liczebno

ść

populacji generalnej.

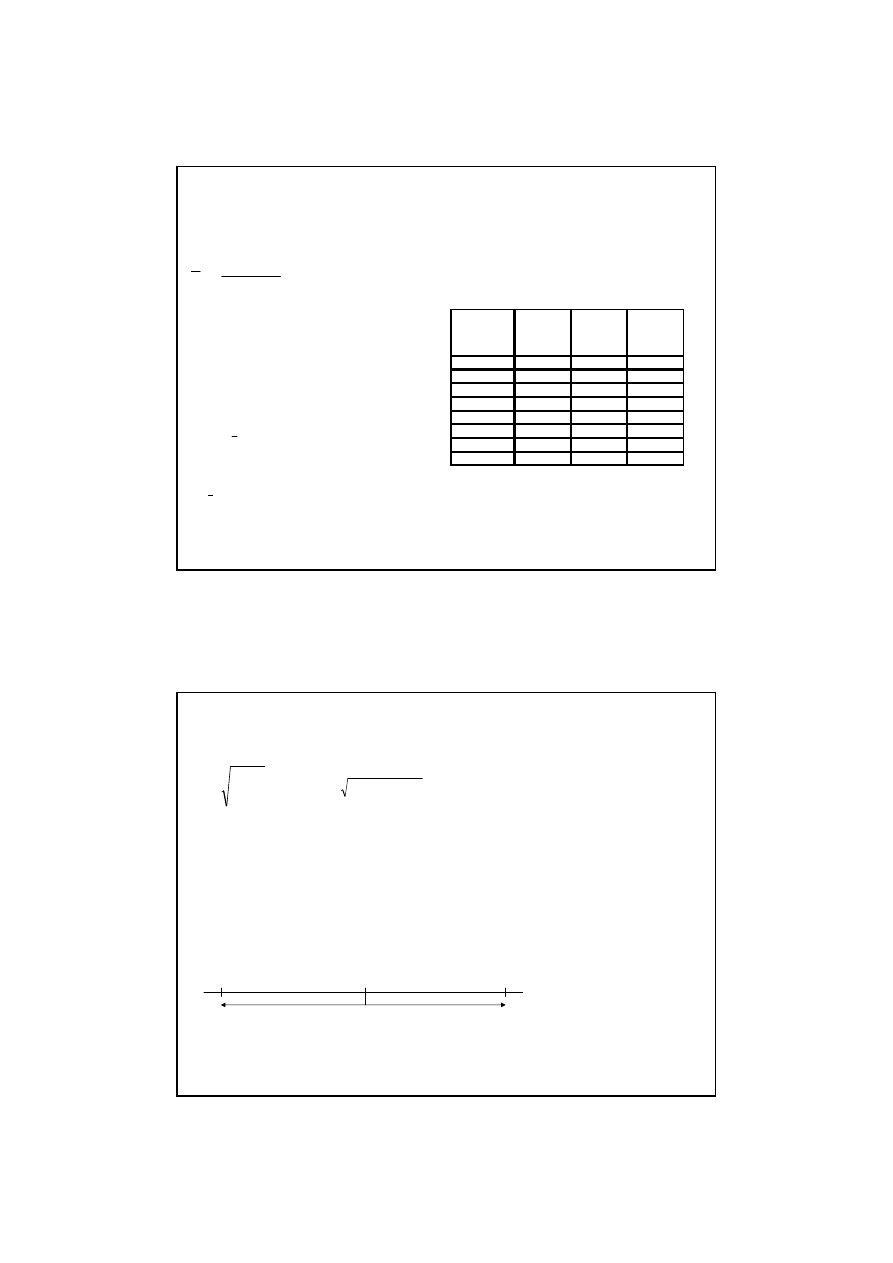
Przykład 1.2

Korzystaj

ą

c z szeregu rozdzielczego dotycz

ą

cego

liczby osób zamieszkuj

ą

cych w wynajmowanych

mieszkaniach oblicz

ś

redni

ą

liczb

ę

mieszka

ń

ców na

jeden wynajmowany lokal (tablica 3.1 z tematu
„Etapy badania statystycznego”)

Tablica 1.2

Liczba

zamieszkuj

ą

cych osób x

i

Liczba

mieszka

ń

n

i

xi *ni

0

3

0

1

1

1

2

3

6

3

6

18

4

4

16

5

4

20

6

3

18

7

1

7

8

2

16

9

1

9

10

1

10

12

1

12

Razem

30

133

2

Maciej St

ę

pi

ń

ski

3

Analiza struktury zbiorowo

ś

ci statystycznej cd.

c) szereg rozdzielczy oparty na cesze ci

ą

g

ł

ej lub inny

szereg posiadaj

ą

cy przedzia

ł

y klasowe

N

n

x

x

k

i

i

i

∑

=

=

1

'

x’

i

–

ś

rodek i-tego przedzia

ł

u klasowego,

n

i

– liczebno

ść

i-tego przedzia

ł

u klasowego,

k – liczba przedzia

ł

ów klasowych,

N – liczebno

ść

populacji generalnej.

Suma odchyle

ń

warto

ś

ci zmiennej od

ś

redniej

arytmetycznej jest równa zero, czyli odchylenia
te wzajemnie si

ę

znosz

ą

:

(

)

∑

=

=

−

N

i

i

x

x

1

0

∑

=

=

⋅

N

i

i

x

x

N

1

Suma warto

ś

ci zmiennej wszystkich jednostek zbiorowo

ś

ci statystycznej jest

równa iloczynowi

ś

redniej arytmetycznej i liczebno

ś

ci populacji.

Ś

redni

ą

arytmetyczn

ą

zawsze mo

ż

na obliczy

ć

dla szeregu szczegó

ł

owego. W przypadku szeregów

rozdzielczych musz

ą

to by

ć

szeregi o zamkni

ę

tych przedzia

ł

ach klasowych.

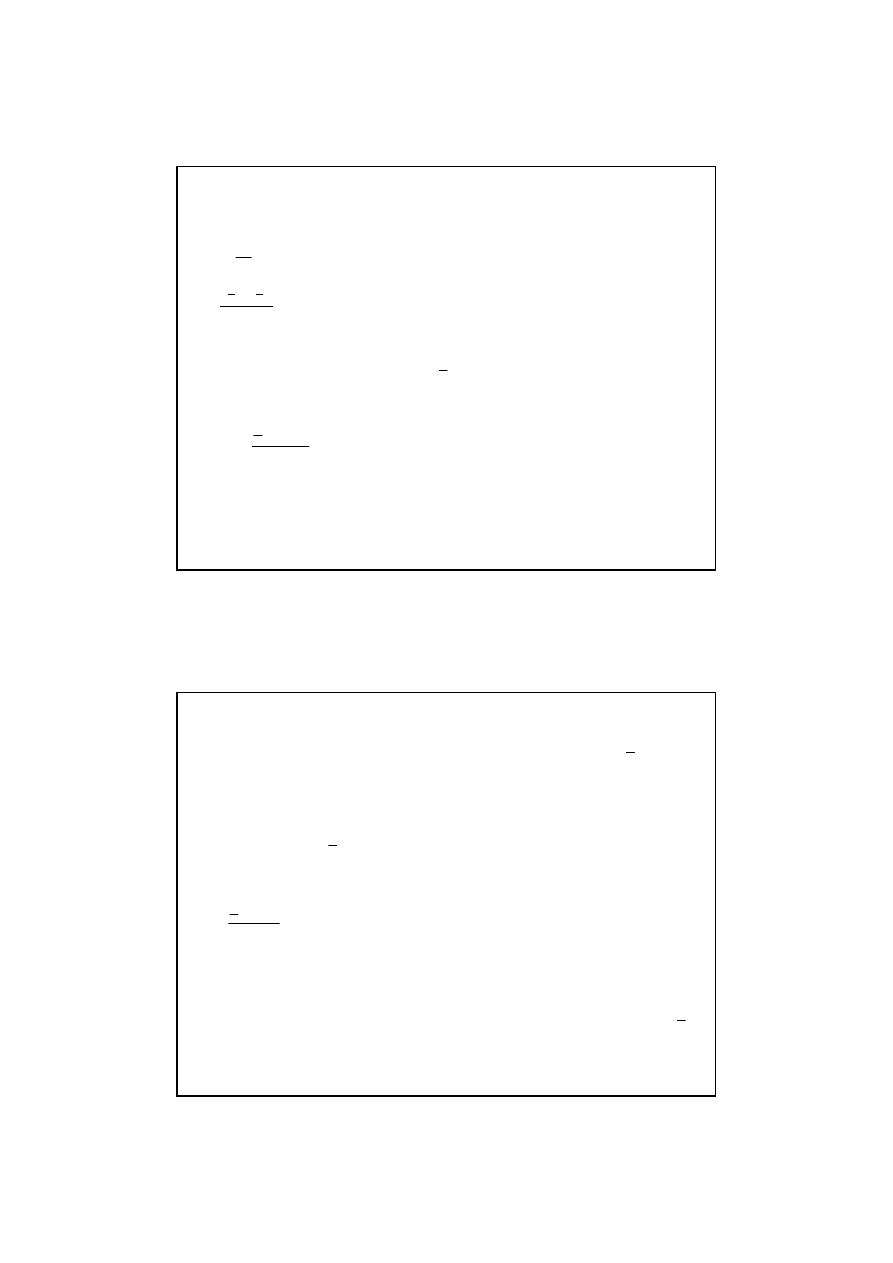
Przykład 1.3

Korzystaj

ą

c z szeregu rozdzielczego dotycz

ą

cego

powierzchni wynajmowanych mieszka

ń

oblicz

ś

redni

ą

powierzchni

ę

lokalu (tablica 3.2 z tematu „Etapy badania

statystycznego)

Tablica 1.3

Powierzchnia

mieszkania

[m

2

]

x

i

min

- x

i

max

Liczba

mieszka

ń

n

i

x

i

'

x

i

*n

i

30-40

6

35

210

40-50

7

45

315

50-60

5

55

275

60-70

3

65

195

70-80

5

75

375

80-90

2

85

170

90-100

2

95

190

Razem

30

1730

Maciej St

ę

pi

ń

ski

4

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Ś

rednia geometryczna

N

N

i

i

x

G

∏

=

=

1

inaczej

N

N

x

x

x

x

G

⋅

⋅

⋅

=

K

3

2

1

x

i

– i-ta warto

ść

badanej zmiennej,

N – liczebno

ść

populacji generalnej.

Ś

rednia geometryczn

ą

stosuje si

ę

, gdy wyst

ę

puje wzgl

ę

dnie du

ż

e ró

ż

nice pomi

ę

dzy warto

ś

ciami zmiennej.

1.2

Ś

rednie pozycyjne

Ś

rednie pozycyjne, to takie

ś

rednie, których warto

ść

wynika z pozycji, któr

ą

zajmuj

ą

w uporz

ą

dkowanym szeregu

statystycznym.

Mediana

Mediana jest warto

ś

ci

ą

zmiennej, któr

ą

w uporz

ą

dkowanym szeregu statystycznym posiada

ś

rodkowa

jednostka.

x

i

min

Me

x

i

max

50%

50%

Warto

ść

mediany interpretuj

ę

si

ę

tak,

ż

e połowa jednostek badanej zbiorowo

ś

ci ma warto

ś

ci zmiennej nie

wi

ę

ksze od mediany, a druga połowa – nie mniejsze.

3

Maciej St

ę

pi

ń

ski

5

Analiza struktury zbiorowo

ś

ci statystycznej cd.

a) szereg szczegółowy

2

1

+

=

N

e

x

M

gdy liczebno

ść

populacji generalnej N jest liczb

ą

nieparzyst

ą

,

2

1

2

2

+

+

=

N

N

e

x

x

M

gdy liczebno

ść

populacji generalnej N jest liczb

ą

parzyst

ą

.

b) szereg rozdzielczy oparty na cesze skokowej

Median

ę

wyznacza si

ę

na podstawie liczebno

ś

ci kumulacyjnej. Mediana jest t

ą

warto

ś

ci

ą

zmiennej, której

liczebno

ść

kumulacyjna obejmuje jednostk

ę

o numerze

.

c) szereg rozdzielczy z przedziałami klasowymi

Warto

ść

mediany szacuje si

ę

na podstawie wzoru interpolacyjnego, po uprzednim zbudowaniu liczebno

ś

ci

kumulacyjnej:

2

N

0

0

1

2

0

c

n

n

x

M

cum

N

e

⋅

−

+

=

−

x

0

– dolna granica przedzia

ł

u, w którym znajduje si

ę

mediana,

n

0

– prosta liczebno

ść

przedzia

ł

u mediany,

c

0

– rozpi

ę

to

ść

przedzia

ł

u mediany,

n

cum-1

– liczebno

ść

kumulacyjna przedzia

ł

u poprzedzaj

ą

cego przedzia

ł

mediany.

Maciej St

ę

pi

ń

ski

6

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Przedzia

ł

mediany to ten, którego liczebno

ść

kumulacyjna obejmuje jednostk

ę

o numerze .

Median

ę

mo

ż

na oblicza

ć

zarówno dla szeregów rozdzielczych o zamkni

ę

tych, jak i otwartych przedzia

ł

ach

klasowych. Zabieg taki nie jest mo

ż

liwy jedynie w przypadku skrajnie asymetrycznych rozk

ł

adów.

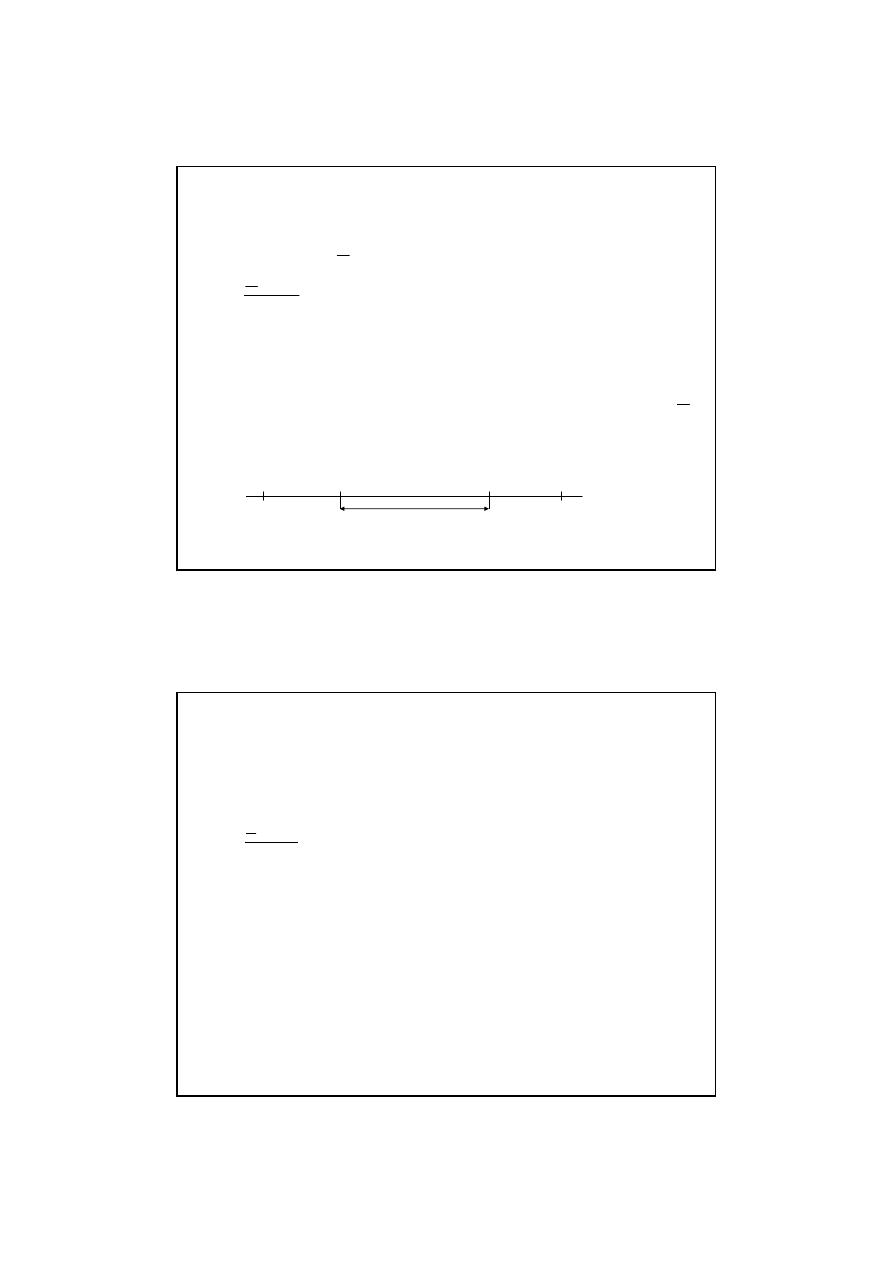
Kwartyl pierwszy

Kwartyl pierwszy jest warto

ś

ci

ą

zmiennej, któr

ą

w uporz

ą

dkowanym szeregu statystycznym posiada

jednostka zajmuj

ą

ca pozycj

ę

.

Kwartyl pierwszy wyznacza si

ę

analogicznie do mediany. W zwi

ą

zku z tym,

ż

e materiał statystyczny

prezentowany jest najcz

ęś

ciej w postaci szeregów o zamkni

ę

tych przedziałach klasowych, podanie formuł

obliczeniowych ograniczone tu zostanie jedynie do takiego wła

ś

nie przypadku. Stosuje si

ę

nast

ę

puj

ą

cy

wzór interpolacyjny:

2

N

4

N

0

0

1

4

0

1

c

n

n

x

Q

cum

N

⋅

−

+

=

−

x

0

– dolna granica przedzia

ł

u, w którym znajduje si

ę

kwartyl pierwszy,

n

0

– prosta liczebno

ść

przedzia

ł

u kwartyla pierwszego,

c

0

– rozpi

ę

to

ść

przedzia

ł

u kwartyla pierwszego,

n

cum-1

– liczebno

ść

kumulacyjna przedzia

ł

u poprzedzaj

ą

cego przedzia

ł

kwartyla pierwszego.

Przedzia

ł

kwartyla pierwszego to przedzia

ł

, którego liczebno

ść

kumulacyjna obejmuje jednostk

ę

o numerze .

Kwartyl pierwszy dostarcza informacji,

ż

e 25% jednostek badanej zbiorowo

ś

ci statystycznej ma warto

ś

ci

zmiennej nie wi

ę

ksze od kwartyla pierwszego, a 75% - nie mniejsze.

4

N

4

Maciej St

ę

pi

ń

ski

7

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Kwartyl trzeci

Kwartyl trzeci jest warto

ś

ci

ą

zmiennej, któr

ą

w uporz

ą

dkowanym szeregu statystycznym posiada

jednostka zajmuj

ą

ca pozycj

ę

.

Wzór interpolacyjny dla szeregu rozdzielczego z przedziałami klasowymi ma posta

ć

:

4

3 N

0

0

1

4

3

0

3

c

n

n

x

Q

cum

N

⋅

−

+

=

−

x

0

– dolna granica przedzia

ł

u, w którym znajduje si

ę

kwartyl trzeci,

n

0

– prosta liczebno

ść

przedzia

ł

u kwartyla trzeciego,

c

0

– rozpi

ę

to

ść

przedzia

ł

u kwartyla trzeciego,

n

cum-1

– liczebno

ść

kumulacyjna przedzia

ł

u poprzedzaj

ą

cego przedzia

ł

kwartyla trzeciego.

Przedzia

ł

kwartyla trzeciego to przedzia

ł

, którego liczebno

ść

kumulacyjna obejmuje jednostk

ę

o numerze .

Kwartyl pierwszy dostarcza informacji,

ż

e 75% jednostek badanej zbiorowo

ś

ci statystycznej ma warto

ś

ci

zmiennej nie wi

ę

ksze od kwartyla pierwszego, a 25% - nie mniejsze.

Z obrazu graficznego przedstawiaj

ą

cego poło

ż

enie kwartyli w ramach przedziału zmienno

ś

ci badanej zmiennej

wynika,

ż

e połowa jednostek zbiorowo

ś

ci statystycznej przyjmuje warto

ś

ci od Q

1

do Q

3

x

i

min

Q

1

Q

3

x

i

max

4

3 N

50%

Maciej St

ę

pi

ń

ski

8

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Decyl i-ty

Je

ż

eli populacje generalne s

ą

bardzo liczne i/lub chcemy dowiedzie

ć

wi

ę

cej na temat rozkładu w

skrajnych regionach obszaru zmienno

ś

ci badanej cechy, wówczas wyró

ż

nienie kwartyli mo

ż

e

okaza

ć

si

ę

niewystarczaj

ą

ce. Stosuje si

ę

wówczas decyle, które dziel

ą

zbiorowo

ść

na

subpopulacje dziesi

ę

cioprocentowe. W tym celu posługuje si

ę

wzorem interpolacyjnym (dla

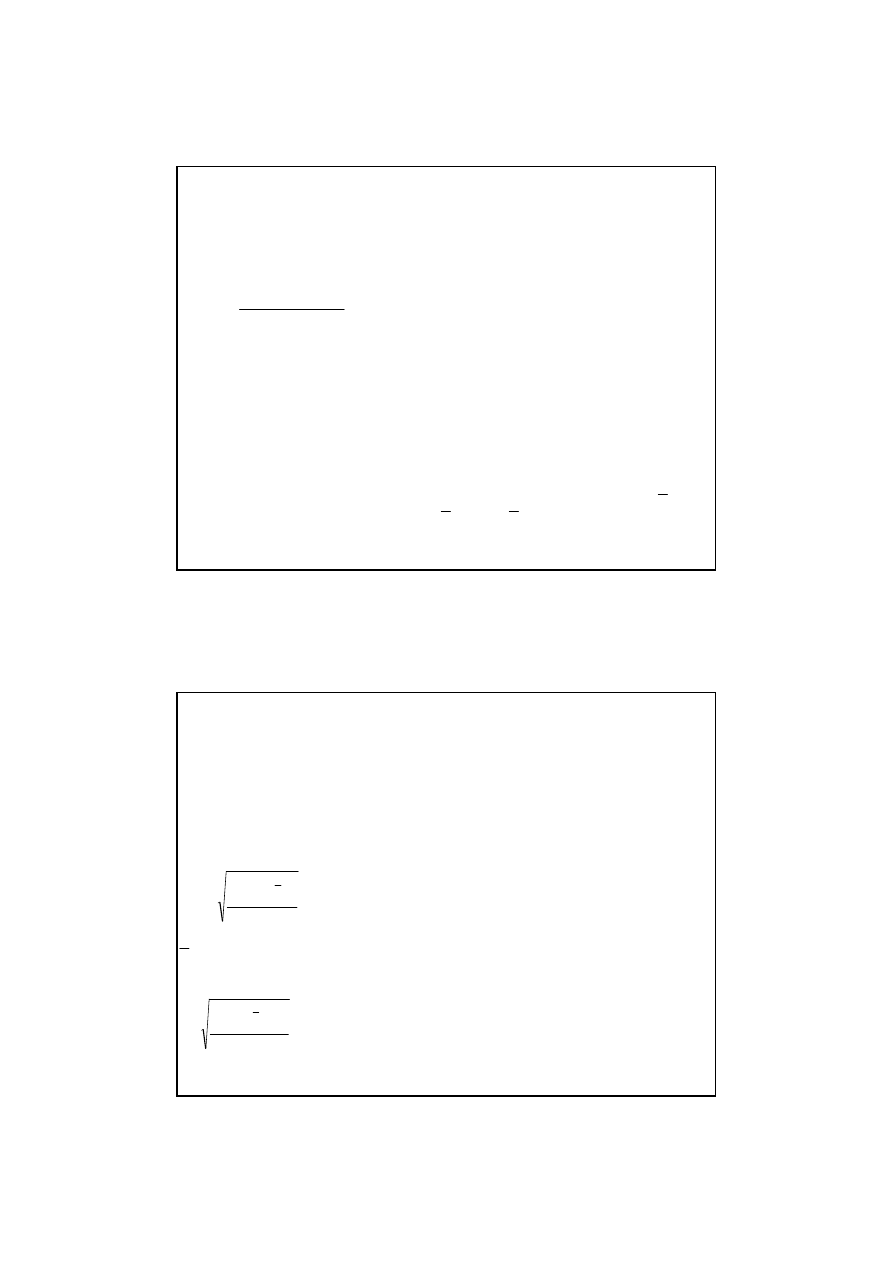
szeregów z przedziałami klasowymi):

0

0

1

10

0

c

n

n

x

D

cum

iN

i

⋅

−

+

=

−

x

0

– dolna granica przedzia

ł

u, w którym znajduje si

ę

i-ty decyl,

n

0

– prosta liczebno

ść

przedzia

ł

u i-tego decyla,

c

0

– rozpi

ę

to

ść

przedzia

ł

u i-tego decyla,

n

cum-1

– liczebno

ść

kumulacyjna przedzia

ł

u poprzedzaj

ą

cego przedzia

ł

i-tego decyla.

W analogiczny sposób konstruuje si

ę

wzór i przeprowadza obliczenia w przypadku centyli, z t

ą

ró

ż

nic

ą

,

ż

e

wówczas dochodzi do podziału zbiorowo

ś

ci generalnej na 100 subpopulacji.

Dla i = 1, 2,….,9

5

Maciej St

ę

pi

ń

ski

9

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Dominanta/Modalna

Dominanta, zwana równie

ż

modaln

ą

, jest t

ą

warto

ś

ci

ą

zmiennej, która w badanej populacji

generalnej wyst

ę

puje z najwi

ę

ksz

ą

cz

ę

sto

ś

ci

ą

.

W przypadku szeregów rozdzielczych z przedzia

ł

ami klasowymi, warto

ść

dominanty szacujemy na

podstawie wzoru interpolacyjnego. Jest ona wtedy warto

ś

ci

ą

abstrakcyjn

ą

, charakteryzuj

ą

c

ą

rozk

ł

ad.

(

) (

)

0

1

0

1

0

1

0

0

c

n

n

n

n

n

n

x

D

⋅

−

+

−

−

+

=

+

−

−

x

0

– dolna granica przedziału dominanty;

n

0

– liczebno

ść

przedziału dominanty;

n

-1

– liczebno

ść

przedziału poprzedzaj

ą

cego przedział dominanty;

n

+1

– liczebno

ść

przedziału nast

ę

puj

ą

cego po przedziale dominanty;

c

0

– rozpi

ę

to

ść

przedziału mediany.

Przedzia

ł

dominanty to ten, który ma maksymaln

ą

liczebno

ść

prost

ą

.

Dominant

ę

mo

ż

na oblicza

ć

tylko dla szeregów rozdzielczych o tej samej rozpi

ę

to

ś

ci przedzia

ł

ów. W innych

przypadkach obliczanie dominanty jest bardziej skomplikowane i wymaga spełnienia dodatkowych warunków.
Szereg mo

ż

e by

ć

natomiast szeregiem o otwartych przedzia

ł

ach klasowych.

Jak oka

ż

e si

ę

podczas analizy asymetrii, wzajemne poło

ż

enie miar

ś

rednich mo

ż

e by

ć

równe (D=Me= ).

Najcz

ęś

ciej jednak wyst

ę

puje sytuacja, w której D>Me> albo D<Me<

x

x

x

Maciej St

ę

pi

ń

ski

10

Analiza struktury zbiorowo

ś

ci statystycznej cd.

2. Analiza rozproszenia czyli dyspersji

Analiza rozproszenia pozwala odpowiedzie

ć

na pytanie, w jakim stopniu jednostki zbiorowo

ś

ci

statystycznej s

ą

zró

ż

nicowane pod wzgl

ę

dem warto

ś

ci badanej zmiennej, czyli jak kszta

ł

tuje si

ę

podobie

ń

stwo jednostek lub ich rozproszenie.

2.1Odchylenie standardowe

Odchylenie standardowe jest parametrem, który informuje, o ile,

ś

rednio rzecz bior

ą

c, warto

ś

ci

zmiennej odchylaj

ą

si

ę

in plus lub In minus o

ś

redniej arytmetycznej.

Odchylenie standardowe oznacza si

ę

symbolem

σ

(

σ

2

to wariancja).

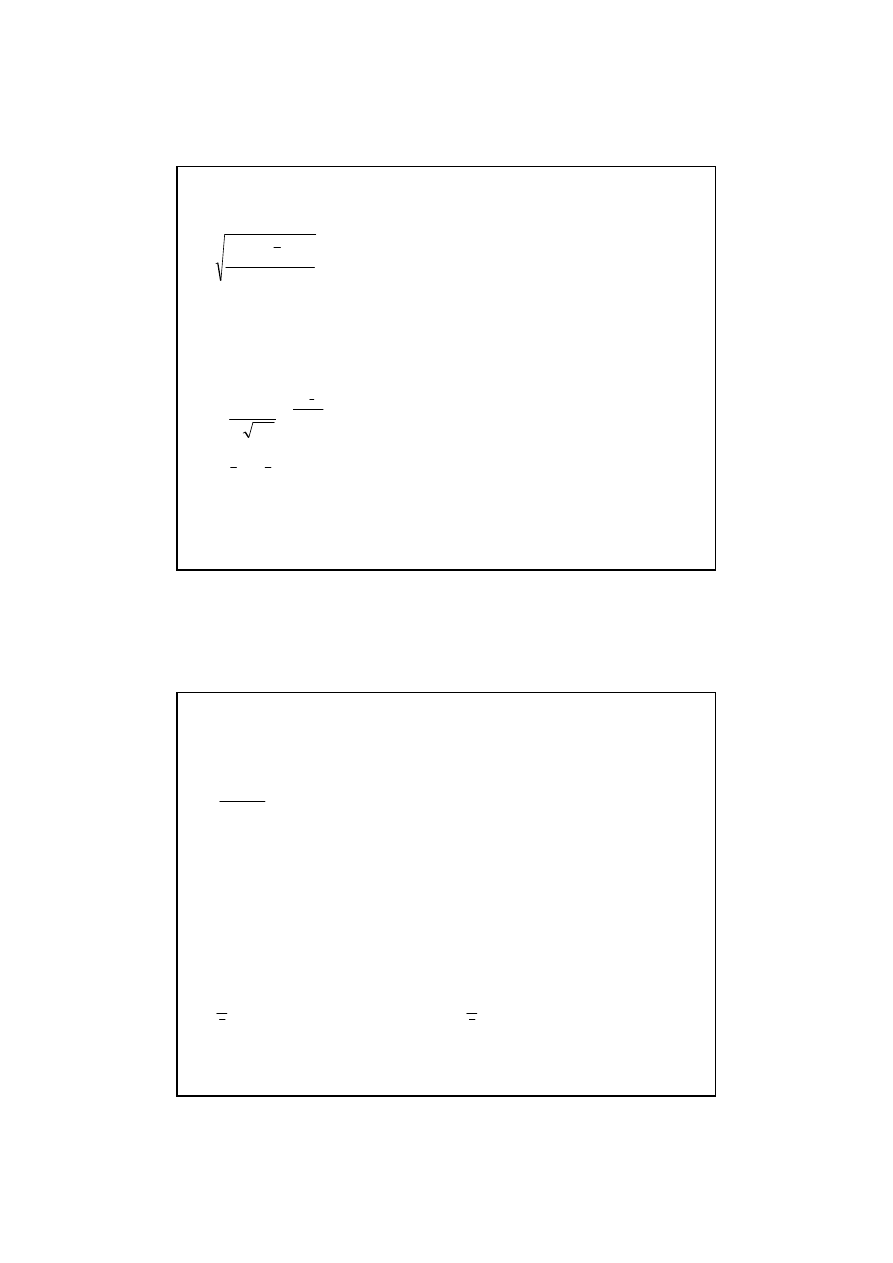
a) szereg szczegółowy

(

)

N

x

x

N

i

i

i

∑

=

−

=

1

2

σ

x

i

– i-ta warto

ść

zmiennej, i = 1, 2, …, N;

–

ś

rednia arytmetyczna;

N – liczebno

ść

populacji generalnej.

b) szereg rozdzielczy oparty na cesze skokowej

x

(

)

N

n

x

x

k

i

i

i

i

∑

=

⋅

−

=

1

2

σ

x

i

– i-ta warto

ść

zmiennej, i = 1, 2, …, k;

n

i

– cz

ę

sto

ść

, z jak

ą

wyst

ę

puje i-ta warto

ść

zmiennej;

k – liczba warto

ś

ci badanej zmiennej.

6

Maciej St

ę

pi

ń

ski

11

Analiza struktury zbiorowo

ś

ci statystycznej cd.

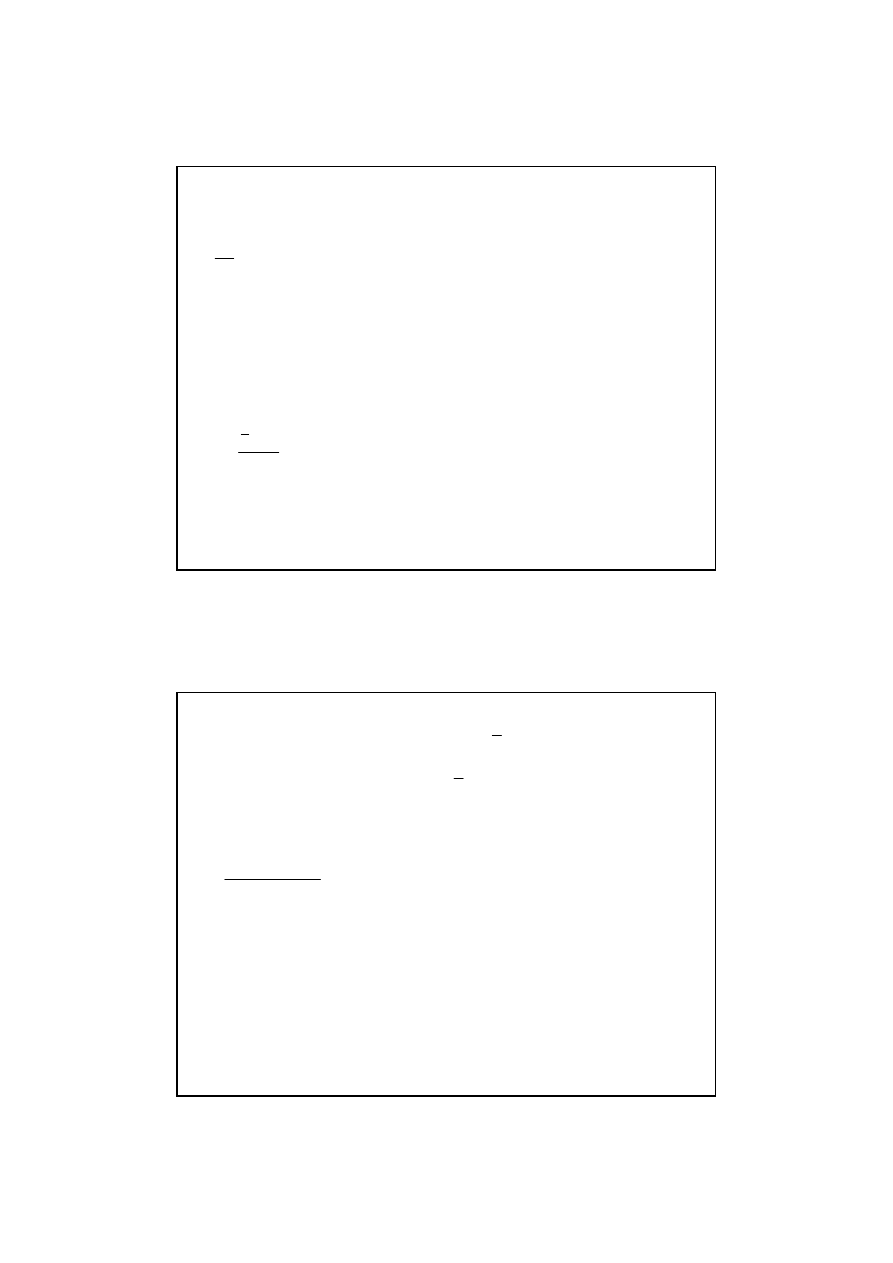
c) szereg rozdzielczy z przedziałami klasowymi

(

)

N

n

x

x

k

i

i

i

i

∑

=

⋅

−

=

1

2

'

σ

x’

i

–

ś

rodek i-tego przedzia

ł

u klasowego, i = 1, 2, …, k;

n

i

– liczebno

ść

i-tego przedzia

ł

u klasowego;

k – liczebno

ść

przedzia

ł

ów klasowych.

Podobnie, jak w przypadku

ś

redniej arytmetycznej, odchylenie standardowe dla szeregów rozdzielczych z

przedzia

ł

ami kasowymi mo

ż

emy obliczy

ć

tylko w przypadku, gdy wszystkie przedzia

ł

y klasowe s

ą

zamkni

ę

te.

Gdy rozk

ł

ad badanej zmiennej jest normalny, jej funkcja g

ę

sto

ś

ci ma posta

ć

:

(

)

2

2

2

2

1

)

(

σ

π

σ

x

x

e

x

f

−

−

=

(rysunek na tablicy)

Mo

ż

na wówczas wyznaczy

ć

tzw. typowy obszar zmienno

ś

ci:

(

)

σ

σ

+

−

=

x

x

x

TYP

;

Obszar ten zajmuje 68,26% jednostek badanej zbiorowo

ś

ci. Oznacza to,

ż

e 68,26% jednostek zbiorowo

ś

ci

generalnej przyjmuje warto

ś

ci z typowego obszaru.

Maciej St

ę

pi

ń

ski

12

Analiza struktury zbiorowo

ś

ci statystycznej cd.

2.2 Odchylenie

ć

wiartkowe.

Je

ż

eli z przyczyn formalnych nie mo

ż

emy obliczy

ć

odchylenia standardowego (szeregi o otwartych

przedzia

ł

ach klasowych), to miar

ą

rozproszenia staje si

ę

odchylenie

ć

wiartkowe (Q).

2

1

3

Q

Q

Q

−

=

Q

1

– kwartyl pierwszy,

Q

3

– kwartyl trzeci.

Odchylenie

ć

wiartkowe informuje, jak du

ż

a jest po

ł

owa obszaru zmienno

ś

ci

ś

rodkowych 50% jednostek

zbiorowo

ś

ci statystycznej. Mo

ż

na te

ż

powiedzie

ć

,

ż

e odchylenie to informuje, jakie jest przeci

ę

tne odchylenie od

mediany.

2.3 Współczynniki zmienno

ś

ci

Odchylenie standardowe i odchylenie

ć

wiartkowe to bezwzgl

ę

dne miary dyspersji. Wyra

ż

ane s

ą

one w tych

samych jednostkach, w których wyra

ż

ana jest badana zmienna.

Stosuje si

ę

równie

ż

wzgl

ę

dne miary dyspersji. S

ł

u

żą

one ocenie intensywno

ś

ci rozproszenia, a tak

ż

e celowi

porównywania dwóch lub wi

ę

cej zbiorowo

ś

ci. To wspó

ł

czynniki zmienno

ś

ci (V

Z

).

Dla miar klasycznych , wspó

ł

czynnik zmienno

ś

ci ma posta

ć

:

x

V

Z

σ

=

i najcz

ęś

ciej wyra

ż

a si

ę

go w procentach

%

100

⋅

=

x

V

Z

σ

Współczynnik zmienno

ś

ci informuje, jak

ą

cz

ęś

ci

ą ś

redniej arytmetycznej jest odchylenie standardowe. Im

mniejsza warto

ść

parametru, tym warto

ś

ci zmiennej s

ą

bardziej do siebie podobne i zbli

ż

one do warto

ś

ci

ś

redniej.

7

Maciej St

ę

pi

ń

ski

13

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Je

ż

eli nie mo

ż

na wyznaczy

ć

parametrów klasycznych, dysponujemy natomiast

ś

rednimi pozycyjnymi, wówczas

wzór ma posta

ć

:

(

)

%

100

⋅

=

e

Z

M

Q

V

Informuje on, jak

ą

cz

ęś

ci

ą

mediany jest odchylenie

ć

wiartkowe. Niska warto

ść

współczynnika informuje o du

ż

ym

skupieniu warto

ś

ci zmiennej wokół mediany. Nale

ż

y jednak pami

ę

ta

ć

,

ż

e miara ta odnosi si

ę

jedynie do

„

ś

rodkowej” połowy jednostek badanej zbiorowo

ś

ci.

3. Analiza asymetrii

Analiza asymetrii zmierza do udzielenia odpowiedzi na pytanie, czy w badanej zbiorowo

ś

ci przewa

ż

aj

ą

jednostki ,

których warto

ś

ci zmiennej s

ą

mniejsze od

ś

redniej, czy jednostki przyjmuj

ą

ce warto

ś

ci zmiennej wi

ę

ksze od

ś

redniej. Badanie mo

ż

e równie

ż

wykaza

ć

równowag

ę

, czyli symetri

ę

rozkładu.

3.1 Asymetria w przypadku szeregów o zamkni

ę

tych przedziałach klasowych

Gdy obliczona została

ś

rednia arytmetyczna, wówczas podstawowym współczynnikiem asymetrii jest parametr,

który wyznacza si

ę

przy u

ż

yciu nast

ę

puj

ą

cego wzoru:

σ

D

x

A

S

−

=

Mo

ż

liwie s

ą

trzy warianty wyników, które odpowiadaj

ą

ró

ż

nym charakterom rozkładu.

Kiedy A

S

= 0, wtedy mamy do czynienia z rozkładem idealnie symetrycznym. Dominanta,

ś

rednia arytmetyczna

i mediana maj

ą

wówczas identyczne warto

ś

ci (rysunek na tablicy). Liczba jednostek maj

ą

cych warto

ś

ci

zmiennej ni

ż

sze od

ś

redniej równa si

ę

liczbie jednostek o wy

ż

szej od

ś

redniej warto

ś

ci zmiennej.

Maciej St

ę

pi

ń

ski

14

Analiza struktury zbiorowo

ś

ci statystycznej cd.

A

S

> 0 Wówczas

ś

rednia arytmetyczna jest wi

ę

ksza od dominanty ( >D). Rozkład charakteryzuje si

ę

asymetri

ą

dodatni

ą

, prawostronn

ą

(rysunek na tablicy). Przewa

ż

aj

ą

w nim jednostki, dla których warto

ś

ci

zmiennej s

ą

mniejsze od

ś

redniej.

A

S

< 0

Ś

rednia arytmetyczna jest mniejsza od dominanty ( <D). Mamy zetem do czynienia z asymetri

ą

lewostronn

ą

, ujemn

ą

. Wi

ę

cej jest jednostek, które przyjmuj

ą

warto

ś

ci zmiennej wi

ę

ksze od

ś

redniej.

x

3.2 Asymetria w przypadku szeregów o otwartych przedziałach klasowych

Je

ś

li z przyczyn obiektywnych nie mo

ż

na obliczy

ć

miar klasycznych, a dysponujemy miarami pozycyjnymi,

wówczas współczynnik asymetrii wyznaczany jest w oparciu o nast

ę

puj

ą

cy wzór:

Q

Me

Q

Q

A

S

2

3

1

−

+

=

Analogicznie do sytuacji w przypadku szeregów o zamkni

ę

tych przedziałach klasowych, współczynnik

zmienno

ś

ci mo

ż

e mie

ć

:

a) warto

ść

równ

ą

0; rozkład jest wtedy symetryczny;

b) warto

ść

dodatni

ą

; rozkład jest asymetryczny dodatnio, prawostronnie; przewa

ż

aj

ą

jednostki o niskich

warto

ś

ciach zmiennej w ramach obszaru jej zmienno

ś

ci;

c) warto

ść

ujemn

ą

; wtedy rozkład wykazuje si

ę

asymetri

ą

ujemn

ą

, lewostronn

ą

. Przewa

ż

aj

ą

w nim jednostki o

wysokich warto

ś

ciach zmiennej w ramach obszaru jej zmienno

ś

ci.

x

8

Maciej St

ę

pi

ń

ski

15

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Zadanie 1.

Na podstawie materiału statystycznego znajduj

ą

cego si

ę

w poni

ż

szym szeregu szczegółowym,

oblicz , , V

Z

, Me, Q

1

, Q

3

i Q.

x

σ

Wielko

ść

ogródka

działkowego

[ar] x

i

i

2,1

1

2,7

2

3,1

3

4,4

4

5,0

5

5,7

6

6,3

7

6,3

8

6,4

9

7,8

10

7,9

11

8,2

12

8,2

13

9,0

14

10,3

15

11,4

16

11,5

17

12,8

18

13,0

19

13,5

20

Razem

155,6

Wielko

ść

ogródka

działkowego

[ar] x

i

i

(x

i

-x

ś

r )

(x

i

-x

ś

r )

2

2,1

1

-5,68

32,2624

2,7

2

-5,08

25,8064

3,1

3

-4,68

21,9024

4,4

4

-3,38

11,4244

5,0

5

-2,78

7,7284

5,7

6

-2,08

4,3264

6,3

7

-1,48

2,1904

6,3

8

-1,48

2,1904

6,4

9

-1,38

1,9044

7,8

10

0,02

0,0004

7,9

11

0,12

0,0144

8,2

12

0,42

0,1764

8,2

13

0,42

0,1764

9,0

14

1,22

1,4884

10,3

15

2,52

6,3504

11,4

16

3,62

13,1044

11,5

17

3,72

13,8384

12,8

18

5,02

25,2004

13,0

19

5,22

27,2484

13,5

20

5,72

32,7184

155,6

1,421E-14

230,052

Maciej St

ę

pi

ń

ski

16

Analiza struktury zbiorowo

ś

ci statystycznej cd.

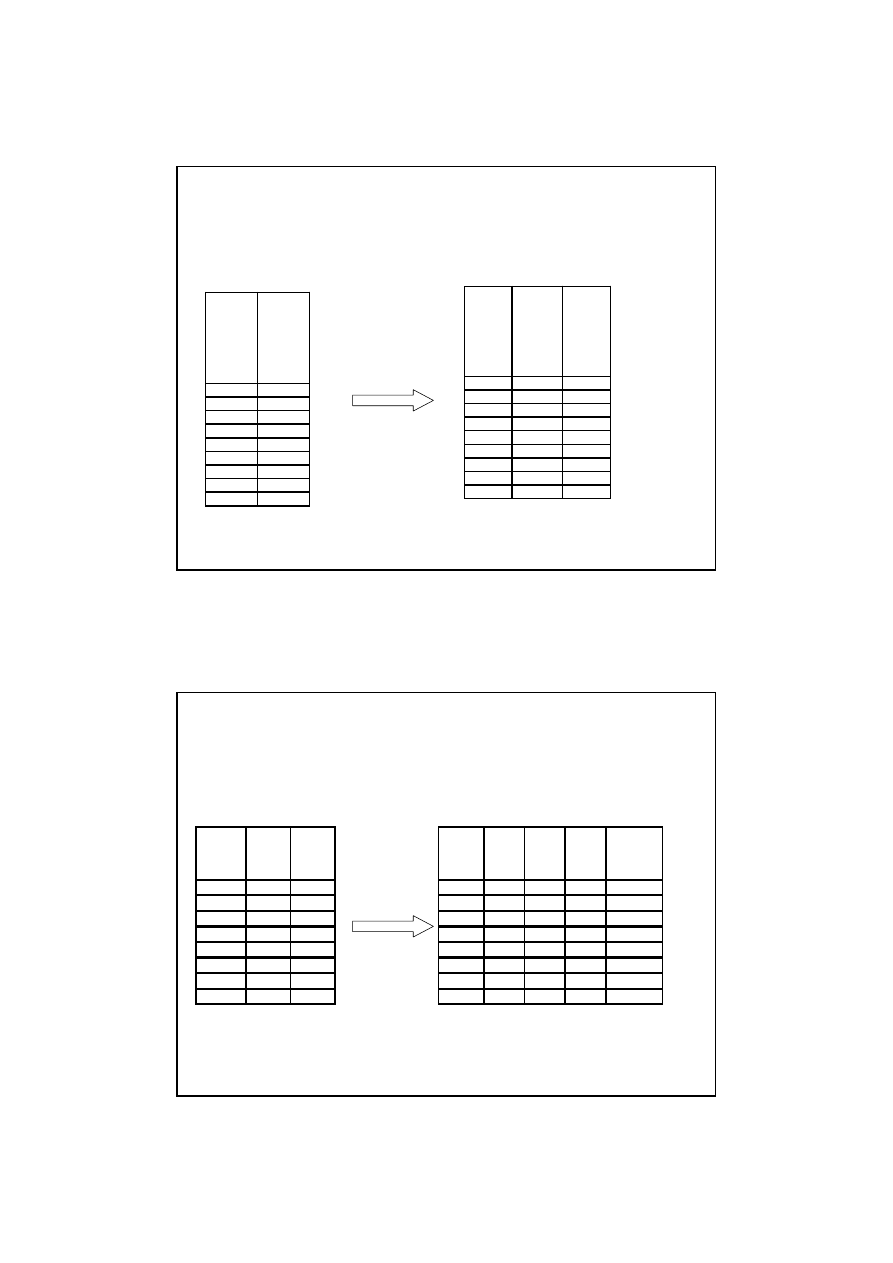
Zadanie 2.

Przeprowad

ź

wszechstronn

ą

analiz

ę

struktury wynajmowanych mieszka

ń

pod wzgl

ę

dem liczby

mieszka

ń

ców:

Liczba

zamieszkuj

ą

cych osób x

i

Liczba

mieszka

ń

n

i

xi *ni

(xi-x

ś

r)

2

(xi-x

ś

r)

2

* n

i

0

3

0

19,6544

58,9633

1

1

1

11,7878

11,7878

2

3

6

5,9211

17,7633

3

6

18

2,0544

12,3267

4

4

16

0,1878

0,7511

5

4

20

0,3211

1,2844

6

3

18

2,4544

7,3633

7

1

7

6,5878

6,5878

8

2

16

12,7211

25,4422

9

1

9

20,8544

20,8544

10

1

10

30,9878

30,9878

12

1

12

57,2544

57,2544

Razem

30

133

251,3667

Liczba

zamieszkuj

ą

cych osób x

i

Liczba

mieszka

ń

n

i

0

3

1

1

2

3

3

6

4

4

5

4

6

3

7

1

8

2

9

1

10

1

12

1

Razem

30

9

Maciej St

ę

pi

ń

ski

17

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Zadanie 3.

Przeprowad

ź

wszechstronn

ą

analiz

ę

struktury gospodarstw domowych pod wzgl

ę

dem liczby

posiadanych telefonów komórkowych:

Liczba

pryw atnych

telefonów

kom. w

gospodarst

w ie

domow ym

Liczebno

ś

ci

w zgl

ę

dne

0

0,048

1

0,074

2

0,112

3

0,269

4

0,218

5

0,123

6

0,083

7 i wi

ę

cej

0,075

Razem

1,00

Liczba

pryw atnych

telefonów

kom. w

gospodarst

w ie

domow ym

Liczebno

ś

ci

w zgl

ę

dne

Liczebno

ś

ci

kumulacyjne

w zgl

ę

dne

[%]

0

0,048

4,8%

1

0,074

12,2%

2

0,112

23,3%

3

0,269

50,2%

4

0,218

72,0%

5

0,123

84,3%

6

0,083

92,5%

7 i wi

ę

cej

0,075

100,0%

Razem

1,00

Maciej St

ę

pi

ń

ski

18

Analiza struktury zbiorowo

ś

ci statystycznej cd.

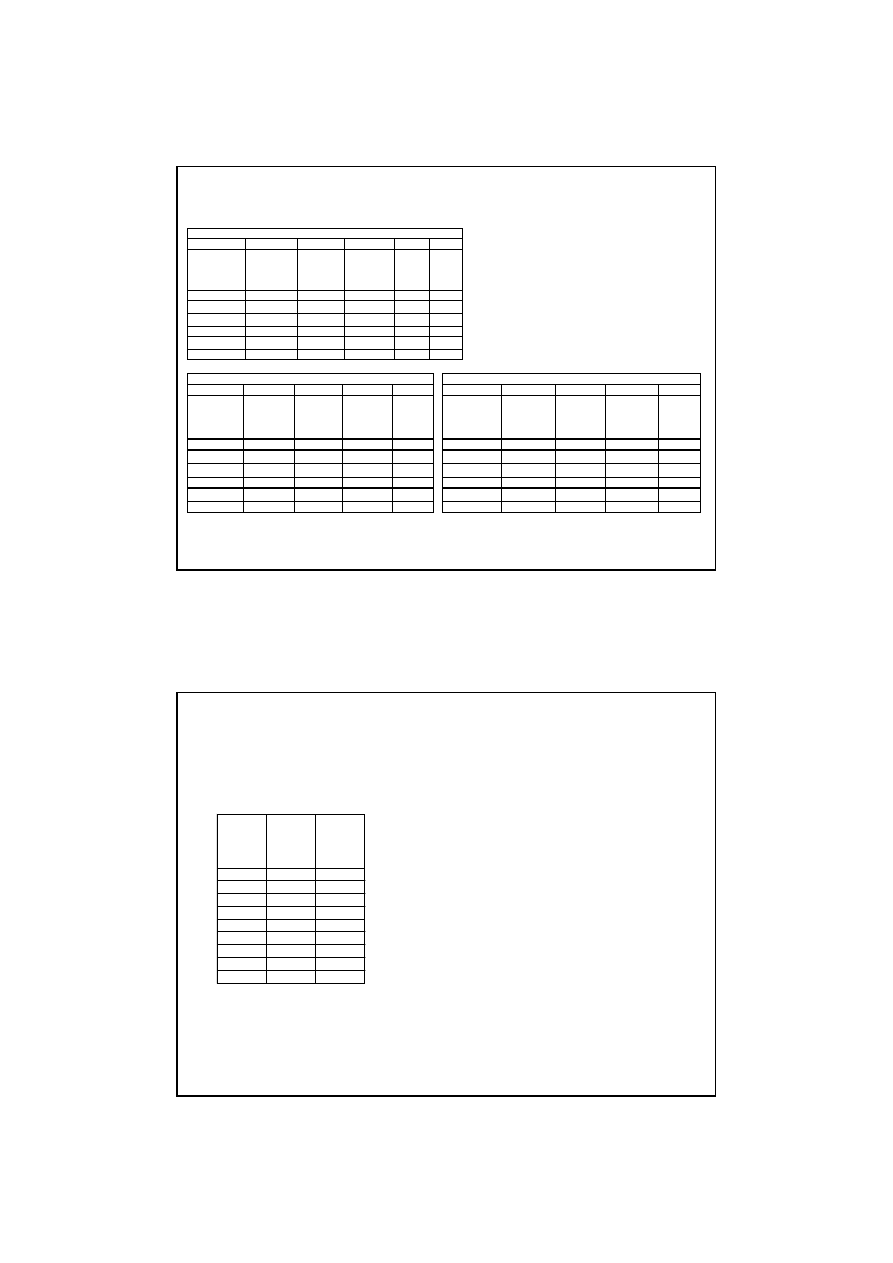
Zadanie 4.

Przeprowad

ź

wszechstronn

ą

analiz

ę

struktury wynajmowanych mieszka

ń

pod wzgl

ę

dem ich

powierzchni:

Powierzchnia

mieszkania

[m

2

]

x

i

min

- x

i

max

Liczba

mieszka

ń

n

i

x

i

'

30-40

6

35

40-50

7

45

50-60

5

55

60-70

3

65

70-80

5

75

80-90

2

85

90-100

2

95

Razem

30

Powierzchnia

mieszkania

[m

2

]

x

i

min

- x

i

max

Liczba

mieszka

ń

n

i

x

i

'

x'

i

*n

i

(xi'-x

ś

ri)2*n

i

30-40

6

35

210

3082,6667

40-50

7

45

315

1123,1111

50-60

5

55

275

35,5556

60-70

3

65

195

161,3333

70-80

5

75

375

1502,2222

80-90

2

85

170

1494,2222

90-100

2

95

190

2787,5556

Razem

30

1730

10186,6667

10

Maciej St

ę

pi

ń

ski

19

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Zadanie 5.

Wielko

ść

gospodarstw rolnych w Polsce w 2000 r. (gosp. indywid.)

Wielko

ść

gospodarstwa

[ha]

Liczba

gospodarstw

n

i

Liczebno

ść

wzgl

ę

dna

Liczebno

ść

wzgl

ę

dna

kumulacyjna

1,01-1,99

448 171

23,83%

23,83%

Me=

2,00-4,99

613 609

32,62%

56,45%

Q

1

=

5,00-9,99

447 677

23,80%

80,25%

Q

3

=

10-14,99

185 668

9,87%

90,12%

Q=

15,00 i wi

ę

cej

185 757

9,88%

100,00%

V

z

=

1 880 882

Wielko

ść

gospodarstw rolnych w Polsce w 2002 r. (gosp. indywid.)

Wielko

ść

gospodarstwa

[ha]

Liczba

gospodarstw

n

i

Liczebno

ść

wzgl

ę

dna

Liczebno

ść

wzgl

ę

dna

kumulacyjna

1,01-1,99

516 836

26,48%

26,48%

Me=

2,00-4,99

629 462

32,25%

58,73%

Q

1

=

5,00-9,99

426 520

21,85%

80,59%

Q

3

=

10-14,99

182 505

9,35%

89,94%

Q=

15,00 i wi

ę

cej

196 403

10,06%

100,00%

V

z

=

1 951 726

Wielko

ść

gospodarstw rolnych w Polsce w 2007 r. (gosp. indywid.)

Wielko

ść

gospodarstwa

[ha]

Liczba

gospodarstw

n

i

Liczebno

ść

wzgl

ę

dna

Liczebno

ść

wzgl

ę

dna

kumulacyjna

1,01-1,99

422 533

23,42%

23,42%

Me=

2,00-4,99

613 978

34,03%

57,45%

Q

1

=

5,00-9,99

399 869

22,16%

79,62%

Q

3

=

10-14,99

166 435

9,23%

88,84%

Q=

15,00 i wi

ę

cej

201 250

11,16%

100,00%

V

z

=

1 804 065

Maciej St

ę

pi

ń

ski

20

Analiza struktury zbiorowo

ś

ci statystycznej cd.

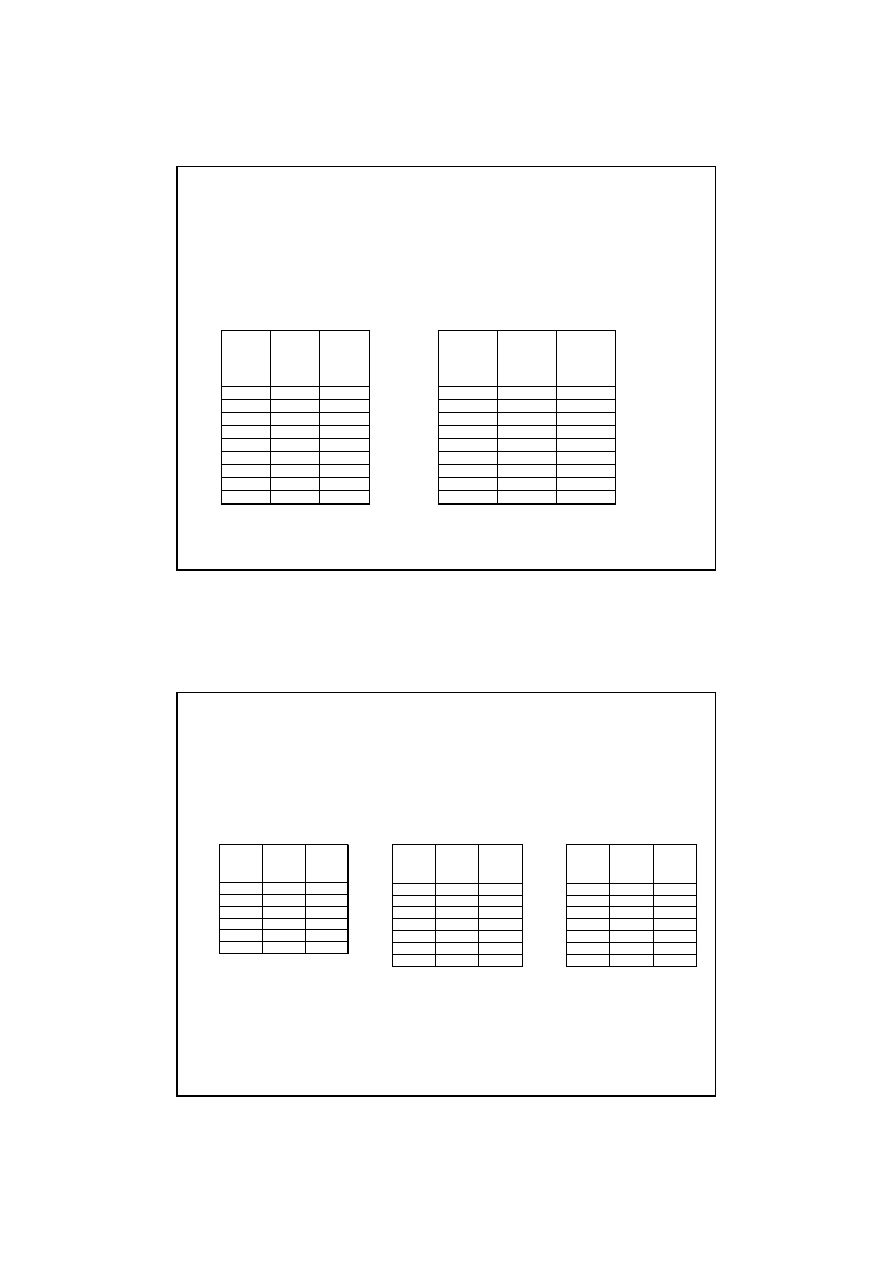
Zadanie 6.

Przeprowad

ź

wszechstronn

ą

analiz

ę

struktury warto

ś

ci koszyka dóbr kupowanych w dniu 30 V

2010 w markecie sieci „Alfa” w miejscowo

ś

ci Sło

ń

ce (Region Północny):

Warto

ść

koszyka

(x

i

)

x

i

'

Liczebno

ś

ć

wzgl

ę

dna

(n

i

)

20-30

25

2,40

30-40

35

7,90

40-50

45

9,30

50-60

55

15,20

60-70

65

18,30

70-80

75

38,40

80-90

85

7,20

90-100

95

1,30

100,00

11

Maciej St

ę

pi

ń

ski

21

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Zadanie 7.

Przeprowad

ź

wszechstronn

ą

analiz

ę

struktury warto

ś

ci koszyka dóbr kupowanych w dniu 30 V

2010 w markecie sieci „Alfa” w miejscowo

ś

ci Ksi

ęż

yc (Region Centralny) i w miejscowo

ś

ci Mars

(Region Południowy)

Warto

ść

koszyka

(x

i

)

x

i

'

Liczebno

ś

ć

wzgl

ę

dna

(n

i

)

20-30

25

3,50

30-40

35

8,10

40-50

45

9,20

50-60

55

24,20

60-70

65

29,80

70-80

75

16,80

80-90

85

5,80

90-100

95

2,60

100,00

Warto

ść

koszyka

(x

i

)

x

i

'

Liczebno

ś

ć

wzgl

ę

dna

(n

i

)

20-30

25

7,20

30-40

35

9,80

40-50

45

19,40

50-60

55

25,80

60-70

65

16,40

70-80

75

9,50

80-90

85

8,70

90-100

95

3,20

100,00

Region Centralny

Region Południowy

Maciej St

ę

pi

ń

ski

22

Analiza struktury zbiorowo

ś

ci statystycznej cd.

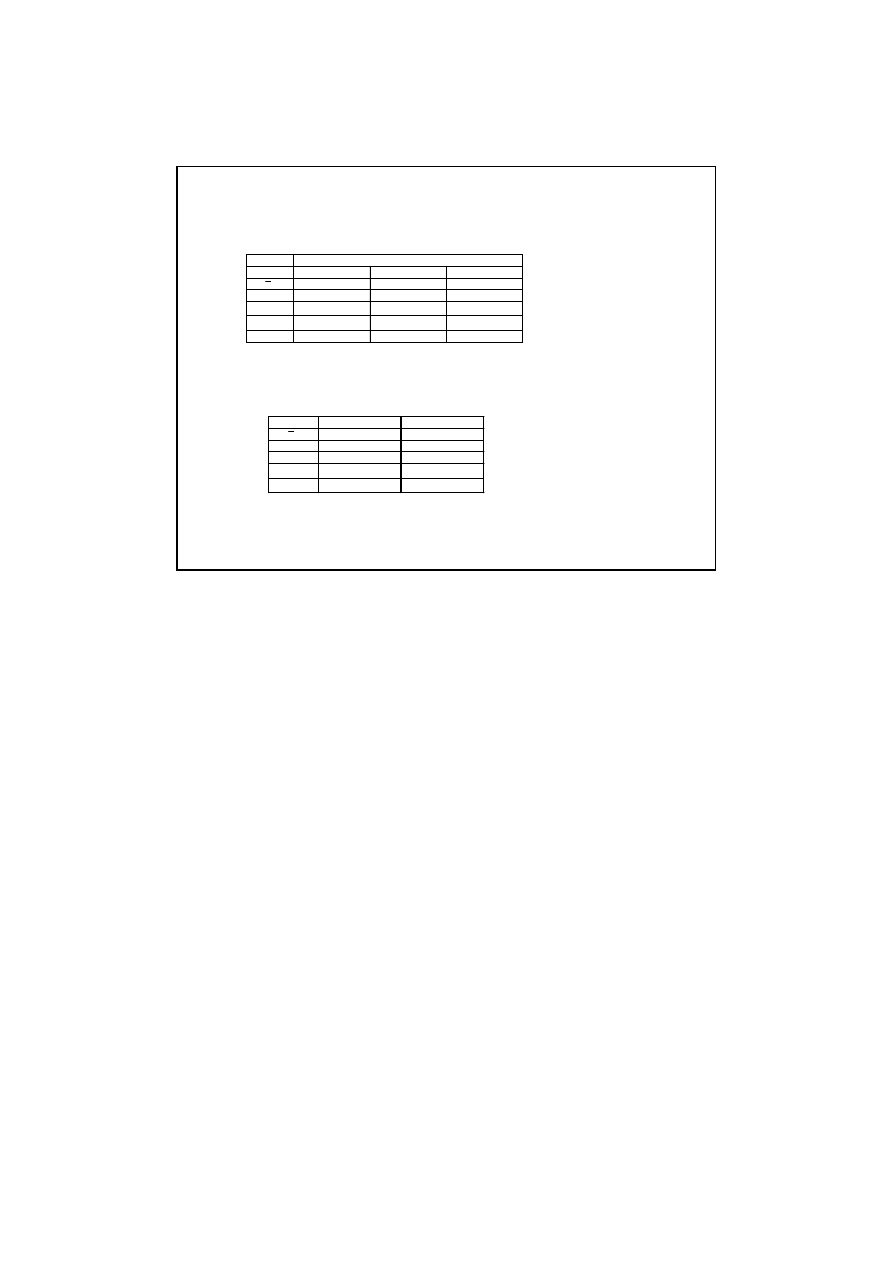
Zadanie 8.

Przeprowad

ź

analiz

ę

struktury wieku posłów na sejm I, II i III kadencji w kraju „Sło

ń

ce” z wykorzystaniem

parametrów klasycznych. Jak zmieniała si

ę

struktura wieku w poszczególnych kadencjach?

Wiek

posłów (x

i

)

x

i

'

Liczba

posłów (n

i

)

20-29

25

9

30-39

35

92

40-49

45

212

50-59

55

120

60-69

65

27

SUMA

460

Struktura wieku posłów na sejm I

Kadencji w kraju Sło

ń

ce

Wiek

posłów (x

i

)

x

i

'

Liczba

posłów (n

i

)

20-29

25

7

30-39

35

57

40-49

45

164

50-59

55

178

60-69

65

42

70-79

75

12

SUMA

460

Struktura wieku posłów na sejm II

Kadencji w kraju Sło

ń

ce

Wiek

posłów (x

i

)

x

i

'

Liczba

posłów (n

i

)

20-29

25

7

30-39

35

84

40-49

45

168

50-59

55

146

60-69

65

52

70-79

75

3

SUMA

460

Struktura wieku posłów na sejm

III Kadencji w kraju Sło

ń

ce

12

Maciej St

ę

pi

ń

ski

23

Analiza struktury zbiorowo

ś

ci statystycznej cd.

Parametry I półrocze 2009 r. II półrocze 2009 r. I półrocze 2010 r.

[kg]

3,1

3,1

3,5

D [kg]

2,7

3,1

3,7

[kg]

0,9

1,1

1

V

z

[%]

29,03

35,48

28,57

A

S

0,44

0

-0,2

Okres

Miesi

ę

czne spo

ż

ycie

ś

wie

ż

ych owoców w gospodarwstwach

domowych Regionu Północnego

x

σ

Zadanie 9.

Czy zaszły zmiany w modelu spo

ż

ycia owoców

ś

wie

ż

ych w Regionie Północnym?

Zadanie 10.

Porówna

ć

dwa województwa pod wzgl

ę

dem wydatków przeznaczonych w roku 2008 na publikacje ksi

ąż

kowe

(poza podr

ę

cznikami szkolnymi) w gospodarstwie domowym.

Parametry Województwo A

Województwo B

[zł]

150

100

D [zł]

170

90

[zł]

17

V

z

[%]

53,33%

A

S

Wydatki na publikacje ksi

ąż

kowe (poza

podr

ę

cznikami szkolnymi) w 2008 r.

x

σ

Zadanie 11.

Porównaj dwa województwa pod wzgl

ę

dem wieku pracowników zatrudnionych w ksi

ę

garniach w dniu 30

listopada 2009 w miejscowo

ś

ci Ksi

ęż

yc. Woj. A: Me= 31 lat, Q

1

= 21 lat, Q= 10 lat. Woj. B: Q

1

= 20 lat, Q

3

= 42

lata, A

s

= -1,28