1

1

Analiza szeregów dynamicznych

1. Opisowo-wska

ź

nikowa analiza szeregów czasowych

y

t

- poziom badanej zmiennej w t-tym momencie lub okresie,

n + 1 okresów, czyli t = 0, 1, 2, …, n.

•przyrosty absolutne;
•wska

ź

niki tempa (przyrosty wzgl

ę

dne);

•indeksy dynamiki;
•

ś

rednia chronologiczna;

•

ś

rednie okresowe tempo wzrostu;

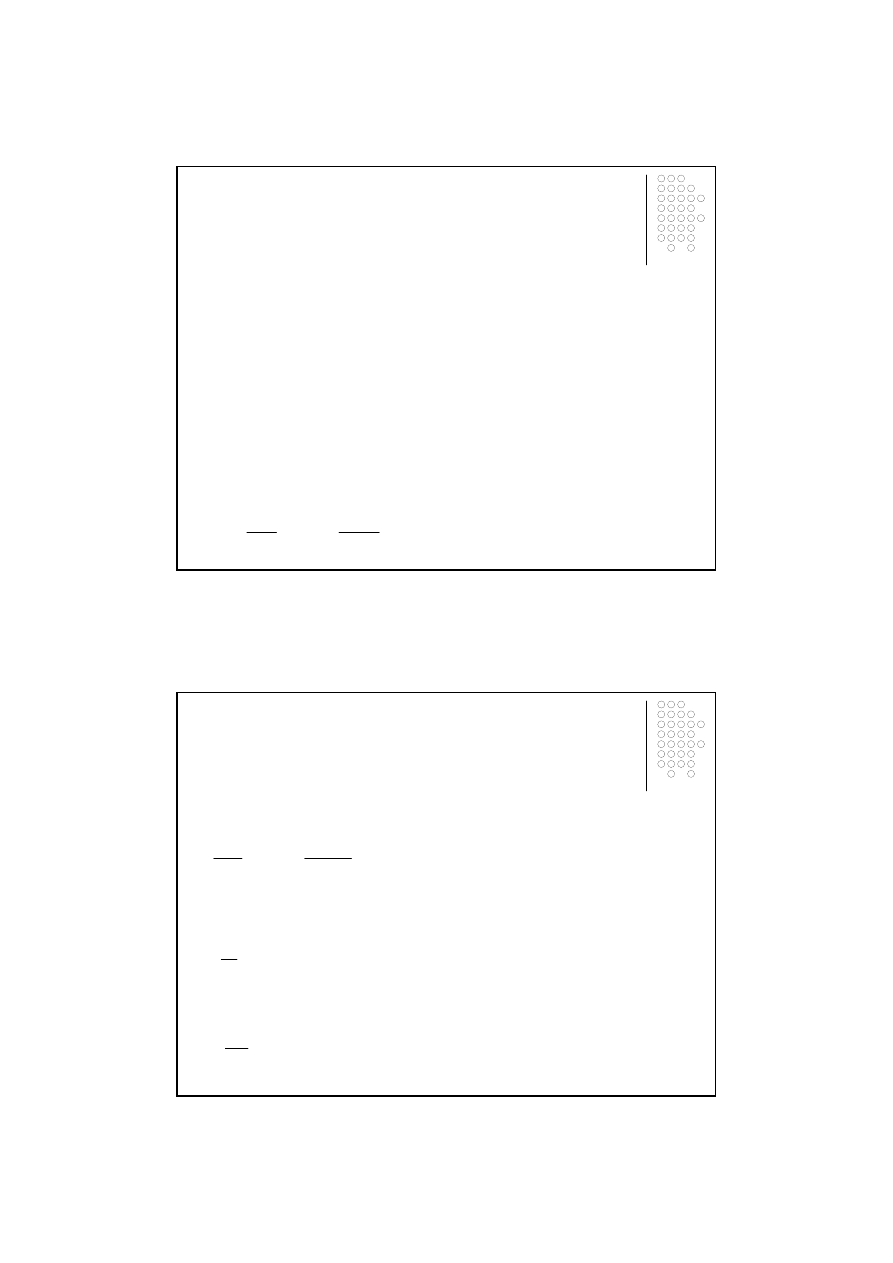
1.1 Przyrost absolutny jednopodstawowy.

dla t = 1, 2, …, n.

Przyrost absolutny jednopodstawowy jest liczb

ą

mianowan

ą

pokazuj

ą

c

ą

, o ile zmienił si

ę

poziom zjawiska

w t-tym momencie (okresie) w porównaniu z momentem (okresem) pocz

ą

tkowym.

1.2 Przyrost absolutny ła

ń

cuchowy.

dla t = 1, 2, …, n.

Jest to liczba mianowana, mówi

ą

ca, o ile zmienił si

ę

poziom zjawiska w jednostce czasu.

1.3 Wska

ź

nik tempa (przyrost wzgl

ę

dny) jednopodstawowy

dla t = 1, 2, …, n.

( )

0

y

y

y

t

j

t

−

=

∆

( )

1

−

−

=

∆

t

t

ł

t

y

y

y

( )

( )

(

)

(

)

%

100

%

100

0

0

0

⋅

−

=

⋅

∆

=

y

y

y

y

y

w

t

j

t

j

t

2

Analiza szeregów dynamicznych

Przyrost wzgl

ę

dny jednopodstawowy mo

ż

e mie

ć

posta

ć

ułamkow

ą

lub procentow

ą

. Wyra

ż

ony w procentach

informuje, o ile zmieni si

ę

poziom zjawiska notowany w t-tym momencie (okresie) w stosunku do poziomu

zjawiska w momencie (okresie) pocz

ą

tkowym analizy (w okresie od pocz

ą

tku badania zjawiska do

momentu/okresu t-tego).

1.4 Wska

ź

nik tempa (przyrost wzgl

ę

dny) ła

ń

cuchowy

dla t = 1, 2, …, n.

Przyrost wzgl

ę

dny ła

ń

cuchowy wyra

ż

ony jest w postaci ułamkowej lub w procentach. W postaci procentowej

informuje, o ile procent zmieni si

ę

poziom zjawiska w jednostce czasu.

1.5 Indeks indywidualny jednopodstawowy

dla t = 1, 2, …, n.

Pokazuje, jak

ą

cz

ęść

poziomu zjawiska w zerowym okresie (momencie) stanowi poziom zjawiska w t-tym

okresie (momencie).

1.6 Indeks indywidualny ła

ń

cuchowy

dla t = 1, 2, …, n.

( )

( )

(

)

(

)

%

100

%

100

1

1

1

⋅

−

=

⋅

∆

=

−

−

−

t

t

t

t

ł

t

ł

t

y

y

y

y

y

w

( )

(

)

%

100

0

⋅

=

y

y

i

t

j

t

( )

(

)

%

100

1

⋅

=

−

t

t

ł

t

y

y

i

( )

( )

(

)

(

)

( )

( )

(

)

(

)

%

100

1

%

100

1

⋅

+

=

⋅

+

=

ł

t

ł

t

j

t

j

t

w

i

w

i

2

3

Analiza szeregów dynamicznych

jednopodsta
wowe y

t

-y

0

ła

ń

cuchowe

y

t

-y

t-1

jednopodstaw

owe

ła

ń

cuchowe

jednopodstawo

we

ła

ń

cuchowe

1991

0

59,0

-

-

-

-

100,00

-

1992

1

61,4

2,4

2,4

4,07

4,07

104,07

104,07

1993

2

62,2

3,2

0,8

5,42

1,30

105,42

101,30

1994

3

70,3

11,3

8,1

19,15

13,02

119,15

113,02

1995

4

89,0

30,0

18,7

50,85

26,60

150,85

126,60

1996

5

115,9

56,9

26,9

96,44

30,22

196,44

130,22

1997

6

146,3

87,3

30,4

147,97

26,23

247,97

126,23

1998

7

174,8

115,8

28,5

196,27

19,48

296,27

119,48

1999

8

215,4

156,4

40,6

265,08

23,23

365,08

123,23

2000

9

261,1

202,1

45,7

342,54

21,22

442,54

121,22

2001

10

304,0

245,0

42,9

415,25

16,43

515,25

116,43

2002

11

342,2

283,2

38,2

480,00

12,57

580,00

112,57

2003

12

366,1

307,1

23,9

520,51

6,98

620,51

106,98

2004

13

381,5

322,5

15,4

546,61

4,21

646,61

104,21

2005

14

388,5

329,5

7,0

558,47

1,83

658,47

101,83

2006

15

391,7

332,7

3,2

563,90

0,82

663,90

100,82

2007

16

408,1

349,1

16,4

591,69

4,19

691,69

104,19

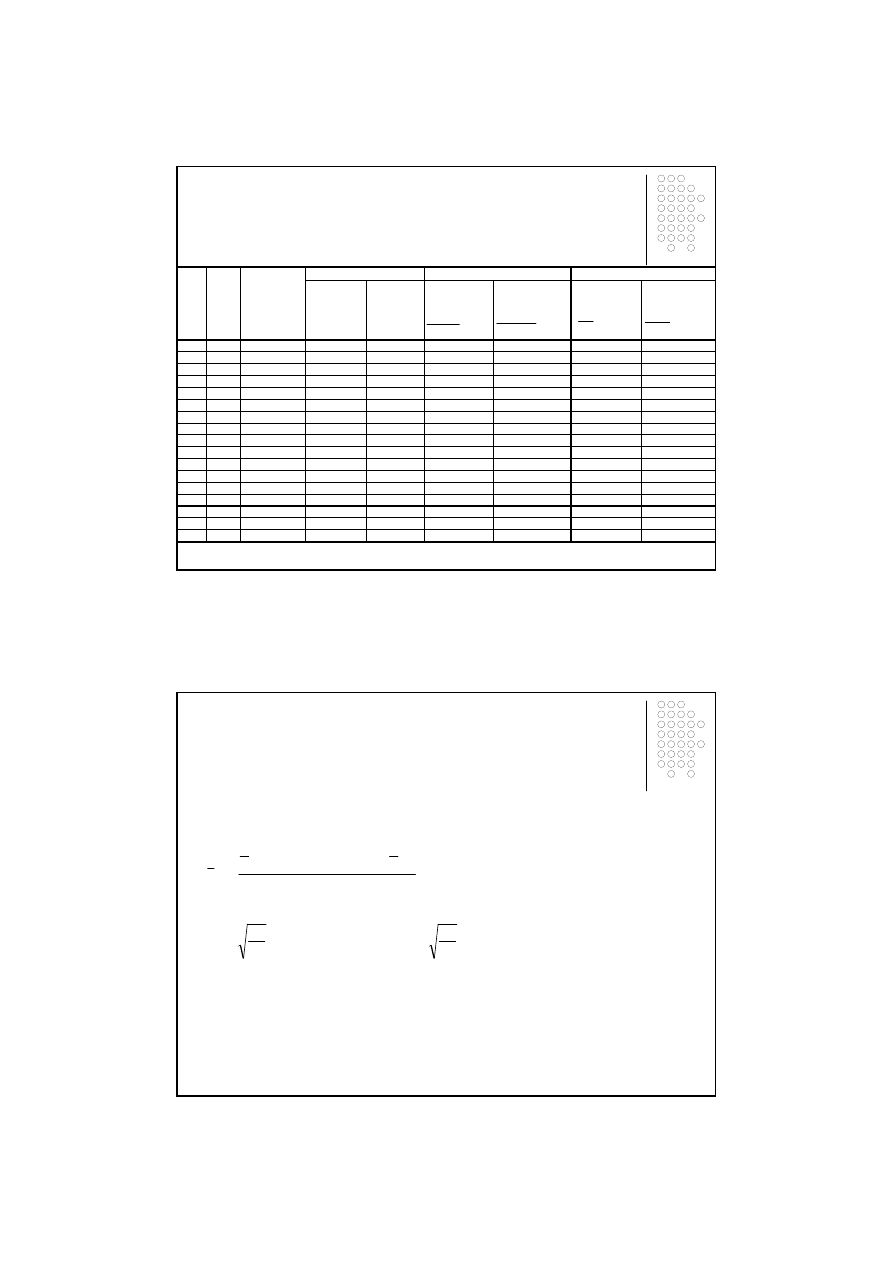
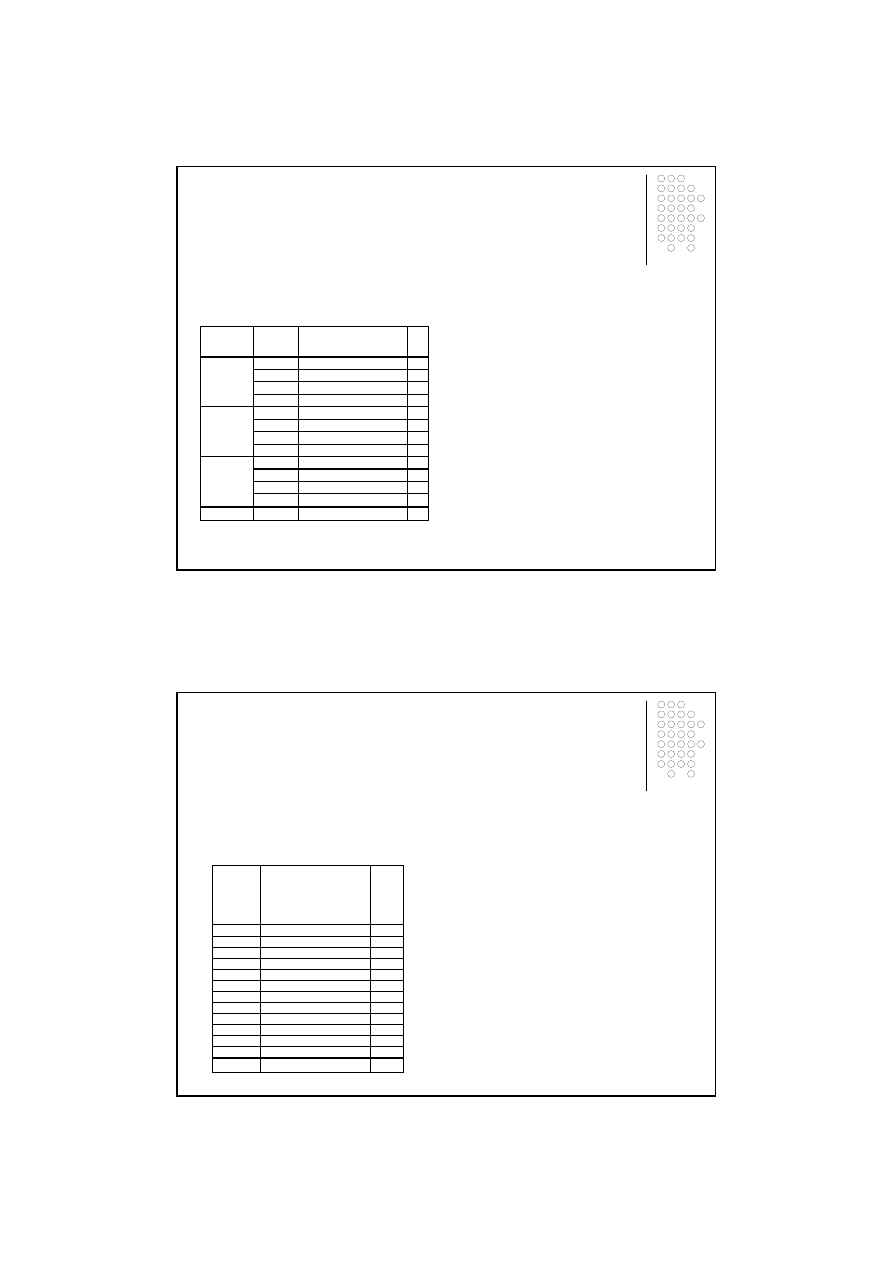
Wska

ź

niki tempa

Indeksy indywidualne

Lata

Okres

t

Liczba

absolwentów

[w tys. osób]

Przyrosty absolutne

%

100

0

0

⋅

−

y

y

y

t

%

100

1

1

⋅

−

−

−

t

t

t

y

y

y

%

100

0

⋅

y

y

t

%

100

1

⋅

−

t

t

y

y

Tablica 1.1

Liczba absolwentów szkół wy

ż

szych w Polsce w latach 1991-2007

Ź

ródło: Rocznik Statystyczny Rzeczypospolitej Polskiej. Wydania z odpowiednich lat, GUS, Warszawa.

4

Analiza szeregów dynamicznych

1.7

Ś

rednia chronologiczna

Obliczaj

ą

c

ś

redni poziom zjawiska w badanym okresie (od momentu/okresu 0 do momentu/okresu n), zaleca

si

ę

stosowanie

ś

redniej w zmodyfikowanej postaci. Modyfikacja zmierza do wyeliminowania potencjalnych

wpływów okresów minionych, a tak

ż

e zarysowuj

ą

cych si

ę

tendencji przyszło

ś

ciowych:

n

y

y

y

y

y

y

n

n

ch

2

1

...

2

1

1

2

1

0

+

+

+

+

+

=

−

1.8

Ś

rednie okresowe tempo wzrostu

lub

Ś

rednie okresowe tempo wzrostu T informuje, o ile procent (o jaki ułamek) zmieniał si

ę

w jednej jednostce

czasu poziom badanego zjawiska.

Ś

rednie okresowe tempo wzrostu mo

ż

e by

ć

wykorzystywane do prognozowania. Musz

ą

jednak zaistnie

ć

okre

ś

lone przesłanki:

•szereg ła

ń

cuchowych wska

ź

ników tempa charakteryzuje si

ę

wzgl

ę

dnie zbli

ż

onymi warto

ś

ciami;

•ła

ń

cuchowe wska

ź

niki tempa nie wykazuj

ą

tendencji;

•horyzont czasowy prognozy jest wzgl

ę

dnie krótki;

•nie s

ą

przewidywane znacz

ą

ce zmiany w otoczeniu.

%

100

1

0

⋅















−

=

n

n

y

y

T

1

0

−

=

n

n

y

y

T

(

)

r

n

r

n

T

y

y

+

=

+

1

3

5

Analiza szeregów dynamicznych

Zadanie 1.

Zaprogramuj wielko

ść

sprzeda

ż

y cementu w Regionie Północnym na rok 2012:

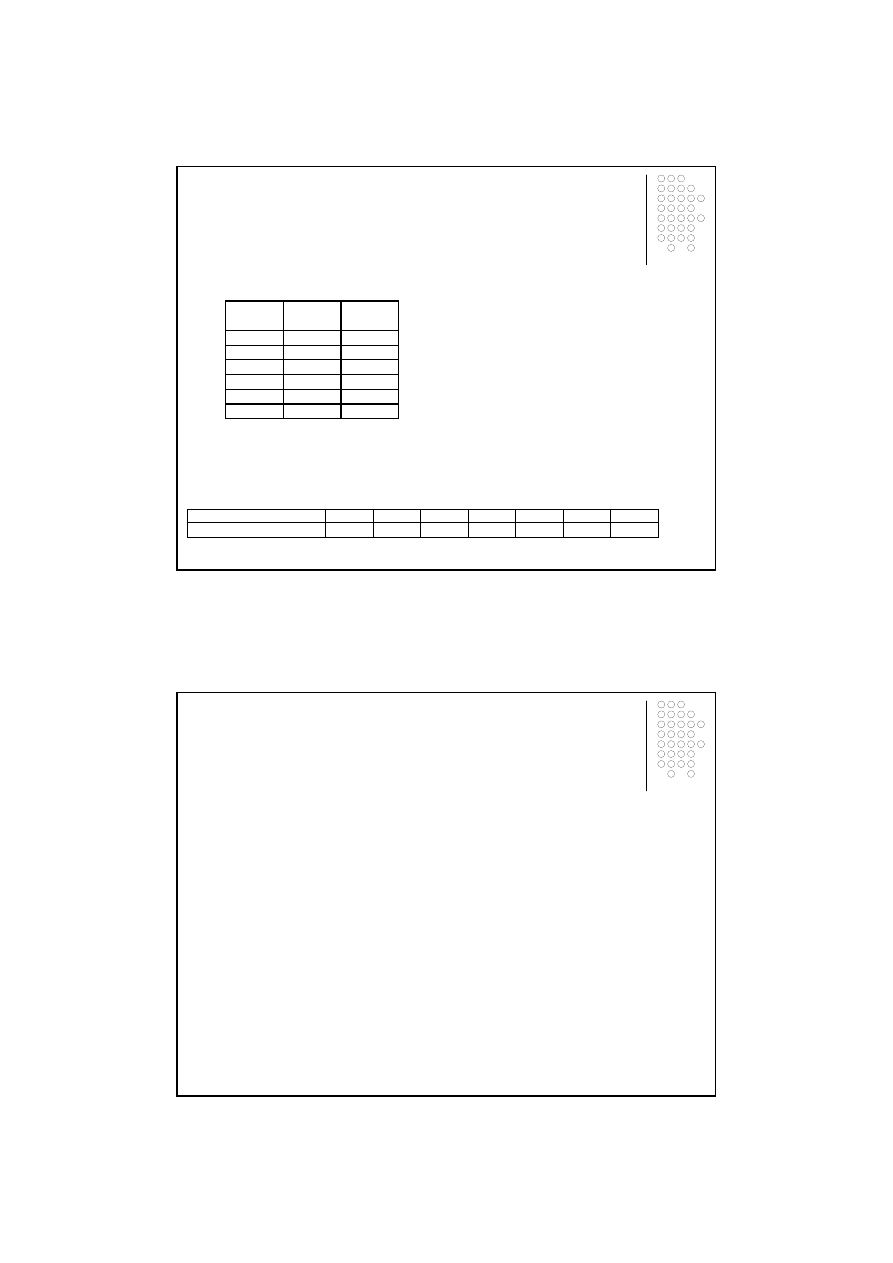
Tablica 1.2

Sprzeda

ż

cementu w Regionie Pn. w latach 2005-2010

Rok

t

Sprzeda

ż

[tys. ton]

2005

0

25,0

2006

1

26,5

2007

2

27,4

2008

3

29,0

2009

4

30,0

2010

5

32,2

Ź

ródło: dane fikcyjne.

Zadanie 2.

Poni

ż

szy szereg dynamiczny przedstawia liczb

ę

absolwentów szkół wy

ż

szych w latach 2000-2006 w Polsce.

Czy mo

ż

na sporz

ą

dzi

ć

prognoz

ę

liczby absolwentów na rok 2009 wykorzystuj

ą

c

ś

rednioroczne tempo zmian?

Odpowied

ź

uzasadnij.

Lata

2000

2001

2002

2003

2004

2005

2006

Liczba absolwentów (w tys.) y

t

261

304

342

366

384

391

394

Ź

ródło: patrz Tablica 1.1.

6

Analiza szeregów dynamicznych

2. Funkcja rozwojowa (trendu).

Funkcja trendu jest specyficzn

ą

funkcja regresji, w której rol

ę

zmiennej niezale

ż

nej pełni czas.

Przesłank

ą

do jej szacowania jest dla badacza posiadanie informacji na temat poziomu interesuj

ą

cego go

zjawiska we wzgl

ę

dnie długim okresie. Dodatkowym warunkiem jest uwidaczniaj

ą

ca si

ę

na podstawie

obserwacji tendencja rozwojowa dotycz

ą

ca badanej zmiennej.

Do oszacowania funkcji rozwojowej potrzebne jest zatem n informacji o poziomie zmiennej Y w kolejnych
momentach (okresach), czyli szereg wielko

ś

ci empirycznych (y

t

): y

1

, y

2

, y

3

,…, y

n

.

Na podstawie szeregu empirycznego szacuje si

ę

funkcj

ę

trendu: (rysunek na tablicy).

Funkcja trendu mo

ż

e mie

ć

posta

ć

liniow

ą

b

ą

d

ź

krzywoliniow

ą

. Jej parametry szacuje si

ę

metod

ą

najmniejszych kwadratów.
Wybór najbardziej wła

ś

ciwej, trafnej funkcji spo

ś

ród oszacowanych odbywa si

ę

na podstawie kryterium

najlepszego dopasowania warto

ś

ci teoretycznych zmiennej Y, obliczonych na podstawie oszacowanej

funkcji, do wielko

ś

ci empirycznych.

( )

t

f

y

=

ˆ

4

7

Analiza szeregów dynamicznych

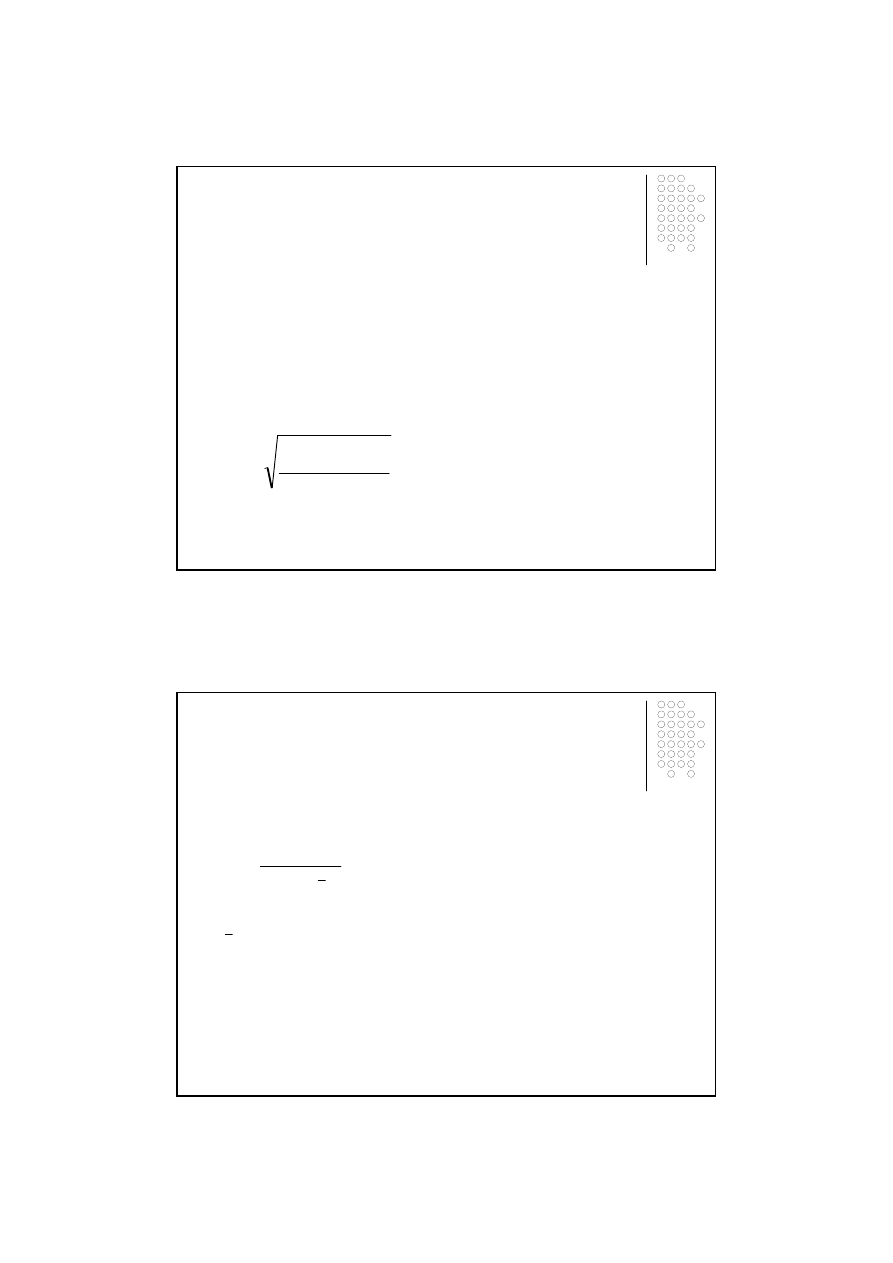
2.1 Liniowa funkcja trendu

Liniowa funkcja trendu ma posta

ć

:

Parametry liniowej funkcji trendu (a,b) szacuje si

ę

, rozwi

ą

zuj

ą

c układ równa

ń

:

Parametr b informuje, o ile

ś

rednio rzecz bior

ą

c zmienia si

ę

warto

ść

badanego zjawiska (zmiennej) w

jednostce czasu.

Po oszacowaniu parametrów liniowej funkcji trendu post

ę

puje si

ę

analogicznie, jak w przypadku linowej

funkcji regresji omówionej podczas zaj

ęć

dotycz

ą

cych analizy współzale

ż

no

ś

ci.

Szacuje si

ę

zatem

ś

redni bł

ą

d szacunku, który ma posta

ć

:

- warto

ść

empiryczna, t = 1, 2, …, n,

- warto

ść

teoretyczna, t = 1, 2, …, n,

- liczba szacowanych parametrów (w przypadku funkcji liniowej 2)

bt

a

y

+

=

ˆ













+

=

⋅

+

=

∑

∑

∑

∑

∑

=

=

=

=

=

n

t

n

t

n

t

t

n

t

n

t

t

t

b

t

a

t

y

t

b

na

y

1

2

1

1

1

1

(

)

k

y

y

gdzie

k

n

y

y

S

t

t

n

t

t

t

y

ˆ

ˆ

2

1

−

−

=

∑

=

8

Analiza szeregów dynamicznych

Ś

redni bł

ą

d informuje, o ile przeci

ę

tnie rzecz bior

ą

c warto

ś

ci zmiennej odchylaj

ą

si

ę

„in plus” lub „in minus”

od oszacowanej funkcji trendu.

Dobro

ć

funkcji oznaczaj

ą

ca dopasowanie funkcji do warto

ś

ci empirycznych oblicza si

ę

wykorzystuj

ą

c

współczynnik zbie

ż

no

ś

ci i współczynnik determinacji R

2

:

-

ś

redni poziom badanego zjawiska w analizowanym okresie

R

2

= 1 -

lub R

2

= 100% -

Współczynnik determinacji, analogicznie jak w przypadku funkcji regresji, informuje, w jakim stopniu
zmienno

ść

badanej zmiennej Y obja

ś

nia szacowana funkcja trendu, za

ś

współczynnik , w jakim stopniu

na zmienno

ść

zmiennej Y wpływa czynnik losowy.

2

Φ

(

)

(

)

(

)

y

gdzie

y

y

y

y

n

t

t

n

t

t

t

%

100

ˆ

1

2

1

2

2

⋅

−

−

=

Φ

∑

∑

=

=

2

Φ

2

Φ

2

Φ

5

9

Analiza szeregów dynamicznych

Zadanie 2.1
Na podstawie danych zawartych w poni

ż

szej tabeli, oszacuj funkcj

ę

trendu sprzeda

ż

y ekspresów

ci

ś

nieniowych do kawy w Regionie Północnym. Oszacuj dobro

ć

funkcji,

ś

redni bł

ą

d szacunku i zaprognozuj

sprzeda

ż

ekspresów w roku 2011.

Tablica 2.1

Kwartalna wielko

ść

sprzeda

ż

y ekspresów ci

ś

nieniowych do kawy w Regionie Północnym w latach 2008-2010

Ź

ródło: dane fikcyjne.

Lata

Kwartały

Wielko

ść

sprzeda

ż

y w

tys. sztuk y

t

t

I

11,3

1

II

12,8

2

III

12,9

3

IV

13,8

4

I

14,9

5

II

15,1

6

III

16,2

7

IV

16,8

8

I

17,3

9

II

18,5

10

III

19,6

11

IV

21,3

12

Σ

190,5

78

2008

2009

2010

10

Analiza szeregów dynamicznych

Zadanie 2.2
Na podstawie danych zawartych w poni

ż

szej tabeli, oszacuj funkcj

ę

trendu kosztów paliwa zu

ż

ywanego przez

samochody słu

ż

bowe w dziale sprzeda

ż

y firmy „Odkurzacze”. Oce

ń

jej dobro

ć

, oblicz

ś

redni bł

ą

d szacunku i

zaprognozuj koszty paliwa dla roku 2012:

Tablica 2.2

Roczne koszty zu

ż

ycia paliwa zu

ż

ywanego przez samochody słu

ż

bowe w dziale sprzeda

ż

y firmy „Odkurzacze”

w latach 1999-2010

Ź

ródło: dane fikcyjne.

Lata

Koszty paliwa

zu

ż

ywanego przez

samochody słu

ż

bowe w

dziale sprzeda

ż

y [tys.

zł] y

t

t

1999

225

1

2000

227

2

2001

228

3

2002

239

4

2003

238

5

2004

240

6

2005

242

7

2006

240

8

2007

248

9

2008

249

10

2009

252

11

2010

254

12

Σ

2882

78