
Politechnika Warszawska
Instytut Automatyki i Robotyki
Prof. dr hab. inż. Jan Maciej Kościelny
PODSTAWY AUTOMATYKI
PODSTAWY AUTOMATYKI
część 3
P
odstawowe elementy liniowe

2
Założenia
Elementy mechaniczne:
•
występuje jedynie tarcie lepkie (wiskotyczne), a nie tarcie suche
- siła tarcia jest proporcjonalna do prędkości
Wiele elementów automatyki można traktować jako liniowe, jeżeli:
•
ograniczy się zakres ich pracy
•
przyjmie następujące założenia upraszczające:
- siła tarcia jest proporcjonalna do prędkości
•
sztywności elementów sprężystych są stałe
Elementy płynowe:
•
opór przepływu jest stały
- natężenie przepływu jest proporcjonalne do różnicy ciśnień
•
współczynnik ściśliwości płynu jest stały
Elementy elektryczne:
•
rezystancje, indukcyjności i pojemności są stałe i niezależne od
przepływającego prądu i napięcia

3
Ze względu na własności dynamiczne:
• bezinercyjne (proporcjonalne)
• inercyjne
• całkujące
• różniczkujące (idealne i rzeczywiste)
• oscylacyjne
• opóźniające
Podział elementów liniowych
Elementy charakteryzują:
Właściwości statyczne:
charakterystyka statyczna y = f(u)
Właściwości dynamiczne:
równanie różniczkowe
transmitancja operatorowa
odpowiedź na zakłócenie skokowe
charakterystyki częstotliwościowe
4
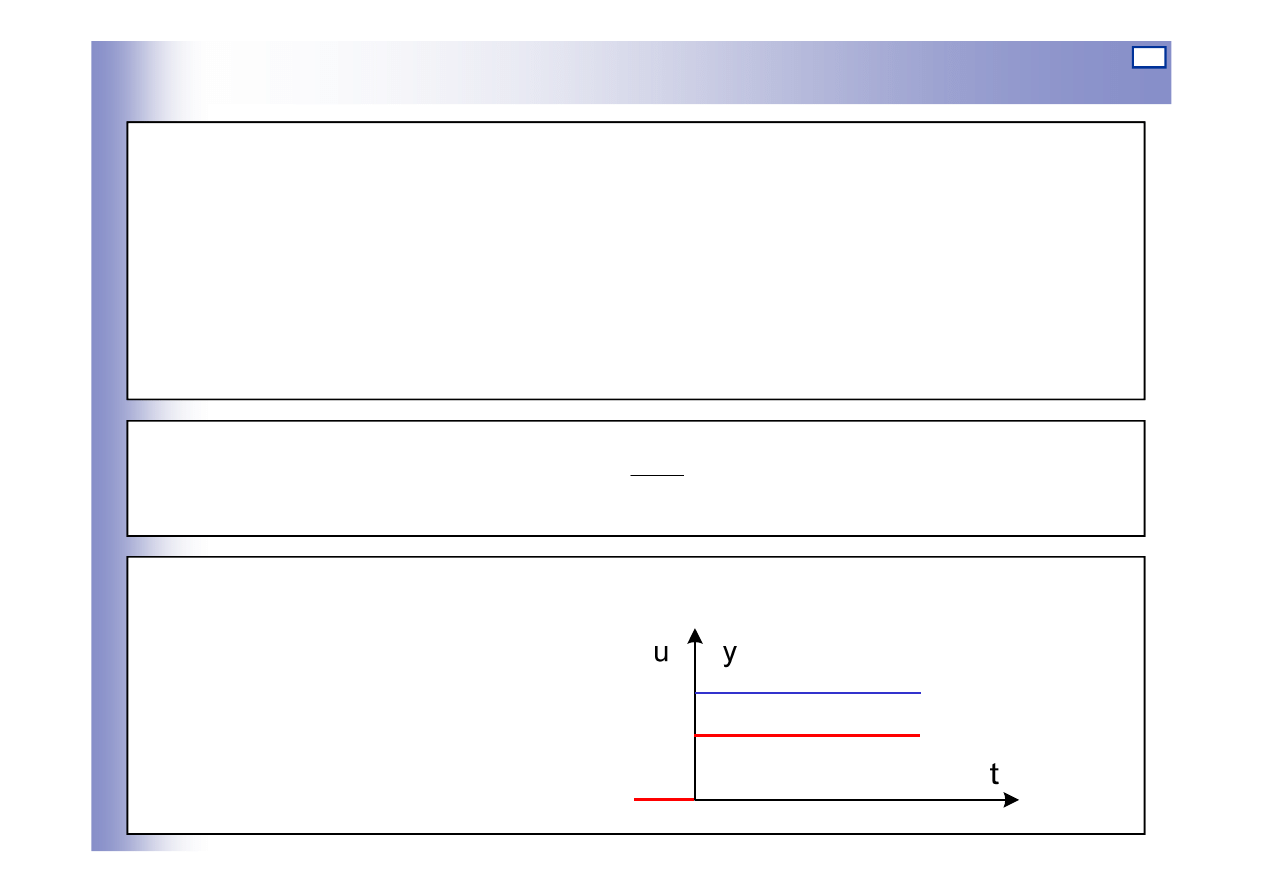
Elementy bezinercyjne (proporcjonalne)
Równanie różniczkowe (równe charakterystyce statycznej y=ku)
y – wielkość wyjściowa
u – wielkość wejściowa
k – współczynnik proporcjonalności (wzmocnienie)
Transmitancja
s
y )
(
)
(
)
(
t
ku
t
y
=
Transmitancja
k
s
u
s
y
s
G
=
=
)
(
)
(
)
(
Odpowiedź na wymuszenie skokowe:
st
ku
t
t
y
)
(
1
)
(
=
st
u
t
t
u
)
(
1
)
(
=
y (t)
u(t)
u
st
ku
st
5
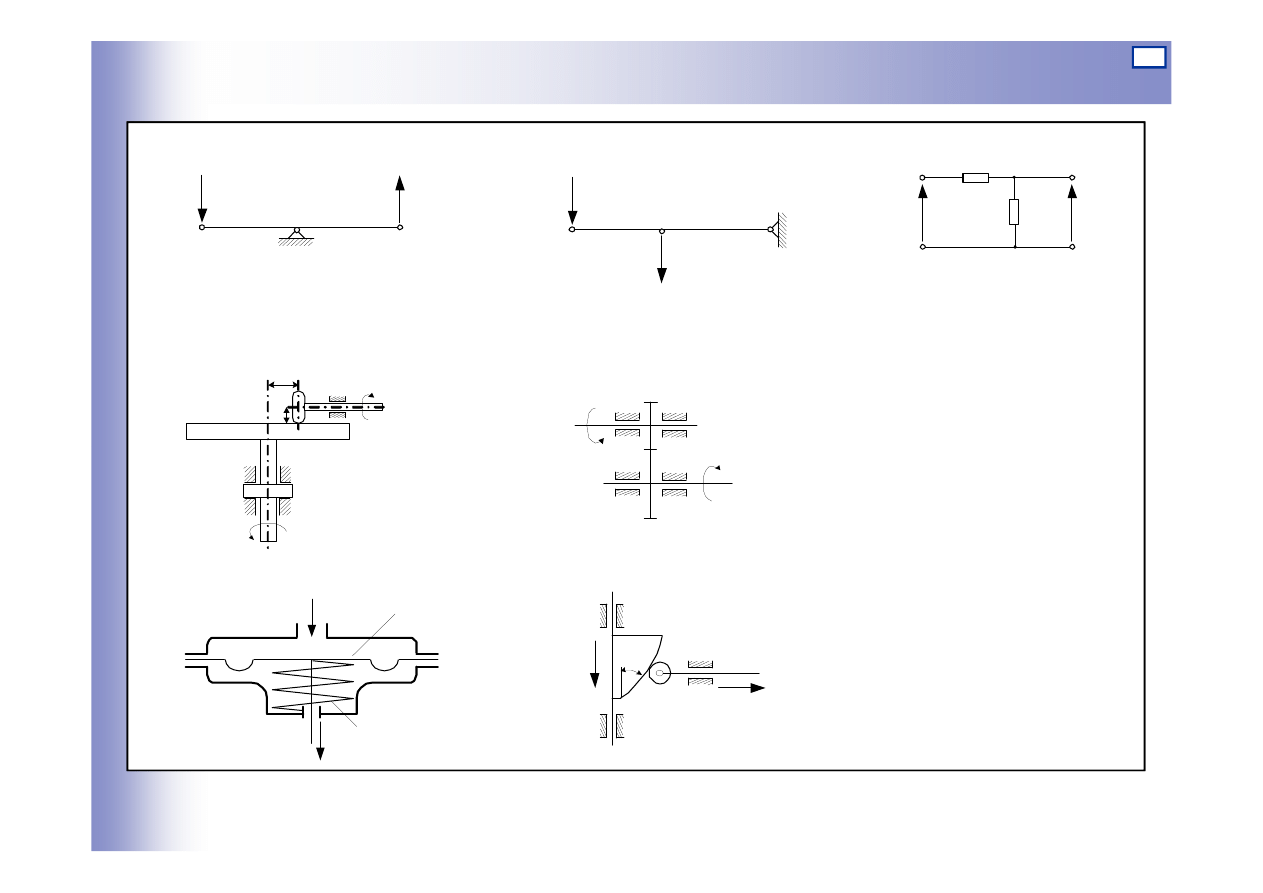
Elementy bezinercyjne – przykłady
a b
u
y
F
u
F
y
a)
a b
u
y
F
u
F
y
b)
u
2
u
1
R
1
R
2
c)
d)
r
x
?
2
n
1
z
1
e)
a, b) dźwignia
?
1
1
n
2
z
2
p
A
c
y
f)
x
y
?
g)
c) dzielnik napięcia
d) przekładnia cierna
e) przekładnia zębata
f) siłownik
pneumatyczny
g) mechanizm
krzywkowy

6
Elementy inercyjne pierwszego rzędu
Równanie różniczkowe
k – współczynnik proporcjonalności (wzmocnienie)
T – stała czasowa
Transmitancja
ku
y
dt
dy
T
=
+
Transmitancja
Odpowiedź na wymuszenie skokowe
1
)
(
)
(
)
(
+
=
=
Ts
k
s
u
s
y
s
G
)
1
(
)
(
T
t
st
e
ku
t
y
−
−
=
7
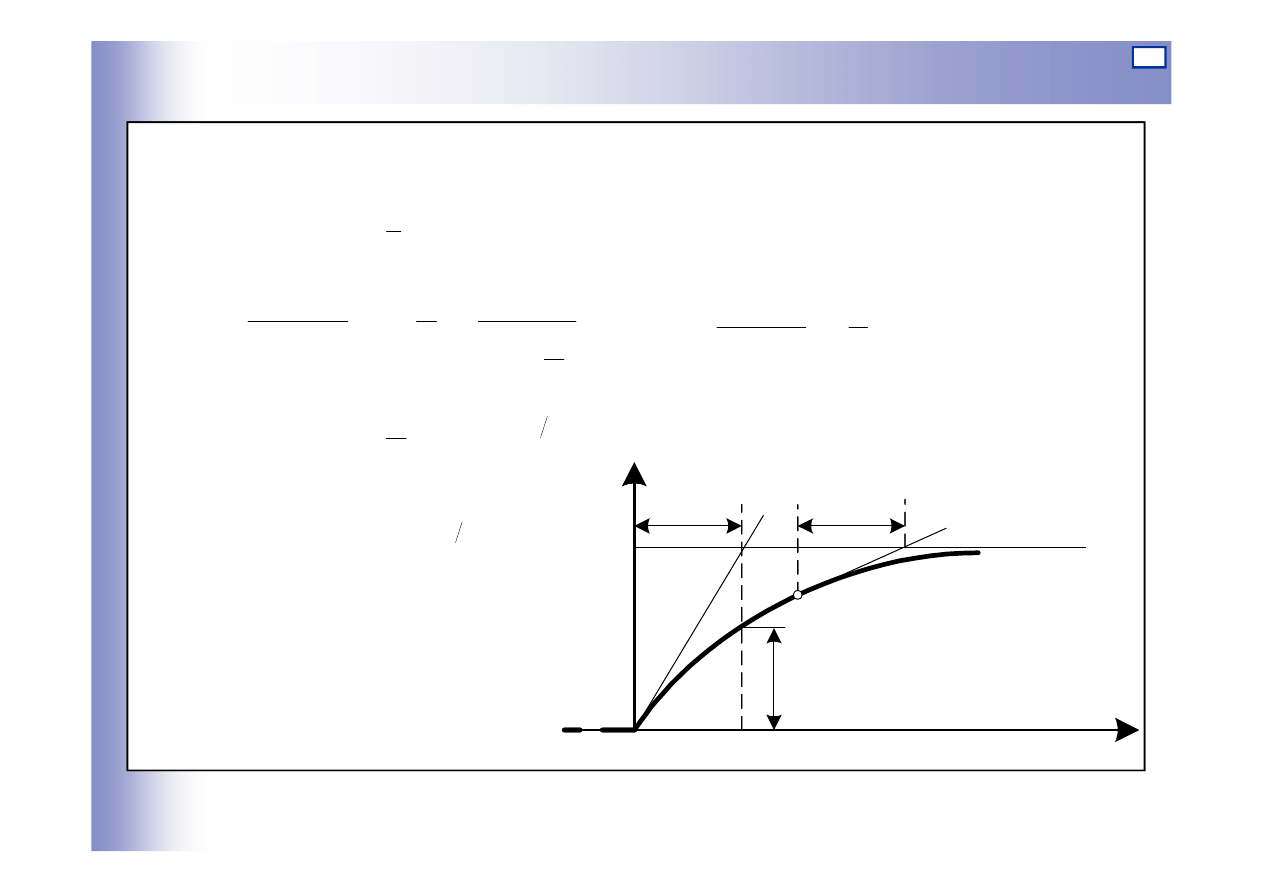
Elementy inercyjne pierwszego rzędu
Odpowiedź na wymuszenie skokowe
st
u
s
s
u
1
)
(
=
)
1
(
1
)
1
(
)
(
T
s
s
u
T
k
u
Ts
s
k
s
y
st
st
+
=
+
=
)
1
(
)]
(
[
)
(
1
T
t
st
e
T
u
T
k
s
y
L
t
y
−
−
−
=
=
)
1
(
1
)
(
1
1
at
e
a
a
s
s
L
−
−
−
=
+
y
t
ku
st
T
T
0,632ku
st
)
1
(
)]
(
[
)
(
st
e
T
u
T
s
y
L
t
y
−
=
=
)
1
(
)
(
T
t
st
e
ku
t
y
−
−
=
8
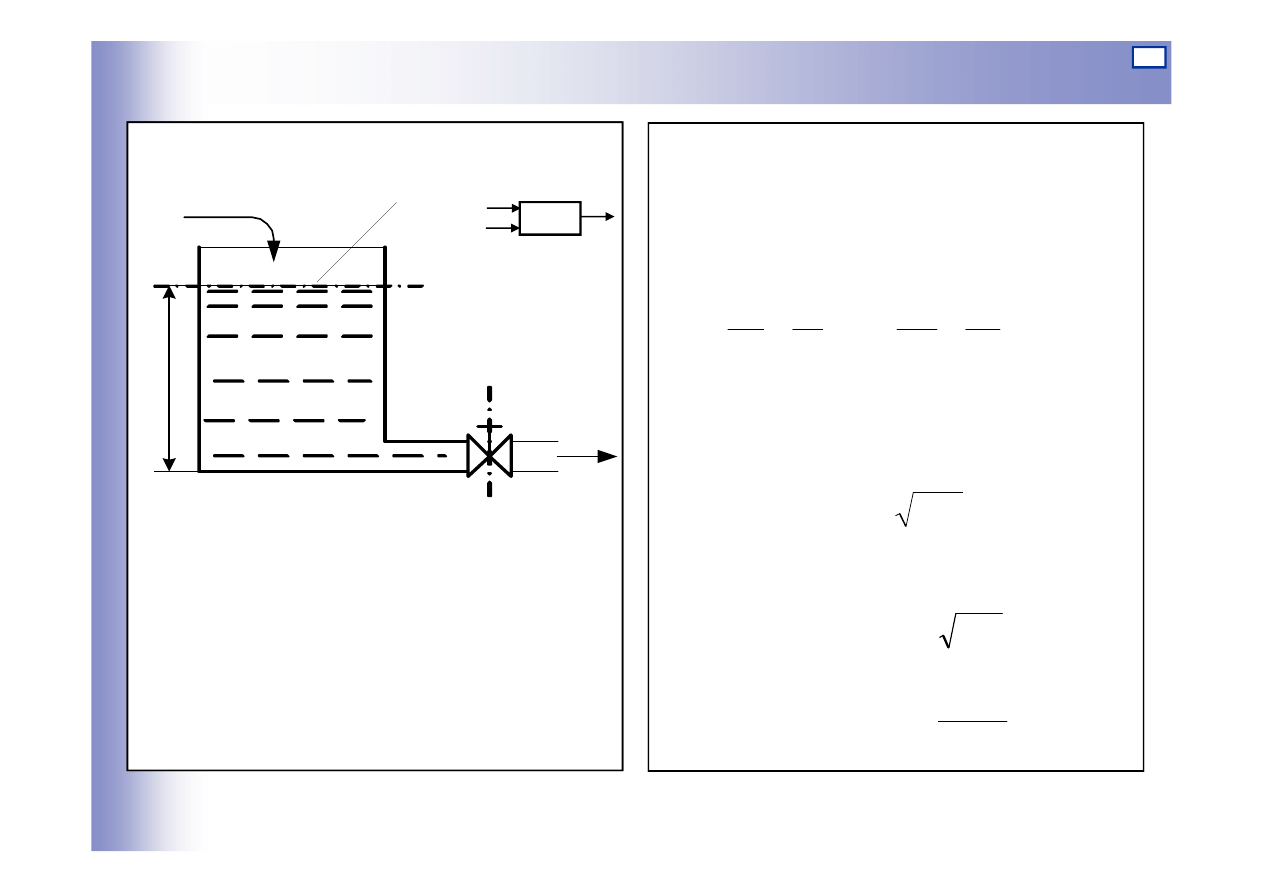
Elementy inercyjne pierwszego rzędu
Przykład
Q
1
A
1
Q
2
2
1
h
f
Warunek stanu ustalonego
Z równania Bernoulliego
zakładając v
1
=0 oraz p
1
=p
2
20
10
Q
Q
=
0
2
2
2
2
2
1
2
1
+
+
=
+
+
γ
γ
p
g
v
h
p
g
v
h
Q
1
f
Wejścia
Q
1
– natężenie przepływu cieczy
f – powierzchnia przekroju zaworu
Wyjście
h – poziom cieczy w zbiorniku
2
2
1
1
2
otrzymujemy:
Z równania ciągłości:
Otrzymujemy:
gh
v
2
2
=
gh
f
fv
Q
2
2
2
=
=
2
0
2
10
0
2gf
Q
h
=
9
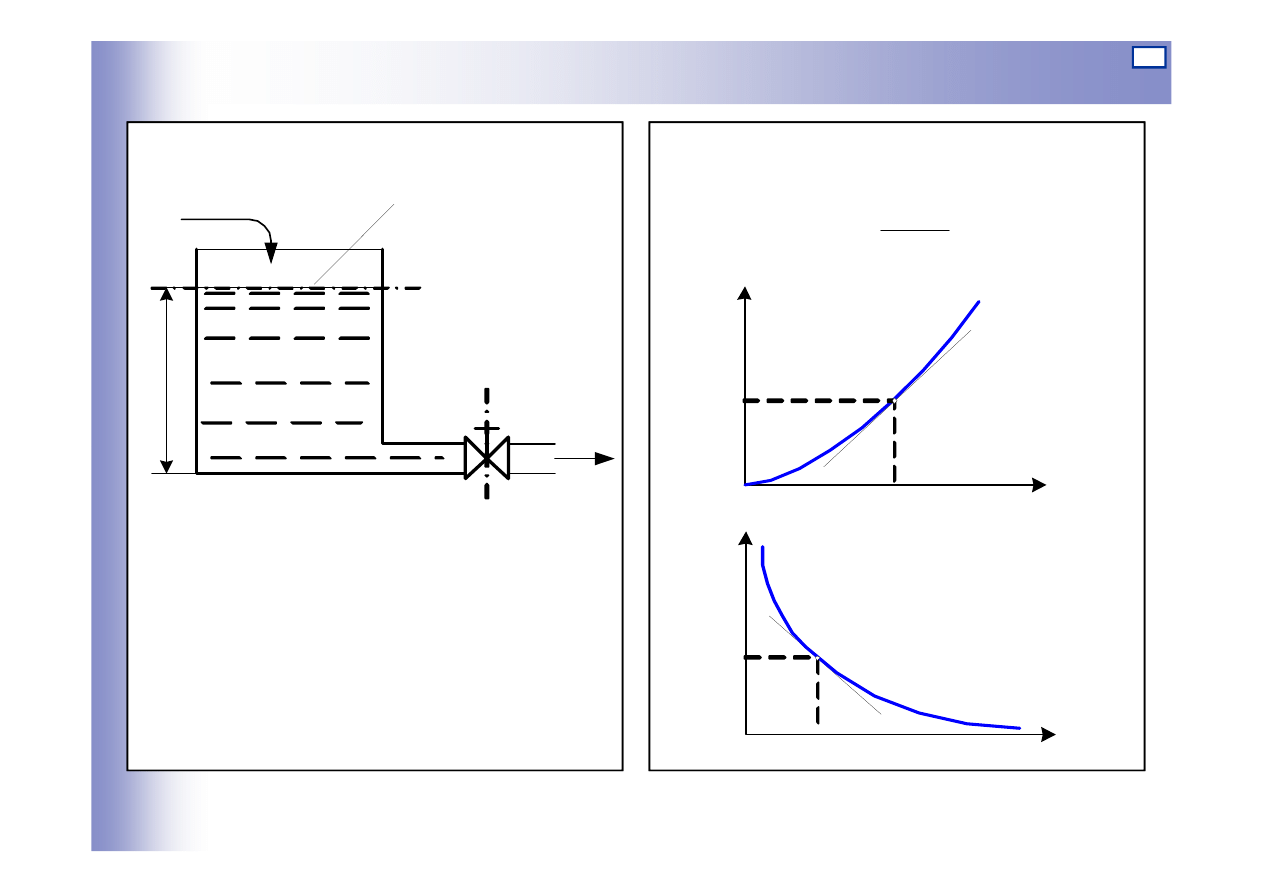
Elementy inercyjne pierwszego rzędu
Przykład
Q
1
A
1
Q
2
2
1
h
f
Charakterystyka statyczna
2
0
2
10
0
2gf
Q
h
=
h
0
h
n
f
0
=const
Wejścia
Q
1
– natężenie przepływu cieczy
f – powierzchnia przekroju zaworu
Wyjście
h – poziom cieczy w zbiorniku
Q
2
2
Q
1n
Q
10
h
0
h
n
f
n
f
0
Q
10
=const
10
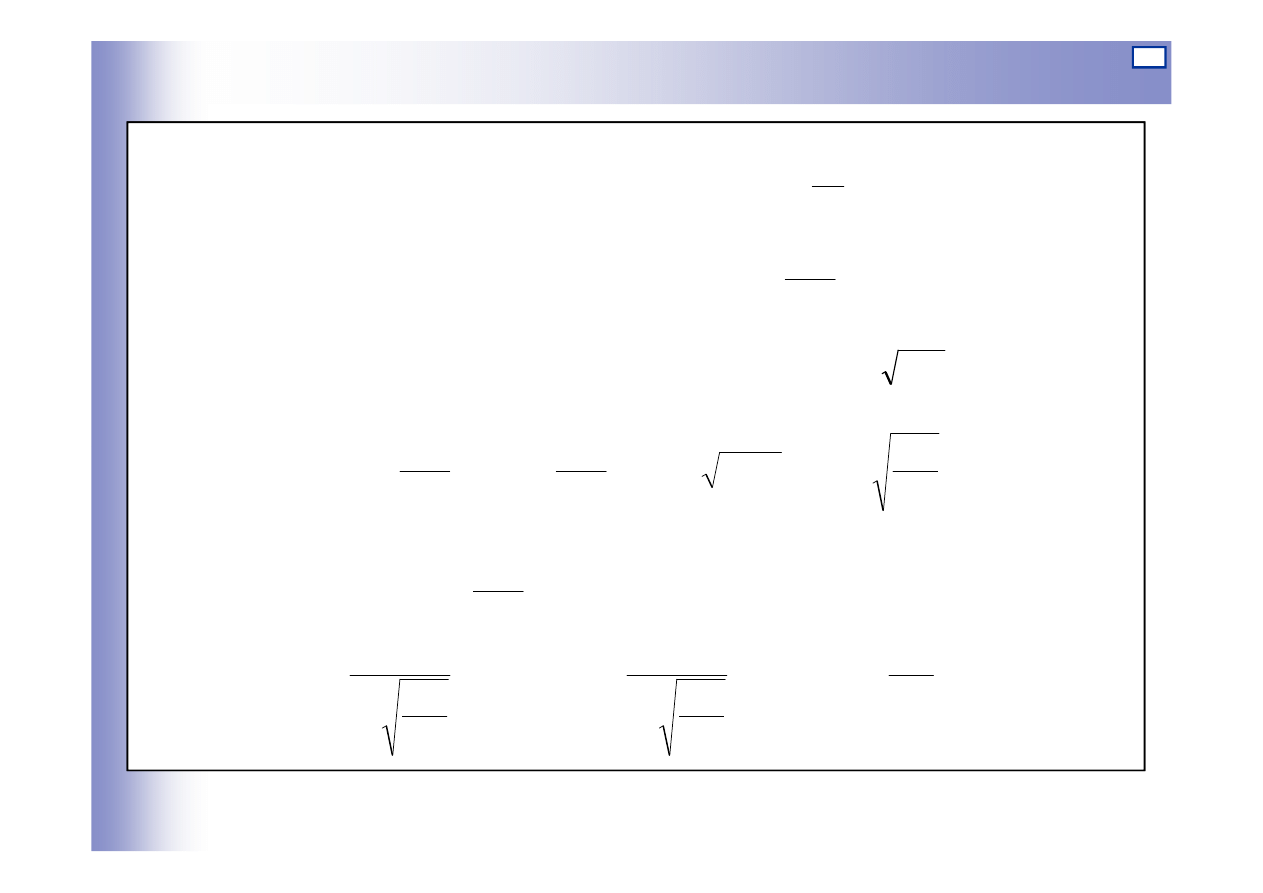
W stanie nieustalonym
linearyzacja dla punktu pracy h
n
, Q
1n
, f
n
Przyrost
∆Q
2
zastępujemy różniczką zupełną
Elementy inercyjne pierwszego rzędu
2
1
Q
Q
dt
dh
A
−
=
2
1
Q
Q
dt
h
d
A
∆
−
∆
=
∆
g
Q
Q
∂
∂
gh
f
Q
2
2
=
otrzymujemy
gdzie:
h
h
g
f
f
gh
h
h
Q
f
f
Q
Q
n
n
n
n
n
∆
+
∆
=
∆
∂
∂
+
∆
∂
∂
=
∆
2
2
2
2
2
f
k
Q
k
h
dt
h
d
T
∆
−
∆
=
∆
+
∆
2
1
1
n
n
h
g
f
A
T
2
=
n
n
h
g
f
k
2
1
1
=
n
n
f
h
k
2
2
=
11
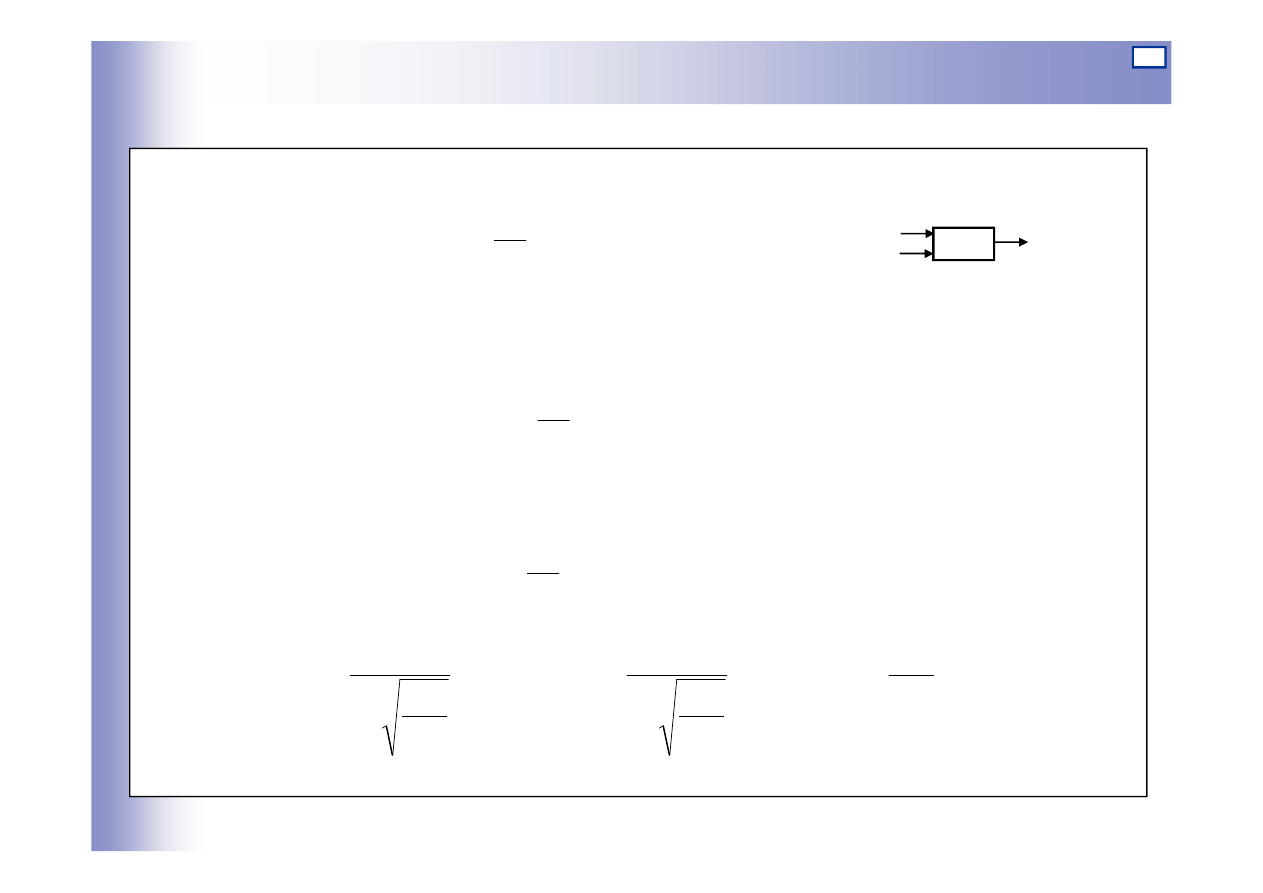
Opuszczając znaki
∆
W przypadku, kiedy f
0
=const (f=0)
Elementy inercyjne pierwszego rzędu
f
k
Q
k
h
dt
dh
T
∆
−
=
+
2
1
1
1
1
Q
k
h
dt
dh
T
=
+
h
Q
1
f
kiedy Q
10
=const (Q
1
=0)
gdzie:
n
n
h
g
f
A
T
2
=
n
n
h
g
f
k
2
1
1
=
n
n
f
h
k
2
2
=
dt
f
k
h
dt
dh
T
∆
−
=
+
2
12
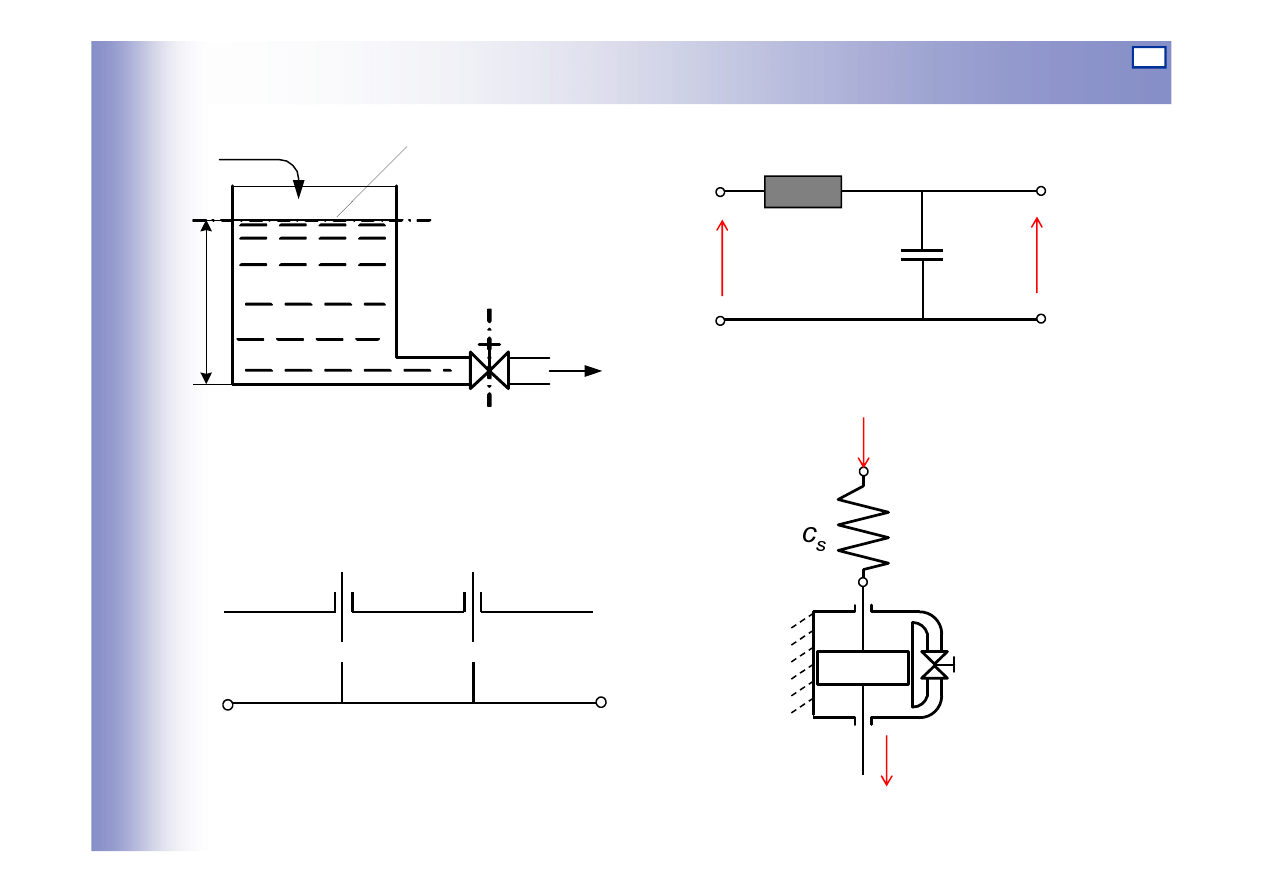
Elementy inercyjne – przykłady
Q
1
A
1
Q
2
2
2
1
h
f
U
1
U
2
R
C
Czwórnik RC
Zbiornik z wypływem swobodnym
u
u=Q
1
y=Q
2
u=u
1
y=u
2
p
1
p
2
p
k
f
1
f
2
Kaskada pneumatyczna
Zbiornik z wypływem swobodnym
y
u
Tłumik hydrauliczny
y=p
k
u
3
=f
1
u
1
=p
1
u
2
=p
2
u
4
=f
2

13
Elementy całkujące
Równanie różniczkowe:
po scałkowaniu, przy zerowych warunkach początkowych:
ku
dt
dy
=
∫
=
t
udt
k
y
Transmitancja:
∫
=
udt
k
y
0
s
k
s
u
s
y
s
G
=
=
)
(
)
(
)
(
14
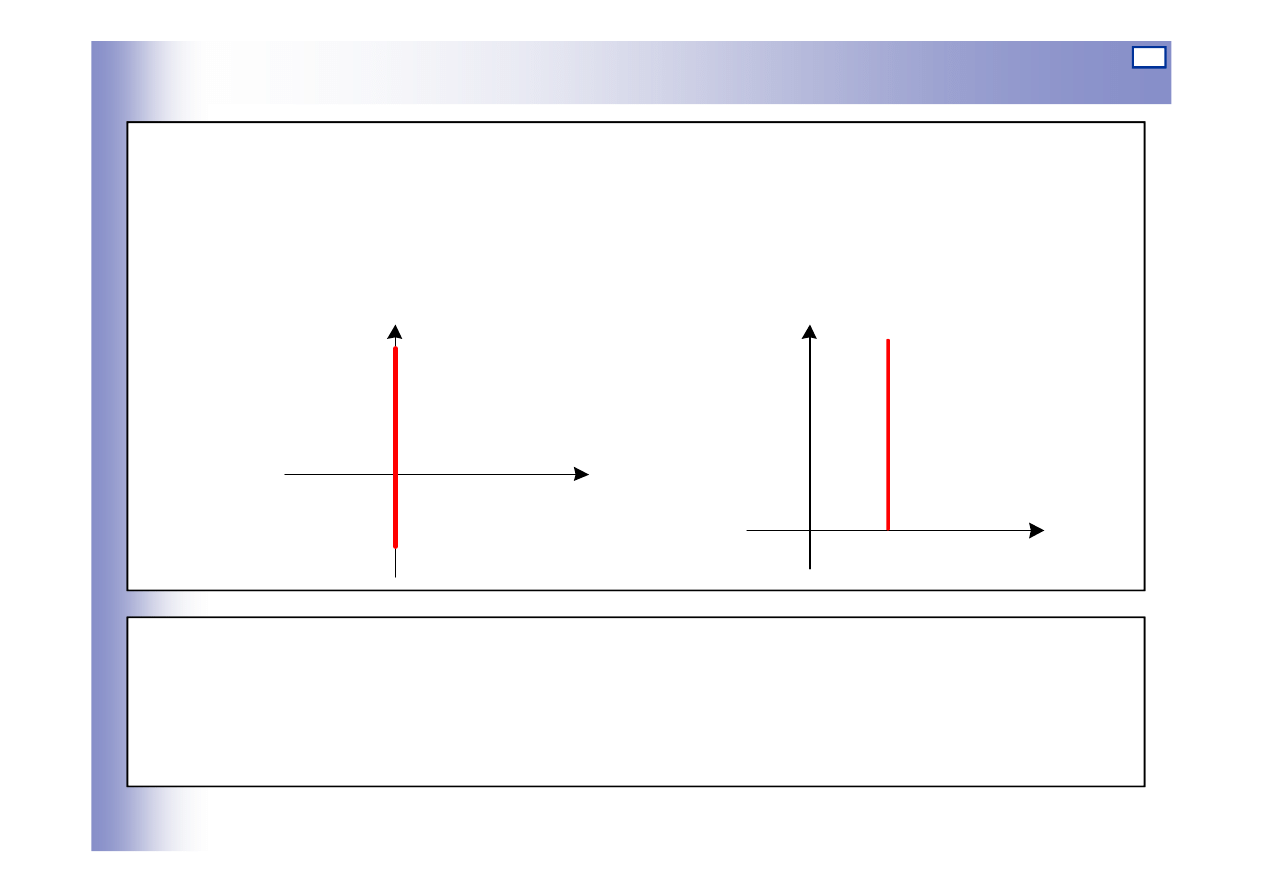
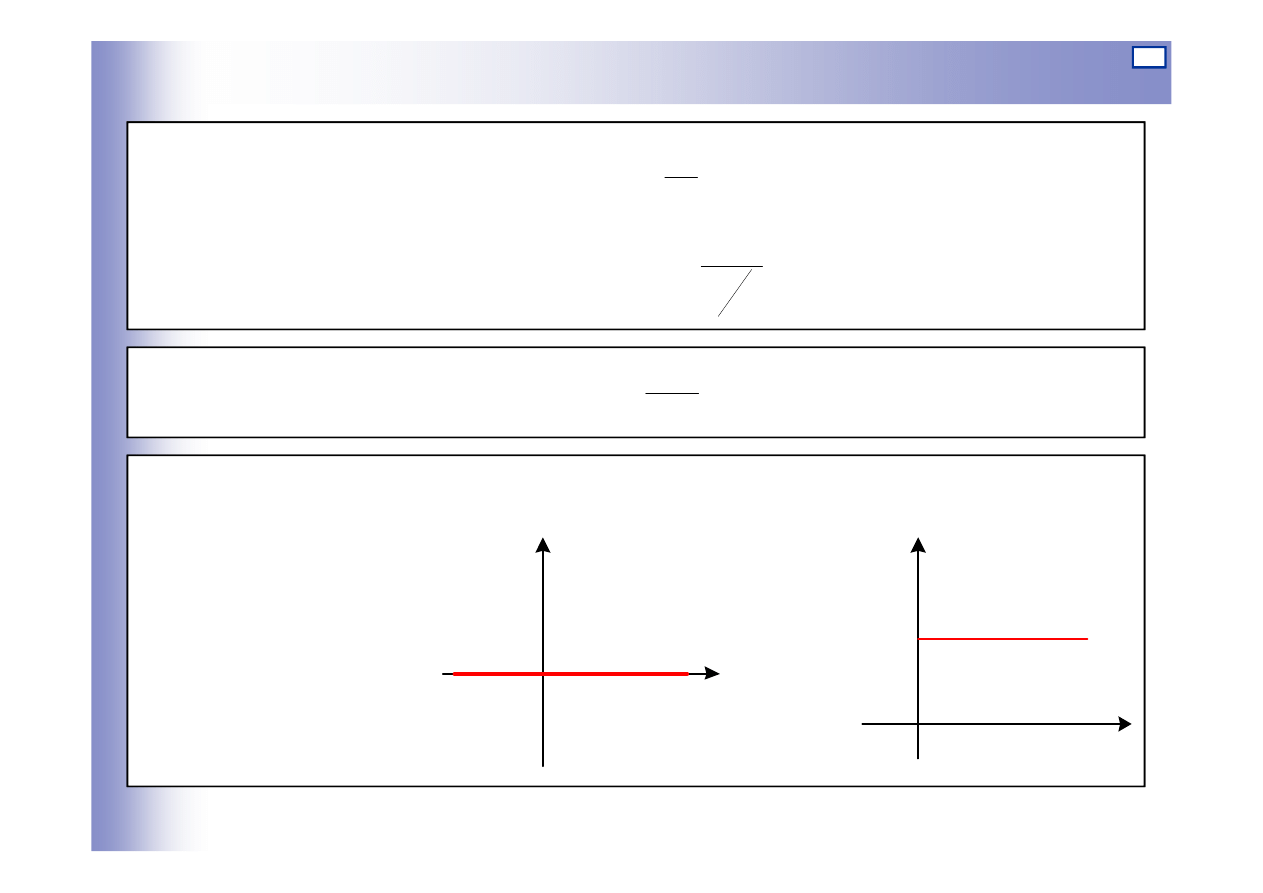
Elementy całkujące
Charakterystyka statyczna
we współrzędnych odchyłek a) i wartości absolutnych b)
0
=
u
y
y
0
a)
b)
Odpowiedź na wymuszenie skokowe
u
u
0
0
u
n
t
ku
s
y
L
t
y
st
=
=
−
)]
(
[
)
(
1
15
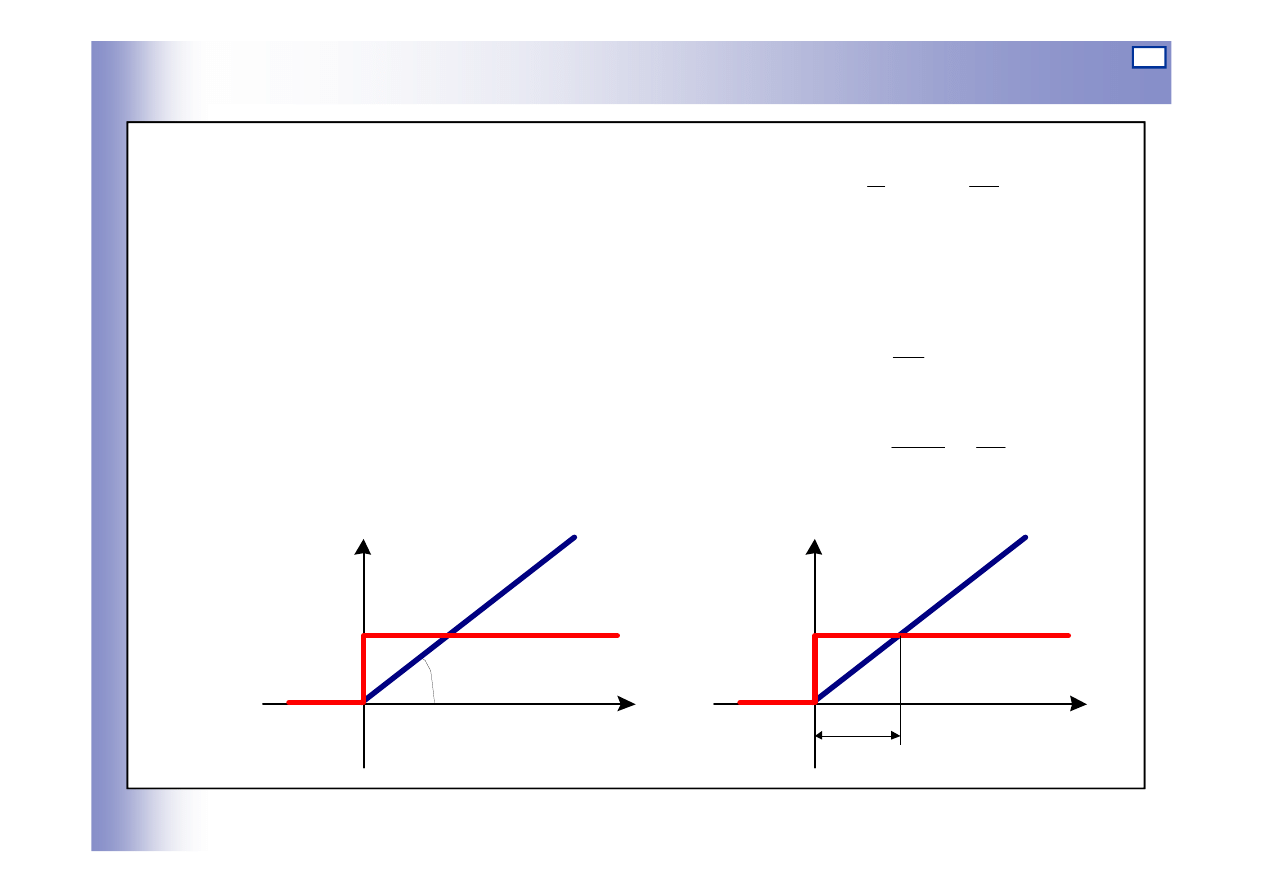
Elementy całkujące
Odpowiedź na wymuszenie skokowe
kiedy wejście i wyjście
są sygnałami jednoimiennymi, to k = 1/T
gdzie T jest stałą czasową akcji całkującej
– stałą całkowania
st
u
s
k
s
u
s
k
s
y
2
)
(
)
(
=
=
t
ku
s
y
L
t
y
st
=
=
−
)]
(
[
)
(
1
u
dt
dy
T
=
s
y
s
G
1
)
(
)
(
=
=
– stałą całkowania
a)
b)
t
u y
u
st
y(t)
u(t)
arctg ku
st
t
u y
u
st
y(t)
u(t)
T
Ts
s
u
s
G
)
(
)
(
=
=
16
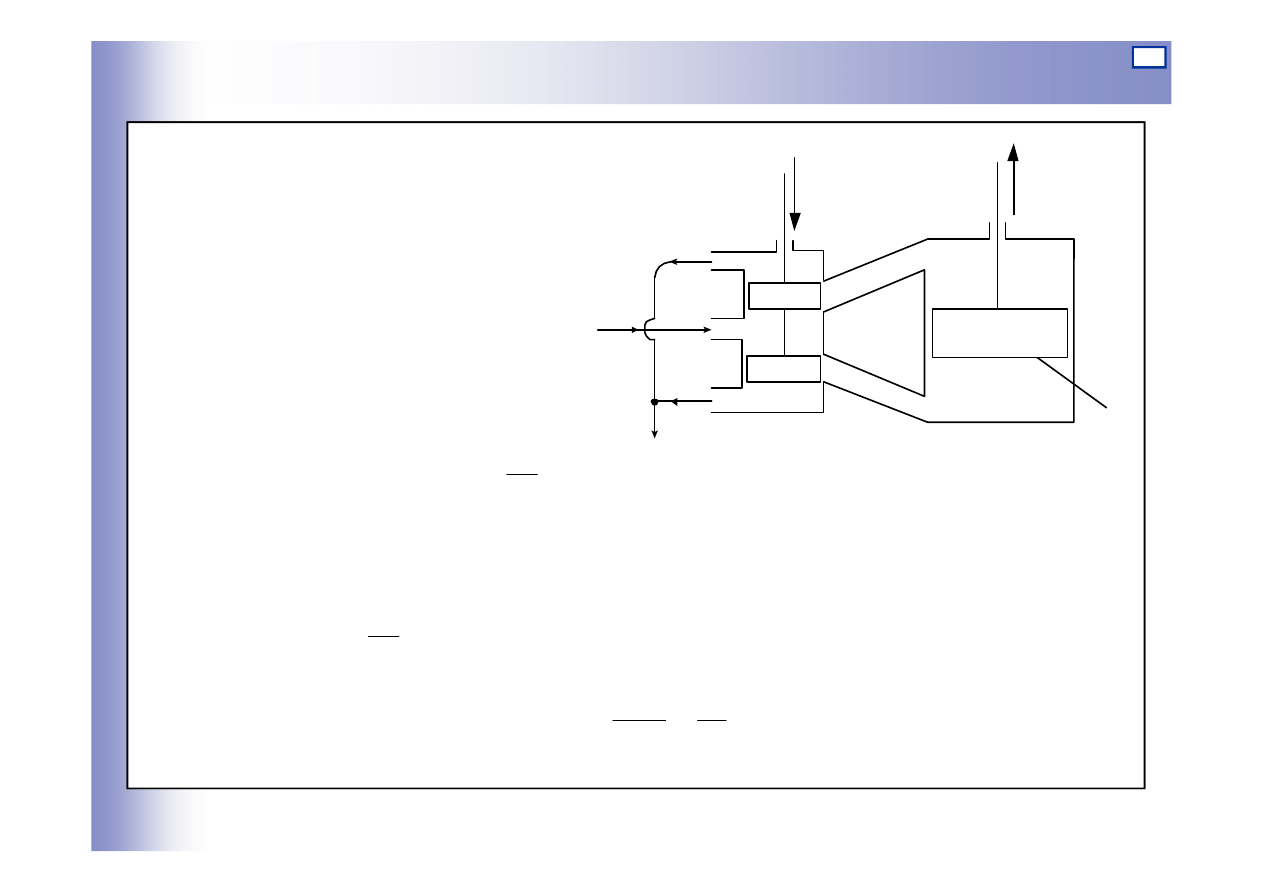
Elementy całkujące
Przykład
Założenia:
a) stałe p
z
i p
s
b) zerowe obciążenie siłownika
c) stały przepływ v medium przez
rozdzielacz
dy
y
A
u
p
z
p
s
Stan dynamiczny:
z równania ciągłości:
gdzie ub – przekrój szczeliny
otrzymujemy:
gdzie
dt
dy
A
Q
=
ubv
Q
=
u
dt
dy
T
=
bv
A
T
/
=
Ts
s
u
s
y
s
G
1
)
(
)
(
)
(
=
=
17
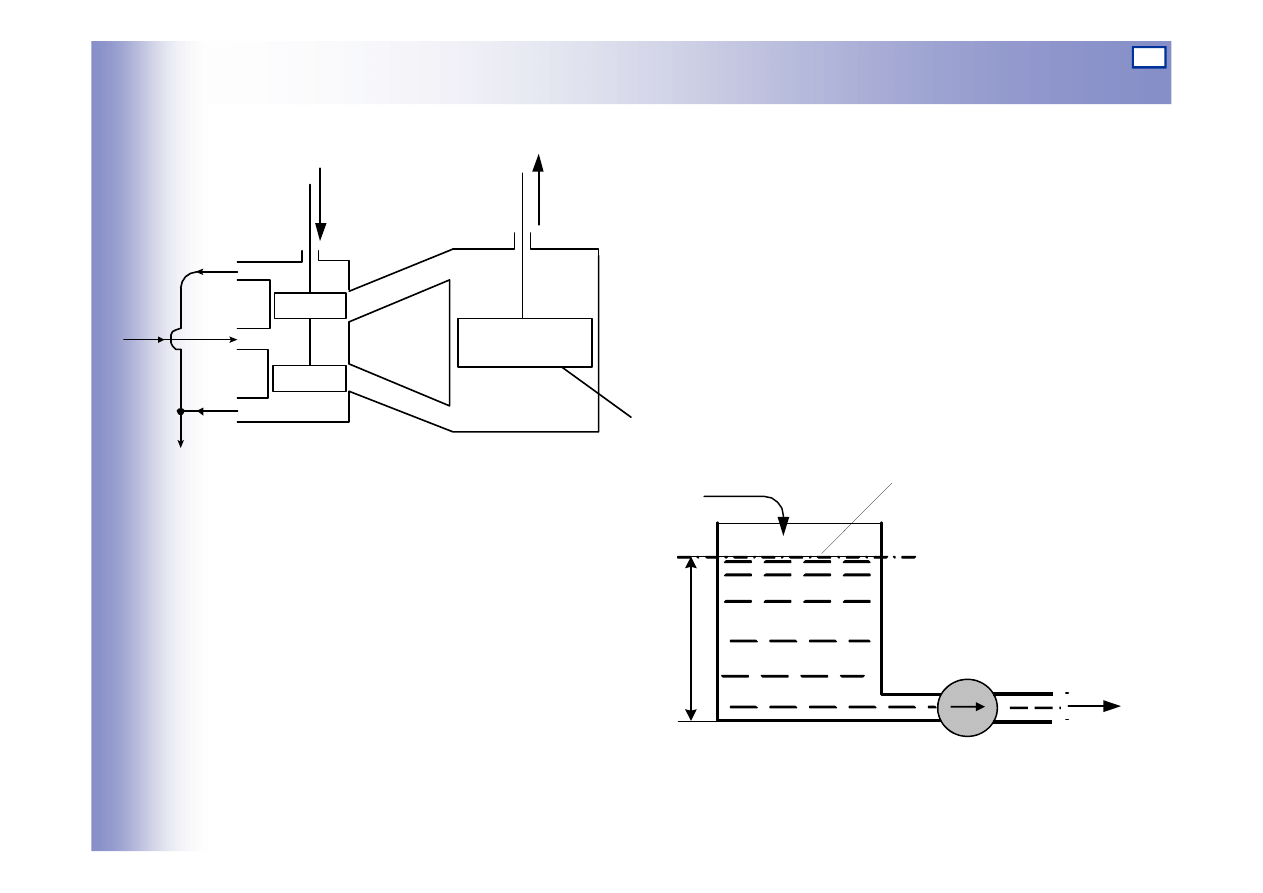
Elementy całkujące - przykłady
y
A
u
p
z
p
s
Zbiornik z wymuszonym
poborem cieczy
Zespół siłownik - rozdzielacz
hydrauliczny
Q
1
A
1
1
h
Q
2
y=h
u=Q
2
18
Elementy różniczkujące
Równanie różniczkowe
k – współczynnik definiowany jako
Transmitancja
dt
du
k
y
=
dt
du
y
k
=
ks
s
u
s
y
s
G
=
=
)
(
)
(
)
(
Charakterystyka statyczna
we współrzędnych:
a) odchyłek
b) wartości absolutnych
u
y
u
0
y
0
0
a)
b)
y
n
19
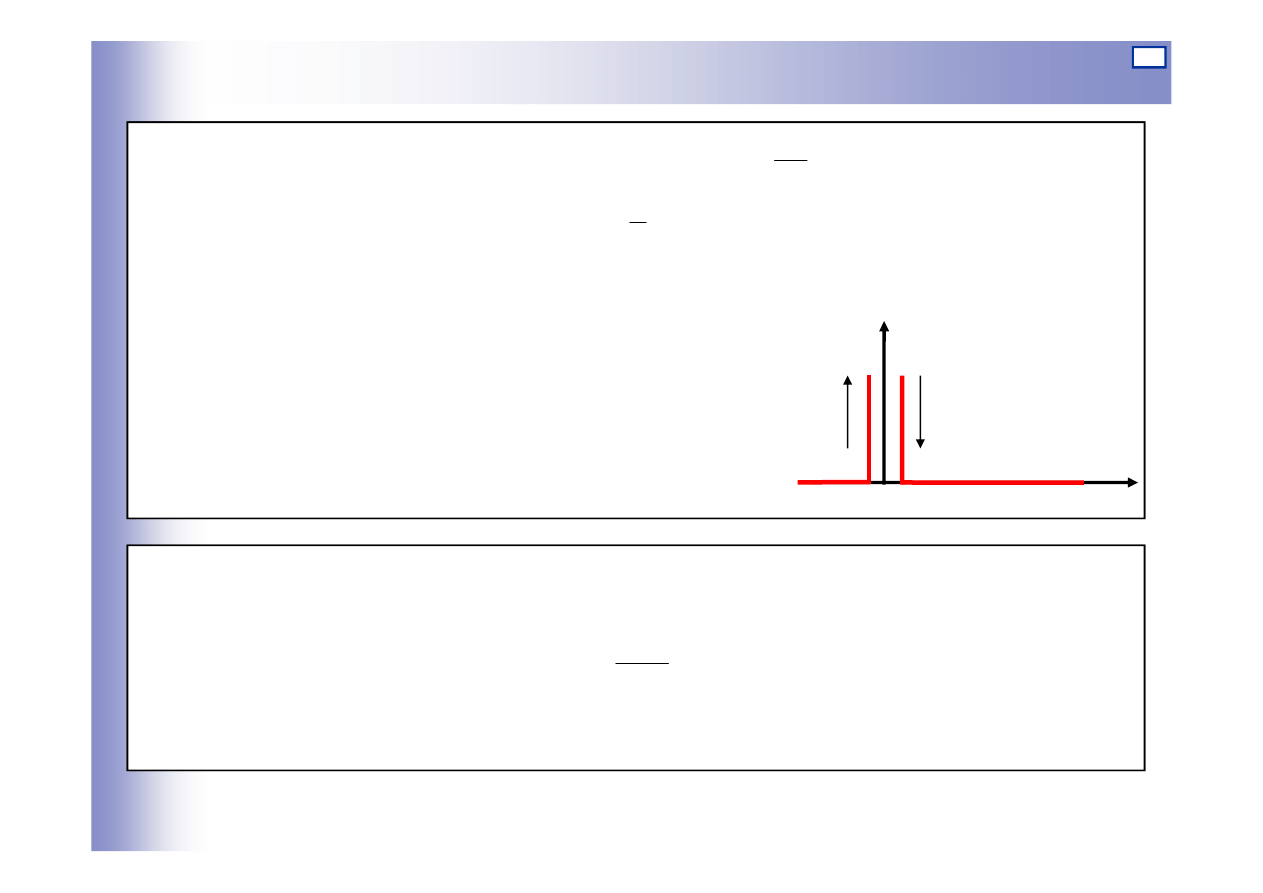
Odpowiedź na wymuszenie skokowe
Elementy różniczkujące
)
(
)
(
s
ksu
s
y
=
)
(
)]
(
[
)
(
1
t
ku
s
y
L
t
y
st
δ
=
=
−
=
∞
<
=
0
dla
0
dla
0
)
(
t
t
t
y
dt
du
k
y
=
st
u
s
s
u
1
)
(
=
st
ku
s
u
=
)
(
t
y
∞
Kiedy wejście i wyjście są sygnałami jednoimiennymi zapisujemy:
gdzie: T jest stałą czasową akcji różniczkującej (stała różniczkowania)
> 0
dla
0
t
Ts
s
u
s
y
s
G
=
=
)
(
)
(
)
(
t
0

20
Elementy różniczkujące rzeczywiste
Równanie różniczkowe
Transmitancja
gdzie:
k – współczynnik proporcjonalności akcji różniczkującej
dt
du
k
y
dt
dy
T
=
+
1
)
(
)
(
)
(
+
=
=
Ts
ks
s
u
s
y
s
G
T – stała czasowa części inercyjnej
Dla sygnałów jednoimiennych u i y:
Charakterystyka statyczna
jak dla elementów różniczkujących idealnych
1
)
(
)
(
)
(
+
=
=
Ts
Ts
s
u
s
y
s
G
21
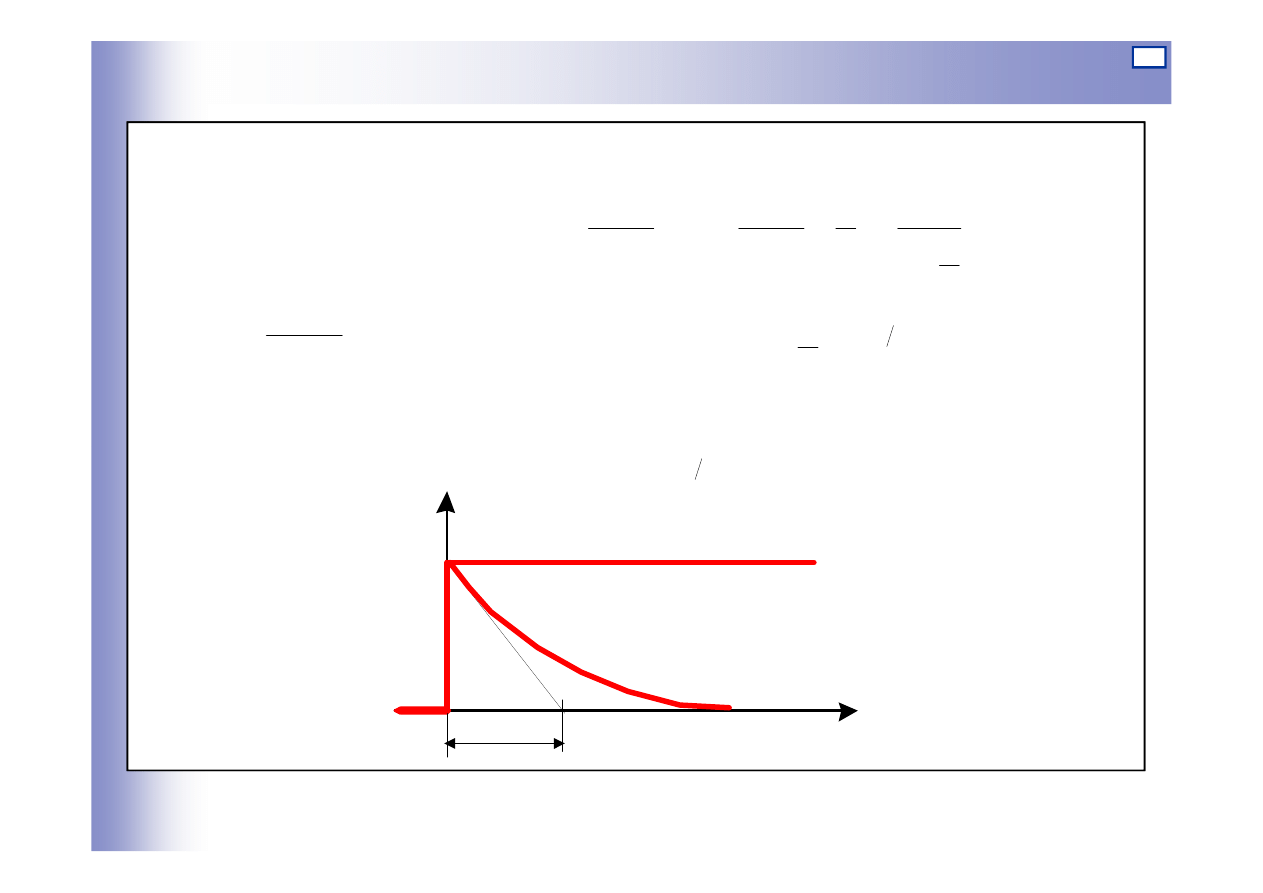
Odpowiedź na wymuszenie skokowe:
dla sygnałów jednoimiennych:
Elementy różniczkujące rzeczywiste
T
s
u
T
k
Ts
ku
s
u
Ts
ks
s
y
st
st
1
1
1
)
(
1
)
(
+
=
+
=
+
=
T
t
st
e
u
T
k
s
y
L
t
y
−
−
=
=
)]
(
[
)
(
1
at
e
a
s
L
−
−
=
+ )
(
1
1
T
t
st
e
u
t
y
−
=
)
(
y
t
ku
st
T
u(t)
y(t)
0
22
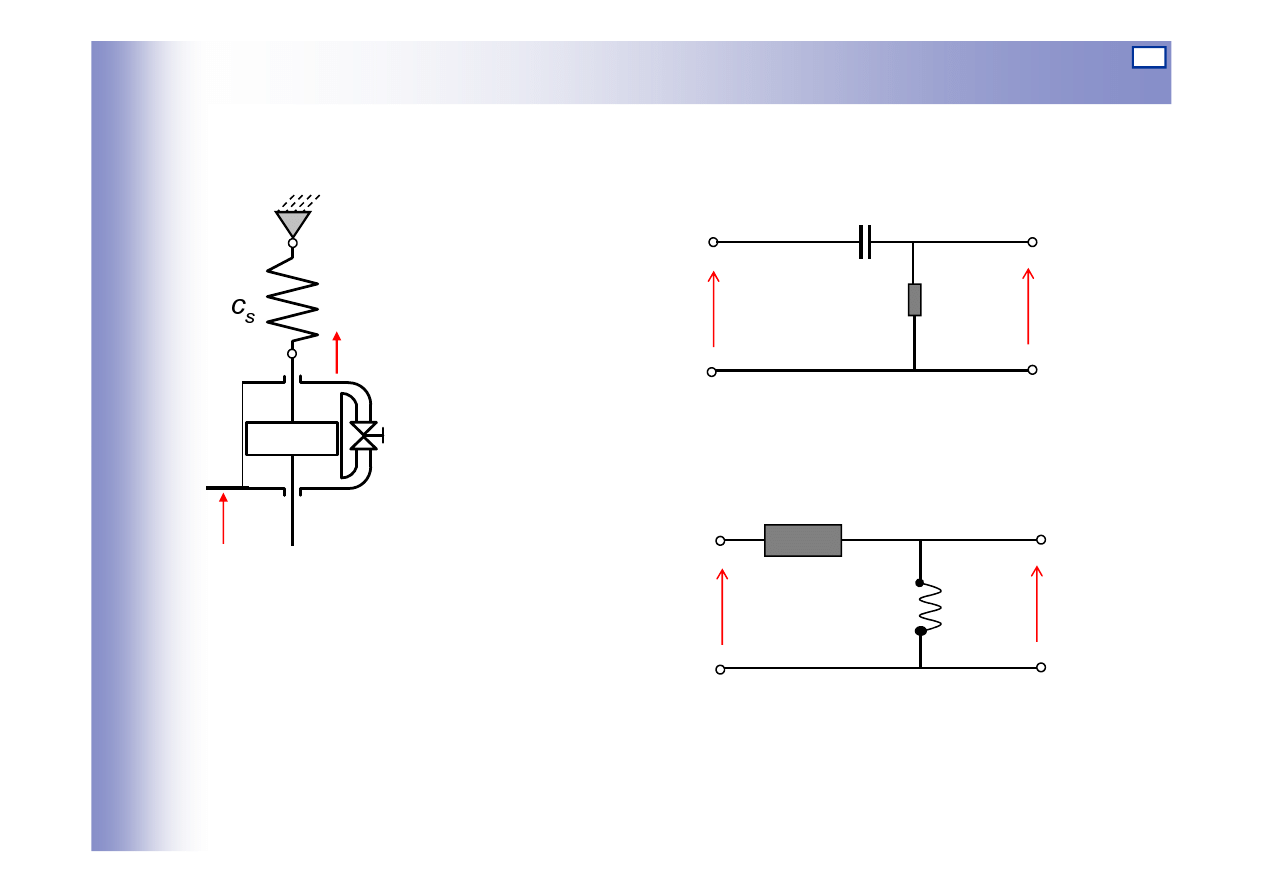
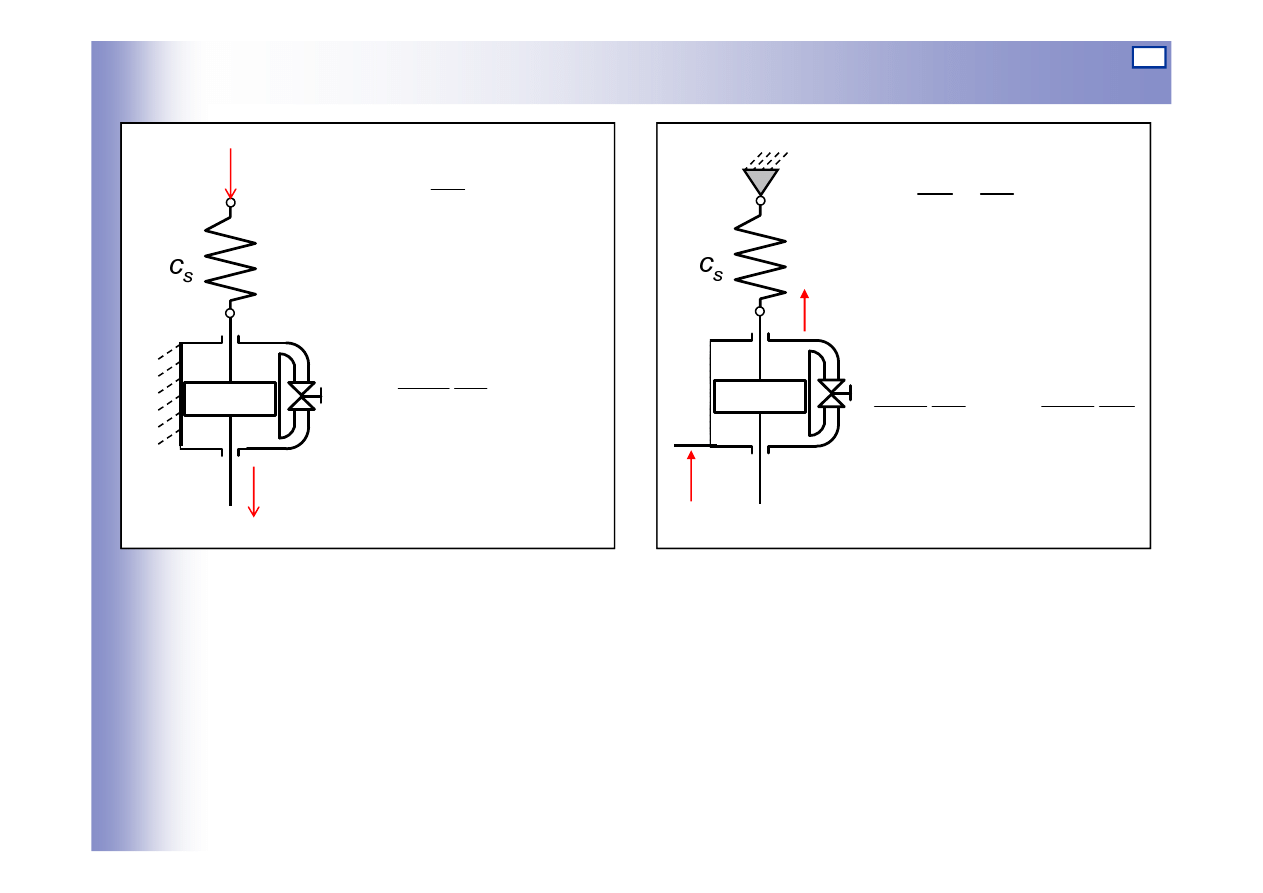
Elementy różniczkujące - rzeczywiste
Czwórnik RC
U
1
U
2
R
C
y=u
2
u=u
1
y
Tłumik hydrauliczny
ze sprężyną
Czwórnik RL
U
1
U
2
R
L
u=u
1
y=u
2
U
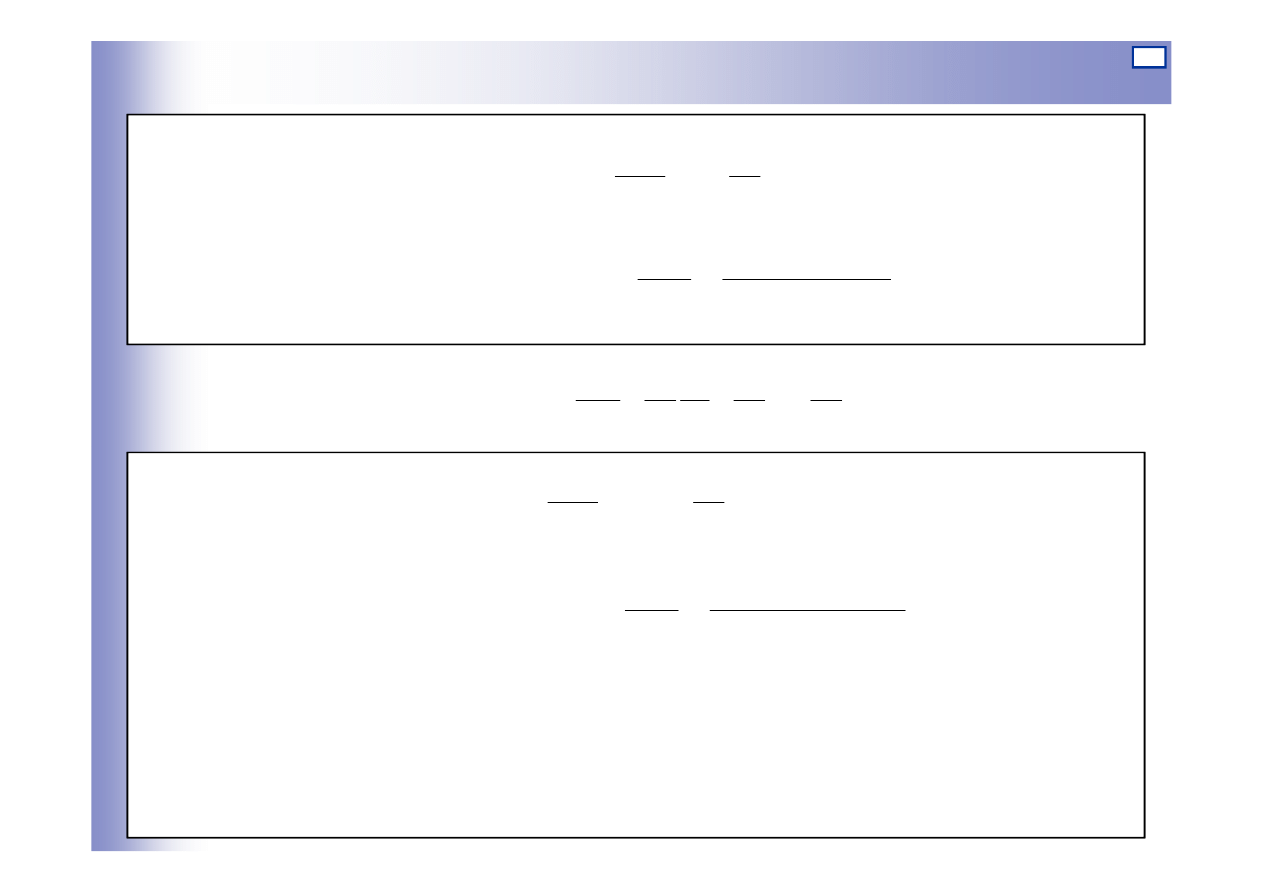
23
Zależność transmitancja od we-wy
pA
C
y
u
s
∆
=
− )
(
p
dt
dy
A
∆
=
α
u
u
y
dt
dy
C
A
s
=
+
α
2
p
dt
dy
dt
du
A
∆
=
−
α
pA
yC
s
∆
=
dt
du
C
A
y
dt
dy
C
A
s
s
α
α
2
2
=
+
y
y
s
s
U
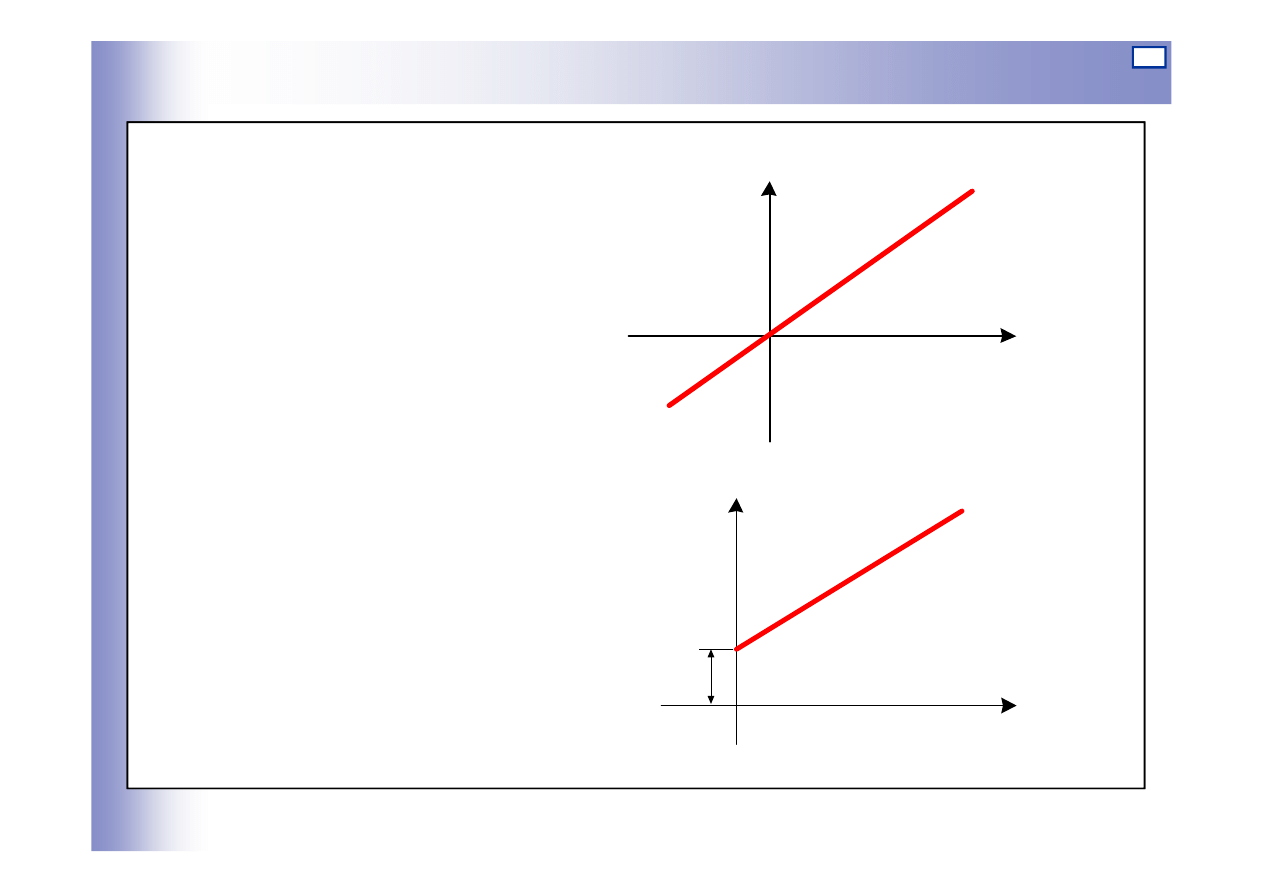
24
Elementy oscylacyjne
Równanie różniczkowe
Transmitancja:
2
1
2
2
4T
T
<
ku
y
dt
dy
T
dt
y
d
T
=
+
+
2
2
2
2
1
1
)
(
)
(
)
(
2
2
2
1
+
+
=
=
s
T
s
T
k
s
u
s
y
s
G
u
T
k
y
T
dt
dy
T
T
dt
y
d
2
1
2
1
2
1
2
2
2
1
=
+
+
Równanie różniczkowe
Transmitancja :
gdzie: k – współczynnik proporcjonalności
– pulsacja oscylacji własnych
– zredukowany (względny) współczynnik tłumienia
u
k
y
dt
dy
dt
y
d
2
0
2
0
0
2
2
2
ω
ω
ζω
=
+
+
2
0
0
2
2
0
2
)
(
)
(
)
(
ω
ζω
ω
+
+
=
=
s
s
k
s
u
s
y
s
G
1
2
<
ζ
1
0
/
1
T
=
ω
1
2
2
/
T
T
=
ζ
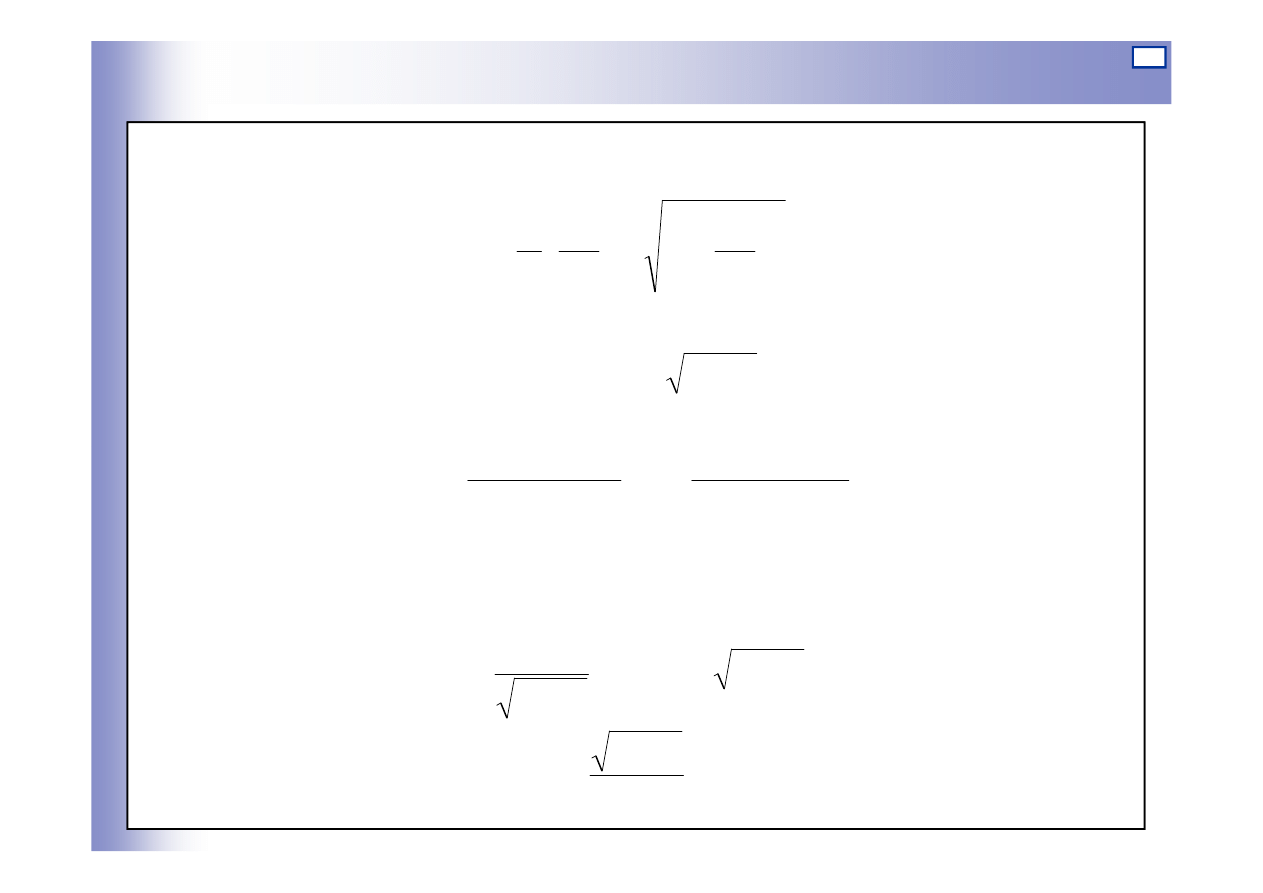
25
Charakterystyka statyczna
we współrzędnych:
a) odchyłek
Elementy oscylacyjne
ku
y
=
u
y
a)
b) wartości absolutnych
C
ku
y
+
=
0
0
u
0
y
0
c
0
b)

26
Odpowiedź na wymuszenie skokowe
pierwiastki wielomianu N(s):
Elementy oscylacyjne
+
+
=
+
+
=
=
−
−
−
)
1
(
1
)
1
(
)
(
)
(
)
(
2
2
2
1
1
2
2
2
1
1
1
s
T
s
T
s
L
ku
u
s
T
s
T
s
k
L
u
s
sN
s
M
L
t
y
st
st
st
−
−
=
−
±
−
=
1
1
4
2
2
2
2
1
2
2
2
2
,
1
T
T
T
T
T
s
m
lub:
lub
to
odpowiedź jest oscylacyjna gdy:
lub
−
−
=
=
1
2
2
2
1
2
1
2
1
2
1
1
2
2
2
,
1
T
T
T
T
s
m
1
0
1
T
=
ω
1
2
2T
T
=
ζ
)
1
(
2
0
2
,
1
−
−
=
ζ
ζ
ω
m
s
2
1
2
2
4T
T
<
1
2
<
ζ
27
Odpowiedź na wymuszenie skokowe
zapisując
lub
otrzymujemy
Elementy oscylacyjne
−
−
=
2
1
2
1
2
1
2
,
1
2
1
2
1
T
T
j
T
T
T
s
m
)
1
(
2
0
2
,
1
ζ
ζ
ω
−
−
=
j
s
m
1
1
Stosując wzory Eulera
można uzyskać:
gdzie:
−
+
−
+
=
t
s
t
s
st
e
s
s
s
T
e
s
s
s
T
ku
t
y
2
1
)
(
1
)
(
1
1
)
(
1
2
2
2
1
2
1
1
2
1
+
−
−
−
=
−
)
1
sin(
1
1
)
(
2
0
2
1
0
ϕ
ζ
ω
ζ
ζω
t
e
e
ku
t
y
t
s
t
st
ζ
ζ
ζ
ϕ
arccos
1
2
=
−
= arctg
)
sin
(cos
v
j
v
e
e
u
jv
u
+
=
+
28
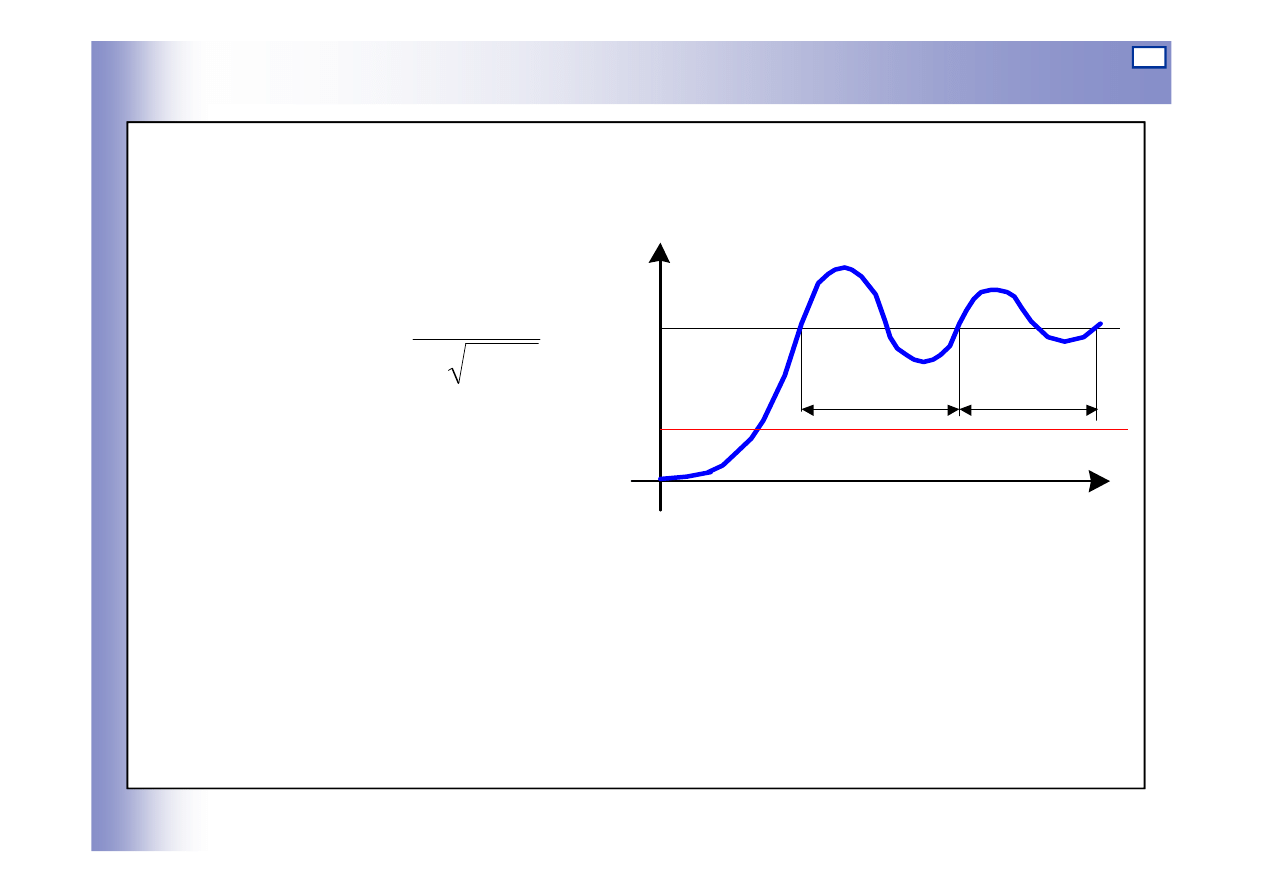
Odpowiedź na wymuszenie skokowe
składowa stała:
okres gasnącej sinusoidy:
Elementy oscylacyjne
y
k u
st
T
T
st
ku
2
0
1
2
ζ
ω
π
−
=
T
y(t)
u(t)
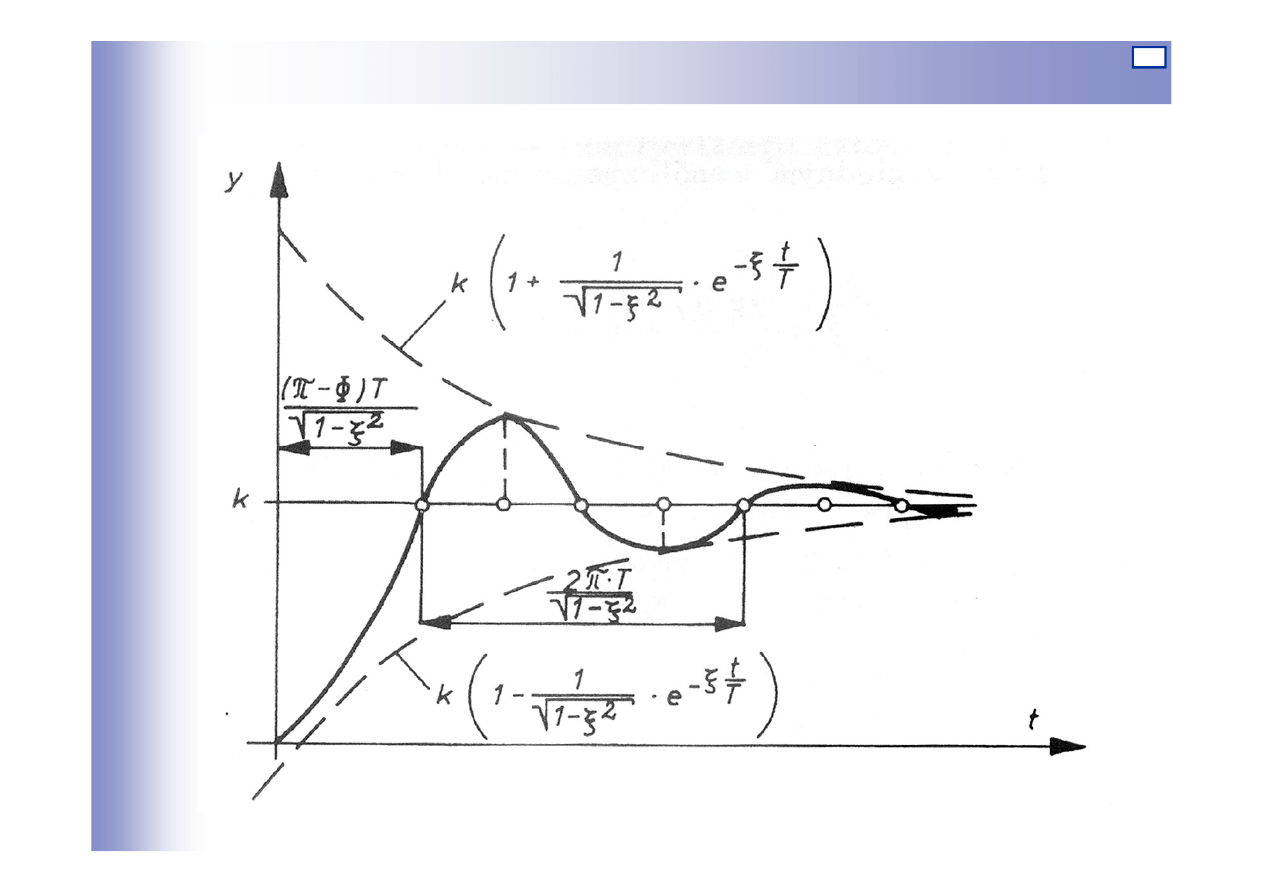
dla
ζ
= 0 (T
2
= 0) występują drgania zachowawcze (nie tłumione)
o pulsacji
ω
0
, wtedy:
t
0
]
cos
1
[
)
(
)]
90
sin(
1
[
)
(
0
0
t
ku
t
y
t
ku
t
y
st
st
ω
ω
−
=
+
−
=
o
u(t)
29
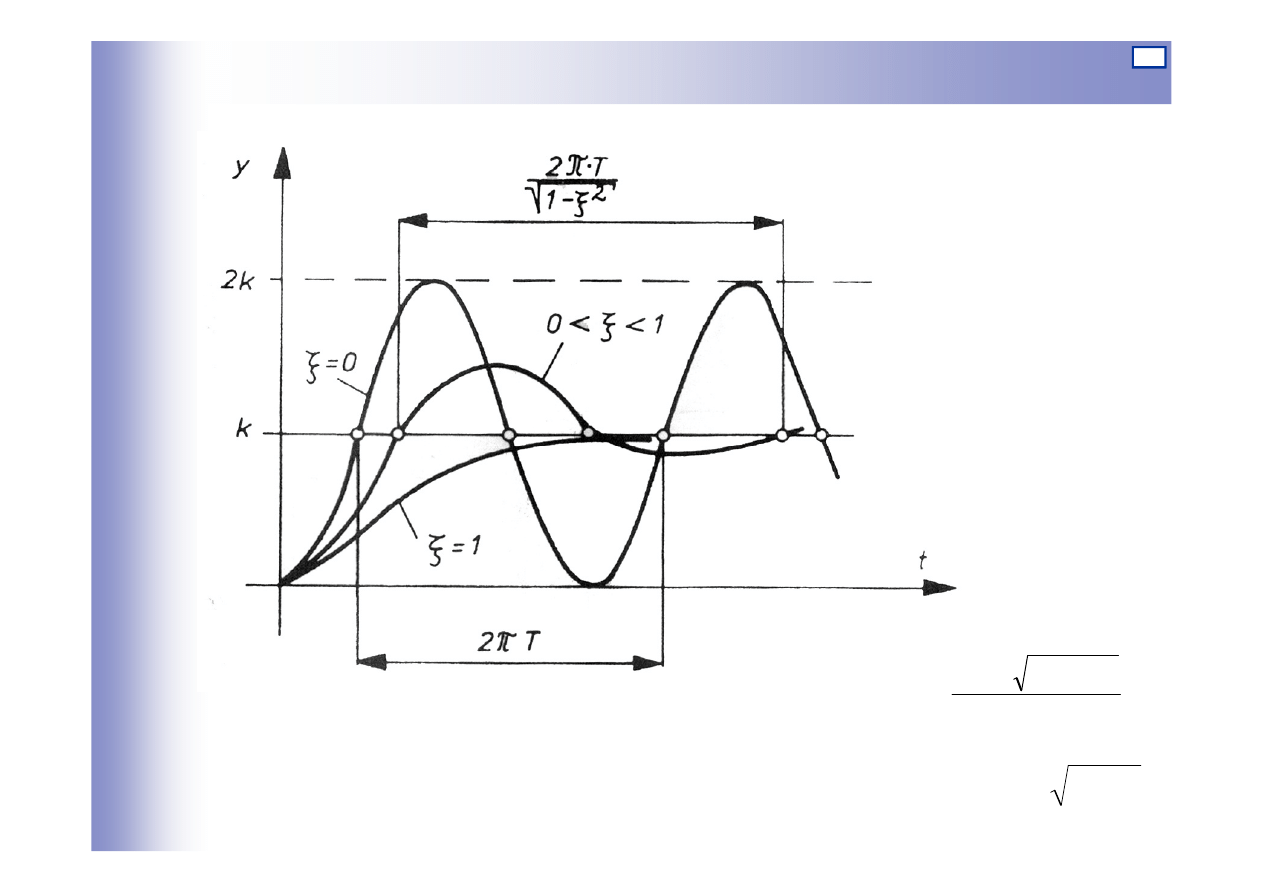
Elementy oscylacyjne
1
T
T
≡
30
Elementy oscylacyjne
1
T
T
≡
2
1
2
1
2
2
2
2
,
1
2
4
T
T
T
T
s
−
±
−
=
)
1
(
2
0
2
,
1
−
−
=
ζ
ζ
ω
m
s
2
1
2
2
4T
T
=
1
2
=
ζ
31
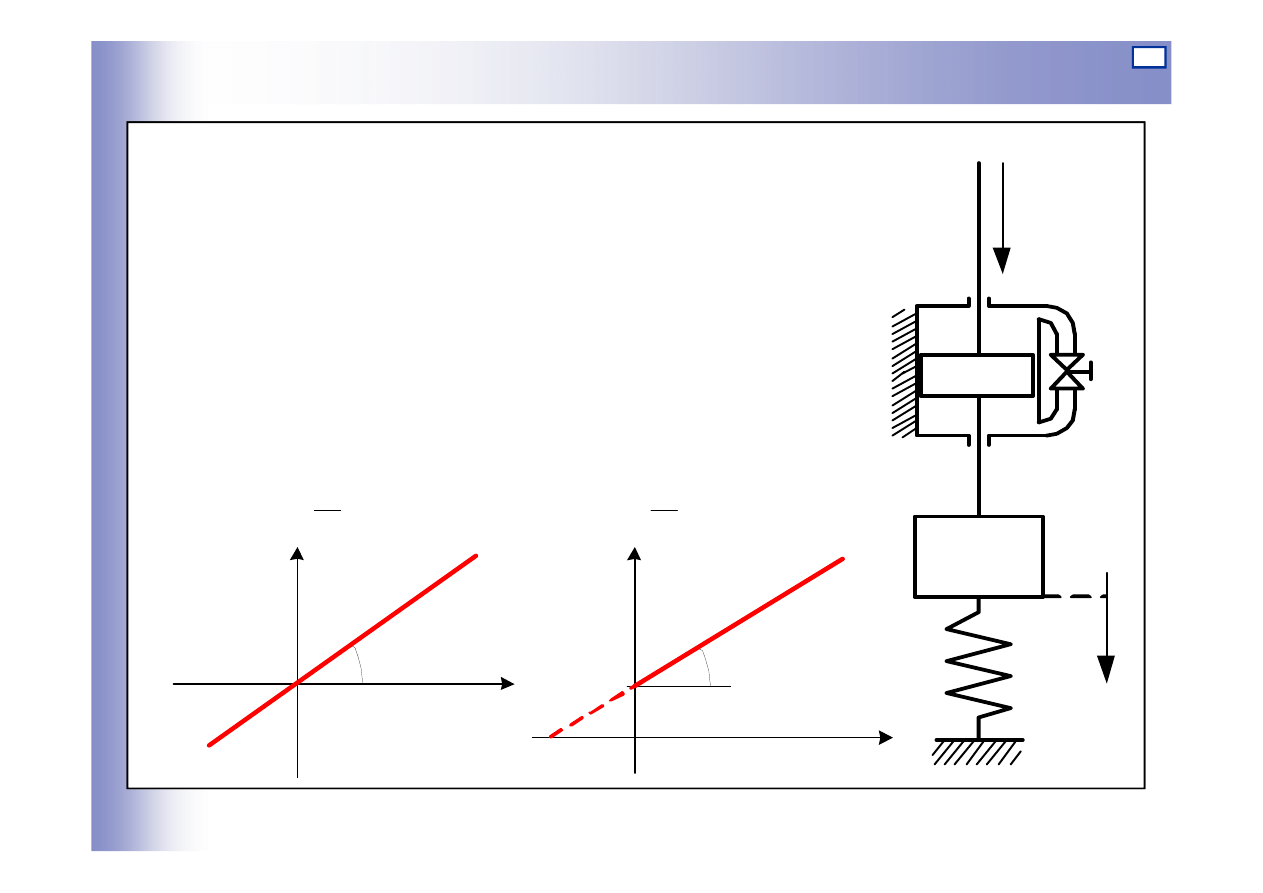
Elementy oscylacyjne
Przykład
siła F – sygnał wejściowy
przesunięcie y – sygnał wyjściowy
W stanie ustalonym:
F
c
t
0
0
y
c
mg
F
s
=
+
m
y
c
s
)
(
1
0
0
mg
F
c
y
s
+
=
F
y
a)
arctg 1/c
s
arctg 1/c
s
F
0
y
0
0
b)
- mg
F
c
y
s
1
=
32
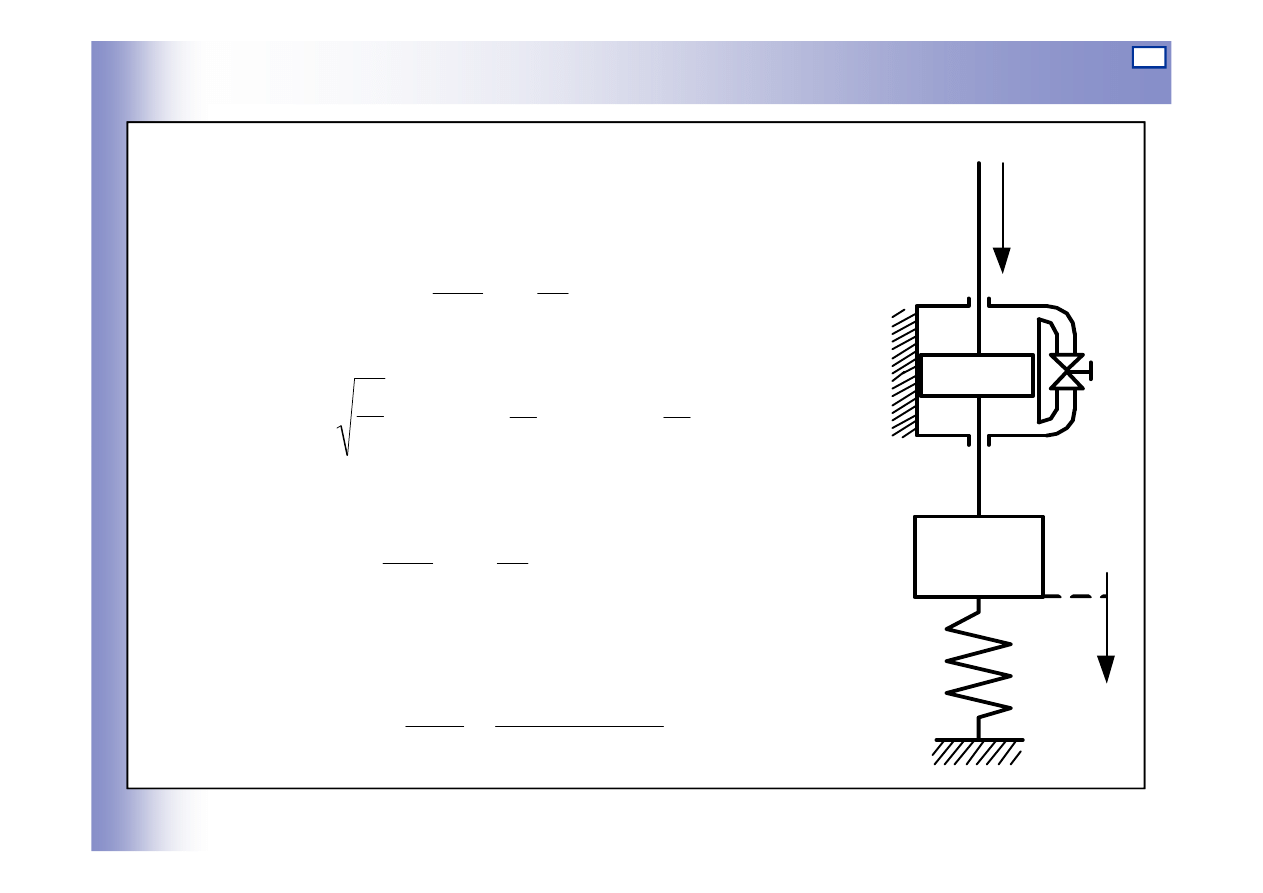
Elementy oscylacyjne
Przykład
równanie równowagi
jeżeli:
F
c
t
y
c
dt
dy
c
dt
y
d
m
F
s
t
+
+
=
2
2
s
c
m
T
=
1
s
t
c
c
T
=
2
s
c
k
1
=
to:
stąd transmitancja:
m
y
c
s
s
c
s
c
s
c
kF
y
dt
dy
T
dt
y
d
T
=
+
+
2
2
2
2
1
1
)
(
)
(
)
(
2
2
2
1
+
+
=
=
s
T
s
T
k
s
F
s
y
s
G
33
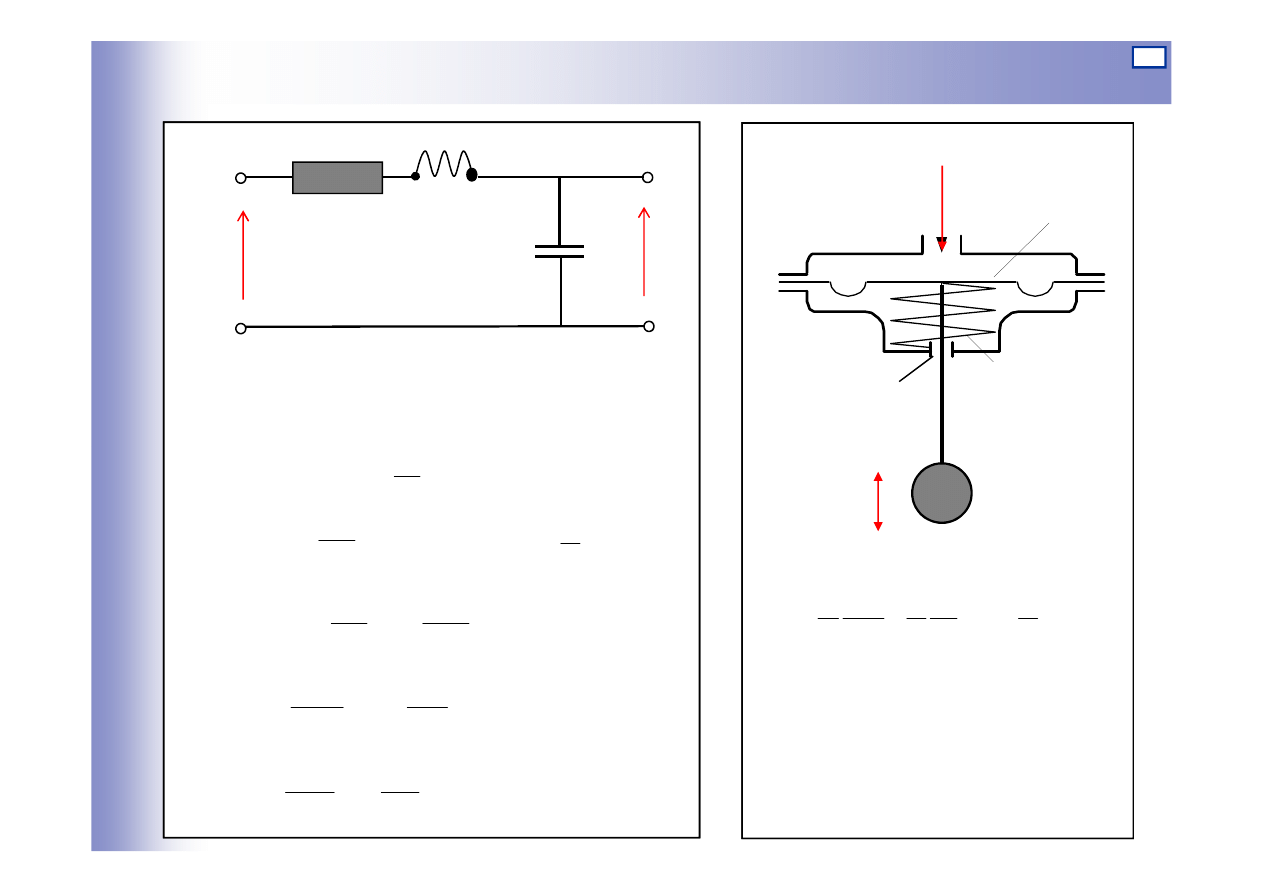
Elementy oscylacyjne
di
L
U
1
U
2
R
C
Czwórnik RLC
p
A
c
f)
c
u=p
B
2
1
u
dt
di
L
Ri
u
+
+
=
∫
∝
−
=
t
idt
C
u
1
2
dt
du
C
i
2
=
1
2
2
2
2
2
u
u
dt
du
RC
dt
u
d
LC
=
+
+
2
2
2
2
2
1
u
dt
u
d
LC
dt
du
RC
u
+
+
=
1
2
2
2
2
2
2
2
1
u
u
dt
du
T
dt
u
d
T
=
+
+
m
y
p
c
A
y
dt
dy
c
B
dt
y
d
c
m
=
+
+
2
2
34
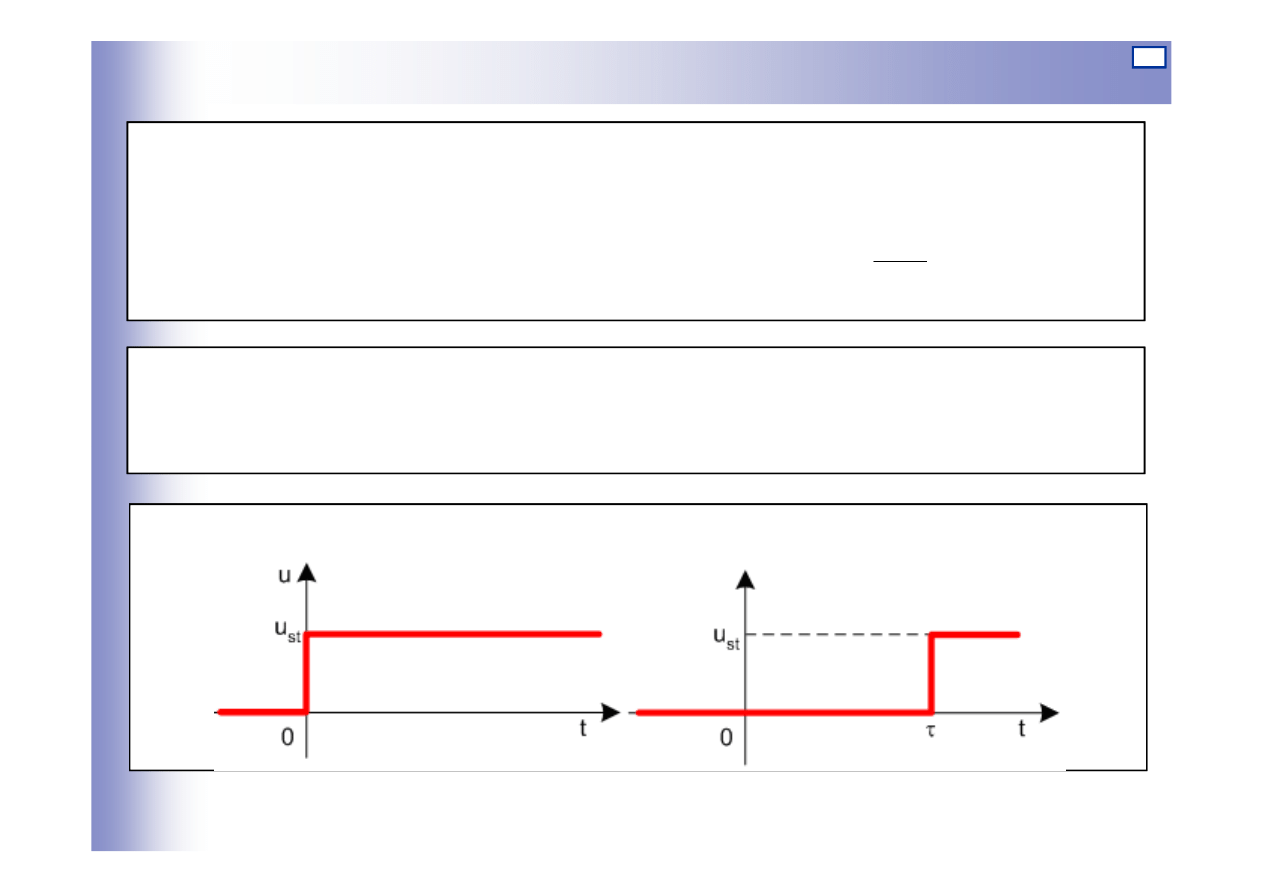
Elementy opóźniające
Równanie elementu opóźniającego:
Skąd wynika transmitancja:
)
(
)
(
τ
−
=
t
u
t
y
s
e
s
u
s
y
s
G
τ
−
=
=
)
(
)
(
)
(
Charakterystyka statyczna
lub
u
y
=
0
0
u
y
=
lub
u
y
=
0
0
u
y
=
Odpowiedź na wymuszenie skokowe:
y(t)
35
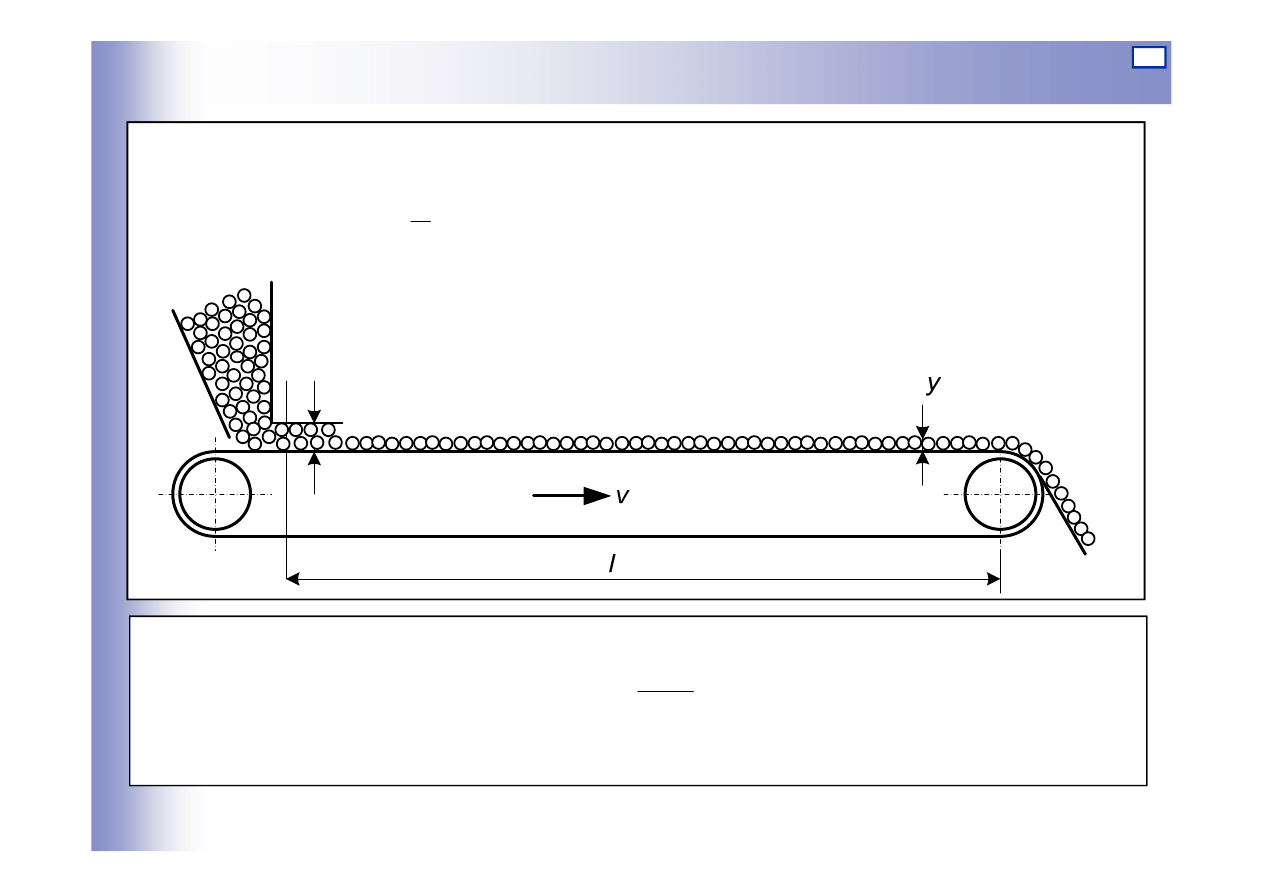
Elementy opóźniające
Przykład 1. Podajnik taśmowy
Opóźnienie:
gdzie: l – odległość [m]
v – prędkość taśmy [m/s]
v
l
τ
=
u
Transmitancja
τ
s
e
u(s)
y(s)
G(s)
−
=
=
36
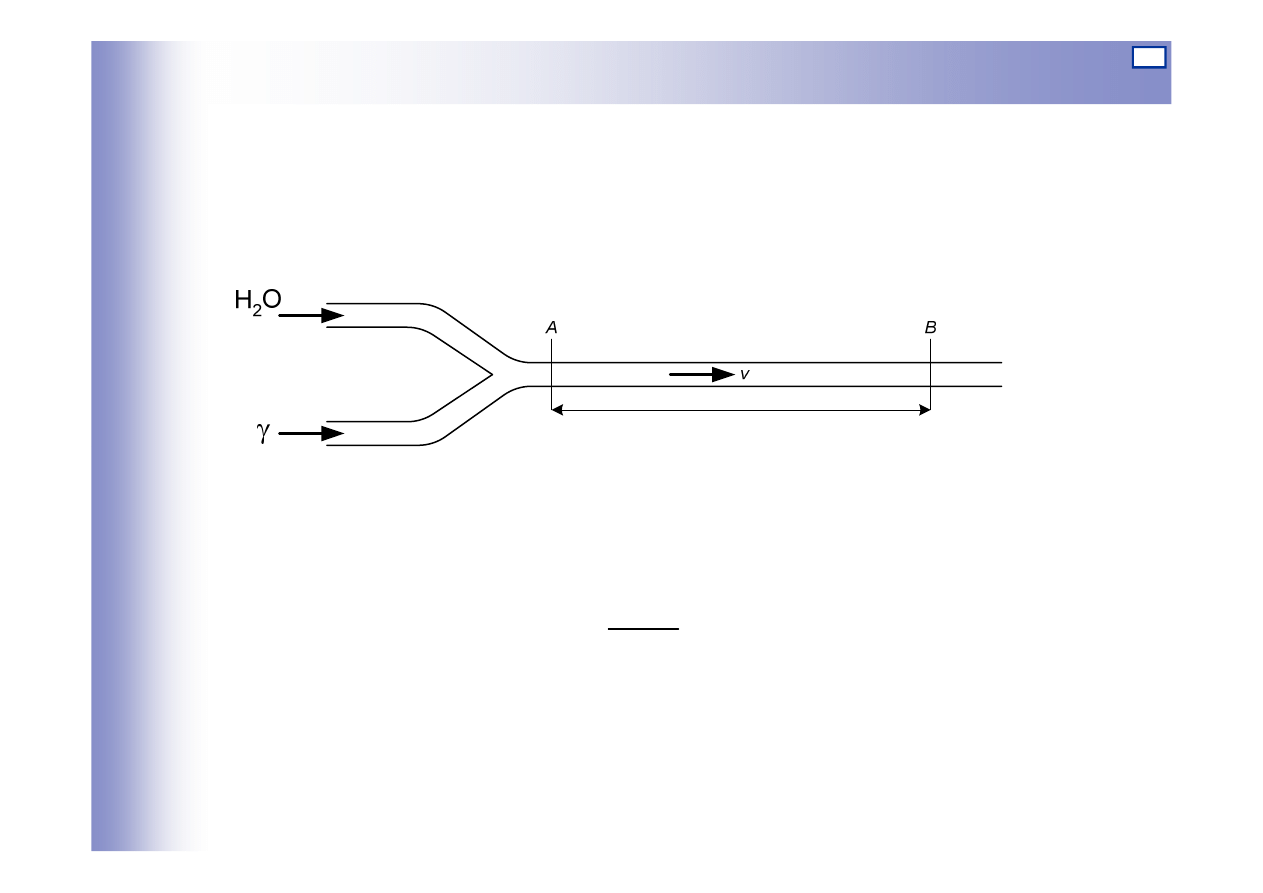
Elementy opóźniające
Schemat elementu podano na rysunku poniżej. Sygnałem wejściowym
jest stężenie substancji
γ w przekroju A, sygnałem wyjściowym –
stężenie substancji w przekroju B rurociągu.
l
Przy założeniu, że następuje dokładne wymieszanie substancji i w
danym przekroju jej stężenie jest jednakowe, otrzymamy:
gdzie: CA – stężenie substancji
γ w przekroju A,
CB – stężenie substancji
γ w przekroju B,
τ
=l/v – opóźnienie
s
A
B
e
s
C
s
C
s
G
τ
−
=
=
)
(
)
(
)
(
l
Wyszukiwarka
Podobne podstrony:
03 Podstawowe elementy liniowe
PA3 podstawowe elementy liniowe [tryb zgodności]
Podstawowe elementy liniowe
Modelowanie i badanie podstawowych elementów liniowych automatyki – symulacja
Podstawowe elementy liniowe
PA3 podstawowe elementy liniowe [tryb zgodności]
03 PODSTAWY GENETYKI
sprawko elementy liniowe i nieliniowe
Podstawowe elementy planowania i podejmowania decyzji
Charakterystyki skokowe wybranych elementow liniowych
(8) Podstawowe elementy organizowaniaid 1180
Metodyka nauczania podstawowych elementów technicznych w mini piłce nożnej
M5 Charakterystyki podstawowych elementów elektronicznych, AGH, MiBM - I rok, Elektrotechnika, Spraw
Sprawozdanie Badanie obwodów prądu stałego zawierającego elementy liniowe i nieliniowe (Moje)x
Zadania Podstawowe Elementy Automatyki
Laboratorium Instalacji I Oświetlenia, Pomiary natężenia oświetlenia i luminancji v2, Celem ćwiczeni
Wykład 7 PODSTAWOWE ELEMENTY ORGANIZOWANIA
Modul 2 Podstawowe elementy stosowane w mikroelektronice
Podstawy algebry liniowej mscierze
więcej podobnych podstron