Politechnika Warszawska

Instytut Automatyki i Robotyki

Prof. dr hab. in

ż

. Jan Maciej Ko

ś

cielny

PODSTAWY AUTOMATYKI

PODSTAWY AUTOMATYKI

3. P

odstawowe elementy liniowe

2

Zało

ż

enia

Elementy mechaniczne

:

•

wyst

ę

puje jedynie tarcie lepkie (wiskotyczne)

,

a nie tarcie suche

- siła tarcia jest proporcjonalna do pr

ę

dko

ś

ci

Wiele elementów automatyki mo

ż

na traktowa

ć

jako liniowe, je

ż

eli

:

•

ograniczy si

ę

zakres ich pracy

•

przyjmie nast

ę

puj

ą

ce zało

ż

enia upraszczaj

ą

ce:

- siła tarcia jest proporcjonalna do pr

ę

dko

ś

ci

•

sztywno

ś

ci elementów spr

ęż

ystych s

ą

stałe

Elementy płynowe

:

•

opór przepływu jest stały

- nat

ęż

enie przepływu jest proporcjonalne do ró

ż

nicy ci

ś

nie

ń

•

współczynnik

ś

ci

ś

liwo

ś

ci płynu jest stały

Elementy elektryczne:

•

rezystancje, indukcyjno

ś

ci i pojemno

ś

ci s

ą

stałe i niezale

ż

ne od

przepływaj

ą

cego pr

ą

du i napi

ę

cia

3

Ze wzgl

ę

du na własno

ś

ci dynamiczne:

• bezinercyjne (proporcjonalne)

• inercyjne

• całkuj

ą

ce

• ró

ż

niczkuj

ą

ce (idealne i rzeczywiste)

• oscylacyjne

• opó

ź

niaj

ą

ce

Podział elementów liniowych

Elementy charakteryzuj

ą

:

Wła

ś

ciwo

ś

ci statyczne:

charakterystyka statyczna y = f(u)

Wła

ś

ciwo

ś

ci dynamiczne:

równanie ró

ż

niczkowe

transmitancja operatorowa

odpowied

ź

na zakłócenie skokowe

charakterystyki cz

ę

stotliwo

ś

ciowe

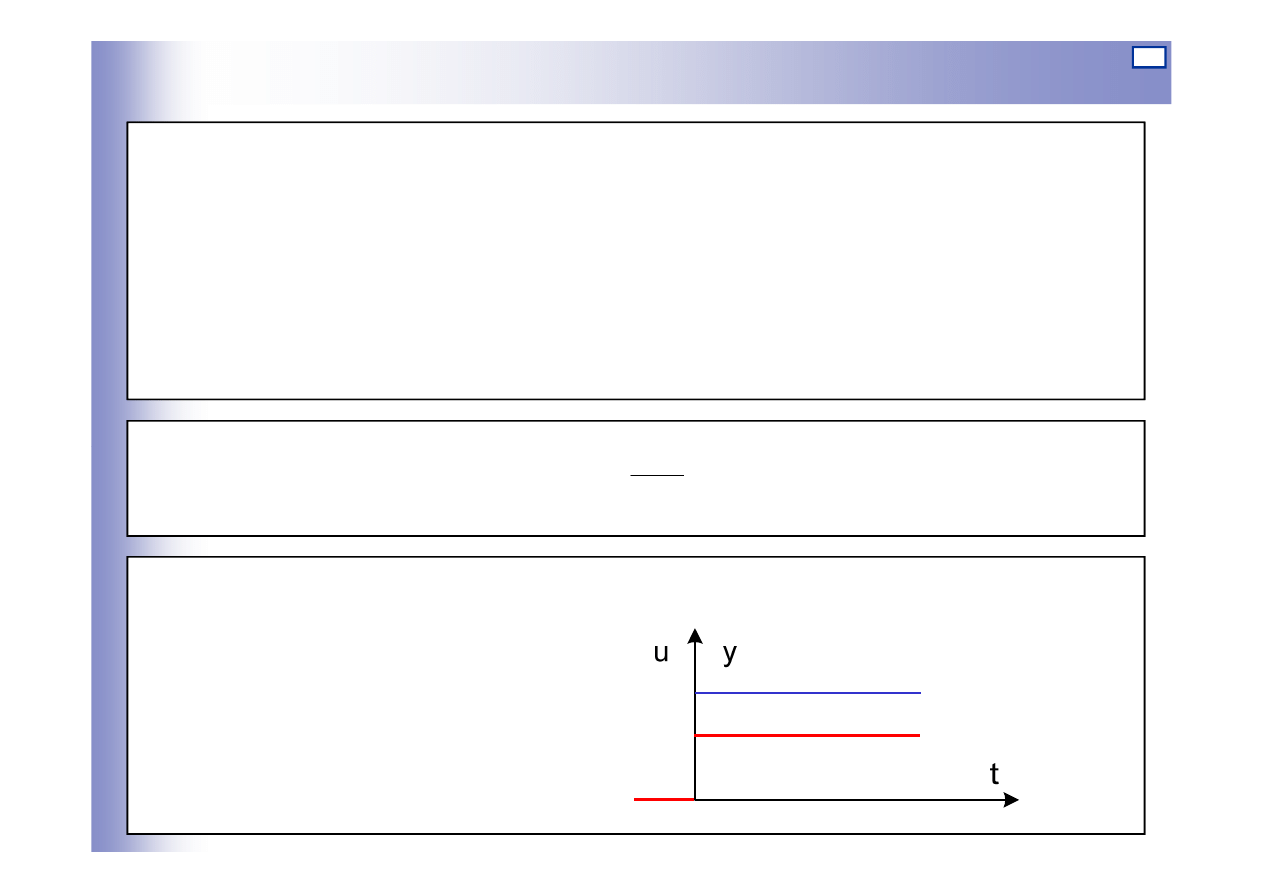
4

Elementy bezinercyjne (proporcjonalne)

Równanie ró

ż

niczkowe (równe charakterystyce statycznej y=ku)

y – wielko

ść

wyj

ś

ciowa

u – wielko

ść

wej

ś

ciowa

k – współczynnik proporcjonalno

ś

ci (wzmocnienie)

Transmitancja

s

y )

(

)

(

)

(

t

ku

t

y

=

Transmitancja

k

s

u

s

y

s

G

=

=

)

(

)

(

)

(

Odpowied

ź

na wymuszenie skokowe:

st

ku

t

t

y

)

(

1

)

(

=

st

u

t

t

u

)

(

1

)

(

=

y (t)

u(t)

u

st

ku

st

5

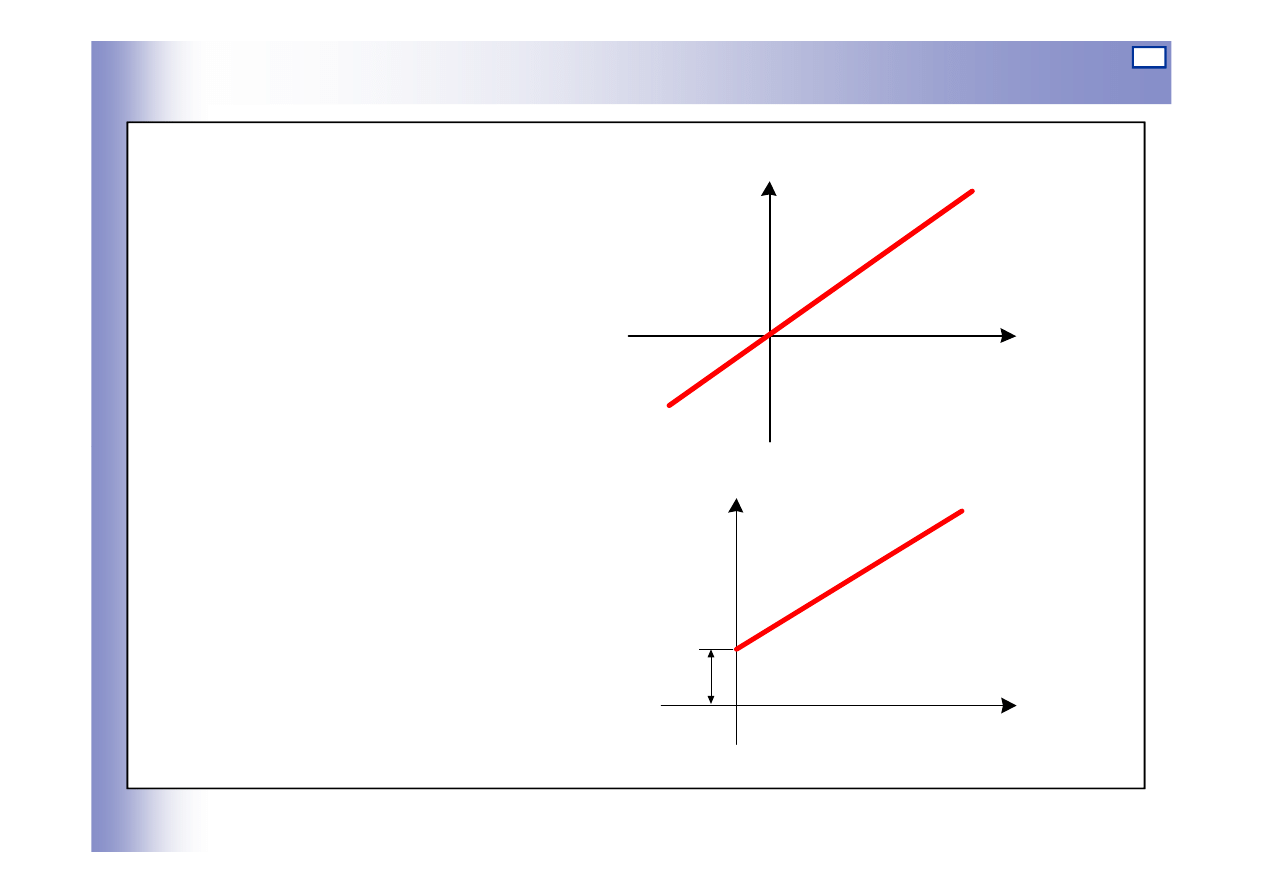
Elementy bezinercyjne (proporcjonalne)

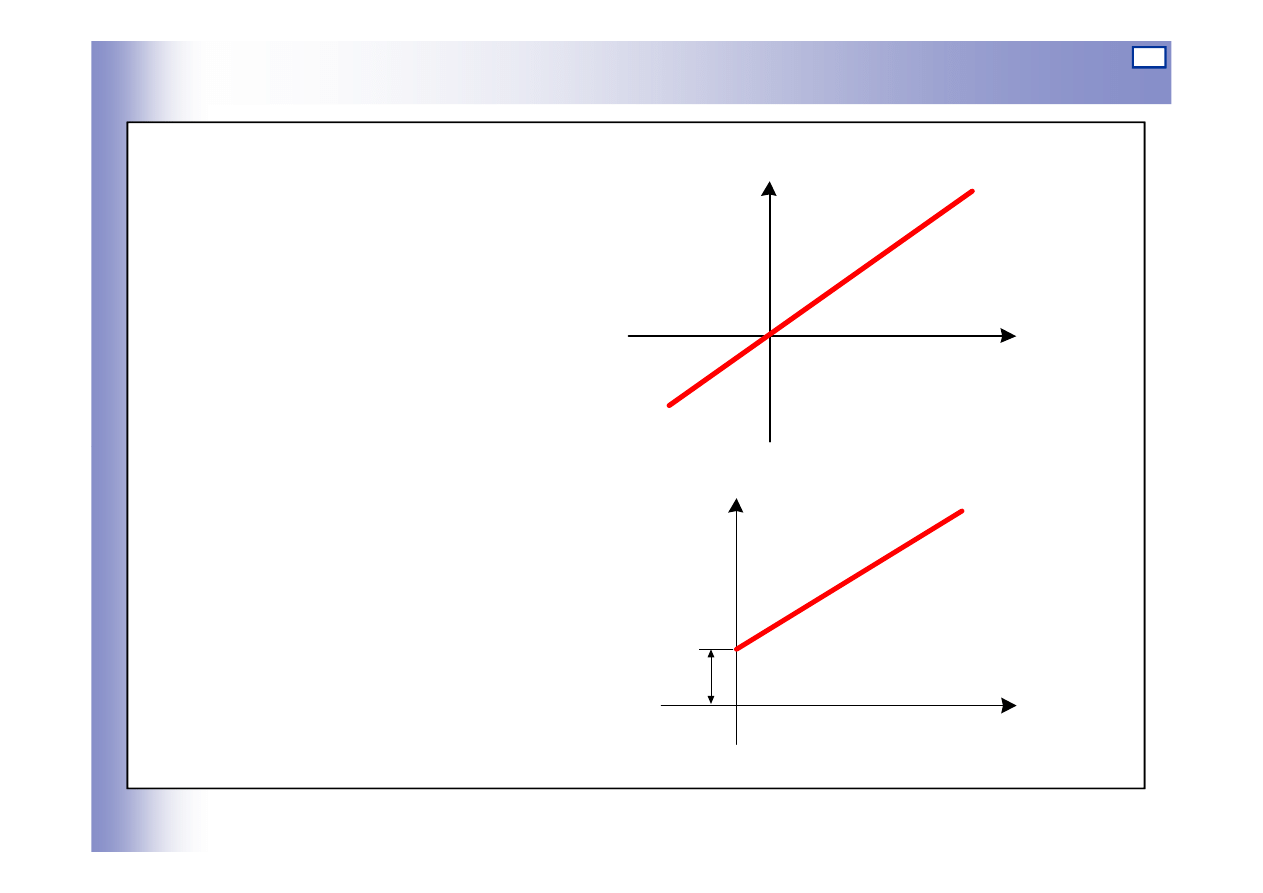
Charakterystyka statyczna

we współrz

ę

dnych:

a) odchyłek

ku

y

=

u

y

a)

b) warto

ś

ci absolutnych

C

ku

y

+

=

0

0

u

0

y

0

c

0

b)

6

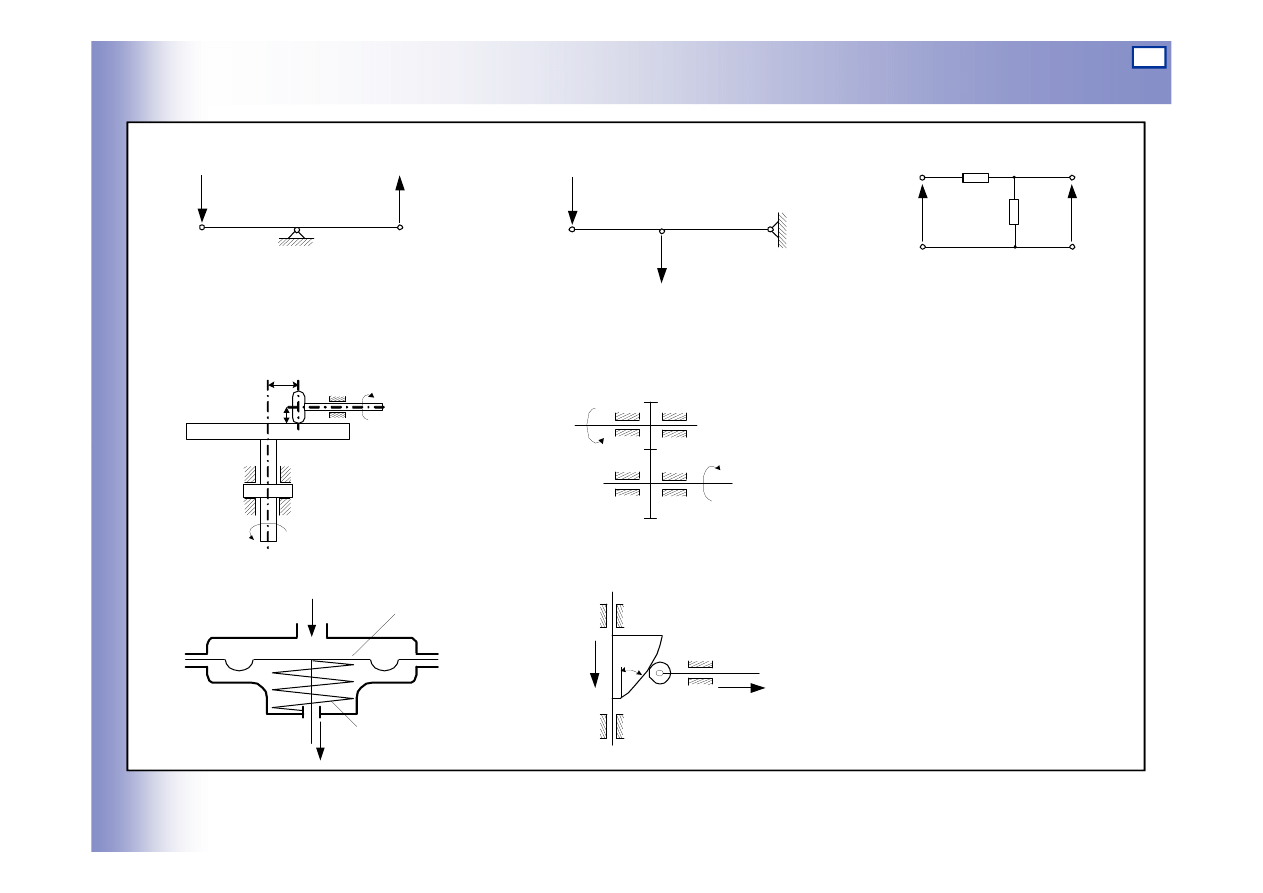
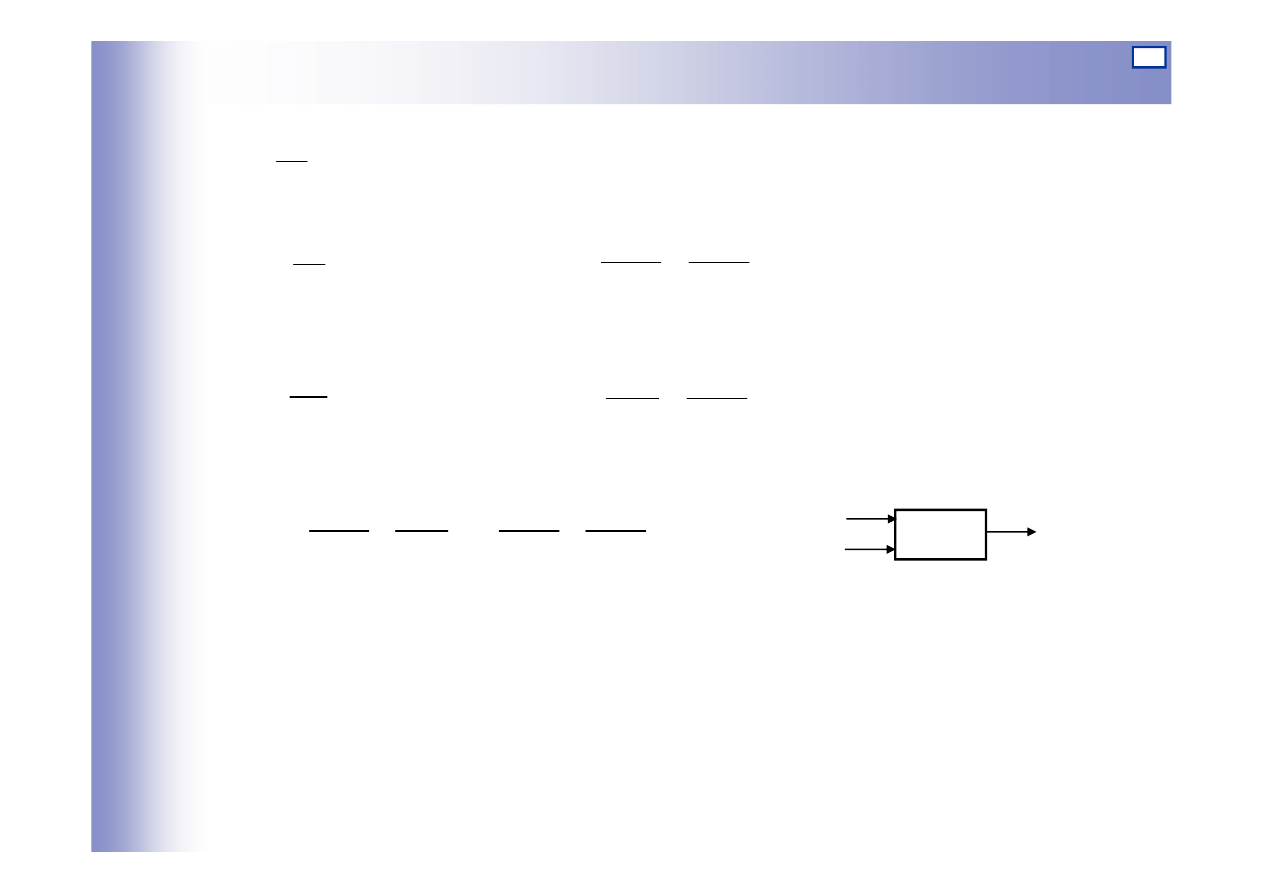
Elementy bezinercyjne – przykłady

a b

u

y

F

u

F

y

a)

a b

u

y

F

u

F

y

b)

u

2

u

1

R

1

R

2

c)

d)

r

x

?

2

n

1

z

1

e)

a, b) d

ź

wignia

?

1

1

n

2

z

2

p

A

c

y

f)

x

y

?

g)

c) dzielnik napi

ę

cia

d) przekładnia cierna

e) przekładnia z

ę

bata

f) siłownik

pneumatyczny

g) mechanizm

krzywkowy

7

Elementy inercyjne pierwszego rz

ę

du

Równanie ró

ż

niczkowe

k – współczynnik proporcjonalno

ś

ci (wzmocnienie)

T – stała czasowa

Transmitancja

ku

y

dt

dy

T

=

+

Transmitancja

Odpowied

ź

na wymuszenie skokowe

1

)

(

)

(

)

(

+

=

=

Ts

k

s

u

s

y

s

G

)

1

(

)

(

T

t

st

e

ku

t

y

−

−

=

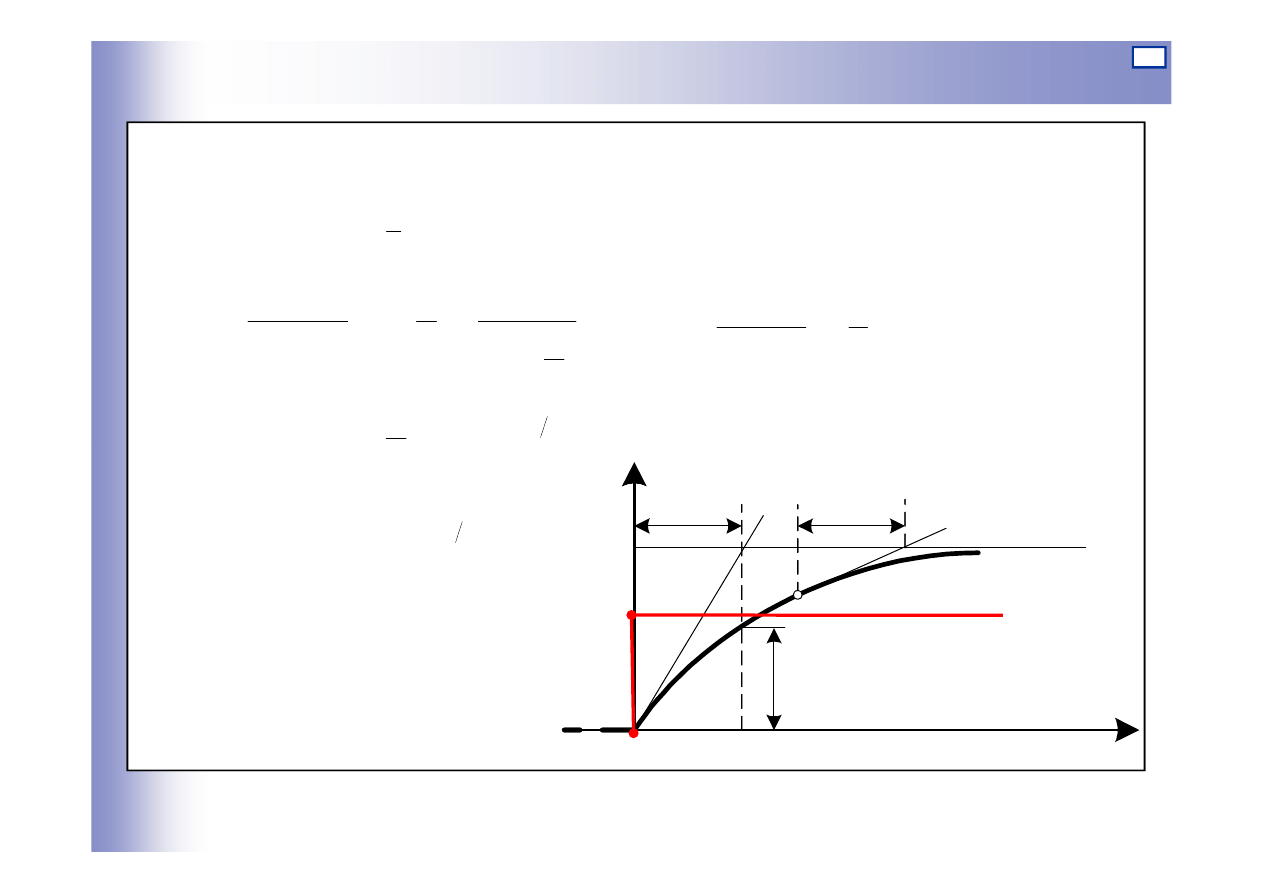
8

Elementy inercyjne pierwszego rz

ę

du

Odpowied

ź

na wymuszenie skokowe

st

u

s

s

u

1

)

(

=

)

1

(

1

)

1

(

)

(

T

s

s

u

T

k

u

Ts

s

k

s

y

st

st

+

=

+

=

)

1

(

)]

(

[

)

(

1

T

t

st

e

T

u

T

k

s

y

L

t

y

−

−

−

=

=

)

1

(

1

)

(

1

1

at

e

a

a

s

s

L

−

−

−

=













+

y

t

ku

st

T

T

0,632ku

st

)

1

(

)]

(

[

)

(

st

e

T

u

T

s

y

L

t

y

−

=

=

)

1

(

)

(

T

t

st

e

ku

t

y

−

−

=

9

Elementy inercyjne pierwszego rz

ę

du

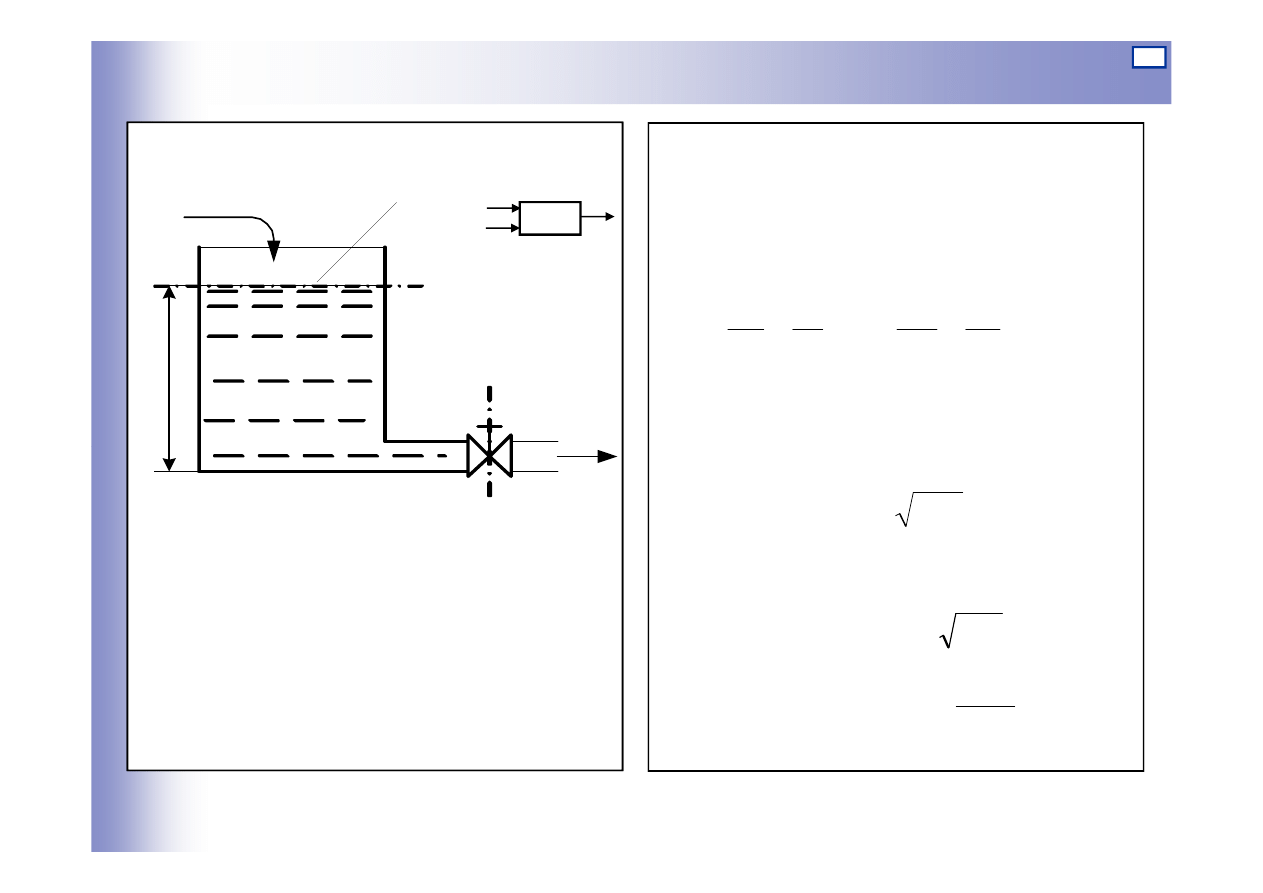
Przykład

Q

1

A

1

Q

2

2

1

h

f

Warunek stanu ustalonego

Z równania Bernoulliego

zakładaj

ą

c v

1

=0 oraz p

1

=p

2

=p

atm

20

10

Q

Q

=

0

2

2

2

2

2

1

2

1

+

+

=

+

+

γ

γ

p

g

v

h

p

g

v

h

Q

1

f

Wej

ś

cia

Q

1

– nat

ęż

enie przepływu cieczy

f – powierzchnia przekroju zaworu

Wyj

ś

cie

h – poziom cieczy w zbiorniku

2

2

1

1

2

atm

otrzymujemy:

Z równania ci

ą

gło

ś

ci:

Otrzymujemy:

gh

v

2

2

=

gh

f

fv

Q

2

2

2

=

=

2

2

2

2gf

Q

h

=

10

Elementy inercyjne pierwszego rz

ę

du

Przykład

Q

1

A

1

Q

2

2

1

h

f

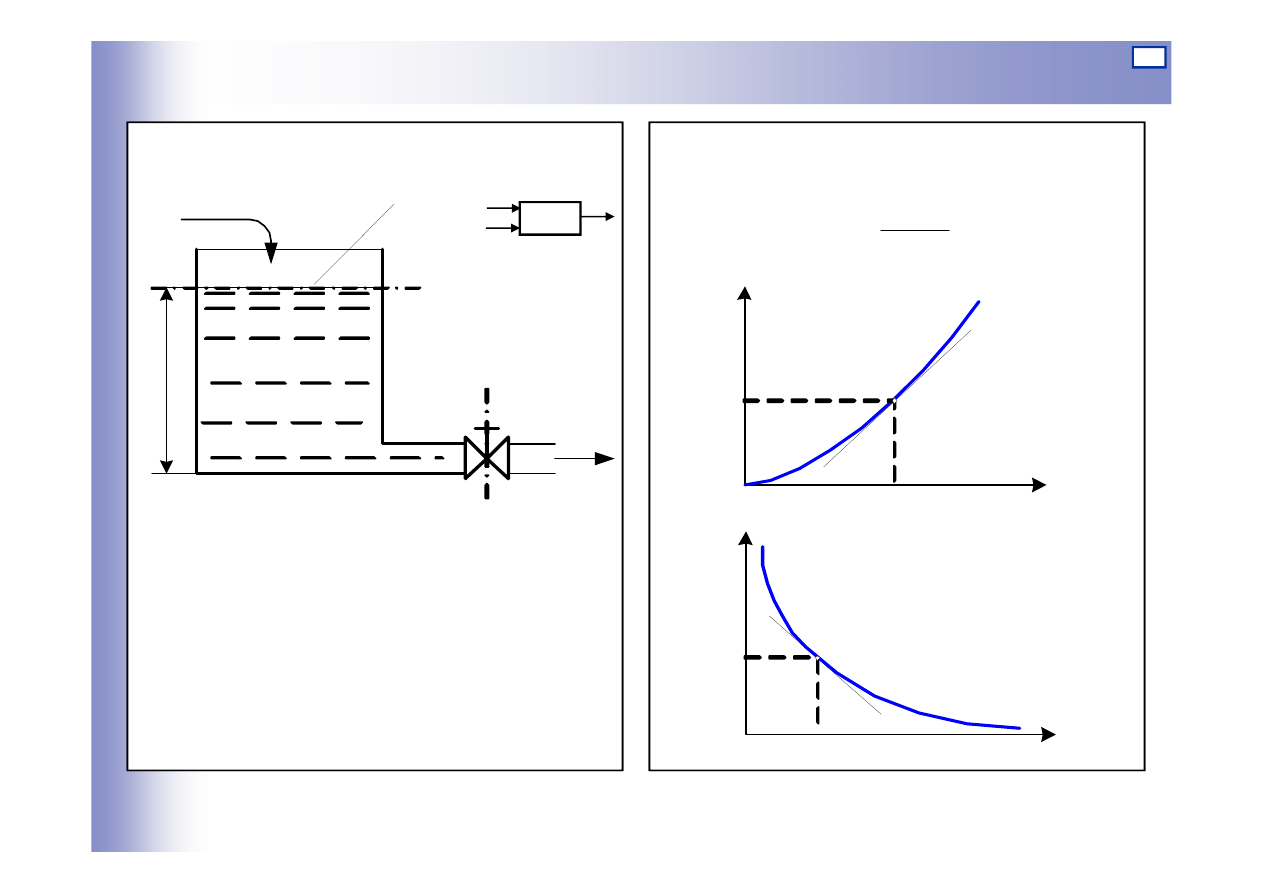
Charakterystyka statyczna

2

0

2

10

0

2gf

Q

h

=

h

0

h

n

f

0

=const

h

Q

1

f

Wej

ś

cia

Q

1

– nat

ęż

enie przepływu cieczy

f – powierzchnia przekroju zaworu

Wyj

ś

cie

h – poziom cieczy w zbiorniku

Q

2

2

Q

1n

Q

10

h

0

h

n

f

n

f

0

Q

10

=const

11

W stanie nieustalonym

linearyzacja dla punktu pracy h

n

, Q

1n

, f

n

Przyrost

∆

Q

2

zast

ę

pujemy ró

ż

niczk

ą

zupełn

ą

Elementy inercyjne pierwszego rz

ę

du

2

1

Q

Q

dt

dh

A

−

=

2

1

Q

Q

dt

h

d

A

∆

−

∆

=

∆

g

Q

Q





∂





∂

gh

f

Q

2

2

=

otrzymujemy

gdzie:

h

h

g

f

f

gh

h

h

Q

f

f

Q

Q

n

n

n

n

n

∆

+

∆

=

∆













∂

∂

+

∆













∂

∂

=

∆

2

2

2

2

2

f

k

Q

k

h

dt

h

d

T

∆

−

∆

=

∆

+

∆

2

1

1

n

n

h

g

f

A

T

2

=

n

n

h

g

f

k

2

1

1

=

n

n

f

h

k

2

2

=

12

Opuszczaj

ą

c znaki

∆

W przypadku, kiedy f

0

=const (f=0)

Elementy inercyjne pierwszego rz

ę

du

f

k

Q

k

h

dt

dh

T

2

1

1

−

=

+

1

1

Q

k

h

dt

dh

T

=

+

h

Q

1

f

kiedy Q

10

=const (Q

1

=0)

gdzie:

n

n

h

g

f

A

T

2

=

n

n

h

g

f

k

2

1

1

=

n

n

f

h

k

2

2

=

dt

f

k

h

dt

dh

T

2

−

=

+

Elementy inercyjne pierwszego rz

ę

du

13

1

1

Q

k

h

dt

dh

T

=

+

f

k

h

dt

dh

T

2

−

=

+

1

)

(

)

(

)

(

1

1

1

+

=

=

Ts

k

s

Q

s

h

s

G

1

)

(

)

(

)

(

2

2

+

−

=

=

Ts

k

s

f

s

h

s

G

f

k

Q

k

h

dt

dh

T

2

1

1

−

=

+

f

0

=const (f=0)

Q

10

=const (Q

1

=0)









+

−

+

=













1

1

)

(

)

(

)

(

)

(

2

1

1

Ts

k

Ts

k

s

f

s

h

s

Q

s

h

h

Q

1

f

14

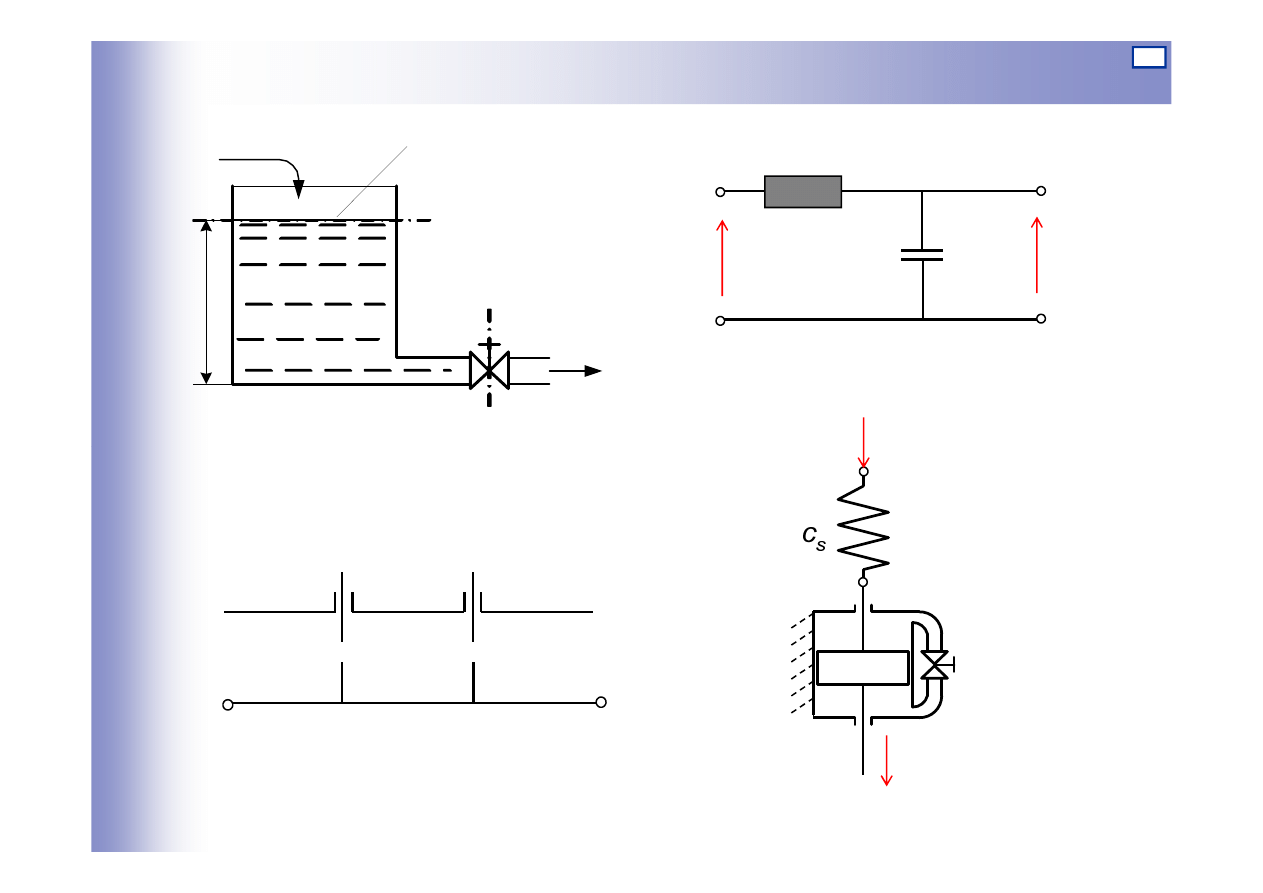
Elementy inercyjne – przykłady

Q

1

A

1

Q

2

2

2

1

h

f

U

1

U

2

R

C

Czwórnik RC

Zbiornik z wypływem swobodnym

u

u=Q

1

y=Q

2

u=u

1

y=u

2

p

1

p

2

p

k

f

1

f

2

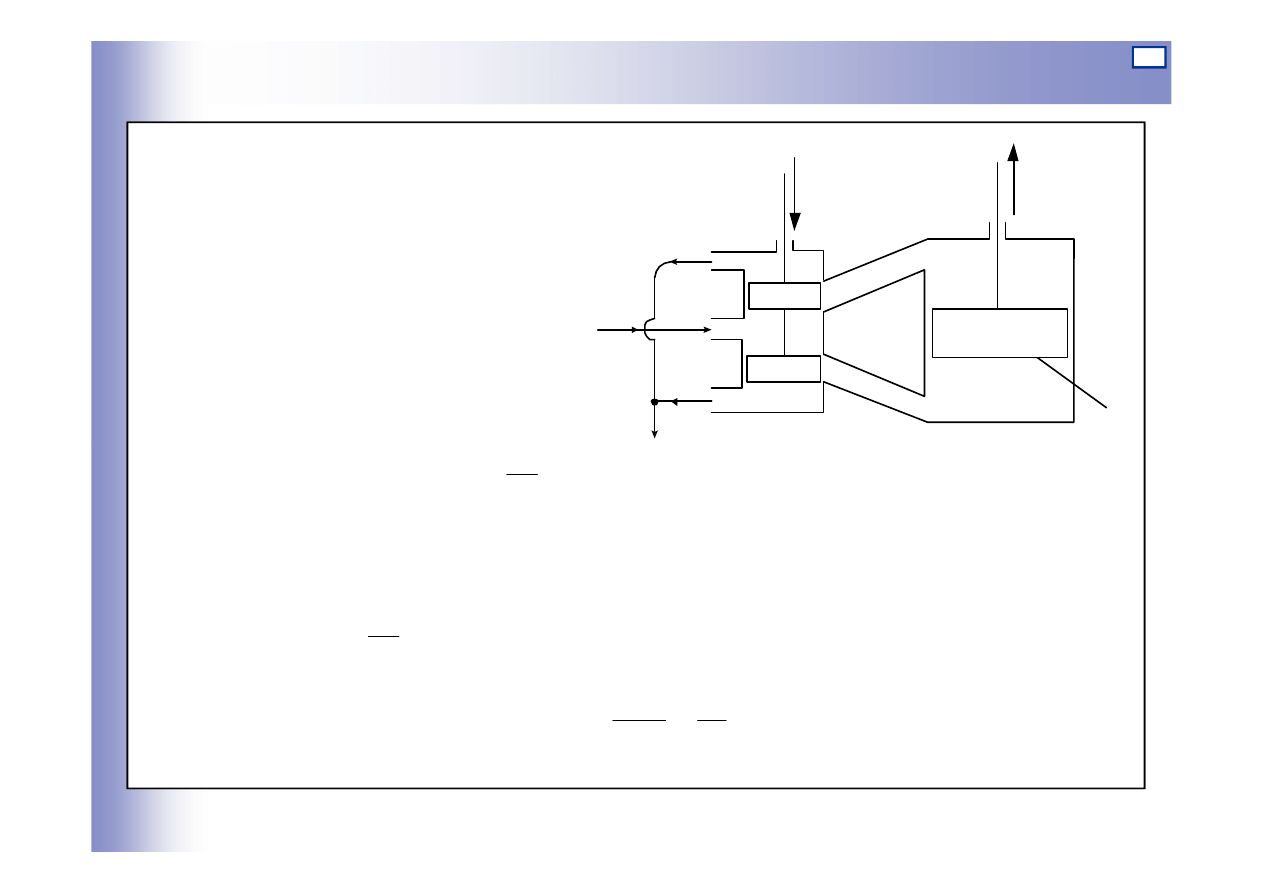
Kaskada pneumatyczna

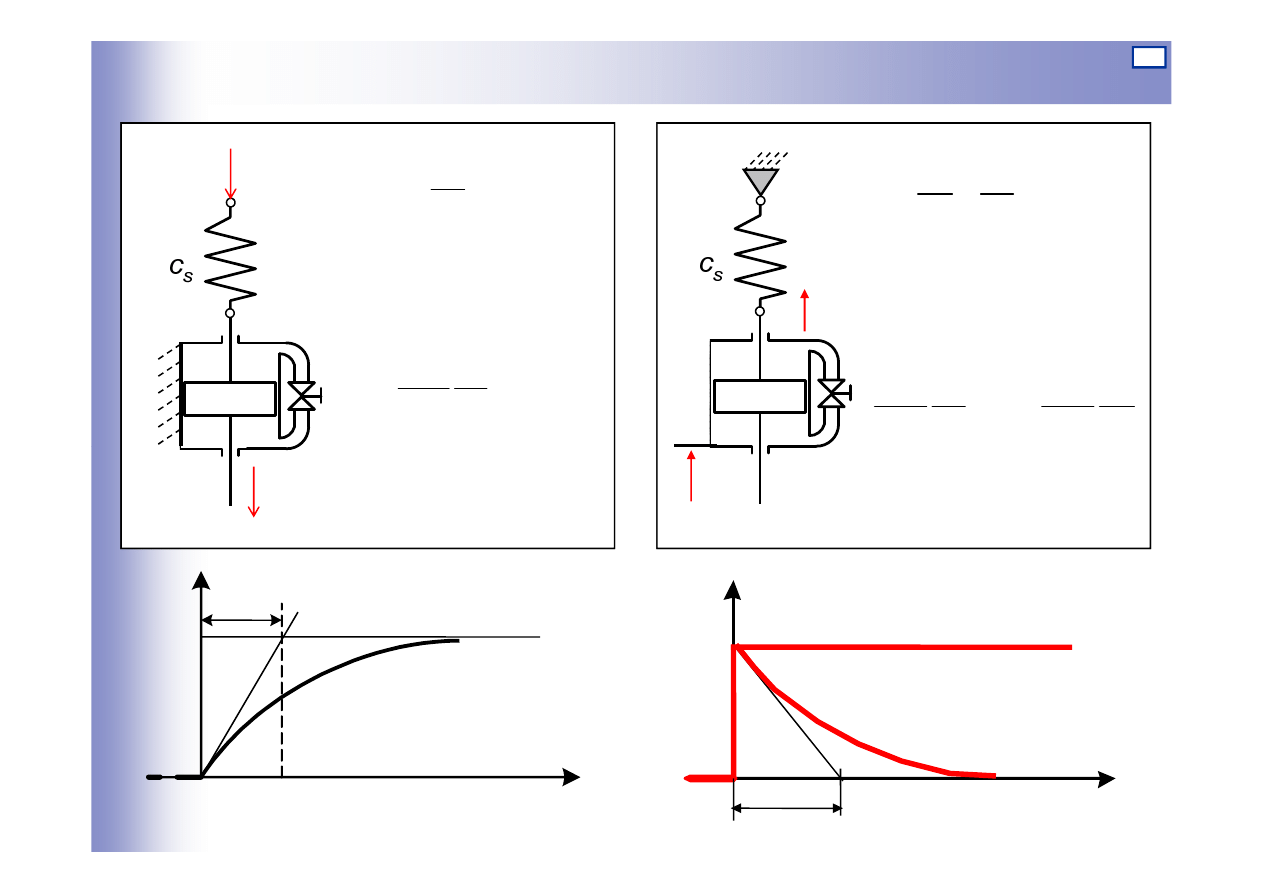
Zbiornik z wypływem swobodnym

y

u

Tłumik hydrauliczny

y=p

k

u

3

=f

1

u

1

=p

1

u

2

=p

2

u

4

=f

2

15

Elementy całkuj

ą

ce

Równanie ró

ż

niczkowe:

po scałkowaniu, przy zerowych warunkach pocz

ą

tkowych:

ku

dt

dy

=

∫

=

t

udt

k

y

Transmitancja:

gdy sygnały jednoimienne:

∫

=

udt

k

y

0

s

k

s

u

s

y

s

G

=

=

)

(

)

(

)

(

Ts

s

u

s

y

s

G

1

)

(

)

(

)

(

=

=

16

Elementy całkuj

ą

ce

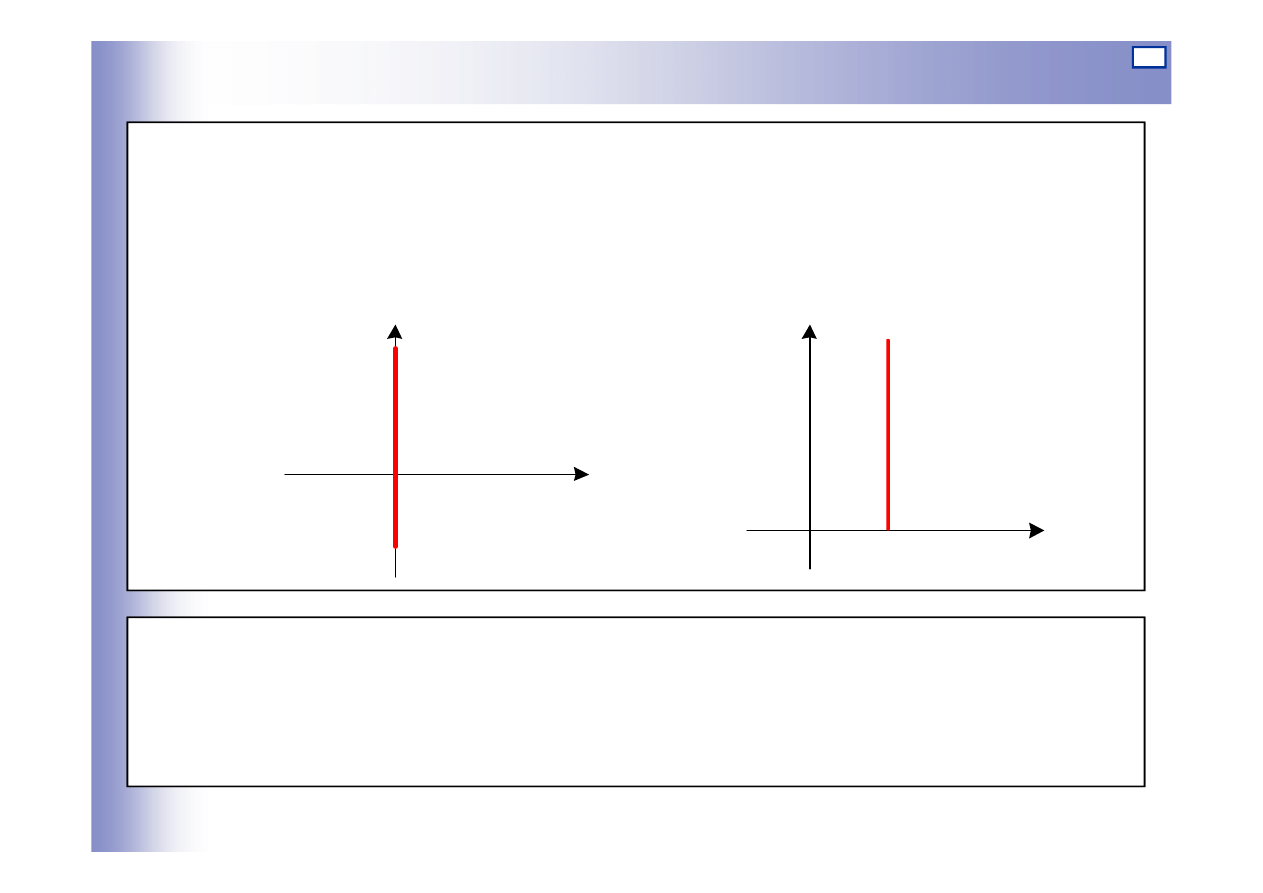
Charakterystyka statyczna

we współrz

ę

dnych odchyłek a) i warto

ś

ci absolutnych b)

0

=

u

y

y

0

a)

b)

Odpowied

ź

na wymuszenie skokowe

u

u

0

0

u

n

t

ku

s

y

L

t

y

st

=

=

−

)]

(

[

)

(

1

17

Elementy całkuj

ą

ce

Odpowied

ź

na wymuszenie skokowe

kiedy wej

ś

cie i wyj

ś

cie

s

ą

sygnałami jednoimiennymi, to k = 1/T

gdzie T jest stał

ą

czasow

ą

akcji całkuj

ą

cej

– stał

ą

całkowania

st

u

s

k

s

u

s

k

s

y

2

)

(

)

(

=

=

t

ku

s

y

L

t

y

st

=

=

−

)]

(

[

)

(

1

u

dt

dy

T

=

s

y

s

G

1

)

(

)

(

=

=

– stał

ą

całkowania

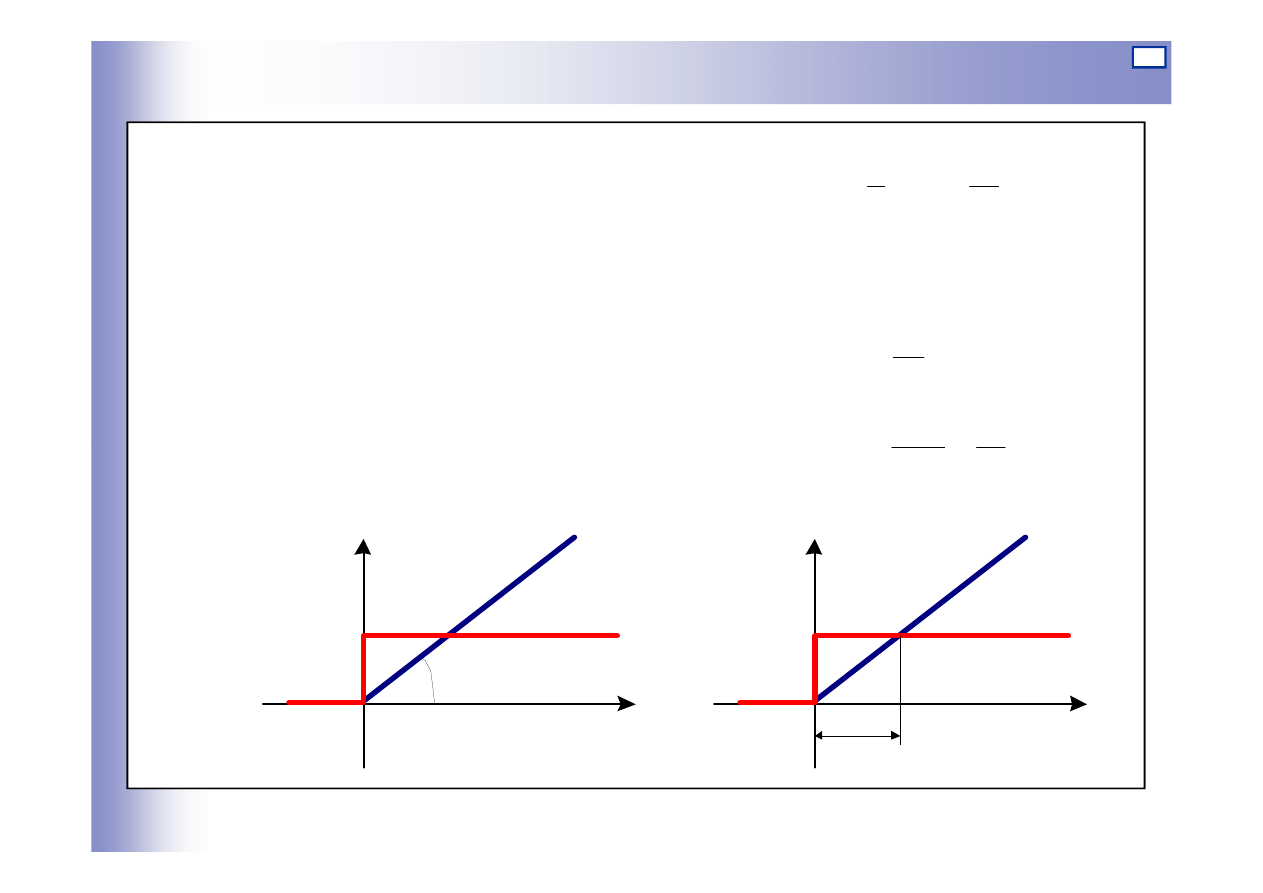
a)

b)

t

u y

u

st

y(t)

u(t)

arctg ku

st

t

u y

u

st

y(t)

u(t)

T

Ts

s

u

s

G

)

(

)

(

=

=

18

Elementy całkuj

ą

ce

Przykład

Zało

ż

enia:

a) stałe p

z

i p

s

b) zerowe obci

ąż

enie siłownika

c) stała pr

ę

dko

ść

v przepływu

medium przez rozdzielacz

dy

y

A

u

p

z

p

s

Stan dynamiczny:

z równania ci

ą

gło

ś

ci:

gdzie ub – przekrój szczeliny

otrzymujemy:

gdzie

dt

dy

A

Q

=

ubv

Q

=

u

dt

dy

T

=

bv

A

T

/

=

Ts

s

u

s

y

s

G

1

)

(

)

(

)

(

=

=

19

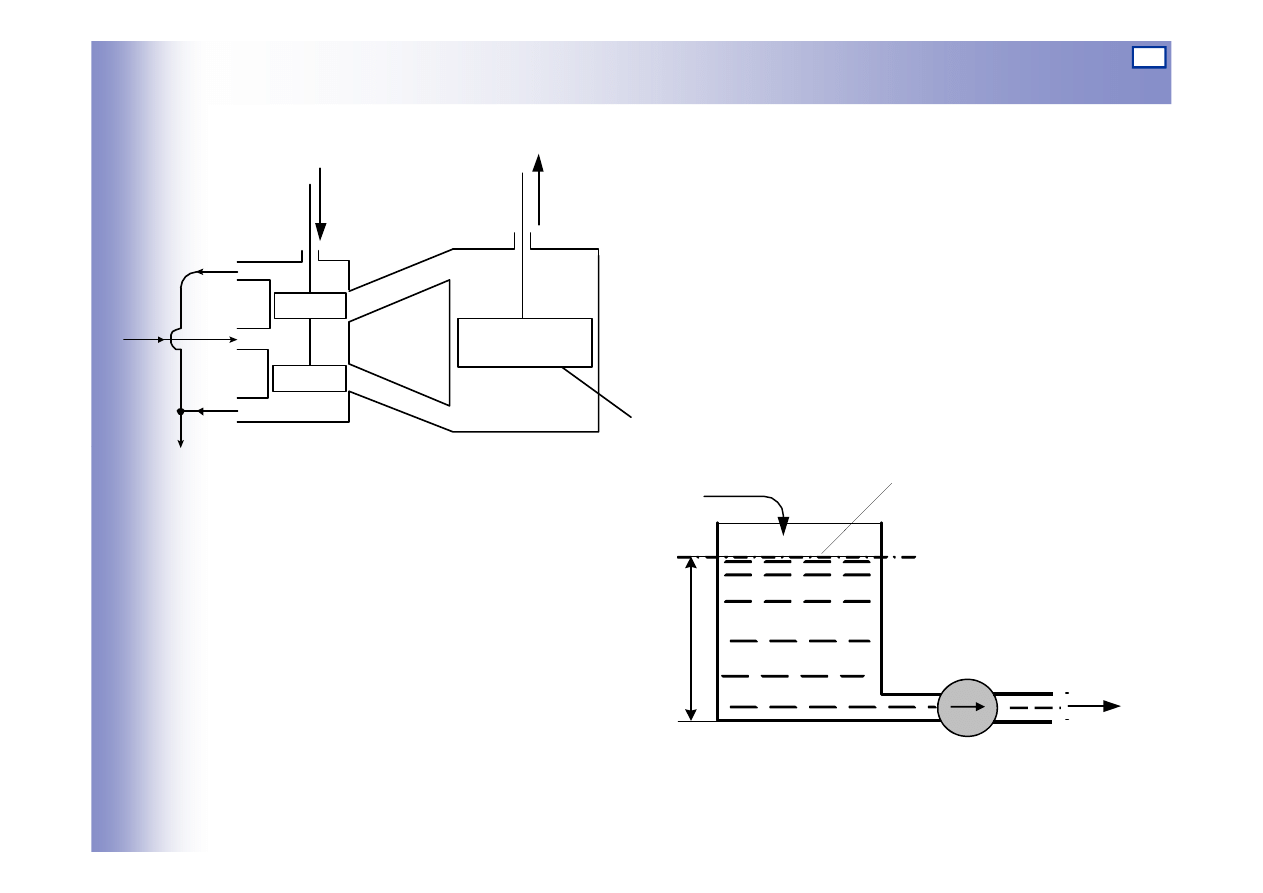
Elementy całkuj

ą

ce - przykłady

y

A

u

p

z

p

s

Zbiornik z wymuszonym

poborem cieczy

Zespół siłownik - rozdzielacz

hydrauliczny

Q

1

A

1

1

h

Q

2

y=h

u=Q

2

20

Elementy ró

ż

niczkuj

ą

ce

Równanie ró

ż

niczkowe

k – współczynnik definiowany jako

Transmitancja

dt

du

k

y

=

dt

du

y

k

=

ks

s

u

s

y

s

G

=

=

)

(

)

(

)

(

Charakterystyka statyczna

we współrz

ę

dnych:

a) odchyłek

b) warto

ś

ci absolutnych

u

y

u

0

y

0

0

a)

b)

y

n

21

Odpowied

ź

na wymuszenie skokowe

Elementy ró

ż

niczkuj

ą

ce

)

(

)

(

s

ksu

s

y

=

)

(

)]

(

[

)

(

1

t

ku

s

y

L

t

y

st

δ

=

=

−









=

∞

<

=

0

dla

0

dla

0

)

(

t

t

t

y

dt

du

k

y

=

st

u

s

s

u

1

)

(

=

st

ku

s

y

=

)

(

t

y

∞

Kiedy wej

ś

cie i wyj

ś

cie s

ą

sygnałami jednoimiennymi zapisujemy:

gdzie: T jest stał

ą

czasow

ą

akcji ró

ż

niczkuj

ą

cej (stała ró

ż

niczkowania)







>

0

dla

0

t

Ts

s

u

s

y

s

G

=

=

)

(

)

(

)

(

t

0

22

Elementy ró

ż

niczkuj

ą

ce rzeczywiste

Równanie ró

ż

niczkowe

Transmitancja

gdzie:

k – współczynnik proporcjonalno

ś

ci akcji ró

ż

niczkuj

ą

cej

dt

du

k

y

dt

dy

T

=

+

1

)

(

)

(

)

(

+

=

=

Ts

ks

s

u

s

y

s

G

T – stała czasowa cz

ęś

ci inercyjnej

Dla sygnałów jednoimiennych u i y:

Charakterystyka statyczna

jak dla elementów ró

ż

niczkuj

ą

cych idealnych

1

)

(

)

(

)

(

+

=

=

Ts

Ts

s

u

s

y

s

G

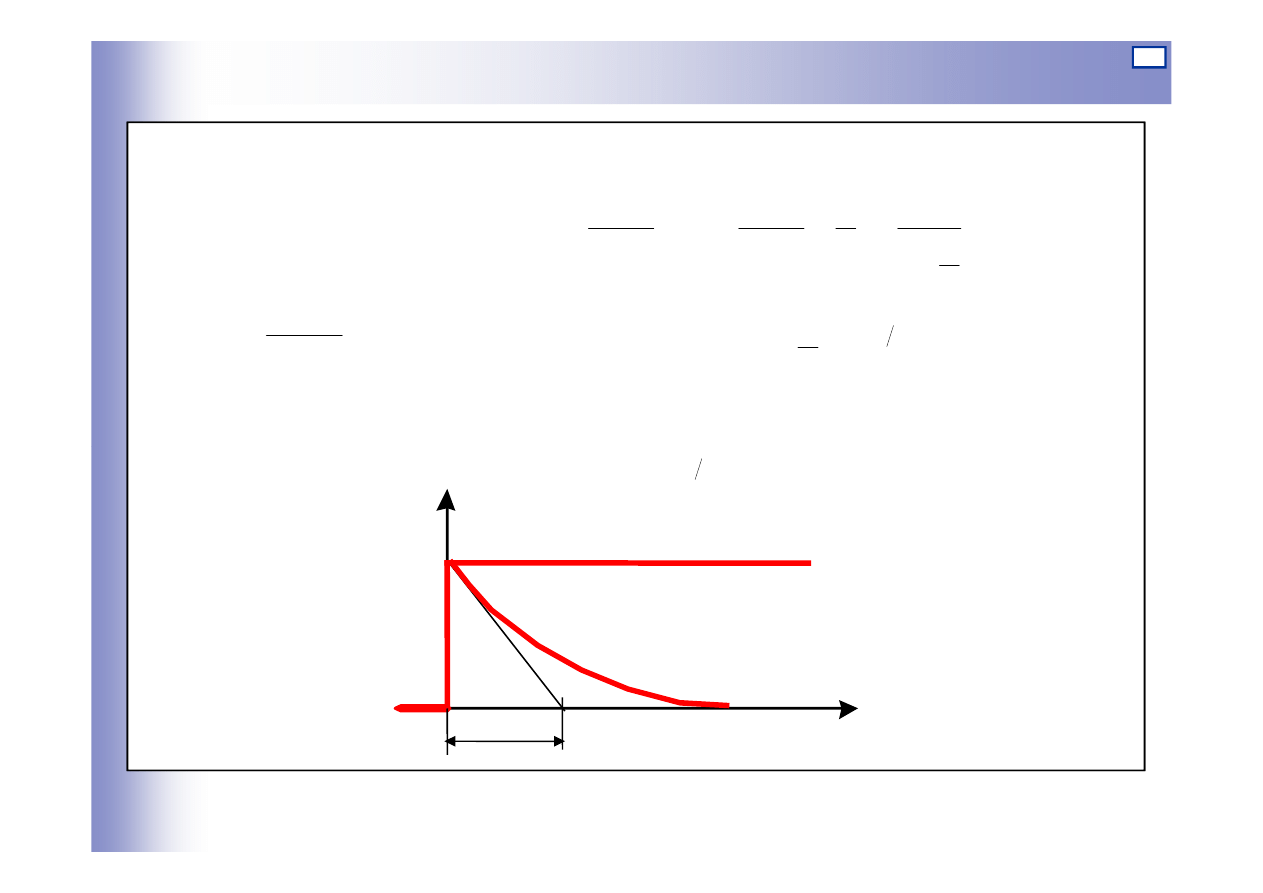
23

Odpowied

ź

na wymuszenie skokowe:

dla sygnałów jednoimiennych:

Elementy ró

ż

niczkuj

ą

ce rzeczywiste

T

s

u

T

k

Ts

ku

s

u

Ts

ks

s

y

st

st

1

1

1

)

(

1

)

(

+

=

+

=

+

=

T

t

st

e

u

T

k

s

y

L

t

y

−

−

=

=

)]

(

[

)

(

1

at

e

a

s

L

−

−

=













+

)

(

1

1

T

t

st

e

u

t

y

−

=

)

(

y

t

u

st

T

u(t)

y(t)

0

24

Elementy ró

ż

niczkuj

ą

ce - rzeczywiste

Czwórnik RC

U

1

U

2

R

C

y=u

2

u=u

1

y

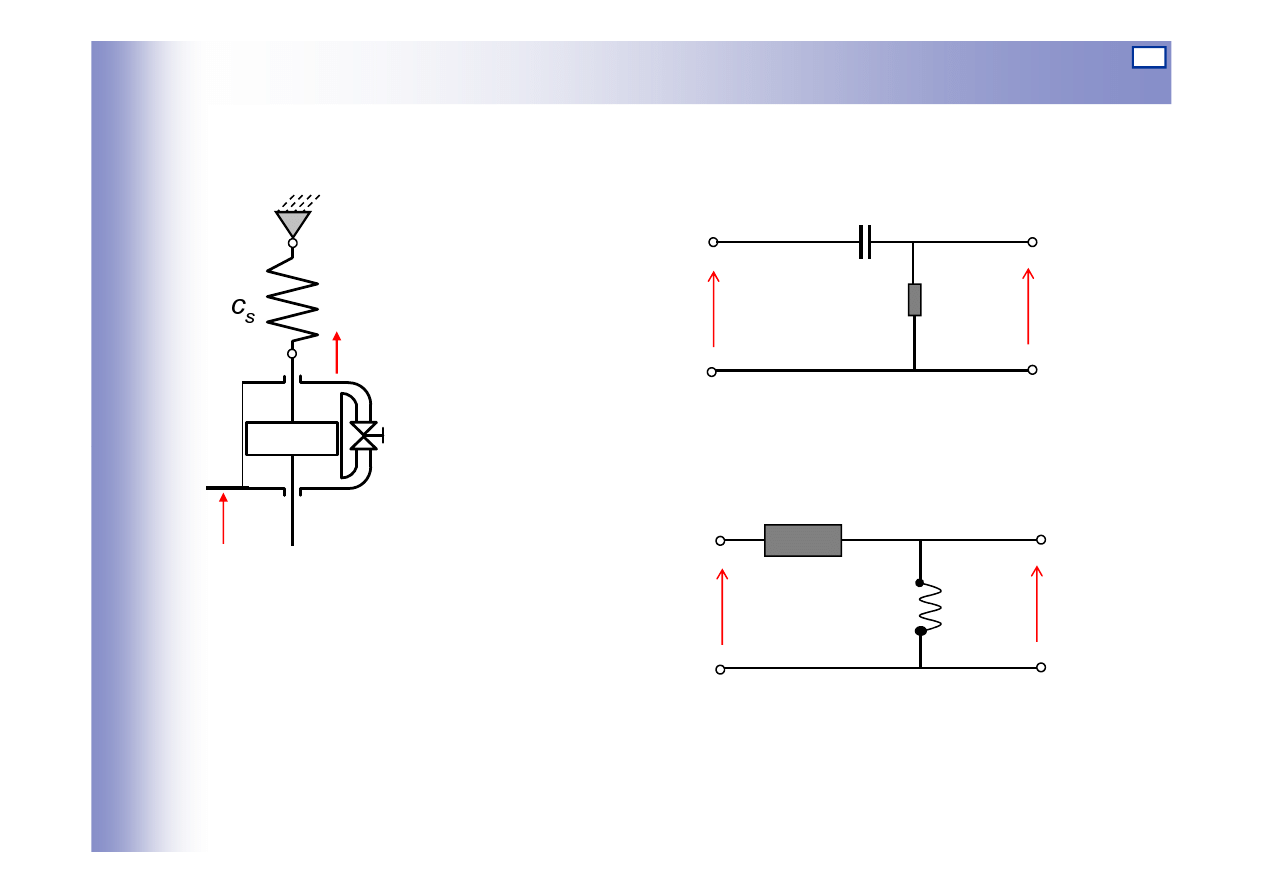
Tłumik hydrauliczny

ze spr

ęż

yn

ą

Czwórnik RL

U

1

U

2

R

L

u=u

1

y=u

2

U

25

Zale

ż

no

ść

transmitancja od we-wy

pA

C

y

u

s

∆

=

−

)

(

p

dt

dy

A

∆

=

α

u

u

y

dt

dy

C

A

s

=

+

α

2

p

dt

dy

dt

du

A

∆

=













−

α

pA

yC

s

∆

=

dt

du

C

A

y

dt

dy

C

A

s

s

α

α

2

2

=

+

y

y

s

s

U

t

u

st

T

u(t)

y(t)

0

y

t

u

st

T

26

Elementy oscylacyjne

Równanie ró

ż

niczkowe

Transmitancja:

2

1

2

2

4T

T

<

ku

y

dt

dy

T

dt

y

d

T

=

+

+

2

2

2

2

1

1

)

(

)

(

)

(

2

2

2

1

+

+

=

=

s

T

s

T

k

s

u

s

y

s

G

u

T

k

y

T

dt

dy

T

T

dt

y

d

2

1

2

1

2

1

2

2

2

1

=

+

+

Równanie ró

ż

niczkowe

Transmitancja :

gdzie: k – współczynnik proporcjonalno

ś

ci

– pulsacja oscylacji własnych

– zredukowany (wzgl

ę

dny) współczynnik tłumienia

u

k

y

dt

dy

dt

y

d

2

0

2

0

0

2

2

2

ω

ω

ζω

=

+

+

2

0

0

2

2

0

2

)

(

)

(

)

(

ω

ζω

ω

+

+

=

=

s

s

k

s

u

s

y

s

G

1

2

<

ζ

1

0

/

1

T

=

ω

1

2

2

/

T

T

=

ζ

27

Charakterystyka statyczna

we współrz

ę

dnych:

a) odchyłek

Elementy oscylacyjne

ku

y

=

u

y

a)

b) warto

ś

ci absolutnych

C

ku

y

+

=

0

0

u

0

y

0

c

0

b)

28

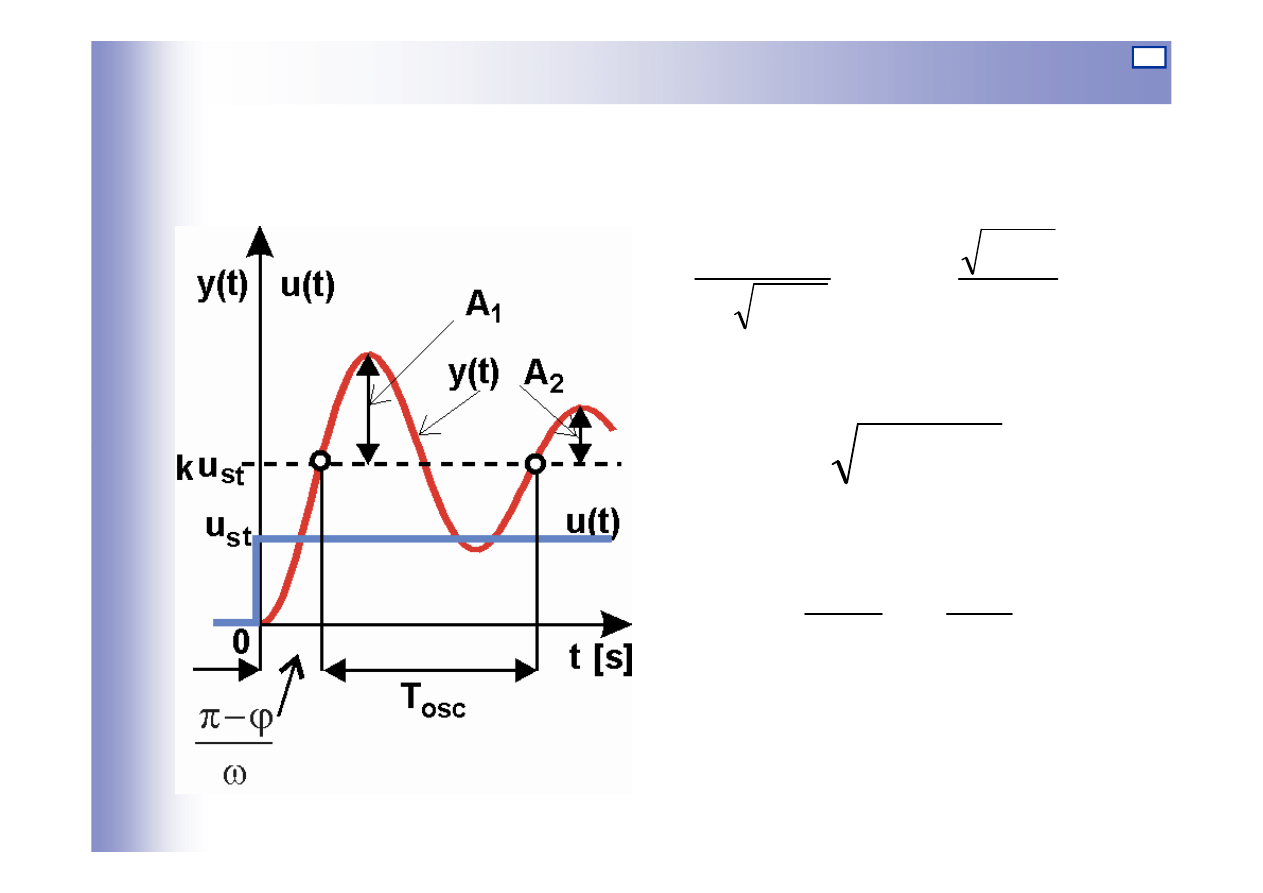
Odpowied

ź

na wymuszenie skokowe

pierwiastki wielomianu N(s):

Elementy oscylacyjne













+

+

=













+

+

=













=

−

−

−

)

1

(

1

)

1

(

)

(

)

(

)

(

2

2

2

1

1

2

2

2

1

1

1

s

T

s

T

s

L

ku

u

s

T

s

T

s

k

L

u

s

sN

s

M

L

t

y

st

st

st









−









−

=

−

±

−

=

1

1

4

2

2

2

2

1

2

2

2

2

,

1

T

T

T

T

T

s

m

lub:

lub

to

odpowied

ź

jest oscylacyjna gdy:

lub











−









−

=

=

1

2

2

2

1

2

1

2

1

2

1

1

2

2

2

,

1

T

T

T

T

s

m

1

0

1

T

=

ω

1

2

2T

T

=

ζ

)

1

(

2

0

2

,

1

−

−

=

ζ

ζ

ω

m

s

2

1

2

2

4T

T

<

1

2

<

ζ

29

Odpowied

ź

na wymuszenie skokowe

zapisuj

ą

c

lub

otrzymujemy

Elementy oscylacyjne



























−

−

=

2

1

2

1

2

1

2

,

1

2

1

2

1

T

T

j

T

T

T

s

m

)

1

(

2

0

2

,

1

ζ

ζ

ω

−

−

=

j

s

m





1

1

Stosuj

ą

c wzory Eulera

mo

ż

na uzyska

ć

:

gdzie:













−

+

−

+

=

t

s

t

s

st

e

s

s

s

T

e

s

s

s

T

ku

t

y

2

1

)

(

1

)

(

1

1

)

(

1

2

2

2

1

2

1

1

2

1

















+

−

−

−

=

−

)

1

sin(

1

1

)

(

2

0

2

1

0

ϕ

ζ

ω

ζ

ζω

t

e

e

ku

t

y

t

s

t

st

ζ

ζ

ζ

ϕ

arccos

1

2

=

−

=

arctg

)

sin

(cos

v

j

v

e

e

u

jv

u

+

=

+

Elementy oscylacyjne

30

2

2

;

α

+

ω

=

ω

k>1

1

0

〈

ξ

〈

;

ξ

ξ

−

=

ϕ

ξ

−

ω

π

=

2

2

0

osc

1

tg

;

1

2

T

,

A

A

ln

T

1

2

1

osc

=

α

o

2

2

o

/

;

ω

α

=

ξ

α

+

ω

=

ω

31

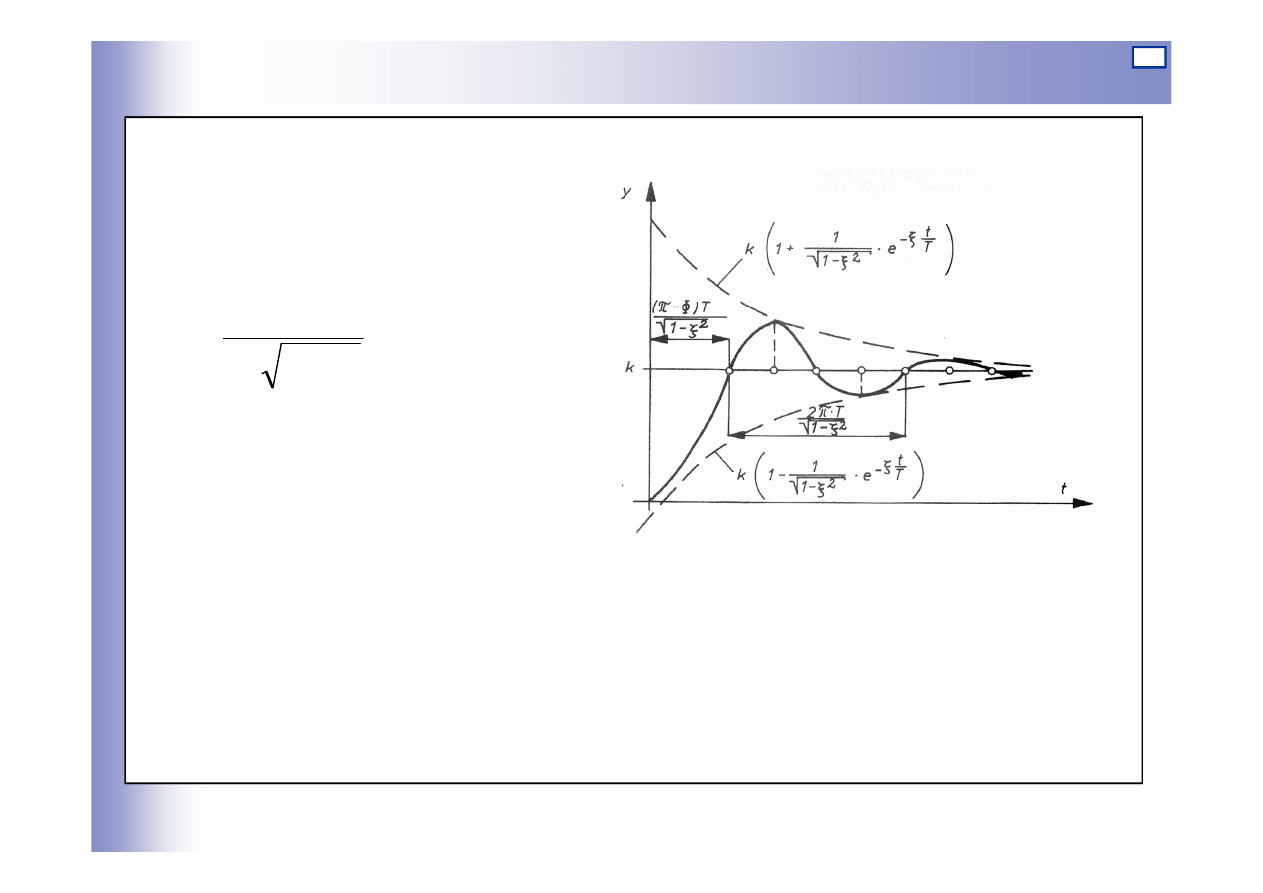
Odpowied

ź

na wymuszenie skokowe

składowa stała:

okres gasn

ą

cej sinusoidy:

Elementy oscylacyjne

st

ku

2

0

1

2

ζ

ω

π

−

1

T

T

≡

dla

ζ

= 0 (T

2

= 0) wyst

ę

puj

ą

drgania zachowawcze (nie tłumione)

o pulsacji

ω

0

, wtedy:

]

cos

1

[

)

(

)]

90

sin(

1

[

)

(

0

0

t

ku

t

y

t

ku

t

y

st

st

ω

ω

−

=

+

−

=

o

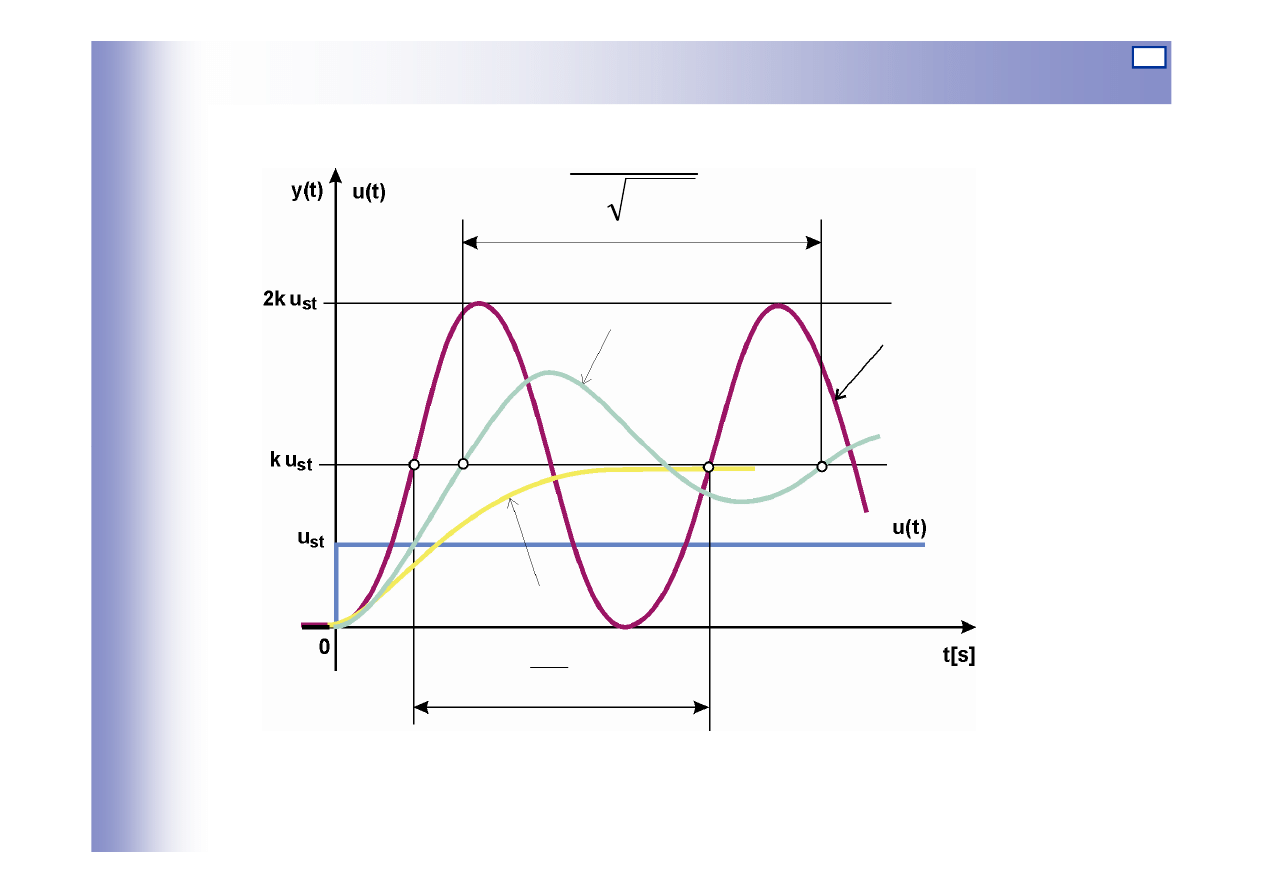
Elementy oscylacyjne

32

2

0

1

2

ξ

−

ω

π

1

0 〈

ξ

〈

0

=

ξ

0

2

ω

π

1

≥

ξ

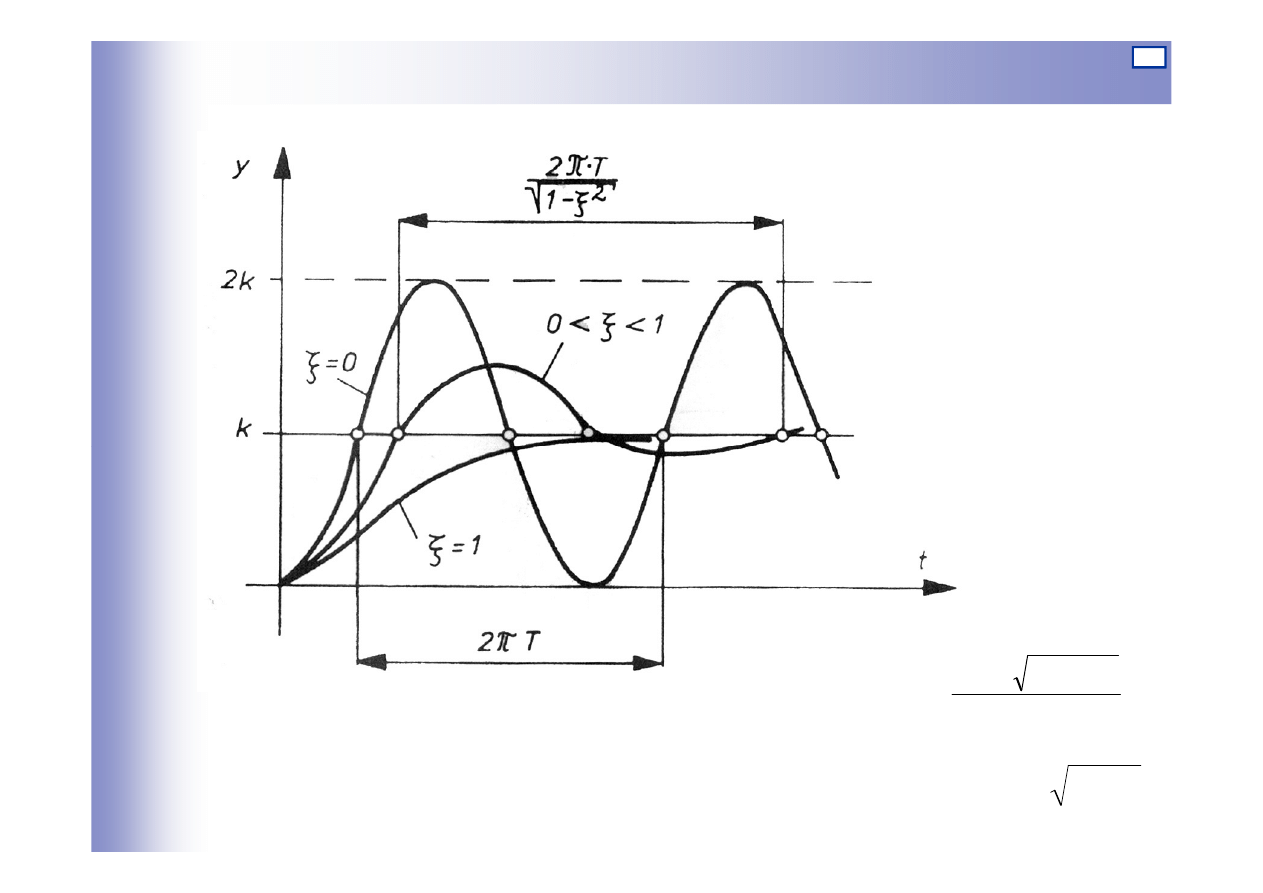
33

Elementy oscylacyjne

1

T

T

≡

2

1

2

1

2

2

2

2

,

1

2

4

T

T

T

T

s

−

±

−

=

)

1

(

2

0

2

,

1

−

−

=

ζ

ζ

ω

m

s

2

1

2

2

4T

T

=

1

2

=

ζ

34

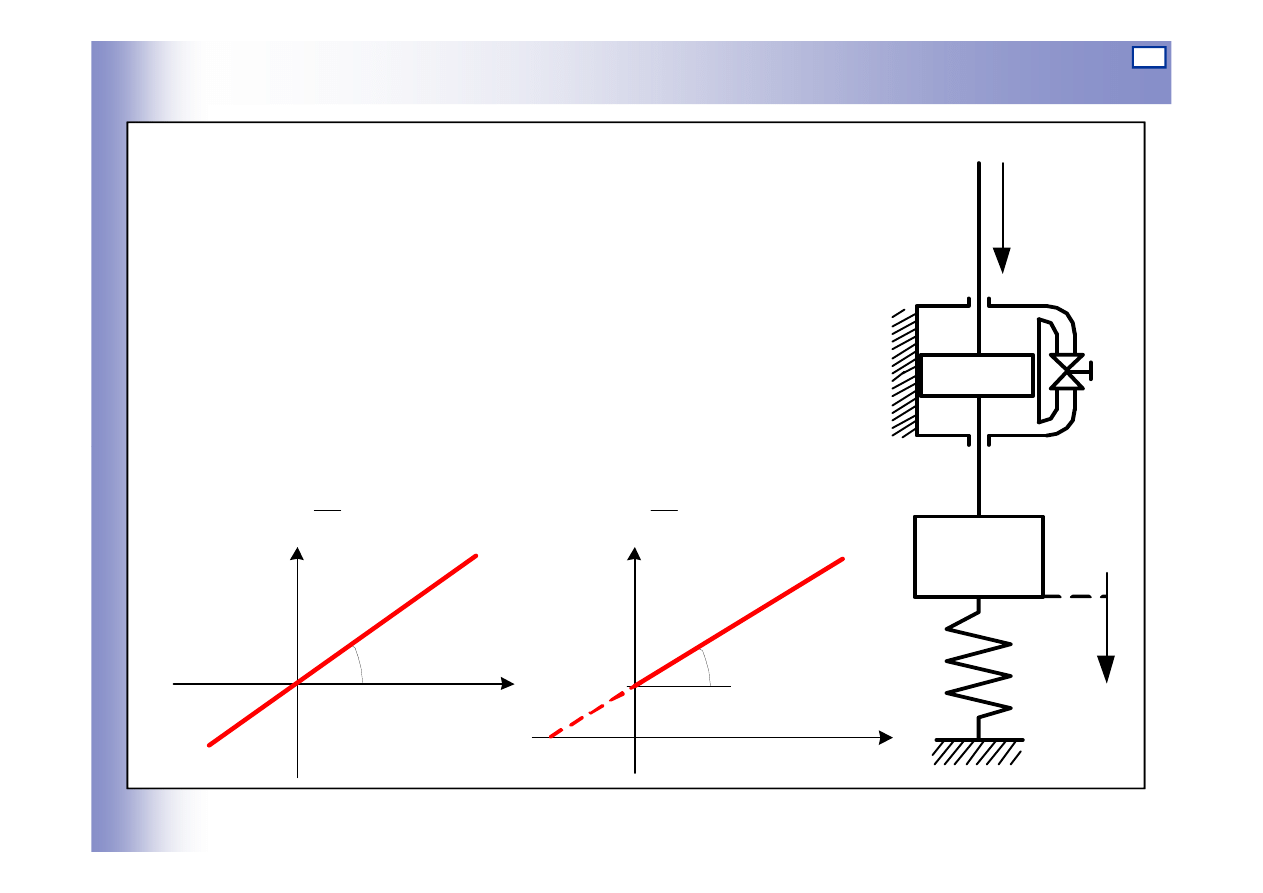
Elementy oscylacyjne

Przykład

siła F – sygnał wej

ś

ciowy

przesuni

ę

cie y – sygnał wyj

ś

ciowy

W stanie ustalonym:

F

c

t

0

0

y

c

mg

F

s

=

+

m

y

c

s

)

(

1

0

0

mg

F

c

y

s

+

=

F

y

a)

arctg 1/c

s

arctg 1/c

s

F

0

y

0

0

b)

- mg

F

c

y

s

1

=

35

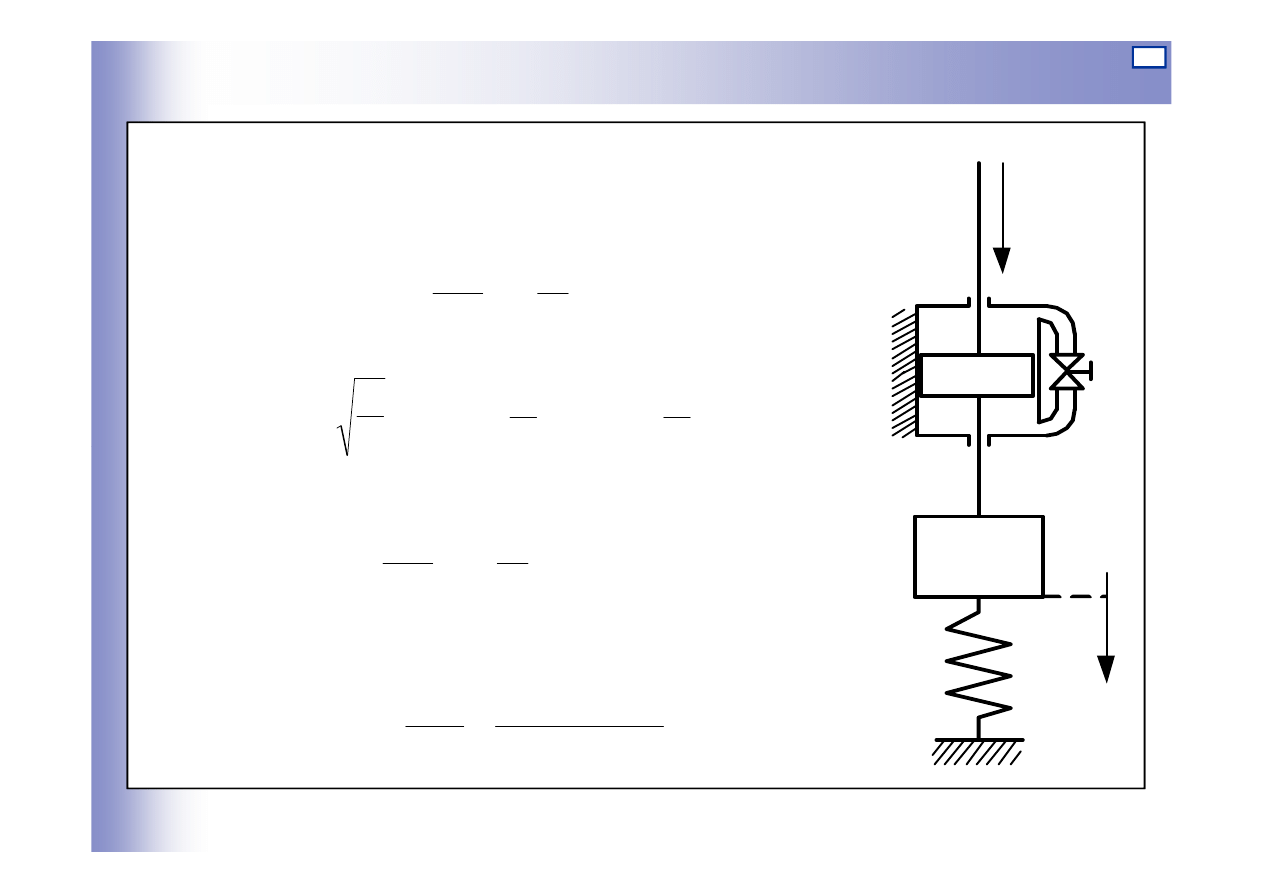
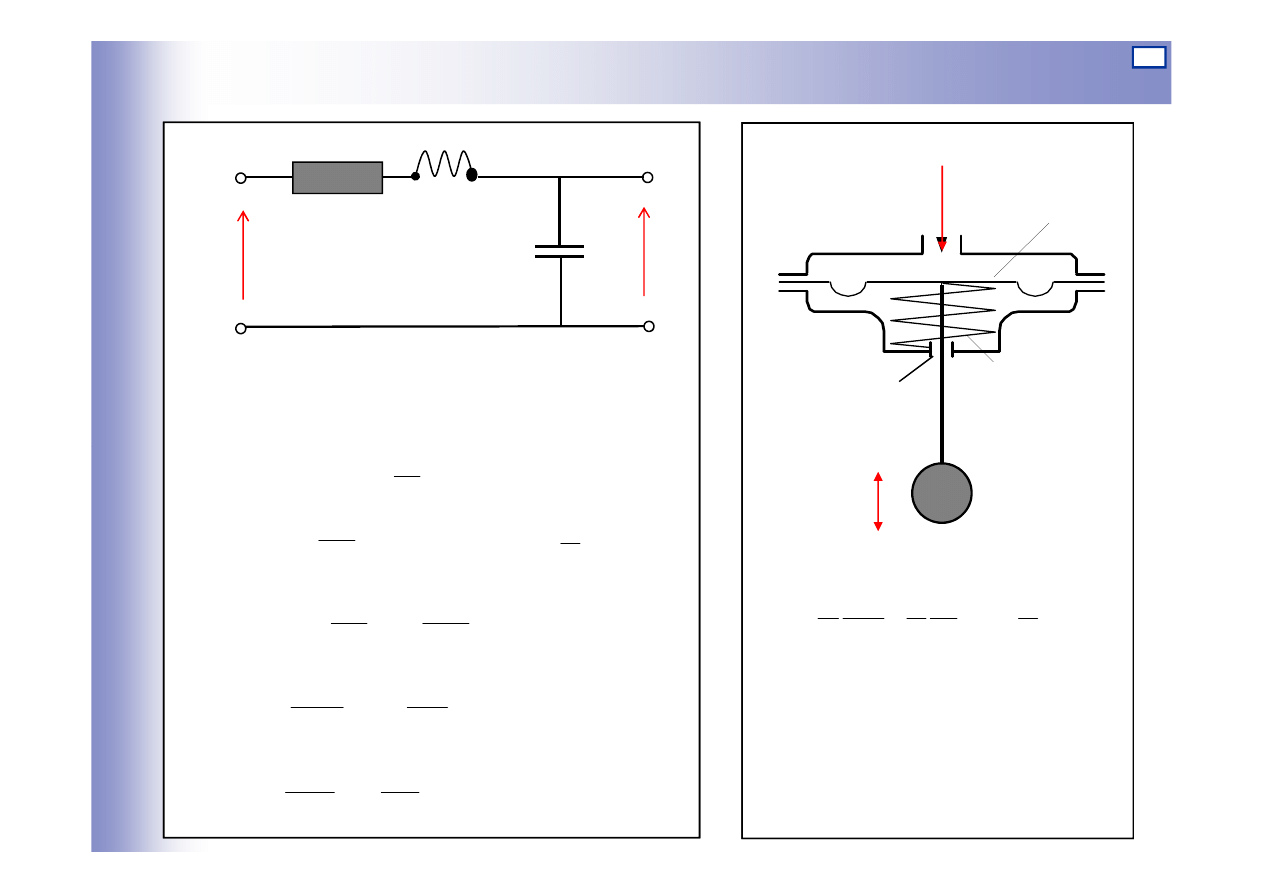
Elementy oscylacyjne

Przykład

równanie równowagi

je

ż

eli:

F

c

t

y

c

dt

dy

c

dt

y

d

m

F

s

t

+

+

=

2

2

s

c

m

T

=

1

s

t

c

c

T

=

2

s

c

k

1

=

to:

st

ą

d transmitancja:

m

y

c

s

s

c

s

c

s

c

kF

y

dt

dy

T

dt

y

d

T

=

+

+

2

2

2

2

1

1

)

(

)

(

)

(

2

2

2

1

+

+

=

=

s

T

s

T

k

s

F

s

y

s

G

36

Elementy oscylacyjne

di

L

U

1

U

2

R

C

Czwórnik RLC

p

A

c

f)

c

u=p

B

2

1

u

dt

di

L

Ri

u

+

+

=

∫

∝

−

=

t

idt

C

u

1

2

dt

du

C

i

2

=

1

2

2

2

2

2

u

u

dt

du

RC

dt

u

d

LC

=

+

+

2

2

2

2

2

1

u

dt

u

d

LC

dt

du

RC

u

+

+

=

1

2

2

2

2

2

2

2

1

u

u

dt

du

T

dt

u

d

T

=

+

+

m

y

p

c

A

y

dt

dy

c

B

dt

y

d

c

m

=

+

+

2

2

37

Elementy opó

ź

niaj

ą

ce

Równanie elementu opó

ź

niaj

ą

cego:

Sk

ą

d wynika transmitancja:

)

(

)

(

τ

−

=

t

u

t

y

s

e

s

u

s

y

s

G

τ

−

=

=

)

(

)

(

)

(

Charakterystyka statyczna

lub

u

y

=

0

0

u

y

=

lub

u

y

=

0

0

u

y

=

Odpowied

ź

na wymuszenie skokowe:

y(t)

38

Elementy opó

ź

niaj

ą

ce

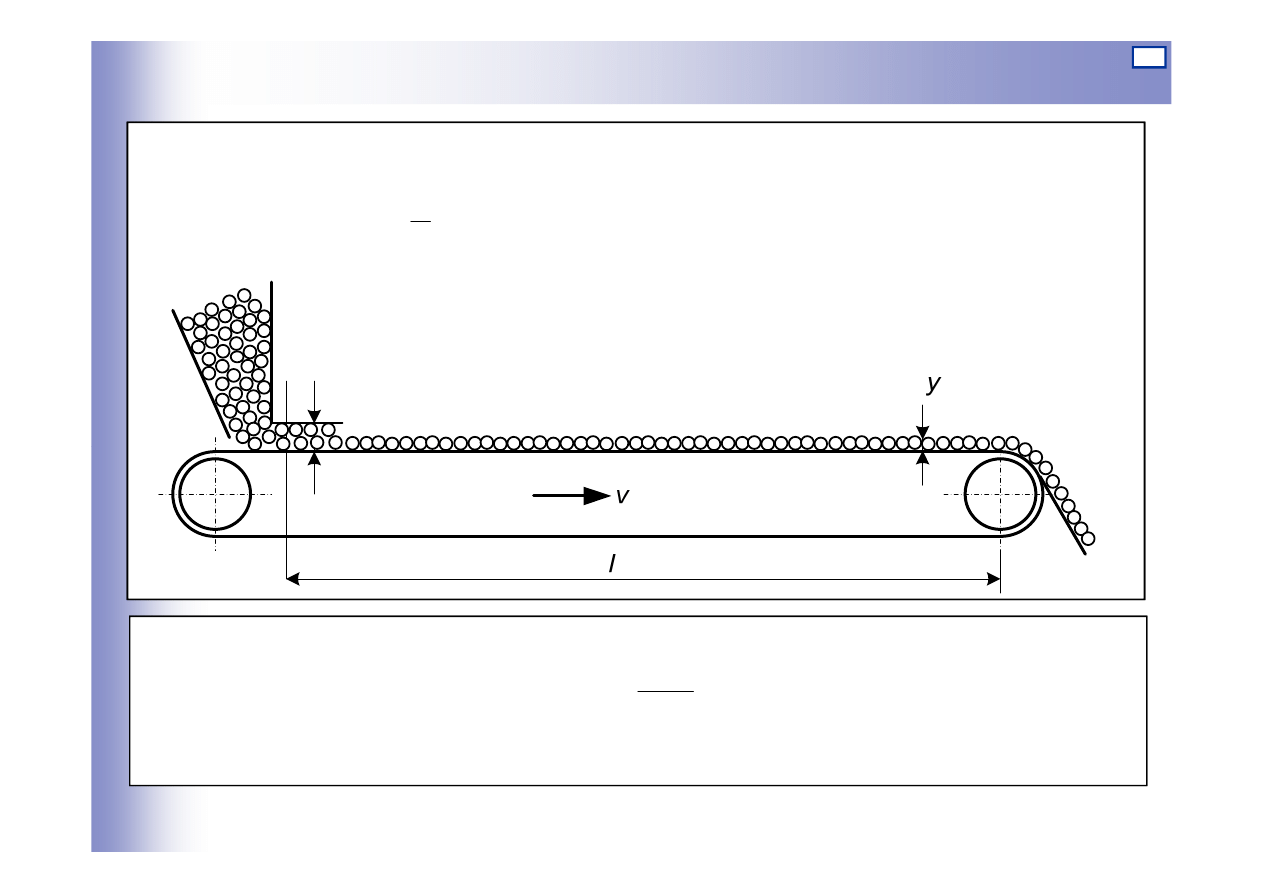
Przykład 1. Podajnik ta

ś

mowy

Opó

ź

nienie:

gdzie: l – odległo

ść

[m]

v – pr

ę

dko

ść

ta

ś

my [m/s]

v

l

τ

=

u

Transmitancja

τ

s

e

u(s)

y(s)

G(s)

−

=

=

39

Elementy opó

ź

niaj

ą

ce

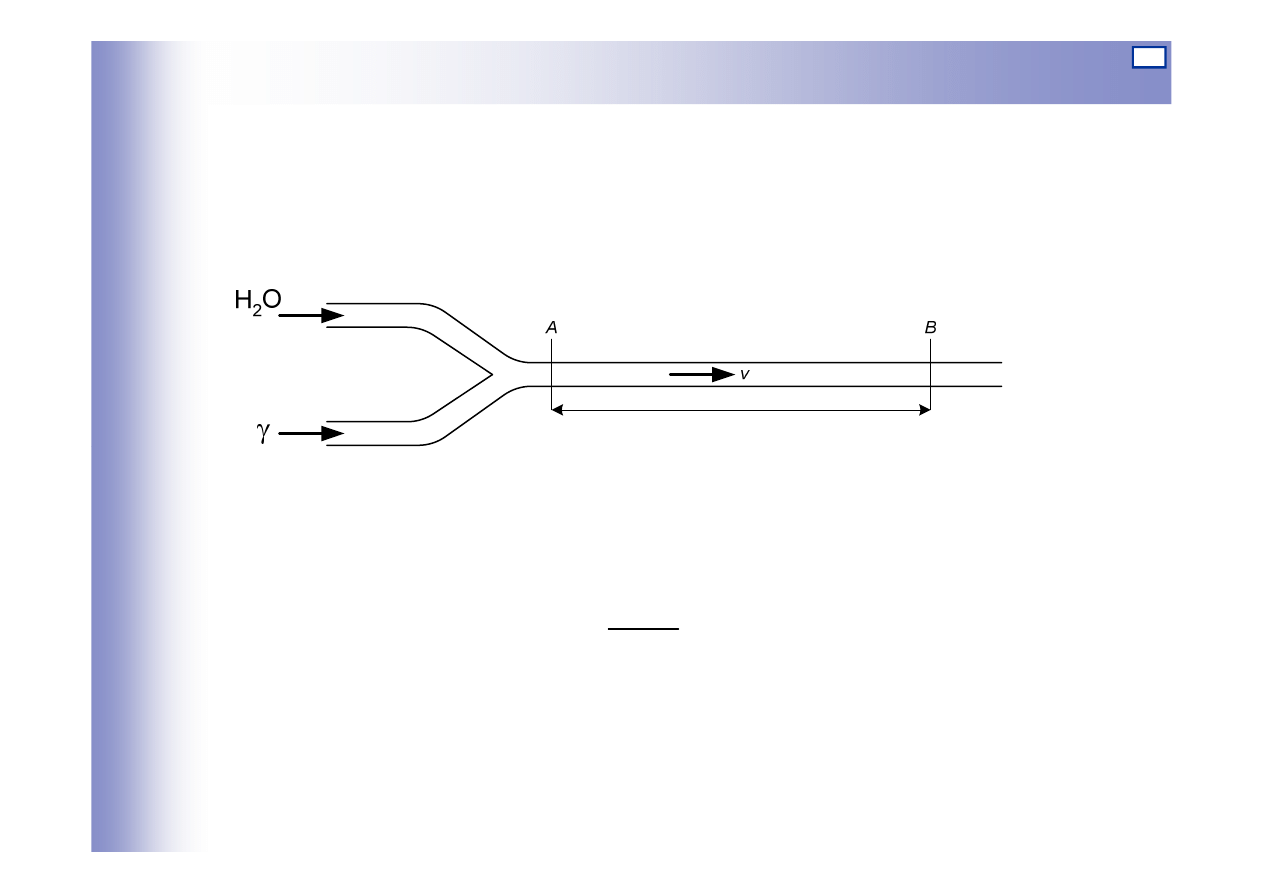
Schemat elementu podano na rysunku poni

ż

ej. Sygnałem wej

ś

ciowym

jest st

ęż

enie substancji

γ

w przekroju A, sygnałem wyj

ś

ciowym –

st

ęż

enie substancji w przekroju B ruroci

ą

gu.

l

Przy zało

ż

eniu,

ż

e nast

ę

puje dokładne wymieszanie substancji i w

danym przekroju jej st

ęż

enie jest jednakowe, otrzymamy:

gdzie: CA – st

ęż

enie substancji

γ

w przekroju A,

CB

–

st

ęż

enie substancji

γ

w przekroju B,

τ

=l/v

–

op

óź

nienie

s

A

B

e

s

C

s

C

s

G

τ

−

=

=

)

(

)

(

)

(

l