Ró

wn

ow

agi

w

roz

two

rac

h

Wprowadzenie

W wielu wypadkach reakcje chemiczne mogą zachodzić

przy spełnieniu pewnych warunków praktycznie w jedną

bądź w drugą stronę !!!

Prawo działania mas

• podczas działania pary wodnej na żelazo w podwyższonej

temperaturze zachodzi reakcja:

3Fe + 4H

2

O

→ Fe

3

O

4

+ 4H

2

(

↑

)

• jeżeli weźmiemy otrzymany tlenek i zadziałamy na niego

wodorem w podwyższonej temperaturze to:

• reakcje które mogą przebiegać w obydwu kierunkach

nazywamy

reakcjami odwracalnymi

Fe

3

O

4

+ 4H

2

→ 3Fe + 4H

2

O

3Fe + 4H

2

O Fe

3

O

4

+ 4H

2

Prawo działania mas

• jeśli weźmiemy najprostszy przykład reakcji odwracalnej:

• miarą szybkości takiej reakcji jest wzrost stężenia produktu

w jednostce czasu:

• dla reakcji przebiegającej w prawo:

v

1

= k

1

[A][B]

A + B AB

t

[AB]

d

d

v

====

v

-1

= k

-1

[AB]

• dla reakcji przebiegającej w lewo:

Prawo działania mas

• Dla reakcji odwracalnej:

w momencie ustalenia się stanu równowagi:

k

1

[A][B] = k

-1

[AB]

A + B AB

v

1

= v

-1

[A][B]

[AB]

=

−1

1

k

k

Prawo działania mas

• stosunek stałych szybkości obu reakcji jest stały i nosi

nazwę

stałej równowagi

reakcji:

m

1

A

1

+ m

2

A

2

+ ...= n

1

B

1

+ n

2

B

2

+ ...

[A][B]

[AB]

=

=

−1

1

k

k

K

...

]

[A

]

[A

...

]

[B

]

[B

2

1

2

1

m

2

m

1

n

2

n

1

=

c

K

• w ogólnym przypadku reakcji chemicznej:

Prawo działania mas

znaczenie

stałej równowagi

reakcji:

m

1

A

1

+ m

2

A

2

+ ...= n

1

B

1

+ n

2

B

2

+ ...

...

]

[A

]

[A

...

]

[B

]

[B

2

1

2

1

m

2

m

1

n

2

n

1

=

c

K

• gdy K >> 1 reakcja przesunięta w stronę

tworzenia produktów

• gdy K << 1 reakcja przesunięta w stronę

tworzenia substratów

Prawo działania mas

znaczenie

stałej równowagi

reakcji:

...

]

[A

]

[A

...

]

[B

]

[B

2

1

2

1

m

2

m

1

n

2

n

1

=

c

K

• gdy K = 10

-6

oznacza to, że iloczyn stężeń

produktów jest milion razy mniejszy niż
iloczyn stężeń substratów

Zmiana warunków reakcji:

Reguła Le Chateliera Browna

Zmieniając warunki reakcji można zwiększyć lub
zmniejszyć wydajności otrzymywanych produktów

• Zmiana

stężenia

poprzez usunięcie produktów lub dodanie

substratów do naczynia reakcyjnego

• Zmiana

ciśnienia cząstkowego

gazowych reagentów i

produktów poprzez zmniejszenie objętości

• Zmiana

temperatury

W przypadku mieszaniny gazowej znamy trzy
sposoby aby wpłynąć na skład równowagowy

Jeżeli na układ znajdujący się w stanie równowagi
działa bodziec zewnętrzny, to w układzie tym
następują zmiany zmniejszające skutki tego bodźca.

Reguła Le Chateliera

mówi że:

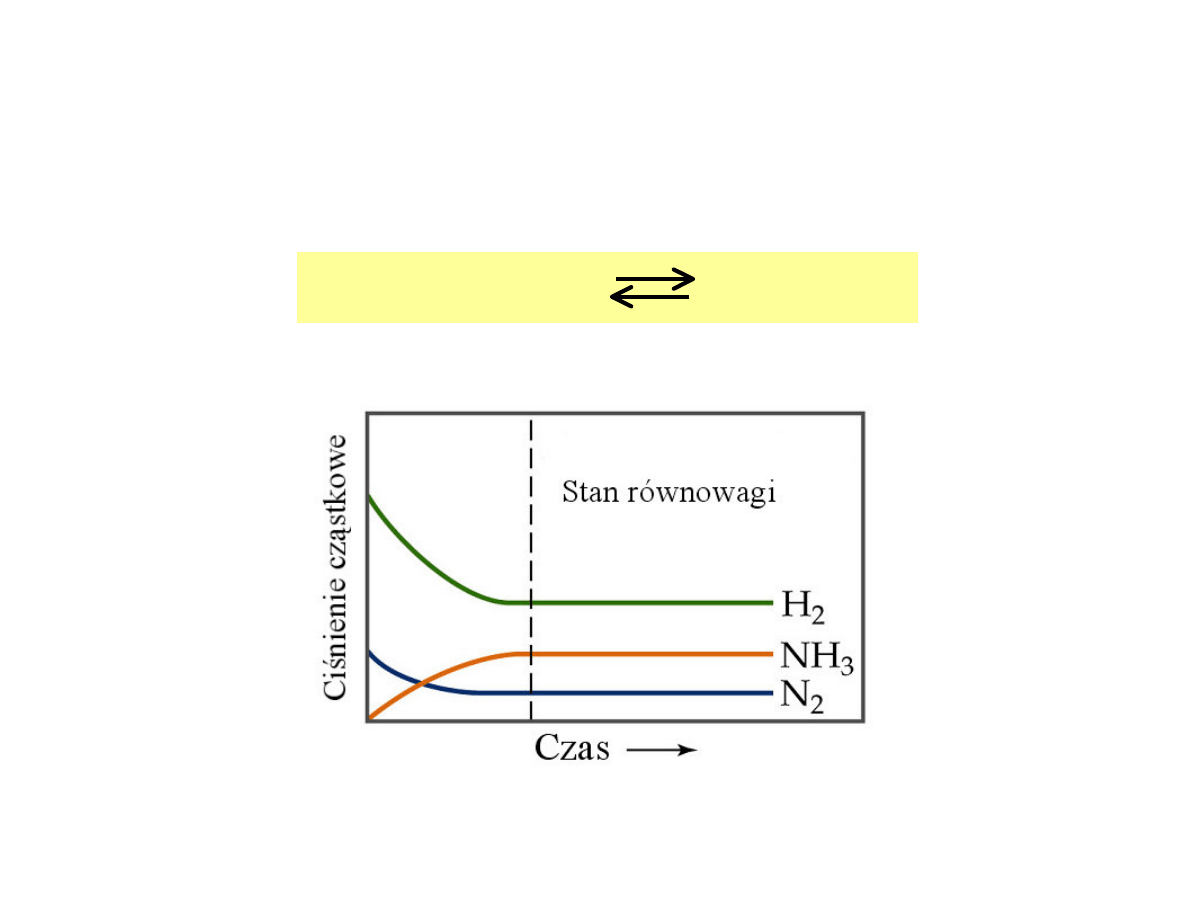
Przykład reakcji z gazowymi reagentami

(synteza amoniaku)

N

2

(g)

+ 3H

2

(g)

2 NH

3

(g)

Efekty zmiany stężeń

Ogólnie:

•

wprowadzenie substratu do układu w stanie równowagi

powoduje jej przesunięcie w stronę tworzenia produktów

N

2

(g)

+ 3H

2

(g)

2 NH

3

(g)

•

wprowadzenie produktu do układu znajdującego sięw stanie

równowagi spowoduje przesunięcie się równowagi w stronę
tworzenia substratów

Przesunięcie równowagi reakcji

N

2

(g)

+ 3H

2

(g)

2 NH

3

(g)

Przesunięcie równowagi reakcji

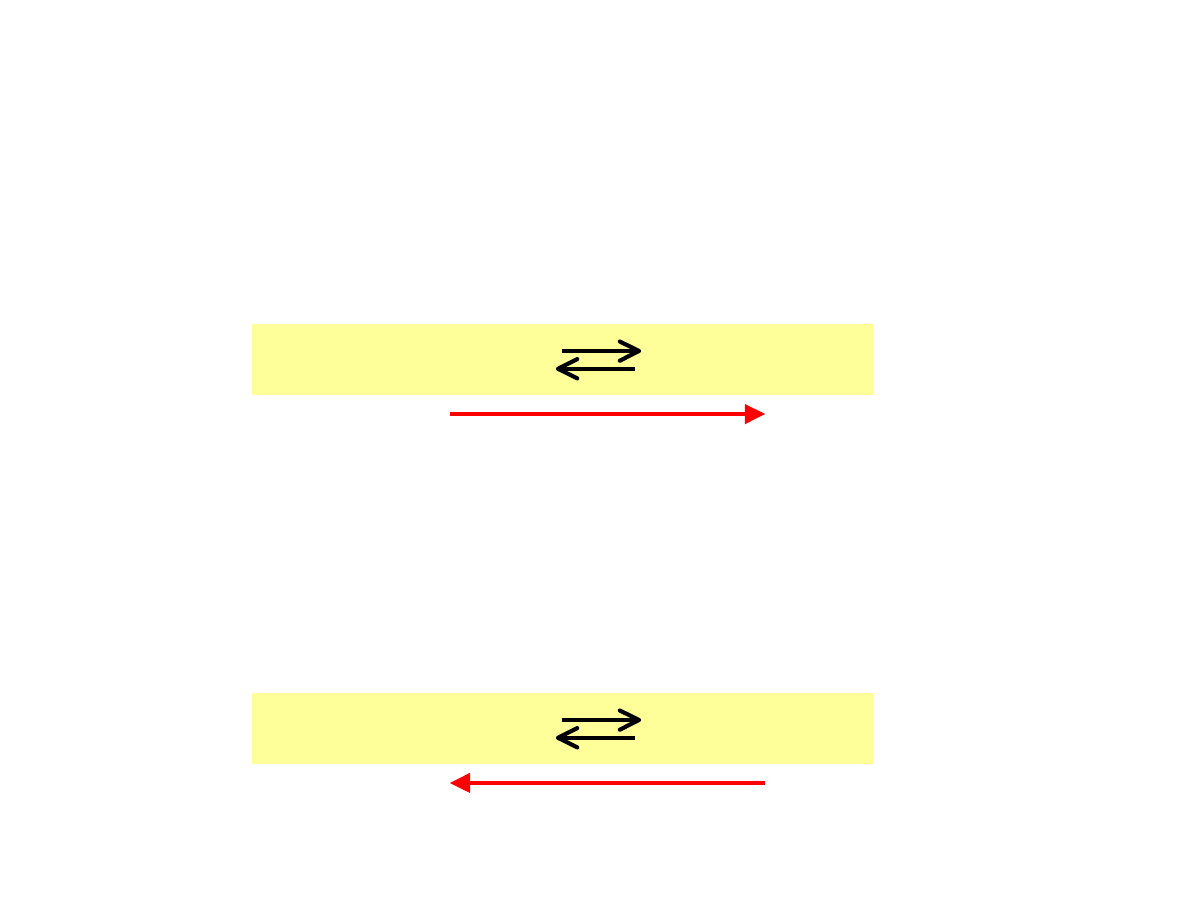
Efekty zmiany stężeń

Ogólnie:

•

usuwanie produktu z układu w stanie równowagi chemicznej

powoduje jej przesunięcie w stronę tworzenia się produktów

N

2

(g)

+ 3H

2

(g)

2 NH

3

(g)

•

usuwanie substratów z układu w stanie równowagi chemicznej

powoduje jej przesunięcie w stronę tworzenia się substratów

Przesunięcie równowagi reakcji

N

2

(g)

+ 3H

2

(g)

2 NH

3

(g)

Przesunięcie równowagi reakcji

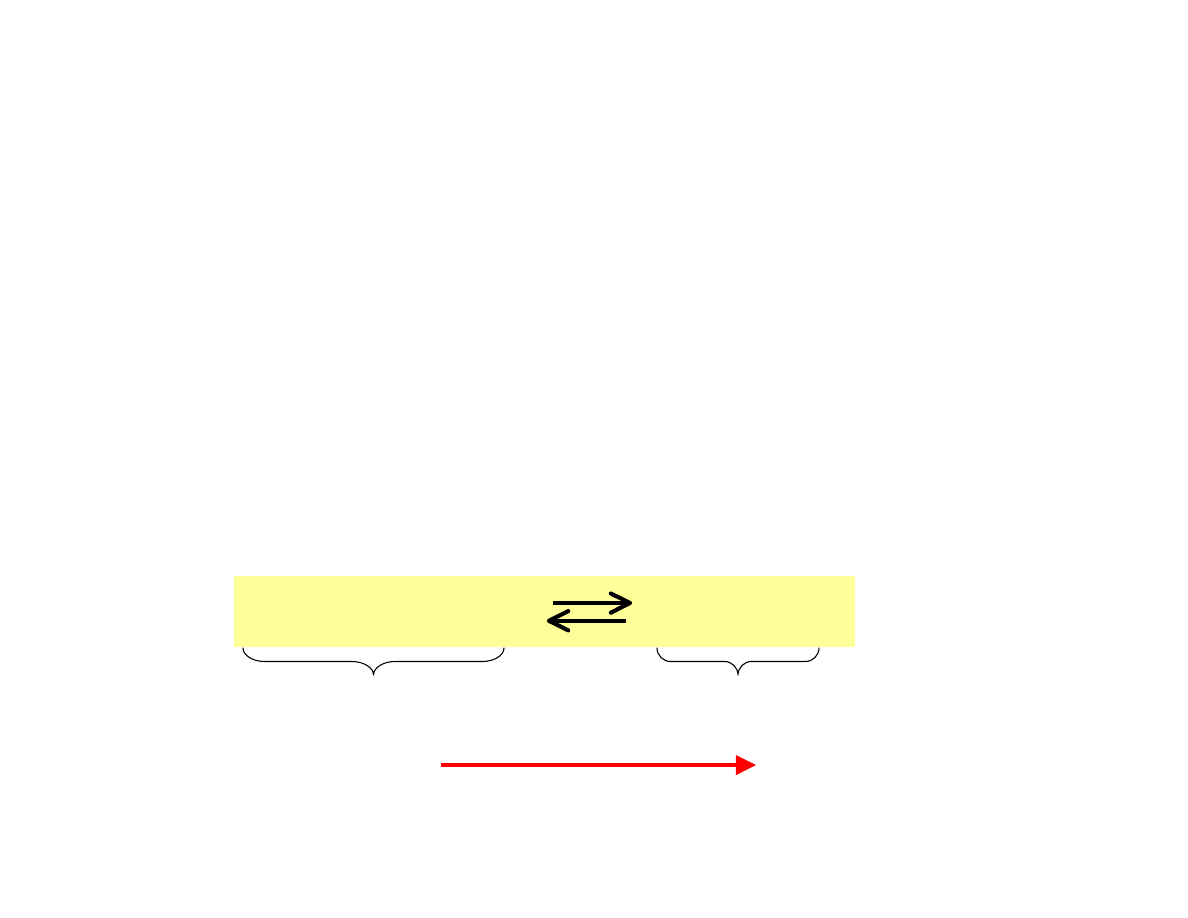
Efekty zmian objętości i ciśnienia

Gdy

zwiększamy ciśnienie

poprzez

zmniejszenie objętości

mieszaniny reakcyjnej,

reakcja

przesuwa się

w kierunku

mniejszej

ilości moli gazu.

Ogólnie:

N

2

(g)

+ 3H

2

(g)

2 NH

3

(g)

Przesunięcie kierunku reakcji

1 + 3 = 4 mole

2 mole

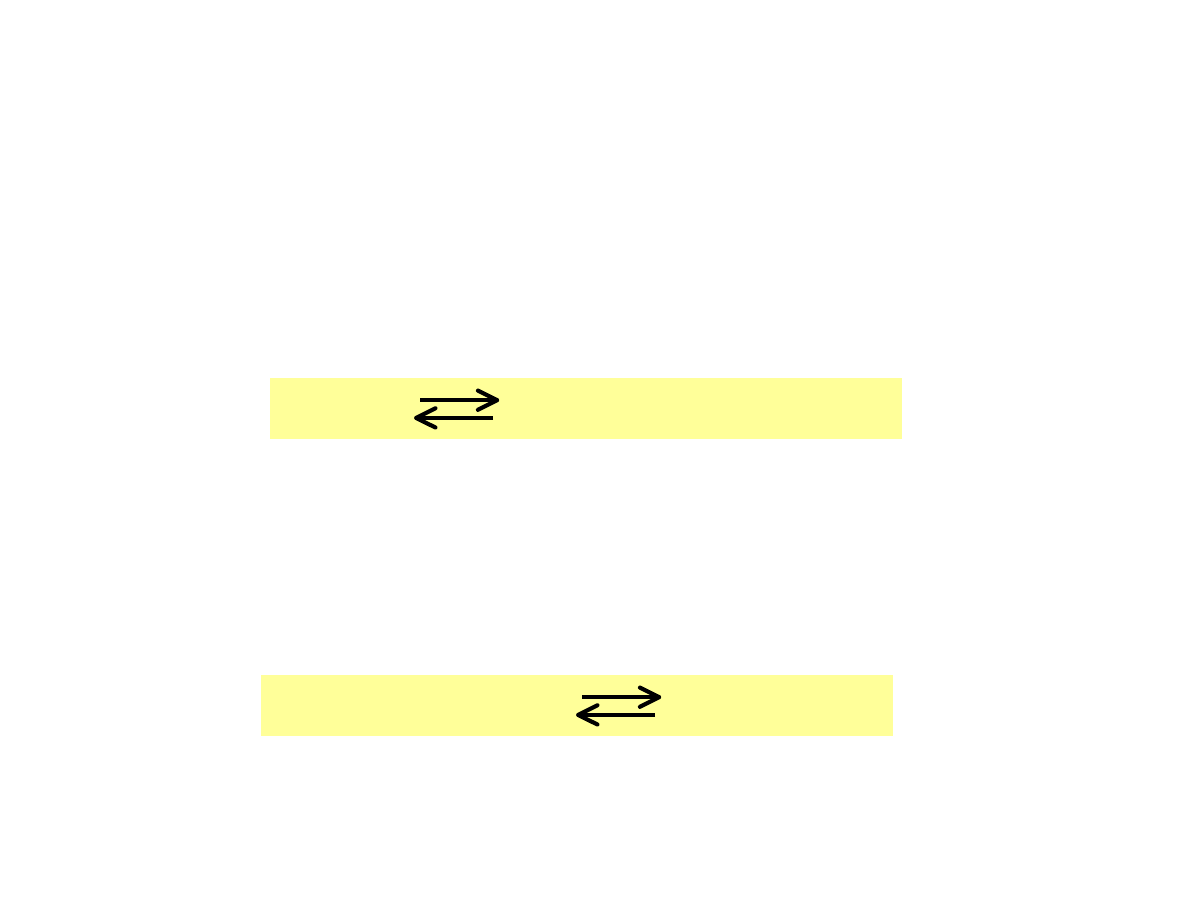
Efekt zmiany temperatury

Dla

reakcji

egzotermicznych

(∆

∆

∆

∆H ujemne), ilość

produktów zmniejsza się w przypadku
podwyższenia temperatury

Dla

reakcji

endotermicznych

(∆

∆

∆

∆H dodatnie),

ilość produktów zwiększa się w przypadku
podwyższenia temperatury

A + B C + D +

ciepło

A + B +

ciepło

C + D

Zastosowanie reguły przekory przy zmianie temperatury

Jednym z etapów produkcji kwasu siarkowego jest
tworzenie trójtlenku siarki(VI) poprzez reakcję SO

2

z O

2

.

W jaki sposób skład równowagowy mieszaniny reakcji
zmieni się gdy podwyższymy temperaturę?

2SO

2(g)

+ O

2(g)

2 SO

3(g)

∆

∆

∆

∆H = -198 kJ

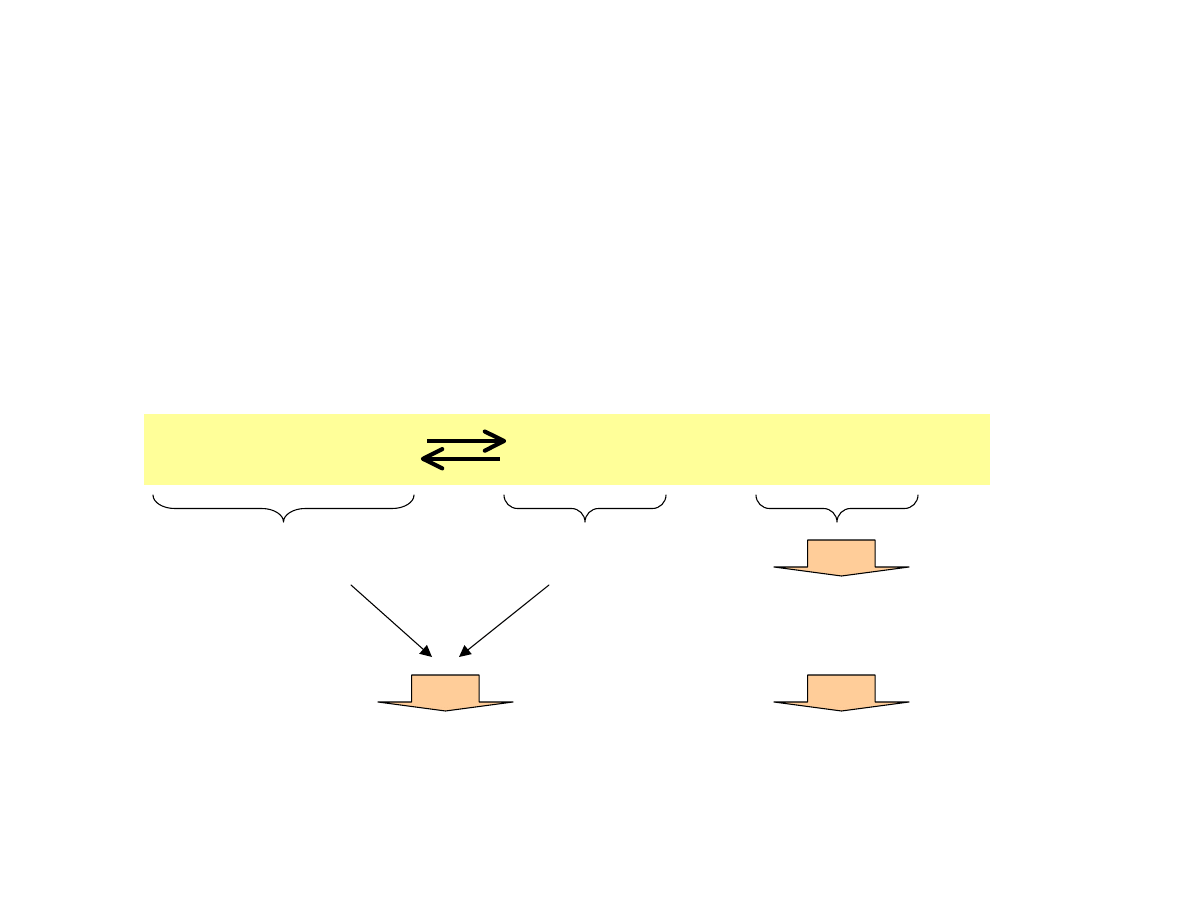
Zastosowanie reguły przekory przy zmianie

temperatury i ciśnienia

Jakie będą optymalne warunki przeprowadzenia
następującej reakcji?

2CO

(g)

+ O

2(g)

2 CO

2(g)

∆

∆

∆

∆H <0

2 + 1 = 3 mole

2 mole

Reakcja egzotermiczna

Obniżenie temperatury

(niska temperatura)

Podwyższenie ciśnienia

(wysokie ciśnienie)

N

2(g)

+ O

2(g)

2 NO

(g)

∆

∆

∆

∆H > 0

Zastosowanie reguły przekory przy zmianie

temperatury i ciśnienia

Jakie będą optymalne warunki przeprowadzenia
następującej reakcji?

1 + 1 = 2 mole

2 mole

Reakcja endotermiczna

Podwyższenie temperatury

(wysoka temperatura)

Ciśnienie nie wpływa

na przebieg reakcji

N

2

(g)

+ 3H

2

(g)

2 NH

3

(g)

∆

∆

∆

∆H <0

Zastosowanie reguły przekory przy zmianie

temperatury i ciśnienia

Jakie będą optymalne warunki przeprowadzenia
następującej reakcji?

1 + 3 = 4 mole

2 mole

Reakcja egzotermiczna

Obniżenie temperatury

(niska temperatura)

Podwyższenie ciśnienia

(wysokie ciśnienie)

Zależność szybkości reakcji od temperatury

Szybkość reakcji w bardzo znacznym
stopniu zależy od temperatury

T

A

ln

−

= B

k

Reguła Van’t Hoffa

orientacyjna reguła stwierdzająca, że podwyższenie temperatury
o 10 K powoduje od 2-4 krotny wzrost szybkości reakcji.

zatem wzrost o 100K

2

10

- 4

10

wzrost szybkości

reakcji

Zależność empiryczna łącząca k z T:

równanie
Arrheniusa

A i B stałe które możemy
obliczyć gdy zostały wykonane
pomiary k w różnych T

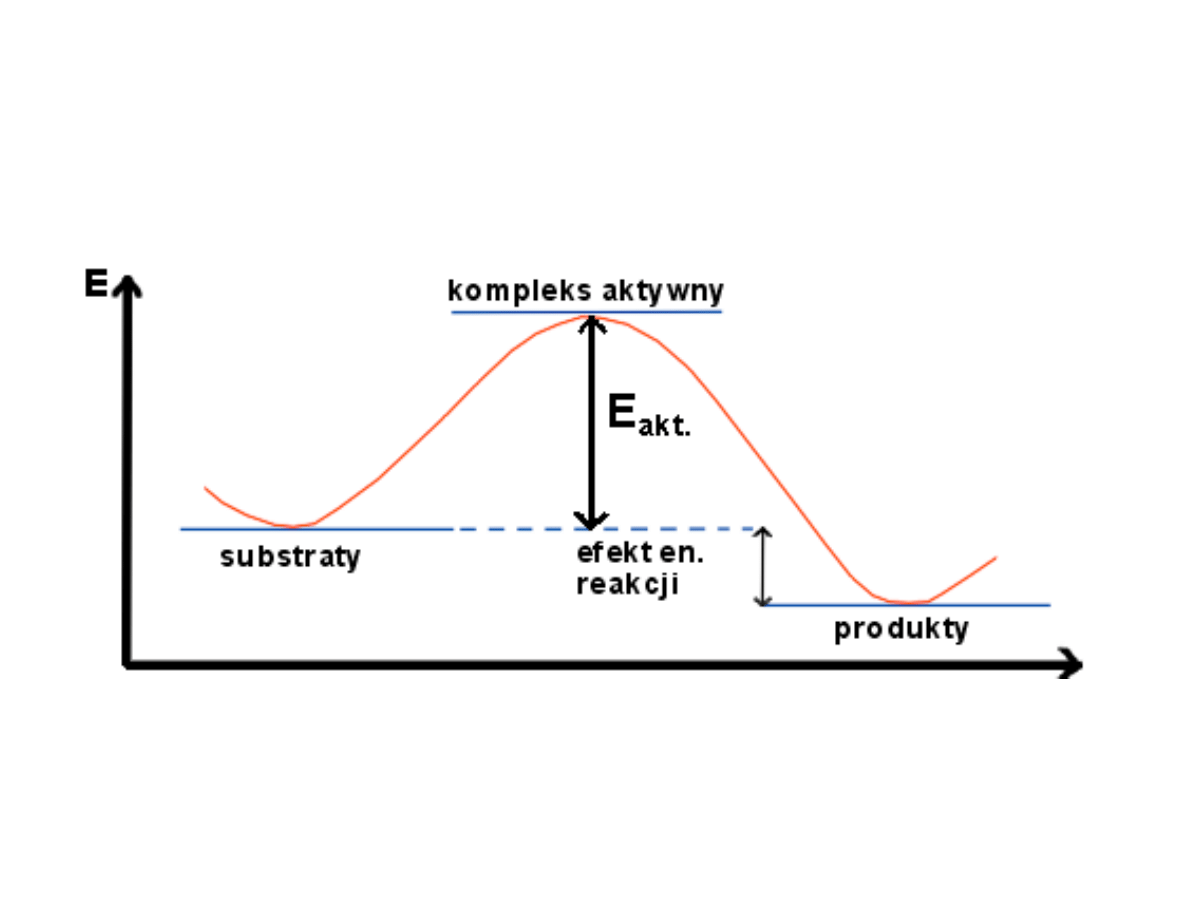
Energia aktywacji

Aktywność i siła jonowa

Roztwory elektrolitów mocnych

AB

→

→

→

→

A

+

+ B

−

to roztwory substancji praktycznie całkowicie zdysocjowanych,
które wykazują znaczną przewodność elektryczną:

przykłady:

• mocne kwasy
• mocne zasady
• większość soli

Roztwory elektrolitów słabych

to roztwory substancji zdysocjowanych w małym stopniu, a
dysocjacja wzrasta w miarę ich rozcieńczania:

przykłady:

• słabe kwasy
• słabe zasady
• niektóre sole

AB A

+

+ B

−

Aktywność i siła jonowa

Roztwory elektrolitów słabych

prawo działania mas wyrażone wzorem:

nie można go stosować do elektrolitów mocnych!!!

AB A

+

+ B

−

[AB]

]

][B

[A

-

+

=

c

K

odnosi się tylko do rozcieńczonych
roztworów elektrolitów słabych:

Aktywność i siła jonowa

Teoria roztworów elektrolitów mocnych
Debye’a i Hückla

uwzględnia wzajemne oddziaływania na siebie wszystkich jonów
istniejących w roztworze

im większe stężenie tym oddziaływania mocniejsze!!!

rzeczywista zdolność cząsteczek do reagowania
nosi nazwę

aktywności (a)

Aktywność i siła jonowa

Termodynamiczna stała równowagi:

prawo działania mas w znacznie ściślejszym wyrażeniu
przedstawia

termodynamiczna stała równowagi

:

f - współczynnik

aktywności

...

...

...

]

[A

]

[A

...

]

[B

]

[B

2

1

2

1

m

2

m

1

n

2

n

1

2

2

1

1

2

2

1

1

m

A

m

A

n

B

n

B

a

f

f

f

f

K

•

=

m

1

A

1

+ m

2

A

2

+ ...= n

1

B

1

+ n

2

B

2

+ ...

...

...

2

2

1

1

2

2

1

1

m

A

m

A

n

B

n

B

a

a

a

a

a

K

=

• rodzaju jonów
• ich ładunków
• stężenia i ładunków innych
jonów obecnych w roztworze

zależy od

Aktywność i siła jonowa

Termodynamiczna stała równowagi:

do obliczenia termodynamicznej stałej równowagi niezbędna jest
znajomość

współczynników aktywności f

:

zależy

od mocy jonowej (µ) oraz ładunku jonów (z)

∑

=

i

i

c

z

2

2

1

µ

z

i

- ładunek jonu i

c

i

- stężenie molowe jonu i

Aktywność i siła jonowa

Zadanie:

Obliczyć siłę jonową roztworu siarczanu potasu o stężeniu 0.2 mol/l

∑

=

i

i

c

z

2

2

1

µ

K

2

SO

4

→

→

→

→

2 K

+

+ SO

4

2

−

µ =

1/2 [1

2

· (2· 0.2) + 2

2

· 0.2] = 0.6

Aktywność i siła jonowa

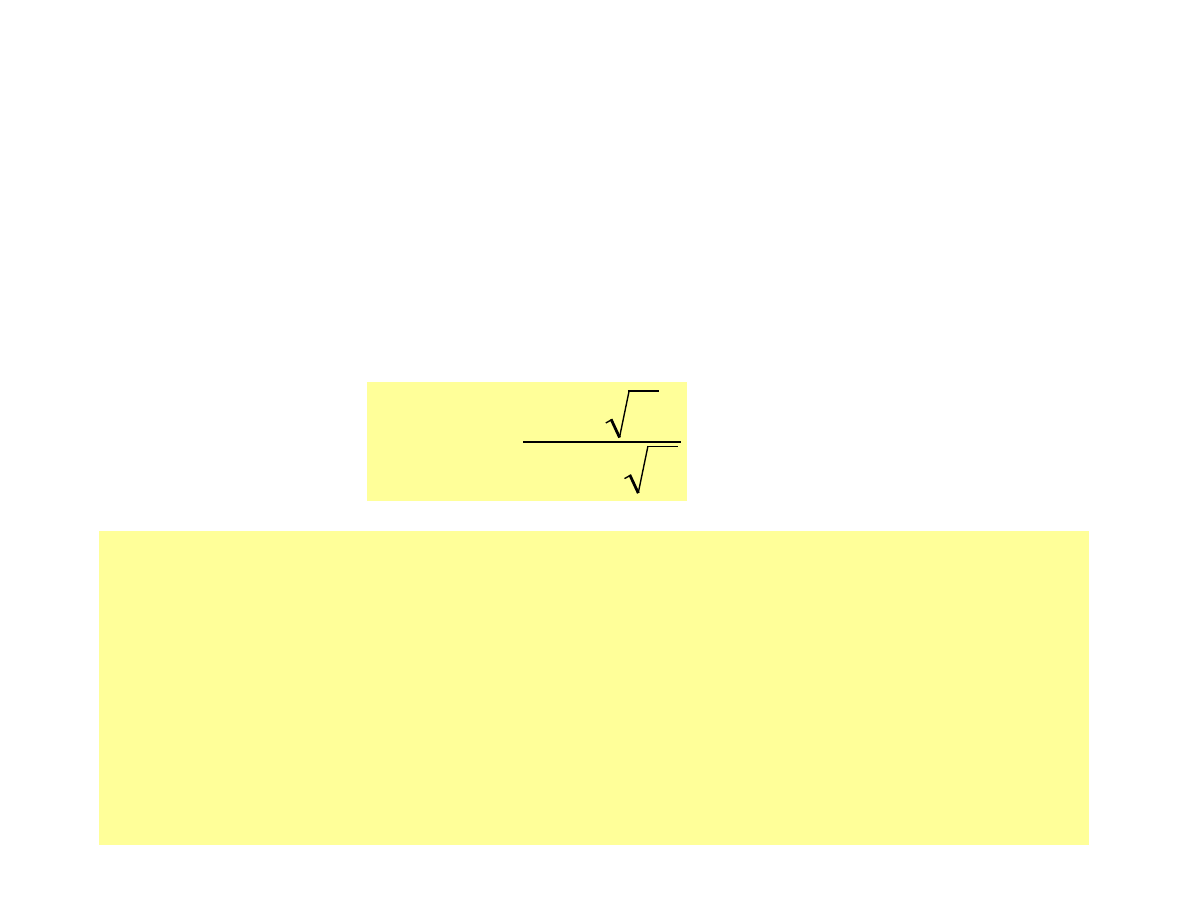
Współczynnik aktywności

znając skład roztworu (siłę jonową i ładunek rozpatrywanego jonu)

współczynnik aktywności f

można obliczyć ze wzoru Debye’a i

Hückla;

µ

µ

Bd

Az

f

i

i

+

−

=

1

log

2

z

i

- ładunek jonu

µ

- moc jonowa roztworu

A i B - stałe zależne od temperatury i właściwości

rozpuszczalnika (dla wody w temp. 25

o

C wynoszą

one 0.51 i 3.3· 10

7

)

d - średnica uwodnionego jonu (3 · 10

-8

do 11 · 10

-8

cm)

Aktywność i siła jonowa

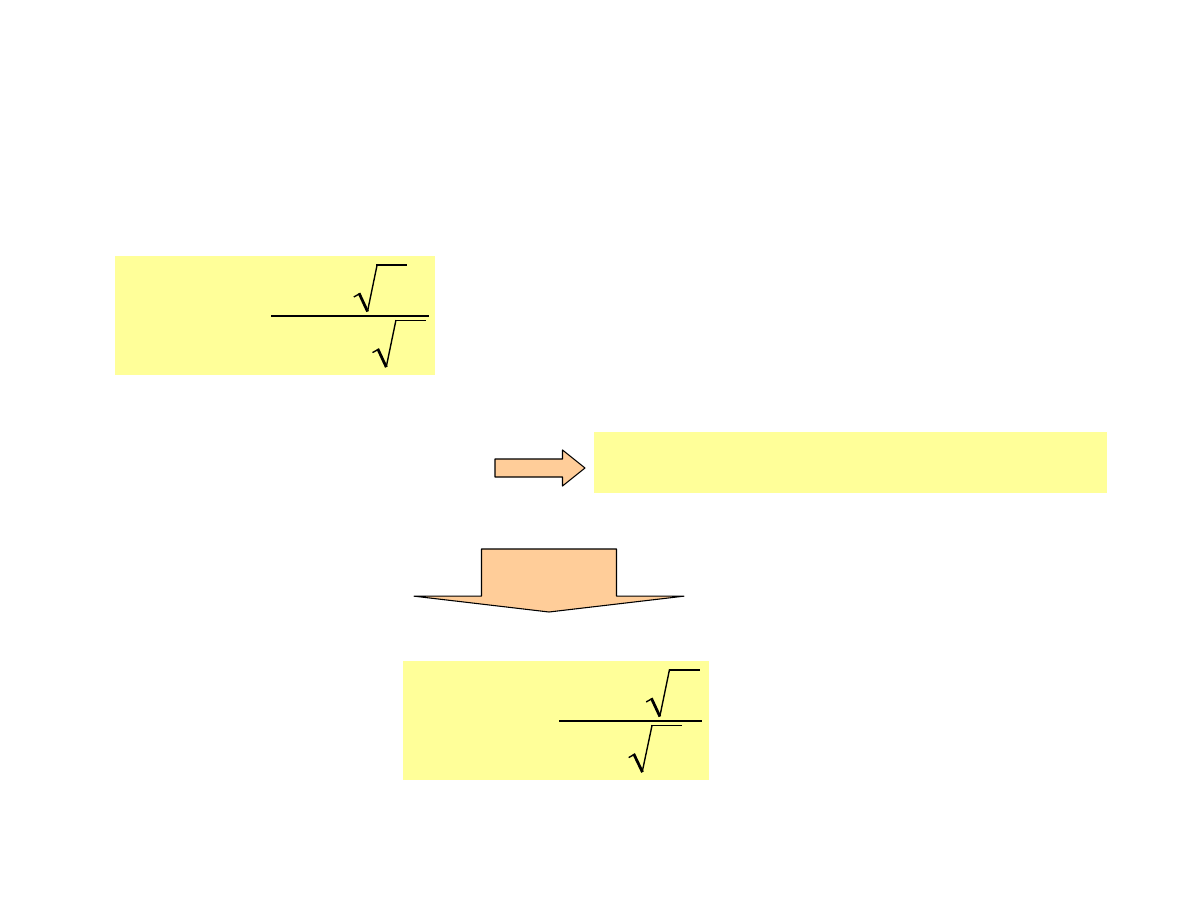
Współczynnik aktywności

poprawna wartość
dla roztworów gdzie

µ

µ

µ

µ

µ

µ

µ

µ

≤≤≤≤

≤≤≤≤

0.1

0.1

µ

µ

Bd

Az

f

i

i

+

−

=

1

log

2

B · d = 3.3· 10

7

· 3 · 10

-8

≈

1

ponieważ w przypadku wielu

jonów wartość d = 3

·

10

-8

cm

µ

µ

+

−

=

1

5

.

0

log

2

i

i

z

f

Aktywność i siła jonowa

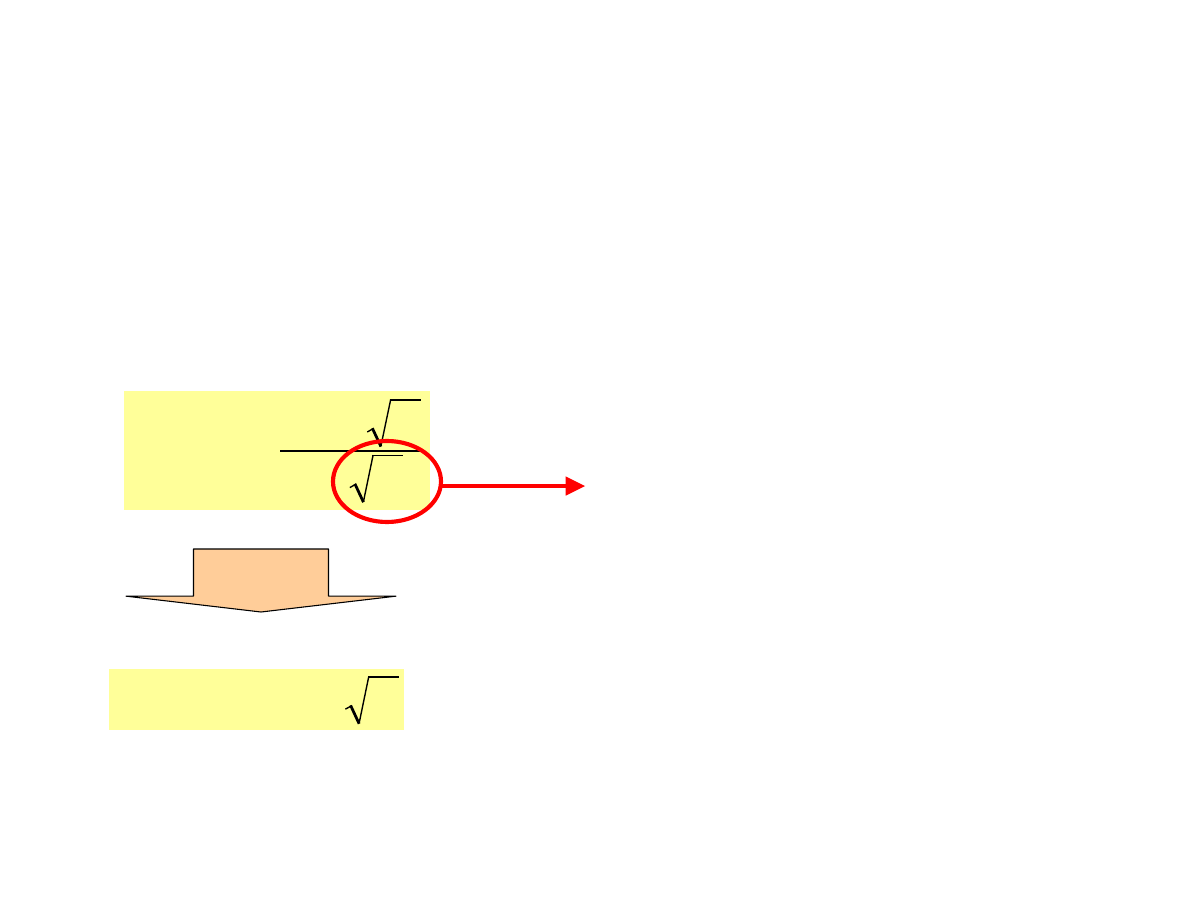
Współczynnik aktywności

można pominąć

µ

µ

+

−

=

1

5

.

0

log

2

i

i

z

f

dla roztworów jeszcze bardziej
rozcieńczonych gdzie

µ

µ

µ

µ

µ

µ

µ

µ

≤≤≤≤

≤≤≤≤

0.02

0.02

µ

2

5

.

0

log

i

i

z

f

−

=

Aktywność i siła jonowa

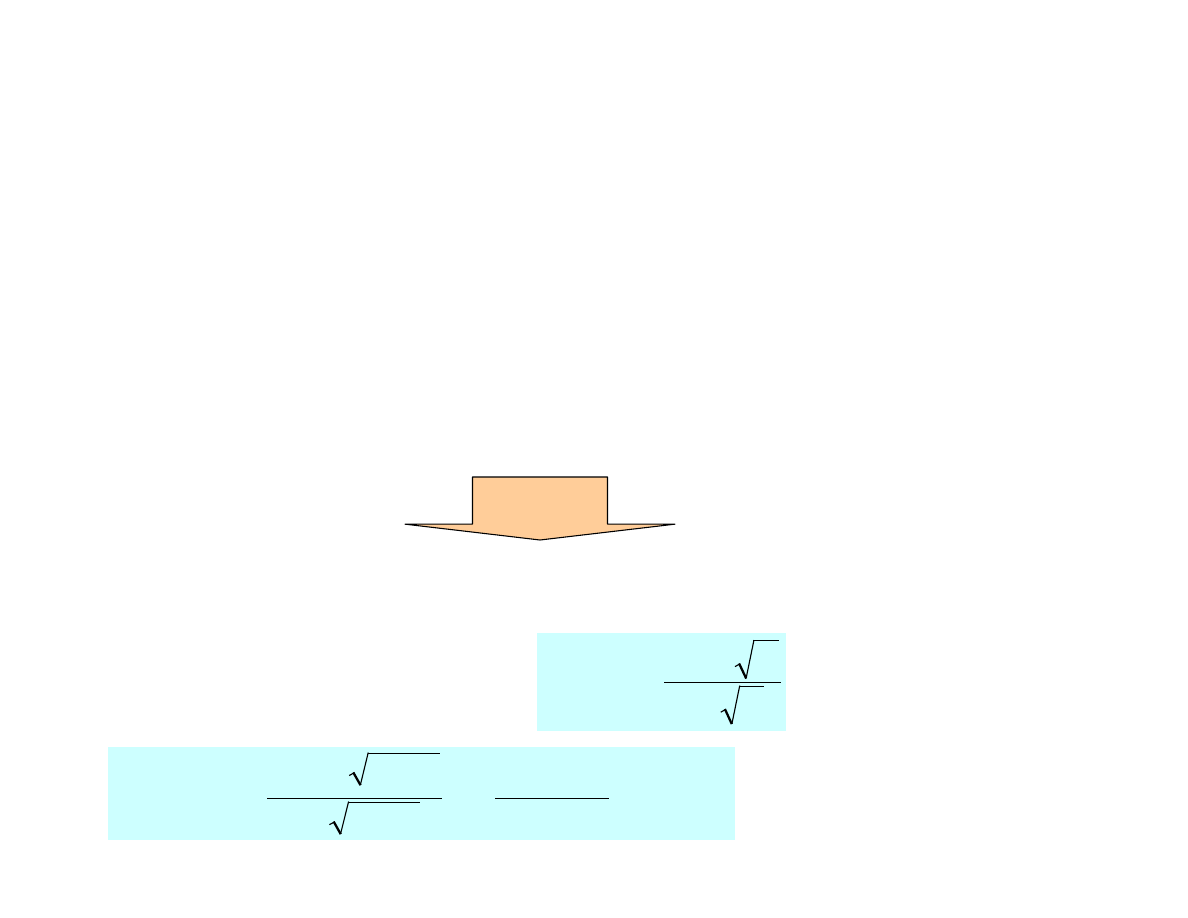
Zadanie

a) 0.001M NaOH + 0.01M Na

2

SO

4

µ

µ

+

−

=

1

5

.

0

log

2

i

i

z

f

Obliczyć współczynniki aktywności jonów OH

-

w 0.001M zasadzie sodowej

NaOH znajdującej się w roztworze

a) 0.01M Na

2

SO

4

i

b) 0.001 M Na

2

SO

4

[OH

-

] - 0.001 mol/L; [SO

4

2-

] - 0.01 mol/L; [Na

+

] - 0.021 mol/L

µ

a

= 1/2(1

2

· 0.001 + 2

2

· 0.01 + 1

2

· 0.021) = 1/2 · 0.062 = 0.031

Ponieważ µ

a

>0.02

076

.

0

18

.

0

1

18

.

0

5

.

0

031

.

0

1

031

.

0

1

5

.

0

log

2

−

=

+

⋅

−

=

+

⋅

−

=

−

OH

f

f = 0.84

Aktywność i siła jonowa

Zadanie

b) 0.001M NaOH + 0.001M Na

2

SO

4

Obliczyć współczynniki aktywności jonów OH

-

w 0.001M zasadzie sodowej

NaOH znajdującej się w roztworze

a) 0.01M Na

2

SO

4

i

b) 0.001 M Na

2

SO

4

µ

2

5

.

0

log

i

i

z

f

−

=

[OH

-

] - 0.001 mol/L; [SO

4

2-

] - 0.001 mol/L; [Na

+

] - 0.003 mol/L

µ

a

= 1/2(1

2

· 0.001 + 2

2

· 0.001 + 1

2

· 0.003) = 1/2 · 0.008 = 0.004

Ponieważ µ

a

< 0.02

032

.

0

063

.

0

5

.

0

004

.

0

1

5

.

0

log

2

−

=

⋅

−

=

⋅

−

=

−

OH

f

f = 0.93

Ag

+

+ Cl

−

AgCl (

↓

)

Iloczyn rozpuszczalności

Charakterystyczną cechą reakcji przebiegających w roztworach
jest tworzenie się związków trudno rozpuszczalnych

]

][Cl

[Ag

[AgCl]

-

+

=

strąc

K

W przypadku osadów trudno rozpuszczalnych szczególne
znaczenie praktyczne ma stała reakcji rozpuszczania tych osadów:

AgCl (

↓

) Ag

+

+ Cl

−

[AgCl]

]

][Cl

[Ag

-

+

=

rozp

K

K

so

- iloczyn rozpuszczalności

]

][Cl

[Ag

-

+

=

so

K

Iloczyn rozpuszczalności

Z definicji
Iloczyny rozpuszczalności

K

so

są wielkościami stałymi dla

danego

rozpuszczalnika

i w danej

temperaturze

mM

n+

+ nA

m

−

M

m

A

n

(

↓)

Termodynamiczny iloczyn rozpuszczalności:

n

A

m

M

a

so

f

f

K

−

+

⋅

⋅

=

+

n

-

m

m

n

]

[A

]

[M

K

so

=[M

n+

]

m

[A

m

−

]

n

pK

so

= -log K

so

często podaje się w postaci ujemnego logarytmu:

w praktyce podczas obliczania iloczynów rozpuszczalności
mamy do czynienia z roztworami o małej sile jonowej
(f

≈≈≈≈

1) stąd korzystamy zazwyczaj ze wzoru uproszczonego:

Iloczyn rozpuszczalności

termin

iloczyn rozpuszczalności

można stosować do substancji

których rozpuszczalność nie przekracza 0.01 mol/L

rozpuszczalność danej substancji można przedstawić:
- jako

iloczyn rozpuszczalności

(K

so

)

- jako

rozpuszczalność

(wyrażoną w gramach na litr (g/L)

bądź w molach na litr (mol/L) )

Uwaga:
Jeśli w roztworze pojawią się w dużych stężeniach obce sole
wówczas należy rozpatrywać

termodynamiczny iloczyn

rozpuszczalności

Iloczyn rozpuszczalności

Zadanie

Obliczyć iloczyn rozpuszczalności AgCl wiedząc, że rozpuszczalność
tego związku wynosi 1.81· 10

-3

g/L (M

AgCl

=143.4)

Rozpuszczalność molowa

w roztworze nasyconym dysocjacja jest całkowita stąd:

1 mol AgCl

→ 1 mol Ag

+

+ 1 mol Cl

−

pK

so,AgCl

= - log (1.6· 10

-10

) = 9.8

mol/L

10

26

.

1

143.4

10

1.81

5

3

−

−

⋅

=

⋅

[Ag

+

] = 1.26· 10

-5

mol/L

[Cl

-

] = 1.26· 10

-5

mol/L

K

so

= [Ag

+

] [Cl

-

] = 1.26· 10

-5

· 1.26· 10

-5

=

1.60· 10

-10

Iloczyn rozpuszczalności

Zadanie
Obliczyć jaka jest rozpuszczalność w g/L siarczku antymonu
jeśli jego iloczyn rozpuszczalności K

so

= 1.0· 10

-30

.

jeżeli przyjmiemy rozpuszczalność molową związku jako

x

Sb

2

S

3

(

↓

) 2Sb

3+

+ 3S

2

−

x = 3.9· 10

-7

mol/L

3

-

2

2

3

]

[S

]

[Sb

+

=

SO

K

w roztworze nasyconym dysocjacja jest całkowita stąd:

1 mol Sb

2

S

3

→ 2 mole Sb

3+

+ 3 mole S

2

−

K

so

= [2x]

2

[3x]

3

= 2

2

· x

2

· 3

3

· x

3

= 108 · x

5

5

30

108

10

0

.

1

−

⋅

=

x

3.9· 10

-7

mol/L · 339.52 g/mol

R = 1.3· 10

- 4

g/L

Iloczyn rozpuszczalności

efekt wspólnego jonu

AgCl (

↓) Ag

+

+ Cl

−

K

so

= [Ag

+

] [Cl

-

]

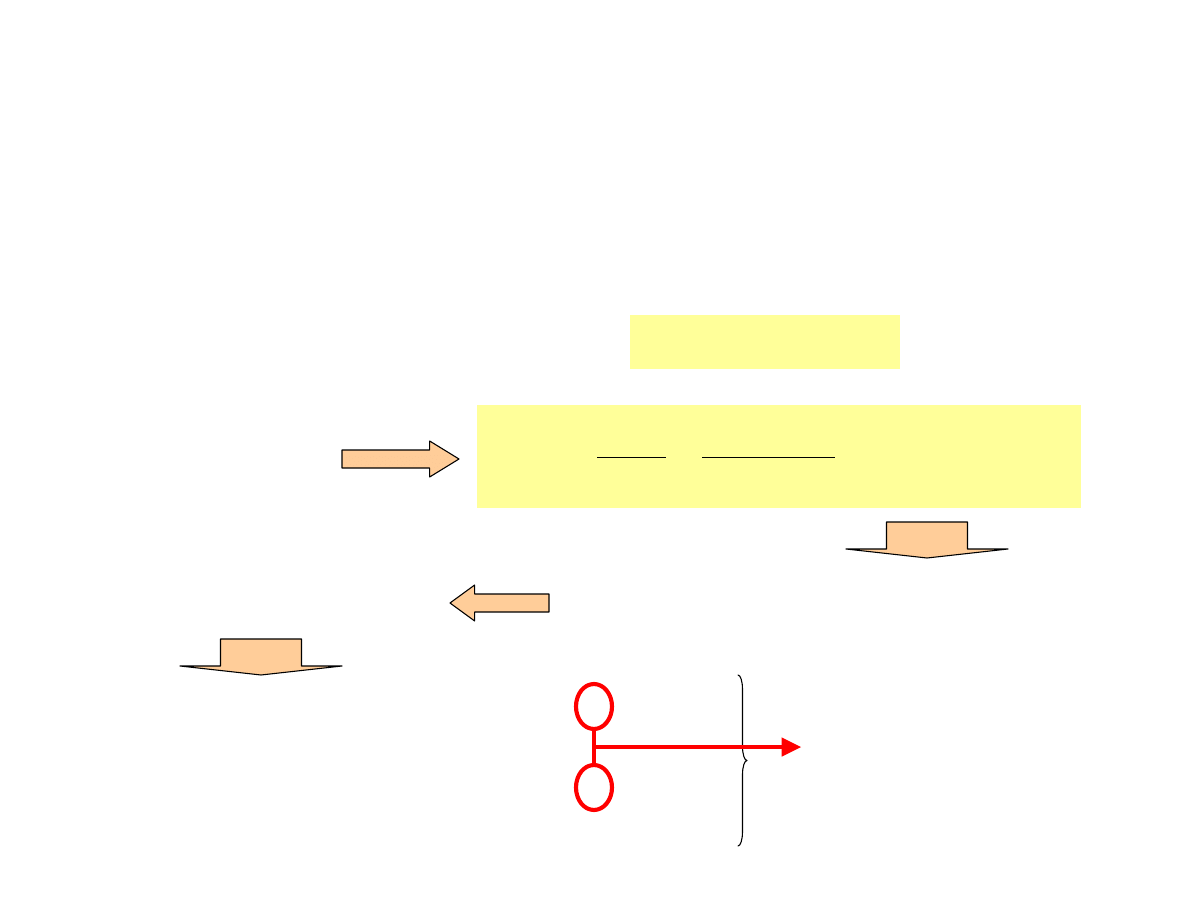
w roztworze nasyconym mamy równowag

ę

:

co si

ę

stanie gdy dodamy jonów Cl

-

?

K

so

= [Ag

+

] [Cl

-

]

wzrasta

maleje

wartość stała
dla danego
rozpuszczalnika

zmniejsza si

ę

zatem rozpuszczalno

ść

AgCl

Efekt wspólnego jonu jest to zmniejszanie rozpuszczalno

ś

ci

trudno rozpuszczalnej soli przez dodanie soli rozpuszczalnej
zawieraj

ą

cej z ni

ą

wspólny jon.

Iloczyn rozpuszczalności

efekt wspólnego jonu

Zadanie

Jaka jest przybliżona wartość rozpuszczalności molowej AgCl w
roztworze KCl o stężeniu 0.10 mol/L? K

so,AgCl

=1.6· 10

-10

[Cl

-

] = 0.10 mol/L

st

ęż

enie jonów Ag

+

w roztworze

rozpuszczalność AgCl =1.6· 10

-9

mol/L

mol/L

10

6

.

1

10

.

0

10

6

.

1

]

[Cl

K

]

[Ag

9

10

-

so

−

−

+

⋅

=

⋅

=

=

K

so

= [Ag

+

] [Cl

-

]

1.6 · 10

-9

mol/L

rozpuszczalno

ść

AgCl = 1.3· 10

-5

mol/L

( w wodzie )

>10 000

razy mniejsza

W przypadku gdy mamy do czynienia z wytr

ą

caniem trudno

rozpuszczalnej soli w układzie w którym znajduj

ą

si

ę

równie

ż

inne jony wpływ

siły jonowej

jest do

ść

znaczny

const (T=const)

Iloczyn rozpuszczalności

efekt solny

AgCl (

↓) Ag

+

+ Cl

−

K

so

= [Ag

+

] [Cl

-

] · f

Ag+

· f

Cl

-

gdy siła jonowa wzrasta

(w miar

ę

wzrostu st

ęż

enie obcych

elektrolitów nie maj

ą

cych wspólnych jonów z rozpuszczanym

osadem)

malej

ą

zatem współczynniki aktywno

ś

ci

(w tym

przypadku f

Ag+

i f

Cl

-

)

Poniewa

ż

K

so

= const (w danej temperaturze)

musz

ą

wzrosn

ąć

st

ęż

enia jonów

rozpuszczanej

soli (w tym przypadku [Ag

+

] i [Cl

-

] )

zwi

ę

ksza si

ę

rozpuszczalno

ść

AgCl

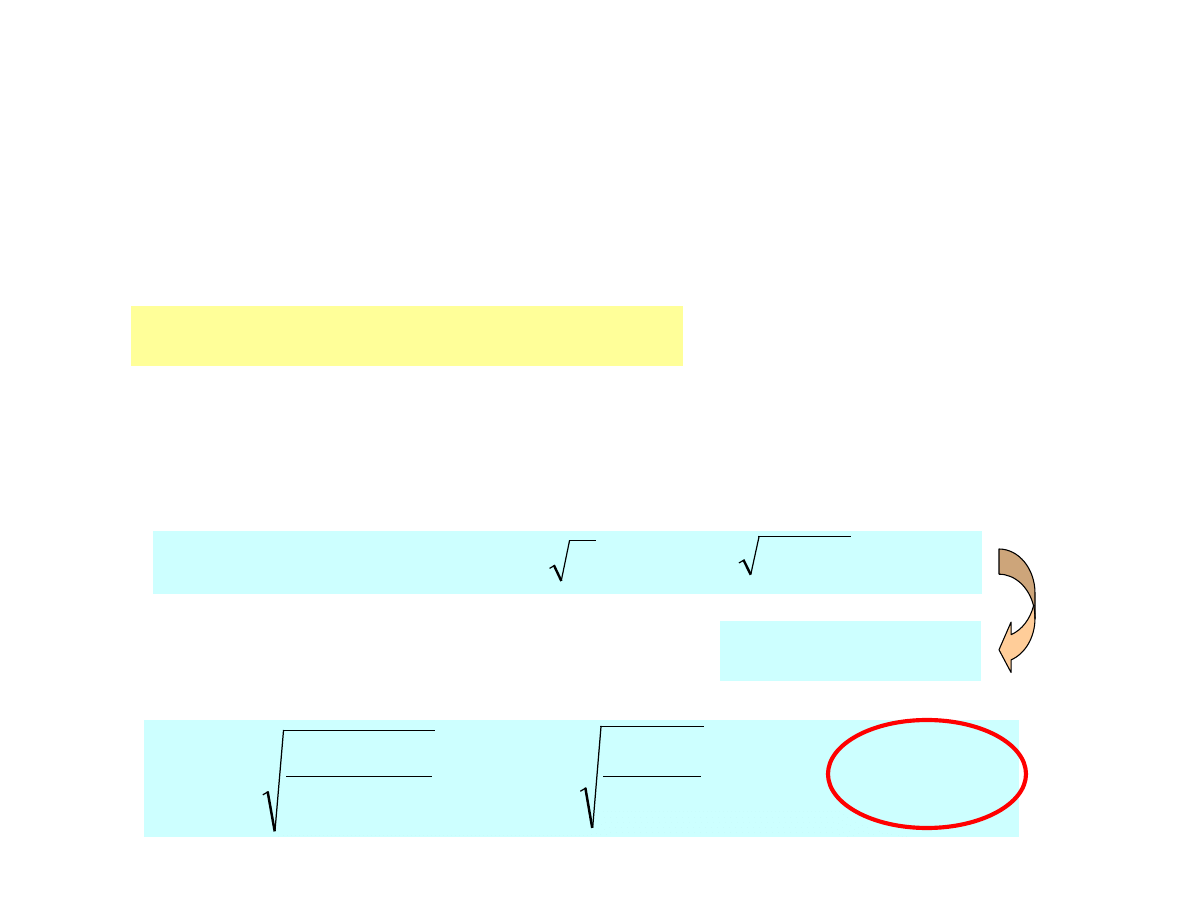
Zadanie
Obliczy

ć

rozpuszczalno

ść

osadu BaSO

4

w

wodzie

i

0.1M NaCl

przy zało

ż

eniu,

ż

e [Ba

2+

] = [SO

4

2-

] = 10

-5

mol/L

Iloczyn rozpuszczalności

efekt solny

10

-

2
4

2

10

1

]

][SO

[Ba

2

4

2

−

+

⋅

=

⋅

⋅

=

−

+

SO

Ba

a

so

f

f

K

µ = 1/2 · (2

2

· 10

-5

+ 2

2

· 10

-5

) = 4 · 10

-5

013

.

0

10

4

2

5

.

0

5

.

0

log

log

5

2

2

2

4

2

−

=

⋅

⋅

−

=

⋅

−

=

=

−

−

+

µ

i

SO

Ba

z

f

f

97

.

0

2

4

2

=

=

−

+

SO

Ba

f

f

L

g

M

f

f

K

R

BaSO

SO

Ba

so

BaSO

/

10

4

.

2

4

.

233

97

.

0

10

1

3

2

10

4

2

4

2

4

−

−

⋅

=

⋅

⋅

=

⋅

⋅

=

−

+

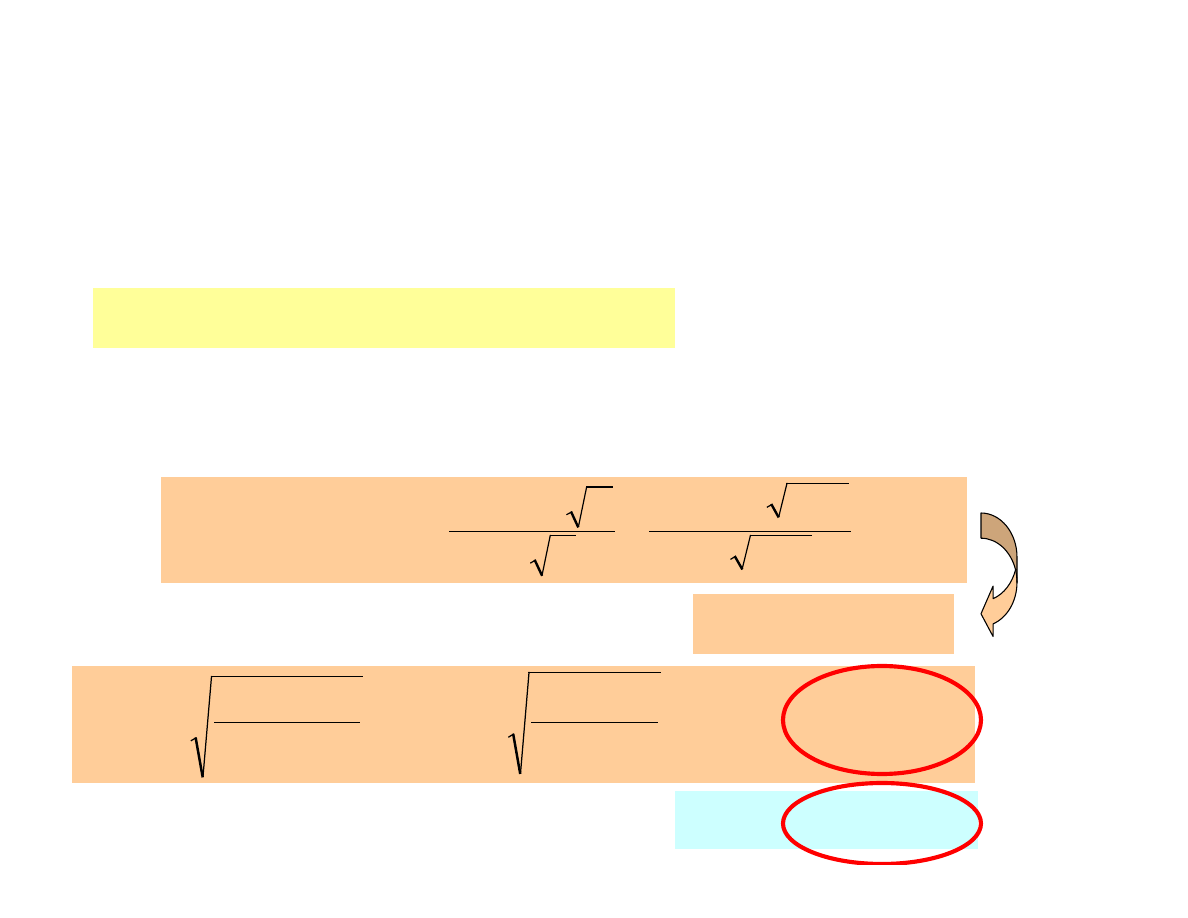
Zadanie
Obliczy

ć

rozpuszczalno

ść

osadu BaSO

4

w

wodzie

i

0.10M NaCl

przy założeniu, że [Ba

2+

] = [SO

4

2-

] = 10

-5

mol/L << [Na

+

]=[Cl

-

]=0.10 mol/L

Iloczyn rozpuszczalności

efekt solny

10

-

2
4

2

10

0

.

1

]

][SO

[Ba

2

4

2

−

+

⋅

=

⋅

⋅

=

−

+

SO

Ba

a

so

f

f

K

µ = 1/2 · (1

2

· 0.10 + 1

2

· 0.10) = 0.10

48

.

0

10

.

0

1

10

.

0

2

5

.

0

1

5

.

0

log

log

2

2

2

4

2

−

=

+

⋅

−

=

+

⋅

−

=

=

−

+

µ

µ

i

SO

Ba

z

f

f

33

.

0

2

4

2

=

=

−

+

SO

Ba

f

f

L

g

M

f

f

K

R

BaSO

SO

Ba

so

BaSO

/

10

1

.

7

4

.

233

33

.

0

10

0

.

1

3

2

10

4

2

4

2

4

−

−

⋅

=

⋅

⋅

=

⋅

⋅

=

−

+

L

g

R

BaSO

/

10

4

.

2

3

4

−

⋅

=

W domu potrenować obliczenia

zadania z Galusa

Iloczyn rozpuszczalno

ś

ci :

4.246 - 4.317

Jedno z tych zada

ń

pojawi si

ę

na pewno

na I kolokwium z pracowni

zadania z Galusa

przeliczanie st

ęż

e

ń

:

3.9, 3.41-3.43, 3.46, 3.47, 3.50, 3.51

rozcie

ń

czanie i przygotowywanie roztworów:

3.76, 3.77, 3.80, 3.86, 3.90, 3.97, 3.100, 3.114, 3.115, 3.117

Jedno z tych zada

ń

równie

ż

na pewno

pojawi si

ę

na I kolokwium z pracowni

Osady analityczne

• osady koloidalne

– serowate (chlorek srebra)

– galaretowate (wodorotlenek

ż

elaza III)

• osady krystaliczne (uporz

ą

dkowana budowa krystaliczna)

– drobnokrystaliczne

– grubokrystaliczne

Osady analityczne

koloidy

• cz

ą

steczki substancji rozpuszczonych zbite w niewielkie

cz

ą

stki tworz

ą

zawiesin

ę

(np. mydło w wodzie)

grupy zbitych (zwartych) cz

ą

steczek -

micele

micele wraz z rozpuszczalnikiem -

koloid

posta

ć

materii składaj

ą

ca si

ę

z ogromnej liczby

cz

ą

stek o

ś

rednicy od 1 nm do 10 mm

rozproszonych w cieczy, ciele stałym lub gazie

Osady analityczne

koloidy

Faza

rozproszona

Ośrodek

rozpraszający

Nazwa

Przykłady

stała

gaz

aerozol

dym

ciekła

gaz

aerozol

lakier w sprayu, mgła

stała

ciecz

zol lub żel

atrament, farba malarska

ciekła

ciecz

emulsja

mleko, majonez

stała

ciało stałe

stała dyspersja szkło rubinowe (Au w

szkle), niektóre stopy

ciekła

ciało stałe

stała emulsja

bitumiczne nawierzchnie
dróg, lody

gazowa

ciało stałe

stała pianka

pianki izolacyjne

Osady analityczne

koloidy

• w procesie tworzenia osadu koloidalnego powstaj

ą

ce

aglomeraty obdarzone jednoimiennym ładunkiem
odpychaj

ą

si

ę

od siebie

zol

(pseudoroztwór)

ż

el

elektrolit

(zobojętnia ładunki)

woda

(przy przemywaniu)

zol

osad nale

ż

y przemywa

ć

roztworem elektrolitu !!!

proces

peptyzacji

koagulacja

Osady analityczne

koloidy

koloidy - du

ż

e skupiska - łatwo adsorbuj

ą

inne jony

aby temu zapobiec stosuje si

ę

podwójne str

ą

canie

Podział koloidów:

• hydrofilowe (emulsoidy) - ch

ę

tnie przył

ą

czaj

ą

ce wod

ę

• hydrofobowe (suspensoidy) - nie maj

ą

ce powinowactwa do wody

Osady analityczne

osady krystaliczne

• w przypadku str

ą

cania osadów krystalicznych ich posta

ć

drobno czy grubokrystaliczna zale

ż

y od sposobu str

ą

cania

po przekroczeniu K

so

wzrost kryształów

zarodki

osad drobnokrystaliczny

osad grubokrystaliczny

szybko

wolno

Osady analityczne

osady krystaliczne

• osad grubokrystaliczny

– mały nadmiar jonów strącających

– powolne dodawanie odczynnika strącającego

– wysoka temperatura

– w przypadku rekrystalizacji powolne schładzanie

• gdy zapewnimy prawidłowe warunki str

ą

cania:

– osad grubokrystaliczny

– osad czysty o prawidłowej sieci krystalicznej

– osad pozbawiony obcych inkluzji

Osady analityczne

osady krystaliczne

• Zjawiska wtórne towarzysz

ą

ce str

ą

caniu

– starzenie osadu

– postr

ą

canie

– współstr

ą

canie