S
TRONA
74
Element mikropaskowy zasilany poprzez sprzężenie z aperturą
jedności. Podane wymiary są oczywiście tylko pierwszym przybliżeniem wymiarów
struktury, które należy poddać optymalizacji w celu uzyskania żądanego pasma pracy.
8. Dopasowanie poprzez zewnętrzny obwód dopasowujący
Dopasowanie impedancji wejściowej anteny do impedancji źródła sygnału, przy
pomocy obwodu dopasowującego, polega na konstrukcji bezstratnego czwórnika klasy SLSS.
Jego zadanie polega na zapewnieniu pożądanego kształtu częstotliwościowej charakterystyki
przenoszenia mocy sygnału między źródłem a anteną oraz odpowiednie tłumienie sygnału
poza pasmem przenoszenia. W przypadku, gdy impedancje źródła i obciążenia są czysto
rzeczywiste, zaprojektowanie obwodu dopasowującego jest względnie proste. Jednak gdy
obie lub tylko jedna z impedancji jest zespolona, problem znalezienia odpowiedniego obwodu
dopasowującego staje się trudnym zagadnieniem.
Ogólne prawa kierujące zasadami impedancyjnego dopasowania układów klasy SLSS
zostały sformułowane w 1945 roku przez H. Bode [44], a następnie rozwinięte w pracach
R. M. Fano i D. C. Youla [45, 46]. Zapostulowane przez nich kryteria mają postać szeregów
lub wyrażeń całkowych, które wiążą ze sobą skuteczne wzmocnienie obwodu
dopasowującego i szerokość jego częstotliwościowego pasma pracy. Istnieje szereg
analitycznych metod syntezy obwodów dopasowujących [47, 48, 49, 50], opracowanych w
oparciu o wymienione kryteria. Jednak ze względu na znaczny stopień złożoności oraz
konieczność znajomości analitycznej funkcji opisującej impedancję obciążenia, metody te są
trudne w zastosowaniu, a w przypadku złożonych obciążeń - prawie nieużyteczne.
Impedancja wejściowa klasycznej anteny mikropaskowej, w okolicy częstotliwości jej
modu podstawowego TM
01
, ma charakter zbliżony do impedancji prostego, pojedynczego
równoległego obwodu rezonansowego, a sama antena jest silnie wąskopasmowa [2].
Obciążenie o takiej postaci daje się dobrze dopasować metodami analitycznymi, ale
uzyskiwana szerokość pasma jest i tak zazwyczaj zbyt mała.
Doskonałe własności szerokopasmowe wykazują natomiast anteny mikropaskowe na grubym
podłożu, dla których impedancja wejściowa formuje pętlę na wykresie Smitha. Wyniki
przedstawione w pracy pokazują jednak, że pętla tworzy się zawsze dla częstotliwości
leżących daleko poza głównym rezonansem anteny, gdzie impedancja ma bardzo złożony
charakter i nie daje się opisać funkcją analityczną niskiego rzędu. Zagadnienie dopasowania
takich obciążeń można dobrze rozwiązać, dla pewnej klasy obwodów dopasowujących,
metodami numerycznymi [31, 47]. Ich główna zaleta polega na zastąpieniu analitycznego
opisu impedancji wejściowej anteny, danymi uzyskanymi w wyniku pomiarów lub obliczeń.
Idea działania tych metod jest zazwyczaj bardzo prosta.
Doskonałe wyniki w projektowaniu obwodów dopasowujących daje metoda SRFT
(Simplified Real Frequency Technique) [31, 49]. Powstała ona na bazie metody opracowanej
przez Carlina [51, 52], znanej pod nazwą RFM (Real Frequency Method) i umożliwia
rozwiązanie zagadnienia podwójnego dopasowania. W technice antenowej prawie zawsze
mamy do czynienia z zagadnieniem pojedynczego dopasowania, polegającego na
dopasowaniu impedancji wejściowej anteny do rezystancji źródła sygnału (rys. 8.1).
Element mikropaskowy zasilany poprzez sprzężenie z aperturą
S
TRONA
75
~
Bezstratny
Z = R + jX
a
a
a
Z = R + jX
o
o
o
R
w
e
g
Z =
wej
R
w
obwód
dopasowujący
Źródło
Antena
s
11
s
12
s
21
s
22
ρ
o
Rys. 8.1. Zagadnienie dopasowania impedancji wejściowej anteny do impedancji źródła sygnału
Idea metody SRFT polega na wyznaczeniu parametrów rozproszenia czwórnika dopaso-
wującego, którego zadaniem jest zapewnienie pożądanego kształtu częstotliwościowej chara-
kterystyki przenoszenia mocy sygnału między źródłem a anteną. W celu zapewnienia prostej
realizacji układowej zakłada się, że obwód dopasowujący jest bezstratny, odwracalny oraz
minimalnej fazy z zerami transmisji tylko w zerze i/lub nieskończoności (
ω
= 0 i/lub
ω
= ∞).
Takie założenia zapewniają, że obwód dopasowujący będzie realizowany w postaci drabinki,
bez sprzężonych indukcyjności, jednak z możliwością wystąpienia transformatorów
impedancji w przypadku obwodów pasmowo-przepustowych.
Jeżeli założymy, że współczynnik odbicia na wejściu obwodu dopasowującego ma następu-
jącą postać
( )
( )
( )
S s
h s
g s
h
h s
h s
h s
g
g s
g s
g s
n
n
n
n
11
0
1
2
2
0
1
2
2
=
=
+
+
+ +
+
+
+ +
...
...
,
(8.1)
w której h(s) i g(s) są wielomianami n-tego stopnia zmiennej zespolonej s, to wobec
poczynionych założeń pozostałe współczynniki rozproszenia obwodu można wyznaczyć na
podstawie znajomości współczynnika S
11
z następujących zależności
( )
( )
( )
S s
h s
g s
11
=
,
(8.2)
( )
( )
( )
S
s
S
s
s
g s
k
12
21
=
= ±
,
(8.3)
( )
(
)
(
)
( )
S
s
h
s
g s
k
22
1
= − −
⋅
−
,
(8.4)
w których k jest liczbą naturalną, określającą liczbę zer transmisji w zerze (
ω
= 0).
Dla bezstratnego obwodu dopasowującego parametry rozproszenia spełniają następujące
równanie
( )
( )
1
2
21
2
11
=
+
ω
ω
S
S
,
(8.5)
z którego bezpośrednio wynika następujący związek między wielomianami h(s) i g(s):
( ) (
)
( ) (
) (
)
g s g
s
h s h
s
s
k
k
−
=
−
+ −1
2
.
(8.6)
Zakładając, że współczynniki wielomianu h(s) są znane, wielomian g(s) można wyznaczyć
metodą faktoryzacji Hurwitza.
Zagadnienie poszukiwania obwodu dopasowującego sprowadza się teraz do poszukiwania
współczynników wielomianu h(s). Dopasowanie anteny do źródła sygnału zależy od
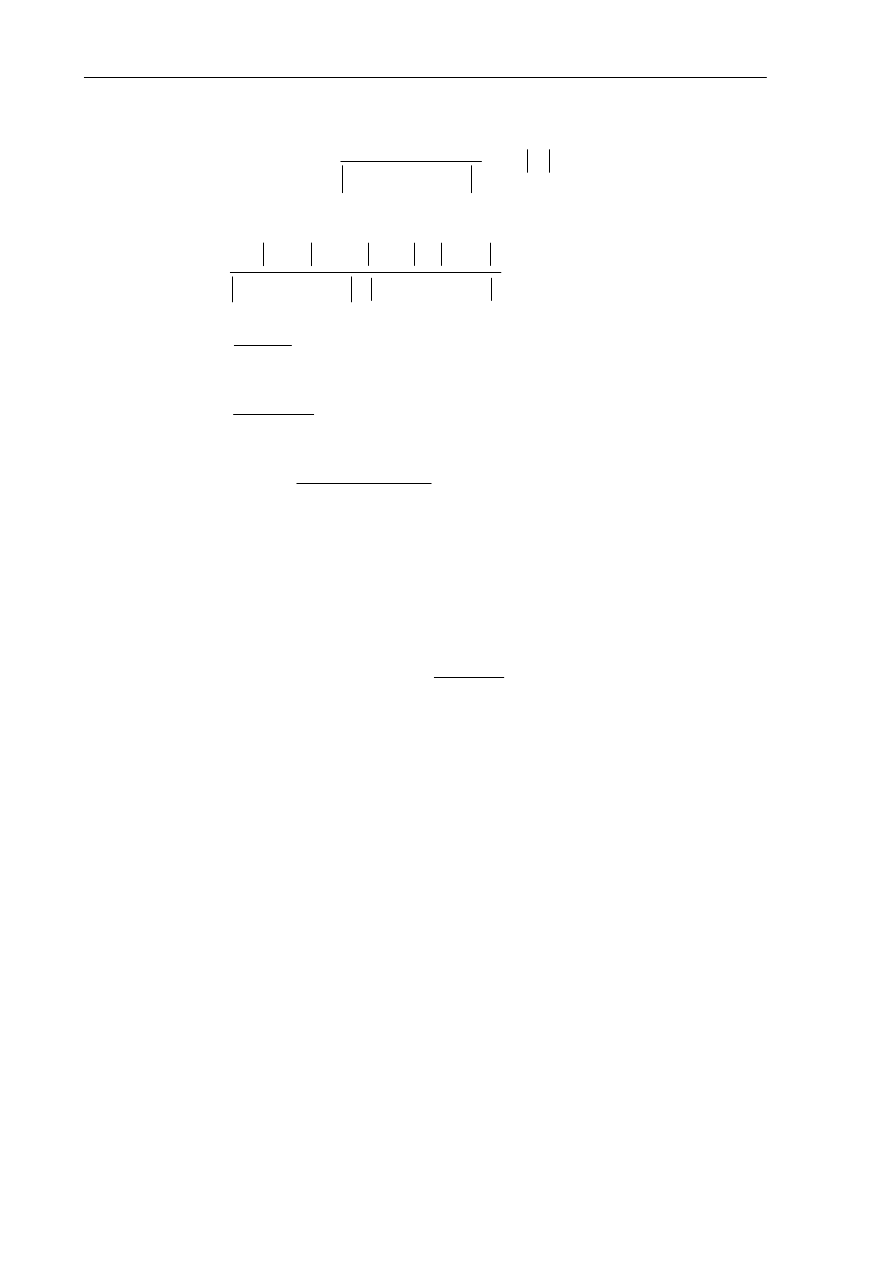
S
TRONA
76
Element mikropaskowy zasilany poprzez sprzężenie z aperturą
parametrów transmisyjnych obwodu dopasowującego, opisanych funkcją skutecznego
wzmocnienia mocy
( )
( )
( )
(
)
(
)
T
R
R
Z j
Z j
a
o
a
q
o
ω
ω
ω
ω
ω
ρ
=
⋅
⋅
+
= −
4
1
2
2
,
(8.7)
którą można również zapisać w zależności od wielomianów h(s) i g(s)
( )
( )
(
)
( )
(
)
( )
( ) ( )
( ) ( )
T
S
S
S
S
S
S
S
G
A
G
A
ω
ω
ω
ω
ω
ω
ω
ω
=
−
⋅
−
⋅
−
⋅ −
1
1
1
1
2
2
21
2
11
2
22
2
'
,
(8.8)
( )
S
R
R
R
R
G
w
n
w
n
ω
=
−
+
,
(8.9)
( )
( )
( )
S
Z
R
Z
R
A
a
n
a
n
ω
ω
ω
=
−
+
,
(8.10)
( )
( )
( )
( ) ( )
( ) ( )
S
S
S
S
S
S
S
A
A
11
11
12
21
22
1
'
ω
ω
ω
ω
ω
ω
ω
=
+
−
,
(8.11)
w których R
n
jest rezystancją normalizacji parametrów S.
Optymalizacja funkcji T(
ω
) na maksimum transmisji mocy ze źródła do obciążenia (anteny)
odpowiada poszukiwaniu optymalnego obwodu dopasowującego, opisanego optymalnym
wielomianem h(s). Impedancję wejściową optymalnego czwórnika dopasowującego
wyznacza się z następującej zależności
( )
( )
( )
Z
R
S
S
wej
n
ω
ω
ω
=
⋅
+
−
1
1
11
11
,
(8.12)
w której S
11
jest współczynnikiem odbicia na wejściu obwodu, zdefiniowanym zależnością
(8.2). Syntezę tak opisanego czwórnika dopasowującego można przeprowadzić metodą
Darlingtona, która kończy procedurę projektowania obwodu dopasowującego.
Metoda SRFT po zaimplementowaniu w programie komputerowym, została z
powodzeniem zastosowana do projektowania szerokopasmowych obwodów dopasowujących.
Optymalizację współczynników wielomianu h(s) wykonano w oparciu o kryterium
najmniejszych kwadratów, a minimum funkcji celu poszukiwano metodą gradientów
sprzężonych.
Na podstawie wyników wielokrotnych obliczeń stwierdzono, że impedancyjne dopasowanie
mikropaskowego elementu promieniującego na grubym podłożu jest możliwe praktycznie dla
dowolnej grubości h
1
podłoża anteny. Jednak zadowalające szerokości pasma pracy (powyżej
20%) uzyskuje się dla struktur promieniujących z pętlą impedancyjną o powierzchni nie
przekraczającej 3·10
4
Ω
2
.
Działanie metody SRFT przedstawiono na przykładzie impedancyjnego dopasowania
modelu elementu promieniującego, opisanego w punkcie 5.1.1.1 (rys. 5.10), z podłożem o
grubości pierwszej warstwy h
1
= 25 mm i położeniem sondy zasilającej y
s
równym 0 mm dla
pierwszego modelu i 16 mm dla drugiego. Elementy takie nie dają się dobrze dopasować
metodą wykorzystującą pojemność w układzie zasilania łaty, dlatego też metoda SRFT jest
w tym przypadku jedynym rozwiązaniem.
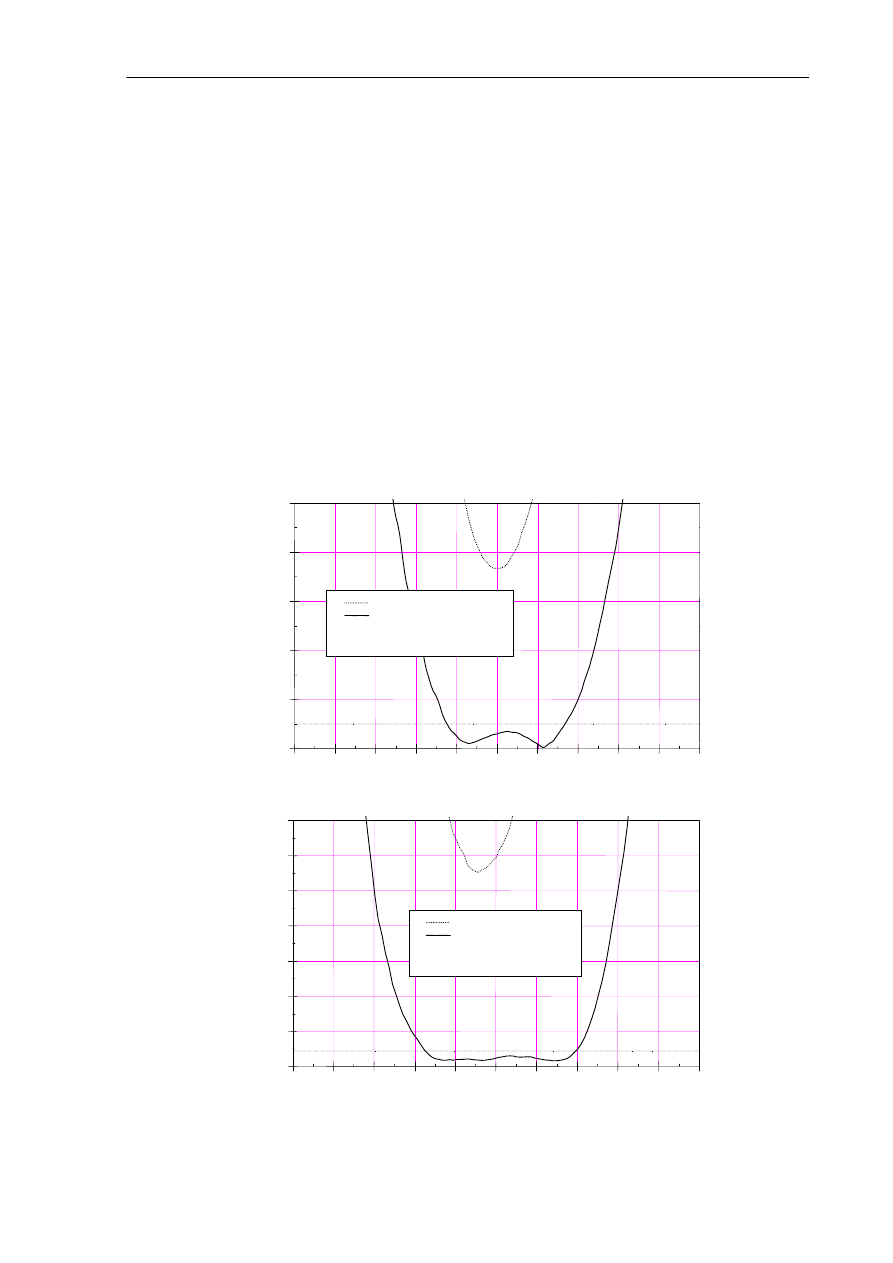
Na rys. 8.2 pokazano przebieg współczynnika fali stojącej na wejściu samej anteny oraz
anteny z filtrem dopasowującym, natomiast na rys. 8.3 pokazano schematy prototypów
obwodów dopasowujących. Obliczenia każdorazowo przerywano dla rzędu filtru, który nie
Element mikropaskowy zasilany poprzez sprzężenie z aperturą
S
TRONA
77
powodował dalszego polepszenia dopasowania. W pracy zamieszczono tylko wyniki obliczeń
dla obwodów dolnoprzepustowych (LP). Obliczenia były wykonywane również dla filtrów
pasmowo-przepustowych (BP) i górno-przepustowych (HP), jednak uzyskiwane wyniki były
niezadowalające.
Otrzymana w wyniku dopasowania względna szerokość częstotliwościowego pasma pracy,
zarówno dla pierwszego jak i drugiego modelu anteny, jest większa od 20%. Dla modelu z
sondą oddaloną od krawędzi łaty o 16 mm sięga ona prawie 30%, co można uznać za bardzo
dobry wynik.
Bardzo ważnym etapem w procesie projektowania obwodów dopasowujących jest
układowa realizacja prototypu filtru. W zakresie częstotliwości mikrofalowych jest ona
praktycznie możliwa tylko w postaci filtrów mikrofalowych. Już przy częstotliwościach
z zakresu pasma L pojawiają się poważne trudności w realizacji filtru na elementach
dyskretnych. Wybór wartości elementów z szeregu oraz brak kontroli efektów pasożytniczych
powodują poważną degradację jego parametrów. Wad tych pozbawiona jest realizacja na
elementach o stałych rozłożonych, np. liniach mikropaskowych. W tym przypadku wartości
elementów prototypu filtru mogą być realizowane z dużą dokładnością. Zaletą konstrukcji
mikropaskowych jest ponadto duża łatwość ich integracji z innymi układami i urządzeniami
mikrofalowymi, realizowanymi w technologii mikropaskowej, np. z antenami mikro-
paskowymi.
a)
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1
2
3
4
5
6
WFS = 1,5
przed dopasowaniem
po dopasowaniu
Szerokość pasma:
B
WFS<1,5
= 22,25% (292,25 MHz)
W
FS
f [GHz]
b)
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1
2
3
4
5
6
7
8
WFS = 1,5
przed dopasowaniem
po dopasowaniu
Szerokość pasma:
B
WFS<1,5
= 29,4% (381.5 MHz)
W
FS
f [GHz]
Rys. 8.2. Przebieg współczynnika fali stojącej na wejściu samej anteny oraz anteny z filtrem dopasowującym dla
modelu promiennika zasilanego sondą z położeniem sondy: a) y
s
= 0 mm, b) y
s
= 16 mm
S
TRONA
78
Element mikropaskowy zasilany poprzez sprzężenie z aperturą
a)
ANTENA
Filtr LP, n=2
C = 0,4 pF
L = 13,4 nH
Z
wej
(WFS)
b)
ANTENA
Filtr LP, n=3
C = 1,5 pF
L1 = 10,6 nH
Z
wej
L2 = 33,5 nH
(WFS)
Rys. 8.3. Struktura prototypu filtru dopasowującego dla modelu anteny z położeniem sondy:
a) y
s
= 0 mm, b) y
s
= 16 mm
W przypadku dolno-przepustowych filtrów drabinkowych istnieją dwie proste metody
zamiany elementów skupionych prototypu na jego odpowiedniki mikropaskowe. Pierwsza z
nich polega na zamianie kolejnych sekcji (elementów) filtru na krótkie odcinki linii
mikropaskowej o małej lub dużej impedancji charakterystycznej. Filtry takie noszą nazwę
stepped-impedance filters [53, 54], są proste w realizacji i mają niewielkie rozmiary
(maksymalna długość odcinków linii wynosi
λ
d
/8). W drugiej metodzie do zamiany
elementów wykorzystuje się przekształcenie Richardsa oraz tożsamości Kurody [54].
Otrzymywane tą metodą filtry mają postać, połączonych ze sobą szeregowo lub równolegle,
odcinków linii mikropaskowych o równej długości (wynoszącej
λ
d
/8) i różnej impedancji
charakterystycznej.
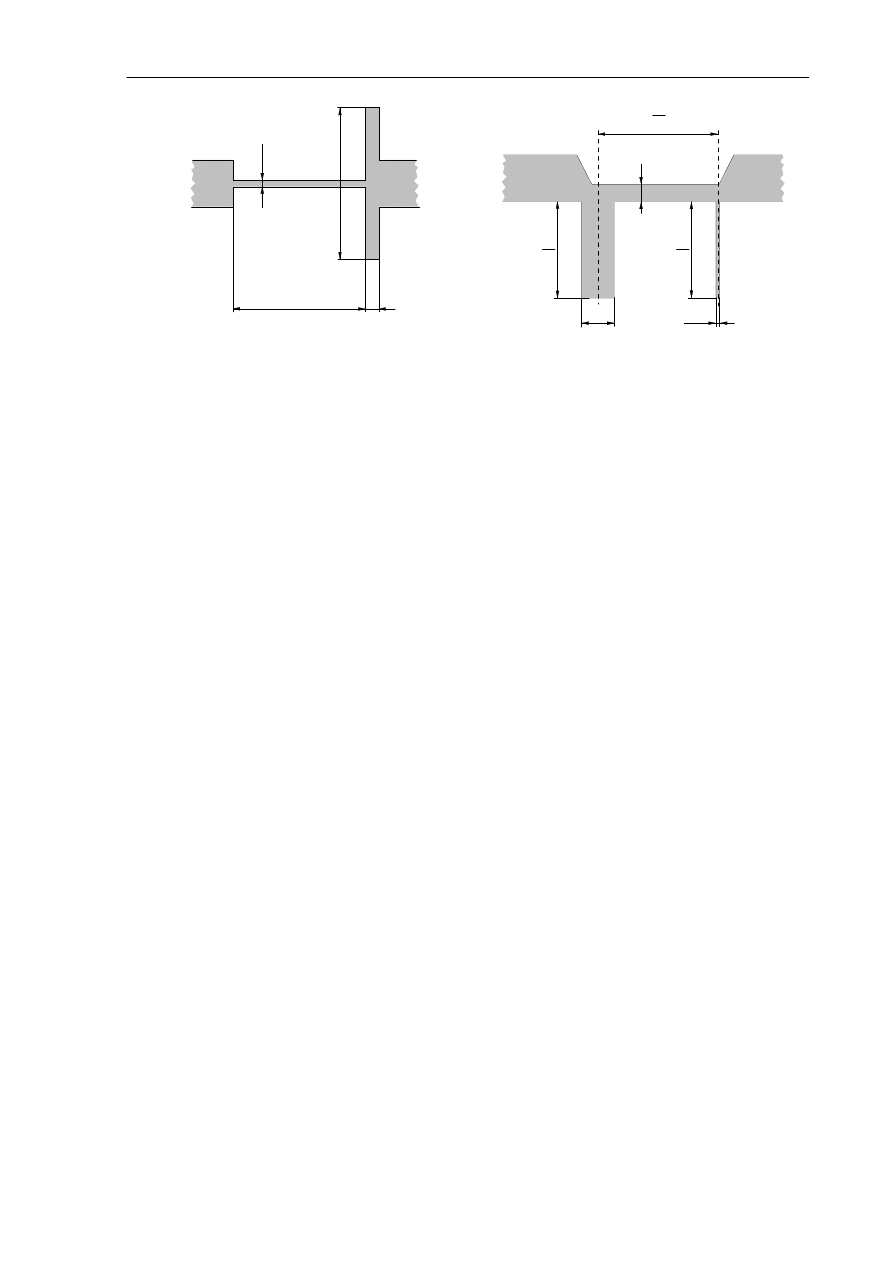
Wyniki syntezy uzyskane przy pomocy wymienionych metod można porównać na
przykładzie realizacji, omówionego wcześniej, prototypu filtru LP z rys. 8.3.a).
Na rys. 8.4.a) pokazano realizację w strukturze stepped-impedance, a na rys. 8.4.b) - strukturę
filtru otrzymaną z przekształcenia Richardsa i tożsamości Kurody. Zarówno w pierwszym jak
i drugim przypadku realizacji pojawiają się linie mikropaskowe o trudnej do osiągnięcia
impedancji
charakterystycznej
(180
Ω i
332 Ω
odpowiednio
dla
struktury
z rys. 8.4 a i b). Połączenie dwóch metod umożliwia ominięcie tych niedogodności i
zwiększenie pewności realizacji prototypu filtru. Otrzymany w ten sposób mikropaskowy
obwód dopasowujący można łatwo zintegrować z elementem promieniującym w postaci
wielowarstwowej struktury mikropaskowej. W tym miejscu należy jednak pamiętać o
wpływie obwodu dopasowującego na parametry polowe anteny. Przejawiają się one
zwiększeniem poziomu listków bocznych oraz listka wstecznego charakterystyki
promieniowania układu. Zjawisko to jest wywołane pasożytniczym promieniowaniem
elementów struktury filtru, oczywiście tylko w przypadku, gdy nie jest ona ekranowana.
Straty w mikropaskowym obwodzie dopasowującym powodują dodatkowo zmniejszenie
zysku promiennika.
Metoda dopasowania mikropaskowego elementu promieniującego na grubym podłożu,
poprzez zewnętrzny obwód dopasowujący, stanowi dobrą alternatywę dla metody
wykorzystującej dodatkową pojemność w układzie zasilania łaty. Przy wyborze metody
należy jednak pamiętać o wszystkich jej zaletach i wadach, a szczególną uwagę zwrócić na
sposób realizacji dopasowania - w postaci małej, zintegrowanej z układem zasilania
pojemności lub dużo większego filtru mikropaskowego.
Metoda SRFT jest z powodzeniem również wykorzystywana do poprawy dopasowania
elementów promieniujących zasilanych poprzez sprzężenie z aperturą [64, 55, 56, 57].
Element mikropaskowy zasilany poprzez sprzężenie z aperturą
S
TRONA
79
a)
50 Ω
50 Ω
w1
w2
l1
l2
180 Ω
20 Ω
b)
50 Ω
w1
50 Ω
w2
w3
λ
8
λ
8
λ
8
~75 Ω
~332 Ω
~151 Ω
Rys. 8.4. Struktura filtru mikropaskowego dla prototypu LP n=2:
a) filtr o strukturze stepped-impedance, b) filtr otrzymany po transformacji Richardsa
9. Zastosowanie mikropaskowych elementów promieniujących o
poszerzonym paśmie pracy w układach antenowych o
kształtowanej charakterystyce promieniowania
9.1. Wprowadzenie
W celu kształtowania charakterystyki promieniowania anteny mikropaskowe buduje się
w postaci układów antenowych. Najczęściej przybierają one postać płaskich prostokątnych
układów antenowych z równomiernie rozmieszczonymi elementami promieniującymi na
aperturze. Przy narzuconych wymaganiach na kształt charakterystyki promieniowania tylko w
jednej płaszczyźnie, układ redukuje się do postaci liniowego układu antenowego: kolumny
lub wiersza. Charakterystyka promieniowania w drugim głównym przekroju ma kształt
charakterystyki promieniowania elementu zastosowanego w układzie liniowym.
Synteza układu antenowego sprowadza się do określenia parametrów układu (zysk,
poziom listków bocznych , kształt charakterystyki promieniowania) i wyznaczenie rozkładu
współczynników pobudzenia elementów (amplitud i faz prądów zasilających), który formuje
charakterystykę promieniowania będącą najlepszym przybliżeniem zadanej charakterystyki
promieniowania, przy ustalonym kryterium optymalizacyjnym.
Kształt charakterystyki promieniowania układu antenowego zależy od rozkładu pola w
aperturze anteny. Charakterystyki promieniowania w głównych przekrojach układu
antenowego zależą od rozkładu współczynników pobudzeń elementów w wierszu oraz
kolumnie. Syntezę charakterystyk promieniowania anteny w głównych przekrojach anteny.
można przeprowadzić oddzielnie (zasada ekwiwalentnych liniowych apertur). Rozważania
nad płaskim układem antenowym można więc sprowadzić do rozważań nad liniowym
układem antenowym.
W zależności od kształtu charakterystyki promieniowania można stosować różne metody
syntezy (Woodworda–Lawsona, Transformaty Fouriera, wielomianów-Schelkunoffa,.....)[11].
W przypadku syntezy charakterystyk promieniowania układu antenowego o założonym
poziomie listków bocznych i kierunkowości D syteza sprowadza się do wybrania typowego
rozkładu amplitud i prądów zasilających (np. Czebyszewa, Tylora lub cos
2.
).
Wyżej wymienione metody syntezy można stosować przy założeniach, że:
− sprzężenia pomiędzy promiennikami są pomijalnie małe