S

TRONA

6

Budowa anten mikropaskowych

2. Budowa promienników mikropaskowych

Apertura anteny w technologii mikropaskowej jest wykonywana w formie druku na

laminacie dwustronnie metalizowanym folią miedzianą . Warstwa miedzi na jednej ze stron
laminatu stanowi ekran anteny, na drugiej natomiast jest trawiony wzór promienników.
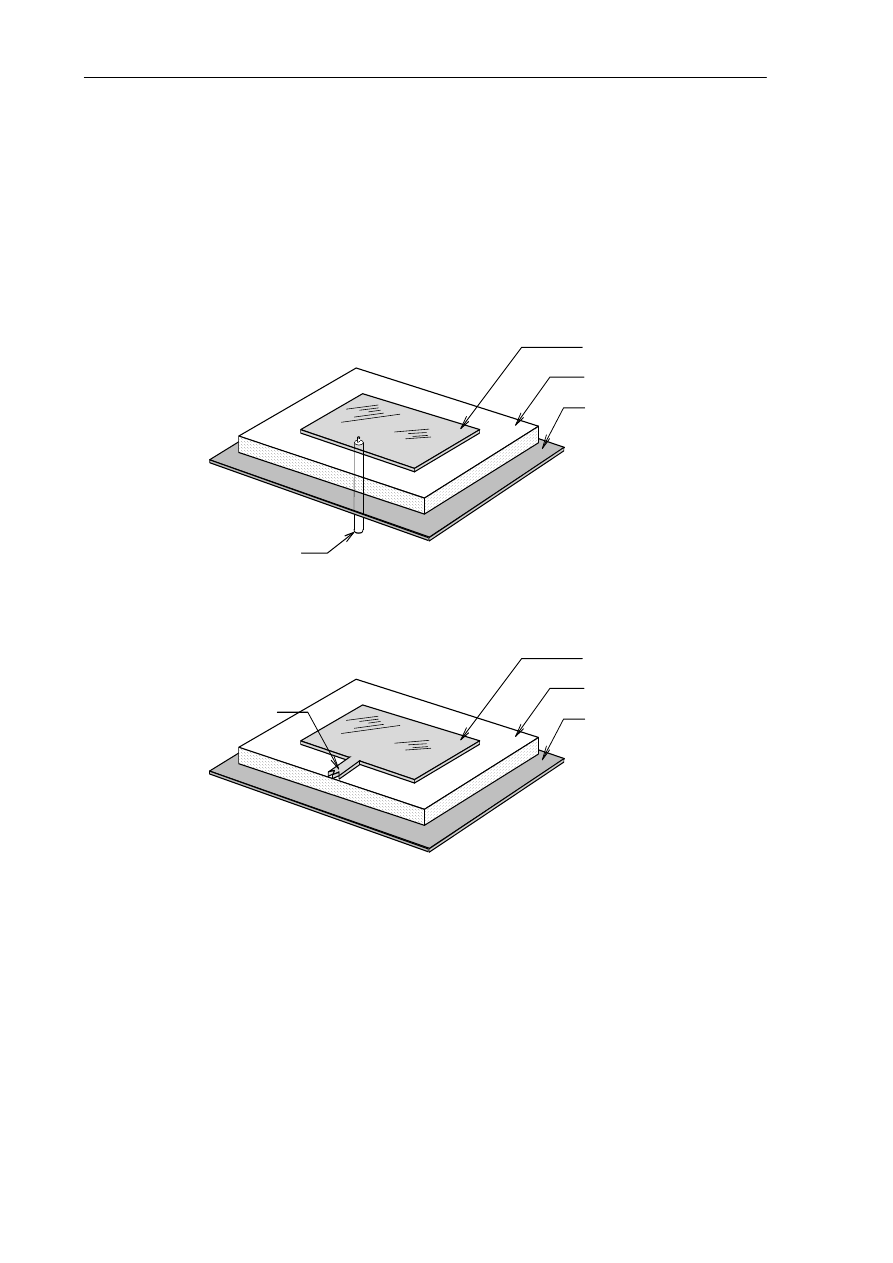
Zasilanie łaty odbywa się poprzez sondę (rys. 2.1) lub też bezpośrednio linią mikropaskową
(rys. 2.2). Zasilanie bezpośrednio poprzez linie mikropaskowe jest korzystne z punktu
widzenia technologicznego, gdyż promienniki oraz sieć zasilająca wykonywana jest na jednej
stronie laminatu. Odpada konieczność lutowania poszczególnych promienników oraz
trawienia dodatkowej płyty laminatu z układem podziału mocy.

Łata

Podłoże

Ekran

Sonda

Rys. 2.1. Budowa promiennika mikropaskowego zasilanego sondą

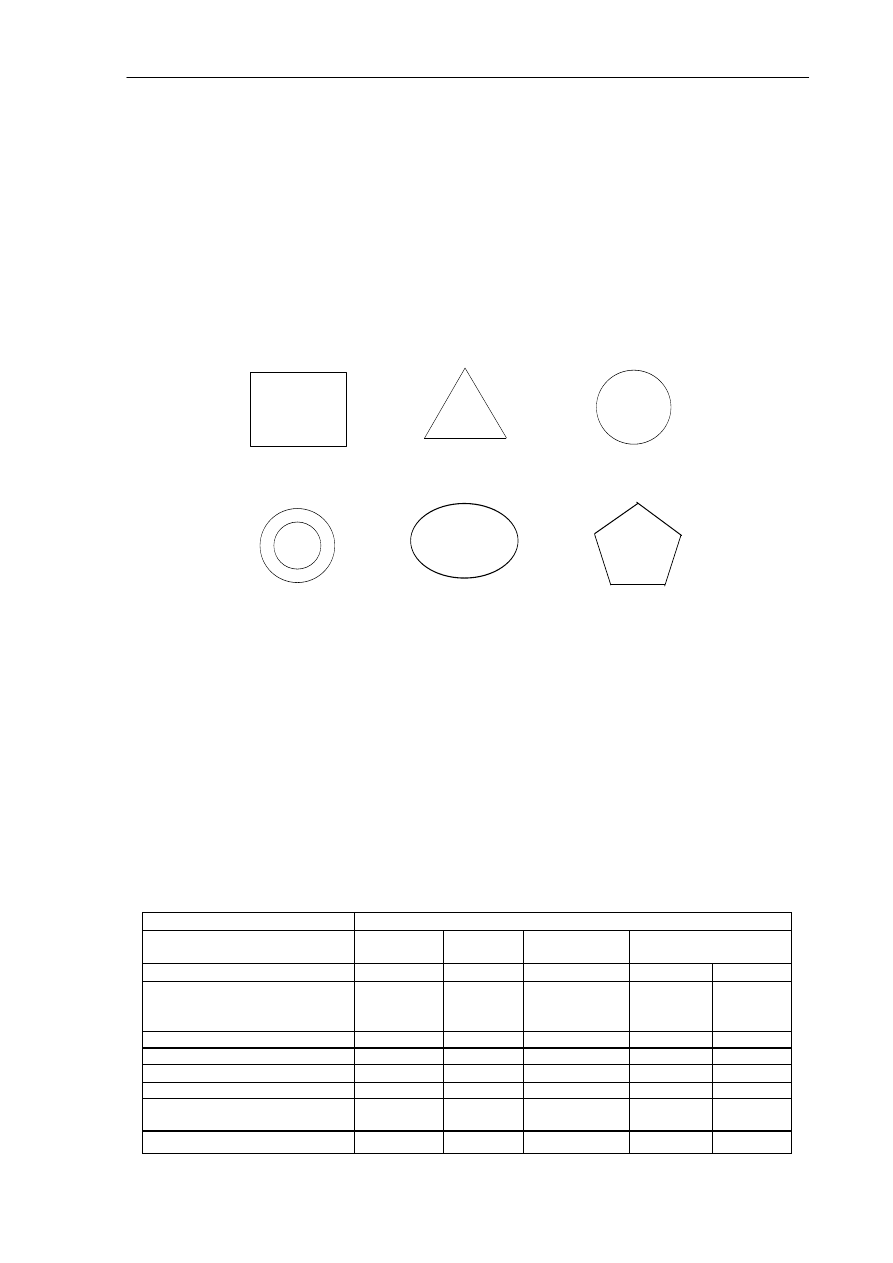
Łata

Podłoże

Ekran

Linia

zasilająca

Rys. 2.2. Budowa promiennika zasilanego linią mikropaskową

Ograniczona ilość miejsca na aperturze uniemożliwia jednak zbytnie rozbudowanie

sieci zasilającej. Ponadto, należy zauważyć, że odcinki sieci są liniami długimi, które również
promieniują zakłócając rozkład pola w aperturze anteny. Powoduje to podniesienie się
poziomu listków bocznych oraz zniekształcenie charakterystyki promieniowania.
Korzystniejszym rozwiązaniem wydaje się zasilanie łat przez sondy. Układ podziału mocy
jest przeniesiony wtedy za ekran anteny, przez co można wyeliminować niekorzystne
zjawiska wprowadzane przez sieć zasilającą. Jednak w przypadku rozbudowanych szyków
antenowych złożonych z dużej ilości łat promieniujących lutowanie może stanowić pewien
problem technologiczny. Ponadto obniża się niezawodność anteny wskutek możliwości
wystąpienia zimnego lutu lub jego rozłączenia pod wpływem naprężeń termicznych.

Poszczególne warstwy anteny łączy się ze sobą metodą klejenia oraz prasowania,

zapewniając między poszczególnymi warstwami laminatów połączenia galwaniczne lub też

Budowa anten mikropaskowych

S

TRONA

7

poprzez sprzężenie polem elektromagnetycznym. Taka technologia wykonania powoduje, że
antena ma cienki profil oraz małą wagę. Ponadto materiał z jakiego są wykonywane laminaty
pozwala w trakcie prasowania nadać antenie kształt powierzchni, na której będzie później
montowana. Oczywiście w ograniczonym zakresie tj. dla powierzchni konforemnych.

2.1. Charakterystyka podstawowych mikropaskowych elementów

promieniujących

Dwa stopnie swobody w płaskim układzie współrzędnych umożliwiają budowę

planarnego elementu promieniującego praktycznie o dowolnym kształcie. Niestety, tylko
kilka z wielu możliwych kształtów zostało dokładnie przebadane w celu określenia ich
podstawowych parametrów zarówno geometrycznych, jak i elektrycznych. Do grupy
najpopularniejszych możemy zaliczyć elementy: prostokątne, kołowe, eliptyczne, trójkątne,
pentagonalne oraz pierścieniowe (rys. 2.3).

Prostokąt

Trójkąt

Koło

Pierścień

Elipsa

Pięciokąt foremny

Rys. 2.3. Podstawowe mikropaskowe elementy promieniujące

Charakterystyki promieniowania wymienionych elementów są podobne, jeśli

pracują z modem podstawowym. Szerokość pasma pracy elementu oraz jego powierzchnia
zależą jednak od kształtu, np.: struktura pierścieniowa umożliwia uzyskanie poszerzonego
pasma pracy oraz zwiększenie zysku w czasie pracy z wyższymi modami fali
elektromagnetycznej, kosztem jednak znacznego powiększenia rozmiarów elementu.
W tabeli 2.1 zestawiono przykładowe parametry elementów mikropaskowych zbudowanych
przy następujących założeniach:

− częstotliwość pracy f

0

=2 GHz,

− grubość podłoża h=1,59 mm,

− przenikalność dielektryczna podłoża

ε

r

=2,32.

Tabela 2.1. Zestawienie podstawowych parametrów promienników mikropaskowych o różnych kształtach

TYP ELEMENTU

Parametr

Prostokątny

(W =1,56⋅L)

Kołowy

Trójkątny

(równoboczny)

Pierścieniowy (b=2a)

Mod pola elektromagnetycznego

TM

10

TM

11

TM

10

TM

11

TM

12

Szerokość wiązki ( 3 dB)
płaszczyzna E
płaszczyzna H

102°

85°

100°

80°

100°

88°

103°

81°

30°
47°

Kierunkowość D [dB]

7,0

7,1

7,1

7,1

10,9

Zysk G [dB]

6,1

6,8

6,2

6,1

10,6

Sprawność promieniowania η [%]

87

94

87

86

97

Szerokość pasma B [%]

0,7

1,1

0,78

0,7

3,8

Rozmiary

W=4,92 cm

L=3,28 cm

a=4,92 cm

a=6,57 cm

b=1,84 cm
a=0,82 cm

b=8,9 cm

a=4,45 cm

Powierzchnia [cm

2

]

16,1

23,3

18,1

10,6

249,0

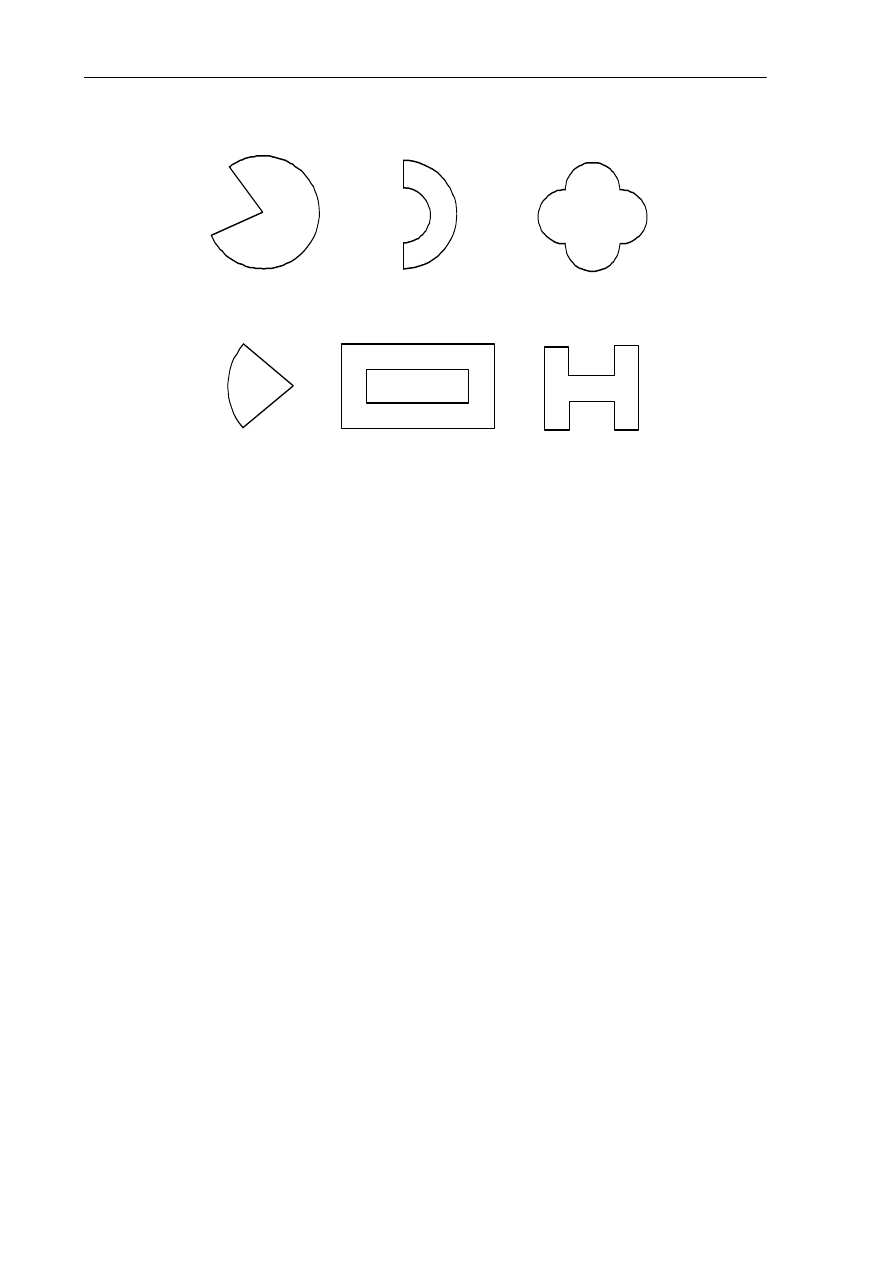
S

TRONA

8

Budowa anten mikropaskowych

Przykłady mniej popularnych wariantów podstawowych kształtów elementów

promieniujących pokazano na rys. 2.4.

Rys. 2.4. Mniej popularne kształty elementów mikropaskowych

Analizę parametrów elektrycznych promienników mikropaskowych na cienkim

podłożu można przeprowadzić w oparciu o model wnękowy[6, 9, 10, 11] lub linii
transmisyjnej, tradycyjny [8] lub zmodyfikowany [1]. Metoda prądowa nie zdobyła takiej
popularności do liczenia promienników typu łata nad ekranem, gdyż wymaga zbyt dużej
mocy obliczeniowej w stosunku do postawionego zagadnienia. Ponadto uzyskana dokładność
obliczeń impedancji wejściowej jest porównywalna (tylko dla cienkich dielektryków
h/λ<0,02). Jednak bez względu na przyjęty model obliczeń w efekcie i tak należy stroić
wykonaną strukturę w celu osiągnięcia wymaganych parametrów elektrycznych.

Modele

zastępcze

anteny

w postaci

rezonatora

wnękowego

ze ściankami

elektrycznymi i magnetycznymi lub linii transmisyjnej obarczone są pewnym błędem, który
wynika z niedoskonałości tych modeli, a także z uproszczeń. Powoduje to, że dokładność
wyników obliczeniowych nie zawsze jest zadowalająca, a ponadto zakres stosowalności tych
metod jest ograniczony warunkiem h/

λ

d

< 0,02 (h - grubość dielektryka,

λ

d

- długość fali

w dielektryku). Wielu autorów na użytek inżynierski wyznaczyło wzory algebraiczne
ze współczynnikami korekcyjnymi uzyskanymi w oparciu o metody numeryczne lub
empiryczne pozwalające z lepszą dokładnością wyznaczyć częstotliwość rezonansową łaty,
a także pozwalają na przekroczenie warunku h/

λ

d

< 0,02. Jest to tym ważniejsze,

że najprostszą metodą poszerzenia pasma pracy elementu mikropaskowego jest zwiększenie
grubości (w pewnym zakresie) dielektryka separującego łatę od ekranu.

Dielektryk użyty do budowy promiennika ma kluczowy wpływ na jego parametry.

Należy więc z dużą skrupulatnością prowadzić jego dobór poddając analizie takie parametry
jak:

ε

r

-względna przenikalność elektryczna,

tgδ -straty w dielektryku,

h -grubość dielektryka

Przenikalność dielektryczna jest kluczowym parametrem podłoża, od którego zależy

częstotliwość rezonansowa łaty, dlatego przy wykonywaniu większej ilości elementów należy
zapewnić jego stałość. Ważny jest też dobór wielkości

ε

r

, gdyż ma on wpływ na sprawność

promieniowania. Wybór laminatu o dużej wartości przenikalności pozwala zmniejszyć
fizyczne wymiary elementu jednakże wymaga większych dokładności trawienia

Budowa anten mikropaskowych

S

TRONA

9

poszczególnych elementów, aby zapewnić powtarzalność parametrów polowych i
obwodowych kolejnych egzemplarzy anteny. Ponadto zastosowanie dielektryka o dużej
przenikalności powoduje zawężenie pracy elementu promieniującego

Stosowanie w promiennikach podłoży o większych przenikalnościach powoduje

również zwiększoną wzrost zjawisk związanych z generacją fali powierzchniowej
w antenie, przez co zmniejsza się zysk promieniowania elementu. Fala elektromagnetyczna
nie jest bowiem wypromieniowywana w przestrzeń, lecz porusza się w warstwie dielektryka,
gdzie jest wytracana.

Wzrost grubości laminatu h ma wpływ na szerokość częstotliwościowego pasma pracy

promiennika. Niestety poszerzanie pasma pracy tą metodą jest mocno ograniczone, gdyż
wzrost grubości h ma również wpływ na wzrost zjawisk związanych z generacją fali
powierzchniowej. Zbyt duża grubość dielektryka doprowadza do sytuacji kiedy antena
przestaje promieniować. Oczywiście granice dopuszczalnej grubości dielektryka oraz jego
przenikalności dielektrycznej zależą od częstotliwości z jaką będzie pracować promiennik.

Z powyższego omówienia widać, że należy pogodzić ze sobą sprzeczne wymagania co

do parametrów dielektryka. Jedynym jednoznacznym parametrem jest stratność dielektryka
i powinna być ona bardzo niska.

Obecnie dobór materiałów na anteny mikropaskowe jest znacznie ułatwiony, gdyż

wielu producentów dostarcza na rynek gotowe laminaty o dobrych i gwarantowanych
parametrach.

Parametry promiennika zależą nie tylko od podłoża na jakim je wykonano, ale jak

wspomniano wcześniej, także od jego kształtu. Zjawiska jakie zachodzą w antenie
mikropaskowej, które omówiono powyżej, mają różny przebieg i charakter w zależności od
kształtu

promiennika.

Poniżej

scharakteryzowano

anteny

mikropaskowe

o

najpopularniejszych kształtach oraz przedstawiono zależności na wyznaczanie ich
częstotliwości rezonansowej wraz z granicami ich stosowalności oraz dokładności.

2.1.1. Element prostokątny

Prostokątny element promieniujący jest najczęściej stosowany w antenach

mikropaskowych. Jego określenie polega na podaniu długości L, szerokości W oraz
parametrów podłoża: względnej przenikalności elektrycznej

ε

r

i grubości h (rys. 2.5).

Pobudzany jest tak, aby pracował z modem fali TM

10

lub TM

01

. Umieszczenie

punktu zasilania na boku W oznacza , że przy modzie TM

10

promieniują krawędzie L,

natomiast przy TM

01

promieniują krawędzie W. Umożliwia to uzyskanie dwóch

ortogonalnych polaryzacji. Uzyskanie polaryzacji kołowej wymaga umieszczenia punktu
zasilania na przekątnej łaty lub zasilania jej na sąsiednich bokach z przesunięciem fazy o 90°.
Wybór sposobu zasilania zależy od wymaganej dokładności spolaryzowania fali oraz
dopuszczalnej komplikacji układowej. Polaryzację o lepszych parametrach zapewnia drugie
rozwiązanie, lecz wymaga dodatkowego dzielnika mocy.

Dla fali typu TM

01

osiąga się najmniejszą dobroć układu Q

,

a tym samym najszersze

pasmo pracy. Przy małych wartościach przenikalności

ε

r

i częstotliwościach powyżej

500 MHz szerokość pasma wzrasta wraz ze wzrostem grubości h i częstotliwością
rezonansową. Przy zastosowaniu podłoży o dużych wartościach przenikalności

ε

r

≥8

zachowanie to nie jest jednoznaczne. Charakterystyka promieniowania zasadniczo nie jest
czuła na zmiany parametru W/L i h, ale ulega zmianie wraz z względną przenikalnością
dielektryczna podłoża

ε

r

.

Impedancja wejściowa anteny ściśle zależy od częstotliwości rezonansowej oraz

położenia punktu zasilania elementu (w przypadku sondy współosiowej). Impedancja
wejściowa wzrasta wraz ze zbliżaniem się do krawędzi elementu i osiąga największą wartość
dla modu TM

10

.

S

TRONA

10

Budowa anten mikropaskowych

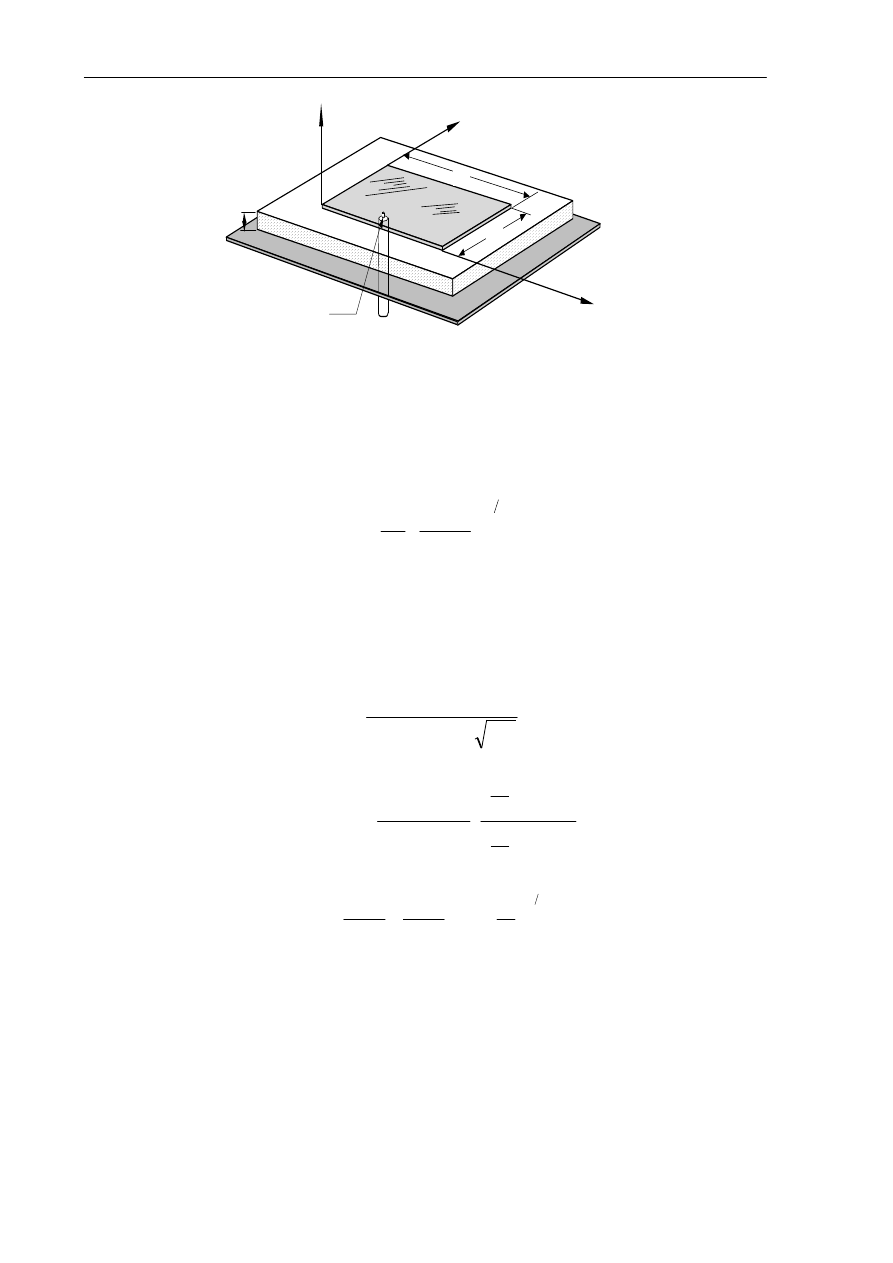
Y

X

Z

W

L

ε

r

h

Punkt zasilania

x

0

,y

0

Rys. 2.5. Geometria prostokątnego elementu mikropaskowego

Wartość maksymalnej impedancji anteny można zwiększać poprzez skrócenie boku W anteny.
Należy jednak pamiętać, że zbyt mała jego długość powoduje obniżenie sprawności
promieniowania anteny, natomiast zbyt duża sprzyja generowaniu wyższych modów fali.
Optymalny wymiar boku W określa zależność [2]

2

1

2

1

2

−













+

=

r

o

W

ε

λ

.

(2.1)

2.1.2. Częstotliwość rezonansowa łaty dla modelu wnęki rezonansowej

Zależność na częstotliwość rezonansową f

ro

dla modelu wnęki rezonansowej przy

uwzględnieniu efektów brzegowych takich jak promieniowanie mocy i moc bierna na
obrzeżach wnęki związanych ze skończoną admitancją ścianek wnęki, opisuje zależność [3]

(

)

eff

ro

L

L

c

f

ε

⋅

∆

+

⋅

=

2

2

,

(2.2)

(

)

(

)













+













+

⋅

−

+

⋅

⋅

=

∆

813

.

0

262

.

0

258

.

0

3

.

0

412

.

0

h

W

h

W

h

L

eff

eff

ε

ε

,

(2.3)

2

1

10

1

2

1

2

1

−











 +

−

+

+

=

W

h

r

r

eff

ε

ε

ε

.

(2.4)

przy czym:

L, W, h - wymiary łaty jak na rys. 2.5,

ε

r

- względna przenikalność elektryczna,

c

- prędkość światła.

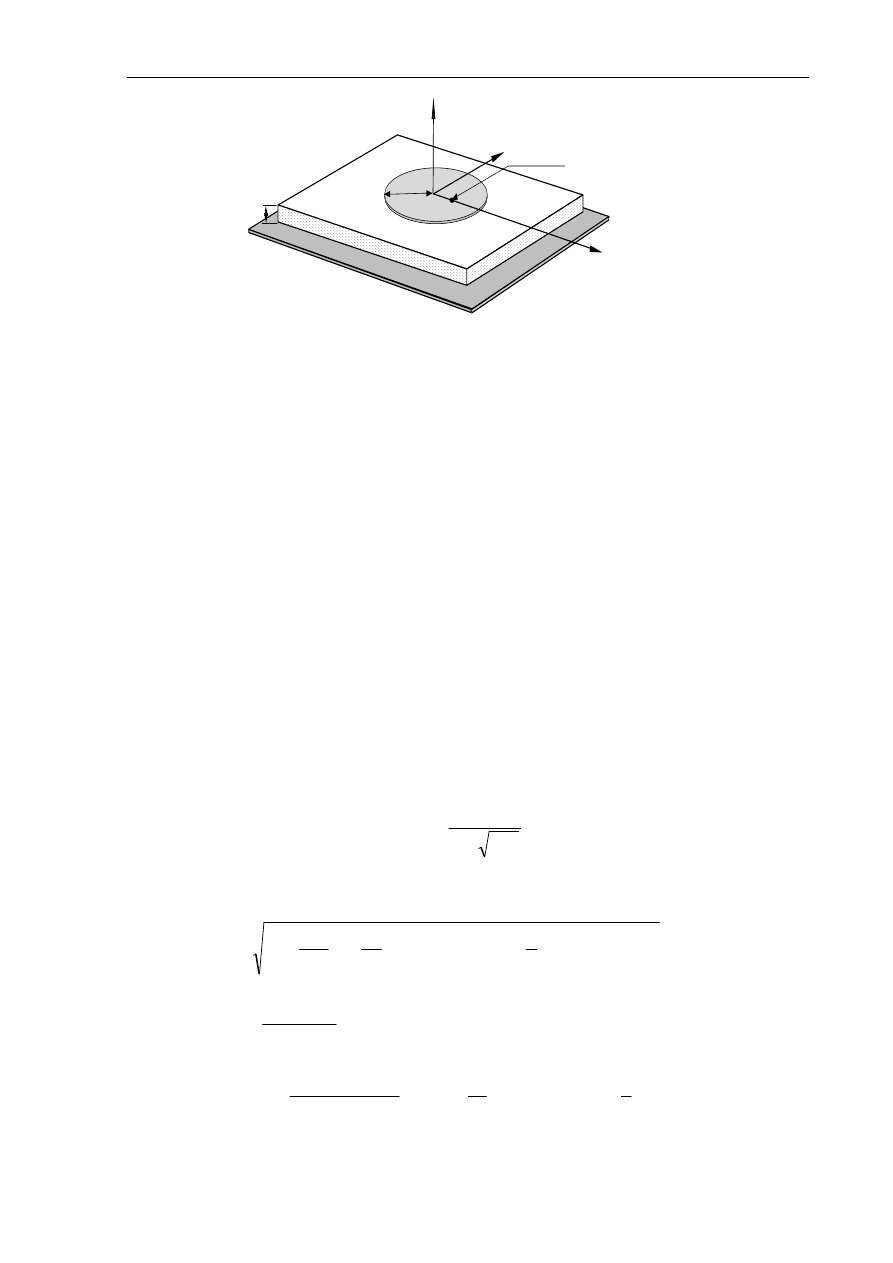
2.1.3. Element kołowy

Geometria elementu kołowego jest określona tylko jednym parametrem,

promieniem a (rys. 2.6).

Budowa anten mikropaskowych

S

TRONA

11

Y

X

Z

ε

r

h

Punkt zasilania

a

Rys. 2.6. Geometria kołowego elementu mikropaskowego

Elementy kołowe są głównie stosowane podczas pracy z modami TM

11

i TM

21

(pierwszy i drugi rezonans). Dla modu TM

11

charakterystyka promieniowania, w dowolnej

płaszczyźnie przekroju prostopadłej do powierzchni elementu, ma kształt funkcji

( )

cos

n

⋅

,

a dla modu TM

21

i wyższych listek główny rozdwaja się dając zero charakterystyki

promieniowania na kierunku prostopadłym do płaszczyzny elementu.

Parametry takie jak dobroć, sprawność promieniowania zachowują się identycznie jak

dla elementu prostokątnego. Impedancja wejściowa zależy od odległości punktu zasilającego
od krawędzi elementu i maleje wraz z jej wzrostem. Wpływ na impedancję mają oczywiście
również parametry geometryczne elementu, jak i parametry podłoża (

ε

r

, h). Kołowy element

promieniujący zasilany w jednym punkcie jest źródłem fali elektromagnetycznej
spolaryzowanej liniowo. Kołową polaryzację możemy osiągnąć stosując zasilanie w dwóch
punktach położonych na wzajemnie prostopadłych średnicach z przesunięciem fazy zasilania
o 90°.

Wzory algebraiczne opisujące związek częstotliwości rezonansowej dla modu TM

11

i wymiarów geometrycznych podano za [4]. Jest oczywiście wiele podejść do problemu
algebraicznego wyznaczenia częstotliwości rezonansowej łaty kołowej. Jednak po
przeanalizowaniu zbieżności wyników obliczeń z pomiarami zamieszczono zależności dające
wyniki z najmniejszym błędem.
Częstotliwość rezonansową łaty określa wzór:

f

r

ef

dyn

11

27 6177

=

.

π

ε

,

(2.5)

w którym

(

)

(

)

r

r

hr

r

h

h

r

ef

r

r

r

=

+







+

+

+

+











2

2

2

1 41

177

0 268

165

πε

ε

ε

ln

.

.

.

.

,

(2.6)

(

)

(

)

ε

ε

ε

dyn

C r h

C r h

=

, ,

, ,

0

,

(2.7)

(

)

(

)

(

)

C r h

r

h

r

r

h

h

r

r

r

r

, ,

.

ln

.

.

.

.

ε

ε ε π

ε

ε

ε

=

⋅

+







+

+

+

+











0 8525

2

1 41

1 77

0 268

1 65

2

0

0

,

(2.8)

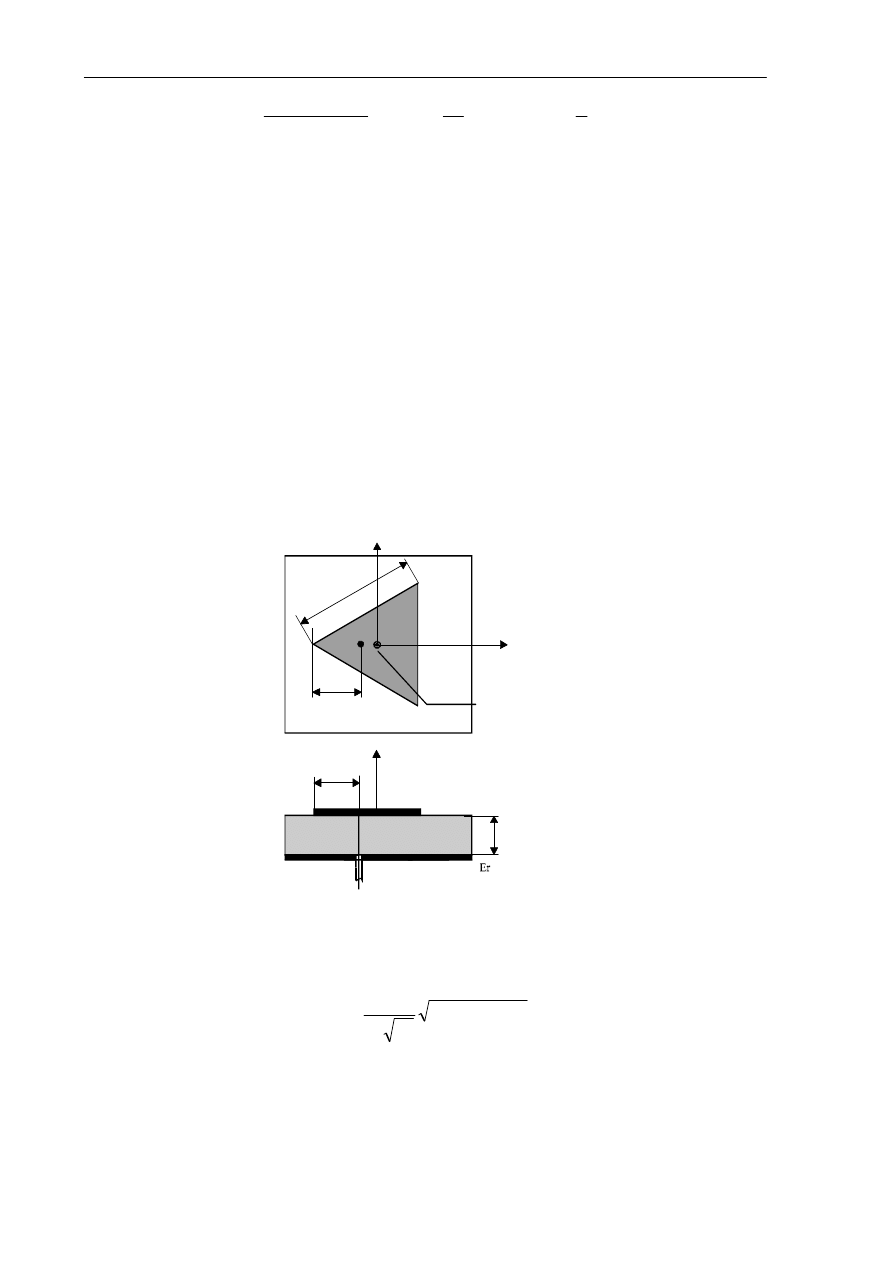
S

TRONA

12

Budowa anten mikropaskowych

(

)

C r h

r

h

r

r

h

h

r

, ,

.

ln

.

.

ε

ε π

ε

0

2

0

0

0 8525

2

318

1918

=

⋅

+







+

+









 ,

(2.9)

r -promień łaty,

ε

r

-względna przenikalność elektryczna podłoża,

ε

0

-przenikalność elektryczna próżni,

h -grubość podłoża.

2.1.4. Element trójkątny

Trójkątny element promieniujący jest charakteryzowany poprzez podanie długości

jego boku a (rys. 2.7). Kształt charakterystyki promieniowania nie zależy od częstotliwości
rezonansowej i wymiarów elementu promieniującego. Maksimum charakterystyki
promieniowania dla modów TM

11

i TM

21

występuje na kierunku prostopadłym do

powierzchni elementu. W odróżnieniu od elementu prostokątnego dobroć oraz pasmo pracy
elementu trójkątnego zachowuje się w sposób jednoznaczny tzn. dobroć maleje, a pasmo
rośnie wraz ze wzrostem grubości laminatu h lub spadkiem przenikalności dielektrycznej
podłoża

ε

r

.

Impedancja elementu promieniującego jak poprzednio, zależy od wyboru położenia

punktu zasilającego. Dla modów fali TM

10

, i TM

21

rezystancja wejściowa elementu maleje

ze wzrostem d, dla modu TM

20

, początkowo maleje, osiągając minimum, a następnie rośnie.

ε

r

t

linia zasilająca

d

X

Y

a

d

Z

Punkt
zasilania

Z

Rys. 2.7. Geometria trójkątnego elementu mikropaskowego

Model wnęki rezonansowej, jako najbardziej rozpowszechniony, posłuży także jako

podstawa do wyznaczenia częstotliwości rezonansowej elementu trójkątnego, która wynosi

f

c

a

m

mn

n

m n

r

,

=

+

+

2

3

2

2

ε

,

(2.10)

gdzie: m, n - wyznaczają numer modu fali z jakim ma pracować antena.

Ponieważ idealne ścianki magnetyczne nie istnieją, to otrzymane wyniki teoretyczne

są obarczone dużym błędem. Podobnie jak dla elementu kołowego w literaturze proponuje
się zastąpienie we wzorze na częstotliwość rezonansową długości rzeczywistej boku
elementu długością efektywną, tak więc wzór przybiera postać

Budowa anten mikropaskowych

S

TRONA

13

f

c

a

m

mn

n

m n

eff

r

,

=

+

+

2

3

2

2

ε

.

(2.11)

W zależności od źródła podawane są różne zależności na a

eff

. Największą zgodność

na częstotliwość rezonansową między wartościami zmierzonymi, a wyliczonymi można
otrzymać z zależności [5]

a

a

h

a

h

a

h

a

h

a

h

a

eff

r

r

r

=

+









 −

























 +

























 +









 −











































1 1199

12 853

1

16 436

1

6 182

9 802

1

2

2

.

.

.

.

.

ε

ε

ε

. (2.12)

Powyższa zależność pozwala na wyznaczenie częstotliwości rezonansowej dla modu
podstawowego TM

10

z błędem nie większym niż 1% przy spełnieniu warunku h/λ

d

≤ 0,2,

a więc o rząd wyższym, niż przy standardowej metodzie wnęki.

2.2. Pasmo pracy anten mikropaskowych

Szerokość częstotliwościowego pasma pracy anteny definiuje się jako przedział

częstotliwości, w którym parametry obwodowe lub polowe zachowują pożądane wartości [6].
Definicja taka może być sformułowana w odniesieniu do:

− impedancji wejściowej anteny,

− zysku energetycznego,

− szerokości listka głównego charakterystyki promieniowania,

− poziomu listków bocznych,

− poziomu tłumienia składowej pola o polaryzacji ortogonalnej.

W niniejszym opracowaniu jako częstotliwościowe pasmo pracy przyjęto definicję odnoszącą
się do impedancji wejściowej anteny.
Szerokość pasma pracy B definiuje się jako przedział częstotliwości, w którym wejściowy
współczynnik fali stojącej anteny (WFS) jest równy lub mniejszy od założonej wielkości S.
Do porównywania częstotliwościowego pasma pracy anten mikropaskowych pracujących z
różną częstotliwością środkową bardziej arbitralną definicją jest względne częstotliwościowe
pasmo pracy
Zakładając, że współczynnik fali stojącej na wejściu anteny spełnia warunek WFS≤S
w przedziale częstotliwości od f

d

do f

g

, a jej częstotliwość rezonansowa wynosi f

r

,

to względna szerokość częstotliwościowego pasma pracy anteny B wyraża się następująco

B

f

f

f

g

d

r

[%]

=

−

⋅100%.

(2.13)

W przypadku wąskopasmowych, jednowarstwowych anten mikropaskowych impedancja
wejściowa w okolicach częstotliwości rezonansowej modu podstawowego TM

01

zachowuje

się podobnie jak impedancja pojedynczego równoległego obwodu rezonansowego [6 ,3 , 7].
Jeżeli dodatkowo założymy, że dla częstotliwości rezonansowej f

r

antena jest dopasowana do

źródła sygnału, to szerokość względnego częstotliwościowego pasma pracy można zapisać
wzorem [8]

B

Q

S

S

[%]

=

⋅

−

⋅

1

1

100% ,

(2.14)

w którym Q oznacza wypadkową dobroć, wyznaczoną dla wnękowego modelu zastępczego
anteny mikropaskowej [6, 3, 7 ,9, 10, 11], a S jest wartością graniczną współczynnika fali
stojącej w pasmie B.

S

TRONA

14

Pasmo pracy

Dobroć wnęki rezonansowej, definiuje się jako stosunek energii zgromadzonej w polu
elektromagnetycznym wnęki do energii pochłoniętej przez straty wnęki. Zgodnie z definicją
dobroć opisuje się następującą zależnością [8, 9]

Q

f W

P

e

d

=

⋅

2

π

,

(2.15)

w której W

e

jest średnią energią gromadzoną w jednym okresie, a P

d

stanowi moc traconą na

stratach wnęki. Parametry modelu wnękowego anteny mikropaskowej mają dobrą
interpretację fizyczną, umożliwiającą między innymi wskazanie źródeł strat i oszacowanie ich
wielkości. Wypadkowa dobroć Q wnęki jest związana ze stratami następującą zależnością

1

1

1

1

1

Q

Q

Q

Q

Q

r

p

c

d

=

+

+

+

,

(2.16)

w której poszczególne składowe oznaczają:

Q

r

- dobroć wnęki dla strat promieniowania,

Q

p.

- dobroć wnęki dla strat promieniowania fali powierzchniowej,

Q

c

- dobroć wnęki dla strat w przewodniku łaty promieniującej,

Q

d

- dobroć wnęki dla strat w dielektryku.

Wielkości Q

c

i Q

d

można oszacować z przybliżonych zależności [8]

Q

h

c

=

2

0

ωµ σ

,

(2.17)

Q

tg

d

=

1

δ

,

(2.18)

w których:
h

- jest grubością dielektryka,

tgδ - jest tangensem kąta strat w dielektryku,
σ

- jest przewodnością właściwą materiału, z którego wykonana jest łata promieniująca.

Główne składowe dobroci wnęki Q

r

i Q

p

można wyznaczyć z zadowalającą dokładnością

tylko poprzez obliczenie wielkości mocy promieniowanej z całki powierzchniowej składowej
radialnej wektora Poytinga w strefie pola dalekiego.
Wypadkowa dobroć może być również wyznaczona na podstawie znajomości efektywnego
(wypadkowego) tangensa kąta strat wnęki [9, 10], reprezentującego wszystkie straty w
antenie mikropaskowej

Q

tg

eff

=

1

δ

.

(2.19)

Efektywny tangens kąta strat można wyrazić w zależności od tangensa kąta strat
w dielektryku, grubości dielektryka, głębokości wnikania dla przewodnika łaty
promieniującej oraz stosunku mocy promieniowanej z anteny i energii zgromadzonej we
wnęce. Przedstawiona interpretacja wypadkowej dobroci modelu wnękowego, umożliwia
powiązanie parametrów anteny mikropaskowej z szerokością częstotliwościowego pasma
pracy.
Jedynym sposobem poszerzenia pasma pracy jest zmniejszenie dobroci wnęki. Można to
osiągnąć zwiększając jej straty. Najbardziej korzystnym rozwiązaniem byłoby zwiększenie
tylko strat promieniowania. Niestety wraz ze wzrostem strat promieniowania rosną również

Pasmo pracy

S

TRONA

15

straty związane z promieniowaniem fali powierzchniowej. Straty w antenie rosną
proporcjonalnie

z

rozmiarami

anteny.

W

przypadku

jednowarstwowych

anten

mikropaskowych szerokość pasma pracy zależy od parametrów podłoża i rozmiarów łaty
promieniującej. Ze względów praktycznych modyfikacji można poddawać tylko parametry
podłoża anteny mikropaskowej. Szerokość pasma rośnie wraz ze wzrostem grubości podłoża,
a maleje wraz ze wzrostem jego względnej przenikalności elektrycznej.

3. Materiały wykorzystywane do budowy anten mikropaskowych

Dobór materiałów wchodzących w skład mikropaskowych struktur promieniujących jest

jednym z najważniejszych zagadnień technologicznych. Parametry zastosowanych
materiałów bezpośrednio wpływają na parametry elektryczne anten mikropaskowych.
Od ich właściwości elektrycznych zależą własności impedancyjne, polowe, mocowe oraz
wymiary anteny. Związek ten jest szczególnie ważny ze względu na rolę dielektrycznego
podłoża w zjawiskach fizycznych zachodzących w antenie.
W mikropaskowych antenach wykorzystuje się różne materiały dielektryczne, których
zasadniczą cechą są małe straty elektryczne (wyrażone parametrem tgδ). Produkowane są one
przeważnie w postaci płyt o różnych grubościach z metalizowaną powierzchnią jedno lub
dwustronnie. W zależności od parametrów elektrycznych oraz właściwości mechanicznych
można je podzielić na cztery grupy zastosowań:

− laminaty dla elementów promieniujących,

− laminaty na sieć zasilającą,

− materiały na powłoki ochronne,

− materiały na elementy mechaniczne struktur promieniujących.

Konstruując mikropaskowy układ antenowy wraz z siecią zasilającą należy mieć na

uwadze odmienność wymagań stawianych przez optymalne projektowanie promienników i
sieci zasilającej. Promienniki mikropaskowe o szerokim względnym częstotliwościowym
paśmie pracy wymagają grubych podłoży o niskiej względnej przenikalności elektrycznej.
Pojedyncze podłoże może być również zastąpione strukturą wielowarstwową, której
zastępcza przenikalność elektryczna musi być również jak najmniejsza.
Układy formowania wiązki złożone z dzielników oraz linii mikropaskowych powinny być
wykonane na cienkim podłożu, aby zminimalizować niepożądane promieniowanie. Wybór
konkretnej przenikalności elektrycznej w przypadku sieci zasilającej nie jest już jednak tak
jednoznaczny jak w przypadku promienników. Duża przenikalność elektryczna podłoża
umożliwia uzyskanie małych rozmiarów elementów wchodzących w skład sieci zasilającej.
Powoduje to jednak zwiększone wymagania na tolerancję wykonania sieci zasilającej. W
wyniku czego fizyczne wykonanie pewnych elementów sieci jest niemożliwe lub skutkuje
dużym odrzutem w trakcie produkcji. Ponadto podłoża o dużej przenikalności elektrycznej
charakteryzują się większymi stratami. W wyniku czego spada zysk energetyczny układu
antenowego Zastosowanie podłoży o niskiej przenikalności elektrycznej pozwala uniknąć
problemów technologicznych. Z reguły jednak ograniczona powierzchnia przeznaczona na
sieć

zasilającą

wymusza

kompromis

pomiędzy

miniaturyzacją,

a

wymogami

technologicznymi.

Bardzo istotnym parametrem materiałów dielektrycznych używanych w układach

mikrofalowych jest powtarzalność ich parametrów elektrycznych. Rynek laminatów
mikrofalowych jest bardzo bogaty. Jednak na uwagę zasługuje tylko kilku wiodących
producentów, których laminaty są dostosowane do wymagań stawianym przez technikę anten
mikropaskowych. Nazwy czołowych producentów wraz z nazwami wybranych produktów
zebrano w tabeli 3.1.

S

TRONA

16

Materiały wykorzystywane do budowy anten mikropaskowych

Tabela 3.1. Wykaz wybranych producentów laminatów mikrofalowych

Producent

Laminat

Grubość

[mm]

Stała dielektryczna

εεεε

r

Współczynni

k strat

tg

δ

Crane

CuFlon CF-A62-7-7

1,57

2,1

0,00045

Rogers

RT Duroit 5880
Ultralam 2000
RO 4003
RO4350

0,79
0,762
0,81
0,762

2,2

±

0,02

2,4

±

0,04

3,38

±

0,05

3,48

±

0,05

0,0009
0,0019
0,002
0,002

3M AG

CuClad 250 LX 0300 55 55
CuClad 250 LX 0600 55 55

0,762
1,524

2,55

±

0,04

2,55

±

0,04

0,0021
0,0021

Taconic

TLY-5A-0310 CH/CH
TLX-8-0310-CH/Ch

0,79
0,79

2,17

±

0,02

2,55

±

0,04

0,0009
0,0019

GIL

MC-5
MC-5
GML 1000
GML 1000

0,762
1,524
0,762
1,524

3,40

±

0,05

3,20

±

0,05

3,20

±

0,05

3,05

±

0,05

0,012
0,011
0,003
0,003

Można wyróżnić kilka typów produkowanych laminatów , których zastosowanie jest możliwe
w antenach mikropaskowych i ich sieciach zasilających:

− laminaty teflonowe ε

r

≈2.1,

− laminaty teflonowo-szklane ε

r

≈2.2÷2,6,

− laminaty teflonowo-ceramiczne, ε

r

≈2.6÷6,

− laminaty ceramiczne ε

r

≈10,

− laminaty poliestrowo-szklane ε

r

≈3÷3,6.

Laminaty do zastosowań mikrofalowych produkowane są przeważnie na bazie

teflonu, który ma najniższe straty elektryczne. Jednak mają one niekorzystne właściwości
mechaniczne (laminaty są miękkie, a do ich klejenia trzeba używać specjalnych folii-tzw.
prepregów) oraz trudne w obróbce elektrochemicznej (metalizacja otworów). Poważną wadą
teflonu jest skokowa zmiana wartości stałej dielektrycznej w temperaturze między 20°a 30°C.
Ponadto koszt takich laminatów jest stosunkowo wysoki.
Wśród producentów na uwagę zasługuje firma GIL, która wprowadziła niedawno na rynek
laminat poliestrowo-szklany (GML-1000) do zastosowań w antenach do systemów
komunikacji ruchowej. Ma on zastąpić na rynku laminat FR-4 firmy Isola. Ze względu na
swoje parametry elektryczne laminat GML1000 stanowi tańszą alternatywę również dla
laminatów teflonowych, szczególnie w aplikacjach poniżej 10 GHz.

W kraju produkowane są tylko laminaty szklano-epoksydowe. Ze względu na

swoje właściwości elektryczne mogłyby być one stosowane w antenach pracujących do
pasma L. Niestety producenci nie gwarantują powtarzalności parametrów elektrycznych
laminatu. Potwierdziły to również wykonane pomiary laminatu.
Do pozostałych materiałów stosowanych w antenach mikropaskowych należy zaliczyć
materiały wykorzystywane do wykonania powłok zabezpieczających oraz elementów
konstrukcyjnych struktur promieniujących.

Zabezpieczenie zewnętrzne anten mikropaskowych przed działaniem czynników

atmosferycznych i mechanicznych może być wykonane przez:
− naniesienie powłoki lakierniczej na laminat

− powleczenie laminatu folią ochronną

− umieszczenie osłony nad anteną.

W wielowarstwowych strukturach promieniujących konieczne jest zastosowanie

elementów dystansujących poszczególne warstwy laminatów na których naniesiony jest wzór

Materiały wykorzystywane do budowy anten mikropaskowych

S

TRONA

17

z elementami mikrofalowymi. Można to zrobić przy pomocy dielektrycznych kołków w kilku
punktach dielektrykiem separującym poszczególne płyty laminatu jest wtedy powietrze.
Ponieważ odległość pomiędzy poszczególnymi płytkami drukowanymi jest zazwyczaj bardzo
istotna, rozwiązanie tego typu jest więc niewygodne ze względu na giętkość płyt laminatu i
konieczność podparcia go w wielu punktach. Lepszym rozwiązaniem jest wprowadzenie
materiału dielektrycznego w postaci płyty, która zapewni podparcie laminatu na całej
powierzchni.

Do głównych skutków ubocznych zastosowania zabezpieczenia oraz wprowadzenie

w strukturę promieniującą dielektrycznych elementów konstrukcyjnych należą zmiany
impedancji wejściowej anteny, przesunięcie się częstotliwościowego pasma pracy
określonego przez kryterium dopasowania (WFS) oraz wprowadzenie dodatkowego
tłumienia.
Do najczęściej stosowanych materiałów konstrukcyjnych stosowanych w antenach
mikropaskowych na elementy dystansujące i osłony zalicza się wszelkiego rodzaju pianki
oraz wypełniacze komórkowe typu plaster miodu.
W czystej formie materiały te stosowane są one raczej sporadycznie . Najczęściej służą do
wykonania różnego rodzaju struktur kompozytowych (warstwowych), które osiągają dużą
wytrzymałość mechaniczną, a zarazem są bardzo lekkie. Technologia ta jest stosowana od lat
w przemyśle lotniczym do produkcji różnego typu elementów konstrukcyjnych oraz osłon w
samolotach.
W uproszczeniu struktura kompozytowa składa się z wypełniacza oklejonego z obu stron
okładkami w postaci cienkiej płyty. Poszczególne elementy struktury kompozytowej
posiadają małą wytrzymałość mechaniczną, dopiero po sklejeniu uzyskują wysoką
wytrzymałość mechaniczną. Jako okładki struktury kompozytowej mogą występować
bezpośrednio laminaty mikrofalowe z naniesionym układem ścieżek i promienników.
Struktury kompozytowe stanowią klucz do produkcji anten mikropaskowych o poszerzonym
paśmie pracy, które z natury mają znacznie wyższy profil od wąskopasmowych, Umożliwiają
budowę anten o zwartej płaskiej lub konforemnej konstrukcji, małej wadze, a zarazem bardzo
wytrzymałych na narażenia klimatyczne i mechaniczne. Ponadto anteny wykonane w
technologii kompozytowej mogą mieć konstrukcję samonośną.

Wiodącym producentem pianek jest firma ROHM GMBH. Produkuje ona różnego

typu pianki pod nazwą ROHACELL, które spełniają wymagania stawiane materiałom
mikrofalowym. Charakteryzuje się niską przenikalnością elektryczną (ε

r

≈1.05) oraz niskim

współczynnikiem strat elektrycznych (tgδ=0.0008). Ze względu na swoje właściwości
mechaniczne może być stosowana w strukturach kompozytowych. Jej podstawową wadą jest
brak odporności na bezpośrednie działanie wody oraz wysoką temperaturę.

Rys. 3.1. Struktura kompozytowa

Innym materiałem wykorzystywanym w strukturach kompozytowych są wypełniacze

komórkowe typu plaster miodu. Materiał wykorzystywany do produkcji wypełniaczy

S

TRONA

18

Materiały wykorzystywane do budowy anten mikropaskowych

komórkowych może być różny: papier aramidowy, capton, aluminium. Najodpowiedniejszy z
punktu widzenia zastosowania na osłony oraz przekładki dystansujące jest papier aramidowy.
Wiodącymi producentami w tej dziedzinie jest firma HEXEL w Stanach Zjednoczonych oraz
EURO-COMPOSITE z siedzibą w Luksemburgu. Na rynku dostępne są wypełniacze o różnej
wysokości oraz wielkości oczek. Ze względu na znikomą ilość dielektryka w objętości
wypełniacza (większość stanowi powietrze), materiały te charakteryzują się niską
przenikalnością elektryczną oraz małymi stratami elektrycznymi.

Parametry elektryczne laminatów mikrofalowych są podawane przez producentów dla

wybranej częstotliwości i temperatury. Parametry elektryczne materiałów zastosowanych w
antenie wpływają bezpośrednio na parametry polowe i obwodowe anten mikropaskowych.
Ponieważ antena może pracować w różnych warunkach ( pasmo częstotliwości , maksymalny
zakres zmian temperatury), dlatego przed zastosowaniem należy precyzyjnie wyznaczyć
parametry elektryczne materiałów w sposób eksperymentalny.

Wyniki pomiarów własności elektrycznych laminatów są rzadko spotykane w literaturze.

Standardowo przy projektowaniu anten mikropaskowych stosuje się wartości parametrów
elektrycznych laminatu podanych przez producenta. Jednak znajomość rzeczywistych
wartości parametrów elektrycznych szczególnie w funkcji temperatury ma duże znaczenie
przy projektowaniu anten drukowanych oraz elementów mikrofalowych (sprzęgacze ,
dzielniki mocy) wchodzących w skład układu antenowego.

Na rys. 3.2-rys. 3.10 zamieszczone zostały wyniki pomiarów wybranych, których

pomiary były wykonane w Instytucie Chemii Uniwersytetu Wrocławskiego pod kierunkiem
prof. Huberta Kołodzieja.

Pomiary dotyczyły względnej przenikalności elektrycznej oraz współczynnika strat.

Wartości poszczególnych parametrów elektrycznych zostały wyliczone na podstawie
pomiarów zespolonej przenikalności elektrycznej, które zostały wykonane metodą skupionej
pojemności [12]. Dokładność pomiaru składowej rzeczywistej

ε

r

’ wynosi 2% natomiast

składowej urojonej

ε

r

’’ nie przekracza 5%.

Na przedstawionych wynikach stałej przenikalności dielektrycznej oraz strat

elektrycznych widać, że ich wartości zmieniają się w funkcji temperatury. Producenci podają
zazwyczaj wartości parametrów elektrycznych laminatów tylko dla temperatury 25°C.
Przyjmując więc dane producenta, może okazać się że zaprojektowana antena będzie
pracować niepoprawnie w niskich temperaturach lub w miejscu mocno nasłonecznionym.
Znając rzeczywiste parametry laminatu można zaprojektować antenę pewnym zapasem (np.
szersze pasmo) tak, aby przy zmianie temperatury antena nie utraciła wymaganego
dopasowania w paśmie.

Jako przykład konieczności weryfikacji parametrów elektrycznych podano laminat

epoksydowo-szklany krajowej produkcji. Badaniu poddano trzy partie laminatu. Widać, że
przenikalność elektryczna partii 3 gwałtownie zmienia się w temperaturze 45 °C.
Według danych producenta laminat spełnia parametry Normy IEC249-1,która określa że
pomiar przenikalności dokonuje w temperaturze 18-28 °C, jednak nie nadaje się on do
zastosowań antenowych.