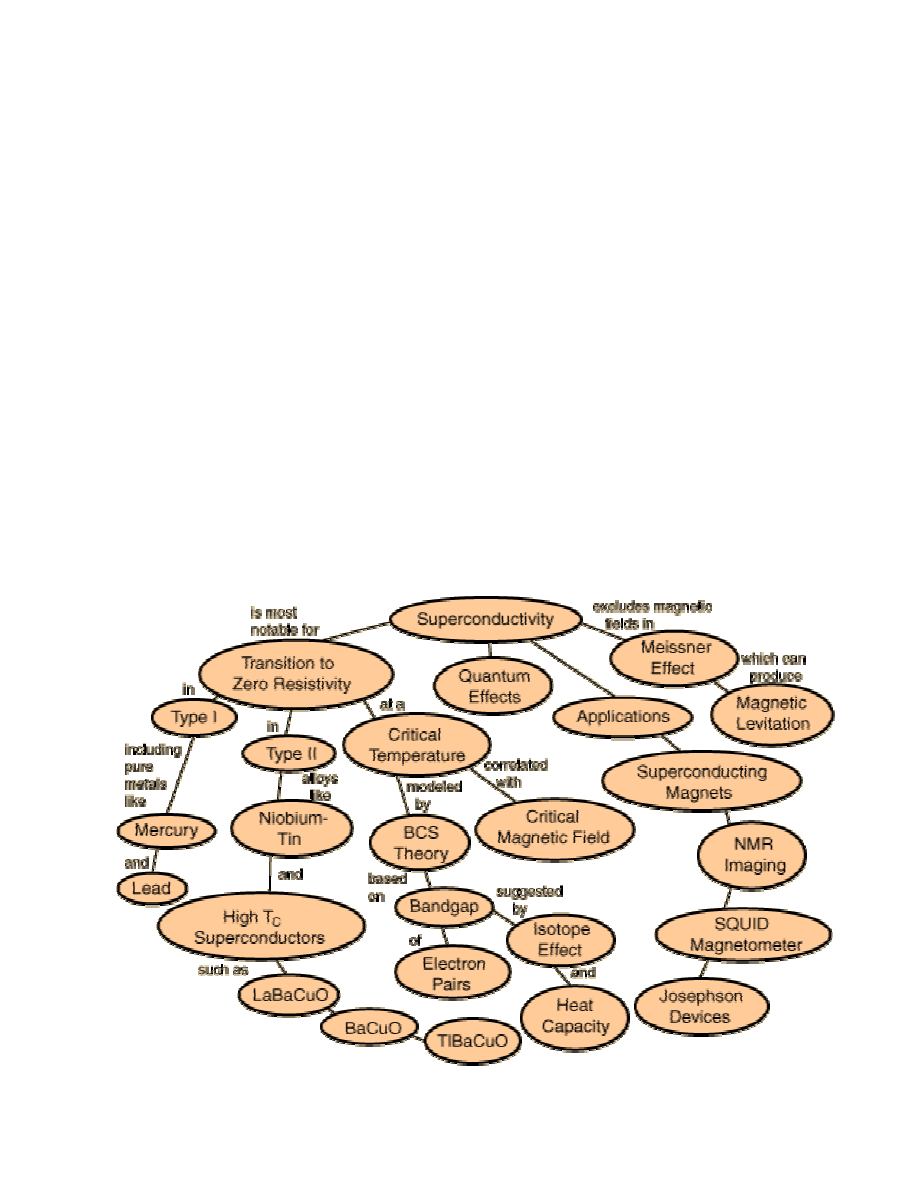
Nadprzewodnictwo

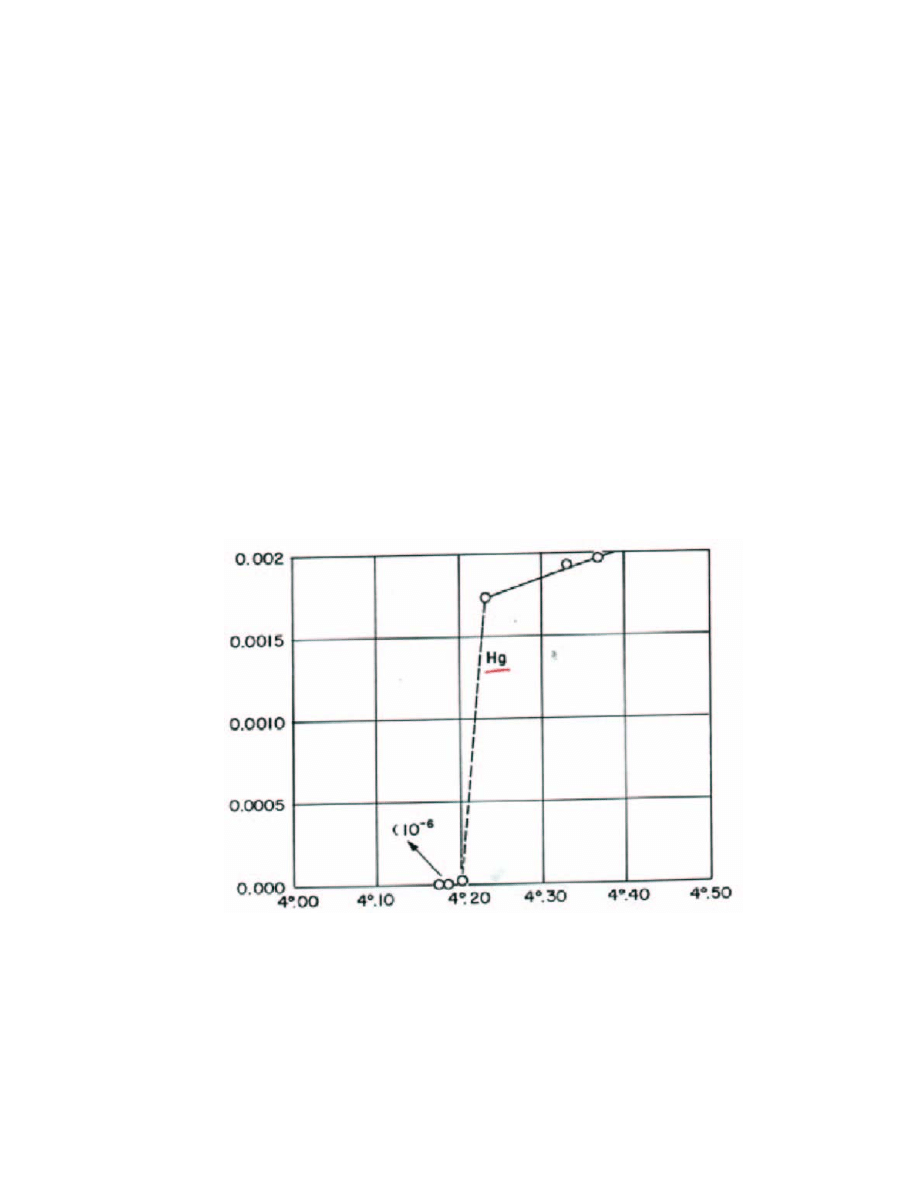
W 1911 roku Kammerlingh Onnes odkrył, że rtęć poniżej
pewnej temperatury zaczyna nadprzewodzić,co oznacza, że jej
opór elektryczny wynosi 0.

Nagroda Nobla 1913

Pierwiastki nadprzewodzące

Materiały nadprzewodzące

Rodzaj

Materiał

T

c

(K) Uwagi

Związki
międzymetaliczne i
stopy

Związki zawierające
tzw. ciężkie fermiony

Nb

1-x

Ti

x

Nb

3

Sn

ErRh

4

B

4

HoMo

6

S

8

RNi

2

B

2

C

CeCu

2

Si

2

UPt

3

CeCoIn

5

UGe

2

10
18.0

< 23

0.65
0.54
2.3
0.8

elektromagnesy do 11 T
A-15, elektromagnesy do 22 T

fazy Chevrela
borki, węgliki

symetria d
symetria p lub f

współistnienie ferromagnetyzmu i
nadprzewodnictwa

Rodzaj

Materiał

T

c

(K)

Uwagi

Tlenki

Nadprzewodniki
wysokotemperatu
rowe

SrTiO

3-

δ

Ba(Pb, Bi)O

3

LiTi

2

O

4

Sr

2

RuO

4

(La,Ba)

2

CuO

4

YBa

2

Cu

3

O

7

HgBaCuO

0.3
13
13
1.5

30
92
135

perowskit
perowskit
spinel
warstwowy perowskit, symetria-p

symetria d

Właściwości w stanie nadprzewodzącym

• Opór elektryczny (dla prądu stałego i o małej

częstotliwości) = 0;

• Opór elektryczny dla prądu o dużej częstotliwości maleje;
• Właściwości magnetyczne: nadprzewodnik jest idealnym

diamagnetykiem;

• Właściwości termiczne (obserwuje się skok ciepła

właściwego, zmniejszenie przewodności cieplnej);

• Istnieją krytyczne wartości pola magnetycznego i

gęstości prądu, powyżej których stan nadprzewodzący
jest niszczony;

Szczegó

ły dalej

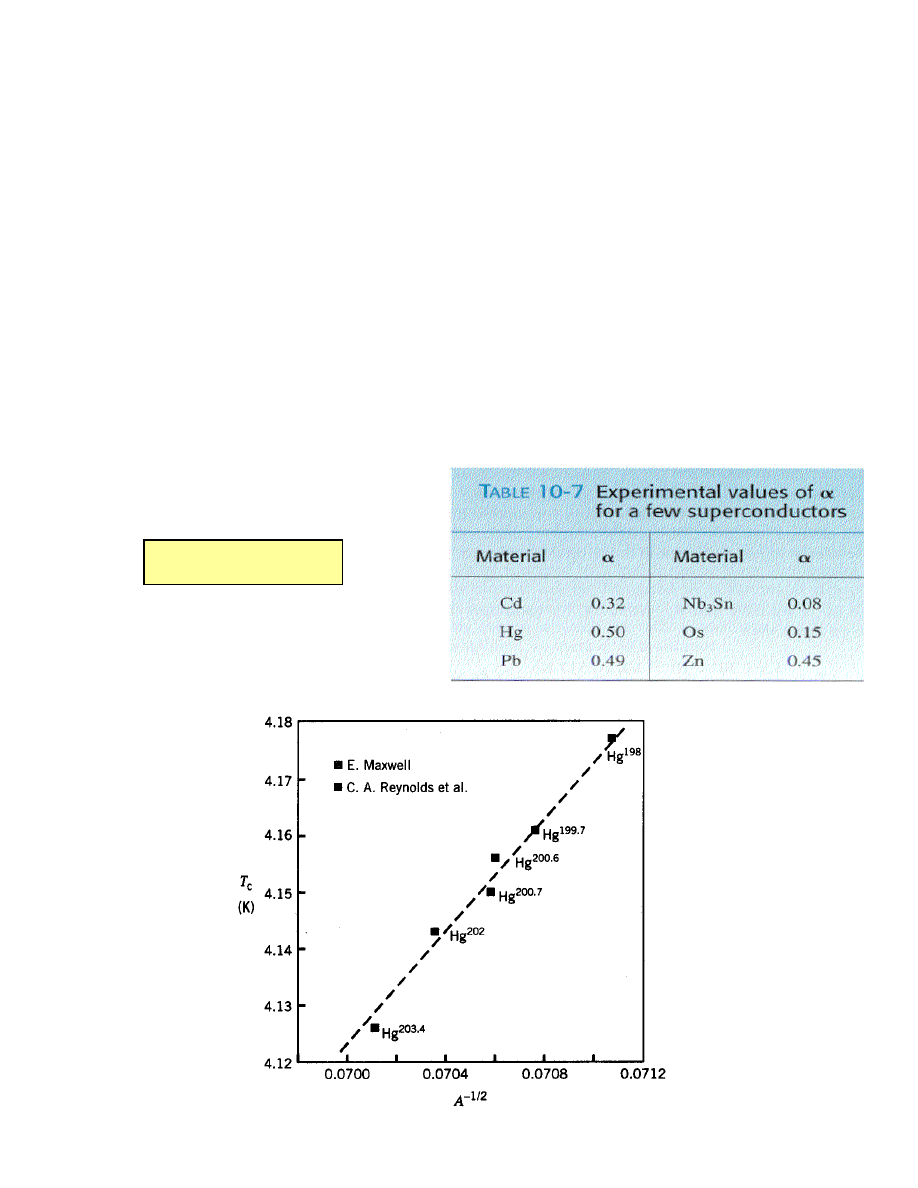
Właściwości w stanie nadprzewodzącym

• Temperatura krytyczna zależy od masy izotopu (efekt

izotopowy)

M

α

T

c

= constant

Właściwości w stanie nadprzewodzącym

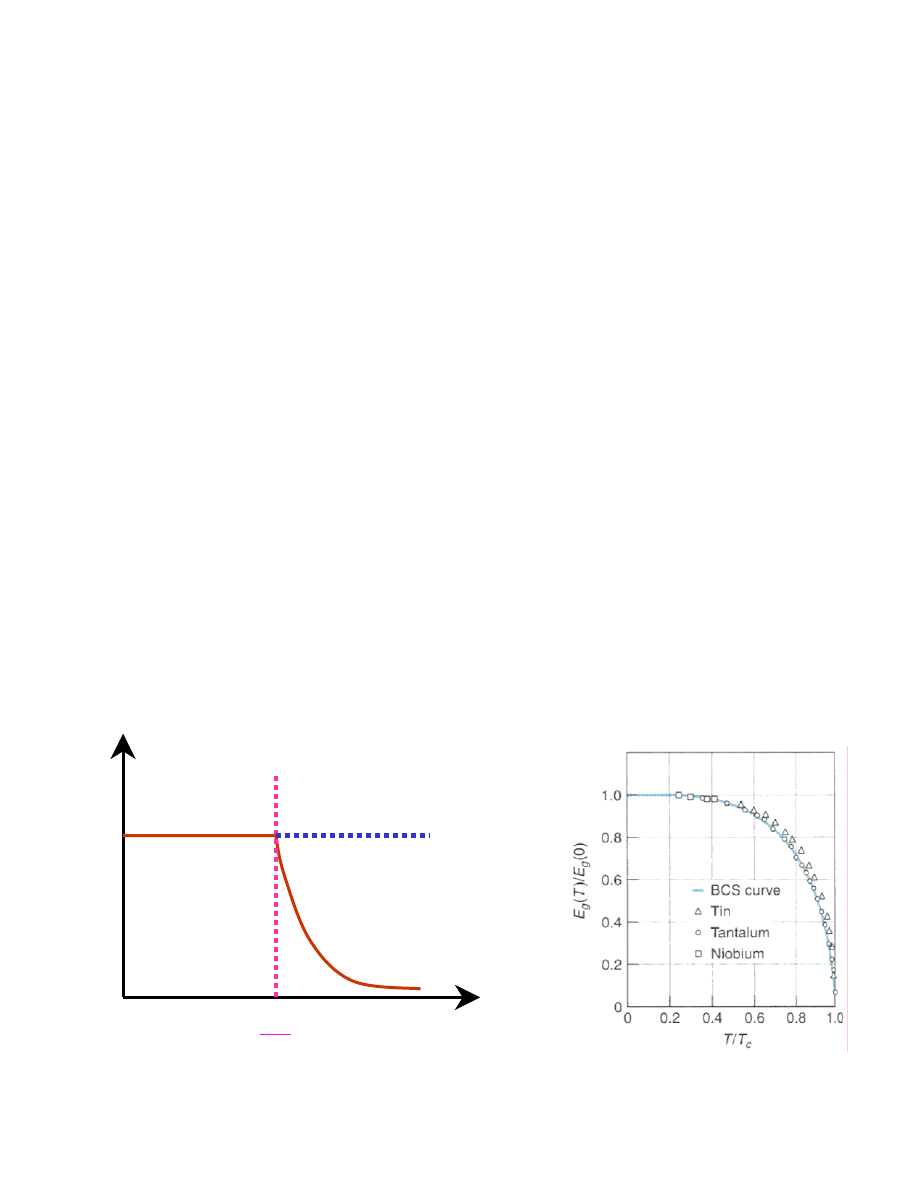
• Zmieniają się rozmaite właściwości związane z absorpcją

energii (np. absorpcja promieniowania
elektromagnetycznego i ultradźwięków). Zjawiska te
wskazują na istnienie przerwy energetycznej. W
temperaturze krytycznej przerwa energetyczna zanika.

Reflec

tion coefficient

h

2

∆

normal

superconducting

ν

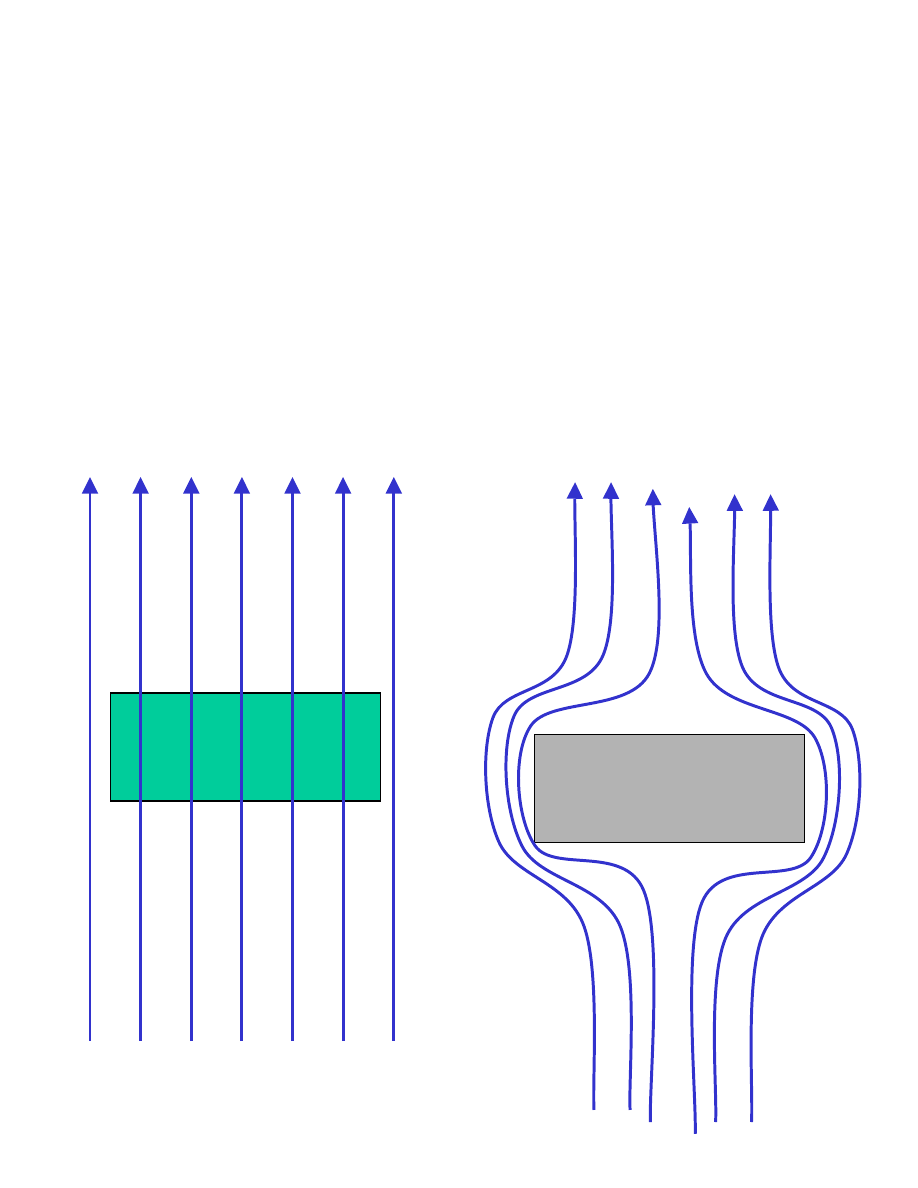
Właściwości w stanie nadprzewodzącym:

diamagnetyzm

Nadprzewodnik jest

idealnym diamagnetykiem

: wypycha

pole magnetyczne ze swojego wnętrza. Fenomenologiczny
opis własności magnetycznych:

RÓWNANIA LONDONÓW

.

Zwykły metal

Nadprzewodnik

Z rozwiązania równań Maxwella w przypadku materiału o zerowym oporze
wynika, że w takim materiale zmiany pola magnetycznego nie przenikają do
wnętrza materiału, tylko zanikają eksponencjalnie:

0

2

1

,

)

0

(

)

(

µ

α

α

n

e

m

gdzie

e

dt

dB

x

dt

dB

x

=

=

−

Z doświadczenia wiadomo, że w nadprzewodnikach nie tylko zmiany pola
magnetycznego ale również pole magnetyczne nie wnika do wnętrza
nadprzewodnika.

F. i H. Londonowie zaproponowali fenomenologiczny opis tego zjawiska w taki
sposób, że

wnikania

a

glebokosci

ą

londonowsk

tzw

jest

n

e

m

gdzie

e

B

x

B

L

x

.

1

,

)

0

(

)

(

0

2

λ

µ

α

α

≡

=

=

−

W rezultacie, powyższy, fenomenologiczny opis zachowania nadprzewodnika w
polu magnetycznym nosi nazwę teorii Londonów, natomiast równania:

s

rotj

ne

m

B

E

m

ne

dt

dj

2

2

;

−

=

=

są to tzw. równania Londonów

x

(

)

λ

− x

exp

B

A

(

)

λ

− x

exp

B

A

A

B

A

B

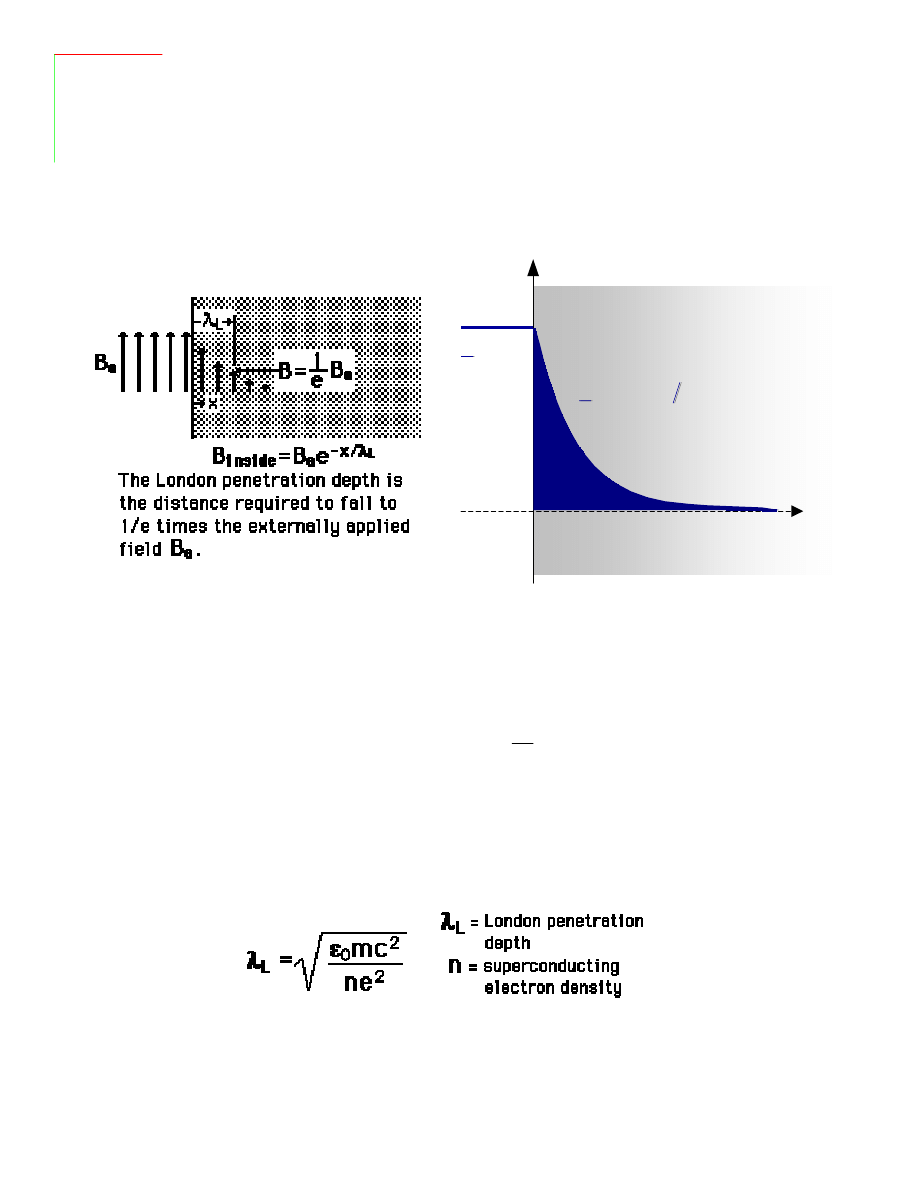
Na granicy między nadprzewodnikiem a otoczeniem, w którym
B

≠0:

λ – głębokość wnikania pola
magnetycznego

λ

x

e

B

x

B

−

=

)

0

(

)

(

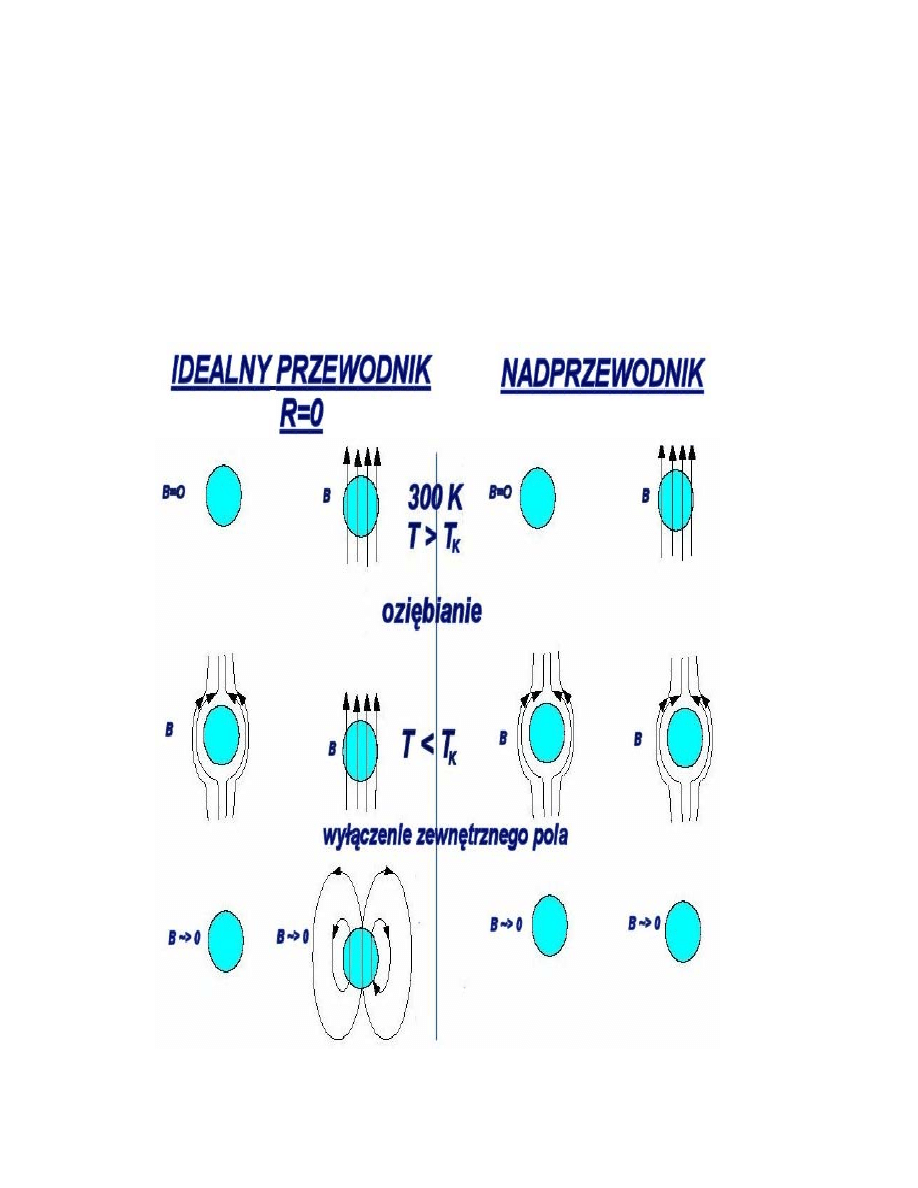
Nadprzewodnik to nie jest tylko idealny przewodnik !

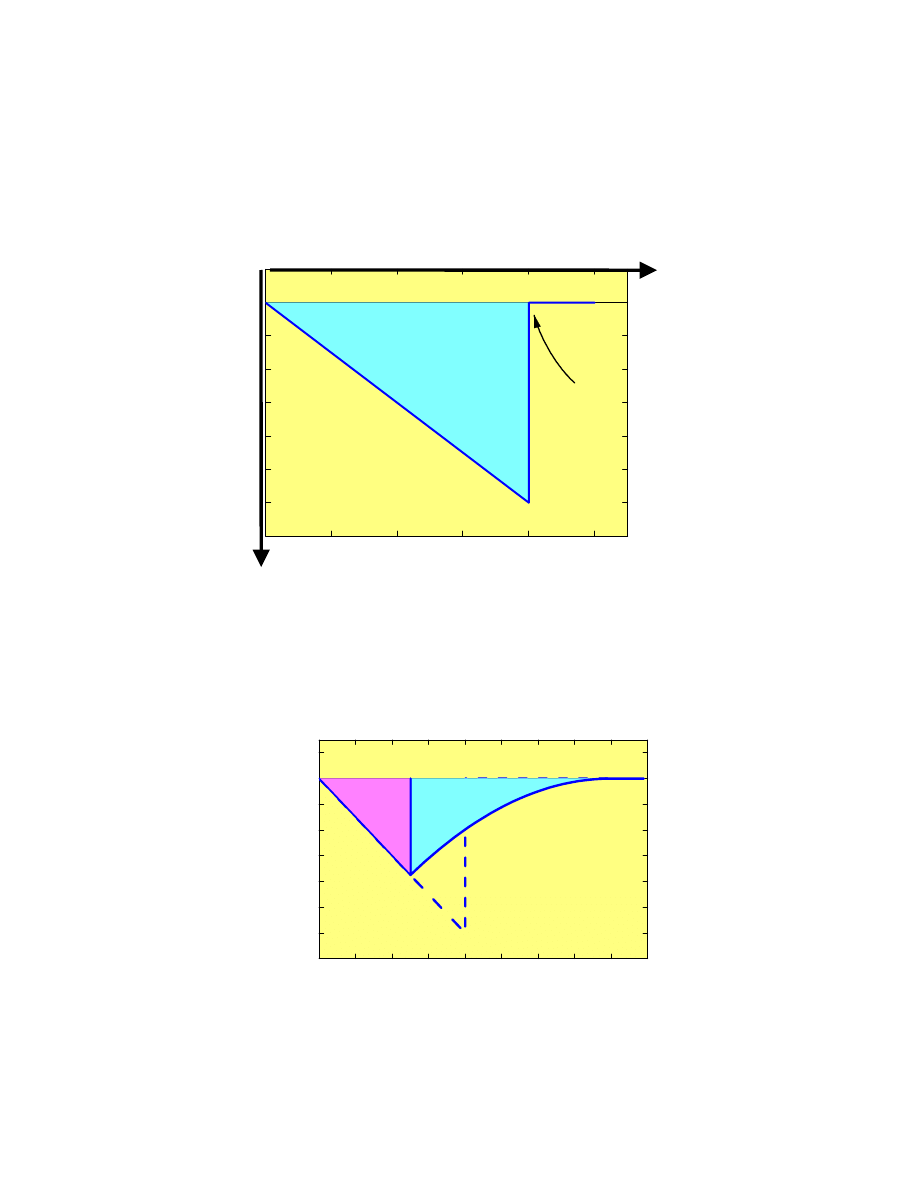
Właściwości w stanie nadprzewodzącym:
pole krytyczne

Nadprzewodniki I rodzaju: zachowują się w polu magnetycznym
tak, jak to zostało opisane: poniżej pola krytycznego całkowicie
wypychają pole z wnętrza materiału, powyżej Hc – pole wnika, jak
do normalnego metalu.

0

1

2

3

4

5

6

7

8

9

-0.7

-0.6

-0.5

-0.4

-0.3

-0.2

-0.1

0.0

0.1

stan
normalny

idealny
diamag
netyk

stan
mieszany

H

c2

H

c1

H

c

magnetisation [emu]

field [tesla]

0

1

2

3

4

5

-0.7

-0.6

-0.5

-0.4

-0.3

-0.2

-0.1

0.0

0.1

nadprzewodnik

H

c

magnetisation [emu]

field [tesla]

namagnesowanie

Pole magnetyczne

Nadprzewodniki II rodzaju: W odróżnieniu od nadprzewodników
pierwszego rodzaju, zachowują się one tak, że w pewnym zakresie
pola magnetycznego, pole częściowo wnika do wnętrza
nadprzewodnika.

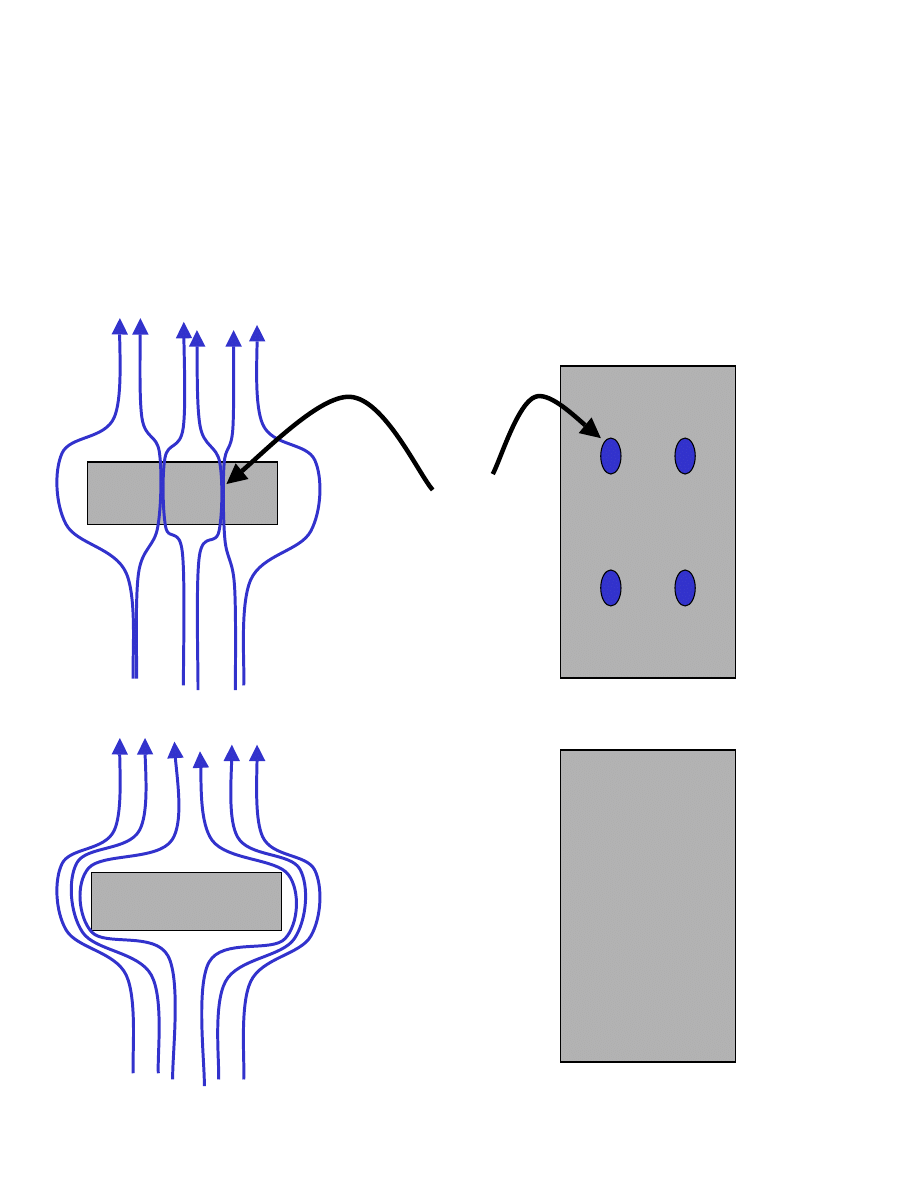
Na czym polega częściowe wnikanie pola magnetycznego:

„

Widok z góry”

Superconductor

Kwant strumienia

pola

magnetycznego

(wir, worteks)

Superconductor

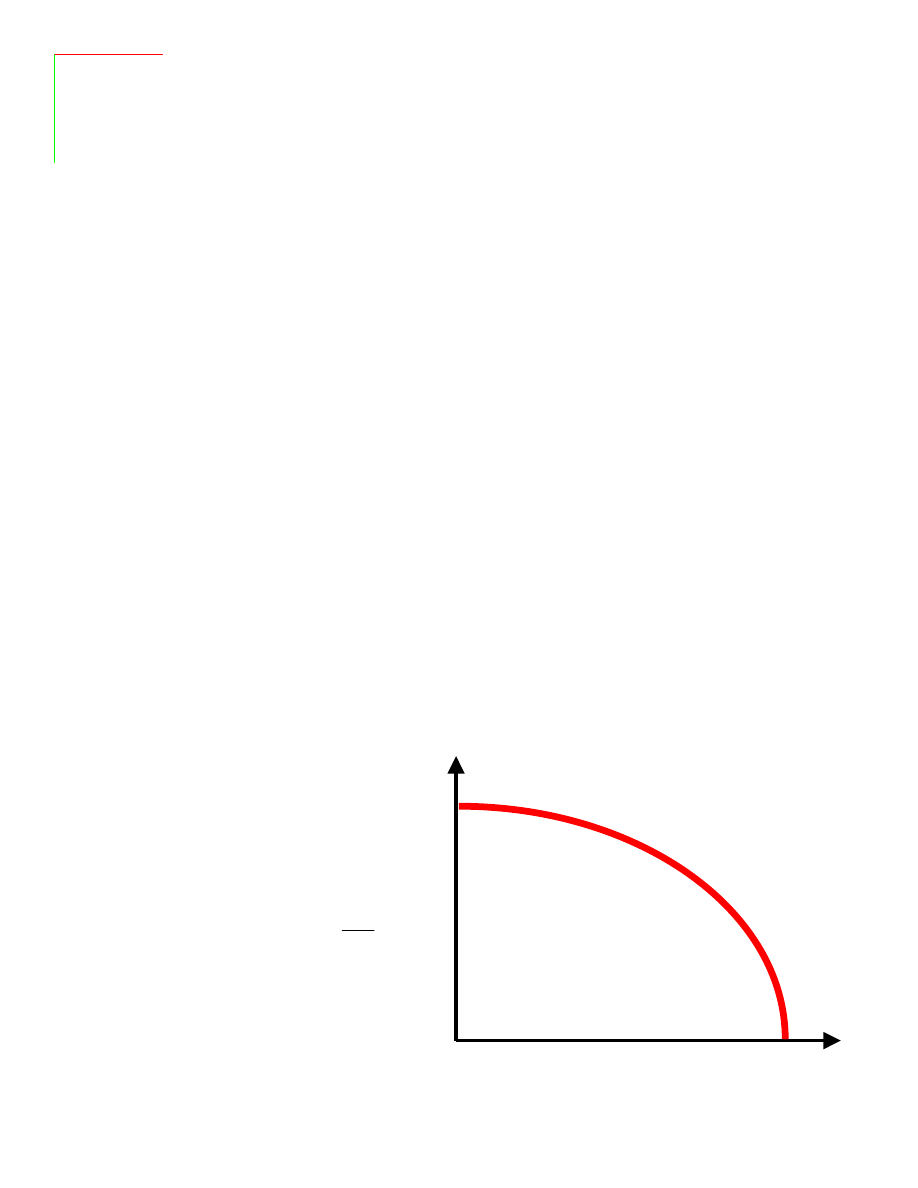
Właściwości w stanie nadprzewodzącym:

prąd krytyczny, pole krytyczne, głębokość

wnikania pola magnetycznego, temperatura

krytyczna

•Stan nadprzewodzący można zniszczyć:

—ogrzewając materiał powyżej temperatury krytycznej;

—umieszczając go w polu magnetycznym większym od
pola krytycznego;

—gdy płynie prąd większy niż prąd krytyczny.

•Pole i prąd krytyczny zależą od temperatury w podobny
sposób:

T

j

c

, H

c

,

T

c

Nadprzewodnik

Normalny

metal

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

2

1

)

0

(

)

(

c

c

c

T

T

H

T

H

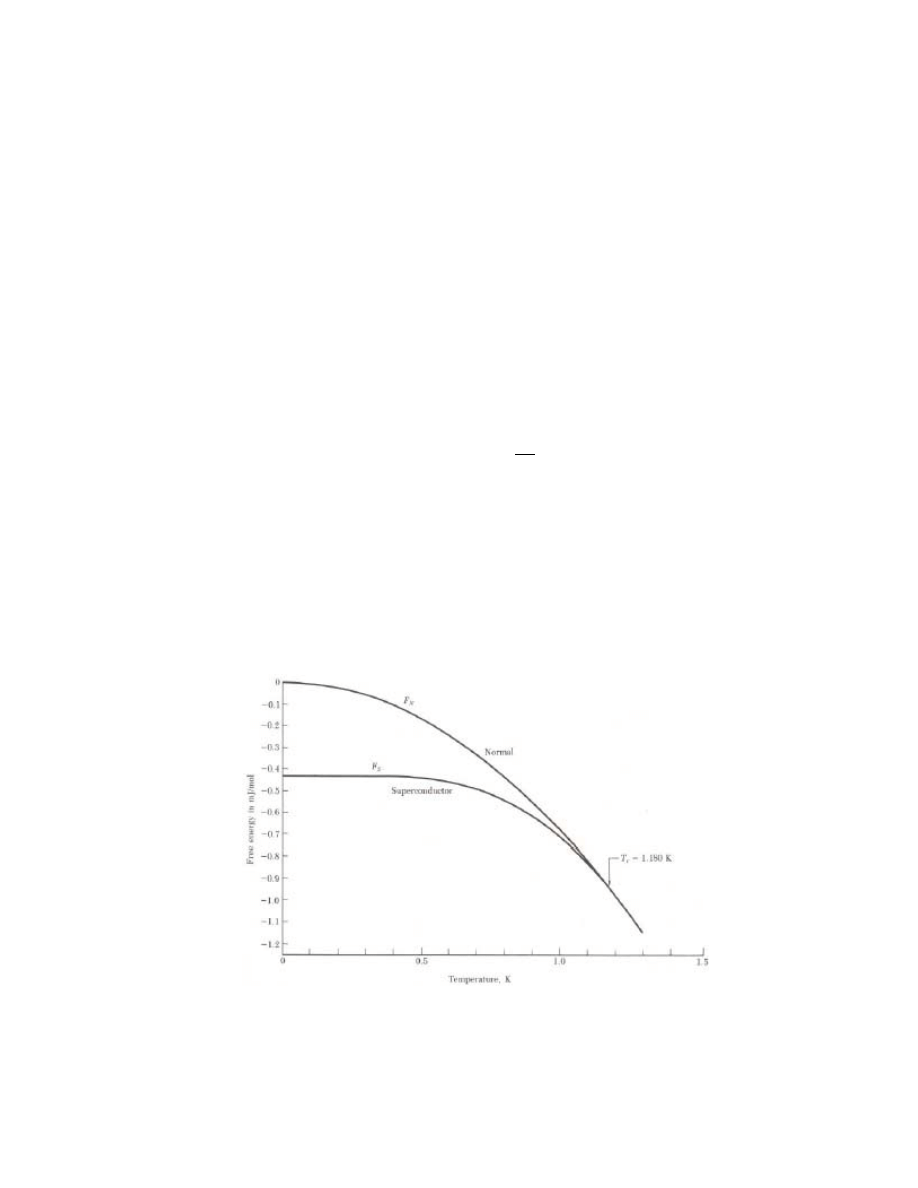
Właściwości w stanie nadprzewodzącym:

termodynamika przejścia do stanu

nadprzewodzącego (energia swobodna)

(

)

(

)

(

)

2

2

0

2

1

,

,

H

H

H

T

G

H

T

G

C

n

S

−

−

=

µ

G

n

G

s

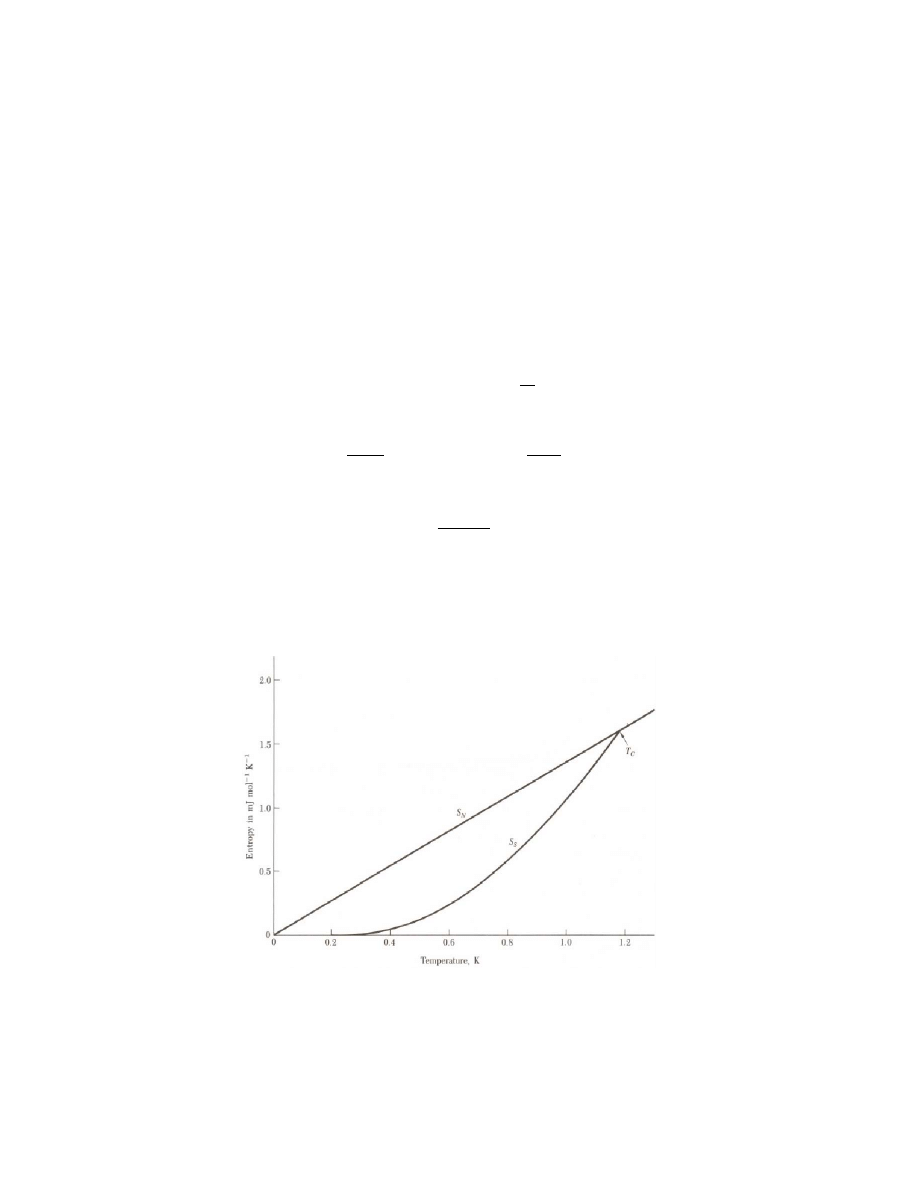
Właściwości w stanie nadprzewodzącym:

termodynamika przejścia do stanu

nadprzewodzącego (entropia)

(

)

(

)

(

)

T

H

H

S

S

T

S

T

C

T

G

S

H

H

H

T

G

H

T

G

C

C

n

S

C

n

S

∂

∂

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

−

=

−

−

=

0

2

2

0

,

2

1

,

,

µ

µ

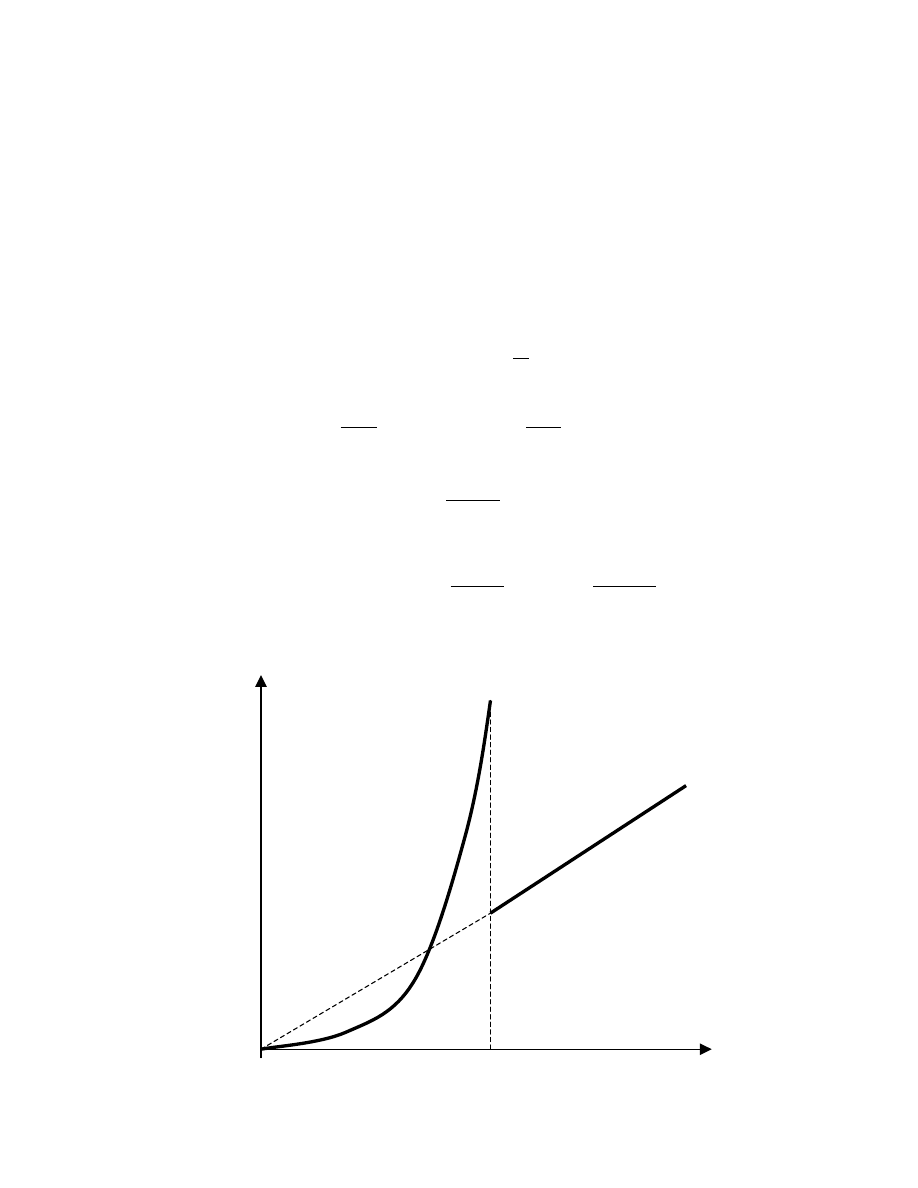
Właściwości w stanie nadprzewodzącym:

termodynamika przejścia do stanu

nadprzewodzącego (ciepło właściwe)

(

)

(

)

(

)

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

∂

∂

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

=

−

∂

∂

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

−

=

−

−

=

2

2

2

0

0

2

2

0

,

2

1

,

,

T

H

H

T

H

T

C

C

T

H

H

S

S

T

S

T

C

T

G

S

H

H

H

T

G

H

T

G

C

C

C

n

S

C

C

n

S

C

n

S

µ

µ

µ

Tc

T

γT

C

V

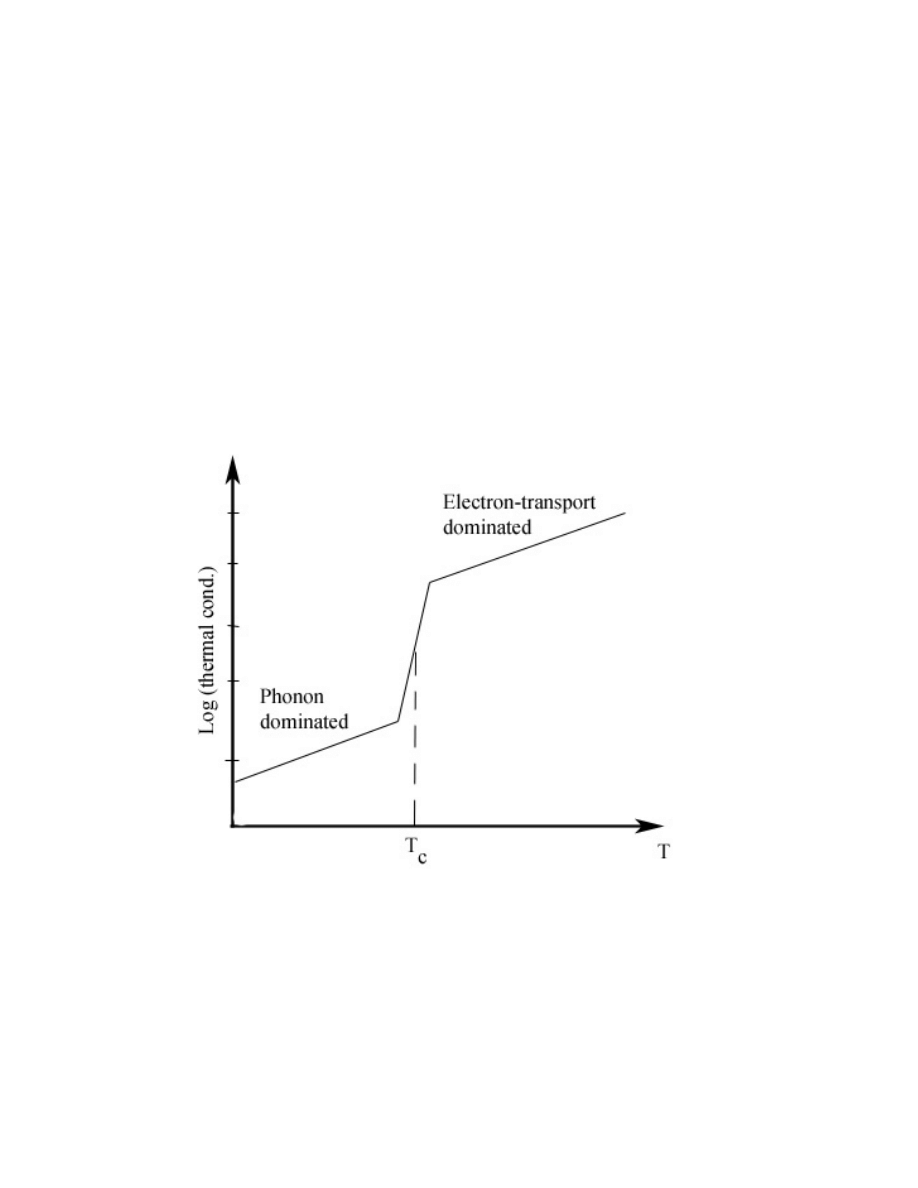
Właściwości w stanie nadprzewodzącym:

termodynamika przejścia do stanu

nadprzewodzącego (przewodność

cieplna)

Mikroskopowa teoria

nadprzewodnictwa: teoria Bardeena,

Coopera, Schrieffera (BCS)

Niezwykłe właściwości stanu

nadprzewodzącego

•

Nadprzewodnictwo związane jest ze zmianą zachowania

elektronów:

– Zerowy opór, brak tłumienia;
– Istnieje jakieś uporządkowanie: entropia maleje;
– Diamagnetyzm;
– Istnieje przerwa energetyczna: absorpcja promieniowania

elektromagnetycznego;

•

Właściwości sieci krystalicznej nie ulegają zmianie przy

przejściu do stanu nadprzewodzącego, ale sieć odgrywa jakąś

rolę:

– Efekt izotopowy;

•

Zbyt dobre przewodniki nie przechodzą do stanu

nadprzewodzącego (miedź, srebro).

•

Ferromagnetyki nie przechodzą do stanu nadprzewodzącego.

•

Przejście do stanu nadprzewodzącego bez pola

magnetycznego jest przemianą fazową drugiego rodzaju (bez

ciepła utajonego, ale z nieciągłą zmianą ciepła właściwego).

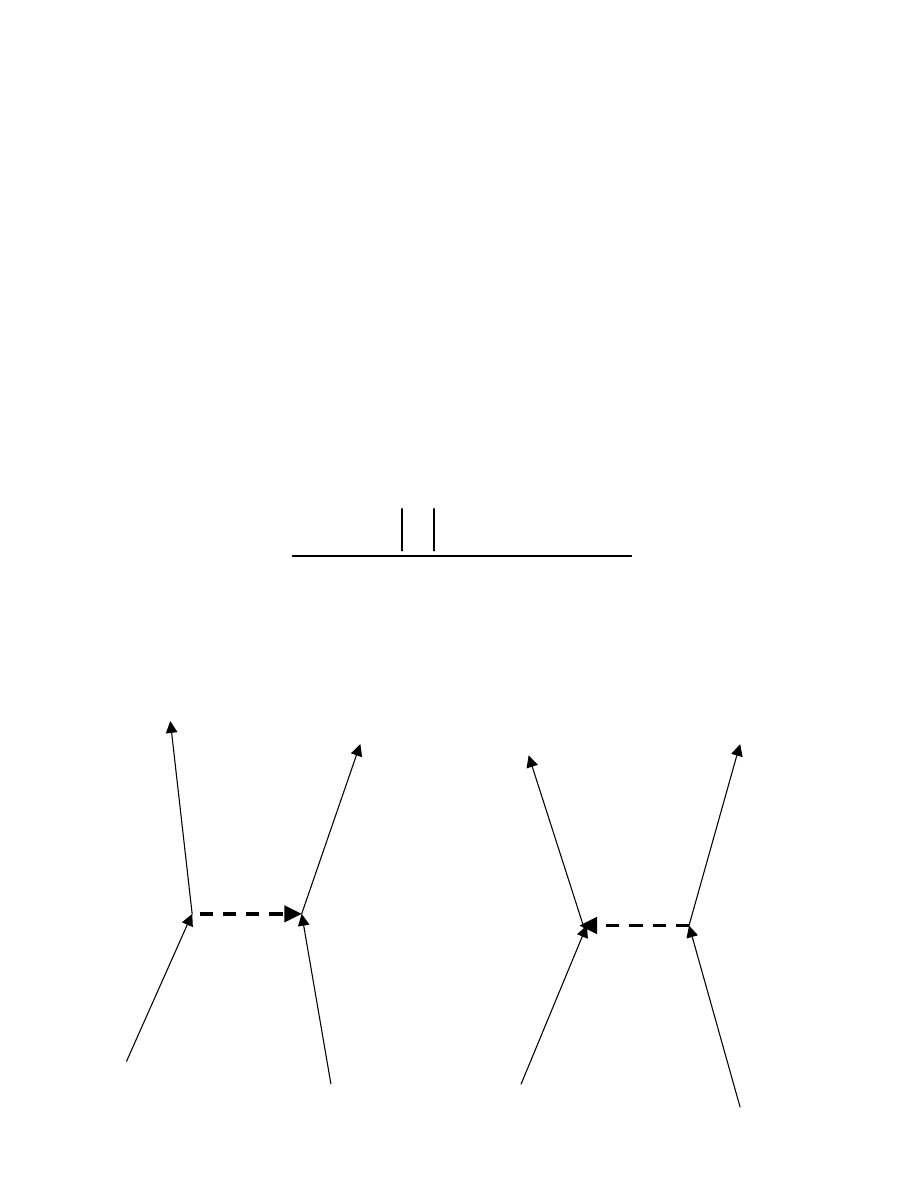
Przesłanki:

1.

Pierwszy krok (Frohlich, 1950): oddziaływanie elektron-

fonon może doprowadzić

do przyciągania pomiędzy

elektronami (gdy E

i

- E

i

jest mniej więcej

ω

q

)

2.

Jeżeli istnieje takie właśnie przyciąganie między

elektronami, to tworzą się pary elektronowe (pary Coopera)

(

) (

)

2

2

2

q

q

k

k

q

V

ω

ε

ε

ω

ε

δ

h

h

−

−

=

+

q

q

k

k

k’

k’

k - q

k’+ q

k +
q

k’-
q

fonon

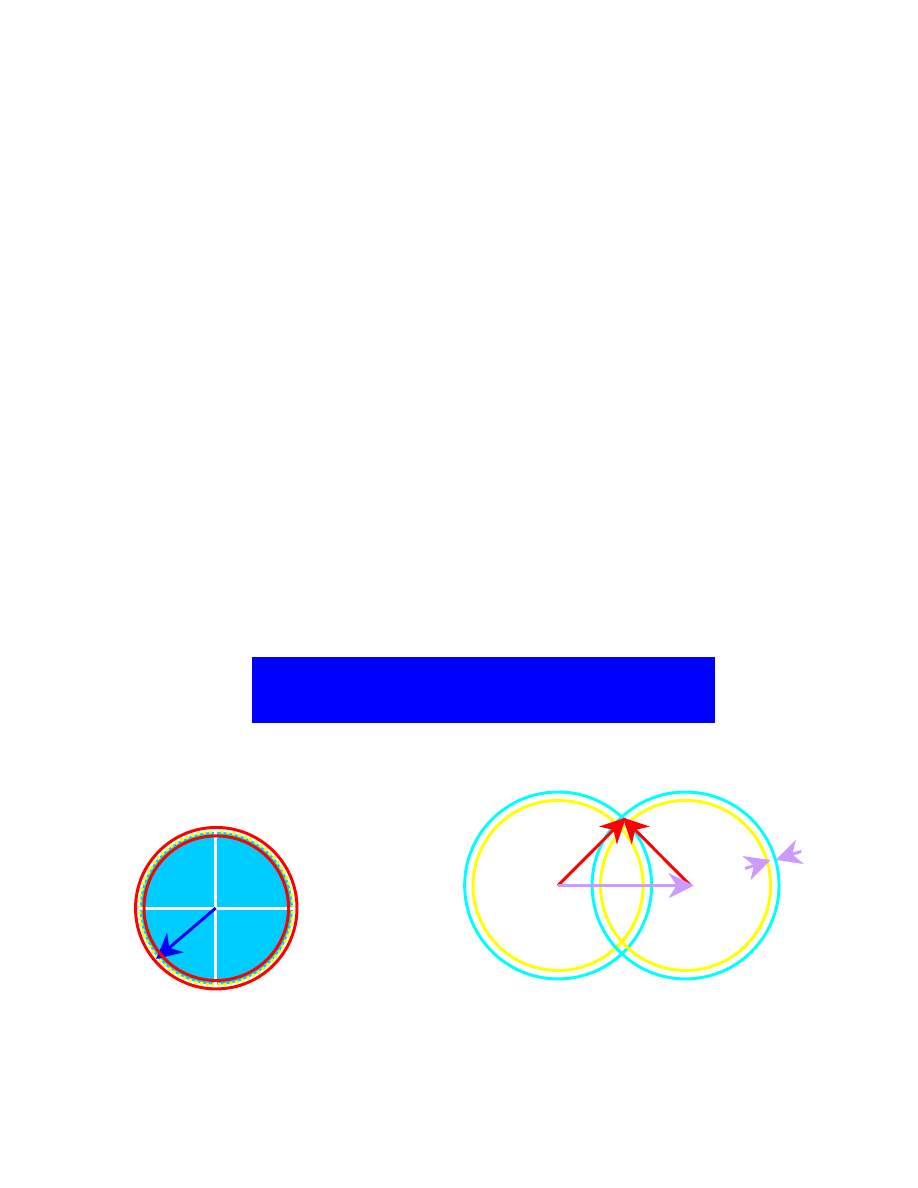
Para Coopera

• Dwa elektrony [k1, E(K1)] i [k2,E(K2)] są w stanach

powyżej E

F

.

• Poniżej Tc pojawia się słabe przyciągające

oddziaływanie pomiędzy nimi.

• Pozostałe elektrony w morzu Fermiego nie oddziałują ze

sobą.

constant

k

k

k

k

'

2

'

1

2

1

=

+

=

+

r

r

r

r

k

F

(outer)
E

F

+

hω

D

E

F

-

hω

D

(inner)

E

F

k

x

k

y

1

k

r

2

k

r

−

k

r

∆

Liczba par k

1

, k

2,

które mogą oddziaływać jest największa gdy k

1

=-k

2

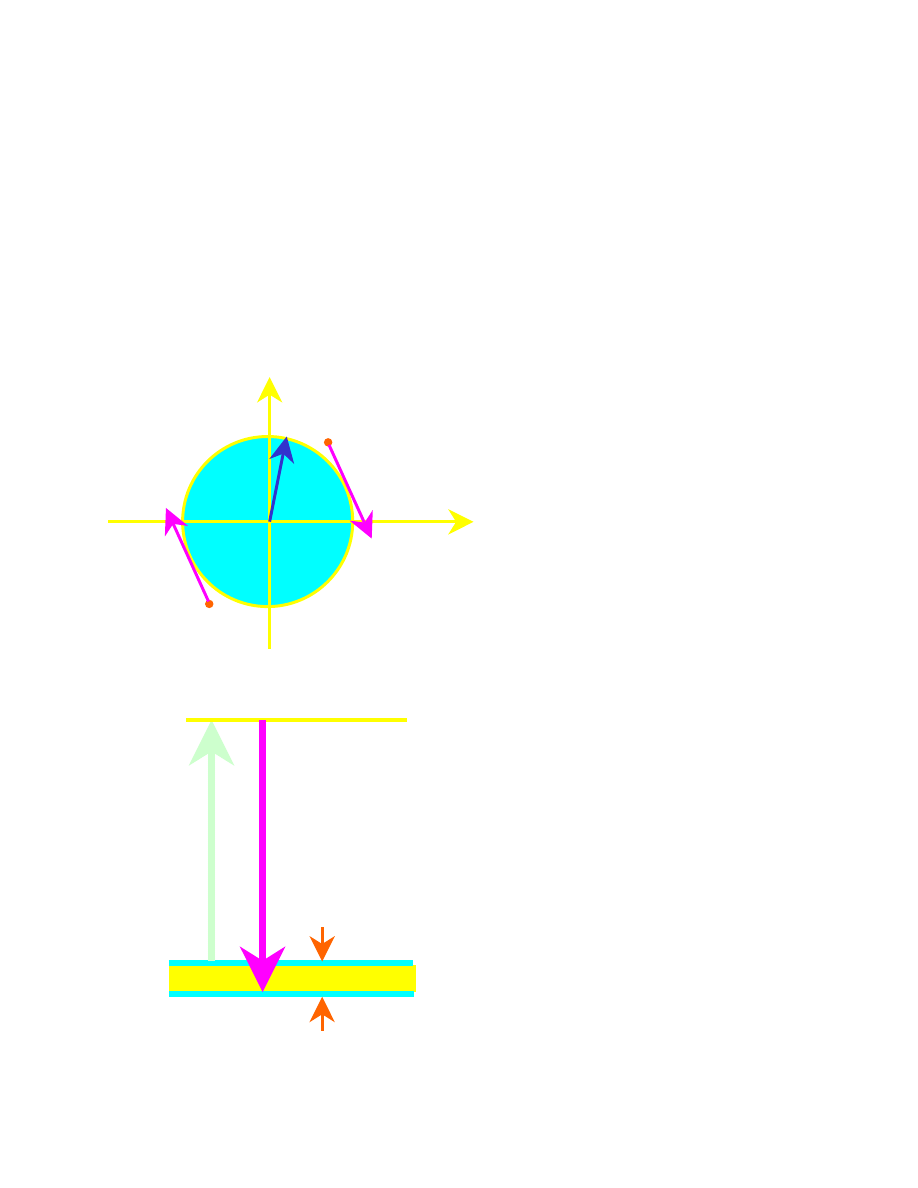
Para Coopera

• Elektrony pary są

wzbudzone
powyżej energii
Fermiego (większa
energia kinetyczna
o KE)

• Elektrony

przyciągają się,
zatem obniża się
ich energia o
energię wiązania
PE.

• Razem: zysk

energetyczny.

k

-k

k’

-k’

k

x

k

y

k

F

E

N

E

s

KE

PE

E

c

Para Coopera bez wzorów:

• Przyczyną powstania nadprzewodnictwa jest

jakieś

oddziaływanie pomiędzy elektronami, które prowadzi do tego,

że

ELEKTRONY SIĘ PRZYCIĄGAJĄ

.

W konwencjonalnych nadprzewodnikach jest to oddziaływanie z
siecią krystaliczną (oddziaływanie elektron-fonon).

Główne tezy teorii BCS:

1

W temperaturze, w której wypadkowe oddziaływanie między

elektronami staje się przyciągające, wówczas stan nieskorelowanych
elektronów w morzu Fermiego staje się niestabilny. Zaczynają tworzyć
się pary Coopera. Proces ten trwa tak długo aż energia swobodna
układu osiągnie minimum.

2.

Pary Coopera tworzą te elektrony, które mają takie wektory

falowe k

i

, że ich energia liczona względem energii Fermiego :

4.

Dwa elektrony tworząc parę Coopera (w przypadku

najkorzystniejszym, czyli k i -k ) mają całkowitą energię: E = 2E

F

-

∆

< 2E

F

, gdzie:

5.

każda para Coopera ma taką samą energię.

q

F

2

2

i

k

E

m

2

k

ω

≤

−

=

ε

h

h

5

,

0

V

)

E

(

N

1

,

0

,

fonon

elektron

nia

oddzialywa

macierzowy

element

V

);

V

)

E

(

N

1

exp(

F

F

D

≤

≤

−

−

−

ω

=

∆ h

3.

Przyciąganie między elektronami odbywa się

za

pośrednictwem fononów.

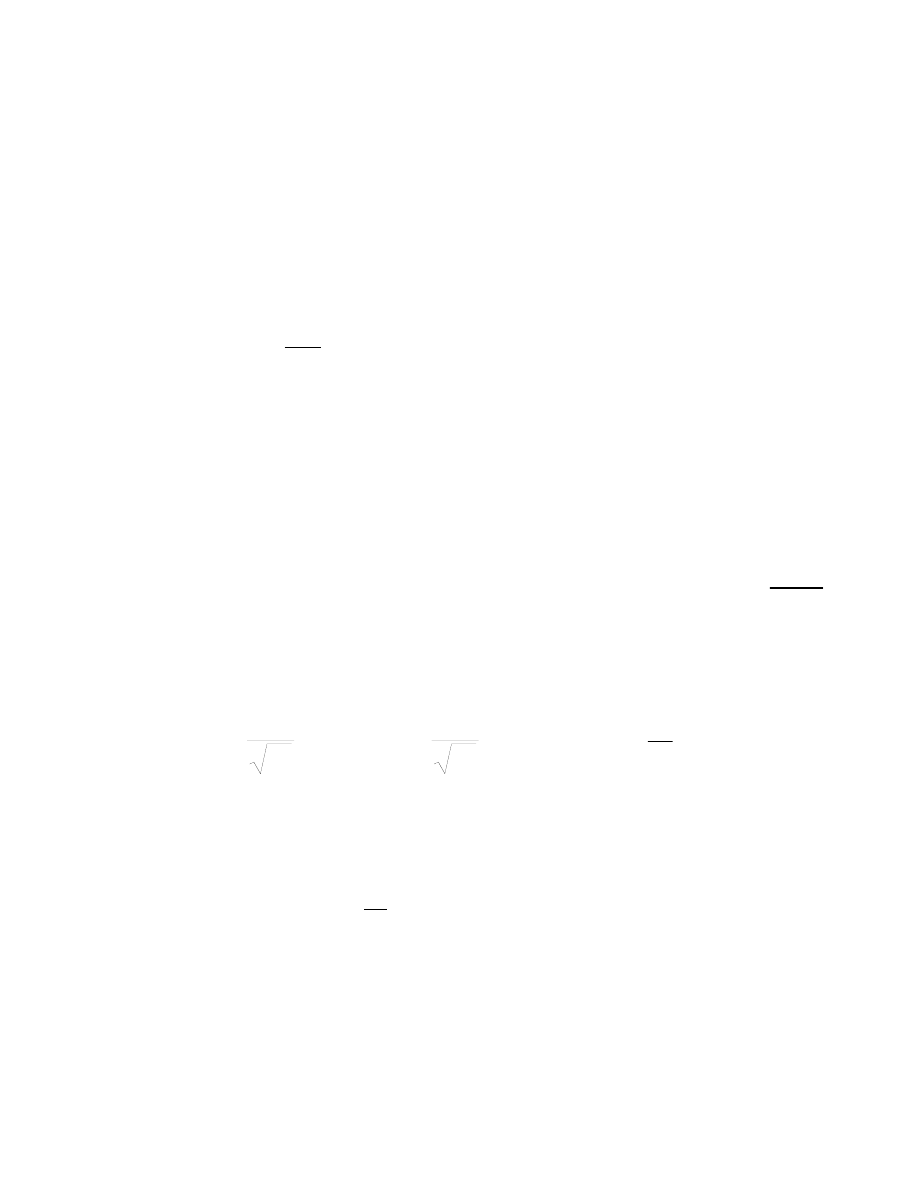
Funkcja falowa pary Coopera

R-nie Schr.
jednej pary

(

)

(

)

)

r

,

r

(

2E

)

r

,

r

(

E

)

r

,

r

(

)

r

,

r

(

V

)

r

,

r

(

m

2

2

1

F

2

1

2

1

2

1

2

1

2
2

2

1

2

r

r

r

r

r

r

r

r

r

r

h

Ψ

+

=

Ψ

=

Ψ

+

Ψ

∇

+

∇

−

ε

gdzie

ε jest energia pary liczoną względem stanu bez oddziaływania

(V=0), kiedy każdy elektron na poziomie Fermiego maję energię E

F

,

m

2

k

E

2
F

2

F

h

=

Funkcja falowa nieoddziałujących dwóch elektronów, V=0

(

)

(

)

(

)

(

)

2

1

2

2

1

1

2

1

r

r

k

exp

V

1

r

k

exp

V

1

r

k

exp

V

1

)

(

r

r

r

r

r

r

r

−

•

=

•

•

=

−

Ψ

i

i

i

r

r

Funkcja falowa oddziałujących dwóch elektronów, V

≠0

(

)

(

)

(

)

∑

−

•

=

−

k

2

1

2

1

r

r

k

i

)exp

k

g(

V

1

r

r

r

r

r

r

r

r

k

ϕ

g(k) jest amplitudą prawdopodobieństwa znalezienia pary k

Przyjmując oznaczenia jak w BCS:

⎟

⎠

⎞

⎜

⎝

⎛

−

⇒

⎟

⎠

⎞

⎜

⎝

⎛

−

↓

↑

↓

↑

'

'

,

,

k

k

k

k

Amplituda prawdopodobieństwa , że stan k, k’ jest:

Zajęty

v

k

v

k’

Pusty

u

k

u

k’

v

k

2

+ u

k

2

= 1 v

k’

2

+ u

k’

2

= 1

c

+

k↑

-

operator kreacji elektronu k↑

c

k↑

-

operator anihilacji elektronu k↑

WYNIKI TEORII BCS

Stan podstawowy BCS (T=0K, j = 0, B = 0) jest to stan utworzony
przez pary Coopera o k↑,-k↓.

Wieloelektronowy stan podstawowy BCS można zapisać jako:

1

v

u

gdzie

,

0

)

c

c

v

u

(

2

k

2

k

k

k

k

k

k

S

=

+

+

=

Ψ

+

↓

−

+

↑

∏

−

↓

−

−

↑

+

↓

−

+

↑

+

↓

−

+

↑

∑

∑

+

ε

=

k

k

k

k

k

,

k

kk

k

k

k

k

c

c

c

c

V

c

c

H

'

Uwaga: podstawowy stan normalny

∏

≤

+

↓

−

+

↑

=

Ψ

F

k

k

k

k

N

c

c

0

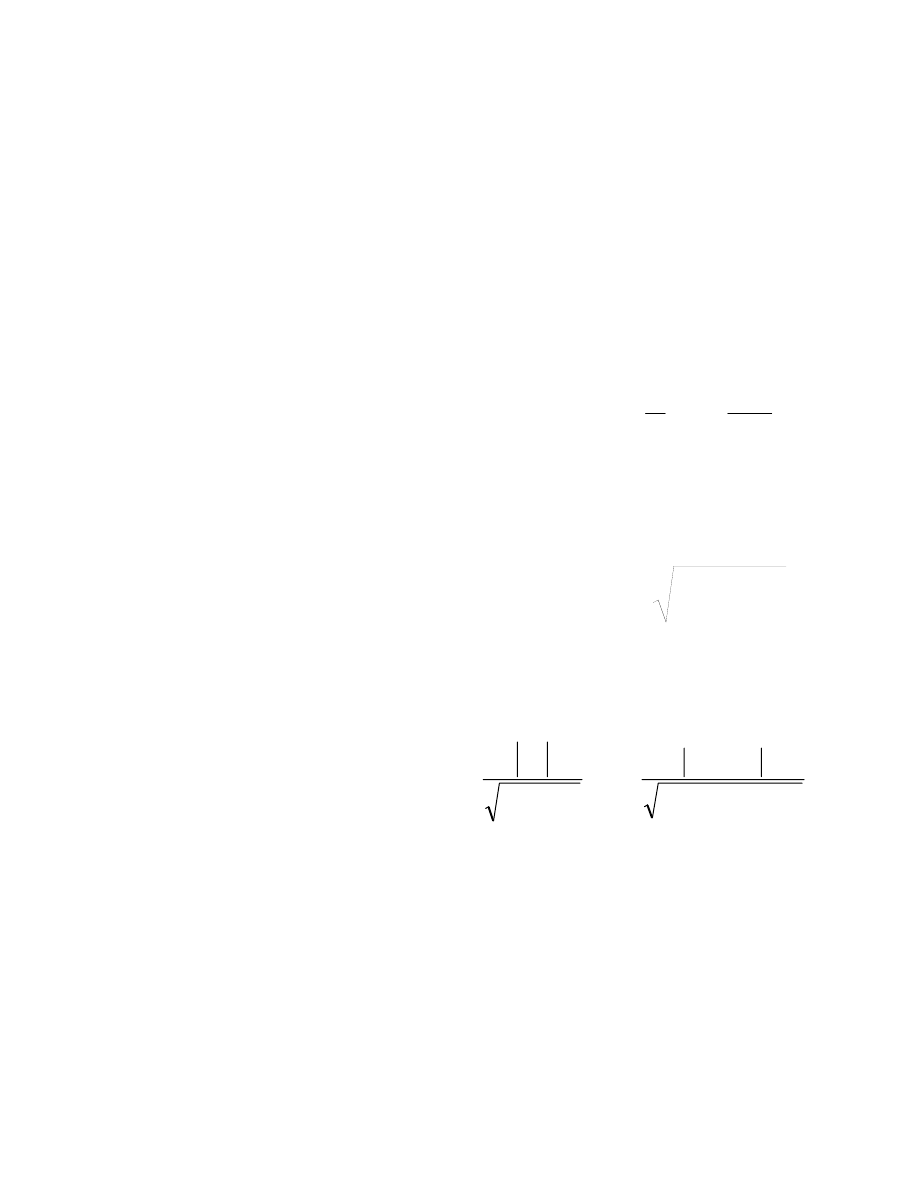
WYNIKI TEORII BCS

Rozwiązania szuka się metoda wariacyjną.

W rezultacie otrzymuje się:

nową funkcję rozkładu:

parametr przerwy energetycznej:

nowy związek dyspersyjny
jednocząstkowego stanu wzbudzonego:

nową gęstość stanów (stanów
wzbudzonych):

)

E

1

(

2

1

v

k

k

2

k

ε

−

=

k

k

k

u

v

V

∑

=

∆

2

2

∆

+

=

k

k

E

ε

(

)

N

2

2

F

k

F

k

N

2

2

'
k

'
k

'
k

D

E

E

E

E

D

E

E

)

D(E

∆

−

−

−

=

∆

−

=

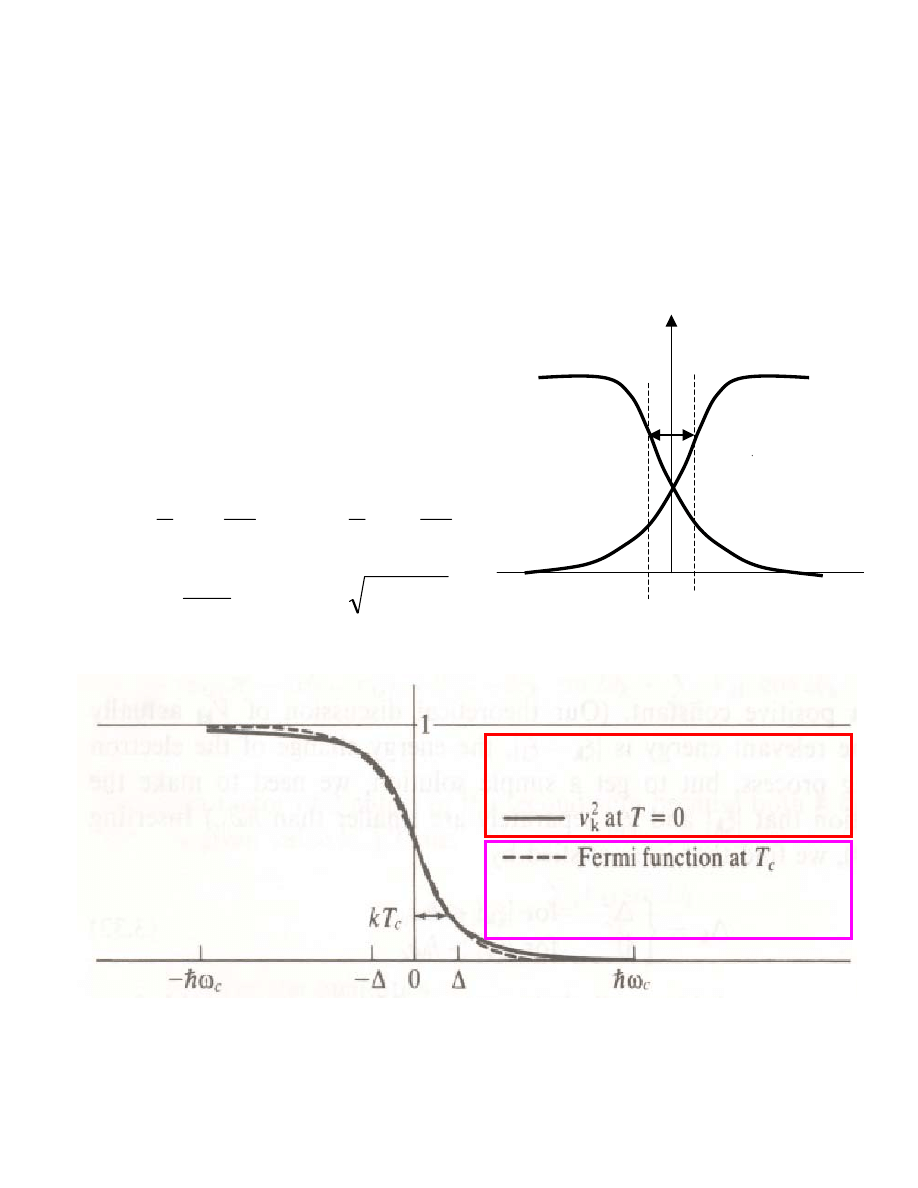
Nowa funkcja rozkładu

2

2

2

2

;

2

;

1

2

1

;

1

2

1

k

k

k

k

k

k

k

k

k

k

k

k

k

E

E

u

v

E

u

E

v

∆

+

=

∆

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

ε

ε

ε

0

=

k

ε

v

k

2

u

k

2

2∆

In reality,
f(T

c

)~v

k

2

(0).

E

k

’

=E

k-

E

F

Probability that e

-

state k

is

occupied.

Probability that pair state

(k,-k) is

occupied.

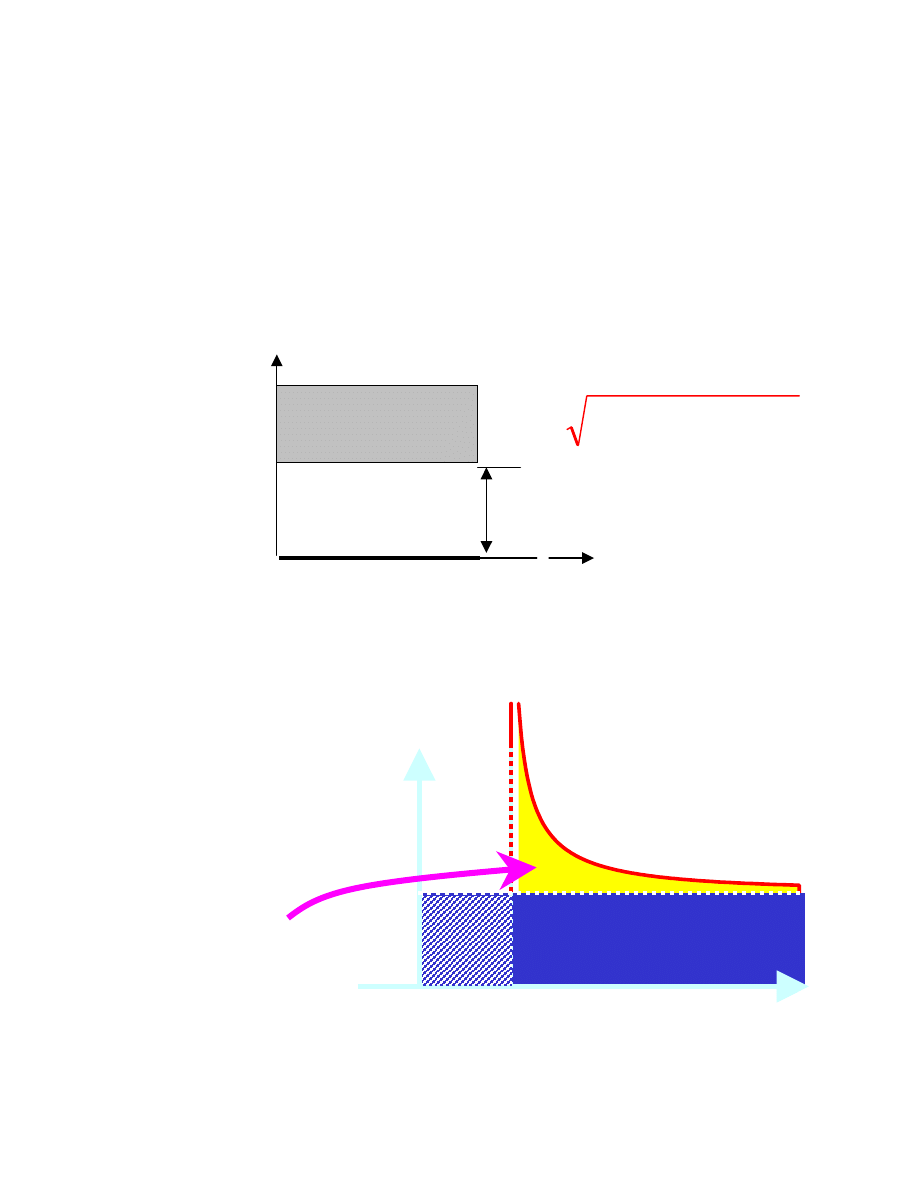
Schemat energetyczny nadprzewodnika,

przerwa energetyczna

Stany
wzbudzone

∆

2

Pary Coopera

(

)

2

k

2

F

k

k

E

E

∆

+

−

=

ε

• Gęstość

jednoelektronowych
stanów wzbudzonych

• Stany z obszaru

przerwy

∆

są

"wypchnięte" do
obszary najniższych
stanów wzbudzonych

•

D(E

k

’)

1xD

N

Normal state

∆

E

k

’

Jak teoria BCS wyjaśnia właściwości

nadprzewodników

Tc, przerwa energetyczna, efekt izotopowy,

zerowy opór, pole i prąd krytyczny, odległość

koherencji, diamagnetyzm, kwantowanie

strumienia magnetycznego, tunelowanie,...

Zerowy opór

Aby rozważać takie własności nadprzewodników jak zerowy opór,
diamagnetyzm itd. trzeba powrócić do zwykłego zapisu funkcji falowej:

)

(

exp(

)

(

)

(

)......

(

)

(

)

1

(

1

2

1

2

1

1

4

3

2

1

r

r

ik

u

v

r

r

r

r

r

r

r

r

V

k

k

k

n

n

P

P

S

−

=

−

−

−

−

−

=

Ψ

∑

∑

−

ϕ

ϕ

ϕ

ϕ

θ

i

s

e

n

2

=

Φ

W warunkach przepływu prądu zmienia się faza funkcji falowej pary (dla
każdej pary tak samo). Można wtedy zapisać funkcję falową wszystkich
par (tzw. makroskopową funkcję falową, lub parametr porządku) jako:

Gdzie n

s

jest koncentracją elektronów biorących udział w tworzeniu par

Coopera.

Gęstość prądu, natomiast obliczamy korzystając ze znanego wyrażenia:

]

}

qA

i

{

}

qA

i

{

[

m

q

j

*

*

Φ

−

∇

Φ

+

Φ

−

∇

−

Φ

=

h

h

Zerowy opór

....)

(

2

2

1

+

+

=

=

Φ

R

R

K

e

n

i

s

r

r

r

θ

θ

]

}

{

}

{

[

*

*

Φ

−

∇

Φ

+

Φ

−

∇

−

Φ

=

qA

i

qA

i

m

q

j

h

h

W nieobecności pola magnetycznego otrzymujemy:

const

K

m

qn

n

m

q

j

s

s

=

=

∇

=

r

h

h

θ

2

2

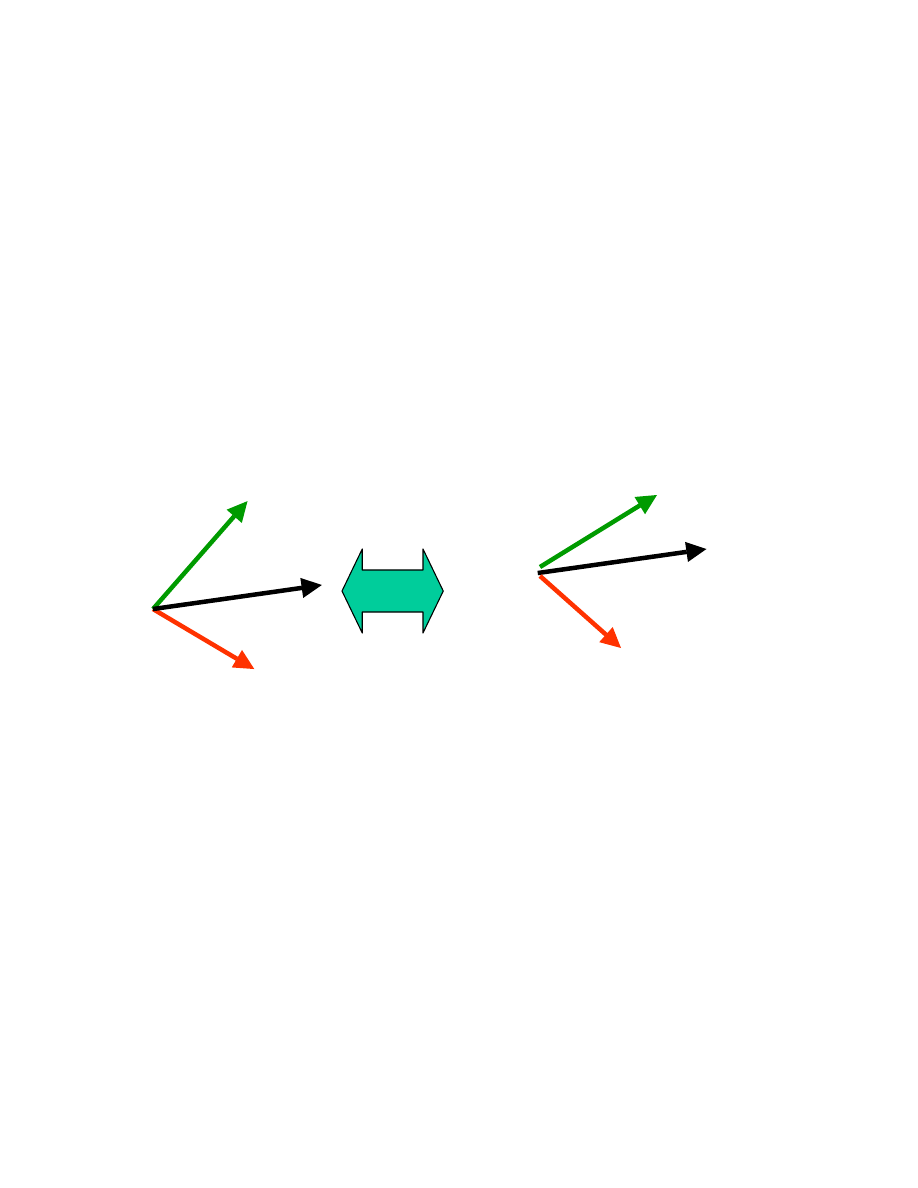
Zerowy opór bez wzorów:

• Wiemy,że opór metali wynika z oddziaływania elektronów z

drganiami sieci krystalicznej (następuje zmiana kierunku
ruchu elektronu, czyli ograniczenie prądu elektrycznego).

• W nadprzewodniku oddziaływanie elektronu z drganiami

sieci prowadzi do powstania pary Coopera.

Elektron zmienia swój pęd, ale para Coopera nie!!!

Diamagnetyzm: równania Londonów

....)

(

2

2

1

+

+

=

=

Φ

R

R

K

e

n

i

s

r

r

r

θ

θ

]

}

{

}

{

[

*

*

Φ

−

∇

Φ

+

Φ

−

∇

−

Φ

=

qA

i

qA

i

m

q

j

h

h

Gęstość prądu w polu magnetycznym:

(

)

rotj

n

q

m

B

B

m

n

q

rotA

m

n

q

rotj

A

m

n

q

K

m

qn

qA

n

m

q

K

m

qn

j

s

s

s

s

s

s

s

2

2

2

2

0

2

2

−

=

=

−

=

−

=

−

+

=

r

r

h

r

h

Ostatnie równanie jest równaniem Londonów

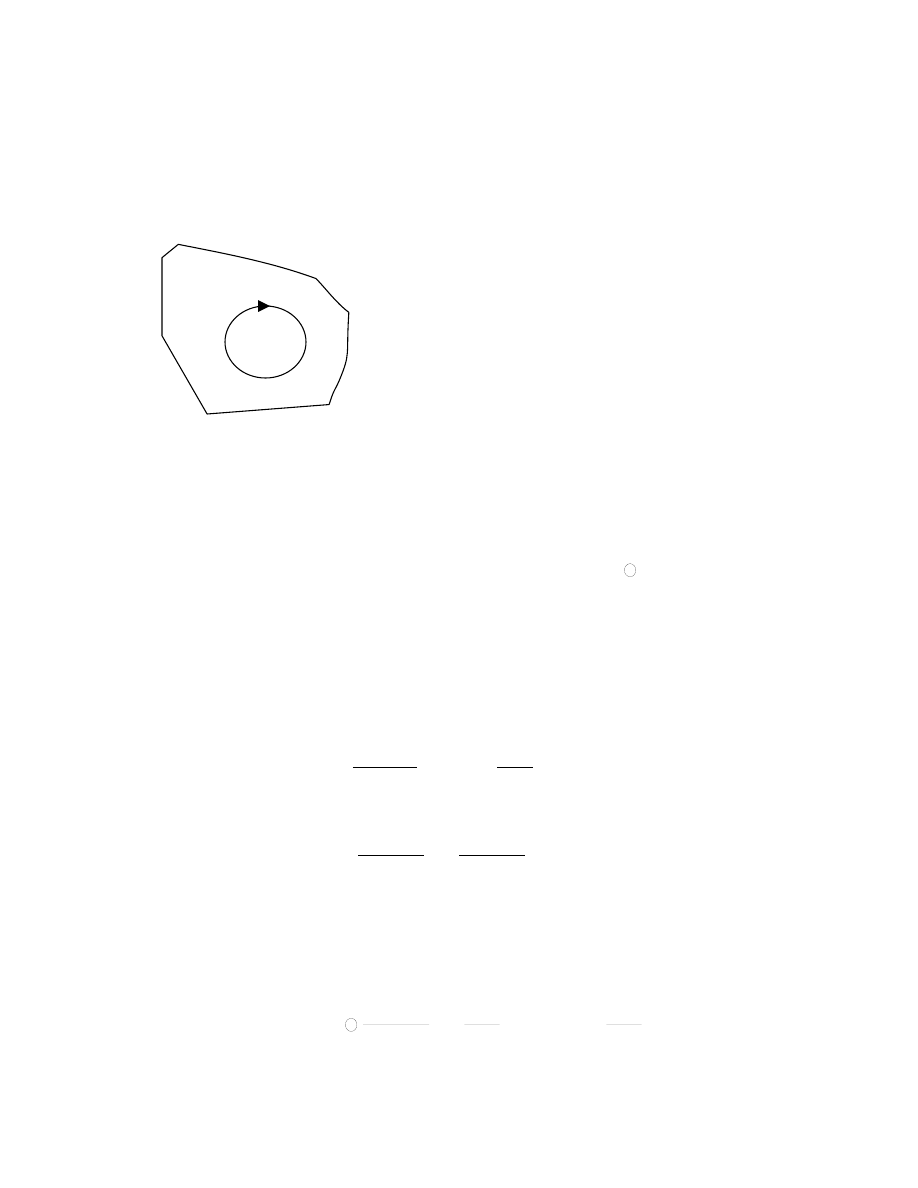
Kwantowanie strumienia pola

magnetycznego

Umieszczamy materiał
nadprzewodzący w polu
magnetyczny. Wewnątrz materiału, z
dala od prądów ekranujących
zataczamy zamkniętą pętlę. Strumień
pola magnetycznego wewnątrz pętli
wynosi:

∫

=

Φ

l

d

A

r

r

Gęstość prądu w polu magnetycznym:

( )

e

q

A

qA

n

m

q

m

qn

j

s

s

2

0

2

θ

θ

θ

∇

=

∇

=

=

−

∇

=

h

h

h

Zatem:

e

h

n

n

e

e

2

2

2

2

=

=

∇

=

Φ

∫

π

θ

h

h

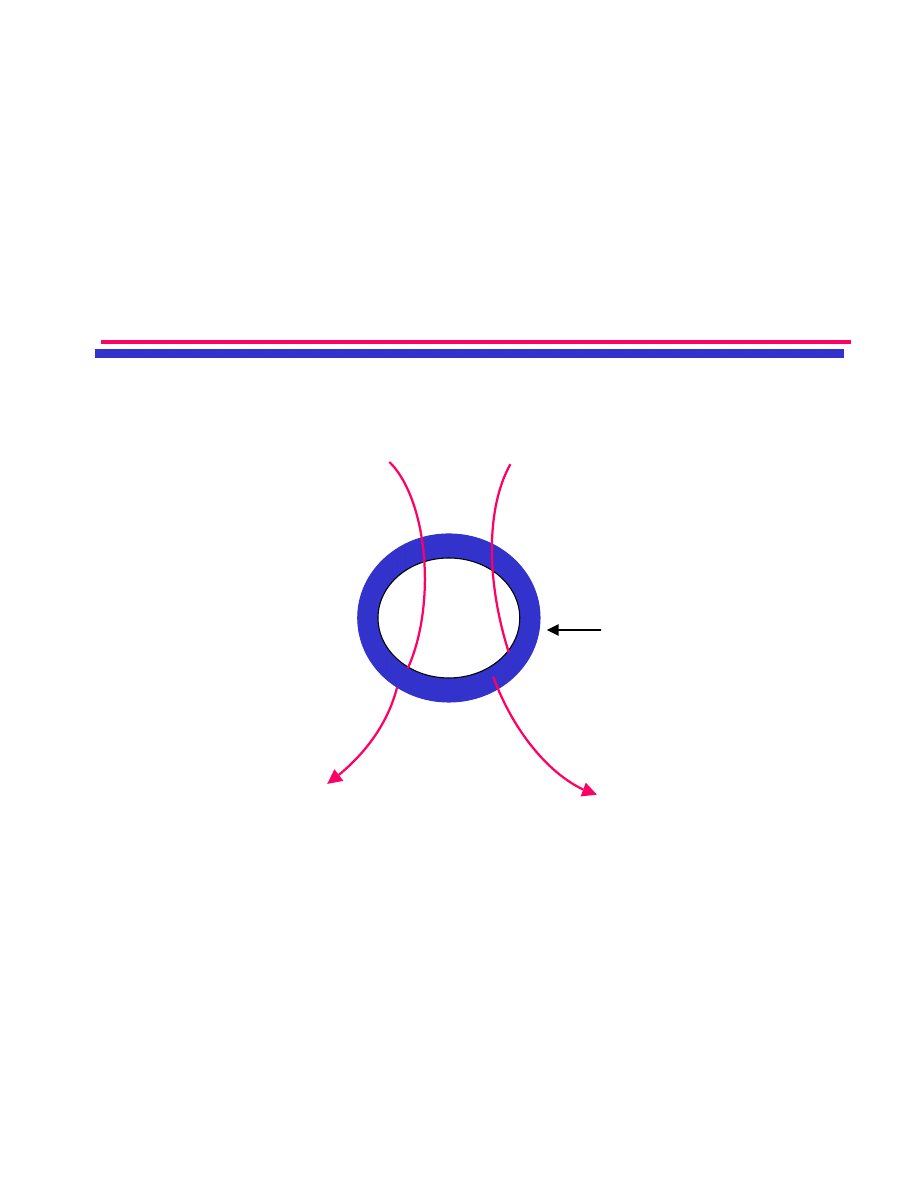
Kwantowanie strumienia pola

magnetycznego

Magnetic
field

B

Pierścień
nadprzewodzący

W nadprzewodnikach, strumień pola magnetycznego jest
skwantowany. Kwant strumienia wynosi:

Φ

0

= h/2e = 2.07 x 10

-15

weber

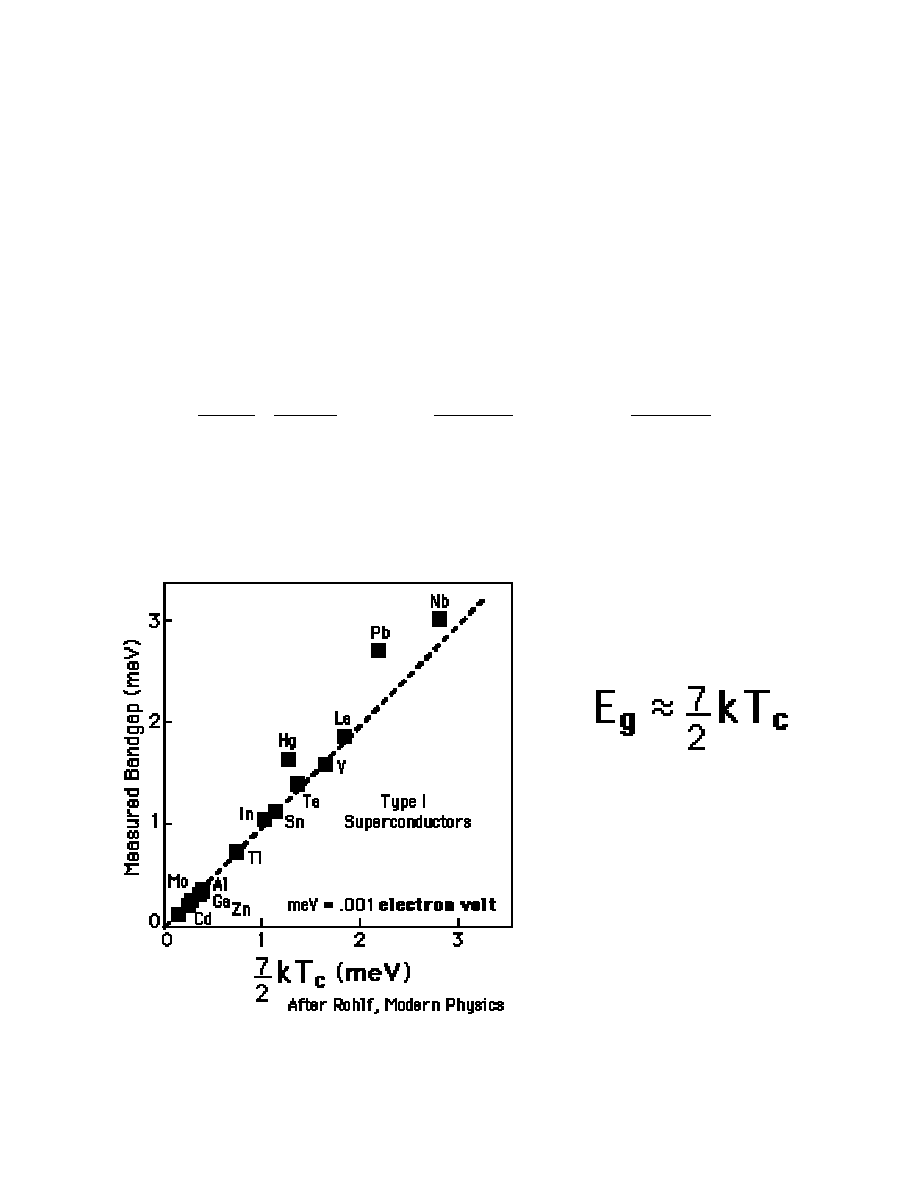
Temperatura krytyczna, efekt izotopowy i

przerwa energetyczna

( )

( )

53

.

3

0

2

0

1

exp

2

=

∆

⇒

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

=

C

B

B

D

e

C

T

k

VN

k

T

ω

π

γ

h

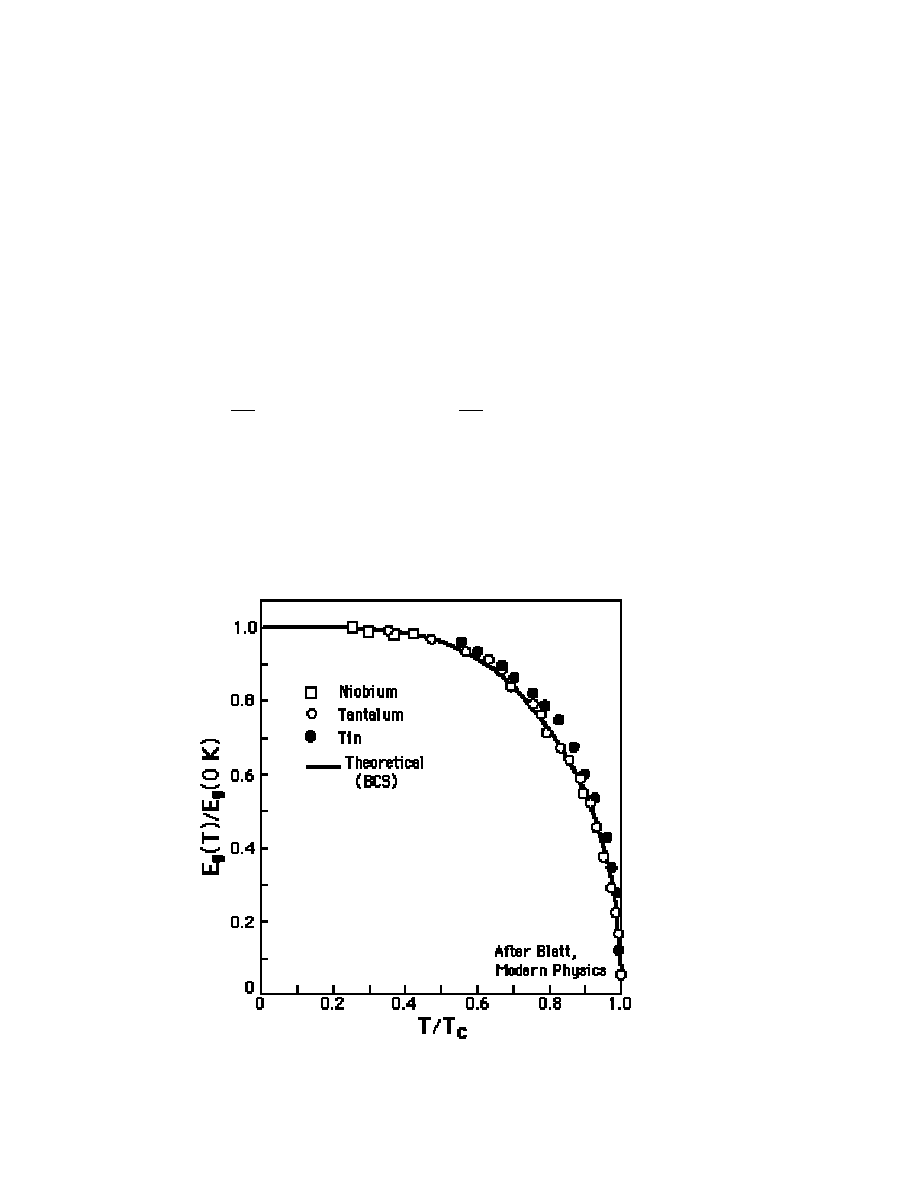
Pole krytyczne

( )

( ) ( )

2

2

0

0

0

2

1

0

2

1

∆

= N

H

C

µ

Prąd krytyczny

• Gęstość prądu par Coopera (K

jest wypadkowym wektorem
falowym pary):

• Ruch pary Coopera powoduje

przyrost jej energii kinetycznej.
Ten przyrost energii
przypadający na jeden elektron
jest równy:

• Jeżeli energia 2

δE przekroczy

wartość 2

∆ para samorzutnie

ulegnie rozpadowi (rozbicie pary
będzie korzystne energetycznie
w porównaniu z płynięciem
prądu nadprzewodzącego).

K

m

en

en

j

2

h

=

=

υ

m

K

k

m

k

m

K

k

E

F

F

F

2

2

)

(

2

)

2

(

2

2

2

2

2

h

h

h

≈

−

+

=

δ

∆

≥ 2

2

m

K

k

F

h

F

c

k

en

j

h

∆

=

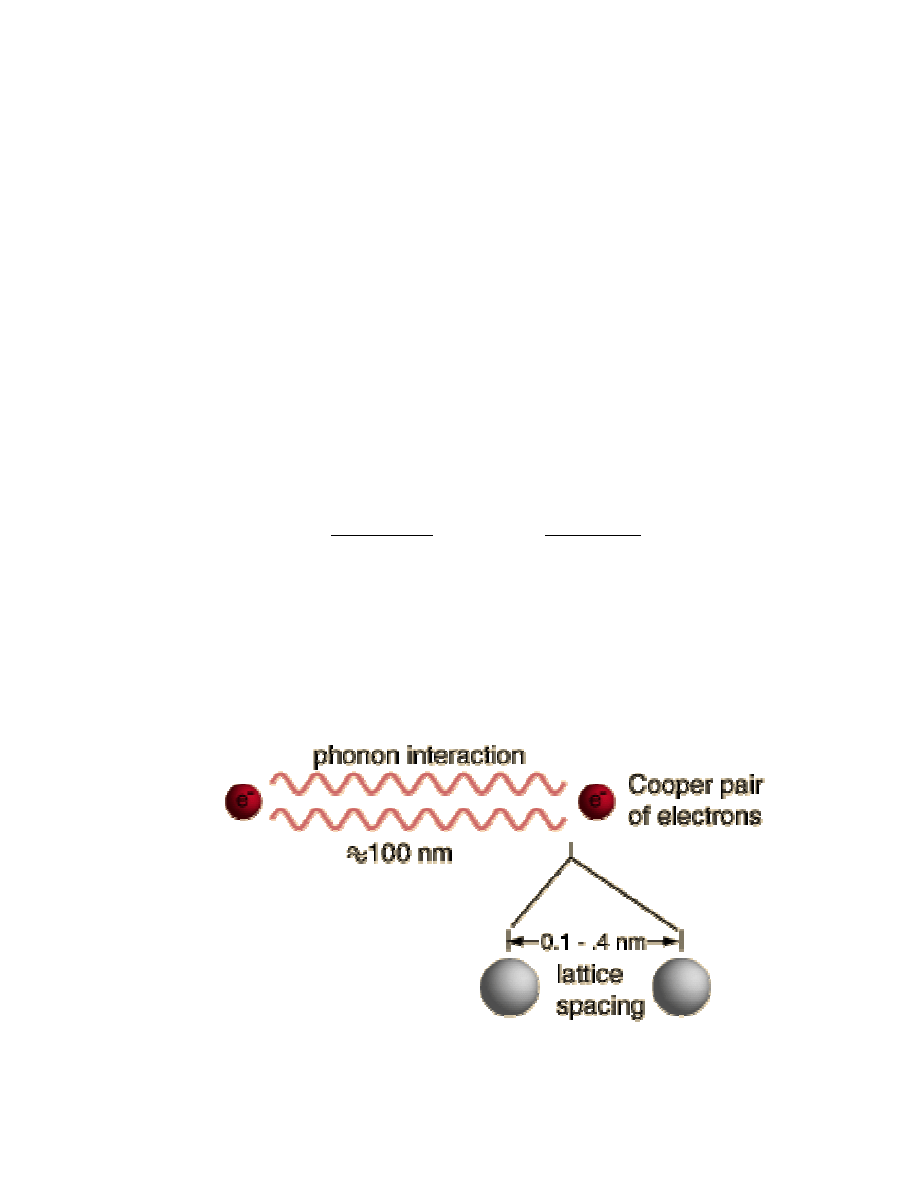
Odległość koherencji

Miara odległości zaniku koherencji fazowej pomiędzy
elektronami ("rozmiar pary Coopera").

( )

( )

C

B

F

F

T

k

v

v

h

h

18

.

0

0

0

=

∆

=

π

ξ

Literatura

• W. A. Harrison, Teoria ciała stałego;
• M. Grinberg, Wydział Fizyki Uniwersytetu Gdańskiego,

Wykłady z fizyki ciała stałego;

• S.Y. Hsu, NCTU;
• Rose-Innes, Nadprzewodnictwo;