MATERIAŁY XXXVI ZJAZDU FIZYKÓW POLSKICH – TORUŃ 2001 – WYKŁADY PLENARNE

Diagram fazowy

nadprzewodników wysokotemperaturowych

Jan Stankowski

Instytut Fizyki Molekularnej Polskiej Akademii Nauk, Poznań

1. Wstęp

Nadprzewodnictwo jest jednym z najbardziej

frapujących zjawisk w fizyce fazy skondensowa-
nej. Odkryte w rtęci w 1911 r., spowodowało roz-
wój prac nad wzbudzeniami silnie skorelowanych
elektronów w ciele stałym. Elektrony w metalu
tworzą ciecz Fermiego (FL), której gęstość za-
leży od gęstości stanów na poziomie Fermiego E

F

.

Korelacje między elektronami sprawiają, że elek-
trony łączą się w tzw. pary Coopera (CP). Są one
wzbudzeniami w krysztale, mają właściwości bo-
zonów (spin S = 0 lub 1), a ich energia leży poni-
żej E

F

. Pary Coopera tworzą ciecz słabo oddzia-

łujących par lokalnych (LP), która jest cieczą bo-
zonów (BL). Różnice w statystykach rządzących
FL i BL powodują, że obsadzenie poziomu CP,
poniżej T

c

, przewyższa gęstość stanów na pozio-

mie Fermiego. Po przekroczeniu gęstości krytycz-
nej CP następuje kondensacja Bosego–Einsteina
(BEC), przejawiająca się w nadprzewodnikach za-
nikiem oporu elektrycznego oraz idealnym diama-
gnetyzmem. Przez kryształ płynie prąd CP bez
strat, bo każda para Coopera charakteryzuje się
taką samą amplitudą |Ψ| i fazą ϕ funkcji falowej
tak, że cały stan nadprzewodnika opisuje jedna
funkcja falowa Ψ = |Ψ| exp(iϕ).

Odkrycie w 1986 r. nadprzewodnictwa wyso-

kotemperaturowego (HTSC) spowodowało pewien
zamęt w zrozumieniu tego zjawiska i dzisiaj, po
15 latach, nadal trwają dyskusje dotyczące dia-
gramu fazowego HTSC. Teoria nadprzewodnic-
twa podana przez Bardeena, Coopera i Schrieffera
(BCS), obowiązująca dla metali, gdzie występuje
duża gęstość stanów na poziomie Fermiego, opi-
suje słabe oddziaływania w parach Coopera za
pośrednictwem wirtualnych fononów o prawie ze-

rowym przekazie pędu: k

↑

+k

↓

≈ 0. Takie przybli-

żenie nie tłumaczy wysokich temperatur krytycz-
nych T

c

i nie opisuje złożonych zjawisk występu-

jących w HTSC w zakresie małych koncentracji
nośników prądu. Ponadto w teorii BCS występuje
jedna temperatura krytyczna T

c

, oddzielająca ob-

szar cieczy Fermiego od obszaru nadprzewodnic-
twa, co oznacza, że w modelu BCS pojawienie się
CP i BEC następuje w tej samej temperaturze.

Nadprzewodnictwo wysokotemperaturowe zo-

stało odkryte w materiałach o bardzo małej kon-
centracji nośników, co sugeruje, że jego istotą są
fluktuacje ładunku w skali nanoskopowej. Fluk-
tuacje te sprawiają, że już w wysokiej tempera-
turze T

∗

= T

LP

> T

c

występują CP jako nie-

zależne wzbudzenia tworzące gaz LP, który do-
piero w T

c

tworzy kondensat Bosego–Einsteina.

Na diagramie fazowym występują więc dwie tem-
peratury charakterystyczne: T

∗

i T

c

. W zakresie

T

c

< T < T

∗

występuje ciecz bozonów (LP),

a jeszcze nie następuje BEC. W tym ciekawym
obszarze diagramu fazowego HTSC występują zja-
wiska polegające na oscylacji stanów spinowych
(SDW) i stanów ładunkowych (CDW) elektronów
wędrujących. Jest on nazywany obszarem z pseu-
doszczeliną (ang. crossover). Omawiane zjawiska
związane ze zmianą koncentracji dzielą płaszczy-
znę diagramu fazowego na dwie części: zakres
poddomieszkowania (ang. underdoped) i zakres
naddomieszkowania (ang. overdoped). Zależności
między temperaturami T

∗

i T

c

podane są w tab. 1.

Diagram fazowy stanu nadprzewodzącego

T

c

(x) pokazuje, że obszar, w którym występuje

nadprzewodnictwo (SC), rozpoczyna się powyżej
krytycznej koncentracji x

1

i T

c

rośnie ze wzrostem

x aż do koncentracji optymalnej x

opt

, a dalszy

wzrost x powoduje spadek temperatury T

c

. Wy-

46

POSTĘPY FIZYKI

TOM DODATKOWY 53D

ROK 2002

MATERIAŁY XXXVI ZJAZDU FIZYKÓW POLSKICH – TORUŃ 2001 – WYKŁADY PLENARNE

stępowanie dwóch temperatur T

LP

i T

c

prowadzi

do różnorakich zjawisk związanych z silnymi ko-
relacjami elektronów.

Tabela 1. Temperatury krytyczne T

∗

i T

c

w nadprze-

wodnikach wysokotemperaturowych.

Koncentracja

Temperatury

BEC

nośników

krytyczne T

c

i T

∗

T < T

c

x < x

1

T

c

= 0, T

∗

= T

LP

nie

x

1

< x < x

opt

(poddomieszkowanie)

T

c

< T

∗

= T

LP

tak

x

opt

< x < x

max

(naddomieszkowanie)

T

c

= T

∗

= T

LP

tak

x > x

max

T

c

= 0

nie

Fulereny, które należą do nadprzewodników

wysokotemperaturowych, mają obydwie tempera-
tury krytyczne: T

LP

i T

c

w zakresie poddomiesz-

kowania i jedną temperaturę w zakresie naddo-
mieszkowania.

Diagram fazowy HTSC wyjaśnia efekty ci-

śnieniowe. Ze wzrostem ciśnienia rośnie wartość
całki przeskoku t, do której jest proporcjonalna
gęstość stanów na poziomie Fermiego. Parametr
dT

c

/dp jest dodatni poniżej koncentracji optymal-

nej x

opt

, gdzie skaluje się jak t

2

/U (U jest we-

wnątrzwęzłową energią korelacji). Powyżej opty-
malnej koncentracji, gdzie ciśnienie obniża T

c

,

skaluje się jak (2zt)

−1

, gdzie z – liczba sąsiadów,

a dT

c

/dp < 0. Złożony diagram fazowy HTSC wy-

nika z dwucząstkowych korelacji fermionów oraz
kondensacji Bosego–Einsteina, będącej procesem
korelacji wielu CP.

2. Przykłady diagramów fazowych nad-

przewodników wysokotemperaturowych

Głównym reprezentantem nadprzewodnictwa

wysokotemperaturowego (HTSC) jest związek
YBa

2

Cu

3

O

6+x

(YBCO), który jest złożonym

tlenkiem o warstwowej strukturze płaszczyzn
CuO połączonych łańcuchami miedziowo-tleno-
wymi. Dobór koncentracji tlenu x w łańcuchach
pozwala na kontrolowaną zmianę koncentracji no-
śników prądu (dziur) płynących równolegle do
tych płaszczyzn. Dzięki temu w YBCO można śle-
dzić korelacje spinowe i ładunkowe w fazie upo-
rządkowania antyferromagnetycznego (AF) dla

x < 0,5 oraz uporządkowania ładunkowego w sta-
nie nadprzewodnictwa (SC), gdy x zmienia się od
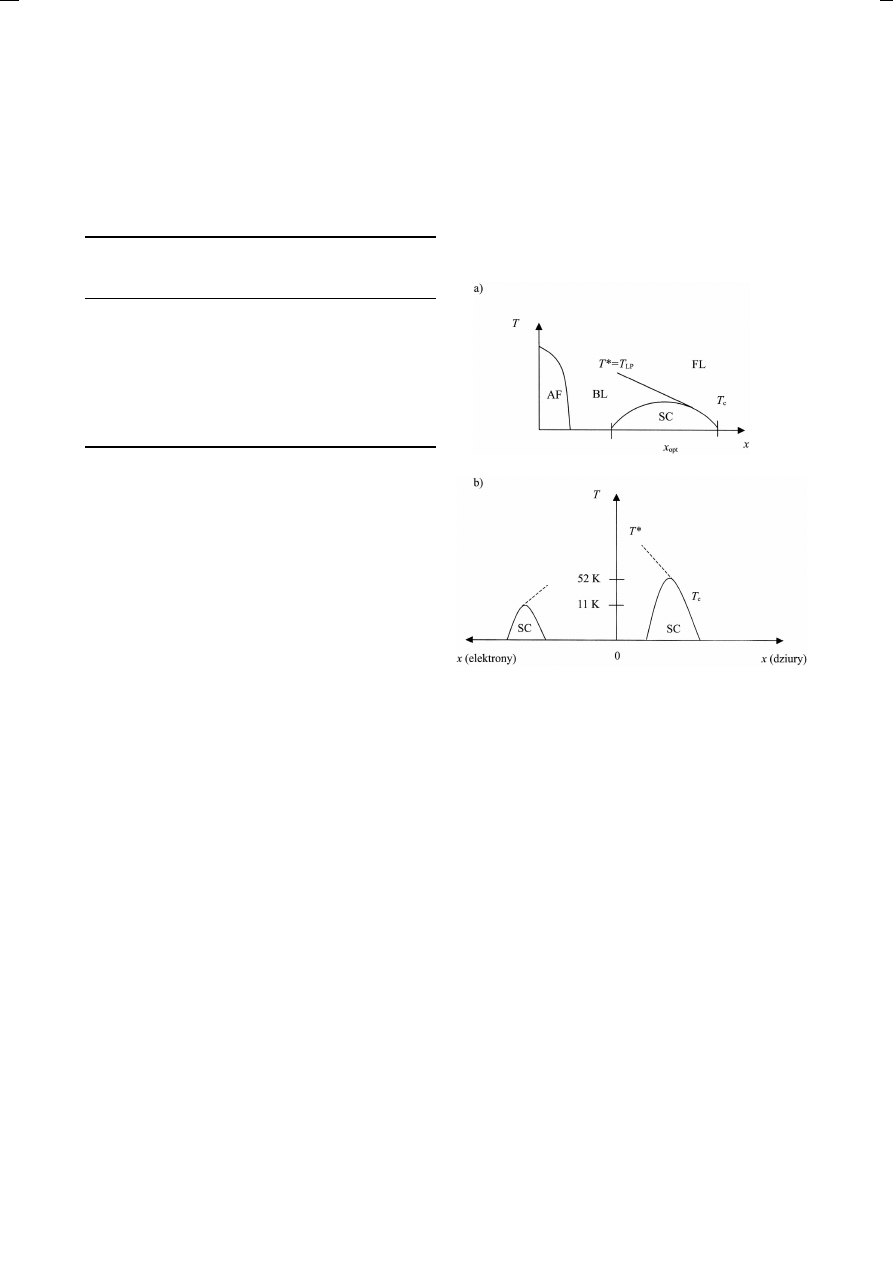
0,5 do 1. Przedstawiony na rys. 1a diagram fa-
zowy ma znamiona uniwersalności, na co wyraź-
nie wskazują ostatnie prace z FulFET-em, czyli
tranzystorem polowym z monokryształem fule-
renu C

60

[2] (rys. 1b).

Rys. l. Diagram fazowy nadprzewodnika wysokotempe-
raturowego przedstawiający zależność temperatur kry-
tycznych T

∗

= T

LP

i T

c

od koncentracji nośników x

(elektronów lub dziur) dla: a) YBCO [1] oraz b) fulere-

nowego tranzystora polowego FulFET [2].

Dla bardzo małej koncentracji nośników

(dziur/elektronów) materiał wykazuje antyferro-
magnetyzm (AF), a ładunki i spiny są zlokalizo-
wanymi stanami w krysztale. W miarę wzrostu
koncentracji nośników prądu rośnie przewodność,
występują korelacje dwójkowe i pojawiają się pary
lokalne (LP) o właściwościach swobodnych bozo-
nów, które kondensują w T

c

.

Odkrycie nadprzewodnictwa indukowanego

w tranzystorze FulFET [2] na krysztale C

60

po-

kazuje, że zależność od koncentracji ma maksi-
mum [T

c

(x)]

h,e

max

tak dla nadprzewodnictwa dziu-

rowego (52 K), jak też elektronowego (11 K)
(rys. 1b). Jest to duże przesunięcie T

c

ku wysokiej

temperaturze, bo w wyniku domieszkowania fule-
ryty K

3

C

60

, Rb

3

C

60

mają niższą temperaturę kry-

tyczną T

c

, która wynosi odpowiednio 19 K i 30 K.

POSTĘPY FIZYKI

TOM DODATKOWY 53D

ROK 2002

47

MATERIAŁY XXXVI ZJAZDU FIZYKÓW POLSKICH – TORUŃ 2001 – WYKŁADY PLENARNE

3. Przewodnictwo fulerenu C

60

i fulerytów A

x

C

60

Przewodnictwo elektryczne w krysztale utwo-

rzonym przez sferyczne molekuły fulerenu C

60

jest

procesem złożonym [3]. Swobodne elektrony prze-
wodnictwa rozpraszane na powierzchni takiej mo-
lekuły przez lokalne drgania dopuszczone przez
symetrię decydują o zależności przewodności elek-
trycznej od temperatury, gdy przeskoki pomię-
dzy sąsiednimi cząsteczkami zachodzą dzięki bez-
stratnemu tunelowaniu. Średnia droga swobodna
elektronu w jego ruchu translacyjnym w fulerenie,
l

tr

= 0,3 nm, jest mniejsza od odległości d = 1 nm

między molekułami C

60

w sieci fcc kryształu.

Ten dwuetapowy proces przewodnictwa w fulere-
nie sprawia, że nie można stosować przybliżenia
swobodnego gazu kwantowego elektronów, lecz ze
wzrostem stopnia nieuporządkowania (ang. disor-
der) trzeba rozpatrywać efekt lokalizacji Ander-
sona, zwiększający opór, lub należy uwzględnić
efekt kondensacji defektów związanych z przesu-
nięciami jonów, który prowadzi do „nasycenia”
oporu. W celu wyjaśnienia tak skomplikowanego
procesu przewodnictwa elektrycznego w fulerenie
postuluje się zastąpienie elektronów nienaładowa-
nymi kwazicząstkami Bogolubowa, które są su-
perpozycją fermionów: ujemnych elektronów i do-
datnich dziur. Modelem takiej kwazicząstki jest
torus, będący rotonowym stanem nadprzewodzą-
cego prądu par Coopera, wewnątrz którego znaj-
duje się spin. Te egzotyczne cząstki mają właści-
wości gazu, lecz ich spin i ładunek są kwanto-
wymi obserwablami wyznaczanymi za pomocą od-
powiednich szczelin energetycznych: spinowej lub
ładunkowej (ang. spin/charge gaps) [4].

Opór właściwy fulerenu domieszkowanego

metalami alkalicznymi był dyskutowany w wielu
pracach, lecz obraz podany przez Hebarda i in. [5]
wydaje się najbliższy rzeczywistości. W obra-
zie tym cząsteczka C

60

jako akceptor elektro-

nów tworzy anionowe stany stabilne C

1−

60

, C

2−

60

i C

3−

60

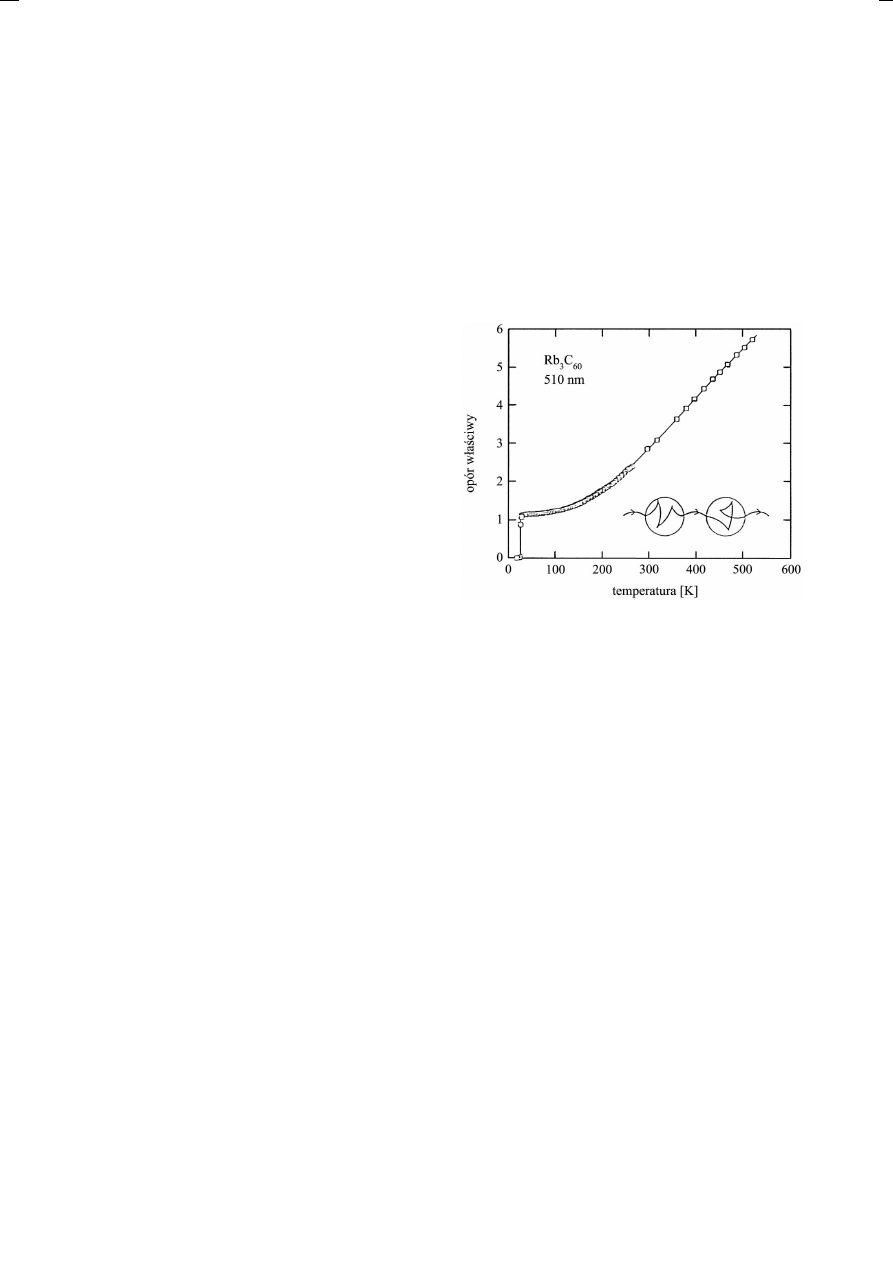
. W tym modelu (rys. 2) uchwycone na po-

wierzchni elektrony przebywają tam przez czas
τ ∼ λ

−l

, gdzie λ jest wielkością oddziaływa-

nia elektron–fonon. Ponieważ cząsteczkę fulerenu
można traktować jako obiekt mezoskopowy, ter-
micznie wzbudzane drgania mają cechy wynika-
jące z symetrii tej cząsteczki. Dlatego silne i krót-
kozasięgowe sprzężenie powoduje skrócenie śred-

niej drogi swobodnej do wartości l

tr

= 0,17 nm,

podczas gdy „optyczna” średnia droga swobodna
elektronu w Rb

3

C

60

w niskiej temperaturze wy-

nosi l

tr

= 8,7 nm. Różnica bierze się stąd, że oby-

dwa parametry dotyczą różnych procesów: mniej-
sza wartość l

tr

jest związana z rozpraszaniem elek-

tronu na powierzchni cząsteczki C

60

, a dłuższa za-

wiera również tunelowe przeskoki między sąsied-
nimi molekułami w sieci krystalicznej fulerenu.

Rys. 2. Zależność oporu właściwego K

3

C

60

od tem-

peratury. Schematyczny rysunek pokazuje dwuetapowy

translacyjny ruch elektronu w krysztale [5].

Przedstawiony na rys. 2 dwuetapowy pro-

ces przewodnictwa elektronowego składa się
z wewnątrzcząsteczkowego rozpraszania na po-
wierzchni molekuły oraz z szybkiego procesu tune-
lowania między sąsiednimi cząsteczkami w krysz-
tale. Na ten złożony proces ruchu elektronów
w krysztale fulerenu nakłada się orientacyjne
nieuporządkowanie molekuł C

60

, zawsze obecne

w temperaturze T > 0 K. Bardzo ciekawym
i istotnym spostrzeżeniem jest to, że w nadprze-
wodzących A

3

C

60

gęstość elektronów jest mniej-

sza niż trzy na molekułę C

60

! Oznacza to, że stan

ładunkowy w fulerenie nigdy nie jest „czysty”,
lecz zawsze mamy do czynienia z superpozycją
anionów o różnej wartościowości.

4. Nadprzewodnictwo fulerenu C

60

i fulerytów A

x

C

60

Własności nadprzewodzące w substancji wę-

glowej obserwowano w interkalowanym graficie
C

8

K, dla którego temperatura krytyczna T

c

była

48

POSTĘPY FIZYKI

TOM DODATKOWY 53D

ROK 2002

MATERIAŁY XXXVI ZJAZDU FIZYKÓW POLSKICH – TORUŃ 2001 – WYKŁADY PLENARNE

bardzo niska, gdyż wynosiła tylko 0,135 K. Silna
anizotropia pola krytycznego sugeruje, że dla
równoległej orientacji pola magnetycznego H
w stosunku do osi c kryształu zmienia się typ
nadprzewodnictwa [4]. Dla orientacji równole-
głej (H

↑

) do osi c występuje nadprzewodnictwo

typu I, bo parametr Ginzburga–Landaua κ =
0,22 < 1/

√

2, a wartość pola krytycznego H

c

=

400–560 A/m, podczas gdy dla orientacji prosto-
padłej H

→

występuje nadprzewodnictwo typu II:

κ = 0,78 > 1/

√

2 i pole krytyczne H

c2

=

960–1500 A/m. O zmianie charakteru nadprze-
wodnictwa ze zmianą kierunku pola magnetycz-
nego świadczy zależność podatności magnetycz-
nej χ od orientacji pola H. Ma ona kształt li-
tery U albo V, gdy pole H jest odpowiednio rów-
noległe albo prostopadłe do osi c kryształu gra-
fitu. Kształt „U” wskazuje na występowanie fazy
Meissnera aż do pola krytycznego, a kształt ”V”
wskazuje na wnikanie strumienia magnetycznego
(worteksów) już od najmniejszych pól i na struk-
turę mieszaną, charakterystyczną dla nadprze-
wodnika typu II.

W przypadku połączeń węgla i siarki dono-

szono o bardzo wysokich temperaturach krytycz-
nych T

c

. Ostatnio dla kompozytu siarki i grafitu

uzyskano temperaturę krytyczną 35 K [7]. W la-
tach 70. sugerowano nadprzewodnictwo amorficz-
nego węgla w temperaturze pokojowej na podsta-
wie oscylacyjnego charakteru zależności przewod-
nictwa od pola magnetycznego [8], lecz te obser-
wacje dotąd nie zostały potwierdzone.

Najlepiej zbadane są nadprzewodniki fulere-

nowe, gdzie kryształ fulerenu jest „gospodarzem”,
do którego wprowadzono gaz elektronów pocho-
dzący od zjonizowanych metali alkalicznych, od-
znaczających się małą energią jonizacji. Przed od-
kryciem nadprzewodnictwa w FulFET-ach [2] wy-
dawało się, że w układzie Me

x

C

60

, gdzie Me = K

lub Rb, tylko skład dla x = 3 jest fazą nadprzewo-
dzącą, a temperatury krytyczne K

3

C

60

i Rb

3

C

60

wynoszą odpowiednio T

c

(K) = 19 K i T

c

(Rb) =

30 K. Dzisiaj wiemy, że temperatura T

c

rośnie od

zera do wartości maksymalnej T

max

, gdy koncen-

tracja nośników prądu rośnie od x

1

do x

opt

. Powy-

żej tej wartości T

c

maleje do zera ze wzrostem x,

jak wynika z diagramu fazowego HTSC (rys. 1b).

Nie tylko jednak diagram fazowy, lecz przede

wszystkim zasięg korelacji ξ = 2 nm i stosunek
2∆/kT

c

≈ 5,25, gdzie ∆ jest szerokością prze-

rwy energetycznej, sytuuje fulereny w rodzinie
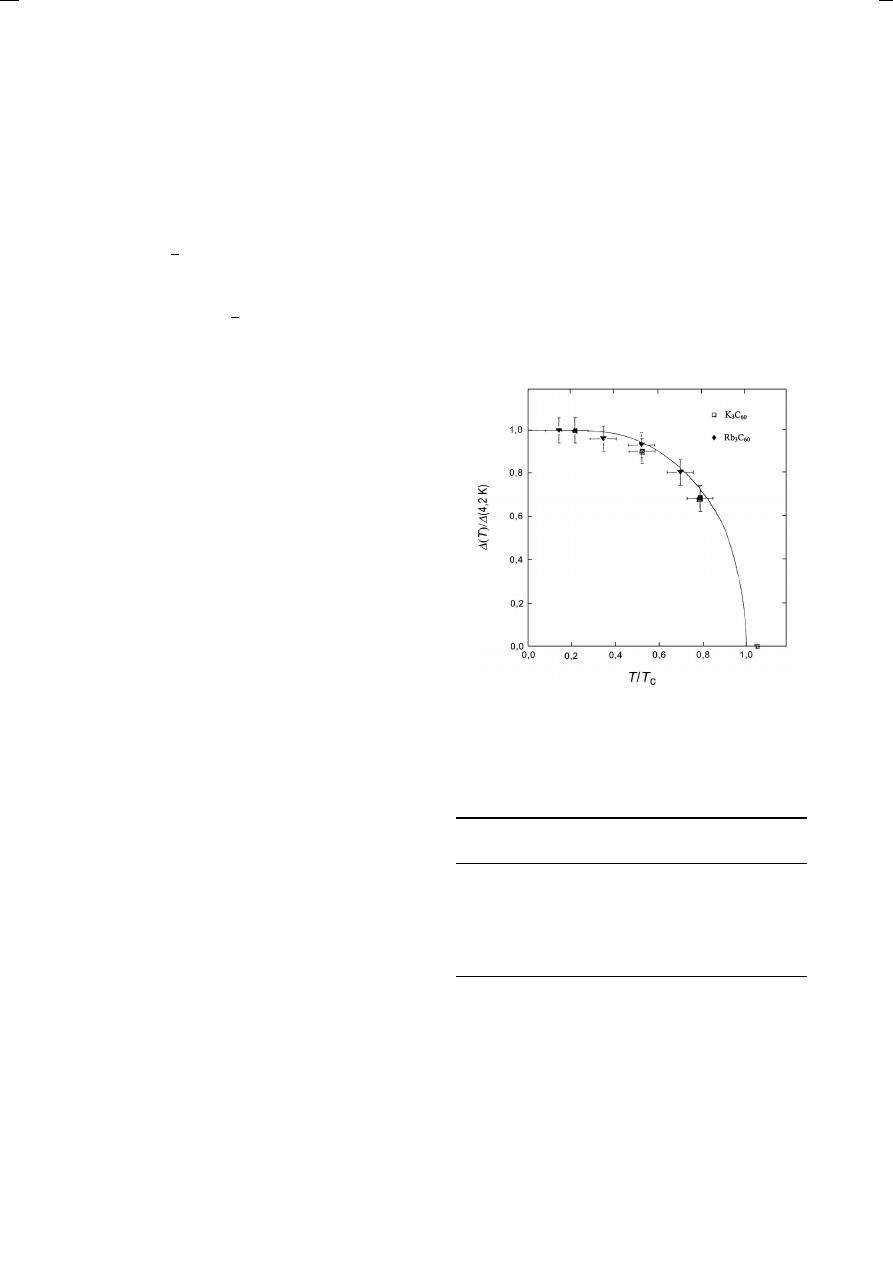
nadprzewodników wysokotemperaturowych. Za-
leżność szerokości przerwy energetycznej od zre-
dukowanej temperatury T /T

c

przedstawiono na

rys. 3. Linia ciągła została wykreślona zgod-
nie z teorią BCS. Podstawowe parametry stanu
nadprzewodzącego w interkalowanych fulerenach
A

x

C

60

przedstawiono w tab. 2. Wartości tych pa-

rametrów wskazują, że fuleryty są nadprzewodni-
kami typu II. Molekuła fulerenu C

60

ma właści-

wości układu nanoskopowego, w którym rozmiar
decyduje o jego strukturze elektronowej.

Rys. 3. Zależność szerokości przerwy energetycznej ∆ od

temperatury dla A

3

C

60

(A = K lub Rb) [9].

Tabela 2. Temperatura T

c

, parametr κ Ginzburga–

–Landaua i zasięg korelacji ξ w fulerytach.

T

c

[K]

κ

ξ [nm]

K

3

C

60

[8]

19,3

92

2,6–3,5

Rb

3

C

60

[8]

29,6

84

2,0–3,0

na granicy
domieszkowania [11]

21

5. Idea tranzystora

na pojedynczej molekule C

60

Stosując analogię między grafitem i fulerenem

wykazano, że współczynnik g wyznaczony za po-
mocą EPR jednoznacznie charakteryzuje poszcze-
gólne aniony: C

1−

60

i C

3−

60

[12]. Po odkryciu mole-

POSTĘPY FIZYKI

TOM DODATKOWY 53D

ROK 2002

49

MATERIAŁY XXXVI ZJAZDU FIZYKÓW POLSKICH – TORUŃ 2001 – WYKŁADY PLENARNE

kuły C

60

zaproponowano tranzystor wykorzystu-

jący fuleren jako element czynny nano-elektrome-
chanicznej struktury, oznaczanej w anglojęzycznej
literaturze akronimem NEMS [13]. Nanoskopowy
tranzystor fulerenowy ma strukturę tranzystora
FET, w którym mamy źródło S wstrzykujące elek-
trony, dren D oraz bramkę G (rys. 4, u góry). Na-
pięciem bramki U

G

steruje się prąd płynący mię-

dzy źródłem i drenem. Złote elektrody S i D zo-
stały osadzone na przekładce dielektryka leżącej
pod metalową bramką G. Szerokość elektrod wy-
nosiła 100 nm, a ich grubość 15 nm. Obserwacje
za pomocą mikroskopu elektronowego pokazały,
że szczelina między elektrodami jest nieregularna
i w najwęższych miejscach węższa od 10 nm. Na
tak przygotowanej szczelinie osadzono z roztworu
C

60

w toluenie molekuły fulerenu, spodziewając

się, że w najwęższym miejscu między elektrodami
znajdzie się pojedyncza cząsteczka C

60

. Standar-

dową techniką zbadano charakterystykę prądowo-
-napięciową I(U ), wiążąc skoki natężenia prądu
płynącego przez tranzystor z kolejnymi zmianami
ładunku molekuły C

60

w zależności od napię-

cia bramki U

G

. Ponieważ potencjały jonizacji ko-

lejnych anionów w sąsiedztwie źródła są znane
z pomiarów elektrochemicznych, można sądzić, że
pierwszy stopień odpowiada generacji jednowarto-
ściowego anionu C

1−

60

, a następne maksima prądu

tunelowego odpowiadają jonom C

2−

60

i C

3−

60

. Tak

więc za pomocą tranzystora udało się uwidocznić
ładunkowe stany fulerenu, traktując tę niezwykłą
molekułę jako kropkę kwantową.

6. Nadprzewodzący tranzystor FulFET

z modulowaną temperaturą krytyczną T

c

Ostatnio odkryto nadprzewodnictwo elektro-

nowe i dziurowe [2] w tranzystorze polowym zbu-
dowanym na czystym monokrysztale fulerenu C

60

.

Odkrycie to jest dlatego niezwykłe, że zaobser-
wowano łączenie się w pary stanów dziurowych,
które do tego odkrycia były uważane za stany fule-
renu C

1+

60

(mimo wielu wątpliwości). W strukturze

tranzystora polowego wykorzystano monokryształ
C

60

o przewodnictwie typu metalicznego (rys. 4).

Powierzchnię monokryształu, który specjalnie

oczyszczano przez wielokrotną sublimację i kon-
densację, poddano działaniu strumienia wodoru
w temperaturze 600

◦

C. Na kryształ o rozmiarach

1–2 mm naparowano źródło S i dren D, tak że

utworzył się między nimi kanał o długości 25 µm
i szerokości 0,5–1 mm. Na te elektrody nanie-
siono izolującą warstwę Al

2

O

3

, na którą nałożono

bramkę G. Badania własności nadprzewodzących
tego osobliwego FET-a przeprowadzono w zakre-
sie temperatury powyżej 1,7 K i w polach magne-
tycznych o indukcji do 9 T, skąd na podstawie
zależności H

c2

od indukcji B wyznaczono zasięg

korelacji ξ.

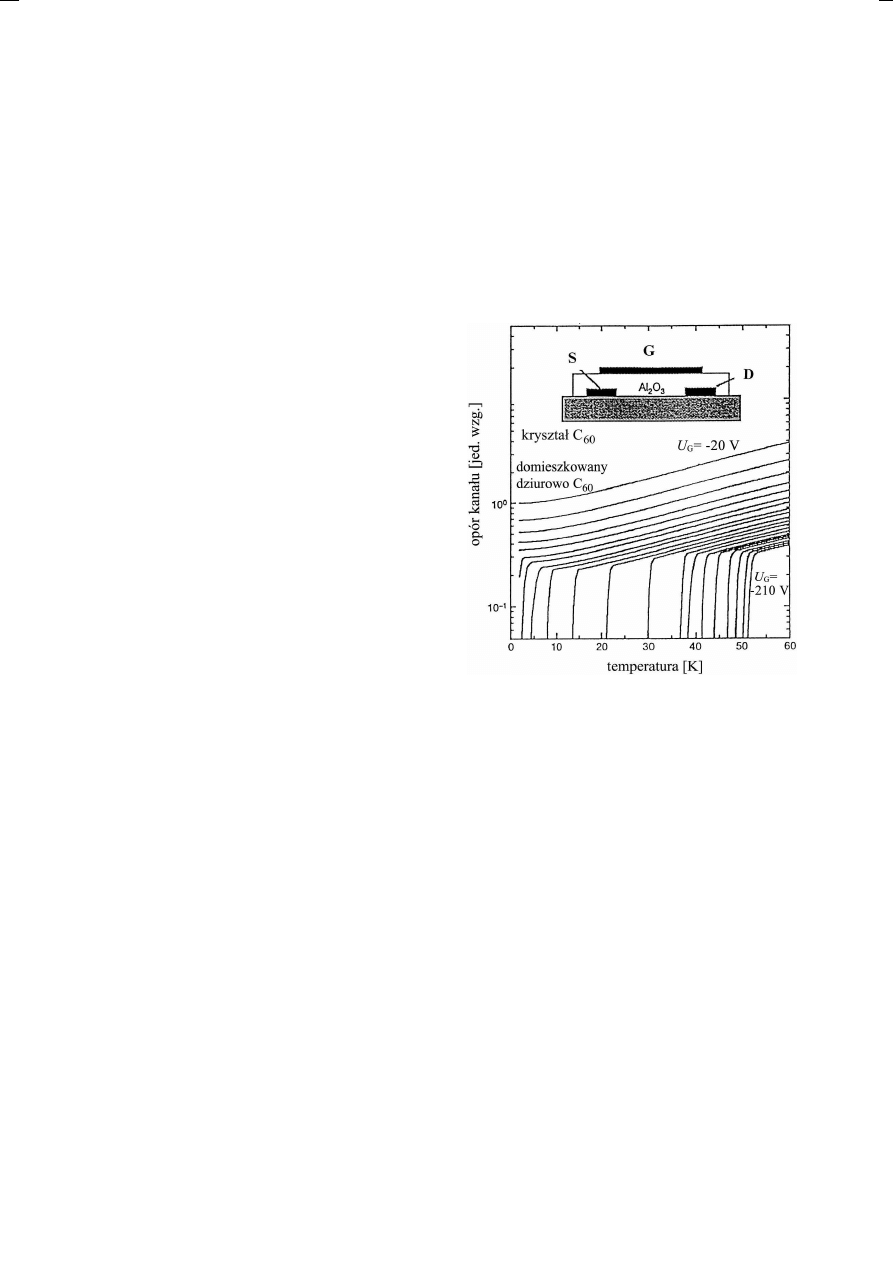
Rys. 4. Struktura fulerenowego tranzystora polowego
(FulFET-a) i zależność oporu właściwego nośników dziu-
rowych pomiędzy źródłem S i drenem D od temperatury

dla różnych napięć bramki G [2].

W zależności od polaryzacji bramki G zmie-

niano gęstość stanów elektronów lub dziur.
W stanie normalnym opór właściwy wynosił kil-
ka mΩ · cm. Na rysunku 4 widzimy typowe dla
nadprzewodników jego zależności od temperatury.
Dla polaryzacji dodatniej U

G

> 0 zaobserwo-

wano nadprzewodnictwo, polegające na łączeniu
się w pary elektronów wstrzykiwanych ze źródła S.
Temperatura krytyczna T

c

nie przekraczała 11 K.

Rewelacyjne okazało się generowanie w krysztale
C

60

dziur, dla których osiągnięto rekordowo wy-

soką temperaturę krytyczną T

c

= 52 K. Ponie-

waż obszar, w którym występuje nadprzewodnic-
two, jest nieokreślony, nie jest pewne, jaki ładu-
nek przypada na jedną molekułę C

60

. Trzy elek-

trony na cząsteczkę odpowiadają anionom C

3−

60

w słabo domieszkowanych związkach K

x

C

60

. Na-

tomiast dziurowe nadprzewodnictwo wskazuje, że

50

POSTĘPY FIZYKI

TOM DODATKOWY 53D

ROK 2002

MATERIAŁY XXXVI ZJAZDU FIZYKÓW POLSKICH – TORUŃ 2001 – WYKŁADY PLENARNE

pojedyncze dziury na molekułach fulerenu two-
rzą objętościowy nadprzewodnik w pobliżu po-
wierzchni kryształu.

Autorzy spodziewali się osiągnąć temperaturę

100 K, co uczyniłoby fuleren silnym konkuren-
tem innych nadprzewodników wysokotemperatu-
rowych. Udało się to [14] dla zmodyfikowanego
fulerenu przez zwiększenie stałej sieci za pomocą
chloro- i bromoformu, którego molekuły umiesz-
czono w lukach oktaedrycznych komórki elemen-
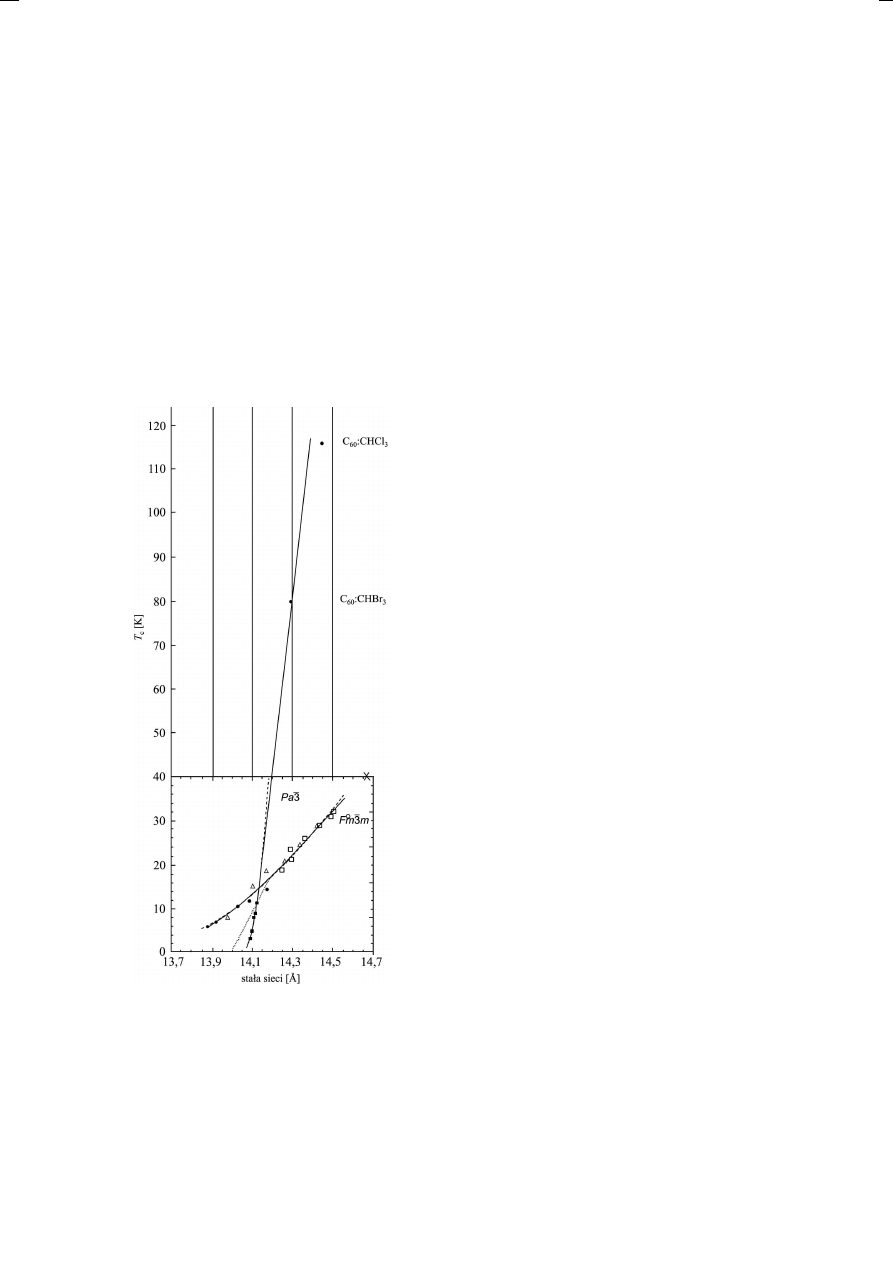
tarnej fcc fulerenu. Rysunek 5 pokazuje, jak zmie-
nia się temperatura krytyczna w zależności od sta-
łej sieci komórki elementarnej.

Rys. 5. Zależność temperatury krytycznej T

c

od stałej

sieci dla różnych struktur fulerenu [15].

Ostatnie wyniki dla chemicznie powiększonej

komórki elementarnej fulerenu sugerują, że struk-
tura obszaru nadprzewodzącego w FulFET-ach
jest typu Pa¯3. Wynika stąd, że tak silną jak w po-
miarach zależność T

c

od stałej sieci można wyja-

śnić przyjmując, że w nadprzewodzącej warstwie
FulFET-a mamy strukturę Pa¯3, a nie Fm¯3m.
Faza Pa¯3 występuje dla C

60

poniżej 260 K, w któ-

rej reorientacje sąsiednich molekuł fulerenu są
skorelowane. Korelacje takie wyjaśniałaby wy-
sokie temperatury T

c

i tak silną zależność od

wzajemnych odległości między molekułami C

60

.

Wskazuje na to również mała różnica między sta-
łymi sieci czystego C

60

i C

60

: HCBr

3

. Taka faza

kryształu o skorelowanym ruchu molekuł C

60

jest

sztywniejsza, dlatego fonony o większej częstości
uczestniczą w procesie parowania się spinów znaj-
dujących się na sąsiednich molekułach, który pro-
wadzi do wzrostu T

c

.

7. Nadprzewodnictwo dziurowe

w fulerenie – lepsze zrozumienie HTSC

Wyjątkowa możliwość dowolnego przesuwa-

nia temperatury krytycznej za pomocą napięcia
przykładanego do bramki fulerenowego tranzy-
stora FET stwarza możliwość ciągłej modyfikacji
stanu nadprzewodzącego. Najważniejszym wnio-
skiem płynącym z tego odkrycia jest to, że nie-
zależnie od sposobu wytworzenia stanu nadprze-
wodzącego procesy łączenia się nośników w pary
przebiegają podobnie i nie zależą od tego, czy
elektrony są wprowadzane przez donory w A

x

C

60

,

czy też są wstrzykiwane z elektrod w tranzysto-
rze FulFET. Stany dziurowe, które wiążą większą
liczbę elektronów, silniej oddziałują z siecią i dla-
tego maksymalna temperatura krytyczna T

c

dla

nadprzewodnictwa dziurowego jest wyższa niż dla
elektronowego. Jednak w obydwóch przypadkach
zasięg korelacji dla najwyższych T

c

jest taki sam

i nie jest mniejszy od 2 nm, tj. podwójnej odle-
głości między sąsiednimi molekułami C

60

w krysz-

tale [14].

Wskazuje to, że proces parowania dotyczy fer-

mionów znajdujących się na sąsiednich moleku-
łach C

60

. Graniczna wielkość zasięgu korelacji jest

taka sama we wszystkich nadprzewodnikach fule-
renowych, a zasięg korelacji, zgodnie z teorią BCS,
zależy od temperatury: ξ ∝ T

−n

c

.

8. Uniwersalny diagram fazowy nad-

przewodnictwa wysokotemperaturowego

Mechanizm nadprzewodnictwa w nadprze-

wodnikach wysokotemperaturowych nie jest do-

POSTĘPY FIZYKI

TOM DODATKOWY 53D

ROK 2002

51

MATERIAŁY XXXVI ZJAZDU FIZYKÓW POLSKICH – TORUŃ 2001 – WYKŁADY PLENARNE

tychczas wyjaśniony. Bezspornie prawidłowy wy-
daje się model parowania, polegający na sil-
nych korelacjach w cieczy fermionów (FL), które
w temperaturze T

∗

= T

LP

tworzą ciecz bozonów

(BL), ulegającą w temperaturze T

c

kondensacji

Bosego–Einsteina (BEC).

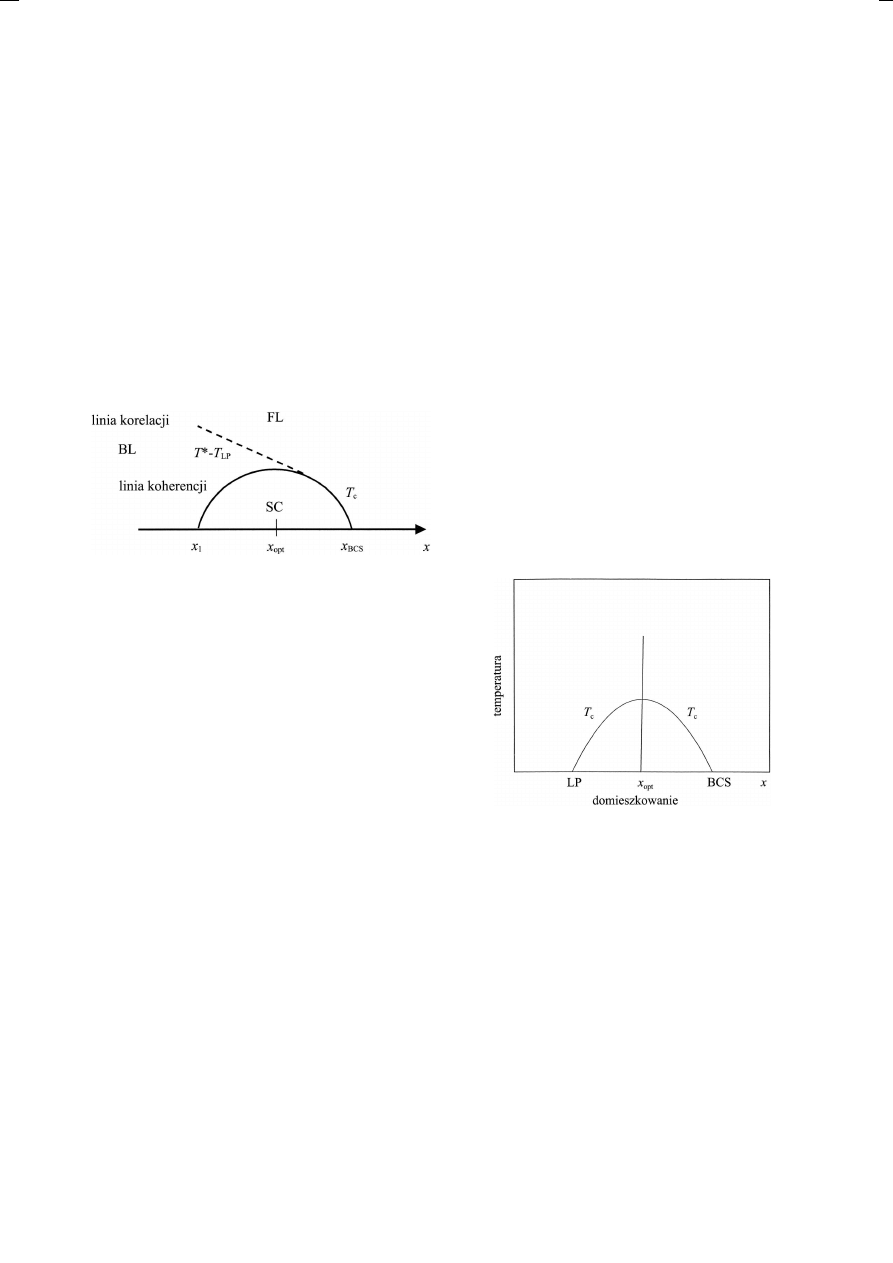
Na diagramie fazowym przedstawionym na

rys. 1 można poprowadzić dwie ważne linie
(rys. 6): l i n i ę k o r e l a c j i dwójkowych, wzdłuż
której elektrony tworzą CP o własnościach bo-
zonów, i

l i n i ę k o h e r e n c j i, poniżej której

występuje kondensat nadprzewodzący (SCBEC),
obejmujący cały kryształ.

Rys. 6. Linie korelacji dwójkowych i synchronizacji ma-
kroskopowej oddzielają obszary FL i BL (LP) oraz FL

i kondensatu SCBEC.

Dla małych koncentracji (x

1

< x < x

opt

) po-

niżej T

∗

= T

LP

fermiony tworzą swobodne bo-

zony, które kondensują poniżej T

c

. W zakresie du-

żych koncentracji nośników (x

opt

< x < x

BCS

)

obydwie linie zbiegają się i T

∗

= T

c

, co oznacza,

że tworzenie się par Coopera (CP) następuje w tej
samej temperaturze, w której pojawia się nad-
przewodzący kondensat. Linię dwójkowych kore-
lacji T

∗

c

można nazwać linią tworzenia się swo-

bodnych kwazicząstek bozonowych, które dopiero
w temperaturze T

c

osiągają spójność funkcji fa-

lowych poszczególnych cząstek i cały makrosko-
powy układ opisuje jedna funkcja falowa. Jest to
istota kondensacji Bosego–Einsteina.

Linie rozdziału między tak określonymi sta-

nami w nadprzewodniku są związane ze spójno-
ścią stanu elektronów. Wzdłuż linii FL–BL wy-
stępują krótkozasięgowe korelacje, gdy w konden-
sacie ich zasięg jest makroskopowy i obejmuje całą
fazę nadprzewodzącą. W zakresie słabych oddzia-
ływań – czyli w zakresie stosowalności teorii BCS
– występuje jedno przejście od FL do BEC w tem-
peraturze T

c

. Dla silnych oddziaływań mamy dwa

przejścia: od FL do BL (ze spinową pseudoszcze-

liną) w temperaturze T

∗

= T

LP

, kiedy powstają

lokalne, nieoddziałujące wzajemnie pary, a do-
piero w T

c

pojawia się nadprzewodnictwo, bo ciecz

bozonów LB przechodzi w kondensat BEC. Sce-
nariusz ten znajduje uzasadnienie w diagramie fa-
zowym proponowanym przez teorię [16,17]. Wy-
stępowanie dwóch temperatur T

∗

i T

c

oraz T

∗

dla x < x

1

zostało potwierdzone doświadczal-

nie w słabo domieszkowanych fulerenach A

x

C

60

(x < 0,5), gdzie A = K lub Rb [18].

9. Efekty ciśnieniowe w HTSC

Obserwowane wartości dT

c

/dp zmieniają się

od wartości dodatnich poprzez zero, czyli czę-
sto obserwowaną niezależność T

c

od ciśnienia, aż

do spotykanych czasem wartości mniejszych od
zera [19]. Taka zależność T

c

od ciśnienia hydro-

statycznego znajduje pełne uzasadnienie w dia-
gramie fazowym nadprzewodników wysokotempe-
raturowych.

Rys. 7. Skalowanie efektu ciśnieniowego po obu stro-

nach x

opt

.

Po obydwu stronach optymalnej koncentra-

cji nośników x

opt

, zgodnie z modelem Micnasa

i in. [16], efekty ciśnieniowe, których miarą jest
współczynnik ciśnieniowy dT

c

/dp, skalują się ina-

czej. Ze wzrostem ciśnienia rośnie całka przeskoku
w rozszerzonym modelu Hubbarda. Dlatego poni-
żej x

opt

współczynnik ciśnieniowy dT

c

/dp jest do-

datni, bo skaluje się jak t

2

/U , a powyżej x

opt

ska-

luje się jak (2zt)

−1

, co sprawia, że jest on ujemny.

W pobliżu T

max

c

współczynnik ciśnieniowy jest

bliski zera. Zatem ciśnienie powoduje podwyż-
szenie T

c

w tym zakresie koncentracji nośników,

gdzie występują dwie temperatury krytyczne T

LP

52

POSTĘPY FIZYKI

TOM DODATKOWY 53D

ROK 2002

MATERIAŁY XXXVI ZJAZDU FIZYKÓW POLSKICH – TORUŃ 2001 – WYKŁADY PLENARNE

i T

c

. Gdy T

LP

= T

c

, współczynnik ciśnieniowy

dT

c

/dp < 0, co oznacza, że T

c

zmniejsza się

ze wzrostem ciśnienia, jak w „klasycznych” nad-
przewodnikach. Taką zależność potwierdziło do-
świadczenie dla kompozytu YBCO–PZT, gdzie
zaobserwowano zarówno dodatnie jak i ujemne
współczynniki ciśnieniowe temperatury krytycz-
nej T

c

[20]. Pokazano, że współczynnik ciśnie-

niowy w zależności od koncentracji dziur może
być dodatni dla zakresu poddomieszkowania lub
ujemny w zakresie naddomieszkowania, co po-
twierdza różne skalowanie efektu ciśnieniowego
w tych dwóch zakresach x, przewidziane przez
teorię.

10. Zakończenie

Ostatnio opublikowane prace Abrikosowa [17]

dotyczące zjawiska nadprzewodnictwa wysoko-
temperaturowego pokazują, że silne fluktuacje wy-
stępują w zakresie małych koncentracji nośników,
podczas gdy w dużym zakresie gęstości nośni-
ków można je pominąć. Fluktuacje będące powo-
dem powstania obszaru pseudoszczeliny na dia-
gramie fazowym HTSC, są związane z linią kore-
lacji na rys. 6 i warunkują pojawienie się tempera-
tury T

∗

, poniżej której występują nieoddziałujące

pary lokalne tworzące ciecz o właściwościach bozo-
nowych. Można na koniec sformułować przypusz-
czenie, że właściwości cieczy fermionów w stanie
normalnym są związane z niejednorodnością roz-
kładu ładunku w krysztale. Obszar „pseudoszcze-
liny” jest tożsamy z cieczą quasi-bozonów, w któ-
rym występuje przerwa spinowa, a nie występuje
przerwa ładunkowa obejmująca cały nadprzewod-
nik. Dlatego w tym obszarze pojawiają się skom-
plikowane struktury wykazujące obecność fal gę-
stości: ładunku (CDW) lub spinu (SDW).

Wydaje się, że zależność T

c

(x) przedstawiona

na rys. 1 i 6 ma charakter uniwersalny i wszel-
kie teorie uwzględniające fluktuacje spinowe oraz
ładunkowe w HTSC zbliżają nas do zrozumienia

zjawiska nadprzewodnictwa wysokotemperaturo-
wego.

Literatura

[1] P.W. Anderson, Science 228, 480 (2000).
[2] J.H. Schoen, Ch. Kloc, B.Batlogg, Nature 408, 549

(2000).

[3] P.B. Allen, Nature 405, 1007 (2000); O. Gunnarsson,

J.E. Han, tamże, s. 1027.

[4] S.A. Kivelson, D. Rokhsar, Phys. Rev. B 41, 11693

(1990).

[5] A.F. Hebard, T.T.M. Palstra, R.C. Haddon, R.M.

Fleming, Phys. Rev. B 48, 9945 (1993).

[6] Y. Koike, H. Suematsu, K. Higuchi, S. Tanuma, Phy-

sica B 99, 503 (1980).

[7] R. da Silva, J.H.S. Torres, Y. Kopelevich, Phys. Rev.,

w druku.

[8] K. Antonowicz, Nature 247, 358 (1974).
[9] Z. Zhang, Chia-Chung Chen, S.P. Kelty, H. Dai,

C.M. Lieber, Nature 353, 333 (1991).

[10] K. Holczer, R.W. Whetten, „Superconducting and

Normal State Properties of the A

3

C

60

Compounds”,

w: The Fullerenes, red. H.W. Kroto, J.E. Fischer,
D.E. Cox (Pergamon Press, 1993), s. 123.

[11] J. Stankowski, T. Luty, W. Kempiński, L. Piekara-

-Sady, Solid State Science 3, 531 (2001).

[12] J. Stankowski, L. Piekara-Sady, W. Kempiński, Appl.

Magn. Res. 19, 539 (2000).

[13] L. Kouwenhhoven, Nature 407, 35 (2000); H. Park

i in., tamże, s. 57.

[14] J.H. Schoen, Ch. Kloc, B. Batlogg, Science 293, 2432

(2001).

[15] T. Yidirm i in., Solid State Commun. 93, 269 (1995);

M.J. Rosseinsky, J. Matter. Chem. 5, 1497 (1995).

[16] R. Micnas, S. Robaszkiewicz, w: High T

c

Supercon-

ductivity 1996; Ten Years after The Discovery, red.
E. Kaldis, E. Liarokapis, K.A. M¨

uller (Kluwer Ac.

Publ., 1996).

[17] A.A. Abrikosov, Phys. Rev. B 63, 134518 (2001);

tamże 64, 104521 (2001).

[18] J. Stankowski, L. Piekara-Sady, W. Kempiński, Phys.

Rev. B, w druku.

[19] R. Griessen, Phys. Rev. B 36, 5284 (1987); A. Dries-

sen i in., tamże, s. 5602.

[20] M. Krupski, J. Stankowski, S. Przybył, B. Andrzejew-

ski, A. Kaczmarek, B. Hilczer, J. Marfaing, C. Cara-
noni, Physica C 320, 120 (1999).

POSTĘPY FIZYKI

TOM DODATKOWY 53D

ROK 2002

53