50 Â

WIAT

N

AUKI

Paêdziernik 1996

J

edno z najbardziej niezwyk∏ych spo-
tkaƒ fizyków odby∏o si´ 18 marca
1987 roku podczas posiedzenia

American Physical Society. Pospiesznie
zorganizowana, obfitujàca w doniesie-
nia zg∏oszone ju˝ po terminie, konferen-
cja zgromadzi∏a w hotelu Hilton w No-
wym Jorku 2 tys. uczestników. St∏oczeni
w sali balowej i przyleg∏ym holu usi∏o-
wali wys∏uchaç pi´ciominutowych wy-
stàpieƒ o najnowszych koncepcjach i ba-
daniach oraz sami zabraç g∏os. Spo-
tkanie, które zyska∏o miano Woodstock
fizyki, rozpocz´∏o si´ o wpó∏ do ósmej
wieczorem i trwa∏o do trzeciej nad ra-

nem, a napi´cie odczuwa∏o si´ do ostat-
niej chwili.

Powodem tego naukowego szaleƒ-

stwa by∏o odkrycie wysokotemperatu-
rowego nadprzewodnictwa. Pod koniec
1986 roku J. Georg Bednorz i K. Alexan-
der Müller z Laboratorium Badawcze-
go IBM w Zurychu stwierdzili, ˝e cera-
miczna substancja – tlenek miedzio-
wo-barowo-lantanowy – traci opór elek-
tryczny w temperaturze –238°C, czyli
35 K. Ta bardzo ju˝ niska temperatura
jest jednak o ponad 10 stopni wy˝sza
ni˝ w przypadku najlepszych znanych
nadprzewodników konwencjonalnych,

które sà metalicznymi pierwiastkami al-
bo stopami. Wkrótce pojawi∏y si´ licz-
ne doniesienia o temperaturze krytycz-
nej wy˝szej ni˝ 90 K, a zamieszanie
wywo∏a∏y komunikaty o nadprzewod-
nictwie w temperaturze 130 i 240 K.
Gdyby odkryto substancj´ nadprzewo-
dzàcà w temperaturze bliskiej pokojo-
wej (oko∏o 300 K), by∏by to prawdopo-
dobnie poczàtek prawdziwej rewolucji
technicznej we wspó∏czesnym Êwiecie.

Podczas tego marcowego spotkania fi-

zycy przedstawili prace poÊwi´cone teo-
rii nowych nadprzewodników i wyko-
nanym doÊwiadczeniom. Jego szalona

Nadprzewodniki

wysokotemperaturowe

pod mikroskopem

Najnowsze doÊwiadczenia wykorzystujàce subtelne efekty kwantowe dostarczajà

wa˝nych informacji o nadprzewodnictwie niektórych materia∏ów ceramicznych

John R. Kirtley i Chang C. Tsuei

CLIFFORD A. PICKOVER

IBM Research

Â

WIAT

N

AUKI

Paêdziernik 1996 51

atmosfera by∏a spowodowana nie tylko
marzeniami o nadprzewodnictwie w
temperaturze pokojowej, ale tak˝e stra-
chem. Niektórzy bali si´, ˝e nowe mate-
ria∏y, cz´sto zwane miedzianami, zosta-
nà zbadane, zanim oni wniosà swój
osobisty znaczàcy wk∏ad. Poza tym za
badania w dziedzinie nadprzewodnic-
twa przyznano jak dotàd najwi´cej Na-
gród Nobla – pi´ç. Prawid∏owa teoria no-
wych nadprzewodników z pewnoÊcià
równie˝ tak zostanie uhonorowana.

DziÊ ju˝ wiadomo, ˝e nie by∏o powo-

dów do zmartwienia. W ciàgu ostatnich
9 lat tysiàce badaczy na ca∏ym Êwiecie
poÊwi´ci∏o miliony godzin, poszukujàc
odpowiedzi na pytanie, dlaczego i jak
miedziany nadprzewodzà w tak wyso-
kiej temperaturze. Mimo znacznego po-
st´pu oba pytania wcià˝ pozostajà bez
odpowiedzi. Dzi´ki wykonanym ostat-
nio doÊwiadczeniom wykazano, ˝e
zwiàzki te ró˝nià si´ istotnie od tradycyj-
nych nadprzewodników, i okreÊlono
kierunki badaƒ teoretycznych. Okaza-
∏o si´, ˝e jeden z postulowanych mecha-
nizmów – fluktuacje magnetyczne
w atomach tworzàcych przewodzàcy
oÊrodek – jest wielce prawdopodobny.

Przewodzenie a pary Coopera

Poglàd, ˝e sednem sprawy mo˝e byç

magnetyzm, jest sprzeczny z dobrze
ugruntowanym zrozumieniem w∏aÊci-
woÊci konwencjonalnych niskotempe-
raturowych nadprzewodników. Takie
nadprzewodnictwo pojawia si´ wtedy,
gdy elektrony ∏àczà si´ w tzw. pary Coo-
pera (od nazwiska fizyka Leona N. Coo-
pera, który pracujàc w University of
Illinois, pierwszy opisa∏ w∏aÊciwoÊci ta-
kich tworów). Pary Coopera, w odró˝-
nieniu od pojedynczych elektronów, nie
zderzajà si´ ze sobà i nie sà rozpraszane
przez defekty oÊrodka przewodzàcego
pràd. Dzi´ki temu mo˝liwy jest prze-
p∏yw pràdu bez oporu. Pràd elektrycz-
ny w nadprzewodniku p∏ynie bez przy-
∏o˝onego napi´cia, a jeÊli obwód ma
kszta∏t p´tli – b´dzie p∏ynàç zawsze,
a wi´c dopóty, dopóki temperatura nad-
przewodnika nie wzroÊnie do tempera-
tury krytycznej.

To niezwyk∏e, ˝e elektrony w meta-

lu mogà ∏àczyç si´ w pary, chocia˝ jako
ujemnie na∏adowane zazwyczaj si´ od-
pychajà. W latach pi´çdziesiàtych Coo-
per oraz jego koledzy – John Bardeen

i J. Robert Schrieffer – wyja-
Ênili to zjawisko. Teoria BCS,
nazwana tak na ich czeÊç,
g∏osi, ˝e elektrony w kon-
wencjonalnym nadprzewod-
niku przezwyci´˝ajà odpy-
chanie na dwa sposoby. Po
pierwsze, ich ∏adunek jest
cz´Êciowo neutralizowany
wskutek „ekranowania” wy-
wo∏anego ruchem innych
elektronów, dzi´ki czemu
maleje si∏a oddzia∏ywania.
Po drugie – i to jest wa˝niej-
sze – istniejà poÊrednicy,
którzy ∏àczà odpychajàce si´ elektrony.
Tymi swatami sà dodatnio na∏adowa-
ne jony atomów tworzàcych nadprze-
wodnik. (Oboj´tne atomy stajà si´ do-
datnimi jonami, gdy oderwà si´ od nich
elektrony przewodzàce pràd.) Porusza-
jàcy si´ elektron mo˝e nieznacznie prze-
sunàç napotkany po drodze jon. Dzi´-
ki takim odkszta∏ceniom, czyli fononom,
tworzà si´ ma∏e obszary o nadmiarze
dodatniego ∏adunku, który przyciàga
inne elektrony. Analogià mo˝e byç za-
chowanie kul bilardowych na matera-
cu: jedna kula wgniata materac, co po-
woduje zbli˝anie si´ drugiej.

Na tym jednak podobieƒstwo si´ koƒ-

czy, bo elektronowe kule bilardowe sil-
nie si´ odpychajà. Lepszà analogi´ poda∏
Bardeen. Wyobraêmy sobie t∏um prze-
pychajàcych si´ ludzi st∏oczonych na
p∏ycie stadionu. Par´ Coopera mo˝emy
przedstawiç jako dwie osoby rozpacz-
liwie starajàce si´ trzymaç razem. Gdy
t∏um zaczyna si´ przesuwaç, trudno nad
nim zapanowaç, zatrzymanie bowiem
jednej osoby wymaga zatrzymania wie-
lu innych. Ma∏e przeszkody nieznacz-
nie wp∏ywajà na ruchy poszczególnych
ludzi w t∏umie.

Fizycy powiadajà, ˝e elektrony ∏à-

czà si´ w pary, wymieniajàc mi´dzy so-
bà fonony, tak jak p´dzàcy do bramki
rugbiÊci podajà sobie pi∏k´. W ramach
teorii BCS nadprzewodnictwo konwen-
cjonalne da si´ doskonale wyt∏umaczyç
mechanizmem tworzenia si´ par z
udzia∏em fononów.

Badacze sà jednak przekonani, ˝e

w ten sposób nie mo˝na wyjaÊniç nad-
przewodnictwa w materia∏ach ceramicz-
nych. Aby teoria BCS opisywa∏a nad-
przewodnik o wysokiej temperaturze
krytycznej, sprz´˝enie elektronów z fo-
nonami musi byç bardzo silne. Jednak

wówczas struktura materia∏u by∏aby tak
zdeformowana, ˝e nie móg∏by on byç
nadprzewodnikiem, a nawet zwyk∏ym
przewodnikiem.

Co wi´cej, teoria BCS zak∏ada, ˝e

energia elektronów jest du˝o wi´ksza
ni˝ energia fononów. Elektrony poru-
szajà si´ znacznie szybciej ni˝ fonony,
elektron zatem oddala si´ na du˝à odle-
g∏oÊç od przesuni´tego jonu, zanim do-
trze tam drugi elektron. Ta du˝a odle-
g∏oÊç mi´dzy elektronami zmniejsza si∏´
wzajemnego odpychania. W nadprze-
wodzàcych ceramikach elektrony i fo-
nony poruszajà si´ jednak z porówny-
walnà pr´dkoÊcià i odleg∏oÊç mi´dzy
elektronami tworzàcymi par´ nie mo˝e
byç du˝a. (Mówimy tu o elektronach ja-
ko noÊnikach pràdu, choç naprawd´
w wi´kszoÊci miedzianów pràd prze-
wodzà „dziury”, czyli czàstki dodatnio
na∏adowane. Dziury powstajà, gdy ma-
teria∏ jest domieszkowany atomami
„wysysajàcymi” cz´Êç elektronów. W
dalszej cz´Êci artyku∏u, mówiàc o pa-
rach Coopera, b´dziemy pos∏ugiwaç si´
poj´ciem „noÊnik” zamiast „elektron”.)

Ze wzgl´du na trudnoÊci w opisie

nadprzewodnictwa wysokotemperatu-
rowego z udzia∏em fononów próbowa-
no zastàpiç je innymi poÊrednikami –
„pi∏kami” rzucanymi przez „graczy
w rugby”. Zamiast fononów propono-
wano ekscytony, które mia∏yby poru-
szaç otaczajàcà je chmur´ ∏adunku, pla-
zmony – kolektywne wzbudzenia
noÊników pràdu, i polarony, w których
powstajà znaczne odkszta∏cenia sie-
ci krystalicznej i zaburzenia ruchu in-
nych noÊników. Pojawi∏y si´ te˝ mode-
le traktujàce ka˝dy ∏adunek jak dwie
czàstki, które mogà przeskakiwaç mi´-
dzy p∏aszczyznami atomów tworzàcych
nadprzewodnik.

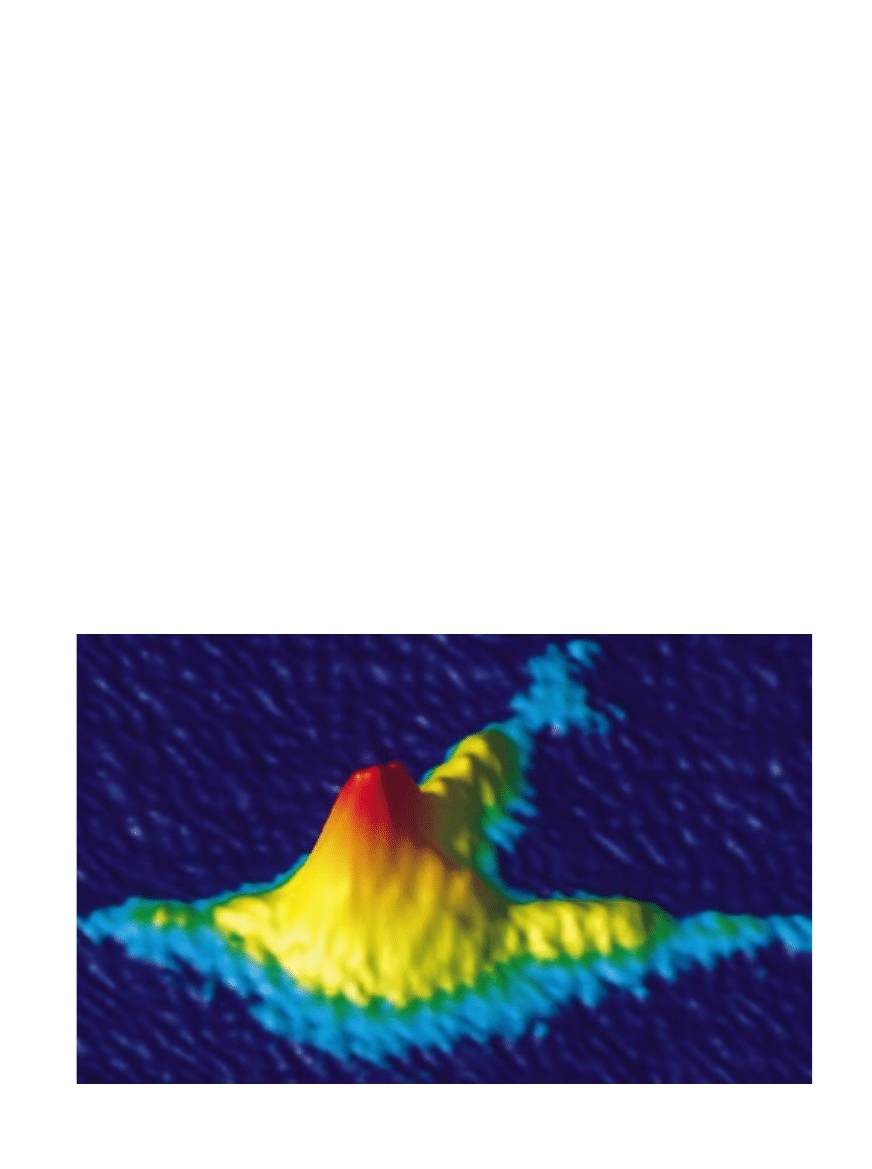
STRUMIE¡ MAGNETYCZNY przenika przez trzy granice ziaren krystalicz-
nych cienkiej warstwy nadprzewodnika

(na stronie obok). ObecnoÊç tzw. po-

∏ówkowego kwantu strumienia wskazuje na g∏´bokie fizyczne podstawy nad-
przewodnictwa wysokotemperaturowego, dzi´ki któremu zostanà mo˝e kiedyÊ
skonstruowane lewitujàce pociàgi. Fotografia po prawej stronie ukazuje ma-
gnes unoszàcy si´ nad nadprzewodnikiem, który zawiera itr.

IBM RESEARCH

czyli typu s. Oznacza to, ˝e znalezienie
jednego z noÊników tworzàcych par´
Coopera w zadanej odleg∏oÊci od dru-
giego maleje (wyk∏adniczo) jednakowo
we wszystkich kierunkach. GdybyÊmy
wykreÊlili funkcj´ falowà, traktujàc je-
den z noÊników jako poczàtek uk∏adu
wspó∏rz´dnych, wówczas powierzch-
nia opisujàca zadane prawdopodobieƒ-
stwo znalezienia drugiego noÊnika mia-
∏aby kszta∏t sfery.

W przypadku miedzianów kolejnym

stanem o wysokiej symetrii jest syme-
tria typu d. Wykres funkcji falowej te-
go stanu przypomina le˝àcà na p∏asz-
czyênie czterolistnà koniczyn´. Ka˝dy
listek oznacza obszar, w którym mo˝e
znajdowaç si´ jeden ze sk∏adników pa-
ry Coopera, podczas gdy drugi zajmu-
je po∏o˝enie centralne. Symetria typu d
oznacza te˝, ˝e partnerzy w parze Coo-
pera nie sà tak blisko siebie, aby ich wza-
jemne odpychanie by∏o znacznie silniej-
sze ni˝ przyciàganie.

W jaki sposób okreÊlenie symetrii sta-

nu nadprzewodzàcego mo˝e u∏atwiç
odkrycie mechanizmu odpowiedzialne-
go za tworzenie par Coopera? Okazuje
si´, ˝e proponowane mechanizmy pro-
wadzà do ró˝nej symetrii. Kilka lat te-
mu wi´kszoÊç teoretyków dzieli∏a si´,
z grubsza rzecz bioràc, na dwie grupy.
Jedni opowiadali si´ za mechanizmami
prowadzàcymi do symetrii typu s;
w przewa˝ajàcej mierze ich teorie by∏y
próbà modyfikacji teorii BCS odwo∏u-
jàcej si´ do wymiany fononów. Inni ba-
dali procesy prowadzàce do symetrii ty-
pu d, co wymaga∏o istotnych zmian
podstawowych koncepcji stanu nad-
przewodzàcego.

SpoÊród teorii prowadzàcych do sy-

metrii typu d najwi´kszà chyba popu-
larnoÊç zdoby∏a ta, która odwo∏uje si´ do
modelu fal spinowych. Jej g∏ównymi
twórcami sà Douglas J. Scalapino z Uni-
versity of California w Santa Barbara
i David Pines z University of Illinois. We-
d∏ug tej teorii poruszajàcy si´ ∏adunek
wp∏ywa na orientacj´ spinu atomów two-
rzàcych nadprzewodnik i pozostawia za
sobà zaburzenie pola magnetycznego (fa-
l´ spinowà). Fala ta przyciàga drugi no-
Ênik, co powoduje powstanie pary Coo-
pera. Czas ˝ycia fal spinowych jest bar-
dzo krótki, dlatego czasami nazywane
sà one fluktuacjami spinu.

Wielu fizyków sàdzi∏o, ˝e symetria

stanu nadprzewodzàcego mo˝e roz-
strzygaç o s∏usznoÊci danej teorii. Ale
sprawa nie jest tak prosta, teoretycy bo-
wiem odkryli w ciàgu ostatnich paru lat,
˝e ró˝ne mechanizmy mogà prowadziç
do identycznej symetrii. OkreÊlenie za-
tem symetrii nie przesàdza jeszcze o od-
rzuceniu mechanizmu. Mówiàc dok∏ad-
niej, doÊwiadczalne okreÊlenie symetrii
pozwoli∏oby teoretykom udoskonaliç
proponowane teorie. Na przyk∏ad wy-
kazanie, ˝e stan nadprzewodzàcy nie
ma symetrii d, wyeliminowa∏oby mo-
del fal spinowych.

Âlady fal o symetrii d

Jednà z w∏aÊciwoÊci fal d, którà mo˝-

na badaç doÊwiadczalnie, jest s∏absze
zwiàzanie par Coopera w pewnych
(okreÊlonych przez struktur´ krystalo-
graficznà) kierunkach ni˝ w innych. Je-
Êli tak jest w istocie, to nale˝y spodzie-
waç si´ obecnoÊci pojedynczych noÊni-
ków poruszajàcych si´ w niektórych kie-
runkach. Przeprowadzono wiele ekspe-
rymentów majàcych na celu wykrycie
tych ∏adunków. Sprawdzano, jak g∏´bo-
ko pole magnetyczne wnika do nad-
przewodnika i jak wiele ciep∏a potrze-
ba, aby zwi´kszyç temperatur´ materia-
∏u. W ogólnoÊci wyniki doÊwiadczeƒ po-
twierdzajà obecnoÊç nie sparowanych
noÊników w niskiej temperaturze, ale
nie przekonujà wi´kszoÊci fizyków. Te-
sty te nie by∏y bowiem bezpoÊrednie,
a wyniki cz´sto dawa∏o si´ wyjaÊniç za
pomocà stanów o innej symetrii (w tym
równie˝ zmodyfikowanych stanów s).

Niektórzy fizycy wi´c, zamiast po-

szukiwaç pojedynczych noÊników, pró-
bowali wyznaczyç kàtowà zale˝noÊç si-
∏y wià˝àcej par´ Coopera. Pomiary te
polega∏y na okreÊleniu, jak promienio-
wanie o du˝ej energii wyrywa noÊniki
z nadprzewodnika, jak zmienia si´ d∏u-
goÊç fali Êwietlnej przenikajàcej nadprze-
wodnik i jak elektrony tunelujà z innych
materia∏ów do nadprzewodnika przez
cienkà izolujàcà barier´.

Badania te wykaza∏y istnienie zale˝-

noÊci si∏y sprz´˝enia pary od kàta, a mi-
mo to nie mog∏y byç dowodem istnie-
nia stanów o symetrii d. Sàsiadujàce ze
sobà listki funkcji typu d ró˝nià si´ zna-
kiem: w obszarze dwóch z nich funkcja
jest dodatnia, a pozosta∏ych dwóch –
ujemna. Przeprowadzane testy nie by-
∏y czu∏e na znak funkcji, ich wyniki za-
tem nie stanowi∏y przekonujàcego do-
wodu zwyci´stwa symetrii typu d.

Jest jednak sposób okreÊlenia znaku

listków funkcji falowej. W metodzie tej
wykorzystuje si´ dobrze znany efekt pu-
∏apkowania pola magnetycznego we-

52 Â

WIAT

N

AUKI

Paêdziernik 1996

Struktura krystalograficzna miedzia-

nów jest niestety bardzo skomplikowa-
na. Ich komórka elementarna sk∏ada si´
z kilku warstw atomów izolujàcych
p∏aszczyzny miedziowo-tlenowe, stano-
wiàce zasadniczà cz´Êç obszaru przewo-
dzàcego. Nie wymyÊlono ˝adnego spo-
sobu rozró˝nienia mechanizmów two-
rzenia si´ par noÊników ani nawet nie
uzgodniono koncepcji takiego testu.
Osiàgni´to jednak post´p w zakresie co
najmniej jednej fundamentalnej cechy
stanu nadprzewodzàcego – symetrii, któ-
ra mo˝e okazaç si´ papierkiem lakmu-
sowym testu wyjaÊniajàcego, w jaki spo-
sób noÊniki ∏àczà si´ w pary.

Symetria funkcji falowej

Chodzi tu o symetri´ obecnà w mate-

matycznym opisie stanu nadprzewodzà-
cego, czyli w funkcji falowej nadprze-
wodnika. Funkcja ta okreÊla m.in., jak
poruszajà si´ wzgl´dem siebie dwa no-
Êniki tworzàce par´ Coopera, i pozwala
obliczyç prawdopodobieƒstwo znalezie-
nia jednego noÊnika w danej odleg∏oÊci
od drugiego.

W konwencjonalnym nadprzewodni-

ku funkcja falowa pary Coopera ma naj-
wy˝szà mo˝liwà symetri´: sferycznà,

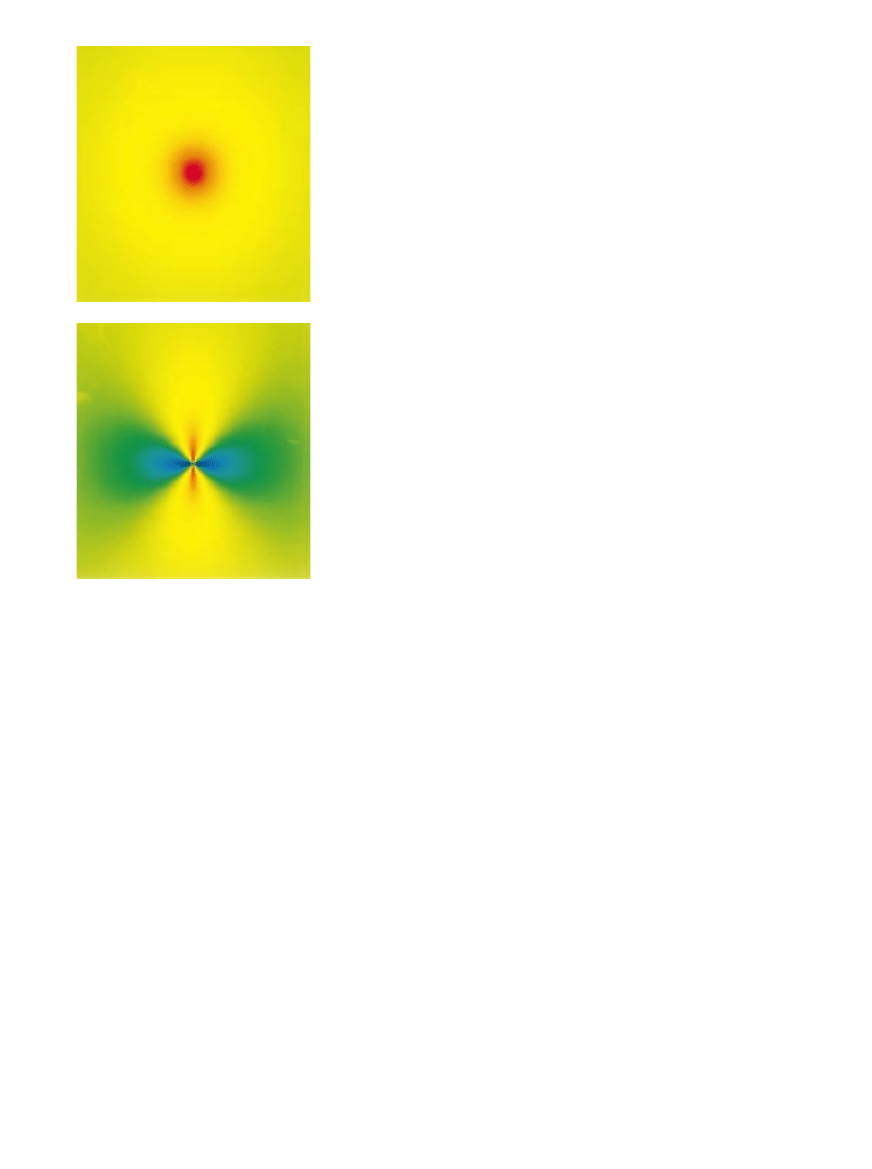
DWA TYPY SYMETRII funkcji falowej sta-
nu nadprzewodzàcego: s i d. W przypadku
funkcji typu s jeden z partnerów w parze
Coopera znajduje si´ w sferycznym otocze-
niu drugiego. W przypadku funkcji o syme-
trii d obszar ten przybiera kszta∏t przy-
pominajàcy czterolistnà koniczyn´, której
dwa listki majà znak ujemny

(niebieski),

a dwa pozosta∏e dodatni

(˝ó∏to-czerwony).

JOHN R. KIRTLEY

SYMETRIA TYPU S

SYMETRIA TYPU D

wnàtrz nadprzewodzàcego pierÊcienia.
Wiadomo te˝, ˝e pu∏apkowany strumieƒ
jest wielokrotnoÊcià okreÊlonej jednost-
ki zwanej kwantem strumienia, który
mo˝na wyobra˝aç sobie jako rurk´ z po-
lem magnetycznym. Ca∏kowity strumieƒ
pola magnetycznego w rurce (iloczyn in-
dukcji pola magnetyczngo i powierzch-
ni przekroju poprzecznego rurki) jest sta-
∏à fundamentalnà, równà h/2e, gdzie h
jest sta∏à Plancka, a e – ∏adunkiem elektro-
nu. PierÊcienie wykonane z konwencjo-
nalnych nadprzewodników o funkcjach
falowych typu s zawierajà ca∏kowità licz-
b´ kwantów strumienia.

PierÊcienie wykonane z nadprzewod-

nika o stanach typu d mogà jednak
kwantowaç strumieƒ w inny sposób.
Obliczenia wykazujà, ˝e w zale˝noÊci
od energii uk∏adu i strumienia pola ma-
gnetycznego jego wielkoÊç mo˝e byç
ca∏kowità wielokrotnoÊcià po∏owy
kwantu strumienia. Okazuje si´, ˝e
obecnoÊç takiej kwantyzacji strumienia

albo jej brak wyznacza, czy i w jaki spo-
sób listki funkcji falowej zmieniajà znak.

Fizycy eksperymentatorzy zdo∏ali za-

obserwowaç po∏ówki kwantu strumie-
nia magnetycznego zaledwie przed trze-
ma laty, choç ich istnienie przewidzia∏
ju˝ pod koniec lat siedemdziesiàtych
Lew N. Bu∏ajewskij z Instytutu Lebie-
diewa w Rosji (obecnie pracuje w Los
Alamos National Laboratory) i inni.

Pierwsze wskazówki przynios∏y po-

miary namagnesowania wykonane
w 1993 roku przez Dietera Wohllebena
z Uniwersytetu Koloƒskie-
go. Póêniej Dave Wollman
i Dale van Harlingen z
University of Illinois do-
starczyli znacznie bardziej
przekonujàcych dowodów,
przedstawiajàc pomiary
charakterystyk pràdowo-
-napi´ciowych pierÊcieni
nadprzewodzàcych wyko-
nanych z monokryszta∏u

tlenku itrowo-barowo-miedziowego
(YBCO) i cienkiej warstwy o∏owiu.

Nasza grupa przeprowadzi∏a ostat-

nio w laboratorium IBM pierwsze ob-
serwacje po∏ówek kwantu strumienia.
WykorzystaliÊmy zaprojektowane spe-
cjalnie w tym celu pierÊcienie wykona-
ne z miedzianów z wbudowanymi cien-
kimi warstwami izolatora. Te izolujàce
bariery zwane z∏àczami Josephsona sà
tak cienkie, ˝e umo˝liwiajà tunelowa-
nie par Coopera. Zjawisko to nosi na-
zw´ efektu Josephsona od nazwiska

Â

WIAT

N

AUKI

Paêdziernik 1996 53

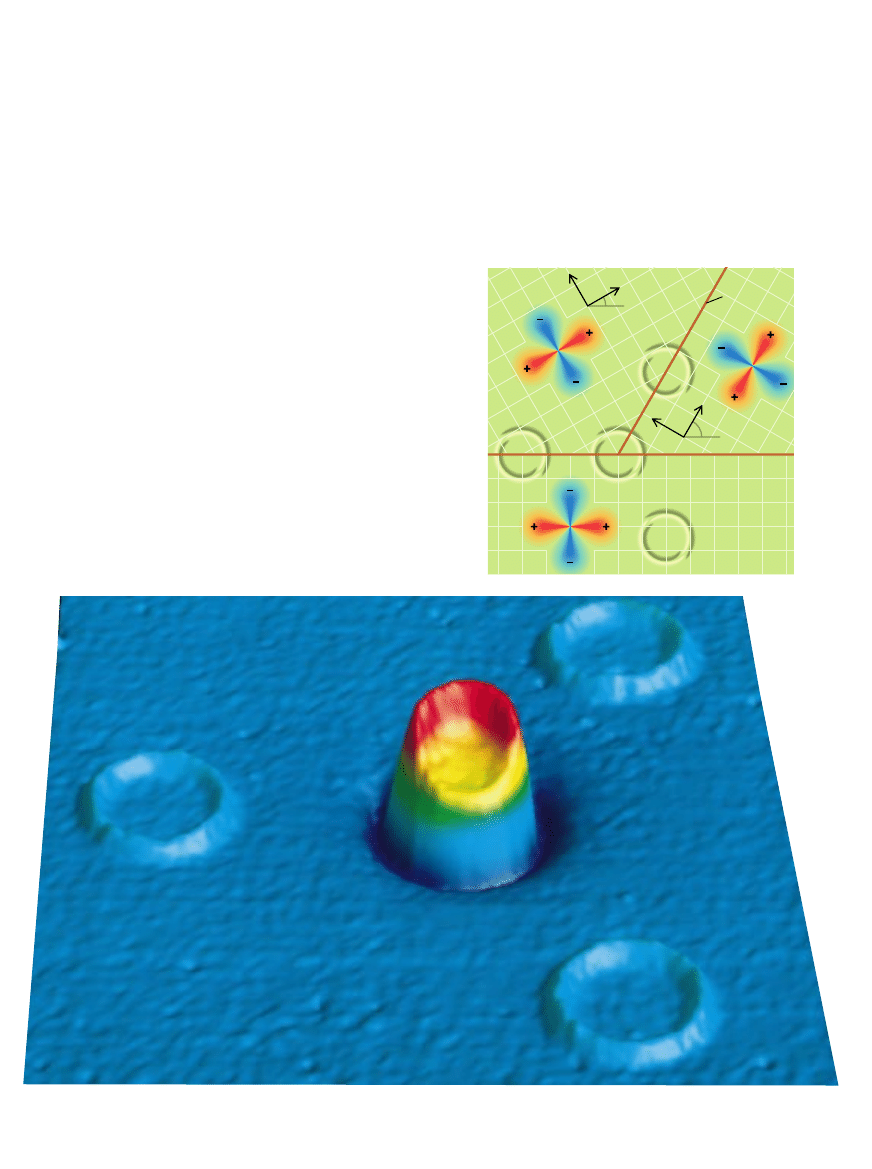
DOÂWIADCZENIE Z „POTRÓJNYM KRYSZTA¸EM” sprawdzajàce hipo-
tez´ o istnieniu funkcji o symetrii d

(z prawej). Granice trzech obszarów

nadprzewodnika zawierajàcego itr tworzà z∏àcza Josephsona. Wytrawione
pierÊcienie zawierajà trzy, dwa z∏àcza Josephsona lub wcale ich nie majà.
JeÊli funkcja falowa nadprzewodnika jest typu d, to wewnàtrz pierÊcienia
z trzema z∏àczami powinien byç zamkni´ty strumieƒ równy po∏owie kwan-
tu strumienia, strumieƒ zaÊ w pierÊcieniach o parzystej liczbie z∏àczy – rów-
ny zeru. Obraz po∏owy kwantu strumienia

(poni˝ej) dowodzi, ˝e teorie po-

winny opisywaç stan nadprzewodzàcy za pomocà funkcji typu d.

60°

30°

TRZY
Z¸ÑCZA

BRAK Z¸ÑCZA

DWA
Z¸ÑCZA

DWA

Z¸ÑCZA

Z¸ÑCZE
JOSEPHSONA

JARED SCHNEIDMAN DESIGN

CLIFFORD A. PICKOVER

IBM Research

Briana Josephsona, laureata Nagrody
Nobla, który przewidzia∏ je w 1962 roku.

Efekt Josephsona zachodzi tylko wte-

dy, gdy pary Coopera po jednej stronie
z∏àcza „sà w przeciwfazie” z parami po
drugiej stronie. „Faza” jest jednà z cech
funkcji falowej (okreÊla, z grubsza rzecz
bioràc, w jakiej cz´Êci okresu drgaƒ jest
w∏aÊnie funkcja). Majàc nadprzewod-
nik o funkcji falowej typu d, mo˝na za-
projektowaç pierÊcienie ze z∏àczami Jo-
sephsona, które automatycznie zmienia-
jà faz´ krà˝àcych par Coopera. Ta zmia-
na fazy jest równowa˝na odwróceniu
znaku funkcji falowej.

PierÊcieƒ wokó∏ strumienia

Tak wi´c dzi´ki wbudowanej zmianie

znaku w ozi´bianym pierÊcieniu pop∏y-
nie spontanicznie pràd otaczajàcy stru-
mieƒ o wartoÊci równej dok∏adnie po∏o-
wie kwantu strumienia. W pierÊcieniu
ozi´bianym w polu magnetycznym zo-
stanie uwi´ziony strumieƒ o wartoÊci
3/2, 5/2, 7/2 itd. kwantu strumienia.

WytworzyliÊmy pierÊcienie nadprze-

wodnika itrowego na specjalnie przy-
gotowanym pod∏o˝u w taki sposób, ˝e
ka˝dy pierÊcien obejmowa∏ trzy sektory.
Ka˝dy sektor by∏ obrócony wzgl´dem
sàsiedniego o 30°, tak ˝e wszystkie gra-
nice utworzy∏y z∏àcza Josephsona. Gdy-
by pary Coopera mia∏y symetri´ d,
wówczas funkcja falowa ka˝dej pary
zmienia∏aby znak po okrà˝eniu pierÊcie-
nia. (Nie wiemy naprawd´, ile razy
funkcja zmienia znak, poza tym ˝e dla
takiej geometrii pierÊcienia musi to za-
chodziç nieparzystà liczb´ razy.)

Z drugiej strony, gdyby funkcja mia-

∏a symetri´ typu s, czyli sta∏y znak, obec-
noÊç granic sektorów by∏aby bez zna-
czenia. Funkcja falowa nie zmienia∏aby
si´ po okrà˝eniu pierÊcienia.

Wytworzone z „trójkryszta∏u” pier-

Êcienie o Êrednicy oko∏o 50

mm ozi´bia-

liÊmy nast´pnie do temperatury ni˝szej
ni˝ krytyczna. Z powodu swej geometrii
pierÊcienie by∏y oczywiÊcie niestabilne,
bioràc pod uwag´ przewodnictwo,
i spontanicznie pojawia∏ si´ w nich ma-

54 Â

WIAT

N

AUKI

Paêdziernik 1996

∏y pràd nadprzewodzàcy. W pewnym
sensie pierÊcieƒ zachowuje si´ tak, jakby
by∏ skr´cony we wst´g´ Möbiusa. Ten-
dencja do „rozkr´cenia” wst´gi sprawia,
˝e ∏adunki zaczynajà si´ poruszaç.
StwierdziliÊmy, ˝e w pierÊcieniu zna-
jdujà si´ tylko po∏ówkowe wartoÊci stru-
mienia. To oczywisty dowód symetrii
typu d (w przypadku funkcji falowej o
symetrii s w pierÊcieniu w ogóle nie
by∏oby strumienia).

ZobrazowaliÊmy rozk∏ad pola magne-

tycznego w pierÊcieniu za pomocà mi-
kroskopu skaningowego z interferome-
trem kwantowym. Interferometr kwan-
towy jest najwra˝liwszym czujnikiem
pola magnetycznego [patrz: John Clar-
ke, „Interferometry kwantowe”; Âwiat
Nauki, paêdziernik 1994]. Staranna kali-
bracja sygna∏u z interferometru wykaza-
∏a na wiele sposobów, ˝e mamy do czy-
nienia z dok∏adnie po∏owà kwantu
strumienia w „trójkrystalicznym pier-
Êcieniu”. Wykonane dla porównania
pierÊcienie z parzystà liczbà z∏àczy nie
obejmowa∏y ˝adnego strumienia (ponie-
wa˝ znak zmienia∏ si´ parzystà liczb´ ra-
zy i powraca∏ do poczàtkowej wartoÊci).

ZmienialiÊmy równie˝ warunki do-

Êwiadczenia, aby upewniç si´, ˝e otrzy-
mane wyniki sà na pewno okreÊlone
przez symetri´ funkcji falowej pary Coo-
pera, a nie inne efekty. WykazaliÊmy, ˝e
niewielkie zmiany geometrii pierÊcienia
powodujà spontaniczne pojawianie si´
i znikanie po∏ówkowych wartoÊci stru-
mienia. Przyk∏adajàc s∏abe pole magne-
tyczne, stwierdziliÊmy, ˝e pozosta∏e pier-
Êcienie obejmowa∏y ca∏kowità wielokrot-
noÊç kwantów strumienia, co oznacza-
∏o, ˝e wszystkie pierÊcienie dzia∏a∏y pra-
wid∏owo. DoÊwiadczenia wykonane na
cienkich warstwach, kropkach i pierÊcie-
niach, których geometria nie by∏a spe-
cjalnie dobierana, potwierdzi∏y istnienie
po∏ówkowych wartoÊci kwantu strumie-
nia, dowodzàc tym samym, ˝e jest to
w∏aÊciwoÊç wynikajàca z symetrii stanu
nadprzewodzàcego, a nie szczególnego
kszta∏tu próbki.

W ciàgu ostatniego roku powtórzyli-

Êmy te doÊwiadczenia z trzema innymi
miedzianami: tlenkiem miedziowo-biz-
mutowo-strontowo-wapniowym (który
ma struktur´ w pewnym sensie bardziej
skomplikowanà ni˝ YBCO), tlenkiem
miedziowo-barowo-gadolinowym (mniej
wi´cej równie z∏o˝onym jak YBCO) i tlen-
kiem miedziowo-barowo-talowym (pro-
stszym ni˝ YBCO). OtrzymaliÊmy te sa-
me rezultaty. DoÊwiadczenia przepro-
wadzone przez nas, a tak˝e te wykonane
w University of Illinois, w Federalnym
Instytucie Technologicznym w Zurychu
i w University of Maryland sà zgodne
z hipotezà o symetrii typu d.

TEMPERATURA (KELWINY)

0

160

140

120

100

80

60

40

20

1910

1950

1960

1970

1990

2000

1980

IV 1986

XII 1986

XII 1986

I 1987

Nb

3

Sn

Nb

3

Ge

Nb

3

N

NIOB

O¸ÓW

CIEK¸Y HEL

RT¢å

CIEK¸Y WODÓR

CIEK¸Y NEON

POWIERZCHNIA PLUTONA

CIEK¸Y AZOT

NOC
NA KSI¢˚YCU

TLENEK

MIEDZIOWO-

-LANTANOWO-BAROWY

II 1987

I 1988

II 1988

V 1993

TLENEK MIEDZIOWO-

-BAROWO-WAPNIOWO-

-RT¢CIOWY

TLENEK MIEDZIOWO-TALOWO-

-BAROWO-WAPNIOWY

TLENEK MIEDZIOWO-BIZMUTOWO-

-STRONTOWO-WAPNIOWY

TLENEK MIEDZIOWO-

-ITROWO-BAROWY

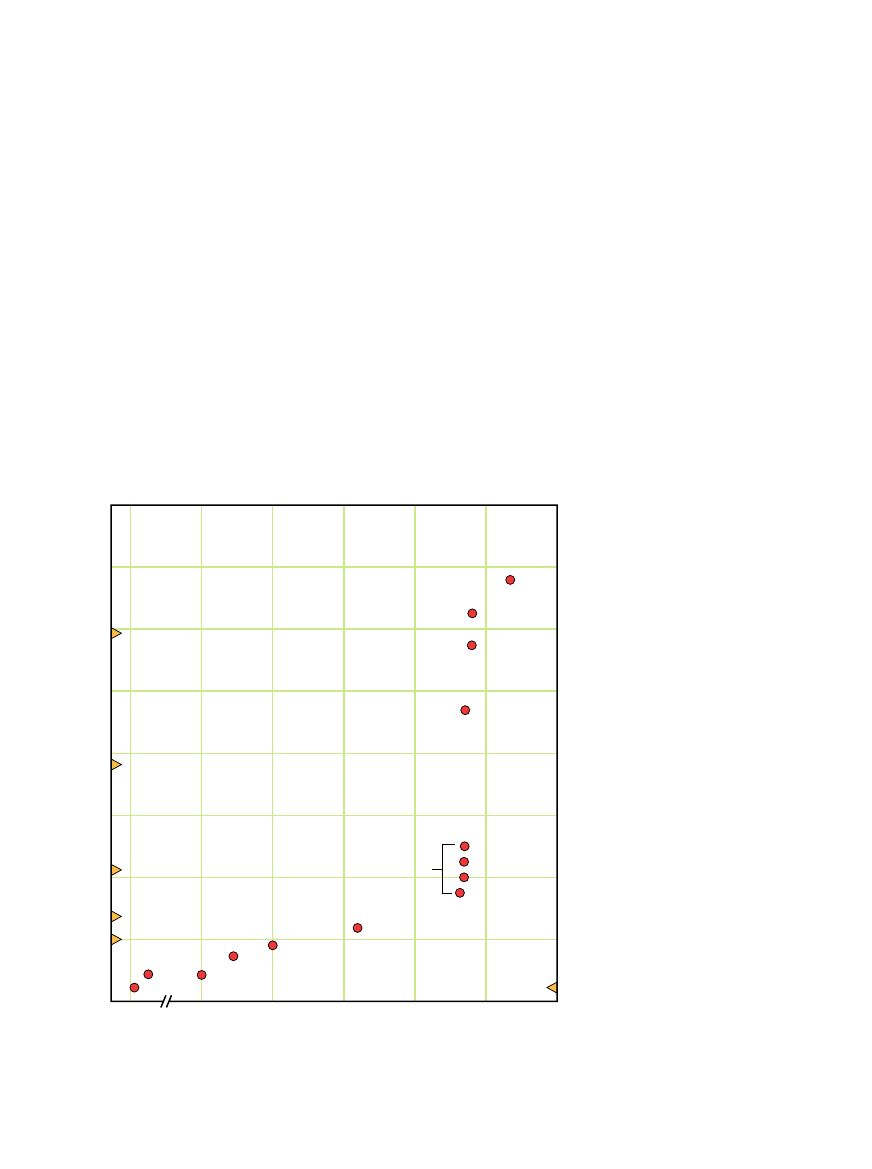
NADPRZEWODNIKI o coraz wy˝szej temperaturze krytycznej otrzymuje si´ ze zwiàz-
ków miedzi. ˚adna z proponowanych dotychczas teorii nie wyklucza istnienia nadprze-
wodnictwa w temperaturze pokojowej, chocia˝ z drugiej strony nie ma doÊwiadczalnych
danych przemawiajàcych za takà mo˝liwoÊcià.

JARED SCHNEIDMAN DESIGN

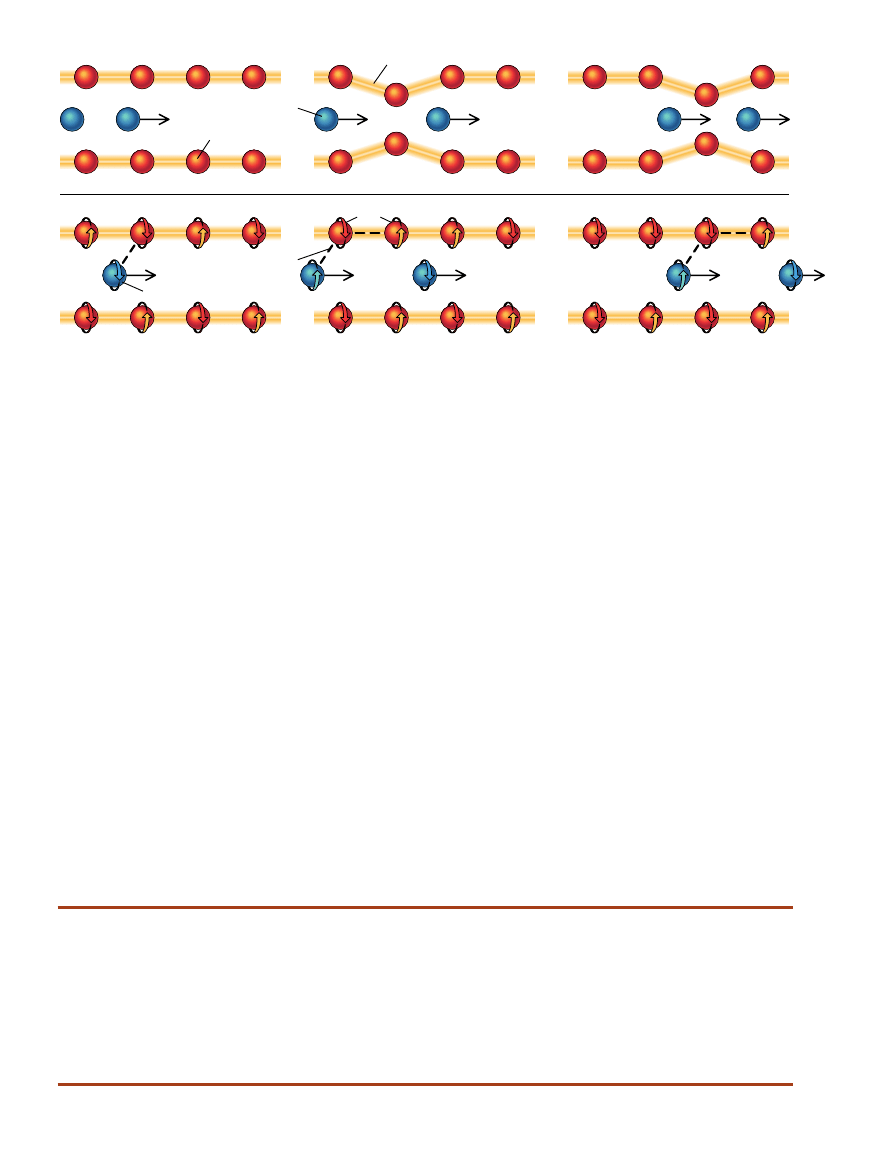
Jest prawie pewne, ˝e funkcja falowa

w kilku nadprzewodzàcych miedzia-
nach ma symetri´ typu d. (Niektóre do-
Êwiadczenia Êwiadczà o symetrii ty-
pu s, ale mo˝e to byç efekt tego, ˝e funk-
cja falowa w pewnych warunkach mie-
wa symetri´ mieszanà.) Nic zatem dziw-
nego, ˝e konwencjonalna teoria BCS nie
nadaje si´ do opisu nadprzewodnictwa
wysokotemperaturowego. Oznacza to
te˝, ˝e wcià˝ mo˝na spodziewaç si´ po-
twierdzenia hipotezy o falach spino-
wych przenoszàcych oddzia∏ywanie
mi´dzy noÊnikami tworzàcymi par´
Coopera.

Co dalej?

Niestety, wyniki doÊwiadczeƒ mogà

przemawiaç prawie za ka˝dym innym
mechanizmem sprz´˝enia (z udzia∏em
ekscytonów, polaronów i innych). Wy-
starczy za∏o˝yç, ˝e ∏adunki w parze
Coopera silnie si´ odpychajà, co Êwiad-
czy∏oby o symetrii ze zmianà znaku.

Niemniej jednak badanie symetrii

mo˝e ograniczyç zakres mo˝liwych me-
chanizmów sprz´gania noÊników. Trze-

ba wykonaç podobne doÊwiadczenia na
innych miedzianach. Na przyk∏ad funk-
cja falowa w tlenku miedziowo-cerowo-
-neodymowym, domieszkowanym w
ten sposób, ˝e przewodnictwo odbywa
si´ dzi´ki elektronom, jest prawdopo-
dobnie typu s. By∏by to cios dla tych,
którzy opowiadajà si´ za mechanizmem
zwiàzanym z fluktuacjami spinu, gdy˝
wielu badaczy sàdzi, ˝e ten sam mecha-
nizm powinien wyjaÊniaç nadprzewod-
nictwo we wszystkich nadprzewodni-
kach wysokotemperaturowych. Ozna-
cza∏oby to te˝, ˝e przyroda jest bardziej
skomplikowana, ni˝ to sobie wyobra-
˝ano. Systematyczne badania symetrii
funkcji falowej w zale˝noÊci od sk∏adu
nadprzewodnika pozwolà wyelimino-
waç b∏´dne teorie.

Na koniec coÊ pocieszajàcego dla osób

zainteresowanych zastosowaniami prak-
tycznymi: otó˝ wi´kszoÊç proponowa-
nych mechanizmów nie wyklucza ist-
nienia nadprzewodnictwa w tempera-
turze pokojowej. Pobie˝ne obliczenia
w zakresie modelu fal spinowych wy-
kazujà na przyk∏ad, ˝e nadprzewodnic-
two mo˝e istnieç w temperaturze znacz-

nie wy˝szej ni˝ 20°C, nawet w kilkuset
stopniach. Chocia˝ ta górna granica wy-
daje si´ nierealna, ewentualnoÊç nad-
przewodzenia w temperaturze pokojo-
wej jest na pewno wielkim osiàgni´ciem
w porównaniu z przewidywaniami
konwencjonalnej teorii BCS, która wy-
znacza t´ granic´ w okolicach –233°C
(40 K). Badanie mechanizmów nadprze-
wodnictwa mo˝e przynieÊç korzyÊci
tym, którzy wytwarzajà nowe nadprze-
wodzàce materia∏y i konstruujà urzà-
dzenia o praktycznym znaczeniu [patrz:
Paul C. W. Chu, „Nadprzewodniki wy-
sokotemperaturowe”; Âwiat Nauki, listo-
pad 1995].

Ostateczne okreÊlenie mechanizmu

sprz´˝enia b´dzie wymaga∏o jeszcze
wiele pracy. Obserwacja kwantów stru-
mienia magnetycznego przenikajàcych
pierÊcienie jest jednak pot´˝nym na-
rz´dziem, które pomo˝e odpowiedzieç
na pytanie, dlaczego te materia∏y o
skomplikowanej strukturze wcià˝ sta-
wiajà opór uczonym, ale nie pràdowi
elektrycznemu.

T∏umaczy∏

Jerzy ¸usakowski

Â

WIAT

N

AUKI

Paêdziernik 1996 55

ELEKTRON

DODATNI JON

STARY MODEL (FONONY)

NOWY MODEL (FALE SPINOWE)

NOÂNIK ¸ADUNKU

PRZYCIÑGANIE

ZA POÂREDNICTWEM

FALI SPINOWEJ

OBRÓT SPINU

ODKSZTA¸CENIE SIECI

STARY I NOWY MODEL NADPRZEWODNICTWA, pokazane tu w sposób bardzo uproszczony, zak∏adajà ∏àczenie si´ noÊników ∏adun-
ku w pary. W starym modelu, który wyjaÊnia nadprzewodnictwo niskotemperaturowe na gruncie starych teorii, poruszajàcy si´ elektron
wytwarza fonony – odkszta∏cenia sieci krystalicznej – przyciàgajàce drugi elektron. W jednej z wielu nowych koncepcji – modelu zak∏a-
dajàcym wzbudzenia fal spinowych – noÊnik ∏adunku zaburza spin jednego jonu, co powoduje zmian´ orientacji spinu sàsiedniego jo-
nu i przyciàgni´cie drugiego noÊnika z przeciwnie skierowanym spinem.

Informacje o autorach

JOHN R. KIRTLEY i CHANG C. TSUEI poszukujà po∏ów-

kowych kwantów strumienia pola magnetycznego w nad-

przewodzàcych pierÊcieniach w IBM Thomas J. Watson Re-

search Center w Yorktown Heights (stan Nowy Jork), gdzie

pracujà od lat siedemdziesiàtych. Kirtley ukoƒczy∏ studia

i obroni∏ prac´ doktorskà w University of California w San-

ta Barbara. Tsuei ukoƒczy∏ studia w Uniwersytecie Tajwaƒ-

skim, a doktorat uzyska∏ w California Institute of Techno-

logy. Obaj sà cz∏onkami American Physical Society. Oprócz

nadprzewodnictwa badajà tak˝e podstawowe elektryczne

i magnetyczne w∏aÊciwoÊci cia∏ sta∏ych.

Literatura uzupe∏niajàca

THE CASE FOR DX2Y2 PAIRING IN THE CUPRATE SUPERCONDUCTORS

. D.J. Scalapino, Phy-

sics Reports, vol. 250, nr 6, ss. 329-365, I/1995.

CALL THEM IRRESISTIBLE

. Tim Folger, Discover, vol. 16, nr 9, ss. 83-91, IX/1995.

DESIGN AND APPLICATIONS OF A SCANNING SQUID MICROSCOPE.

J. R. Kirtley, M. B. Ket-

chen, C. C. Tsuei, J. Z. Sun, W. J. Gallagher, Lock-See Yu-Jahnes, A. Gupta,

K. G. Stawiasz i S. J. Wind, IBM Journal of Research and Development, vol. 39, nr 6,

ss. 655-668, XI/1995.

EXPERIMENTS PROBE THE WAVEFUNCTION OF ELECTRON PAIRS IN HIGH-Tc SUPERCONDUC-

TORS

. Barbara Levi, Physics Today, vol. 49, nr 1, ss. 19-22, I/1996.

ELECTRON PAIRS AND WAVES: TACKLING THE PUZZLE OF HIGH-TEMPERATURE SUPERCON-

DUCTIVITY

. Ivars Peterson, Science News, vol. 149, nr 10, ss. 156-157, 9 III 1996.

JARED SCHNEIDMAN DESIGN