2.

Obwody prądu zmiennego

2.1.

Definicje i wielkości charakteryzujące

Spośród wielu możliwych przebiegów zmiennych w czasie zajmiemy się jedynie

przebiegami harmonicznymi (sinusoidalnymi lub cosinusoidalnymi). Prądy i napięcia o takim
kształcie spotykamy w technice najczęściej. Ich analiza jest stosunkowo prosta, dlatego wiele
innych, podobnych do nich przebiegów staramy się przybliżyć harmonicznymi.
Przebiegi okresowe można scharakteryzować za pomocą następujących parametrów:

(

)

( )

1

- definicja przebiegu okresowego,

1

,

2

,

2

- częstotliwość przebiegu [Hz],

- częstość [s ],

- okres przebiegu [s].

u t

T

u t

f

f

T

T

f

T

ω

ω

ω

−

+

=

=

= π

= π ;

(2.1)

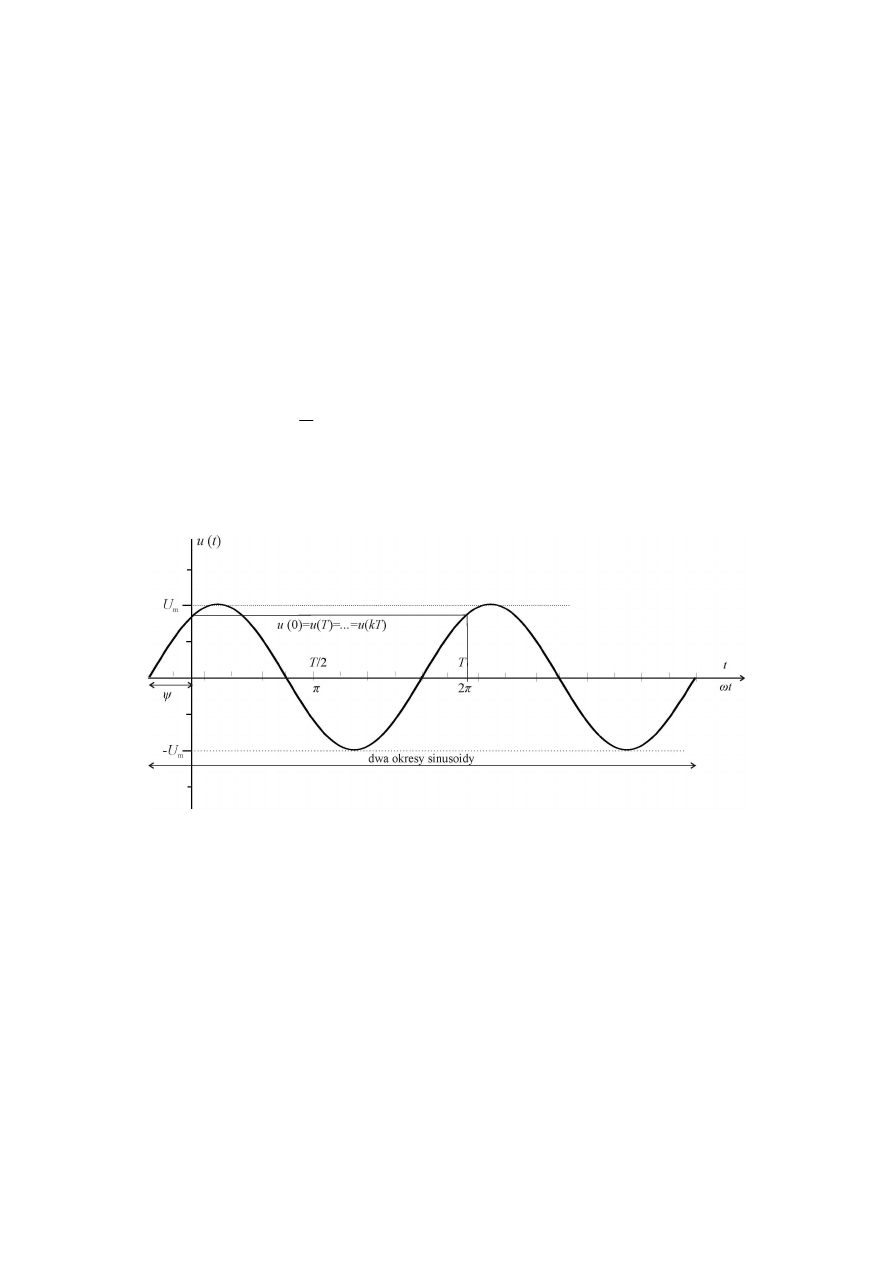
Rys. 2.1. Przebieg okresowy harmoniczny

Na rys. 2.1 przedstawiony jest przebieg okresowy harmoniczny. Może on zostać opisany
wzorem:

(

)

m

m

( )

sin

wartość maksymalna,

częstość,

początkowy kąt fazowy.

u

u t

U

t

U

ω ψ

ω

ψ

=

=

+

−

−

−

(2.2)

Kąt fazowy Ψ można określić tylko względem innego przebiegu o tej samej częstotliwości.
Zapisywanie każdego prądu lub napięcia wzorem 2.2 byłoby uciążliwe, stąd wynika potrzeba
zdefiniowania wielkości charakteryzujących przebiegi. Spróbujmy zdefiniować wartość
ś

rednią całookresową:

Obwody prądu zmiennego

2/15

( )

0

0

0

1

1

( ) d

( ) d

0 ;

t

T

T

t

u t

u t

t

u t

t

T

T

+

=

⇒

=

∫

∫

(2.3)

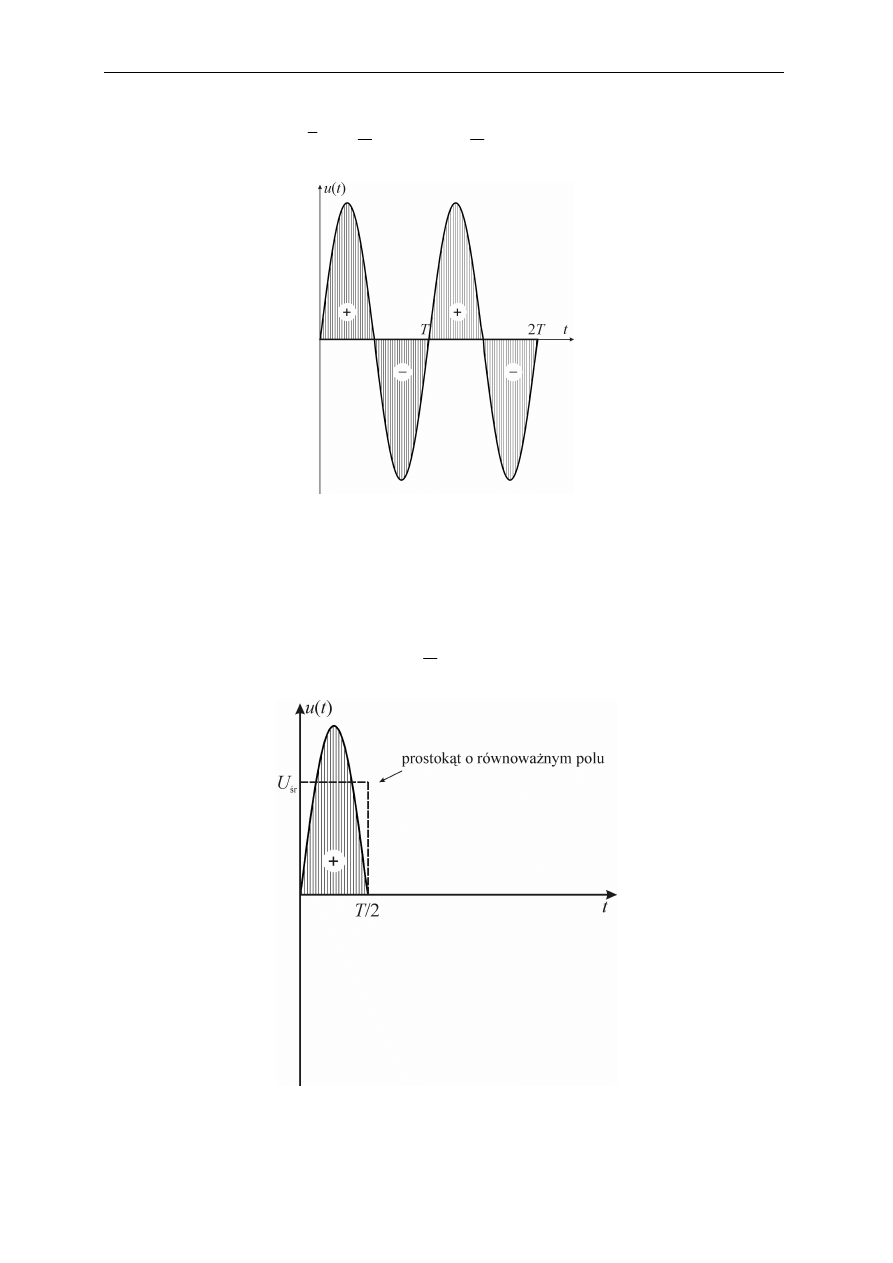
Rys. 2.2. Całka z przebiegu sinusoidalnego za całkowitą liczbę okresów

Ze względu na symetryczne położenie przebiegu nad i pod osią czasu (x), całka
uwzględniająca tą samą liczbę pól „+” co „

−

” będzie w wyniku dawać zero. Tak więc wartość

ś

rednia całookresowa jest nieprzydatna. Zdefiniujmy i wyliczmy w takim razie wartość

ś

rednią półokresową:

/ 2

ś

r

0

2

( ) d

T

U

u t

t

T

=

∫

.

(2.4)

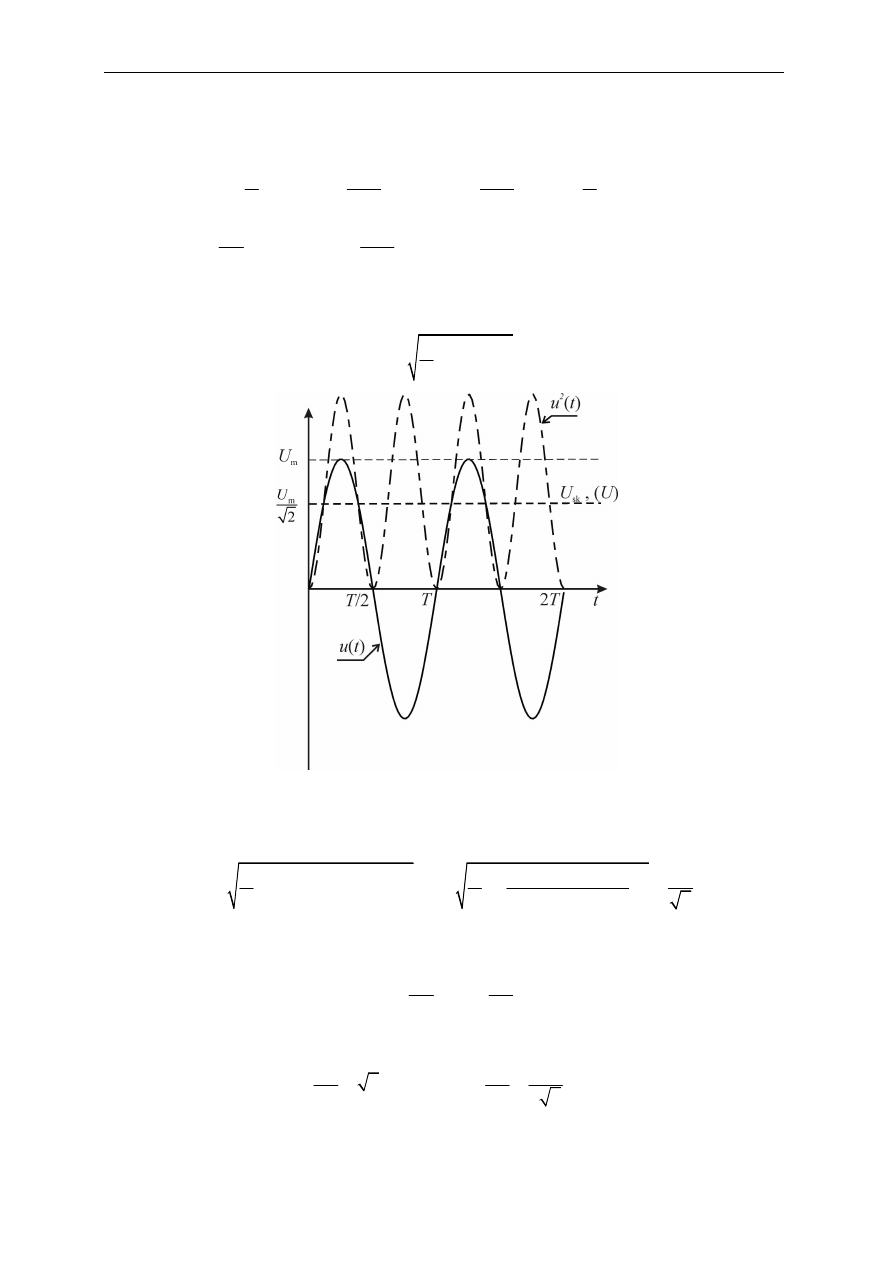
Rys. 2.3. Interpretacja geometryczna wartości średniej półokresowej

Obwody prądu zmiennego

3/15

Tak zdefiniowana wartość średnia będzie różna od zera i po scałkowaniu jej dla przebiegu
sinusoidalnego otrzymujemy wartość:

(

)

/ 2

/ 2

m

m

ś

r

0

0

m

m

2

2

2

( ) d

sin

d

cos(

)

cos(0)

2

2

cos(

.

T

T

U

U

T

U

u t

t

t t

T

T

T

U

U

ω

ω

ω





=

=

=

−

+

=









=

−

π) +1 =

π

π

∫

∫

(2.5)

Od wartości średniej większą przydatność praktyczną ma wartość skuteczna. Definicja
wartości skutecznej (przykładowo napięcia) jest następująca:

2

0

1

( ) d

T

U

u t

t

T

=

∫

.

(2.6)

Rys. 2.4. Interpretacja sposobu obliczania wartości skutecznej

Wyznaczenie wartości skutecznej przebiegu sinusoidalnego prowadzi do jej zależności od
wartości maksymalnej:

(

)

(

)

2

2

m

m

m

0

0

1 cos 2

1

1

sin

d

d

2

2

T

T

t

U

U

U

t

t

U

t

T

T

ω ψ

ω ψ

−

+

=

+

=

=

∫

∫

.

(2.7)

Do opisu przebiegów odkształconych w stosunku do harmonicznych używa się
współczynnika amplitudy

k

a

i współczynnika kształtu

k

k

m

a

k

ś

r

,

U

U

k

k

U

U

=

=

.

(2.8)

Dla przebiegów harmonicznych te współczynniki wynoszą

m

ś

r

2

1, 41 ;

1,11.

a

k

U

U

k

k

U

U

π

=

=

=

=

=

=

2 2

(2.9)

Obwody prądu zmiennego

4/15

Interpretacja fizyczna wartości skutecznej

Interpretacja opiera się o wartość energii wydzieloną przez prąd o wartości skutecznej I:

2

0

1

( ) d

T

I

i t

t

T

=

∫

.

(2.10)

Energia wydzielona przez prąd i(t) w rezystorze R i w czasie T wynosi:

2

0

( ) d

T

W

R

i t

t

=

∫

.

(2.11)

Na podstawie wzoru (2.10) stwierdzamy, że ta energia może być łatwo wyrażona przez
wartość skuteczną I

2

W

R I T

= ⋅

.

(2.12)

Gdyby I oznaczało wartość prądu stałego, wzór (2.12) miałby taką samą postać. Stwierdzamy
wobec tego, że:

wartość skuteczna prądu zmiennego odpowiada takiej wartości prądu stałego,

która powoduje wydzielenie w rezystorze tej samej energii (i ten sam skutek cieplny).

Ważnym pojęciem dotyczącym przebiegów harmonicznych jest przesunięcie fazowe między
dwoma przebiegami, koniecznie o tej samej częstotliwości.

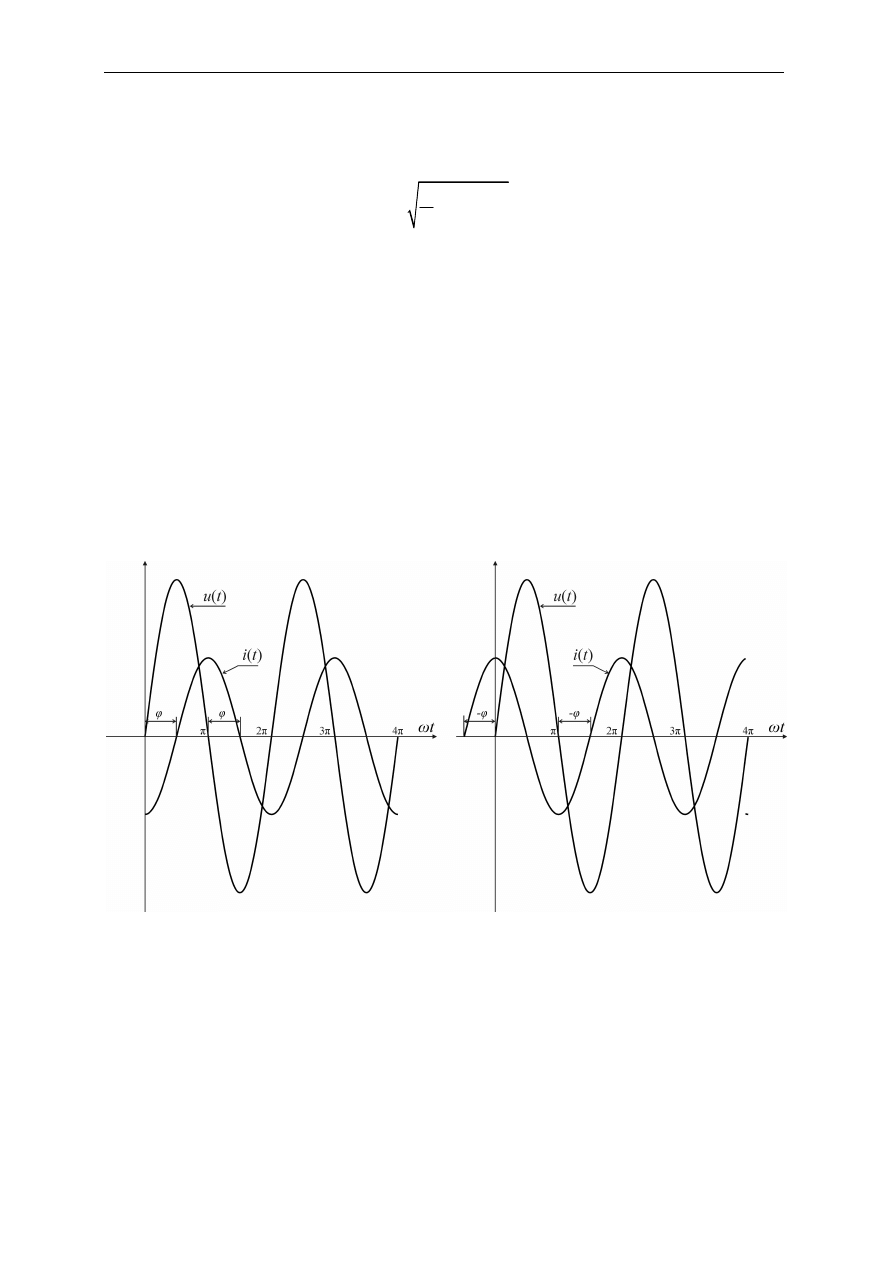
Rys. 2.5. Prąd opóźniający się za napięciem (po lewej) i prąd wyprzedzający napięcie

Przebiegi pokazane na rys. 2.5 możemy zaobserwować na ekranie oscyloskopu. W przypadku

niewielkich kątów

ϕ

(-90

o

≤

ϕ

≤

90

o

)

łatwo jest określić wzrokowo, czy prąd się opóźnia, czy

też wyprzedza napięcie.

Obwody prądu zmiennego

5/15

2.2.

Wytwarzanie napięć zmiennych

Wytwarzanie napięć zmiennych odbywa się w generatorach. Zasada działania generatora

wynika z prawa Faraday’a

( )

d

.

d

e t

t

Φ

= −

(2.13)

Mówi ono, że zmianom strumienia magnetycznego towarzyszy indukowanie siły
elektromotorycznej (napięcia). Warunkiem koniecznym jest zmienność strumienia. Jeżeli
przyczyną zmiany jest ruch cewki wzbudzającej pole magnetyczne względem drugiej cewki,
to w tej drugiej cewce powstanie siła elektromotoryczna, a po zamknięciu obwodu popłynie
prąd. Generator prądu jest urządzeniem przemieniającym energię mechaniczną ruchu
obrotowego turbiny na energię prądu elektrycznego. Schemat najprostszego generatora
pokazany jest na rys. 2.6.

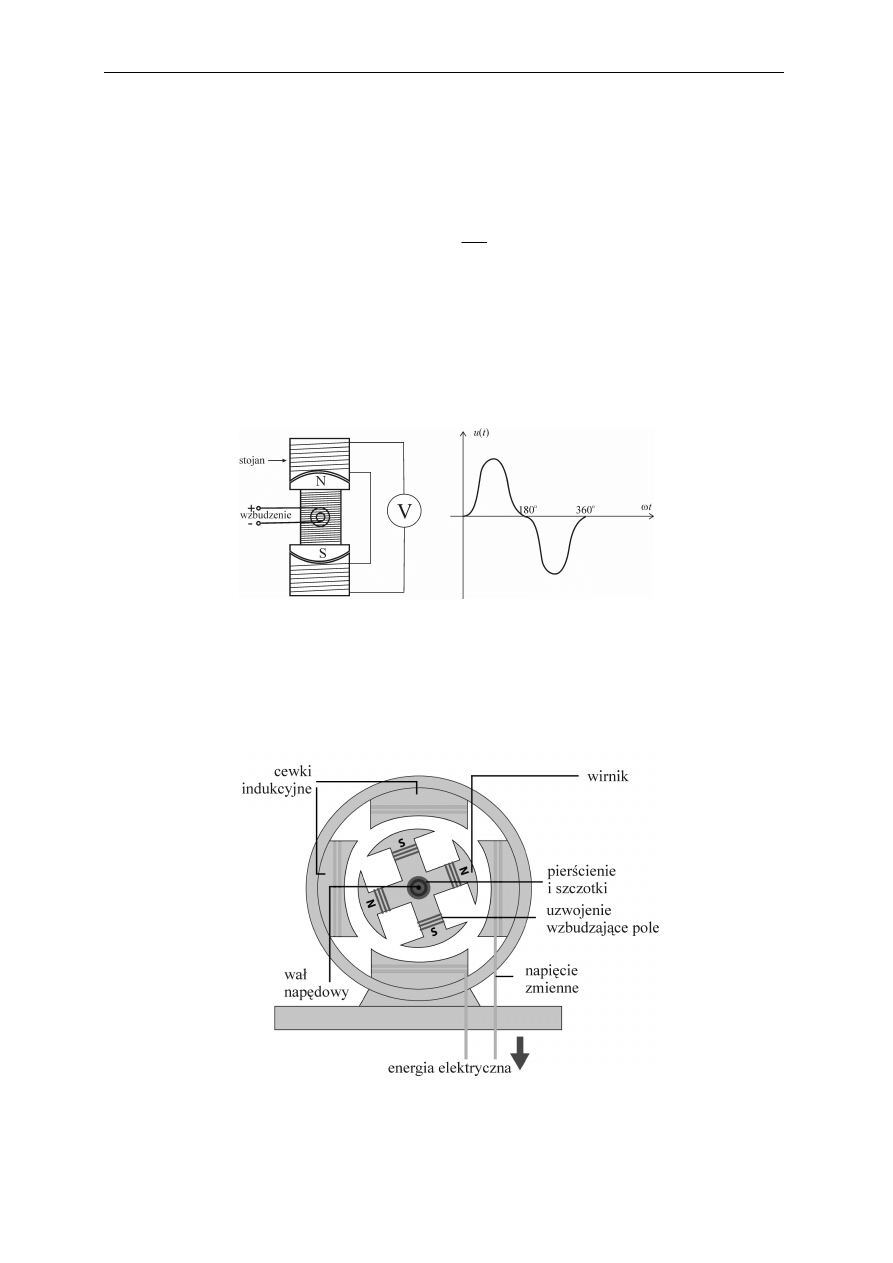
Rys. 2.6. Budowa generatora napięcia przemiennego oraz kształt napięcia

W wyniku obrotu wzbudnika zasilanego prądem stałym w cewkach stojana indukuje się
napięcie przemienne, którego kształt w tak prostym generatorze mocno odbiega od sinusoidy.
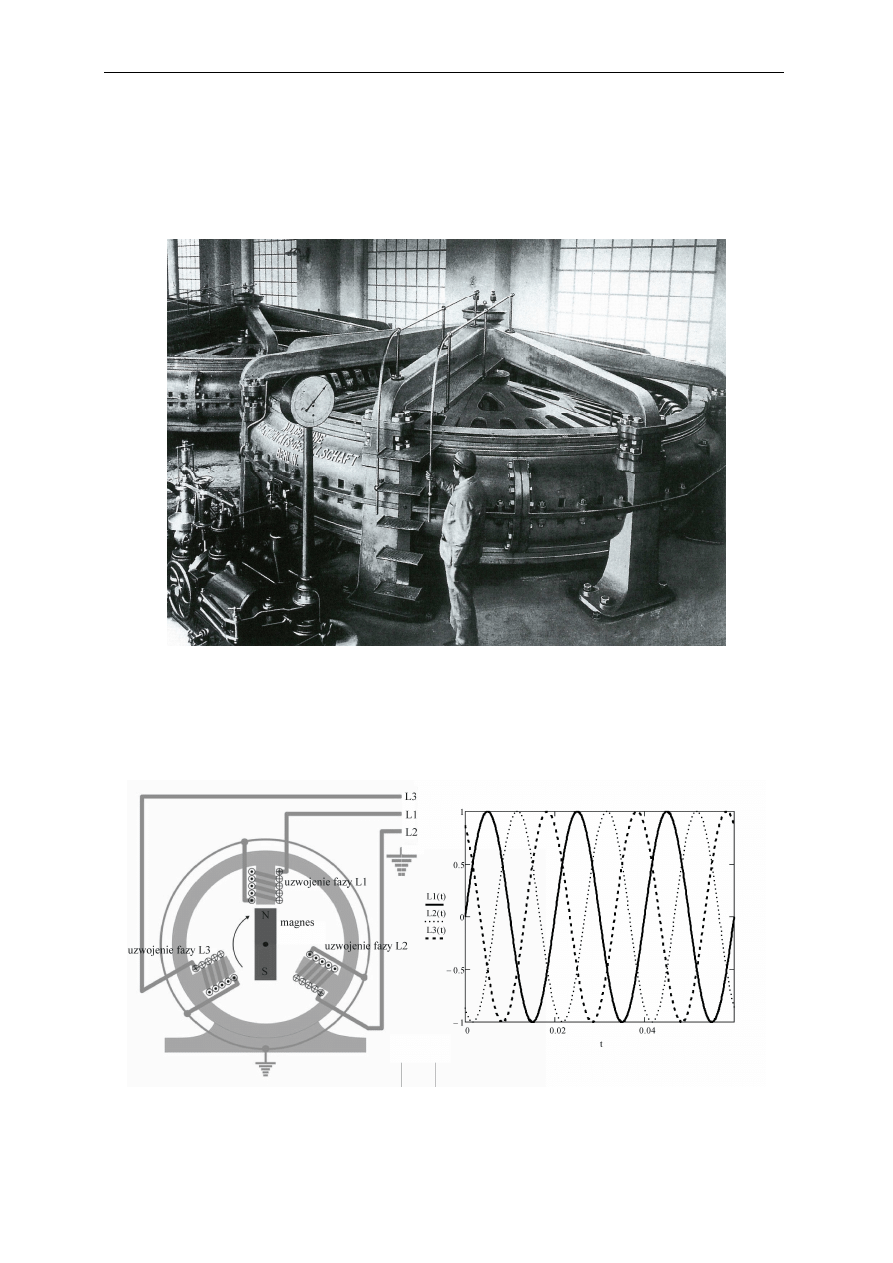
Na kolejnym rysunku pokazano bardziej zaawansowany generator w układzie
wielobiegunowym. Posiada on dwie pary biegunów, tak więc do wytworzenia częstotliwości
sieciowej 50Hz powinien się obracać z prędkością 1500obr/min.

Rys. 2.7. Generator wielobiegunowy

Obwody prądu zmiennego

6/15

Ilość par biegunów determinuje prędkość obrotową generatora. Generatory napędzane
turbinami parowymi pracują zwykle przy wysokich obrotach, ponieważ sprawność turbiny
jest wtedy wyższa. Natomiast generatory napędzane turbinami wodnymi mają bardzo małe
obroty, a w związku z tym dużą liczbę biegunów. Taki generator ma również bardzo dużą
ś

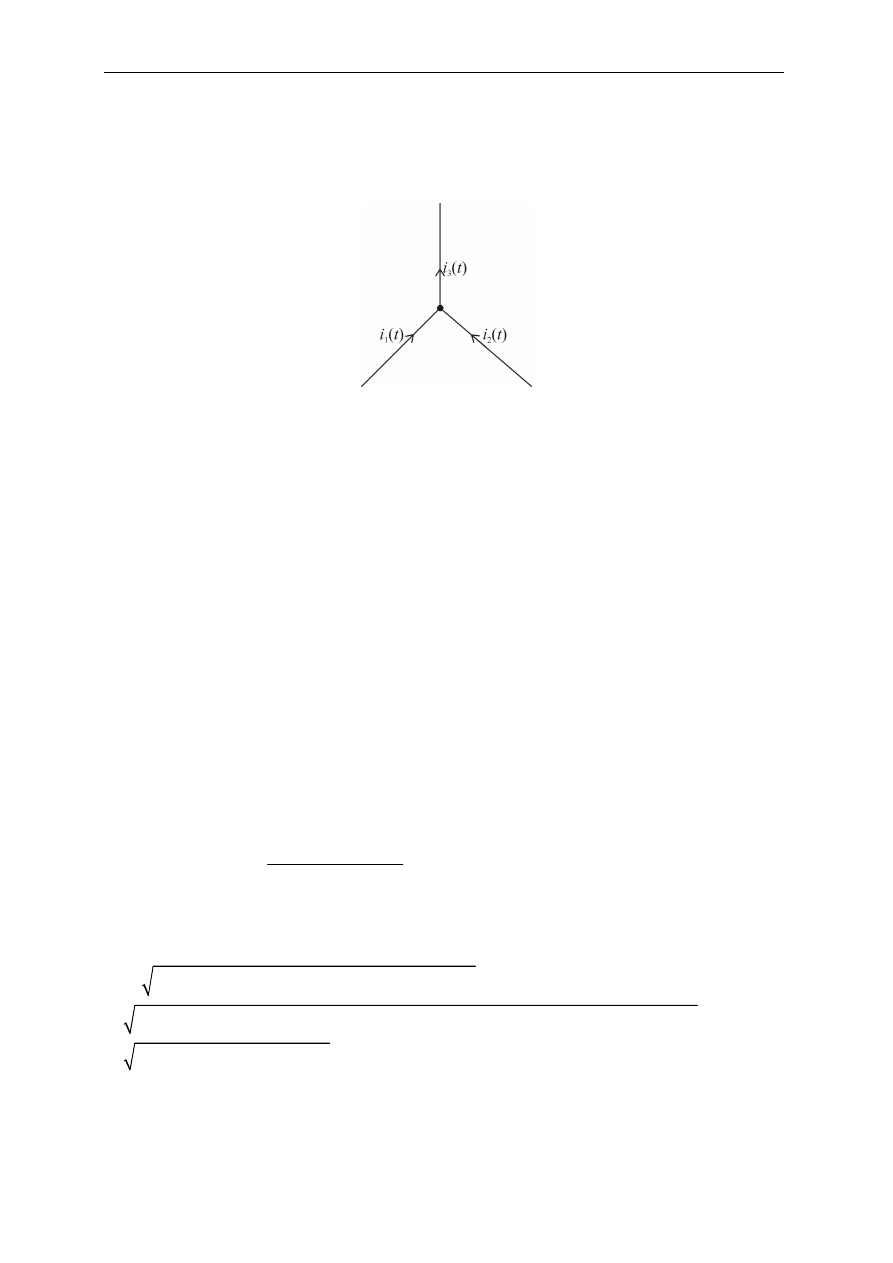
rednicę. Na rysunku 2.8 widoczny jest generator elektrowni wodnej w Rheinfelden

zbudowany ok. 1900 roku.

Rys. 2.8. Generator elektrowni wodnej w Rheinfelden ok. 1900r. (źródło: Wikipedia)

Schemat budowy generatora trójfazowego pokazano na rys. 2.9. Generator ten składa się z
trzech cewek, w środku między którymi obraca się wzbudnik. Cewki te są przesunięte w

przestrzeni o 120

o

, co powoduje, że napięcia kolejnych faz są również przesunięte o 120

o

.

Otrzymuje się w ten sposób symetryczny, trójfazowy układ napięć.

Rys. 2.9. Schemat budowy generatora trójfazowego

Obwody prądu zmiennego

7/15

2.3.

Dodawanie przebiegów harmonicznych

Na przykładzie uzyskiwania sumy dwóch prądów wpływających do wspólnego węzła

(rys. 2.10) zostanie pokazane sumowanie funkcji harmonicznych.

Rys. 2.10. Prądy i

1

(t) oraz i

2

(t) sumują się dając prąd i

3

(t)

Na podstawie pierwszego prawa Kirchhoffa dla każdej chwili czasu t zachodzi

3

1

2

( )

( )

( )

i t

i t

i t

=

+

. Jeżeli prądy i

1

oraz i

2

mają kształt sinusoidy, można je dodać tylko wtedy,

gdy obydwa mają tą samą częstotliwość. Jeżeli dodatkowo miałyby one ten sam kąt fazowy,
można byłoby dodać bezpośrednio ich amplitudy. W większości przypadków takie proste
postępowanie nie jest możliwe i trzeba przeprowadzić dodawanie funkcji. Prąd i

3

chcielibyśmy otrzymać w postaci podanej poniżej:

(

)

(

)

(

)

3

1

1

2

2

3

3

( )

sin

sin

sin

i t

I

t

I

t

I

t

ω ϕ

ω ϕ

ω ϕ

=

+

+

+

=

+

.

(2.14)

W tym celu zamienimy sinusy zgodnie z wzorem na sinus sumy dwóch kątów:

1

1

1

1

2

2

2

2

3

3

3

3

sin

cos

cos

sin

sin

cos

cos

sin

sin

cos

cos

sin

.

I

t

I

t

I

t

I

t

I

t

I

t

ω

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

+

+

+

=

=

+

(2.15)

Aby lewa strona tego równania równała się prawej, współczynniki przy sinusach i cosinusach
po obu stronach równania muszą być równe. Otrzymujemy stąd dwa równania

1

1

2

2

3

3

1

1

2

2

3

3

cos

cos

cos

,

sin

sin

sin

.

I

I

I

I

I

I

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

+

=

+

=

(2.16)

Dzieląc drugie przez pierwsze upraszczamy I

3

i otrzymujemy kąt fazowy

1

1

2

2

3

1

2

3

1

1

2

2

sin

sin

,

jeśli kąty są równe :

.

cos

cos

I

I

arctg

k

I

I

ϕ

ϕ

ϕ

ϕ ϕ

ϕ

ϕ

ϕ

+



=

± π

=

⇒

=



+



(2.17)

W celu otrzymania amplitudy I

3

oba równania podnosimy do kwadratu i dodajemy stronami.

Korzystamy z wzoru jedynkowego (

( )

( )

2

2

sin

cos

1

x

x

+

=

) otrzymując

(

) (

)

(

)

(

)

(

)

(

)

2

2

3

1

1

2

2

1

1

2

2

2

2

2

2

2

2

1

1

1

2

2

2

1 2

1

2

1

2

2

2

1

2

1 2

1

2

3

1

2

3

1

2

cos

cos

sin

sin

sin

cos

sin

cos

2

cos

cos

sin

sin

2

cos

,

jeśli :

.

I

I

I

I

I

I

I

I I

I

I

I I

I

I

I

I

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ ϕ

ϕ ϕ

=

+

+

+

=

=

+

+

+

+

+

=

=

+ +

−

=

=

⇒

= +

(2.18)

Przedstawione zależności pokazują, jak trudne byłoby posługiwanie się funkcjami
sinusoidalnymi w celu rozwiązywania obwodów.

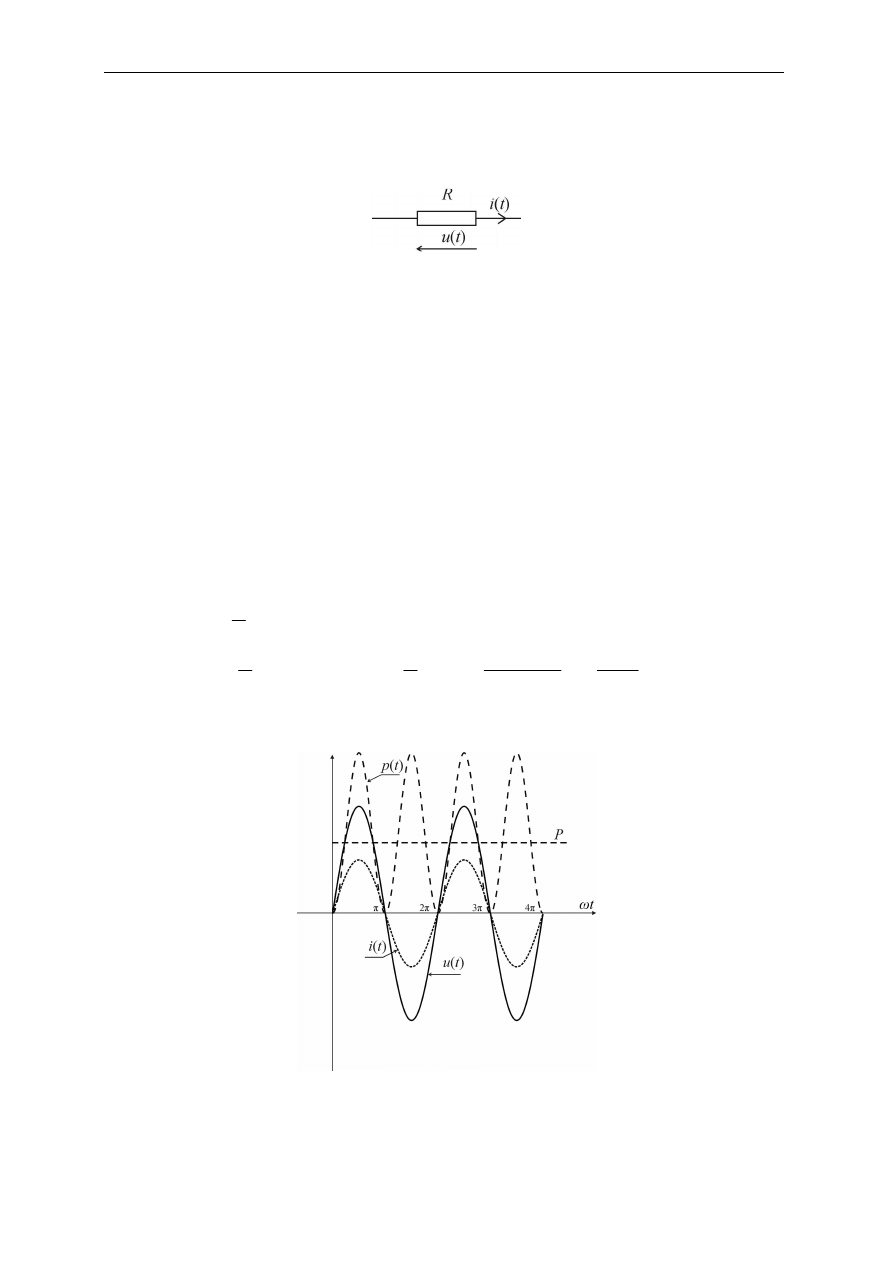
Obwody prądu zmiennego

8/15

2.4.

Zachowanie się podstawowych elementów przy prądzie sinusoidalnie zmiennym

Rezystor

Rys. 2.11. Rezystor, przez który płynie prąd i(t)

Załóżmy, że przez rezystor płynie sinusoidalny prąd

m

( )

sin

i t

I

t

ω

=

. Zgodnie z prawem

Ohma dla każdej chwili czasu

m

m

m

m

( )

( )

sin

sin

czyli:

, a wartości skuteczne:

.

u t

R i t

RI

t

U

t

RI

U

RI

U

ω

ω

= ⋅

=

=

=

=

(2.19)

Celem zrozumienia zjawisk zachodzących w różnych elementach trzeba przeanalizować
transfer mocy między źródłem a elementem. Zdefiniujmy moc chwilową:

2

m

m

m m

( )

( ) ( ), dla przebiegów sinusoidalnych na rezystorze:

( )

sin

sin

sin

p t

u t i t

p t

U

t I

t

U I

t

ω

ω

ω

=

⋅

=

=

(2.20)

Moc chwilowa jest nieujemna, co oznacza, że moc jest przekazywana ze źródła do rezystora,
a nigdy w przeciwnym kierunku. Na podstawie mocy chwilowej zdefiniujemy moc czynną
jako wartość średnią:

0

2

m m

R

m m

m m

0

0

1

( )d , dla rezystora będzie to:

1

1

1 cos 2

sin

d

d

.

2

2

T

T

T

P

p t

t

T

t

U I

P

U I

t t

U I

t

U I

T

T

ω

ω

=

−

=

=

=

= ⋅

∫

∫

∫

(2.21)

Dla rezystora moc czynna wyraża się prostym iloczynem wartości skutecznych prądu i
napięcia. Komplet przebiegów dla rezystora pokazuje rys. 2.12.

Rys. 2.12. Przebiegi prądu, napięcia, mocy chwilowej i linia mocy czynnej

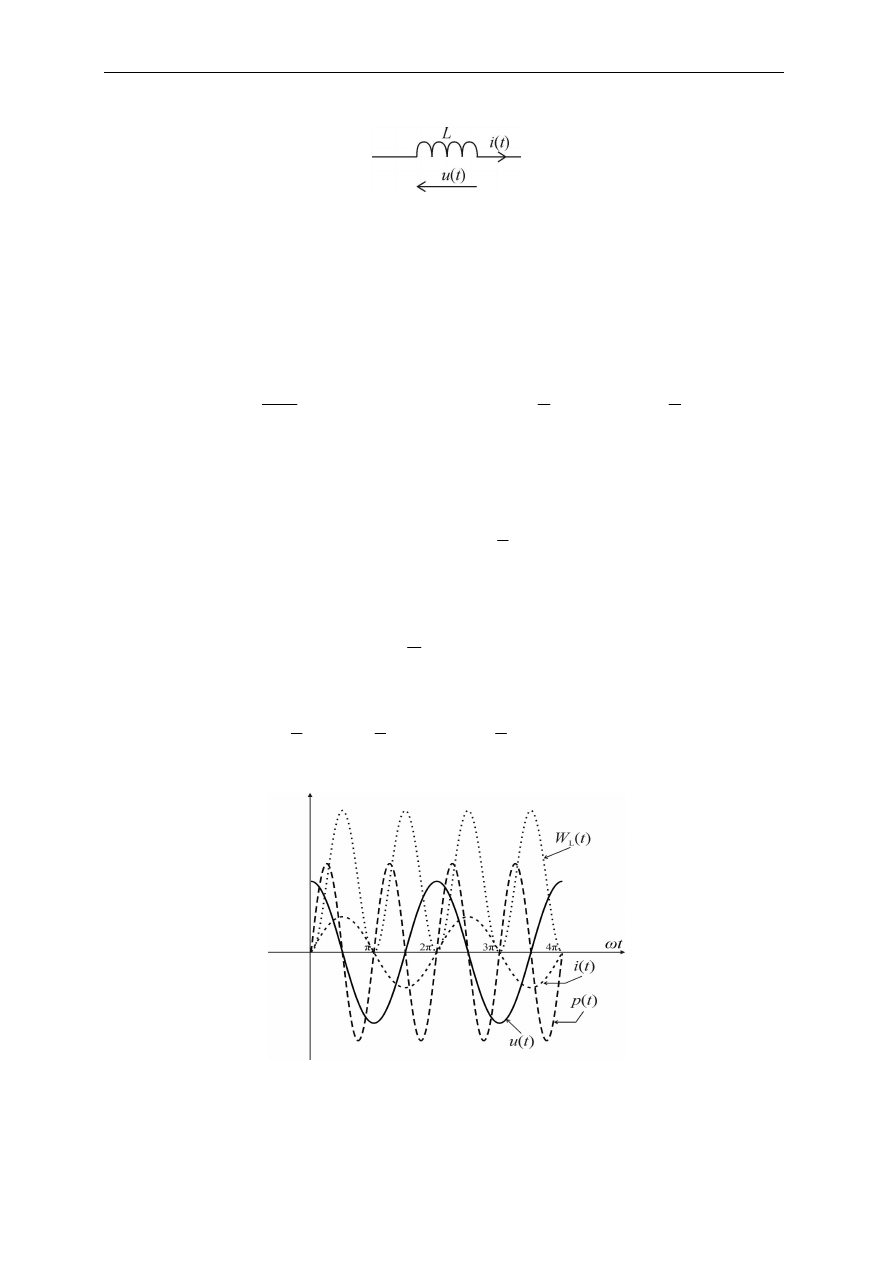
Obwody prądu zmiennego

9/15

Cewka

Rys. 2.13. Cewka, przez którą płynie prąd i(t)

Załóżmy, że przez cewkę płynie sinusoidalny prąd

m

( )

sin

i t

I

t

ω

=

. Spadek napięcia na cewce

wynika z prawa Faraday’a: ( )

d

( ) / d

e t

t

t

Φ

= −

. Jeżeli przez cewkę przenika zmienny strumień

magnetyczny, indukuje się w niej siła elektromotoryczna e(t)=

−

u(t). Można ją traktować jako

spadek napięcia na cewce u(t) z przeciwnym znakiem. Ponieważ indukcyjność cewki jest
definiowana jako współczynnik proporcjonalności pomiędzy prądem, a strumieniem
magnetycznym:

( )

( )

t

L i t

Φ

= ⋅

, stąd:

m

m

m

m

m

d ( )

( )

cos

sin

sin

d

2

2

, a dla wartości skutecznych:

.

i t

u t

L

LI

t

L I

t

U

t

t

L I

U

L I

U

ω

ω ω

ω

ω

ω

ω

π

π









=

=

=

⋅

+

=

+

















⋅

=

⋅ =

(2.22)

Wielkość L

ω

występującą we wzorze nazywamy reaktancją indukcyjną i oznaczamy jako X

L

.

Moc chwilowa dla cewki

m

m

m m

1

( )

cos

sin

sin 2

2

p t

U

t I

t

U I

t

ω

ω

ω

=

⋅

=

(2.23)

jest funkcją oscylującą wokół osi x, co oznacza, że moc jest przekazywana w obu kierunkach
w różnych chwilach czasu. Stąd moc czynna wynosi:

0

1

( )d

0,

T

P

p t t

T

=

=

∫

(2.24)

a energia zgromadzona w cewce jest nieujemna:

(

)

2

2

2

2

L

m

1

1

1

( )

sin

1 cos 2

2

2

2

W

L i t

L I

t

L I

t

ω

ω

=

⋅

=

⋅

=

⋅

−

.

(2.25)

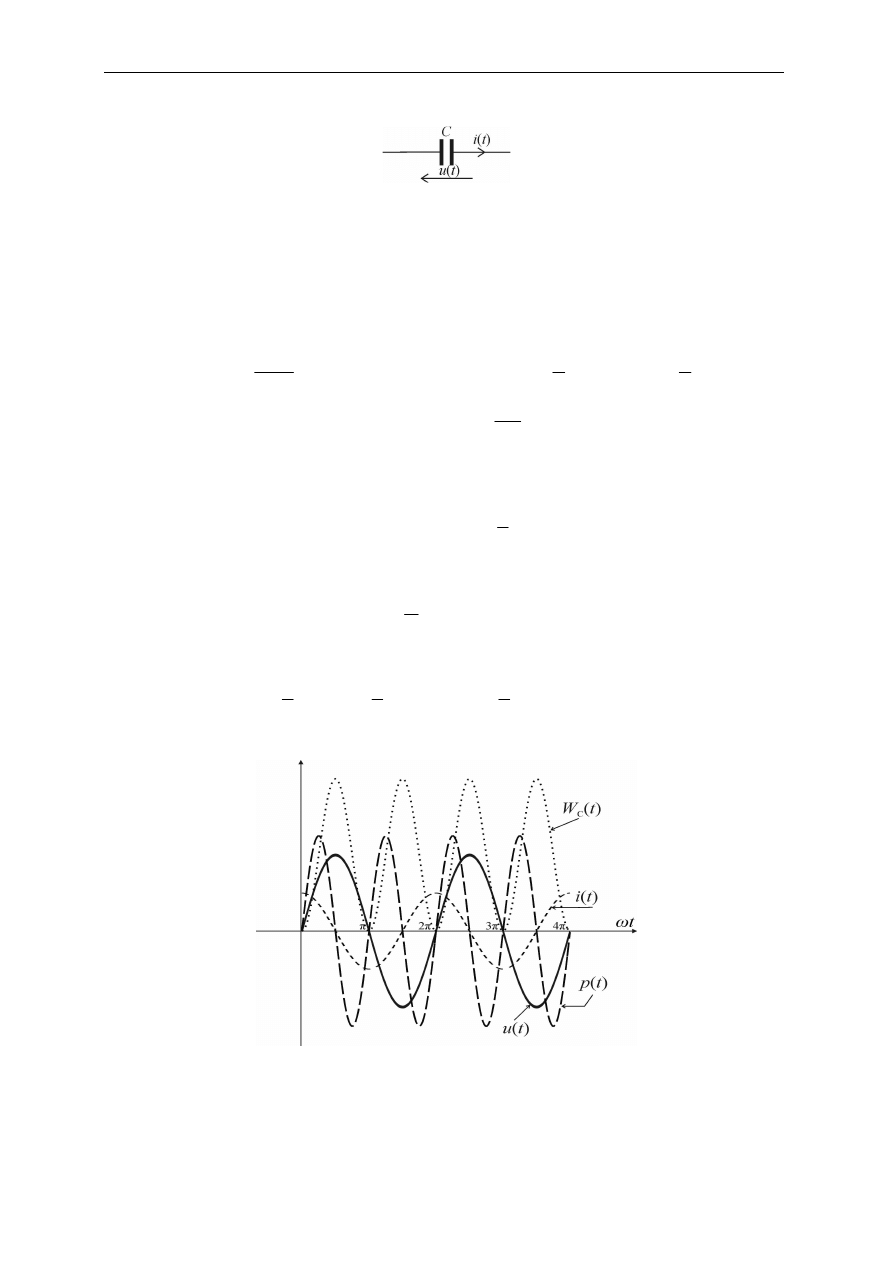
Rysunek 2.14 pokazuje przebiegi wszystkich wielkości występujących w cewce.

Rys. 2.14. Przebiegi prądu, napięcia, mocy chwilowej i energii zgromadzonej w cewce

Obwody prądu zmiennego

10/15

Kondensator

Rys. 2.15. Kondensator, do którego przyłożono napięcie u(t)

Załóżmy, że do kondensatora przyłożono napięcie sinusoidalne

m

( )

sin

.

u t

U

t

ω

=

Prąd w

obwodzie z kondensatorem może płynąć tylko wtedy, gdy zmienia się ładunek na jego
okładzinach ( )

d ( ) / d .

i t

q t

t

=

Współczynnikiem proporcjonalności pomiędzy ładunkiem, a

napięciem jest pojemność kondensatora

( )

( ).

q t

C u t

= ⋅

Wtedy prąd płynący „przez”

kondensator wyraża się wzorem

m

m

m

m

m

d ( )

( )

cos

sin

sin

d

2

2

1

, a dla wartości skutecznych:

u t

i t

C

C U

t

C I

t

I

t

t

C U

I

I

U

C

ω

ω ω

ω

ω

ω

ω

π

π









=

=

⋅

=

⋅

+

=

+

















⋅

=

⋅ =

(2.26)

Wielkość 1/ C

ω

występująca we wzorze jest nazywana reaktancją pojemnościową (X

C

). Moc

chwilowa dla kondensatora przyjmuje podobną postać, jak dla cewki

m

m

m m

1

( )

sin

cos

sin 2

2

p t

U

t I

t

U I

t

ω

ω

ω

=

⋅

=

(2.27)

i jest funkcją oscylującą wokół osi x. Dlatego moc czynna

0

1

( )d

0

T

P

p t

t

T

=

=

∫

,

(2.28)

a energia zgromadzona w kondensatorze jest również nieujemna:

(

)

2

2

2

2

C

m

1

1

1

( )

sin

1 cos 2

2

2

2

W

C u t

C U

t

C U

t

ω

ω

=

⋅

=

⋅

=

⋅

−

.

(2.29)

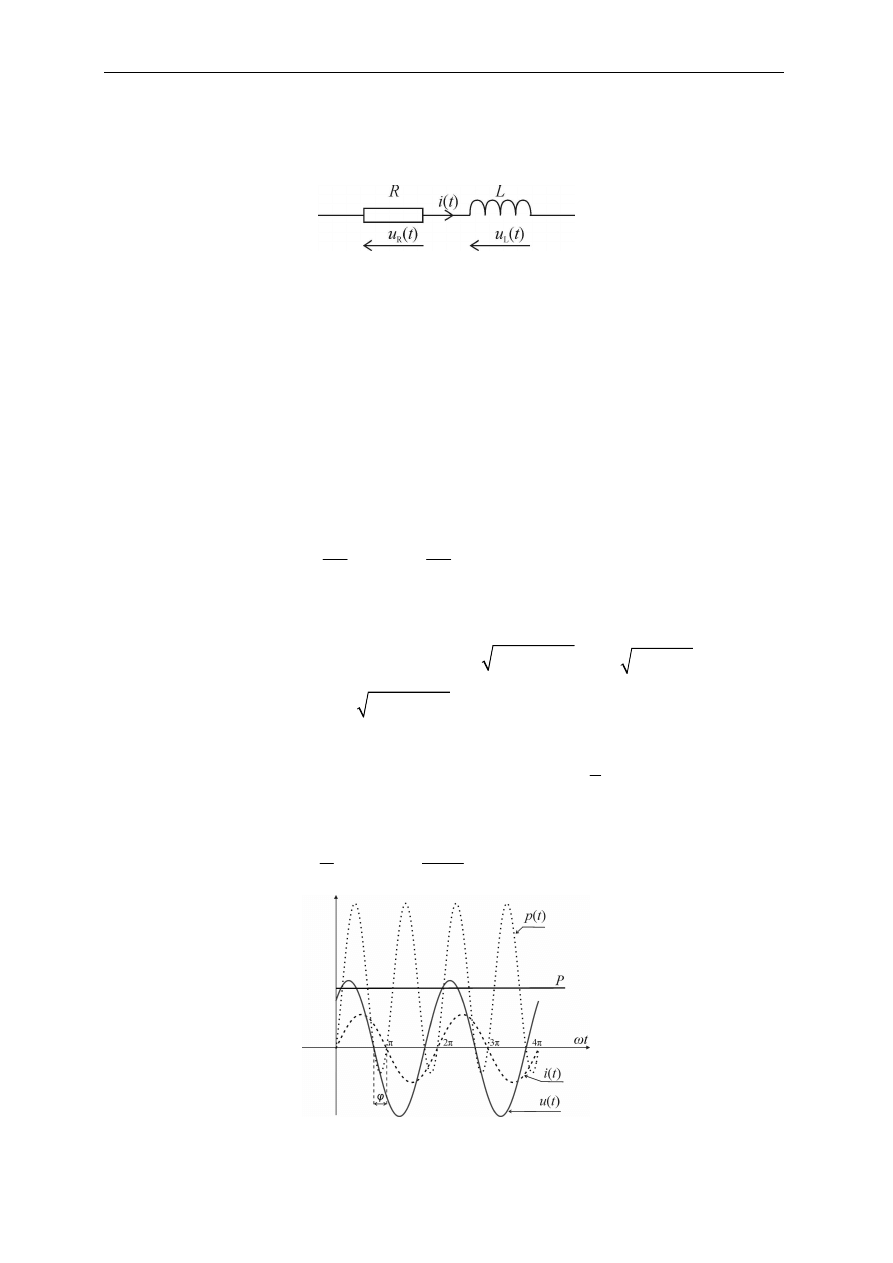
Wszystkie przebiegi dla obwodu z kondensatorem pokazano na rys.2.16.

Rys. 2.16. Przebieg napięcia, prądu, mocy chwilowej i energii w obwodzie kondensatora

Obwody prądu zmiennego

11/15

2.5.

Gałęzie szeregowe RL, RC oraz RLC przy prądzie sinusoidalnie zmiennym

Na rysunku 2.17 widoczna jest gałąź RL, przez którą przepływa prąd

m

( )

sin

i t

I

t

ω

=

.

Rys. 2.17. Gałąź szeregowa RL

Na podstawie wzorów 2.19 oraz 2.22 można podać napięcie całkowite w postaci

(

)

R

L

m

m

m

( )

( )

( )

sin

cos

sin

u t

u t

u t

R I

t

L I

t

U

t

ω ω

ω

ω ϕ

=

+

= ⋅

+

⋅

=

+

.

(2.30)

Naszym zadaniem jest wyznaczenie wartości U

m

oraz

ϕ

opisujących napięcie całkowite u(t).

W tym celu po przekształceniu prawej strony trzeba porównać współczynniki przy sin i cos

(

)

m

m

m

m

m

m

m

sin

cos

sin

cos

cos

sin

cos

sin

R I

t

L I

t

U

t

t

R I

U

L I

U

ω ω

ω

ω

ϕ

ω

ϕ

ϕ

ω

ϕ

⋅

+

⋅

=

+

⋅

=





⋅

=



(2.31)

Podzielenie tych dwóch wzorów przez siebie powoduje uproszczenie U

m

i daje kąt fazowy

ϕ

,

arctg

(wystarczy =0)

L

L

tg

k

k

R

R

ω

ω

ϕ

ϕ

=

=

± π

.

(2.32)

Podniesienie obustronne do kwadratu i dodanie równań stronami, po uwzględnieniu wzoru
jedynkowego, daje U

m

:

(

) (

)

(

)

(

)

2

2

2

2

2

2

2

2

2

m

m

m

m

m

R

L

sin

cos

;

RI

LI

U

U

I

R

L

U

U

U

ω

ϕ

ϕ

ω

+

=

+

⇒

=

+

=

+

(2.33)

Wielkość występująca we wzorze

(

)

2

2

R

L

ω

+

jest impedancją Z gałęzi szeregowej RL.

Moc chwilowa pulsuje wokół osi x z przewagą części dodatnich:

(

)

2

m

m

m m

1

( )

sin

sin

sin

cos

sin 2

sin

2

p t

U

t

I

t

U I

t

t

ω ϕ

ω

ω

ϕ

ω

ϕ





=

+

⋅

=

+









,

(2.34)

skąd wynika wartość mocy czynnej dla obwodu szeregowego RL:

m m

0

1

( )d

cos

cos

2

T

U I

P

p t

t

U I

T

ϕ

ϕ

=

=

= ⋅ ⋅

∫

.

(2.35)

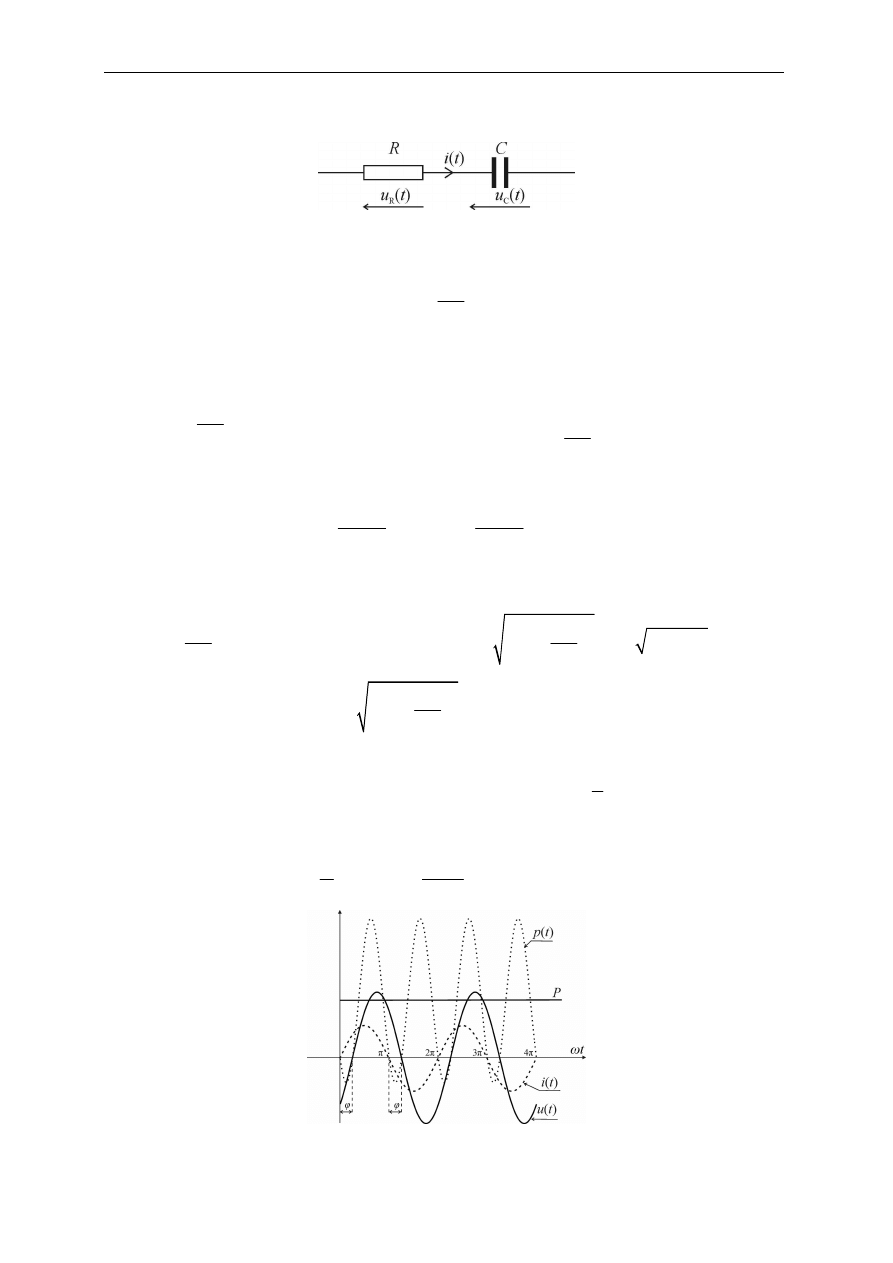
Rys. 2.18. Przebiegi napięcia, prądu i mocy dla gałęzi szeregowej RL

Obwody prądu zmiennego

12/15

Na rysunku 2.19 widoczna jest gałąź RC, przez którą przepływa prąd

m

( )

sin

i t

I

t

ω

=

.

Rys. 2.19. Gałąź szeregowa RC zasilana prądem i(t)

Na podstawie wzorów 2.19 oraz 2.26 można podać napięcie całkowite w postaci

(

)

(

)

o

R

C

m

m

m

1

( )

( )

( )

sin

sin

90

sin

u t

u t

u t

R I

t

I

t

U

t

C

ω

ω

ω ϕ

ω

=

+

= ⋅

+

−

=

+

(2.36)

Naszym zadaniem jest wyznaczenie wartości U

m

oraz

ϕ

opisujących napięcie całkowite u(t).

W tym celu po przekształceniu prawej strony trzeba porównać współczynniki przy sin i cos

(

)

m

m

m

m

m

m

m

cos

1

sin

cos

sin

cos

cos

sin

1

sin

RI

U

RI

t

I

t

U

t

t

C

I

U

C

ϕ

ω

ω

ω

ϕ

ω

ϕ

ω

ϕ

ω

=





−

=

+



−

=



(2.37)

Podzielenie tych dwóch wzorów przez siebie powoduje uproszczenie U

m

i daje kąt fazowy

ϕ

1

1

tg

,

arctg

k

k

R

C

R

C

ϕ

ϕ

ω

ω

= −

= −

± π ( = 0)

⋅

⋅

(2.38)

Podniesienie obustronne do kwadratu i dodanie równań stronami, po uwzględnieniu wzoru
jedynkowego, daje U

m

:

(

)

(

)

2

2

2

2

2

2

2

2

2

m

m

m

m

m

R

C

1

1

sin

cos

;

RI

I

U

U

I

R

U

U

U

C

C

ϕ

ϕ

ω

ω









+

=

+

⇒

=

+

=

+

















(2.39)

Wielkość występująca we wzorze

2

2

1

R

C

ω





+









jest impedancją Z gałęzi szeregowej RC.

Moc chwilowa pulsuje wokół osi x z przewagą części dodatnich:

(

)

2

m

m

m m

1

( )

sin

sin

sin

cos

sin 2

sin

2

p t

U

t

I

t

U I

t

t

ω ϕ

ω

ω

ϕ

ω

ϕ





=

+

⋅

=

+









(2.40)

skąd wynika wartość mocy czynnej dla obwodu szeregowego RC:

m m

0

1

( )d

cos

cos

2

T

U I

P

p t

t

U I

T

ϕ

ϕ

=

=

= ⋅ ⋅

∫

.

(2.41)

Rys. 2.20. Przebiegi napięcia, prądu i mocy dla gałęzi szeregowej RC

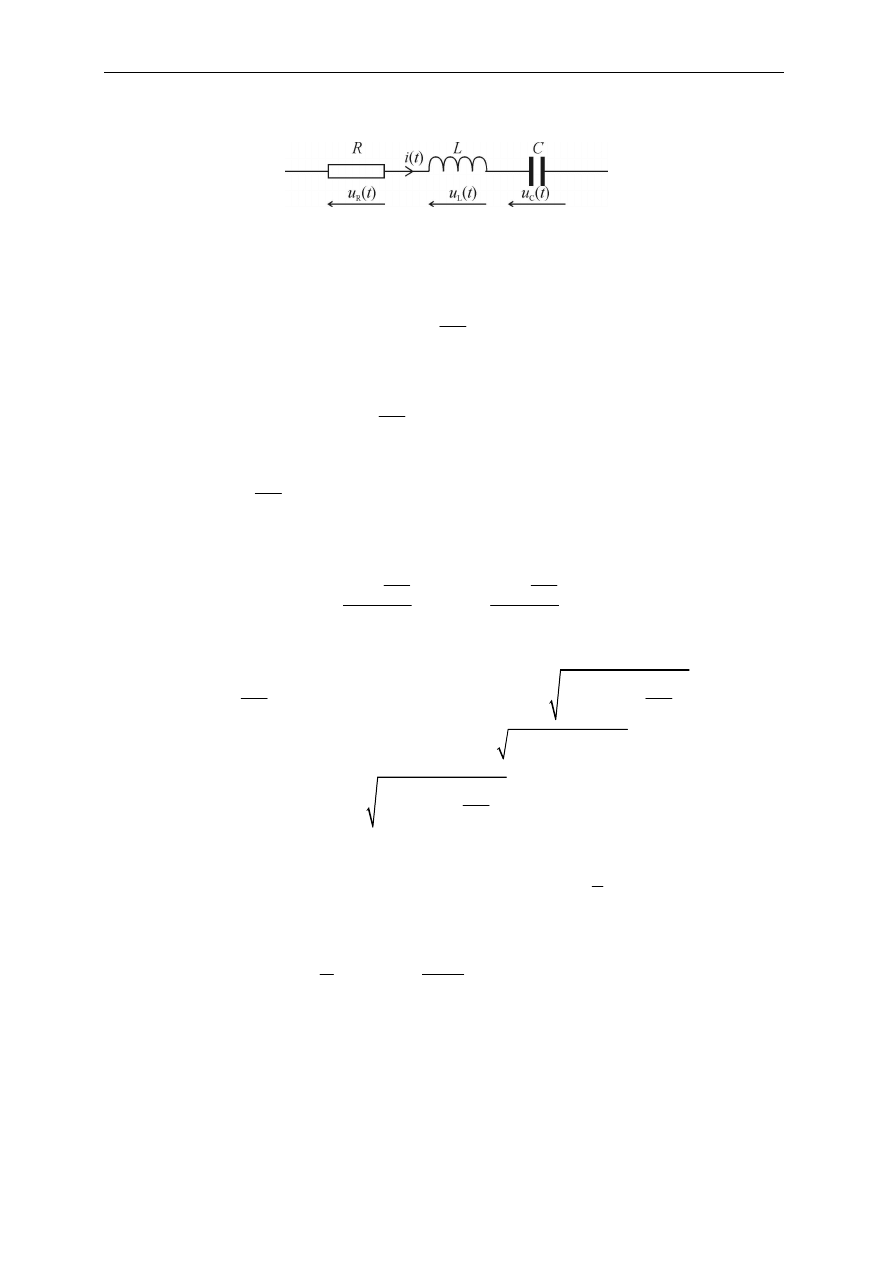
Obwody prądu zmiennego

13/15

Na rysunku 2.21 widoczna jest gałąź RLC, przez którą przepływa prąd

m

( )

sin

i t

I

t

ω

=

.

Rys. 2.21. Gałąź szeregowa RLC zasilana prądem i(t)

Na podstawie wzorów (2.19), (2.22) oraz (2.26) można podać napięcie całkowite w postaci

(

)

(

)

(

)

m

R

L

C

o

o

m

m

m

m

( )

sin

,

( )

( )

( )

( )

1

sin

sin

90

sin

90

sin

i t

I

t u t

u t

u t

u t

RI

t

LI

t

I

t

U

t

C

ω

ω ω

ω

ω

ω ϕ

ω

=

=

+

+

=

=

+

+

+

−

=

+

(2.42)

W celu wyznaczenia wartości U

m

oraz

ϕ

trzeba porównać współczynniki przy sin i cos

(

)

m

m

m

m

m

m

m

m

m

1

sin

cos

cos

sin

cos

cos

sin

cos

1

sin

RI

t

LI

t

I

t

U

t

t

C

RI

U

LI

I

U

C

ω ω

ω

ω

ω

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

ω

+

−

=

+

=







−

=



(2.43)

Podzielenie tych dwóch wzorów przez siebie powoduje uproszczenie U

m

i daje kąt fazowy

ϕ

1

1

,

arctg

L

L

C

C

tg

k

R

R

ω

ω

ω

ω

ϕ

ϕ

−

−

=

=

± π

(2.44)

Podniesienie obustronne do kwadratu i dodanie równań stronami daje U

m

:

(

)

(

)

(

)

2

2

2

2

2

2

2

m

m

m

m

m

m

2

2

R

L

C

1

1

sin

cos

;

RI

LI

I

U

U

I

R

L

C

C

U

U

U

U

ω

ϕ

ϕ

ω

ω

ω









+

−

=

+

⇒

=

+

−

















=

+

−

(2.45)

Wielkość występująca we wzorze

2

2

1

R

L

C

ω

ω





+

−









jest impedancją Z gałęzi szeregowej

RLC. Moc chwilowa pulsuje wokół osi x z przewagą części dodatnich:

(

)

2

m

m

m m

1

( )

sin

sin

sin

cos

sin 2

sin

2

p t

U

t

I

t

U I

t

t

ω ϕ

ω

ω

ϕ

ω

ϕ





=

+

⋅

=

+









(2.46)

skąd wynika wartość mocy czynnej dla obwodu szeregowego RLC:

m m

0

1

( )d

cos

cos

2

T

U I

P

p t

t

U I

T

ϕ

ϕ

=

=

= ⋅ ⋅

∫

.

(2.47)

Obwody prądu zmiennego

14/15

2.6.

Wykresy trójkątowe dla gałęzi RL, RC oraz RLC

Wykresy trójkątowe pozwalają na graficzne przedstawienie relacji pomiędzy

impedancjami, napięciami lub mocami występującymi w obwodzie. Wykorzystują one fakt,
ż

e wzory opisujące uzyskiwanie impedancji obwodu Z (2.33), (2.39) i (2.45) są analogiczne

do wzorów opisujących boki trójkąta prostokątnego:

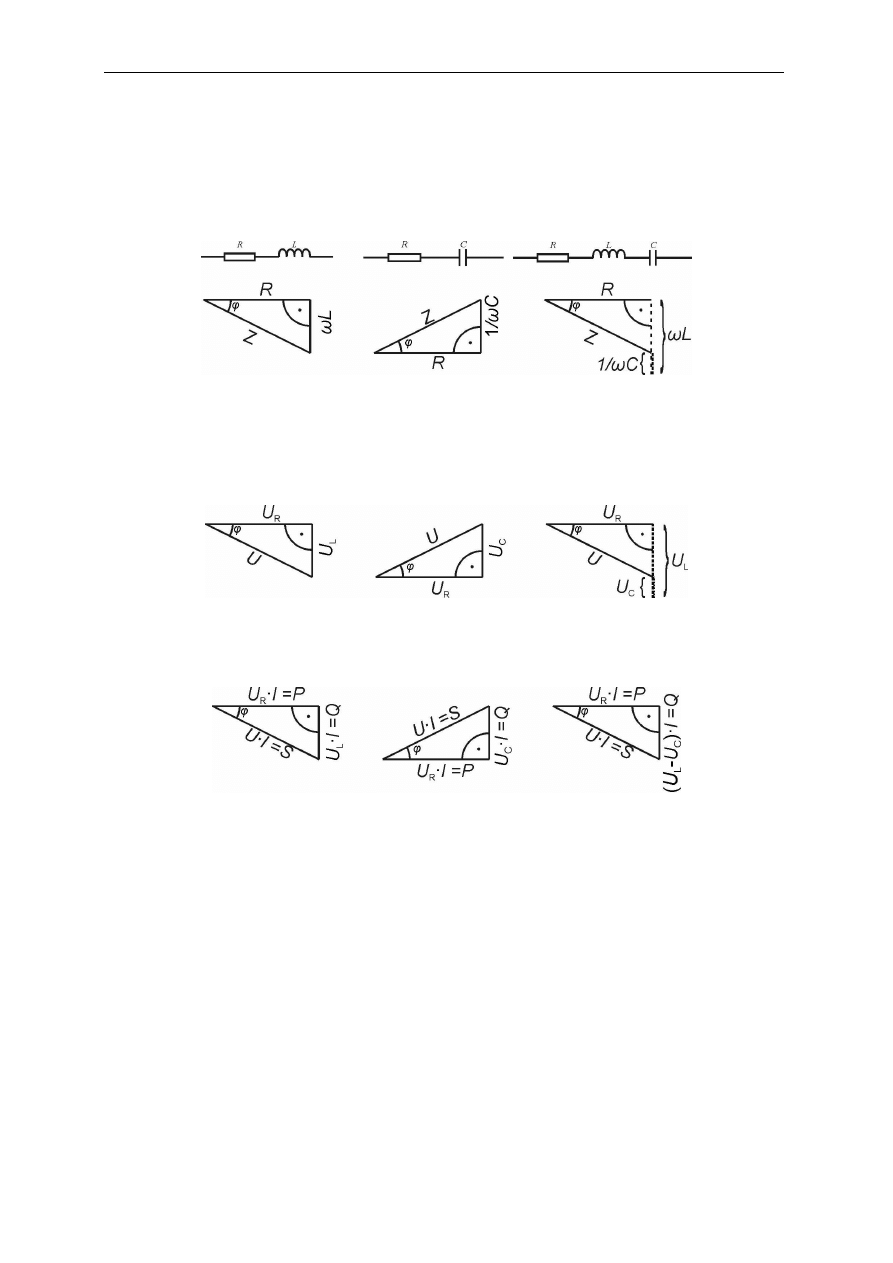
Rys. 2.22. Wykresy trójkątowe impedancji gałęzi RL, RC oraz RLC

W przypadku wykresu po prawej stronie, dotyczącego gałęzi RLC, założono wartość
reaktancji indukcyjnej większą od reaktancji pojemnościowej.
Po pomnożeniu boków trójkątów przez wartość skuteczną prądu płynącego w obwodzie
wykresy te przeskalowywują się na wykresy napięć na elementach obwodu.

Rys. 2.23. Wykresy trójkątowe napięć na elementach obwodów RL, RC oraz RLC

Po powtórnym pomnożeniu boków trójkątów przez wartość prądu stają się one mocami
występującymi w obwodzie:

Rys. 2.24. Moce występujące w gałęziach RL, RC oraz RLC

Moc czynna

cos

P

U I

ϕ

= ⋅ ⋅

jest już znana z wyprowadzeń przeprowadzonych powyżej.

Iloczyn napięcia i prądu jest zwany mocą pozorną S

U I

= ⋅

. Trzeci bok trójkąta jest mocą

„uzupełniającą” nazywaną mocą bierną

sin

Q

U I

ϕ

= ⋅ ⋅

. Występowanie mocy biernej jest

związane z obecnością w obwodzie elementów zachowawczych, które nie rozpraszają energii,
lecz ją gromadzą oddając następnie z powrotem. Jest to moc bezproduktywna, którą w
układach energetycznych staramy się minimalizować.

Obwody prądu zmiennego

15/15

2.7.

Moce w obwodach prądu sinusoidalnie zmiennego

Przedstawiono tu zebrane razem definicje wszystkich mocy, którymi posługujemy się w
obwodach z prądem zmiennym.

0

Moc chwilowa:

( )

( ) ( )

1

Moc czynna:

( )d

T

p t

u t i t

P

p t

t

T

=

⋅

=

∫

(2.48)

Te dwie definicje można stosować przy przebiegach zmieniających się w sposób dowolny. W
szczególnym przypadku przebiegów sinusoidalnie zmiennych otrzymujemy wzory:

2

2

2

Moc czynna:

cos ;

Moc bierna:

sin ;

Moc pozorna:

;

Stąd wynikają zależności:

cos ;

sin ;

;

P

U I

Q

U I

S

U I

P

S

Q

S

P

Q

S

ϕ

ϕ

ϕ

ϕ

= ⋅ ⋅

= ⋅ ⋅

= ⋅

= ⋅

= ⋅

+

=

(2.49)