III. Diody półprzewodnikowe
1
III. Diody półprzewodnikowe
Wstęp
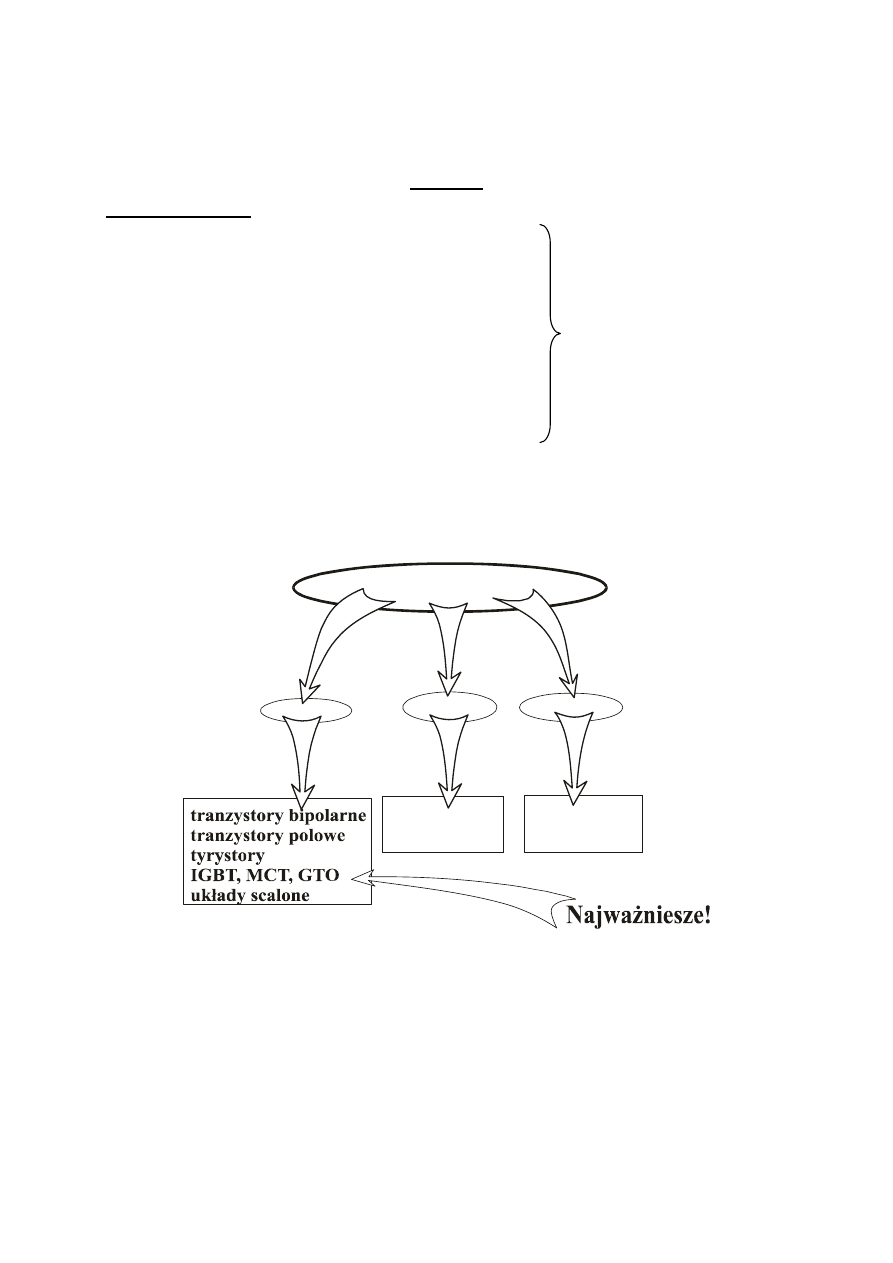
Podział złączy
•
złącza p-n, w którym styk tworzą obszary
p oraz n z tego samego materiału
półprzewodnikowego, np. krzemu,
•
złącza m-s, w których w kontakcie
pozostają obszary półprzewodnika i metalu,
•
heterozłącza, w których pozostają w
kontakcie dwa różne materiały
półprzewodnikowe, (Ge – Si)
•
struktura MIS (metal–izolator–półprzewodnik)
⇐
p-n
m-s
MIS
diody
Schottky
tranzystory
polowe
Praktyczne wykorzystanie złączy
diody
Schottky
tranzystory
polowe
Rys. 3.1
ch – ki
i(u)
ch – ki
C(u)
III. Diody półprzewodnikowe
2
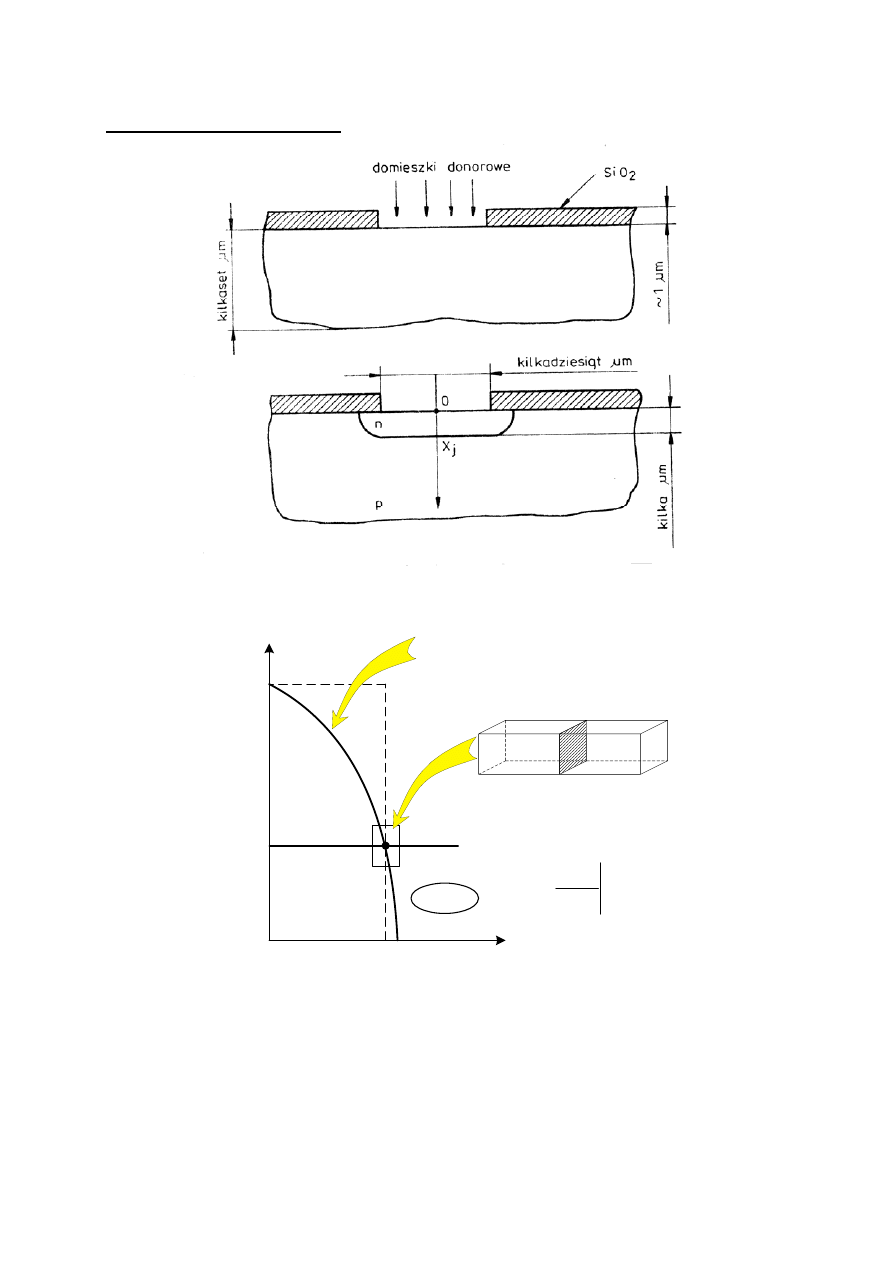
Technologia złącza p-n
Zależność N
D
, N
A
= f(x)
10
18
10
17
10
16
10
15
x
j
N
A
x
N
D
N
A
(baza)
x
j
[cm
-3
]
N
D
,N
A
baza
( )
( )
j
A
j
D
x
N
x
N
=
∞
→
x
dx
dN
j
D
N
D
Rys. 3.3
x
Si, typ p, N
A
= 10
15
cm
-3
a)
b)
Rys. 3.2
III. Diody półprzewodnikowe
3
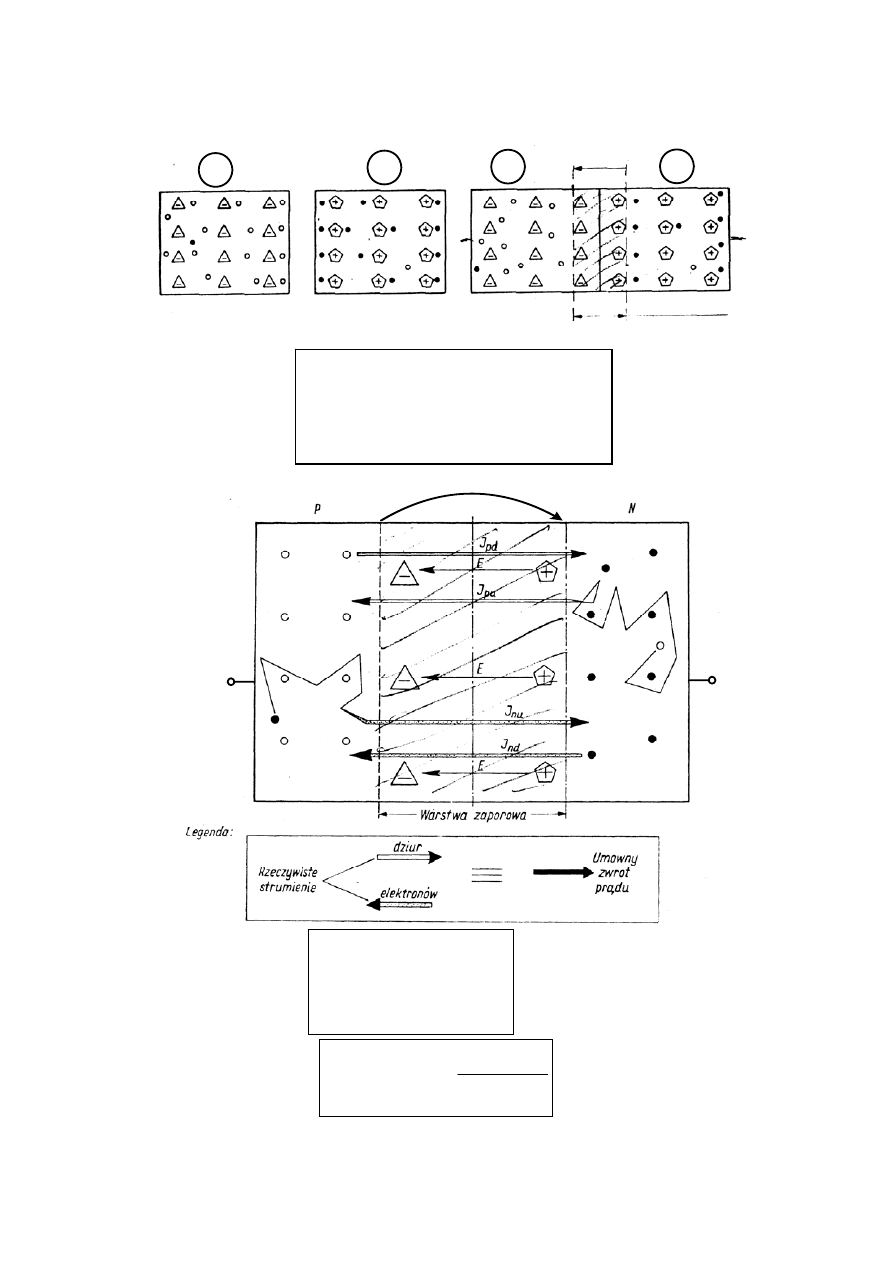
Złącze niespolaryzowane (u = 0)
Rys. 3.4
obszar ładunku przestrzennego
obszar opróżniony złącza
obszar przejściowy
warstwa zaporowa złącza
napięcie kontaktowe
napięcie dyfuzyjne
napięcie bariery
napięcie wbudowane
2
i
D
A
T
B
n
N
N
ln
U
U
⋅
⋅
=
(3.2)
dla S
i
w temperaturze 300K →
mV
700
U
B
≈
n
p
<<
p
n
<<
2
i
n
np
=
P
P
N
N
Warstwa zaporowa
U
B
Rys. 3.5
III. Diody półprzewodnikowe
4
p
n
-x
n
x
p
x
x
-x
n
x
p
x
p
Q
-x
n
obszar
neutralny
obszar
neutralny
U
B
D
N
q
⋅
warstwa
zaporowa
A
N
q
⋅
−
E
mx
E
x
a)
b)
c)
U
D
>
N
A
•
Słuszna jest zależność
p
D
n
A
x
N
x
N
⋅
=
⋅
(3.4)
•
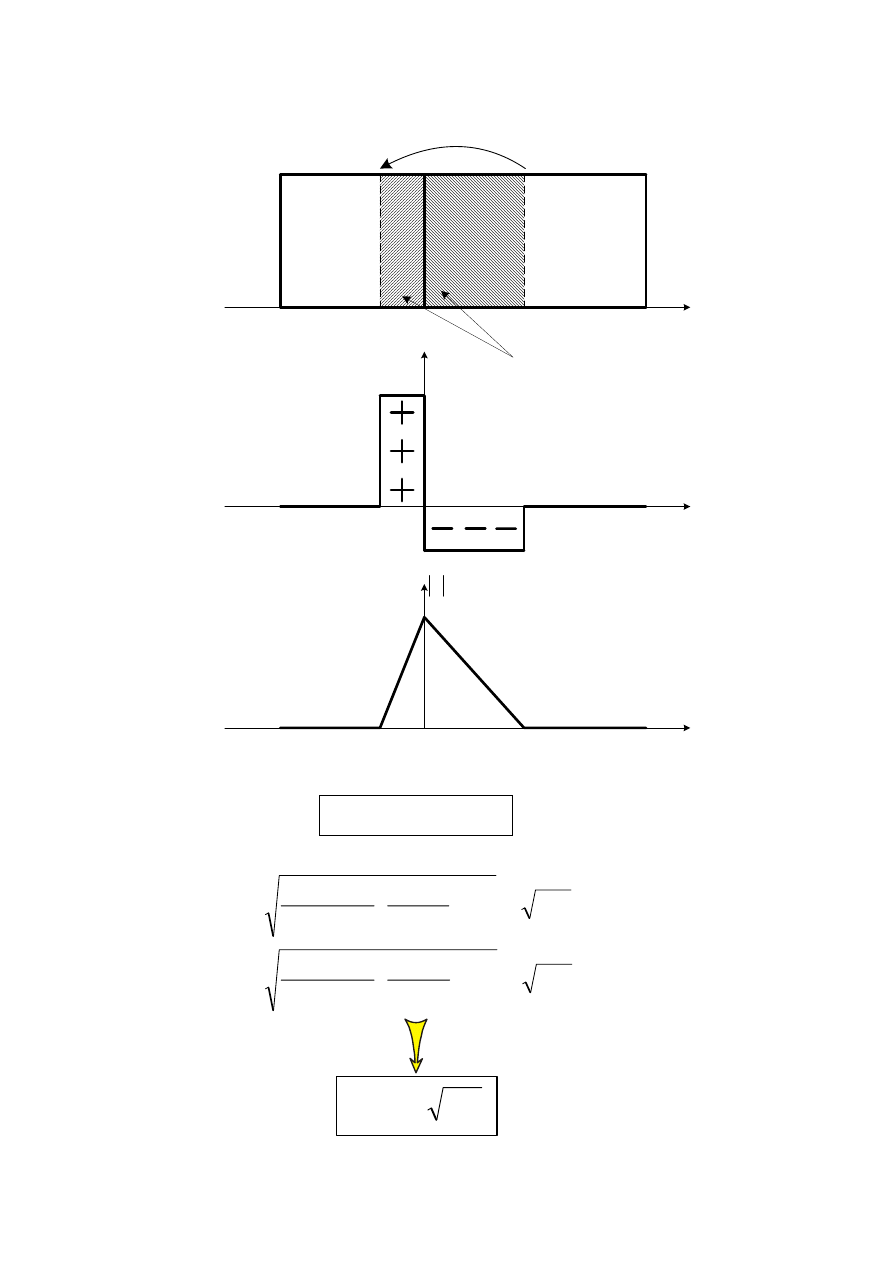
Grubość obszarów opróżnionych
B
B
D
A
D
A
0
n
U
~
U
N
q
N
N
N
2
x
⋅
⋅
⋅
+
εε
=
(3.6a)
B
B
A
D
D
A
0
p
U
~
U
N
q
N
N
N
2
x
⋅
⋅
⋅
+
εε
=
(3.6b)
B
p
n
U
~
,
x
Rys. 3.6
III. Diody półprzewodnikowe
5
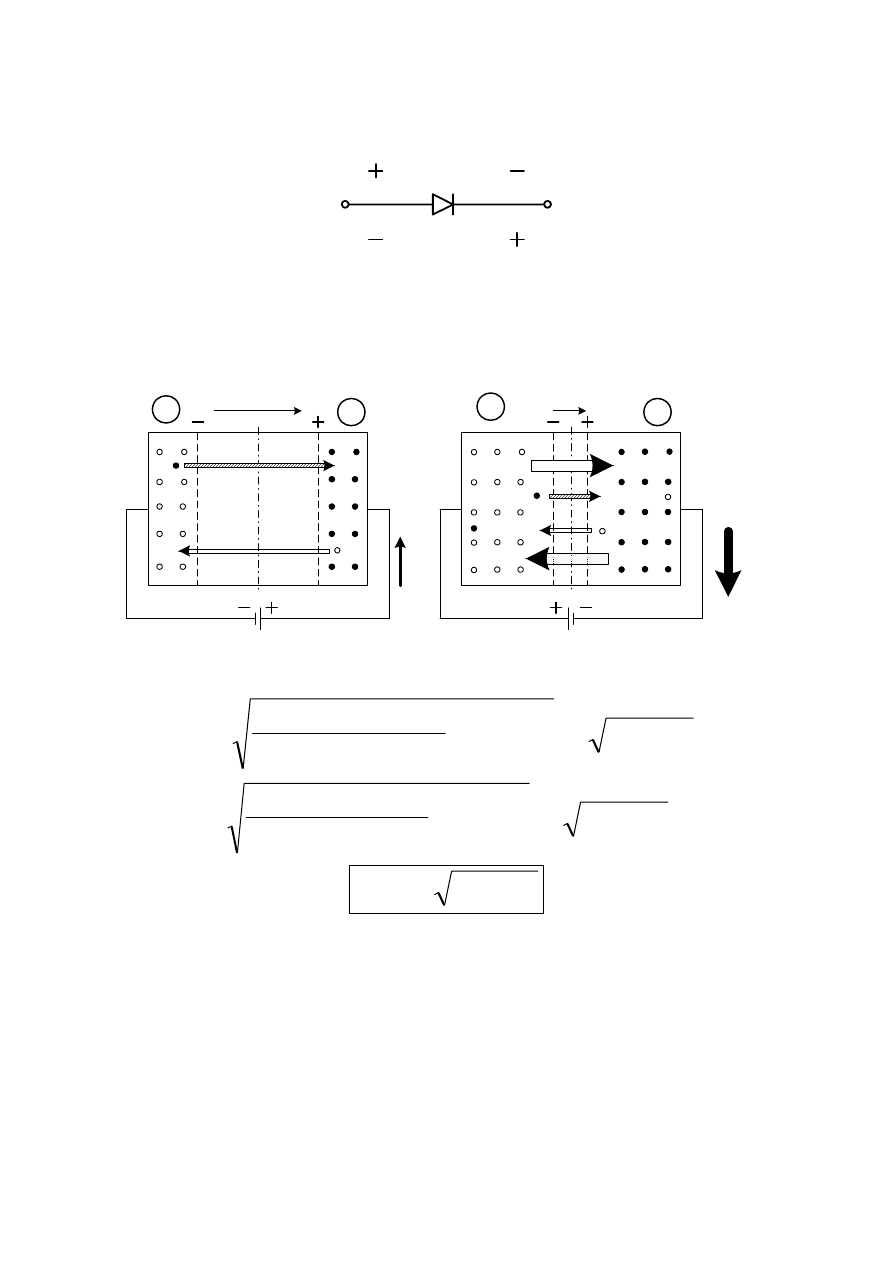
Złącze spolaryzowane
Kierunek
przewodzenia
Kierunek
zaporowy
Rys. 3.7
•
Kierunek zaporowy
•
Kierunek przewodzenia
E
I
u
U
B
+ E
E
I
d
-I
u
U
B
- E
a)
b)
I
nu
I
pu
I
pd
I
nu
I
pu
I
nd
N
P
N
P
Rys. 3.8
(
)(
)
u
U
N
N
qN
N
2
X
B
D
A
D
A
0
n
−
+
εε
=
~
u
U
B
−
(3.7a)
(
)
u
U
N
)
N
N
(
q
N
2
X
B
A
d
A
D
0
p
−
+
εε
=
~
u
U
B
−
(3.7b)
u
U
~
,
x
B
p
n
−
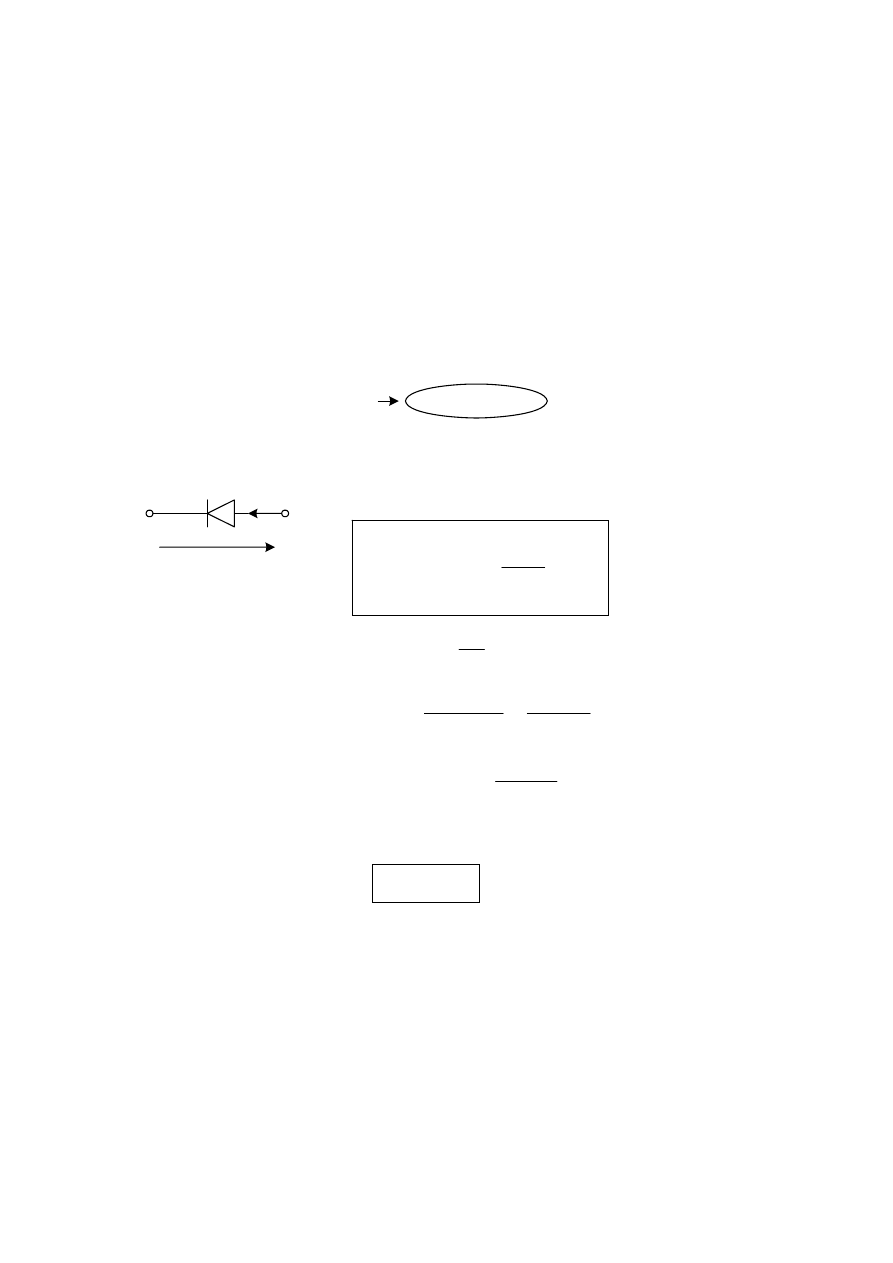
III. Diody półprzewodnikowe
6
Charakterystyka statyczna i(u) złącza idealnego
•
złącze skokowe
•
jednowymiarowy charakter zjawisk w złączu
•
niski poziom wprowadzania
•
pole elektryczne występuje tylko w warstwie zaporowej
•
rezystywność obszarów neutralnych = 0
•
brak procesów gen.– rekomb. w obszarze ładunku przestrz.
•
nie występują efekty przebicia
złącze idelane
Gdy warunki te są spełnione
Wzór na statyczną charakterystykę prądowo – napięciową i(u) złącza
idealnego ma postać
gdzie:
•
potencjał termiczny
q
kT
U
T
=
(3.9)
•
prąd nasycenia
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⋅
⋅
⋅
=
D
p
p
A
n
n
2
i
S
N
L
D
N
L
D
n
S
q
I
(3.10)
•
dla złącza
p+n
D
p
p
2
i
S
N
L
D
n
S
q
I
⋅
⋅
=
(3.11)
p+n
Dla krótkiej bazy
L
p
→ W
n
•
Można napisać, że:
2
i
S
n
S
~
I
⋅
(3.12)
∈
S
I
(nanoampery, pikoampery)
Model wielkosygnałowy
statyczny
B
u
A
i
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⋅
=
1
U
u
exp
I
i
T
S
(3.8)
III. Diody półprzewodnikowe
7
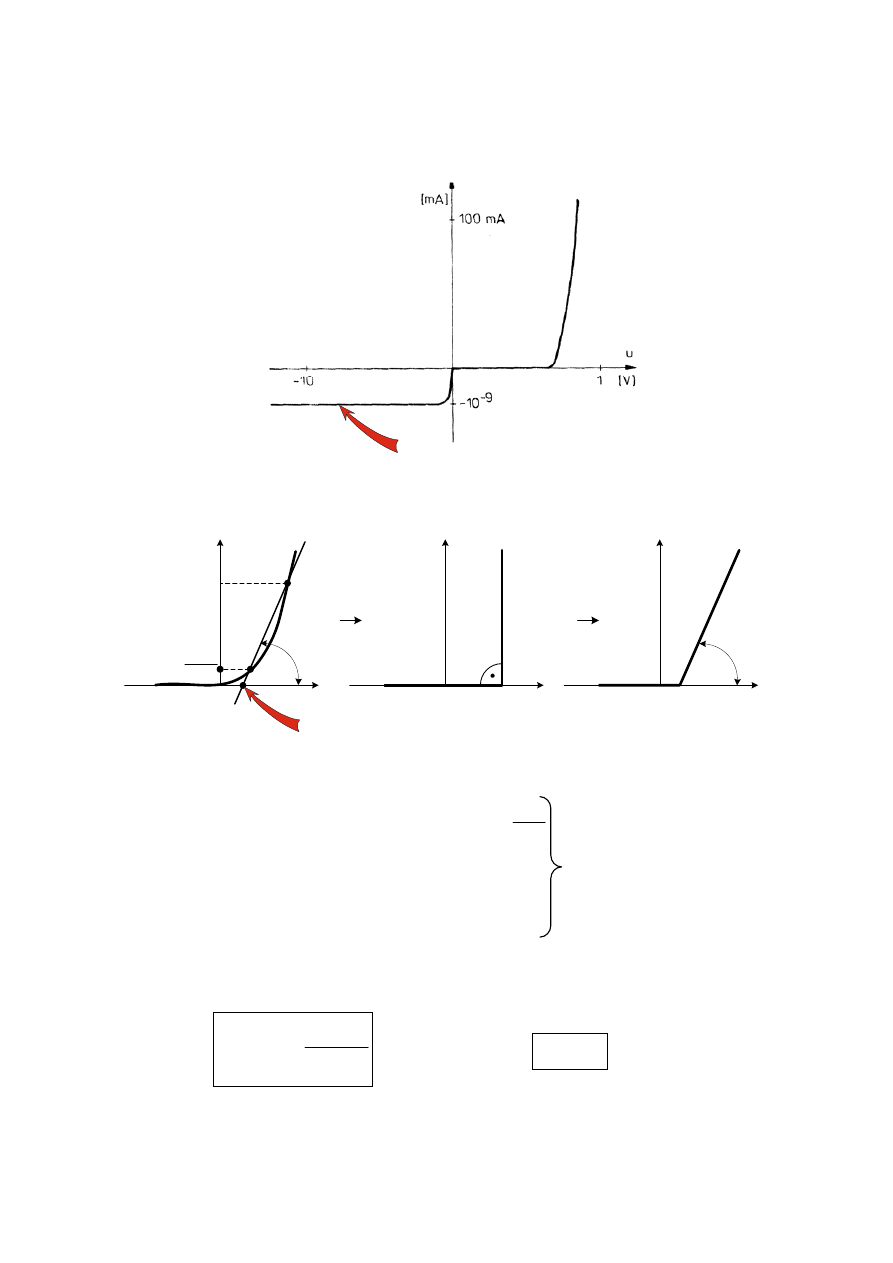
Postać graficzna modelu
•
Skala log-lin (przykład liczbowy)
Rys. 9
•
Charakterystyka odcinkowo – liniowa
U
p
i
u
100
i
max
max
i
U
p
i
u
U
p
i
u
a)
b)
c)
α
α
Rys. 3.10
Uproszczenia
• dla
T
U
4
u
⋅
≥
:
T
S
U
u
exp
I
i
=
(3.13a)
błąd < 1-2%
• dla
T
U
4
u
⋅
≤
:
s
I
i
−
=
(3.13b)
Inercja elektryczna
•
Pojemność dyfuzyjna (C
d
)
T
S
d
U
I
i
C
+
⋅
τ
=
czyli
i
~
C
d
(3.14)
-I
S
III. Diody półprzewodnikowe
8
•
Pojemność złączowa (C
j
)
B
U
u
0
j
j
1
C
C
−
=
(3.16)
C
j0
=C(u = 0)
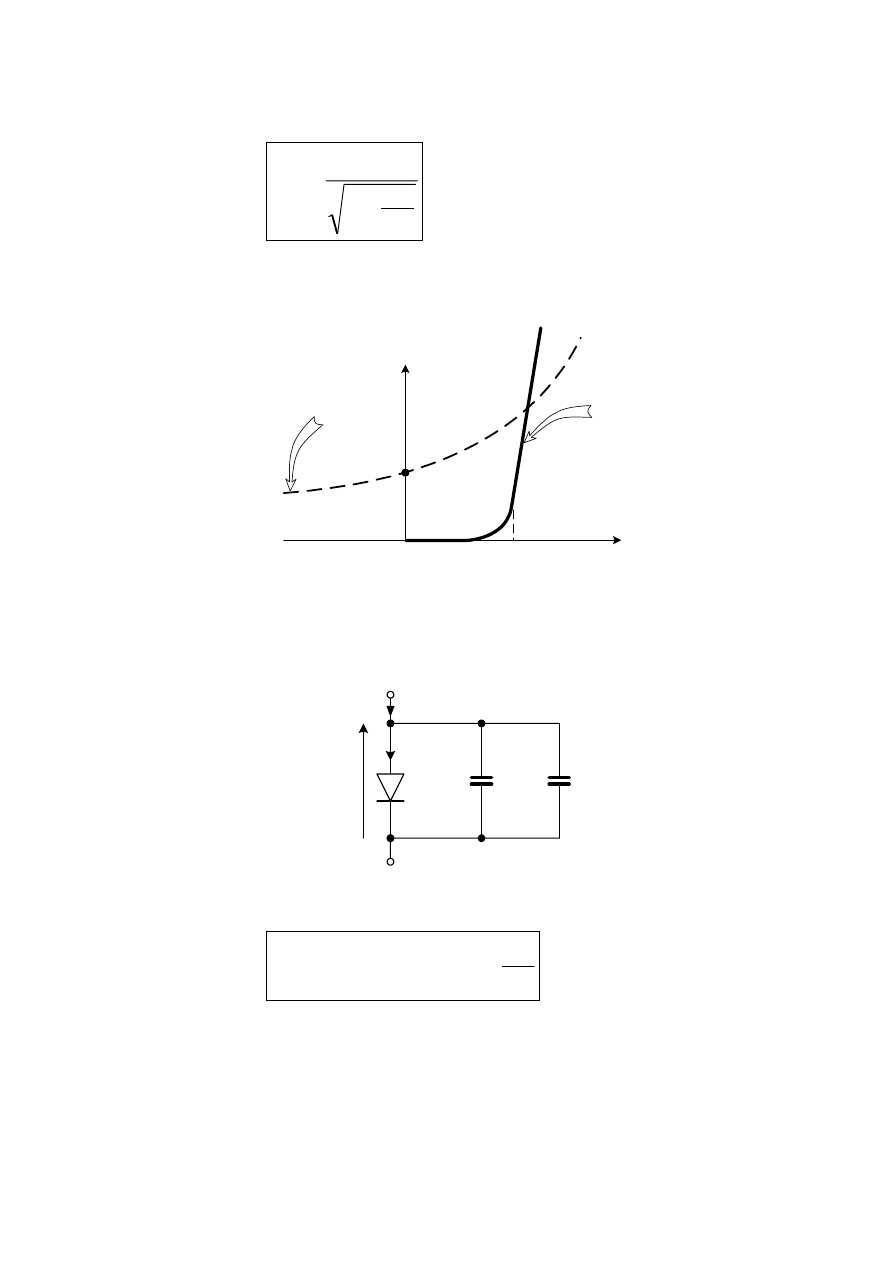
Zależność graficzna pojemności od napięcia na złączu
C
j
(0)
u
C
j
C
d
U
p
C
d
C
j
Rys. 3.11
Wielkosygnałowy dynamiczny model diody p-n
•
postać symboliczna
u
)
u
(
i
t
i
j
C
d
C
Rys. 3.12
•
postać analityczna
( )
(
)
dt
du
C
C
u
i
i
d
j
t
⋅
+
+
=
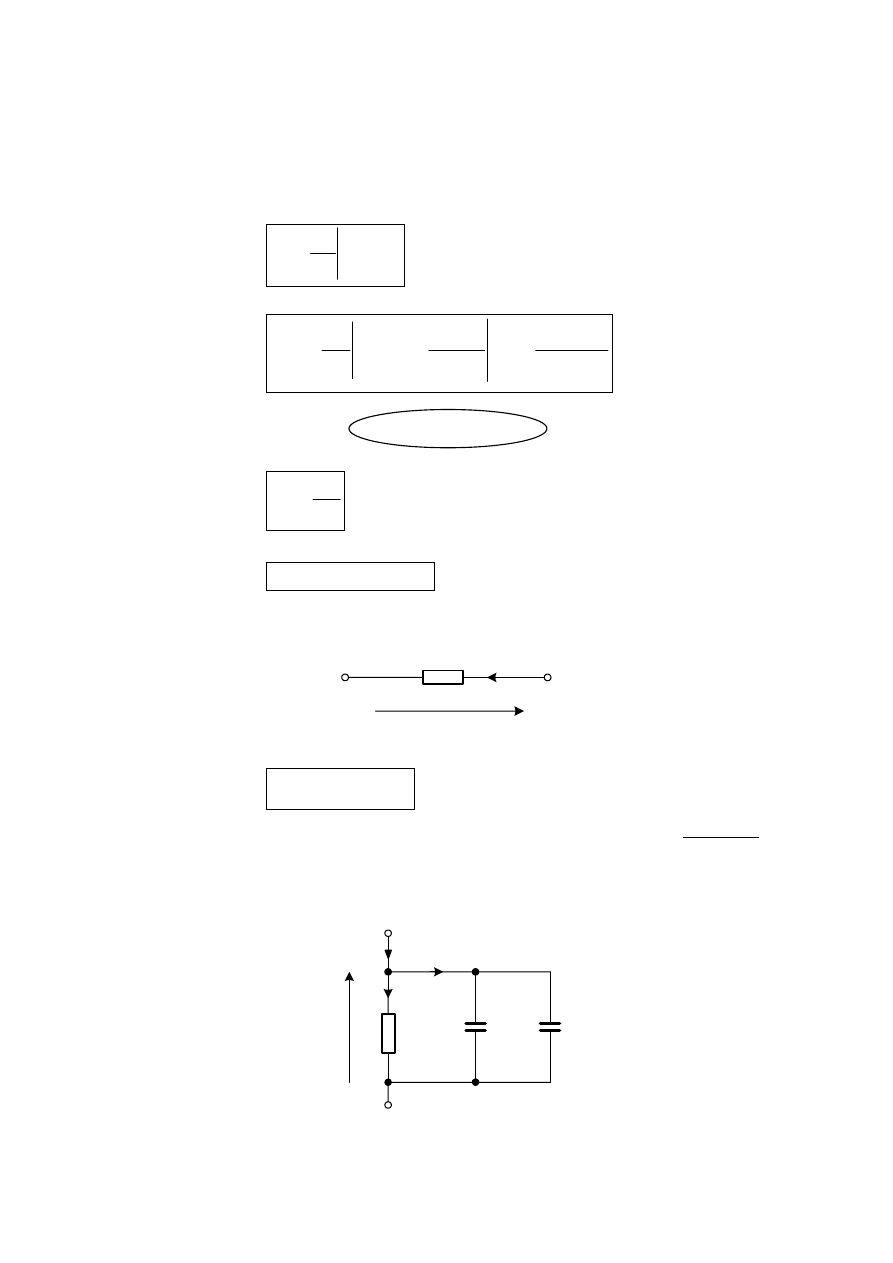
III. Diody półprzewodnikowe
9
Parametry małosygnałowe idealnego złącza p-n
Jak wynika z rozdz. 1 mały przyrost prądu
I
a
diody opisanej wzorem
i
A
= f(u
AB
)
wokół pkt. pracy o współrzędnych
(I
0
,U
0
)
jest równy różniczce
funkcji opisującej zależność i od u.
ab
P
a
U
du
di
I
⋅
=
(3.19)
gdzie przewodność dyfuzyjna:
T
S
0
I
T
S
U
,
I
d
U
I
I
U
I
i
du
di
g
0
0
0
+
=
+
=
=
(3.20)
np.: dla I
0
=1mA, T=300K,
g
d
=40mS, r
d
=25Ω
Rezystancja dyfuzyjna:
d
d
g
1
r
=
(3.21)
Przy polaryzacji zaporowej
I
0
= -I
S
→ g
d
= 0
(3.22)
W analizie małosygnałowej konduktacja (rezystancja) dyfuzyjna może być
przedstawiona za pomocą rezystora liniowego.
d
g
a
I
ab
U
A
B
Rys. 3.13
A zatem dla małych amplitud sygnału harmonicznego można zapisać
a
d
ab
I
r
U
⋅
=
(3.23)
Konduktancja dyfuzyjna opisuje związek między
U
ab
oraz
I
a
jaki ustali się po
czasie >>
τ
p
i τ
n
.
•
model małosygnałowy dla w. cz.
ab
U
a
I
t
I
j
C
d
C
A
B
d
g
dj
I
Rys. 3.14
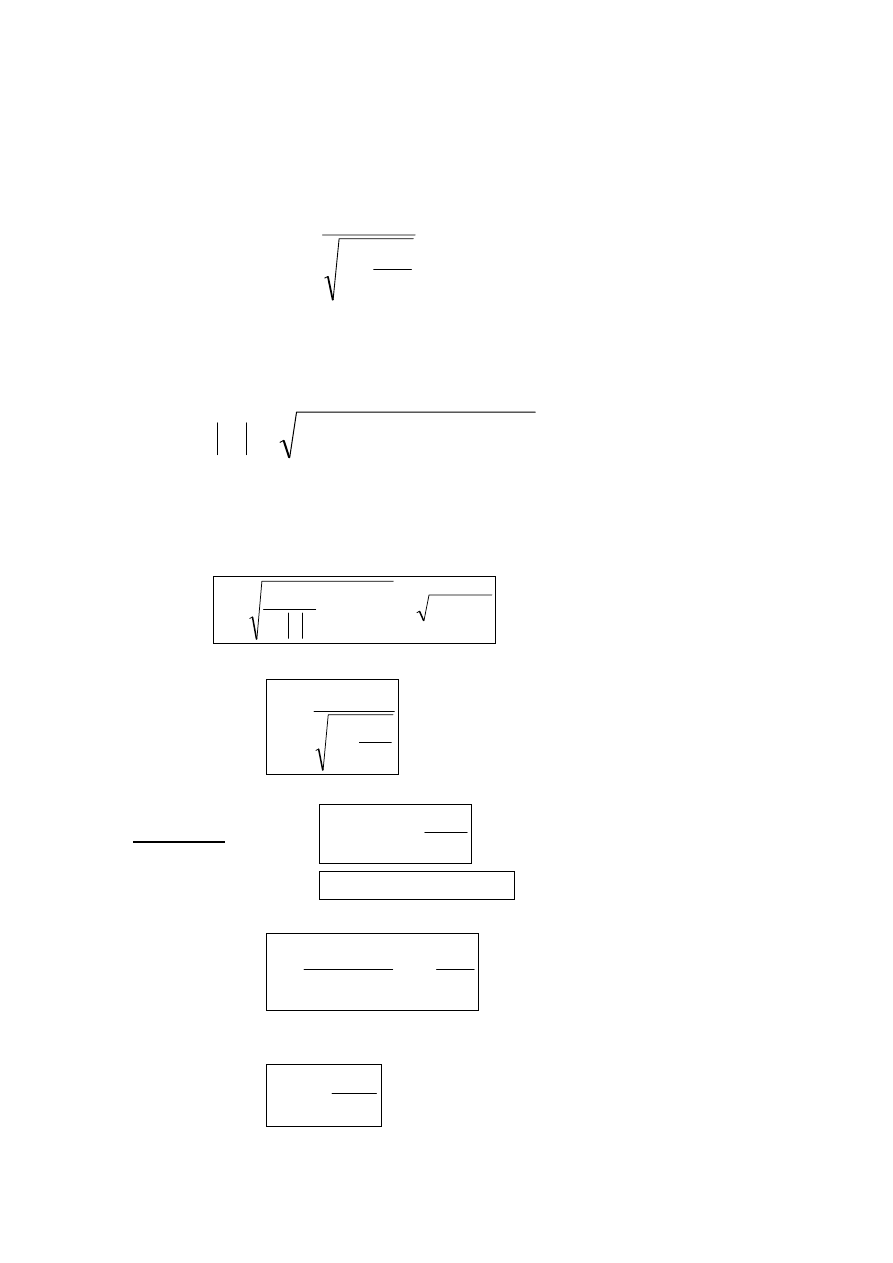
III. Diody półprzewodnikowe
10
Stąd
(
)
j
d
d
C
C
j
g
Y
+
ω
+
=
(3.24)
gdzie
0
d
I
~
C
( )
B
0
j
j
U
U
1
0
C
C
−
=
dla przedstawionego modelu zachodzą związki
j
d
a
t
I
I
I
+
=
(3.25a)
ab
t
U
Y
I
⋅
=
(3.25b)
(
)
ab
2
j
d
2
2
d
t
U
C
C
g
I
⋅
+
ω
+
=
(3.25c)
Właściwości diod rzeczywistych
Liniowy rozkład domieszek
•
szerokości obszaru opróżnionego
(
)
3
B
3
B
0
u
U
~
u
U
a
q
12
d
−
−
εε
=
(3.26)
•
pojemności złączowej
3
B
0
j
j
U
u
1
C
C
−
=
(3.27)
Wysoki poziom wprowadzania (WPW)
Dla WPW
:
T
ws
nU
U
exp
I
i
⋅
=
(3.28)
gdzie:
n>1
,
I
ws
>> I
S
, 1 < n < 2
Inny stosowany opis:
T
H
S
U
u
exp
I
/
i
1
I
i
+
=
(3.29)
gdzie
I
H
– tzw. prąd kolana (prąd graniczny)
Jeżeli
i >> I
H
wówczas:
T
U
2
u
exp
~
i
tzn.
n = 2
we wzorze (3.28)
III. Diody półprzewodnikowe
11
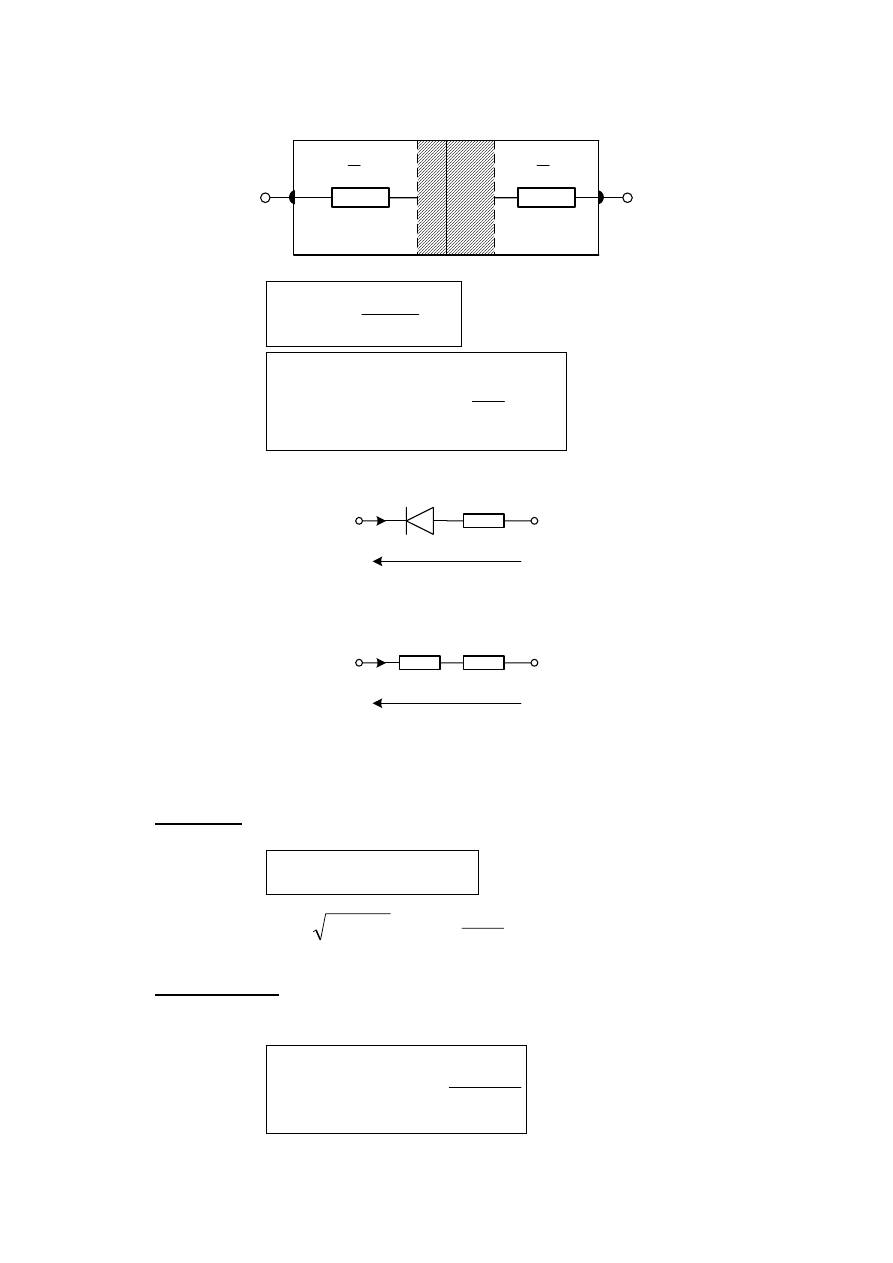
Rezystancja szeregowa diody
s
r
2
1
s
r
2
1
Rys. 3.15
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
=
1
U
i
r
u
exp
I
i
T
S
S
(3.31)
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
=
1
I
i
ln
U
ir
u
S
T
S
(3.32)
•
dla przypadku stałoprądowego
AB
u
s
r
A
i
B
A
Rys. 3.16
•
dla małego sygnału
(po zróżniczkowaniu zależności (3.32))
ab
U
s
r
a
I
B
A
d
r
Rys. 3.17
Procesy generacji i rekombinacji nośników w warstwie
zaporowej złącza
•
generacja
– dla kierunku zaporowego, dodatkowa składowa prądu
generacyjnego.
)
u
(
d
n
g
i
i
G
⋅
⋅
=
(3.34)
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⋅
−
kT
2
W
exp
u
U
~
i
0
g
B
G
(3.35)
•
rekombinacja
– dla kierunku przewodzenia część nośników w obszarze
bariery rekombinuje, stąd dodatkowa składowa prądu rekombinacyjnego
I
R
wynosi:
T
RS
R
mU
u
exp
I
i
⋅
=
(3.37)
III. Diody półprzewodnikowe
12
Zjawiska przebić złącza
•
zjawisko Zenera
•
zjawisko jonizacji zderzeniowej
(powielanie lawinowe
→
gdy duże napięcie)
0
w
i
M
i
⋅
=
(3.39)
gdzie:
i
w
– prąd wsteczny w zakresie powielania lawinowego
i
0
– prąd przy braku powielania
M
– współczynnik powielania lawinowego (formalnie też zjawisko
Zenera) o postaci:
η
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
Z
U
u
1
1
M
(3.40)
U
Z
– napięcie przebicia przy którym prąd
→ ∞
η – zależy od rodzaju złącza
( )
6
,
2
∈
η
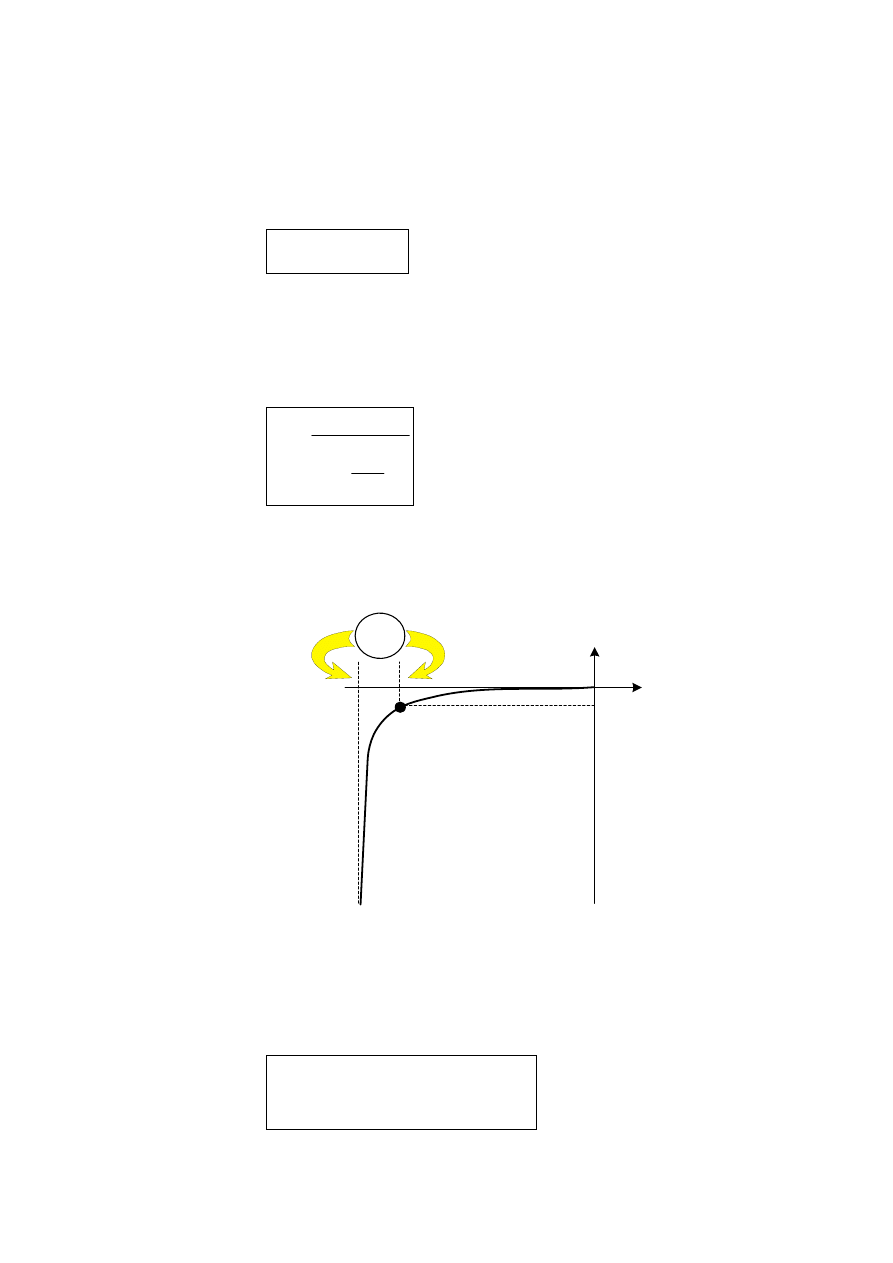
10mA
u
Definicja
formalna
i
Definicja
praktyczna
Z
U
Rys. 3.18
Podsumowanie diod rzeczywistych
•
Kierunek zaporowy
(
)
u
i
S
G
CW
I
I
i
M
i
0
+
+
⋅
=
4
8
47
6
(3.50)
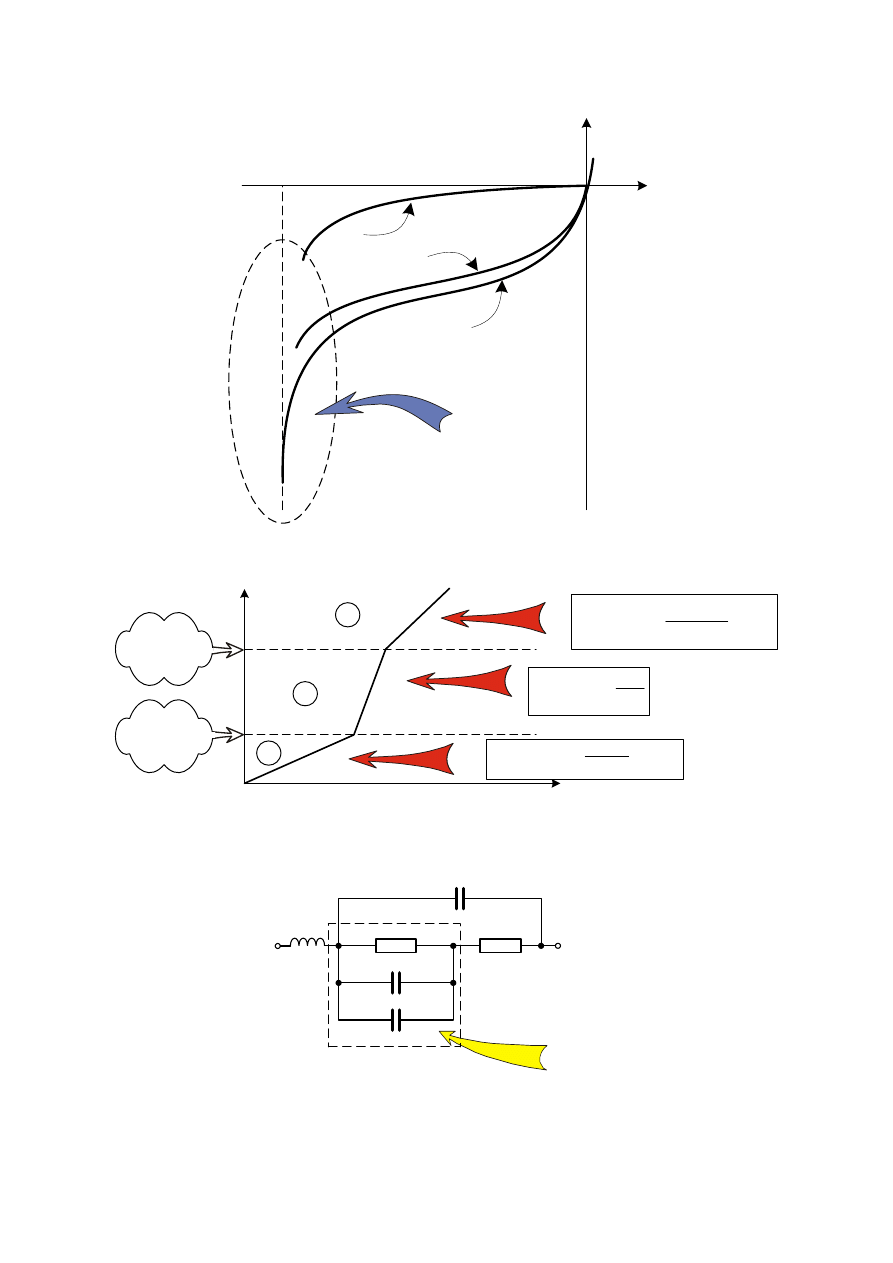
III. Diody półprzewodnikowe
13
U
Z
i
u
M
!
i
CW
i
G
I
S
Rys. 17
• Kierunek przewodzenia
I
II
III
lni
1
n
,
nU
i
r
U
exp
I
i
T
s
WS
>
⋅
−
=
T
S
U
u
exp
I
i
⋅
=
1
m
,
mU
u
exp
I
i
T
RS
>
⋅
=
u
A
kilkaset
μ
H
I
Rys. 3.20
•
Model małosygnałowy
A
j
C
d
r
d
C
B
Dioda
idealna
d
L
s
r
o
C
Rys. 3.21
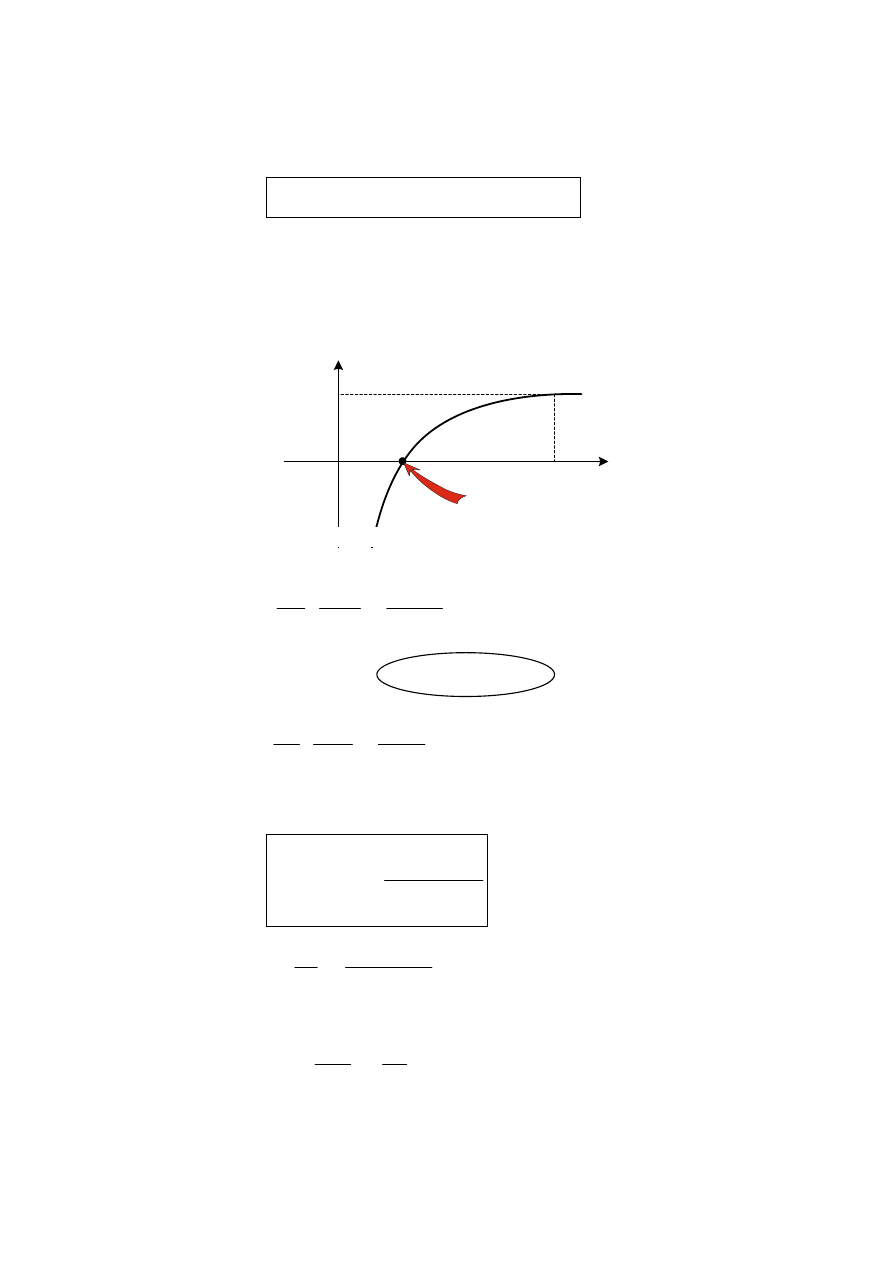
III. Diody półprzewodnikowe
14
Wpływ temperatury
Charakterystyka wsteczna
(
)
[
]
0
Z
0
Z
Z
T
T
1
U
U
−
β
+
=
(3.42)
Z
β
<0 – Przebicie Zenera
Z
β
>0 – przebicie lawinowe
Z
β
≈ 0 dla u ≈ 6V
Β
Z
≈ 10
-3
K
-1
≈ const. – dla diod o napięciu przebicia U
Z
>20V
20V
10
-3
K
-1
Z
β
ok. 6V
Rys. 23
2
0
g
G
G
iG
kT
2
W
dT
di
i
1
=
⋅
=
γ
(3.43)
dla krzemu (T = 300 K) →
8
iG
≈
γ
1
K
%
−
2
go
S
S
IS
kT
W
dT
dI
I
1
=
⋅
=
γ
(3.44)
Kierunek przewodzenia
T
go
U
U
u
exp
A
i
−
=
(3.47)
T
0
g
U
U
u
A
i
ln
−
=
stąd:
go
U
A
i
ln
q
kT
u
+
=
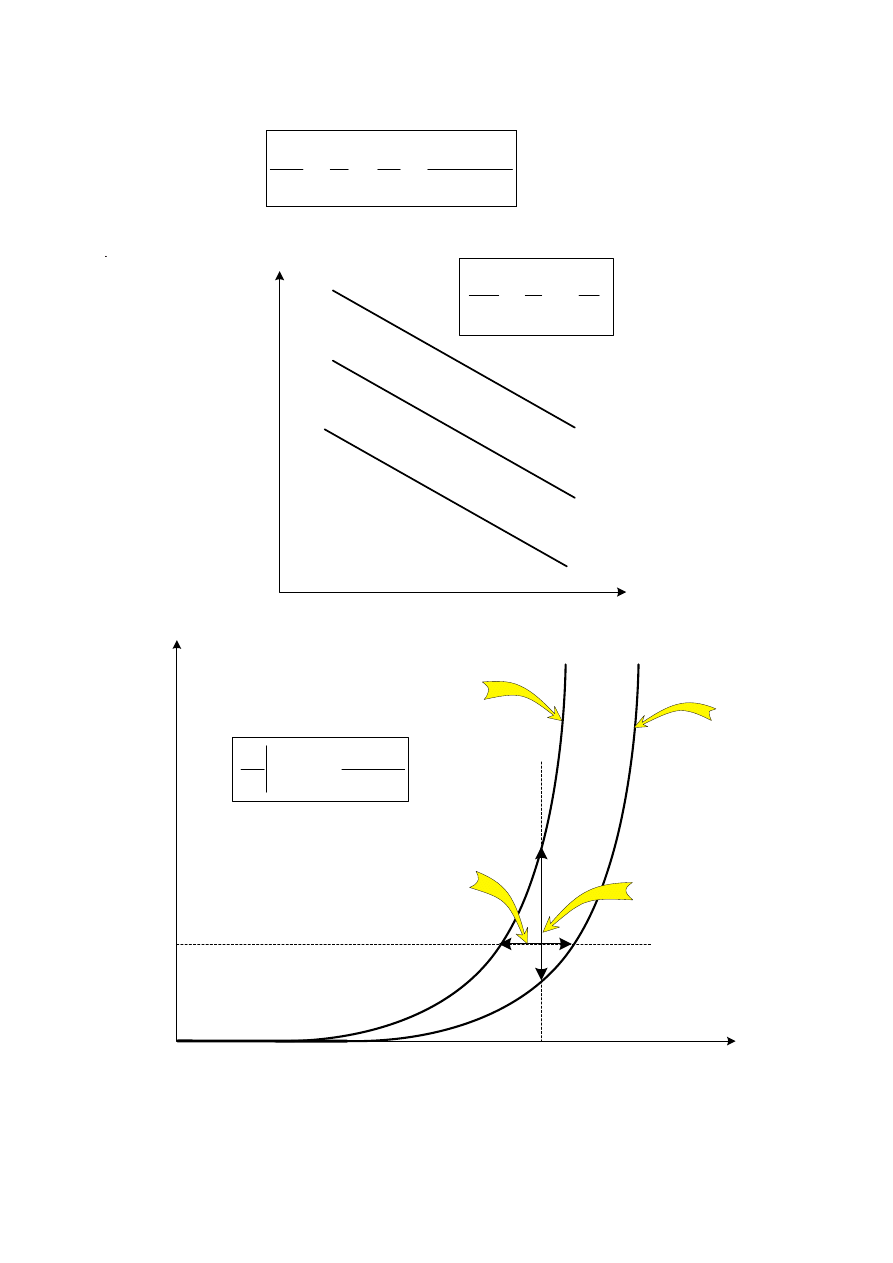
III. Diody półprzewodnikowe
15
Ostatecznie:
T
U
u
A
i
ln
q
k
T
u
0
g
−
=
=
∂
∂
Graficzna interpretacja zależności
A
i
ln
q
k
T
u
⋅
=
∂
∂
i
3
i
2
i
1
u
T
Rys. 3.24
-2mV/K
kilka %/K
i
T>T
O
T
U
u
T
u
go
.
const
i
−
=
∂
∂
=
I
O
T
O
u
Rys. 3.25
III. Diody półprzewodnikowe
16
Parametry małosygnałowe
T
S
0
d
U
I
I
g
+
=
d
d
g
C
⋅
τ
=
Pojemność
B
0
j
j
U
/
u
1
C
C
−
=
zależy od temperatury poprzez
2
i
D
A
B
n
N
N
ln
q
kT
U
=
•
Dopuszczalna temperatura złącza
P
R
T
T
th
a
j
⋅
+
=
th
a
max
j
max
R
T
T
P
−
=
Zasady analizy układu z elementami
półprzewodnikowymi
A) Obliczanie składowej stałej napięcia/prądu
Usunąć źródła zmiennoprądowe
U
m
, I
m
= 0
B) Obliczanie składowej zmiennej napięcia/prądu
Model małosygnałowy układu (zasada tworzenia):
•
elementy nieliniowe układu zastępujemy odpowiednimi modelami
małosygnałowymi tych elementów
•
zwieramy źródła napięcia stałego
•
rozwieramy źródła prądu stałego
•
pozostałe elementy pozostawiamy bez zmian
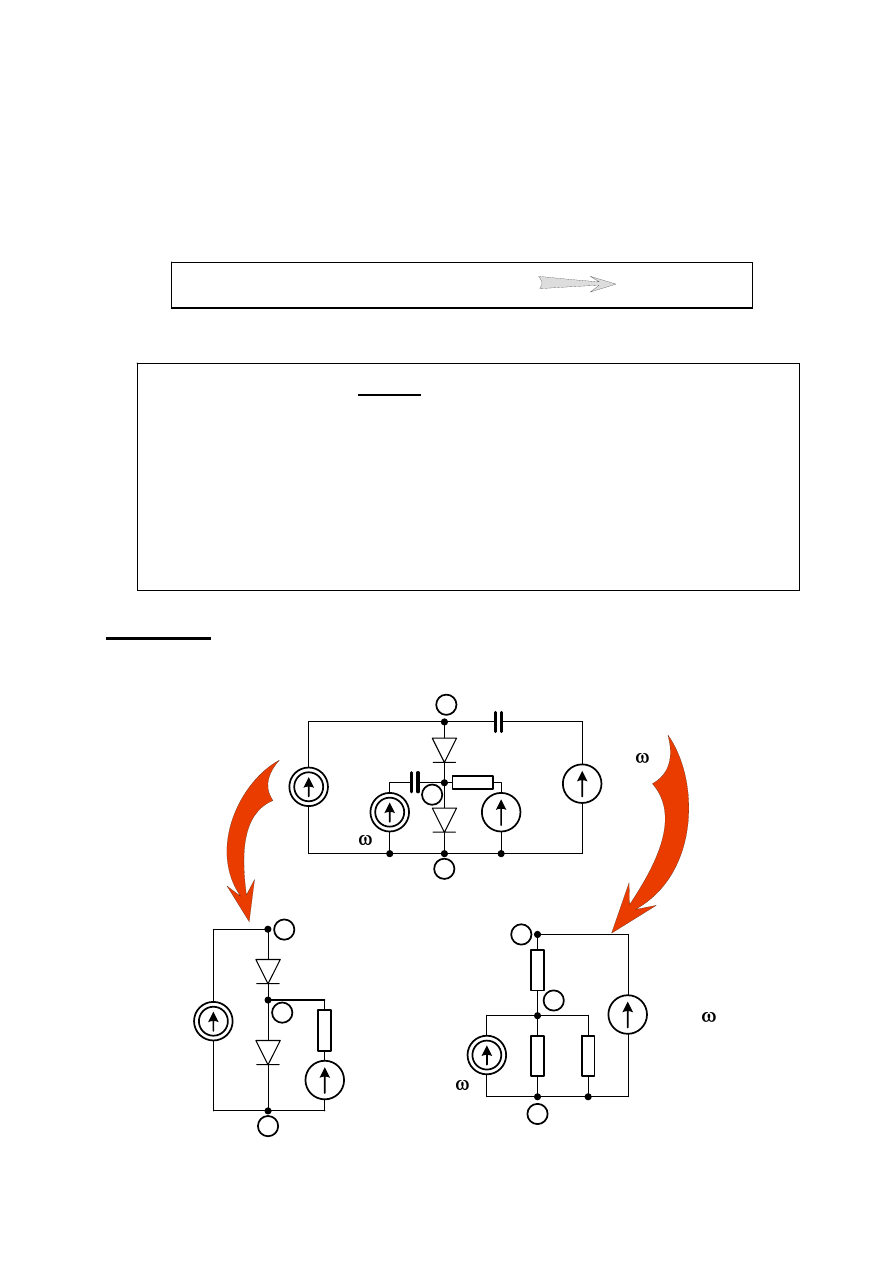
Przykład
•
Analizowany układ nieliniowy
D
1
D
2
U
0
U
1
sin
2
t
I
1
sin
1
t
I
0
C =
∞
C =
∞
R
1
2
1
● ad. A
● ad. B (przypadek m.cz.)
D
1
D
2
R
1
U
0
I
0
I
1
sin
1
t
U
1
sin
2
t
r
d1
r
d2
R
1
1
2
3
1
2
3
3
2
1
Document Outline