Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
1
Temat ćwiczenia: Algorytmy stratnej kompresji sygnałów
Algorytm kompresji jest to algorytm kodowania oraz algorytm rekonstrukcji
dekompresji). Algorytm kodowania dla pewnych danych wejściowych X generuje pewną
reprezentację X
C
, która wymaga mniejszej ilości bitów. Algorytm rekonstrukcji na podstawie
skompresowanej reprezentacji danych X
C
, tworzy rekonstrukcję Y.Kompresja bezstratna
wymaga, aby sygnał wejściowy (źródłowy) X był identyczny z sygnałem rekonstruowanym.
Natomiast kompresja stratna dopuszcza, aby X i Y były różne od siebie.
1. Kompresja stratna
Kompresję stratną (nieodwracalną) stosuje się w przypadku rzeczywistych sygnałów
multimedialnych, czyli mowy, muzyki, obrazów oraz sekwencji cyfrowego sygnału
telewizyjnego. W procesie dekompresji nie otrzymuje się tej samej sekwencji bitów,
co w sygnale oryginalnym. Jego dolnoczęstotliwościowa aproksymacja jest pozbawiona
wysokoczęstotliwościowych szczegółów. Im sygnał zostaje pozbawiony mniejszej ilości
detali w procesie kompresji, tym uzyskany zostaje mniejszy stopień kompresji, lecz
zrekonstruowany sygnał bliższy będzie oryginałowi.
Na rysunku 1 zawarty jest schemat kompresji stratnej . Informacje generowane przez
źródło opisuje zmienna losowa X. Koder przekształcane dane wejściowe na ich wersję
skompresowaną X
C
. Blok Kanał symbolizuje wszelkie przekształcenia, którym poddawane są
dane skompresowane przed rekonstrukcją. Kanał oznacza przekształcenia wzajemnie
równoważne
C
C
X
X
∧
=
. Na podstawie wersji skompresowanej
C
X
∧
dokonuje się rekonstrukcji
danych po stronie odbiorcy [1].
Źródło
Odbiorca
Koder
Dekoder
Kanał
X
X
c
X
c
Y
Rys. 1. Ogólny schemat kompresji stratnej
Proces eliminacji wysokoczęstotliwościowych szczegółów z sygnału może być realizowany w
różny sposób:
•
drogą śledzenia i upraszczania zmian dynamicznych np. metoda ADPCM (ang.Adaptive
Differential Pulse Code Modulation),
•
drogą przekształcania sygnału do dziedziny częstotliwościowej i usunięciu
współczynników widmowych niskoczęstotliwościowych np. standard kompresji
nieruchomych obrazów JPEG (ang. Joint Photographic Experts Group), gdzie stosuje się
dwuwymiarową dyskretną transformatę kosinusową 2-DCT (ang. Two Dimesional
Discrete Cosine Transform),
•
drogą modelowania w sposób uproszczony źródeł generacji sygnałów i wyznaczania
parametrów tych modeli na podstawie analizowanych sygnałów np. algorytmy kompresji
mowy. Oblicza się parametry modelu generacji mowy, a następnie przesyła się je do
dekodera, który syntezuje sygnał,
•
drogą eliminacji z sygnału składowych, których brak jest nie zauważalny np. w MPEG
(ang. Moving Pictures Exprets Group) audio gdzie kompresowany sygnał rozkładany jest
na
wiele
sygnałów
podpasmowych
(wysokoczęstotliwościowych).
Następnie
wykorzystuje się model psychoakustyczny ludzkiego słuchu, adaptacyjnie przydziela się
bity na sygnały podpasmowe zgodnie z ich istotą modelu psychoakustycznego .

Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
2
2.
Efektywność kompresji
Efektywność kompresji jest rozumiana na wiele sposobów w zależności od rodzaju
kompresowanych danych, zastosowania lub sprzętowych możliwości implementacji.
Najbardziej powszechnym rozumieniem tego pojęcia jest zdolność do maksymalnego
zredukowania rozmiaru nowej reprezentacji kompresowanego sygnału. Do ilościowych miar
tak rozumianej efektywności kompresji należą:
•
stopień kompresji CR,
•
procent kompresji CP,
•
średnia bitowa BR,
•
energia i entropia sygnału.
Miary kompresji wykorzystujące różnice pomiędzy wartościami oryginalnymi
i zrekonstruowanymi tzn. zniekształceń powstałych w trakcie kompresji:
•
kwadratowa miara błędu SEM oraz bezwzględna miara błędu ADM,
•
błąd średniokwadratowy MSE,
•
stosunek szumu do sygnału SNR
3. Stratne metody kompresji oraz ich zastosowanie
Poniżej zostaną przedstawione wybrane stratne metody kompresji sygnałów, które
obecnie znalazły zastosowanie w wielu dziedzinach. W wielu przypadkach jest tak, że jedna
metoda jest używana do kilku zastosowań.
3.1
Kodowanie różnicowe sygnałów
W przypadku danych takich jak np. dźwięki, obrazy, zachodzi duża korelacja
pomiędzy kolejnymi próbkami strumienia danych. Możliwe jest przewidywanie wartości
każdej próbki sygnału na podstawie wartości próbek poprzednich. Kodować oraz wysyłać
można jedynie różnicę między przewidywaną a rzeczywistą wartością próbki. Ta przesłanka
jest podstawą algorytmów kodowania różnicowego, których implementacja jest dużo prostsza
w porównaniu z innymi algorytmami kompresji stratnej.
Podstawowy algorytm kodowania różnicowego nazywany jest systemem różnicowej
modulacji kodowo – impulsowej (ang. Differential Pulse Code Modulation, DPCM). System
DPCM został opracowany w USA w laboratoriach Bell’a. Jest powszechnie stosowany do
kodowania mowy, zwłaszcza w komunikacji telefonicznej. Daje również efektywne podejście
do kompresji bezstratnej obrazów, lecz aspekt ten nie został jeszcze w pełni zbadany.
3.1 Algorytm podstawowy DPCM
W wielu sygnałach próbkowane dane źródła {x
n
} nie zmieniają się w znaczący sposób
z próbki na próbkę. Wariancja jak i wartości różnic {d
n
= x
n
- x
n-1
} są znacznie mniejsze niż
wariancja i wartości danych źródła.
Rozważmy ciąg {x
n
}, który jest ciągiem danych źródłowych. Na jego podstawie
generujemy ciąg różnic {d
n
} zgodnie z zależnością:
1
−
−
=
n
n
n
x
x
d
Ciąg {d
n
} jest kwantyzowany N poziomowym kwantyzatorem.
Otrzymujemy ciąg {
∧
n
d }:
n
n
n
n
q
d
d
Q
d
+
=
=
∧
]
[
gdzie q
n
jest błędem kwantyzacji.

Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
3
Odbiorca otrzyma zrekonstruowaną sekwencję {
n
x
∧
} przez dodanie {
∧
n
d } do poprzedniej
rekonstruowanej wartości
1
−
∧
n
x
:
n
n
n
d
x
x
∧
−
∧
∧
+
=
1
Zakładając, że zarówno nadawca, jak i odbiorca mają na początku tą samą wartość x
0
, czyli
0
x
x
n
=
∧
. Proces kwantyzacji dla pierwszych paru próbek wygląda następująco :
0
1
1
x
x
d
+
=
1
1
1
1
]
[
q
d
d
Q
d
+
=
=
∧
1
1
1
1
1
1
0
1
q
x
q
d
x
d
x
x
+
=
+
+
=
+
=
∧
∧
1
2
2
x
x
d
+
=
2
2
2
2
]
[
q
d
d
Q
d
+
=
=
∧
2
1
2
2
2
1
1
2
1
2
q
q
x
q
d
q
x
d
x
x
+
+
=
+
+
+
=
+
=
∧
∧
∧
Kontynuując ten proces, dla n - tej iteracji otrzymamy
∑
=
∧
+
=
n
k
k
n
n
q
x
x
1
Należy zauważyć, że w trakcie procesu rekonstrukcji błąd kwantyzacji narasta.
Teoretycznie błąd ten ma średnią zero i powinien się znosić podczas długiego przebiegu
jednak w praktyce może być tak, że dla pewnej próbki pojawi się błąd nadmiaru.
Koder jak i dekoder korzystają z różnych informacji. Koder generuje ciąg różnic
opierając się na oryginalnych wartościach próbek, natomiast dekoder dodaje z powrotem
kwantyzowane różnice do zniekształconej wersji oryginalnego sygnału. W celu rozwiązania
tego problemu należy spowodować, aby koder i dekoder korzystały z tej samej informacji
przy obliczaniu różnic i rekonstruowaniu wartości próbek.
Jedyną informacją o ciągu oryginalnym {
n
x } dostępną odbiorcy jest ciąg danych
rekonstruowanych {
∧
n
x
}. Tą informację posiada również nadawca, zatem można
zmodyfikować operację liczenia różnic tak, aby zamiast wartości rzeczywistej poprzedniej
próbki używana była jej wartości zrekonstruowana, to znaczy
1
−
∧
+
=
n
n
n
x
x
d
Po uwzględnieniu powyższych nowych założeń liczenia różnic, proces kwantyzacji
i rekonstrukcji wygląda następująco:
Ponownie zakładamy, że
0
x
x
n
=
∧
.
0
1
1
x
x
d
+
=
1
1
1
1
]
[
q
d
d
Q
d
+
=
=
∧
1
1
1
1
0
1
0
1
q
x
q
d
x
d
x
x
+
=
+
+
=
+
=
∧
∧
1
2
2
∧
+
=
x
x
d
2
2
2
2
]
[
q
d
d
Q
d
+
=
=
∧
Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
4
2
2
2
2
1
2
1
2
q
x
q
d
x
d
x
x
+
=
+
+
=
+
=
∧
∧
∧
∧
Podczas n – tej iteracji mamy
n
n
n
q
x
x
+
=
∧
W tym przypadku, nie nastąpiła żadna akumulacja szumu kwantyzacyjnego. Szum
kwantyzacji związany z kwantyzowaniem n – tej rekonstruowanej próbki jest szumem
wywołanym podczas kwantyzacji n – tej różnicy. Błąd kwantyzacji dla ciągu różnic jest
znacząco mniejszy od błędu kwantyzacji ciągu oryginalnego. Ta procedura prowadzi do
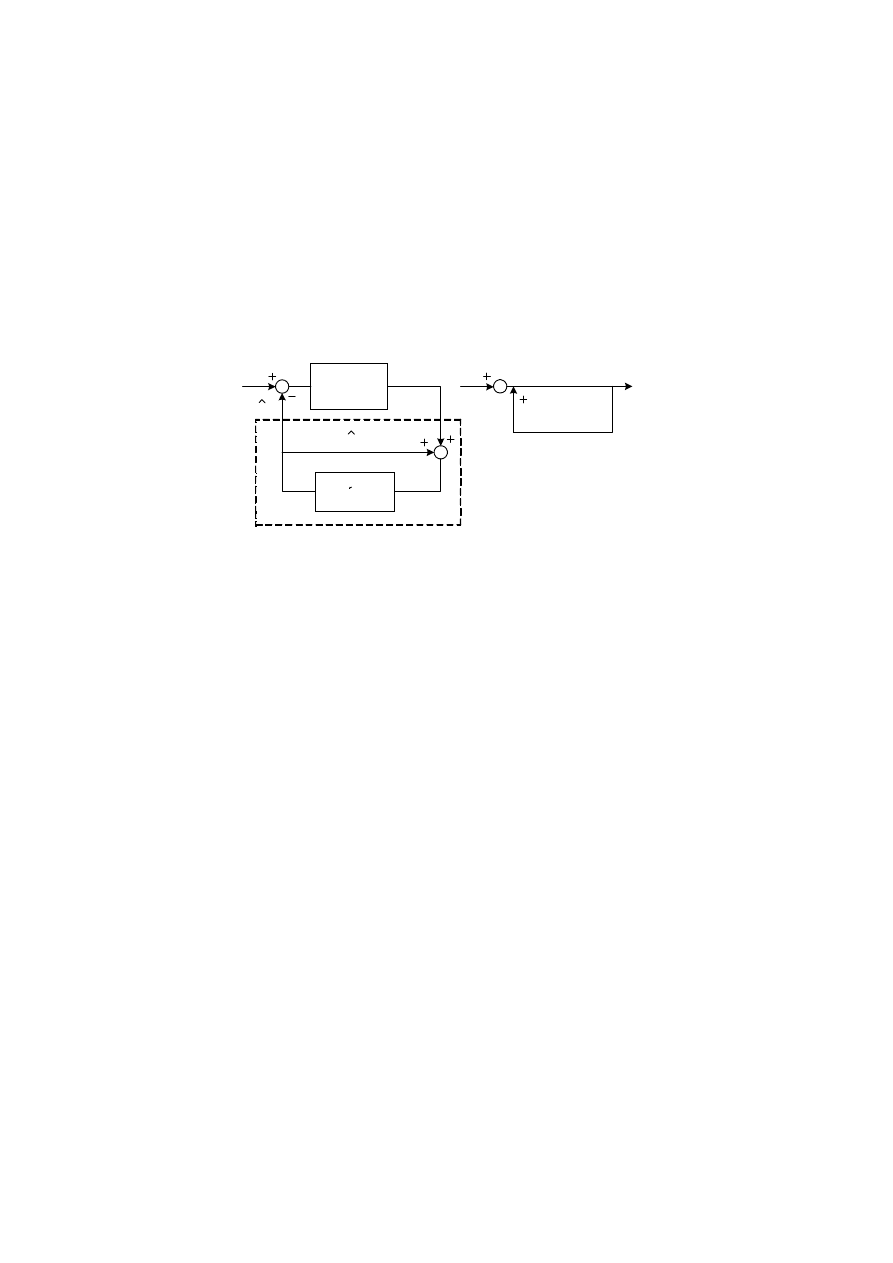
zmniejszenia całkowitego błędu kwantyzacji. Na rysunku 2.1 zamieszczony został
przykładowy schemat blokowy prostego systemu kodowania różnicowego.
K w a n tyz a to r
O p ó z n ie n ie
∧
n
x
1
−
n
x
1
−
n
x
n
x
n
d
∧
n
d
D e k o d e r
∧
n
d
∧
n
x
K o d e r
Rys. 2 Prosty system kodowania różnicowego.
4. Kodowanie transformacyjne
Metoda kompresji stratnej zwana kodowaniem transformacyjnym TC (ang. Transform
coding) jest najpopularniejszym sposobem kompresji danych. Znalazła zastosowanie
w kompresji stratnej obrazów JPEG, MPEG oraz dźwięków (mp3 – MPEG I Layer III).
Stosowanie metod transformacyjnych ma duże walory praktyczne ze względu na niewielkie
koszty obliczeniowe oraz łatwość realizacji koderów, zarówno programowych jak
i sprzętowych.
Ogólny schemat kodowania transformacyjnego jest techniką, w której sygnał dzielony
jest na pewną liczbę składowych, gdzie każda składowa jest kodowana niezależnie. Celem
transformacji jest usunięcie korelacji występującymi pomiędzy próbkami sygnału.
Dekorelację osiąga się zasadniczo poprzez fakt, iż po transformacji energia sygnału zawarta
jest w niewielkiej liczbie współczynników transformaty. Umożliwia to efektywną kompresję
wskutek usunięcia wielu wartości pozostałych współczynników procesie kwantyzacji.
Odpowiedni dobór współczynników kwantyzacji pozwala przy zastosowaniu technik
transformacyjnych na osiągnięcie metod kodowania stratnego i bezstratnego.
5.
Dyskretne przekształcenie kosinusowe DCT i sinusowe DST
Dyskretne przekształcenie kosinusowe DCT (ang. Discrete Cosine Transform) jest
typem przekształcenia częstotliwościowego. W tego typu metodzie liczba bitów używana do
kodowania poszczególnych składowych może być niezależna od liczby bitów używanych do
pozostałych składowych. Dokładność kodowania może być dostosowywana do aktualnych
potrzeb dla danej składowej częstotliwościowej. W poszczególnych przypadkach składowa
częstotliwościowa o małej lub zerowej energii może nie być wcale kodowana.
W technikach transformacyjnych, współczynnikom posiadającym bardziej istotną
informację można przydzielić większą ilość bitów. Najczęściej są to składowe
niskoczęstotliwościowe. W ten sposób, można zredukować liczbą bitów wymaganych do

Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
5
przesyłu sygnału i tym samym ograniczyć pasmo sygnału. Redukcja szerokości pasma jest
podstawowym celem większości technik kompresji.
DCT jest dyskretnym ciągiem
)
1
(
,....,
2
,
1
,
0
)
(
−
=
N
n
x
i jest wyrażane następującą
zależnością [5]:
∑
−
=
+
⋅
=
1
0
cos
2
)
1
2
(
cos
)
(
)
(
2
)
(
N
k
N
k
n
n
x
k
C
N
k
X
π
)
1
(
,...,
2
,
1
,
0
−
=
N
k
,
2
1
)
(
=
k
C
dla k=0,
1
)
(
=
k
C
dla
)
1
(
,...,
2
,
1
,
0
−
=
N
k
.
gdzie
n – numer próbki,
k – numer bazy.
Podobnie transformata odwrotna do DCT, IDCT (ang. Inverse Discrete Cosine Transform)
wyraża się równaniem [5]:
∑
−
=
+
⋅
⋅
=
1
0
2
)
1
2
(
cos
)
(
)
(
2
)
(
N
k
N
k
n
k
X
k
C
N
n
x
π
Za pomocą IDCT można zrekonstruować sygnał, wcześniej przetransformowany metodą
DCT. Zostaje on odtworzony na podstawie zakodowanych współczynników.
Dyskretne przekształcenie sinusowe DST (ang. Discrete Sine Transform) jest
przekształceniem komplementarnym do przekształcenia DCT.
DST wyraża się zależnością [7]:
+
+
+
+
=
1
)
1
)(
1
(
sin
1
2
)
(
sin
N
n
k
n
N
K
X
)
1
(
,...,
2
,
1
,
0
−
=
N
k
,
)
1
(
,...,
2
,
1
,
0
−
=
N
n
.
DCT daje efekty bliskie optymalnemu KLT (algorytm Korhunena - Loévego) dla dużych
wartości współczynnika korelacji ρ , który definiuje się zależnością:
]
[
]
[
2
1
n
n
n
x
E
x
x
E
+
=
ρ
Jako E oznaczona została oznaczona energia sygnału. Z kolei DST daje pod względem
zagęszczenia wyniki bliskie optymalnemu KLT, gdy ρ jest małe. Dzięki tym własnościom
DST jest uzupełnieniem DCT w kodowaniu sygnałów. Ze względu na charakter niniejszej
pracy możliwości transformaty DCT i DST zostaną przedstawione oddzielnie.
6. Algorytm metody kompresji LPC-10 (prosty)
Algorytm kompresji mowy LPC-10 składa się z następujących bloków:
ANALIZA-koder
1. Preemfaza – uwydatnienie wyższych częstotliwości w sygnale przy zastosowaniu
filtracji nierekursywnej typu FIR,
)
1
(
9375
.
0
)
(
)
(
1
−
⋅
−
=
n
s
n
s
n
s
2. Okno – przemnożenie sygnału s(n) z oknem Hamminga w(n) o długości N=240
próbek,

Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
6
)),
1
/(
2
cos(
46
.
0
54
.
0
)
(
−
−
=
N
n
n
w
π
1
0
−
≤
≤
N
n
)
(
)
(
)
(
1
2
n
w
n
s
n
s
⋅
=
3. Filtr traktu głosowego – wyliczenie współczynników filtru traktu głosowego
{a
k
, k=1,2,…,p} oraz wzmocnienia G
∑
−
−
=
+
=
k
N
n
k
n
s
n
s
k
r
1
0
2
2
)
(
)
(
)
(
,
p
k
,.....,
2
,
1
=
a = - R
-1
r
,
)
(
)
2
(
)
1
(
)
0
(
)
2
(
)
1
(
)
2
(
)
0
(
)
1
(
)
1
(
)
1
(
)
0
(
1
2
1
−
−
−
−
−
=
−
p
r
r
r
r
p
r
p
r
p
r
r
r
p
r
r
r
a
a
a
p
M
L
M
O
M
M
L
L
M
∑
=
+
=
p
k
k
k
r
a
r
G
1
)
(
)
0
(
4. Filtracja dolnoprzepustowa – przy zastosowaniu filtru o odpowiedzi h(k) i górnej
częstotliwości granicznej f
g
=900 Hz
∑
=
−
=
M
k
k
n
s
k
h
n
s
0
2
3
)
(
)
(
)
(
.
5. Progowanie sygnału:
−
≤
+
≥
−
=
pozostale
P
n
s
P
n
s
P
n
s
P
n
s
n
s
,
0
)
(
,
)
(
)
(
,
)
(
)
(
3
3
4
gdzie
))
(
max(
3
.
0
n
s
P
=
lub
8
.
0
6
.
0
,
),
,
min(
3
/
3
3
/
1
÷
=
=
K
A
A
K
P
6. Funkcja autokorelacji sygnału po sprogowaniu:
∑
−
−
=
+
=
k
N
n
p
k
n
s
n
s
k
r
1
0
4
4
)
(
)
(
)
(
,
1
,...,
2
,
1
−
=
N
k
7. Decyzja „dźwięczna/bezdźwięczna” – sprawdzanie warunku kiedy fragment mowy
zostaje uznany za dźwięczny,
.
160
,...,
20
),
0
(
]
35
.
0
3
.
0
[
))
(
max(
=
⋅
÷
≥
k
r
k
r
p

Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
7
8. Okres tonu podstawowego T dla mowy dźwięcznej:
max
k
T
=
k
max
– maksimum funkcji autokorelacji z przedziału 20<k<160.
9. Strumień wyjściowy – zapisanie danych wyjściowych jako {T, G, a
1
, a
2
, … ,a
p
}
SYNTEZA-dekoder
1. Odtworzenie danych wyjściowych z kodera czyli parametrów {T, G, a
1
, a
2
, … ,a
p
}
2. Zsyntetyzowanie próbek mowy.
1
,...,
2
,
1
,
0
,
)
(
)
(
)
(
1
1
1
−
=
−
−
⋅
=
∑
=
M
k
k
n
s
a
n
e
G
n
s
p
k
k
,
3. Deemfaza – tłumienie wyższych częstotliwości poprzez filtracje rekursywną typu IIR,
jest to operacja odwrotna do preemfazy kodera.
)
1
(
9375
.
0
)
(
)
(
1
−
⋅
+
=
n
s
n
s
n
s
Powyższy algorytm jest przykładem najprostszego przedstawienia metody kompresji
LPC-10, w którym do obliczania współczynników filtru traktu głosowego wykorzystana
została transmitancja H(z) .
7. LPC-10 z zastosowaniem algorytmu Durbina - Levinsona
Algorytm Durbina – Levinsona służy do iteracyjnego wyznaczenia współczynników filtru
traktu głosowego, dzięki czemu możliwe jest zastosowanie w praktycznej implementacji
kodera LPC-10 czasu rzeczywistego. W ten sposób unika się odwracania macierzy R, tym
samym ułatwia to implementację algorytmu kodera na procesorach sygnałowych
powszechnego użytku.
8.
Format kompresji dźwięku MP3 (MPEG
– 1 Layer 3)
Format MP3 jest najbardziej popularnym spośród wszystkich formatów zapisu fonii,
w którym dopuszczana jest pewna informacji, tak jak przy obróbce obrazów cyfrowych.
Format ten został opracowany przez podgrupę JTC 1 (ang. Joint Technical Commitee 1),
MPEG (ang. Motion Picture Export Group) i zarejestrowany przez ISO (ang. International
Standards Organization) jako ISO MPEG – 1 Layer 3.
Standard MPEG – 1 opisuje trzy warstwy kompresji Layer 1, Layer 2 i Layer 3.
Wszystkie te warstwy sa zdolne do wytworzenia dźwięku o jakości bliskiej CD. W tabeli 2
zamieszczono krótką charakterystykę trzech warstw MPEG.
Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
8
Tabela 1: Rodzaje standardu MPEG-1
Metoda
Współ
czynnik
kompresji
Opis
Layer 1
1:4
Sygnał stereo generuje strumień bitów 384 kbit/s
Layer 2
1:6 – 1:8
Sygnał stereo generuje strumień bitów 256
– 192 kbit/s
Layer 3
1:10 – 1:12
Sygnał stereo generuje strumień bitów 128
– 192 kbit/s
Są one hierarchicznie kompatybilne, co oznacza, że dekoder dla warstwy Layer 3
trzeciej może być zastosowany także dla warstw 1 i 2. Nie jest jednak możliwe w odwrotną
stronę. Im wyższy numer warstwy, tym bardziej złożony staje się koder i tym samym
otrzymujemy wyższy stopień kompresji. W tabeli 3 zamieszczono stopnie kompresji możliwe
do uzyskania w Layer 3 oraz ich zastosowanie.
Tabela 2: Przykładowe stopnie kompresji
Jakość dźwięku
Stopień
kompresji
Szerokość pasma
(kHz)
Tryb
Strumień bitów
(kb/s)
Telefoniczna
1:96
2,5
mono
8
Krótkofalowa
1:48
4,5
mono
16
Średniofalowa
1:24
7,5
mono
32
Radio FM
1:24 – 1:26
11
stereo
56 - 64
Niemal CD
1:16
15
stereo
96
CD
1:12 – 1:14
> 15
stereo
112 - 128
Wszystkie trzy warstwy mają tą samą strukturę. Zastosowana w nich technika
kodowania jest znana jako perceptualne kształtowanie szumu lub perceptualne kodowanie
transformaty pasma. Koder dokonuje analizy składowych widmowych sygnału za pomocą
banku filtrów pasmowoprzepustowych korzystających z modelu psychoakustycznego
do określenia dostrzegalnych poziomów szumów. W tym podrozdziale zostanie
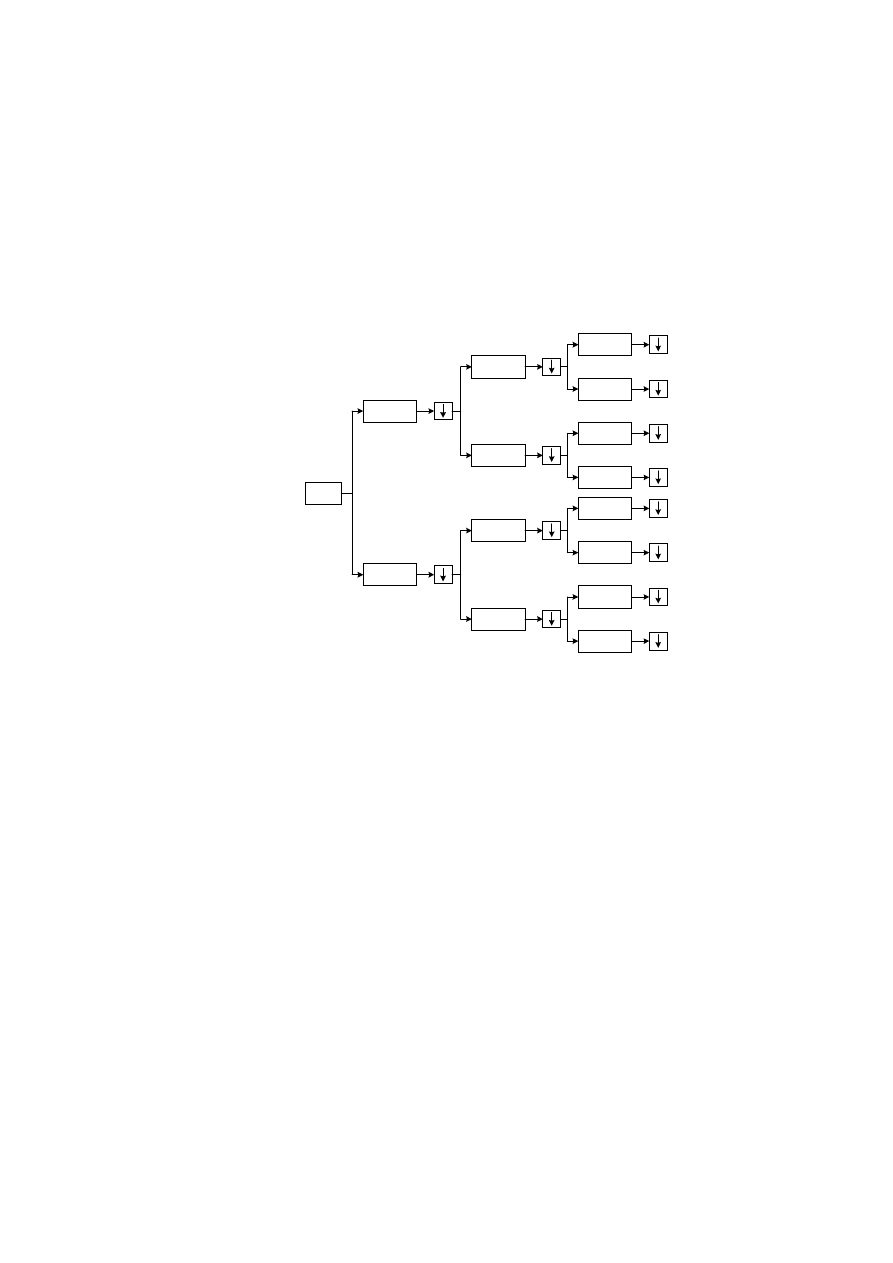
przedstawiony algorytm MP3 z bankiem filtrów w układzie równoległym i kaskadowym.
Filtr 1
0-2.8 kHz
Filtr 2
2.8-5.5 kHz
Filtr 8
16.5-22 kHz
Filtr 7
16.5-19.3 kHz
Filtr 4
8.8-11 kHz
Filtr 3
5.5-8.8 kHz
Filtr 6
13.8-16.5 kHz
Filtr 5
11-13.8 kHz
Wejście
Rys. 3. Bank filtrów w układzie równoległym.
Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
9
W tej pracy został zaimplementowany uproszczony algorytm MP3, który posiada 8 –
kanałowy bank filtrów. O uproszczonym algorytmie będzie mowa w dalszej części tego
podrozdziału. W algorytmie standardowym MP3, wszystkie trzy warstwy mają 32 – kanałowy
bank filtrów. Wszystkie dopuszczają częstotliwości próbkowania 32 kHz, 44,1 kHz, 48 kHz i
są w stanie przetworzyć strumień bitów 32 kb/s lub większe.
Dla uzyskania redukcji szerokości pasma cyfrowego, w MPEG – 1 Layer 3 stosowane
są następujące techniki :
•
dolny próg słyszalności, dla ludzkiego słuchu nie jest liniowy, wznosi się pomiedzy 2 kHz
i 5 kHz. Nie jest konieczne kodowanie dźwięku leżącego poniżej progu, ponieważ
słuchacz i tak nie jest w stanie go usłyszeć,
HPF
11-22 kHz
LPF
0-11 kHz
Wejście
HPF
16.5-22 kHz
LPF
11-16.5 kHz
HPF
11-22 kHz
LPF
0-11 kHz
LPF
11-13.8 kHz
HPF
13.8-16.5 kHz
LPF
16.5-19.3 kHz
HPF
19.3-22 kHz
HPF
8.3-11 kHz
LPF
5.5-8.3 kHz
HPF
2.8-5.5 kHz
LPF
0-2.8 kHz
Rys. 4. Bank filtrów w układzie kaskadowym.
•
efekt maskowania wykorzystuje fakt, że słuch ludzki nie postrzega słabych dźwięków,
które są częściowo lub całkowicie zamaskowane przez inne dźwięki. Na skutek
maskowania część dźwięków nie musi być kodowana, co pozwala w dużym stopniu
zaoszczędzić pamięć. Dlatego też wszystkie kodery MPEG – 1 Layer 3 posiadają model
psychoakustyczny, który ma właściwości ucha ludzkiego ,
•
kodowanie Huffmana stosuje się do zakodowania informacji cyfrowej tzn. do kompresji
rzeczywistej. Algorytm Huffmana generuje kod o zmiennej długości i całkowitej liczbie
bitów. Kody Huffmana doskonale się dekodują, pomimo swojej zmiennej długości.
8.1 Algorytm standardowy MP3
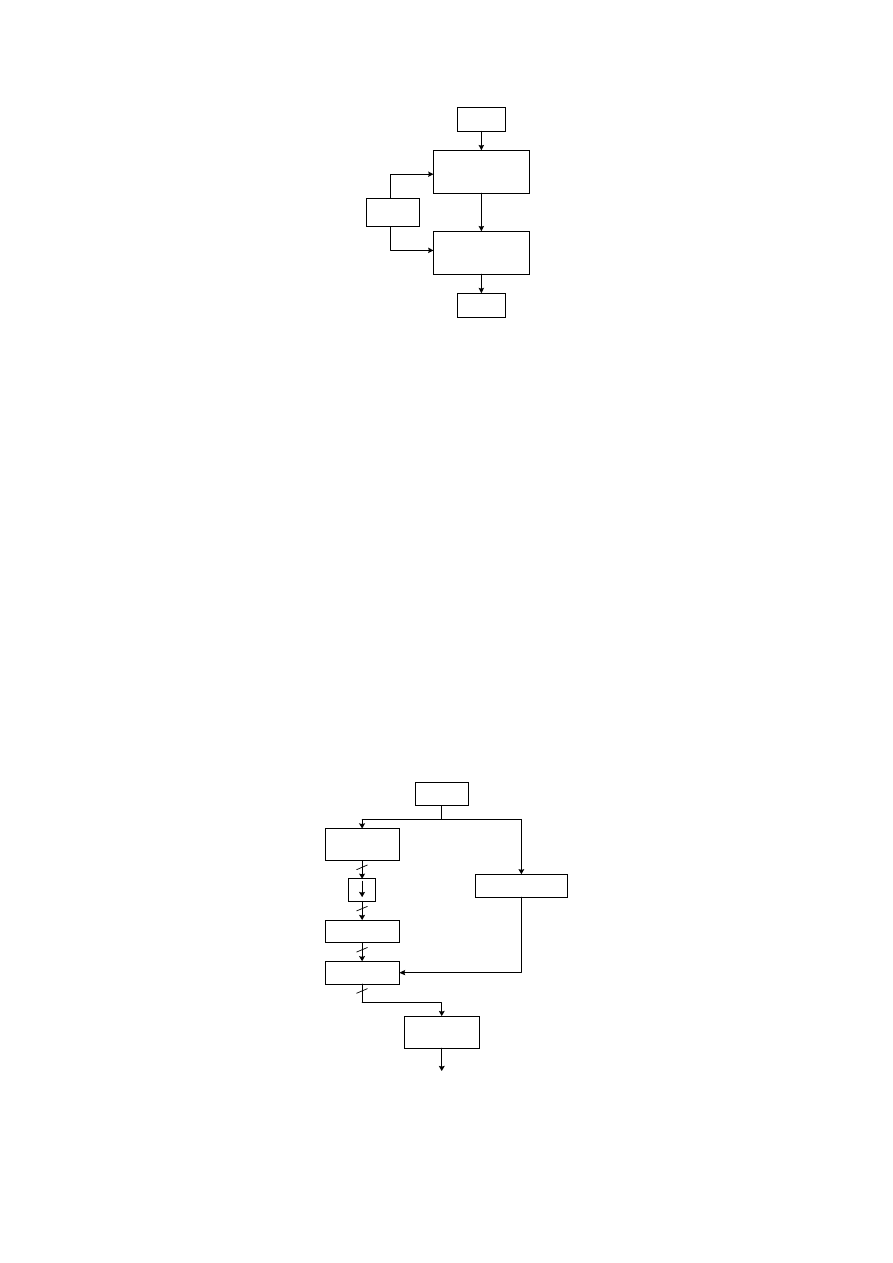
Na rysunku 5 przedstawiono uproszczony schemat funkcjonalny algorytmu, dzięki
któremu łatwiej jest zrozumieć podstawowe działanie całego systemu kodowania MP3.
Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
10
Wejście
Blok Kodera
Blok Dekodera
Wyjście
Zakodowany strumień
danych
Blok
Kontroli
Rys. 5. Funkcjonalny schemat blokowy algorytmu MP3.
Algorytm MP3 posiada dwa główne systemy, koder i dekoder. Koder generuje
strumień bitów poprzez kodowanie sygnału wejściowego według specyfikacji MPEG–1.
W najlepszym przypadku algorytm kompresji jest w stanie wygenerować sygnał o jakości CD
o współczynniku kompresji 1:12 przy niewielkiej utracie jakości dźwięku. Dekoder
przetwarza zakodowany strumień bitów i tworzy sygnał wyjściowy. Działanie bloku kodera
i dekodera jest nadzorowane przez blok kontrolny, który zawiera podstawowe informacje
o sygnale wejściowym tj. częstotliwość próbkowania, ilość bitów czy typ sygnału
(monofoniczny lub stereofoniczny) .
8.2 Koder podstawowy
Kluczowym
elementem
algorytmu
warstwy
Laser
3
jest
bank
filtrów
pasmowoprzepustowych (rys. 2.9), pokrywający cały zakres widma sygnału. W koderze
podstawowym, bank filtrów dzieli sygnał na 32 równe podpasma częstotliwościowe
w zależności od częstotliwości Nyquist’a oryginalnego sygnału. Na przykład, jeżeli
częstotliwość Nyquist’a oryginalnego sygnału wynosi 24 kHz to bank filtrów podzieli sygnał
na pasma o szerokości 750 Hz. Następnie w procesie podpróbkowania (decymacji)
redukowana jest ilość danych w każdym podpaśmie. Jest to proces pozostawiania co N – tej
próbki sygnału [7].
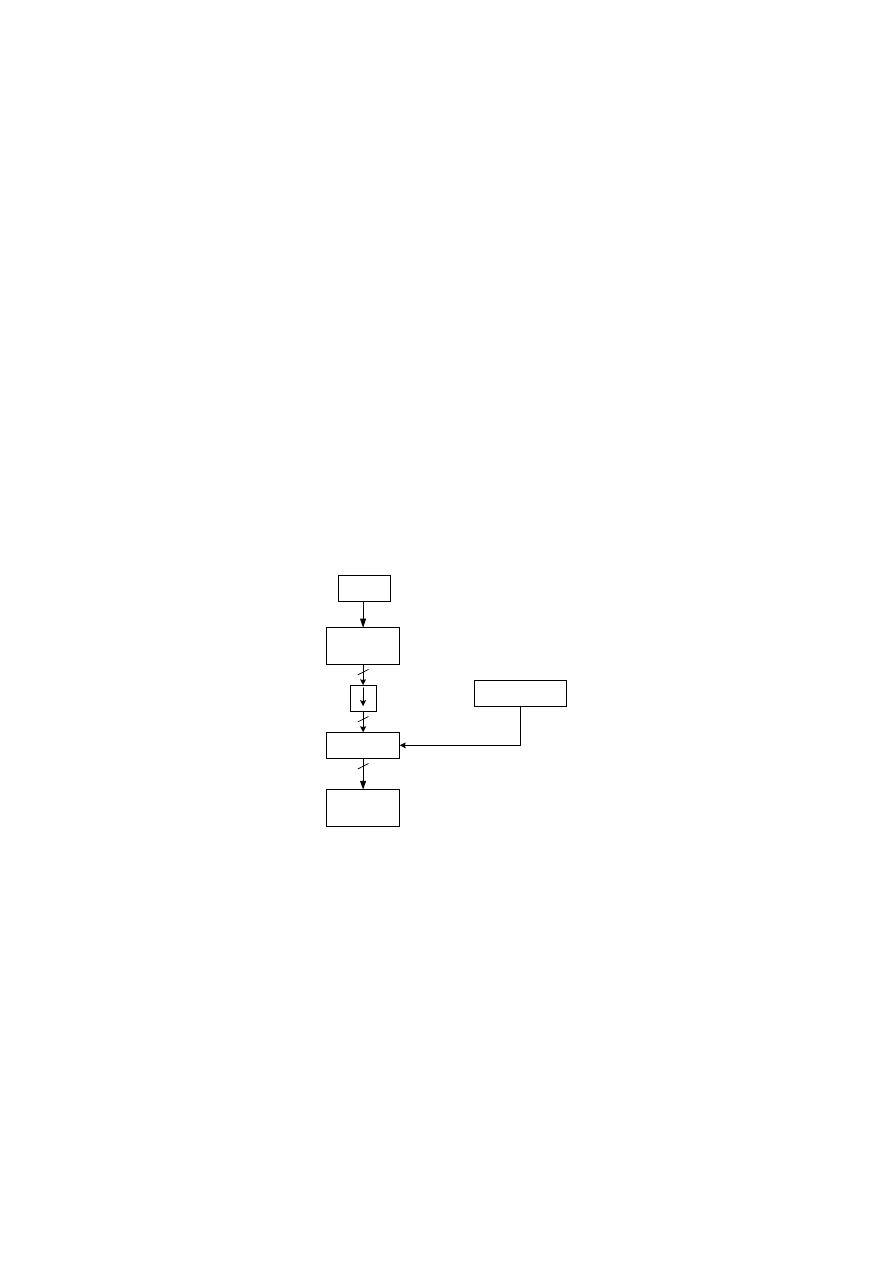
Wejście
Zespół filtrów
750 Hz
MDCT
Koder
Model
Psychoakustyczny
Formatowanie
Strumienia
Zakodowany strumień
Rys. 6. Schemat podstawowego systemu kodera MP3.
Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
11
Pomimo tego całkowita ilość danych jest taka sama, ponieważ mamy 32 podpasma.
Na przykład jeśli mamy 100 oryginalnych próbek sygnału, bank filtrów tworzy 32 podpasma,
każdy po 10 próbek. Wtedy liczba próbek wzrasta do 3200 (32*100). Po podpróbkowaniu ta
liczba znowu jest zredukowana do 100. Blok MDCT (ang. Modified Discrete Cosine
Transform) zwiększa dokładność banku filtrów poprzez rozłożenie 32 podpasm na 576
(32*18),(18 – punktowa MDCT). Równocześnie model psychoakustyczny w odniesieniu do
sygnału wejściowego, decyduje jakie pasma częstotliwości powinny być zachowane. Model
korzysta z możliwości maskowania słuchu ludzkiego by zidentyfikować elementy
niedostrzegane w sygnale oryginalnym. Koder używa danych dostarczonych przez model
psychoakustyczny, aby zadecydować jak ma być zakodowane 576 podpasm sygnału. Koder
kodując dane, ignoruje podpasma, które sa zamaskowane przez inne elementy. Dodatkowo
maskowane podpasma są kodowane z mniejszą dokładnością niż pasma dominujące.
W końcu blok formatujący strumień składa sygnał wyjściowy kodera w strumień danych
według standardu MPEG – 1. W zależności od aplikacji, dane te mogą być przesłane lub
zapisane w pamięci.
8.3 Koder uproszczony
Program zaimplementowany w środowisku Matlab na podstawie algorytmu
kodowania MP3 z zastosowaniem standardowego systemu kodowania, potrzebowałby dużo
czasu na wykonanie obliczeń nawet dla krótkich sygnałów. W związku z tym na potrzeby
symulacji tej metody kompresji został stworzony model uproszczonego kodera .
Wejście
Zespół filtrów
2.7 kHz
Koder
Model
Psychoakustyczny
Próbkowanie
Rys.7 Schemat uproszczonego systemu kodera MP3.
Wprowadzone zmiany dotyczyły usunięcia bloku MDCT oraz bloku formatującego
dane wyjściowe z kodera. Zmodyfikowano bank filtrów pasmowoprzepustowych (szerokość
pasma 2,7 kHz), aby dzieliły sygnał na 8 podpasm, a nie 32.W układzie podpróbkującym
dokonano zmiany wartości N z 32 na 8.
8.4 Dekoder podstawowy
W przeciwieństwie do podstawowego algorytmu kodera, ten algorytm nie zostanie
poddany modyfikacjom. Na rysunku 2.11 został przedstawiony schemat blokowy dekodera
MP3. Zadaniem dekodera jest przeanalizowanie strumienia danych wygenerowanych przez
system kodowania i zrekonstruowanie sygnału.

Katedra Elektroniki PL - Cyfrowe przetwarzanie sygnałów
Algorytmy stratnej kompresji sygnałów
12
Wyjście
Bank filtrów
odzyskujących
IMDCT
Analiza
Strumienia
Zakodowany strumień
∑
Rys. 8 Schemat standardowego systemu dekodera MP3.
Pierwszym krokiem w odzyskaniu oryginalnego sygnału jest pobranie zakodowanych
informacji ze strumienia bitów. W wyniku analizy strumienia dane są odczytywane
i przesyłane do bloku IMDCT (ang. Inverse Modified Discrete Cosine Transform), który
łączy 576 podpasm z powrotem na 32 podpasma wytworzone przez koder. Potem sygnał jest
przetwarzany przez układ nadpróbkujący, w którym pasma są interpolowane poprzez dodanie
N-1 próbek w miejsce usuniętych przez koder. Proces nadpróbkowania (interpolacji) jest
konieczny w celu odtworzenia tej samej szerokości pasma, jak w sygnale oryginalnym.
Następnie bank filtrów rekonstrukcji przetwarza te dane, usuwając błędy powstałe w wyniku
nadpróbkowania. W końcu 32 podpasma zostają dodane, co daje pojedynczy sygnał, który
percepcyjnie powinien być identyczny z oryginałem.
Wyszukiwarka
Podobne podstrony:
Kompresja danych (FAQ), Informatyka -all, INFORMATYKA-all
Test kompresyjny otworw midzykrgowych, biomechanika kliniczna testy
Lab 2 Visual Analyser oraz kompresje v2
kompresja danych
Kompresja wielopasmowa
Kompresory- podstawy parametry, Realizacja Audio - recording, mix
Kompresja klatki piersiowej skuteczniejsza niż standardowa RKO, MEDYCYNA, RATOWNICTWO MEDYCZNE, BLS,
Kompresja?nych Rzędzian i?rbórka
Kompresja klatki piersiowej skuteczniejsza niż standardowa resuscytacja krążeniowo – oddechowa
kompresjoterapia
hossa,kompresja informacji L,Kompresja algebraiczna w oparciu o przekształcenie Karhunena Loeve (2)
Kompresja?nych na partycjach NTFS
komprespr barwa
kompresja
09 kompresja pasy nasuwcze na szelfachid 8086 ppt
Kodowanie i kompresja danych
08 kompresja orogenyid 7583 ppt
KOMPRESJA DZWIĘKÓW
więcej podobnych podstron