1

Wymiarowanie

konstrukcji nośnych

H.Jakubczak
IMRC PW

Konstrukcje nośne

2

Algorytm projektowania konstrukcji nośnych

1. Określenie możliwych rodzajów uszkodzenia w zależności

od obciążeń i warunków eksploatacji

2. Sformułowanie kryteriów (warunków) projektowania

konstrukcji dla uniknięcia tych uszkodzeń

3. Określić obciążenia eksploatacyjne, wywołujące rozważane

rodzaje uszkodzeń

4. Przeprowadzić analizę naprężeń według:

•

Norm, o ile istnieją (dźwignice, zbiorniki ciśnieniowe, ...)

•

Wytyczne branżowe (statki, ...)

•

Potencjalnych obciążeń maszyny (maszyny do robót ziemnych, ...)

5. Przeprowadzić analizy odpowiednie dla rozważanych

rodzajów uszkodzenia i wyznaczyć odpowiednie wymiary

konstrukcji

3

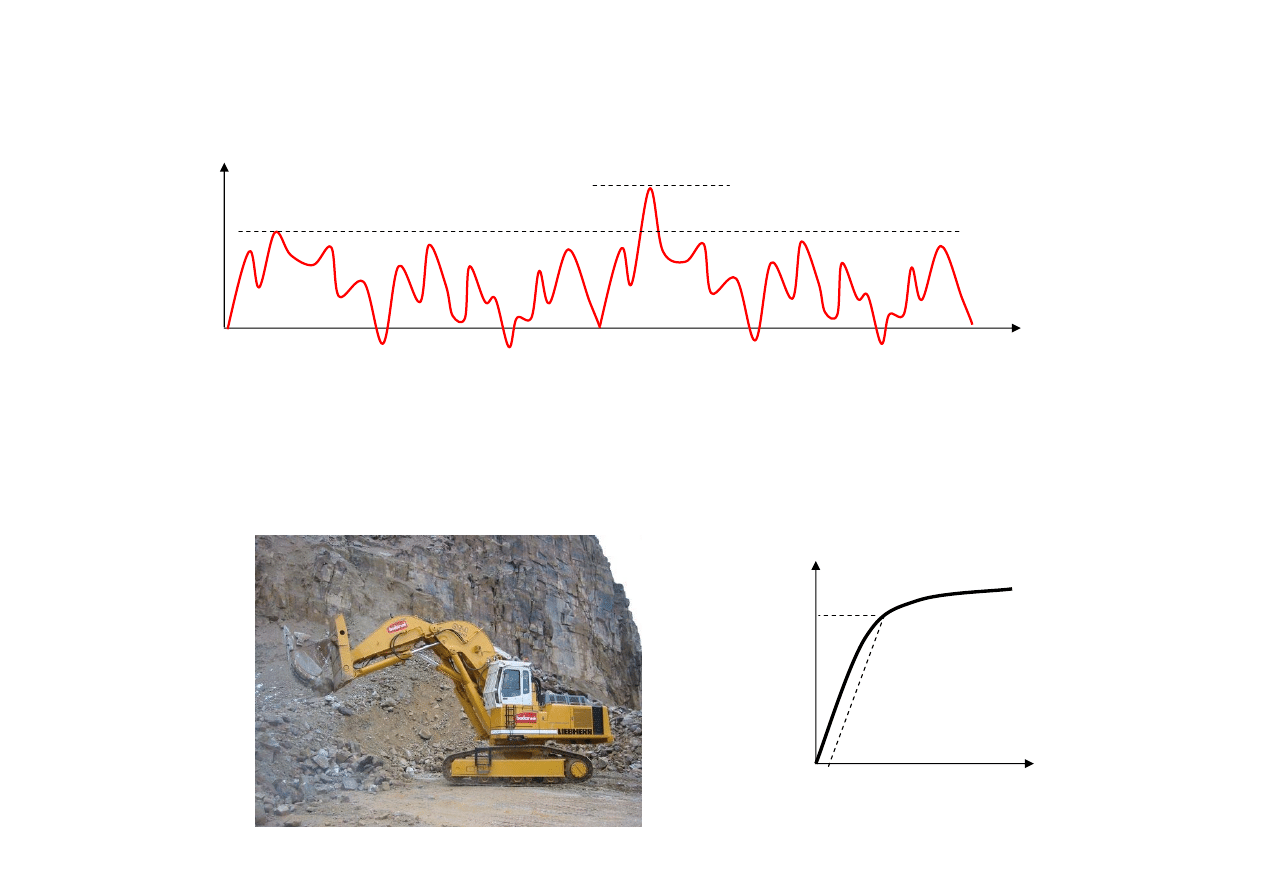
Obciążenia eksploatacyjne

Wymiarowanie:

1. Wytrzymałość doraźna - obciążenia ekstremalne
2. Wytrzymałość zmęczeniowa – obciążenia regularne

czas

odkształcenie

naprężenie

R

02

0.2%

Obciążenie ekstremalne

Obciążenie regularne

4

Wytrzymałość

na obciążenia jednorazowe

(statyczne)

5

Kryteria projektowe dla rodzajów uszkodzeń

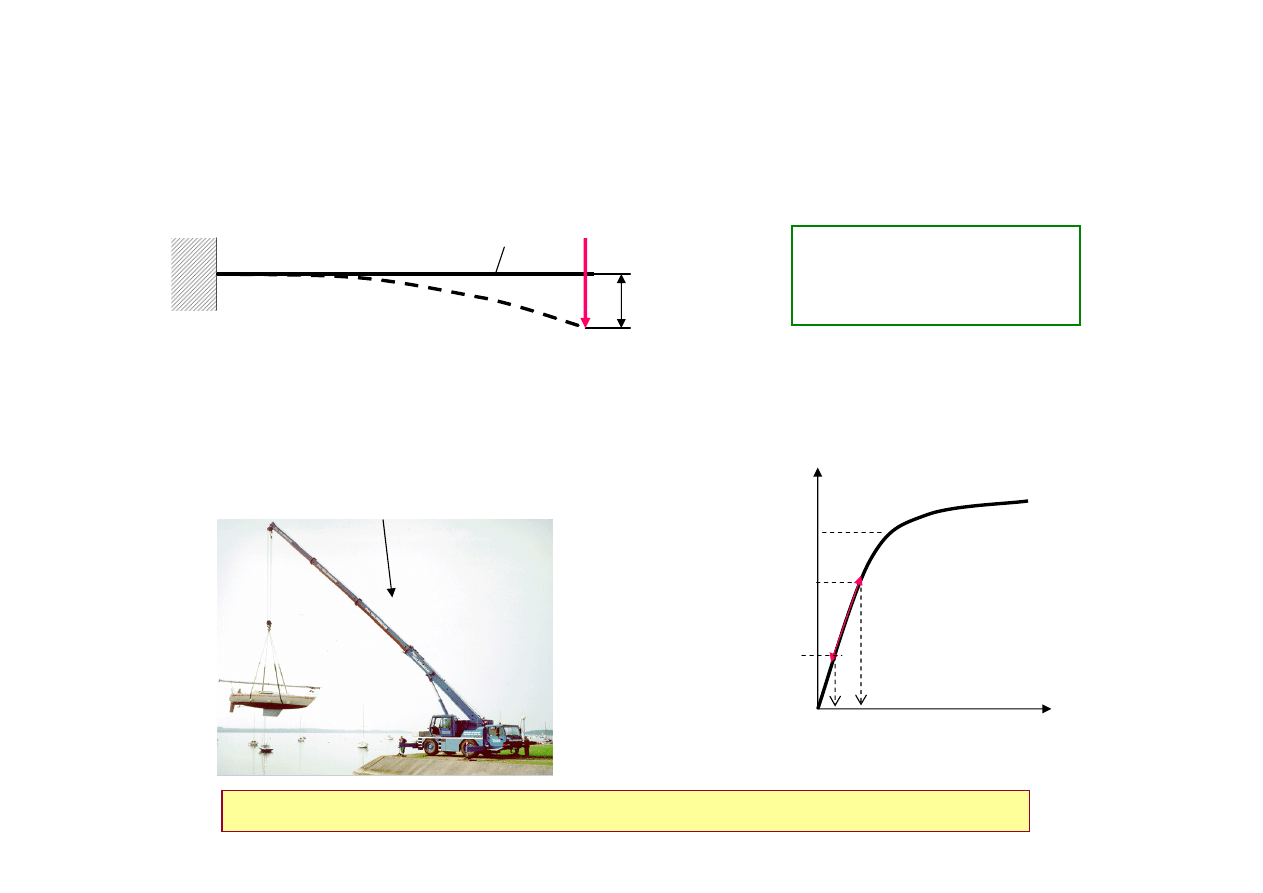
Nadmierna deformacja sprężysta

d o p

f

f

<

Przykłady:

1. Belka główna suwnicy (+)

2. Wysięgnik teleskopowy (?)

f

odciążenie

f = f(L, J, E, Obc. nominalne)

odkształcenie

naprężenie

R

02

f

1

S

2

obciążenie

S

1

f

2

Czy warto stosować stale wysokowytrzymałe na konstrukcje o małej f

dop

?

6

(

) (

)

(

)

(

)

n

R

R

o

red

zx

yz

xy

x

z

z

y

y

x

red

02

2

2

2

2

2

2

6

2

1

=

<

σ

τ

+

τ

+

τ

+

σ

−

σ

+

σ

−

σ

+

σ

−

σ

=

σ

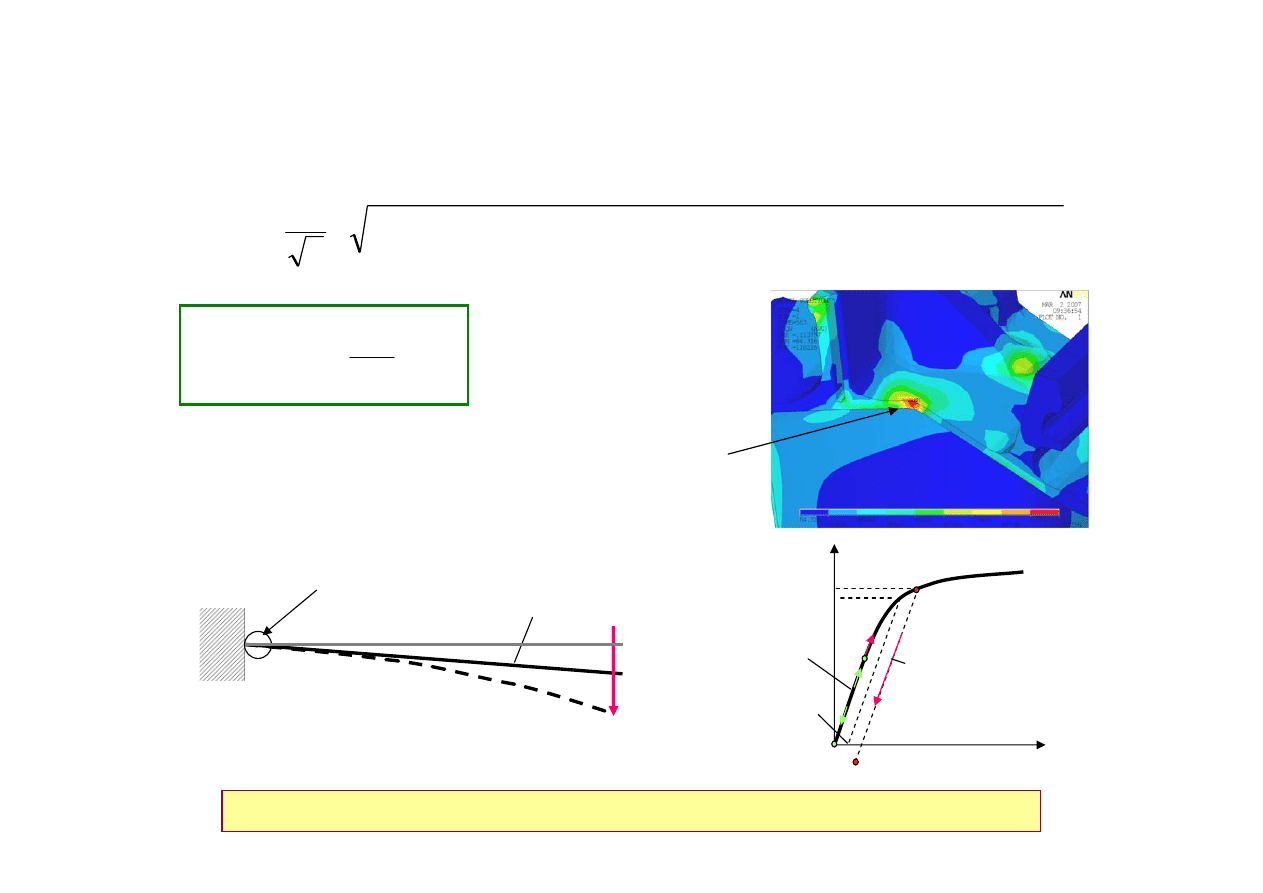
Przykłady:

odciążenie

Trwałe

odkształcenie

Max naprężenie
zredukowane

σ

red

> R

02

(?)

0

1

2

Kryteria projektowe dla rodzajów uszkodzeń

Deformacja trwała (wytrzymałość doraźna)

Ten warunek w konstrukcjach nośnych odnosi się do naprężeń nominalnych

obciążenie max

odkształcenie

naprężenie

R

02

0.2%

0

1

2

naprężenie

lokalne

naprężenie

nominalne

1

7

Ic

max

K

K

<

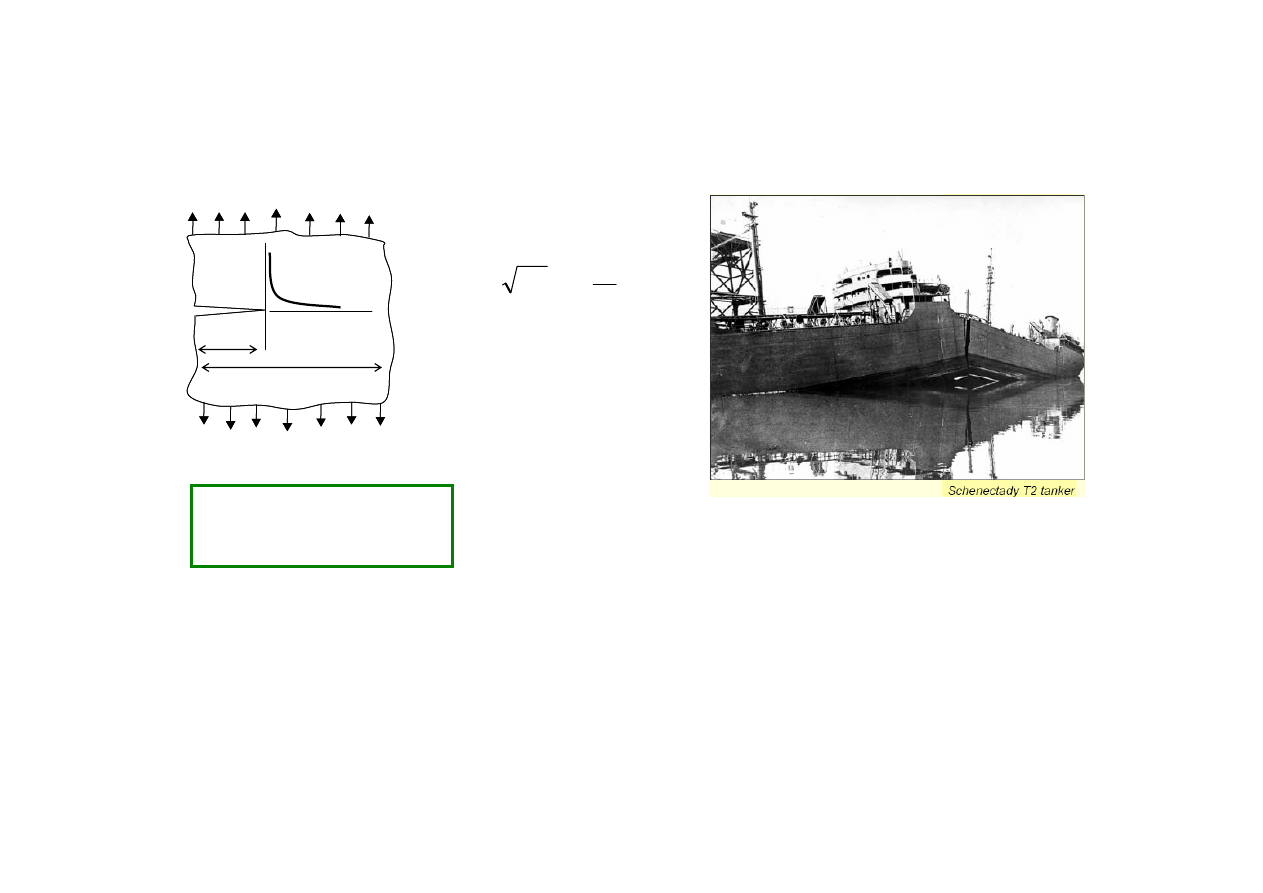
Przykłady:

Elementy zawierające wady

(spawanie)

As part of the government project during World

War II, United States planed continuous block

construction of all-welded cargo vessels (DWT

11000, "Liberty Ship"). The construction was

started with outbreak of the Pacific war from 1942.

2708 Liberty Ships were constructed from 1939

to 1945. 1031 damages or accidents due to

brittle fracture were reported by April 1, 1946.

More than 200 Liberty Ships were sink or

damaged beyond all hope of repair

(KOBAYASHI, Hideo)

⎟

⎠

⎞

⎜

⎝

⎛

⋅

π

=

w

a

Y

a

S

K

I

Współczynnik
intensywności
naprężeń

S

S

σ

y

a

Kryteria projektowe dla rodzajów uszkodzeń

Kruche pękanie

K = f(Obciążenie, Geometria, Rozmiar wady
K

Ic

= f(Materiał) – odporność na pękanie

w

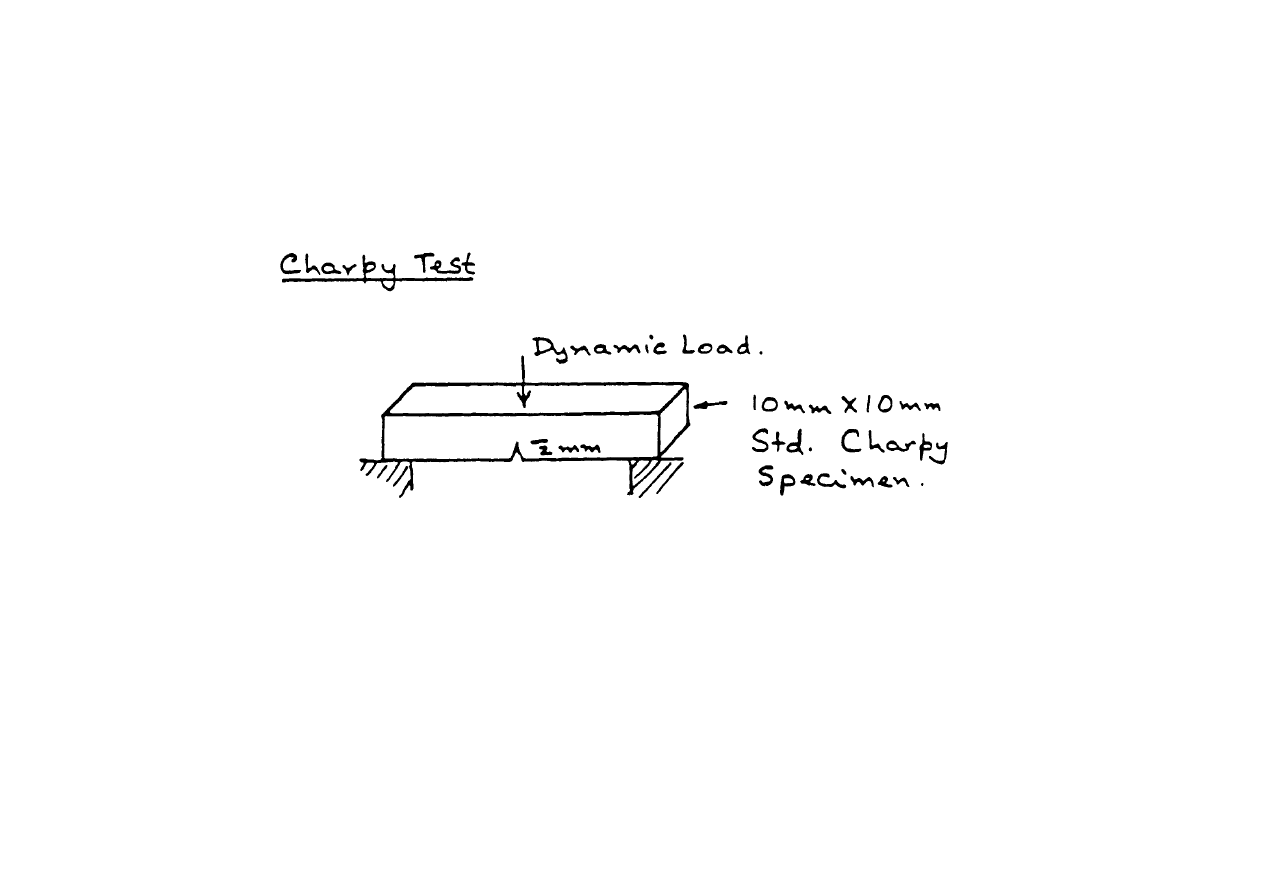
8

8

•

Próbka jest równomiernie podgrzewana/chłodzona do zadanej

temperatury, a potem ustawiana na stanowisku badawczym

•

Próbka pęka na skutek obciążenia dynamicznego wywołanego

wahadłem

•

Próbka jest badana metallurgicznie celem określenia udziału

procentowego przełomu ciągliwego i kruchego

Test Charpy (1905) pozwala ocenić kruche pękanie materiałów

Kryteria projektowe dla rodzajów uszkodzeń

9

9

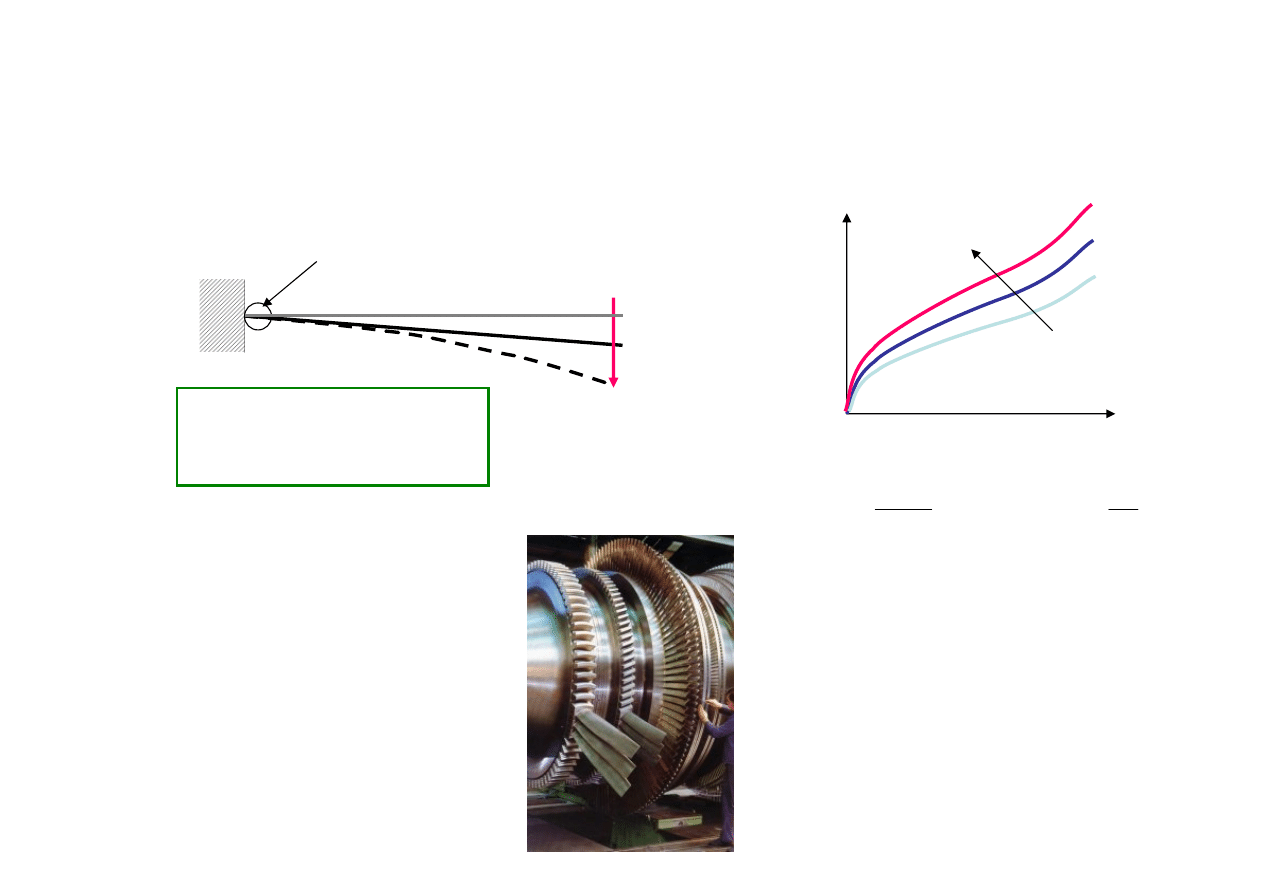
• Temperatura przejścia wskazuje znaczny spadek energii wymaganej do złamania próbki
• Temperatura przejścia jest kryterium wyboru materiału do pracy w niskich temperaturach

Przykład wyników testu Charpy

Absorbowana

energia

Temperatura przejścia

Kryteria projektowe dla rodzajów uszkodzeń

10

lim

h

t

L

L

Δ

<

Δ

=10000

Przykłady:

1. Długie belki (suwnice)
2. Łopatki turbin

Odkształcenie

plastyczne

czas

⎟

⎠

⎞

⎜

⎝

⎛

−

Δ

⋅

⋅

+

Δ

=

Δ

T

C

exp

t

C

C

t

C

n

C

eqv

n

ctn

4

2

3

1

3

1

σ

ε

Naprężenie+

Temperatura+

Trwałe odkształcenie

na skutek pełzania

0

t >> 0

t = 0

Kryteria projektowe dla rodzajów uszkodzeń

Pełzanie

11

Stateczność

konstrukcji nośnych

12

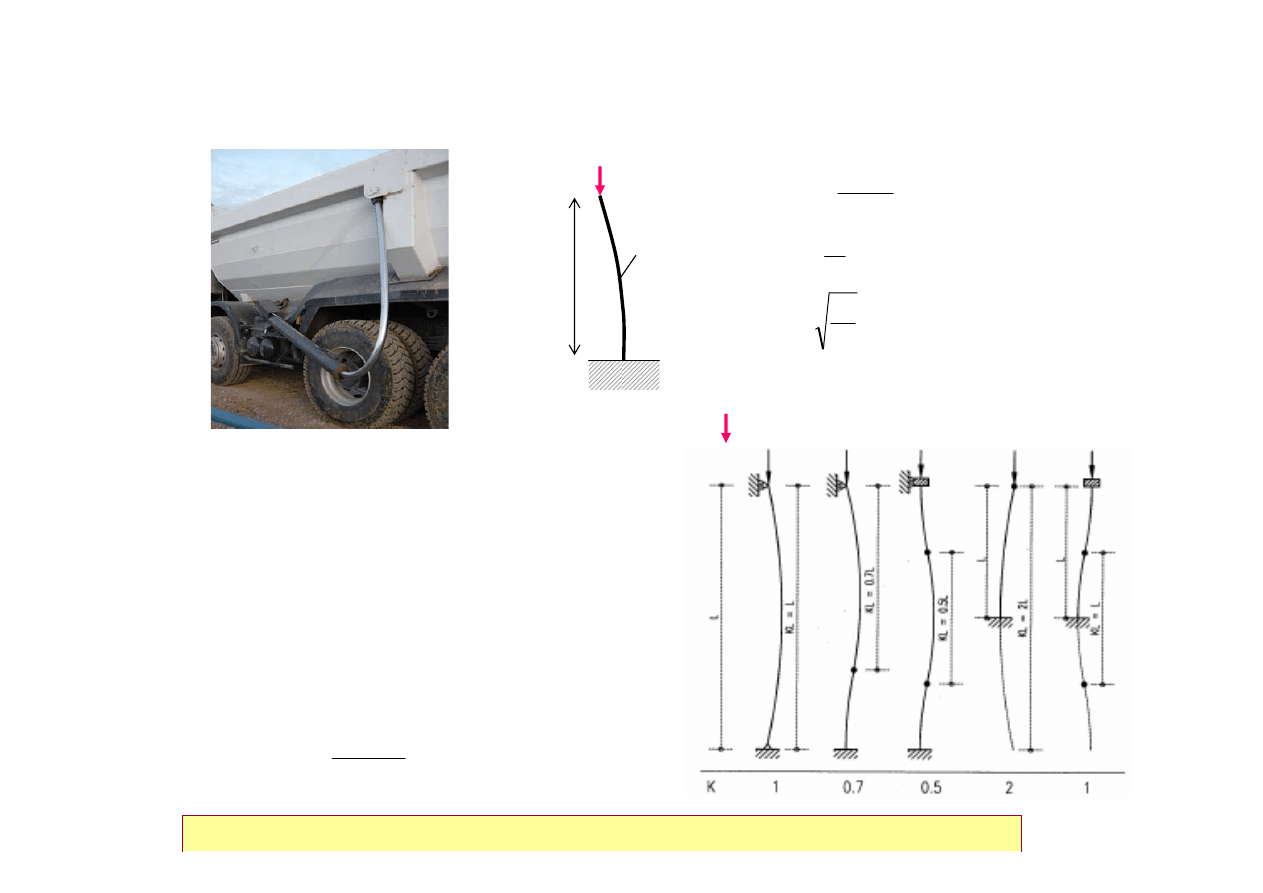
Stateczność ogólna konstrukcji

l

k

l

A

J

i

i

l

E A

P

w

x

w

k r

⋅

=

=

=

λ

λ

π

=

2

2

kolumna

P

l

Siła krytyczna

Smukłość

Promień
bezwładności

Badania wskazują, że siła krytyczna Eulera jest rzadko osiągana

w rzeczywistych konstrukcjach. Powody tego są następujące:

• Elementy ściskane nie są zupełnie proste,
• W elementach występują naprężenia własne o nierównomiernym

rozkładzie,

• Zamocowania na końcach nie są idealnie sworzniowe lub

zamurowane,

• Obciążenia nie są idealnie osiowe.

Długość wyboczeniowa, l

w

1

≤

⋅

ϕ

o

A R

P

Warunek stateczności (

ϕ < 1 zależy od smukłości λ):

Szczegóły obliczeń w zakresie stateczności konstrukcji nośnych: PN-90/B-3200 lub inne

13

Stateczność ogólna słupów zestawnych

x

y

x

y

α

=

=

λ

α

α

t g

A

A ,

n A

A

.

D

v

3

5

Gałęzie

l

1

1

1

i

l

v

=

λ

F

N

x

y

Smukłość zastępcza dla osi niefizycznej (N)

1

l

1

A

D

α

2

2

2

v

m

m

λ

+

λ

=

λ

λ – smukłość jak dla elementu pełnościennego
m – liczba gałęzi w płaszczyźnie skratowania

a

b

A – pole powierzchni wszystkich gałęzi
A

D

– pole przekroju krzyżulców (A

α

< A

D

)

n – liczba płaszczyzn skratowania

1

≤

⋅

ϕ

o

A R

P

Warunek stateczności (

ϕ < 1 zależy od smukłości λ

m

):

n=2

n=2

n=1.5

Inne warunki stateczności obejmują ściskanie i zginanie słupów

14

-25

-20

-15

-10

-5

0

5

10

15

20

25

0

5

10

15

20

25

Wysięg, R [m ]

Q

[k

N

],

M

[k

N

m

]

Qogr

MQogr

MQ=0

MGw

MGp

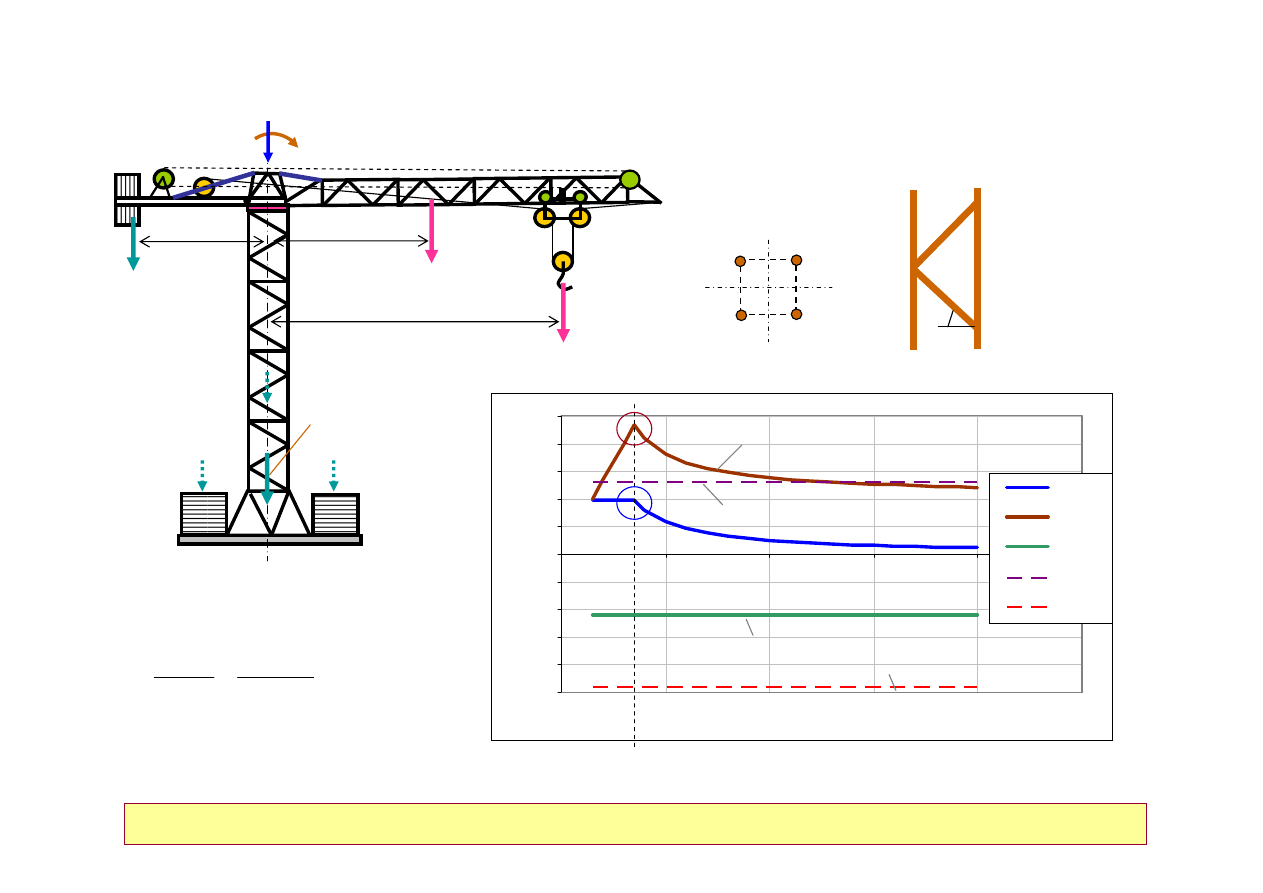
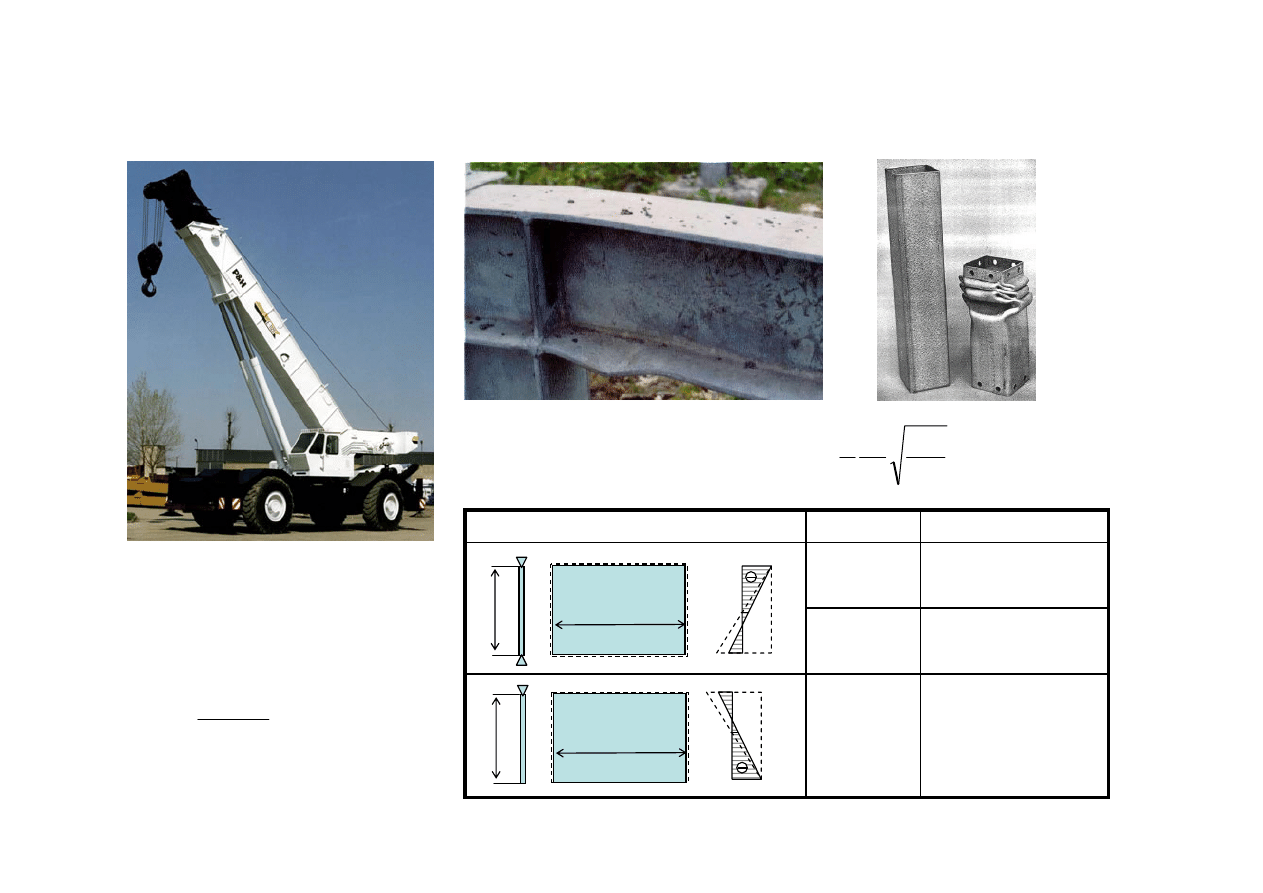
Stateczność wieży żurawia wieżowego

G

p

M+

R

Q

G

s1

/2

G

s1

/2

G

sw

G

w

G

s

r

p

r

w

Moment od przeciwwagi

Moment przy Q = 0

Moment przy Q dopuszczalnym

Moment od wysięgnika

Krytyczne obciążenie dla wieży

α

P

p

w

o

x

Rc

o

Rc

Rc

L

x

Rc

G

G

Q

P

R

W

M

;

AR

P

M

M

P

P

+

+

=

=

=

≤

⋅

ϕ

β

+

⋅

ϕ

1

Warunek stateczności
(

ϕ,

ϕ

L

zależą od smukłości

λ

m

):

x

y

Można również rozpatrywać warunek stateczności przy ściskaniu i podwójnym zginaniu wieży

15

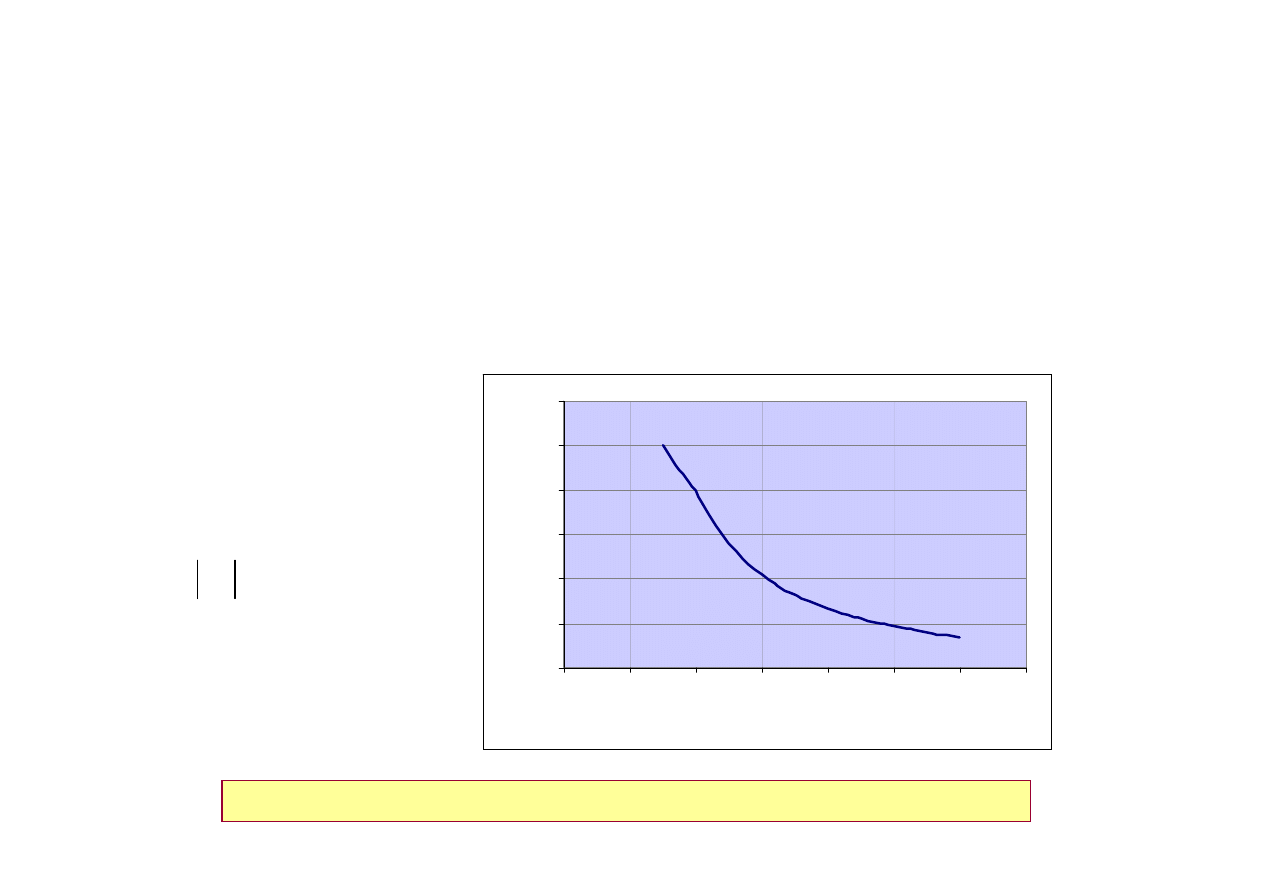
Stateczność miejscowa konstrukcji

1

≤

⋅

ϕ

σ

o

p

c

R

215

56

o

p

R

K

t

b

=

λ

Smukłość względna

λ

p

Współczynnik K

Zakres

Schemat podparcia i obciążenia ścianki

β ≥ 1
0

≤ ν ≤ 1

K = 0.4 + 0.6

ν

β ≥ 1.6
0

≤ ν ≤ 1

K = 2.2 + 0.8

ν

β ≥ 1

ν ≤ 0

K = 0.4 / (1-

ν

)

ν = (σ

1

+σ

2

)/2/σ

1

νσ

1

σ

1

νσ

1

σ

1

b

a =

βb

b

a =

βb

σ

2

σ

2

Warunek stateczności:

σ

c

=

σ

1

(ściskanie)

ϕ

p

zależy od smukłości

λ

p

16

Stateczność miejscowa konstrukcji

o

p

c

R

ϕ

≤

σ

Warunek stateczności
(

ϕ

p

zależy od smukłości

λ

p

)

ν

−

=

λ

≤

λ

25

0

75

0

0

.

.

p

p

Współczynnik

ϕ

p

dla:

1

=

ϕ

p

35

1

0

.

p

p

≤

λ

<

λ

(

)

ν

−

λ

−

ν

−

=

ϕ

2

0

8

0

3

0

6

1

.

.

.

.

p

p

35

1

.

p

>

λ

0

0.2

0.4

0.6

0.8

1

1.2

0

0.5

1

1.5

2

2.5

3

3.5

lambda_p

fi

_p

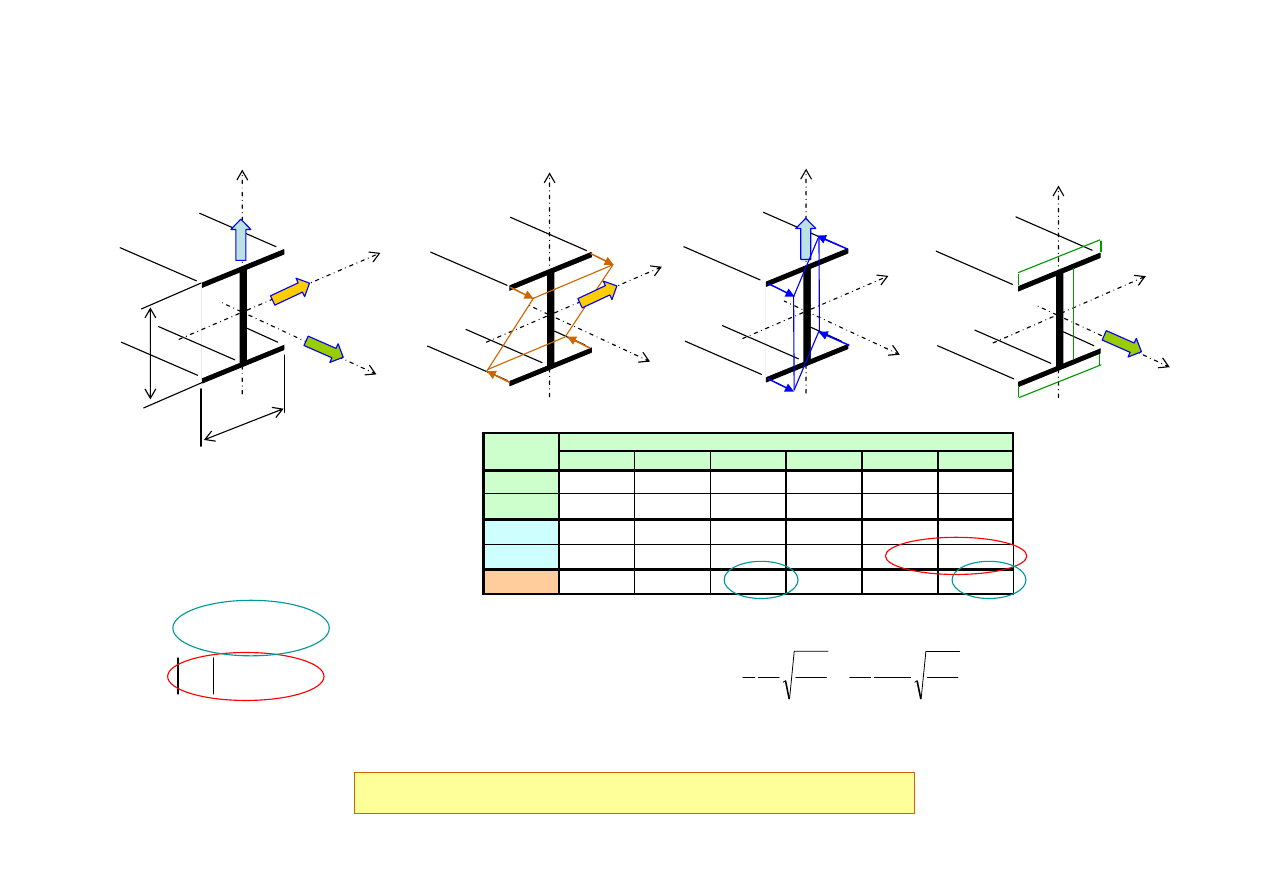
Wykres

ϕ

p

Stateczność miejscowa może ograniczać wytrzymałość konstrukcji nośnej

17

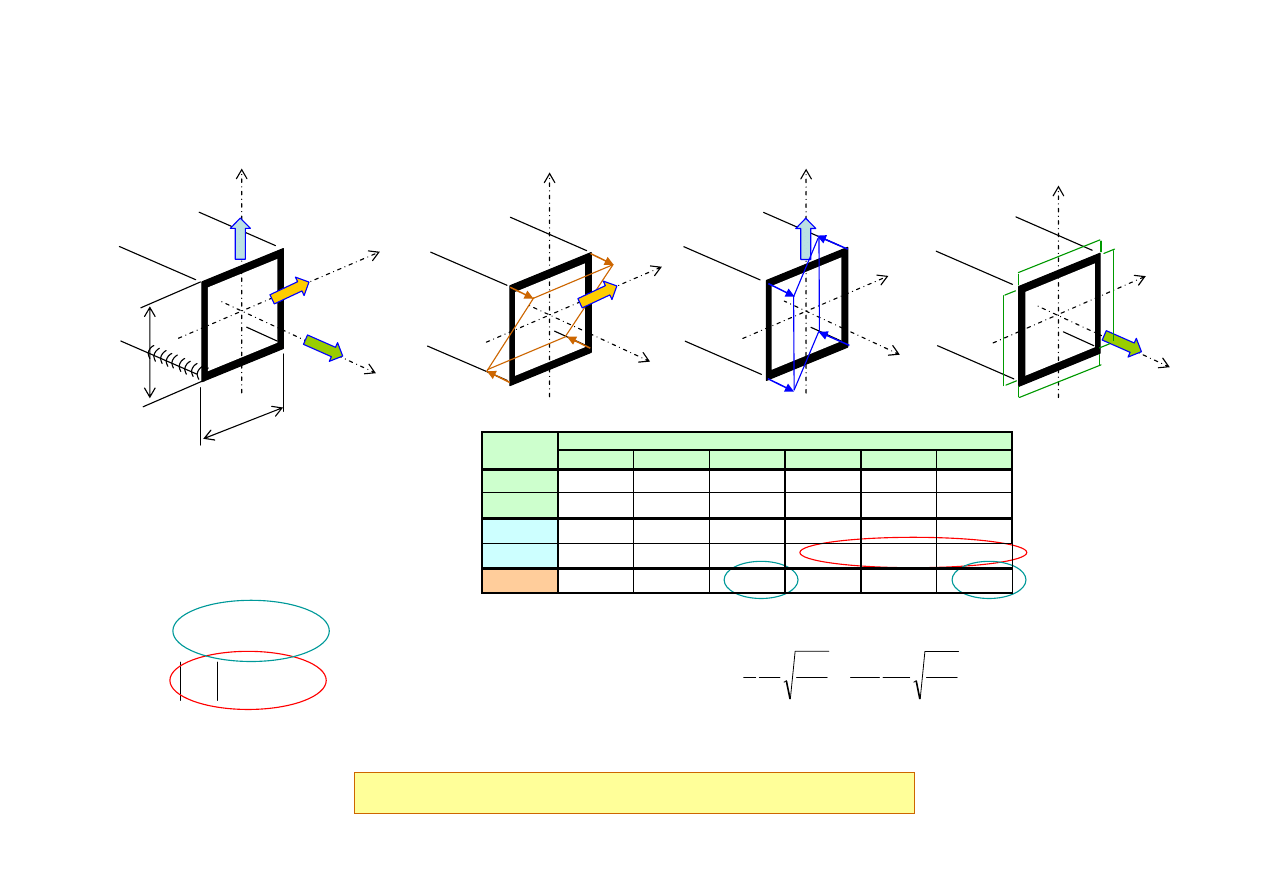
Rodzaj
naprężeń

1

2

3

4

5

6

σ

x,y

94.2

94.2

94.2

-94.2

-94.2

-94.2

σ

x,z

-103.6

0

103.6

103.6

0

-103.6

τ

s

119.0

119.0

119.0

119.0

119.0

119.0

σ

n

-9.4

94.2

197.8

9.4

-94.2

-197.8

σ

red

206.4

226.7

285.7

206.4

226.7

285.7

Punkt przekroju

Wytrzymałość doraźna

y

z

x

M

x

M

y

M

z

b

h

M

y

= 25 kNm

M

z

= 5 kNm

M

x

= 2 kNm

b = 120 mm
h = 200 mm

δ = 10 mm

Materiał
R

o

= 300 MPa

σ

1

= -197.8,

σ

2

= -94.2,

ν = (-197.8-94.2)/2/(-197.8) = 0.74

K = 2.2 + 0.8

ν = 2.79

353

0

215

300

56

79

2

10

60

215

56

.

.

R

K

t

b

o

p

=

=

=

λ

0

1

565

0

25

0

75

0

.

;

.

.

.

p

p0

=

ϕ

=

ν

−

=

λ

Oba warunki wytrzymałości doraźnej są spełnione

y

z

x

M

z

y

z

x

M

y

σ

x,y

σ

x,z

o

p

c

o

red

R

.

R

.

ϕ

≤

σ

≤

σ

2

1

Warunki

y

z

M

s

τ

s

1

2

3

4

5

6

18

Wytrzymałość doraźna

Materiał
R

o

= 300 MPa

σ

1

= -101.4,

σ

2

= -57.9,

ν = (-101.4-57.9)/2/(-101.4) = 0.43

K = 0.4/(1 –

ν) = 0.70

177

0

215

300

56

7

0

10

120

215

56

.

.

R

K

t

b

o

p

=

=

=

λ

0

1

565

0

25

0

75

0

.

;

.

.

.

p

p0

=

ϕ

=

ν

−

=

λ

Oba warunki wytrzymałości doraźnej są spełnione

o

p

c

o

red

R

.

R

.

ϕ

≤

σ

≤

σ

2

1

Warunki

y

z

x

M

x

M

y

M

z

b

h

M

y

= 25 kNm

M

z

= 5 kNm

M

x

= 2 kNm

b = 120 mm
h = 200 mm

δ = 10 mm

y

z

x

M

y

σ

x,y

y

z

x

M

z

σ

x,z

1

2

3

4

5

6

y

z

M

s

τ

s

Rodzaj
naprężeń

1

2

3

4

5

6

σ

x,y

79.6

79.6

79.6

-79.6

-79.6

-79.6

σ

x,z

-21.7

0

21.7

21.7

0

-21.7

τ

s

4.8

4.8

4.8

4.8

4.8

4.8

σ

n

57.9

79.6

101.4

-57.9

-79.6

-101.4

σ

red

58.5

80.0

101.7

58.5

80.0

101.7

Punkt przekroju

19

Wytrzymałość

na obciążenia cykliczne

(zmęczeniowa)

20

.

ogr

nie

trwalosc

S

S

.

ogr

trwalosc

N

N

L

a

wym

−

<

−

>

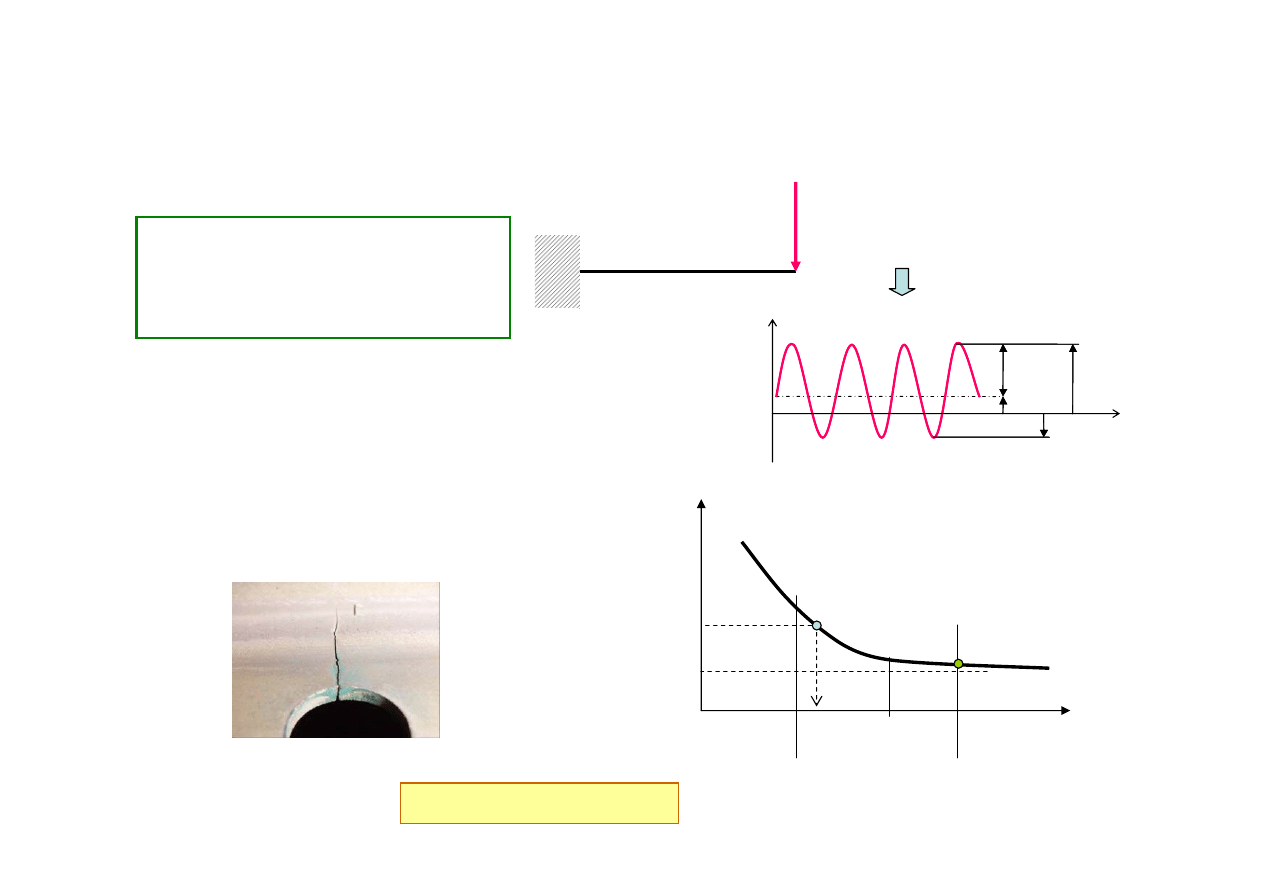
Przykłady:

Elementy

zawierające karby

(koncentracja naprężeń)

S

m

S

min

S

max

S

a

0

S

czas

Obciążenie:

F = f(czas)

Amplituda na

pr

ęż

eń

Cykle

Sa

Charakterystyka zmęczeniowa

N

Kryteria projektowe dla rodzajów uszkodzeń

Pękanie zmęczeniowe

N

wym

< N

G

trwałość

ograniczona

N = f(Obciążenie, Geometria, Materiał, …)
N

wym

= f(Element konstrukcyjny, Obciążenia)

Jak określić trwałość T?

N

wym

> N

G

trwałość

nieograniczona

N

G

S

L

Naprężenie:

Sa

21

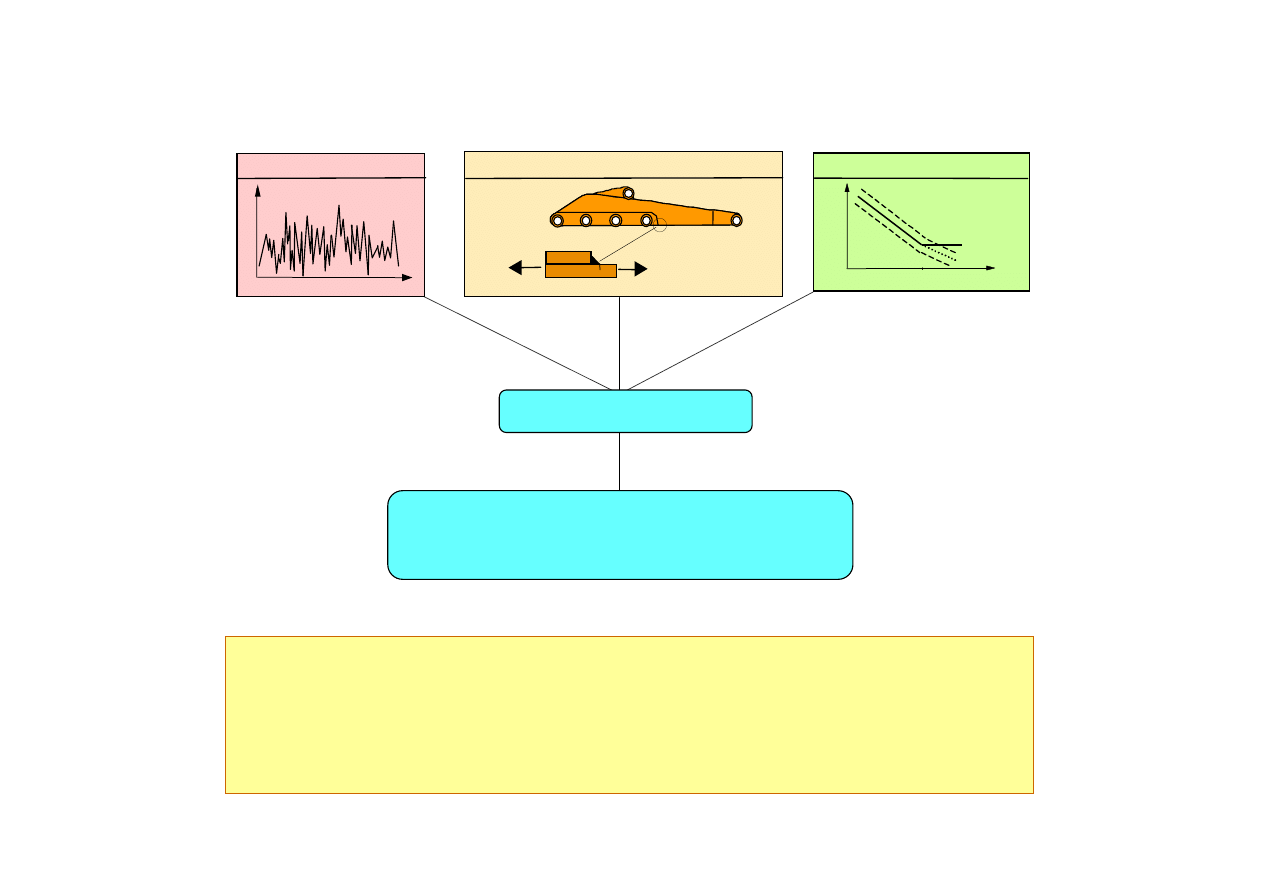
Prognozowanie trwałości zmęczeniowej

W ocenie trwałości należy:
1. Określić potencjalne najsłabsze miejsce (miejsca) w konstrukcji (PSO)
2. Dobrać charakterystykę zmęczeniową adekwatną dla geometrii PSO
3. Określić obciążenia eksploatacyjne i ich efekty (naprężenia) dla PSO
4. Przeprowadzić stosowne obliczenia.

ELEMENT KONSTRUKCYJNY

PSO

KRZYWA S-N

N

o

N

ΔS

R

w

OBCIĄŻENIE

S

t

OBLICZANIE TRWAŁOŚCI

T > T

r

TRWAŁOŚĆ OBLICZONA > TRWAŁOŚĆ WYMAGANA

22

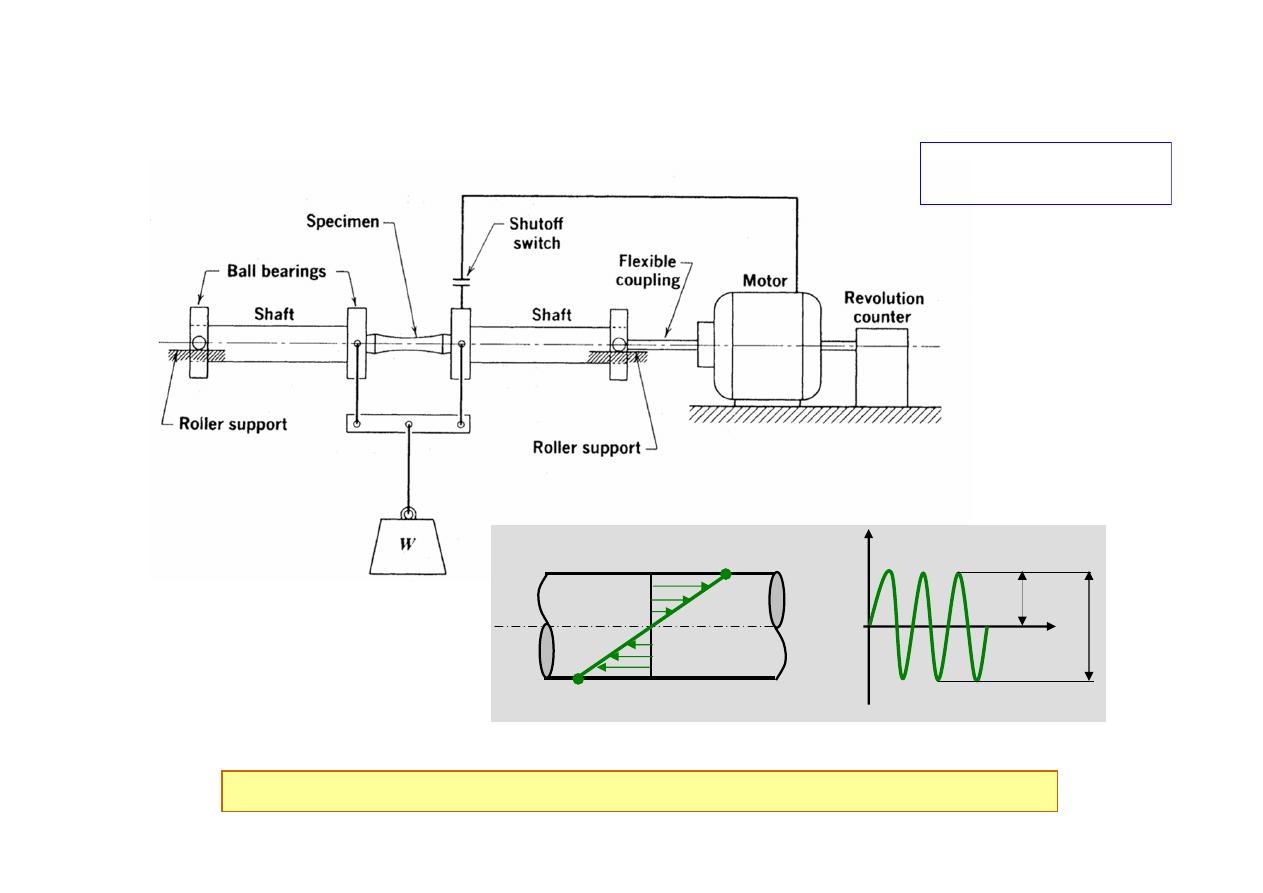
Charakterystyka zmęczeniowa – krzywa S-N

Łatwy sposób wywoływania naprężeń w próbce, ale badania tylko przy r = -1

(Collins)

Wyznaczanie krzywej S-N (Woehlera)

Współczynnik asymetrii cyklu
r = S

min

/S

max

(+) S

max

(-) S

min

S

max

S

min

czas

Napr

ęż

.

0

S

a

∆

S

S-N = Stress-Life
(Naprężenie – Trwałość)

23

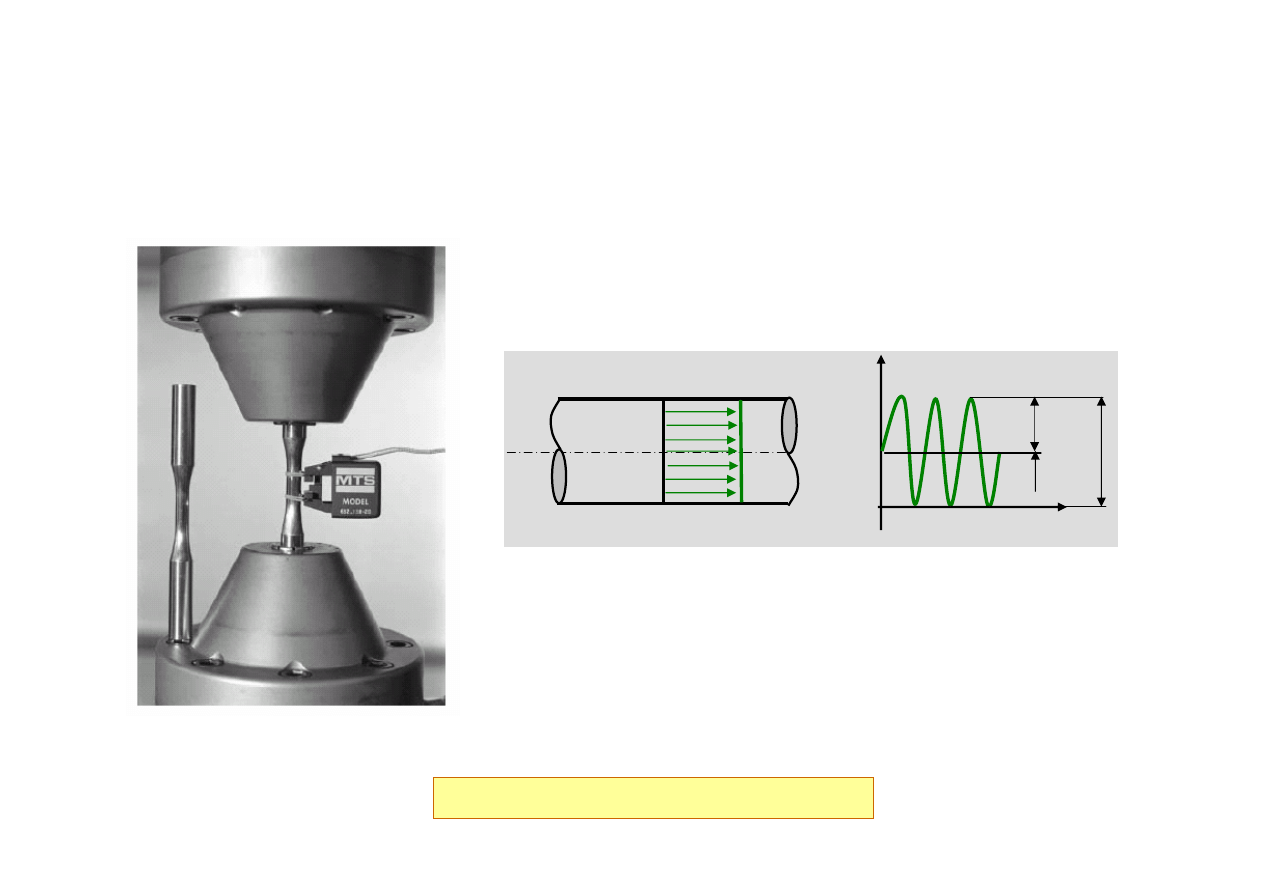
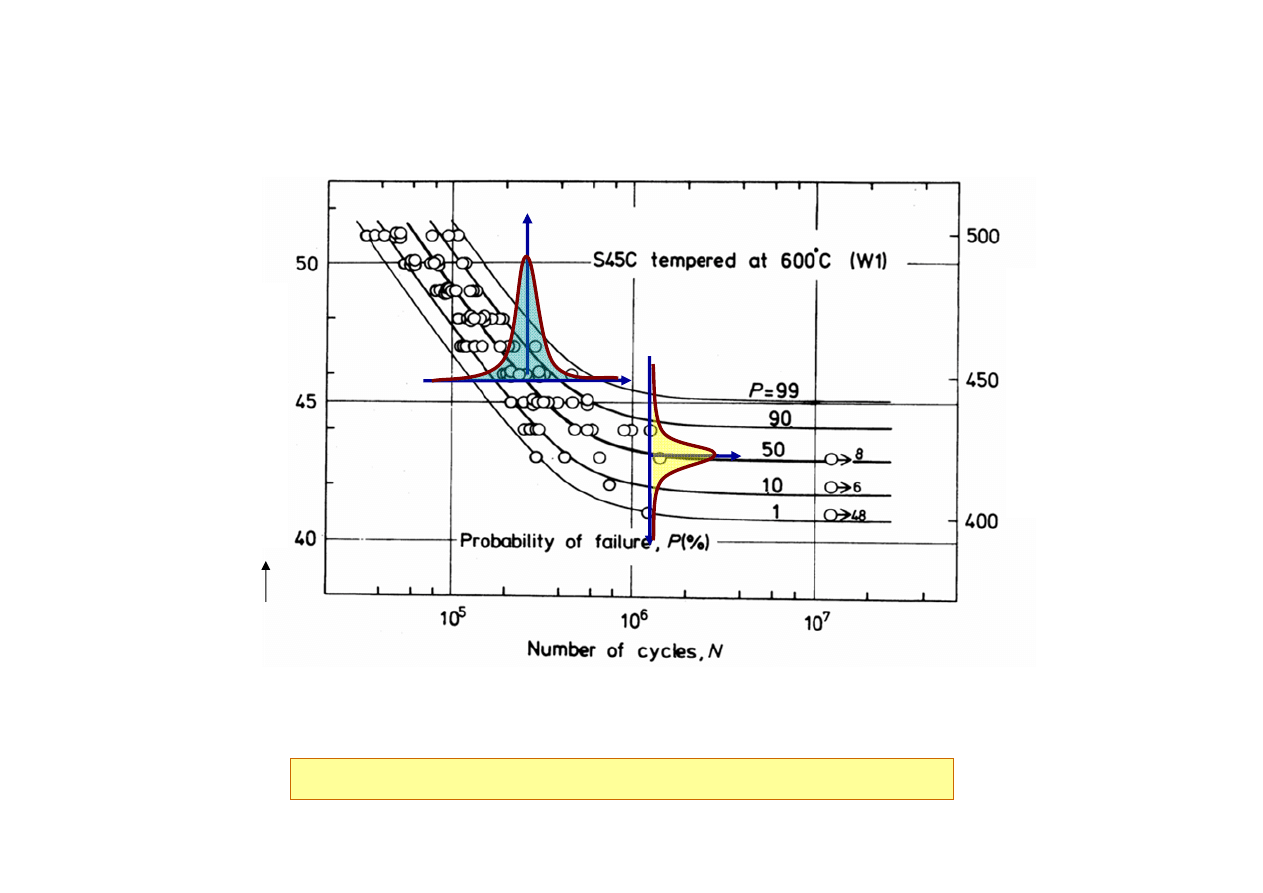
Charakterystyka zmęczeniowa – krzywa S-N

Porównać z poprzednimi badaniami…

S

max

S

max

S

min

czas

Napr

ęż

.

0

S

a

∆

S

S

m

Wyznaczanie krzywej S-N

24

Alt.

 Stress,

 Sa

(kgf/mm

2

)

Alt.

 Stress,

 Sa

(N/mm

2

)

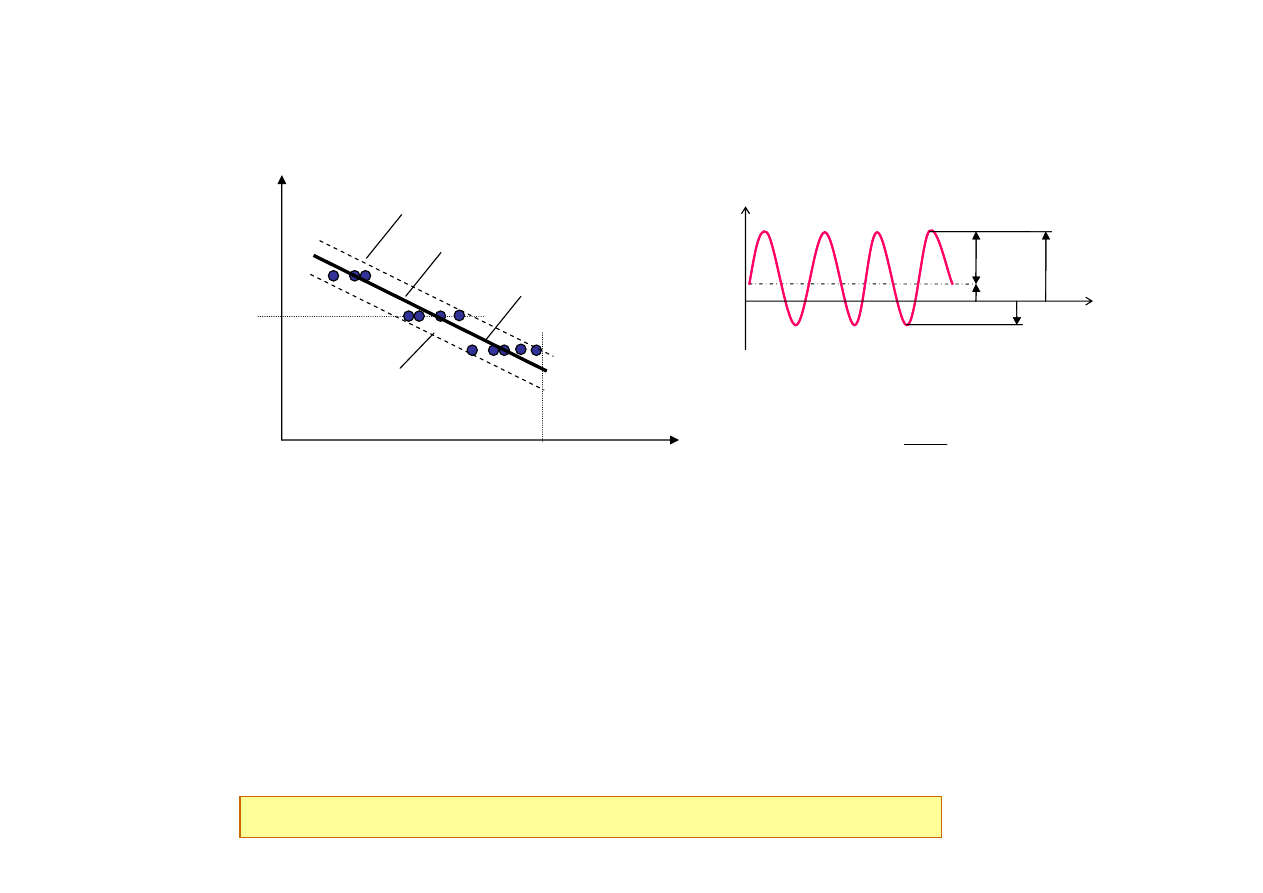
Charakterystyka zmęczeniowa – krzywa S-N

f(N)

f(S)

Charakterystykę zmęczeniową (krzywą S-N) cechuje rozrzut

(S. Nishijima)

Jakich informacji brak na tym wykresie?

Krzywa S-N opisana jest
zwykle za pomocą
amplitudy naprężeń,
czasem za pomocą
naprężeń max

25

S

m

S

min

S

max

S

a

0

S

czas

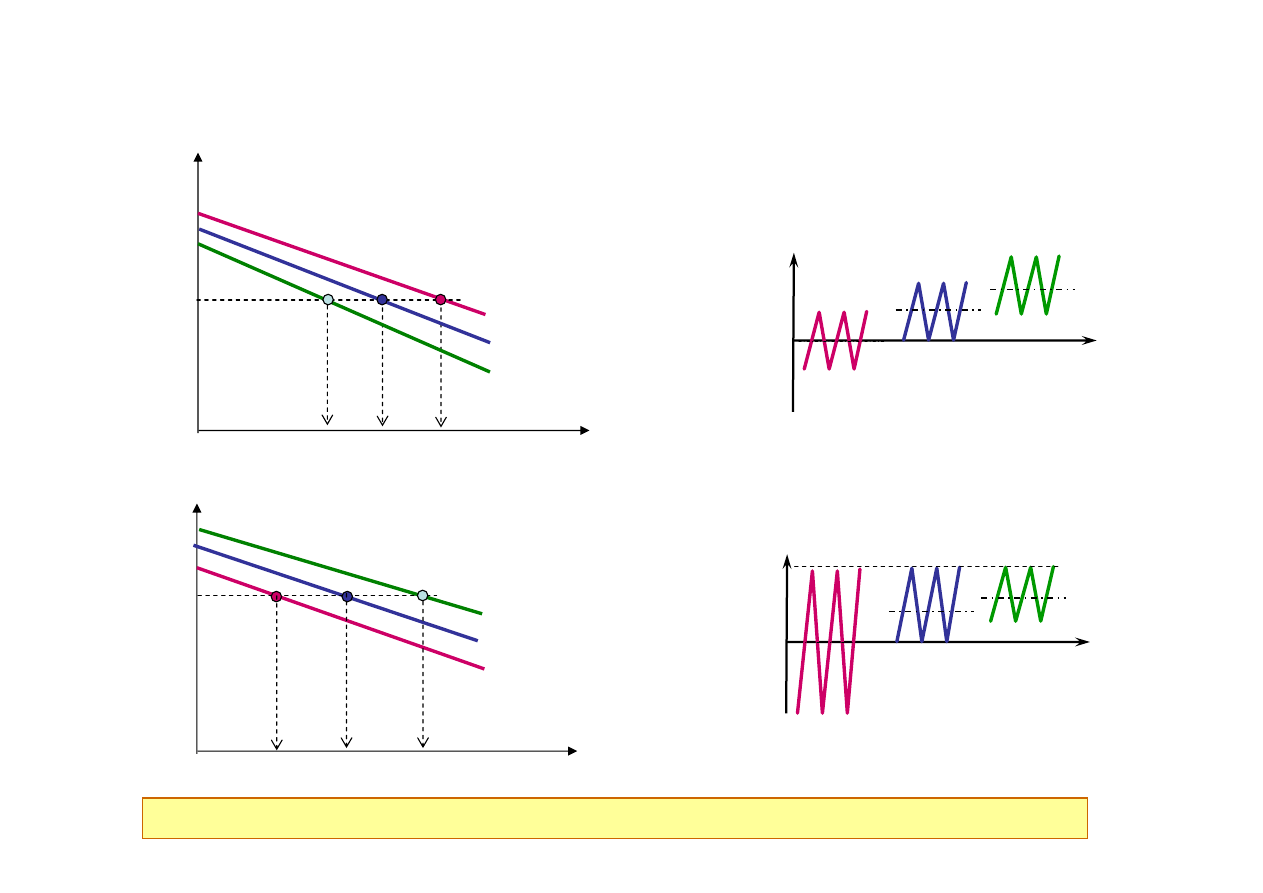
Charakterystyka zmęczeniowa – krzywa S-N

Czynniki wpływające na krzywą S-N:
1. Materiał
2. Naprężenie średnie cyklu (współczynnik r > 0

↓)

3. Gradient naprężeń (rozciąganie

↓, zginanie ↑)

4. Temperatura (wyższa

↓)

5. Chropowatość powierzchni (wzrost

↓)

6. Obróbka powierzchniowa (pokrycia

↓, śrutowanie ↑)

7. Rozmiar próbki (wzrost

↓)

8. Częstotliwość zmian naprężeń (wzrost

↑)

9. Środowisko (korozja

↓)

max

min

S

S

r

=

Cykl obciążenia opisują 2 parametry

Współczynnik asymetrii cyklu

Log Sa

Sa1

Cykle

Amplituda

naprężeń

N

0

Log N

S

D

+2

σ (Pf = 97.7%)

-2

σ (Pf = 2.3%)

AVG (Pf = 50%)

S

a

m.

N = C

Powyższe informacje powinny być podane w opisie krzywej S-N

26

r = 0.2

r = 0

r = -1

Trwałość

Ampl. napr., Sa

S

a1

czas

S

m

= 0

S

m

= S

a

S

m

> 0

Napr

ęż

eni

e, S

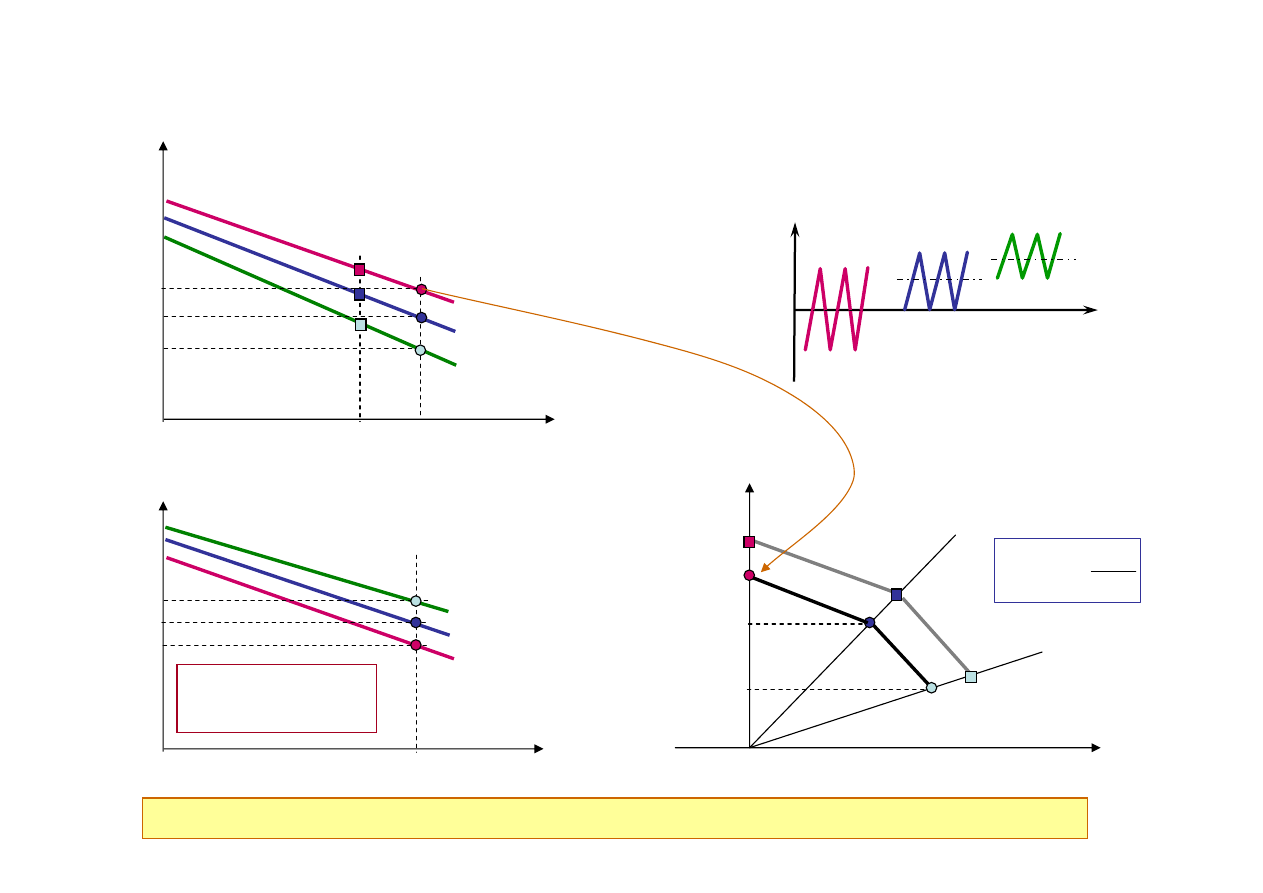
Charakterystyka zmęczeniowa

Wpływ naprężeń średnich

r = -1

r = 0

r = 0.2

Naprężenie średnie cyklu obciążenia ma ujemny wpływ na wytrzymałość zmęczeniową

Jednakowa amplituda Î różna trwałość

r = 0.2

r = 0
r = -1

Trwałość

Napr. max, S

max

(

!

)

S

mx1

czas

S

m

= 0

S

m

= S

a

S

m

> 0

Napr

ęż

eni

e, S

r = -1

r = 0

r = 0.2

Jednakowe S

max

Î

różna trwałość

S

mx1

27

N1

r = 0.2

r = 0

r = -1

Trwałość

Ampl. napr., Sa

S

a0.2

S

a0

S

a-1

N2

r

r

S

S

a

m

−

+

=

1

1

Napr. średnie, S

m

Ampl. napr., Sa

S

a0.2

S

a0

S

a-1

N2

N1

r = 0.2

r = 0

r = -1

0

czas

S

m

= 0

S

m

= S

a

S

m

> 0

Napr

ęż

eni

e, S

Charakterystyka zmęczeniowa

Wpływ naprężeń średnich

r = -1

r = 0

r = 0.2

Naprężenie średnie cyklu obciążenia ma ujemny wpływ na wytrzymałość zmęczeniową

r = 0.2
r = 0

r = -1

Trwałość

Napr. max, S

max

(

!

)

S

mx0.2

S

mx0

S

mx-1

N

S

mx-1

= Z

rc

S

mx0

= Z

rj

dla N = N

G

S

a1

Cykle równoważne Î jednakowa trwałość

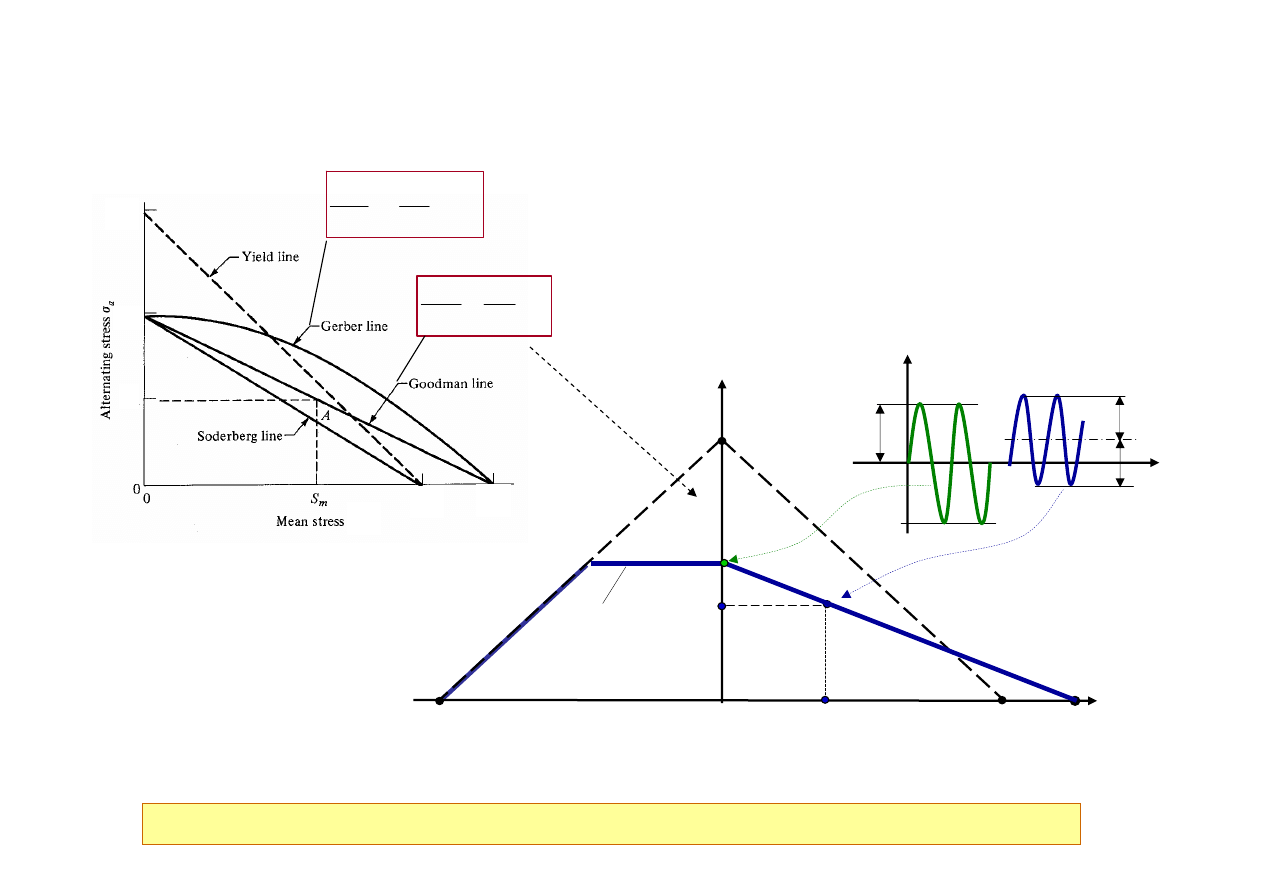
28

S

m

S

a

Naprężenie średnie, S

m

R

e

R

e

R

m

0

R

e

S

a-1

S

a

S

a

S

a

S

m

S

S

a-

1

S

m

= 0

0

N

Równoważne cykle

obciążenia, dające

jednakową trwałość N

1

1

=

+

−

m

m

a

a

R

S

S

S

1

2

1

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

−

m

m

a

a

R

S

S

S

R

e

S

a-1

S

a

S

m

R

e

R

m

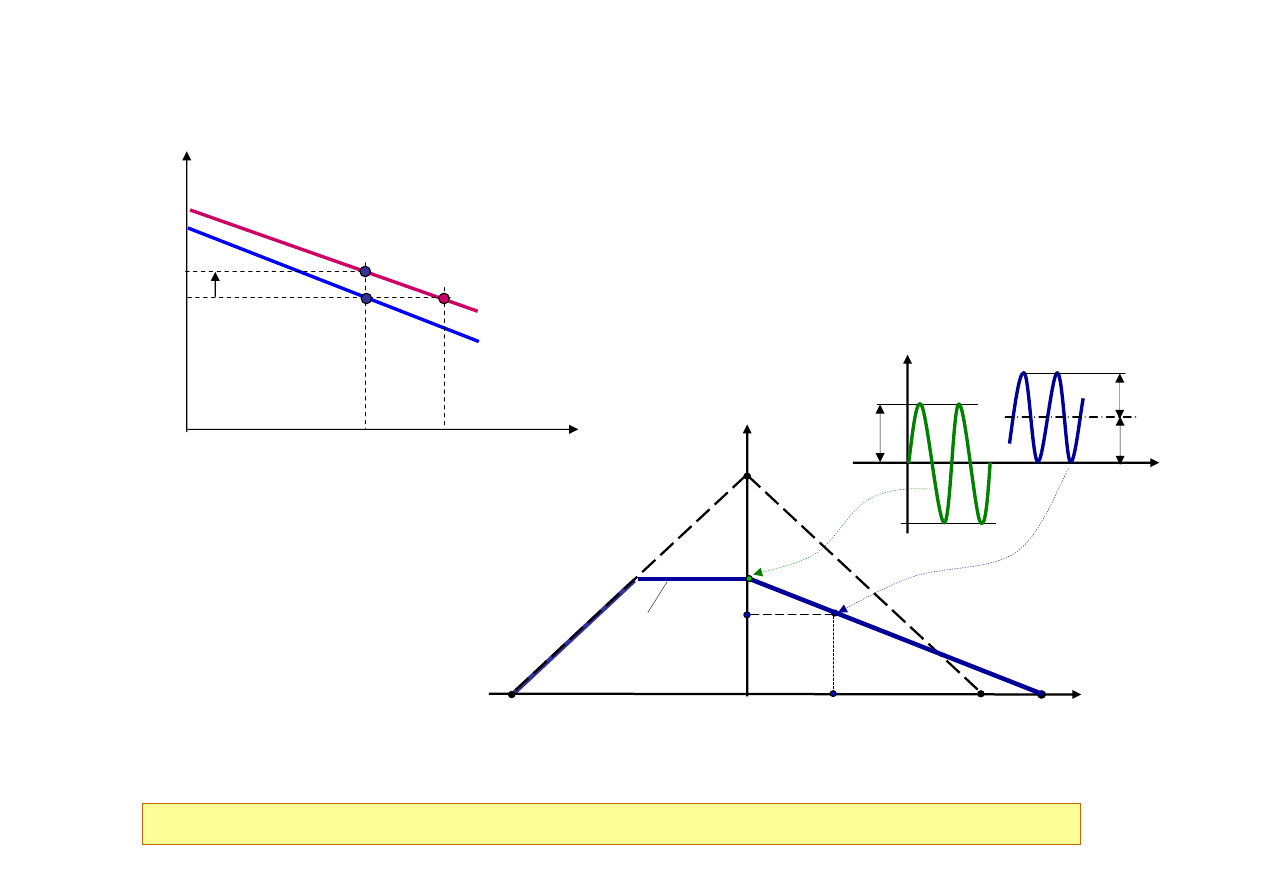
Charakterystyka zmęczeniowa

Modelowanie wpływu naprężeń średnich

Modelowanie wpływu naprężeń średnich jest konieczne dla poprawnej oceny trwałości

Modelowanie wpływu naprężeń średnich ma
na celu wyznaczenie amplitudy naprężeń
cyklu równoważnego, o innej wartości
naprężeń średnich (współczynnika r).

r = -1

r > -1

Gdy krzywa S-N jest wyznaczona
dla r = -1, to cykl obciążeń (S

a

, S

m

)

musi zostać zastąpiony cyklem
równoważnym o r = -1 (S

a-1

,0)

Î

Umożliwia to model

Goodmana lub Gerbera.

29

R

m

S

m

S

a

Naprężenie
średnie, S

m

R

e

R

e

0

R

e

S

a-1

S

a

N

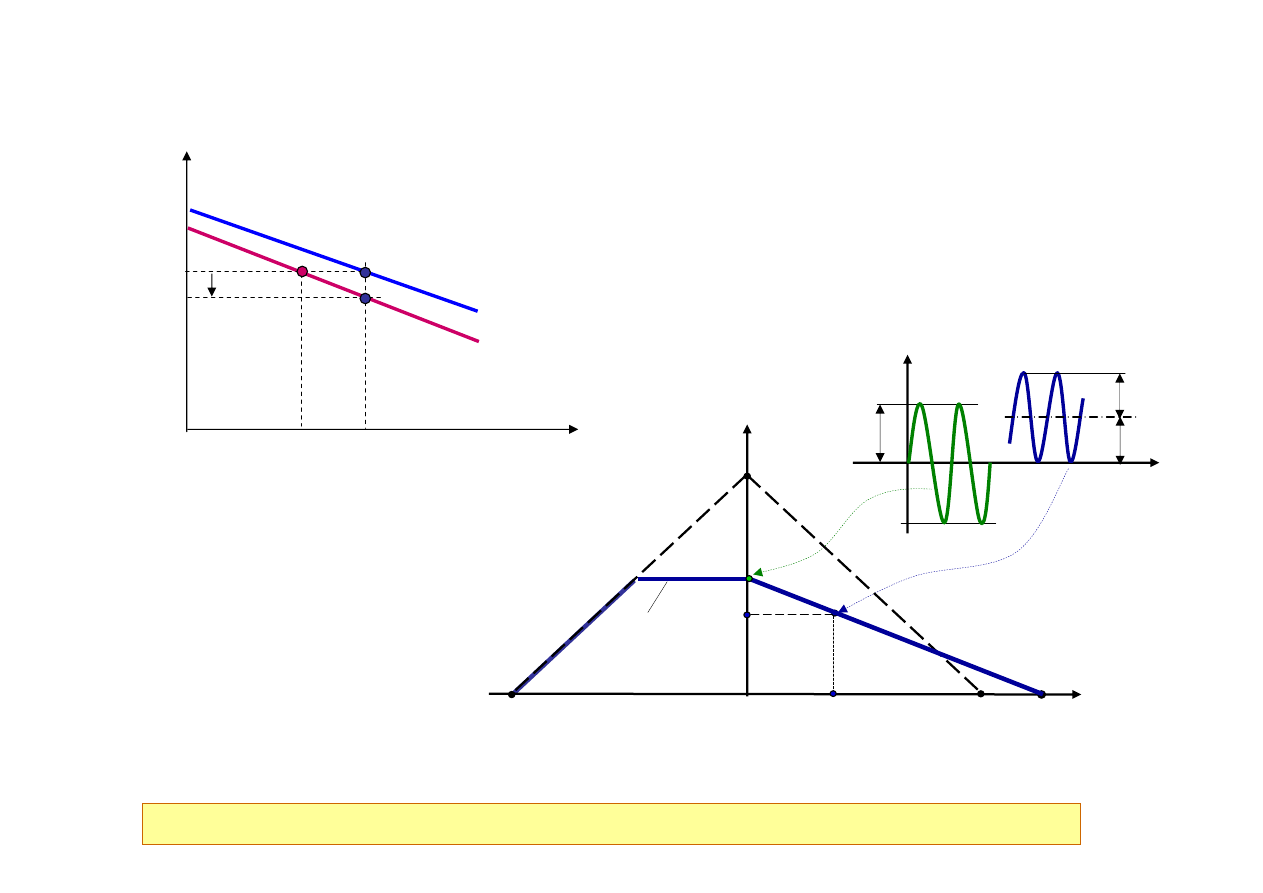
Scenariusz 1

1. Cykl obciążenia elementu: r = 0, S

a

= S

a0

2. Dostępna jest krzywa S-N wyznaczona

przy r = -1

Charakterystyka zmęczeniowa

Modelowanie wpływu naprężeń średnich

Modelowanie wpływu naprężeń średnich jest konieczne dla poprawnej oceny trwałości

S

m

S

a0

S

S

a-

1

S

m

= 0

0

r = -1

r = 0

• Gdybyśmy mieli krzywą dla r = 0, to

prognozowana trwałość byłaby N*.

• Przy użyciu krzywej r = -1

prognozowana trwałość wynosi N

• Dla poprawnej oceny trwałości cykl

obciążeń z S

m

> 0 musi zostać

zastąpiony cyklem równoważnym
o r = -1 (S

a-1

> S

a0

).

N*

r = 0 (brak)

r = -1 (dostępna)

Trwałość

Sa

S

a0

S

a-1

N

30

R

m

S

m

S

a

Naprężenie
średnie, S

m

R

e

R

e

0

R

e

S

a-1

S

a

N

Scenariusz 2

1. Cykl obciążenia elementu: r = -1, S

a

= S

a-1

2. Dostępna jest krzywa S-N wyznaczona

przy r = 0

Charakterystyka zmęczeniowa

Modelowanie wpływu naprężeń średnich

Modelowanie wpływu naprężeń średnich jest konieczne dla poprawnej oceny trwałości

S

m

S

a0

S

S

a-

1

S

m

= 0

0

r = -1

r = 0

• Gdybyśmy mieli krzywą dla r = -1,

to prognozowana trwałość byłaby N*.

• Przy użyciu krzywej r = 0

prognozowana trwałość wynosi N

• Dla poprawnej oceny trwałości cykl

obciążeń z S

m

= 0 musi zostać

zastąpiony cyklem równoważnym
dla r = 0 (S

a0

< S

a-1

).

N*

r = 0 (dostępna)

r = -1 (brak)

Trwałość

Sa

S

a0

S

a-1

N

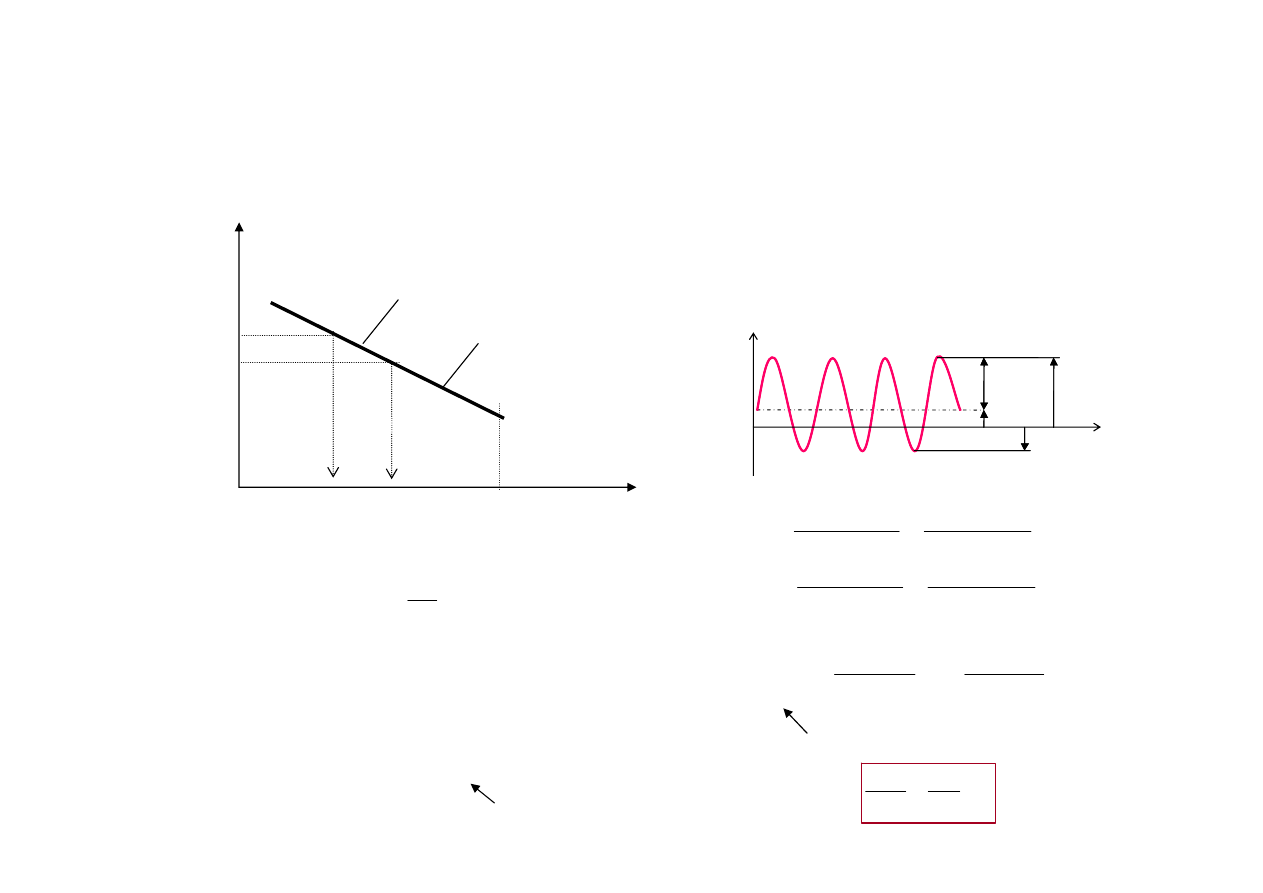
31

S

m

S

min

S

max

S

a

0

S

czas

Log S

a

S

a

Amplituda

naprężeń

N

0

= 2E+6

Log N

S

D

= 60 MPa

(Pf = 50%)

S

min

= -30 MPa, S

max

= 150 MPa

r = -30/150 = -0.2 Î

należy wyznaczyć cykl

równoważny o r = -1

S

a

m.

N = const

Charakterystyka zmęczeniowa

Wpływ naprężeń średnich

N

(

)

(

)

MPa

S

R

R

S

S

)

S

(

równowazny

cykl

MPa

S

S

S

MPa

S

S

S

m

m

m

a

a

m

min

max

m

min

max

a

108

60

360

360

90

0

60

2

30

150

2

90

2

30

150

2

1

=

−

=

−

=

=

=

−

+

=

+

=

=

−

−

=

−

=

−

Krzywa S-N

(m = 5, r = -1, R

m

= 360 MPa)

Trwałość:

S

a

= 90 MPa Î N = 263374 cykle

S

a

* = S

a-1

= 108 MPa Î N* = 105844 cykle

N*/N = 105844/263374 = 0.40

m

a

D

o

S

S

N

N

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

Z modelu Goodmana

Ujemny wpływ
naprężeń średnich

1

1

=

+

−

m

m

a

a

R

S

S

S

S

a

*

N*

Naprężenie w elemencie

32

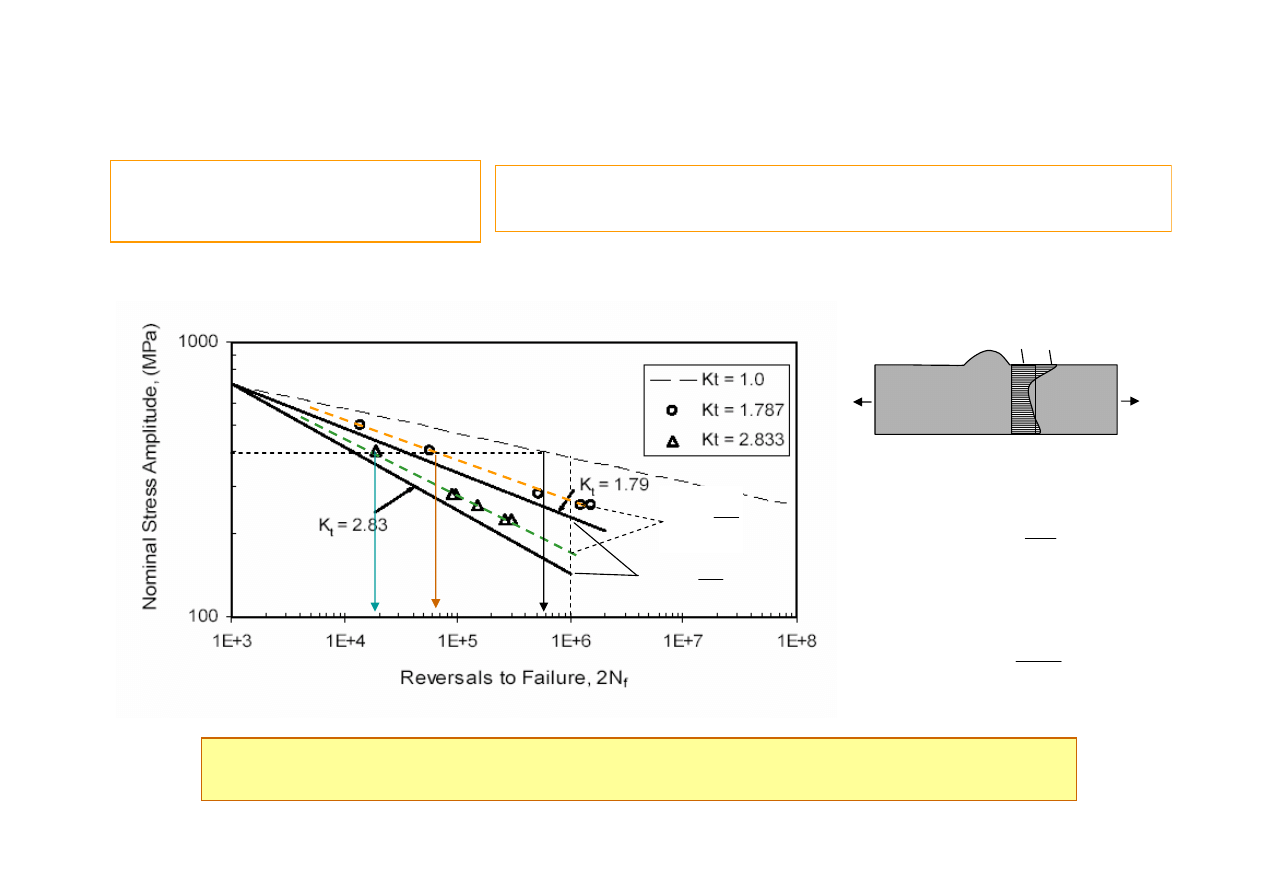
A. Fatemi, D. Fang, and Z. Zeng

THE EIGHT INTERNATIONAL FATIGUE CONGRESS,

STOCKHOLM, SWEDEN, JUNE 2002

• Circumferentially grooved round bars were tested under axial loading.

• Notch root radii were 1.59 mm and 0.53 mm, to produce a Kt of 1.79 and 2.83.

1. Takie krzywe S-N otrzymuje się gdy badanie prowadzi się do całkowitego pęknięcia próbki
2. Wpływ działania karbu zwiększa się dla dużych trwałości

S

K

L

K

t

σ

=

α

=

Wsp. koncentracji naprężeń

(geometria):

σ

L

S

Charakterystyka zmęczeniowa dla elementów

Wpływ działania karbu

Krzywe S-N dla próbek z karbem opisuje się za pomocą

naprężeń nominalnych, S

DK

D

K

f

S

S

K

=

β

=

Wsp. działania karbu
(eksperyment):

t

D

DK

K

S

'

S

=

f

D

DK

K

S

S

=

33

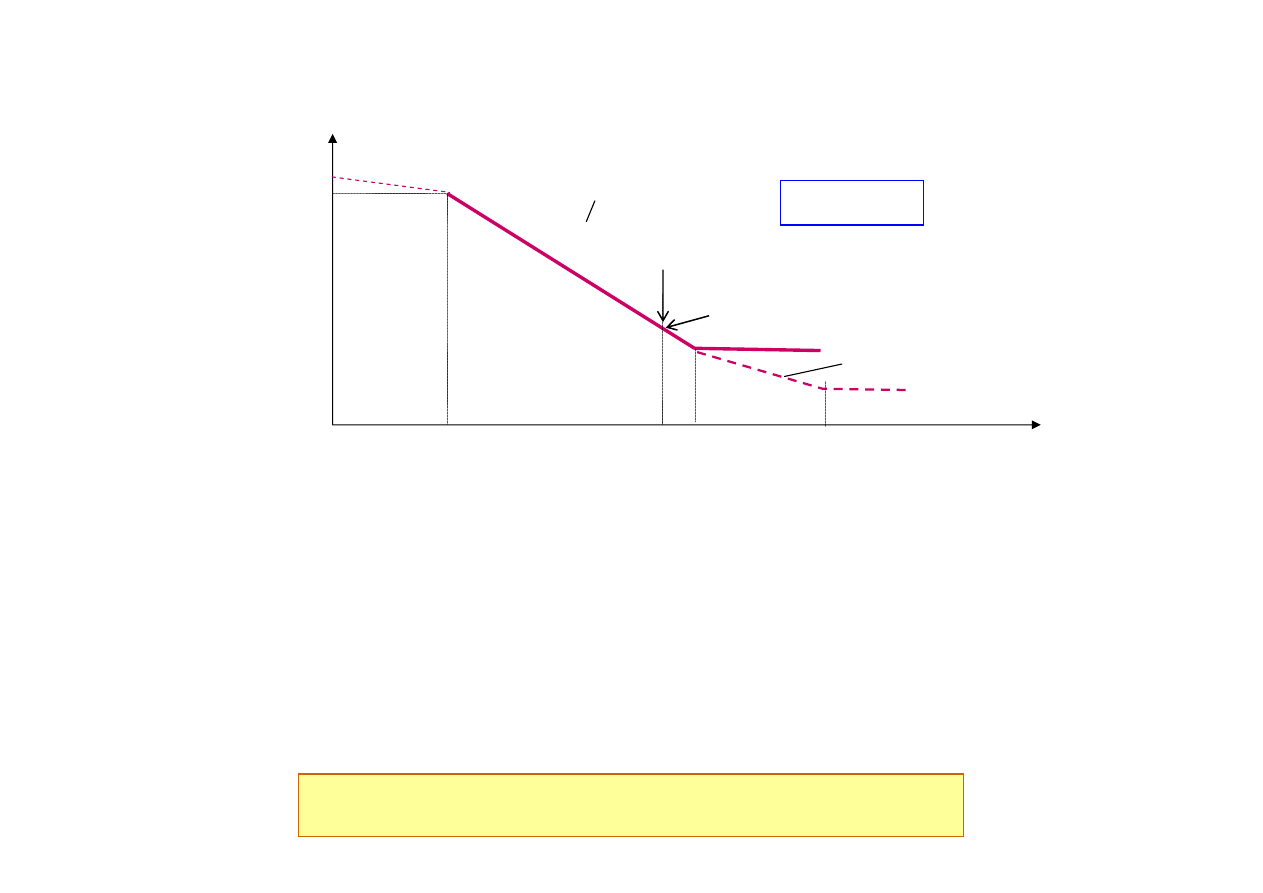
Teoretyczna krzywa S-N

Szacunkowe parametry krzywej S-N dla stali o R

m

< 1400 MPa (

próbka gładka, r = -1

):

S

1

– wytrzymałość zmęczeniowa (amplituda)

przy N1 = 1000 cykli: S

1

= 0.75 R

m

(rozciąganie)

S

D

= 0.9 R

m

(zginanie)

S

D

– wytrzymałość zmęczeniowa (amplituda)

przy No = 1E+6 cykli : S

D

= 0.4 R

m

(rozciąganie)

S

D

= 0.5 R

m

(zginanie)

gdzie: R

m

– wytrzymałość materiału

N

1

N

0

log N

log S

a

R

m

S

1

1

Próbka
gładka

Próbka / element
z karbem

1. Jak można wyznaczyć wykładnik ‘m’ krzywej S-N ?
2. Jak można wyznaczyć współczynnik ‘

β

K

’ dla elementu z karbem?

S

a

m

.N = C

5E+6

1E+8

m

m1 = m+2

S

DK

= S

D

/

β

K

– krzywa S-N dla elementu z karbem

S

D

34

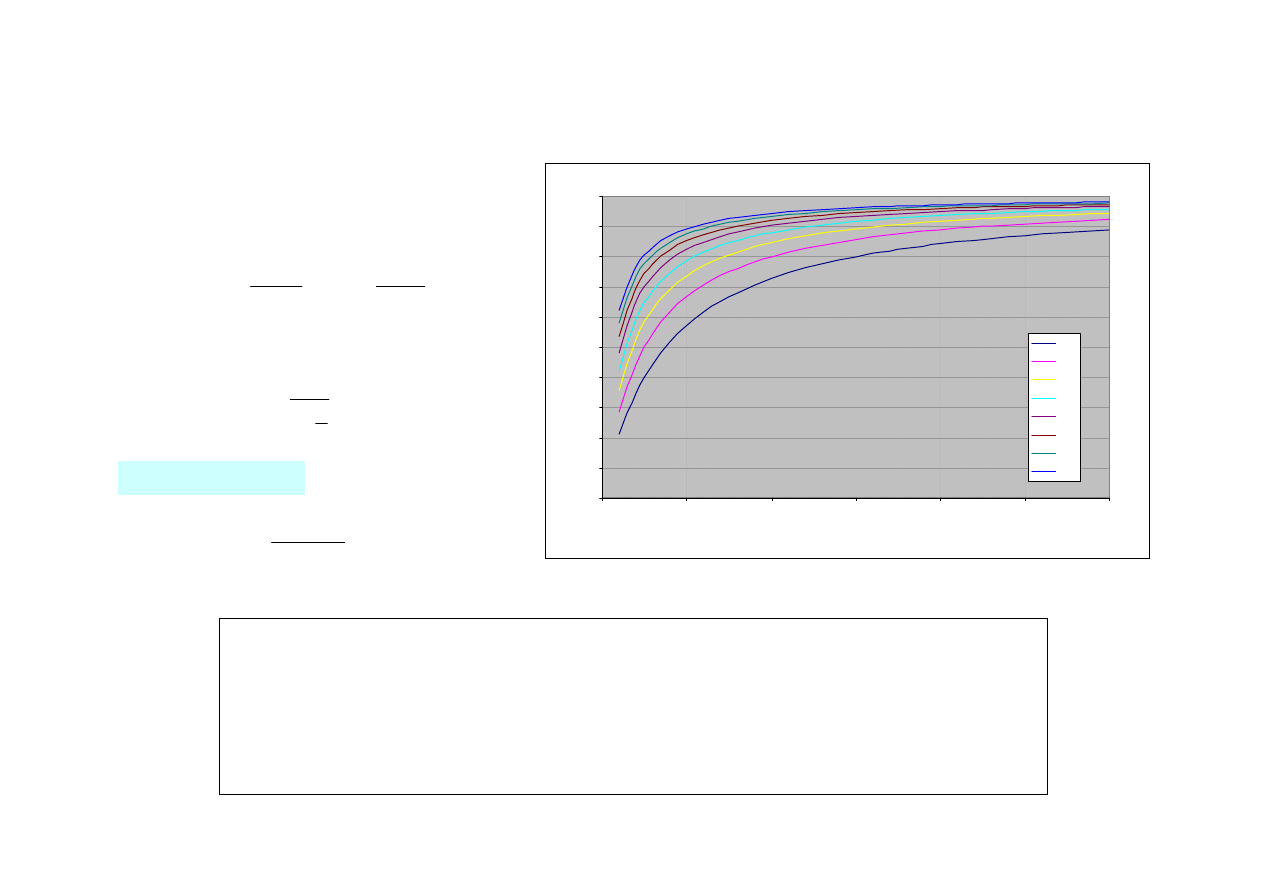
Wrażliwość na działanie karbu,

η, zależy od wytrzymałości materiału oraz gradientu

naprężeń (promienia karbu):

• Duża wrażliwość Î K

f

≈ K

t

• Duża wytrzymałość materialu Î duża wrażliwość (K

f

≈ K

t

)

• Mały gradient naprężeń (duży promień karbu) Î duża wrażliwość (K

f

≈ K

t

)

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.05

0.1

0.15

0.2

0.25

0.3

r [in]

q

40

50

60

70

80

90

100

110

Rm

= 275 MPa

Rm

= 760 MPa

1

1

−

α

−

β

=

η

K

K

Peterson
zaproponował uproszczony wzór do obliczania

η:

r

a

+

=

η

1

1

)

mm

(

)

MPa

(

R

a

.

m

8

1

269

⎥

⎦

⎤

⎢

⎣

⎡

=

Dla stopów żelaza:

Współczynnik wrażliwości materiału
na działanie karbu

η (q) wyznacza się

z krzywych S-N dla próbki gładkiej
i próbki z karbem (eksperyment):

Wyznaczanie współczynnika działania karbu

1

1

−

−

=

t

f

K

K

q

35

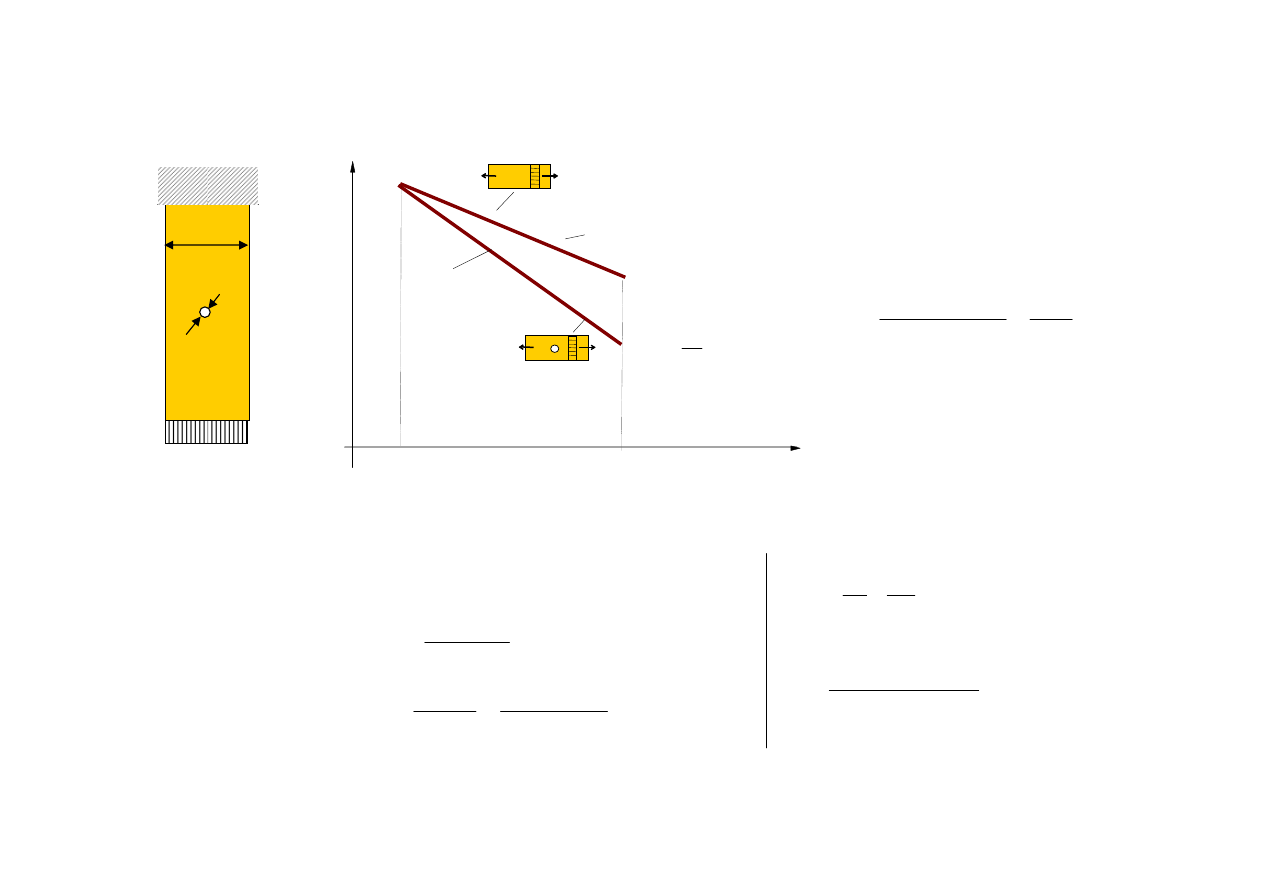
Próbka gładką (materiał):

Uproszczony sposób wyznaczania krzywej S-N

d

w

S

w = 50 mm
d = 3 mm
R

m

= 400 MPa

cykli

S

D

N (S

a

)

m

= C

S

a

Ampl. napr

ęż

eń

S

f

D

DK

K

S

S

=

N (S

a

)

m

= C

1

N

1

= 10

3

S

N

0

= 10

6

10

2

3

1

1

0

≈

=

−

−

=

log

S

log

S

log

N

log

N

log

m

D

MPa

360

400

0.9

R

0.9

S

m

1

=

⋅

=

=

MPa

180

400

0.45

R

0.45

S

m

D

=

⋅

=

=

Element z karbem:

3

4

1

1

0

.

S

log

S

log

N

log

N

log

m

DK

=

−

−

=

3.0

K

t

=

49

0

269

8

1

.

)

mm

(

)

MPa

(

R

a

.

m

=

⎥

⎦

⎤

⎢

⎣

⎡

=

75

0

5

1

49

0

1

1

1

1

.

.

/

.

r

/

a

q

=

+

=

+

=

(

)

5

2

1

1

.

K

q

K

t

f

=

+

−

=

Pa

M

.

K

S

S

f

D

DK

72

5

2

180=

=

=

S

1

36

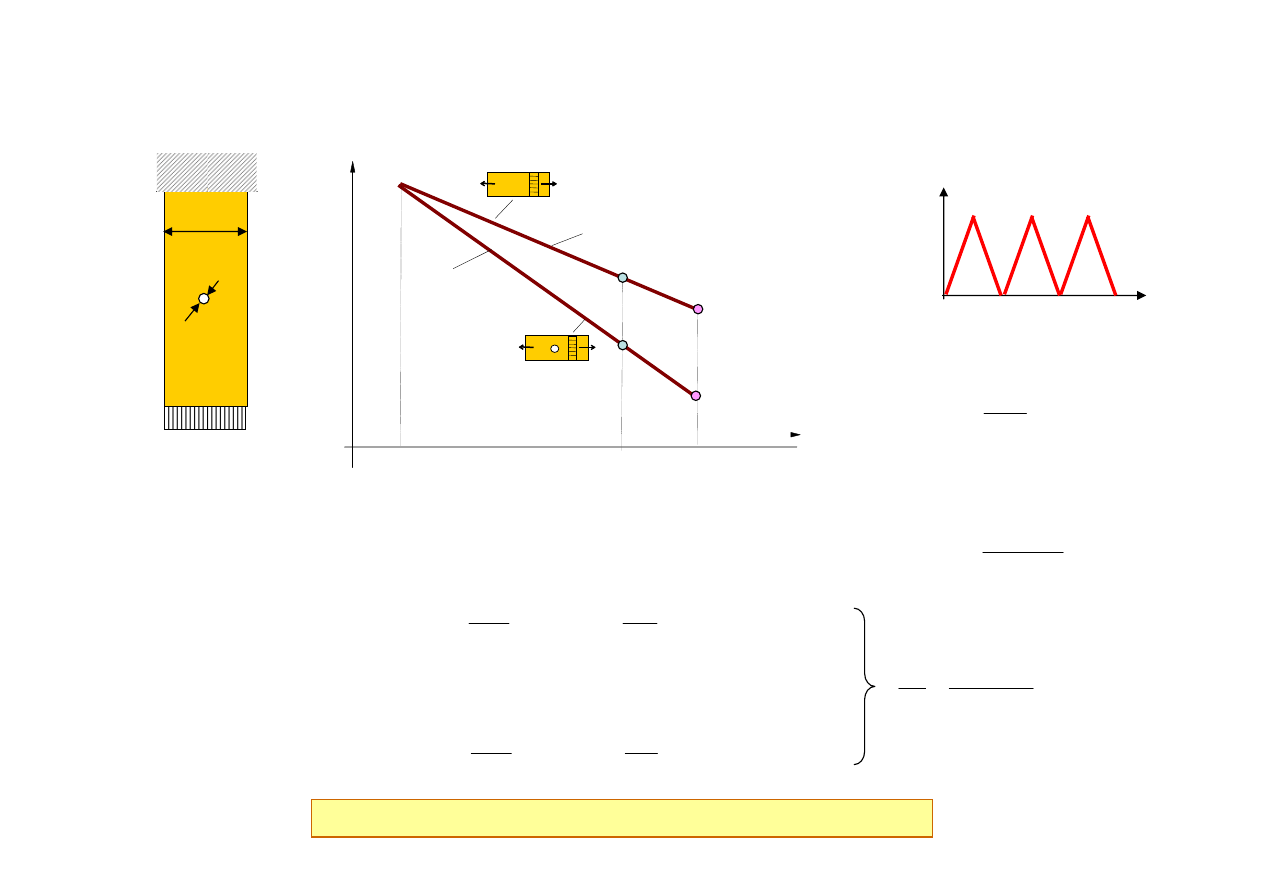
Wpływ karbu na trwałość

d

w

S

w = 50 mm
d = 3 mm
R

m

= 400 MPa

cykli

S

D

= 180 MPa, m = 10

N (S

a

)

m

= C

S

a

Ampl. napr

ęż

eń

S

N (S

a

)

m

= C

1

N

1

= 10

3

S

10

6

S

1

t

S

Obciążenie eksploatacyjne

Krzywe S-N (r = -1)

S

max

= 240 MPa

S

DK

= 72 MPa, m = 4.3

5

.

10

6

S

e

= 157 MPa

S

ek

= 50 MPa

MPa

S

S

max

a

120

2

=

=

Amplituda napr

ęż

e

ń

(r = 0):

Efektywna amplituda
napr

ęż

e

ń

(r = -1):

MPa

S

R

R

S

S

m

m

m

a

a

171

1

=

−

=

−

Próbka gładka (materiał):

Trwałość:

cykli

E

.

E

S

S

N

N

m

a

D

o

6

67

1

171

180

6

1

10

1

+

=

⎟

⎠

⎞

⎜

⎝

⎛

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

−

Element z karbem:

cykli

E

.

E

S

S

N

N

.

m

a

DK

o

K

4

42

2

171

72

6

1

3

4

1

+

=

⎟

⎠

⎞

⎜

⎝

⎛

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

−

015

0

6

67

1

4

42

2

.

E

.

E

.

N

N

K

=

+

+

=

Wp

ł

yw dzia

ł

ania karbu zale

ż

y od warto

ś

ci obci

ąż

enia (i trwa

ł

o

ś

ci)

37

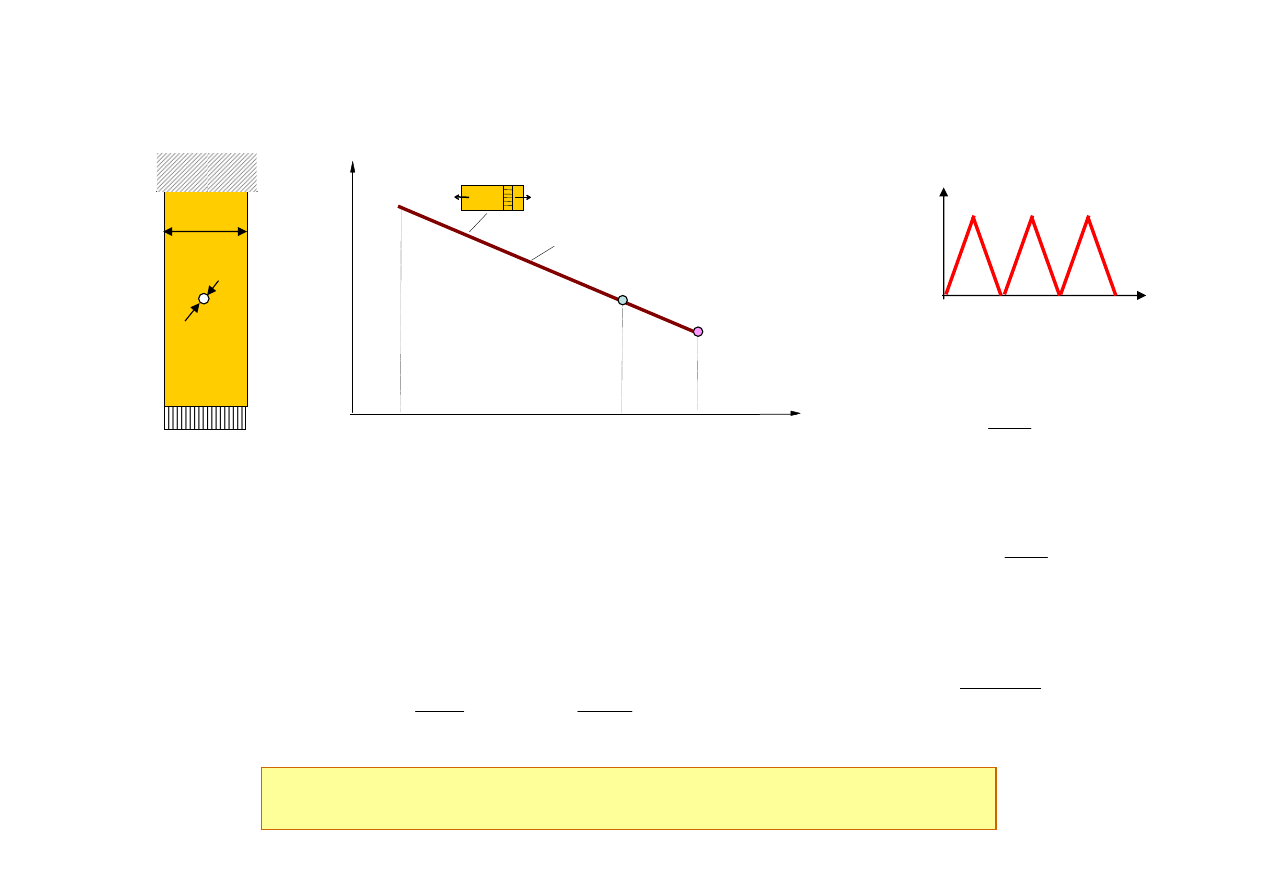
Wpływ karbu na trwałość

d

w

S

w = 50 mm
d = 3 mm
R

m

= 400 MPa

cykli

S

D

= 180 MPa, m = 10

N (S

a

)

m

= C

S

a

Ampl. napr

ęż

eń

S

N

1

= 10

3

10

6

S

1

t

S

Obciążenie eksploatacyjne

Krzywe S-N (r = -1)

S

max

= 240 MPa

5

.

10

6

S

e

= 157 MPa

MPa

S

S

max

a

120

2

=

=

Amplituda napr

ęż

e

ń

nominalnych (r = 0):

Efektywna amplituda
napr

ęż

e

ń

(r = -1):

MPa

S

R

R

S

S

m

m

m

La

a

L

171

3

1

⋅

=

−

=

−

Element z karbem:

Trwałość:

cykli

E

S

S

N

N

m

a

L

D

o

28

171

3

180

6

1

10

1

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

−

Trwa

ł

o

ść

tak okre

ś

lona dotyczy inicjacji p

ę

kni

ę

cia w karbie w przeciwie

ń

stwie

do poprzedniej analizy, gdzie prognoza dotyczy

ł

a p

ę

kni

ę

cia elementu

Gdy do oceny trwa

ł

o

ś

ci elementu z karbem u

ż

ywamy

napr

ęż

e

ń

lokalnych (skoncentrowanych), np. z analizy

MES, to do oceny trwa

ł

o

ś

ci stosujemy krzyw

ą

S-N

materia

ł

u (próbka g

ł

adka).

MPa

S

S

max

K

La

360

2

=

α

=

Amplituda napr

ęż

e

ń

lokalnych (r = 0):

38

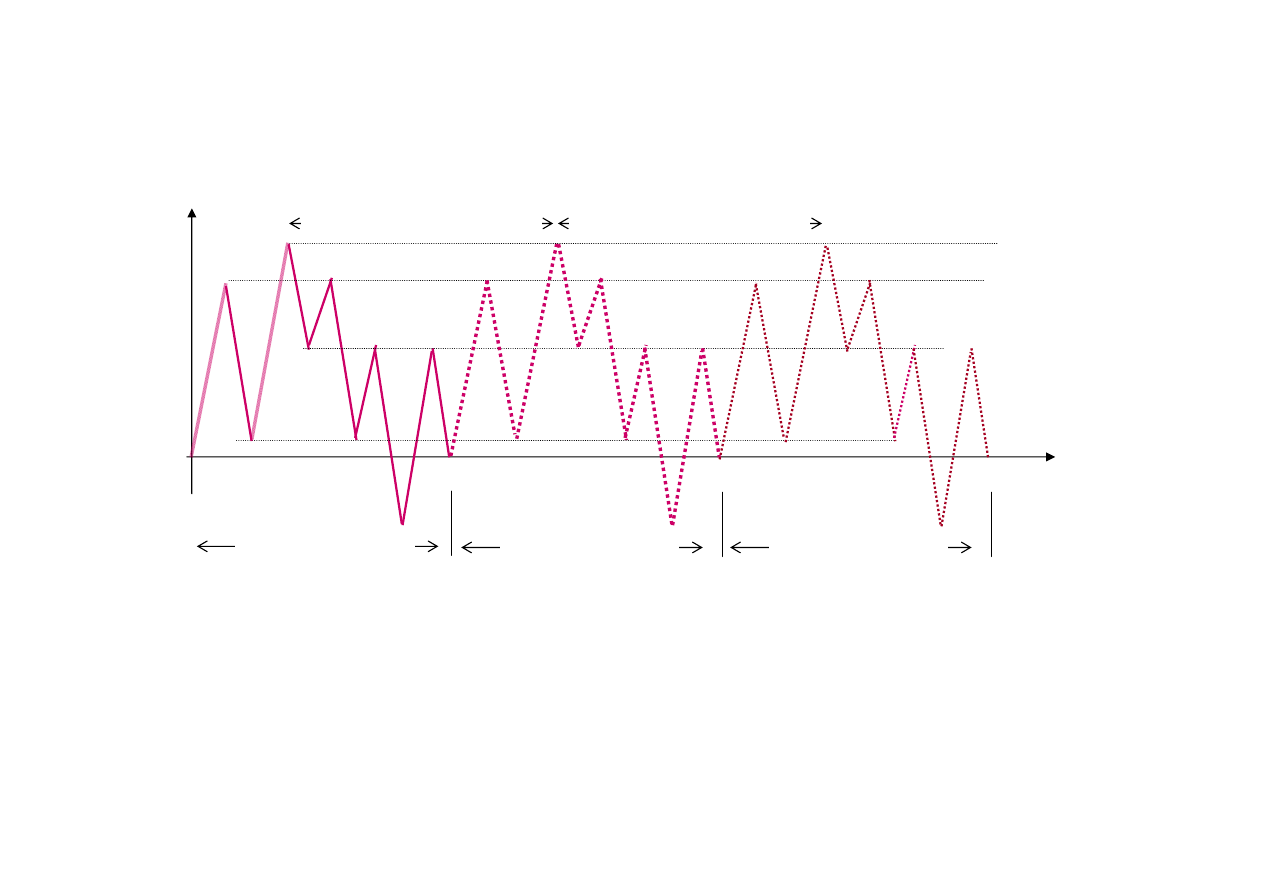
Algorytm zliczania cykli metod

ą

rainflow wymaga przeorganizowania przebiegu napr

ęż

e

ń

wg

najwi

ę

kszego (bezwzgl

ę

dnie) napr

ęż

enia – zak

ł

ada si

ę

, ze analizowany przebieg obci

ąż

e

ń

(blok

obci

ąż

e

ń

) b

ę

dzie si

ę

powtarza

ć

w eksploatacji. Jest to konieczne, aby zliczy

ć

wszystkie cykle.

Zliczanie cykli (harmonicznych) metodą rainflow

Złożone przebiegi naprężeń

czas

N

apr

ęż

eni

e

3

0

4

6

5

7

8

2’

3’

1

2

9

10

1’

Blok obciążenia
(np. cykl pracy koparki)

Zreorganizowany blok obciążenia

4’

6’

5’

7’

8’

9’

10’

Blok obciążenia
(np. cykl pracy koparki)

2”

3”

1”

4”

6”

5”

7”

8”

9”

10”

Blok obciążenia
(np. cykl pracy koparki)

Zreorganizowany blok obciążenia

39

Algorytm zliczania cykli metod

ą

rainflow:

1. Cykl napr

ęż

e

ń

(j) jest okre

ś

lany z nast

ę

puj

ą

cego warunku:

2. Po zliczeniu cyklu, nale

ż

y usun

ąć

punkty (i, i-1) z przebiegu (dokona

ć

enumeracji przebiegu),

po czym wróci

ć

do punktu (i-2)

Co to są cykle harmoniczne? Î

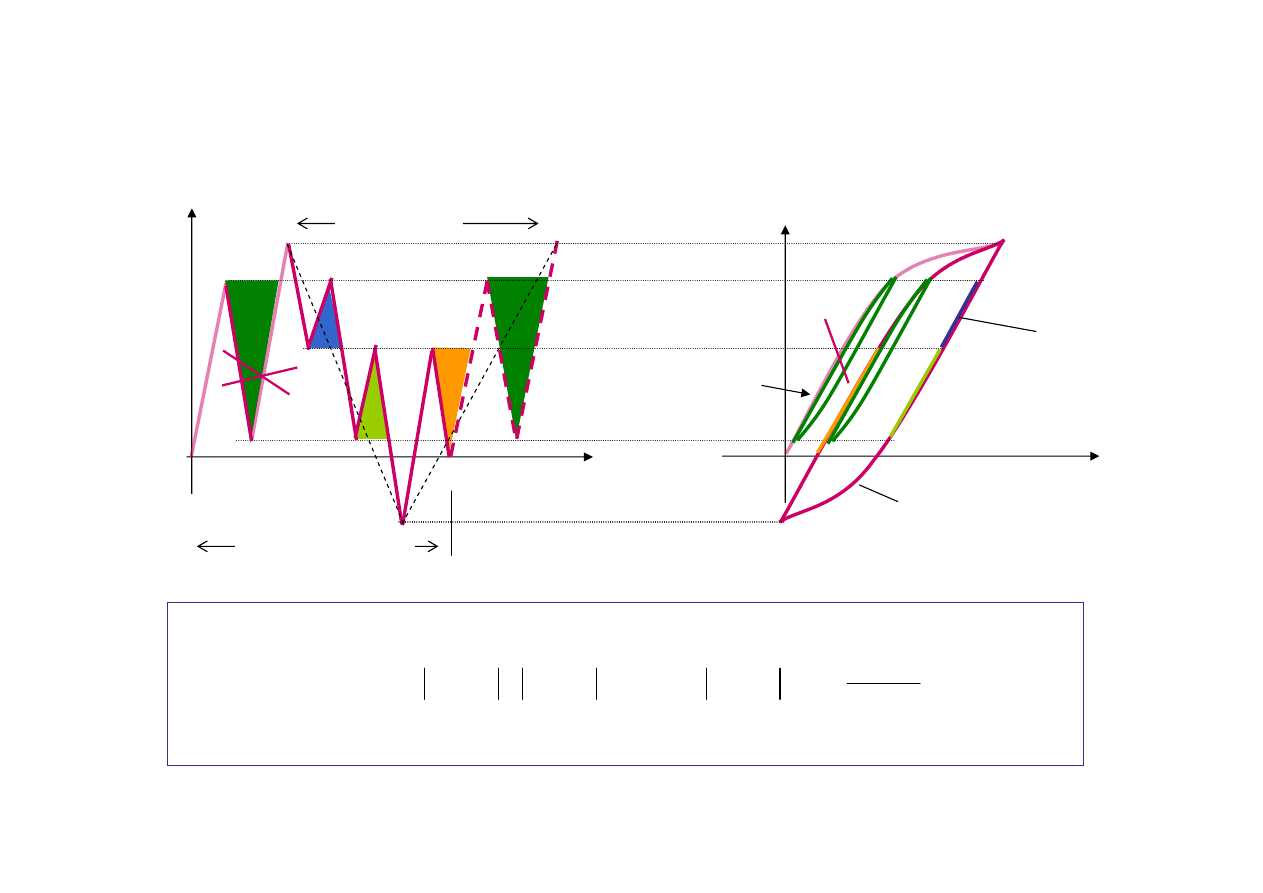
Zliczanie cykli (harmonicznych) metodą rainflow

Cykle harmoniczne tworzą zamknięte pętle histerezy

2

1

1

1

1

−

−

−

+

+

=

−

=

Δ

>

−

−

−

>

−

i

i

mj

i

i

j

i

i

i

i

S

S

S

,

S

S

S

S

S

S

S

Złożone przebiegi naprężeń

Cykl
4-5

czas

N

apr

ęż

eni

e

3

0

4

6

5

7

8

2’

3,3’

4

5

6

7

8

2’

9

1’

3’

10

0

Cykl (pętla histerezy)
3-8-3’

odkształcenie

1

2

9

10

1’

1

2

N

apr

ęż

eni

e

Blok obciążenia
(np. cykl pracy koparki)

Blok obciążenia

Tylko przy
pierwszym
przejściu

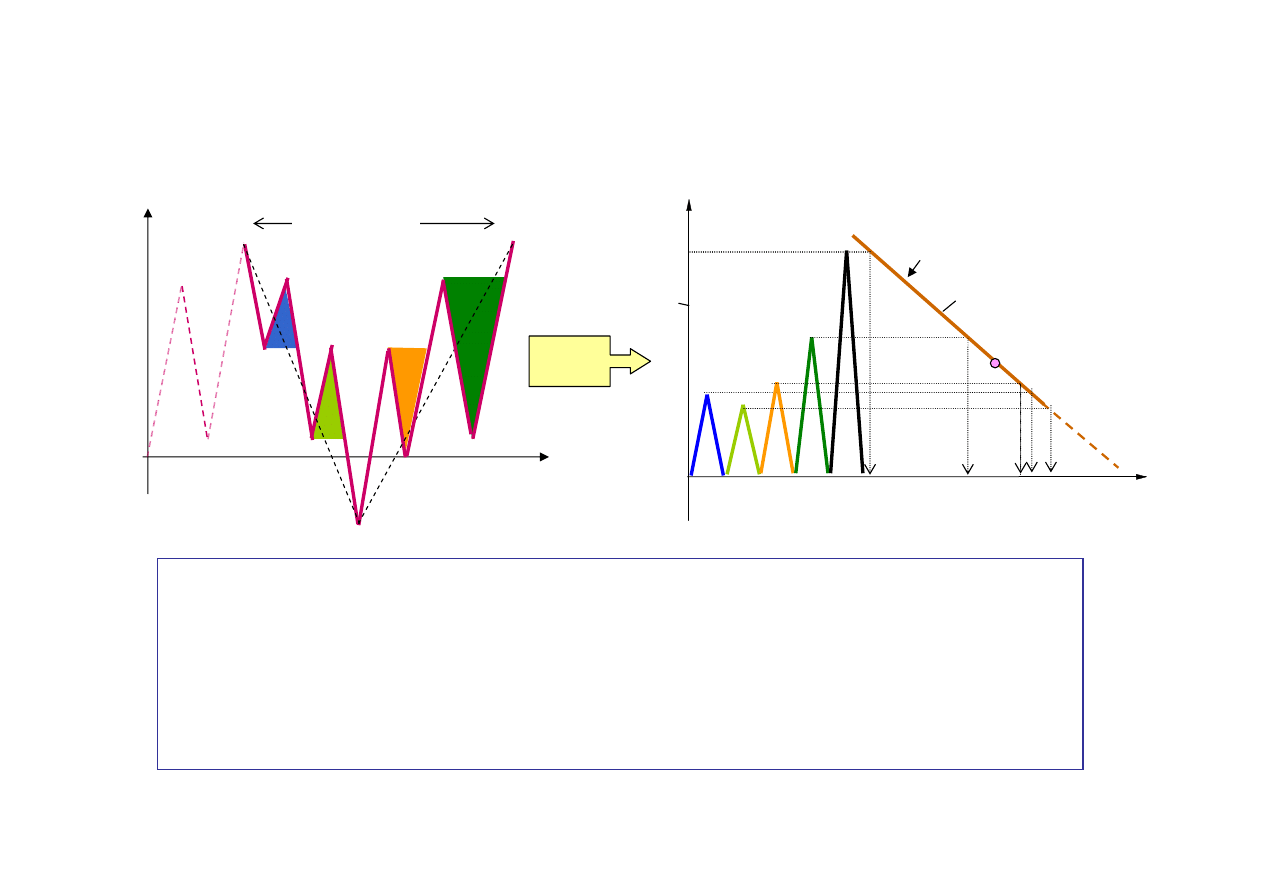
40

Post

ę

powanie:

1. Dla zliczonych cykli (S

aj

, r

i

) oblicz amplitudy napr

ęż

e

ń

efektywnych dla S*

aj

dla r = -1

(z zale

ż

no

ś

ci Goodmana)

1. Oblicz uszkodzenia, D

j

dla ka

ż

dego cyklu: D

j

= 1/N

j

2. Oblicz sum

ę

uszkodze

ń

od wszystkich cykli bloku obci

ąż

e

ń

(Palmgren-Miner): D =

ΣD

j

3. Oblicz trwa

ł

o

ść

jako liczb

ę

powtórze

ń

bloku obci

ąż

e

ń

(cykli pracy): N

BLK

= 1/D

4. Oblicz trwa

ł

o

ść

jako czas pracy: T = N

BLK

* t

BLK

Obciążenia eksploatacyjne

Sumowanie uszkodzeń – ocena trwałości

Obliczanie uszkodzeń zmęczeniowych

(znana krzywa S-N: S

D

,N

o

,m, r = -1)

cykle

S

a

Amp

lit. napr

ęż

eń

N

5

1

2

3

4

5

N

4

N

1

D=0

D=1

0

czas

N

apr

ęż

eni

e

3

0

4

6

5

7

8

2’

3’

1

2

9

10

1’

Blok obciążenia

N

3

N

4

S

*

aj

m

.N

j

= S

D

m

.N

o

Model
Goodmana

(S

D

,N

o

)

41

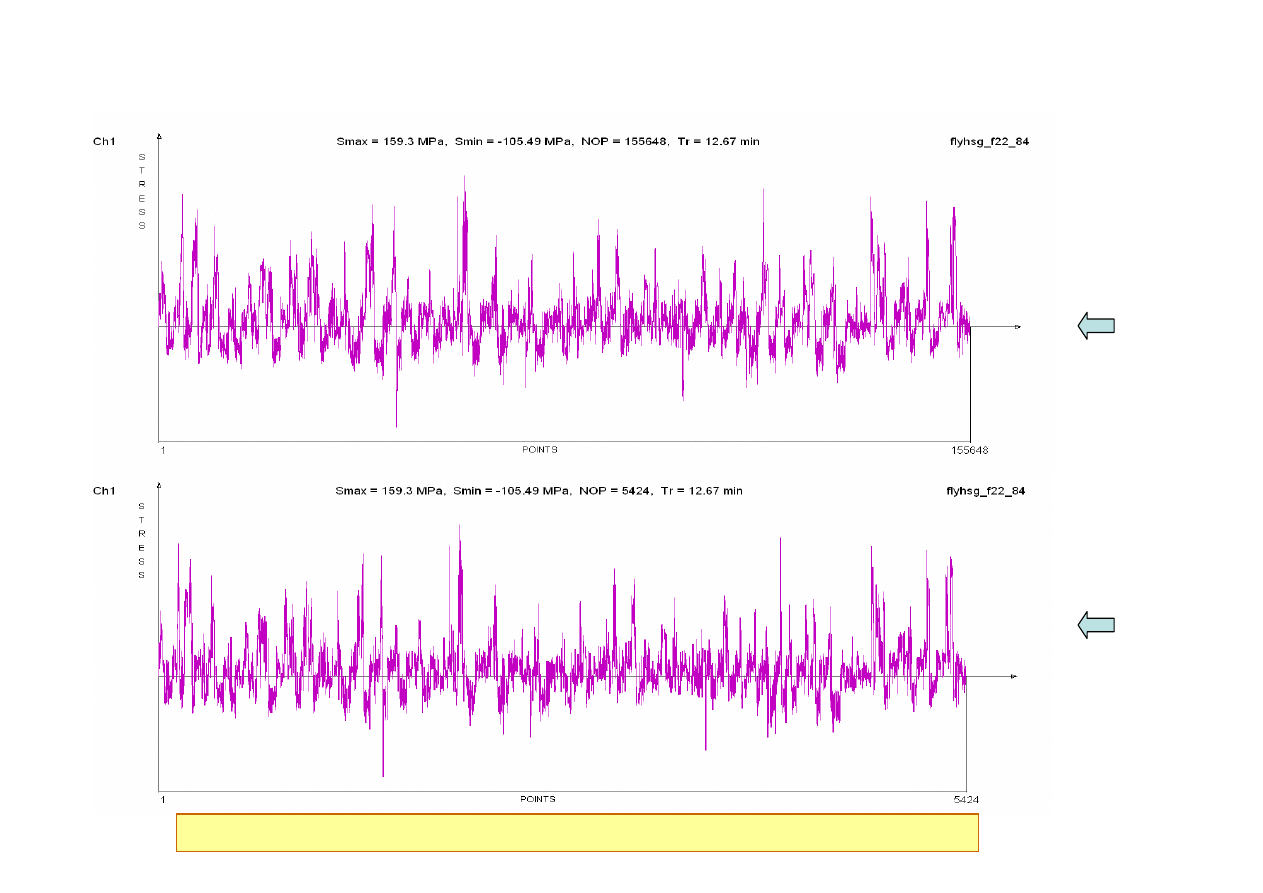
Zarejestrowany
przebieg naprężeń

Usuni

ę

cie punktów po

ś

rednich oraz ma

ł

ych zmian znacznie zmniejsza liczb

ę

danych

Zarejestrowany
przebieg naprężeń
bez pktów pośrednich
+ filtr 1%

Analiza obciążeń eksploatacyjnych

42

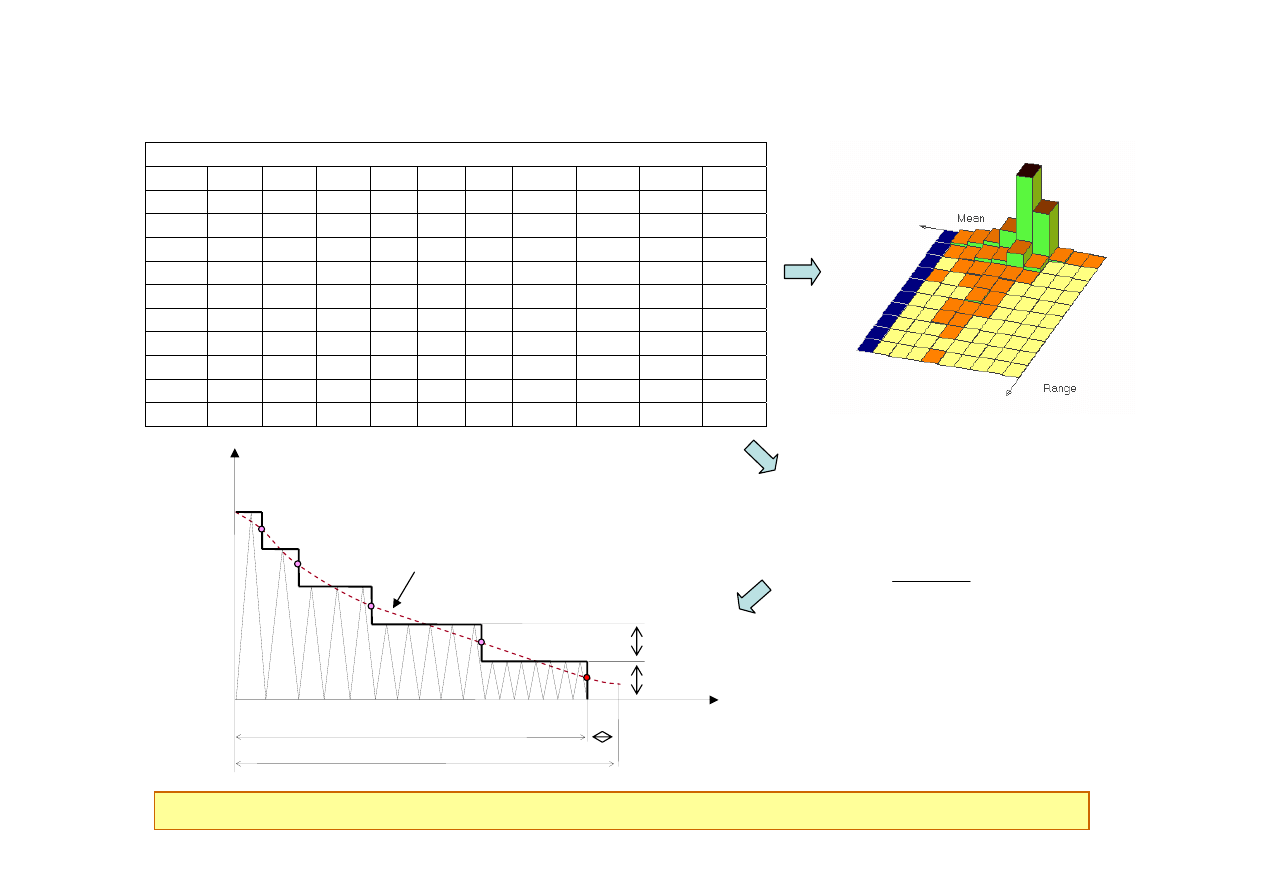
Widmo obciążeń – jak i po co?

Widmo obci

ąż

e

ń

jest prostszym zapisem ale pomija wiele informacji (kolejno

ść

cykli , napr.

ś

rednie)

Naprężenia średnie

Zakres

127.1

102.5

77.9

53.4

28.8 4.2 -20.3 -44.9 -69.5 -94.1

264.78

0

0

0

0

1

0

0 0 0 0

238.3

0

0

0

0

0

0

0 0 0 0

211.83

0

0

0

0

1

0

0 0 0 0

185.35

0

0

0

2

3

0

0 0 0 0

158.87

0

0

0

4

1

1

0 0 0 0

132.39

0

0

0

0

5

3

0 0 0 0

105.91

0

1

0

1

10

4

0 0 0 0

79.43

0

0

4

5

8

10

3 0 0 0

52.96 0 1 7 18 27 63 15

0

0

0

26.48 0 10 24 40 92 318 185

7

1

1

Uszeregowane zliczone cykle

Widmo obciążeń

n

p

n

m

n

1

dS

n

ΔS

ΔS

max

zak

res

ΔS

min

≥ dS

n

2

n

3

n

4

n

5

n

o

n

m

– Liczba cykli zliczonych z przebiegu

n

o

– Liczba cykli pominiętych (

ΔS < ΔS

min

/2)

Î

zależy od liczby stopni widma

Tablica rainflow

Efektywna amplituda
napr

ęż

e

ń

(r = -1):

m

m

m

S

R

R

S

S

−

Δ

=

Δ

−1

43

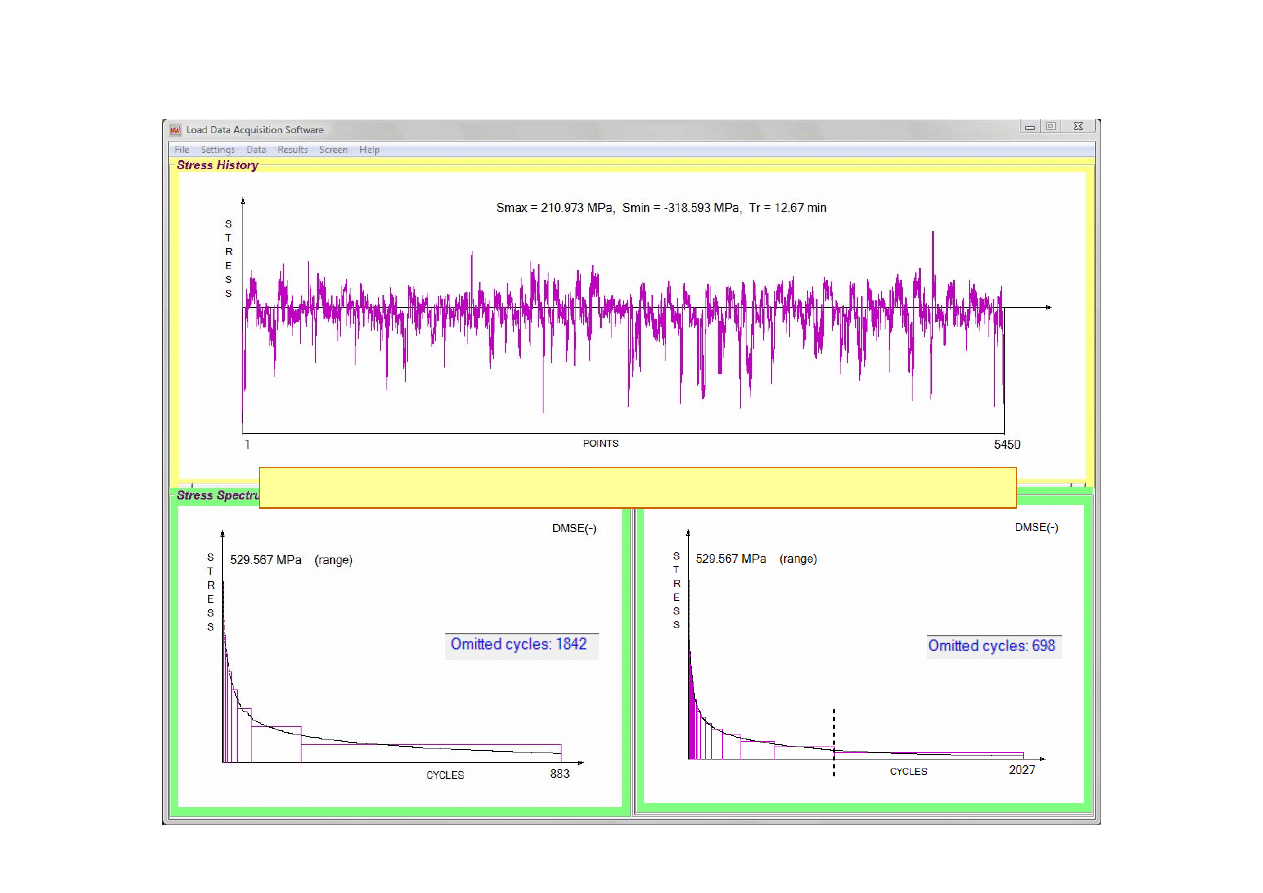
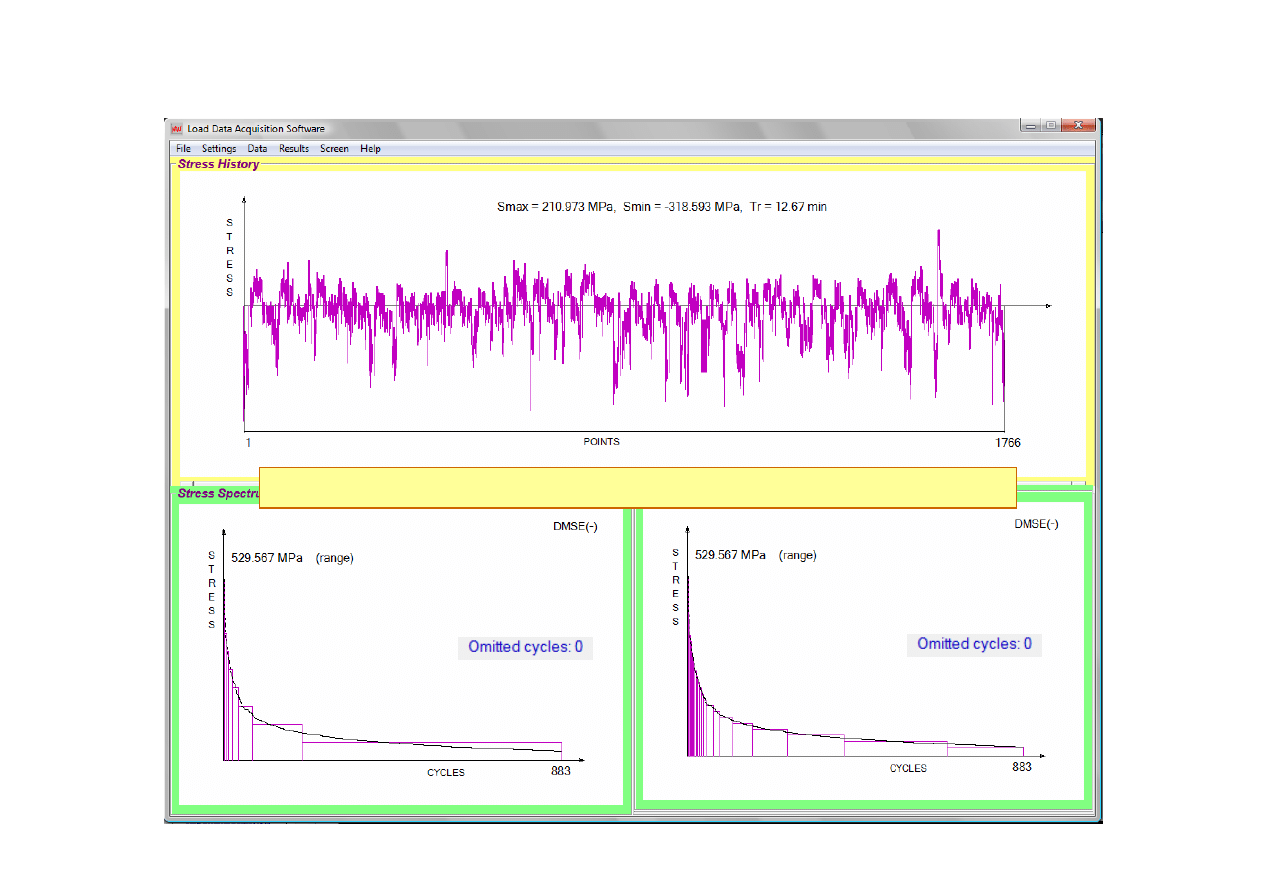
Stopni widma: 30

Obciążenia eksploatacyjne (1%)

883

Jakich wyników oceny trwałości należy oczekiwać dla tych obciążeń?

Stopni widma: 10

44

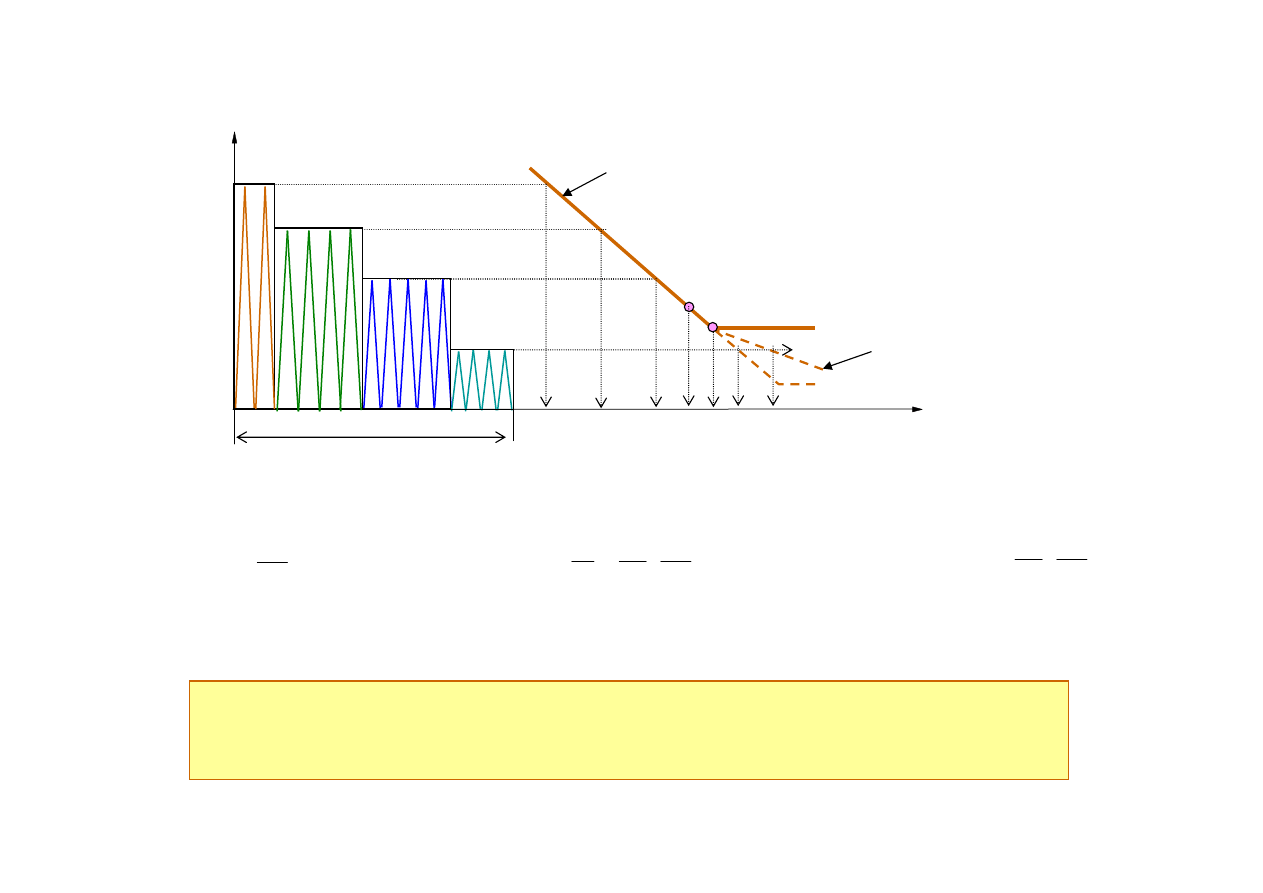
Obciążenia eksploatacyjne (5%)

Stopni widma: 10

Stopni widma: 30

Jakich wyników oceny trwałości należy oczekiwać dla tych obciążeń?

45

Sumowanie uszkodzeń – widmo obciążeń

cykle

S

amax

Amp

lituda nap

ręż

eń

N

2

n1

N

4

N

1

0

N

3

N

4

S

aj

m

.N

j

= S

D

m

.N

o

(S

D

,N

o

)

n2

N

4

(S

E

,N

E

)

N

0

N

D

n3

n4

1. Liczba cykli dla stopnia ‘i’:

m

ai

D

o

i

S

S

N

N

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

2. Uszkodzenie od stopnia ‘i’:

m

D

ai

o

i

i

i

S

S

N

n

N

1

D

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

=

3. Uszkodzenie od widma obc:

∑

∑

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

=

m

D

ai

o

i

i

S

S

N

n

D

D

n

p

=

Σ n

i

m’ = 2m - 1 (Haibach)
m’ = m + 2 (BS)

• Trwała granica zmęczenia występuje tylko przy obciążeniu o stałej amplitudzie
• Przy innych obciążeniach należy uwzględniać cykle poniżej granicy zmęczenia
• Sposób uwzględnienia takich cykli ma wpływ na prognozowaną trwałość

46

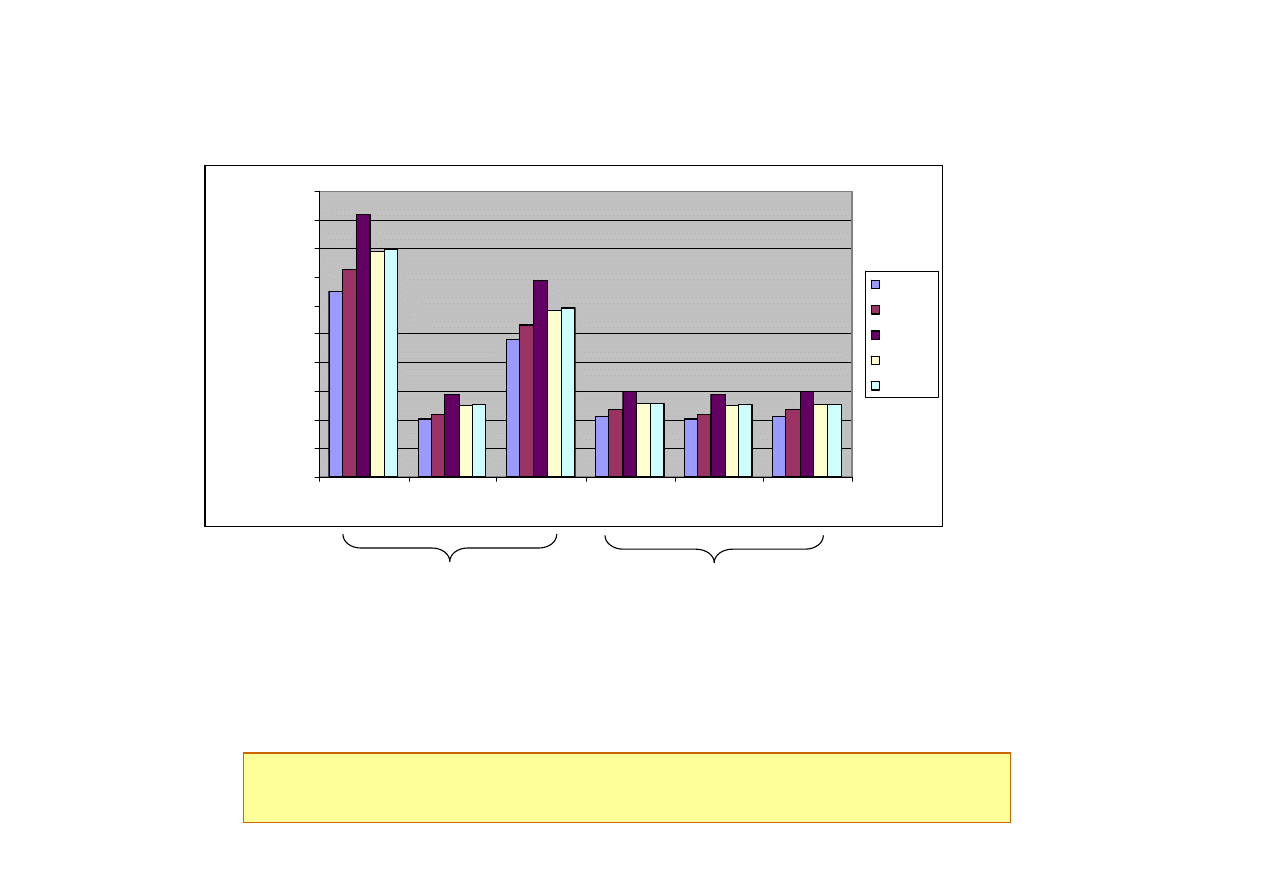
Widoczny wpływ różnej
liczby cykli w bloku
obciążenia (stopni widma)

Wyrażanie prognozowanej trwałości za pomocą cykli zmian naprężeń

jest mało przydatne dla użytkownika

Brak wpływu liczby stopni
widma (jednakowa liczba
cykli w bloku obciążenia)

0.0E+00

5.0E+06

1.0E+07

1.5E+07

2.0E+07

2.5E+07

3.0E+07

3.5E+07

4.0E+07

4.5E+07

5.0E+07

H-1%

W10_1%

W30-1%

H-5%

W10_5%

W30-5%

Tr

w

al

o

ść

[c

yk

li

]

PM_0
PM_05
PM_1
H_0
W

P-M, S

D

’/ S

D

= 0

P-M, S

D

’/ S

D

= 0.5

P-M, S

D

’/ S

D

= 1

HAIB, S

D

’/ S

D

= 0

HAIB, N

C

= 1E+8

Klasyczna hipoteza Palmgrena – Minera jest najbardziej optymistyczna

Prognozowana trwałość [cykle]

S

D

’ – granica

przedłużenia
krzywej S-N

47

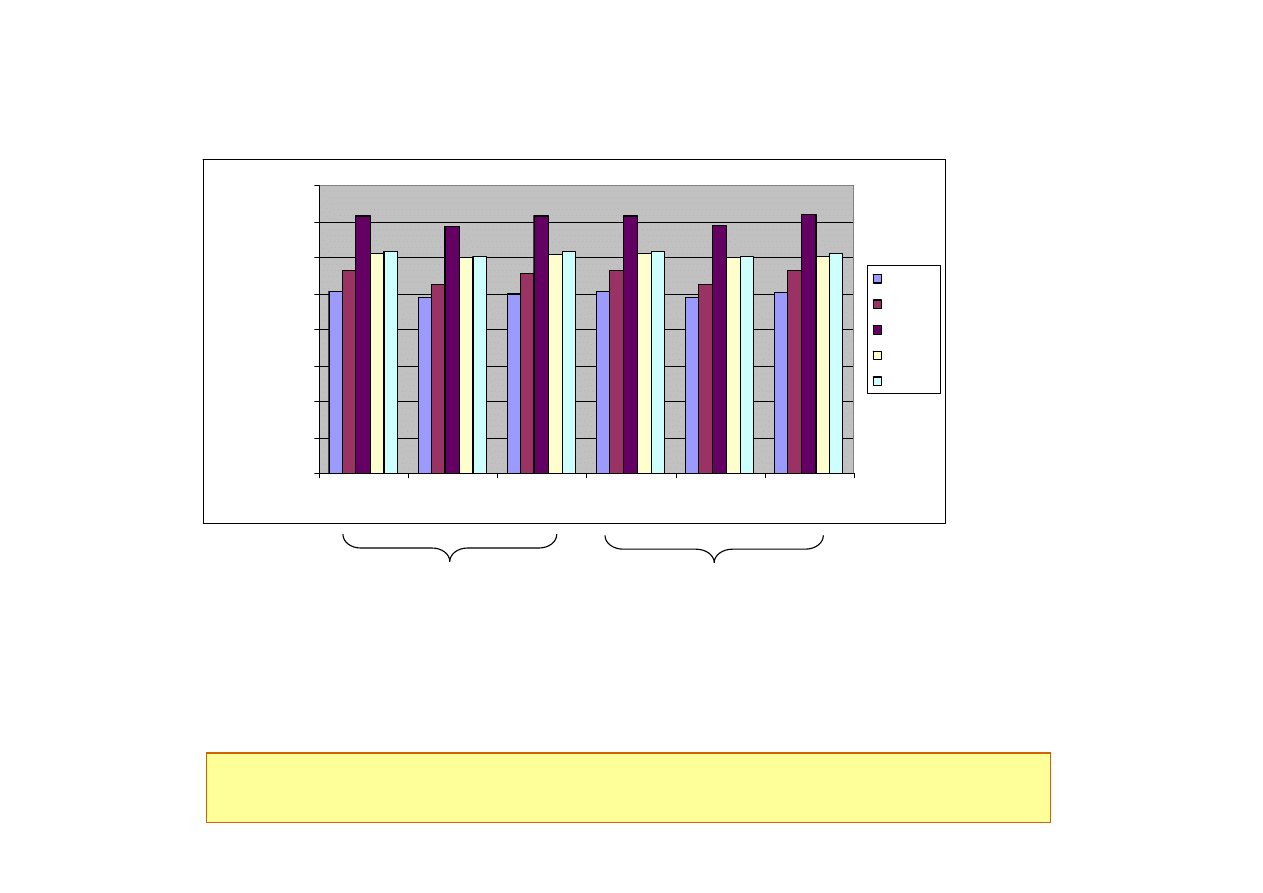
Brak wpływu różnej liczby
cykli w bloku obciążenia
(stopni widma)

Wyrażanie prognozowanej trwałości za pomocą czasu pracy (lub cykli pracy)

jest bardzo przydatne dla użytkownika

Brak wpływu liczby stopni
widma (jednakowa liczba
cykli w bloku obciążenia)

P-M, S

D

’/ S

D

= 0

P-M, S

D

’/ S

D

= 0.5

P-M, S

D

’/ S

D

= 1

HAIB, S

D

’/ S

D

= 0

HAIB, N

C

= 1E+8

0.0E+00

5.0E+02

1.0E+03

1.5E+03

2.0E+03

2.5E+03

3.0E+03

3.5E+03

4.0E+03

H-1%

W10_1%

W30-1%

H-5%

W10_5%

W30-5%

Tr

w

al

o

ść

[h

]

PM_0
PM_05
PM_1
H_0
W

Usuwanie cykli o malej amplitudzie (filtrowanie przebiegu obciążeń, mała

liczba stopni widma) nie wpływa znacząco na prognozowaną trwałość.

Prognozowana trwałość [godz]

S

D

’ – granica

przedłużenia
krzywej S-N

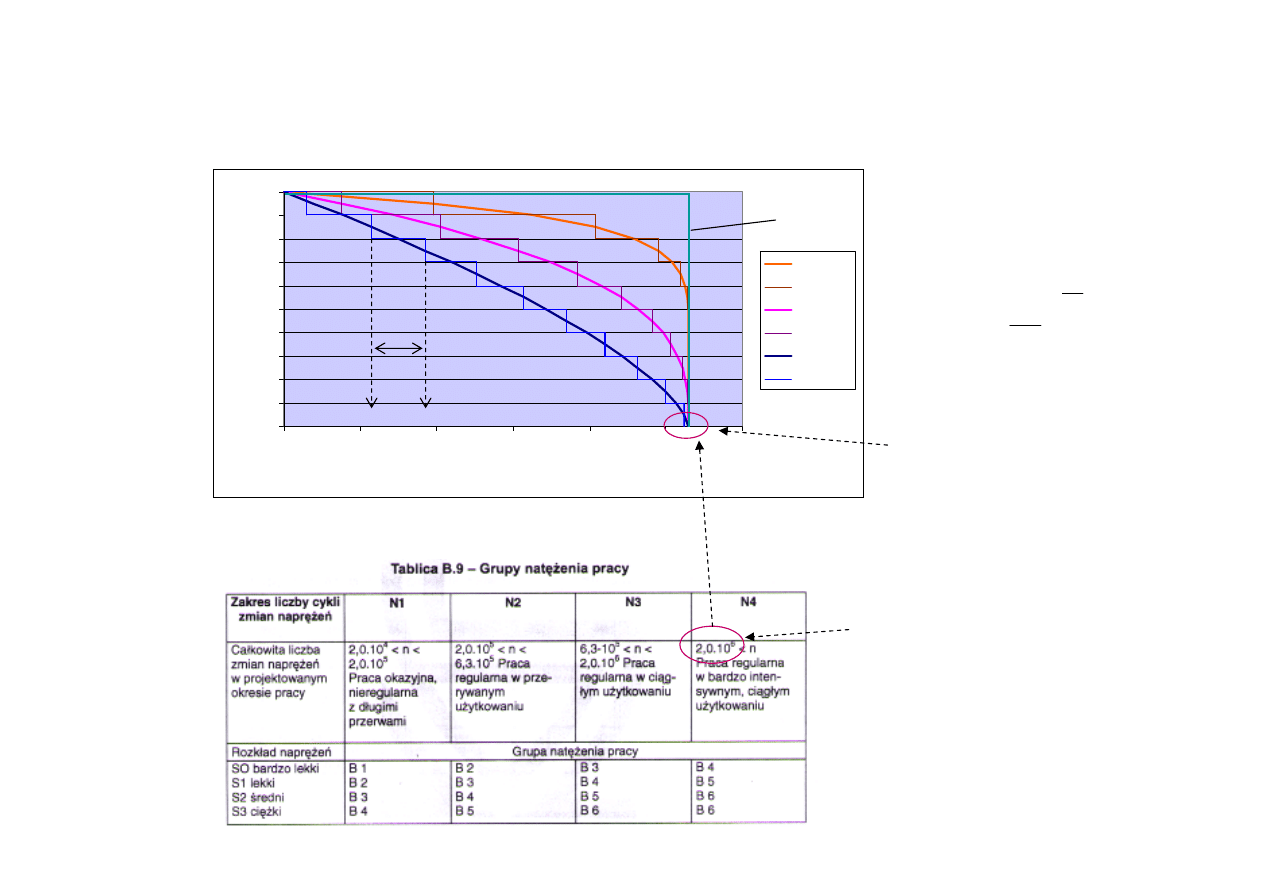
48

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

1.E+00

1.E+01

1.E+02

1.E+03

1.E+04

1.E+05

1.E+06

n [cykli]

σ

ai

/

σ

p

s=9 (S2)
n(i) = 9
s=3 (S1)
n(i) = 3
s=1 (S0)
n(i) = 0.5

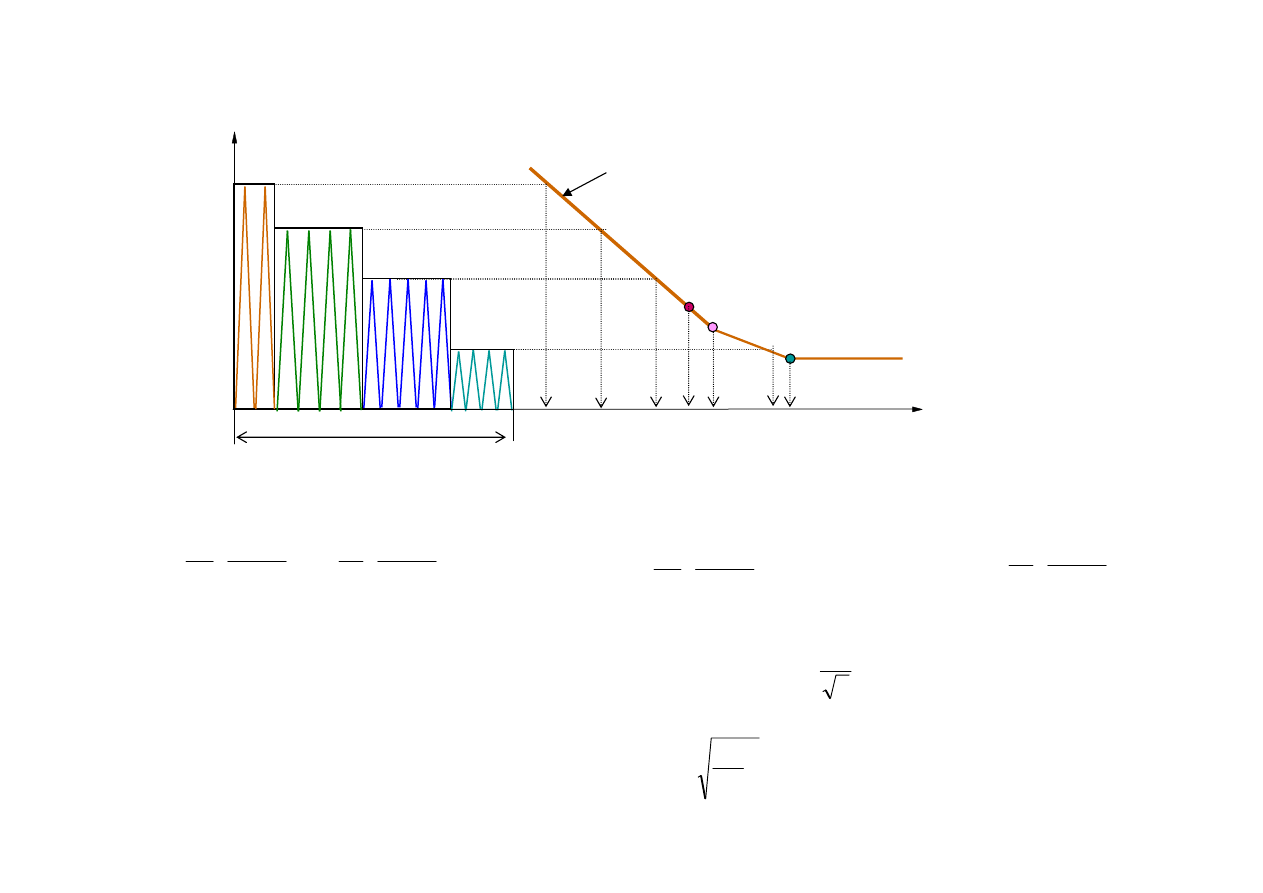
Obciążenia normowe dźwignic

s

p

ai

m

p

m

si

n

n

n

n

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

σ

σ

⎥

⎦

⎤

⎢

⎣

⎡

=

Normowe widmo obciążeń można określić na podstawie opisu grupy natężenia pracy

Grupa natężenia pracy jest opisana przez liczbę cykli widma (n

p

) oraz jego kształt (s)

S3

Wymagana liczba cykli
zmian naprężeń w widmie,
to jest raczej liczba cykli
pracy

n

s3

Cykle widma
skumulowanego

n

s2

n

3

n

p

= 1

n

m

= 2E+5

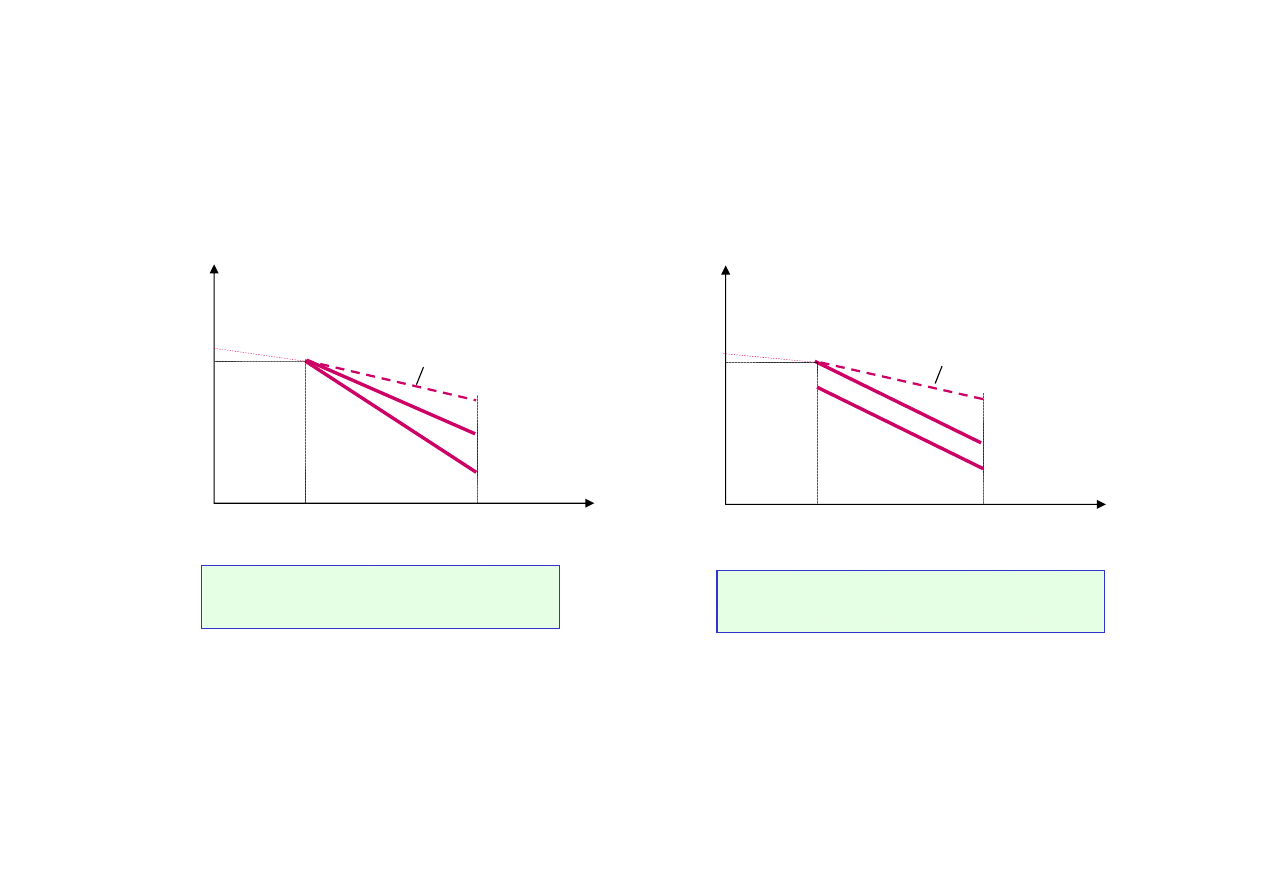
49

Dwie koncepcje krzywych S-N dla próbek specjalnych

(węzły konstrukcyjne)

Wpływ karbu zmienia się z liczbą
cykli do pęknięcia próbki

N

1

N

0

log N

log S

a

R

m

S

1

S

DK1

S

DK2

1

N

1

N

0

log N

log S

a

R

m

S

1

S

DK1

S

DK2

1

Próbka
gładka

Wpływ karbu nie zmienia się z liczbą
cykli do pęknięcia próbki

S

D

Próbki
(elementy)
z karbem

Próbka
gładka

S

D

Doświadczalne wyznaczanie krzywych S-N

Próbki
(elementy)
z karbem

50

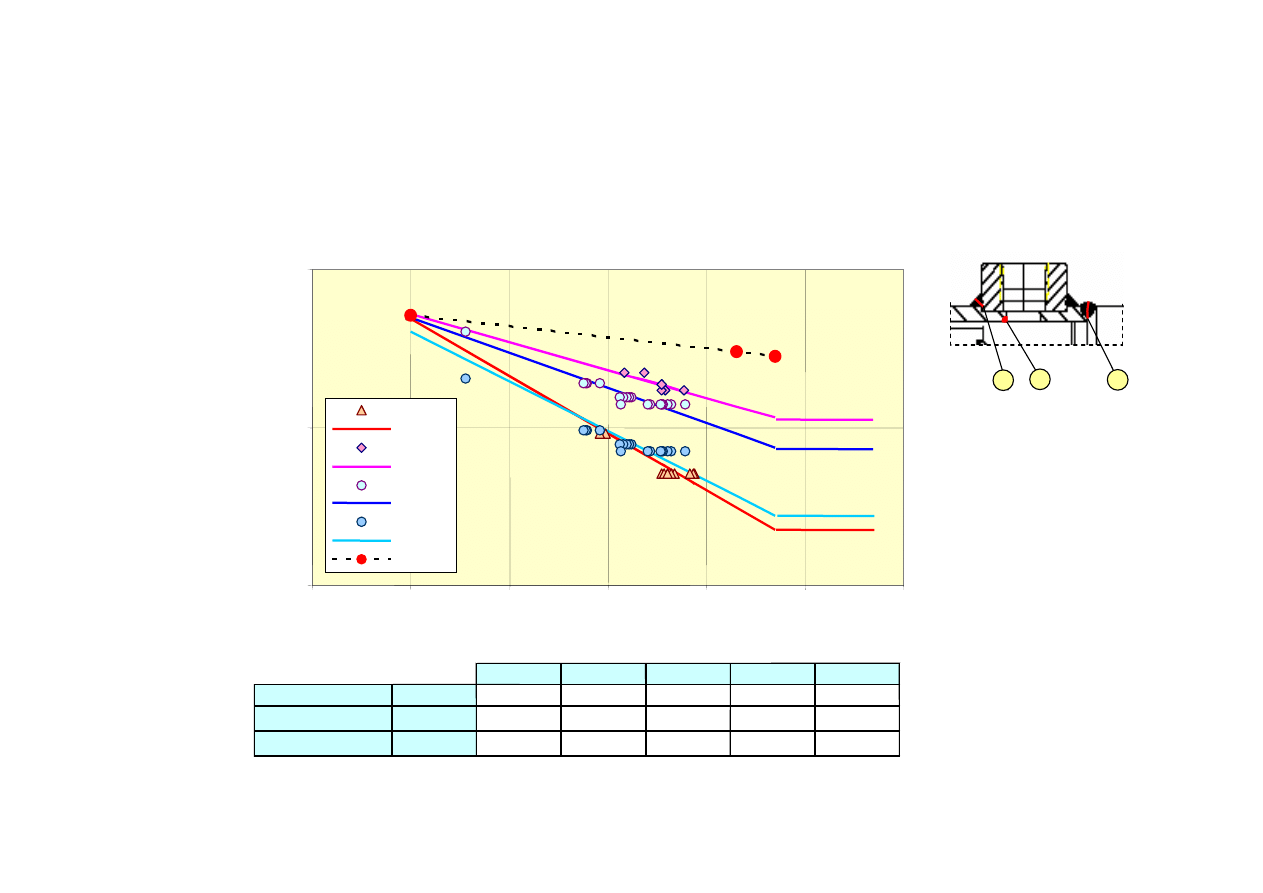
Krzywe S-N elementów konstrukcyjnych

1

3

4

Krzywe S-N wyznacza się w ten sposób raczej rzadko

CL1

CL3

CL4

Czy można wyznaczy krzywą S-N dla złożonego elementu?

51

Krzywe S-N wyznaczono przyjmując wspólny punkt (S1, N1)

10.0

100.0

1000.0

1.E+02

1.E+03

1.E+04

1.E+05

1.E+06

1.E+07

1.E+08

N [cyc]

Si

gma (r

an

ge) [MPa]

exp

CL1

exp

CL3

exp

CL4ab

exp

CL4ax

BM

1

3

4

BM

CL1

CL3

CL4ax

CL4ab

BM

m

2.8

5.6

3.2

4.5

14.0

S

D2

30.9

135.9

36.9

90.4

300.0

S

D5

22.2

115.6

27.6

73.6

281.0

S-N exponent
End. Limit [MPa]
End. Limit [MPa]

Krzywe S-N elementów konstrukcyjnych

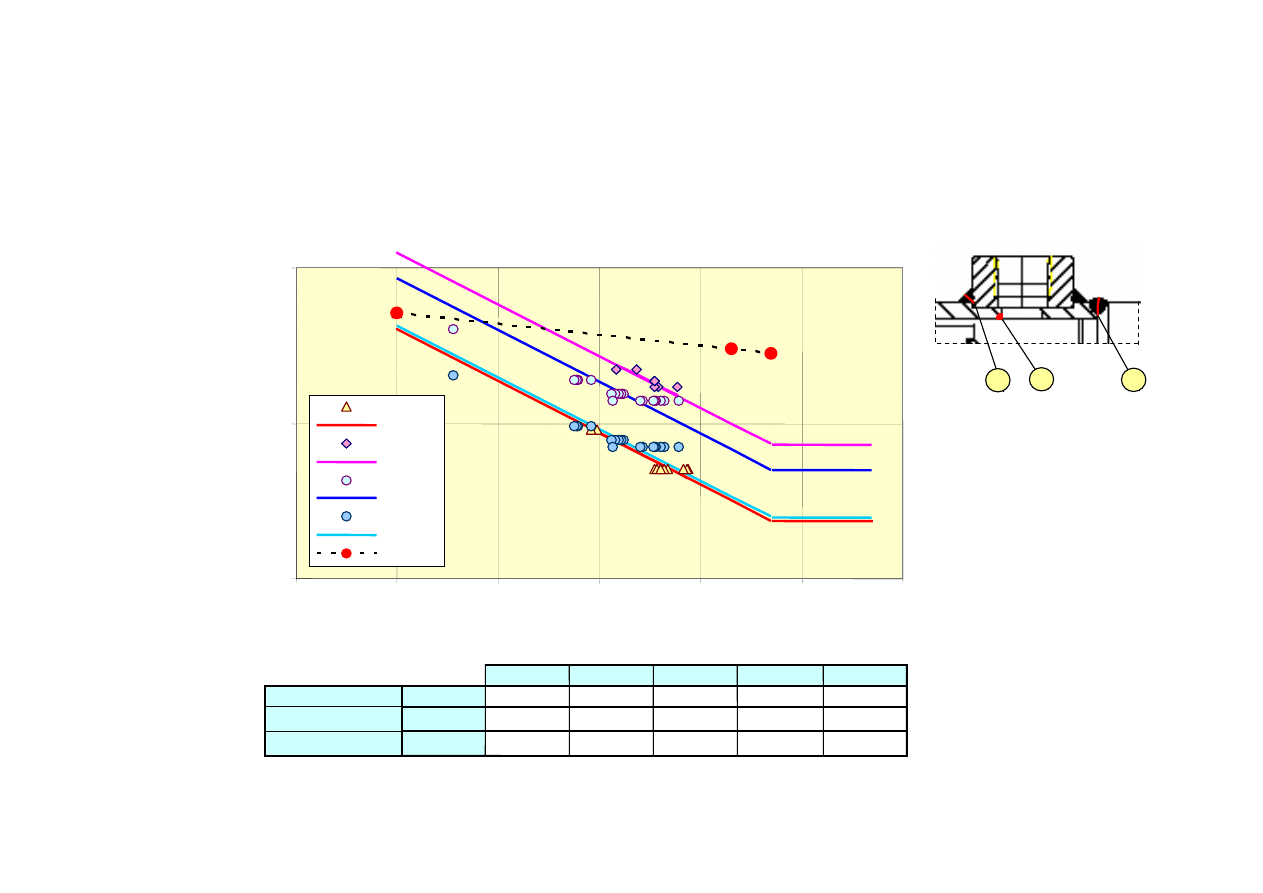
52

10.0

100.0

1000.0

1.E+02

1.E+03

1.E+04

1.E+05

1.E+06

1.E+07

1.E+08

N [cyc]

Si

gma (r

an

ge) [MPa]

exp

CL1

exp

CL3

exp

CL4ab

exp

CL4ax

BM

1

3

4

BM

CL1

CL3

CL4ax

CL4ab

BM

m

3.0

3.0

3.0

3.0

14.0

S

D2

32.0

100.0

34.0

68.0

300.0

S

D5

23.6

73.7

25.1

50.1

281.0

S-N exponent
End. Limit [MPa]
End. Limit [MPa]

Krzywe S-N wyznaczono przyjmując jednakowe nachylenie (m =3)

Krzywe S-N elementów konstrukcyjnych

53

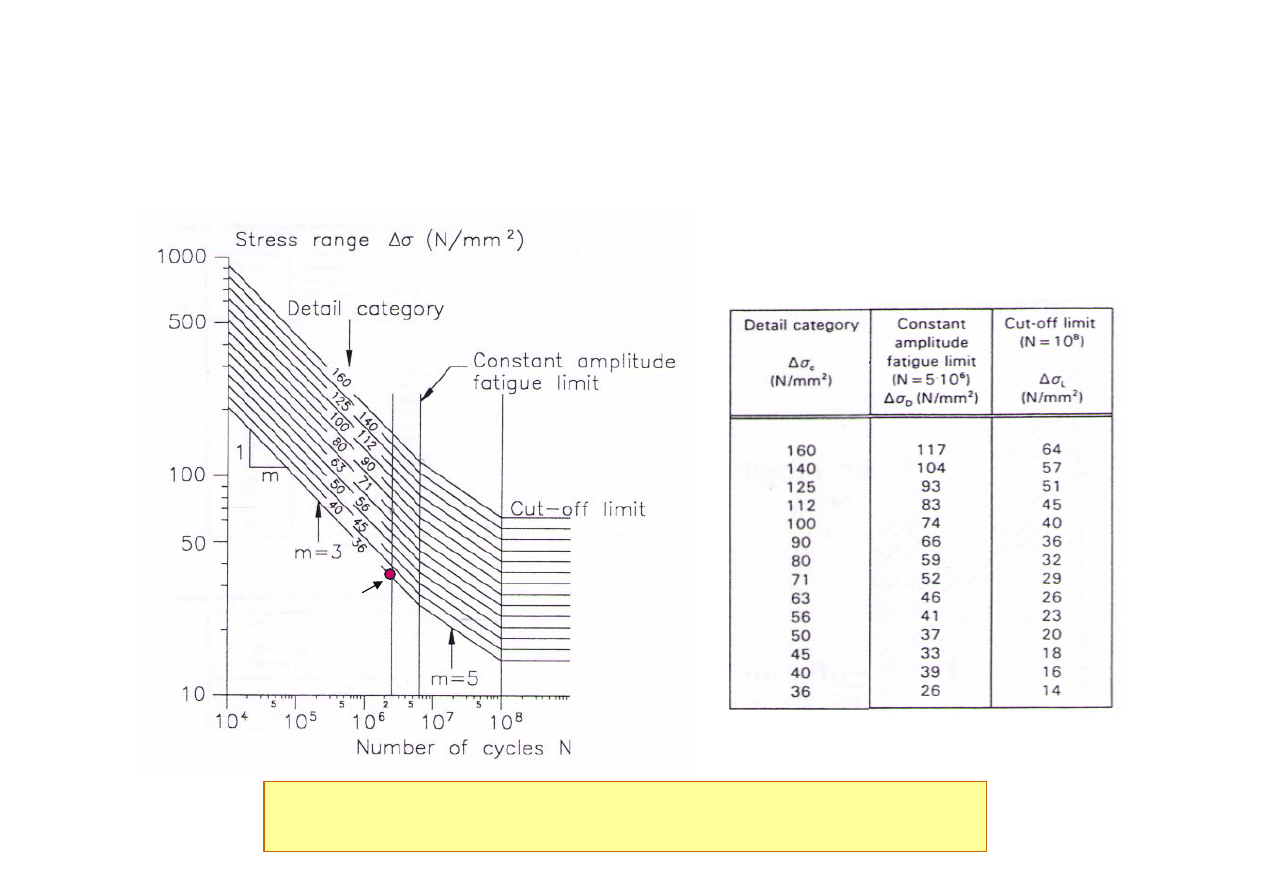
Krzywe S-N dla konstrukcji nośnych: ISO 10721-1

(

Δσ

C

@N

o

=2E+6 cykli, P

f

= 5%,

r = ?

)

Krzywe S-N węzłów spawanych

W konstrukcjach spawanych pomija się wpływ naprężeń średnich

ze względu na duże naprężenia własne

Δσ

C

=36

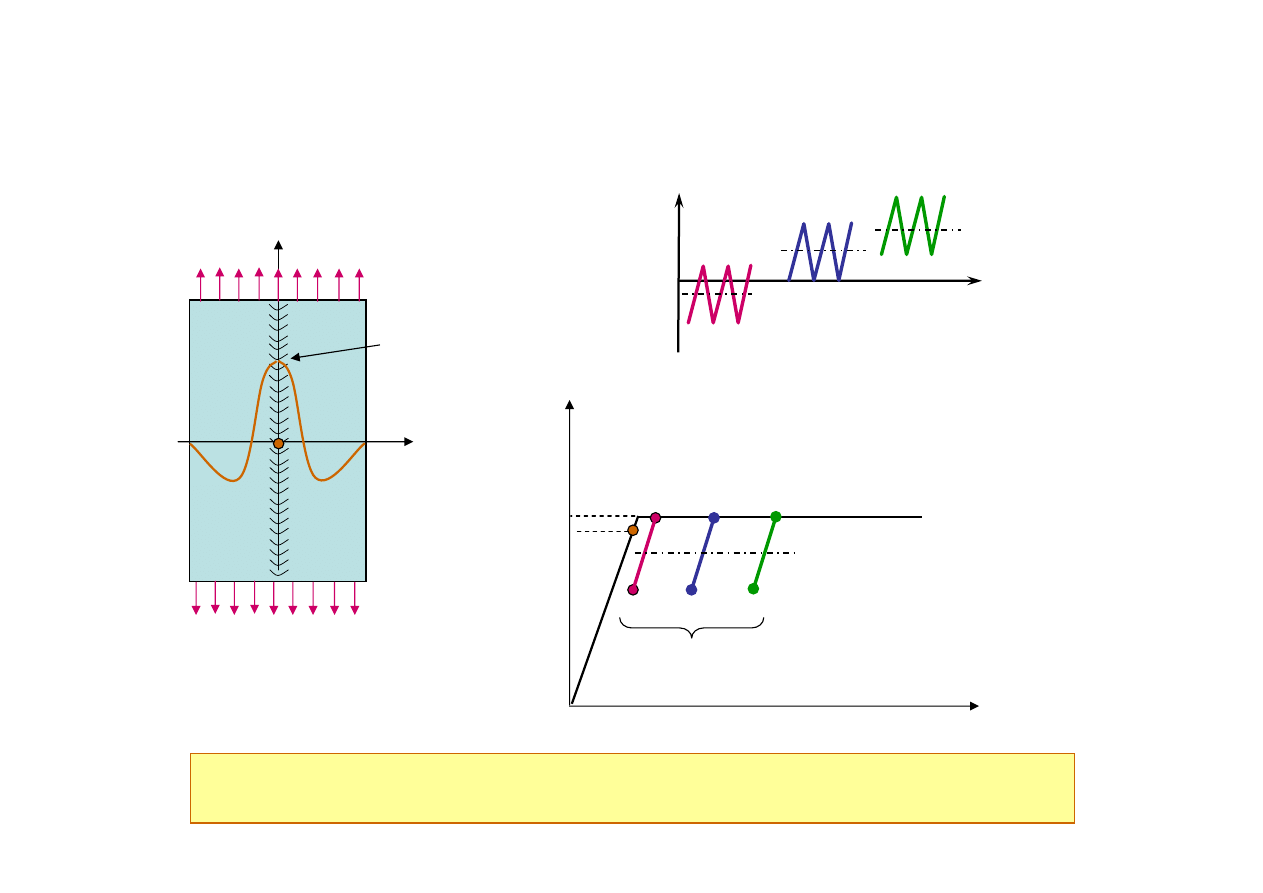
54

Efekt naprężeń własnych w węzłach spawanych

x

y

σ

ry

(x)

(-)

(-)

σ

ry

≈ R

e

czas

S

m

< 0

S

m

= S

a

S

m

> 0

Napr

ęż

eni

e, S

r < -1

r = 0

r > 0

Cykle obciążeń o jednakowej amplitudzie naprężeń

σ

ry

R

e

σ

ε

S

m

> 0 r > 0

Element konstrukcyjny spawany

(naprężenia własne po spawaniu)

Naprężenie, S

S

m

1

2

0

0

1

2

Uproszczona krzywa rozciągania

W obecności dużych rozciągających naprężeń własnych rzeczywista wartość

naprężeń średnich w spoinie zależy tylko od amplitudy naprężeń

1

2

1

2

1

2

1

2

Łą

czny efekt napr

ęż

e

ń

w

ł

asnych

i obci

ąż

e

ń

zewn

ę

trznych

55

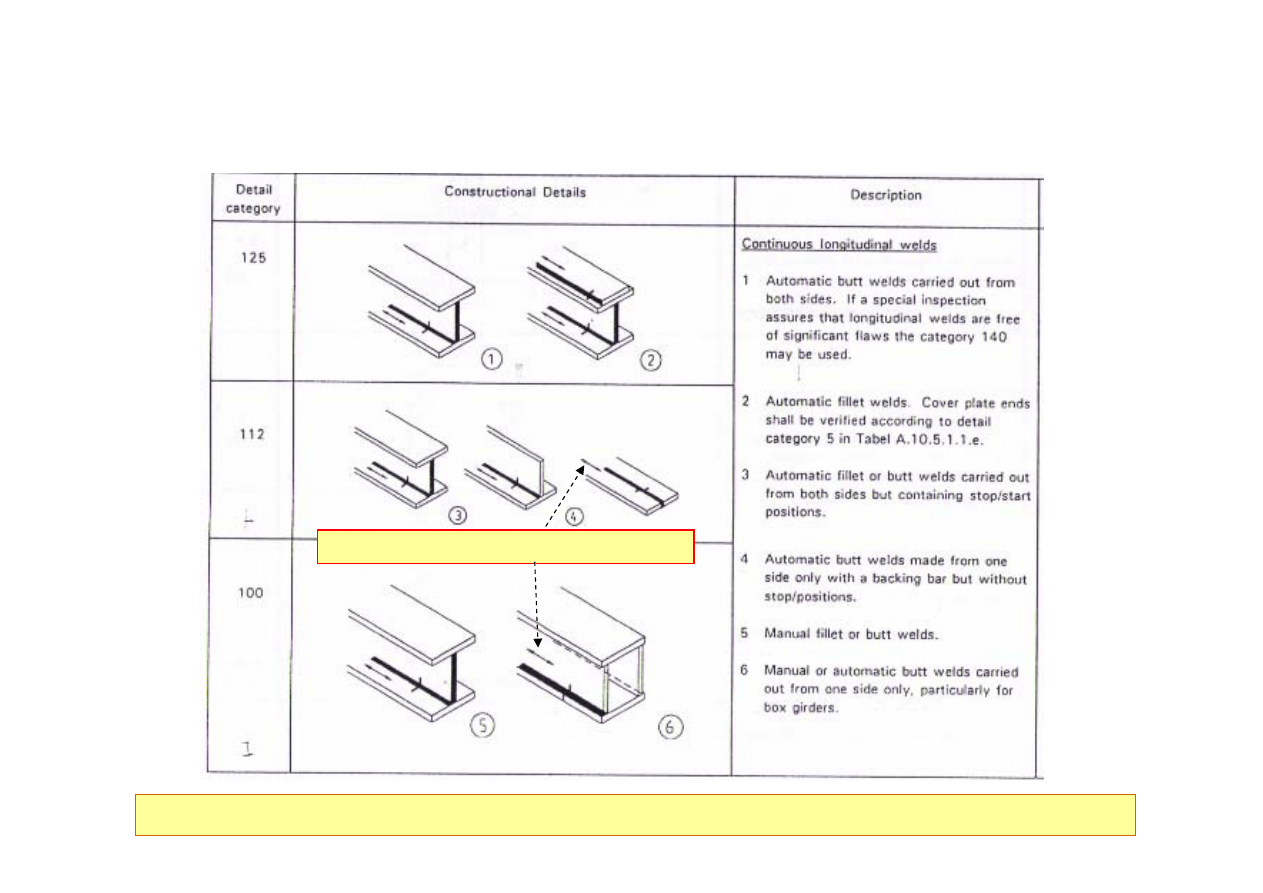
Krzywe S-N węzłów spawanych

ISO 10721-1

Krzywe S-N są opisane poprzez nominalne naprężenia normalne w p-kcie inicjacji pęknięcia

Kierunek nominalnych naprężeń normalnych

56

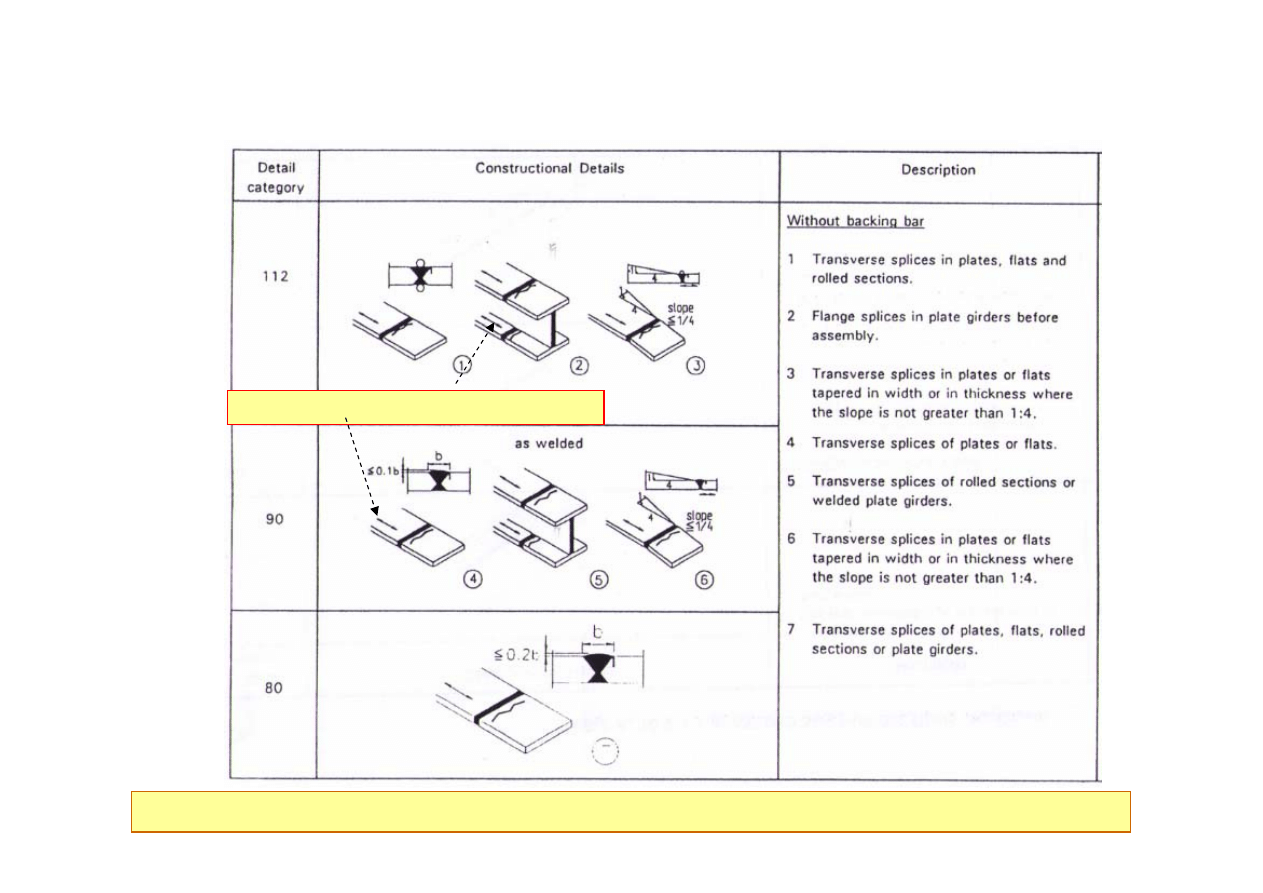
Krzywe S-N węzłów spawanych

ISO 10721-1

Krzywe S-N są opisane poprzez nominalne naprężenia normalne w p-kcie inicjacji pęknięcia

Kierunek nominalnych naprężeń normalnych

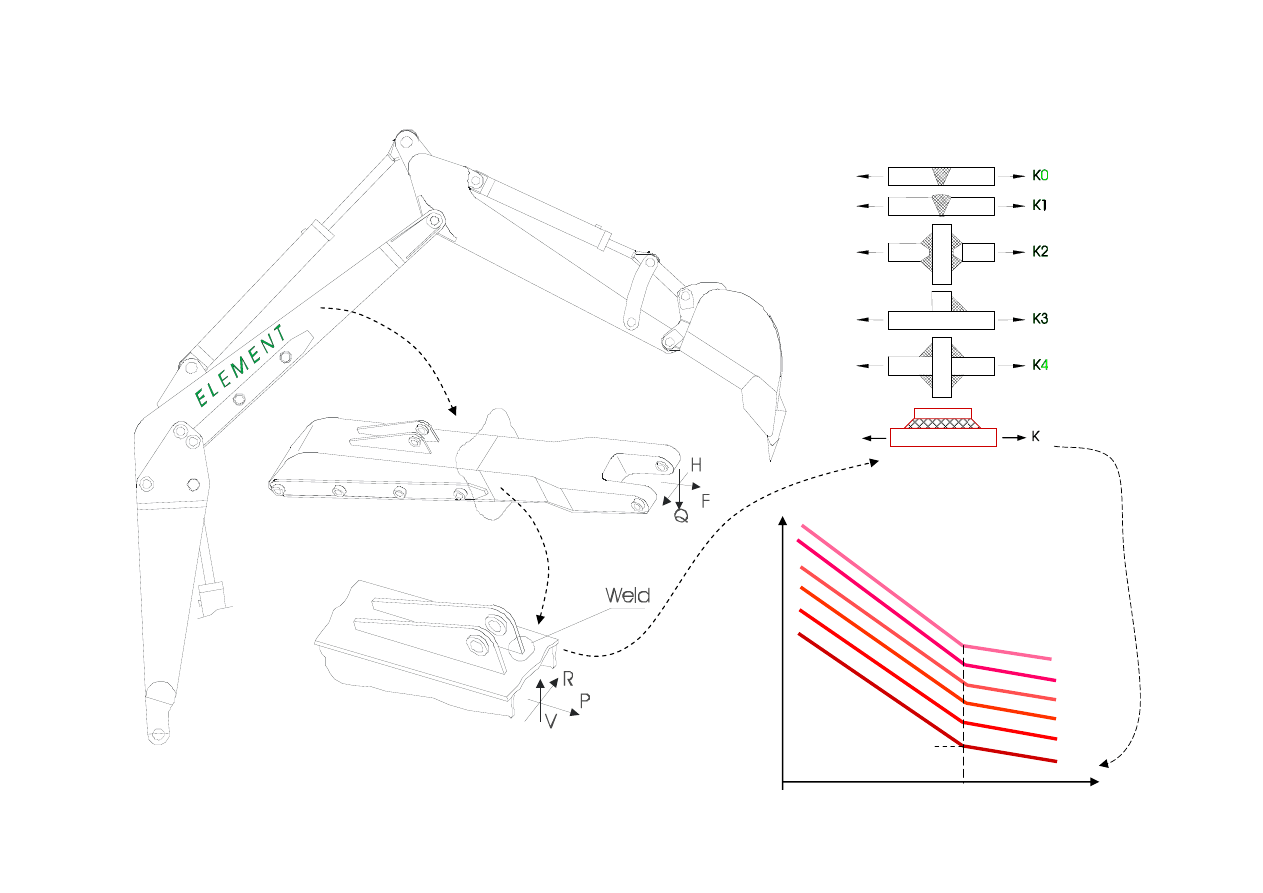
57

5

d) Standard welded joints

K0
K1

K2

K3
K4
K5

Stress

a

m

plitude,

Δσ

n

/2

e) Standard S-N curves

Number of cycles, N

a) Structure

b) Component

c) Section with welded joint

Zasada podobieństwa w prognozowaniu trwałości

S

D

N

o

C

5

= S

D

m

N

o

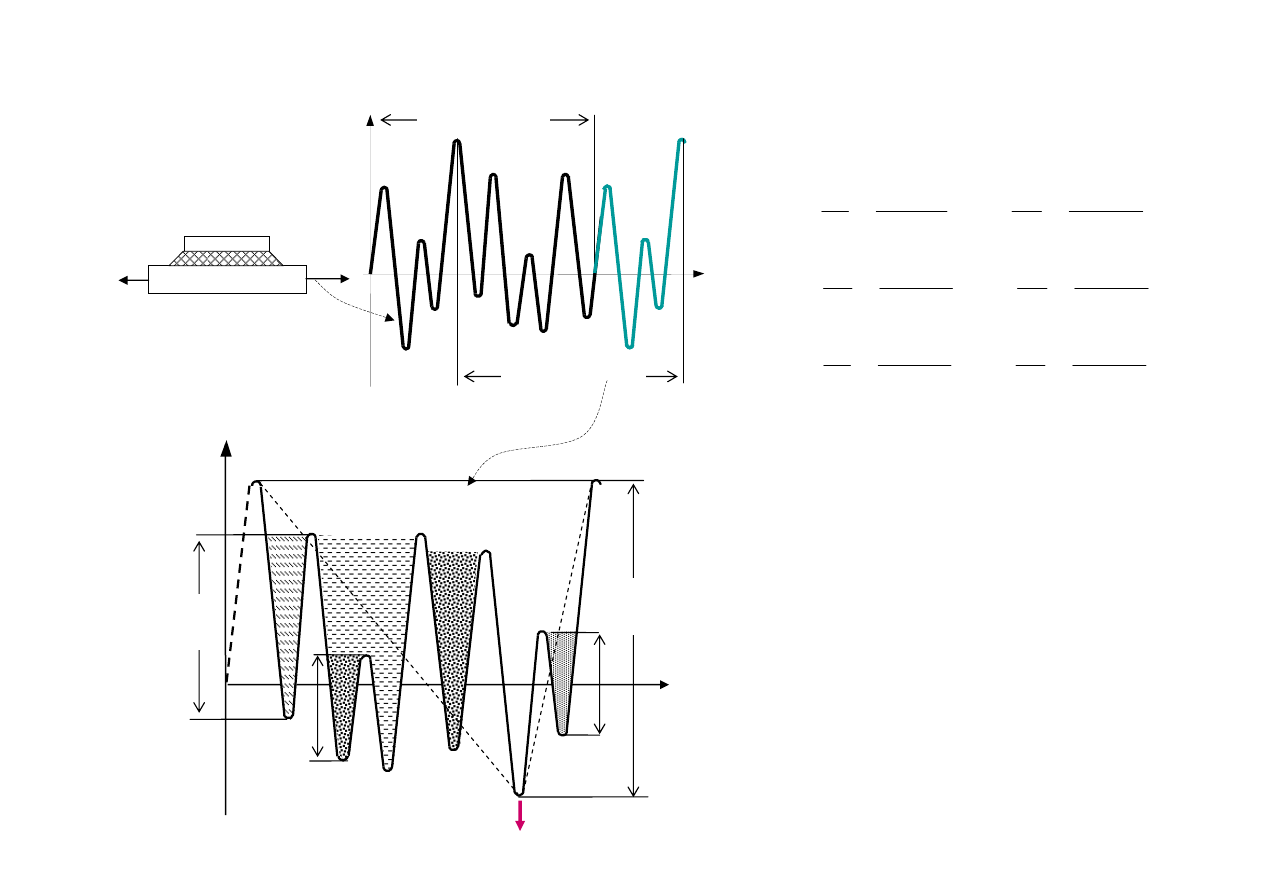
58

t

h) Uszkodzenia zmęczeniowe

Suma uszkodzeń zmęczeniowych
dla bloku obciążeń (Palmgren-Miner)

Trwałość [blk]: N

blk

= 1/D

Trwałość [czn]: N = N

blk *

n

blk

Trwałość [godz]: T = N

blk *

t

blk

f) Blok obciążeń

(napr. nomin.)

t

K5

σ

n

Obliczanie uszkodzeń w analizie trwałości

Stress,

σ

n

Blok obciążeń

Blok obciążeń *

( )

(

)

(

)

(

)

(

)

(

)

5

6

6

6

5

5

1

5

5

4

4

4

5

3

3

3

5

2

2

2

5

1

1

1

1

1

1

1

1

1

C

N

D

;

C

N

D

C

N

D

;

C

N

D

C

N

D

;

C

N

D

m

m

m

m

m

m

σ

Δ

=

=

σ

Δ

=

=

σ

Δ

=

=

σ

Δ

=

=

σ

Δ

=

=

σ

Δ

=

=

6

5

4

3

2

1

D

D

D

D

D

D

D

blk

+

+

+

+

+

=

cp – cykle pracy, gdy 1blk = 1cykl pracy

czn – cykle zmian naprężeń

n

blk

– liczba cykli w bloku obciążeń

Δσ

5

Δσ

2

Stress

g) Zliczanie cykli (rainflow) - metoda rezerwuaru

Δσ

1

Δσ

3

Δσ

6

Δσ

4

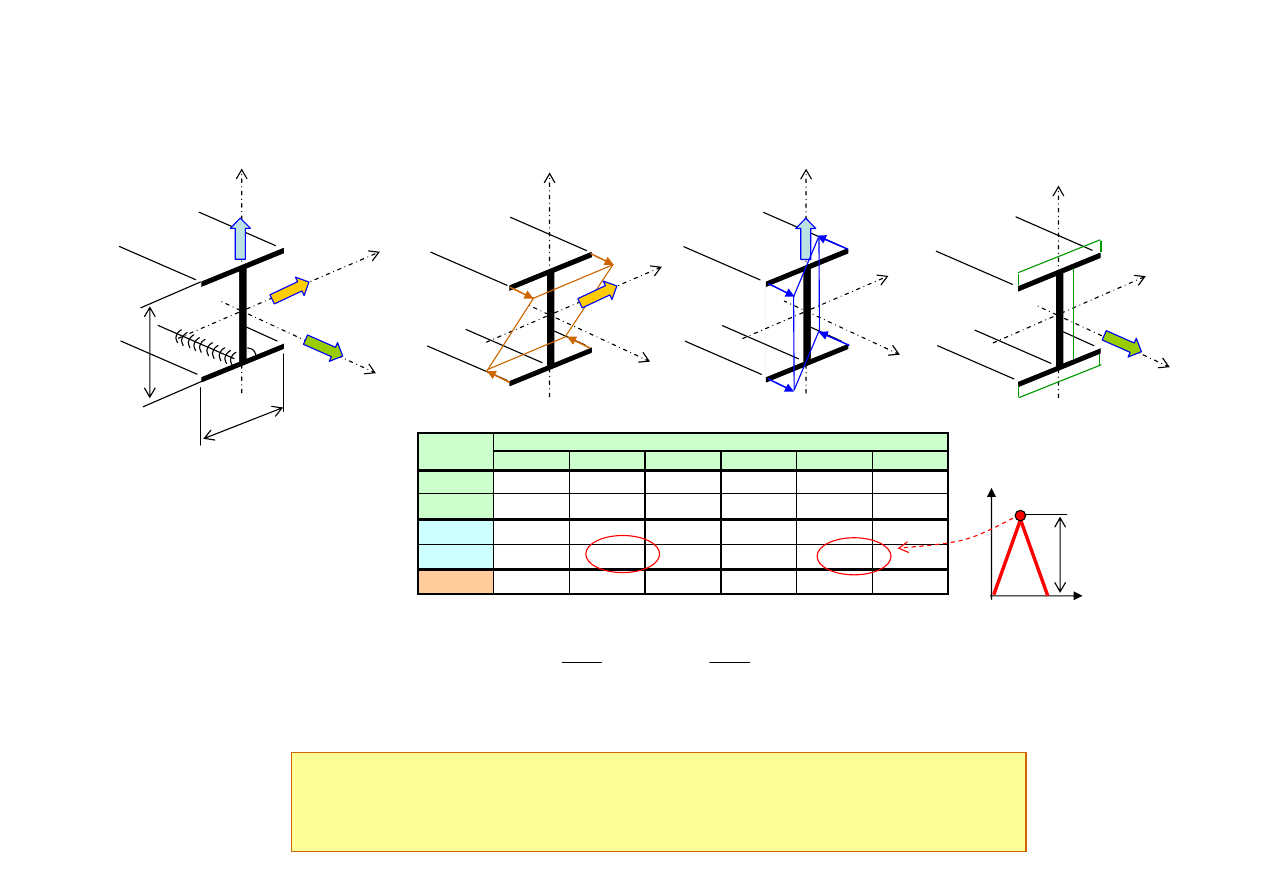
59

Rodzaj
naprężeń

1

2

3

4

5

6

σ

x,y

94.2

94.2

94.2

-94.2

-94.2

-94.2

σ

x,z

-103.6

0

103.6

103.6

0

-103.6

τ

s

119.0

119.0

119.0

119.0

119.0

119.0

σ

n

-9.4

94.2

197.8

9.4

-94.2

-197.8

σ

red

206.4

226.7

285.7

206.4

226.7

285.7

Punkt przekroju

Wytrzymałość zmęczeniowa

y

z

x

M

x

M

y

M

z

b

h

M

y

= 25 kNm

M

z

= 5 kNm

M

x

= 2 kNm

b = 120 mm
h = 200 mm

δ = 10 mm

PSO:

Spoina wzdłużna

Δσ

c

= 100 MPa

N

o

= 2E+6 cykli

m = 3

cykli

E

.

.

E

S

N

N

n

c

o

6

39

2

2

94

100

6

2

3

3

+

=

⎟

⎠

⎞

⎜

⎝

⎛

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Δ

σ

Δ

=

Warunek wytrzymałości zmęczeniowej spełniony *)

*) w obecności naprężeń stycznych dokładniejsza analiza wymaga
stosowania naprężeń głównych zamiast normalnych w spoinie

y

z

x

M

z

y

z

x

M

y

σ

x,y

σ

x,z

w

N

N

>

Warunek

y

z

M

s

τ

s

Wymagana trwałość:

N

w

= 10lat * 200 dni/rok * 6 h/dz * 120 c/h = 1.44E+6 cykli

1

2

3

4

5

6

t

σ

Uproszczony
cykl obciążenia
(naprężenia min-max)

ΔS

n

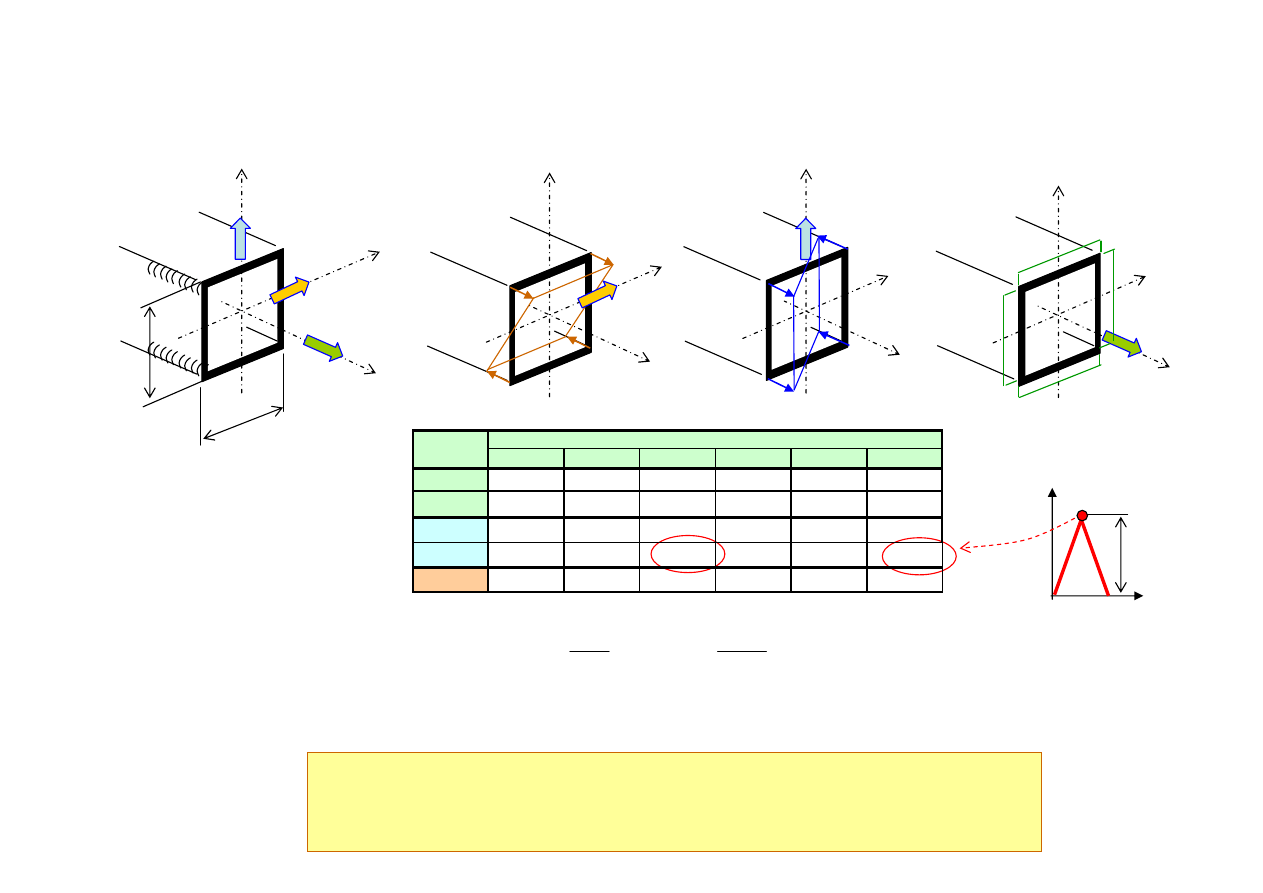
60

Wytrzymałość zmęczeniowa

y

z

x

M

x

M

y

M

z

b

h

M

y

= 25 kNm

M

z

= 5 kNm

M

x

= 2 kNm

b = 120 mm
h = 200 mm

δ = 10 mm

PSO:

Spoina wzdłużna

Δσ

c

= 100 MPa

N

o

= 2E+6 cykli

m = 3

cykli

E

.

.

E

S

N

N

n

c

o

6

92

1

4

101

100

6

2

3

3

+

=

⎟

⎠

⎞

⎜

⎝

⎛

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Δ

σ

Δ

=

y

z

x

M

y

σ

x,y

y

z

x

M

z

σ

x,z

w

N

N

>

Warunek

Wymagana trwałość:

N

w

= 15lat * 200 dni/rok * 6 h/dz * 120 c/h = 2.16E+6 cykli

1

2

3

4

5

6

y

z

M

s

τ

s

Rodzaj
naprężeń

1

2

3

4

5

6

σ

x,y

79.6

79.6

79.6

-79.6

-79.6

-79.6

σ

x,z

-21.7

0

21.7

21.7

0

-21.7

τ

s

16.7

16.7

16.7

16.7

16.7

16.7

σ

n

57.9

79.6

101.4

-57.9

-79.6

-101.4

σ

red

64.7

84.7

105.4

64.7

84.7

105.4

Punkt przekroju

t

σ

Uproszczony
cykl obciążenia

ΔS

n

Warunek wytrzymałości zmęczeniowej spełniony *)

*) w obecności naprężeń stycznych dokładniejsza analiza wymaga
stosowania naprężeń głównych zamiast normalnych w spoinie

61

Wady oceny trwałości przy użyciu

krzywych S-N:

1. Krzywe S-N Nie obejmują zmęczenia

niskocyklowego (LCF)

2. Metoda dobrze działa przy stosowaniu

naprężeń nominalnych (trudno je określić
w obliczeniach MES)

3. Krzywe S-N odnoszą się zwykle do

całkowitego pęknięcia próbki (trwałość
zawiera etap inicjacji i wzrostu pęknięcia)

4. Trudne oszacowanie wielkości

uszkodzenia w elemencie
konstrukcyjnym (krzywa S-N dotyczy
często tylko małej części elementu)

5. Trudność wykorzystania wyników analizy

MES

Ocena trwałości – metoda S-N

Zalety oceny trwałości przy użyciu

krzywych S-N:

1.

Duża baza danych krzywych S-N dla
różnych węzłów głównie spawanych
(normy: konstrukcje stalowe,
dźwignice, zbiorniki ciśnieniowe, …)

2.

Krzywe S-N zawierają efekt jakości
wytwarzania (mikrostruktura,
naprężenia własne)

3.

Łatwe badania próbek

4.

Proste obliczanie trwałości

5.

Duże doświadczenie w zakresie
stosowania tej metody

62

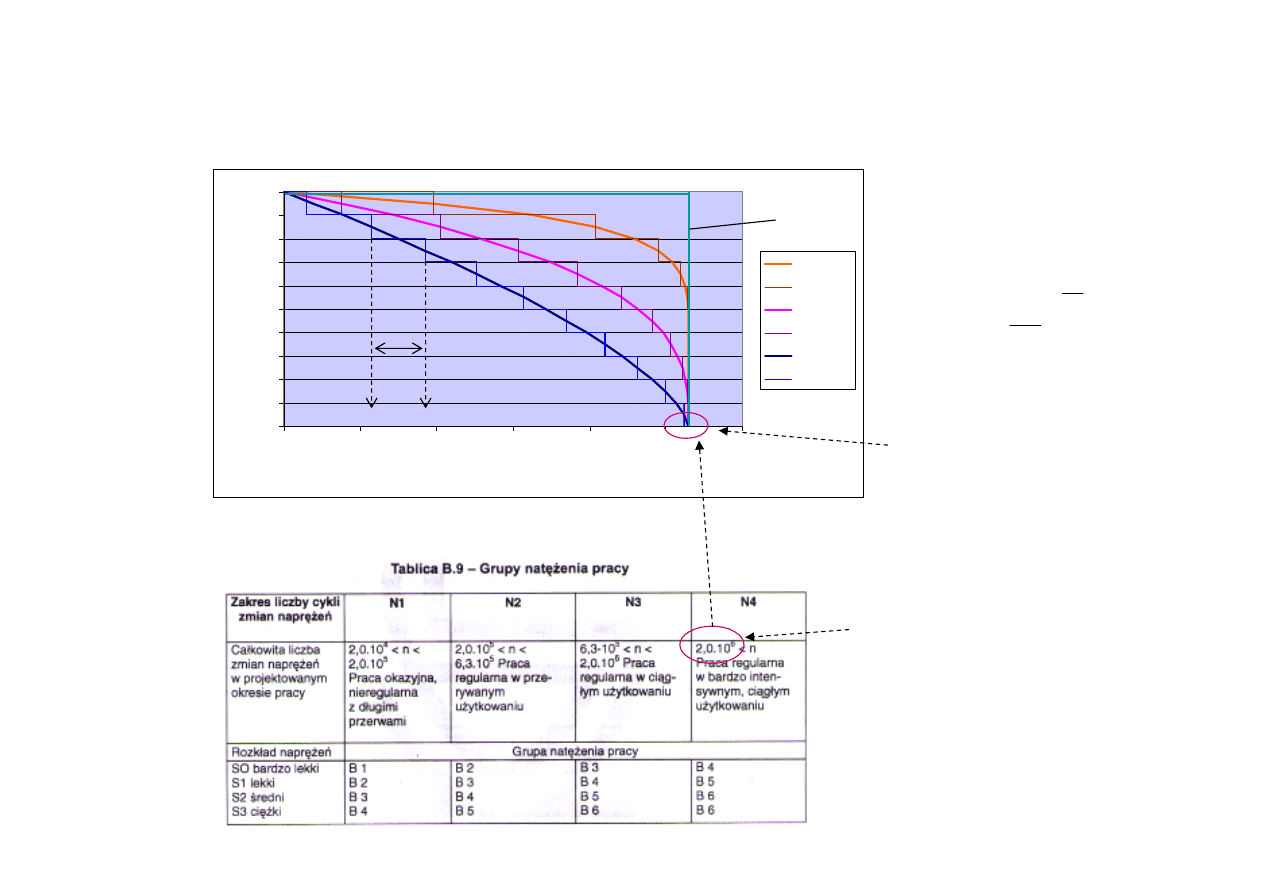
Widmo obciążeń - dźwignice

cykle

Δσ

max

Z

ak

res

napr

ęż

eń

N

2

n1

N

4

N

1

0

N

3

N

L

Δσ

j

m

.N

j

=

Δσ

C

m

.N

o

(

Δσ

C

,N

o

)

n2

(

Δσ

D

,N

E

)

N

0

N

D

n3

n4

n

p

=

Σ n

i

1. Uszkodzenie od widma obc:

∑

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

σ

Δ

σ

Δ

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

σ

Δ

σ

Δ

=

m

max

i

p

i

m

C

max

o

p

n

n

N

n

D

2. Uszkodzenie od widma obc:

k

N

n

D

m

C

max

o

p

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

σ

Δ

σ

Δ

=

∑

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

σ

Δ

σ

Δ

=

m

max

i

p

i

n

n

k

3. Wsp. widma obc:

4. Warunek naprężeniowy (dla D = 1,

gdzie N

w

– wymagana liczba cykli):

m

C

max

s

1

σ

Δ

≤

σ

Δ

N

0

= 2

.

10

6

cykli

N

D

= 5

.

10

6

cykli

N

L

= 10

8

cykli

(

Δσ

L

,N

F

)

m

o

w

k

N

N

s

=

5. Parametr klasy dźwignicy:

63

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

1.E+00

1.E+01

1.E+02

1.E+03

1.E+04

1.E+05

1.E+06

n [cykli]

σ

ai

/

σ

p

s=9 (S2)
n(i) = 9
s=3 (S1)
n(i) = 3
s=1 (S0)
n(i) = 0.5

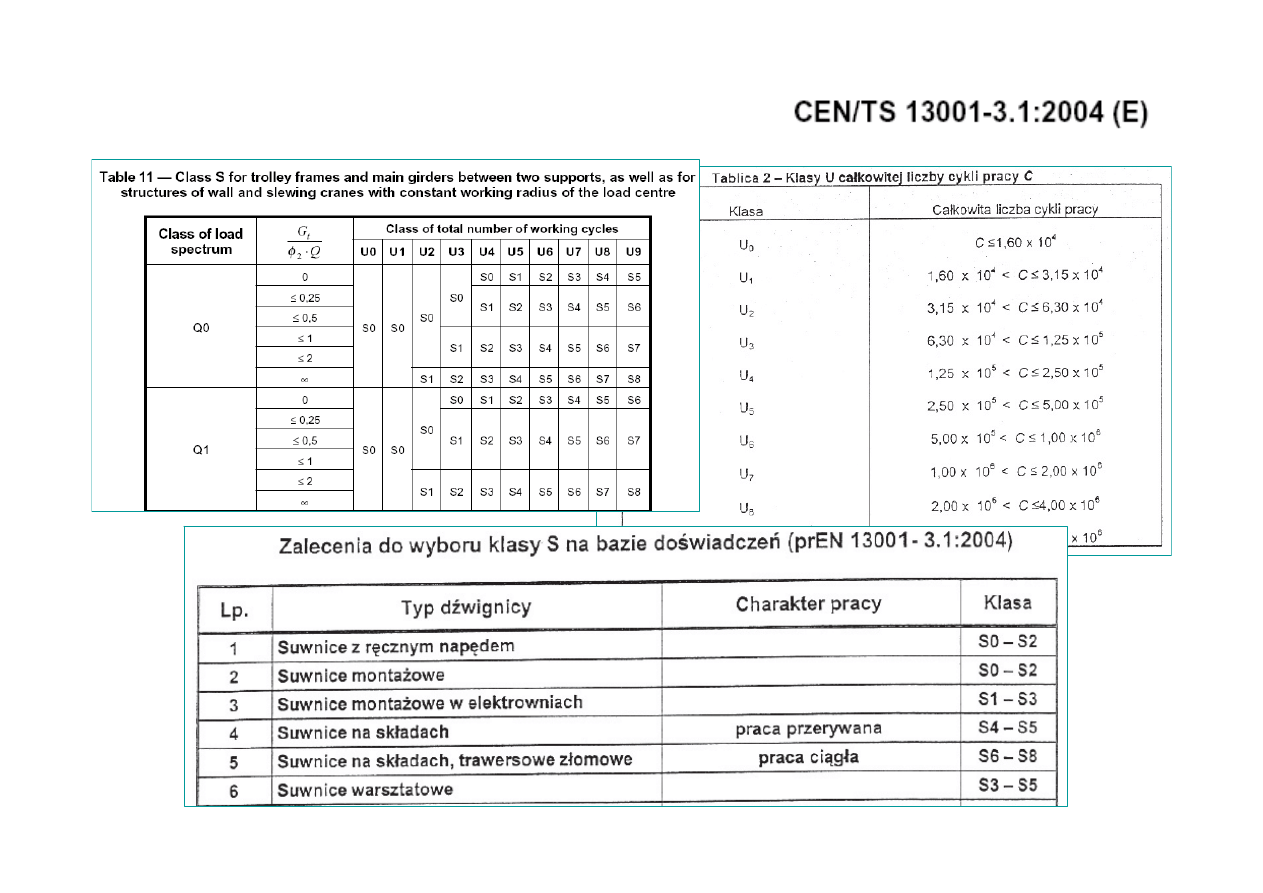
Obciążenia normowe dźwignic

s

p

ai

m

p

m

si

n

n

n

n

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

σ

σ

⎥

⎦

⎤

⎢

⎣

⎡

=

Normowe widmo obciążeń można określić na podstawie opisu grupy natężenia pracy

Grupa natężenia pracy jest opisana przez liczbę cykli widma (n

p

) oraz jego kształt (s)

S3

Wymagana liczba cykli
zmian naprężeń w widmie,
to jest raczej liczba cykli
pracy

n

s3

Cykle widma
skumulowanego

n

s2

n

3

n

p

= 1

n

m

= 2E+5

64

Ujęcie normowe - dźwignice

65

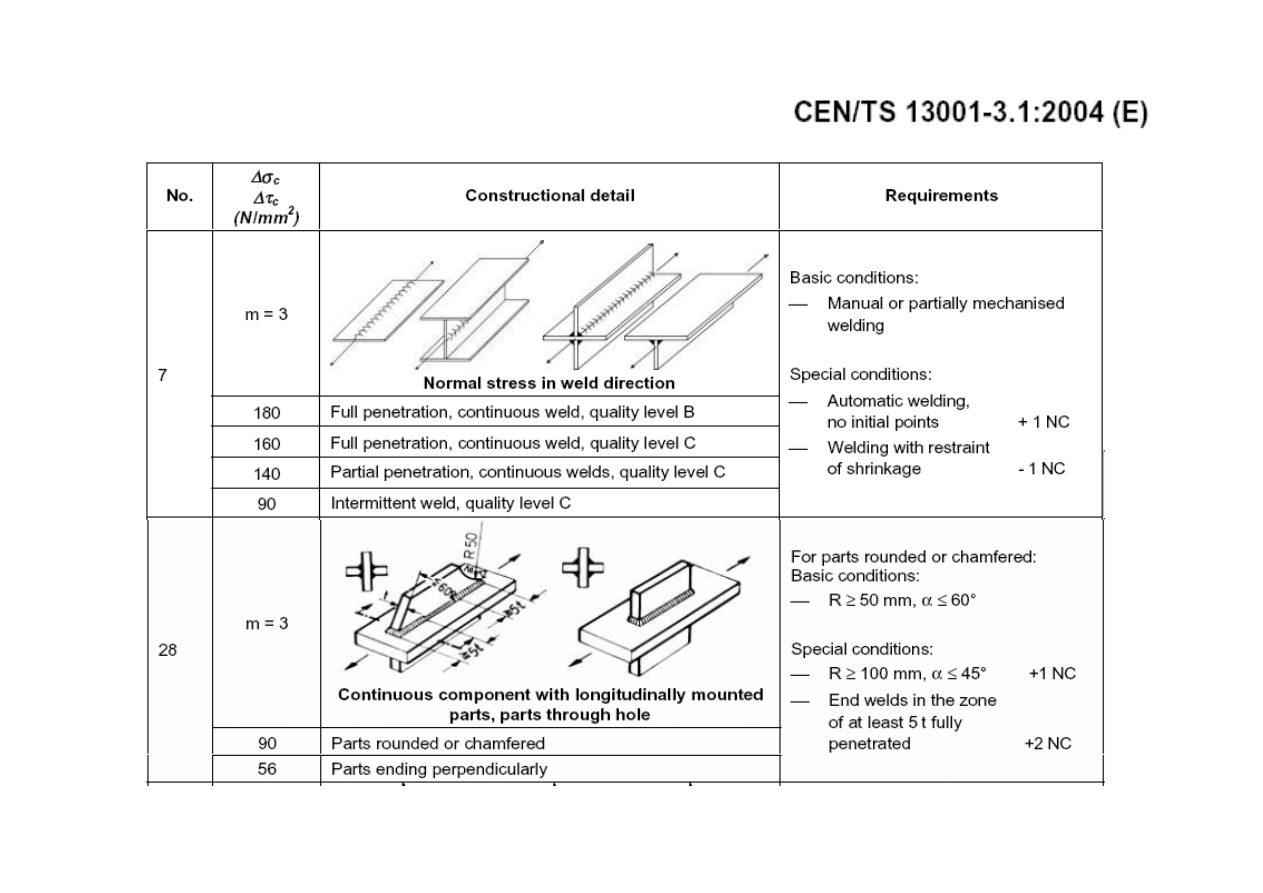
Ujęcie normowe - dźwignice

66

Ujęcie normowe - dźwignice

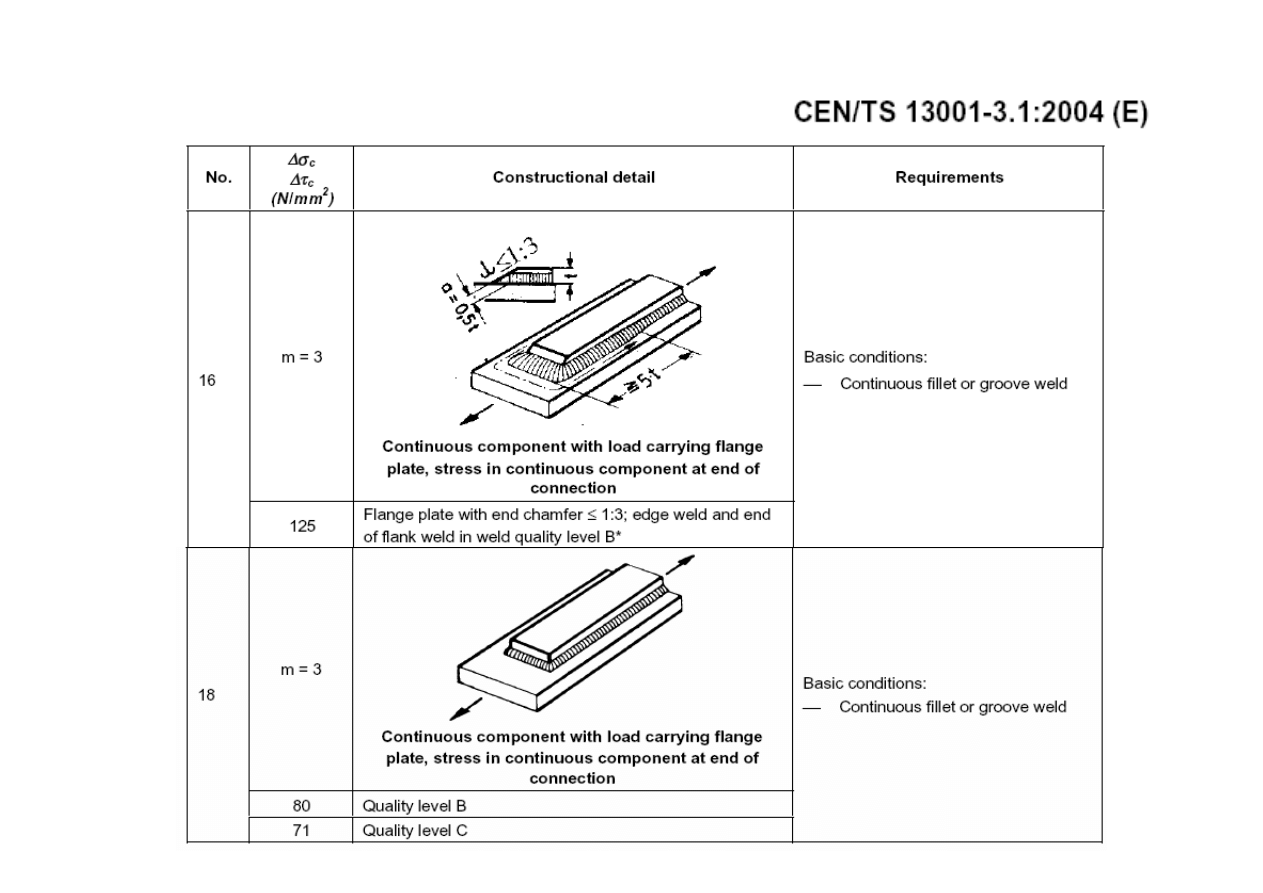
67

Ujęcie normowe - dźwignice

68

Literatura

1. PN-EN 12999: Żurawie przeładunkowe, 2005

2. ISO 10721-1: Steel Structures, Part 1: Materials and design, 1997

3. ISO 2032-1: Cranes – Proof of competence of steel structures – Part 1:

General, 2005

4. PN-EN 13001-2:2011E: Bezpieczeństwo dźwignic - Ogólne zasady

projektowania - Część 2: Obciążenia

5. PN-EN 13001-3-1+A1:2013-09E: Dźwignice - Ogólne zasady

projektowania - Część 3-1: Wyznaczanie ograniczeń i właściwości
stalowych ustrojów nośnych

69

???