Analiza wymiarowa

Analiza wymiarowa

1. Analiza wymiarowa

Element przestrzeni wymiarowej
np. (5 kg), (7,8 m/s

2)

, (15 m

3

/s), (100kPa),…..

Elementy przestrzeni wymiarowej są wymiarowo
niezależne wtedy i tylko wtedy gdy:

3

1

2

1

2

3

n

a

a

a

a

n

A A A

A

a

� � � � =

�

K

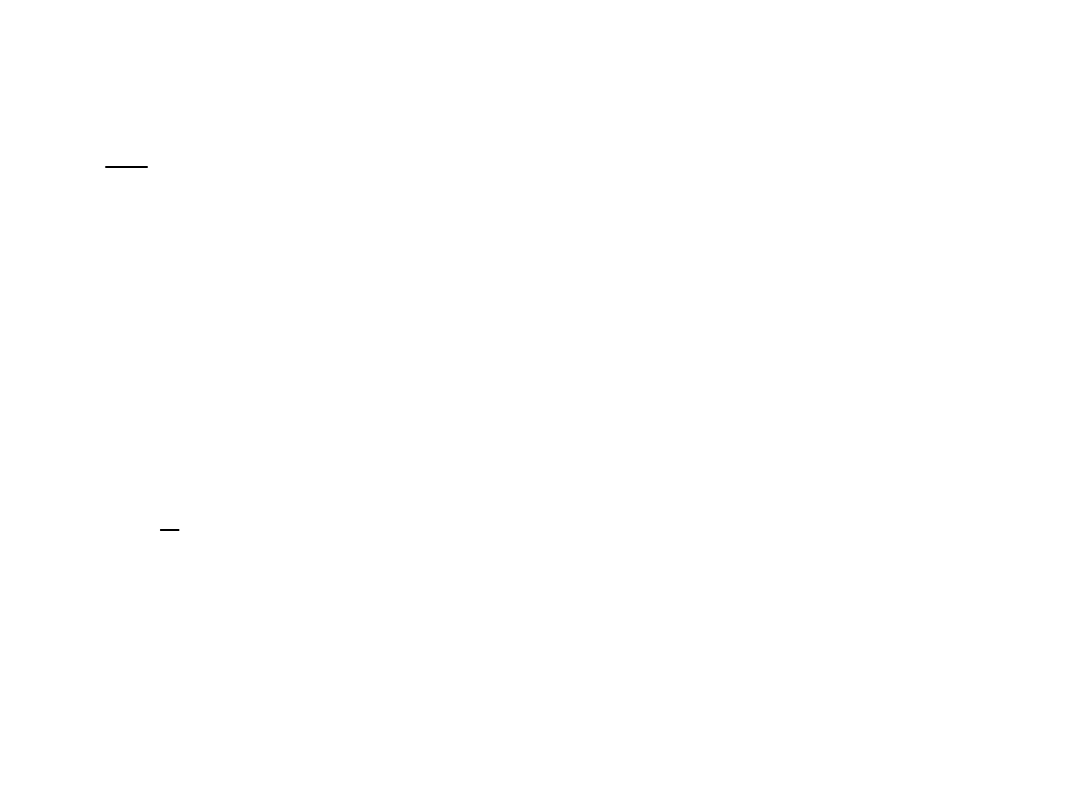
Przykład1:

( )

1

2

3

5

2

a

a

m

s

s

a

�

�

=

�

�

�

�

( )

2

1

1

2

3

a

a

s

s

a

� � =

�

� �

� �

Przykład2:

Elementy są wymiarowo niezależne.

Elementy są wymiarowo zależne.

Przestrzeń wymiarowa ma n jednostek jeżeli
istnieje w niej
n wymiarowo niezależnych wymiarowo elementów.

Każdy zbiór elementów wymiarowo niezależnych

A

1

, A

2

, A

3

,…., A

n

tworzy bazę.

Każdy element przestrzeni można zapisać jako
kombinację elementów bazy

A=

a

- wielkość
bezwymiarowa

Jak sprawdzić czy elementy tworzą bazę (są
wymiarowo niezależne)?

Jeśli znamy zbiór

który wiemy, że tworzy bazę (jest wymiarowo
niezależny) to

zbiór

generowany jest poprzez bazę X

{

}

1

2

3

,

,

,

,

n

X

X X X

X

=

K

{

}

1

2

3

, , ,

,

m

B

B B B

B

=

K

31

32

33

3

1

2

3

1

2

3

3

1

2

3

1

2

3

n

m

m

m

mn

a

a

a

a

n

a

a

a

a

m

m

n

B
B
B

X

X

X

X

B

X

X

X

X

a

a

=

=

= �

�

�

� �

=

�

�

�

� �

K

M

K

11

12

1

21

22

2

1

2

n

n

m

m

mn

a

a

a

a

a

a

rank

a

a

a

=

K
K

M

M O

M

K

to zbiór B tworzy bazę (jest wymiarowo
niezależny).

Jeśli spełniony jest warunek

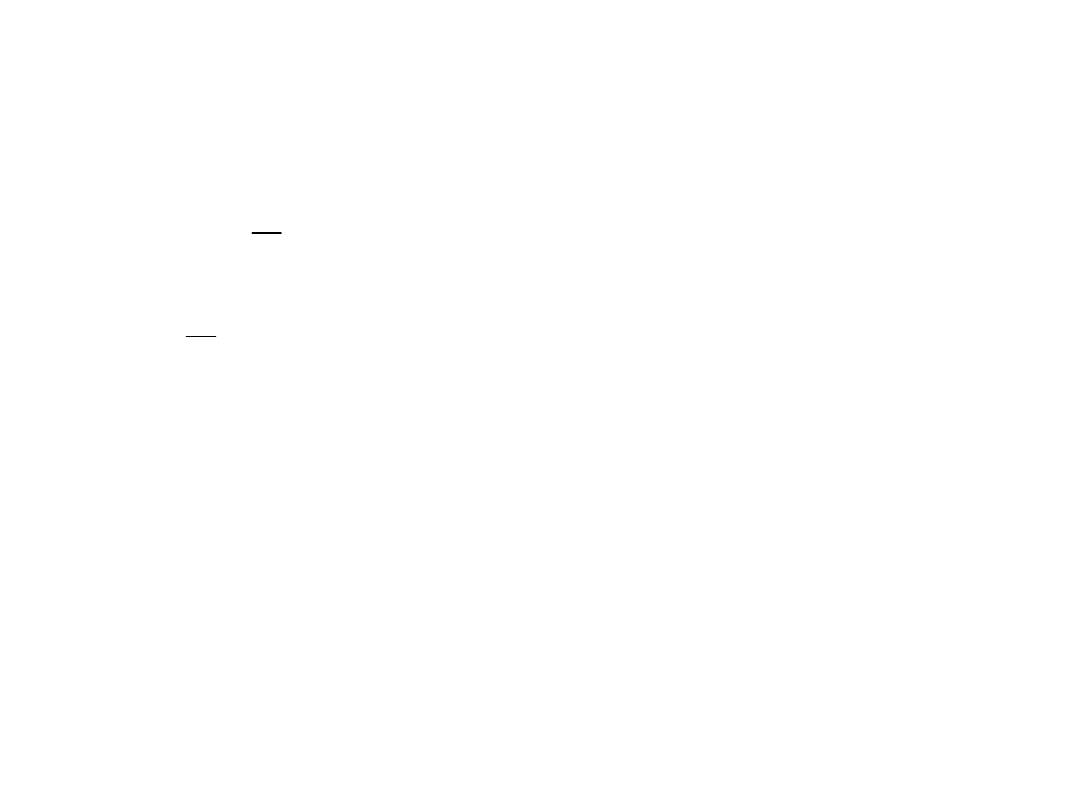
Przykład3:

{

}

1 ,1 ,1

X

m kg s

=

2 ,1 , 4

m

B

m Pa

s

�

�

=�

�

�

jest bazą?

Czy

2

1

4

m

s

m

Pa

�

=

�

�

=

�

�

=

�

�

Czyli zbiór B tworzy bazę.

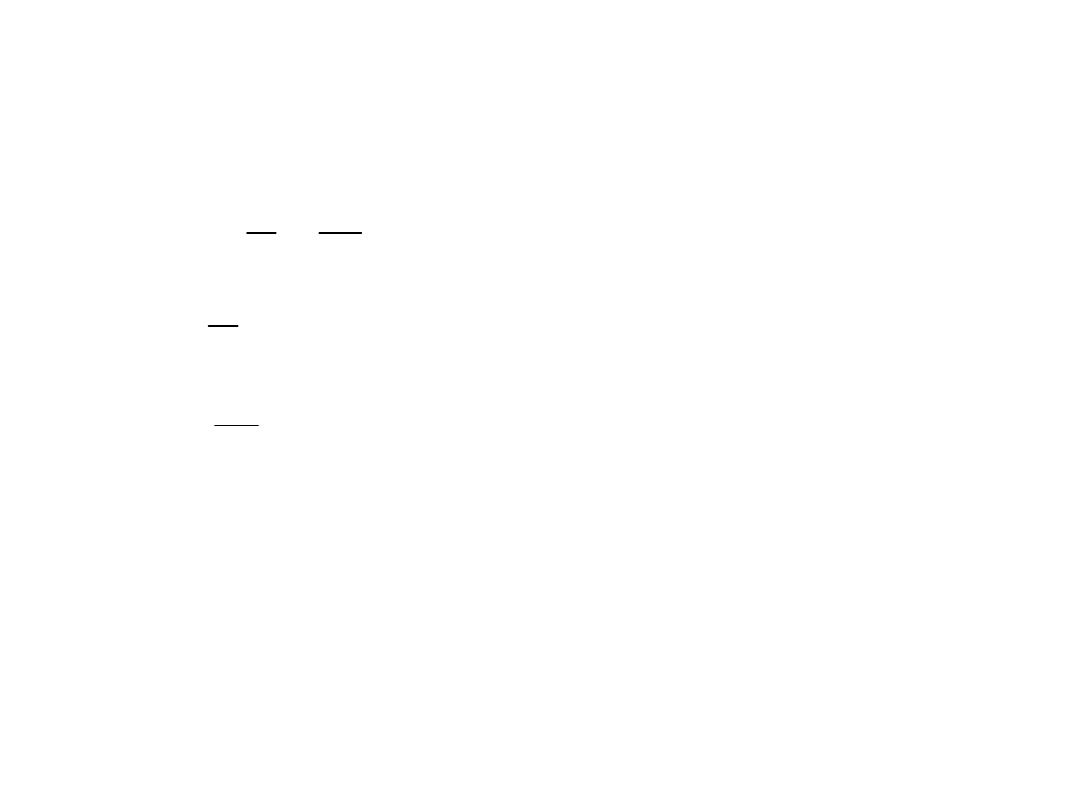
Przykład4:

{

}

1 ,1 ,1

X

m kg s

=

3

1 , 2

, 5

m m

B

s

s

s

�

�

=�

�

�

jest bazą?

Czy

3

1

2

5

m

s

m

s

s

�

=

�

�

�

=

�

�

=

�

�

�

Czyli zbiór B nie tworzy bazy.

Funkcja wymiarowa jest to funkcja określona na
zbiorze elementów wymiarowych.

gdzie Z, Z

1

, Z

2

, …, Z

m

– elementy przestrzeni

wymiarowej

1

2

( , ,

)

m

Z

f Z Z

Z

=

K

Przykład5: Wyznaczyć funkcję wymiarową
określającą spadek ciśnienia przypadający na
jednostkę długości przewodu o średnicy d wskutek
przepływu płynu o gęstości ρ z prędkością v.

( , , )

sl

p

f d

v

l

r

D

=

[ ]
[ ]
[ ]

d

m kg s

mkg s

v

m kg s

r

=

=

=

Sprawdzamy czy argumenty funkcji są wymiarowo
niezależne

Zapisujemy funkcję wymiarową jako kombinację
elementów wymiarowo niezależnych w postaci:

sl

p

l

D

=

3

1

2

(

)

(

) (

) (

)

a

a

a

mkg s

mkg s

mkg s

mkg s

a

= �

Tworzymy układ 3 równań dla m, kg, s

2

1

2

- =

�

� =

�

�- =

�

Rozwiązaniem układu równań jest

a

1

=

a

2

=

a

3

=

Czyli funkcja wymiarowa ma postać

sl

sl

p

l

p

l

D

=

D

=

Twierdzenie Buckinghama (twierdzenie

Twierdzenie Buckinghama (twierdzenie





)

)

1

2

2

3

( , ,

, ,

)

m

r

Z

Y Y

Y A A

A

=F

K

K

Dana jest funkcja wymiarowa

Y

1

,Y

2

, …, Y

m

– elementy wymiarowo niezależne

Z, A

2

, A

3

, …., A

r

– elementy wymiarowo zależne.

Dla funkcji wymiarowo niezmienniczej i
jednorodnej argumenty zależne wyrażają się
wzorem

1

2,3, ,

ji

m

a

j

j

i

i

A

Y

j

r

p

=

=

=

�

K

1

1

1

i

m

a

i

i

Z

Y

p

=

=

�

to funkcja Φ ma postać

1

1,2,3, ,

ji

j

j

m

a

i

i

A

j

r

Y

p

=

=

=

�

K

1

p =

j

p

- bezwymiarowe

1

1

1

i

m

a

i

i

Z

Y

p

=

=

�

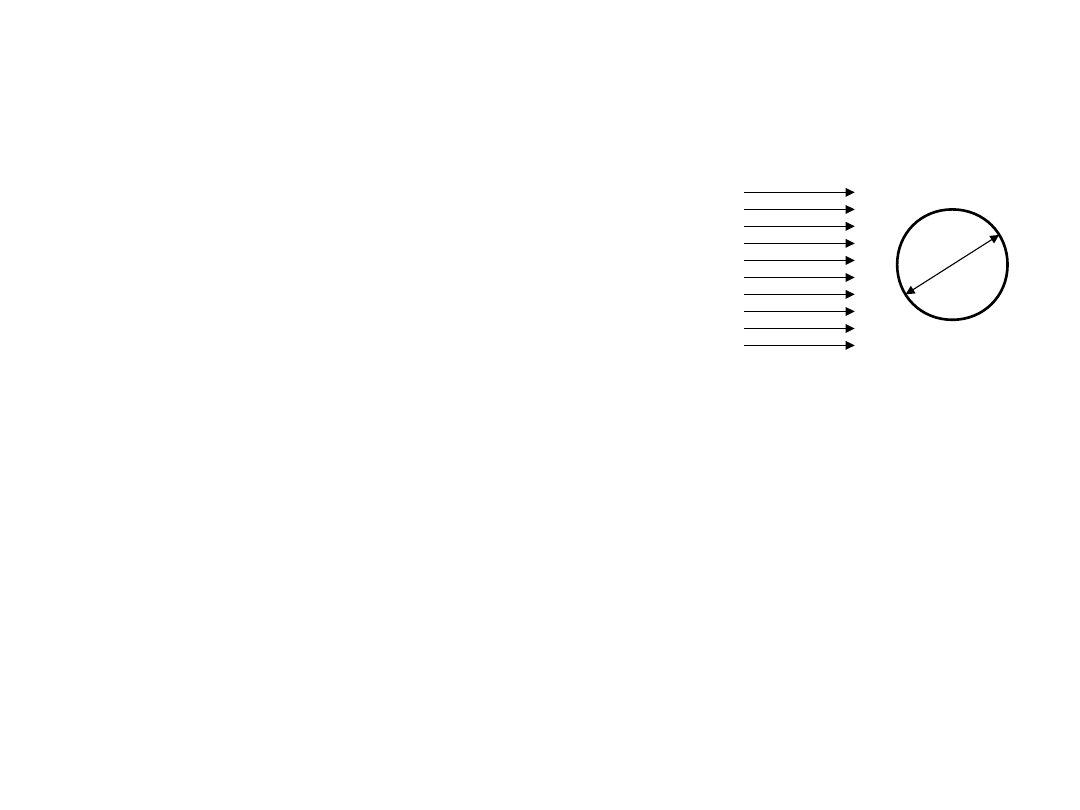
Przykład 1:

Kula o średnicy d opływana jest przez płyn o gęstości ρ i
kinematycznym współczynniku lepkości μ z prędkością u. Wyznaczyć
równanie na silę oporu kuli F.

F - siła oporu kuli, N=m kg/s

2

d - średnica kuli, m

u - prędkość przepływu płynu, m/s

ρ – gęstość płynu, kg/m

3

μ – dynamiczny współczynnik lepkości płynu, Pa s=(kg/ms)

Sprawdzamy czy zestaw ρ, u, d tworzy bazę?

m k

g

s

ρ

u
d

u

Zestaw ρ, u, d tworzy bazę.

d

1

F

p =

�

=

(

)

(

) (

) (

)

11

12

13

1

a

a

a

mkg s

mkg s

mkg s

mkg s

p

=

1
1

2

=

�

� =

�

�- =

�

2

p

m

=

�

=

(

)

(

) (

) (

)

21

22

23

2

a

a

a

mkg s

mkg s

mkg s

mkg s

p

=

1

1

1

- =

�

� =

�

�- =

�

( )

1

2

f

p

p

=

2 2

F

f

u d

u d

m

r

r

�

�

= �

�

�

�

F =

ponieważ

Re=

2

2

1

4

4

2

d

A

A

A

d

C

p

p

=

�

=

=

stąd

F =

F =

Przykład 2:

p/l - spadek ciśnienia na jednostkę długości, Pa/m=kg/(m

2

s

2

)

d - średnica przewodu, m

v – średnia prędkość przepływu płynu, m/s

ρ – gęstość płynu, kg/m

3

μ – dynamiczny współczynnik lepkości płynu, Pa s=(kg/ms)

k – chropowatość bezwględna, m

Sprawdzamy czy zestaw ρ, v, d tworzy bazę?

m k

g

s

ρ

u
d

Zestaw ρ, v, d tworzy bazę.

11

12

13

1

1

11

12

13

/

a

a

a

a

a

a

p l

p

v d

v d

l

p

p r

r

=

�

=

V

V

(

)

(

) (

) (

)

11

12

13

2

1

2

3

1 0

1

0

1

1

0 0

1

a

a

a

m kg s

m kg s

mkg s

mkg s

p

-

-

-

-

=

11

12

13

11

12

2

3

1

2

a

a

a

a

a

- =-

+

+

�

� =

�

�- =

-

�

1

p =

21

22

23

2

2

21

22

23

a

a

a

a

a

a

v d

v d

m

p

m p r

r

=

�

=

(

)

(

) (

) (

)

21

22

23

1

1

1

3

1 0

1

0

1

1

0 0

2

a

a

a

m kg s

m kg s

mkg s

mkg s

p

-

-

-

-

=

21

22

23

21

22

1

3

1

1

a

a

a

a

a

- =-

+

+

�

� =

�

�- =

-

�

2

p =

31

32

33

3

3

31

32

33

a

a

a

a

a

a

k

k

v d

v d

p

p r

r

=

�

=

(

)

(

) (

) (

)

31

32

33

1

0 0

3

1 0

1

0

1

1

0 0

3

a

a

a

mkg s

m kg s

mkg s

mkg s

p

-

-

=

31

32

33

31

32

1

3

0
0

a

a

a

a

a

=-

+

+

�

� =

�

� =

-

�

3

p =

1

p =

2

p d

l

u

r

=

V

p=

V

p

h

g

r

=

=

V

V

h=

V

ostatecznie

PODOBIEŃSTWO MODELOWE

PODOBIEŃSTWO MODELOWE

Najczęściej występujące siły oddziaływujące w
przepływie płynu

•siły grawitacji,
•siły ciśnieniowe,
•siły lepkości,
•siły napięcia powierzchniowego,
•siły bezwładności,
•siły sprężystości.

1. Liczba Reynoldsa

Jeśli ściśliwość płynu może zostać pominięta i nie
występuje w przepływie powierzchnia swobodna
(np. przepływ w rurze, samolot w powietrzu,
zanurzona łódź podwodna) to pod uwagę można
brać tylko siły lepkości i bezwładności.

Wybrane liczby podobieństwa dotyczące

Wybrane liczby podobieństwa dotyczące

przepływu płynu

przepływu płynu

Liczba Reynoldsa stosowana jest jako podstawowe
kryterium stateczności ruchu płynów (przepływ
laminarny, turbulentny).

2. Liczba Froude’a

Jeśli o przepływie decyduje siła grawitacji.

3. Liczba Webbera

Liczbę Webera wykorzystuje przy przepływach
wielofazowych (co najmniej dwufazowymi, gdy
jeden płyn graniczy z innym płynem), szczególnie
gdy powierzchnia rozdziału faz jest silnie
zakrzywiona (np. kropla płynu, poruszająca się w
innym płynie).

4. Liczba Macha

Jeśli płyn płynie z dużą prędkością lub ciało stałe
porusza się z dużą prędkością w płynie
pozostającym w spoczynku dominująca jest
ściśliwość płynu.
Liczba Macha przedstawia stosunek prędkości
przepływu płynu w danym miejscu do prędkości
dźwięku w tym płynie w tym samym miejscu
Lub stosunek prędkości obiektu poruszającego się
w płynie do prędkości dźwięku w tym płynie
niezakłóconym ruchem obiektu, czyli formalnie –
w nieskończoności.

Przepływ jest

•nieściśliwy (wpływ ściśliwości można pominąć) :
Ma << 1

•poddźwiękowy: Ma < 1

•dźwiękowy: Ma = 1

•okołodźwiękowy: 0,8 < Ma < 1,2

•naddźwiękowy: Ma > 1

•hiperdźwiękowy: Ma >> 1