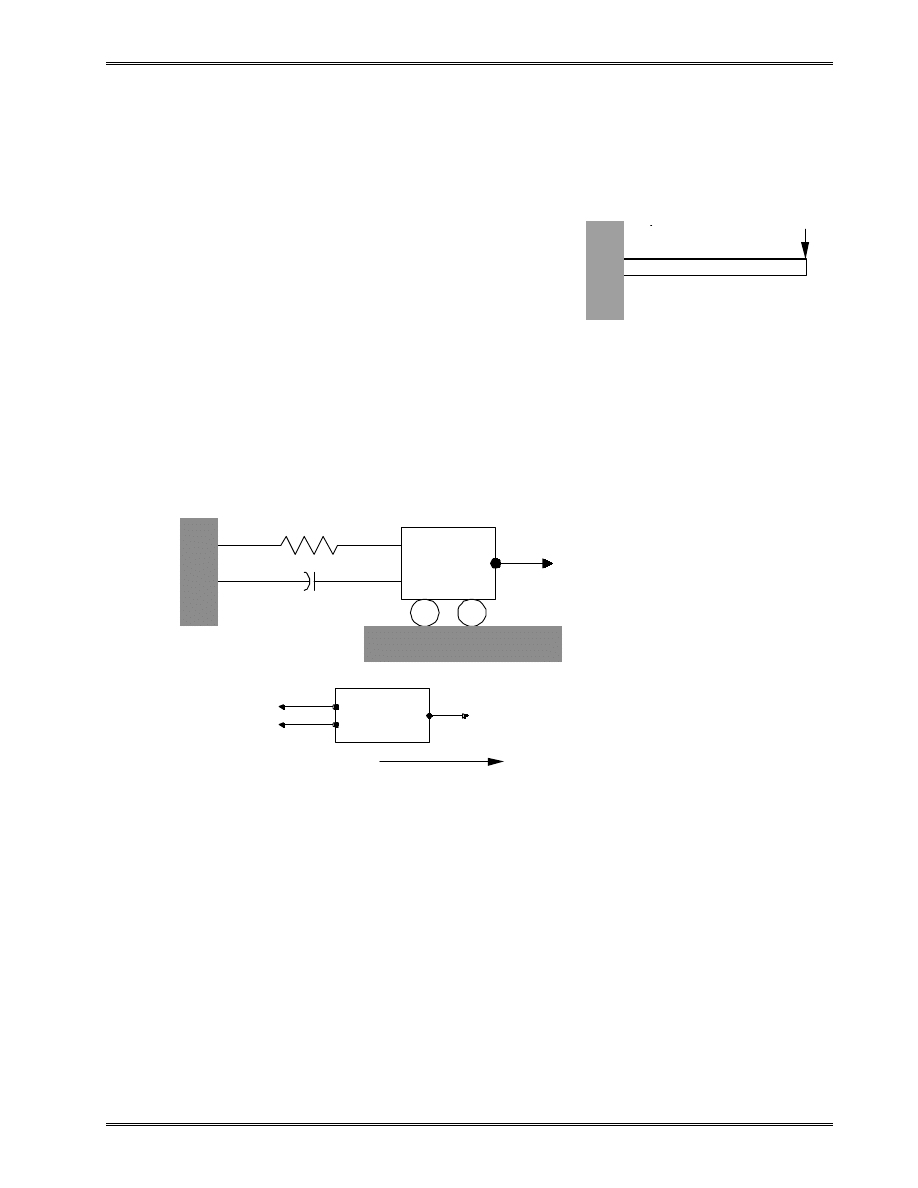
Lecture Notes: Introduction to Finite Element Method Chapter 7. Structural Vibration and Dynamics
© 1999 Yijun Liu, University of Cincinnati
157
Chapter 7. Structural Vibration and Dynamics
•
Natural frequencies and modes
•
Frequency response (F(t)=F
o
sin
ωt)
•
Transient response (F(t) arbitrary)
I. Basic Equations
A. Single DOF System
From Newton’s law of motion (ma = F), we have
u
c
u
k
f(t)
u
m
&
&&
−
−
=
,
i.e.
f(t)
u
k
u
c
u
m
=
+
+
&
&&
, (1)
where u is the displacement,
dt
du
u
/
=
&
and
.
/
2
2
dt
u
d
u
=
&
&
F(t)
m
m
f=f(t)
k
c
f(t)
u
c
ku
&
force
-
)
(
damping
-
stiffness
-
mass
-
t
f
c
k
m
x, u
Lecture Notes: Introduction to Finite Element Method Chapter 7. Structural Vibration and Dynamics
© 1999 Yijun Liu, University of Cincinnati
158
Free Vibration:
f(t) = 0 and no damping (c = 0)
Eq. (1) becomes
0
=
+
u
k
u
m &
&
.
(2)
(meaning: inertia force + stiffness force = 0)
Assume:
t)
(
U
u(t)
ω
sin
=
,
where
ω
is the frequency of oscillation, U the amplitude.
Eq. (2) yields
0
sin
sin
2
=
+
−
t)
ù
(
U
k
t)
ù
(
m
ù
U
i.e.,
[
]
0
2
=
+
−
U
k
m
ω
.
For nontrivial solutions for U, we must have
[
]
0
2
=
+
−
k
m
ω
,
which yields
m
k
=
ω
.
(3)
This is the circular natural frequency of the single DOF
system (rad/s). The cyclic frequency (1/s = Hz) is
π
ω
2
=
f
,
(4)
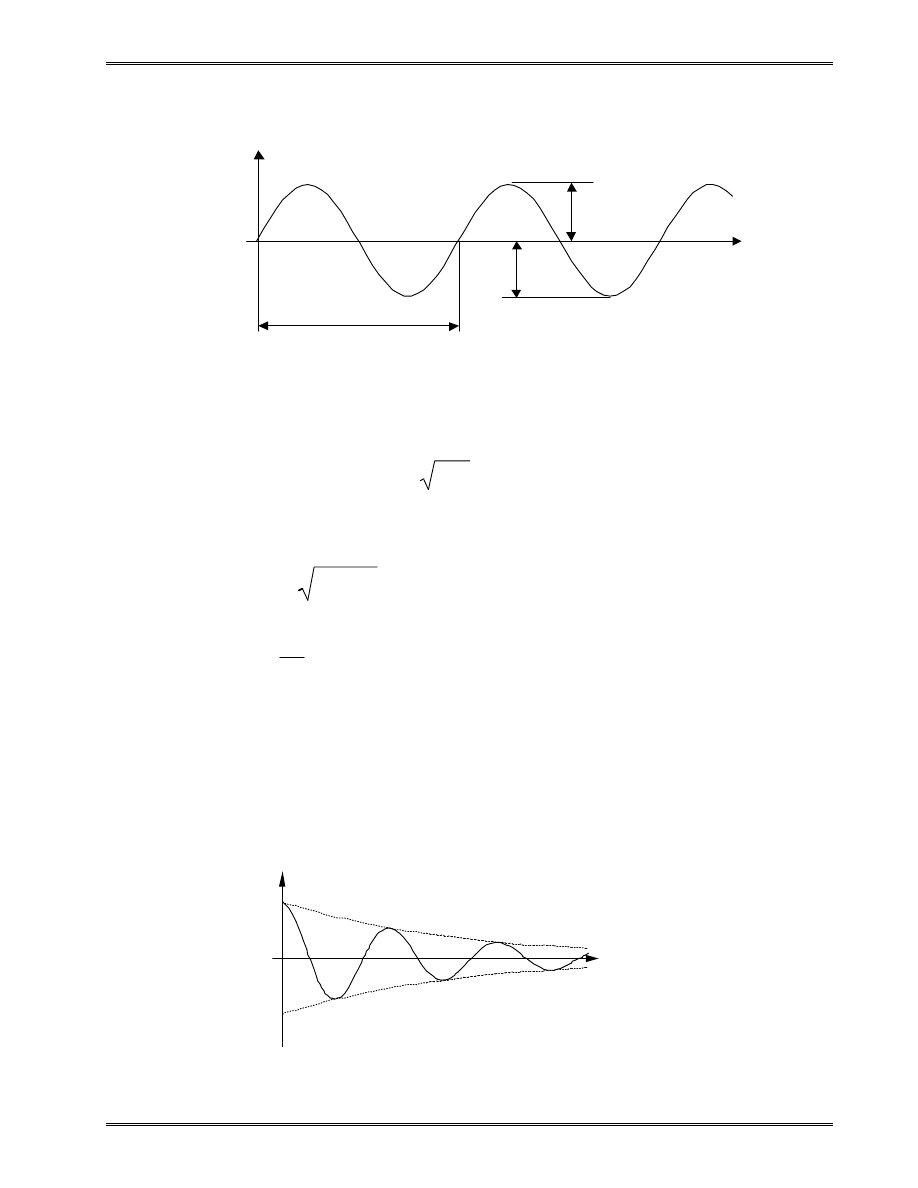
Lecture Notes: Introduction to Finite Element Method Chapter 7. Structural Vibration and Dynamics
© 1999 Yijun Liu, University of Cincinnati
159
With non-zero damping c, where
m
k
m
c
c
c
2
2
0
=
=
<
<
ω
(c
c
= critical damping) (5)
we have the damped natural frequency:
2
1
ξ
ω
ω
−
=
d
,
(6)
where
c
c
c
=
ξ
(damping ratio).
For structural damping:
15
.
0
0
<
≤
ξ
(usually 1~5%)
ω
ω
≈
d
.
(7)
Thus, we can ignore damping in normal mode analysis.
u
t
U
U
T = 1 / f
U n d a m p e d F r e e V i b r a t i o n
u = U s i n w t
u
t
Damped Free Vibration
Lecture Notes: Introduction to Finite Element Method Chapter 7. Structural Vibration and Dynamics
© 1999 Yijun Liu, University of Cincinnati
160
B. Multiple DOF System
Equation of Motion
Equation of motion for the whole structure is
)
(t
f
Ku
u
C
u
M
=
+
+
&
&
&
,
(8)
in which:
u
nodal displacement vector,
M
mass matrix,
C
damping matrix,
K
stiffness matrix,
f
forcing vector.
Physical meaning of Eq. (8):
Inertia forces + Damping forces + Elastic forces
= Applied forces
Mass Matrices
Lumped mass matrix (1-D bar element):
1
ρ,A,L 2
u
1
u
2
Element mass matrix is found to be
4
4 3
4
4 2
1
matrix
diagonal
2
0
0
2
=
AL
AL
ρ
ρ
m
2
1
AL
m
ρ
=
2
2
AL
m
ρ
=
Lecture Notes: Introduction to Finite Element Method Chapter 7. Structural Vibration and Dynamics
© 1999 Yijun Liu, University of Cincinnati
161
In general, we have the consistent mass matrix given by
dV
V
T
∫
=
N
N
m
ρ
(9)
where N is the same shape function matrix as used for the
displacement field.
This is obtained by considering the kinetic energy:
( )
( ) ( )
u
N
N
u
u
N
u
N
u
m
u
m
&
43
42
1
&
&
&
&
&
&
&
&
∫
∫
∫
∫
=
=
=
=
=
Κ
V
T
T
V
T
V
T
V
T
dV
dV
dV
u
u
dV
u
mv
ρ
ρ
ρ
ρ
2
1
2
1
2
1
2
1
)
2
1
(cf.
2
1
2
2
Bar Element (linear shape function):
[
]
3
/
1
6
/
1
6
/
1
3
/
1
1
1
2
1
u
u
AL
ALd
V
&
&
&
&
=
−
−
=
∫
ρ
ξ
ξ
ξ
ξ
ξ
ρ
m
(10)
Lecture Notes: Introduction to Finite Element Method Chapter 7. Structural Vibration and Dynamics
© 1999 Yijun Liu, University of Cincinnati
162
Element mass matrices:
⇒
local coordinates
⇒
to global coordinates
⇒
assembly of the global structure mass matrix M.
Simple Beam Element:
4
22
3
13
22
156
13
54
3
13
4
22
13
54
22
156
420
2
2
1
1
2
2
2
2
θ
θ
ρ
ρ
&
&
&
&
&
&
&
&
v
v
L
L
L
L
L
L
L
L
L
L
L
L
AL
dV
T
−
−
−
−
−
−
=
=
∫
V
N
N
m
(11)
Units in dynamic analysis (make sure they are consistent):
Choice I
Choice II
t (time)
L (length)
m (mass)
a (accel.)
f (force)
ρ (density)
s
m
kg
m/s
2
N
kg/m
3
s
mm
Mg
mm/s
2
N
Mg/mm
3
1
1
θ
v
2
2
θ
v
ρ, A, L