Podstawy programowania

wykład 12

Dr inż. Jakub Bauman

[e-mail]

Rekurencja

Dr inż. Jakub Bauman

[e-mail]

Rekurencja

Często stajemy przed problemem, który
łatwo byłoby rozwiązać, gdybyśmy
mieli w ręku odpowiedź dla mniejszych
danych.

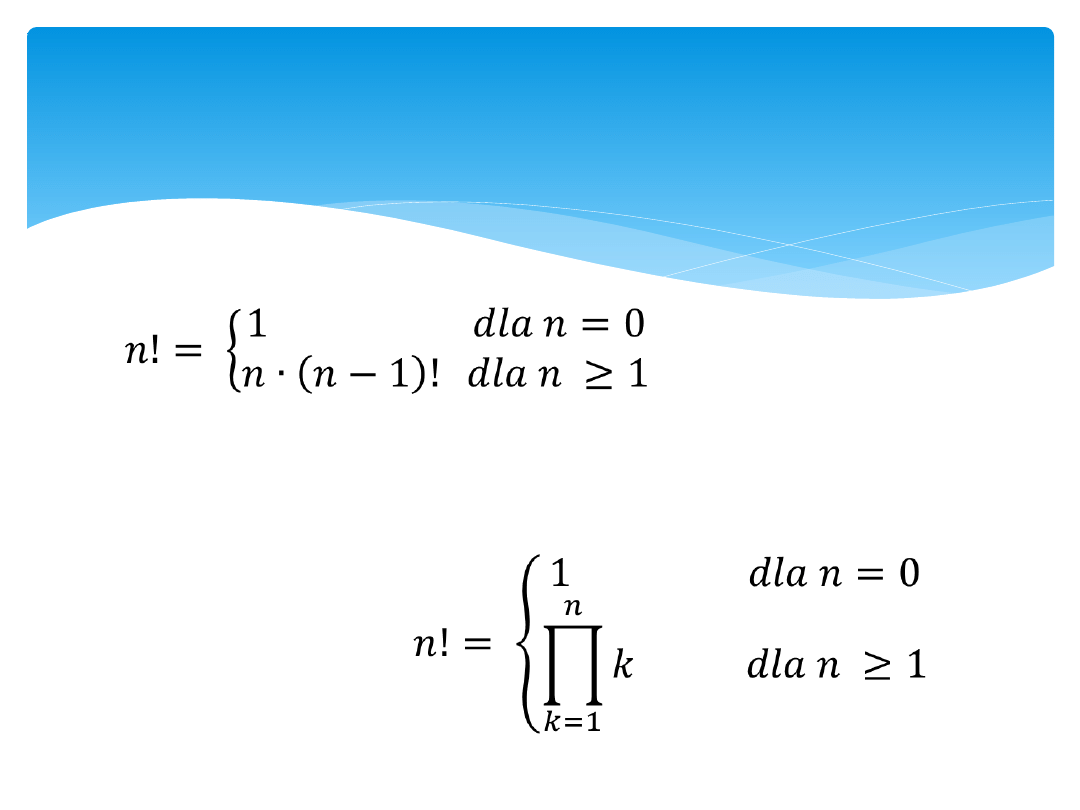
Silnia

Definicja rekurencyjna

definicja nierekurencyjna

int silnia(int n){
if (n==0){

return 1;

}
else {

return n*

silnia(n-1)

;

}
}

Silnia – funkcja rekurencyjna

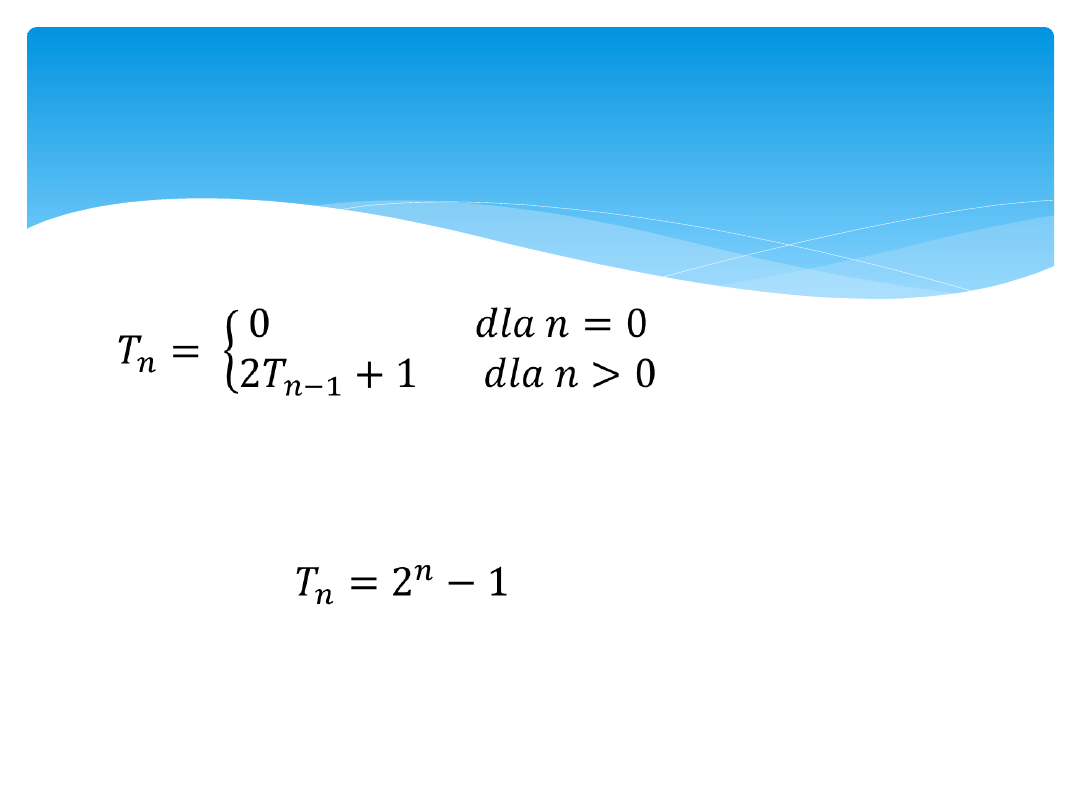
Postać rekurencyjna

i nierekurencyjna

Ciąg T0, T1…

Za pomocą indukcji matematycznej możemy
udowodnić że:



Istnieją problemy, dla których nie znamy postaci
nierekurencyjnej



lub nie możemy w prosty sposób jej zastosować

Problemy

Ciąg Fibonacciego

Definicja rekurencyjna

Wzór Bineta

int Fibo(int n) {
if (n <= 1) {
Fibo = n;
}
else {
Fibo =

Fibo(n-2)

+

Fibo(n-1)

;

}
}

Fibo – algorytm rekurencyjny



Fibo(4) = Fibo(2) + Fibo(3)



Program obliczy: Fibo(2)



I będzie obliczał Fibo(3) = Fibo(1) + Fibo(2)



Ponieważ wartość Fibo(2) nie jest znana musi obliczyć
ją obliczyć jeszcze raz

Problem



Problem wielokrotnego obliczania tych samych liczb
należy zastosować tablicę zapamiętującą obliczone
już wartości



Przykład oprogramowania takiej funkcji

Problem

Wieże Hanoi

Pytania

Dyskusja

Dziękuję za uwagę!

Dr inż. Jakub Bauman

[e-mail]