Bayesian

Bayesian

Option

Option

pricing

pricing

model

model

using

using

asymmetric

asymmetric

GARCH

GARCH

models

models

Luc

Luc

Bauwens

Bauwens

, Michel

, Michel

Lubrano

Lubrano

Bartosz Anacki

Bartosz Anacki

Anna

Anna

Ś

Ś

leszy

leszy

ń

ń

ska

ska

Jest to pierwszy artyku

Jest to pierwszy artyku

ł

ł

, w kt

, w kt

ó

ó

rym zastosowano

rym zastosowano

wnioskowanie

wnioskowanie

Bayesowskie

Bayesowskie

do zagadnienia

do zagadnienia

wyceny instrument

wyceny instrument

ó

ó

w pochodnych

w pochodnych

Por

Por

ó

ó

wnano wycen

wnano wycen

ę

ę

opcji z wykorzystaniem

opcji z wykorzystaniem

wnioskowania

wnioskowania

Bayesowskiego

Bayesowskiego

z wycen

z wycen

ą

ą

przy

przy

u

u

ż

ż

yciu modelu

yciu modelu

Blacka

Blacka

-

-

Scholesa

Scholesa

z

z

wykorzystaniem modeli GARCH.

wykorzystaniem modeli GARCH.

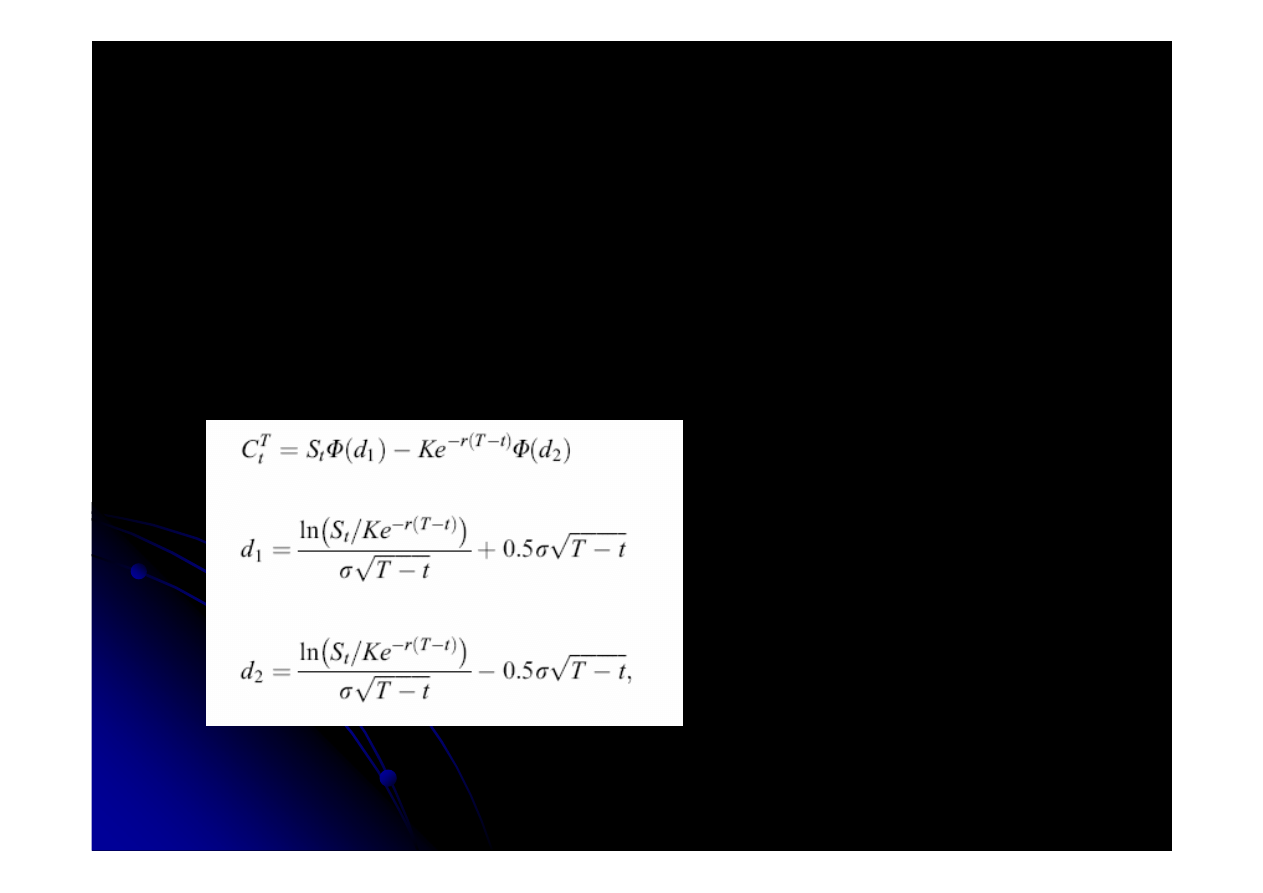
Model

Model

Blacka

Blacka

-

-

Scholesa

Scholesa

Wyp

Wyp

ł

ł

ata z europejskiej opcji kupna wynosi:

ata z europejskiej opcji kupna wynosi:

P

P

T

T

=max(S

=max(S

T

T

-

-

K,0)

K,0)

Formu

Formu

ł

ł

a

a

Blacka

Blacka

-

-

Scholesa

Scholesa

do wyceny opcji:

do wyceny opcji:

Model

Model

Blacka

Blacka

-

-

Scholesa

Scholesa

Je

Je

ś

ś

li znajdziemy neutraln

li znajdziemy neutraln

ą

ą

wzgl

wzgl

ę

ę

dem na ryzyka miar

dem na ryzyka miar

ę

ę

martynga

martynga

ł

ł

ow

ow

ą

ą

Q, to zdyskontowana warto

Q, to zdyskontowana warto

ść

ść

oczekiwana

oczekiwana

wzgl

wzgl

ę

ę

dem miary Q przysz

dem miary Q przysz

ł

ł

ej wyp

ej wyp

ł

ł

aty jest warto

aty jest warto

ś

ś

ci

ci

ą

ą

opcji.

opcji.

Gdzie E[(S

Gdzie E[(S

t

t

-

-

S

S

t

t

-

-

1

1

)/S

)/S

t

t

-

-

1

1

]=r dla ka

]=r dla ka

ż

ż

dego t

dego t

Standardowy model GARCH

Standardowy model GARCH

Podstawowy model GARCH(1,1):

Podstawowy model GARCH(1,1):

jest warunkow

jest warunkow

ą

ą

warto

warto

ś

ś

ci

ci

ą

ą

oczekiwan

oczekiwan

ą

ą

stopy

stopy

zwrotu

zwrotu

jest now

jest now

ą

ą

informacj

informacj

ą

ą

pojawiaj

pojawiaj

ą

ą

c

c

ą

ą

si

si

ę

ę

w

w

momencie t

momencie t

-

-

parametry modelu >=0

parametry modelu >=0

Symetryczny model GARCH zak

Symetryczny model GARCH zak

ł

ł

ada,

ada,

ż

ż

e reakcja

e reakcja

warunkowej zmienno

warunkowej zmienno

ś

ś

ci na pozytywne i negatywne

ci na pozytywne i negatywne

zmiany na rynku jest taka sama.

zmiany na rynku jest taka sama.

Wycena

Wycena

Przewidywana

Przewidywana

g

g

ę

ę

sto

sto

ś

ś

c

c

P

P

T

T

wzgl

wzgl

ę

ę

dem miary Q:

dem miary Q:

Gdzie:

Gdzie:

jest g

jest g

ę

ę

sto

sto

ś

ś

ci

ci

ą

ą

aposteriori parametr

aposteriori parametr

ó

ó

w z modelu:

w z modelu:

jest g

jest g

ę

ę

sto

sto

ś

ś

ci

ci

ą

ą

przysz

przysz

ł

ł

ych wyp

ych wyp

ł

ł

at

at

y to stopy zwrotu u

y to stopy zwrotu u

ż

ż

yte do estymacji

yte do estymacji

Wyznaczona przewidywana g

Wyznaczona przewidywana g

ę

ę

sto

sto

ść

ść

da nam

da nam

wszystkie informacje, kt

wszystkie informacje, kt

ó

ó

rych potrzebujemy do

rych potrzebujemy do

wyznaczenia oczekiwanej ceny opcji, kt

wyznaczenia oczekiwanej ceny opcji, kt

ó

ó

ra wynosi

ra wynosi

E[P

E[P

T

T

(1+r)

(1+r)

-

-

(T

(T

-

-

t)

t)

]

]

Wyznaczanie warunkowego rozk

Wyznaczanie warunkowego rozk

ł

ł

adu

adu

T=t+1, czyli chcemy wyznaczy

T=t+1, czyli chcemy wyznaczy

ć

ć

przewidywan

przewidywan

ą

ą

cen

cen

ę

ę

tylko o jeden okres do przodu (ns=1), warunkowa

tylko o jeden okres do przodu (ns=1), warunkowa

g

g

ę

ę

sto

sto

ść

ść

jest g

jest g

ę

ę

sto

sto

ś

ś

ci

ci

ą

ą

rozk

rozk

ł

ł

adu normalnego:

adu normalnego:

Wszystkie parametry rozk

Wszystkie parametry rozk

ł

ł

adu warunkowego s

adu warunkowego s

ą

ą

znane, gdy

znane, gdy

ż

ż

y

y

T

T

i

i

h

h

T

T

s

s

ą

ą

ju

ju

ż

ż

zaobserwowane lub

zaobserwowane lub

wyznaczone

wyznaczone

Gdy ns>1 g

Gdy ns>1 g

ę

ę

sto

sto

ść

ść

otrzymujemy wyznaczaj

otrzymujemy wyznaczaj

ą

ą

c ca

c ca

ł

ł

k

k

ę

ę

:

:

Nie znamy bowiem nie tylko parametru, ale r

Nie znamy bowiem nie tylko parametru, ale r

ó

ó

wnie

wnie

ż

ż

y

y

t+1

t+1

…

…

y

y

T

T

-

-

1

1

s

s

ą

ą

one bowiem jeszcze nie

one bowiem jeszcze nie

zaobserwowane (

zaobserwowane (

Bauwens

Bauwens

1999 rozdzia

1999 rozdzia

ł

ł

7)

7)

Wyznaczanie ceny opcji

Wyznaczanie ceny opcji

Wyznaczamy N pr

Wyznaczamy N pr

ó

ó

bek (y

bek (y

t+1,

t+1,

y

y

t+2,

t+2,

…

…

,

,

y

y

T

T

)

)

a

a

nast

nast

ę

ę

pnie S

pnie S

T

T

i P

i P

T

T

:

:

Znaj

Znaj

ą

ą

c S

c S

T

T

i P

i P

T

T

wyznaczamy cen

wyznaczamy cen

ę

ę

opcji:

opcji:

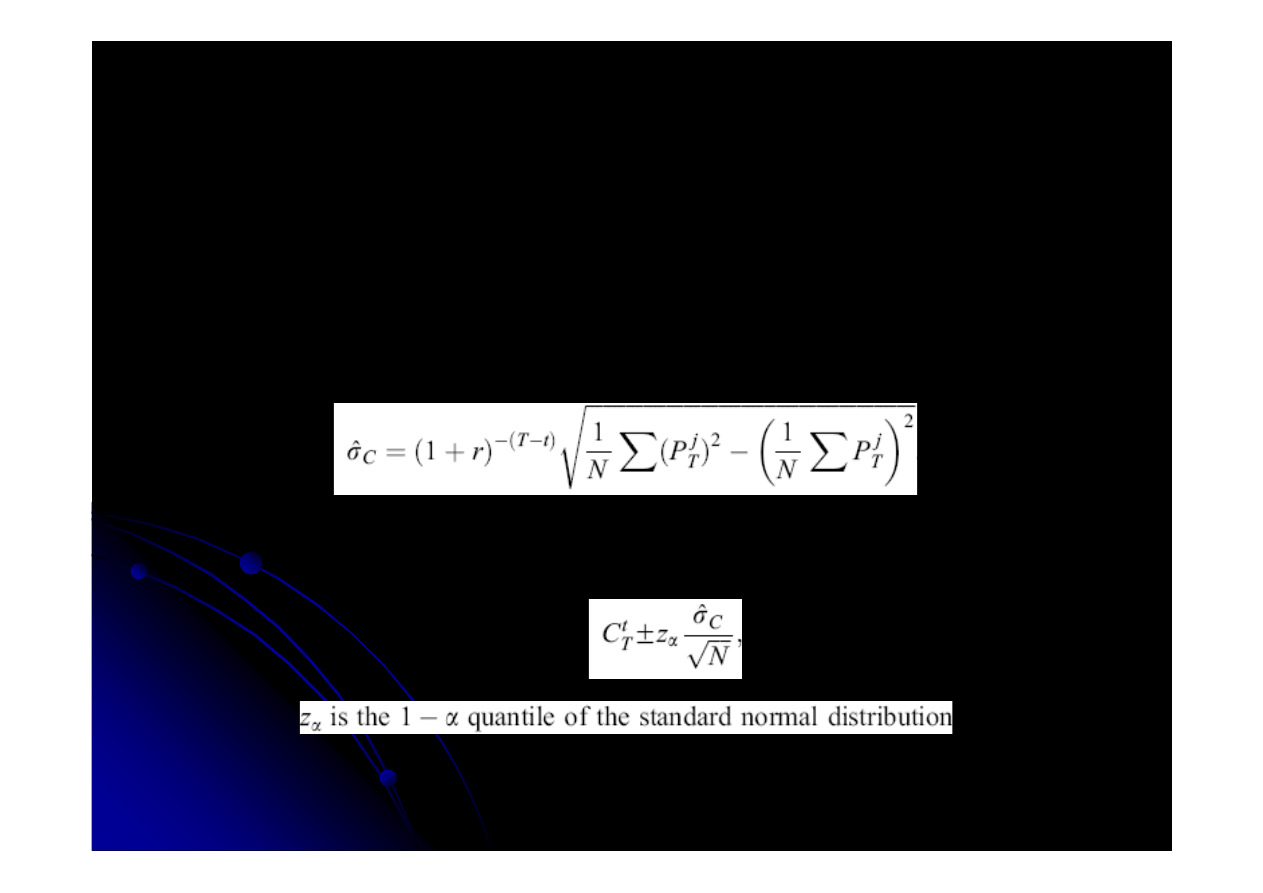
Weryfikacja

Weryfikacja

Aby sprawdzi

Aby sprawdzi

ć

ć

precyzj

precyzj

ę

ę

szacowania

szacowania

wyznaczamy empiryczne odchylenie

wyznaczamy empiryczne odchylenie

standardowe

standardowe

C

C

t

t

T

T

:

:

Gdy N jest du

Gdy N jest du

ż

ż

e, a pr

e, a pr

ó

ó

bki s

bki s

ą

ą

niezale

niezale

ż

ż

ne,

ne,

b

b

łą

łą

d ma asymptotycznie rozk

d ma asymptotycznie rozk

ł

ł

ad normalny,

ad normalny,

Przedzia

Przedzia

ł

ł

ufno

ufno

ś

ś

ci:

ci:

Gdzie

Gdzie

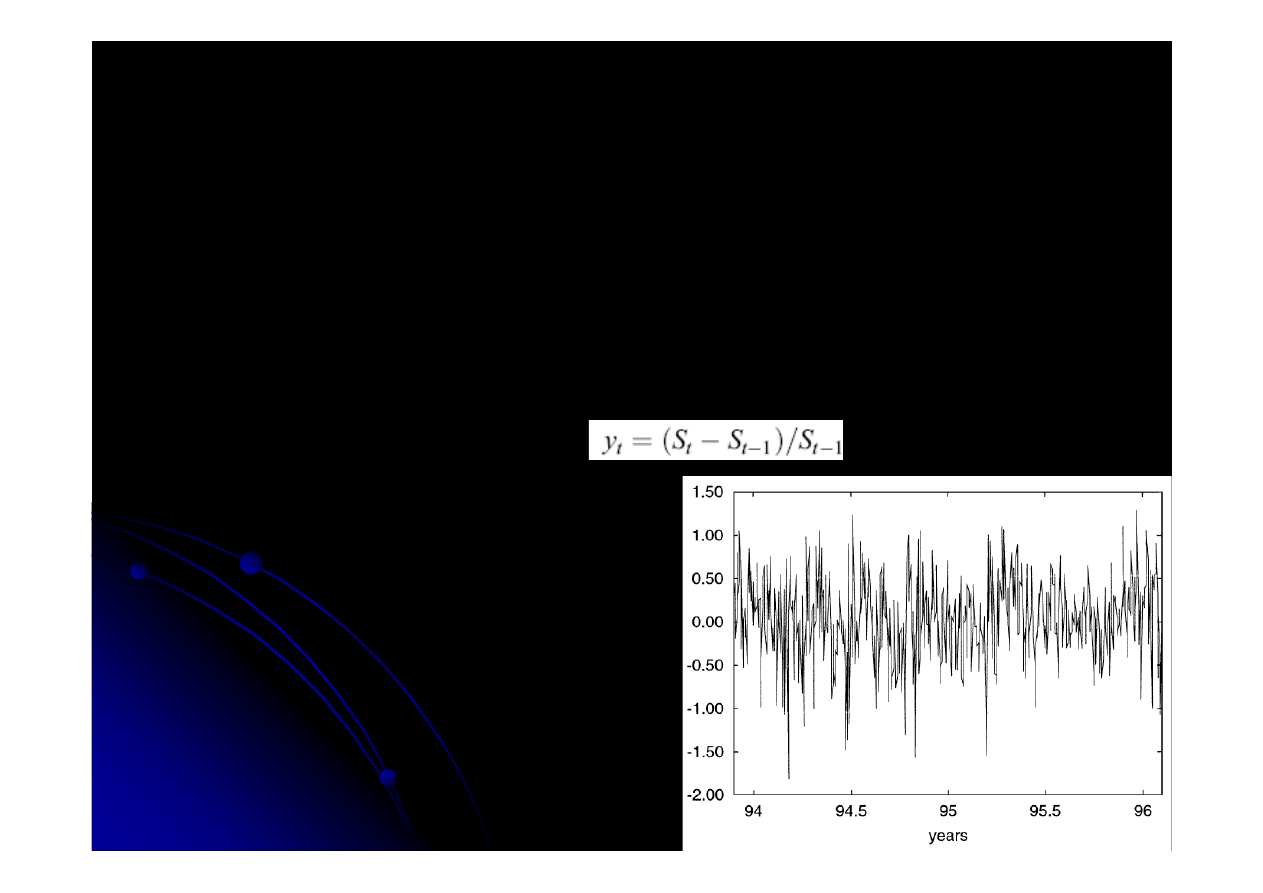
Estymacja modeli GARCH

Estymacja modeli GARCH

Dzienne stopy zwrotu (na podstawie cen

Dzienne stopy zwrotu (na podstawie cen

zamkni

zamkni

ę

ę

cia) dla

cia) dla

Brussels

Brussels

spot market

spot market

index

index

z okresu 23.11.1993

z okresu 23.11.1993

–

–

30.01.1996,

30.01.1996,

w sumie 550 obserwacji.

w sumie 550 obserwacji.

Zmienna zale

Zmienna zale

ż

ż

na: razy 100

na: razy 100

Wykres st

Wykres st

ó

ó

p zwrotu

p zwrotu

Estymacja modeli GARCH

Estymacja modeli GARCH

Og

Og

ó

ó

lna forma estymowanych modeli GARCH:

lna forma estymowanych modeli GARCH:

Dla GARCH

Dla GARCH

Dla GJR

Dla GJR

-

-

GARCH

GARCH

Dla STR

Dla STR

-

-

GARCH

GARCH

Estymacja modeli GARCH

Estymacja modeli GARCH

Podej

Podej

ś

ś

cie

cie

Bayesowskie

Bayesowskie

:

:

O parametrach modelu

O parametrach modelu

μ

μ

,

,

ρ

ρ

,

,

ω

ω

,

,

β

β

,

,

α

α

zak

zak

ł

ł

adamy,

adamy,

ż

ż

e maj

e maj

ą

ą

rozk

rozk

ł

ł

ady a priori jednostajne na sko

ady a priori jednostajne na sko

ń

ń

czonym przedziale.

czonym przedziale.

Dla STR

Dla STR

-

-

GARCH zak

GARCH zak

ł

ł

adamy,

adamy,

ż

ż

e

e

γ

γ

ma rozk

ma rozk

ł

ł

ad a priori:

ad a priori:

Podej

Podej

ś

ś

cie

cie

klayczne

klayczne

:

:

Parametry modelu dobieramy tak,

Parametry modelu dobieramy tak,

ż

ż

eby maksymalizowa

eby maksymalizowa

ł

ł

y

y

funkcj

funkcj

ę

ę

wiarygodno

wiarygodno

ś

ś

ci.

ci.

Wyniki estymacji

Wyniki estymacji

Analiza wynik

Analiza wynik

ó

ó

w

w

Negatywne zmiany maj

Negatywne zmiany maj

ą

ą

wi

wi

ę

ę

kszy wp

kszy wp

ł

ł

yw na warunkow

yw na warunkow

ą

ą

wariancj

wariancj

ę

ę

ni

ni

ż

ż

szoki pozytywne

szoki pozytywne

GJR:

GJR:

λ

λ

=

=

α

α

2

2

-

-

α

α

1

1

ma

ma

ś

ś

redni

redni

ą

ą

posteriori 0.09; odchylenie 0.066

posteriori 0.09; odchylenie 0.066

Prawdopodobie

Prawdopodobie

ń

ń

stwo posteriori

stwo posteriori

ż

ż

e

e

λ

λ

<0 jest ma

<0 jest ma

ł

ł

e (<6%)

e (<6%)

STR: prawdopodobie

STR: prawdopodobie

ń

ń

stwo

stwo

ż

ż

e

e

α

α

2

2

<0 jest zero

<0 jest zero

Estymatory klasyczne i

Estymatory klasyczne i

bayesowske

bayesowske

zbli

zbli

ż

ż

one dla

one dla

μ

μ

i

i

ρ

ρ

Du

Du

ż

ż

e r

e r

ó

ó

ż

ż

nice mi

nice mi

ę

ę

dzy estymatorami

dzy estymatorami

ω

ω

,

,

β

β

i

i

γ

γ

Bayesowskie

Bayesowskie

odchylenia standardowe s

odchylenia standardowe s

ą

ą

znacz

znacz

ą

ą

co

co

wy

wy

ż

ż

sze dla

sze dla

ω

ω

,

,

α

α

i

i

β

β

lepiej ukazuj

lepiej ukazuj

ą

ą

niepewno

niepewno

ść

ść

parametr

parametr

ó

ó

w nich odchylenia klasyczne

w nich odchylenia klasyczne

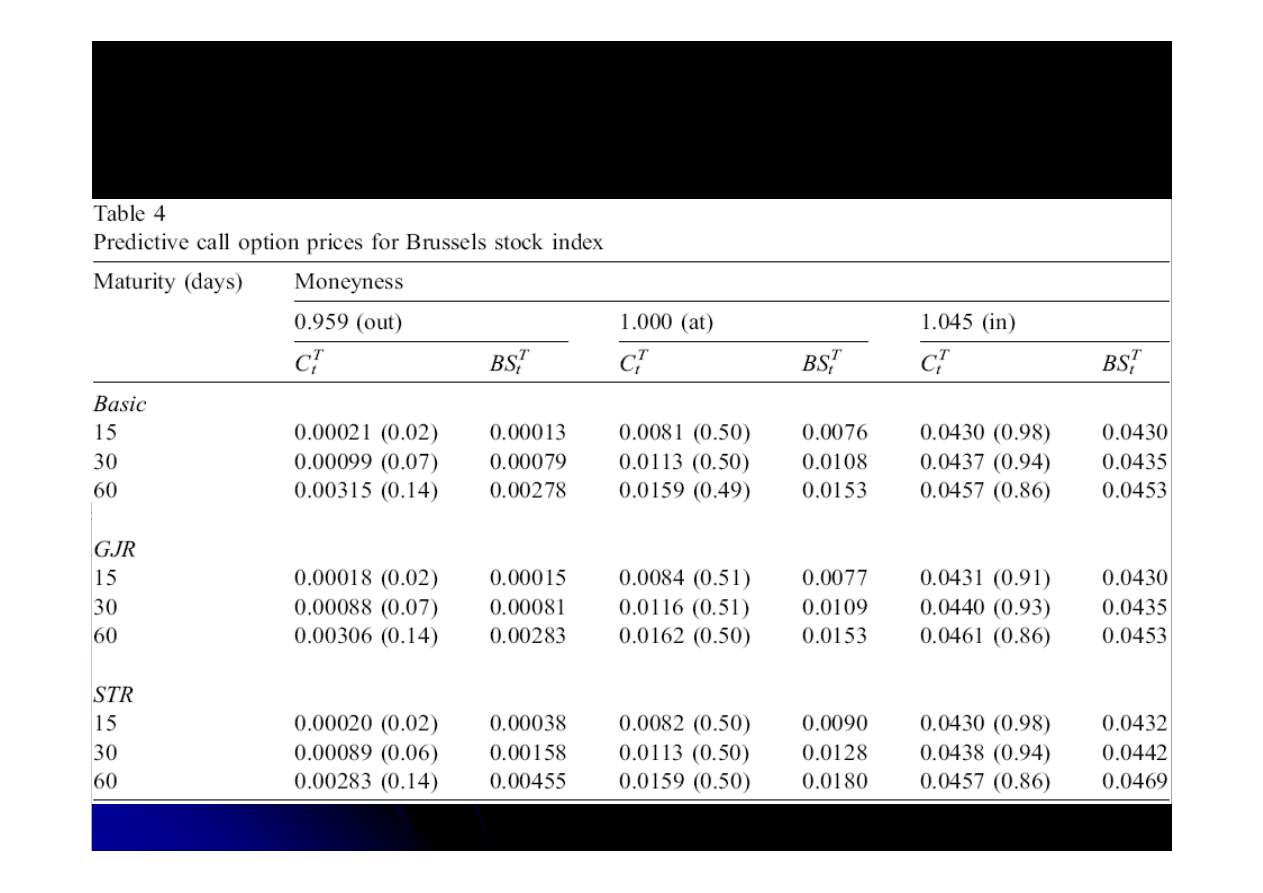
Przewidywanie ceny

Przewidywanie ceny

Estymacja klasyczna a

Estymacja klasyczna a

bayesowska

bayesowska

Wyniki estymacji klasycznej nie zosta

Wyniki estymacji klasycznej nie zosta

ł

ł

y

y

pokazane, s

pokazane, s

ą

ą

zbli

zbli

ż

ż

one do

one do

bayesowskich

bayesowskich

R

R

ó

ó

ż

ż

nice s

nice s

ą

ą

:

:

niewielkie dla

niewielkie dla

out

out

-

-

of

of

-

-

the

the

-

-

money

money

mniejsze dla

mniejsze dla

at

at

-

-

the

the

-

-

money

money

niezauwa

niezauwa

ż

ż

alne dla

alne dla

in

in

-

-

the

the

-

-

money

money

Estymacja

Estymacja

bayesowska

bayesowska

a BS

a BS

opcja

opcja

In

In

-

-

the

the

-

-

money

money

nie ma ekonomicznie znacz

nie ma ekonomicznie znacz

ą

ą

cych r

cych r

ó

ó

ż

ż

nic

nic

☺

☺

Estymacja

Estymacja

bayesowska

bayesowska

a BS

a BS

opcja

opcja

At

At

-

-

the

the

-

-

money

money

Pojawiaj

Pojawiaj

ą

ą

si

si

ę

ę

r

r

ó

ó

ż

ż

nice znacz

nice znacz

ą

ą

ce

ce

ponad 5% przy precyzji oblicze

ponad 5% przy precyzji oblicze

ń

ń

1%

1%

R

R

ó

ó

ż

ż

nice spadaj

nice spadaj

ą

ą

wraz z dojrzewaniem

wraz z dojrzewaniem

opcji

opcji

BS niedocenia opcji dla

BS niedocenia opcji dla

GARCH i GJR

GARCH i GJR

-

-

GARCH,

GARCH,

przecenia dla STR

przecenia dla STR

-

-

GARCH

GARCH

Estymacja

Estymacja

bayesowska

bayesowska

a BS

a BS

opcja

opcja

Out

Out

-

-

the

the

-

-

money

money

BS mocno niedocenia opcji o kr

BS mocno niedocenia opcji o kr

ó

ó

tkim

tkim

okresie trwania

okresie trwania

dla 15 dni 38% w modelu standardowym

dla 15 dni 38% w modelu standardowym

Niedocenianie spada wraz ze wzrostem

Niedocenianie spada wraz ze wzrostem

okresu trwania i gdy wykorzystujemy

okresu trwania i gdy wykorzystujemy

modle GJR

modle GJR

-

-

GARCH

GARCH

Przy STR BS silnie przecenia opcje

Przy STR BS silnie przecenia opcje

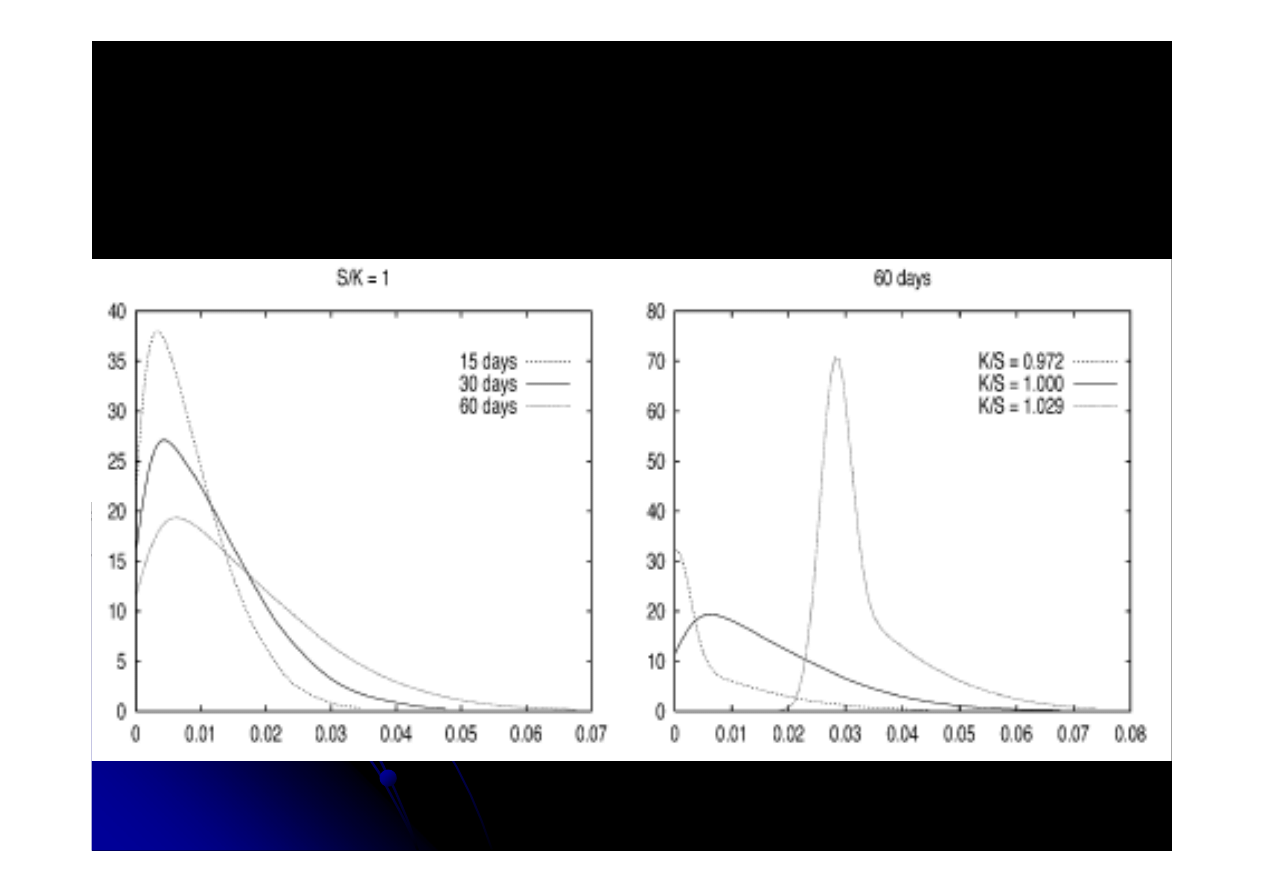
Warunkowy rozk

Warunkowy rozk

ł

ł

ad funkcji wyp

ad funkcji wyp

ł

ł

aty

aty

dla modelu GARCH

dla modelu GARCH

Warunkowy rozk

Warunkowy rozk

ł

ł

ad funkcji wyp

ad funkcji wyp

ł

ł

aty

aty

dla modelu GARCH

dla modelu GARCH

Wykres przedstawia

Wykres przedstawia

Wykres pierwszy

Wykres pierwszy

–

–

niepewno

niepewno

ść

ść

ro

ro

ś

ś

nie

nie

wraz z dojrza

wraz z dojrza

ł

ł

o

o

ś

ś

ci

ci

ą

ą

opcji

opcji

Wykres drugi

Wykres drugi

–

–

cena opcji jest bardzo

cena opcji jest bardzo

wra

wra

ż

ż

liwa na stosunek S

liwa na stosunek S

T

T

/K

/K

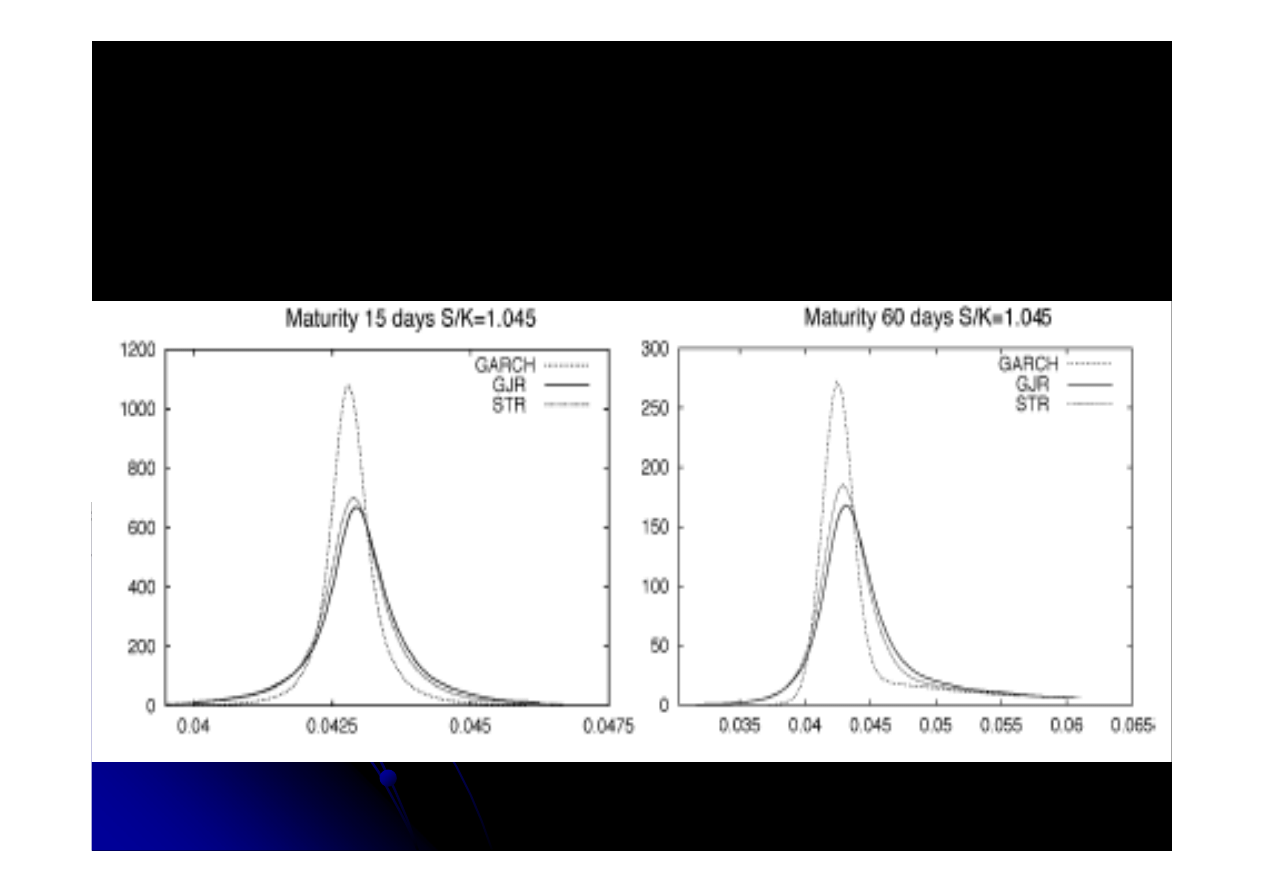
Warunkowy rozk

Warunkowy rozk

ł

ł

ad funkcji wyp

ad funkcji wyp

ł

ł

aty

aty

por

por

ó

ó

wnanie r

wnanie r

ó

ó

ż

ż

nych modeli

nych modeli

dla opcji

dla opcji

out

out

-

-

of

of

-

-

the

the

-

-

money

money

Warunkowy rozk

Warunkowy rozk

ł

ł

ad funkcji wyp

ad funkcji wyp

ł

ł

aty

aty

por

por

ó

ó

wnanie r

wnanie r

ó

ó

ż

ż

nych modeli

nych modeli

dla opcji

dla opcji

out

out

-

-

of

of

-

-

the

the

-

-

money

money

Dwa modele asymetryczne zachowuj

Dwa modele asymetryczne zachowuj

ą

ą

si

si

ę

ę

podobnie

podobnie

Model symetryczny daje bardzo wysok

Model symetryczny daje bardzo wysok

ą

ą

ś

ś

redni

redni

ą

ą

cen

cen

ę

ę

opcji

opcji

Efekt wyst

Efekt wyst

ę

ę

puje niezale

puje niezale

ż

ż

nie od dojrza

nie od dojrza

ł

ł

o

o

ś

ś

ci

ci

KONIEC

KONIEC

Dzi

Dzi

ę

ę

kujemy za uwag

kujemy za uwag

ę

ę

☺

☺