Modele Panelowe

The Predictive Value of Subjective

Labour Supply Data:

A Dynamic Panel Data Model with

Measurement Error

Rob Euwals

Dane panelowe

Dane panelowe- termin ten odnosi się do

zbioru obserwacji określonych jednostek
(tych samych) w kolejnych okresach czasu.

Przykłady

USA (dane zaczęto gromadzić w latach 60tych)
Š Panel Study of Income Dynamics (PSID)
Š National Longitudinal Surveys of Labor Market Experience (NLS)
Kanada
Š Survey of Labour Income Dynamics (SLID)
Europa (od lat 80-tych)
Š Niemiecki panel socjo-ekonomiczny (GSEOP)
Š Francuski panel gospodarstw domowych (1985-1990)
Š Węgierski panel gospodarstw domowych (1992-1996)
Š Brytyjski panel gospodarstw domowych (BHSP), od 1991
Š EuroStat -The European Community Household Pane (ECHP), od

1994

Zalety wykorzystywania
danych panelowych

Š Kontrola indywidualnej heterogeniczności

W przeciwieństwie do badań przekrojowych i szeregów czasowych
panele zakładają heterogeniczność indywidualnych gospodarstw
domowych czy firm.

Š Dane panelowe zawierają więcej informacji, więcej zmienności,

mniejsza korelacja miedzy zmiennymi, więcej stopni swobody,
większa efektywność

Š Lepsze do badania dynamiki dostosowań
Š Umożliwiają identyfikacje i zmierzenie efektów, których nie da się

zauważyć za pomocą szeregów czasowych czy badań przekrojowych

Š Pozwalają konstruować i testować bardziej złożone modele zachowań
Š Gromadzone są na poziomie mikro dzięki temu unika się błędów

związanych z agregacją

Ograniczenia związane z
wykorzystaniem paneli

Š Problemy z gromadzeniem danych (braki danych)
Š Błąd pomiaru (odpowiedzi danej jednostki mogą być

sprzeczne z danymi z roku poprzedniego)

Š Problemy selekcji:

„

Samoselekcja (cenzorowana lub ucięta zmienna)

„

Braki odpowiedzi

Š Krótkookresowe serie badań

Przedmiot badania –
subiektywna podaż pracy

Š Przydatności do prognozowania rzeczywistego

czasu pracy w następnym okresie.

Š Oszacowania preferencji jednostek dotyczących

czasu pracy w przypadku osób bezrobotnych

Š Kwestie „uelastycznienia” czasu pracy.
Š Czy zawiera prawdziwe informacje dotyczące

preferencji?

Š Tradycyjna metodologia - tylko działania

(ujawnione preferencje) są odpowiednie do badania
indywidualnych preferencji

Wykorzystane zmienne.

Aktualny czas pracy

Š Total actual working hours (ht)– zarówno

opłacony jak i nieopłacony czas pracy.

Š Paid actual working hours (hp) – czas

pracy, za który otrzymuje się wynagrodzeni.

hp

it

= hc

it

+ I(or

it

=‘A’)(ht

it

-hc

it

)+

½ I(or

it

=‘C’)(ht

it

-hc

it

)

Dynamiczne modele panelowe

Š

Obciążenie estymatorów RE i FD FE

(nieobciążony gdy TÆ∞) w modelu dynamicznym

Š możliwość zastosowania metody zmiennych

instrumentalnych.

)

(

)

(

ˆ

1

y

Z'

X

Z'

β

⋅

=

−

IV

)

(

)

(

ˆ

1

y

Z'

ZW

X'

X

Z'

ZW

X'

β

N

N

GIVE

⋅

=

−

Metoda Arellano - Bonda

it

1

t

i,

i

it

ε

γy

α

y

+

+

=

−

)

ε

(ε

)

y

γ(y

y

-

y

1

-

t

i,

it

2

t

i,

1

t

i,

1

-

t

i,

it

−

+

−

=

−

−

(

)

{

}

0

2

,

1

,

=

−

−

−

t

i

t

i

it

y

E

ε

ε

Rozpatrzmy prosty model o postaci:

i zapiszmy go w postaci pierwszych różnic:

Rozwiązanie: Wykorzystanie instrumentu, który będzie niezależny od
składnika losowego ale skorelowany ze zmienną objaśniającą w estymacji
FD

Przykład instrumentu: y

i, t-2

- skorelowane z (y

i,t-1

-y

i,t-2

)ale niezależne od

ε

i,t

- ε

i,t-1

(o ile składnik losowy nie wykazuje autokorelacji, co zakładamy)

Æ czyli

Arellano i Bond (1991)

proponują

wykorzystanie wszystkich możliwych

instrumentów, których

liczba

różni się w kolejnych okresach

Model na poziomach

Š β

2

>0 Æ na podstawie subiektywnej podaży pracy można

przewidywać przyszły czas pracy.

„

H0 : β

2

=0

„

H1 :β

2

>0

)

(

)

(

)

)

1

(

(

1

2

1

1

2

1

1

2

1

1

0

*

*

*

1

2

*

1

1

0

*

d

it

a

it

d

it

it

d

i

a

i

i

it

it

it

d

it

d

i

it

it

a

it

a

i

it

it

it

i

it

it

it

v

v

v

v

v

hd

ha

ha

v

v

hd

hd

v

v

ha

ha

hd

ha

ha

−

−

−

−

−

−

−

−

+

+

−

−

+

+

+

+

=

+

+

=

+

+

=

+

+

+

+

=

β

β

ε

β

β

ε

β

β

β

ε

ε

β

β

β

Sposób estymacji

Š Założenie: błąd pomiaru jest nieskorelowany w czasie, dzięki czemu zmienne

z innego okresu czasu niż badany mogą być użyte jako instrumenty.

Š Pierwsze różnice

Š Instrumenty

„

ha

it-2

- nieskorelowany z ε

it

-ε

it-1

, ale skorelowany z υ

a

it-2

„

Prawidłowy instrument : ha

it-3

Š Wektor pierwszych opóźnień Δha – rozmiar N*(T-3)
Š Macierz instrumentów Z – N(T-3)*(T-3)(T-2)

„

Z=[Z

1

’,...,Zn’], gdzie Zi - macierz blokowo-diagonalna (T-3)*(T-3)(T-2), każdy

wiersz zawiera instrumenty prawidłowe dla danego okresu.

β

GMM

= ([

∆ha

-1

,

∆hd

-1

]’Z W

N

Z’[

∆ha

-1

,

∆hd

-1

])

-1

([

∆ha

-1

,

∆hd

-1

]’Z W

N

Z’

∆ha)

)

(

)

(

)

(

)

(

)

(

)

(

2

1

2

2

1

1

1

1

2

1

2

2

1

1

1

d

it

d

it

a

it

a

it

a

it

a

it

it

it

it

it

it

it

it

it

v

v

v

v

v

v

hd

hd

ha

ha

ha

ha

−

−

−

−

−

−

−

−

−

−

−

−

−

−

−

+

+

−

+

−

+

−

=

−

β

β

ε

ε

β

β

Model z ograniczeniem –model
na różnicach

Š Czy różnica między pożądanym a rzeczywistym czasem pracy

dobrze prognozuje zmianę czasu pracy w następnym okresie?

)

(

)

(

)

(

)

(

)

(

1

2

1

2

1

2

1

1

2

0

1

*

1

*

1

2

0

*

1

*

a

it

d

it

a

it

a

it

it

a

i

d

i

it

it

it

it

it

it

it

it

it

v

v

v

v

v

v

ha

hd

ha

ha

ha

hd

ha

ha

−

−

−

−

−

−

−

−

−

−

−

−

+

+

−

+

−

+

=

−

+

−

+

=

−

β

β

ε

β

β

β

ε

β

β

•Ograniczenie β

1

+β

2

=1

•Problem endogeniczności, mimo, że nie jest to typowy model
dynamiczny (nie zawiera opóźnionej zmiennej zależnej)

•Estymacja analogiczna jak w przypadku modelu na poziomach

Wykonane estymacje

Š Na poziomach:

„

LEV-OLS – klasyczny model liniowy nieuwzględniający
„dynamiczności” modelu

„

LEV-ME – GMM, jako instrumenty wykorzystane są
opóźnienia o 3 i więcej okresów (wykorzystane
wszystkie możliwe instrumenty) – wcześniej omówiona

Š Na różnicach

„

DIF-FE – model stałych efektów indywidualnych

„

DIF-AB – model Arellano i Bonda, jako instrumenty
wykorzystane opóźnienia o dwa i więcej okresów

„

DIF-ME

Dane

Š Niemiecki panel socjo-ekonomiczny

(GSEOP)

Š Zatrudnieni w wieku 18-60 lat z

wykluczeniem imigrantów

Š Lata: 1988-1996

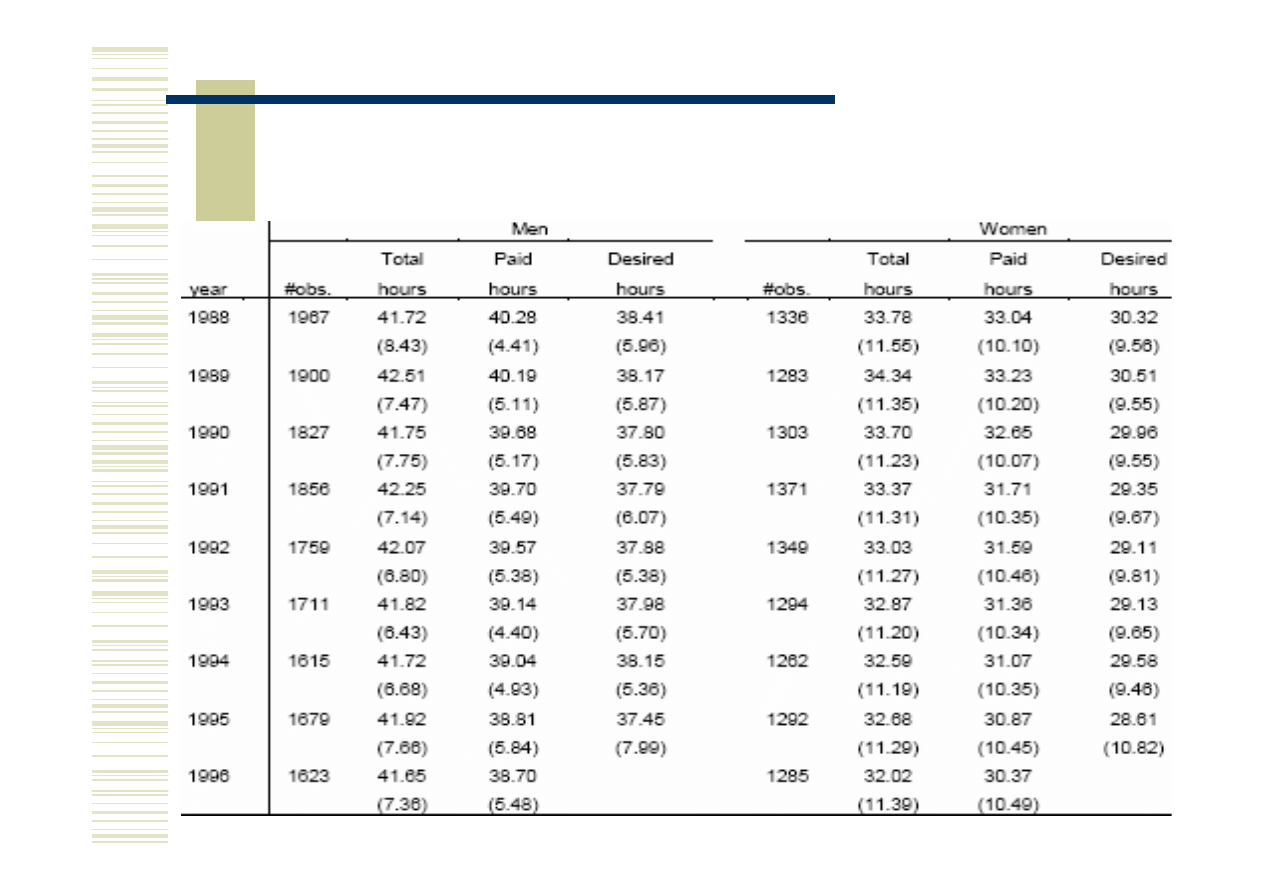
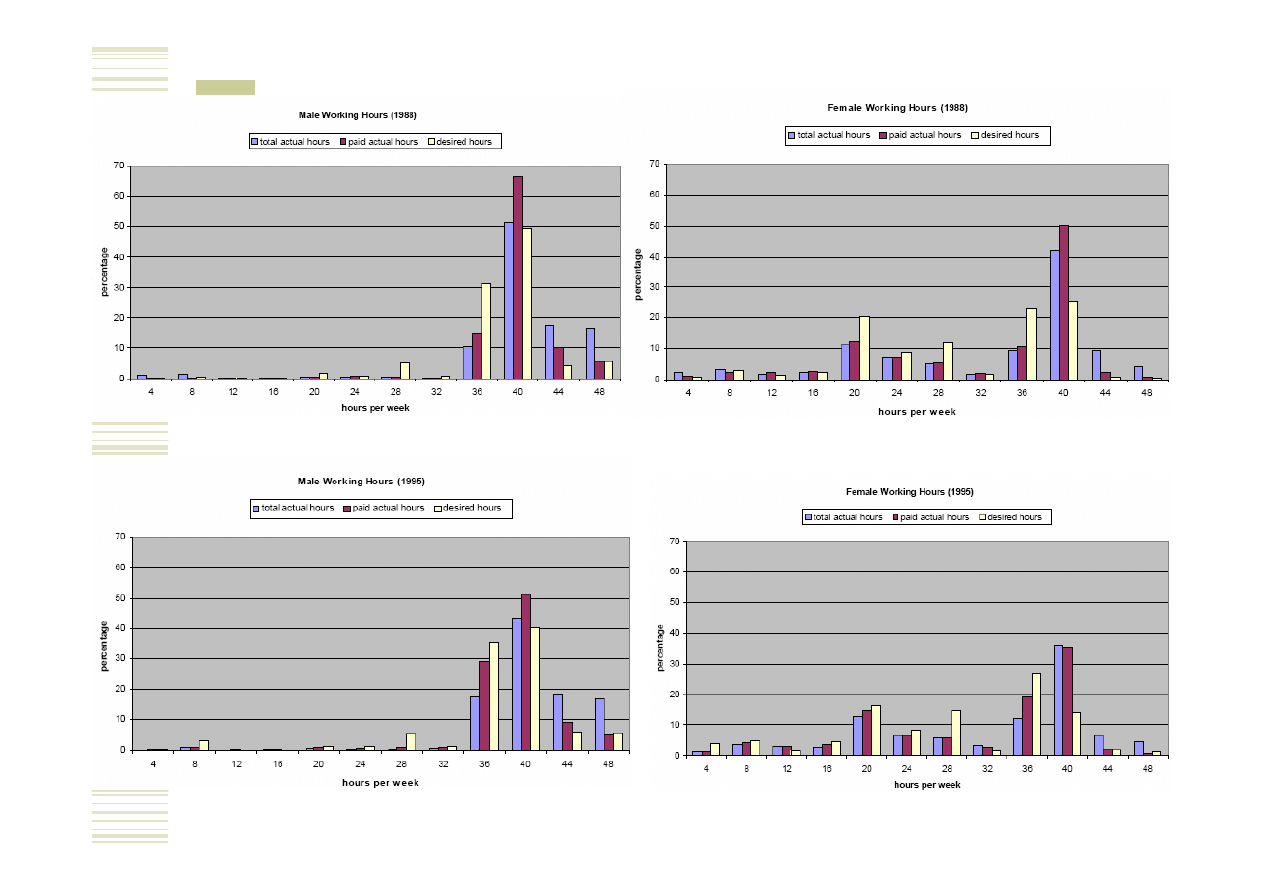
Statystyki opisowe

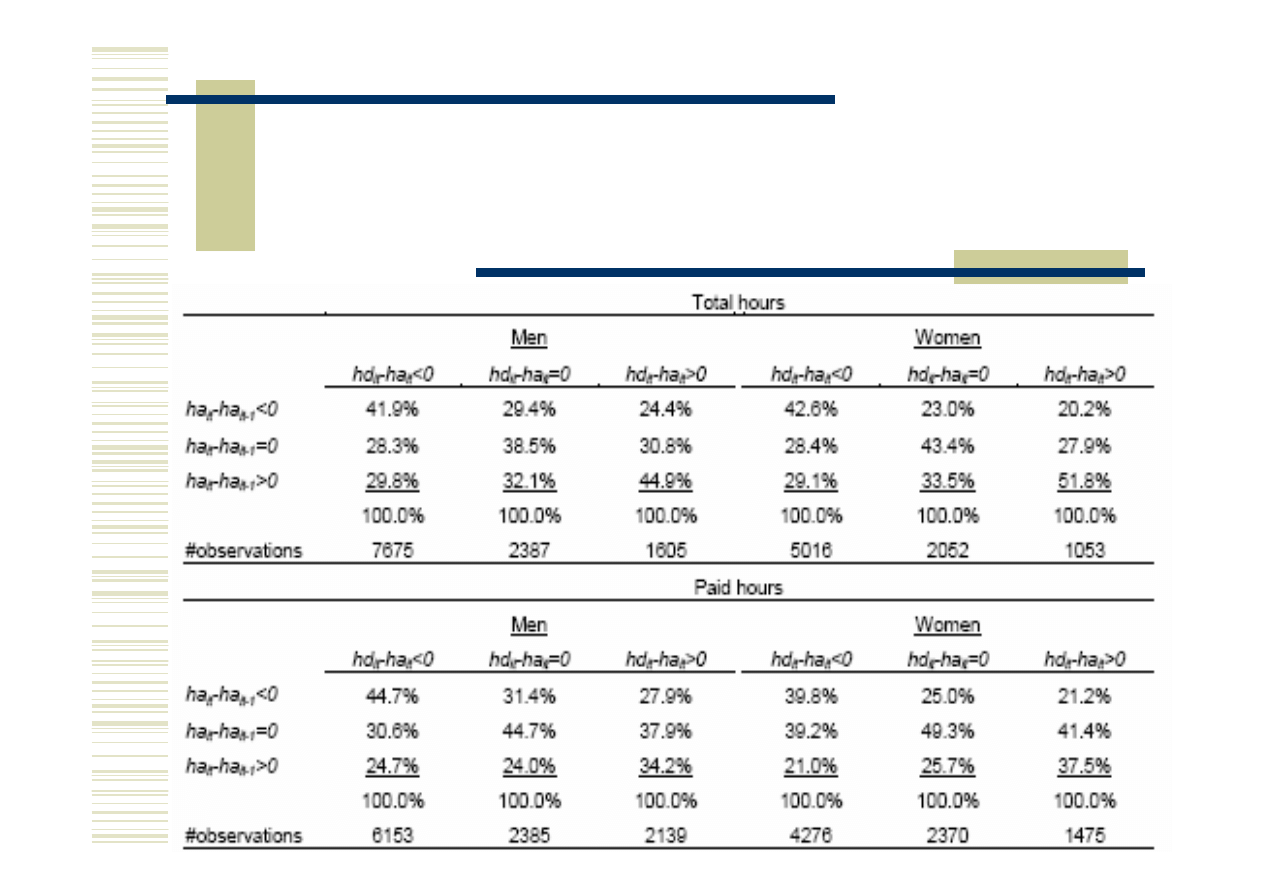
Plany a rzeczywistość

Plany a rzeczywistość

Š Sukces predykcji mierzony średnią ważoną
Š Mężczyźni

„

41,9% dla płatnych godzin pracy

„

41,6% dla łącznych godzin pracy

Š Kobiety

„

42,1% dla płatnych godzin pracy

„

44% dla łącznych godzin pracy

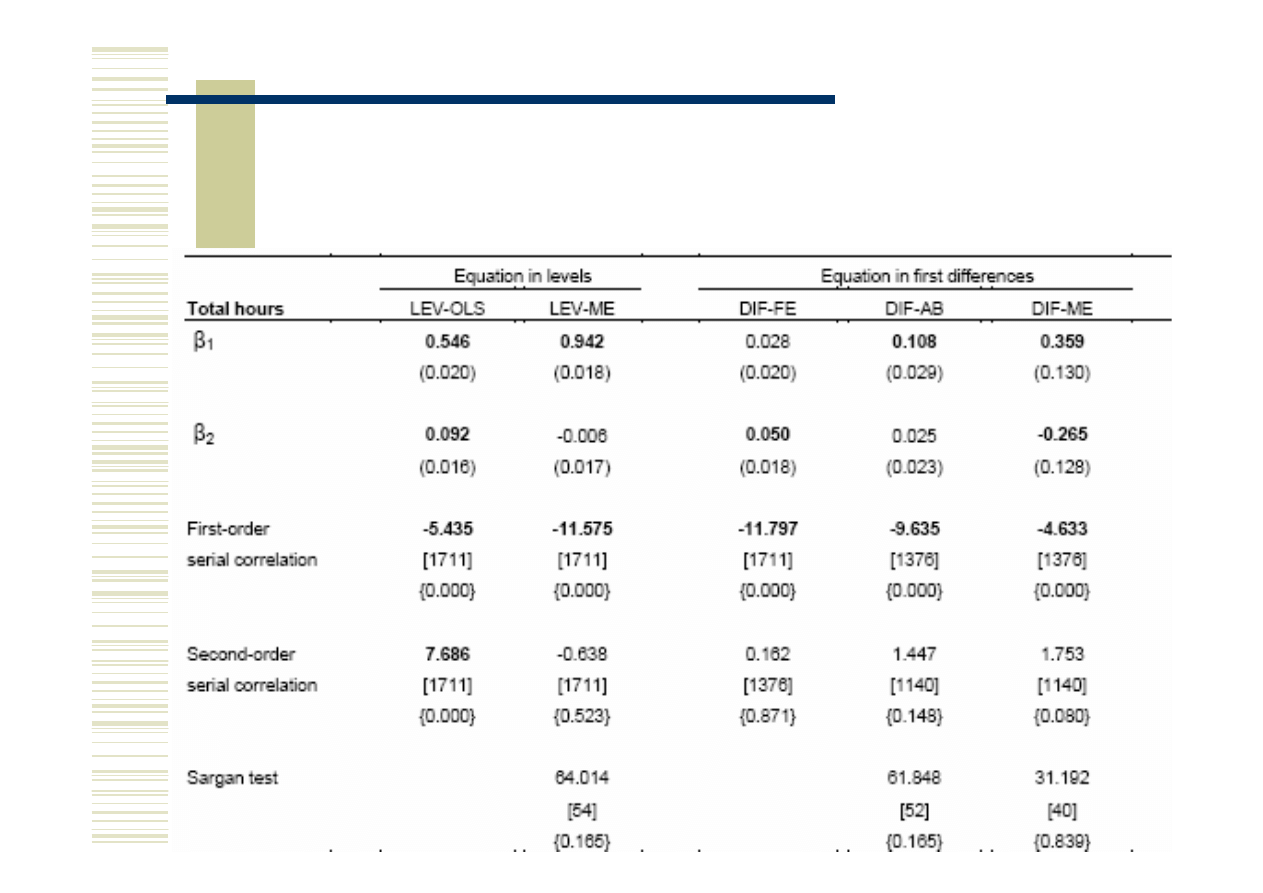
Wyniki estymacji- mężczyźni

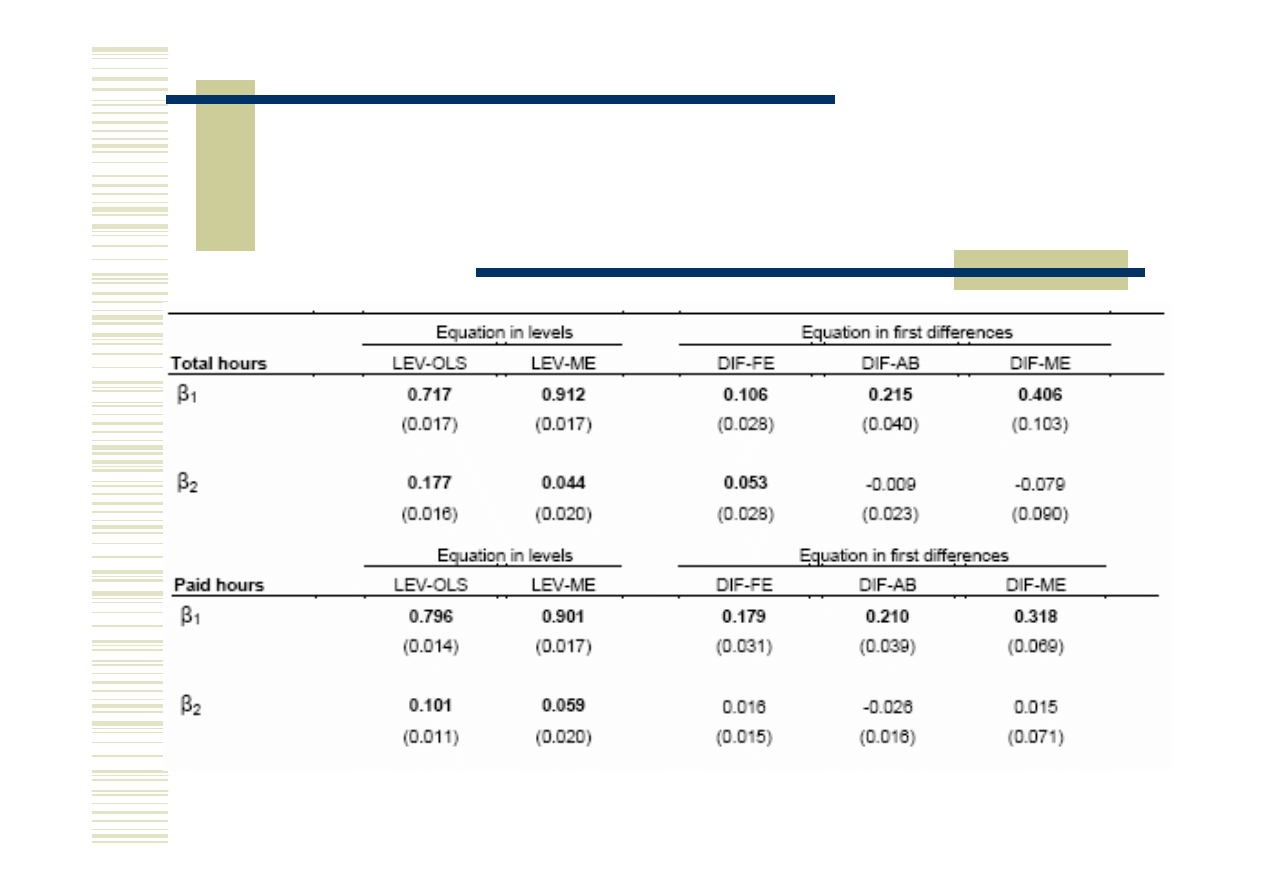
Wyniki estymacji, mężczyźni

Š LEV-OLS

Współczynniki, zarówno dla łącznych jak i opłacanych
godzin pracy, są dodatnie i istotne. Ale mamy tu
autokorelację pierwszego rzędu, co oznacza, że estymator
nie jest zgodny. Nie możemy zatem interpretować wyników.

Š LEV-ME

Model uwzględnia autokorelację. Brak autokorelacji
drugiego rzędu oznacza, że zostały użyte dobre instrumenty.
Współczynniki okazują się jednak mało różne od zera.

Š DIF-FE Współczynniki, zarówno dla łącznych jak i

opłacanych godzin pracy, są dodatnie i istotne.

Š DIF-AB Brak autokorelacji drugiego rzędu oznacza, że

zostały użyte dobre instrumenty.

Š DIF-ME Współczynniki są nieistotne.
Š Na podstawie testu Hausmana należy odrzucić H0 mówiącą

o nieobecności efektów indywidualnych.

Š Wniosek: wyniki różnych estymacji są sprzeczne i na ich

podstawie nie można orzec, że subiektywne dane mogą
służyć

do predykcji. Wniosek ten dotyczy zarówno

mężczyzn jak i kobiet.

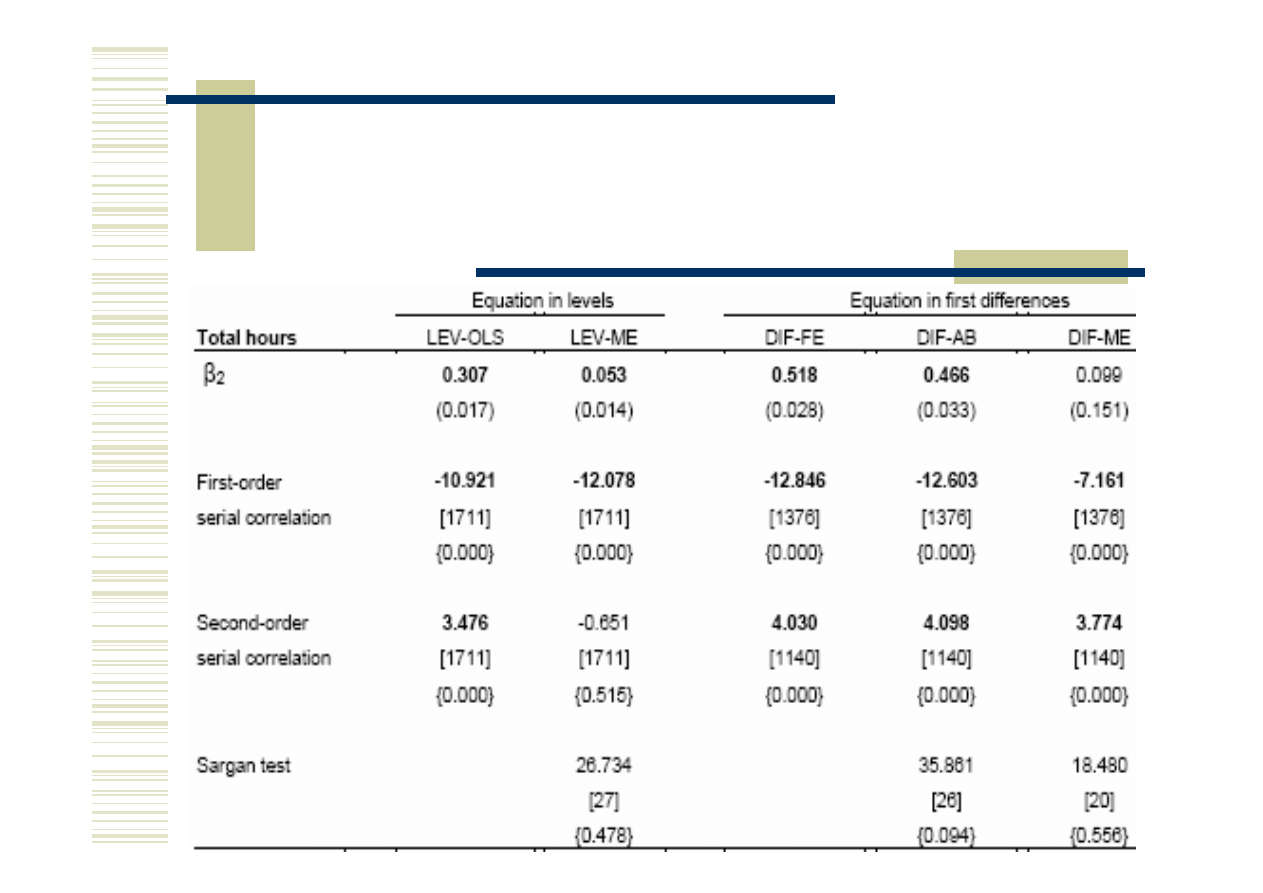
Wyniki estymacji, mężczyźni

Wyniki estymacji, kobiety

Restricted model

Model z ograniczeniem.

Š LEV-ME

Model uwzględnia autokorelację. Brak

autokorelacji drugiego rzędu oznacza, że zostały użyte dobre
instrumenty. Współczynniki, zarówno dla łącznych jak i
opłacanych godzin pracy, są dodatnie i istotne. Jeśli zatem
założenie o braku efektów indywidualnych jest prawdziwe,
to można stwierdzić, że subiektywne dane mogą służyć do
predykcji.

Š Test Hausmana na brak efektów indywidualnych: nie ma

podstaw do odrzucenia H0 (dla mężczyzn)

Š DIF-ME Współczynniki są nieistotne.
Š Dla kobiet Test Hausmana wskazuje na istnienie efektów

indywidualnych dla opłacanych godzin pracy, a brak dla

łącznych.

Podsumowanie

Š Opóźnione planowane godziny nie mają

zdolności do przewidywania wartości
poziomu aktualnych godzin pracy.

DZIĘKUJEMY ZA UWAGĘ