E K O N O M E T R I A

LITERATURA:

Ekonometria,

Ekonometria, red. M. Krzysztofiak, PWE, Warszawa 1984

Ekonometria,

Ekonometria, S. Bartosiewicz, PWE, Warszawa 1978

Matematyczne Techniki Zarz

Matematyczne Techniki Zarz

¹

¹

dzania

dzania, skrypt AGH, rozdziaù V

Statystyka w zarz¹dzaniu, Aczel A. D., PWN, Warszawa 2000

Zespóù realizuj¹cy przedmiot:

dr in¿. Alicja Byrska R¹paùa - wykùadowca
dr Izabela Stach
mgr in¿.. Mateusz Wiernek

Zajêcia:

Wyk

Wyk

ù

ù

ady

ady

-

-

30 godz.

30 godz.

Laboratorium

Laboratorium

-

-

15 godz.

15 godz.

Ã

Ã

wiczenia

wiczenia

-

-

15 godz.

15 godz.

Ekonometria

Ekonometria

-

-

1

1

Ekonometria

—

nauka o mierzeniu zwi¹zków wystêpuj¹cych miêdzy zjawiskami lub procesami ekonomicznymi

a innymi zjawiskami (innymi zjawiskami ekonomicznymi, przyrodniczymi, technicznymi, demograficznymi i

socjologicznymi) w celach poznawczych i dla prognozowania

(Bartosiewicz S.)

—

nauka zajmuj¹ca siê ustalaniem, za pomoc¹ metod matematyczno-statystycznych, iloœciowych prawidùowoœci

zachodz¹cych w ¿yciu gospodarczym

Specyficzne warunki prowadzenia badañ ekonometrycznych

- brak mo¿liwoœci powtórzenia eksperymentu (nie dziaùaj¹ prawa statystyki matematycznej)

- zaostrzone kryteria matematyczne (n>100)

- trudnoœci z danymi: dostêpnoœã, iloœã, wiarygodnoœã, porównywalnoœã

NARZ

NARZ

Æ

Æ

DZIEM BADAWCZYM EKONOMETRII JEST MODEL EKONOMETRYCZNY

DZIEM BADAWCZYM EKONOMETRII JEST MODEL EKONOMETRYCZNY

–

–

opis fragmentu ekonomicznej rzeczywisto

opis fragmentu ekonomicznej rzeczywisto

œ

œ

ci, uwzgl

ci, uwzgl

ê

ê

dniaj

dniaj

¹

¹

cy tylko istotne jej elementy;

cy tylko istotne jej elementy;

–

–

konstrukcja my

konstrukcja my

œ

œ

lowa, kt

lowa, kt

ó

ó

ra w uproszczony spos

ra w uproszczony spos

ó

ó

b przedstawia funkcjonowanie lub wzrost gospodarki lub jej

b przedstawia funkcjonowanie lub wzrost gospodarki lub jej

cz

cz

êœ

êœ

ci

ci

–

–

def

def

. dla ekonomii

. dla ekonomii

–

–

konstrukcja formalna, kt

konstrukcja formalna, kt

ó

ó

ra za pomoc

ra za pomoc

¹

¹

pewnego r

pewnego r

ó

ó

wnania lub uk

wnania lub uk

ù

ù

adu r

adu r

ó

ó

wna

wna

ñ

ñ

przedstawia zasadnicze

przedstawia zasadnicze

powi

powi

¹

¹

zania wyst

zania wyst

ê

ê

puj

puj

¹

¹

ce pomi

ce pomi

ê

ê

dzy rozpatrywanymi zjawiskami ekonomicznymi (spo

dzy rozpatrywanymi zjawiskami ekonomicznymi (spo

ù

ù

eczno

eczno

-

-

ekonomicznymi

ekonomicznymi

).

).

Model ekonometryczny za pomoc

Model ekonometryczny za pomoc

¹

¹

r

r

ó

ó

wna

wna

ñ

ñ

przedstawia zale

przedstawia zale

¿

¿

no

no

œ

œ

ci wyst

ci wyst

ê

ê

puj

puj

¹

¹

ce pomi

ce pomi

ê

ê

dzy zmiennymi.

dzy zmiennymi.

ELEMENTY MODELU:

ELEMENTY MODELU:

•

•

Zmienne,

Zmienne,

•

•

Parametry

Parametry

•

•

Elementy losowe

Elementy losowe

Ekonometria

Ekonometria

-

-

2

2

W

W

£

£

A

A

Ú

Ú

CIWO

CIWO

Ú

Ú

CI MODELU EKONOMETRYCZNEGO:

CI MODELU EKONOMETRYCZNEGO:

Ø

Ø

sp

sp

ó

ó

jno

jno

ϋ

ϋ

ekonomicznych i spo

ekonomicznych i spo

ù

ù

ecznych zjawisk i proces

ecznych zjawisk i proces

ó

ó

w;

w;

Ø

Ø

powi

powi

¹

¹

zanie (skorelowanie) za pomoc

zanie (skorelowanie) za pomoc

¹

¹

formalnych konstrukcji zjawisk

spo

formalnych konstrukcji zjawisk

spo

ù

ù

eczno

eczno

-

-

ekonomicznych

ekonomicznych

wchodz

wchodz

¹

¹

cych do wyodr

cych do wyodr

ê

ê

bnionego systemu;

bnionego systemu;

Ø

Ø

mierzalno

mierzalno

ϋ

ϋ

zjawisk;

zjawisk;

Ø

Ø

jednoznaczno

jednoznaczno

ϋ

ϋ

formalna w zapisie, odczytywaniu i interpretacji uzyskanych wyn

formalna w zapisie, odczytywaniu i interpretacji uzyskanych wyn

ik

ik

ó

ó

w;

w;

Ø

Ø

jest zasad

jest zasad

¹

¹

,

,

¿

¿

e ka

e ka

¿

¿

de r

de r

ó

ó

wnanie modelu przedstawia mechanizm kszta

wnanie modelu przedstawia mechanizm kszta

ù

ù

towania si

towania si

ê

ê

jednej i tylko jednej

jednej i tylko jednej

zmiennej.

zmiennej.

Je

Je

¿

¿

eli wi

eli wi

ê

ê

c model ma przedstawi

c model ma przedstawi

ã

ã

mechanizm kszta

mechanizm kszta

ù

ù

towania si

towania si

ê

ê

jednej tylko zmiennej, b

jednej tylko zmiennej, b

ê

ê

dzie sk

dzie sk

ù

ù

ada

ada

ù

ù

si

si

ê

ê

z

z

jednego r

jednego r

ó

ó

wnania.

wnania.

Je

Je

¿

¿

eli natomiast celem modelu b

eli natomiast celem modelu b

ê

ê

dzie opis mechanizmu kszta

dzie opis mechanizmu kszta

ù

ù

towania si

towania si

ê

ê

G

G

zmiennych, to musi sk

zmiennych, to musi sk

ù

ù

ada

ada

ã

ã

si

si

ê

ê

z

z

G

G

r

r

ó

ó

wna

wna

ñ

ñ

.

.

Terminologia

formalny podziaù zmiennych

• zmienna objaœniana (Y)

• zmienne objaœniaj¹ce (X1, X2...)

ze wzglêdu na wùaœciwoœci teoretyczne i praktyczne modelu

§ zmienne endogeniczne

§ zmienne egzogeniczne

ze wzglêdu na opóênienie w czasie

• zmienne ù¹cznie wspóùzale¿ne

• zmienne z góry ustalone

Ekonometria

Ekonometria

-

-

3

3

KLASYFIKACJA MODELI EKONOMETRYCZNYCH

I. Klasyfikacja wedùug wnoszonej informacji:

• modele przyczynowo-skutkowe

)

k

x

,...,

x

,

x

(

f

y

1

2

1

-

=

y — skutek
X

i

— przyczyny

•

modele tendencji rozwojowej

)

t(

f

y

=

y — analizowane zjawisko
t — czas

II. Klasyfikacja wedùug stopnia uwzglêdniania czasu:

• modele statyczne
• modele dynamiczne

III. Klasyfikacja wedùug liniowoœci:

• modele liniowe
• modele nieliniowe (konieczna transformacja liniowa)

IV. Klasyfikacja wedùug powi¹zania równañ:

Jest to podziaù ze wzglêdu na zaùo¿one powi¹zania miêdzy ró¿nymi zmiennymi endogenicznymi modelu.

Postaã strukturalna modelu:

Y

1

, Y

2

, Y

3

– zmienne endogeniczne

X

1

– zmienna egzogeniczna

a

ij

– wspóùczynnik przy j-tej zmiennej endogenicznej w i-tym równaniu

t,

t,

Y

t,

Y

t,

Y

t,

t,

Y

t,

Y

t,

t,

X

t,

Y

t,

Y

3

3

2

32

1

31

3

2

2

1

21

2

1

1

1

12

1

1

11

1

x

+

a

+

a

+

a

=

x

+

a

+

a

=

x

+

a

+

a

+

-

a

=

ú

ú

ú

û

ù

ê

ê

ê

ë

é

a

-

a

-

a

-

1

32

31

0

1

21

0

0

1

A=

Y1

Y2 Y3

Ekonometria

Ekonometria

-

-

4

4

•

modele proste:

macierz A jest macierz¹ diagonaln¹ i ka¿dy element przek¹tnej równy 1 (macierz

diagonalna: elementy poza przek¹tn¹=0);

nie wystêpuj¹ zwi¹zki miêdzy nie opóênionymi zmiennymi endogenicznymi

• modele rekurencyjne

: macierz A jest macierz¹ trójk¹tn¹; zmienna Y

jt

zale¿eã mo¿e od nie opóênionych

zmiennych endogenicznych, których wskaênik bie¿¹cy jest mniejszy od j, od zmiennych endogenicznych

opóênionych oraz od zmiennych egzogenicznych.

• modele o równaniach wspóùzale¿nych

: macierz A dowolna; istnieje sprzê¿enie zwrotne miêdzy zmiennymi

endogenicznymi w okresie t.

JEDNO RÓWNANIE LUB KILKA

ODDZIELNYCH

)

t,

x

,t

,

x

,t

,

x

,t

,

x

,t

,

x

(

f

t,

Y

)

t,

x

,t

,

x

,t

,

x

,t

,

x

(

f

t,

Y

)

t,

x

,t

,

x

,t

,

x

(

f

t,

Y

5

4

3

2

1

3

4

3

2

1

2

3

2

1

1

=

=

=

)

t,

x

,t

,

x

,t

,

x

,

1

-

t

3,

Y

,t

,

Y

(

f

t,

Y

)

t,

x

,t

,

x

,t

,

x

,

t,

Y

,t

,

Y

(

f

t,

Y

)

t,

x

,t

,

x

,t

,

x

(

f

t,

Y

3

2

1

2

3

3

2

1

1

2

1

2

3

2

1

1

=

-

=

=

Ekonometria

Ekonometria

-

-

5

5

ETAPY BUDOWY MODELU EKONOMETRYCZNEGO

1. Sformuùowanie problemu

a. wybór zmiennych:

y, x

1

, x

2

,...

b. wybór postaci matematycznej modelu:

liniowa, potêgowa,...

2. Zebranie danych statystycznych

(ró¿ne êródùa)

3. Selekcja zmiennych objaœniaj¹cych

(celem podziaùu na dwie grupy — nadaj¹ce siê do modelu i

niepotrzebne w nim)

4. Estymacja parametrów modelu:

a. parametrów strukturalnych:

a

0

, a

1

, a

2

,...

b. parametrów stochastycznych:

s(a

i

), s(y), R

2

, R

5. Weryfikacja modelu

(przy u¿yciu hipotez i testów statystycznych)

6. Interpretacja modelu

• wyci¹gniêcie wniosków dla celów zarz¹dzania
• sprzedanie go klientowi

Ekonometria

Ekonometria

-

-

6

6

ANALIZA REGRESJI I KORELACJI

•

umo¿liwia badanie wpùywu czynników mierzalnych, takich jak: zu¿ycie materiaùów, wielkoœã

produkcji, iloœã placówek wychowania pozaszkolnego, iloœã spo¿ywanego alkoholu itd.

•

umo¿liwia ustalanie przyczyn zachowania siê danego zjawiska:

• jest to bardzo popularna metoda, zgodna z nasz¹ intuicj¹
• obliczeñ parametrów modelu dokonuje siê

metod¹ najmniejszych kwadratów (MNK)

• stosuje siê: estymacjê, testowanie hipotez, analizê wariancji itd.

Podstawowe pojêcia i terminy

KORELACJA

— fakt

powi¹zania, wspóùzale¿noœci, zwi¹zku zmiennych ze sob¹

WSPÓ£CZYNNIK KORELACJI

— liczba

okreœlaj¹ca siùê i kierunek tego zwi¹zku

• wspóùczynnik korelacji liniowej dwu zmiennych: r lub r

xy

Wspóùczynnik r niesie dwie informacje poprzez

swój znak i moduù

1

0

1

1

£

£

£

£

-

r

r

Znak

informuje o kierunku zale¿noœci

Moduù

informuje o sile zale¿noœci

Ekonometria

Ekonometria

-

-

7

7

•

wspóùczynnik korelacji liniowej wielu zmiennych (korelacji wielokrotnej lub wielorakiej): R

Interpretacja:
• im wy¿sza wartoœã R, tym silniejsza wspóùzale¿noœã (R=0: brak korelacji, R=1: zale¿noœã funkcyjna, nie ma

skùadnika losowego)
• R okreœla siùê powi¹zania zmiennej Y z wszystkimi zmiennymi X

i

, bez wzglêdu na to jak poszczególne z nich s¹

skorelowane z Y

• wspóùczynnik korelacji cz¹stkowej dwu zmiennych

j

i

x

x

r

REGRESJA

— statystyczna metoda modelowania zwi¹zków miêdzy zmiennymi; opisuje j¹ funkcja

odzwierciedlaj¹ca powi¹zanie zmiennych (czynników)

• w mowie potocznej regresja to cofanie siê, spadek, zanik
• sk¹d siê wziêùo to sùowo w statystyce?

i

x

,

y

r

1

0

£

£

R

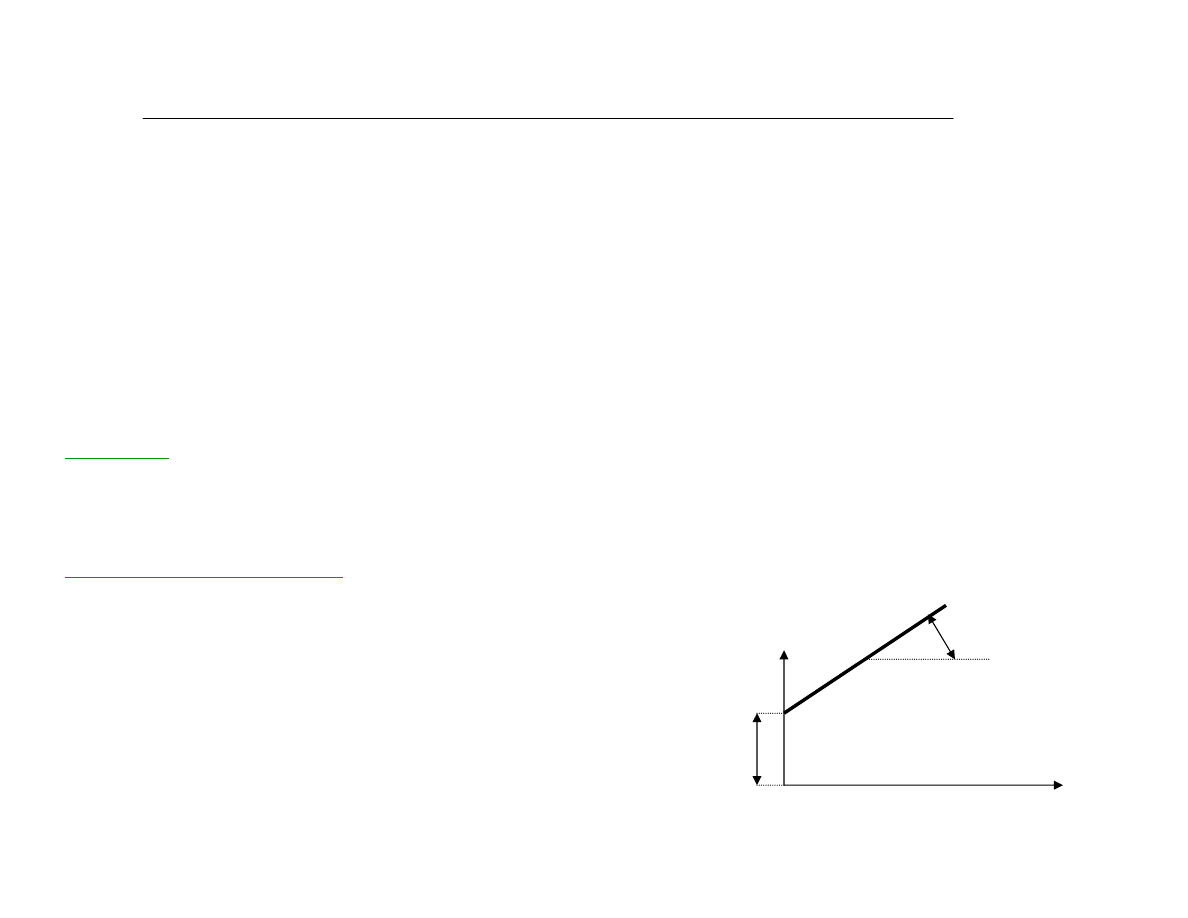
WSPÓ£CZYNNIK REGRESJI

— liczba

stoj¹ca przy ka¿dej zmiennej X, okreœlaj¹ca jej wpùyw na zmienn¹ Y

x

+

+

=

i

bx

a

i

y

a

— wyraz wolny (staùa), wspóùrzêdna punktu przeciêcia z osi¹ Y

b

— wspóùczynnik regresji, tangens k¹ta

g

nachylenia prostej

— skùadnik losowy N(0,

s

2

)

x

xi

a

g

yi

Ekonometria

Ekonometria

-

-

8

8

Trzy rodzaje zwi¹zków pomiêdzy Y i X

• zwi¹zek funkcyjny (deterministyczny)

Y

X

x

i

y

i

i

bx

a

i

y

+

=

KAÝDEJ WARTOÚCI x

i

ODPOWIADA JEDNA I TYLKO

JEDNA WARTOÚÃ y

i

•

zwi¹zek stochastyczny (losowy), probabilistyczny

KAÝDEJ WARTOÚCI x

i

ODPOWIADA CA£Y ZBIÓR WARTOÚCI y

i

TWORZ¥CYCH OKREÚLONY ROZK£AD

x

+

b

+

b

=

X

Y

1

0

•

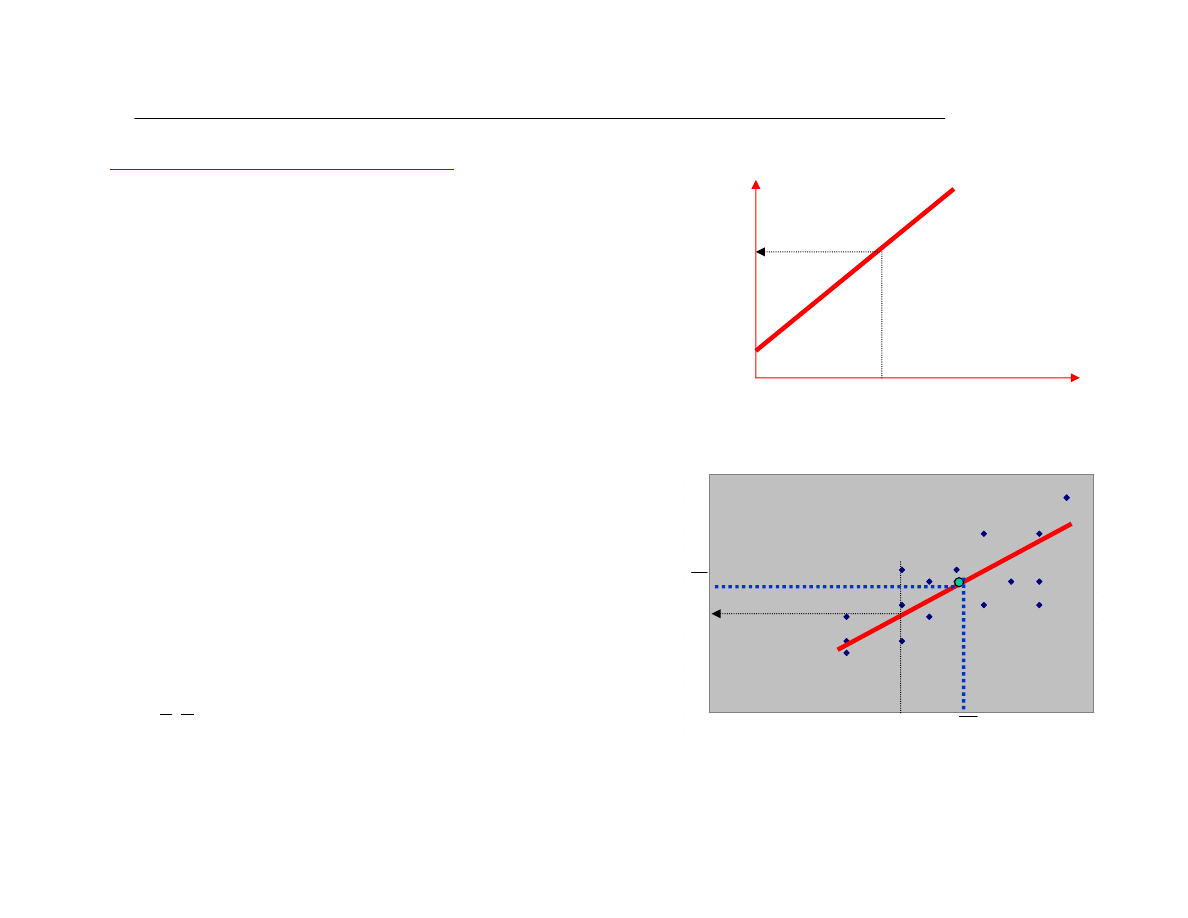
zwi¹zek statystyczny

X

Y

x

i

i

yˆ

i

yˆ

—

œrednia rozkùadu dla ustalonej

wartoœci x

i

x

—

obrazuje rozrzut

y

,

x

—

œrodek ciê¿koœci zbioru

x

y

x

+

+

=

i

bx

a

i

yˆ

Ekonometria

Ekonometria

-

-

9

9

Funkcja regresji I i II rodzaju

• regresja I rodzaju dotyczy populacji (jest nieznana)

e

+

+

a

+

a

+

a

=

...

X

X

Y

2

2

1

1

0

•

regresja II rodzaju dotyczy próbki (jest znana

)

x

+

+

+

+

=

...

x

a

x

a

a

y

2

2

1

1

0

Wspóùczynniki regresji to

a

i

oraz a

i

; tak jak przy estymacji innych parametrów mamy to do czynienia z

estymatorami, ich odchyleniami standardowymi (czyli bùêdami oszacowania) oraz z wartoœciami

oszacowanymi.

Regresja liniowa I rodzaju

Zaùó¿my, ¿e mamy dany rozkùad zmiennej losowej dwuwymiarowej.
Przyjmuje ona wartoœci (x

i

; y

j

) z prawdopodobieñstwem P

ij

,

a odpowiednie rozkùady brzegowe maj¹ postaã h(x

i

) i g(y

j

).

Zmienna losowa dwuwymiarowa

Tablica dwudzielna

1

P

m

P

j

P.

2

P.

1

Suma

Rozk

ù

ad brzegowy g(y

j

)

P

n

P

nm

P

nj

P

n2

P

n1

x

n

P

i

P

im

P

ij

P

i2

P

i1

x

i

P

2

P

2m

P

2j

P

22

P

21

x

2

P

1

P

1m

P

1j

P

12

P

11

x

1

Suma

Rozk

ù

ad brzegowy h(x

i

)

y

m

y

i

y

2

y

1

Statystyka

Statystyka

-

-

10

10

Dla rozkùadu warunkowego zmiennej losowej Y wzglêdem X wartoœã oczekiwana dla rozkùadu dyskretnego i

ci¹gùego dana jest wzorem:

dy

)

x

(

h

)

y

,

x

(

f

y

dy

)

x

/

y

(

f

y

)

x

X

/

Y

(

E

j

)

k

x

(

h

ij

P

j

y

)

k

x

X

/

Y

j

(

P

j

y

)

k

x

X

/

Y

(

E

×

¥

+

¥

-

=

×

¥

+

¥

-

=

=

×

=

=

×

=

=

ò

ò

å

å

Definicja

Definicja

Zbiór punktów (x,y) speùniaj¹cy równanie: y=E(Y/X=x) nazywamy lini¹ regresji I rodzaju

zmiennej losowej Y wzglêdem X.

RÓWNANIE REGRESJI

(model deterministyczny)

X

Y

1

0

b

b

+

=

RÓWNANIE REGRESJI

(model probabilistyczny)

x

b

b

+

+

=

X

Y

1

0

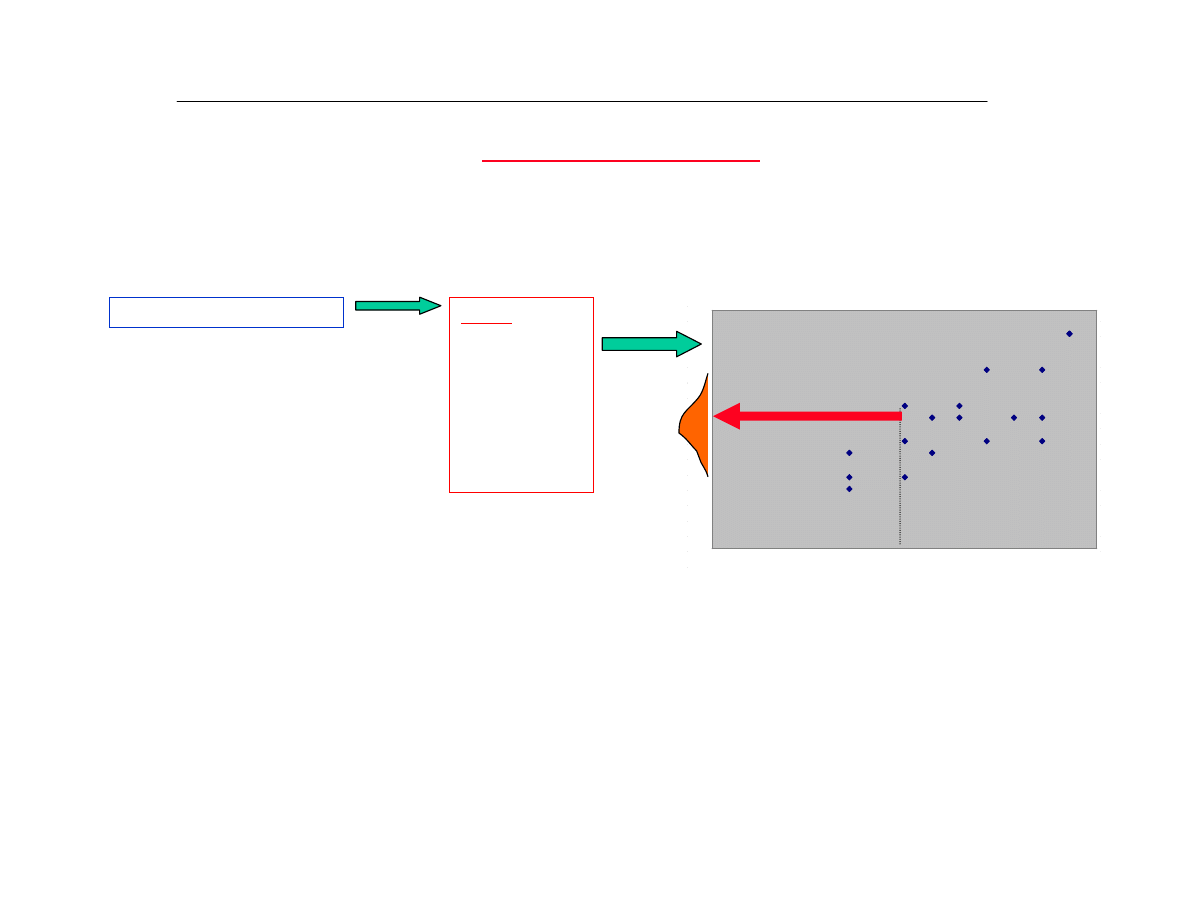
Regresja liniowa II rodzaju

Statystyka

Statystyka

-

-

11

11

KAÝDEJ WARTOÚCI x

i

ODPOWIADA CA£Y ZBIÓR WARTOÚCI y

i

TWORZ¥CYCH OKREÚLONY ROZK£AD

X

Y

DANE
Lp. x

i

y

i

1 x

1

y

1

2 x

2

y

2

3 x

3

y

3

............

x

i

Obserwacja rzeczywistoœci

x

+

+

=

i

bx

a

i

y

Je¿eli ten rozkùad jest normalny to zale¿noœã Y(X) jest liniowa.

Ekonometria

Ekonometria

-

-

12

12

Zmienna

(czynnik)

Wartoϋ

oszacowana

Bù¹d

oszacowania

Statystyka

t

obl

Rzeczywisty po-

ziom istotnoœci P

Wyraz wolny

Czynnik X

1

Czynnik X

2

Czynnik X

3

a

0

a

1

a

2

a

3

s(a

0

)

s(a

1

)

s(a

2

)

s(a

3

)

t(a

0

)

t(a

1

)

t(a

2

)

t(a

3

)

P(a

0

)

P(a

1

)

P(a

2

)

P(a

3

)

Wspóùczynniki: determinacji R

2

, zbie¿noœci

j

2

, bù¹d resztowy s(y) i inne

Wydruk komputerowy równania regresji

Peùny zapis równania regresji

Y

— zmienna zale¿na, skutek, zmienna objaœniana, endogeniczna

y

i

— zaobserwowane wartoœci zmiennej zale¿nej dla obiektów

(jednostka próby)

X

k

— zmienne niezale¿ne, przyczyny, zmienne objaœniaj¹ce - egzogeniczne

x

ki

— zaobserwowane wartoœci zmiennych niezale¿nych

i

x

a

x

a

x

a

a

i

yˆ

x

+

+

+

+

=

3

3

2

2

1

1

0

2

3

2

1

0

2

3

3

2

2

1

1

0

j

x

+

+

+

+

=

)

y

(

s

)

a

(

s

)

a

(

s

)

a

(

s

)

a

(

s

)

R

(

R

i

x

a

i

x

a

i

x

a

a

i

yˆ

Ekonometria

Ekonometria

-

-

13

13

a

i

...

— oszacowane wartoœci wspóùczynników regresji; okreœlaj¹ wpùyw poszczególnych zmiennych X

i

na

zmienn¹ Y

x

— skùadnik losowy, reprezentuj¹cy rozrzut punktów wokóù pùaszczyz-ny regresji; skùadnik ten jest

zmienn¹

losow¹;

jego wartoœci nazywaj¹ siê

reszty

a jego rozkùad jest rozkùadem normalnym o E(

x

)=0 i V(

x

)=s

2

(y)

s(a

0

)

— bù¹d oszacowania wyrazu wolnego; sùu¿y do budowy przedziaùu ufnoœci dla nieznanej wartoœci

wyrazu wolnego

a

0

dla populacji oraz do weryfikacji istotnoœci

a

0

(H

0

:

a

0

=0)

s(a

i

)

— bùêdy oszacowania wspóùczynników regresji; sùu¿¹ do budowy przedziaùu ufnoœci dla nieznanych

wartoœci

a

i

wspóùczynników regresji dla populacji oraz do weryfikacji ich istotnoœci (H

0

:

a

i

=0)

s(y)

— bù¹d resztowy; odchylenie standardowe skùadnika losowego

x

;

okreœla œredni¹ wielkoœã reszty e

i

a

0

— oszacowana wartoœã wyrazu wolnego, estymator

parametry strukturalne i stochastyczne

i

yˆ

i

y

i

e

-

=

R

2

(r

2

)

— wspóùczynnik determinacji; okreœla jaka czêœã zmiennoœci caùko-witej

SSTO

zostaùa wyjaœniona przez

równanie regresji

j

2

— wspóùczynnik zbie¿noœci (zgodnoœci); okreœla jaka czêœã zmien-noœci caùkowitej

SSTO

nie zostaùa

wyjaœniona przez równanie regresji

å

-

2

)

y

i

y

(

=

SSTO

(zmiennoœã caùkowita)

Ekonometria

Ekonometria

-

-

14

14

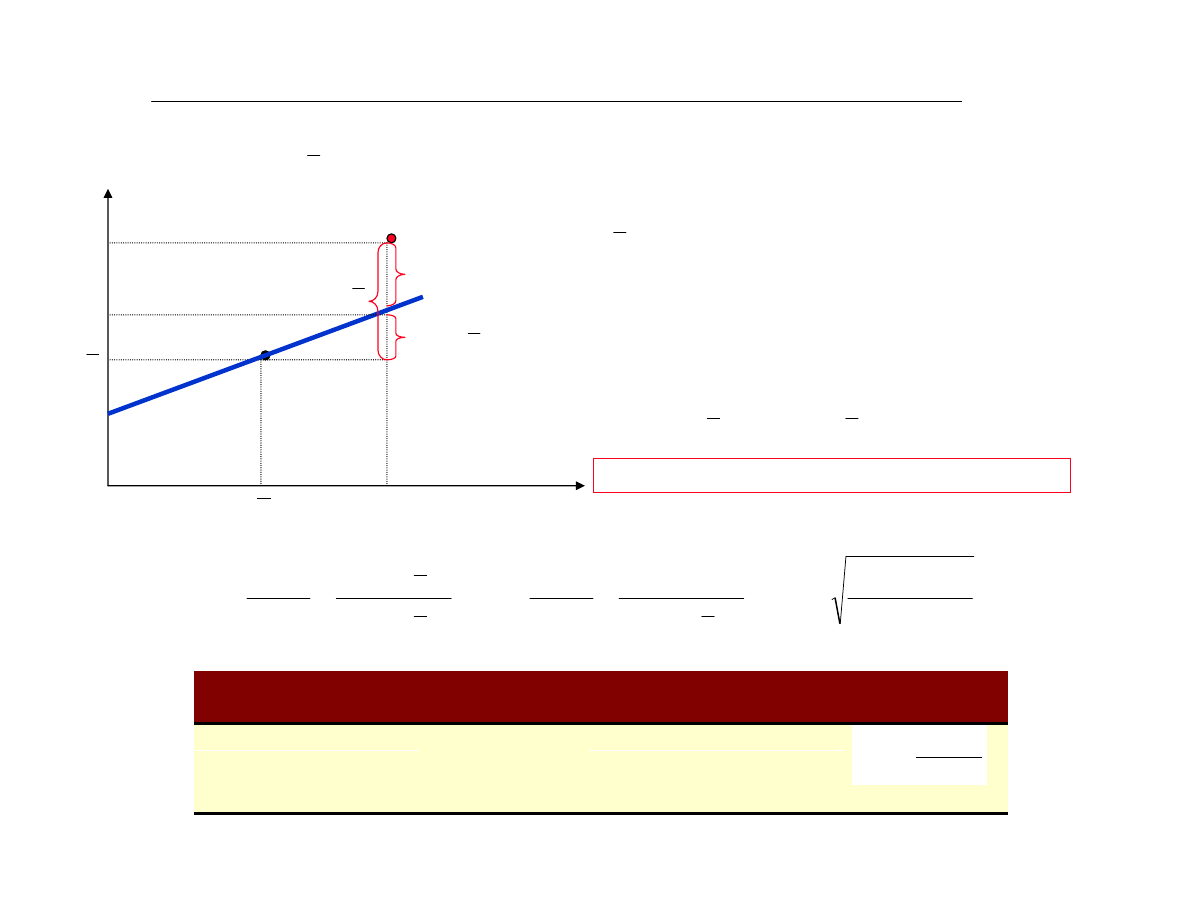
X

Y

x

y

i

x

i

y

i

yˆ

y

y

i

-

i

i

y

y ˆ

-

y

y

i

-

ˆ

å

-

2

)

y

i

y

(

=

SSTO

(zmiennoœã caùkowita)

å

-

2

)

y

i

yˆ

(

=

SSTR

(zmiennoœã wyjaœniona)

å

-

2

)

i

yˆ

i

y

(

=

SSE

(zmiennoœã niewyjaœniona)

å

å

å

-

+

-

=

-

2

2

2

)

i

yˆ

i

y

(

)

y

i

yˆ

(

)

y

i

y

(

SSTO = SSTR +

SSE

k

n

)

i

yˆ

i

y

(

)

y

(s

)

y

i

y

(

)

i

yˆ

i

y

(

SSTO

SSE

)

y

i

y

(

)

y

i

yˆ

(

SSTO

SSTR

R

-

-

=

-

-

=

=

j

-

-

=

=

å

å

å

å

å

2

2

2

2

2

2

2

•ródùo

Zmiennoœci

Liczba stopni

swobody

Suma

kwadratów

Úredni

kwadrat

Statystyka

F

Model (czynniki)

Bù¹d (reszta)

k

-

1

n

-

k

SSTR

SSE

MSTR

MSE

MSE

MSTR

F

obl

=

Razem

n

-

1

SSTO

Ekonometria

Ekonometria

-

-

15

15

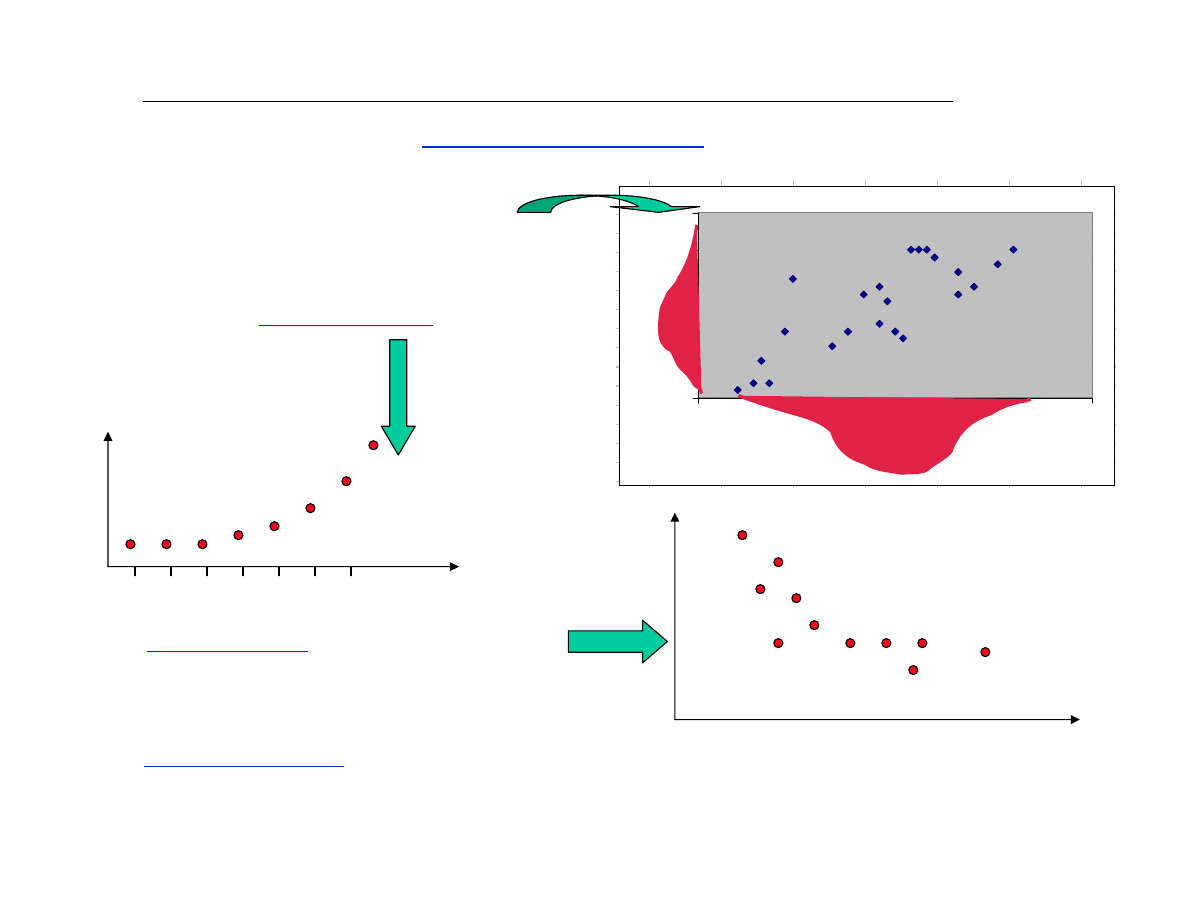
Regresja krzywoliniowa

0

5

10

15

20

25

0

10

20

30

40

50

zmienna X

zm

ie

nn

a

Y

Kiedy wystêpuje regresja liniowa?

— gdy obie

zmienne maj¹ rozkùad normalny!

W wielu przypadkach dane ukùadaj¹ siê w zale¿noœci

nieliniowe:
• gdy maj¹ postaã szeregu czasowego

Y

)

(czas

t

•

gdy dane przekrojowe ukùadaj¹ siê w smugê

nieliniow¹

Y

X

•

gdy krzywoliniowa funkcja wielu zmiennych lepiej opisuje rzeczywistoœã ni¿ funkcja liniowa; (tego nie widaã,

która lepsza mo¿na poznaã tylko po R

2

)

Ekonometria

Ekonometria

-

-

16

16

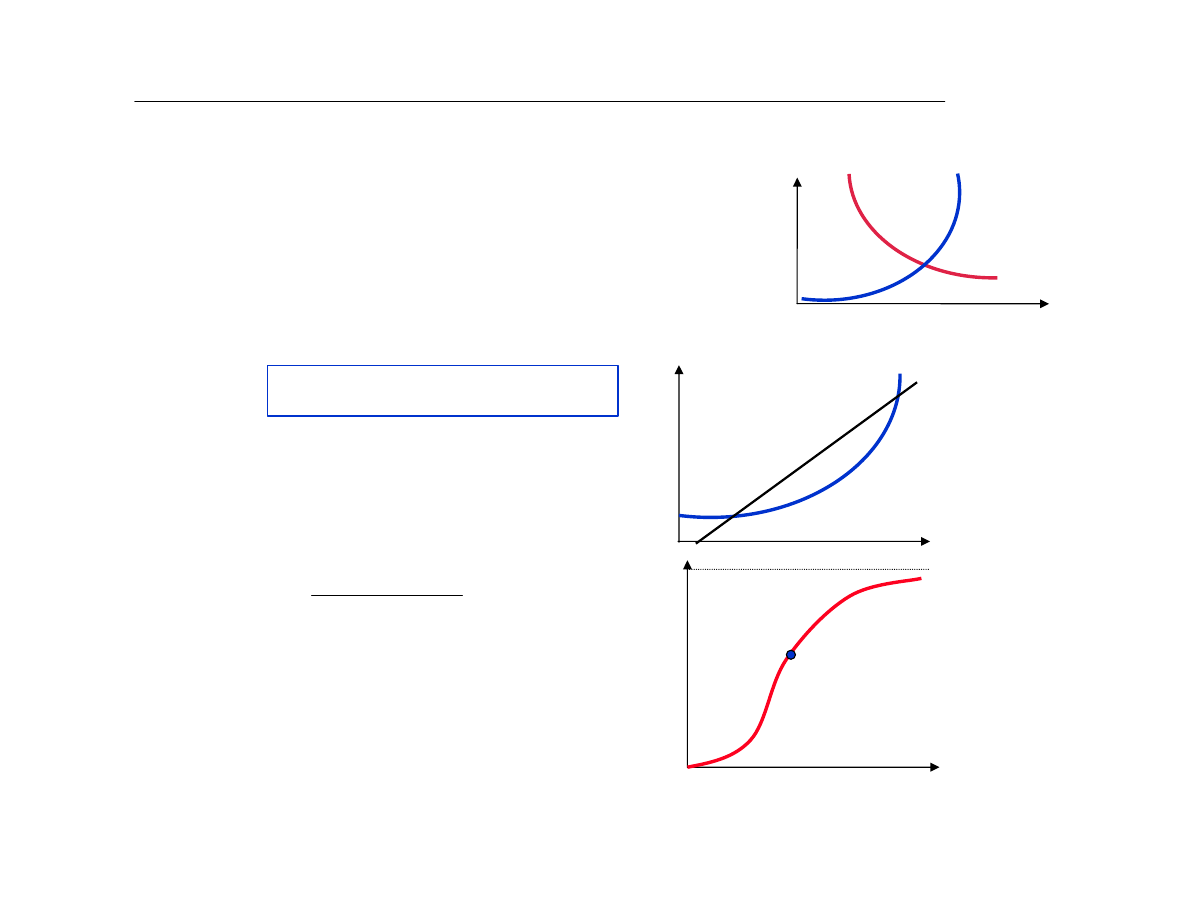
Do opisu takich zjawisk stosujemy rozmaite funkcje krzywoliniowe:

1.

proste funkcje (rosn¹ce lub malej¹ce) dwu zmiennych:

•

wykùadnicze

•

potêgowe itp.

x

×

a

×

a

=

1

0 x

y

1

1

<

a

1

1

>

a

x

y

x

×

×

a

×

a

=

x

e

y

1

0

2. wielomiany ró¿nego stopnia (ich fragmenty)

linia prosta

krzywa

x

y

)

2

(a

x

a

x

a

a

yˆ

0

2

2

1

0

>

+

+

=

3. funkcje bardziej zùo¿one:
• krzywe logistyczne

)

x

(

e

)

x

(

e

y

×

a

+

a

+

×

a

+

a

=

1

0

1

0

1

x

•

funkcje potêgow¹ wielu zmiennych

e

=

...

a

x

a

x

a

x

a

y

3

2

1

3

2

1

0

•

funkcje wykùadnicze wielu zmiennych

x

×

×

a

+

×

a

a

=

+

2

2

1

1

0

x

x

e

y

Ekonometria

Ekonometria

-

-

17

17

ABY MOÝNA BY£O STOSOWAÃ METODÆ NAJMNIEJSZYCH KWADRATÓW, FUNKCJE TE MUSZ¥ BYÃ

SPROWADZONE DO POSTACI LINIOWEJ

1. Uliniowienie przez podstawianie np.

x

+

×

a

+

a

=

=

=

x

+

×

a

+

a

=

'

x

'

y

'

x

x

ln

;'

y

y

ln

x

ln

y

ln

1

0

1

0

2. Transformacja logarytmiczna

e

=

...

a

x

a

x

a

x

a

i

y

3

2

1

3

2

1

0

x

+

+

+

+

+

=

...

x

ln

a

x

ln

a

x

ln

a

a

ln

i

y

ln

3

3

2

2

1

1

0

Kolejnoœã czynnoœci przy estymacji funkcji regresji krzywoliniowej:

1. zebranie danych empirycznych

2. dobranie modelu (funkcji nieliniowej)

3. transformacja modelu do liniowego (logarytmowanie — transformata)

4. przeliczenie danych na ukùad liniowy (robi to komputer)

5. oszacowanie równania regresji liniowej

6. retransformacja do postaci pierwotnej (odlogarytmowanie)

Retransformacji podlegaj¹ tylko parametry strukturalne, natomiast wszystkie parametry stochastyczne

dotycz¹ tylko transformaty

Ekonometria

Ekonometria

-

-

18

18

Klasyczna metoda najmniejszych kwadratów (KMNK)

å

-

-

=

+

=

2

)

i

bx

a

i

y

(

min

SSE

i

bx

a

i

yˆ

å

å

å

å

å

=

+

=

+

i

y

i

x

i

x

a

i

x

b

i

y

i

x

a

bn

2

å

=

=

=

-

n

i

min

SSE

)

i

yˆ

i

y

(

1

2

Metody estymacji równania regresji

• klasyczna metoda najmniejszych kwadratów (KMNK) w wielu wariantach obliczeniowych
• podwójna MNK
• regresje specjalne: grzbietowa (ridge regression), odporna (robust) itd.
• metoda najwiêkszej wiarygodnoœci

Ekonometria

Ekonometria

-

-

19

19

Wersja 2. Metoda „sigma prim” (uproszczona reguùa obliczeniowa ró¿nicy kwadratów)

n

)

i

y

(

i

y

)

y

i

y

(

y

2

2

2

2

S

-

S

=

-

S

=

S¢

Wersja 3. Metoda mno¿ników Gaussa,

posùuguje siê formularzami obliczeniowymi opartymi o wartoœci „sigma

prim”.

Wersja 4. Metoda przeksztaùceñ Jordana
Wersja 5. Metoda macierzowa

x

+

-

-

+

+

+

+

=

1

1

2

2

1

1

0

k

x

k

a

...

i

x

a

i

x

a

a

i

y

y

T

X

)

X

T

X

(

a

1

-

=

ú

ú

ú

ú

û

ù

ê

ê

ê

ê

ë

é

-

=

1

1

0

k

a

...

a

a

a

ú

ú

ú

ú

û

ù

ê

ê

ê

ê

ë

é

-

-

-

=

n

,

k

x

.

n

x

...

.

...

.

,

k

x

.

x

,

k

x

.

x

X

1

1

1

2

1

12

1

1

1

11

1

ú

ú

ú

ú

û

ù

ê

ê

ê

ê

ë

é

=

n

y

.

y

y

y

2

1

X

T

X — wspóùczynniki ukùadu r. n.

X

T

y — prawe strony ukùadu r. n.

1

2

2

1

2

-

=

-

-

=

)

X

T

X

(

s

)

a

(

D

]

a

T

)

y

T

X

(

y

T

y

[

k

n

s

na gùównej przek¹tnej tej macierzy znajduj¹ siê

wariancje

s

2

(a

0

), s

2

(a

1

)

...

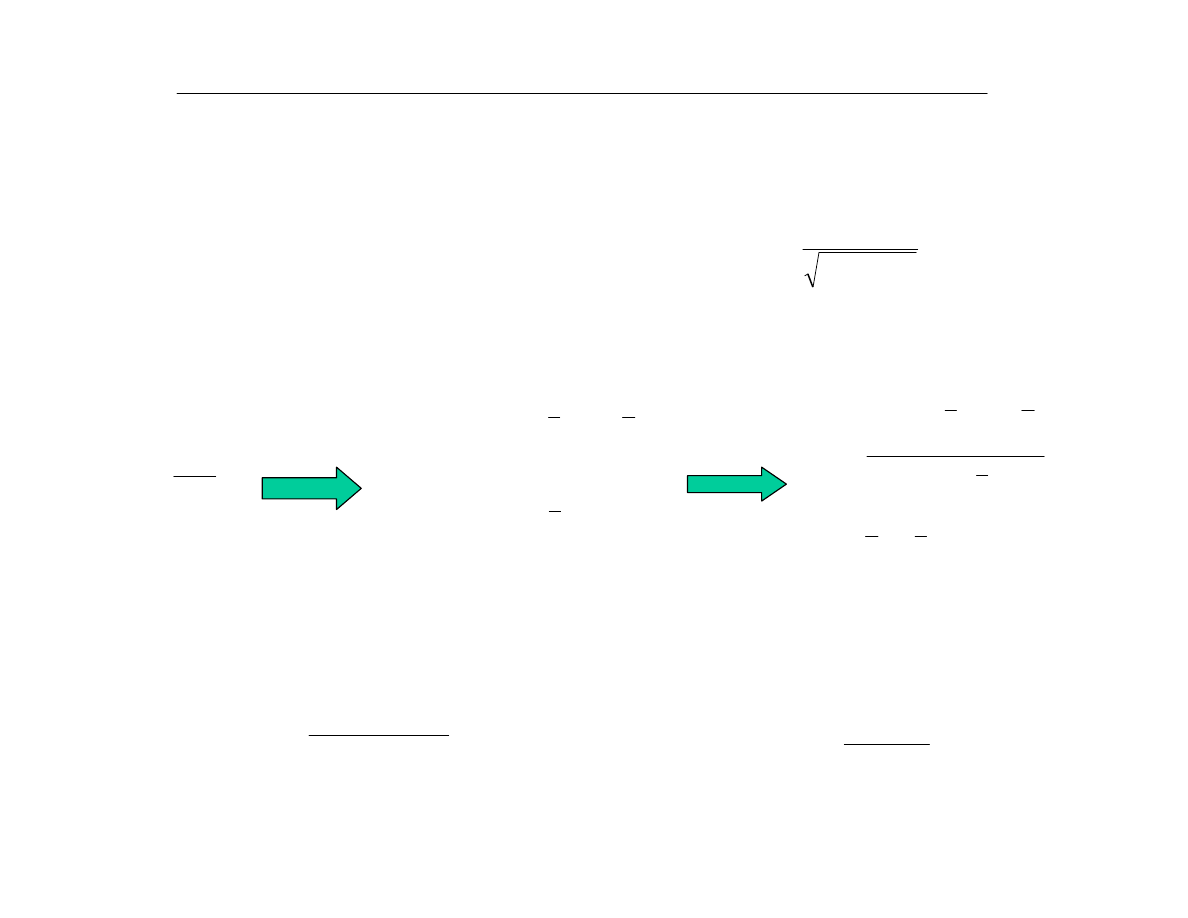
Wersja 6. Metoda uproszczona Hellwiga

Dzielimy zbiór na 2 podzbiory i wyznaczamy ich œrodki ciê¿koœci

x

y

I

II

II

y

,

II

x

I

y

,

I

x

po czym budujemy prost¹ przechodz¹c¹

przez te punkty

Ekonometria

Ekonometria

-

-

20

20

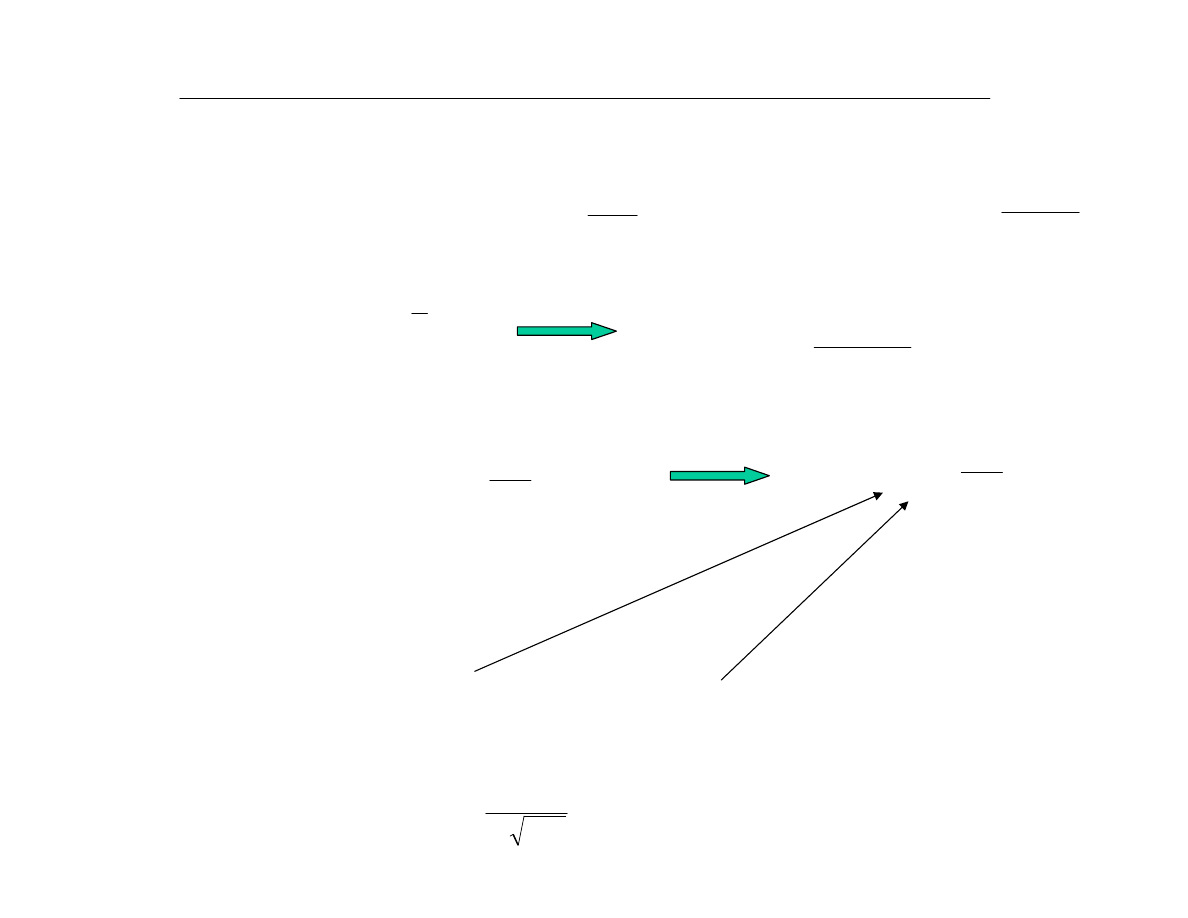
ANALIZA REGRESJI LINIOWEJ

Dla poznania rzeczywistoœci czêsto konieczne jest badanie kilku zmiennych losowych równoczeœnie, wraz ze

zwróceniem uwagi na ich wzajemne powi¹zania.

x

+

+

=

i

bx

a

i

y

Linia regresji II rodzaju zmiennej Y wzglêdem X

yy

S

xx

S

xy

S

r

×

=

Metoda najmniejszych kwadratów MNK pozwala wyznaczyã wspóùczynniki

a

i

b

prostej, która najlepiej

pasuje do zmierzonych punktów.

Wzory na obliczanie wyrazu wolnego

a

i wspóùczynnika regresji

b

KMNK:

x

b

y

a

i

)

x

i

x

(

i

)

y

i

y

)(

x

i

x

(

b

-

=

-

-

-

=

å

å

2

xx

S

xy

S

b

=

(

)

2

å

-

=

i

x

i

x

xx

S

(

)(

)

y

i

y

i

x

i

x

xy

S

-

-

=

å

n

i

i

x

i

i

x

xx

S

2

2

÷

÷

ø

ö

ç

ç

è

æ

-

=

å

å

å

å

å

÷

÷

ø

ö

ç

ç

è

æ

÷

÷

ø

ö

ç

ç

è

æ

-

=

i

n

i

i

y

i

i

x

i

y

i

x

xy

S

Uproszczona reguùa obliczania sumy kwadratów odchyleñ SS

Ekonometria

Ekonometria

-

-

21

21

Estymatorem wariancji

jest s

2

KAÝDEJ WARTOÚCI x

i

ODPOWIADA CA£Y ZBIÓR WARTOÚCI y

i

TWORZ¥CYCH OKREÚLONY ROZK£AD a

p

arametrami tego rozkùadu s¹ E(Y/X) i wariancja

2

s

(

)

å

-

=

i

y

i

y

yy

S

2

( )

xx

S

xy

S

yy

S

xy

S

b

yy

S

SSE

2

-

=

×

-

=

2

2

-

=

n

SSE

s

n

i

i

y

i

i

y

yy

S

2

2

÷

÷

ø

ö

ç

ç

è

æ

-

=

å

å

2

s

Estymator wspóùczynnika regresji

xx

S

b

2

2

s

=

s

)

b

(

E

1

b

=

xx

S

s

b

s

2

2

=

Analiza wspóùczynnika regresji

Test Studenta (t)

xx

S

/

s

b

t

=

a

-

=

×

-

a

+

<

b

<

×

-

a

-

1

2

2

1

2

2

)

b

s

n

;

/

t

b

b

s

n

;

/

t

b

(

P

•

weryfikuj¹c hipotezê — H

0

: â

1

=0 wobec H

1

: â

1

¹

0

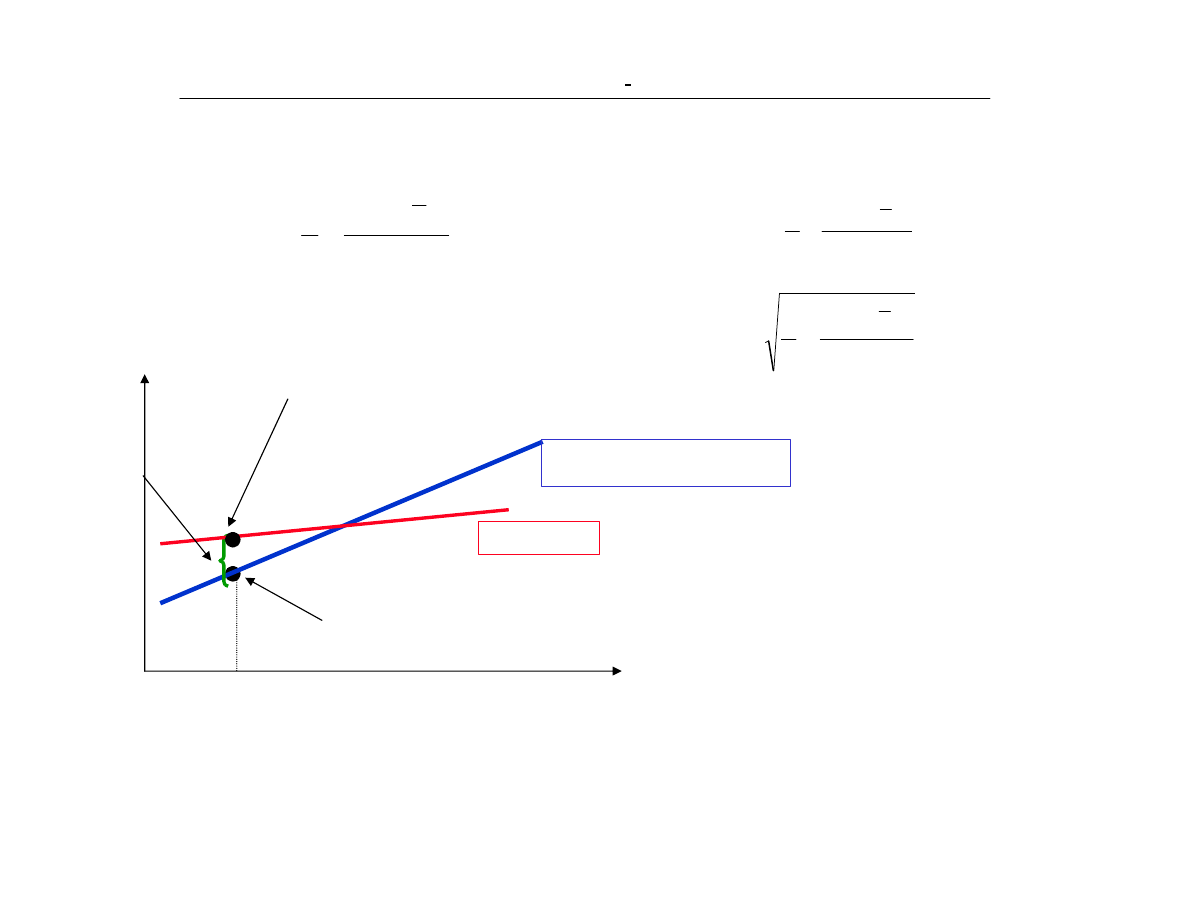
Estymacja E(Y/X) wartoœci oczekiwanej y dla danej wartoœci X

Ekonometria

Ekonometria

-

-

22

22

Y

p

x

X

E(Y|X=x

p

)

Prognozowana wartoϋ y|x

p

Bù¹d

•

przedziaù ufnoœci dla

a

-

=

×

-

a

+

<

<

×

-

a

-

1

2

2

2

2

)

y

s

n

;

/

t

p

y

)

p

x

/

Y

(

E

y

s

n

;

/

t

p

y

(

P

p

p

X

)

p

x

X

|

Y

(

E

1

0

b

+

b

=

=

E(Y|X=x

p

)

i

bx

a

i

yˆ

+

=

(

)

xx

S

x

p

x

n

s

yˆ

s

p

2

1

-

+

=

estymator

(

)

ú

ú

û

ù

ê

ê

ë

é

-

+

=

xx

p

p

y

S

x

x

n

2

2

2

ˆ

1

s

s

(

)

ú

ú

û

ù

ê

ê

ë

é

-

+

=

xx

p

y

S

x

x

n

s

p

s

2

2

2

ˆ

1

X

)

X

|

Y

(

E

1

0

b

+

b

=

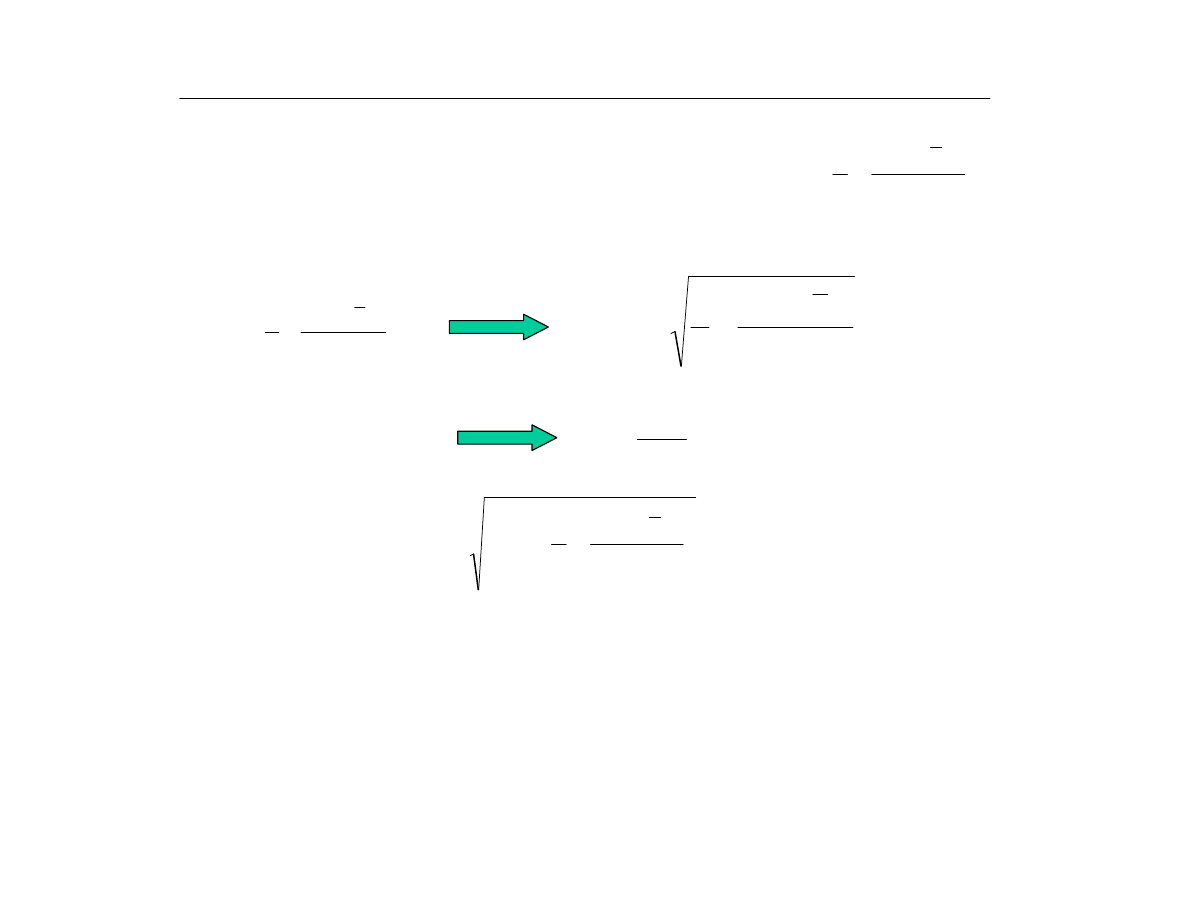
Ekonometria

Ekonometria

-

-

23

23

•

przedziaù ufnoœci dla prognozy y

p

2

2

-

=

n

SSE

s

2

s

(

)

ú

ú
û

ù

ê

ê
ë

é

-

+

+

s

=

s

+

s

=

-

s

xx

S

x

p

x

n

yˆ

yˆ

y

p

p

2

1

1

2

2

2

2

(

)

ú

ú
û

ù

ê

ê
ë

é

-

+

s

=

s

xx

S

x

p

x

n

yˆ

p

2

1

2

2

(

)

xx

p

p

y

S

x

x

n

s

s

2

ˆ

1

-

+

=

Z zale¿noœci:

a

-

=

-

×

-

a

+

<

<

-

×

-

a

-

1

2

2

2

2

)

yˆ

y

s

n

;

/

t

p

yˆ

p

x

/

y

yˆ

y

s

n

;

/

t

p

yˆ

(

P

p

p

(

)

ú

ú
û

ù

ê

ê
ë

é

-

+

+

=

-

xx

S

x

p

x

n

s

yˆ

y

s

p

2

1

1

2

obliczamy:

Wydruk komputerowy równania regresji

Peùny zapis równania regresji liniowej

Y

— zmienna zale¿na, zmienna-skutek, zmienna objaœniana

y

i

— zaobserwowane wartoœci zmiennej zale¿nej dla jednostek próbki

X

— zmienna niezale¿ne, zmienna-przyczyny, zmienna objaœniaj¹ca

x

i

— zaobserwowane wartoœci zmiennej niezale¿nej

a

— oszacowana wartoœã wyrazu wolnego

parametry strukturalne i stochastyczne

Ekonometria

Ekonometria

-

-

24

24

Wspóùczynniki: korelacji liniowej Persona r, determinacji r

2

, zbie¿noœci

j

2

, bù¹d resztowy

s(y) i inne

P(a)

P(b)

t(a)

t(b)

s(a)

s(b)

a

b

Wyraz wolny

Czynnik X

Rzeczywisty poziom

istotnoœci P

Statystyka

t

obl

Bù¹d

oszacowania

Wartoϋ

oszacowana

Zmienna

(czynnik)

)

b

(

s

)

a

(

s

bx

a

i

yˆ

x

+

+

=

r

b

— oszacowana wartoœci wspóùczynnika regresji; okreœla wpùyw zmiennej X na zmienn¹ Y

x

— skùadnik losowy, reprezentuj¹cy rozrzut punktów wokóù prostej regresji; skùadnik ten jest

zmienn¹

losow¹;

jego wartoœci nazywaj¹ siê

reszty

i

yˆ

i

y

i

e

-

=

a jego rozkùad jest rozkùadem normalnym o E(

x

)=0 i V(

x

)=s

2

(y)

s(a)

— bù¹d oszacowania wyrazu wolnego; sùu¿y do budowy przedziaùu ufnoœci dla nieznanej wartoœci

wyrazu wolnego dla populacji oraz do weryfikacji jego istotnoœci (H

0

:

b

0

=0)

s(b)

— bù¹d oszacowania wspóùczynnika regresji; sùu¿y do budowy przedziaùu ufnoœci dla nieznanej wartoœci

b

1

wspóùczynnika regresji dla populacji oraz do weryfikacji jego istotnoœci (H

0

:

b

1

=0)

s(y)

— bù¹d resztowy; jest odchyleniem standardowym skùadnika losowego

x

;

okreœla œredni¹ wielkoœã

reszty e

i

r

2

— wspóùczynnik determinacji; okreœla jaka czêœã zmiennoœci caùkowitej

SSTO

zostaùa wyjaœniona przez

równanie regresji

j

2

— wspóùczynnik zbie¿noœci (zgodnoœci); okreœla jaka czêœã zmiennoœci caùkowitej

SSTO

nie zostaùa

wyjaœniona przez równanie regresji

Ekonometria

Ekonometria

-

-

25

25

x

+

+

=

i

bx

a

i

y

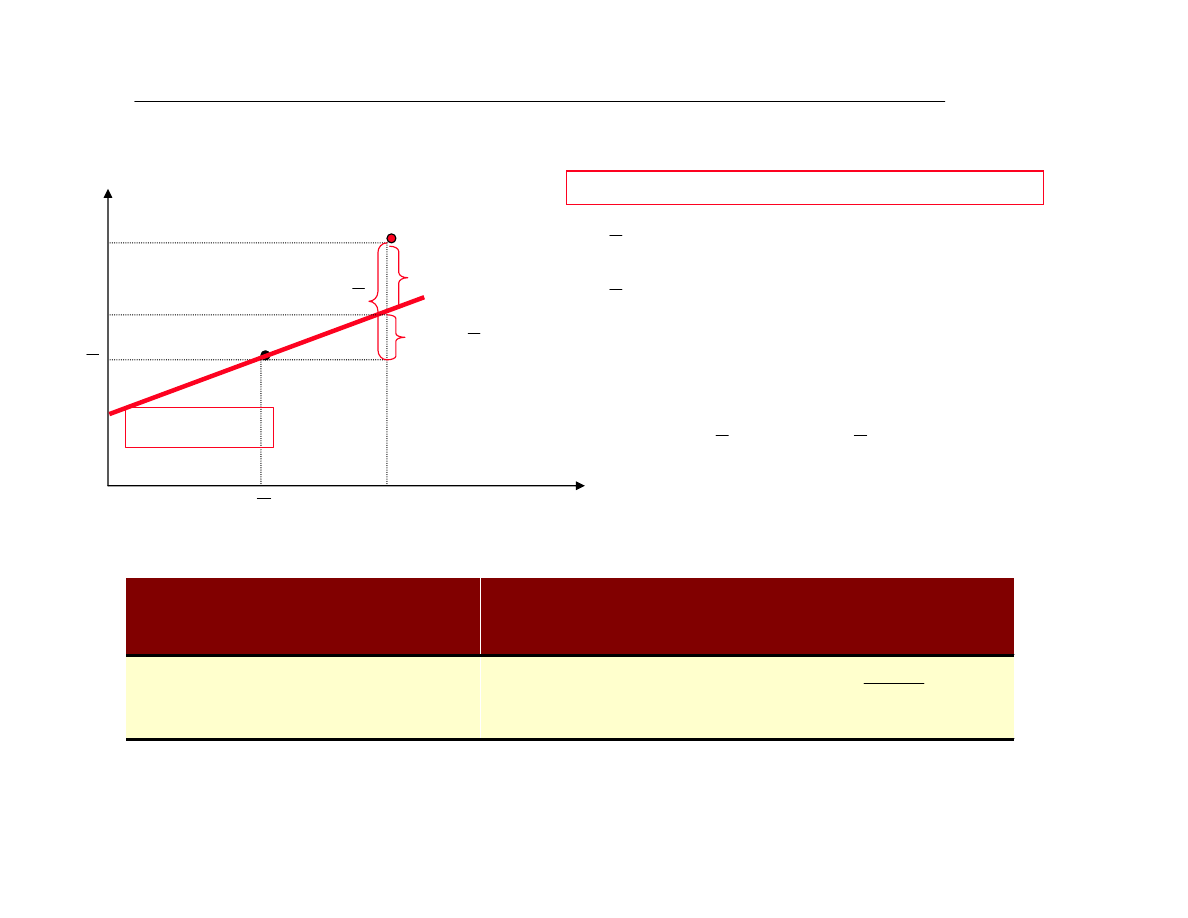
X

Y

x

y

i

x

i

y

i

yˆ

y

y

i

-

i

i

y

y ˆ

-

y

y

i

-

ˆ

å

-

2

)

y

i

y

(

=

SSTO

(zmiennoœã caùkowita)

å

-

2

)

y

i

yˆ

(

=

SSTR

(zmiennoœã wyjaœniona)

å

-

2

)

i

yˆ

i

y

(

=

SSE

(zmiennoœã niewyjaœniona)

å

å

å

-

+

-

=

-

2

2

2

)

i

yˆ

i

y

(

)

y

i

yˆ

(

)

y

i

y

(

SSTO = SSTR +

SSE

•ródùo

Zmiennoœci

Liczba

stopni

swobody

Suma

kwadratów

Úredni

kwadrat

Statystyka

F

Model (czynniki)

Bù¹d (reszta)

2

-

1

n

-

2

SSTR

SSE

MSTR

MSE

MSE

MSTR

F

obl

=

Razem

n

-

1

SSTO

Ekonometria

Ekonometria

-

-

26

26

ANALIZA WARIANCJI

i

i

bx

a

y

+

=

ˆ

Ekonometria

Ekonometria

-

-

27

27

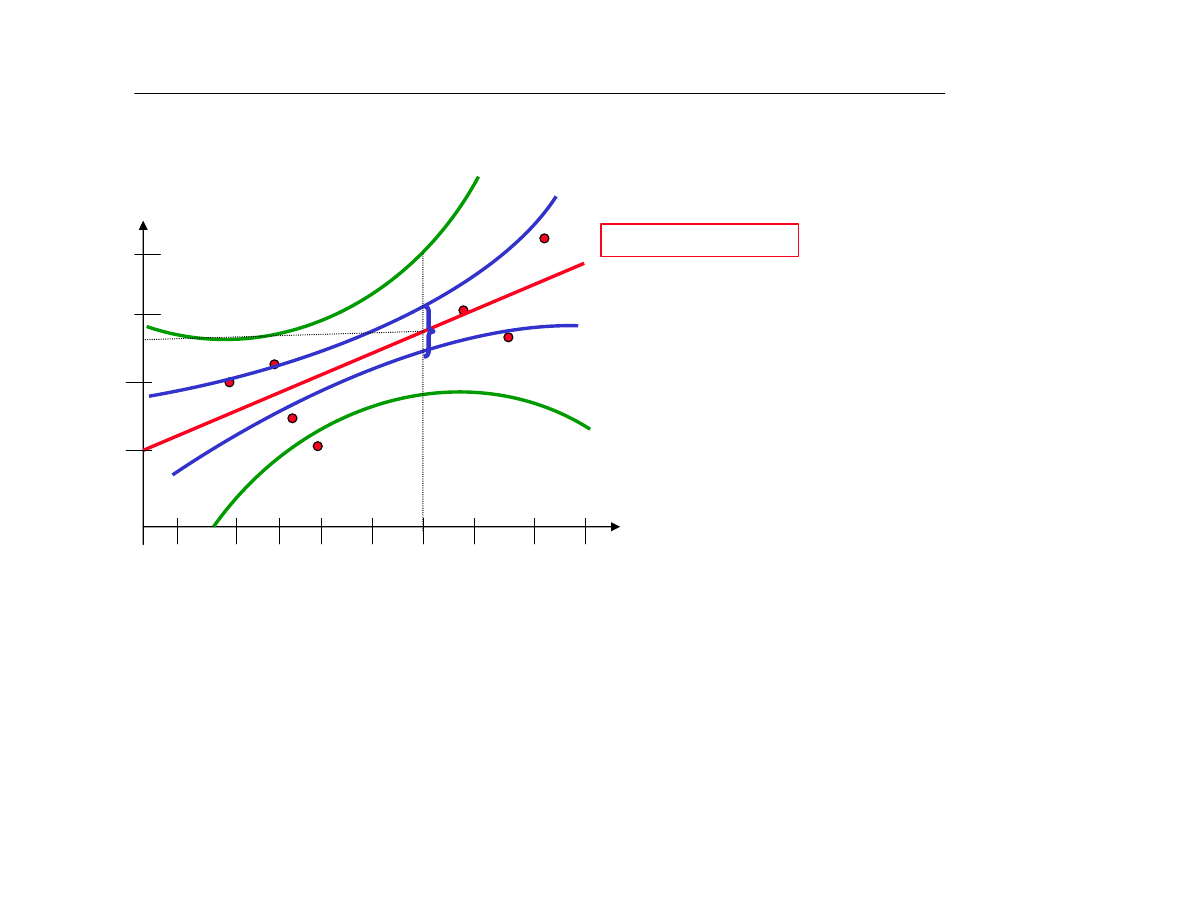
Przykùad

Wpùyw wydatków na reklamê na wielkoœã sprzeda¿y

Miesi¹c

Wydatki na reklamê (X)

(mln zù)

Wartoœã sprzeda¿y (Y)

(mln zù)

1.

1,2

101

2.

0,8

92

3.

1,0

110

4.

1,3

120

5.

0,7

90

6.

0,8

82

7.

1,0

93

8.

0,6

75

9.

0,9

91

10.

1,1

105

Regression Analysis - Linear model: Y = a+bX

----------------------------------------------------------------------------------

Standard

T

Prob.

Parameter

Estimate

Error

Value

Level

----------------------------------------------------------------------------------

Intercept

46.4865

9.8846

4.7029

0.00154

Slope

52.5676

10.2609

5.1231

0.00090

----------------------------------------------------------------------------------

Correlation Coefficient = 0.8754 R-squared = 76.64 (%)

Stnd. Error of Est. = 6.83715

= 46,49 + 52,57x

i

+

x

r=0,88

r=0,88

9,88

10,26

6,84

i

yˆ

Ekonometria

Ekonometria

-

-

28

28

X

Y

p

x

*

p

y

0,6

0,7

0,8 0,9 1,0 1,1 1,2 1,3

x

,

,

i

yˆ

57

52

49

46

+

=

120

110

90

70

50

Estymacja E(y/ x=1,0) wartoœci oczekiwanej y dla x

p

=1,0

95

0

24

104

0

1

88

93

,

)

,

)

,

x

/

Y

(

E

,

(

P

=

<

=

<

Prognozowanie wartoœci y dla x=1,0

Prognoza punktowa:

06

,

99

)

0

,

1

)(

57

,

52

(

49

,

46

ˆ

=

+

=

y

Prognoza przedziaùowa:

95

0

66

115

0

1

46

82

,

)

,

,

x

/

yˆ

,

(

P

=

<

=

<

Przedziaù ufnoœci dla wspóùczynnika regresji

Interpretacja:
Zmiana miesiêcznych wydatków na reklamê o jedn¹ jednostkê (1 mln zù) spowoduje zmianê

wielkoœci sprzeda¿y w przedziale od 28,9 do 76,24 mln zù.

Ekonometria

Ekonometria

-

-

29

29

95

,

0

)

24

,

76

90

,

28

(

P

1

=

<

b

<

Badanie parametrów strukturalnych modelu

ANALIZA WARIANCJI

•ródùo

Zmiennoœci

Liczba

stopni

swobody

Suma

kwadratów

Úredni

kwadrat

Statystyka

F

Model (czynniki)

Bù¹d (reszta)

1
8

1226,9

374,0

1226,9

46,7

MSE

MSTR

F

obl

=

=26,25

Razem

9

1600,9

H

0

:

b

1

= 0

H

1

:

b

1

¹

0

F

MSE

MSTr

xx

S

s

b

t

=

=

÷÷ø

ö

ççè

æ

=

2

2

F

1;8;0,025

=7,57

Wniosek: 77% zmiennoœci y wyjaœnia wyestymowany model