Prezentowany artykuª

I

Matteo Ciccarelli, Alessandro Rebucci Measuring contagion

with a bayesian, time-varying coecient model, ECB working

paper no. 263, wrzesie« 2003

I

Efekt zara»enia (contagion) to transmisja szoków mi¦dzy

rynkami (krajami). Na potrzeby tej pracy efekt zara»enia to

czasowa zmiana charakteru wzajemnych oddziaªywa« mi¦dzy

rynkami nast¦puj¡ca na skutek szoku na jednym lub wielu z

tych rynków.

Ogólna specykacja modelu

Model VAR ze wspóªczynnikami zmiennymi w czasie:

A

t

(

L)Y

t

=

B

t

(

L)W

t

+

D

t

+

U

t

gdzie:

I

Y

t

= [

y

1

t

, . . . ,

y

n

t

]

0

- wektor cen lub wielko±ci aktywów

I

W

t

= [

w

1

t

, . . . ,

w

m

t

]

0

- wektor zmiennych b¦d¡cych ¹ródªem

szoków

I

L - operator opó¹nienia;

I

A

t

i B

t

macierze wielomianowe operatora opó¹nie« p i q

odpowiednio

I

D

t

wektor staªych, U

t

- wektor szoków specycznych dla

danego kraju lub rynku o macierzy wariancji-kowariancji Σ

Charakterystyka modelu

Zaªo»enia modelu:

I

wspóªczynniki zmienne w czasie

I

heteroskedastyczno±¢

I

zmienne pomini¦te

Zalety modelu:

I

jednoczesne badanie wspóªzale»no±ci rynków i efektu zara»enia

I

brak konieczno±ci okre±lenia momentu rozpocz¦cia kryzysu

I

w tym podej±ciu mo»liwa jest modykacja modelu, dzi¦ki

której pod uwag¦ wzi¦te s¡ te» zmienne pomini¦te.

Dokªadna specykacja modelu

Y

t

=

X

t

β

t

+

t

,

gdzie X

t

jest macierz¡ rozmiaru n × k, β

t

rozmiaru k × 1, gdzie

k = np + mq + 1, a Y

t

i

t

to wektorowe procesy stochastyczne

Zaªo»enia:

I

t

|

X

t

∼

iid, gdzie E[

t

|

X

t

] =

0 i E[

t

0

t

|

X

t

] = Σ

;

I

β

t

=

Gβ

t−1

+

F β

0

+

Hζ

t

, gdzie ζ

t

∼

iid N(0, Φ);

I

X

t

,

t

i ζ

t

s¡ warunkowo niezale»ne;

I

t

|

X

t

∼

iid t

ν

(

0, Ω), gdzie Ω =

ν−

2

ν

Σ

i ν > 2.

Dokªadna specykacja modelu

Przyjmuj¡c powy»sze zaªo»enia otrzymujemy nast¦puj¡cy model:

Y

t

=

X

t

˜

β

t−1

+ ˜

t

,

gdzie

˜

β

t−1

=

Gβ

t−1

+

F β

0

i ˜

t

=

X

t

Hζ

t

+

t

,

i

E[Y

t

|

X

t

] =

X

t

˜

β

t−1

i V [Y

t

|

X

t

] = Σ +

X

t

HΦH

0

X

0

t

Y

t

jest warunkowo heteroskedastyczny, z nieliniow¡ warunkow¡

±redni¡; co wi¦cej nie ma rozkªadu normalnego, co jest

charakterystyczne dla danych nansowych o wysokiej cz¦sto±ci.
Rozkªady a priori s¡ przypisywane hiperparametrom modelu - Σ, ˜β

0

,

Φ

i ν.

Estymacja Bayesowska

Wªasno±ci priorów:

I

Niezale»no±¢ priorów: p(Σ, β

0

, Φ, ν) =

p(Σ)p(β

0

)

p(Φ)p(ν),

I

p(Σ

−

1

) =

W (ς, S),

I

p(β

0

) =

N(β

∗

0

, Ω)

,

I

p(Φ

−

1

) =

W (q, Q),

I

p(ν) = Uniform(2, r)

W oznacza rozkªad Wisharta; zakªadamy, »e parametry tych

rozkªadów s¡ znane.
Estymacja metod¡ losowania Gibbsa - estymatory obci¡»one.
Korekta zmiennych pomini¦tych metod¡ Leamera.

Werykacja estymacji

I

dla wygenerowanych danych o najwi¦kszym obci¡»eniu

(metod¡ Monte Carlo) w celu sprawdzenia, czy procedura

estymacji poka»e nieprawdziwo±¢ hipotezy efektu zara»enia,

I

dla prawdziwych danych porównanie wyników modelu z

modelem uwzgledniaj¡cym istotnie wi¦ksz¡ liczb¦ danych

Werykacja estymacji dla danych wygenerowanych

Zaªo»enia:

I

poª¡czenia mi¦dzy rynkami s¡ stabilne w czasie,

I

wyst¦puj¡ wspóªzale»no±ci mi¦dzy rynkami,

I

na skutek szoku wspólnego dla obydwu rynków zmienia si¦

zmienno±¢,

I

model mierz¡cy efekt zara»enia pomija zmienn¡ wyra»aj¡c¡

ten szok (na przykªad dla tego, »e jest nieobserwowalna),

I

procedura estymacji zawiera w sobie korekt¦ obci¡»enia

wynikaj¡cego ze zmiennych pomini¦tych.

Werykacja estymacji dla danych wygenerowanych

Dane generowane s¡ za pomoc¡ nast¦puj¡cego modelu:

y

t

= β

x

t

+ γ

z

t

+

t

,

gdzie x

t

= δ

z

t

+

u

t

, z

t

= ρ

z

t−1

+ η

t

, t = 1, . . . , 200.

I

z

t

- zmiena pomijana; pewien specyczny dla kraju czynnik;

I

x

t

- ¹ródªo szoku lub krysysu;

I

y

t

- zmienne charakterystyczne dla kraju ulegaj¡cego zara»eniu.

Rozkªady parametrów modelu s¡ tak dobrane, »eby reprezentowaªy

najgorszy mo»liwy przypadek.

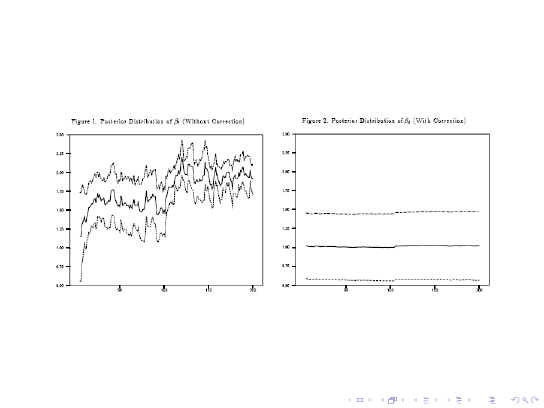
Rozkªad aposteriori parametru β

t

Przykªad Chile

Badanie efektu zara»enia rynku walutowego w Chile przez kryzys

argenty«ski w 2001 roku - odwoªanie do wcze±niejszego modelu

jednego z autorów.
Pomini¦cie zmiennych u»ywanych w tamtym modelu celem

sprawdzenia, czy model o ograniczonej informacji da takie same

wyniki jak model z peªniejsz¡ informacj¡.
Estymacja obydwu modeli bez korekty i z korekt¡ Leamera.
Prezentowany model dobrze nadaje si¦ do tego typu zjawiska ze

wzgl¦du na charakter kryzysu argenty«skiego.
Dane do modeli s¡ danymi dziennymi i pochodz¡ z okresu od 2

czerwca 1999 do 31 stycznia 2002 roku, co daje 641 obserwacji.

Specykacja modelu

Z peªn¡ informacj¡:

DLe

t

= α

0

t

+ α

1

t

DLe

t−1

+

Z

0

t

γ

t

+

t

,

gdzie e

t

jest kursem peso do dolara, Dx

t

=

x

t

−

x

t−1

,

Lx

t

=

log(x

t

)

, a Z

t

reprezentuje zbiór kilkunastu potencjalnych

zmiennych obja±niaj¡cych.
Z ograniczon¡ informacj¡:

DLe

t

= α

0

t

+ α

1

t

DLe

t−1

+ γ

t

Di

AR

t

+

t

,

gdzie i

A

t

R jest argenty«skim indeksem gieªdowym.

Uwagi

I

Model z peªn¡ informacj¡ te» mo»e wykazywa¢ obci¡»enie

zwi¡zane ze zmiennymi pomini¦tymi.

I

W modelu z ograniczon¡ informacj¡ nie uwzgl¦dniono nawet

tych zmiennych, o których wiadomo z poprzedniego

opracowania, »e w sposób istotny wyja±niaj¡ zmian¦ kursu

peso.

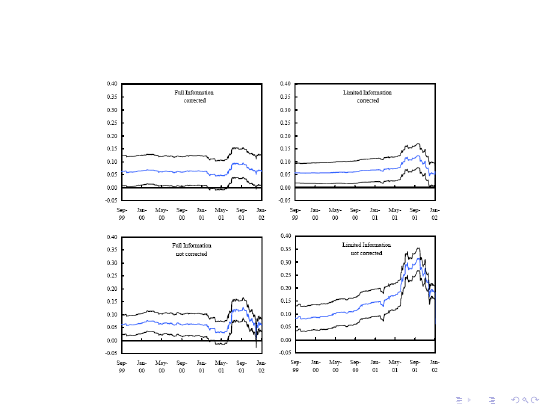
‘rednia w rozkªadzie aposteriori parametru γ

t

Podsumowanie

I

Estymacja daje dobre wyniki nawet dla modelu

heteroskedastycznego z pomini¦tymi zmiennymi.

I

Model nie wymaga znajomo±ci dokªadnego czasu kryzysu i

pozwala na odró»nienie efektu zara»enia od wspóªzale»no±ci i

zaªama« strukturalnych.

I

Model nadaje si¦ do mierzenia zarówno pozytywnych jak i

negatywnych efektów zara»enia.

I

Wyniki otrzymane w prezentowanym modelu z ograniczon¡

informacj¡ skorygowanym o potencjalne obci¡»enie wynikaj¡ce

ze zmiennych pomini¦tych s¡ porównywalne z wynikami

estymacji z u»yciem peªniejszej informacji.