Podatki i wielko
Podatki i wielko
ść
ść
szarej
szarej
strefy: Analiza
strefy: Analiza
nieparametryczna na
nieparametryczna na
podstawie Nowej Zelandii
podstawie Nowej Zelandii
Na
Na
podstawie
podstawie
: David E. A. Giles & Betty J. Johnson,
: David E. A. Giles & Betty J. Johnson,
Maj
Maj
2000
2000
Department
Department
of
of
Economics
Economics
,
,
University
University
of
of
Victoria,
Victoria,
Canada
Canada
Opracowali
Opracowali
: Monika
: Monika
Mroczek
Mroczek
, Adam
, Adam
Wo
Wo
ź
ź
ny
ny
Wst
Wst
ę
ę
p
p
Autorzy tekstu postanowili zbada
Autorzy tekstu postanowili zbada
ć
ć
zwi
zwi
ą
ą
zek
zek
mi
mi
ę
ę
dzy efektywn
dzy efektywn
ą
ą
stop
stop
ą
ą
opodatkowania a
opodatkowania a
wzgl
wzgl
ę
ę
dn
dn
ą
ą
wielko
wielko
ś
ś
ci
ci
ą
ą
szarej strefy,
szarej strefy,
Oszacowany zosta
Oszacowany zosta
ł
ł
model, maj
model, maj
ą
ą
cy
cy
symulowa
symulowa
ć
ć
skutki hipotetycznych zmian
skutki hipotetycznych zmian
podatkowych na rozmiar szarej strefy w
podatkowych na rozmiar szarej strefy w
Nowej Zelandii
Nowej Zelandii
Analiza zosta
Analiza zosta
ł
ł
a przeprowadzona za pomoc
a przeprowadzona za pomoc
ą
ą
nieparametrycznej regresji korzystaj
nieparametrycznej regresji korzystaj
ą
ą
c z
c z
danych z okresu 1968
danych z okresu 1968
-
-
1994
1994
Podstawy teoretyczne
Podstawy teoretyczne
Ju
Ju
ż
ż
pierwsze modele zak
pierwsze modele zak
ł
ł
ada
ada
ł
ł
y hipotez
y hipotez
ę
ę
o
o
dodatnim zwi
dodatnim zwi
ą
ą
zku miedzy wielko
zku miedzy wielko
ś
ś
ci
ci
ą
ą
stopy
stopy
opodatkowania a wielko
opodatkowania a wielko
ś
ś
ci
ci
ą
ą
szarej strefy
szarej strefy
Model
Model
Trandel
Trandel
&
&
Snow
Snow
wyr
wyr
ó
ó
ż
ż
nia dwa obszary,
nia dwa obszary,
pierwszy o dosy
pierwszy o dosy
ć
ć
niskim potencjalnym dochodzie,
niskim potencjalnym dochodzie,
co za tym idzie do
co za tym idzie do
ść
ść
niskimi p
niskimi p
ł
ł
aconymi podatkami.
aconymi podatkami.
(Przyjmujemy ze kary za uchylanie si
(Przyjmujemy ze kary za uchylanie si
ę
ę
od p
od p
ł
ł
acenia
acenia
podatku s
podatku s
ą
ą
proporcjonalne do wielko
proporcjonalne do wielko
ś
ś
ci
ci
niezap
niezap
ł
ł
aconego podatku). W takiej sytuacji sektor
aconego podatku). W takiej sytuacji sektor
ten ch
ten ch
ę
ę
tniej b
tniej b
ę
ę
dzie si
dzie si
ę
ę
stara
stara
ł
ł
uchyli
uchyli
ć
ć
od p
od p
ł
ł
acenia
acenia
podatku ze wzgl
podatku ze wzgl
ę
ę
du na relatywnie niski poziom
du na relatywnie niski poziom
kary, a drugi obszar odwrotnie.
kary, a drugi obszar odwrotnie.
Wst
Wst
ę
ę
p
p
cd
cd
.
.
Forma hipotezy jest dosy
Forma hipotezy jest dosy
ć
ć
skomplikowana gdy
skomplikowana gdy
ż
ż
np
np
. znak zwi
. znak zwi
ą
ą
zku mi
zku mi
ę
ę
dzy stop
dzy stop
ą
ą
podatkow
podatkow
ą
ą
i
i
stopniem uchylania si
stopniem uchylania si
ę
ę
od podatk
od podatk
ó
ó
w zale
w zale
ż
ż
y czy
y czy
przyj
przyj
ę
ę
te jest za
te jest za
ł
ł
o
o
ż
ż
enie o niech
enie o niech
ę
ę
ci ryzyka os
ci ryzyka os
ó
ó
b
b
p
p
ł
ł
ac
ac
ą
ą
cych podatki
cych podatki
Podstawowym problem jest dost
Podstawowym problem jest dost
ę
ę
pno
pno
ść
ść
danych
danych
dotycz
dotycz
ą
ą
cych rozmiaru szarej strefy
cych rozmiaru szarej strefy
Dane te s
Dane te s
ą
ą
szacowane raczej na podstawie
szacowane raczej na podstawie
warto
warto
ś
ś
ci "ukrytej" produkcji, ni
ci "ukrytej" produkcji, ni
ż
ż
na podstawie
na podstawie
wielko
wielko
ś
ś
ci
ci
łą
łą
cznej si
cznej si
ł
ł
y roboczej. Aby u
y roboczej. Aby u
ł
ł
atwi
atwi
ć
ć
mi
mi
ę
ę
dzynarodowe por
dzynarodowe por
ó
ó
wnania, liczby te zwykle s
wnania, liczby te zwykle s
ą
ą
odniesione jako stopa procentowa zmierzonego
odniesione jako stopa procentowa zmierzonego
GDP
GDP
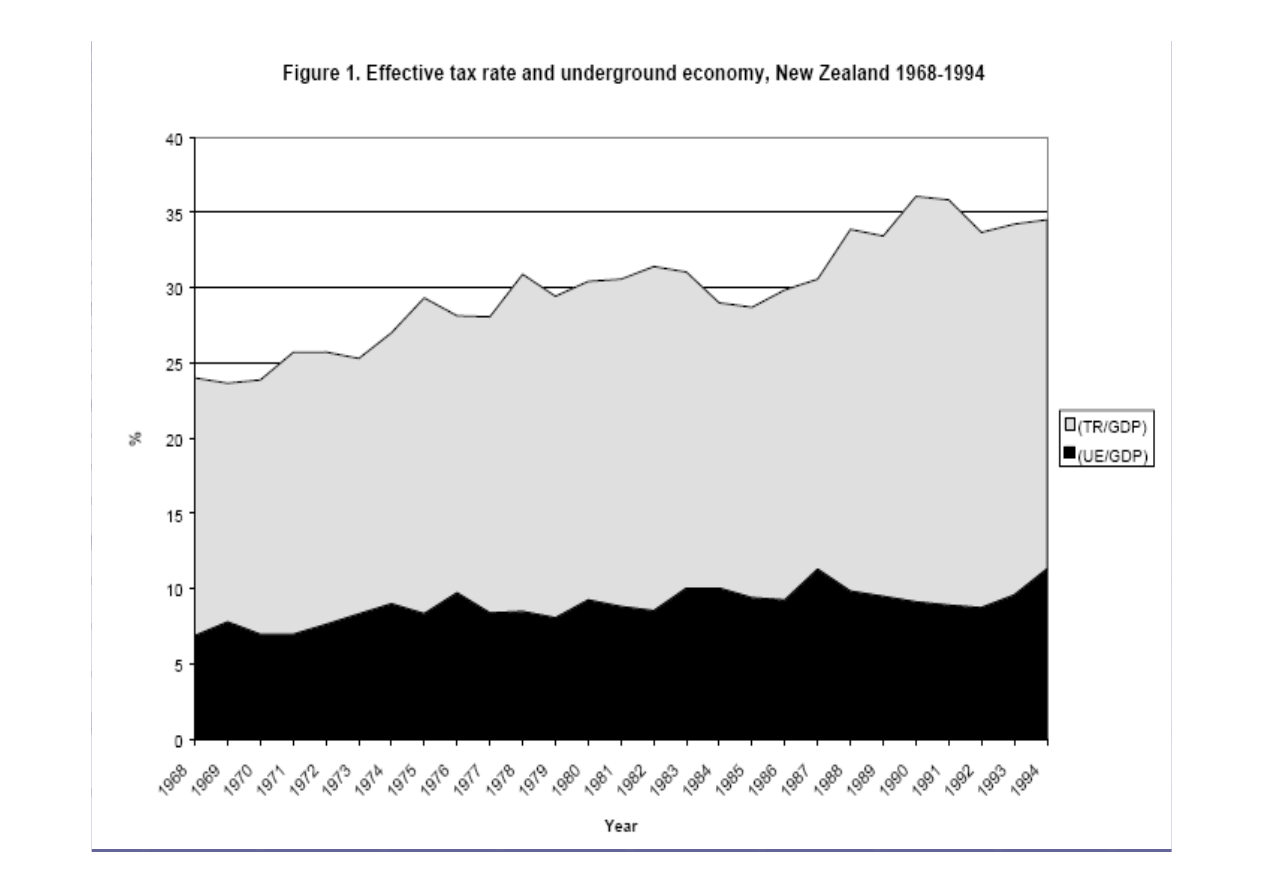
w poni
w poni
ż
ż
szym modelu rozmiar szarej strefy
szym modelu rozmiar szarej strefy
zosta
zosta
ł
ł
zdefiniowany jako (UE / GDP)
zdefiniowany jako (UE / GDP)
a efektywna stopa podatkowa jako:
a efektywna stopa podatkowa jako:
(TR / GDP),
(TR / GDP),
gdzie TR jest ca
gdzie TR jest ca
ł
ł
kowitym przychodem
kowitym przychodem
podatkowym
podatkowym
Wst
Wst
ę
ę
pne testy
pne testy
Przed rozpocz
Przed rozpocz
ę
ę
ciem estymacji
ciem estymacji
przeprowadzono nast
przeprowadzono nast
ę
ę
puj
puj
ą
ą
ce testy :
ce testy :
testy na stacjonarno
testy na stacjonarno
ść
ść
zmiennych
zmiennych
testy na
testy na
kointegracje
kointegracje
test na przyczynowo
test na przyczynowo
ść
ść
Testy na stacjonarno
Testy na stacjonarno
ść
ść
zmiennych
zmiennych
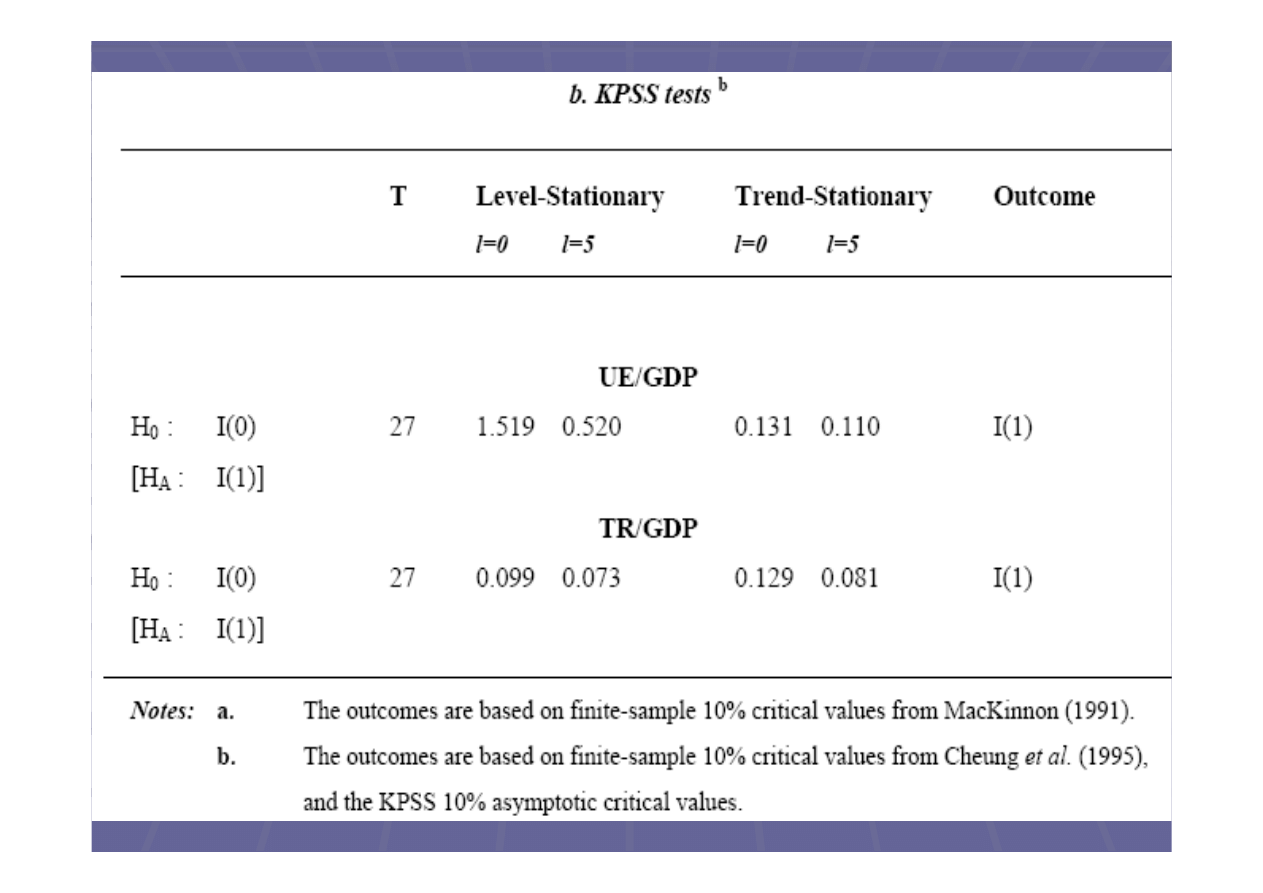
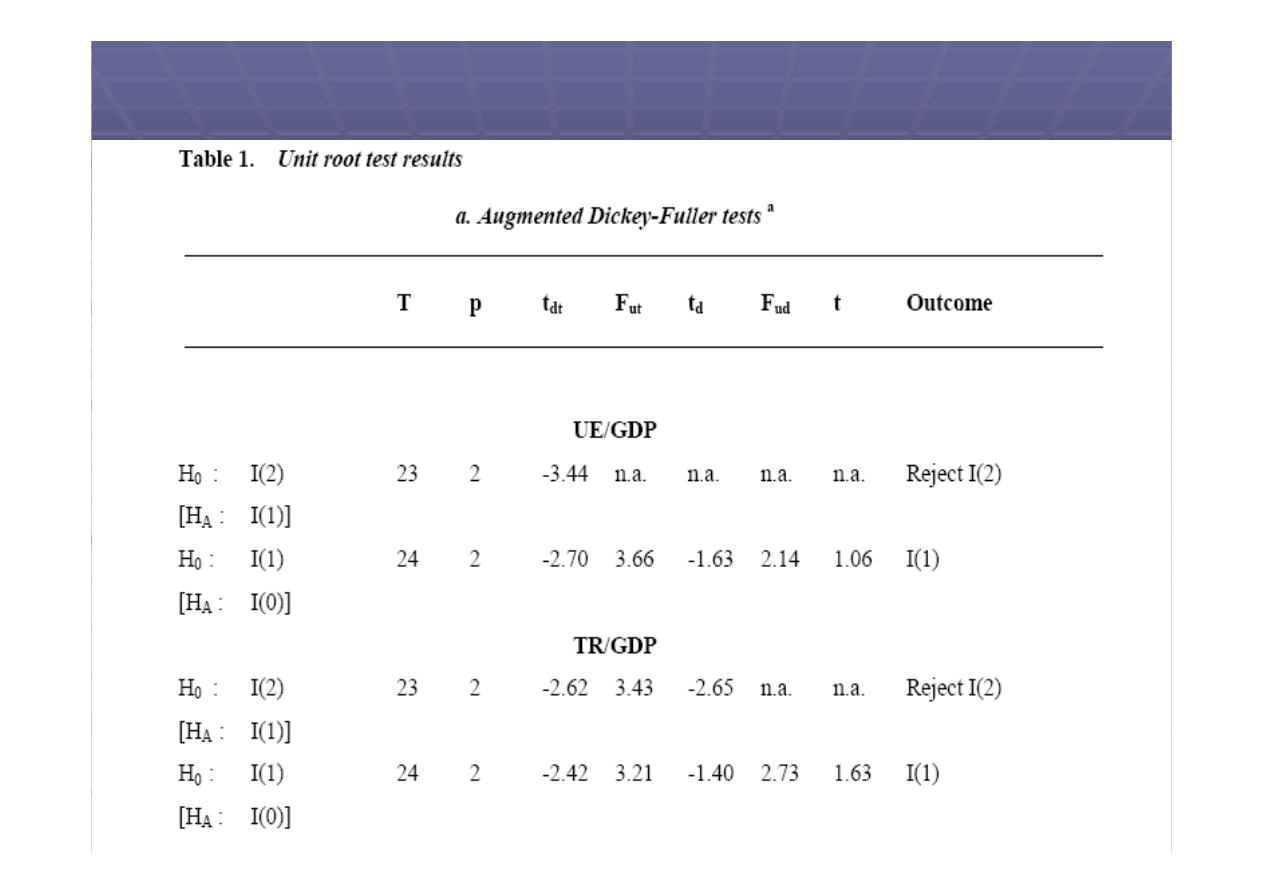
W powy
W powy
ż
ż
szej tabeli zosta
szej tabeli zosta
ł
ł
y przedstawione
y przedstawione
nast
nast
ę
ę
puj
puj
ą
ą
ce testy na stacjonarno
ce testy na stacjonarno
ść
ść
,
,
test
test
Dickey
Dickey
-
-
Fullera
Fullera
(ADF) sprawdzaj
(ADF) sprawdzaj
ą
ą
cego
cego
hipotez
hipotez
ę
ę
zerow
zerow
ą
ą
o niestacjonarno
o niestacjonarno
ś
ś
ci
ci
oraz
oraz
test
test
Kwiatowskiego
Kwiatowskiego
(KPSS) w kt
(KPSS) w kt
ó
ó
rym testuje
rym testuje
si
si
ę
ę
hipotez
hipotez
ę
ę
zerow
zerow
ą
ą
o stacjonarno
o stacjonarno
ś
ś
ci
ci
zmiennych .
zmiennych .
Przyj
Przyj
ę
ę
ty zosta
ty zosta
ł
ł
10% poziom istotno
10% poziom istotno
ś
ś
ci
ci
Testy
Testy
cd
cd
.
.
Wyniki uzyskane w Tabeli 1 wskazuj
Wyniki uzyskane w Tabeli 1 wskazuj
ą
ą
,
,
ż
ż
e zar
e zar
ó
ó
wno (UE / GDP) i (TR / GDP) s
wno (UE / GDP) i (TR / GDP) s
ą
ą
niestacjonarne, sensowne jest wi
niestacjonarne, sensowne jest wi
ę
ę
c
c
przetestowanie mo
przetestowanie mo
ż
ż
liwej
liwej
kointegracji
kointegracji
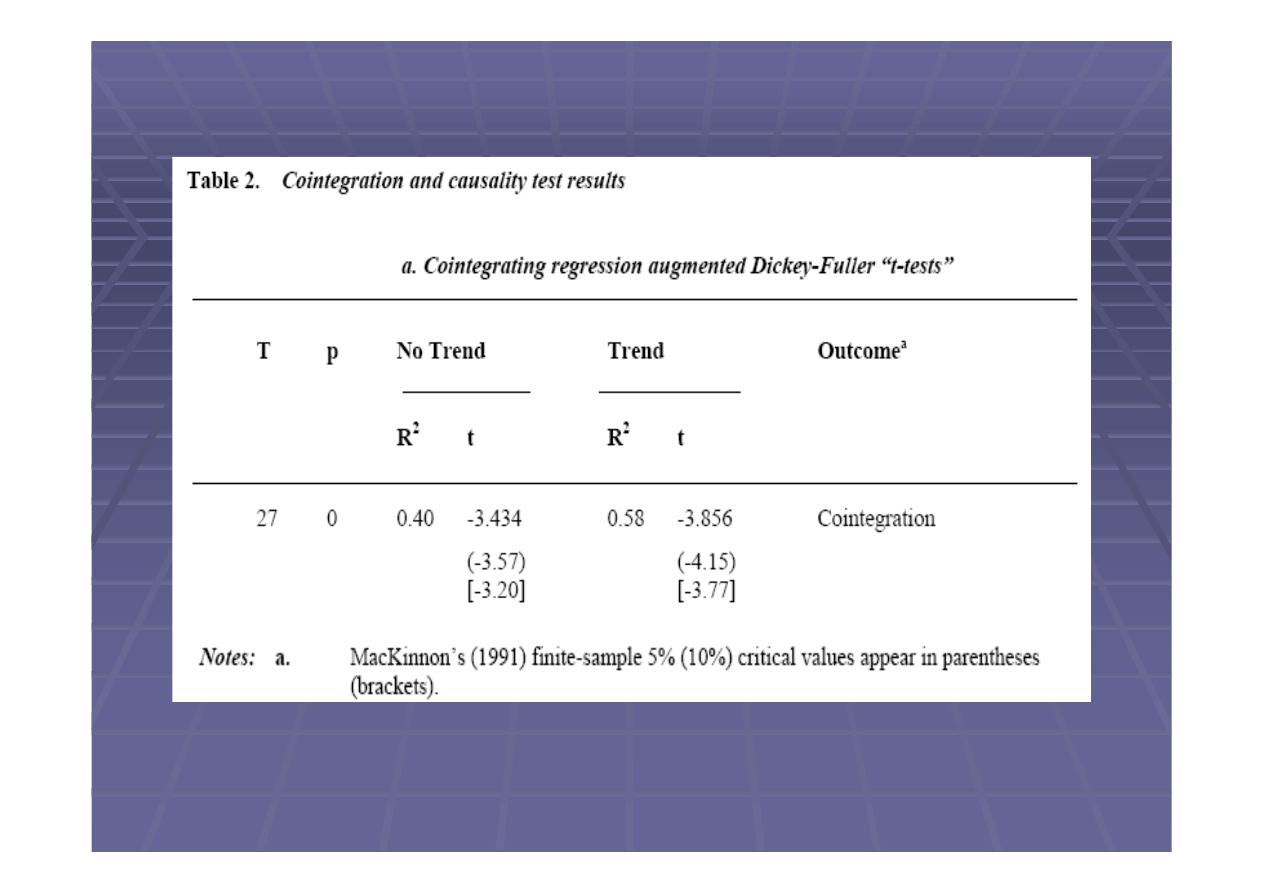
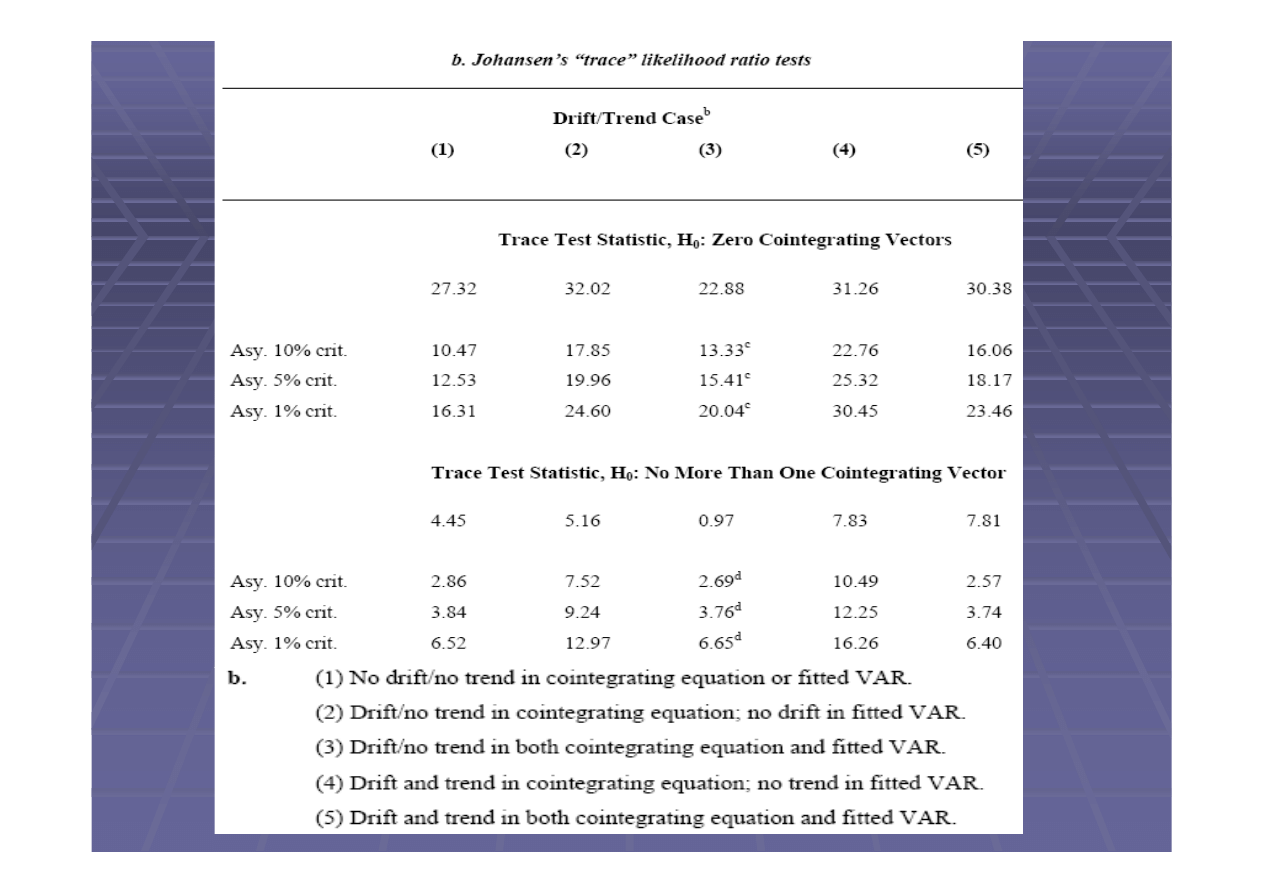
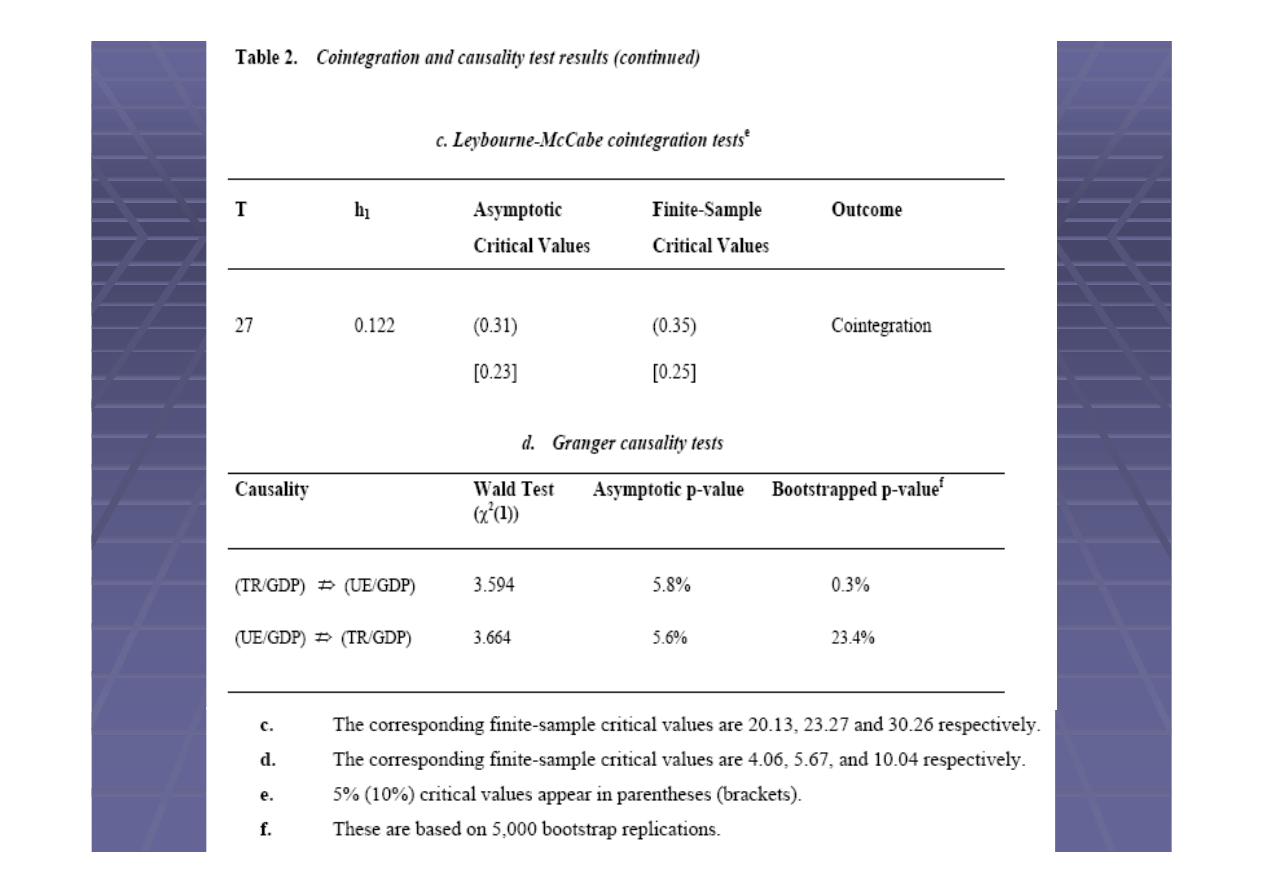
Powy
Powy
ż
ż
sze testy potwierdzaj
sze testy potwierdzaj
ą
ą
wyst
wyst
ę
ę
powanie
powanie
kointegracji
kointegracji
Przetestowano tak
Przetestowano tak
ż
ż
e przyczynowo
e przyczynowo
ść
ść
mi
mi
ę
ę
dzy
dzy
zmiennymi (UE / GDP) i (TR / GDP), u
zmiennymi (UE / GDP) i (TR / GDP), u
ż
ż
ywaj
ywaj
ą
ą
c
c
podej
podej
ś
ś
cia
cia
Toda
Toda
-
-
Yamamoto
Yamamoto
(1995). Wyniki
(1995). Wyniki
ś
ś
wiadcz
wiadcz
ą
ą
o przyczynowo
o przyczynowo
ś
ś
ci od drugiej
ci od drugiej
zmiennej do pierwszej , ale tylko ograniczony
zmiennej do pierwszej , ale tylko ograniczony
dow
dow
ó
ó
d odwrotnej przyczynowo
d odwrotnej przyczynowo
ś
ś
ci.
ci.
(potwierdza to empiryczny model z (UE /
(potwierdza to empiryczny model z (UE /
GDP) jako zmienn
GDP) jako zmienn
ą
ą
zale
zale
ż
ż
n
n
ą
ą
)
)
Estymacja
Estymacja
Forma funkcyjna
Forma funkcyjna
(UE/
(UE/
GDP)
GDP)
t
t
=
=
m{(TR
m{(TR
/
/
GDP)
GDP)
t
t
} +
} +
ε
ε
t
t
Gdzie
Gdzie
funkcja m
funkcja m
–
–
warunkowa
warunkowa
ś
ś
rednia
rednia
ε
ε
t
t
–
–
maj
maj
ą
ą
rozk
rozk
ł
ł
ad normalny, s
ad normalny, s
ą
ą
niezale
niezale
ż
ż
ne i
ne i
homoskedastyczne
homoskedastyczne
Spos
Spos
ó
ó
b estymacji
b estymacji
Estymacja r
Estymacja r
ó
ó
wnania przeprowadzona zosta
wnania przeprowadzona zosta
ł
ł
a
a
za pomoc
za pomoc
ą
ą
procedury NONPAR, kt
procedury NONPAR, kt
ó
ó
ra
ra
wykorzystuje estymator
wykorzystuje estymator
Nadaraya
Nadaraya
-
-
Watson`a
Watson`a
z normalnym j
z normalnym j
ą
ą
drem (
drem (
kernel
kernel
) i rozmiarem
) i rozmiarem
okna (
okna (
bandwidth
bandwidth
) wybranym za pomoc
) wybranym za pomoc
ą
ą
„
„
optymalnej
optymalnej
”
”
metody
metody
Silvermana
Silvermana
.
.
Przeprowadzone testy dowiod
Przeprowadzone testy dowiod
ł
ł
y, i
y, i
ż
ż
wyniki
wyniki
nie s
nie s
ą
ą
w szczeg
w szczeg
ó
ó
lny spos
lny spos
ó
ó
b wra
b wra
ż
ż
liwe na
liwe na
wyb
wyb
ó
ó
r j
r j
ą
ą
dra oraz rozmiaru okna.
dra oraz rozmiaru okna.
Inne formy funkcyjne
Inne formy funkcyjne
Aby upewni
Aby upewni
ć
ć
si
si
ę
ę
czy ta prosta forma
czy ta prosta forma
funkcyjna jest odpowiednia, autorzy brali
funkcyjna jest odpowiednia, autorzy brali
r
r
ó
ó
wnie
wnie
ż
ż
pod uwag
pod uwag
ę
ę
takie zmienne jak wzrost
takie zmienne jak wzrost
realnego GDP oraz op
realnego GDP oraz op
ó
ó
ź
ź
nione zmienne
nione zmienne
UE/GDP i TR/GDP.
UE/GDP i TR/GDP.
Ż
Ż
adna z nowo utworzonych form funkcyjnych
adna z nowo utworzonych form funkcyjnych
nie zosta
nie zosta
ł
ł
a wskazana jako ta lepsza przez
a wskazana jako ta lepsza przez
standardowe kryteria informacyjne, wi
standardowe kryteria informacyjne, wi
ę
ę
c
c
oszacowany zosta
oszacowany zosta
ł
ł
podstawowy model.
podstawowy model.
Wyniki estymacji
Wyniki estymacji
Bandwidth
Bandwidth
Parameter
Parameter
0.548
0.548
R2 (
R2 (
Adjusted
Adjusted
R2)
R2)
0.492 (0.428)
0.492 (0.428)
Cross
Cross
-
-
Validation
Validation
Mean
Mean
Square
Square
Error
Error
0.794
0.794
AIC (SC) [FPE]
AIC (SC) [FPE]
0.842 (1.016) [0.844]
0.842 (1.016) [0.844]
Durbin
Durbin
-
-
Watson
Watson
Statistic
Statistic
1.433
1.433
Runs
Runs
Test,
Test,
Normal
Normal
Statistic
Statistic
(
(
p
p
-
-
value
value
)
)
-
-
0.975
0.975
(0.330)
(0.330)
Coefficient
Coefficient
of
of
Skewness
Skewness
(Standard
(Standard
Deviation
Deviation
)
)
0.956
0.956
(0.448)
(0.448)
Coefficient
Coefficient
of
of
Excess
Excess
Kurtosis
Kurtosis
(Standard
(Standard
Deviation
Deviation
)
)
0.665
0.665
(0.872)
(0.872)
Jarque
Jarque
-
-
Bera
Bera
,
,
Chi
Chi
-
-
Square
Square
, asy.
, asy.
χ
χ
2(2) (
2(2) (
p
p
-
-
value
value
)
)
3.681
3.681
(0.159)
(0.159)
Chi
Chi
-
-
Square
Square
Goodness
Goodness
of
of
Fit, asy.
Fit, asy.
χ
χ
2(3) (
2(3) (
p
p
-
-
value
value
)
)
6.094
6.094
(0.107)
(0.107)
Analiza reszt
Analiza reszt
Testy LM
Testy LM
LM(1), asy. Standard
LM(1), asy. Standard
Normal
Normal
(
(
p
p
-
-
value
value
)
)
1.006 (0.157)
1.006 (0.157)
LM(2), asy. Standard
LM(2), asy. Standard
Normal
Normal
(
(
p
p
-
-
value
value
)
)
0.208 (0.418)
0.208 (0.418)
LM(3), asy. Standard
LM(3), asy. Standard
Normal
Normal
(
(
p
p
-
-
value
value
)
)
0.205 (0.419)
0.205 (0.419)
LM(4), asy. Standard
LM(4), asy. Standard
Normal
Normal
(
(
p
p
-
-
value
value
)
)
0.152 (0.440)
0.152 (0.440)
Test FRESET
Test FRESET
AIC (SC) [FPE]
AIC (SC) [FPE]
0.842 (1.016) [0.844]
0.842 (1.016) [0.844]
FRESETS(1)a: AIC (SC) [FPE]
FRESETS(1)a: AIC (SC) [FPE]
0.995 (1.479) [1.016]
0.995 (1.479) [1.016]
FRESETS(2)a: AIC (SC) [FPE]
FRESETS(2)a: AIC (SC) [FPE]
1.110 (2.086) [1.215]
1.110 (2.086) [1.215]
FRESETS(3)a: AIC (SC) [FPE]
FRESETS(3)a: AIC (SC) [FPE]
1.330 (2.395) [1.333]
1.330 (2.395) [1.333]
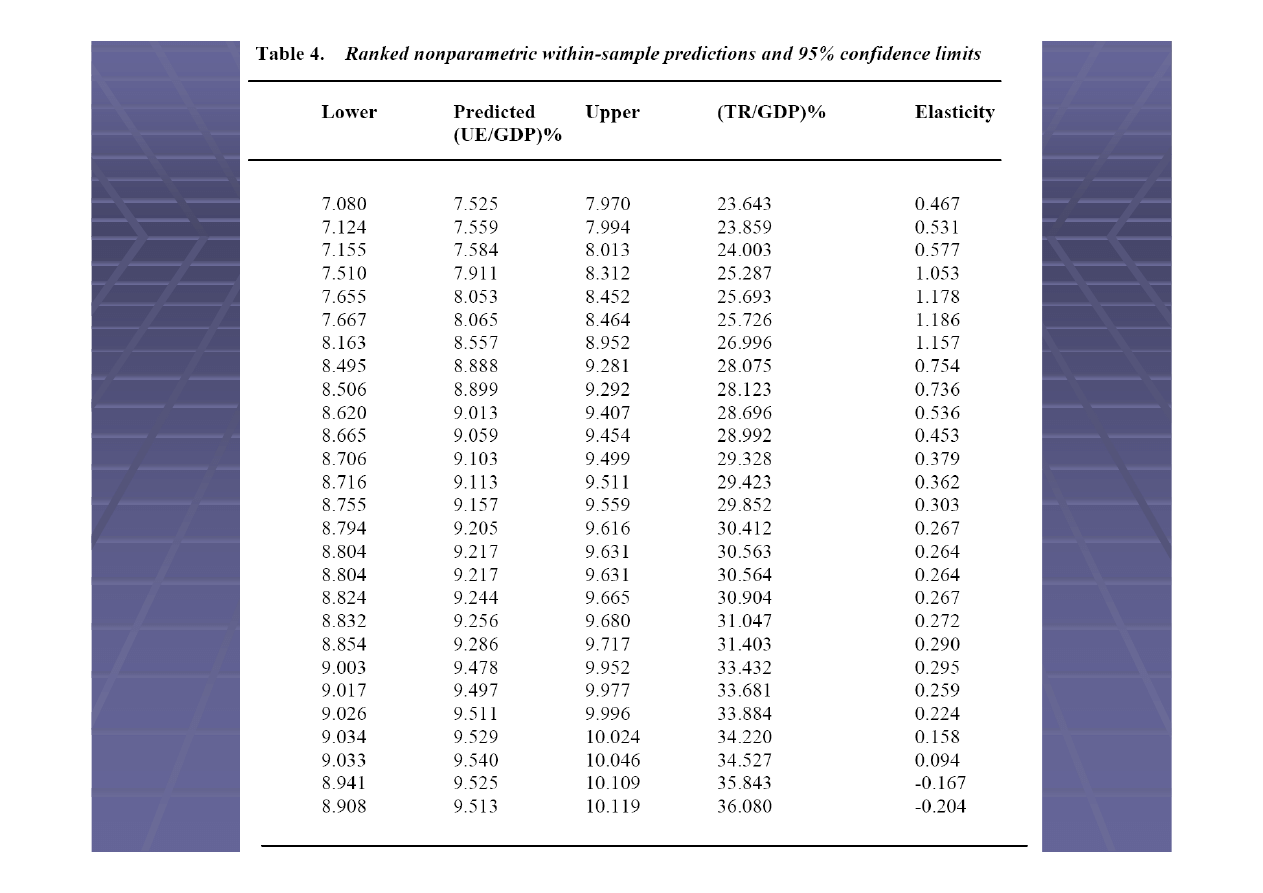
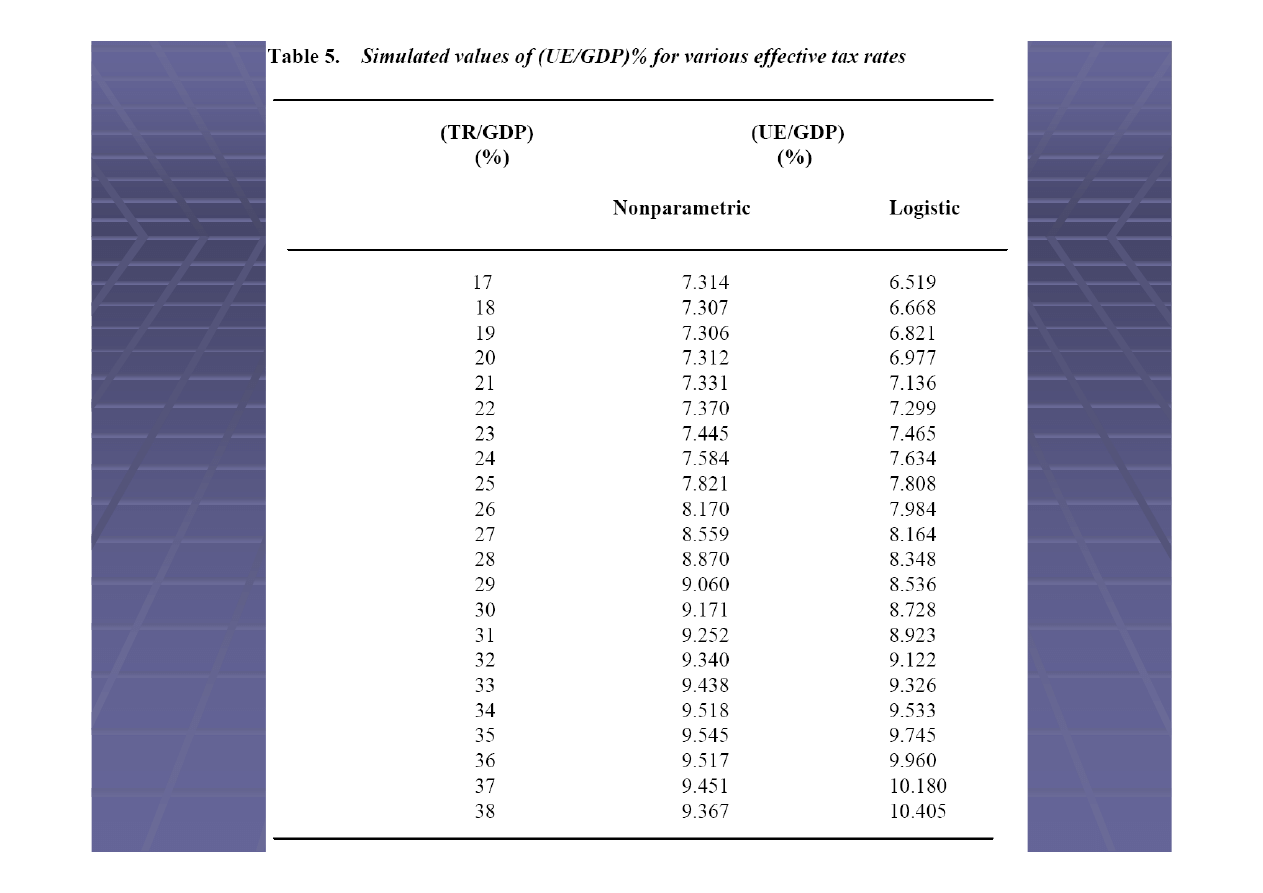
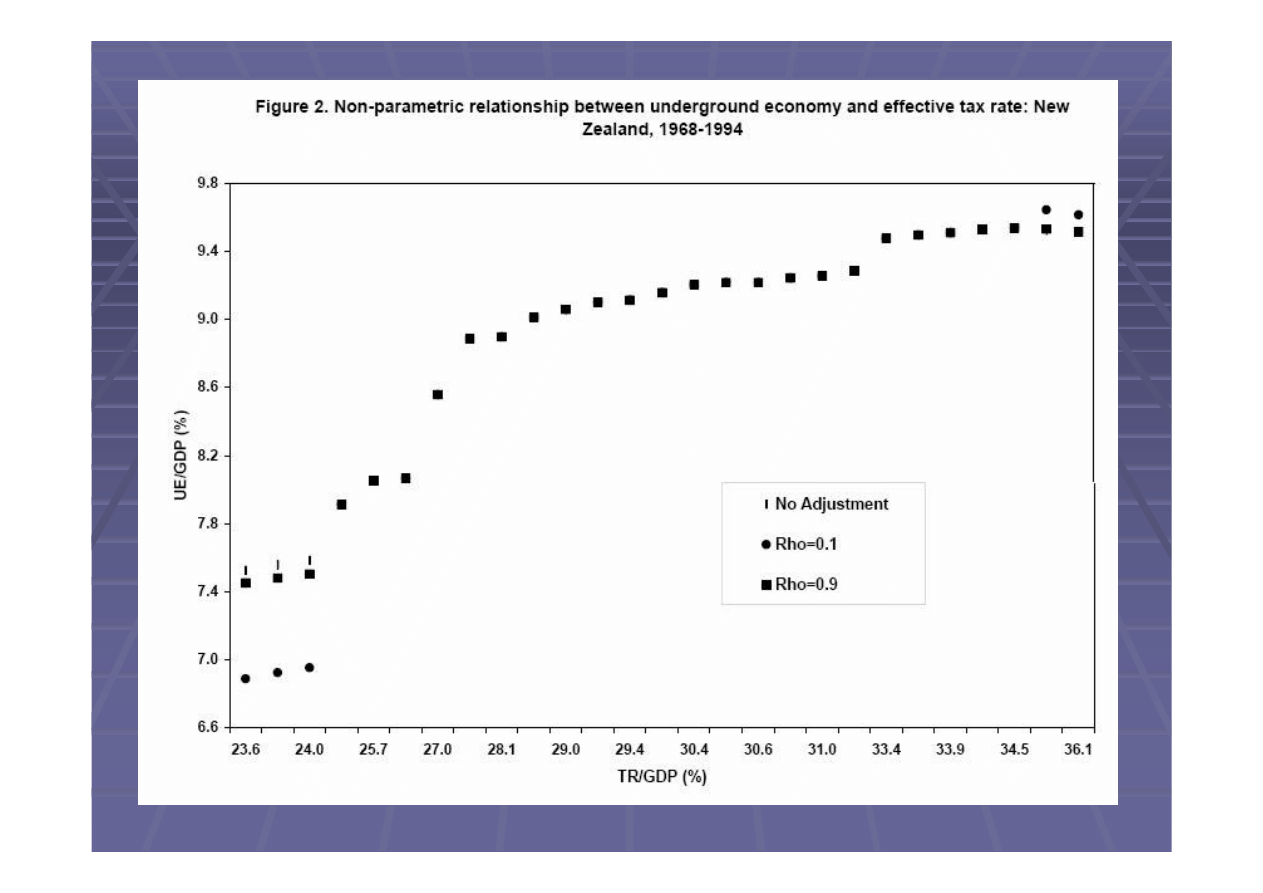
Wniosek
Wniosek
Istnieje zgodno
Istnieje zgodno
ść
ść
pomi
pomi
ę
ę
dzy poziomem
dzy poziomem
opodatkowania niezb
opodatkowania niezb
ę
ę
dnym z punktu
dnym z punktu
widzenia wzrostu gospodarczego, a
widzenia wzrostu gospodarczego, a
opodatkowania z punktu widzenia
opodatkowania z punktu widzenia
problemu powi
problemu powi
ę
ę
kszaj
kszaj
ą
ą
cej si
cej si
ę
ę
szarej
szarej
strefy.
strefy.
Dzi
Dzi
ę
ę
kujemy za
kujemy za
uwag
uwag
ę
ę