Taxes, Risk-Aversion, and the Size of the Underground
Economy: A Nonparametric Analysis With New
Zealand Data
David E. A. Giles & Betty J. Johnson
Department of Economics, University of Victoria
Victoria, B. C., V8W 2Y2, Canada
Revised, May 2000
Opracowali: Monika Mroczek
Adam Woźny
Ekonometria II: regresja nieparametryczna
Warszawa 2006
Podatki, niechęć do ryzyka i wielkość szarej strefy : Analiza nieparametryczna na
podstawie Nowej Zelandii
Wstęp
Autorzy tekstu postanowili zbadać związek między efektywną stopą
opodatkowania a względną wielkością szarej strefy. Oszacowany został model,
mający symulować skutki hipotetycznych zmian podatkowych na rozmiar szarej
strefy w Nowej Zelandii. Analiza została przeprowadzona za pomocą
nieparametrycznej regresji korzystając z danych z okresu 1968 -1994.
Podstawy teoretyczne
Już pierwsze modele zakładały hipotezę o dodatnim związku miedzy
wielkością stopy opodatkowania a wielkością szarej strefy. Model Trandel & Snow
wyróżnia dwa obszary, pierwszy o dosyć niskim potencjalnym dochodzie, co za tym
idzie dość niskimi płaconymi podatkami. (Przyjmujemy ze kary za uchylanie się od
płacenia podatku są proporcjonalne do wielkości niezapłaconego podatku). W takiej
sytuacji sektor ten chętniej będzie się starał uchylić od płacenia podatku ze względu
na relatywnie niski poziom kary, a drugi obszar odwrotnie.
Formułowanie hipotezy testowej
Forma hipotezy jest dosyć skomplikowana gdyż np. znak związku między
stopą podatkową i stopniem uchylania się od podatków zależy czy przyjęte jest
założenie o niechęci ryzyka osób płacących podatki. Według modelu Trandel &
Snow - jeśli podatki są progresywne i jeśli preferencje osób płacących podatki
pokazują zmniejszającą absolutną niechęć ryzyka i niemalejącą względną niechęć
ryzyka, wtedy model przewiduje dodatni związek między stopą podatkową a
udziałem całkowitej siły robotniczej w unikającym podatków sektorze. Dodatni
związek jest też prognozowany między stopą podatku progresywnego a względną
wielkością siły roboczej szarej strefy. Podstawowym problem jest dostępność danych
dotyczących rozmiaru szarej strefy. Dane te są szacowane raczej na podstawie
wartości "ukrytej" produkcji, niż na podstawie wielkości łącznej siły roboczej. Aby
ułatwić międzynarodowe porównania, liczby te zwykle są odniesione jako stopa
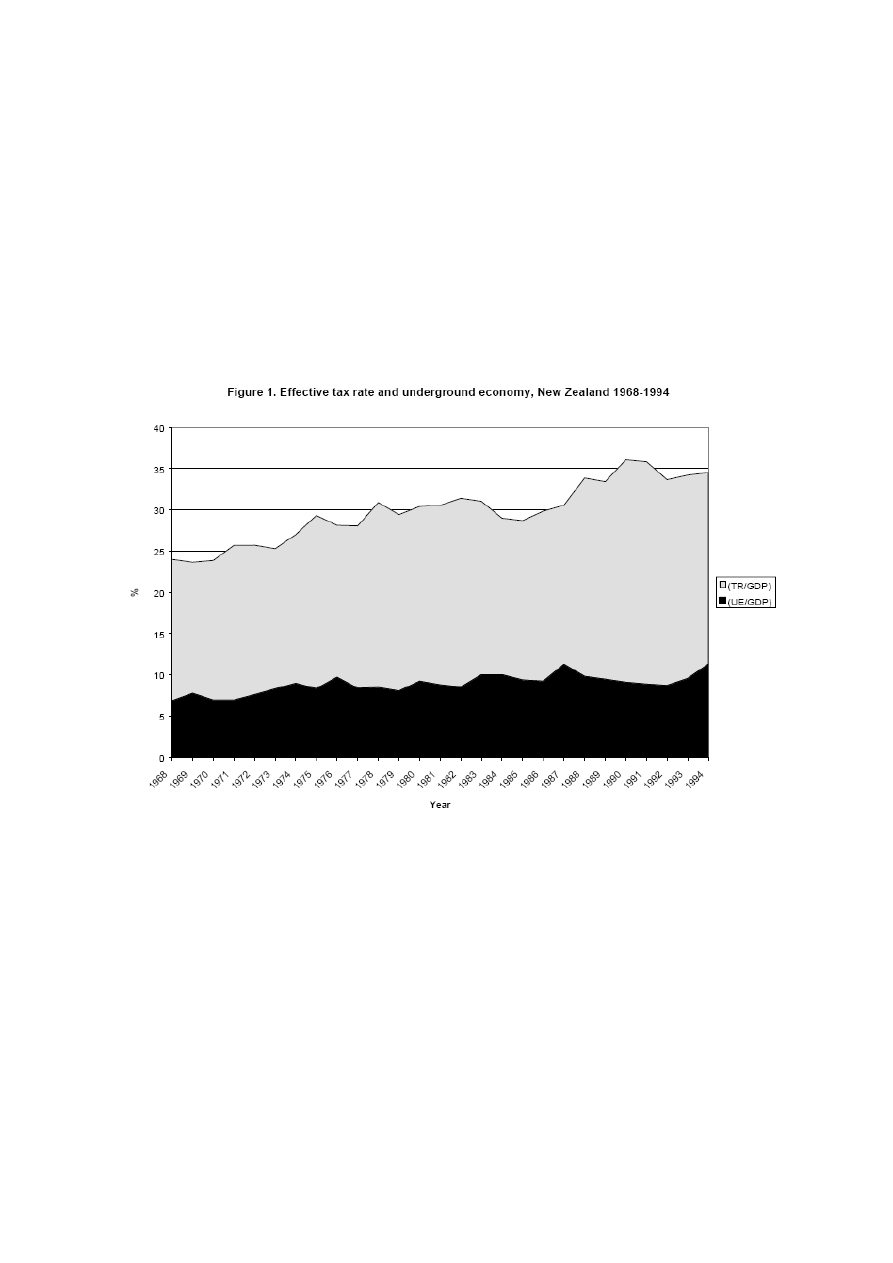
procentowa zmierzonego GDP. W poniższym modelu rozmiar szarej strefy został
zdefiniowany jako (UE / GDP),a efektywna stopa podatkowa jako: (TR / GDP),
gdzie TR jest całkowitym przychodem podatkowym
Hipoteza: wielkość szarej strefy rośnie albo ze wzrostem średniej stopy podatkowej
sektorze nie nieunikającym płacenia podatków , albo ze spadkiem (oczekiwanej)
średniej stopy podatkowej w sektorze unikającym płacenia.
Wstępne testy
• przed rozpoczęciem estymacji przeprowadzono następujące testy
o
testy na stacjonarność zmiennych
o
testy na kointegracje
o
test na przyczynowość
Testy na stacjonarność zmiennych:
W tabeli 1 przetestowano każdą serię na niestacjonarność, uwzględniając możliwości
z I(2), I(1) albo I(0). Użyto testu Dickey-Fullera (ADF) sprawdzającego hipotezę
zerową o niestacjonarności, jak również test Kwiatowskiego (KPSS) (1993) (test
Kwiatkowski, Phillips, Schmidt i Shin – weryfikuje hipotezę o stacjonarności procesu
lub drugą sytuację trendo-stacjonarności procesu). Test ADF i test KPSS pozwala
ocenić całkowity rząd integracji, który dla procesów ekonomicznych najczęściej
przyjmuje wartość I(0) lub I(1), a bardzo rzadko I(2). ) Przyjęty został, 10% poziom
istotności by poradzić sobie z małymi siłami tych testów, chociaż wyniki nie są
wrażliwe na taki wybór.
W przypadku testu ADF, poziom powiększenia (p) został wybrany przez domyślną
metodę SHAZAM (1997), jak pokazuje Dods i Giles (1995), podejście to prowadzi do
niewielkiego przekręcenia (wypaczenia) w średniej ruchomej błędów z podanej
próbki. Autorzy poszli, więc za następną strategią Dolado. (1990) by zająć się
zagadnieniem włączenia / wykluczenia dyfu (odchylenień) i okresów trendu w
regresji Dickey-Fullera. I Tak, w Tabeli 1:
tdt wskazuje ADF unit root test z odchyleniem (dryfem) i okresem trendu
włączonych w dopasowaną regresje;
Fut - odpowiedni ADF z zerowym trendem
td -ADF z dryfem i zerowym trendem w dopasowanej regresji;
Fud – ADF dla zerowego dryfu;
t –wartość ADF bez uwzględnienia dryfu i trendu.
W teście KPSS użyta została wartość dla parametru okna Bartletta, l=0, l = 5. KPSS
dostarcza asymptotycznych wartości krytycznych dla próby z h(0) mówiącą o
stacjonarności zmiennej i stacjonarności trendu. (Cheung (1995) dostarcza
zewnętrznej informacji, która ułatwia określić wartości krytyczne w przypadku
stacjonarnośći trendu) .
Wyniki uzyskane w Tabeli 1 wskazują, że zarówno (UE / GDP) i (TR / GDP) są
niestacjonarne, sensowne jest więc przetestowanie możliwej kointegracji.
Jeśli obydwa szeregi są niestacjonarne, to jest całkiem możliwe, że istnieje między
nimi długookresowa stabilna zależność mająca swoje źródło w złożonych procesach
ekonomicznych, występujących w gospodarce. Jeśli tak jest, to mówimy, że szeregi
są skointegrowane.
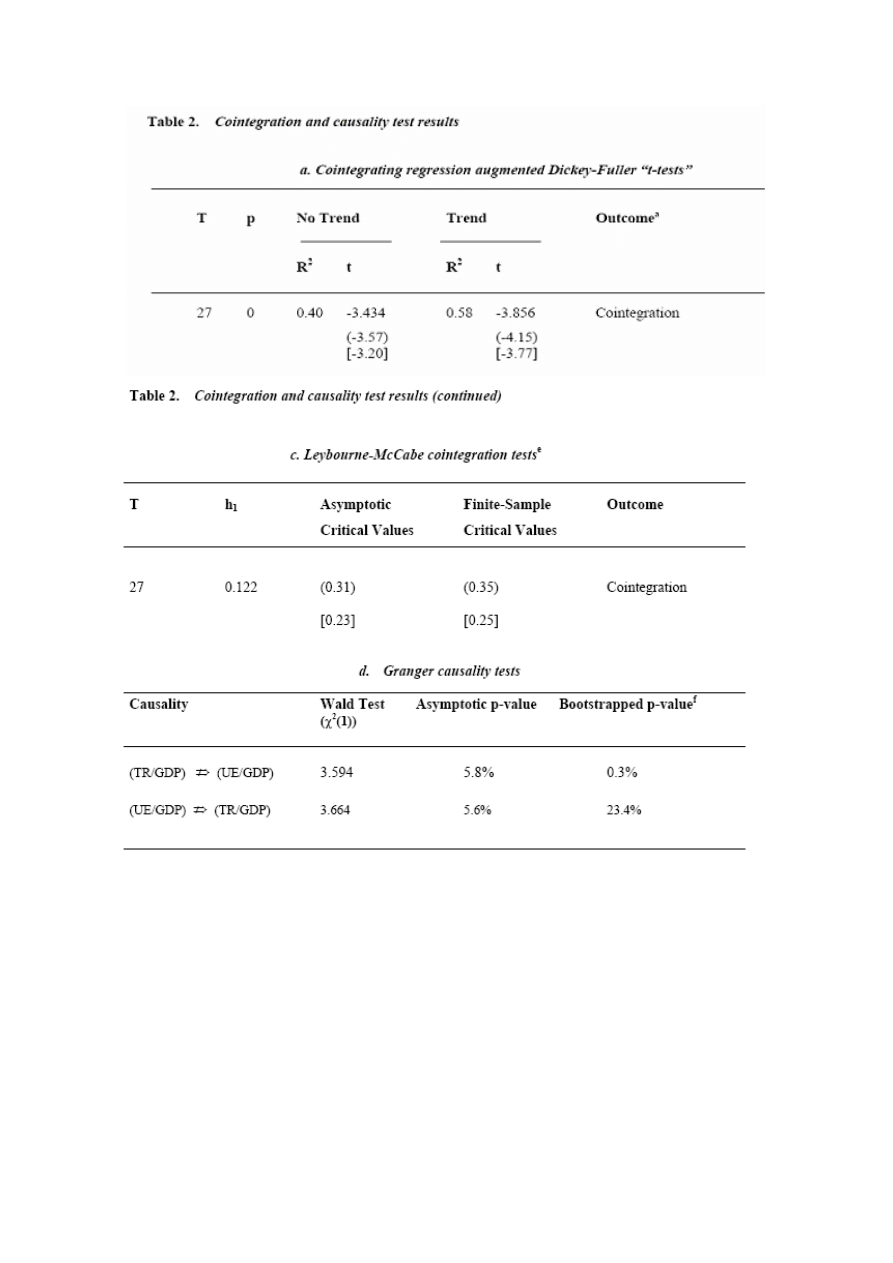
W Tabeli 2 pokazane zostały wyniki testu na kointegracje (CRADF), w którym h(0)
oznacza brak kointegracji, (używając (1991) wartości krytycznych MacKinnona).
Widzimy, przyzwoity dowód na kointegracje na 10% poziomie istotności. Został
także użyty test Leybournea – McCabe’a (1994), w którym h(0) – mówi o istnieniu
kointegracji. Została wygenerowana ograniczona próbka wartości krytycznych dla
tej próby przez symulację Carlo Monte, używając testu Leybourne i McCabe i kod
SHAZAM (1998). Wyraźnie nie możemy odrzucić h(0) o istnieniu kointegracji w
jakimś rozsądnym przedziale istotności.
Przetestowano także przyczynowość (x jest przyczyną w sensie Grangera dla y jeśli
bieżąca wartość zmiennej y może być przewidywana z większą dokładnością przy
wykorzystaniu minionych wartości zmiennej x niż bez nich, przy pozostałej
niezmienionej informacji, a więc przy założeniu ceteris paribus) między zmiennymi
(UE / GDP) i (TR / GDP), używając podejścia Toda - Yamamoto (1995). Wyniki
świadczą o przyczynowości od drugiej zmiennej do pierwszej , ale tylko ograniczony
dowód odwrotnej przyczynowości (popiera to empiryczny model z (UE / GDP) jako
zmienną zależną).
Estymacja
Biorąc pod uwagę poprzednie rozważania, autorzy postanowili modelować
długookresowe zależności pomiędzy UE/GDP i TR/GDP przy pomocy „poziomów”
tych dwóch zmiennych. Różnicowanie zmiennych nie jest wymagalne.
Wyniki estymacji innych autorów pokazywały pozytywną aczkolwiek malejącą
zależność pomiędzy wskaźnikiem czarnego rynku pracy a poziomem podatków.
Oszacowania te były przy wskaźniku R2 w pobliżu 30%. Te wyniki utwierdziły
autorów tekstu do zastosowaniu elastycznej regresji nieparametrycznej. Model
prezentuje prosta forma:
t
t
t
GDP
TR
m
GDP
UE
ε
+
=
}
)
/
{(
)
/
(
(1)
gdzie
funkcja m – warunkowa średnia
ε
t
– „Normalne” błędy standardowe, niezależne i homoskedastyczne
Estymacja równania (1) przeprowadzona została za pomocą procedury NONPAR,
która wykorzystuje estymator Nadaraya-Watson`a z normalnym jądrem (kernel) i
rozmiarem okna (bandwidth) wybranym za pomocą „optymalnej” metody
Silvermana. Przeprowadzone testy dowiodły, iż wyniki nie są w szczególny sposób
wrażliwe na wybór jądra oraz rozmiaru okna.
Ta odporność na błędy wyników uzyskanych jest zachęcająca szczególnie, gdy
nieparametryczna estymacja opiera się na małej próbie. Również brano pod uwagę
wersje (1) zawierającą wzrost realnego GDP i/lub jedno lub dwu-okresowe
opóźnione zmiennych UE/GDP i TR/GDP jako dodatkowe zmienne objaśniające.
Jednakże, żadna z powyższych form nie była faworyzowana przez standardowe
kryteria informacyjne.
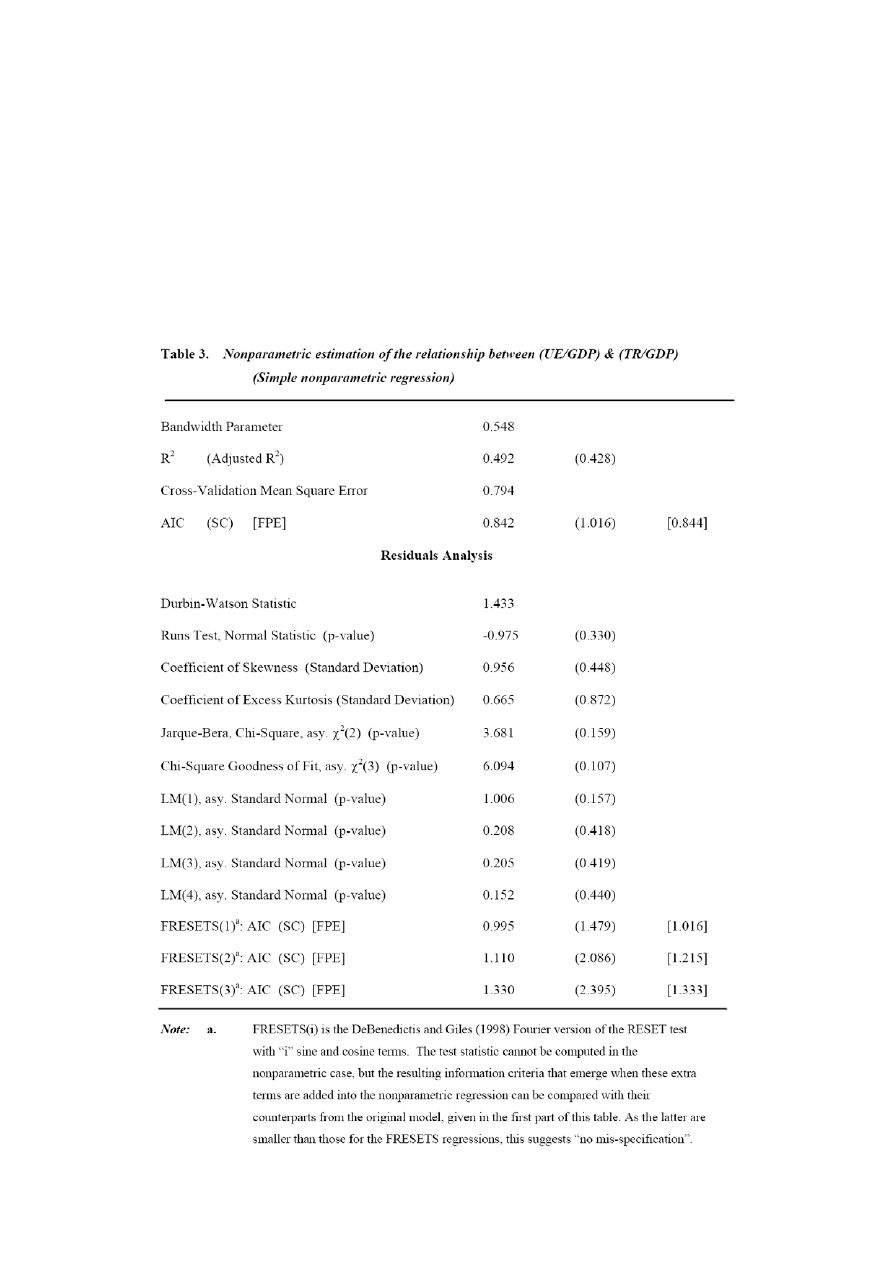
Wyniki oszacowań modelu z najprostszą forma funkcyjną przedstawia Tabela 3.
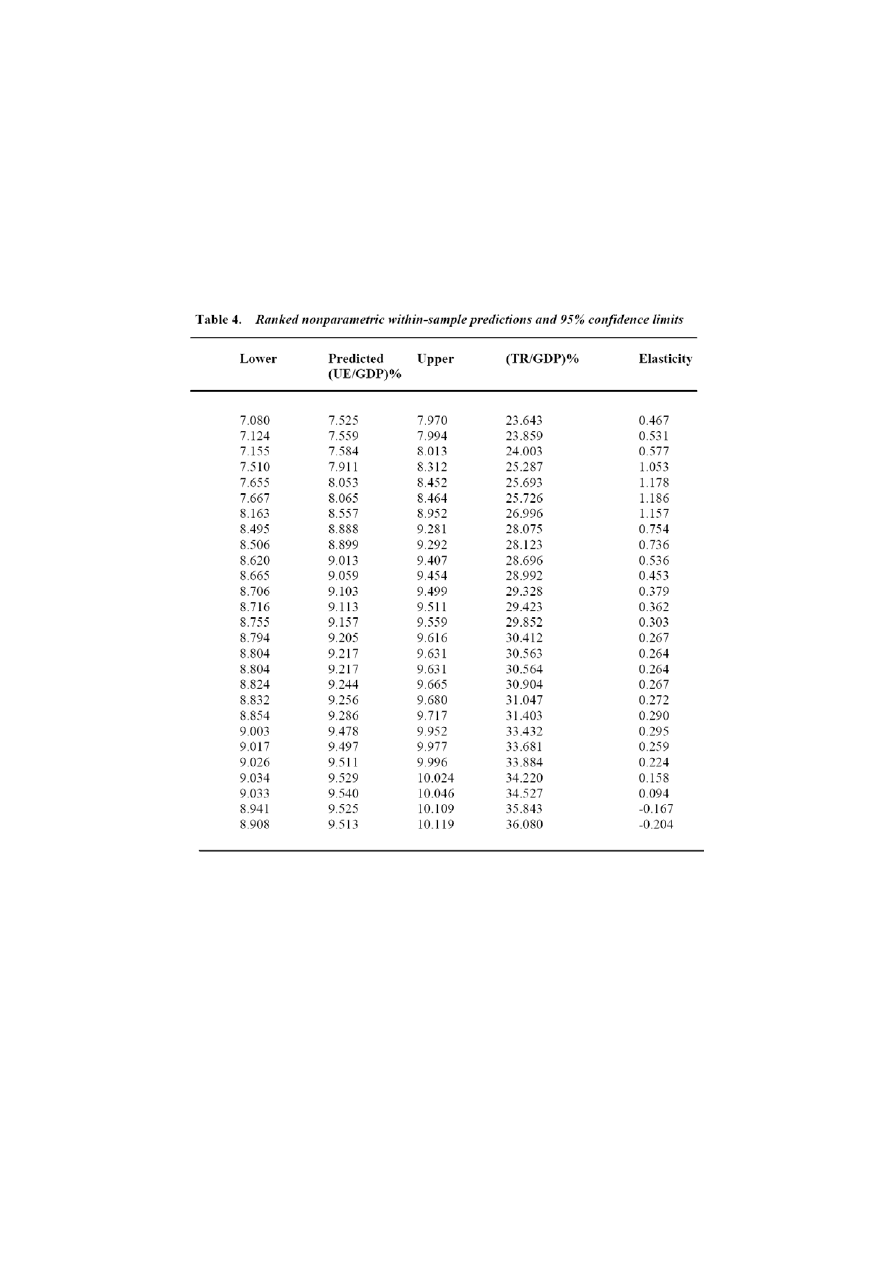
Tabela 4. przedstawia wartości dopasowane dla UE/GDP razem z dolnymi i
górnymi wartościami dla 95% przedziału ufności. Dopasowania mieszczą się w
przedziale od 7,52% do 9,51% GDP. W tej samej tabeli widzimy również
elastyczności pomiędzy efektywną stopą opodatkowania, a UE/GDP. Interesujący
jest fakt, iż poniżej poziomu podatku 25~26% występuje dość drastyczny spadek
elastyczności.
W Tabeli 5. przedstawione są wyniki estymacji równania (1), które prezentują
predykcje zmiennej UE/GDP dla hipotetycznych wartości efektywnego
opodatkowania z przedziału pomiędzy 17% a 38%. Bardzo interesującym jest fakt, iż
gdy poziom opodatkowania spada to wpływ na szarą strefę zaczyna się
„wypłaszczać” dla opodatkowania poniżej 25%. Chociaż estymacja
nieparametryczna nie zezwala na ekstrapolowanie poniżej zakresu danych, to ta
obserwacja bardzo wyraźnie odpowiada wnioskom zawartym w tekście Caragata i
Giles. Przy pomocy kryterium maksymalizacji reakcji szarej strefy na zmiany
opodatkowania autorzy Ci wnioskowani, iż optymalnym poziomem opodatkowania
jest 21%, Scully natomiast sugerował poziom 20%. Dowodzi to, iż jest pewna
konsekwencja pomiędzy poziomem efektywnej stopy opodatkowania ze względu na
wzrost gospodarczy oraz ze względu na poziom stosowania się do tego
opodatkowania.
Wnioski
Według autorów tekstu powyższe wyniki wskazują, że jest pewna
konsekwencja określająca optymalny poziom efektywnej stopy opodatkowania z
punktu widzenia wzrostu gospodarczego oraz z punktu widzenia problemu
uchylania się od płacenia podatków. Nieparametryczna metoda estymacji sugeruje,
iż reakcja szarej strefy na obciążenie podatkowe spada wyraźnie, kiedy poziom
efektywnego opodatkowania spada poniżej 25%.