
Algorytm obliczeń konstukcyjnych podnośnika
śrubowego
1
Wysokość podnoszenia
Wysokość podnoszenia oblicza się na podstawie empirycznej zależności:
H
pod
[
mm]=1,6⋅
√
Q[ N ]
lub
H
pod
[
cm]=0,5⋅
√
Q [kG]
1.1
Podnośnik jednostopniowy
W podnośniku jednostopniowym długość śruby roboczej wynosi w przybliżeniu:
l
śr
≃
H
pod
+
50÷70 [mm]
1.2
Podnośnik dwustopniowy
W podnośniku dwu stopniowym wysokość podnoszenia rozdziela się na dwie śruby robocze. Ich
długości w przybliżeniu są równe:
l
śr wew
≃
H
pod
2
+
50÷70 [mm]
l
śr zew
≃
H
pod
2
+
50÷70[mm ]
2
Dobór gwintu wewnętrznej śruby roboczej
2.1
Podnośnik jednostopniowy
Długość wyboczeniowa jedynej śruby wynosi:
l
w
=
2⋅l
śr
2.2
Podnośnik dwustopniowy
Długość wyboczeniowa wewnętrznej śruby wynosi:
l
w
=
2⋅l
śr wew
Na podstawie obciążenia oblicza się wartość siły krytycznej:
P
kr
=
Q⋅X
wew
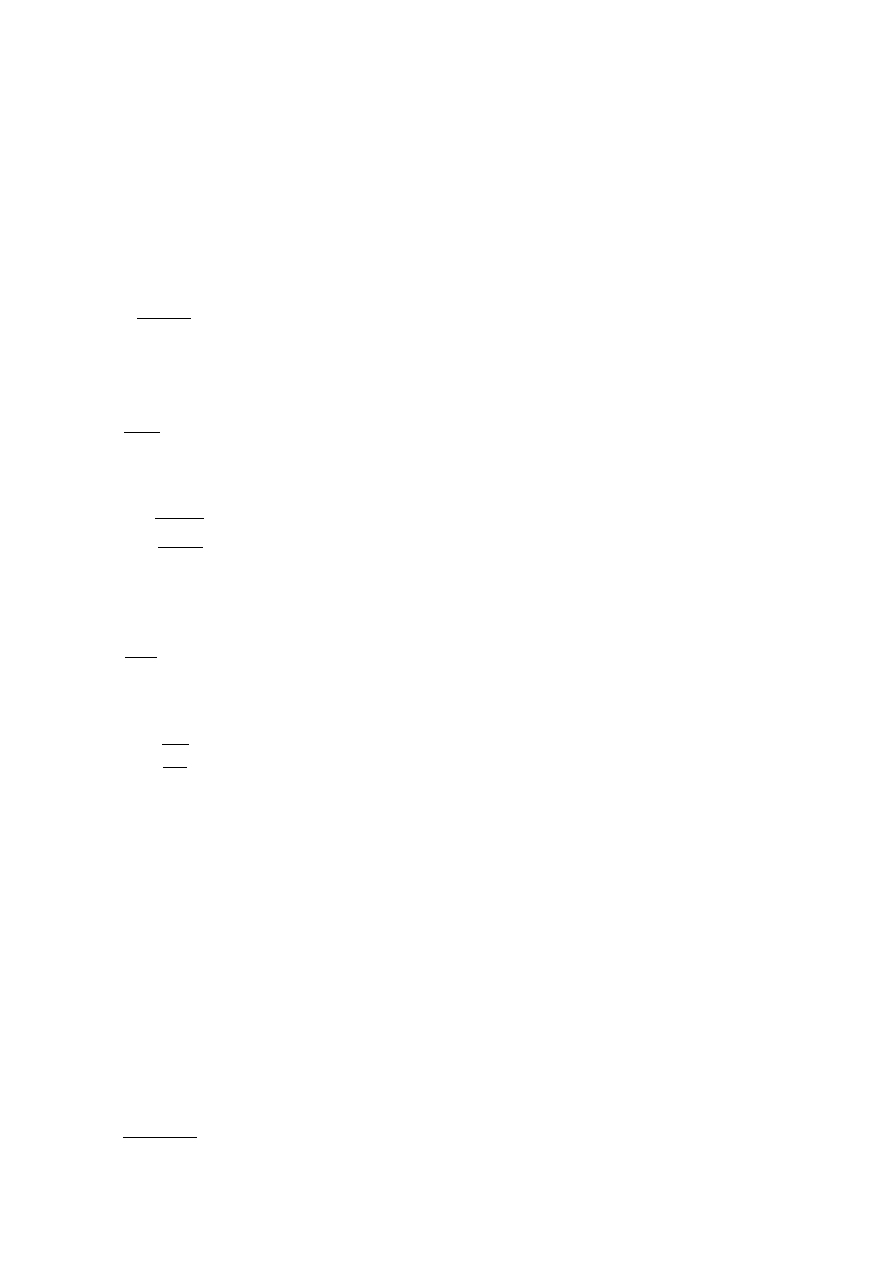
gdzie:
X
wew
=
6÷10
W celu dalszych obliczeń należy wybrać materiał, z którego zostanie wykonana śruba. Powinna być
to stal konstrukcyjna.
Na podstawie wzoru Eulera oblicza się średnicę rdzenie śruby wewnętrznej (wstępnie zakłada się,
że wyboczenie jest spreżyste):
P
kr
=
π
2
⋅
E⋅I
l
w
2
,
gdzie:
I =
π⋅
d
r
4
64
Stąd wzór na średnicę rdzenia ma postać:
d
r
=
4⋅
4
√
l
w
2
⋅
P
kr
π
3
⋅
E
Dodatkowo oblicza się smukłość:
λ=
4⋅l
w
d
r
Następnie należy określić smukłość graniczną z zależności:
λ
gr
=π⋅
√
E
σ
H
Jeśli obliczona smukłość jest mniejsza od smukłości granicznej tzn.
λ <λ
gr
,
wtedy zależność na siłę krytyczną jest nieprawdziwa (wyboczenie nie jest sprężyste jak zostało to
założone na początku). W takiej sytuację stosuje się hipotezę T-J lub J-O.
Hipoteza T-J
σ
kr
=
a⋅λ +b
gdzie:
b=σ
plast
b=
σ
H
−σ
plast
λ
gr
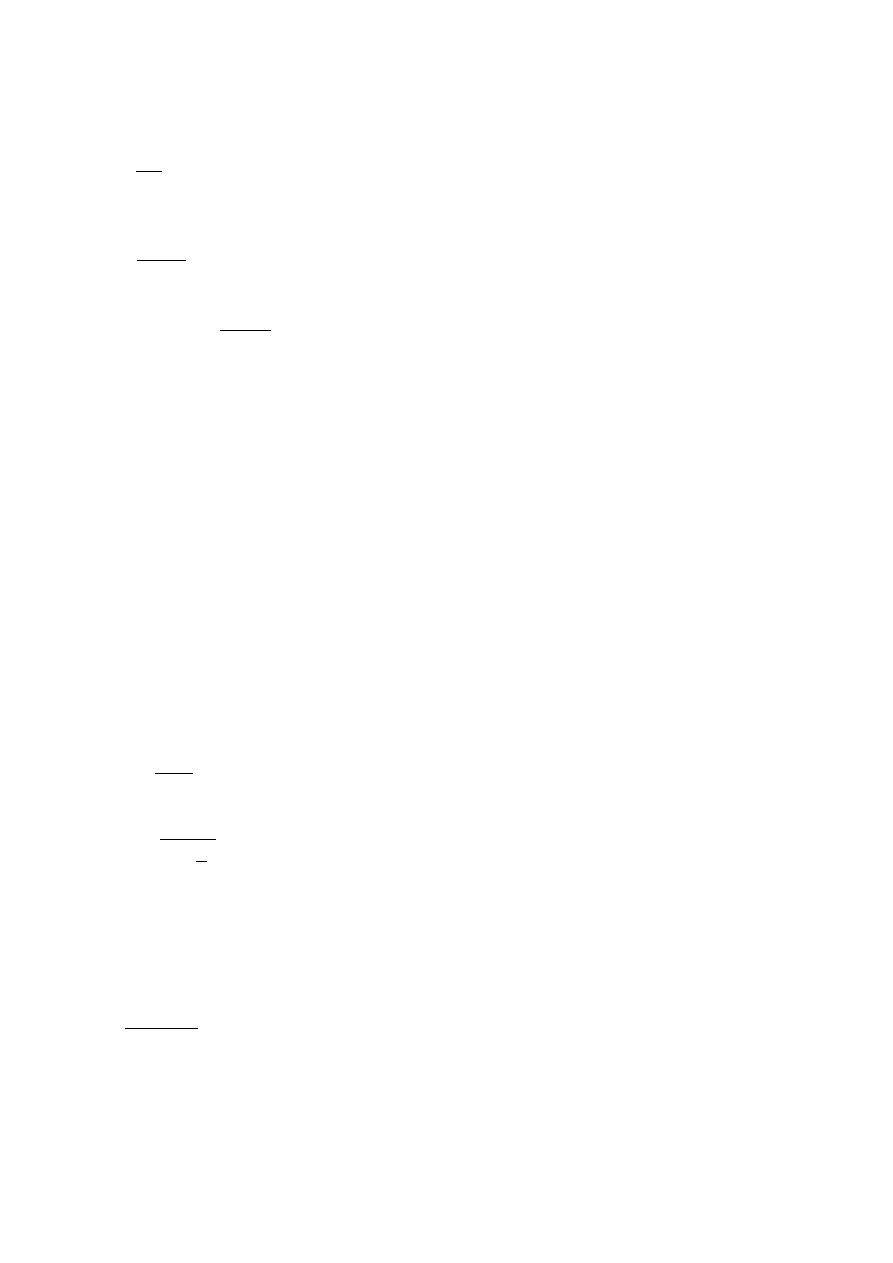
Na podstawie hipotezy T-J, oblicza się się średnicę rdzenia śruby:
σ
kr
=
P
kr
A
=
a⋅λ+b
P
kr
=(
a⋅λ +b)⋅A
P
kr
=
a⋅4⋅l
w
d
r
⋅
A+b⋅A
P
kr
=
a⋅π⋅l
w
⋅
d
r
+
b⋅π⋅d
r
2
4
Wykorzystując dowolną technikę rozwiązywania rownań drugiego stopnia, należy znaleźć
pierwiastki znalezionej równości.
d
r
=
?
Ostatnim krokiem jest dobór gwintu trapezowego symetrycznego z normy, dla którego, średnica
wewnętrzna gwintu jest pierwszą większą od średnicy rdzenia d
r
.
Tr
❑
x
❑
3
Sprawdzenie samohamowności dobranego gwintu
Warunek samohamowności:
γ⩽ρ
'
gdzie:
tg (γ)=
P
π⋅
d
p
tg (ρ ')=
μ
cos
(
β
2
)
4
Sprawność dobranego gwintu
Sprawność gwintu wynosi:
η=
tg(γ)
tg(γ+ρ ')
5
Dobór wysokości nakrętki śruby wewnętrznej
Wysokokość nakrętki określa się na podstawie warunku na nacisku powieszchniowe:

p
dop
⩾
Q
A
n zwoi
gdzie:
A
n zwoi
=
n⋅A
z
A
z
= π
4
⋅
(
d
śr
2
−
D
o nak
2
)
Do obliczenia jest minimalana liczba zwoi czynnych, wymagana do przeniesienia zadanego
obciążenia.
n⩾
Q
A
z
⋅
p
dop
Obliczoną liczbę zwoi zaokrągla się do góry do całkowitej liczby n
z
.
Ponieważ w nakrętce jest 3/4 zwoja wejściowego i 3/4 zwoja wyjściowego nie współpracujacego w
pełni, liczbę zwoi czynnych należy odpowiednio powiększyć.
n
cał
=
n
z
+
1,5
Dodatkowo, minimalna liczba współpracujących zwoi, ze względu niedogładności wykonania
wynosi n=3 .
Ostatecznie całkowita liczba zwoi wynosi:
n
cał
=
max (n
z
+
1,5 ; 4,5)
6
Dobór średnicy zewnętrznej nakrętki śruby wewnętrznej
Średnicę zewnętrzną nakrętki określa się na podstawie warunku na nacisku powieszchniowe:
p
dop
⩾
Q
A
pod
gdzie:
A
pod
= π
4
⋅
(
d
zew obl
2
−
D
r nak
2
)
Stąd:
A
pod
⩾
Q
p
dop

π
4
⋅
(
d
zew obl
2
−
D
r nak
2
)
⩾
Q
p
dop
d
zew obl
⩾
√
4⋅Q
π⋅
p
dop
+
D
r nak
2
Tak obliczoną średnicę należy powiększyć o około 1÷2 mm, aby możliwe było wykonanie fazy
ułatwiającej wciśnięcie nakrętki w gniazdo
d
zew
=
d
zew obl
+
1÷2[mm]
Document Outline
- 1 Wysokość podnoszenia
- 2 Dobór gwintu wewnętrznej śruby roboczej
- 3 Sprawdzenie samohamowności dobranego gwintu
- 4 Sprawność dobranego gwintu
- 5 Dobór wysokości nakrętki śruby wewnętrznej
- 6 Dobór średnicy zewnętrznej nakrętki śruby wewnętrznej
Wyszukiwarka
Podobne podstrony:
algorytm obliczen podnosnika srubowego 2013 03 11(1)
algorytm obliczen podnosnika srubowego 2013 04 07
algorytm obliczen podnosnika srubowego 2013 04 07
2013-03-11, histopatologia
PKM-II(obliczeniania) - podnośnik śrubowy, POLITECHNIKA W-W, PKM
2013 03 11
OBLICZENIA PODNOŚNIKA ŚRUBOWEGO
2013 03 11 Tranwestyta na spotkaniu z Pawłowicz
TPL WYK 2013 03 11 Synonimy
2013 03 11 Jak lewica obchodzi sie z kobietami
2013 03 11 Wałęsa Drodzy Geje
2013 03 11 Wałęsa jako katolik będzie bronił rodziny
2013 03 11 Dlaczego w Szwecji jest najwięcej gwałtów
2013 03 11 Relacja z Manify
03 11 2013 Choroba wysokościowa
Podnośnik śrubowy obliczenia
Podnosnik srubowy obliczenia id 399352
Podnośnik śrubowy obliczenia
więcej podobnych podstron