Dane :
Rozpiętość podciągu :
L
12.4
m
Rozstaw podciągów :
B
6.3
m
Ciężar żelbetu:
γ
z
25
kN
m
3
Grubość płyty stropowej:
d
12
cm
Ciężar płyty stropowej:
g
p
d γ
z
3
kN
m
2
Ciężar warstw wykończeniowych:
g
war
0.4
kN
m
2
Obciążenie użytkowe stropu:
q
5.2
kN
m
2
Rozstaw belek stropowych:
a
roz
2.067
m
Stal gatunku: S275
Granica plastyczności:
f
y
275
N
mm
2
Moduł sprężystości:
E
210000
N
mm
2
γ
M0
1
Przyjmuję dwuteownik IPE330
h
330
mm
h
w
307
mm
t
w
7.5
mm
b
f
160
mm
t
f
11.5
mm
r
18
mm
A
62.6
cm
2
I
y
11770
cm
4
I
z
788
cm
4
I
T
28.8
cm
2
I
w
199100
cm
6
W
pl_y
t
f
b
f
h t
f
t
w
h
2
t
f
2
4
r
2
h
2
t
f
r
2
π
r
2
h
2
t
f
r
4
r
3
π
8
105
mm
3
g
w
0.49
kN
m
1. Zebranie obciążeń:
Obciążenia stałe:
G
k
g
w
g
p
g
war
a
roz
7.518
kN
m
Obciążenia zmienne:
Q
k
q a
roz
10.748
kN
m
Współczynniki:
γ
G_sup
1.35
γ
Q
1.5
ξ
0.85
F
uls
ξ γ
G_sup
G
k
γ
Q
Q
k
24.749
kN
m
2. Obliczenia statyczne belki stropowej
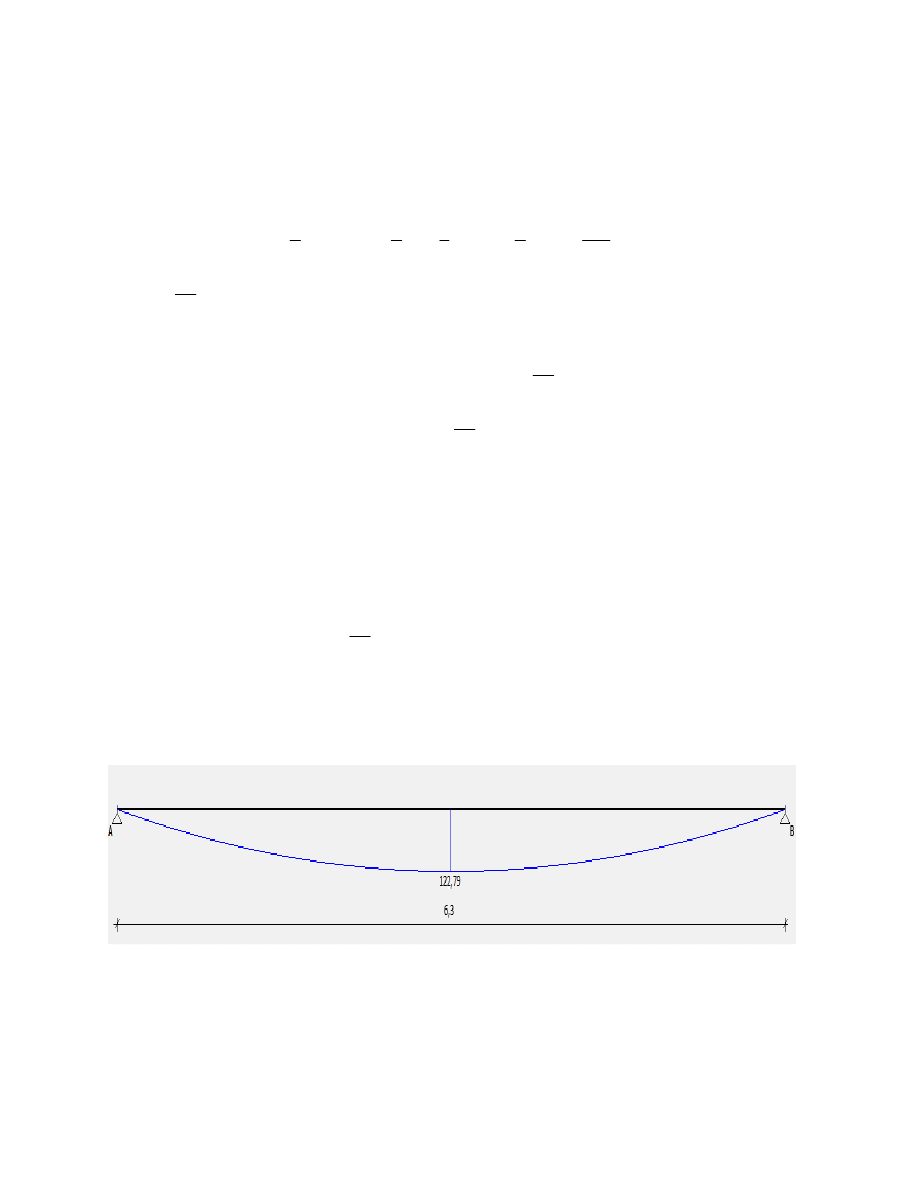
Wykres momentu zginającego:
Maksymalny moment przęsłowy:
M
y_Ed
0.125
F
uls
B
2
122.787
kN·m
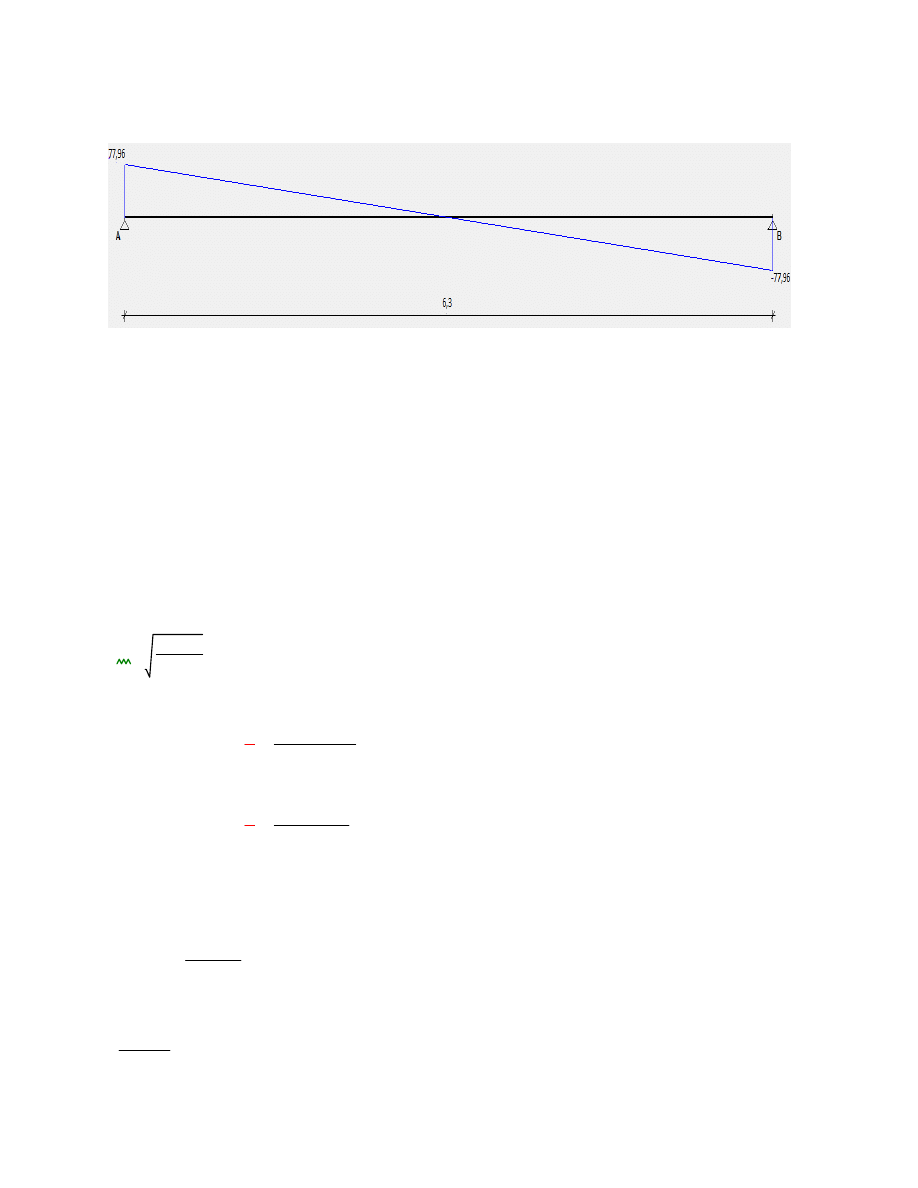
Wykres siły poprzecznej
Maksymalna siła poprzeczna przy podporze:
V
z_Ed
0.5
F
uls
B
77.96
kN
3. Wymiarowanie belki stropowej
3.1 Sprawdzenie stanu granicznego nośności belki stropowej z dwuteownika walcowanego,
zabezpieczonej przed zwichrzeniem
3.1.1. Klasa przekroju przy zginaniu względem osi y-y
ε
235
MPa
f
y
0.924
Stosunek szerokości do grubości:
środnik
c
t
h
2
t
f
2
r
t
w
36.133
c
t
< 66.53
stopka
c
t
b
f
t
w
2
r
2
t
f
5.065
c
t
< 8,316
Przy zginaniu względem osi y-y przekrój jest klasy 1.
3.1.2. Nośność obliczeniowa przekroju klasy 1 przy zginaniu
M
c_y_Rd
W
pl_y
f
y
γ
M0
221.191
kN·m
3.1.3. Warunek nośności belki ze względu na zginanie:
M
y_Ed
M
c_y_Rd
0.555
3.1.4. Sprawdzenie nośności belki przy ścinaniu na podporze
Warunek stateczności miejscowej przy ścinaniu:
η
1.2
h
w
t
w
40.933
<
72
ε
η
55.465
Środnik nie jest wrażliwy na utratę stateczności przy ścinaniu.
Pole przekroju czynnego:
A
v_z
A
2
b
f
t
f
t
w
2
r
t
f
3.08
103
mm
2
lecz nie mniej niż:
η
t
w
h
w
2.763
103
mm
2
Obliczeniowa nośność przekroju przy ścinaniu:
V
c_z_Rd
A
v_z
f
y
3
γ
M0
489.055
kN
Warunek nośności przy ścinaniu:
V
z_Ed
V
c_z_Rd
0.159
< 1
Warunek jest spełniony.
3.2. Sprawdzenie stanu granicznego użytkowalności.
Kombinacja obciążeń:
G
k
Q
k
18.266
kN
m
Maksymalne ugięcie belki:
w
max
5
G
k
Q
k
B
4
384
E
I
y
15.158
mm
Wartość graniczna ugięcia:
w
s
B
350
18
mm
w
max
<
w
s
Warunek jest spełniony.
4. Obliczenia statyczne podciągu
Przyjmuję dwuteownik spawany, środnik z blachy 8x1000, półki 16x260
a
5
mm
h
wp
1000
mm
t
wp
8
mm
b
fp
260
mm
t
fp
16
mm
A
p
105
cm
2
I
yp
b
fp
h
wp
2.
t
fp
3
h
wp
3
b
fp
t
wp
12
3
109
mm
4
W
el_y
2
I
yp
h
wp
2
t
fp
5
106
mm
3
I
zp
h
wp
t
wp
3
12
4
t
fp
b
fp
2
3
12
t
fp
b
fp
2
t
fp
4
2
1.189
107
mm
4
i
zp
I
zp
A
p
33.655
mm
W
pl_yp
t
fp
b
fp
h
wp
t
fp
t
wp
h
wp
2
2
6.2
106
mm
3
g
wp
0.63
kN
m
Zebranie obciążeń:
G
kp
g
wp
g
p
g
war
g
w
a
roz
B
23.543
kN
m
Q
kp
q B
32.76
kN
m
F
ulsp
ξ γ
G_sup
G
kp
γ
Q
Q
k
43.139
kN
m
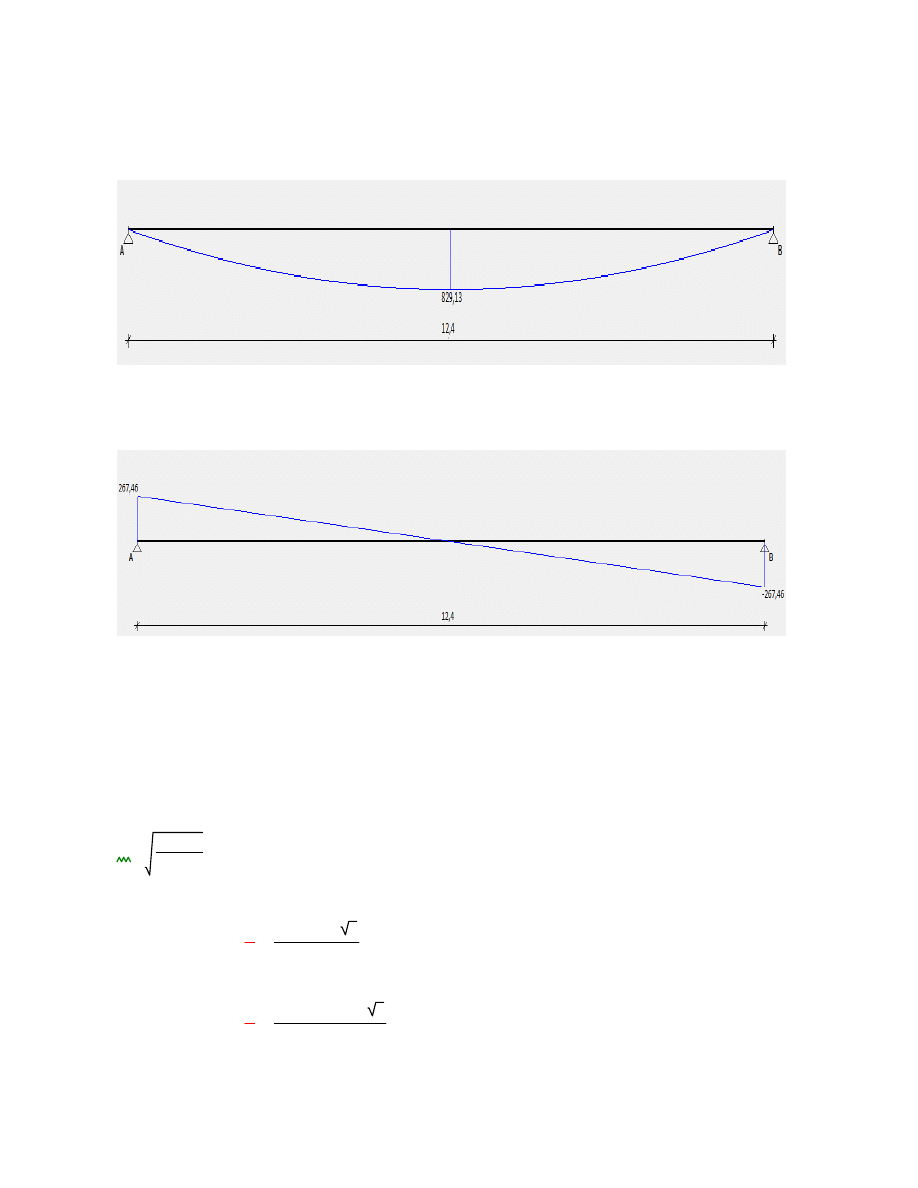
Wykres momentu zginającego:
Maksymalny moment przęsłowy:
M
y_Ed_cp
0.125
F
ulsp
L
2
829.13
kN·m
Wykres siły poprzecznej:
Maksymalna siła poprzeczna przy podporze:
V
z_Ed_cp
0.5
F
ulsp
L
267.46
kN
5. Wymiarowanie podciągu.
5.1. Sprawdzenie stanu granicznego nośności i podciągu spawanego, stężonego bocznie
punktowo, w przekroju przęsłowym i podporowym.
5.1.1. Klasa przekroju przy zginaniu.
ε
235
MPa
f
y
0.924
Stosunek szerokości do grubości:
środnik
c
t
h
wp
2
a
2
t
wp
123.232
c
t
> 114.6 - klasa 4
stopka
c
t
b
fp
t
wp
2
a
2
2
t
fp
7.433
c
t
< 8.3 - klasa 1
Przy zginaniu względem osi y-y przekrój jest klasy 4, a wrażliwy na niestateczność miejscową jest
środnik.
5.1.2. Nośność obliczeniowa przekroju klasy 4 przy zginaniu.
Stateczność miejscowa środnika
Parametr niestateczności miejscowej ścianki przęsłowej o współczynniku
ψ
1
k
σ
23.9
Smukłość płytowa ścianki
λ
p
h
wp
2
a
2
t
wp
1
28.4
ε
k
σ
0.96
Współczynnik redukcyjny
ρ
λ
p
0.055
3
ψ
(
)
λ
p
2
0.922
Szerokość strefy ściskanej i rozciąganej środnika
b
c
h
wp
2
a
2
2
492.929
mm
b
t
b
c
492.929
mm
Szerokość współpracująca
b
eff
ρ
b
c
454.571
mm
Szerokość części przylegających do pasa ściskanego b
e1
i od osi obojętnej b
e2
b
e1
0.4
b
eff
181.828
mm
b
e2
0.6
b
eff
272.742
mm
Przesunięcie położenia osi obojętnej przekroju współpracującego
Δ
z
t
wp
b
c
b
eff
b
e2
0.5
b
c
0.5
b
eff
A
p
t
wp
b
c
b
eff
8.788
mm
Moment bezwładności przekroju współpracującego
I
eff_y
I
yp
A
p
Δ
z
2
t
wp
b
c
b
eff
3
12
t
wp
b
c
b
eff
h
wp
2
a
2
Δ
z
b
e1
b
c
b
eff
2
2
2.787
109
mm
4
Wskaźnik sprężysty skrajnych włókien ściskanych przekroju współpracującego
W
eff_y
I
eff_y
h
wp
2
t
fp
Δ
z
5.311
106
mm
3
Nośność obliczeniowa przekroju klasy 4 przy zginaniu względem osi y-y
M
c_y_Rdp
W
eff_y
f
y
γ
M0
1460
kN·m
5.1.3. Uproszczona ocena zwichrzenia w budynkach.
Smukłość graniczna pasa zastępczego
λ
_c0
0.4
λ
_1
π
E
f
y
86.815
I
f_z
I
zp
h
wp
2
3
t
wp
3
12
2
5932338
mm
4
A
f_z
A
p
h
wp
2
3
t
wp
2
2.583
103
mm
2
Promień bezwładnośći pasa zastępczego
i
f_z
I
f_z
A
f_z
47.921
mm
Rozkład momentu zginającego w przęśle między stężeniami jest bliski stałemu, tym samym można
przyjąć
k
c
1
Rozstaw między stężeniami
L
c
1650
mm
λ
1
λ
_1
ε
80.253
M
c_y_Rd
221.191
kN·m
λ
_f
k
c
L
c
i
f_z
λ
1
0.429
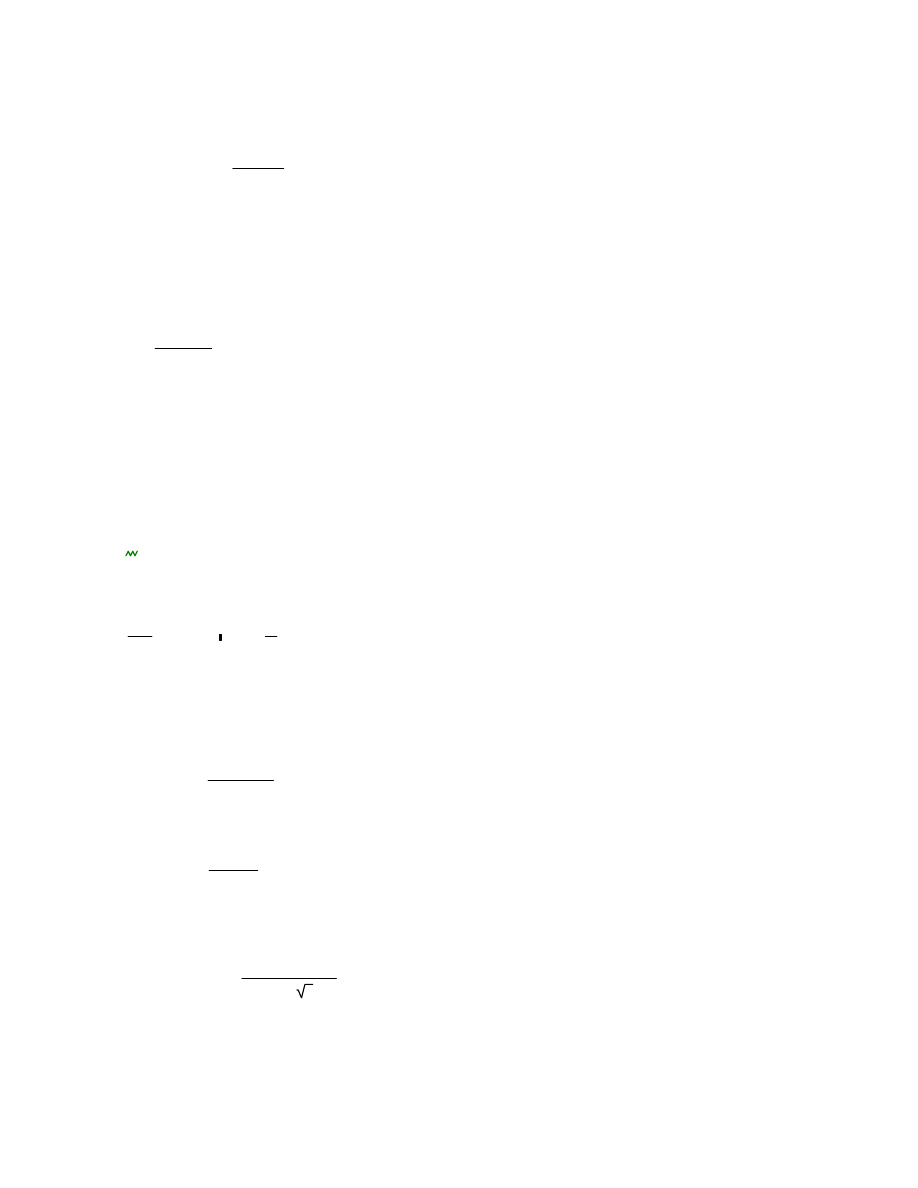
λ
_c0
M
c_y_Rd
M
y_Ed
0.721
λ
_f
0.429
<
0.721
Warunek jest spełniony, belka nie jest narażona na zwichrzenie.
5.1.4. Sprawdzenie nośności podciągu przy zginaniu w przęśle.
M
y_Ed_cp
M
c_y_Rdp
0.568
< 1
Warunek jest spełniony.
5.1.5. Sprawdzenie nośności podciągu przy ścinaniu na podporze.
Przyjmuję żebra podporowe i pośrednie.Przy podporze przyjmuję rozstaw 1000mm, na długości
przęsła 1650mm.
Przy podporze:
a
1000
mm
V
z_Ed_cp
267.46
kN
h
wp
t
wp
125
72
ε
η
55.465
Środnik jest wrażliwy na utratę stateczności miejscowej przy ścinaniu.
Względna smukłość płytowa
λ
w
h
wp
86.4
t
wp
ε
1.565
Współczynnik niestateczności przy ścinaniu
χ
w
1.37
0.7
λ
w
0.605
gdy λ
w
> 1,08
γ
M1
1.0
Nośność obliczeniowa przekroju przy ścinaniu
V
b_w_z_Rd
χ
w
f
y
h
wp
t
wp
γ
M1
3
768.253
kN
Warunek nośności przy ścinaniu
V
c_Rd
V
b_w_z_Rd
768.253
kN
V
z_Ed_cp
V
c_Rd
0.348
Warunek jest spełniony
5.2 Sprawdzenie stanu granicznego użytkowalności.
G
kp
Q
kp
56.303
kN
m
w
tot
5
G
kp
Q
kp
L
4
384
E
I
yp
29.331
mm
w
s
L
250
49.6
mm
w
tot
<
w
s
Warunek jest spełniony.
5.3 Sprawdzenie nośności spoin pachwinowych łączących pas ze środnikiem w strefie
przypodporowej.
Grubość spoin
a
5
mm
V
z_Ed_cp
267.46
kN
f
u
360
MPa
Współczynnik częściowy
γ
M2
1.25
Współczynnik korelacji spoin pachwinowych
β
w
0.85
h
p
h
wp
2
t
fp
1.032
103
mm
Moment statyczny pasa względem osi y-y:
S
y_f
0.5
b
fp
t
fp
h
w
t
f
6.625
105
mm
3
Moment bezwładności przekroju względem osi y-y
I
y
h
p
3
b
fp
h
wp
3
b
fp
t
wp
12
3
109
mm
4
Naprężenia styczne równoległe do osi spoiny:
τ
II
V
z_Ed_cp
S
y_f
I
y 2
a
6.297
MPa
Warunek nośności spoin:
τ
II
6.297
MPa
<
f
u
3
β
w
γ
M2
201.64
MPa
Warunek jest spełniony.
5.4. Dobór przekroju żebra w miejscu połączenia belek stropowych z podciągiem.
Żebro podporowe przyjęto jako zdwojone żebro dwustronne z płaskownika 10x120 w odstępie
osiowo 160mm.
b
st
120
mm
t
st
10
mm
e
160
mm
b
st
t
st
12
<
14
ε
12.942
Żebro jest stateczne
A
st
4
b
st
t
st
4.8
103
mm
2
>
4
h
w
t
w
2
e
431.719
mm
2
e
160
mm
0.1
h
wp
100
mm
Warunek jest spełniony. Przyjmuję zdwojone żebro dwustronne z płaskownika 10x120 w odstępie
osiowo 160mm.
6. Wymiarowanie połączenia belki stropowej z podciągiem.
Siła poprzeczna:
V
Ed
V
z_Ed
77.96
kN
Połączenie kategorii A. Przyjmuję 3 śruby M16, kl. 8.8
d
16
mm
d
0
18
mm
f
yb
640
MPa
f
ub
800
N
mm
2
A
s
161
mm
2
Obliczeniowa nośność śrub na docisk do otworu
e
1
60
mm
e
2
50
mm
p
1
90
mm
W przypadku docisku do górnego brzegu otworów (poprzecznie do osi belki)
e
1
3d
0
1.111
f
ub
f
u
2.222
1 0
Przyjmuję najmniejszą wartość
α
bz
1
k
1z
2.8
e
2
d
0
1.7
6.078
1.4
p
1
d
0
1.7
5.3
2.5
Przyjmuję najmnniejszą wartość
k
1z
2.5
W przypadku docisku do bocznego brzegu otworów (wzdłuż osi belki)
e
2
3d
0
0.926
f
ub
f
u
2.222
1 0
Przyjmuję najmniejszą wartość
α
bx
0.926
k
1x
2.8
e
1
d
0
1.7
7.633
1.4
p
1
d
0
1.7
5.3
2.5
Przyjmuję najmnniejszą wartość
k
1x
2.5
Obliczeniowa nośność pojedynczej śruby na docisk poprzecznie do osi belki:
F
b_i_z_Rd
k
1z
α
bz
f
u
d
t
w
γ
M2
86.4
kN
Obliczeniowa nośność pojedynczej śruby na docisk wzdłuż osi belki:
F
b_i_x_Rd
k
1x
α
bx
f
u
d
t
w
γ
M2
80.006
kN
Obliczeniowa nośność śrub na ścinanie w jednej płaszczyźnie
α
v
0.6
Obliczeniowa nośność pojedynczej śruby na ścinanie:
F
v_i_Rd
α
v
f
ub
A
s
γ
M2
62
kN
Siły w śrubach w połączeniu obciążonym mimośrodowo
Siła poprzeczna:
V
z_Ed
77.96
kN
Mimośród :
e
68
mm
Moment :
M
Ed
V
z_Ed
e
5.301
kN·m
Składowe sił w poszczególnych śrubach:
od siły poprzecznej
F
V_i_Ed
V
z_Ed
3
25.987
kN
od momentu
F
M_i_Ed
M
Ed
p
1
2
p
1
2
29.452
kN
Siła wypadkowa w skrajnej śrubie:
F
Ed
F
V_i_Ed
2
F
M_i_Ed
2
39.277
kN
Warunki nośności śrub
O nośności śrub decyduje obliczeniowa nośność pojedynczej śruby na docisk wzdłuż osi belki:
F
v_i_Rd
61.824
kN
Warunek nośności
F
Ed
F
v_i_Rd
0.635
Rozerwanie blokowe
Przekrój netto rozciągany:
A
nt
t
w
e
2
0.5
d
0
307.5
mm
2
Przekrój netto ścinany:
A
nv
t
w
p
1 2
e
1
2.5
d
0
1.462
103
mm
2
Obliczeniowa nośność na rozerwanie blokowe:
V
eff_2_Rd
0.5
f
u
A
nt
γ
M2
f
y
A
nv
γ
M0
3
276.483
kN
Warunek nośności
V
Ed
V
eff_2_Rd
0.282