Dane
Obliczenia i rysunki
Wyniki
[ ]
kW
P
80
=
=
min
820
obr
n
]
[
63
,
931
m
N
M
O
⋅
=
]
[
400 mm
d
p
=
[ ]
N
F
o
15
,
4658
=
o
20
=
α
[ ]
N
F
r
23
,
1755
=
]
[
210 mm
a
=
]
[
420 mm
b
=
1. Obliczenie momentu przenoszonego przez wał:
n
P
M
o
⋅
⋅
=
π
2
⋅
⋅
⋅
⋅
⋅
=
s
s
m
N
M
o
60
1
820
2
10
80
3
π
[
]
m
N
M
o
⋅
=
63
,
931
2. Wyznaczenie siły obwodowej na kole zębatym:
p
o
o
d
M
F
⋅
=
2
m
m
N
F
o
4
,
0
63
,
931
2
⋅
⋅
=
N
F
o
15
,
4658
=
3. Wyznaczenie siły promieniowej:
α
tan
⋅
=
o
r
F
F
o
r
N
F
20
tan
15
,
4658
⋅
=
N
F
r
23
,
1755
=
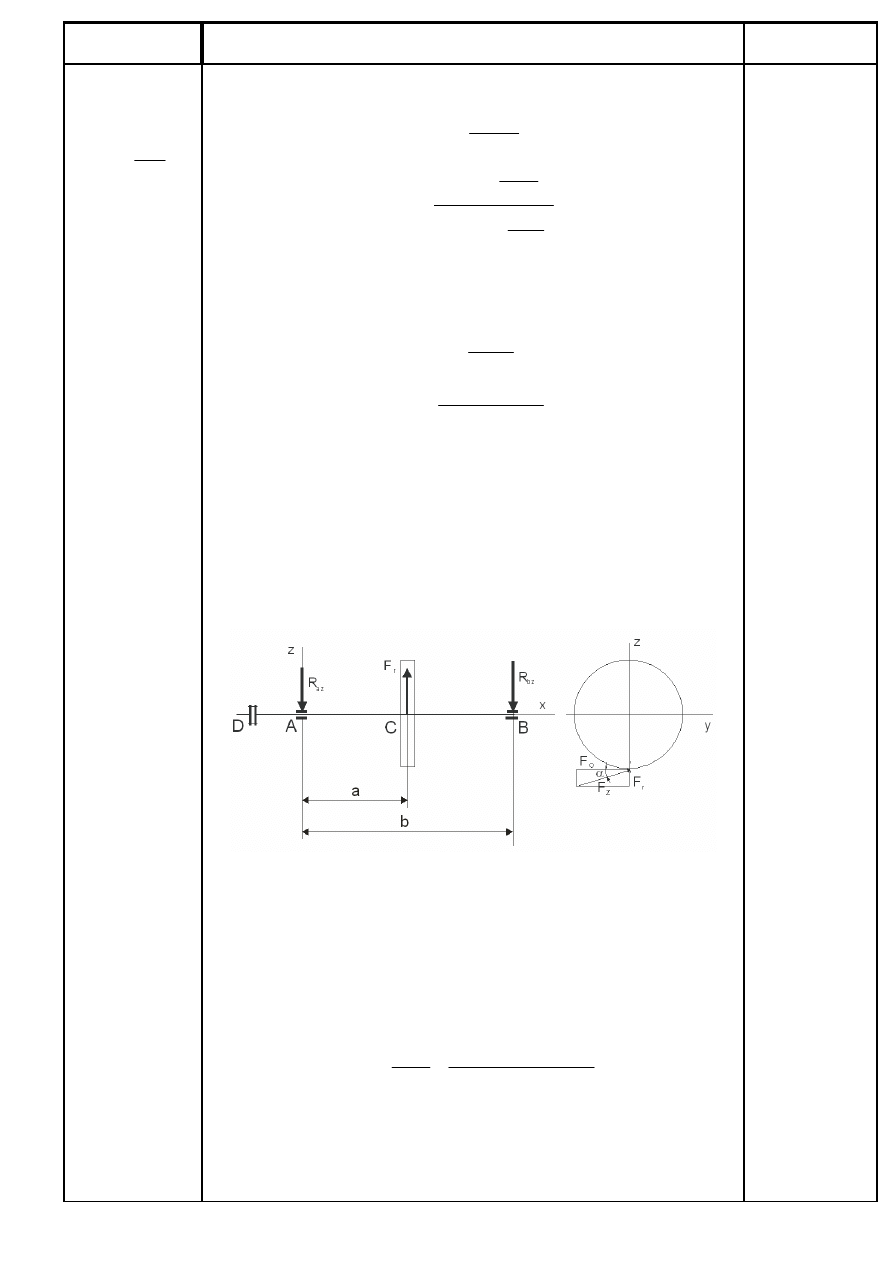
4. Ustalenie punktów przyłożenia, kierunków i wartości sił
obciążających wał w płaszczyźnie X –Z.
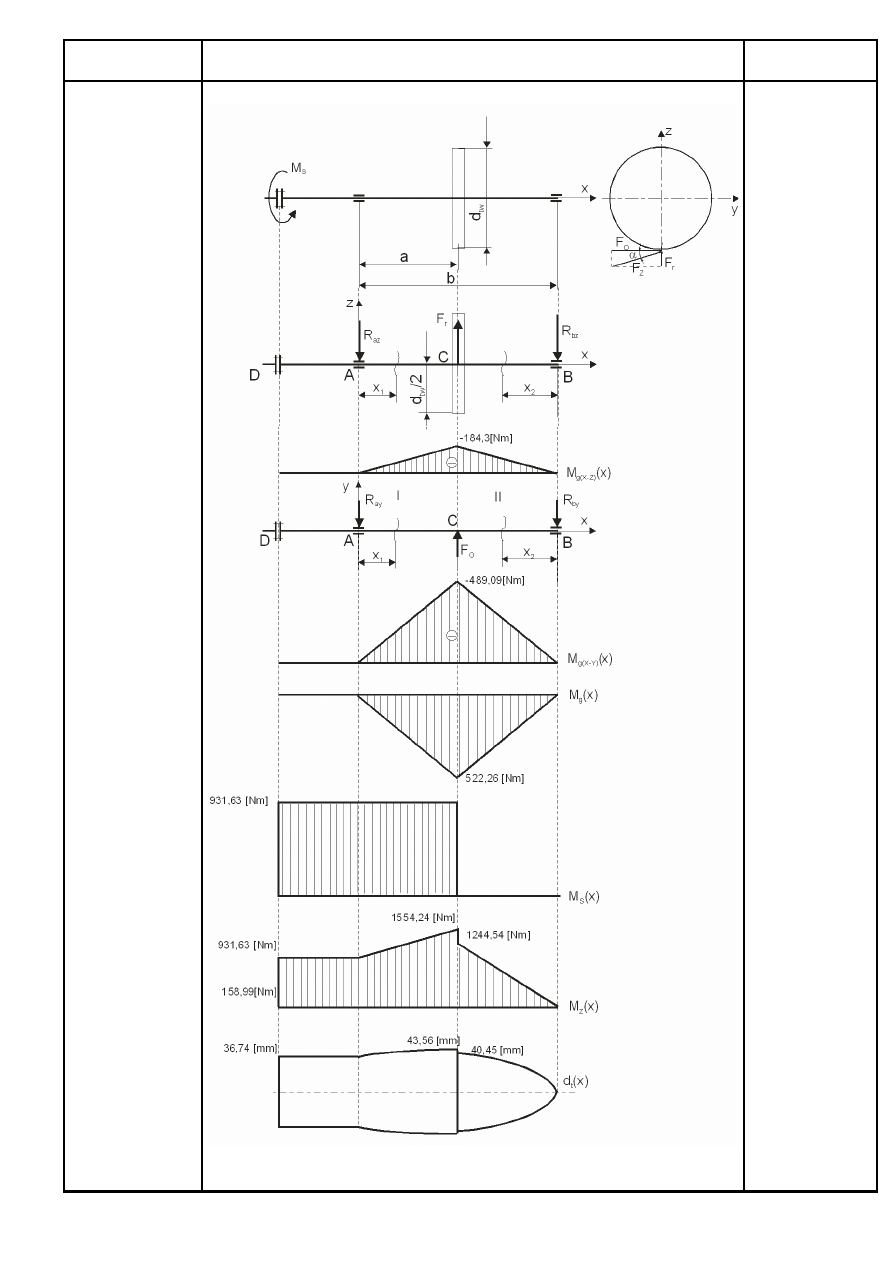
Rys. 1. Punkty przyłożenia sił w płaszczyźnie X – Z
5. Obliczenie reakcji R
az
, R
bz
w płaszczyźnie X –Z korzystając z
układu równowagi statyki:
0
)
(
1
=
−
+
−
=
∑
=
n
i
bz
r
az
i
R
F
R
z
F
0
)
(
1
=
⋅
−
⋅
=
∑
=
n
i
bz
r
i
b
R
a
F
A
M
]
42
,
0
]
[
21
,
0
]
[
23
,
1755
m
m
N
b
a
F
R
r
bz
⋅
=
⋅
=
]
[
52
,
877
N
R
bz
=
bz
r
az
R
F
R
−
=
]
[
62
,
877
]
[
23
,
1755
N
N
R
az
−
=
]
[
62
,
877
N
R
az
=
]
[
63
,
931
m
N
M
O
⋅
=
[ ]
N
F
o
15
,
4658
=
[ ]
N
F
r
23
,
1755
=
]
[
52
,
877
N
R
bz
=
]
[
62
,
877
N
R
az
=
Dane
Obliczenia i rysunki
Wyniki
]
[
210 mm
a
=
]
[
420 mm
b
=
[ ]
N
F
o
15
,
4658
=
]
[
62
,
877
N
R
az
=
]
[
02
,
2329
N
R
ay
=
]
[
62
,
877
N
R
bz
=
]
[
02
,
2329
N
R
by
=
]
[
62
,
877
N
R
az
=
]
[
210 mm
a
=
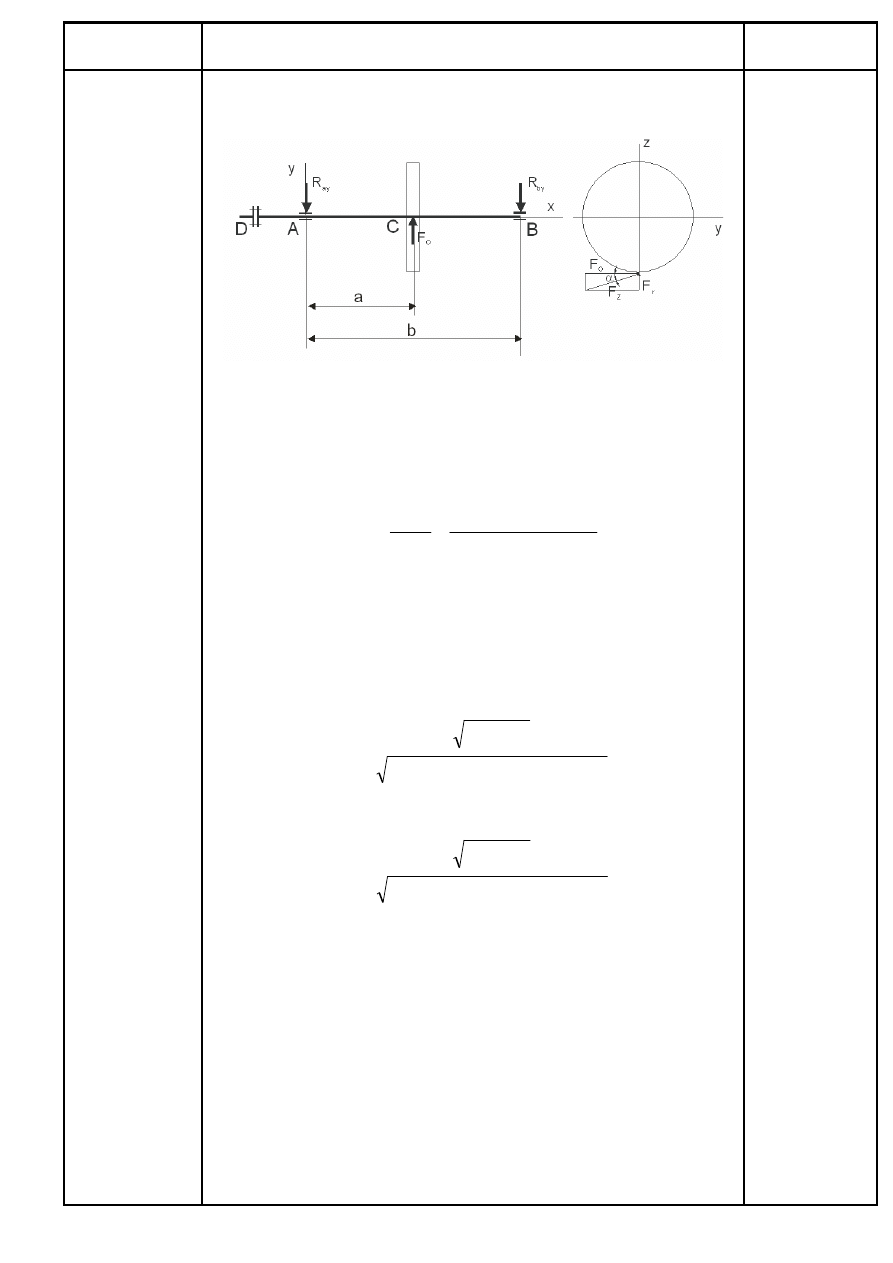
6. Ustalenie punktów przyłożenia, kierunków podparcia i wartości
sił obciążających wał w płaszczyźnie X – Y.
Rys.2. Punkty przyłożenia sił w płaszczyźnie X – Y
0
)
(
1
=
−
+
−
=
∑
=
n
i
by
O
ay
i
R
F
R
y
F
0
)
(
1
=
⋅
−
⋅
=
∑
=
n
i
by
O
i
b
R
a
F
A
M
]
[
42
,
0
]
[
21
,
0
]
[
15
,
4658
m
m
N
b
a
F
R
O
by
⋅
=
⋅
=
]
[
02
,
2329
N
R
by
=
by
O
ay
R
F
R
−
=
]
[
02
,
2329
]
[
15
,
4658
N
N
R
ay
−
=
]
[
02
,
2329
N
R
ay
=
7. Obliczenie wypadkowych Reakcji R
a
, R
b
w podporach: A i B
2
2
ay
az
a
R
R
R
+
=
(
) (
)
2
2
]
[
02
,
2329
]
[
62
,
877
N
N
R
a
+
=
]
[
89
,
2488
N
R
a
=
2
2
by
bz
b
R
R
R
+
=
(
) (
)
2
2
]
[
02
,
2329
]
[
62
,
877
N
N
R
b
+
=
]
[
89
,
2488
N
R
b
=
8. Obliczenie momentów gnących w charakterystycznych
punktach wału i przedstawienie wykresu momentów gnących
M
gz
w płaszczyźnie X – Z na wykresie (rys.3b)
8.1. Obliczenie momentu gnącego w przedziale I dla 0<x
1
<a
1
)
(
)
(
x
R
x
M
az
Z
X
gI
⋅
−
=
−
0
)
0
(
1
=
=
x
gA
M
]
[
21
,
0
]
[
62
,
877
)
(
1
m
N
a
R
M
az
a
x
gC
⋅
=
⋅
−
=
=
]
[
3
,
184
)
(
1
Nm
M
a
x
gC
−
=
=
]
[
02
,
2329
N
R
by
=
]
[
02
,
2329
N
R
ay
=
]
[
89
,
2488
N
R
a
=
]
[
89
,
2488
N
R
b
=
]
[
3
,
184
)
(
1
Nm
M
a
x
gC
−
=
=
Dane
Obliczenia i rysunki
Wyniki
]
[
62
,
877
N
R
bz
=
]
[
210 mm
a
b
=
−
]
[
02
,
2329
N
R
ay
=
]
[
210 mm
a
=
]
[
02
,
2329
N
R
by
=
]
[
210 mm
a
b
=
−
]
[
3
,
184
)
(
1
Nm
M
a
x
gC
−
=
=
]
[
09
,
489
)
(
1
Nm
M
a
x
gC
−
=
=
8.2. Obliczenie momentu gnącego w przedziale II 0<x
2
<b
2
)
(
)
(
x
R
x
M
bz
Z
X
gII
⋅
−
=
−
0
)
0
(
2
=
=
x
gB
M
]
[
21
,
0
]
[
62
,
877
)
(
)
(
2
m
N
a
b
R
M
bz
a
b
x
gC
⋅
−
=
−
⋅
−
=
−
=
]
[
3
,
184
)
(
2
Nm
M
a
b
x
gC
−
=
−
=
8.3. Sporządzenie wykresu momentów gnących (rys.3b).
9. Obliczenie momentów gnących w charakterystycznych
punktach wału i przedstawienie wykresu momentów gnących
M
gz
w płaszczyźnie X – Y na wykresie (rys.3c).
9.1. Obliczenie momentu gnącego w przedziale I dla 0<x
1
<a
1
)
(
)
(
x
R
x
M
ay
Y
X
gI
⋅
−
=
−
0
)
0
(
1
=
=
x
gA
M
]
[
21
,
0
]
[
02
,
2329
)
(
1
m
N
a
R
M
ay
a
x
gC
⋅
−
=
⋅
−
=
=
]
[
09
,
489
)
(
1
Nm
M
a
x
gC
−
=
=
9.2. Obliczenie momentu gnącego w przedziale II 0<x
2
<b
2
)
(
)
(
x
R
x
M
by
Y
X
gII
⋅
=
−
0
)
0
(
2
=
=
x
gB
M
(
)
]
[
21
,
0
]
[
02
,
2329
)
(
2
m
N
a
b
R
M
by
a
b
x
gC
⋅
−
=
−
⋅
−
=
−
=
]
[
09
,
489
)
(
2
Nm
M
b
x
gC
−
=
=
9.3. Sporządzenie wykresu momentów gnących (rys.3c).
10. Obliczenie momentów wypadkowych w charakterystycznych
punktach i przedstawienie ich na wykresie (rys.3d).
0
=
gA
M
2
)
(
2
)
(
Y
X
gC
Z
X
gC
gC
M
M
M
−
−
+
=
(
) (
)
2
2
]
[
09
,
489
]
[
3
,
184
Nm
Nm
M
gC
−
+
−
=
]
[
66
,
522
Nm
M
gC
=
0
=
gB
M
]
[
3
,
184
)
(
2
Nm
M
a
b
x
gC
−
=
−
=
]
[
09
,
489
)
(
1
Nm
M
a
x
gC
−
=
=
]
[
09
,
489
)
(
1
Nm
M
a
x
gC
−
=
=
0
=
gA
M
]
[
66
,
522
Nm
M
gC
=
0
=
gB
M

Dane
Obliczenia i rysunki
Wyniki
]
[
63
,
931
Nm
M
o
=
Mat. Wału
Stal maszynowa
E360
]
[
670 MPa
R
m
=
]
[
4
,
281
MPa
Z
go
=
4
,
3
=
z
x
]
[
180 MPa
Z
sj
=
11. Wyznaczenie momentu skręcającego przenoszonego przez wał
i przedstawienie go na wykresie (rys.3e).
Moment skręcający przenoszony przez wał jest równy momentowi
obrotowemu przenoszonemu przez wał na odcinku D-C między
sprzęgłem a kołem zębatym
]
[
63
,
931
Nm
M
M
o
s
=
=
12. Obliczenie momentów gnących zastępczych w
charakterystycznych punktach wału.
12.1. Przyjęcie naprężeń dopuszczalnych dla materiału, z którego
wykonany jest wał:
Z normy PN-EN 10025:2002 dobrano dla stali E360:
]
[
670 MPa
R
m
=
]
[
360 MPa
R
e
=
12.2. Obliczenie naprężenia dopuszczalnego na zginanie
obustronne i skręcanie jednostronne.
12.2.1. Obliczenie wytrzymałości zmęczeniowej Z
go
z zależności:
12.2.2.
]
[
500
42
,
0
42
,
0
MPa
R
Z
m
go
⋅
=
⋅
=
]
[
4
,
281
MPa
Z
go
=
12.2.3. Obliczenie wytrzymałości zmęczeniowej Z
sj
z zależności:
]
[
670
5
,
0
5
,
0
MPa
R
Z
m
sj
⋅
=
⋅
=
]
[
335 MPa
Z
sj
=
12.2.4. Przyjęcie współczynnika bezpieczeństwa dla
wytrzymałości zmęczeniowej x
Z
Przyjęto współczynnik x
Z
= 3,5 (x
Z
= 3,5
÷4)
12.2.5. Obliczenie naprężenia dopuszczalnego na zginanie k
go.
5
,
3
]
[
4
,
281
MPa
x
Z
k
Z
go
go
=
=
]
[
80 MPa
k
go
=
12.2.6. Obliczenie naprężenia dopuszczalnego na skręcanie
jednostronne.
5
,
3
]
[
335 MPa
x
Z
k
Z
sj
sj
=
=
]
[
71
,
95
MPa
k
sj
=
]
[
63
,
931
Nm
M
s
=
]
[
670 MPa
R
m
=
]
[
360 MPa
R
e
=
]
[
4
,
281
MPa
Z
go
=
]
[
180 MPa
Z
sj
=
4
,
3
=
z
x
]
[
80 MPa
k
go
=
]
[
71
,
95
MPa
k
sj
=
Dane
Obliczenia i rysunki
Wyniki
]
[
80 MPa
k
go
=
]
[
71
,
95
MPa
k
sj
=
0
=
gA
M
]
[
63
,
931
Nm
M
s
=
]
[
66
,
522
Nm
M
gC
=
0
=
gB
M
]
[
71
,
95
MPa
k
sj
=
]
[
99
,
158
Nm
M
zA
=
]
[
75
,
951
Nm
M
zCL
=
]
[
38
,
938
Nm
M
zCP
=
0
=
zB
M
12.3. Wyznaczenie współczynnika α
]
[
43
,
191
]
[
80
2
MPa
MPa
k
k
sj
go
=
⋅
=
α
42
,
0
=
α
12.4. Obliczenie momentów zredukowanych w
charakterystycznych punktach i przedstawienie ich na
wykresie (rys. 3f):
2
2
2
1
s
g
z
M
M
M
+
=
α
2
2
2
1
s
gA
z
M
M
M
+
=
α
2
]
[
63
,
931
0
Nm
M
zA
+
=
]
[
63
,
931
Nm
M
zA
=
2
2
2
1
s
gC
zCL
M
M
M
+
=
α
2
2
])
[
63
,
931
(
])
[
66
,
522
(
67
,
5
Nm
Nm
M
zCL
+
⋅
=
]
[
24
,
1554
Nm
M
zCL
=
2
2
2
1
s
gC
zCP
M
M
M
+
=
α
2
2
])
[
0
(
])
[
66
,
522
(
67
,
5
Nm
Nm
M
zCP
+
⋅
=
]
[
54
,
1244
Nm
M
zCP
=
0
=
zB
M
13. Obliczenie średnic teoretycznych wału w charakterystycznych
punktach i przedstawienie ich na wykresie (rys. 3g).
gj
Z
k
M
d
⋅
⋅
=
π
16
]
[
74
,
36
]
[
03674
,
0
10
71
,
95
]
[
63
,
931
16
3
2
6
mm
m
m
N
Nm
d
A
=
=
⋅
⋅
⋅
=
π
]
[
56
,
43
]
[
04356
,
0
10
71
,
95
]
[
24
,
1554
16
3
2
6
mm
m
m
N
Nm
d
CL
=
=
⋅
⋅
⋅
=
π
]
[
45
,
40
]
[
04045
,
0
10
71
,
95
]
[
55
,
1244
16
3
2
6
mm
m
m
N
Nm
d
CP
=
=
⋅
⋅
⋅
=
π
0
=
B
d
47
,
0
=
α
]
[
99
,
158
Nm
M
zA
=
]
[
75
,
951
Nm
M
zCL
=
]
[
38
,
938
Nm
M
zCP
=
0
=
zB
M
]
[
74
,
36
mm
d
A
=
]
[
47
,
54
mm
d
CL
=
]
[
21
,
54
mm
d
CP
=
0
=
B
d
Dane
Obliczenia i rysunki
Wyniki
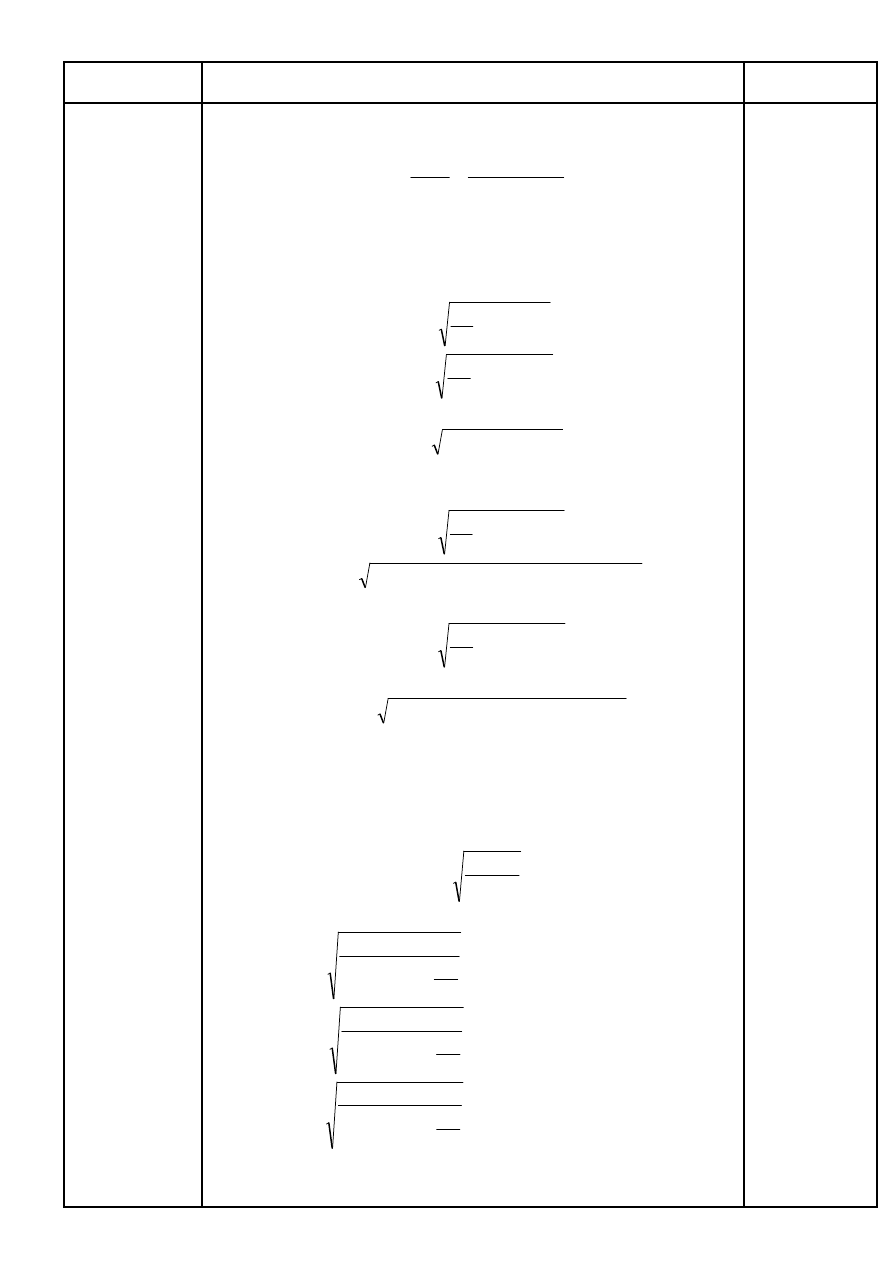
Rys. 3. Wykresy momentów i średnic teoretycznych
Dane
Obliczenia i rysunki
Wyniki
]
[
74
,
36
mm
d
A
=
]
[
63
,
931
Nm
M
o
=
]
[
42
1
mm
d
=
]
[
33
,
44363
N
F
=
]
[
8 mm
h
=
]
[
75 MPa
p
dop
=
14. Obliczenie połączenia wpustowego pod sprzęgło
14.1. Wyznaczenie teoretycznej średnicy wału pod sprzęgłem
Średnice wału pod wpust wyznacza się uwzględniając
osłabienie wału wpustem z zależności:
]
[
41
,
40
]
[
74
,
36
1
,
1
1
,
1
1
mm
mm
d
d
A
t
=
⋅
=
⋅
=
przyjęto średnicę wału pod wpustem d
1
= 42 [mm]
tolerowaną na k6 (zgodnie z normą)
zgodnie z szeregu czopów walcowych zgodnie z
PN-89/M-85000.
14.2. Dobór wymiarów wpustu z PN-70/M-85005
Z PN-70/M-85005 dobrano wymiary wpustu
bxh = 12x8 [mm]
14.3. Wyznaczenie nacisków dopuszczalnych dla elementu
„słabszego” (tarcza sprzęgła stal E360).
W projekcie tarcza sprzęgła i wał zostały wykonane z tego
samego materiału (E360). Naprężenie dopuszczalne na
naciski powierzchniowe przyjmuje się w granicach
(60
÷ 90) MPa dla pary wpust wykonany z E335 lub E360 –
stal lub staliwo w zależności od jakości materiału elementu
słabszego (czopa lub piasty).
Przyjęto p
dop
= 75 MPa dla stali E335.
14.4. Obliczenie siły stycznej przenoszonej przez wpust:
]
[
33
,
44363
]
[
10
42
]
[
63
,
931
2
2
3
N
m
Nm
d
M
F
o
=
×
⋅
=
⋅
=
−
14.5. Obliczenie wstępnej czynnej długości wpustu l
0
dop
p
A
F ≤
o
l
h
A
⋅
=
2
dop
p
h
F
l
⋅
⋅
≥
2
0
]
[
88
,
147
]
[
14788
,
0
]
[
75
]
[
10
8
]
[
33
,
44363
2
0
3
0
mm
m
l
MPa
mm
N
l
=
≥
⇒
⋅
×
⋅
≥
−
]
[
14788
,
0
0
m
l
≥
]
[
88
,
147
0
mm
l
≥
Ponieważ długość wpustu wychodzi z obliczeń zbyt duża (nie ma
możliwości doboru takiego wpustu a dodatkowo nie będzie
możliwości dobrać odpowiedniej długości czopa pod sprzęgło,
gdyż dla średnicy 42 [mm] długość czopa krótkiego wynosi
82 [mm] a długiego 110 [mm]) należy ponownie wykonać
obliczenia wpustu przyjmując większe naciski dopuszczalne
zakładając oczywiście obróbkę cieplną zarówno wpustu, czopa i
piasty. Z tablicy 2.2. PKM pod redakcją Z Osińskiego przyjęto p
dop
= 150 [MPa].
]
[
41
,
40
1
mm
d
t
=
]
[
42
1
mm
d
=
]
[
8
12
mm
h
b
×
=
×
]
[
75 MPa
p
dop
=
]
[
33
,
44363
N
F
=
]
[
88
,
147
0
mm
l
≥
Dane
Obliczenia i rysunki
Wyniki
]
[
33
,
44363
N
F
=
]
[
8 mm
h
=
]
[
150 MPa
p
dop
=
]
[
42
1
mm
d
=
14.6. Obliczenie czynnej długości wpustu l
0
dla p
dop
= 150 [MPa]
dop
p
A
F ≤
gdzie:
o
l
h
A
⋅
=
2
dop
p
h
F
l
⋅
⋅
≥
2
0
]
[
93
,
73
]
[
07393
,
0
]
[
150
]
[
10
8
]
[
33
,
44363
2
3
0
mm
m
MPa
mm
N
l
=
=
⋅
×
⋅
=
−
]
[
07393
,
0
0
m
l
≥
]
[
93
,
73
0
mm
l
≥
14.7. Dobór znormalizowanej długości wpustu
Rzeczywista długość wpustu typu A powiększona o
szerokość b wynikającą z promieni zaokrągleń wyniesie
85,97 [mm]
Z PN-70/M-85005 l
2
= 90 [mm]
Pozostałe wymiary rowka wpustowego takie jak t
1
–
głębokość rowka w czopie, t
2
– głębokość rowka w piaście,
szerokość rowków wraz z tolerancjami, promieniami
zaokrągleń i chropowatościami powierzchni dobrano z tej
samej normy.
14.8. Dobór długości czopa wału pod sprzęgło
W przypadku czopów końcowych, na które zostaje założona
tarcza sprzęgła długość czopa dobiera się z PN-89/M-85000.
Dla średnicy d
1
= 42 [mm] długość czopów odmiany krótkiej
równej 80 [mm] lub długiej równej 110 [mm].
Dobrano czop końcowy odmiany długiej: t
1
= 110 [mm] i
średnicy d
1
= 42 [mm] tolerowanej na k6
Środek czopa końcowego ”jest ruchomy” z uwagi na fakt, że
czop przenosi tylko moment skręcający, a jego oddalenie od
osi łożyska wynikać będzie z jego długości, długości czopa
pod pierścień uszczelniający oraz z połowy szerokości
łożyska.
15. Dobór średnicy i długości czopa pod pierścień uszczelniający:
Średnicę czopa pod pierścień uszczelniający dobrano z PN
uwzględniając zależność:
2
,
1
≤
d
D
16. Przyjęto średnicy pod pierścień uszczelniający d
2
= 50 [mm] a
długość czopa po uwzględnieniu szerokość pierścienia,
położenia łożyska i środka sprzęgła) t
2
= 32 [mm] Dobór
pierścienia gumowego uszczelniającego z lewej strony wału
Dla d
2
= 50 [mm]
Z PN PN-72/M-86964 dobrano gumowy pierścień uszczelniający
Dla którego
Średnica zewnętrzna D = 65 [mm]
Szerokość pierścienia b = 8 [mm]
]
[
93
,
73
0
mm
l
≥
]
[
90
2
mm
l
=
]
[
110
1
mm
t
=
]
[
50
2
mm
d
=
]
[
32
2
mm
t
=
D = 65 [mm]
b = 8 [mm]
Dane
Obliczenia i rysunki
Wyniki
L
h
= 24000 [h]
n = 820
obr/min]
t = 120 [
°C]
]
[
52
,
26292
N
C
=
17. Dobór średnicy pod lewe łożysko oraz wielkości łożysk
tocznych.
Średnicę pod łożyskiem dobrano zgodnie z PN-85/M-86100
d
3
= 55 [mm]
W praktyce dobiera się dwa takie same łożyska, dlatego
łożysko obliczamy w tej podporze gdzie jest większa reakcja.
Dane dodatkowe:
Żądana trwałość łożyska L
h
= 24000 [h]
Prędkość obrotowa n = 820 [obr/min]
Maksymalna temperatura pracy łożyska t = 120 [
°C]
17.1. Obliczenie nośności ruchowej łożyska
n
t
h
f
f
f
C
⋅
=
17.1.1. Obliczenie współczynnika prędkości obrotowej
344
,
0
3
1
33
3
=
=
n
f
h
17.1.2. Obliczenie współczynnika trwałości
634
,
3
500
3
=
=
h
h
L
f
17.1.3. Dobór współczynnika temperatury
Dla t< 150 [
°C] f
t
= 1
]
[
52
,
26292
3028
,
0
634
,
3
]
[
89
,
2488
N
N
f
f
f
R
C
n
t
h
a
=
=
⋅
=
]
[
52
,
26292
N
C
=
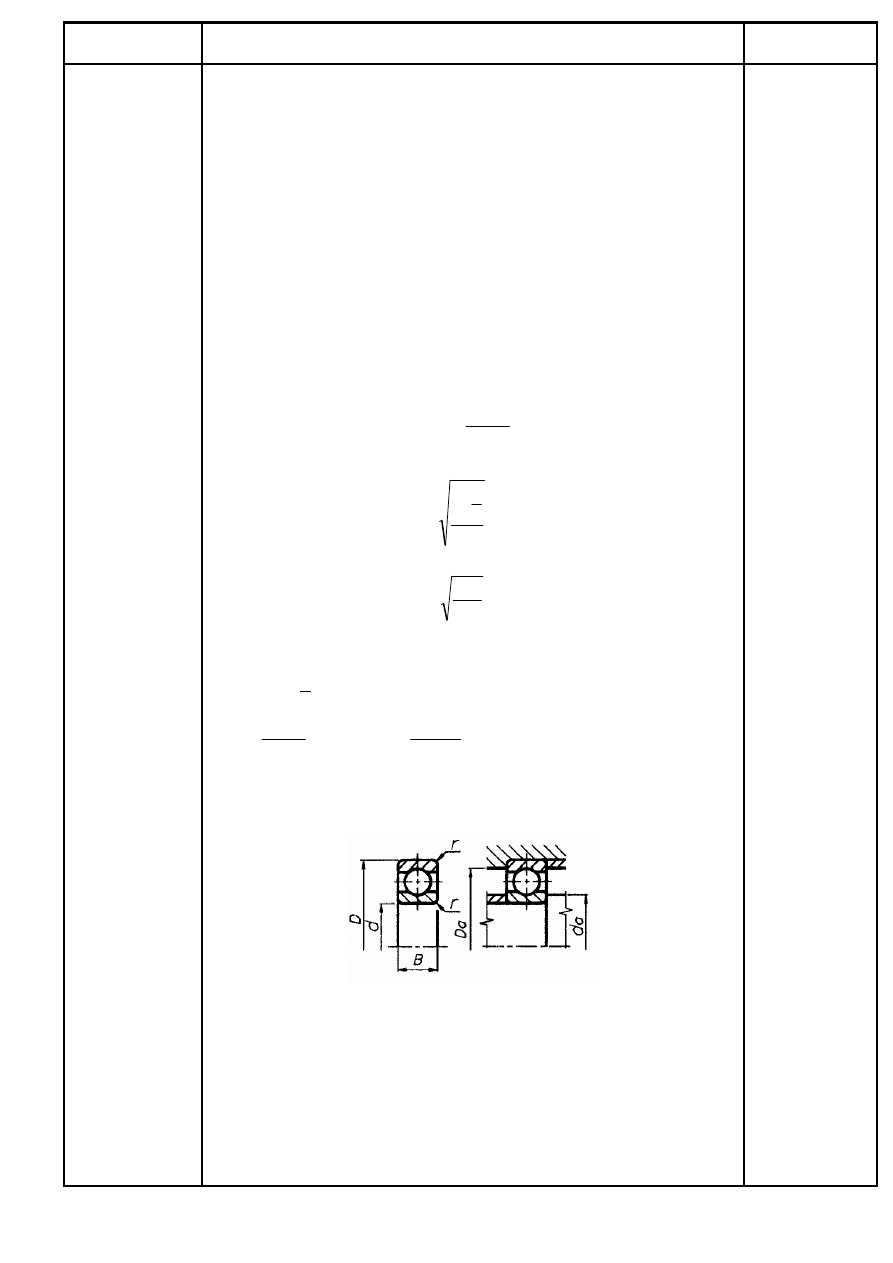
Z PN-85/M-86100 dobierano łożyska kulkowe zwykłe 6210 o
nośności ruchowej 36630 [N], dla którego:
D = 90 [mm]
B = 21 [mm]
r = 1,1 [mm]
d
a
= 57 [mm]
D
a
= 83 [mm]
]
[
55
3
mm
d
=
344
,
0
=
h
f
634
,
3
=
h
f
1
=
t
f
]
[
52
,
26292
N
C
=
D = 90 [mm]
B = 21 [mm]
r = 1,1 [mm]
d
a
= 57 [mm]
D
a
= 83 [mm]

Dane
Obliczenia i rysunki
Wyniki
18. Dobór pierścieni osadczych sprężynujących.
Zaprojektowano ustalenie pierścienia wewnętrznego lewego
łożyska na wale za pomocą pierścienia osadczego sprężynującego z
lewej strony, z prawej zaś pierścień wewnętrzny łożyska ustalony
będzie poprzez tuleję redukcyjną z kołem zębatym.
Pierścień zewnętrzny lewego łożyska ustalono z prawej strony
występem w obudowie, z prawej zaś przewidziano dociśnięcie
pokrywą.
Dobrano z PN-81/M-85111 2 pierścień osadcze sprężynujące o
średnicy wewnętrznej D
0
= 50,8 [mm] i szerokości g = 2 [mm]
tolerowaną na h11
Na podstawie tej samej normy dobrano szerokość rowka pod
pierścień osadczy f = 2,15 [mm] tolerowaną na H13 oraz średnice
rowków d
r
= 52 [mm] i odległość rowków od końców czopów
łożyskowych h = 4,5 [mm] dla obu łożysk.
Prawe łożysko zaprojektowano w podobny sposób z
uwzględnieniem wyjściowych danych jego położenia na wale.
Pierścień wewnętrzny prawego łożyska ustalono takim samym
pierścieniem osadczym sprężynującym z prawej strony z lewej
oparte jest na odsadzeniu przy końcu wału.
Uwzględniając szerokość rowka pod pierścień oraz odległość
rowka od końca wału wraz z sfazowaniem, podobnie jak na łożysku
lewym, ustalono długość czopu pod prawe łożysko t
6
= 27,5 [mm]
]
[
52 mm
d
r
=
]
[
2 mm
g
=
]
[
15
,
2
mm
f
=
]
[
5
,
4
mm
h
=
]
[
5
,
27
6
mm
t
=

Dane
Obliczenia i rysunki
Wyniki
]
[
56
,
43
mm
d
cl
=
]
[
33272 N
F
=
p
dop
= 75 MPa
h = 11 [mm]
19. Obliczenie połączenia wpustowego pod kołem zębatym
19.1. Wyznaczenie teoretycznej średnicy wału pod wpust pod
kołem zębatym
Średnice wału pod wpust wyznacza się uwzględniając
osłabienie wału wpustem z zależności:
]
[
91
,
47
]
[
56
,
43
1
,
1
1
,
1
4
mm
mm
d
d
cl
t
=
⋅
=
⋅
=
Z warunków konstrukcyjnych poprzednich stopni wału
przyjęto średnicę wału pod wpustem d
4
= 60 [mm].
Przewidziano tolerancję p6 tworzącą z piastą koła
pasowanie: H7/p6
Uwzględniając warunek:
2
,
1
≤
d
D
19.2. Dobór wymiarów wpustu z PN-70/M-85005
Z PN-70/M-85005 dobrano wymiary wpustu
bxh = 18x11 [mm]
19.3. Wyznaczenie nacisków dopuszczalnych dla elementu
„słabszego”
W projekcie koło zębate i wał zostały wykonane z tego
samego materiału (E360). Naprężenie dopuszczalne na
naciski powierzchniowe przyjmuje się w granicach
(60
÷ 90) MPa dla pary wpust wykonany z E335 lub E360 –
stal lub staliwo w zależności od jakości materiału elementu
słabszego (czopa lub piasty).
Przyjęto p
dop
= 75 MPa dla stali E360.
19.4. Obliczenie siły stycznej przenoszonej przez wpust:
]
[
33272
]
[
10
56
]
[
63
,
931
2
2
3
N
m
Nm
d
M
F
=
×
⋅
=
⋅
=
−
19.5. Obliczenie czynnej długości wpustu l
0
dop
p
A
F ≤
o
l
h
A
⋅
=
2
dop
p
h
F
l
⋅
⋅
≥
2
0
]
[
75
]
[
10
11
]
[
33272
2
3
0
MPa
mm
N
l
⋅
×
⋅
≥
−
]
[
08066
,
0
0
m
l
≥
]
[
66
,
80
0
mm
l
≥
]
[
91
,
47
4
mm
d
t
=
]
[
60
4
mm
d
=
]
[
11
18
mm
h
b
×
=
×
p
dop
= 75 MPa
]
[
33272 N
F
=
]
[
66
,
80
0
mm
l
≥

Dane
Obliczenia i rysunki
Wyniki
19.6. Dobór znormalizowanej długości wpustu
Rzeczywista długość wpustu powiększona od szerokość b
wynikającą z promieni zaokrągleń wyniesie 98,66 [mm]
Z PN-70/M-85005 l
2
= 100 [mm]
Pozostałe wymiary rowka wpustowego takie jak t
1
–
głębokość rowka w czopie, t
2
– głębokość rowka w piaście,
szerokość rowków wraz z tolerancjami, promieniami
zaokrągleń i chropowatościami powierzchni dobrano z tej
samej normy.
19.7. Dobór długości czopa wału pod koło zębate
Długość czopa powinna być mniejsza od długości piasty,
przy czym odległość od odsadzenia i kolejnego skoku wału
powinna być większa o b/2.
Przyjęto odległość od odsadzenia a
3
= 8 [mm], odległość od
kolejnego skoku średnic wału a
4
również 8 [mm]. Stąd
całkowita długość czopa
t
4
= l
2
+a
3
+a
4
=116 [mm].
19.8. Dobór średnicy odsadzenia
Średnicę odsadzenia dobieramy z zależności D/d< 1,2
średnica ta powinna być z kolei większa od średnicy czopa o
15% stąd d
2
= 1,15 * d
1
= 1,15 * 60 [mm] = 69 [mm].
Przyjęto d
5
= 72 [mm].
19.9. Dobór szerokości odsadzenia t
5
Szerokość odsadzenia t
5
przyjmuje się w zależności od
układu pozostałych części wału wynikających z
rozmieszczenia łożysk nie mniejszą jednak niż 0,1 * d
5
Przyjęto szerokość odsadzenia t
5
= 38,5 [mm].
Dodatkowo, aby uniknąć spiętrzenia naprężeń pod prawym
łożyskiem wykonano stożkowe odsadzenie schodząc ze
średnicy 72 [mm] na 64 [mm]
d
6
= 64 [mm]
19.10. Dobór szerokości piasty koła zębatego.
Szerokość piasty koła zębatego powinna być większa od
szerokości czopa ze względu na jego podparcie za pomocą
tulei redukcyjnej.
Przyjęto szerokość piasty t
p
= 118 [mm]
l
2
= 100 [mm]
t
4
= 116 [mm]
d
5
= 72 [mm]
t
5
= 38,5 [mm]
d
6
= 64 [mm]
t
p
= 118 [mm]
Wyszukiwarka
Podobne podstrony:
Projekt2 poprawiony id 400268 Nieznany
Projekt2 poprawiony id 400268 Nieznany
EiZI Projekt GiG4 2012 id 15450 Nieznany
mechanika do poprawki id 290847 Nieznany
Projekt KD remik id 398914 Nieznany
Projekt badan czII id 400460 Nieznany
dobry poprawiony id 138426 Nieznany
Beta laktamy poprawione2 id 829 Nieznany (2)
ProjektKKa 01 Koncepcja id 4003 Nieznany
projekt stropu akermana id 3996 Nieznany
Projekt Luku Poziomego id 39852 Nieznany
poprawkowy id 375499 Nieznany
PROJEKT nr 1 STUDENT id 399181 Nieznany
projekt mechanizm nac id 399063 Nieznany
Projekt KKa Wrzesinski id 40012 Nieznany
PROJEKT Z FIZYKI BUDOWLI id 399 Nieznany
projekt sumator 8bit id 399618 Nieznany
projekt wymiennika ciepla id 39 Nieznany
Projektowanie ukl cyfr id 40045 Nieznany
więcej podobnych podstron