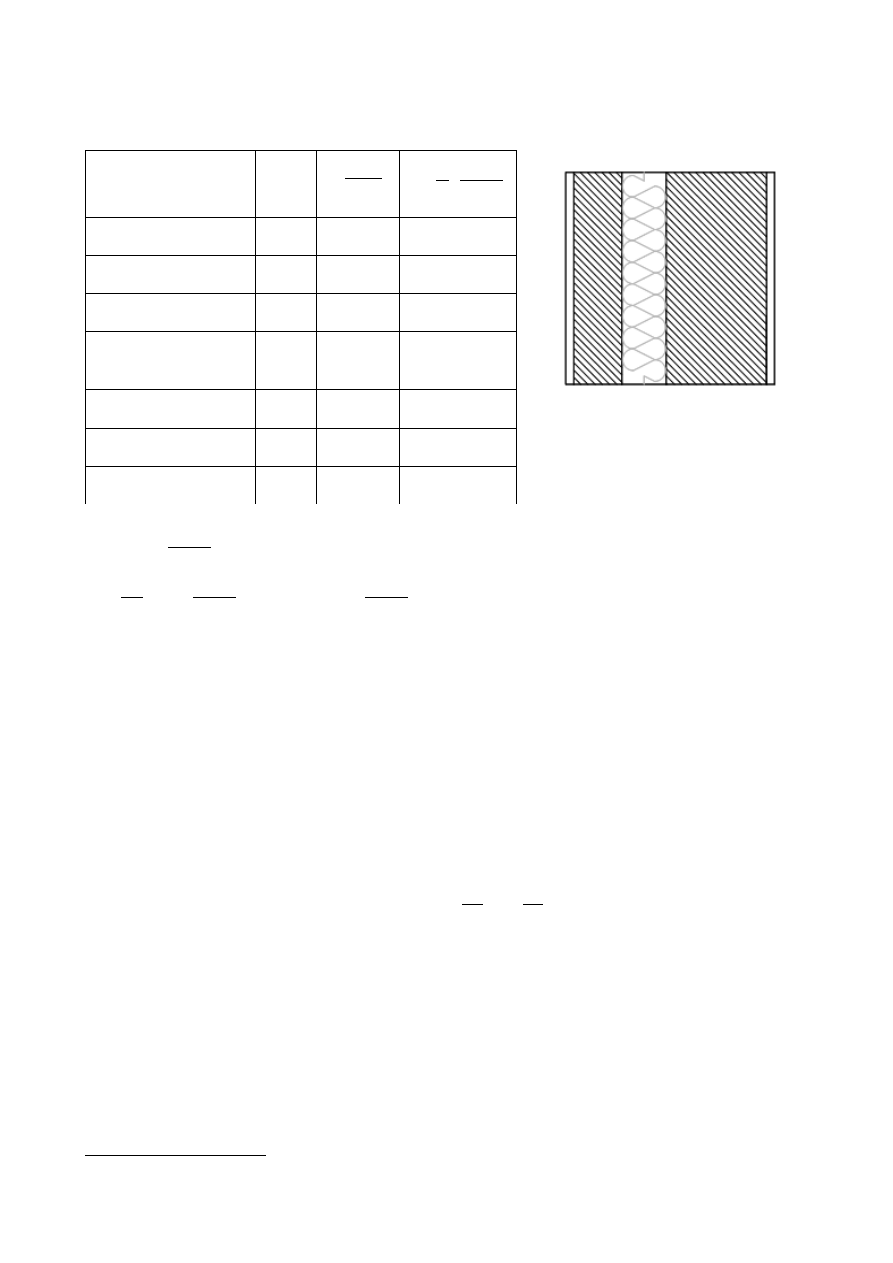
1. Izolacyjność termiczna ściany zewnętrznej

materiał

d [m]



[

W

m⋅K

]

R=

d


[

m

2

⋅

K

W

]

R

se

-

-

0,040

tynk

0,015

0,82

0,018

cegła klinkierowa

0,12

1,05

0,114

wełna mineralna

ROCKMUR

0,12

0,036

3,333

cegła pełna

0,25

0,77

0,325

tynk

0,015

0,82

0,018

R

si

-

-

0,130

R

T

=

3,978

m

2

⋅

K

W

U =

1

R

T

≈

0,25

W

m

2

⋅

K



U

MAX ZEWN.

=

0,3

W

m

2

⋅

K

Zatem grubości poszczególnych warstw zostały dobrane poprawnie.

Założenia

a) Informacje dotyczące stropu:

•

strop Ackermana

•

rozstaw osiowy żeber : 0,31 m

•

stosowany beton klasy: C16/20

•

zbrojenie wykonane ze stali: RB500

•

grubość warstwy konstrukcyjnej stropu:

h

1

25

⋅

l

M

=

1

25

⋅

5,70 m=0,228 m

. Przyjęto

h=24 cm (pustak 20 cm + 4 cm płyty), gdyż jest to również wielokrotność wysokości

jednej warstwy muru z cegły (8 cm)

•

ciężar własny stropu: g

sk

=

3,15 kN /m

2

- odczytany z tabeli 3.13 (na stronie 120

*

)

* Cz. Malinowski, R. Peła: „Projektowanie konstrukcji murowych i stropów w budownictwie tradycyjnym. Część I”

Rysunek 1: Szkic przekroju

przez warstwy przegrody

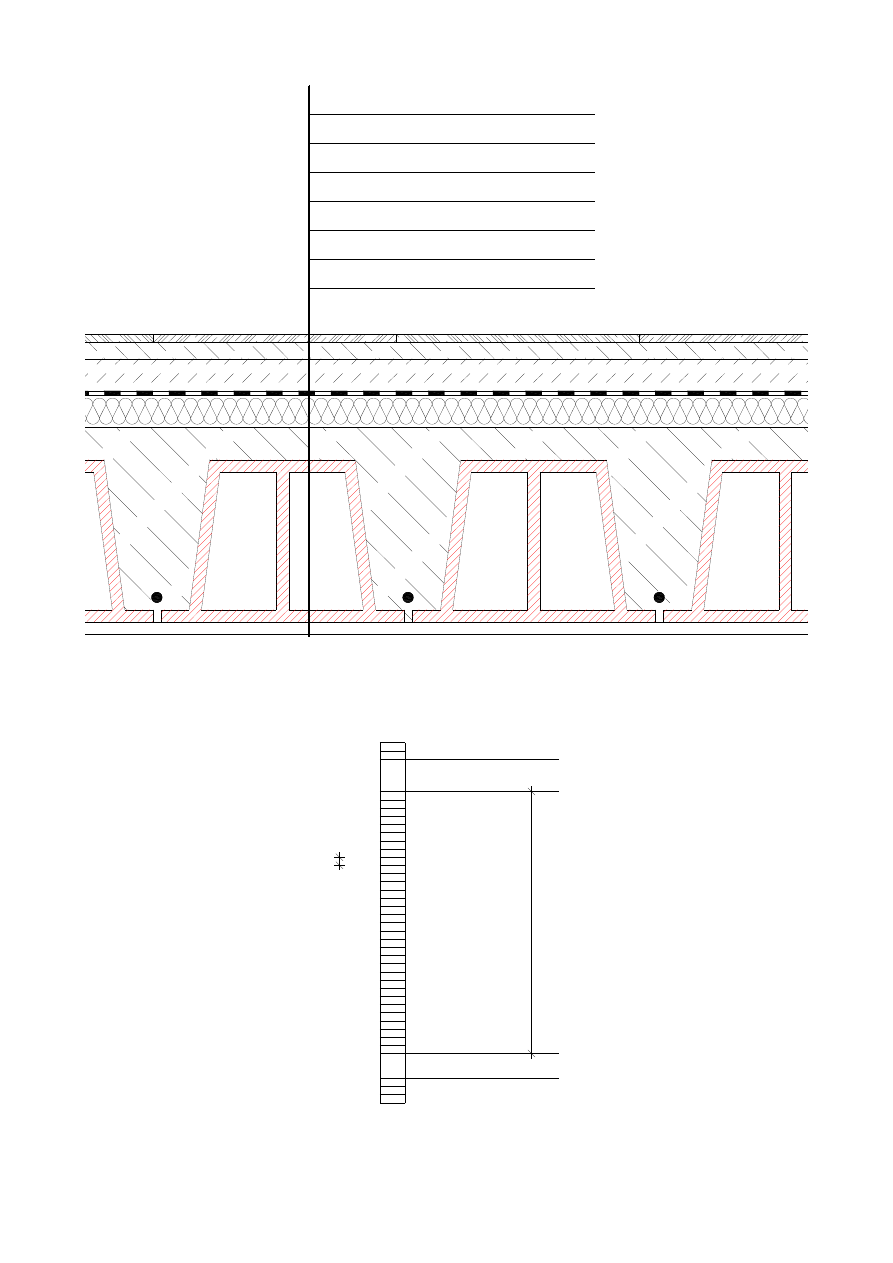
terakota

0,8 cm

zaprawia klejowa

0,2 cm

podkład

4 cm

papa

0,5 cm

płyty wełny mineralnej

4 cm

strop Ackerman 20

24 cm

tynk cementowo-wapienny 1,5 cm

b) Ustalenie wysokości kondygnacji

Rysunek 3: Szkic pokazujący wysokość kondygnacji w świetle

6,51,5=8 cm

H =n⋅8 cm2,5 m

n32
n=32

H =2,56 m

Rysunek 2: Szkic przekroju przez warstwy stropu

c) Ciężar własny stropu (konstrukcja + wykończenie):

obciążenie charakterystyczne

kN/m

2

•

terakota:



0,0080,002⋅21=0,21

•

podkład cementowy grubość 4cm:

0,04⋅21=0,84

(ciężar objętościowy 21 kN/m

3

według normy PN-82/B-02001)

•

papa, przyjęto:

0,05

•

wełna mineralna, grubość 4 cm:

0,04⋅1,2=0,05

(ciężar objętościowy 1,2 kN/m

3

według normy PN-82/B-02001)

•

ciężar własny stropu:

3,15

•

tynk cementowo-wapienny:

0,015⋅19=0,29

(ciężar objętościowy 19 kN/m

3

według normy PN-82/B-02001)

g

k

=

4,59 kN /m

2

d) Obciążenie użytkowe:

p

k

=

2,0 kN /m

2

e) Ciężar ścianki działowej:

obciążenie charakterystyczne

kN/m

•

ciężar muru – pustaki Porotherm 11,5 P+W:

1,2⋅2,56=3,07

(ciężar muru: 1,2 kN/m

2

przyjęto na podstawie opracowania producenta)

•

2 x tynk cementowo-wapienny:

2⋅0,01⋅19⋅2,56=0,97

(ciężar objętościowy 19 kN/m

3

według normy PN-82/B-02001)

g

sk

=

4,04 kN / m

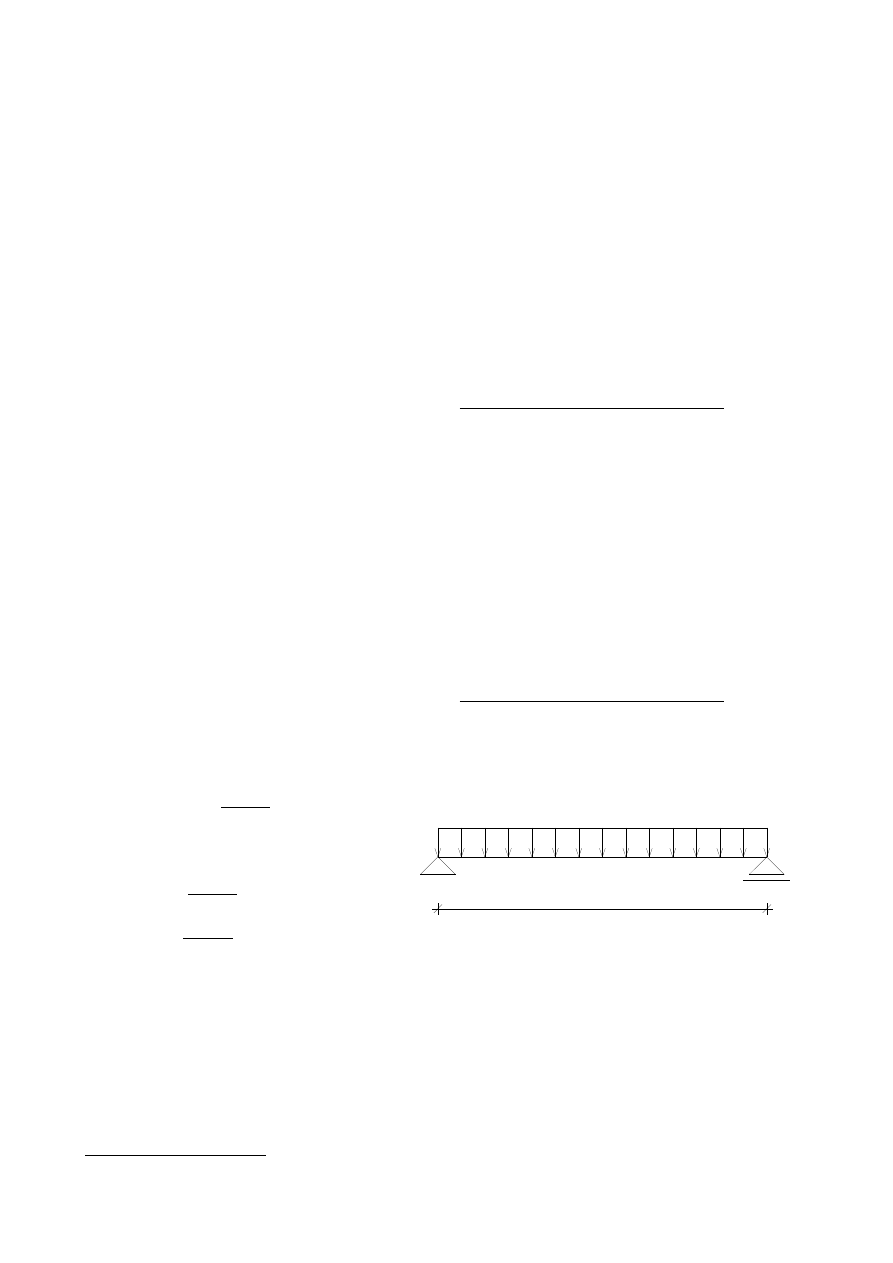
f) Schemat statyczny belki:

l

n

=

5,70 m−2⋅

0,25 m

2

=

5,45 m

l

eff

=

l

n



a

1



a

2

a

i

=

min

{

0,24 m

2

=

0,12 m

0,25 m

2

=

0,125 m

l

eff

=

5,45 m2⋅0,12 m=5,69 m

Na podstawie wysokości pustaka i grubości płyty nadbetonu można zgodnie z tabelą 3.14
(na stronie 121

**

) przyjąć, że schemat statyczny stropu to belka swobodnie podparta oraz

M =0,125⋅q

d

⋅

l

eff

2

.

** Cz. Malinowski, R. Peła: „Projektowanie konstrukcji murowych i stropów w budownictwie tradycyjnym. Część I”

Rysunek 4: Schemat statyczny stropu

q

d

l

eff

2. Obliczenia statyczne stropu

2.1. Obliczenia dla żebra nr 1 (50 % obciążenia od ścianki działowej):

•

według wzoru 6.10a:

q

d

=

1,35⋅



4,59⋅0,310,50⋅4,04





1.05⋅2⋅0,31−0,135

q

d

=

5,02 kN /m

•

według wzoru 6.10b:

q

d

=

1,15⋅



4,59⋅0,310,50⋅4,04





1.5⋅2⋅0,31−0,135

q

d

=

4,48 kN / m

Zatem: M

1

=

0,125⋅5,02⋅5,69

2

=

20,32 kNm

Zgodnie z tablicą nośności stropu Ackermana
w żebrze nr 1 należy zastosować zbrojenie ze stali
RB500 =18 mm . Takich dużych średnic nie stosuje
się jednak w zbrojeniu stropu Ackermana, więc należy
rozsunąć pustaki i zastosować inne zbrojenie, dzięki
któremu żebro nr 1 przeniesie 100% obciążenia
ścianki działowej.
Do dalszych obliczeń przyjmę, że pustaki odsunięto
dodatkowo na 12 cm.

2.2. Obliczenia dla żebra nr 2 (brak obciążenia od ścianki działowej):

•

według wzoru 6.10a:

q

d

=

1,35⋅4,59⋅0,311.05⋅2⋅0,31

q

d

=

2,57 kN / m

•

według wzoru 6.10b:

q

d

=

1,15⋅4,59⋅0,311.5⋅2⋅0,31

q

d

=

2,57 kN / m

Zatem:

M

1

=

0,125⋅2,57⋅5,69

2

=

10,40 kNm

Zgodnie z tablicą nośności stropu
Ackermana w żebrze nr 2 należy
zastosować zbrojenie ze stali RB500

=

12/14 mm

.

Wtedy: A

s średnie

=

1,335 cm

2

Rysunek 5: Schemat wstępnego

rozmieszczenia żebra nr 1

1

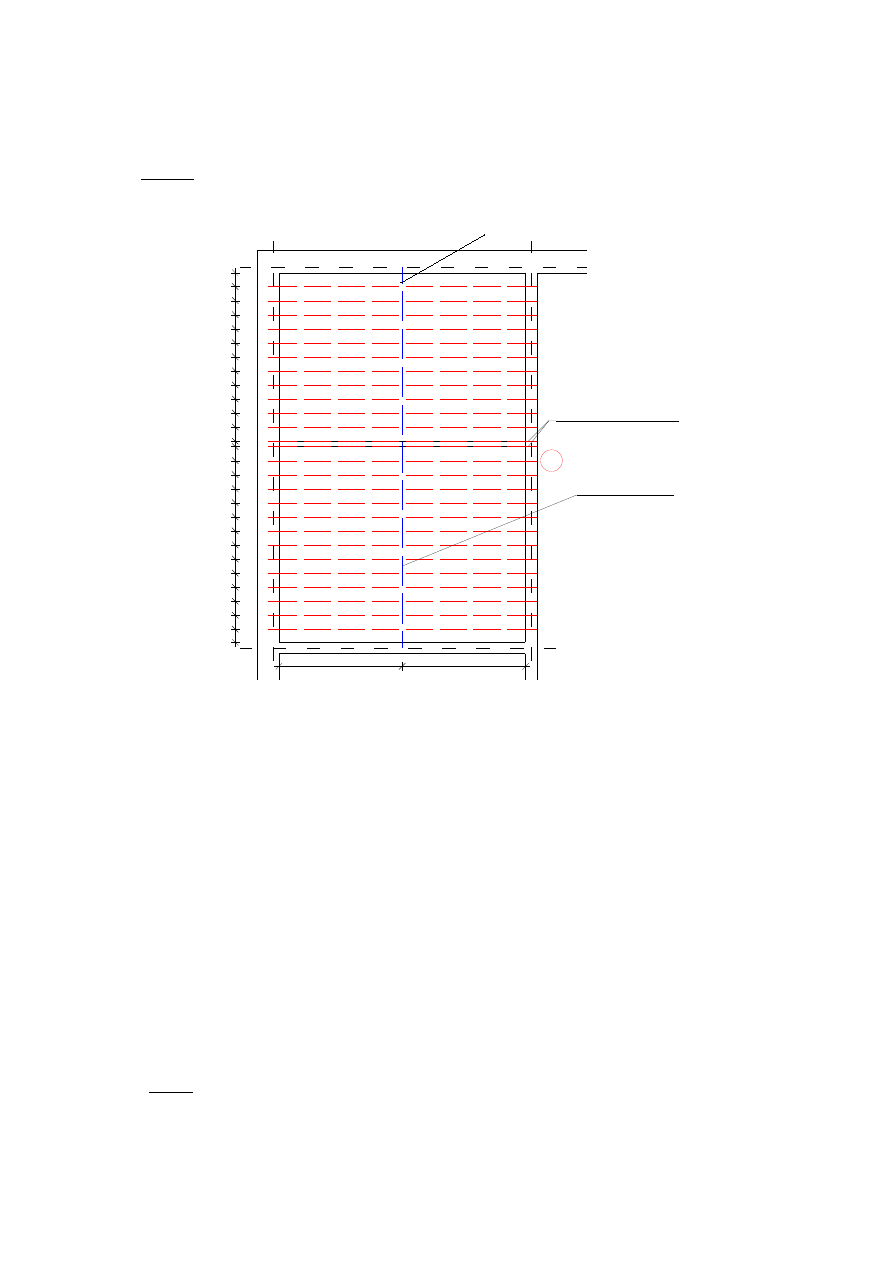
Rysunek 6: Schemat pokazujący usytuowanie żeber w

stropie

31

31

31

31

31

28

,5

3

1

poszerzone żebro nr 1

2

12

3

1 3

1

31

31

31

31

31

31

31

31

31

3

0,

5

31

31

31

31

31

31

31

2.3. Żebro rozdzielcze

F =20⋅l

n

F =20⋅5,45=109 kN

A=

109⋅10

500

=

2,18 cm

2

Należy zatem zastosować zbrojenie ze stali RB500

2 12

( A=2,26 cm

2

).

2.4. Zbrojenie nad podporami

A=20 %⋅A

s

=

0,2⋅1,335=0,267 cm

2

Jest to jednak mała wartość, warto więc rozważyć zbrojenie w co drugim żeberku (co 62 cm).
Wtedy:

A=2⋅0,267=0,534 cm

2

Należy zatem zastosować zbrojenie ze stali RB500



10

( A=0,785 cm

2

) co 62 cm.

Podstawowa długość zakotwienia, przyjęto:

l

b , rqd

=

52⋅=52 cm

2.5. Zbrojenie w wieńcu

F =70 kN

A

w

=

70⋅10

500

=

1,4 cm

2

Należy zatem zastosować zbrojenie ze stali RB500 4 8 (

A=2,01 cm

2

).

Rysunek 7: Schemat pokazujący usytuowanie żebra

rozdzielczego w stropie

3

1
3

1

3

1

3

1
3

1

2

8

,5

3

1

poszerzone żebro nr 1

2

1

2 3

1

3

13

1

3

1

3

13

1

3

1

3

13

1

3

1

3

13

0

,5

3

1
3

1

3

1

3

1
3

1

3

1

3

1

żebro rozdzielcze

272,5

272,5

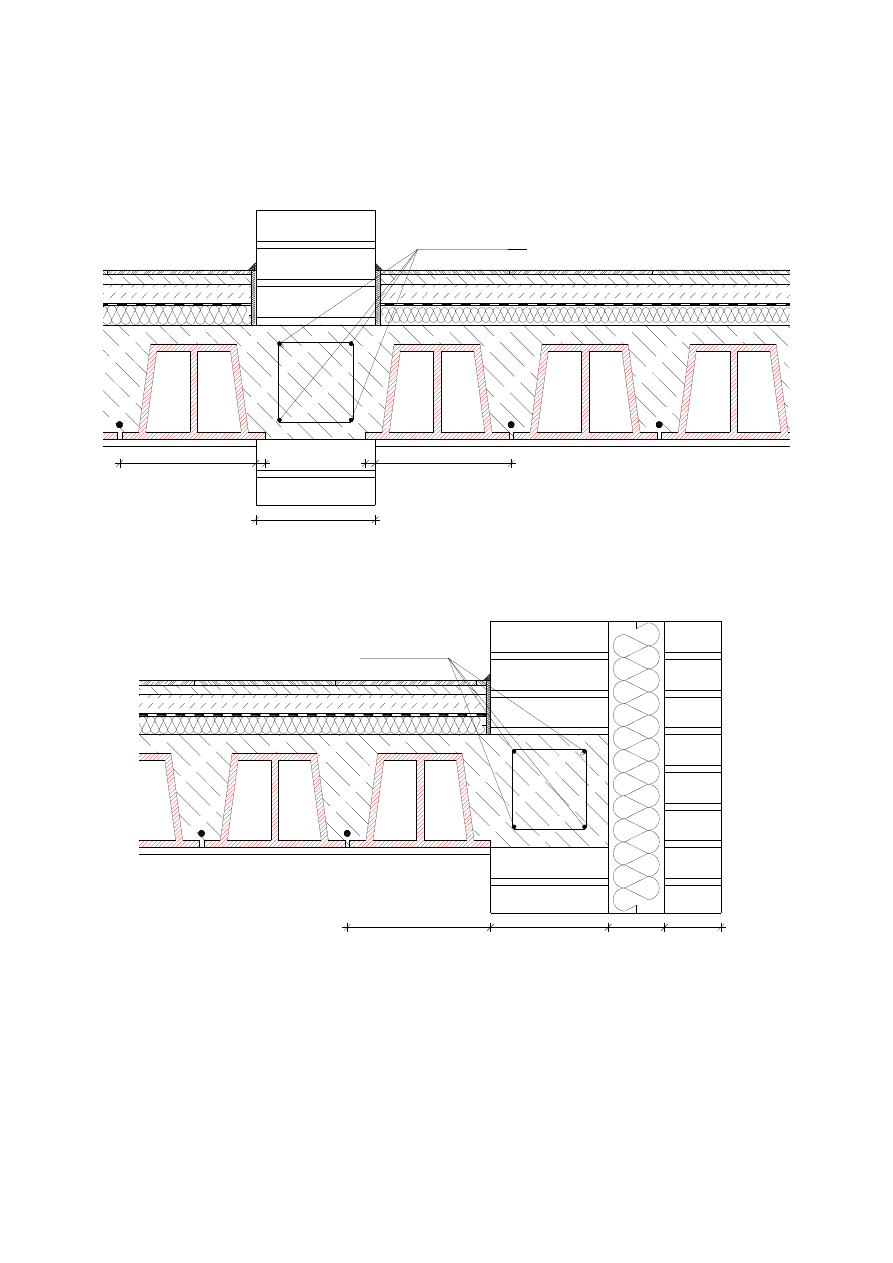
3. Detale

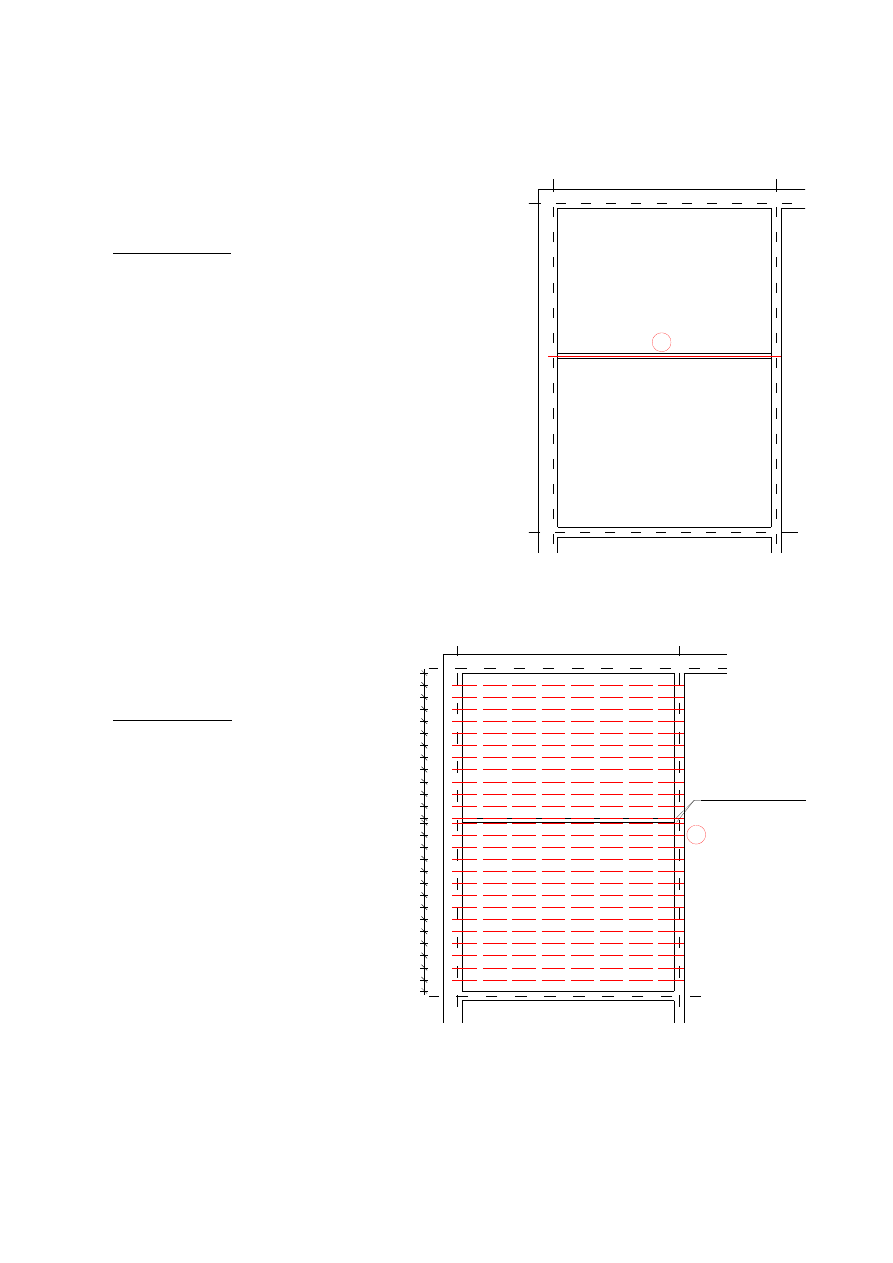
3.1. Dojście do ściany wewnętrznej

3.2. Dojście do ściany zewnętrznej

25

30,5

12

12

2

28,5

2

25

28,5

4 8

4 8

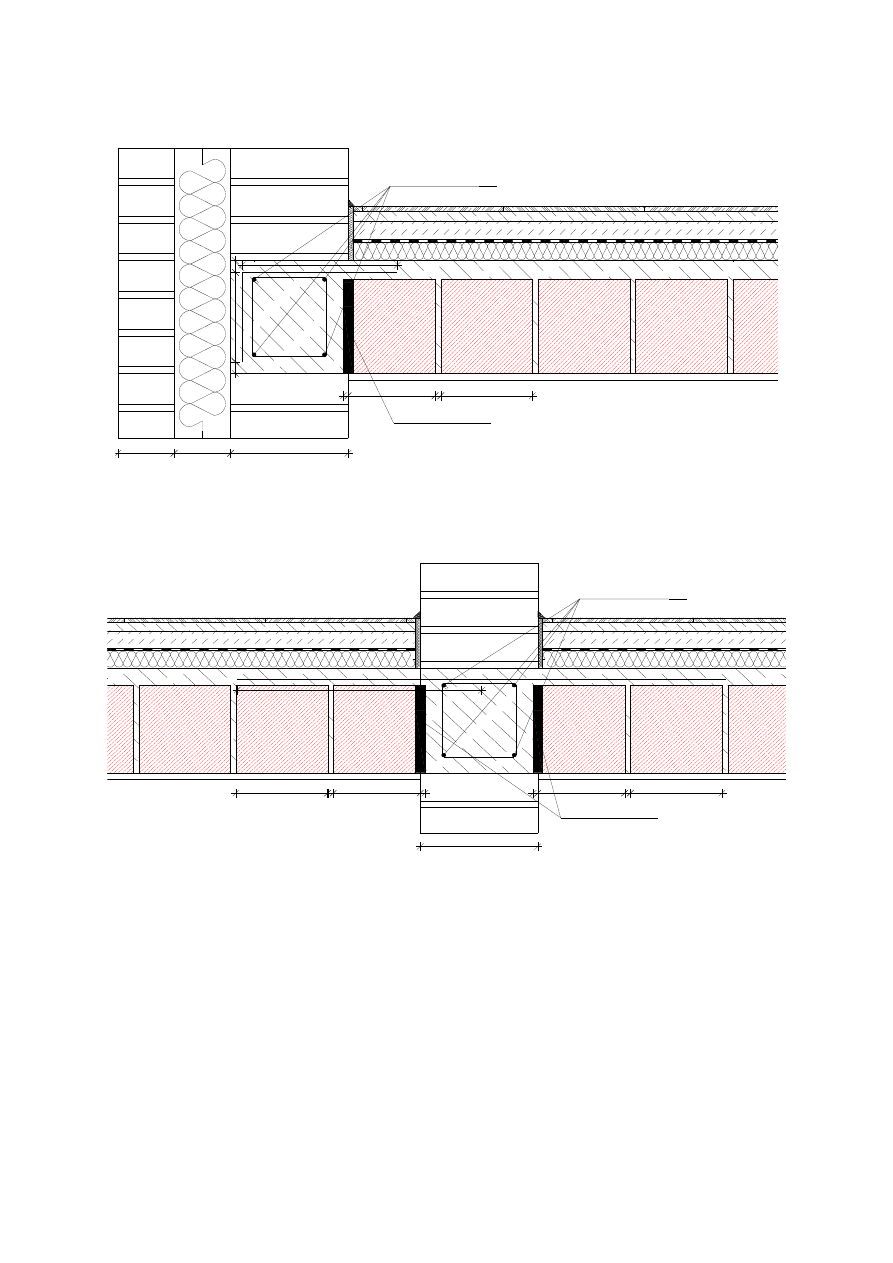
3.3. Oparcie na ścianie zewnętrznej

3.4. Oparcie na ścianie wewnętrznej

25

1

18,5

1,2

19,5

zaślepienie 2 cm

1

18,5

1,2

19,5

52

25

12

12

2,

5

19

2,

5

1

18,5

1,2

19,5

zaślepienie 2 cm

33

4 8

4 8