- 2 -
Elektryczność i magnetyzm
Źródłami sił elektrycznych i magnetycznych są ładunki elektryczne. Materia w stanie
równowagi jest neutralna, lecz wiemy, ze składa się z ładunków. Ładunek
należy do podstawowych własności atomu. W atomach ładunek jest
umieszczony w jądrze atomowym na powłokach elektronowych.
Powłoka zawiera Z elektronów, każdy o ładunku –e, jadro zawiera Z
protonów, każdy o ładunku +e. Pomiędzy jądrem a elektronami działają
siły elektromagnetyczne.
Ładunek elektryczny
Ładunek występuje zawsze w ustalonych wielkościach. Podstawowym „kwantem”
ładunku jest ±e. Wartość ładunku elementarnego wynosi e=1.6*10
-19
[C]
dV
dQ
dS
dQ
dl
dQ
Ładunki zauważa się, gdy zaburzymy neutralność. Ładunki
można rozdzielić i stwierdzić ich istnienie. Poruszać się mogą
tylko elektrony.
Ładunek dodatni – deficyt elektronów ładunek ujemny –
nadmiar elektronów
Rozdział ładunku następuje np. przez kontakt różnych materiałów, lub przez tarcie.
Elektroskop
Do wykrywania ładunku elektrycznego służy elektroskop
- 3 -
Prosty elektroskop listkowy składa się z pionowego metalowego pręta, w środku którego
jest przymocowane przegubowo ruchome ramie. Wykorzystuje się zjawisko odpychania się
jednoimiennych ładunków elektrycznych. Przy zetknięciu pręta z obiektem naładowanym
cześć ładunku przepływa z tego obiektu do elektroskopu, ruchome ramie oddziaływuje z
prętem
Ładunek elektryczny
W rożnych ciałach ładunki mogą się przemieszczać w rożnym stopniu
Ciała w których ładunki mogą przemieszczać się swobodnie na odległości makroskopowe
nazywamy przewodnikami
Ciała w których ładunki przemieszczają się w ograniczony sposób (na odległości
mikroskopowe) nazywamy izolatorami.
Ładunki mogą wiec przemieszczać się pomiędzy różnymi ciałami jeśli połączymy je
przewodnikiem
Jednym z podstawowych praw dotyczących ładunków jest Prawo Zachowania Ładunku
Sumaryczny ładunek układu odizolowanego elektrycznie pozostaje stały. Nie można
zniweczyć ani wytworzyć odosobnionych ładunków jednego znaku
He
Th
U
4
2
234
90
238
92
Rozpad α uranu
238
U – sumaryczny ładunek produktów rozpadu nie zmienia się.
ELEKTROSTATYKA
Zajmuje się badaniami pól elektrycznych wytworzonych przez ładunki nieruchome.
Prawo Culomba
Siła działającą miedzy dwoma ładunkami punktowymi jest wprost proporcjonalna do
iloczynu tych ładunków i odwrotnie do kwadratu odległości miedzy nimi:
r
r
r
q
q
F
2
2
1
0
4
1
2
2
12
0
10
85
.
8
m
N
C
r jest wektorem wyprowadzonym od ładunku q
1
do q
2
Dla układu ładunków pkt. siła działająca na wybrany ładunek (k-ty) będzie równa (zasada
superpozycji):
ik
k
i
ik
i
k
k
k
k
k
r
r
q
q
F
F
F
F
3
1
0
3
2
1
)
(
4
1
...
- 4 -
Natężenie pola elektrycznego
Ładunki wytwarzają wokół siebie pole sil, które działa na każdy ładunek wprowadzony do
tego pola. Pole to charakteryzujemy wektorem natężenia pola elektrycznego E równym sile
działającej na próbny jednostkowy ładunek dodatni.
]
[
C
N
q
F
E
Dla ładunku punktowego Q:
r
r
Q
E
3
0
4
1
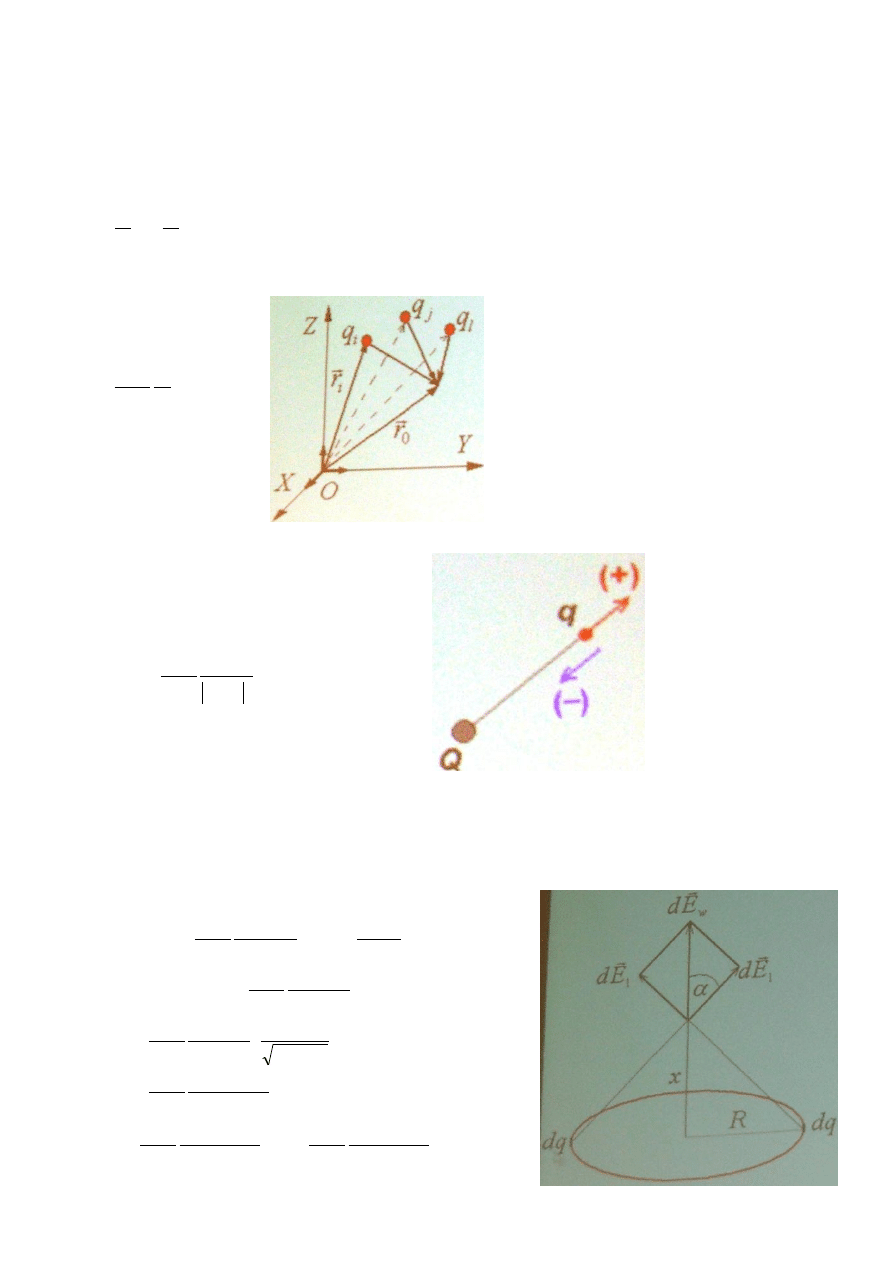
Dla układu ładunków punktowych
)
(
4
1
)
(
0
3
0
0
0
i
i
i
i
r
r
r
r
q
r
E
Przykład
Znaleźć natężenie pola elektrycznego wytwarzanego przez ładunek Q
rozmieszczony równomiernie na pierścieniu o promieniu R na osi pierścienia w odległości x
od jego środka.
rysunek!
2
2
0
1
4
1
x
R
dq
dE
dl
R
Q
dq
2
cos
4
1
2
cos
2
2
2
0
1
x
R
dq
dE
dE
w
2
2
2
2
0
4
1
2
x
R
x
x
R
dq
dE
w
w
w
w
dE
E
x
R
dq
x
dE
2
/
3
2
2
0
4
1
2
2
/
3
2
2
0
2
/
3
2
2
0
4
1
4
1
2
x
R
x
Q
dq
x
R
x
E
w
- 5 -
Linie sił pola elektrycznego
Natężenie opisuje się również poprzez tzw. linie sil, zgodne w każdym punkcie ze zwrotem
E. Przyjmuje się, ze ilość linii sil na jednostkę powierzchni prostopadłej do tych linii jest
równa natężeniu pola E.
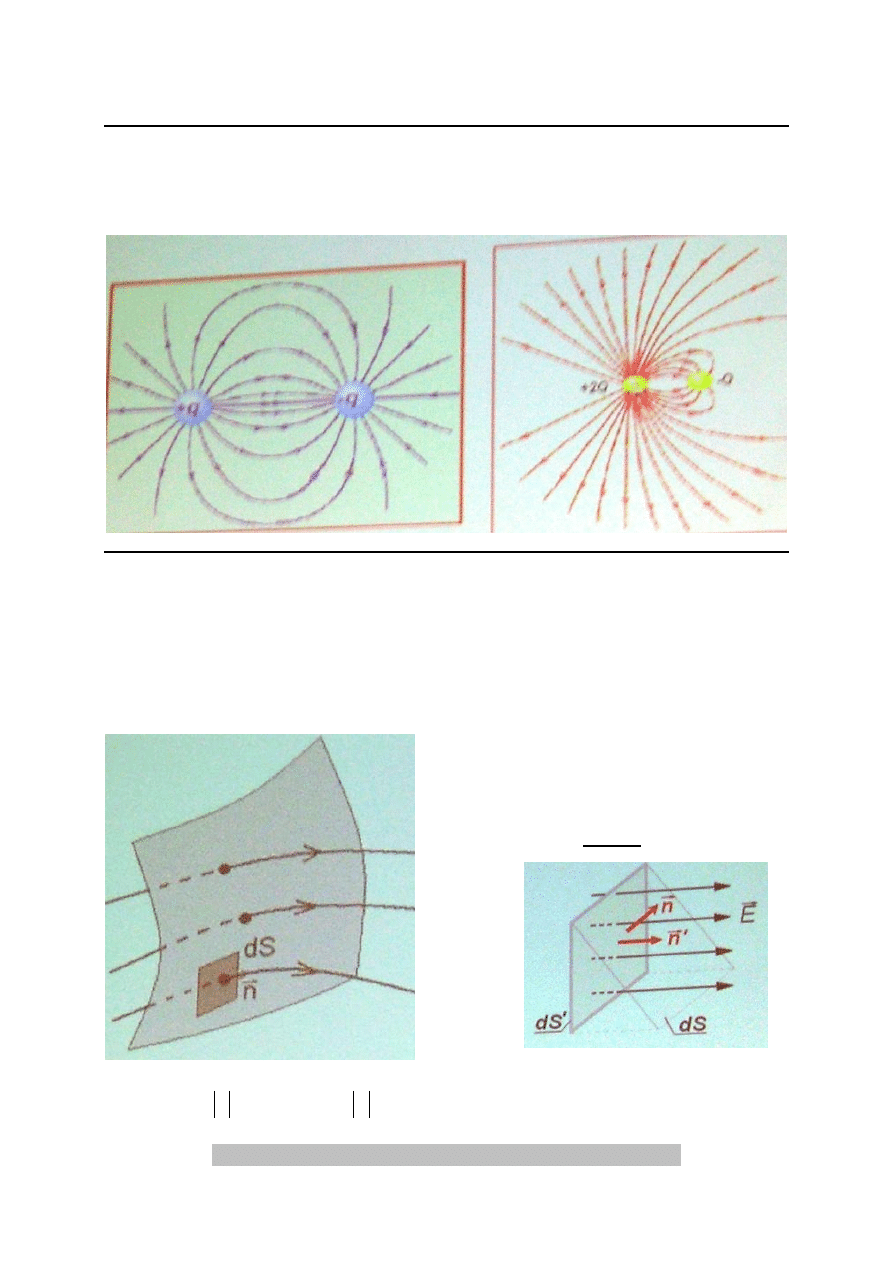
Linie sil pola elektrycznego dla ładunku punktowego dodatniego i ujemnego.
Linie sił dla dwóch różnoimiennych
ładunków punktowych
Linie sił dla dwóch ładunków punkowych
dodatnich
- 6 -
Porównanie linii sil ładunków różnoimiennych – jednakowych i różniących się od
siebie.
Strumień natężenia pola elektrycznego
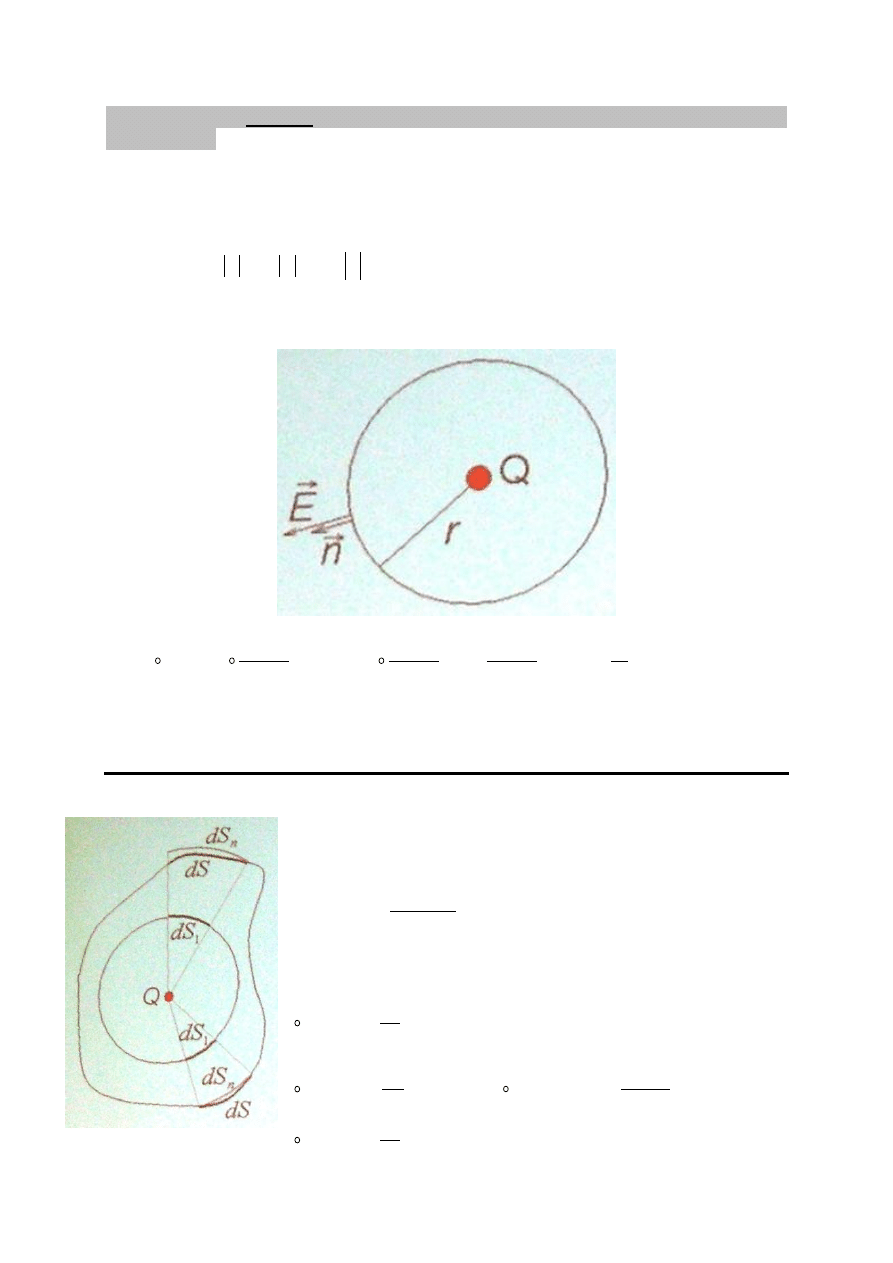
Rozważmy powierzchnię, która przecinają linie sil pola elektrycznego. Elementowi tej
powierzchni przyporządkowujemy wektor skierowany prostopadle do powierzchni ds.
i równy liczbowo dS:
dS
n
S
d
Przez powierzchnię przechodzi taka sama
ilość linii sil, co przez powierzchnię dS’
prostopadłą do E –
rysunek
Strumieniem dΦ pola E przez dowolną powierzchnię ds. nazywamy iloczyn skalarny:
S
d
E
E
n
dS
E
S
d
E
d
)
,
cos(
E
n
'
Strumień dΦ jest miara liczby linii sil przez powierzchnię dS
- 7 -
Strumień przez dowolną powierzchnię S jest miara liczby linii sił przez daną
powierzchnię:
S
d
E
d
2
4 r
E
dS
E
dS
E
S
d
E
S
d
E
||
Obliczamy strumień natężenia pola elektrycznego wytworzonego przez ładunek
punktowy Q przez powierzchnię sfery o promieniu r w środku której jest ładunek:
0
2
2
0
2
0
3
0
4
4
4
4
Q
r
r
Q
dS
r
Q
dS
n
r
r
Q
S
d
E
Udowodnimy, że otrzymany wynik byłby taki sam dla dowolnej powierzchni
zamkniętej.
Prawo Gaussa
Rozważamy dowolną powierzchnię ograniczająca ładunek Q
Przez dS przechodzi taka sama ilość linii, co przez dS
1
i dS
2
0
1
1
Q
S
d
E
V
Sumując wszystkie elementy stronami:
0
2
2
Q
S
d
E
V
0
i
i
V
i
i
Q
S
d
E
0
i
V
i
Q
S
d
E
- 8 -
Strumień natężenia pola elektrycznego przez dowolną powierzchnię zamkniętą
ograniczającą obszar V równy jest całkowitemu ładunkowi zgromadzonemu w tej
objętości:
0
Q
S
d
E
V
gdy
0
Q
0
V
S
d
E
Wzór ten jest jednym z czterech równań Maxwella – podstawowych równań teorii
zjawisk elektromagnetycznych.
Z prawa Gaussa wynika, że źródłem pola elektrycznego są ładunki elektryczne –
wypływ linii sił pola elektrycznego obserwuje przez tą powierzchnię, która ogranicza
znajdujące się w niej ładunki elektryczne.
Prawo Gaussa – przykłady
Przykład (1)
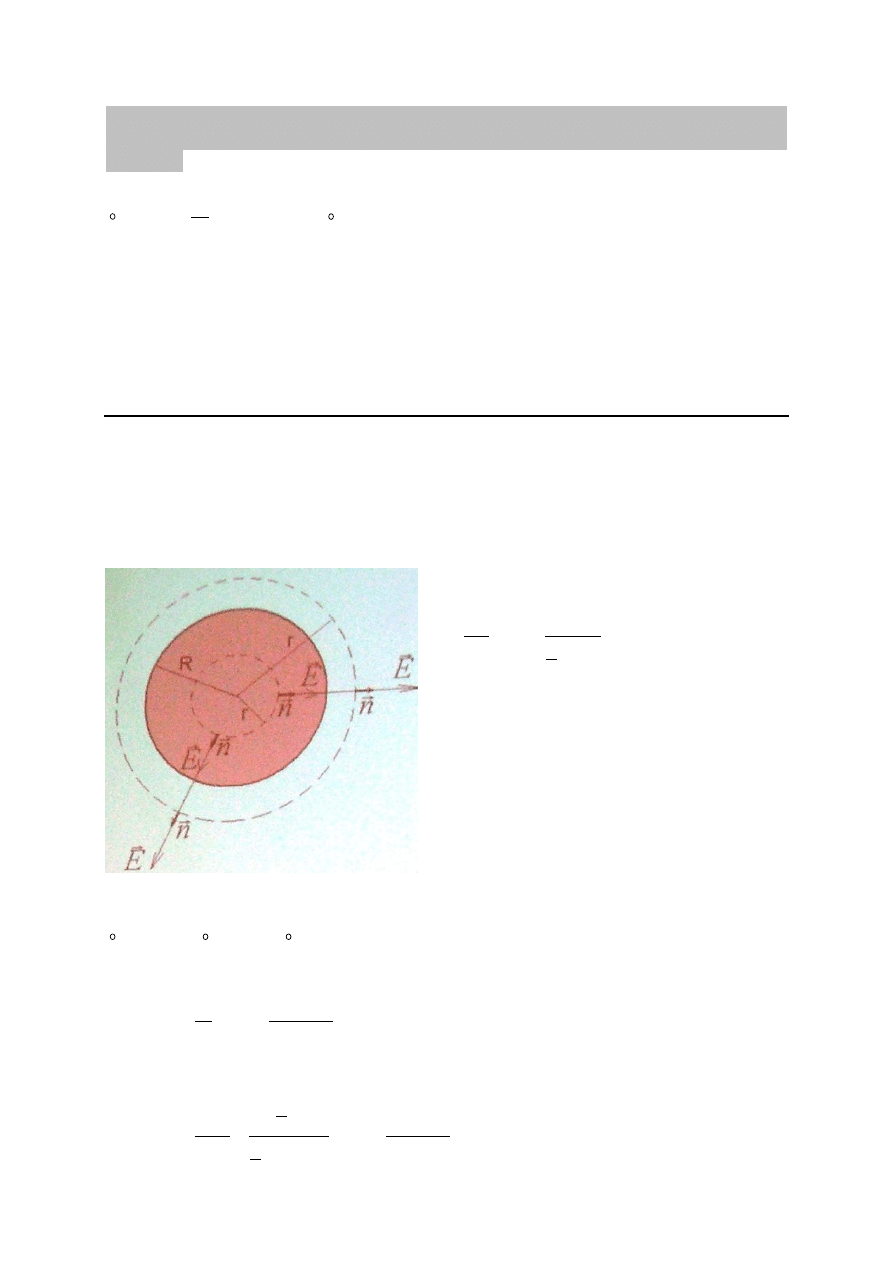
Kulę o promieniu R naładowano równomiernie ładunkiem Q w jej
objętości. Znaleźć natężenie pola elektrycznego na zewnątrz i wewnątrz kuli.
Rozważyć sytuacje, gdy ładunek jest rozmieszczony równomiernie wyłącznie na
powierzchni kuli
Gęstość objętościowa ładunku:
const
R
Q
dV
dQ
3
3
4
Wektor natężenia E=E(r) – jest stały dla
wszystkich punktów równoodległych od
środka kuli. Linie pola musza rozchodzić się
radialnie ze środka (nie mogą wyginać się w
żadna stronę, bo ani prawa ani lewa nie jest
wyróżniona)
Strumień pola elektrycznego przez powierzchnię dowolnej kuli:
2
4
r
E
dS
E
dS
E
dS
n
E
Na zewnątrz kuli:
3
0
0
2
4
4
R
Q
E
Q
r
E
Wewnątrz kuli:
3
0
0
3
3
0
2
4
3
4
3
4
4
R
r
Q
E
R
r
Q
V
r
E
- 9 -
Na zewnątrz kuli:
2
0
0
2
4
4
r
Q
E
Q
r
E
Wewnątrz kuli:
0
)
(
0
4
2
r
E
r
E
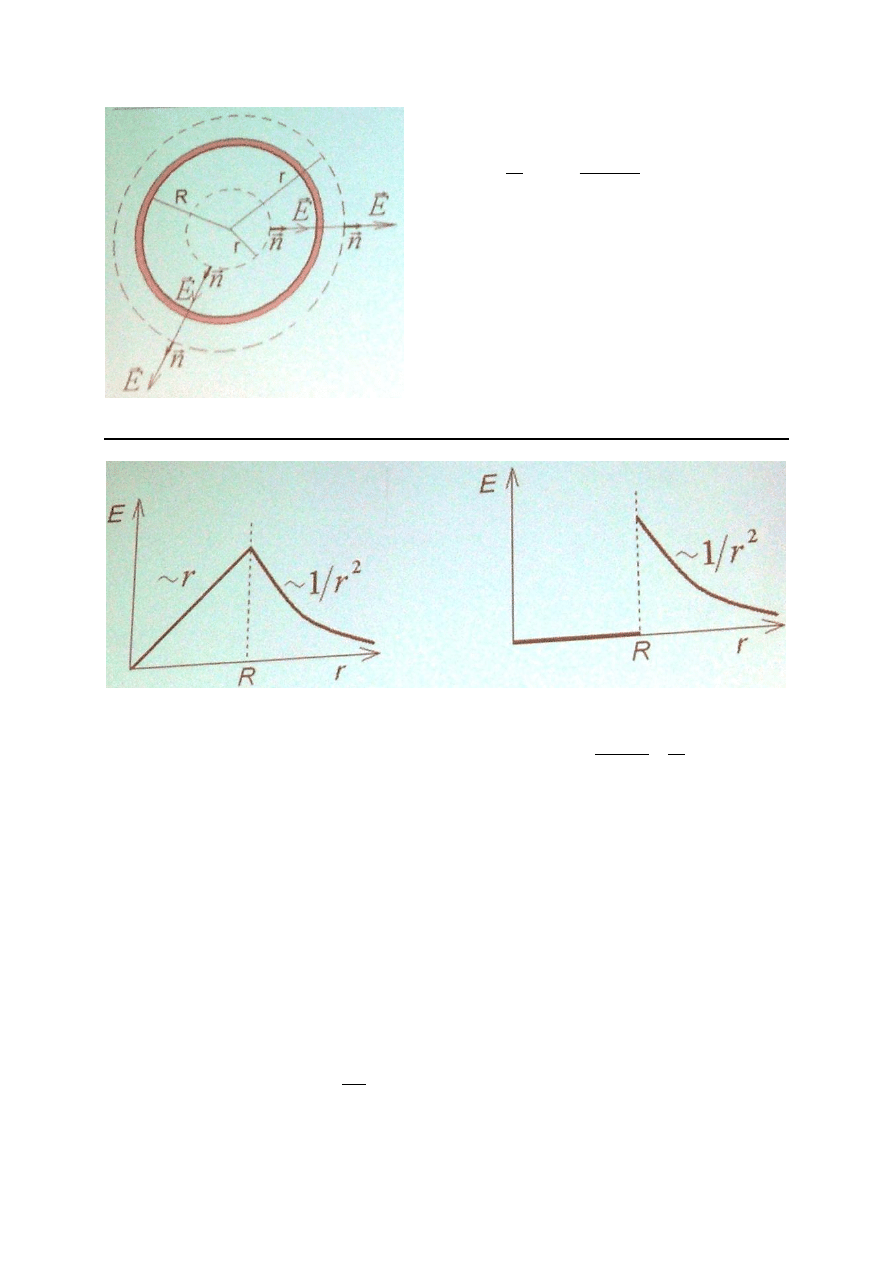
Kula naładowana równomiernie w całej
swojej objętości
0
)
(
)
(
1
2
R
E
R
E
Kula naładowana powierzchniowo
0
2
0
1
2
4
)
(
)
(
R
Q
R
E
R
E
nieciągłość
pola
spowodowana
powierzchniowym rozkładem ładunku
Przykład (2)
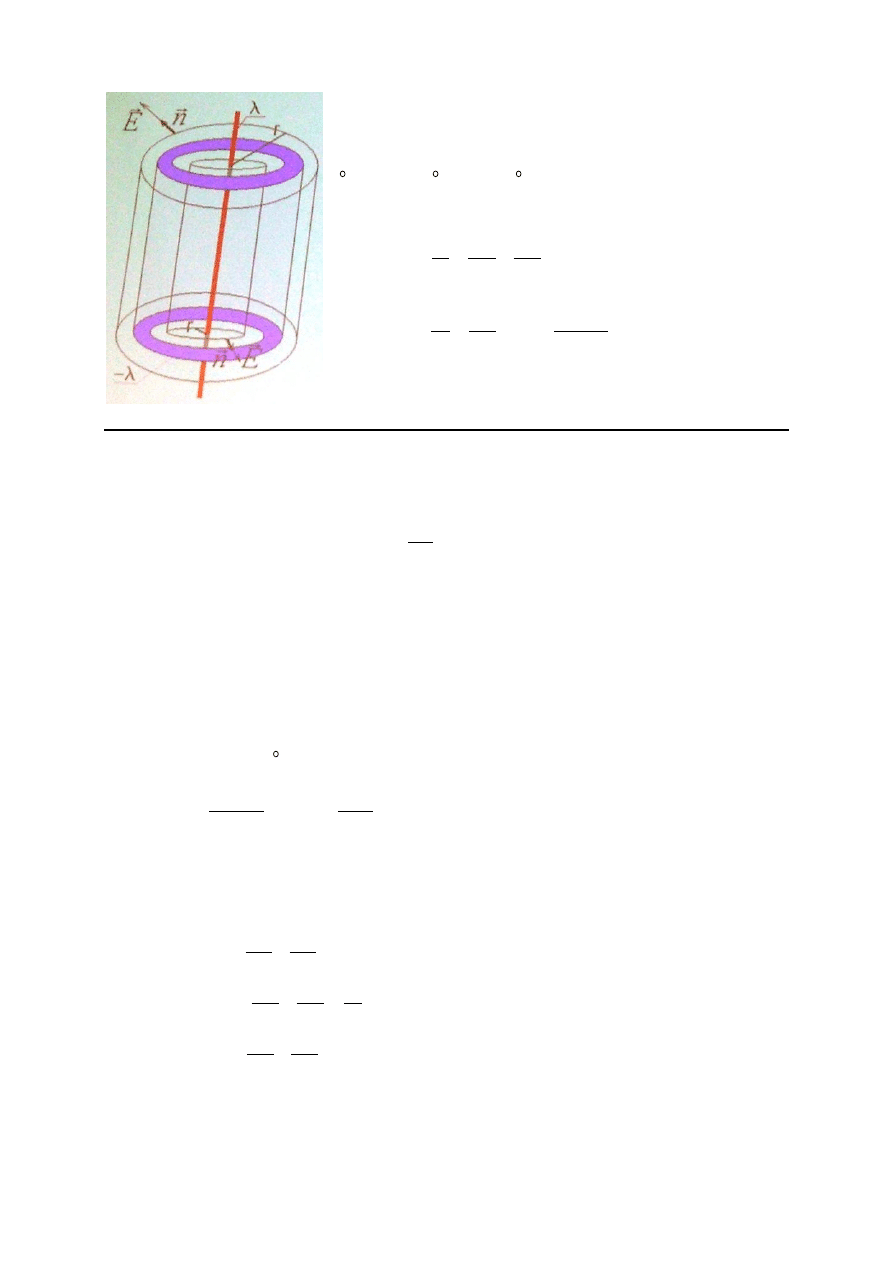
Kabel koncentryczny (współosiowy) składa się z drutu otoczonego
wydrążonym przewodnikiem walcowym. Liniowe gęstości ładunku na tych
przewodnikach są równe λ i –λ. Znaleźć natężenie pola elektrycznego na zewnątrz
kabla i wewnątrz wydrążenia.
Wektor natężenia E=E(r) – jest stały dla wszystkich punktów równoodległych osi
walca i skierowany radialnie.
Gęstość liniowa ładunku:
dl
dQ
Strumień pola elektrycznego przez powierzchnię boczna dowolnego walca o długości
l:
- 10 -
l
r
E
dS
E
dS
E
dS
n
E
2
Na zewnątrz kabla
0
0
2
0
0
0
E
l
l
Q
l
r
E
Wewnątrz kabla:
r
E
l
Q
l
r
E
0
0
0
2
2
Przykład (3)
Znaleźć natężenie pola elektrycznego wytworzonego przez ładunek
rozmieszczony ze stałą gęstością powierzchniowa σ na nieskończonej płaszczyźnie.
Gęstość powierzchniowa ładunku
dS
dQ
Wektor natężenia jest w każdym punkcie prostopadły do naładowanej płaszczyzny.
RYSUNEK
RYSUNEK
Strumień pola elektrycznego przez powierzchnię boczna dowolnego walca równy jest
0.
Całkowity strumień:
B
P
S
S
dS
E
S
d
E
S
d
E
S
d
E
2
2
0
0
2
2
E
dS
dS
E
Obliczamy pole wytwarzane przez dwie płyty naładowane ładunkami jednakowej
wielkości i przeciwnego znaku.
Rysunek
(1)
0
2
2
0
0
1
E
E
E
(2)
0
0
0
2
2
2
E
E
E
(3)
0
2
2
0
0
3
E
E
E