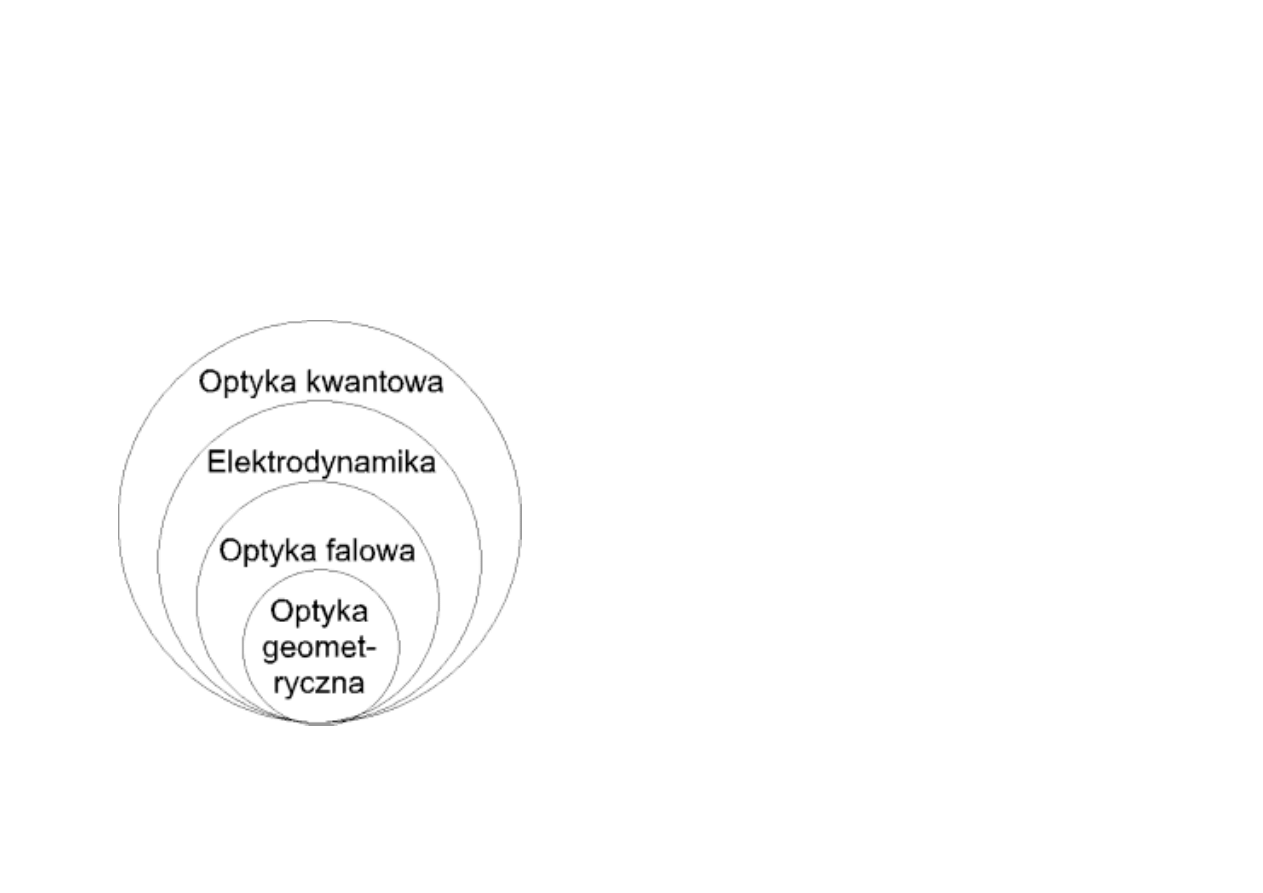
Historyczny rozwój

? ? ? ?

- ?

optyka

→

→

→

→ fotonika

Optyka geometryczna

- promień świetlny

Optyka falowa

- fala nieznanej natury

Elektrodynamika

–

fala ELM

Optyka kwantowa

- kwant

R.Jóźwicki:

Podstawy inżynierii fotonicznej

. Of.Wyd. PW, 2006

? ? ?

Elektrodynamika - wstęp

Prawo Biota-Savarta w ośrodkach materialnych

Przepływ prądu wywoływał odpowiednio ukierunkowane pole magnetyczne

Pierwsze prawo Maxwell’a w dowolnym ośrodku

( )

J

=

∂

ε

∂

−

t

rot

EEEE

HHHH

H, E

– natężenie pola magnetycznego i elektrycznego

J

– gęstość prądu elektrycznego

εεεε

- przenikalność elektryczna ośrodka

Prawo Faradaya

Zmiana pola magnetycznego w czasie wywołuje prąd elektryczny w

ośrodku materialnym

( )

0

t

rot

=

∂

µ

∂

+

HHHH

EEEE

Drugie prawo Maxwell’a w dowolnym ośrodku

µ

– przenikalność magnetyczna ośrodka

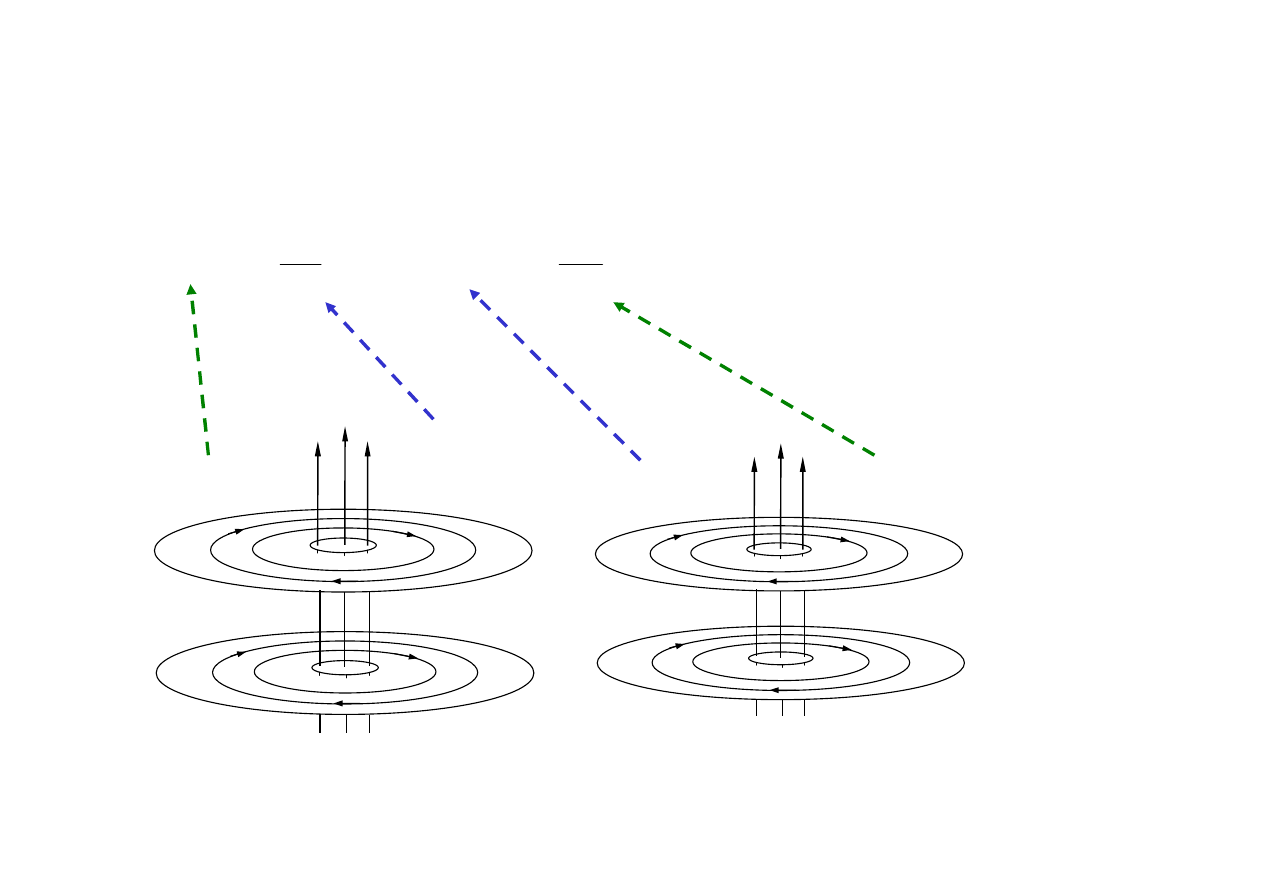
Elektrodynamika optyczna

Równania (James’a) Maxwell’a (1831-1879) w próżni

0

rot

0

t

rot

0

=

∂

∂

µ

+

=

∂

∂

ε

−

t

H

E

E

H

0

E H

– wektory natężenia pola elektrycznego i magnetycznego

ε

0

µ

0

– przenikalność

elektryczna i magnetyczna

próżni

Zmiana w czasie jednego pola generuje drugie pole wirowe

wirowe pole H

zmiana E

wirowe pole E

zmiana H

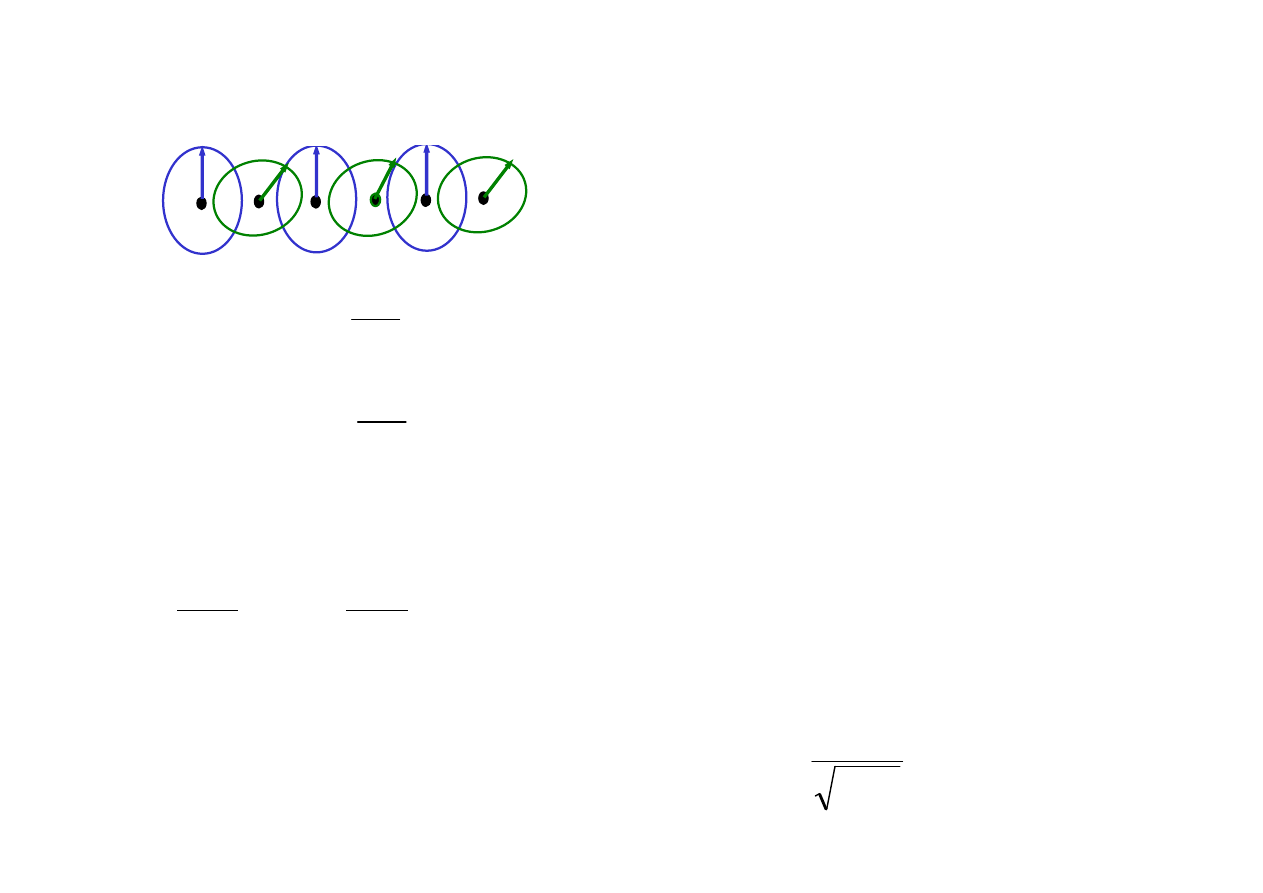
Elektrodynamika

Równanie falowe dla składowej

E

pola elektrycznego

0

t

E

z

E

2

2

0

0

2

2

=

∂

∂

−

∂

∂

εεεε

µ

µµ

µ

(

)

ct

z

E

E

−

=

→

→

→

→

Rozwiązaniem jest dowolna

funkcja argumentu

z - ct

Prędkość fali

0

0

1

c

ε

µ

=

E

E

H

H

E

H

Poglądowy rysunek propagacji

fali elektromagnetycznej

eliminując zmienną np. H

→

równanie falowe

dla

E

0

rot

0

t

rot

0

=

∂

∂

µ

+

=

∂

∂

ε

−

t

H

E

E

H

0

Zalety i trudności elektrodynamiki

Zalety

Trudności

Elektrodynamika nie jest w stanie wyjaśnić mechanizmów

generacji fali w paśmie optycznym

Prawa optyki geometrycznej przy założeniu

pomijalnie małej wartości długości fali

λλλλ →

→

→

→ 0

Wyjaśnia zjawiska propagacji, absorpcji i odbicia

w różnych ośrodkach (dielektrycznych, metalowych

i innych)

Światło jest falą elektromagnetyczną

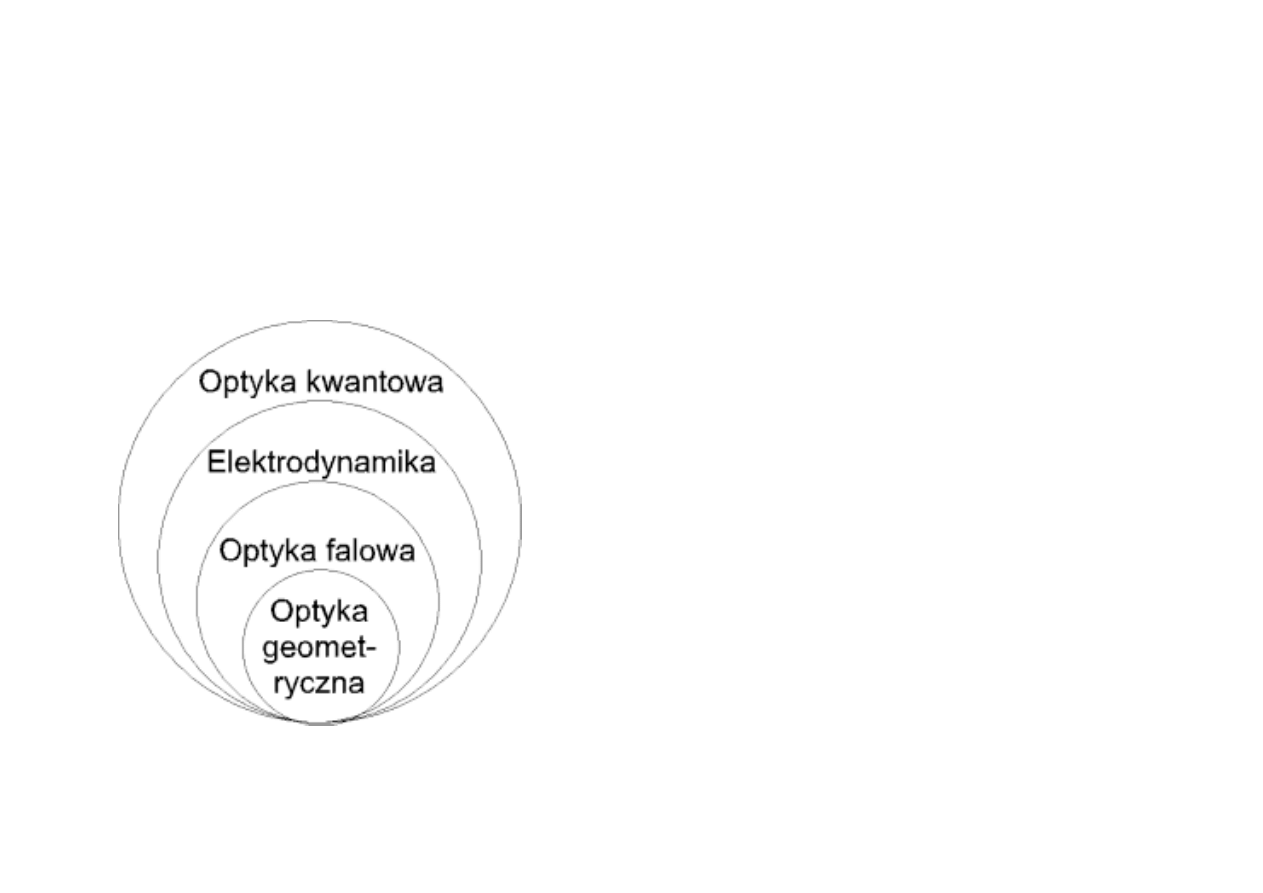
Historyczny rozwój

? ? ? ?

- ?

optyka

→

→

→

→ fotonika

Optyka geometryczna

- promień świetlny

Optyka falowa

- fala nieznanej natury

Elektrodynamika

–

fala ELM

Optyka kwantowa

- kwant

R.Jóźwicki:

Podstawy inżynierii fotonicznej

. Of.Wyd. PW, 2006

? ? ?

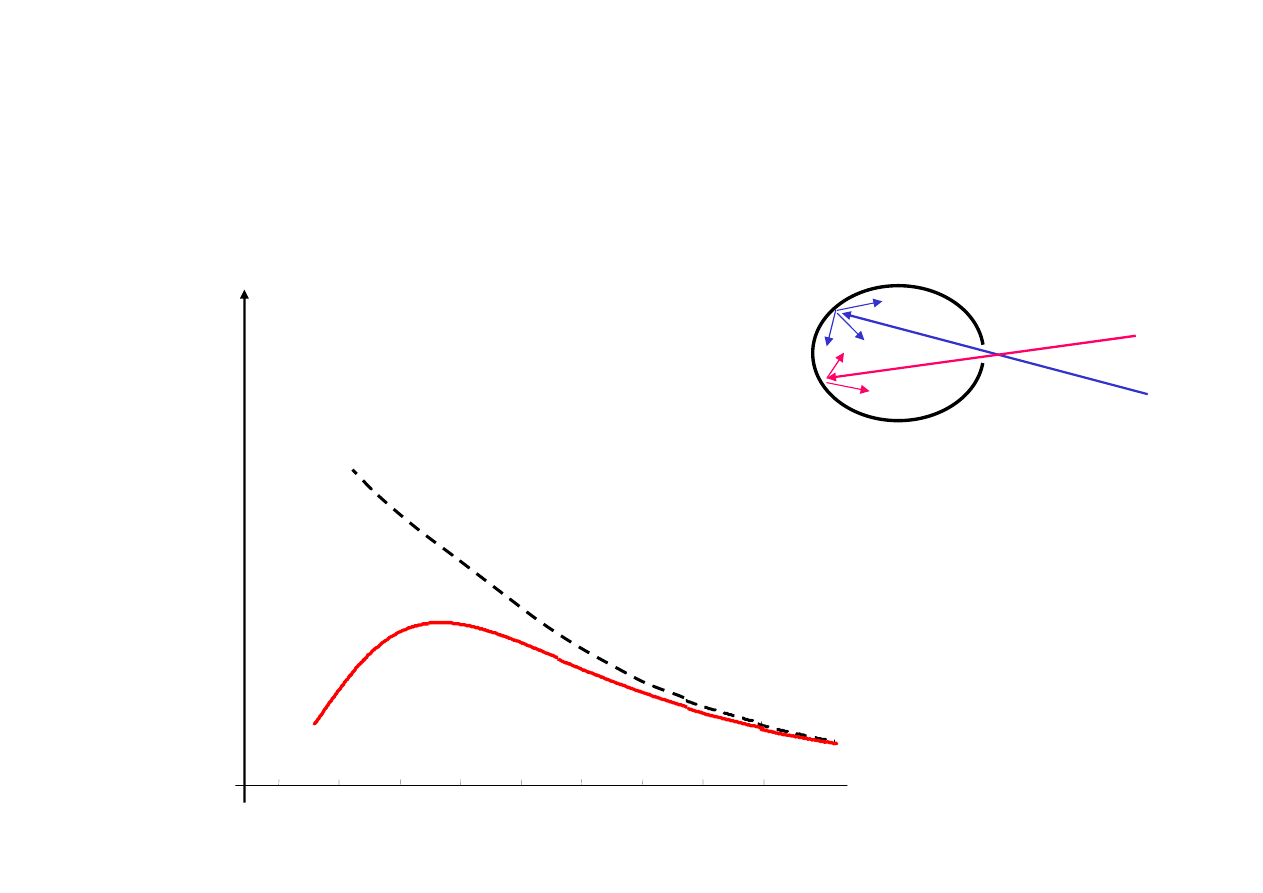
Promieniowanie ciała doskonale czarnego - wstęp

λλλλ

M

λ

J

e

d

n

o

s

tk

i

w

z

g

lę

d

n

e

spektralna emitancja

prawo Jeans’a według klasycznej termodynamiki

promieniowania oscylatorów

rzeczywiste

wyniki

Ciało dosk. czarne absorbuje całe promieniowanie z każdego kierunku,

dla każdej długości fali

λ

i w każdej temperaturze

T

Model ciała czarnego

Promieniowanie ciała doskonale czarnego

(Albert) Einstein (1879-1955) kwant promieniowania nazwał

fotonem

Atom (molekuła) jest dipolem absorbującym i emitującym fotony

(Max) Planck (1858-1947) wykazał w 1900 roku, że empiryczna

zależność dla

spektralnej emitancji

ciała doskonale czarnego

1

2

5

1

cz

,

1

T

c

exp

c

M

−

−













−













=

λλλλ

λλλλ

λλλλ

prawo Plancka

może być udowodniona dla skwantowanej struktury energii

c

1

= 37 418.44 Wcm

2

µm

4

i c

2

= 14 387.69

µmK

– stałe promieniowania

T

[K]

– temperatura

Wyznaczenie ekstremum M

λλλλ,cz

0

M

cz

,

=

λ

∂

∂

λ

Po pomnożeniu i podzieleniu M

λ,cz

przez

(

)

5

2

c

/

T

( )

[

]

1

x

exp

x

1

c

T

c

1

T

c

exp

c

M

5

5

2

1

1

2

5

1

cz

,

−













=













−













λ

λ

=

−

−

−

λ

gdzie

T

c

x

2

λ

=

Warunek ekstremum M

λ,cz

(

)

[

]

(

)

0

x

exp

x

1

x

exp

x

5

1

x

exp

x

5

6

5

=

+

−

−

=

−

λ

∂

∂

−

−

−

(

)

x

exp

1

x

exp

x

5

=

−

Dla

5

x

1

x

exp

ext

≈

⇒

>>

Dokładnie

96511423

.

4

T

c

x

max

2

ext

=

λ

=

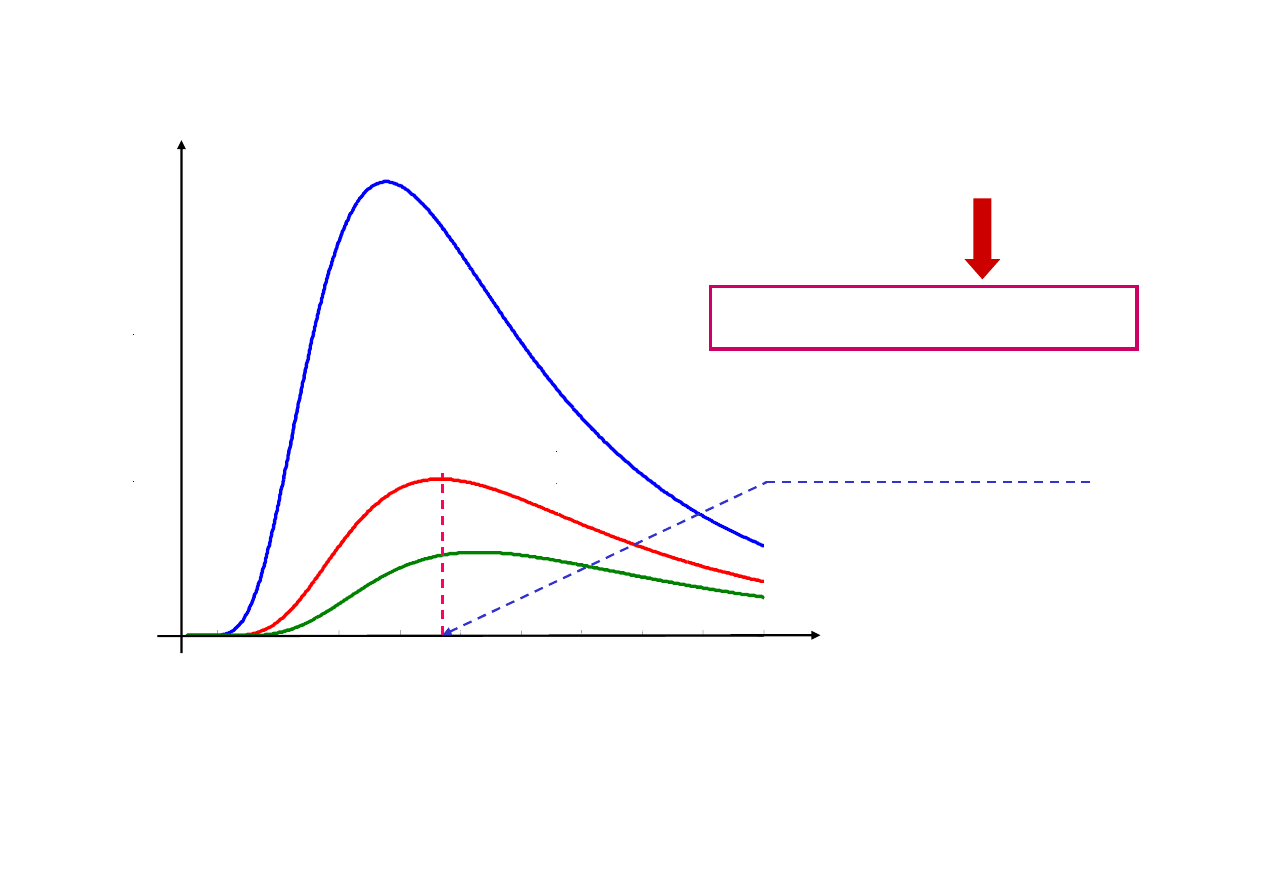
Prawo

(Willy)

Wien’a (1864-1928)

2

6

10

14

18

λλλλ

[

µ

µµ

µm

]

M

λ

J

e

d

n

o

s

tk

i

w

z

g

lę

d

n

e

t = 100

0

C

t = 36

0

C

t = 0

0

C

Maksimum spektralnej emitancji dla

λ

max

]

K

m

[

885

.

2897

T

max

⋅

µ

=

λ

Im wyższa temperatura, tym wyższe wartości

M

λλλλ,cz

dla każdego

λλλλ

i tym krótsza długość fali

λλλλ

max

Dla t = 36

0

C T

≈ 309 K

λλλλ

max

≈ 9.6 µm

Emisja promieniowania przez dowolne ciało

Każde ciało dla

T > 0

jest źródłem promieniowania elektromagnetycznego

( )

( )

( )

T

M

T

T

M

cz

,

λ

λ

λ

ε

=

Dowolne ciało nie w pełni absorbuje padające na nie

promieniowanie, więc w równowadze termicznej jego

współczynnik emisyjności

εεεε

λλλλ

(T)

spełnia zależność

( )

1

T

0

≤

ε

≤

λ

εεεε

λλλλ

= 0

- ciało całkowicie odbijające lub całkowicie przezroczyste

Przypadki spełniające lokalnie zależności w widmie lub przedziale

temperatury :

εεεε

λλλλ

= 1

- ciało doskonale czarne w tym obszarze widma i temperatury

Współczynniki emisyjności wybranych materiałów

0.43

0.33

0.6

µm

1.0

µm

3200

Wolfram

0.85

IR

-10

Śnieg

0.96

IR

-10

Lód

0.98

IR

32

Skóra (in vivo)

0.93

IR

20

Papier biały

0.98

widzialne i IR

20

Grafit

0.07

0.79

widzialne i IR

100

200

Stal polerowana

utleniona

ε

λ

λ

t [

0

C]

Materiał

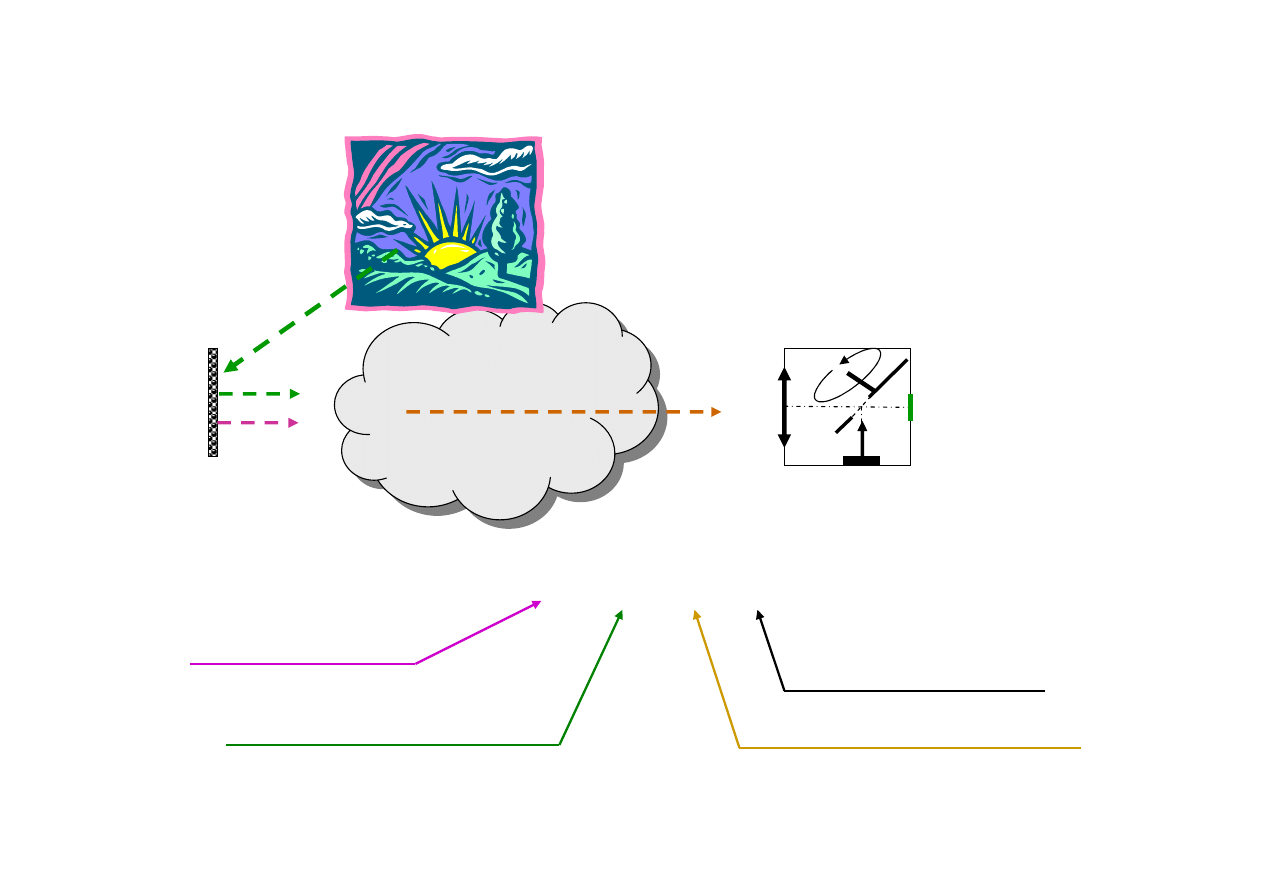
Termografia

S

at

S

r

Sygnał pomiarowy

w

at

r

c

S

S

S

S

dS

−

+

+

=

Odbiornik CCD

kamera

S

c

obiekt

Wzorzec ciała

doskonale czarnego

S

w

Sygnał od obiektu

Sygnał

pasożytniczy

promieniowania odbitego

Sygnał wzorcowy od

ciała czarnego

Promieniowanie atmosfery

Kamera termowizyjna

Wyznaczenie położenia rurociągu

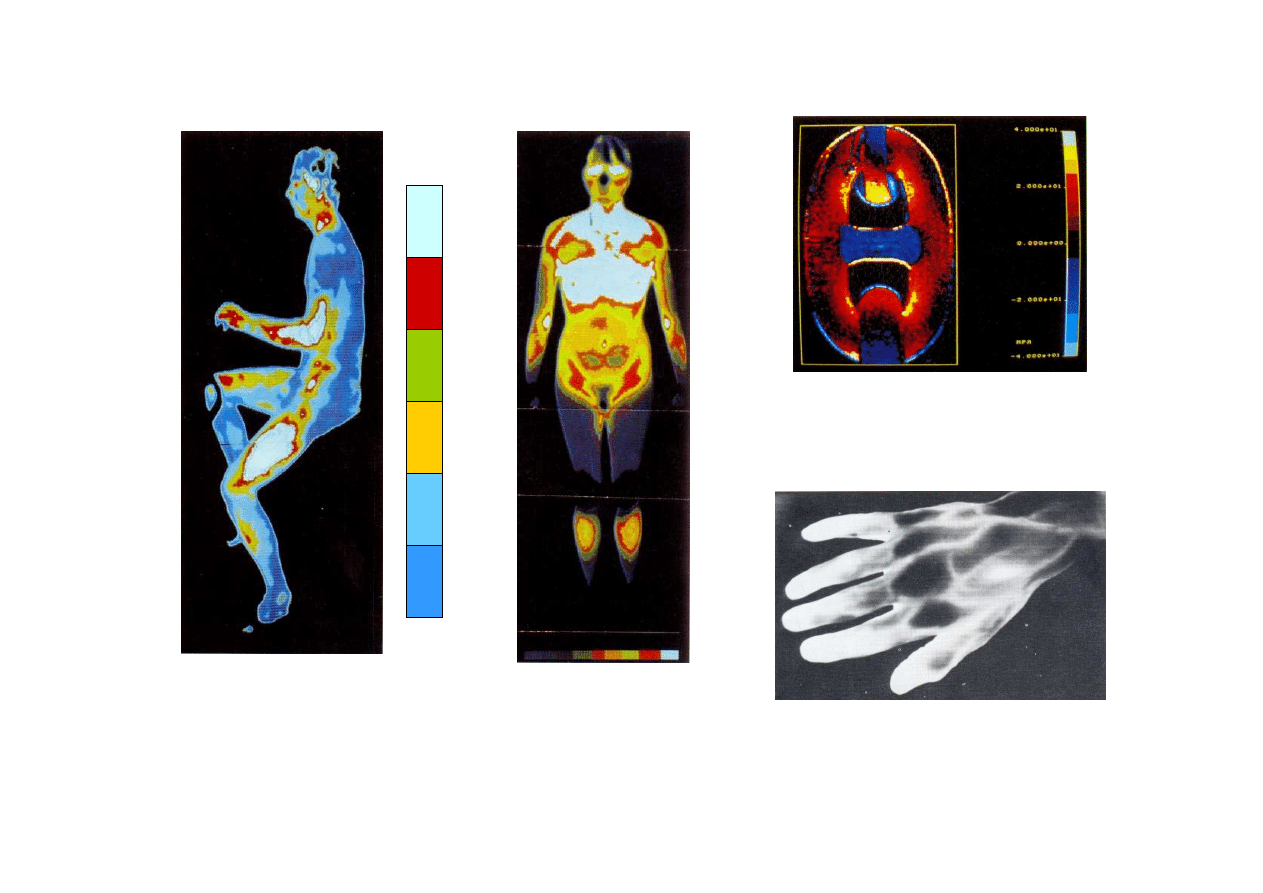
Pomiar rozkładu temperatur w zakresie 26-34

0

C

Mężczyzna

podczas ćwiczeń

26

0

34

0

Kobieta w

ciąży

Element łańcucha ze

zmiennym obciążeniem

Badanie stopnia

ukrwienia dłoni

Czujnik termowizyjny (kamera CCD) umożliwiający na

monitorze obserwację w podczerwieni w celu rozpoznania

terenu podczas oślepienia kierowcy przez reflektory

nadjeżdżającego pojazdu

Możliwości uzyskania promieniowania cieplnego

poza pasmem optycznym

Pasmo optyczne

λλλλ ∈

∈

∈

∈ (1 nm, 1 mm)

Promieniowanie cieplne praktycznie jest wyłącznie

domeną pasma optycznego

Z prawa Wiena

λ

max

< 1nm

odpowiada temperaturze

T > 3 milionów K

realizacja przez eksplozje jądrowe

λ

max

> 1mm

dla T < 3 K

bardzo niska wartość mocy

Podwyższając temperaturę zwiększamy moc i w mikrofalach, ale

większość emisji poza mikrofalami

Zawężanie widma źródeł promieniowania

Metody:

W epoce

przedlaserowej:

Niskociśnieniowe lampy spektralne

Wydzielanie części widma za pomocą monochromatora

Wysoki stopień monochromatyczności promieniowania

wymagają:

nośniki przesyłania informacji

na duże odległości

dyspersja ośrodka materialnego – światłowodu – zmniejsza gęstość

upakowania

układy interferencyjne

w celu uzyskania dużego kontrastu prążków

sód

wodór

rtęć

hel

neon

Linie widmowe lamp spektralnych

Długość fali

λλλλ

600

550

500

450

400

nm

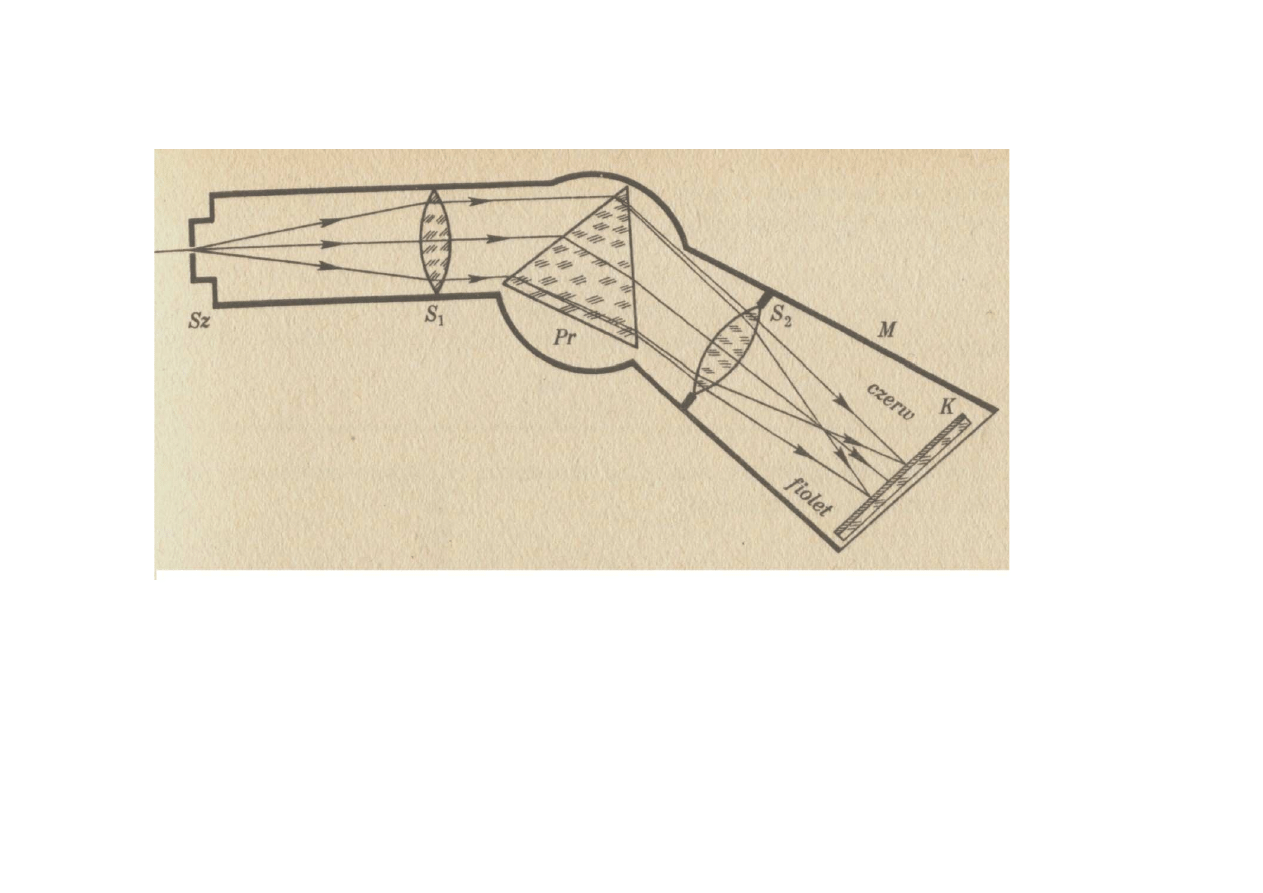
Wydzielanie części widma za pomocą monochromatora

Przełom:

laserowe źródła promieniowania

Niska sprawność metody

Dodając do spektrometru szczelinę

→

monochromator

Optyka kwantowa

operuje narzędziami statystyki i teorii prawdopodobieństwa co jest

niewygodne z punktu widzenia inżynierskiego

Współcześnie najogólniejsza teoria

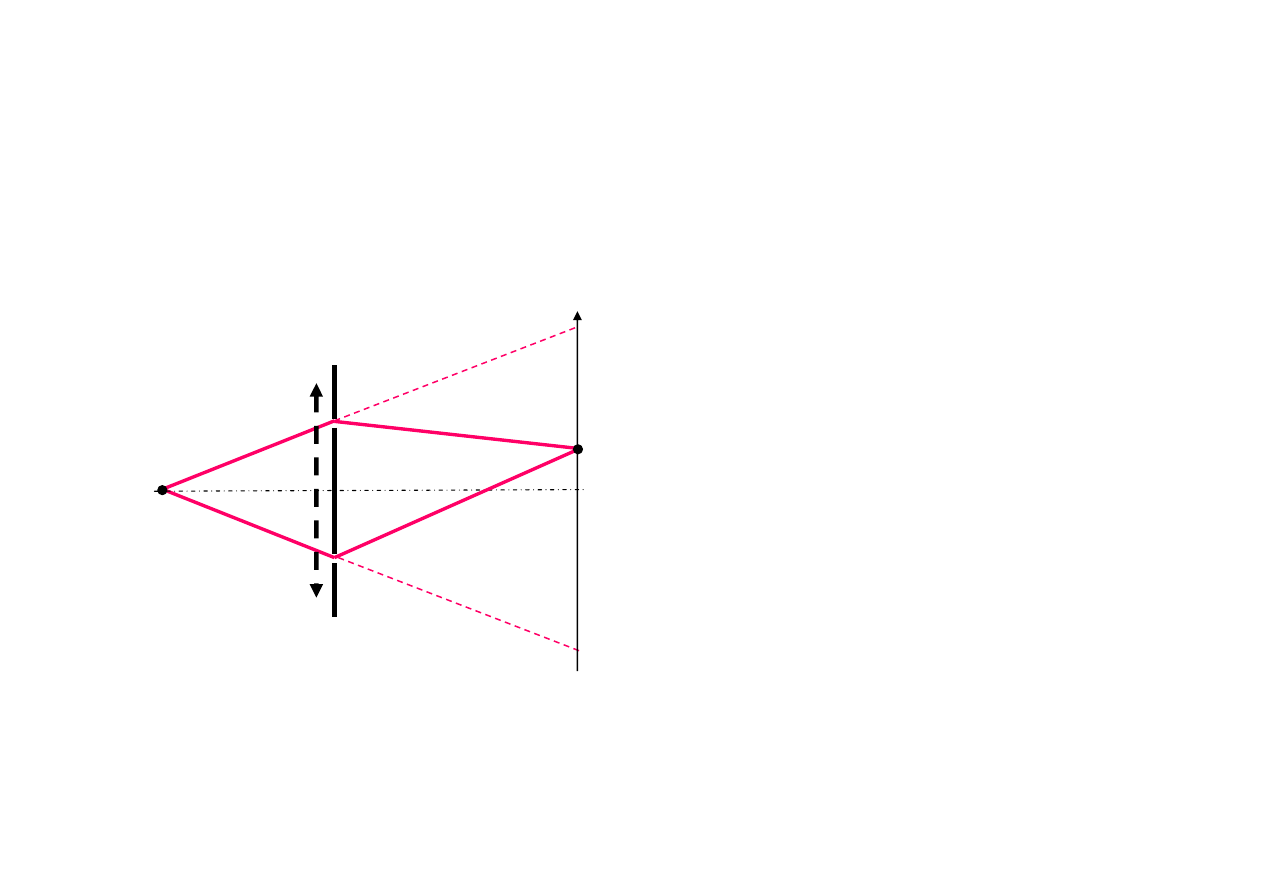
Foton jako korpuskuła

propagować się może przez

jedną ze szczelin

Wynik interferencji temu

przeczy

Przy statystyce pojedynczych fotonów odtwarza się struktura prążkowa

Wątpliwości przy myśleniu tradycyjnym

G

S

1

S

2

x

0

r

1

r

2

M

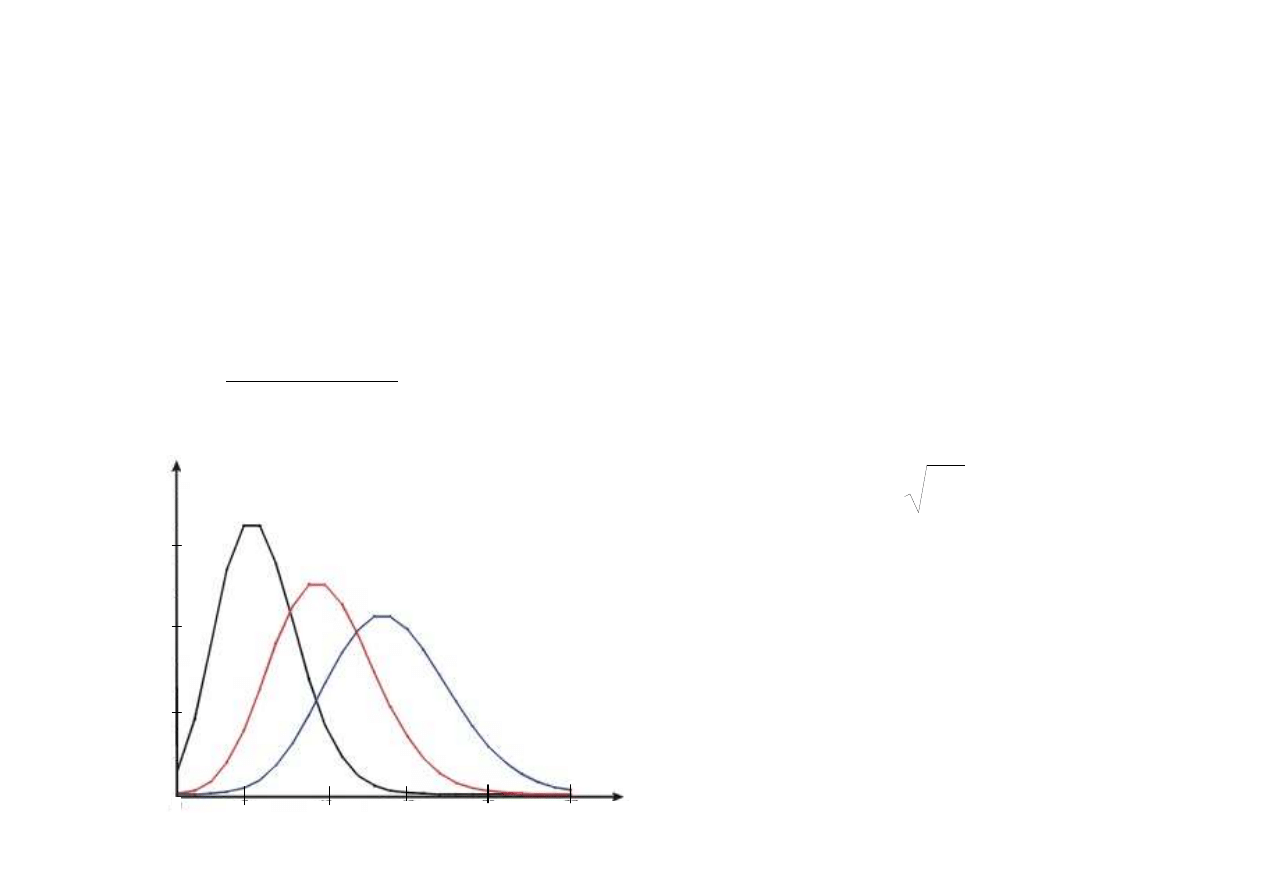
Statystyka fotonów słabych sygnałów

10

6

fotonów na sekundę i cm

2

daje światło gwiazd

n

s

- średnia liczba propagujących się fotonów w przedziale

∆t

Prawdopodobieństwo

p(n)

zarejestrowania

n

fotonów opisane jest

rozkładem

(Simeon’a)

Poissona dla małych wartości

p

( )

(

)

,..

3

,

2

,

1

n

!

n

n

exp

n

n

p

s

n

s

=

−

=

rozkład prawdopodobieństwa

rzadkich zdarzeń

n

s

= 5

n

s

= 10

n

s

= 15

5

10

0

15

20

25

n

p(n)

0.15

0.10

0.05

0.00

n

s

σ

n

%n

s

100

10 10

10

6

1000 0.1

Standardowe odchylenie

s

n

n

=

σ

σ

σ

σ

Rej_fot.exe

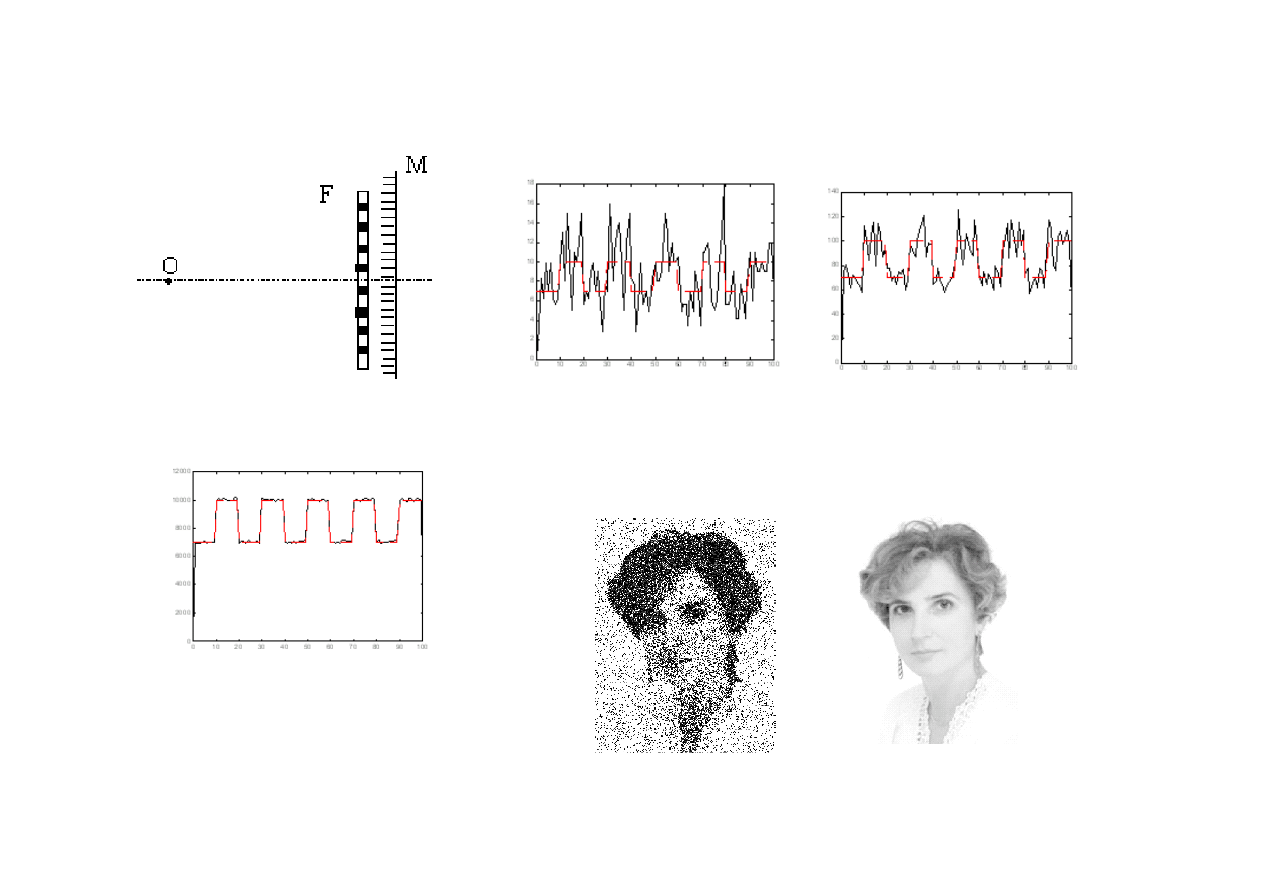
Rejestracja fotonów przez macierz odbiorników

= 10

4

= 10

6

n = 10

3

n – liczba fotonów

Czerwoną linią - obraz oczekiwany

Rejestracja przy małej i dużej liczbie fotonów

Cyfrowy tor przenoszenia informacji

Średni strumień fotonów n

s

=

100

Poziom dyskryminacji n

d

=

50

0

bit

50

n

1

bit

50

n

<

≥

Przesyłamy bit 1

Prawdopodobieństwo błędu

(

)

( )

8

49

0

n

p

10

4

.

2

n

p

50

n

p

−

=

⋅

=

=

<

∑

Wartość nie do zaakceptowania w EMC

Prawidłowy wybór poziomu
dyskryminacji

(

) (

)

d

d

n

n

p

n

n

p

≥

=

<

daje

n

d

= 38

i

p

p

= 10

-12

Mniejsza średnia liczba fotonów obniża zużycie energii przy

przesyłaniu informacji, ale kosztem wzrostu szumów

Istnieje problem fotoniki słabych sygnałów

Wątpliwości przy myśleniu tradycyjnym cd

Na podstawie dotychczasowego pojmowania optyki kwantowej i

elektrodynamiki brak jest spójnego wyjaśnienia zjawisk związanych

z dwoistością natury

fala i korpuskuła jednocześnie

Interferencję wyjaśnia model falowy (ale nie kwantowy)

zasadę pracy lasera - model kwantowy

Co przyniesie wiek XXI ?

?

Generacja promieniowania przez atom

ττττ

a

→

→

→

→ ∞

∞

∞

∞

brak tłumienia

Atom pobiera energię

absorpcja fotonu

– atom przechodzi w stan

wzbudzony

Spontaniczna emisja fotonu

atom przechodzi w stan energetycznie niższy

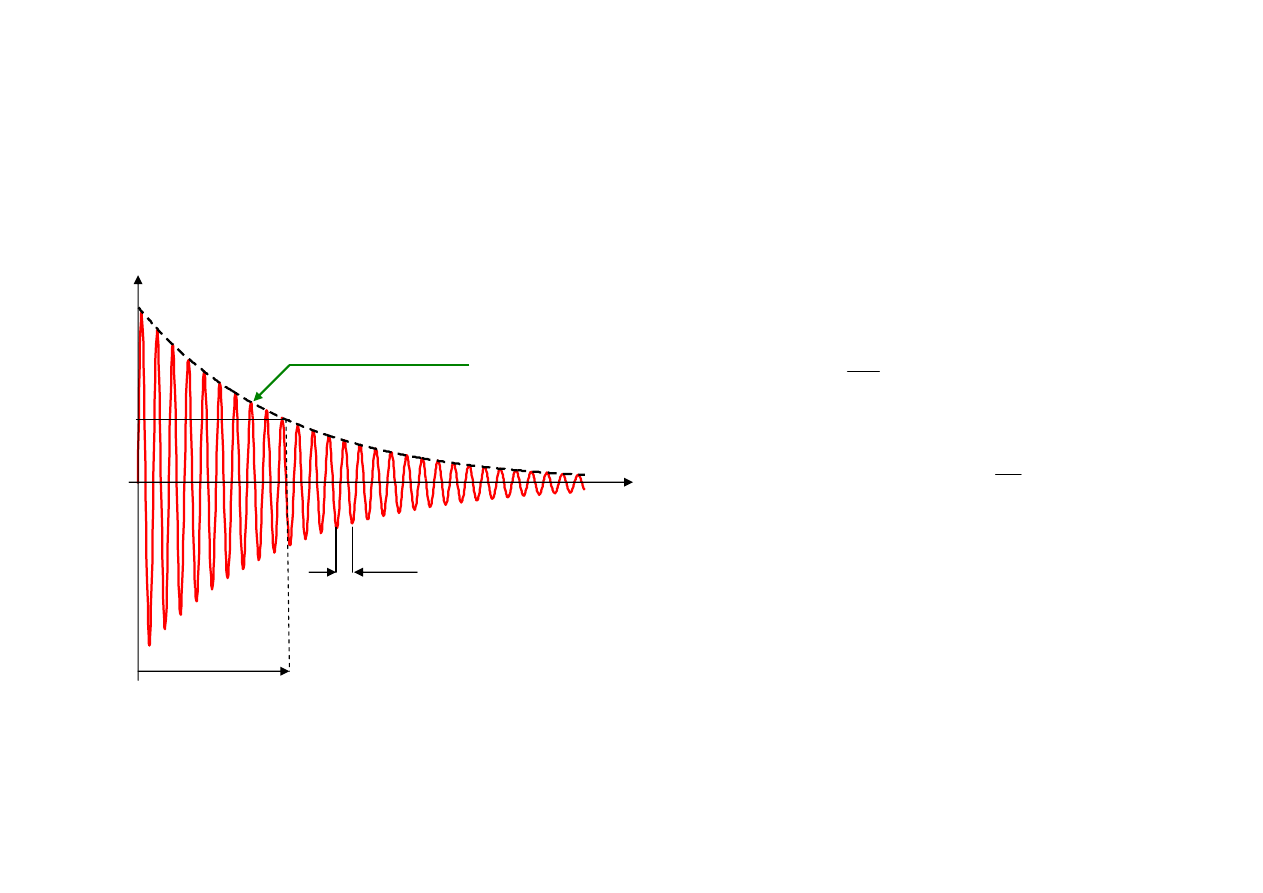
Emisja – tłumiony przebieg harmoniczny

( )

(

)

0

t

t

i

exp

t

exp

V

t

V

0

a

0

≥

ω













τ

−

=

T

1

2

0

0

0

=

ν

πν

=

ω

ν

0

– częstotliwość

T

– okres

ττττ

a

– parametr tłumienności

Re[V/V

0

]

t

(

)

a

/

t

exp

τ

−

ττττ

a

T

1

e

-1

Generacja promieniowania przez atom cd

Częstotliwość

ν

0

jest bardzo wysoka

rzędu 10

14

Hz

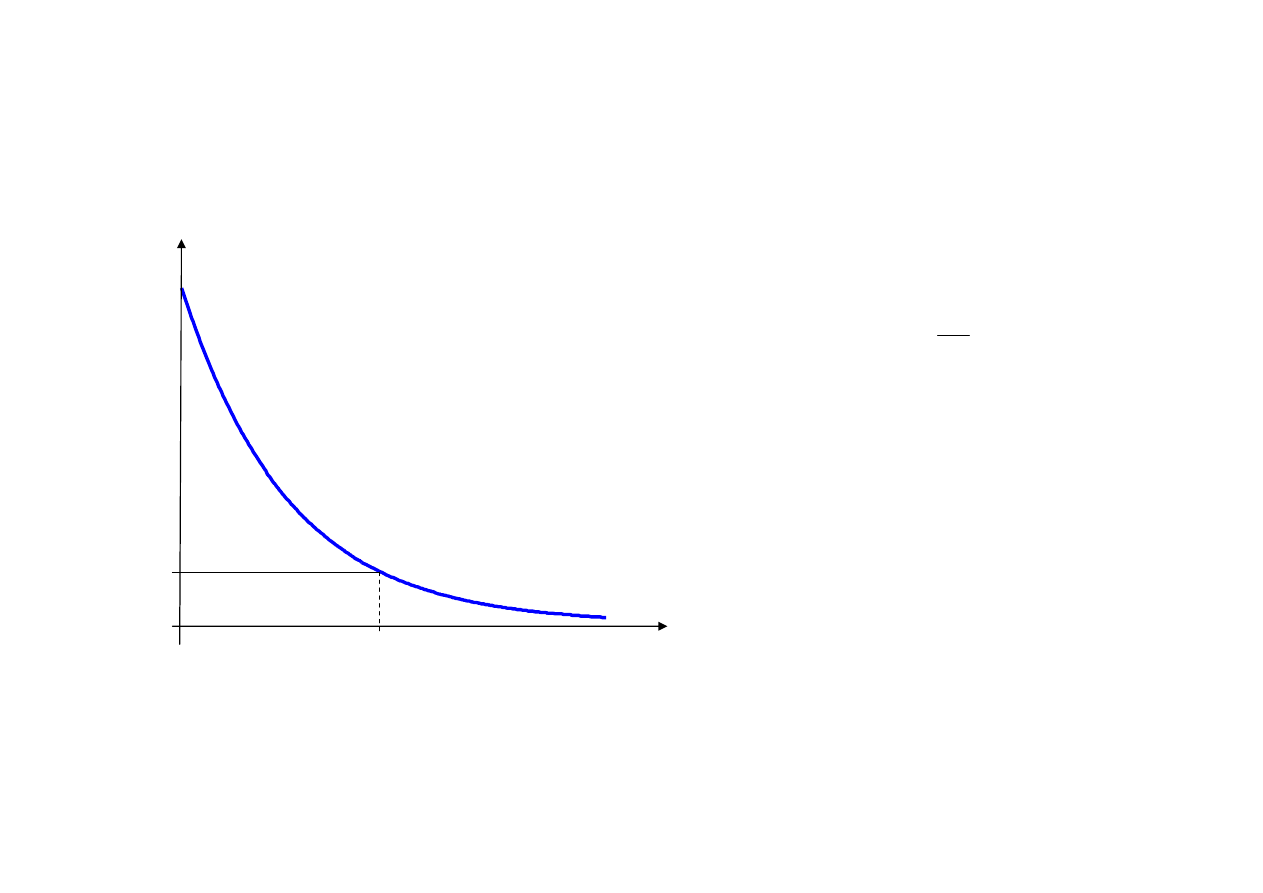
Odbiornik rejestruje średnią wartość mocy – intensywność

I(t)

( )

( ) ( )













τ

−

=

=

∗

a

0

t

2

exp

I

t

V

t

V

t

I

∗

=

0

0

0

V

V

I

Parametr tłumienia

τ

a

odpowiada czasowi, po którym intensywność

zmniejsza się

e

-2

= 0.135

razy

I/I

0

1

t

0

0

e

-2

ττττ

a

Widmo promieniowania atomu

(Jean)

Fourier (1768-1830) wykazał, że każdą funkcję

f(t)

można rozłożyć

na zbiór harmonicznych o różnych częstotliwościach kołowych

ω

ω

ω

ω

Fala o jednej częstotliwości

( )

t

cos ω

)

,

(

t

∞

−∞

∈

Harmoniczna w postaci zespolonej

( )

t

i

exp ω

Czy promieniowanie może być monochromatyczne ?

Kluczowy problem:

( )

( ) ( )

ω

ω

ω

π

=

∫

∞

∞

−

d

t

i

exp

F

2

1

t

f

gdzie widmo funkcji

( )

( ) (

)

dt

t

i

exp

t

f

F

ω

−

=

ω

∫

∞

∞

−

Odwrotne przekształcenie Fouriera

Przekształcenie Fouriera

Widmo promieniowania atomu cd

Aby znaleźć widmo funkcji

( )

(

)

0

t

t

i

exp

t

exp

V

t

V

0

a

0

≥

ω













τ

−

=

należy znaleźć jej transformatę Fouriera, to znaczy

( ) (

)

(

)

∫

∫

∞

∞

∞

−

ω

























τ

−

ω

−

ω

=

ω

−

=

0

a

0

0

dt

t

1

i

exp

V

dt

t

i

exp

t

V

V

Rozkład intensywności w

widmie fotonu

(

)

2
a

2

0

2

0

1

4

I

V

V

I

τ

+

ν

−

ν

π

=

=

∗

ω

ω

ν

Po rozwiązaniu całki przez podstawienie

(

)

a

0

0

ω

τ

1

ω

ω

i

V

V

−

−

−

=

(

)

y

t

1

i

a

0

=













τ

−

ω

−

ω

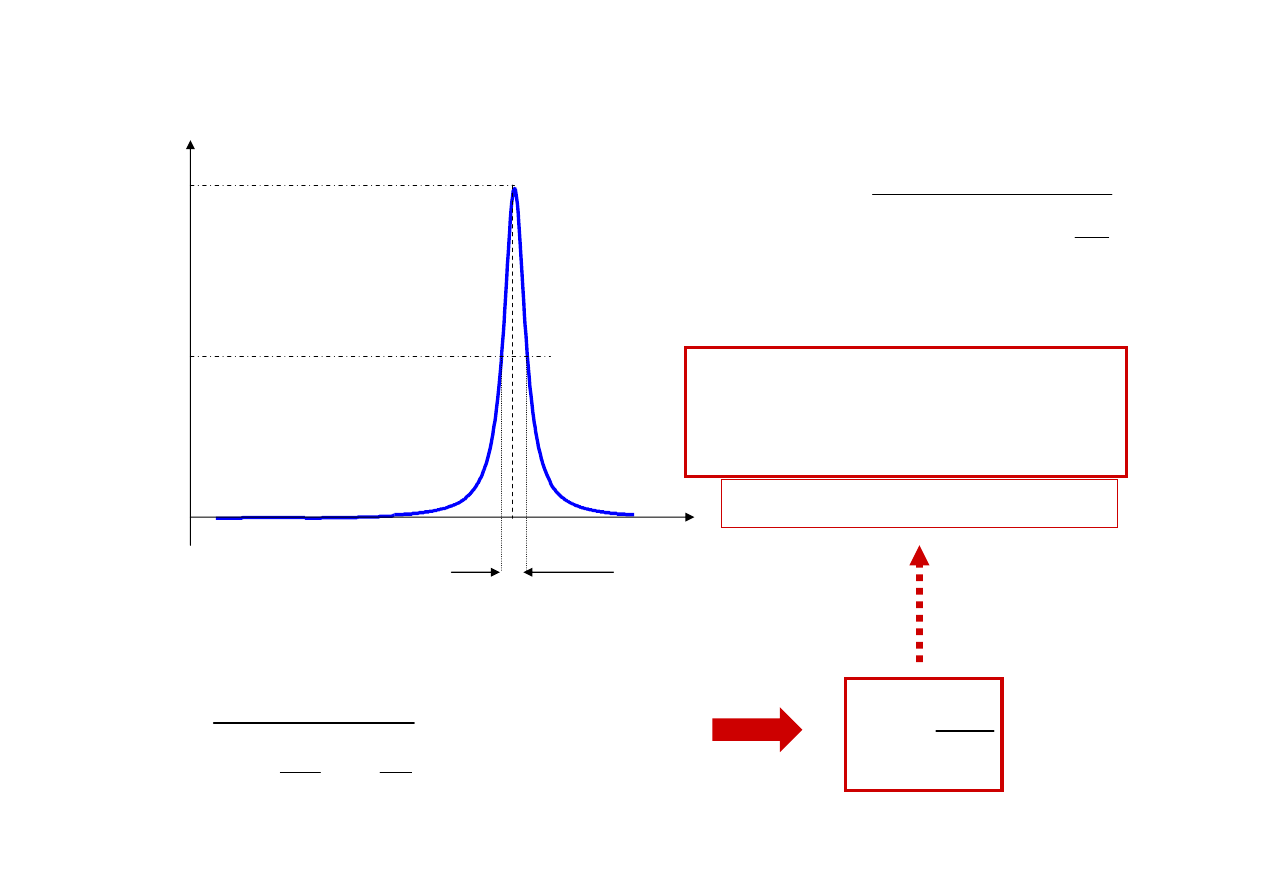
Widmo promieniowania atomu cd

(

)

2
a

2

0

2

0

1

4

I

V

V

I

τ

+

ν

−

ν

π

=

=

∗

ω

ω

ν

νννν

νννν

0

∆ν

∆ν

∆ν

∆ν

I

ν

/I

0

2
a

τ

2
a

5

.

0 τ

Połówkowa szerokość

∆ν

wyznacza się z zależności

2
a

0

max

2
a

2

2

0

I

5

.

0

I

5

.

0

1

2

4

I

τ

=

=

τ

+











 ν

∆

π

ν

a

1

πτ

=

ν

∆

Promieniowanie

monochromatyczne

∆ν

∆ν

∆ν

∆ν = 0

tylko dla

ττττ

a

=

∞

∞

∞

∞

Harmoniczna nietłumiona

Widmo promieniowania atomu cd

Atom nigdy nie promieniuje

światłem monochromatycznym

Im

większe tłumienie

(współczynnik

ττττ

a

mniejszy)

tym

szersze widmo promieniowania

K !!

Promieniowanie monochromatyczne

jest pojęciem abstrakcyjnym

wprowadzonym dla wygody rozważań

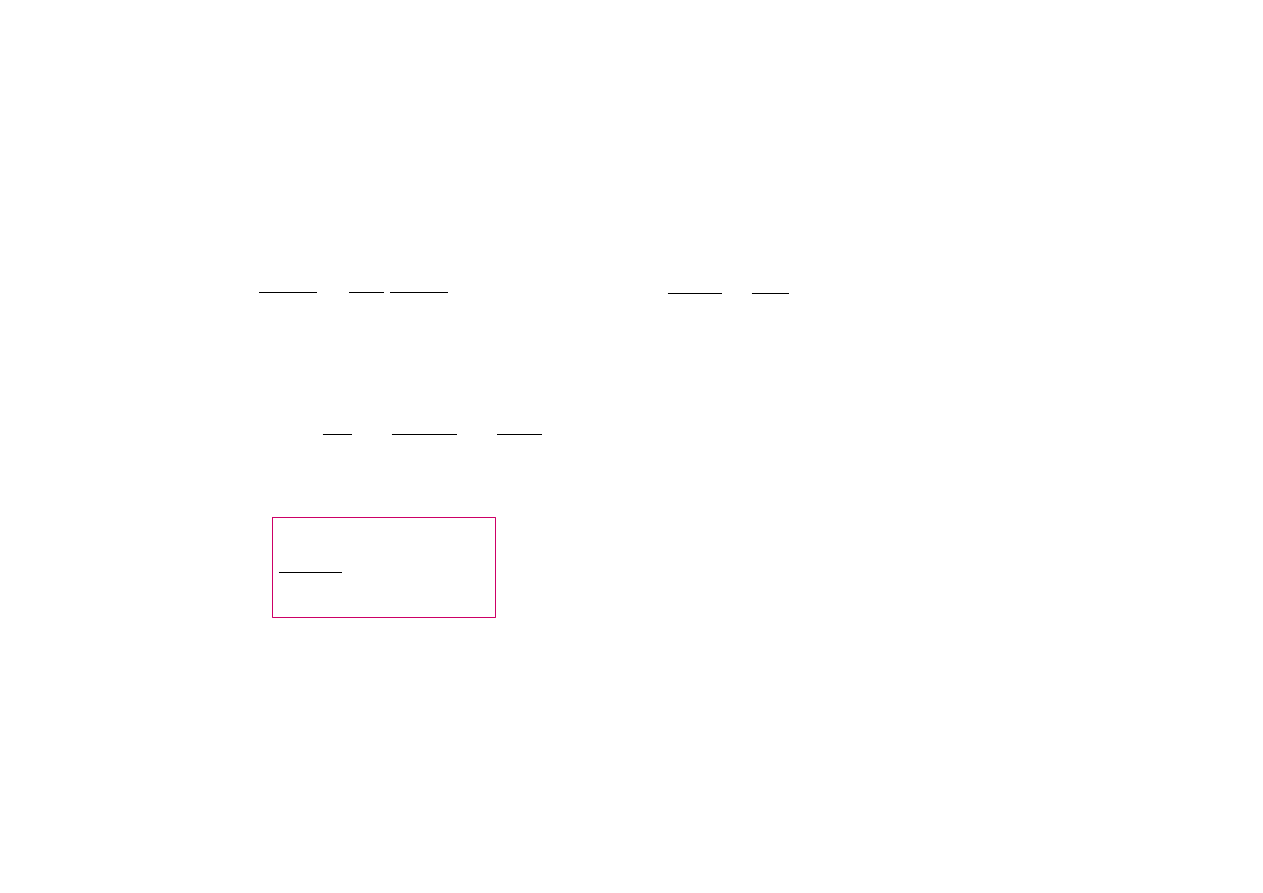
Fala monochromatyczna

( )

( ) ( )

t

i

exp

z

V

t

,

z

E

ω

ω

ω

ω

=

Po podstawieniu do równania falowego

0

t

E

c

1

z

E

2

2

2

2

2

=

∂

∂

−

∂

∂

( )

0

t

i

exp

V

c

z

V

2

2

2

2

=













+

∂

∂

ω

ω

ω

ω

ω

ω

ω

ω

→

→

→

→

ponieważ

0

0

k

2

c

2

c

=

=

=

λλλλ

ππππ

πν

πν

πν

πν

ω

ω

ω

ω

– kołowa liczba falowa w próżni

→

→

→

→

0

V

k

z

V

2
0

2

2

=

+

∂

∂

równanie

(Hermann’a)

Helmholtz’a

Dla

fali monochromatycznej

pomija się zmiany pola w funkcji czasu,

wystarczy wyznaczać zmiany pola w przestrzeni

Literatura uzupełniająca

Literatura

podstawowa

poziom wyższy

naukowa

J.Petykiewicz: Optyka falowa. PWN, Warszawa 1986, rozdziały 1 i 2

E.Hecht, A.Zajac: Optics. Addison-Wesley Publ. Co., Reading Mass.

1974, rozdziały 3,4 i 13

R.Jóźwicki: Podstawy inżynierii fotonicznej. Ofic,Wyd. PW, Warszawa

2006

B.E.A.Saleh, M.C.Teich : Fundamentals of Photonics, John Wiley &

Sons, New York 1991, rozdziały 5 i 11

M.Born, E.Wolf: Principles of Optics. Perg. Press, Oxford 1980, rozdz. III;