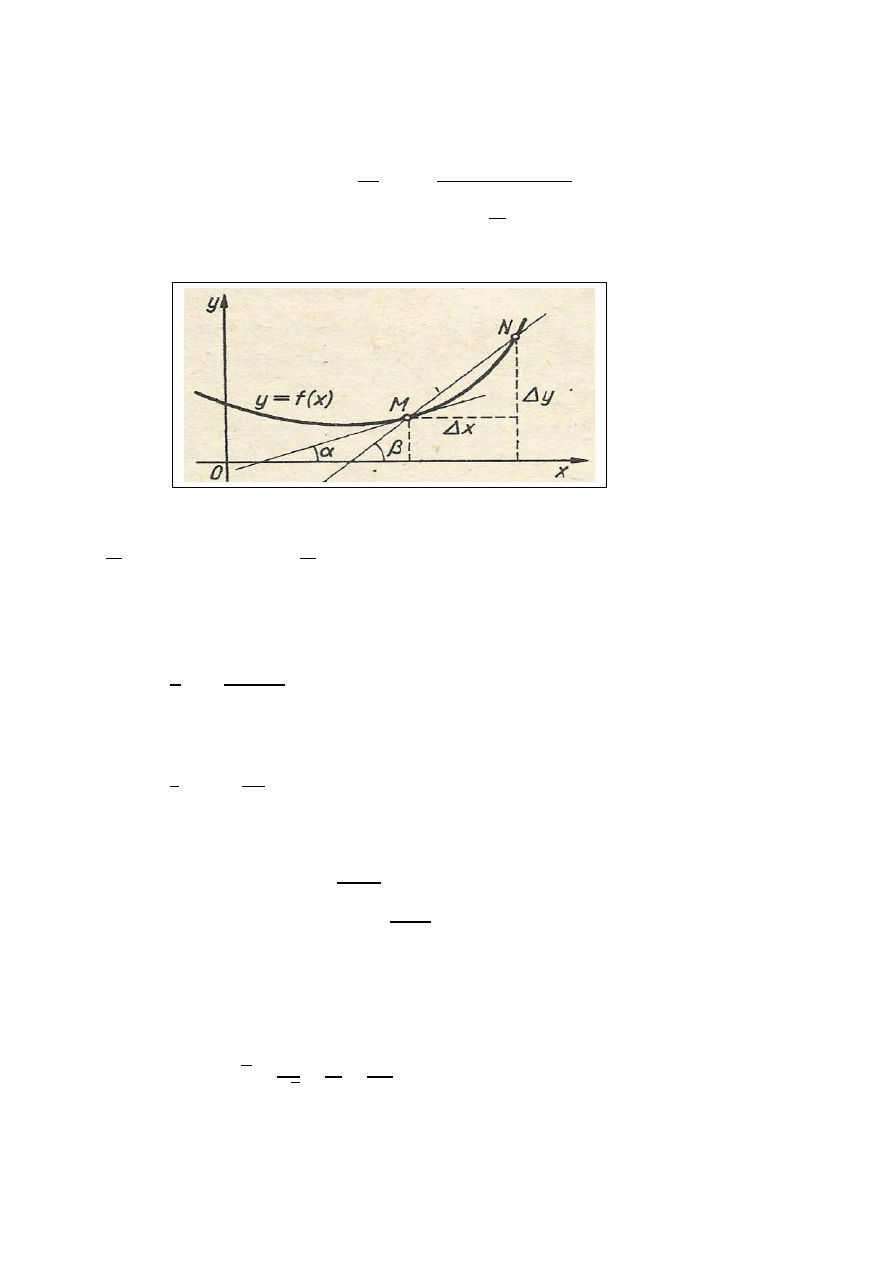
Pochodna funkcji i jej sens geometryczny. Różniczkowalność funkcji.
Pochodną funkcji nazywany granicę:
Pochodną oznaczamy symbolami
lub
, albo
Proces wyznaczania pochodnej nazywamy różniczkowaniem.
Pochodną
funkcji interpretujemy jako tangens kąta stycznej do wykresu funkcji.
,
Pochodne funkcji algebraicznych i trygonometrycznych
1.
2.
3. (
)
4.
5.
6. (
)
7.
8.
9.
10.
11.
Obliczyć pochodne:
1.
2. √
√
(
)
√
√
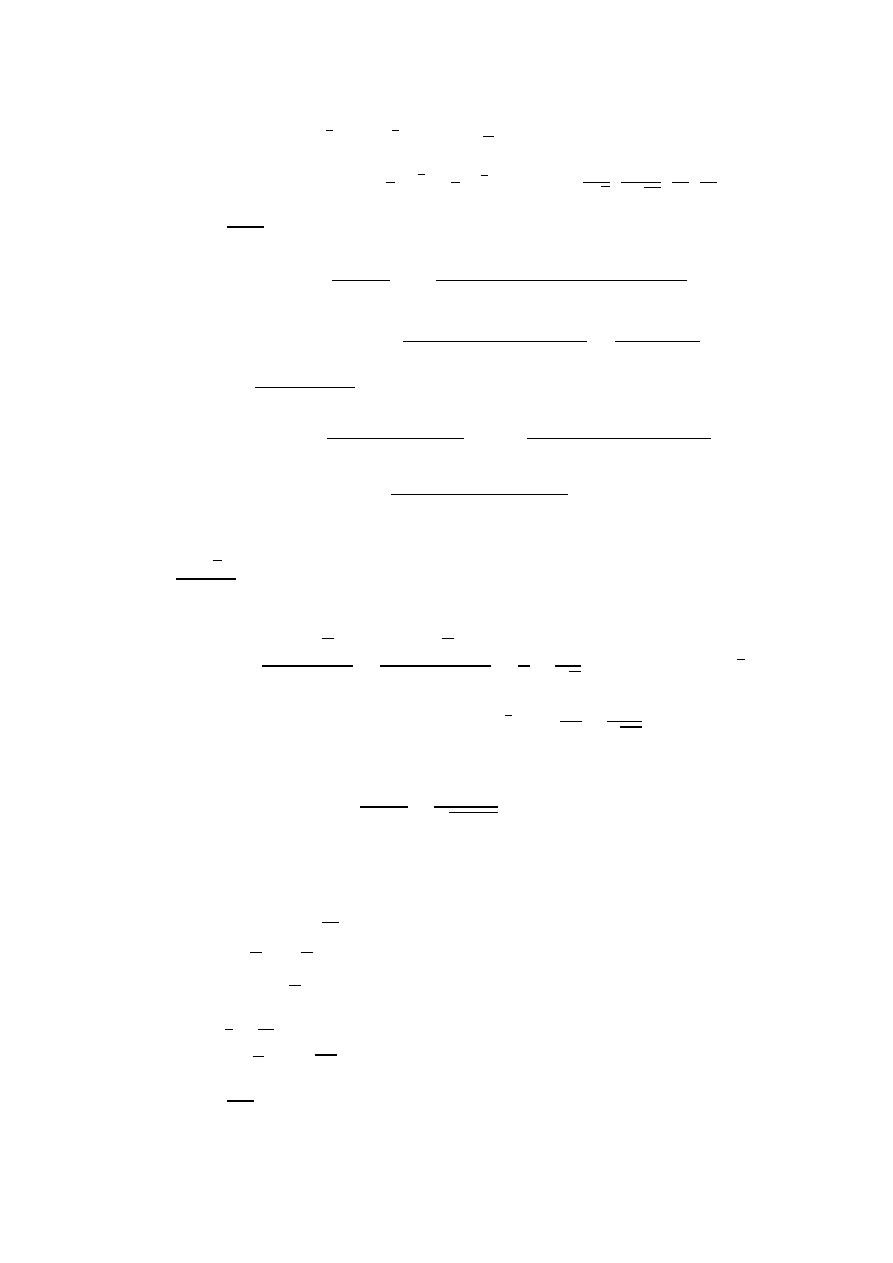
3.
(
)
4.
(
)
Wyznaczyć pochodną funkcji:
( √ )
,dla
( √ )
√
√
√
Podstawiając , otrzymujemy
√
Obliczyć pochodne:
Zadania:
1.
2. (√ √ )
3. √
4.
5. √
√
6.
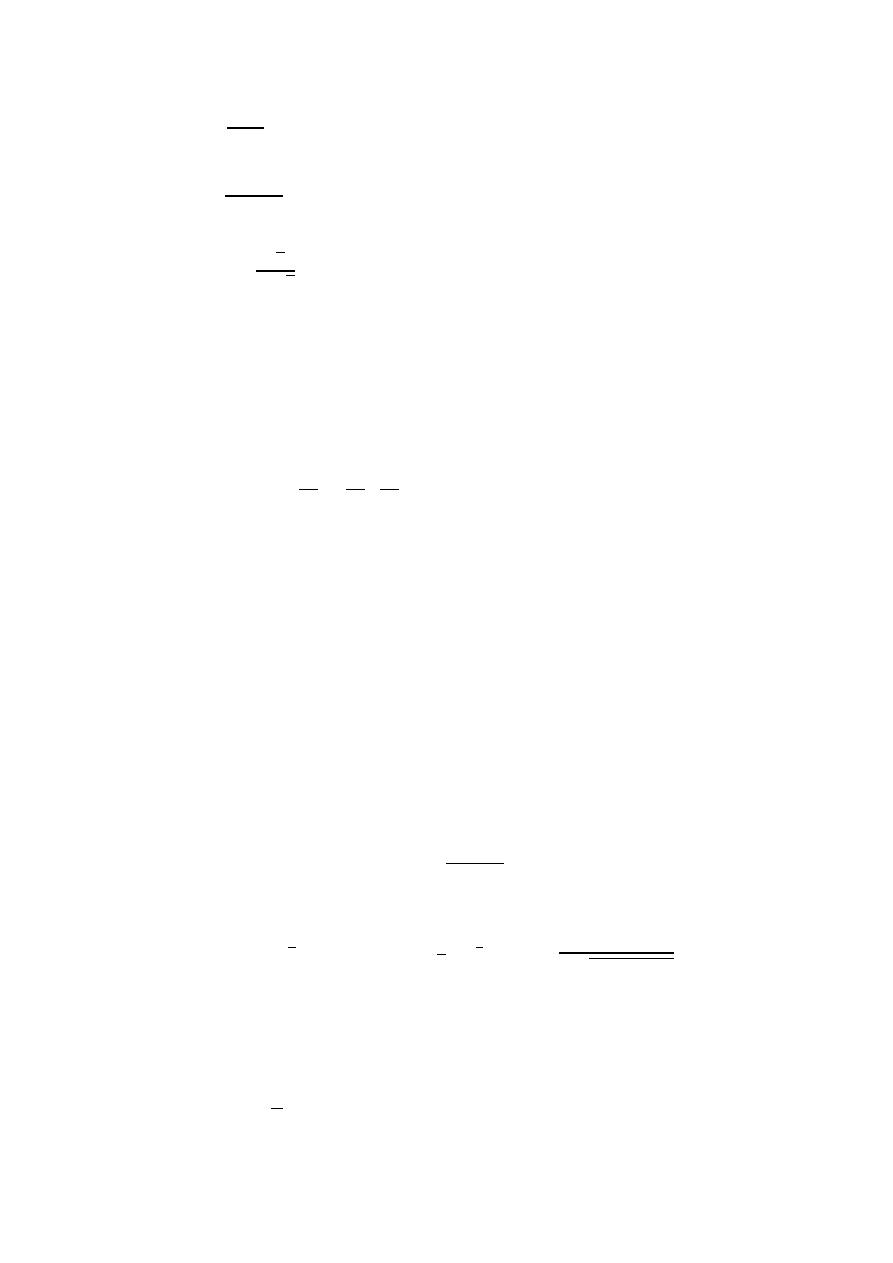
7.
8.
9.
10.
11.
√
√
; Obliczyć
Pochodna funkcji złożonej.
Jeżeli , gdzie . Funkcja jest zależne od argumentu
w sposób pośredni i nazywamy ją funkcją złożoną. Pochodna funkcji złożonej
równa się iloczynowi pochodnej funkcji względem argumentu pośredniego i
pochodnej pośredniego argumentu względem zmiennej niezależnej:
albo
Przykładowo możemy podać wzory:
1.
2.
Przykład 1.
Podstawiamy i otrzymujemy:
Przykład 2.
Podstawiamy
i otrzymujemy:
Przykład 3.
√
Podstawiamy
i otrzymujemy:
(
)
√
Zadania:
Wyznaczyć pochodne następujących funkcji:
1.
2.
3. √
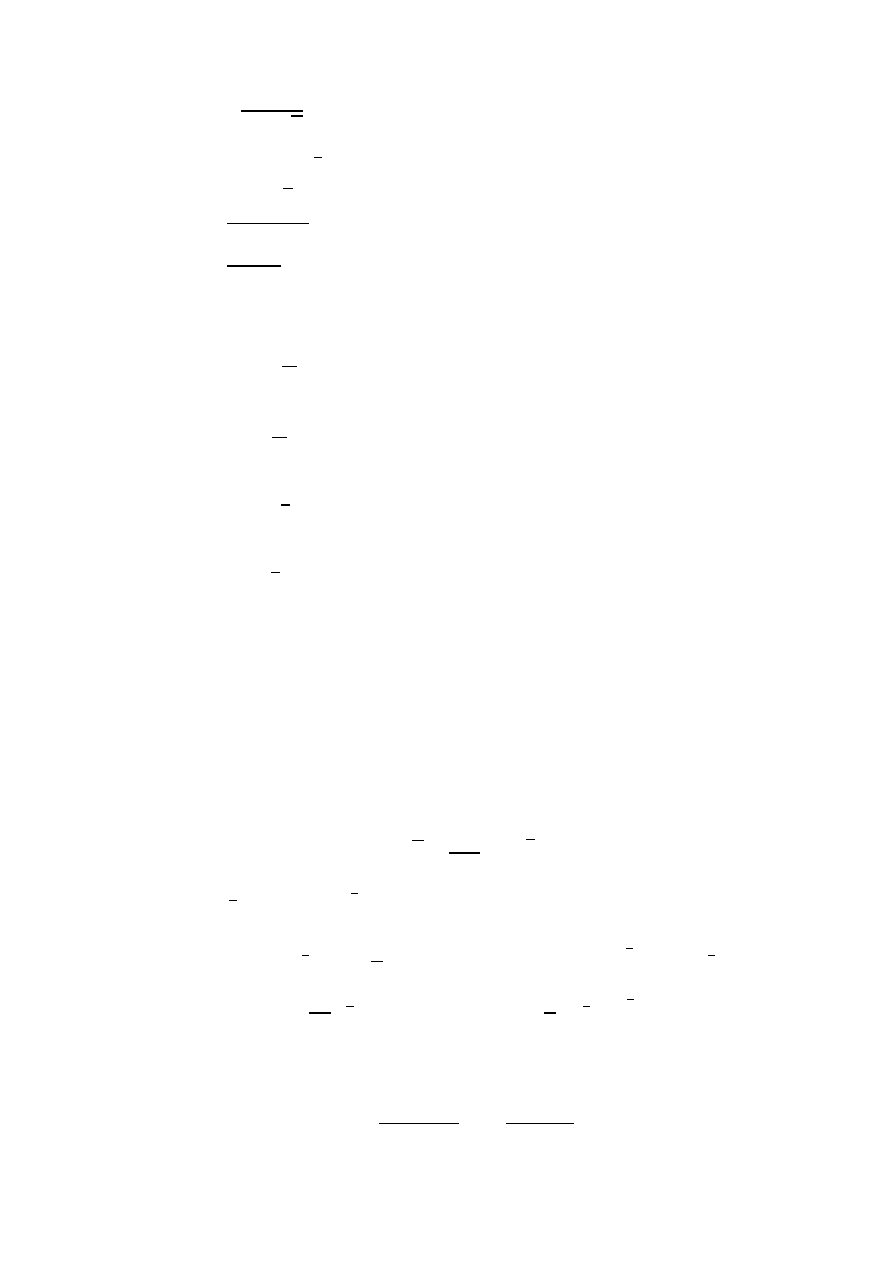
4. √ √
5.
6.
7.
8.
Pochodna funkcji wykładniczych i logarytmicznych.
1.
2.
3.
4.
5.
6.
7.
8.
Przy różniczkowaniu funkcji logarytmicznej o podstawie wyrażamy ją
najpierw przez funkcję logarytmiczną o podstawie , a następnie podstawie
wzoru:
Przykład 1.
Przykład 2.
√
√
(
)
(
)
(
)
Przykład 3.
Zadania.
Oblicz pochodne następujących funkcji:
1.
2.
3. √
4.
5.
6.
7.
8.
9.
10. √