Algorytmy i struktury danych

laboratorium – część 1

1. Algorytmy z rozgałęzieniami, algorytmy cykliczne

Zad. 1.1.
Narysuj schemat blokowy algorytmu rozwiązywania równania kwadratowego o postaci

0

2







c

bx

ax

, gdzie a, b i c są stałymi podawanymi przez użytkownika, ale przyjmij, że stała a

będzie zawsze różna od zera. Zapisz algorytm jako program w języku C/C++.

Zad. 1.2.
Rozszerz algorytm utworzony w zad. 1 o przypadek kiedy stała a jest równa 0.

Zad. 1.3.
Napisz algorytm obliczania podatku dochodowego przy danej podstawie obliczenia podatku.

Podstawa obliczenia podatku

w złotych

Podatek wynosi

ponad

do

85528

18% podstawy obliczenia minus kwota 556 zł 2 gr

85528

14839 zł 2 gr + 32% nadwyżki ponad 85528 zł

Zad. 1.4.
Napisz algorytm wyznaczania wartości funkcji signum dla argumentu rzeczywistego podawanego
przez użytkownika. Funkcja signum określona jest wzorem:























0

1

0

0

0

1

sgn

)

(

x

dla

x

dla

x

dla

x

x

f

Zad. 1.5.
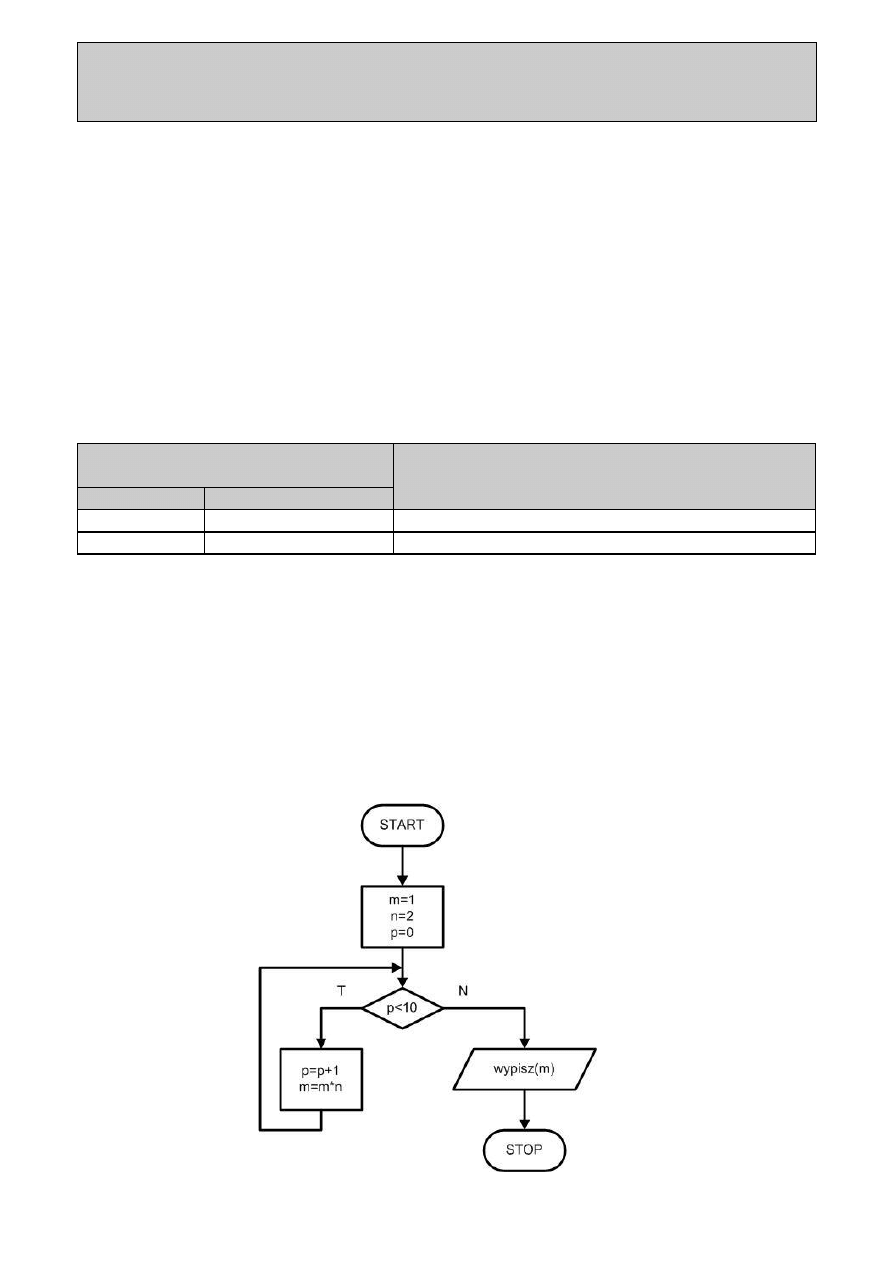
Określ jaką wartość będzie mieć zmienna m po wykonaniu następującego algorytmu:

2. Algorytmy iteracyjne, operacje na tablicach

Zad. 2.1.
Napisz algorytm znajdowania największego wspólnego dzielnika (NWD) dwóch liczb naturalnych
m i n metodą Euklidesa.

Zad. 2.2.
Napisz iteracyjny algorytm obliczania wartości wyrażenia

n

2 dla podanej liczby naturalnej n.

Zad. 2.3.
Napisz algorytm wczytywania i wyświetlania elementów tablicy 10-elementowej.

Zad. 2.4.
Napisz algorytm wyszukiwania w dziesięcioelementowej tablicy liczb całkowitych liczby
największej oraz określania jej pozycji.

Zad. 2.5.
Napisz algorytm określania ilości liczb podzielnych przez 3, lecz niepodzielnych przez 2 w danej
tablicy liczb naturalnych.

3. Algorytmy rekurencyjne

Zad. 3.1.
Napisz rekurencyjny algorytm obliczania silni danej liczby naturalnej n.
Wskazówka:
Korzystamy z definicji silni:















n

n

n

n

n

1

dla

)!

1

(

0

dla

1

!

Zad. 3.2.
Zaproponuj rekurencyjny algorytm odwracania kolejności elementów w tablicy.

Zad. 3.3.
Napisz rekurencyjny algorytm mnożenia dwóch liczb naturalnych m i n (gdzie

0

,



n

m

). Narysuj

drzewo wywołań rekurencyjnych dla

5

,

5





n

m

.

Wskazówka:
Korzystamy z definicji mnożenia:





















n

n

m

m

n

m

n

m

1

dla

)]

1

(

[

1

dla

Zad. 3.4.
Podaj rekurencyjny opis następujących ciągów:

a) ciągu arytmetycznego o pierwszym wyrazie równym 1 i różnicy równej 2,
b) ciągu geometrycznego o pierwszym wyrazie równym 5 i ilorazie równym 2.

Napisz rekurencyjne algorytmy obliczania n-tych wyrazów tych ciągów. Narysuj drzewa wywołań
rekurencyjnych dla tych algorytmów przy

6



n

.

4. Złożoność obliczeniowa algorytmów

Zad. 4.1.
Uporządkuj w kierunku rosnącym następujące złożoności obliczeniowe algorytmów:

)

2

(

),

!

(

),

(log

),

(

n

O

n

O

n

O

n

O

.

Zad. 4.2.
Dana jest tablica n-elementowa. Oszacuj złożoność czasową algorytmu sortowania bąbelkowego tej
tablicy:

for(int i=1; i<n; i++)
{

for(int j=n-1; j>=i; j--)

{

if(tab[j-1]>tab[j])

{

t=tab[j-1]; tab[j-1]=tab[j]; tab[j]=t;

}

}

}

Zad. 4.3.
Dana jest tablica n-elementowa. Oszacuj złożoność czasową algorytmu sortowania przez selekcję
tej tablicy:

for(int i=0; i<n-1; i++)
{

min=i;
for(int j=i+1; j<n; j++)

{

if(tab[j]<tab[min]) min=j;

}

t=tab[min]; tab[min]=tab[i]; tab[i]=t;

}

Zad. 4.4.
Oszacuj złożoność czasową algorytmu mnożenia dwóch macierzy kwadratowych o rozmiarze

n

n



. Dla dwóch macierzy

n

n

ij

a

A





]

[

oraz

n

n

ij

b

B





]

[

elementy macierzy

B

A

C





wyznaczane są

ze wzoru:









n

k

kj

ik

ij

b

a

c

1

dla

n

i

,...,

2

,

1



,

n

j

,...,

2

,

1



.

Zad. 4.5.
Rozwiąż równania rekurencyjne:

a)

















1

1

1

)

1

(

)

(

n

dla

n

dla

n

n

T

n

T

b)





























1

1

1

1

2

)

(

n

dla

n

dla

n

T

n

T