Algebra z geometri

ą

2013-01-12

1

MiNI PW

ALGEBRA

1

UZUPEŁNIENIE i ROZSZERZENIE

Ogólna postać powierzchni walcowych

i stożkowych w przestrzeni

R

3

.

Powierzchnie walcowe i sto

ż

kowe

Powierzchnie walcowe i sto

ż

kowe

MiNI PW

ALGEBRA

2

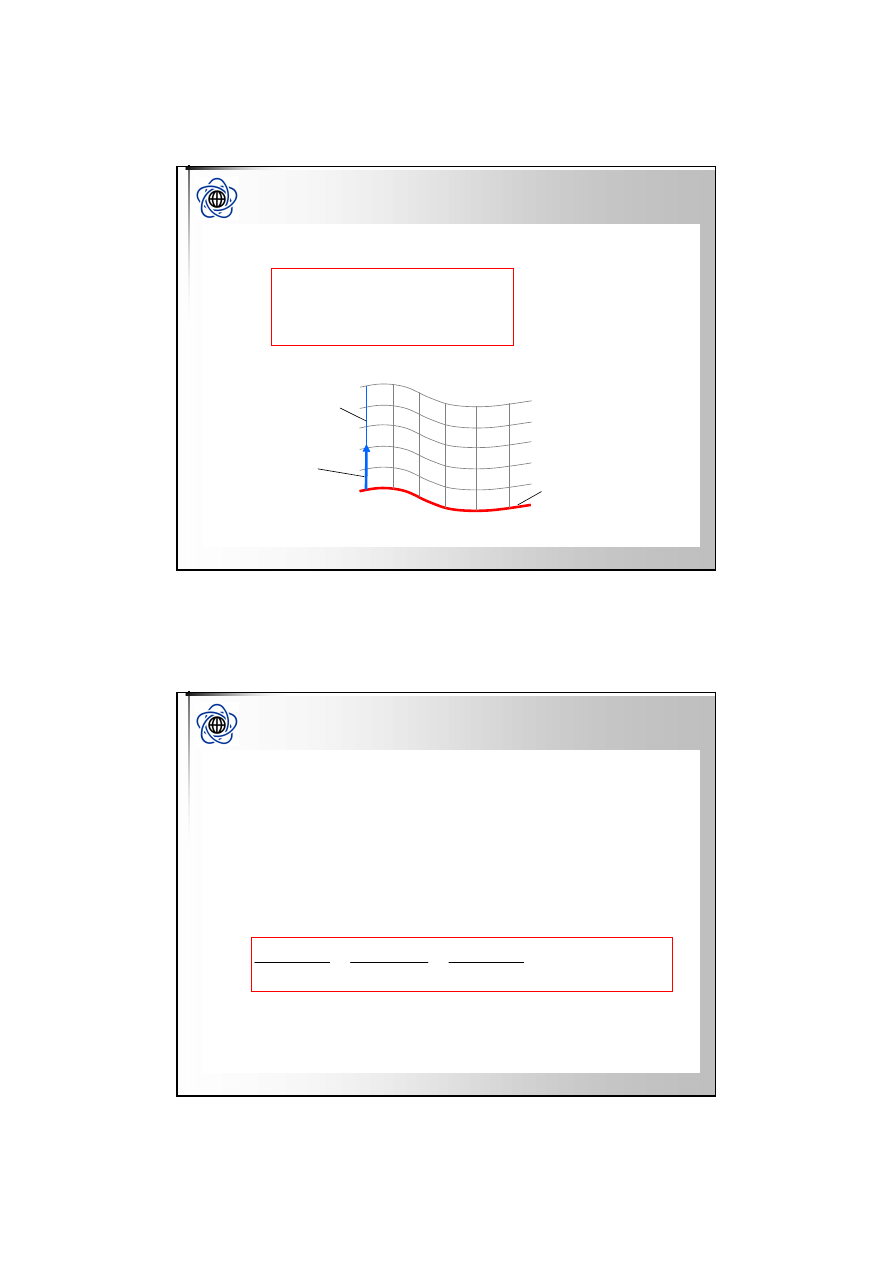
Niech

L

będzie pewną krzywą płaską (leżącą na

pewnej płaszczyźnie) w przestrzeni

R

3

.

Definicja

Powierzchnią walcową nazywamy powierzchnię
utworzoną przez rodzinę prostych równoległych do
danej prostej i przechodzących przez punkty
krzywej

L

.

Krzywą

L

nazywamy kierownicą.

Każdą prostą tej rodziny tworzącą powierzchni
walcowej.

Powierzchnie walcowe i sto

ż

kowe

Powierzchnie walcowe i sto

ż

kowe

Algebra z geometri

ą

2013-01-12

2

MiNI PW

ALGEBRA

3

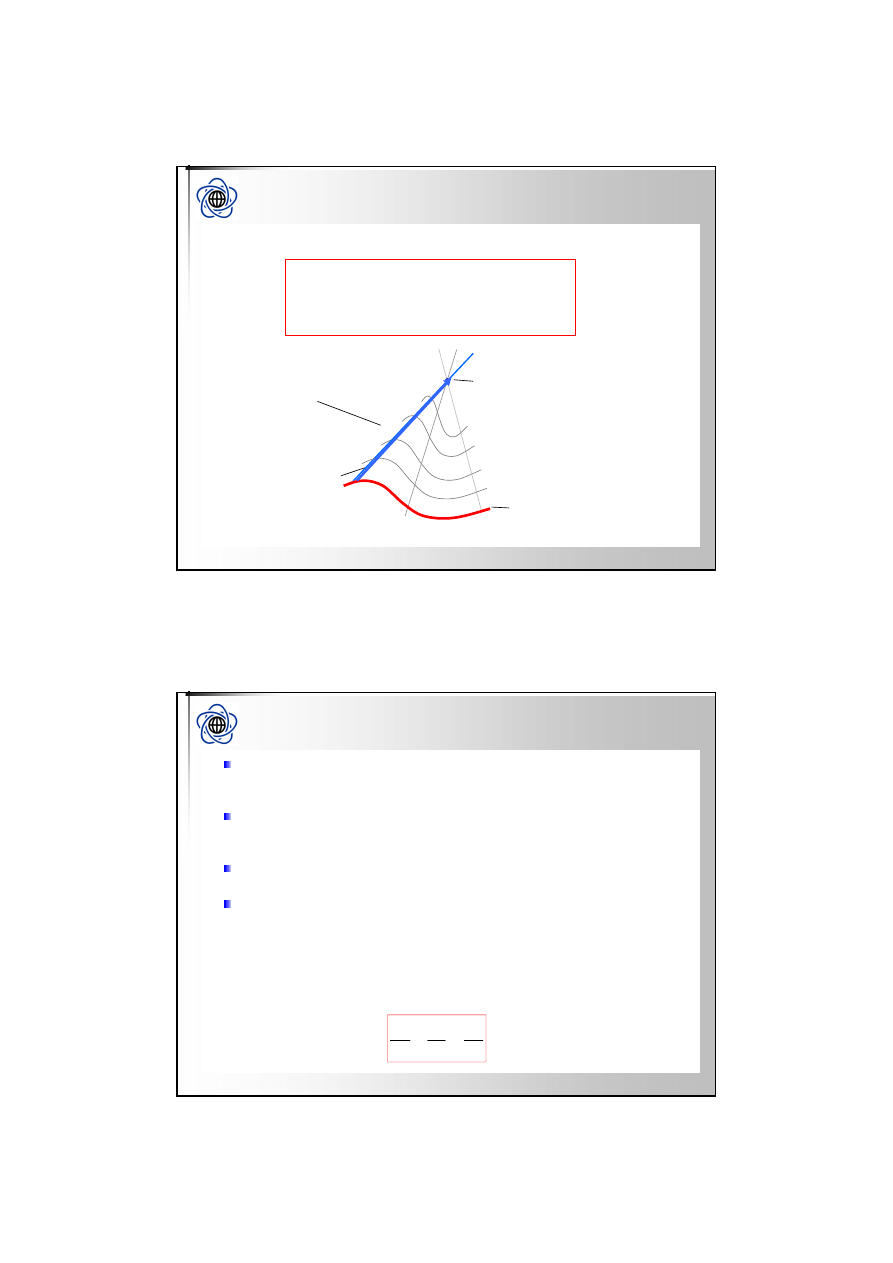
N

iech

L

będzie pewną krzywą płaską (leżącą na pewnej

płaszczyźnie) w przestrzeni

R

3

, zaś

W

ustalonym punktem tej

przestrzeni (

W

∉

L

).

Definicja

Powierzchnią stożkową nazywamy zbiór punktów
współliniowych z punktami

W

i

P

, gdzie

P

należy do

krzywej

L

(tzn. powierzchnię utworzoną przez rodzinę

prostych przechodzących przez punkt

W

i punkty krzywej

L)

.

Krzywą

L

nazywamy kierownicą.

Punkt

W

nazywamy wierzchołkiem stożka.

Każdą prostą tej rodziny tworzącą powierzchni stożkowej.

Powierzchnie walcowe i sto

ż

kowe

Powierzchnie walcowe i sto

ż

kowe

MiNI PW

ALGEBRA

4

Jeżeli krzywa

L

leżąca w pewnej płaszczyźnie ma przedstawienie parametryczne

L

:











=

=

=

)

(

)

(

)

(

3

2

1

t

f

z

t

f

y

t

f

x

,

t

∈

[

t

0

, t

1

]

zaś prosta

l jest równoległa do wektora

[

]

z

y

x

v

v

v

v

,

,

=

r

,

to równanie powierzchni walcowej ma postać

]

[

gdzie

)

(

)

(

)

(

1

0

3

2

1

t

,

t

t

v

t

f

z

v

t

f

y

v

t

f

x

z

y

x

∈

−

=

−

=

−

Powierzchnie walcowe

Powierzchnie walcowe

Algebra z geometri

ą

2013-01-12

3

MiNI PW

ALGEBRA

5

Równanie powierzchni walcowej w postaci parametrycznej











+

=

∈

∈

+

=

+

=

s

v

t

f

z

R

s

t

,

t

t

s

v

t

f

y

s

v

t

f

x

z

y

x

)

(

,

]

[

)

(

)

(

3

1

0

2

1

]

,

,

[

z

y

x

v

v

v

kierownica

K

tworz

ą

ca

Powierzchnie walcowe

Powierzchnie walcowe

MiNI PW

ALGEBRA

6

Jeżeli krzywa

L

ma przedstawienie parametryczne

L

:











=

=

=

)

(

)

(

)

(

3

2

1

t

f

z

t

f

y

t

f

x

,

t

∈

[

t

0

, t

1

]

i

W(x

w

, y

w

, z

w

)

jest ustalonym punktem przestrzeni,

to równanie powierzchni stożkowej ma postać

]

[

gdzie

)

(

)

(

)

(

1

0

3

2

1

t

,

t

t

t

f

z

z

z

t

f

y

y

y

t

f

x

x

x

w

w

w

w

w

w

∈

−

−

=

−

−

=

−

−

Powierzchnie sto

ż

kowe

Powierzchnie sto

ż

kowe

Algebra z geometri

ą

2013-01-12

4

MiNI PW

ALGEBRA

7

Równanie powierzchni stożkowej w postaci parametrycznej











−

+

=

∈

∈

−

+

=

−

+

=

s

t

f

z

z

z

R

s

t

,

t

t

s

t

f

y

y

y

s

t

f

x

x

x

))

(

(

,

]

[

))

(

(

))

(

(

3

0

0

1

0

2

0

0

1

0

0

kierownica

K

tworz

ą

ca

)]

(

),

(

),

(

[

3

0

2

0

1

0

t

f

z

t

f

y

t

f

x

−

−

−

wierzchołek

W

Powierzchnie sto

ż

kowe

Powierzchnie sto

ż

kowe

Sto

ż

ek

Sto

ż

ek

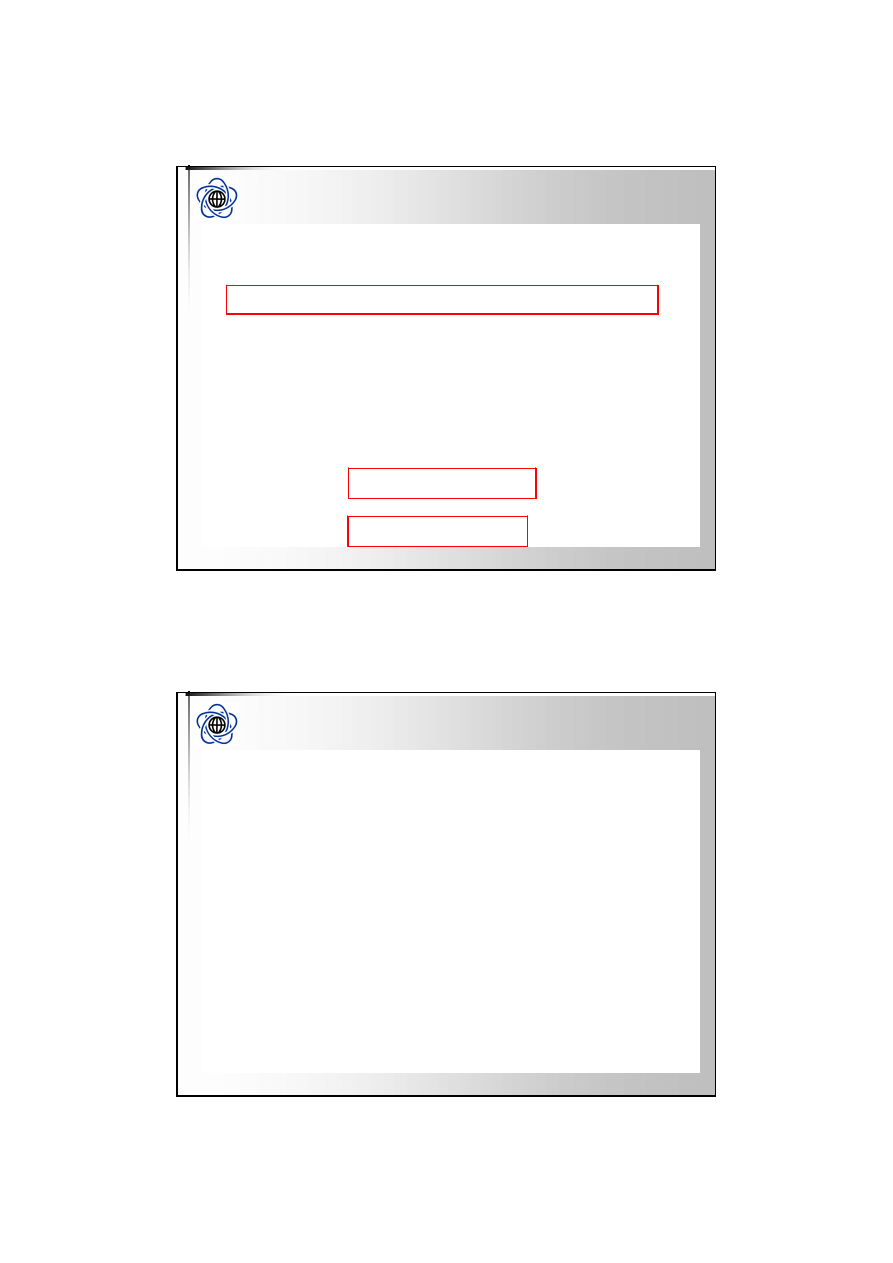
Przekroje sto

ż

ka płaszczyznami prostopadłymi do osi Oz s

ą

elipsami

(z wyj

ą

tkiem płaszczyzny przechodz

ą

cej przez pocz

ą

tek układu

współrz

ę

dnych – wówczas cz

ęś

ci

ą

wspóln

ą

jest punkt).

Przekroje sto

ż

ka płaszczyznami prostopadłymi do osi Ox i Oy s

ą

hiperbolami, a gdy zawieraj

ą

o

ś

Oz par

ą

prostych, b

ę

d

ą

cych tworz

ą

cymi

sto

ż

ka.

Przekroje sto

ż

ka płaszczyznami równoległymi do tworz

ą

cej s

ą

parabolami.

Podane równanie (oraz rysunek) prezentuje powierzchni

ę

otwart

ą

wzdłu

ż

osi Oz.
Aby uzyska

ć

równanie sto

ż

ka otwartego wzdłu

ż

innej osi nale

ż

y

odpowiednio zmodyfikowa

ć

równanie. Zmienna przeniesiona na drug

ą

stron

ę

równania, dla zachowania tego samego znaku współczynników,

wskazuje o

ś

wzdłu

ż

której sto

ż

ek jest otwarty.

Przykładowo - sto

ż

ek otwarty wzdłu

ż

osi Ox ma równanie:

ALGEBRA

8

2

2

2

2

2

2

a

x

c

z

b

y

=

+

MiNI PW

Algebra z geometri

ą

2013-01-12

5

MiNI PW

ALGEBRA

9

Definicja (bardzo ogólna)

Powierzchni

ą

stopnia drugiego (kwadryk

ą

) nazywamy zbiór punktów

przestrzeni trójwymiarowej, spełniaj

ą

cych równanie

0

2

2

2

=

+

+

+

+

+

+

+

+

+

K

Iz

Hy

Gx

Fyz

Exz

Dxy

Cz

By

Ax

gdzie

A, B, …, K

s

ą

stałymi i przynajmniej jedna ze stałych

A, B, C, D, E, F

jest ró

ż

na od zera.

Równanie to nazywamy

ogólnym równaniem powierzchni drugiego

stopnia

.

Mo

ż

na wykaza

ć

,

ż

e istnieje takie przekształcenie płaszczyzny (zło

ż

enie

obrotu i przesuni

ę

cia) w wyniku którego otrzymamy tzw. posta

ć

kanoniczn

ą

równania powierzchni:

0

~

~

~

~

2

2

2

=

+

+

+

K

z

C

y

B

x

A

lub

0

~

~

~

~

2

2

=

+

+

+

K

z

C

y

B

x

A

Powierzchnie stopnia drugiego

Powierzchnie stopnia drugiego

MiNI PW

ALGEBRA

10

Spo

ś

ród 17 ró

ż

nych powierzchni stopnia drugiego, 9 to kwadryki wła

ś

ciwe.

Pozostałe to kwadryki zdegenerowane (niewła

ś

ciwe).

Kwadryki wła

ś

ciwe to:

−

elipsoida (w tym sfera),

−

hiperboloida jednopowłokowa,

−

hiperboloida dwupowłokowa,

−

sto

ż

ek,

−

paraboloida eliptyczna,

−

paraboloida hiperboliczna,

−

walec eliptyczny,

−

walec hiperboliczny,

−

walec paraboliczny,

Powierzchnie stopnia drugiego

Powierzchnie stopnia drugiego

Algebra z geometri

ą

2013-01-12

6

MiNI PW

ALGEBRA

11

Przykłady kwadryk niewła

ś

ciwych:

−

Równanie

x

2

+

y

2

+

z

2

= 0

przedstawia punkt

O

(0,0,0),

−

Równanie

x

2

+

y

2

+

z

2

= −1

przedstawia zbiór pusty,

−

Równanie

x

2

+

y

2

= 0

przedstawia prost

ą (

o

ś

Oz

),

−

Równanie

x

2

−

y

2

= 0

przedstawia sum

ę

dwóch płaszczyzn

o równaniach

:

x

−

y

= 0

i

x

+

y

=0.

Powierzchnie stopnia drugiego

Powierzchnie stopnia drugiego

MiNI PW

ALGEBRA

12

Zmienna przed którą stoi znak minus wskazuje oś wzdłuż której
hiperboloida jest „otwarta” (oś symetrii dla hiperboloidy obrotowej).

Powierzchnie stopnia drugiego

Powierzchnie stopnia drugiego

Algebra z geometri

ą

2013-01-12

7

MiNI PW

ALGEBRA

13

Hiperboloida dwupowłokowa

2

2

2

2

2

2

1

z

x

y

c

a

b

−

−

=

Powierzchnie stopnia drugiego

Powierzchnie stopnia drugiego

MiNI PW

ALGEBRA

14

Przekroje hiperboloidy płaszczyznami prostopadłymi do osi

Oz

są

elipsami.

Przekroje hiperboloidy płaszczyznami prostopadłymi do osi

Ox i

Oy

są hiperbolami.

Szczególnym przypadkiem hiperboloidy dwupowłokowej jest

hiperboloida obrotowa, powstała przez obrót hiperboli wokół osi
rzeczywistej.

Powierzchnie stopnia drugiego

Powierzchnie stopnia drugiego