Satelitarne Techniki Pomiarowe

••

!"#

• $

%

& '(&

)

*

+

• $

%

& '(&

)

*

+

,'

-

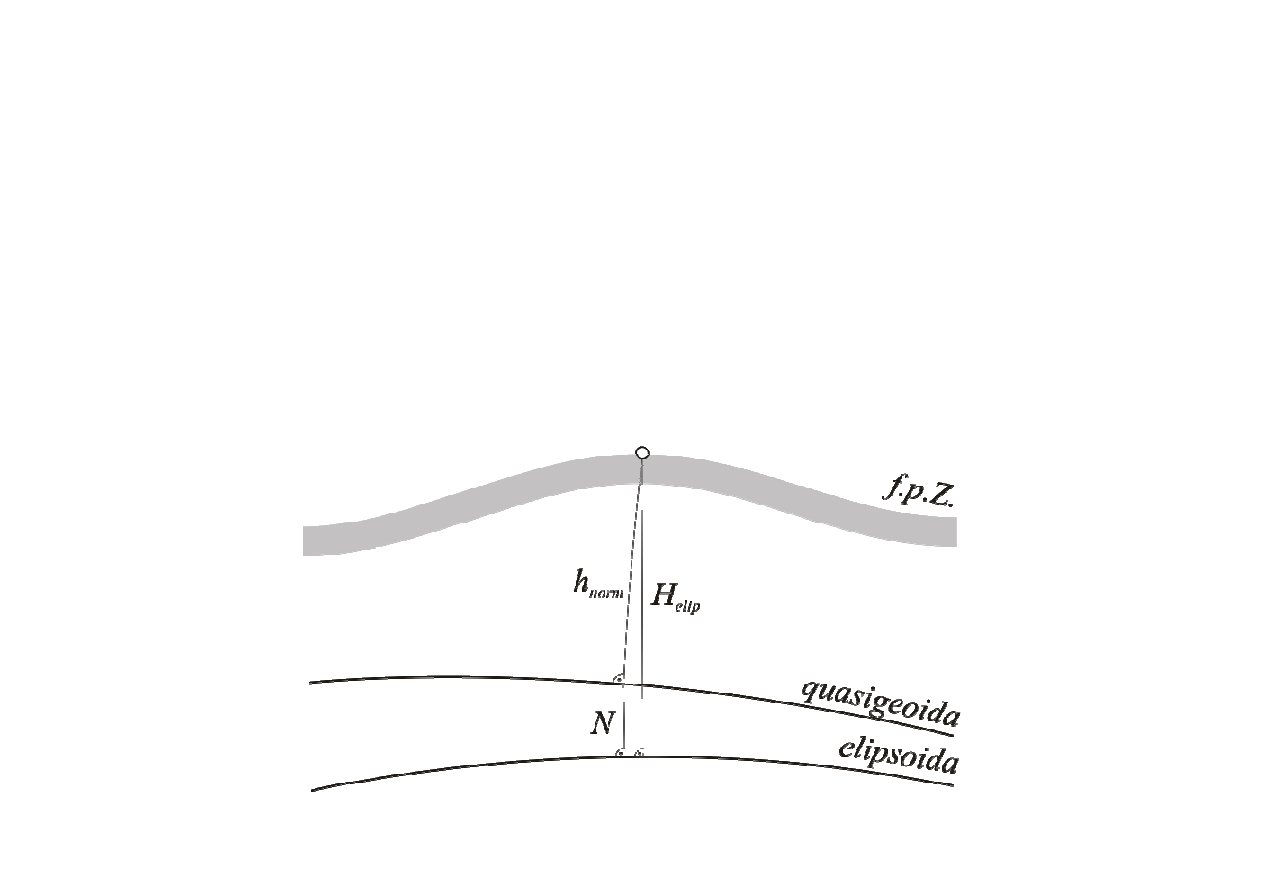
./!0#

H

= h

+ N

H

elip

= h

Norm

+ N

'

(& 1 2

• % 1

'

&

*

3

4

5 '

45 #

3

4

5 '

45 #

• % 1

1

!"

• % 1

1

!"

6'

* % &

'

•

%

'

&

•

%

'

&

'

# ,

,7

'

#

•

8

(

%

(

•

8

(

%

(

•

8

% 9& (

(

•

8

9

'

(

,

+

•

8

9

'

(

,

+

,

+

9

+% 1

% #

•

(

9

1

( % &

(

•

(

9

1

( % &

(

5 4

%

% :

; %

(

)

<

(

(

-

<

(

(

-

= >

% &

9

#

% &

9

#

?

(

#

•

% 1

9

&

%'

(

,

•

(

1

9

&

%'

(

,

,

•

8

' '

'

(

1

'

;

@

9

A

% :

;

B &

A

% :

/CD

4

5 '

45

<

(

<

(

( )

( )

( )

( )

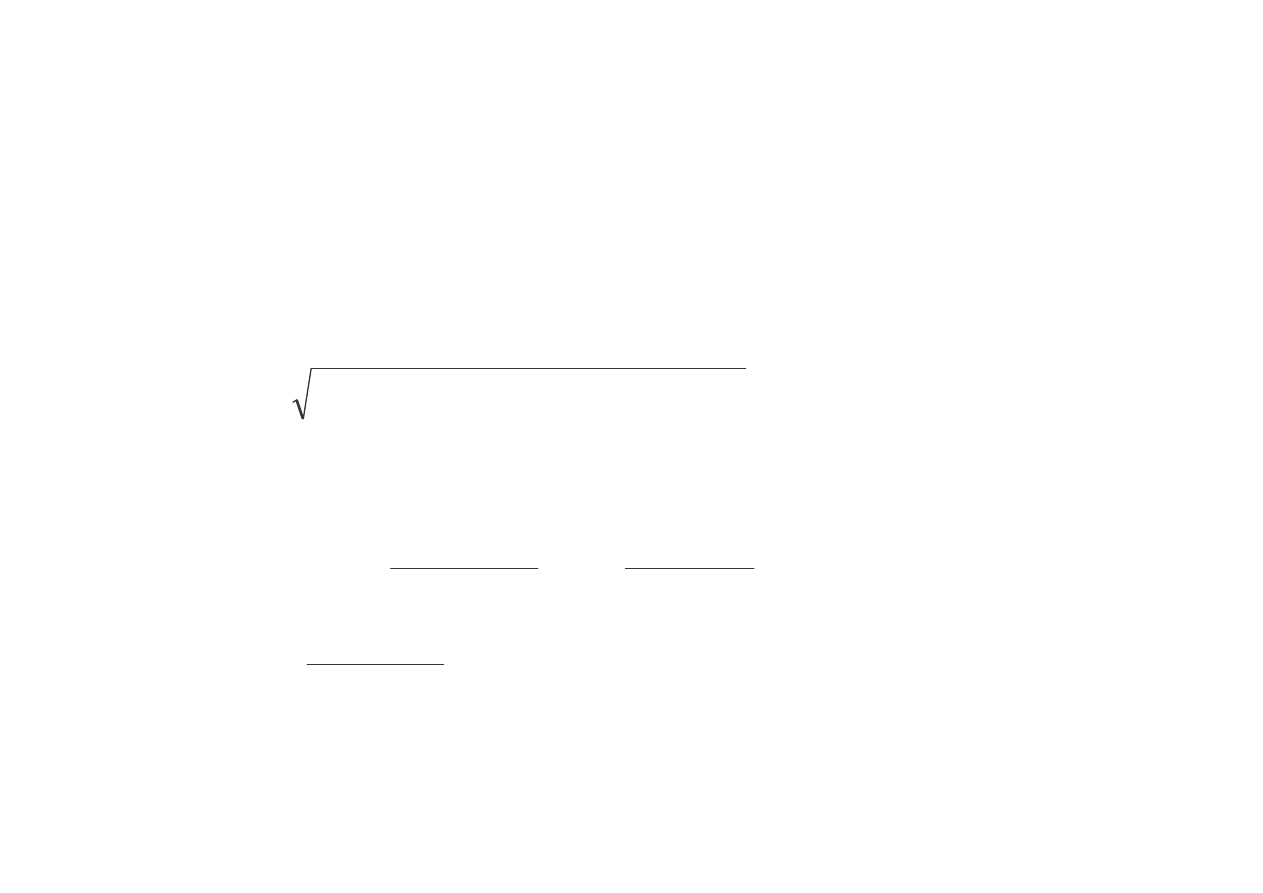
t

c

t

c

t

t

R

s

r

s

r

s

r

δ

δ

ρ

−

+

=

'

( )

t

R

s

r

( )

(

) (

) (

)

2

2

2

r

s

r

s

r

s

s

r

Z

Z

Y

Y

X

X

t

−

+

−

+

−

=

ρ

( )

t

s

r

ρ

<

( )

( )

( )

( )

Y

t

Y

X

t

X

s

s

s

s

ρ

−

∆

−

−

∆

−

−

=

( )

( )

( )

( )

( )

( )

( )

( )

( )

t

c

t

c

Z

Z

t

Z

Y

t

Y

t

Y

X

t

X

t

X

t

t

R

s

r

s

r

s

r

r

r

s

r

r

s

r

s

r

δ

δ

ρ

ρ

ρ

−

+

∆

−

−

−

∆

−

−

∆

−

−

=

0

0

0

0

0

0

( )

( )

( )

( )

t

c

t

c

Z

t

Z

t

Z

s

r

r

s

r

r

δ

δ

ρ

−

+

∆

−

−

0

0

( )

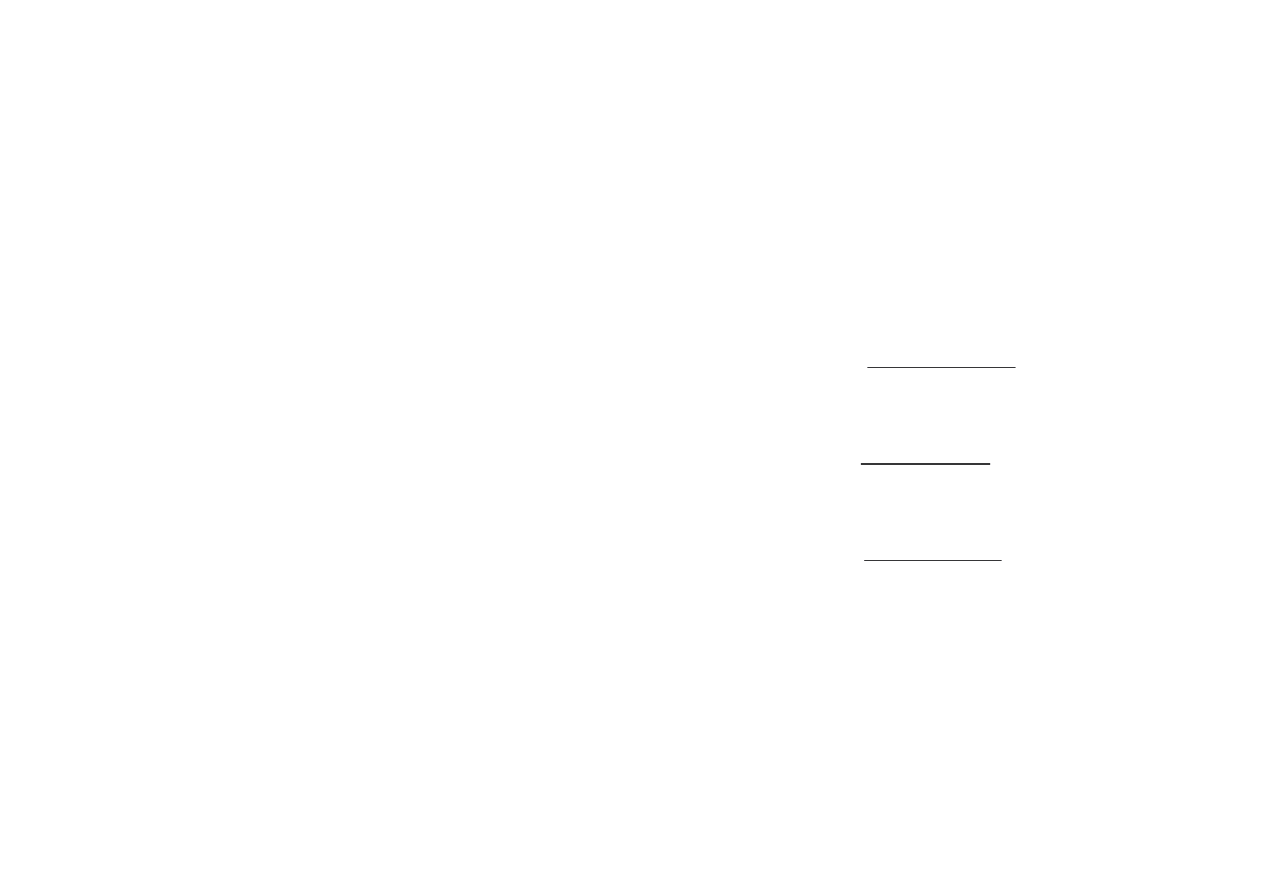
X

t

X

s

s

−

−

=

( )

( )

( )

t

c

t

t

R

l

s

s

r

s

r

s

δ

ρ

+

−

=

0

:

( )

( )

( )

Y

t

Y

a

t

X

t

X

a

r

s

s

s

r

r

s

s

X

r

0

0

0

ρ

−

−

=

−

−

=

:

c

a

a

a

Z

Y

X

r

r

r

1

1

1

( )

( )

( )

Z

t

Z

a

t

Y

t

Y

a

r

s

s

s

r

r

s

Y

r

0

0

0

ρ

−

−

=

−

−

=

=

c

a

a

a

A

s

Z

s

Y

s

X

r

r

r

r

r

r

( )

( )

t

Z

t

Z

a

s

r

r

s

Z

r

0

0

ρ

−

−

=

<

∆X

∆

∆

∆

=

Z

Y

X

x

r

r

( ) ( )

L

A

A

A

X

T

T

1

−

=

( )

∆

=

t

Z

x

r

r

δ

<

(

,

<

(

,

( )

( )

( )

( )

s

r

s

r

s

r

s
r

N

t

c

t

c

t

t

λ

δ

δ

ρ

λ

+

−

+

=

Φ

( )

( )

( )

t

c

t

t

l

s

s

r

s
r

s

δ

ρ

λ

+

−

Φ

=

0

( )

( )

( )

c

t

a

t

a

t

a

Z

Y

X

r

r

r

λ

0

0

0

1

1

1

( )

( )

( )

=

c

t

a

t

a

t

a

A

s

Z

s

Y

s

X

r

r

r

r

r

r

λ

0

0

0

( )

[

]

T

r

s

r

r

r

r

r

t

N

N

Z

Y

X

x

δ

1

∆

∆

∆

=

( )

1

−

=

A

A

Q

T

( )

1

−

=

A

A

Q

T

E%

+ +'

9

(

( &

,

'

'

( &

,

'

'

cos

cos

L

B

−

=

cos

sin

sin

sin

cos

L

B

B

L

B

u

<

(

[

]

u

e

n

R

=

−

−

=

=

cos

sin

sin

cos

sin

B

L

B

L

B

dB

du

n

[

]

u

e

n

R

=

−

−

−

=

L

B

L

L

B

L

B

L

L

B

R

sin

cos

cos

sin

sin

cos

cos

sin

cos

sin

−

=

=

0

cos

sin

cos

L

L

BdL

du

e

−

=

B

B

L

B

L

L

B

R

sin

0

cos

sin

cos

cos

sin

sin

0

T

topo

RQR

Q

=

!

!

•

% 1

('

(

FGAGC

h

Norm

= H

elip

– N

•

% 1

('

(

FGAGC

"#$

%&'&(

•

(&

9

1

2

% &

9

(

1 '

(

:

H

∆

h

Norm

=

∆

H

elip

–

∆

N

% &

9

(

1 '

(

:

H

•

( III

•

' (

'

(&

9

9

1

'

'

*

9

1

'

'

*

'

A

!

)&&*

!

)&&*

&

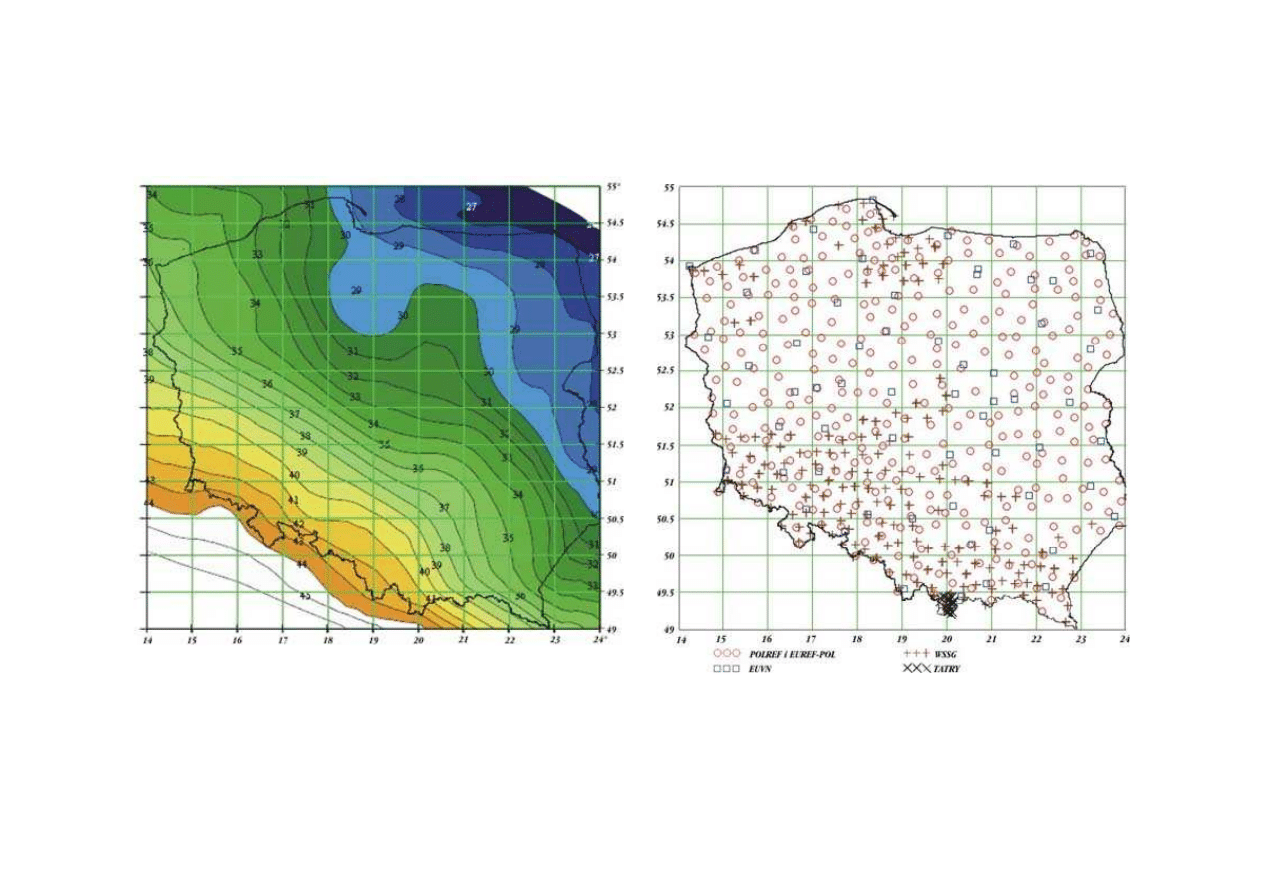
J

' B?

?GAG.K

./LG+./L!# *

6'

/0%

@$ 3

0J#+@$ =@M ); ..#+); =@M NNG#+

' B?

?GAG.K

% &

1

FGAGN

@$ 3

0J#+@$ =@M ); ..#+); =@M NNG#+

NJ0#+OEO=P JN#

III

Q,'

(

(

!

)&&*

!

)&&*

•

&

' (

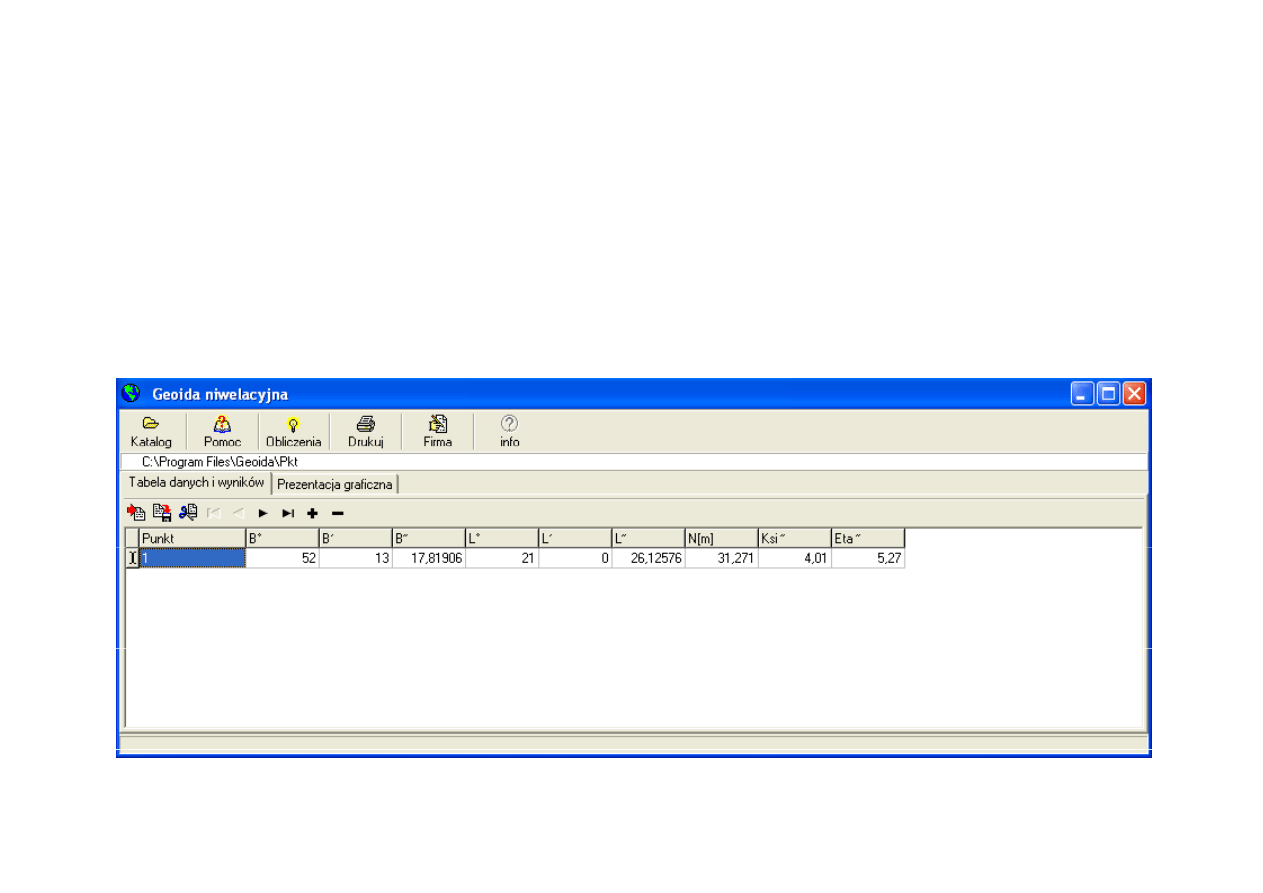
J

•

*

RA >

•

*

RA >

• +BK+BS+BABBT+ K+S+ A T

+!

)&&,

+!

)&&,

•

%

<

( '

•

,

( '

(

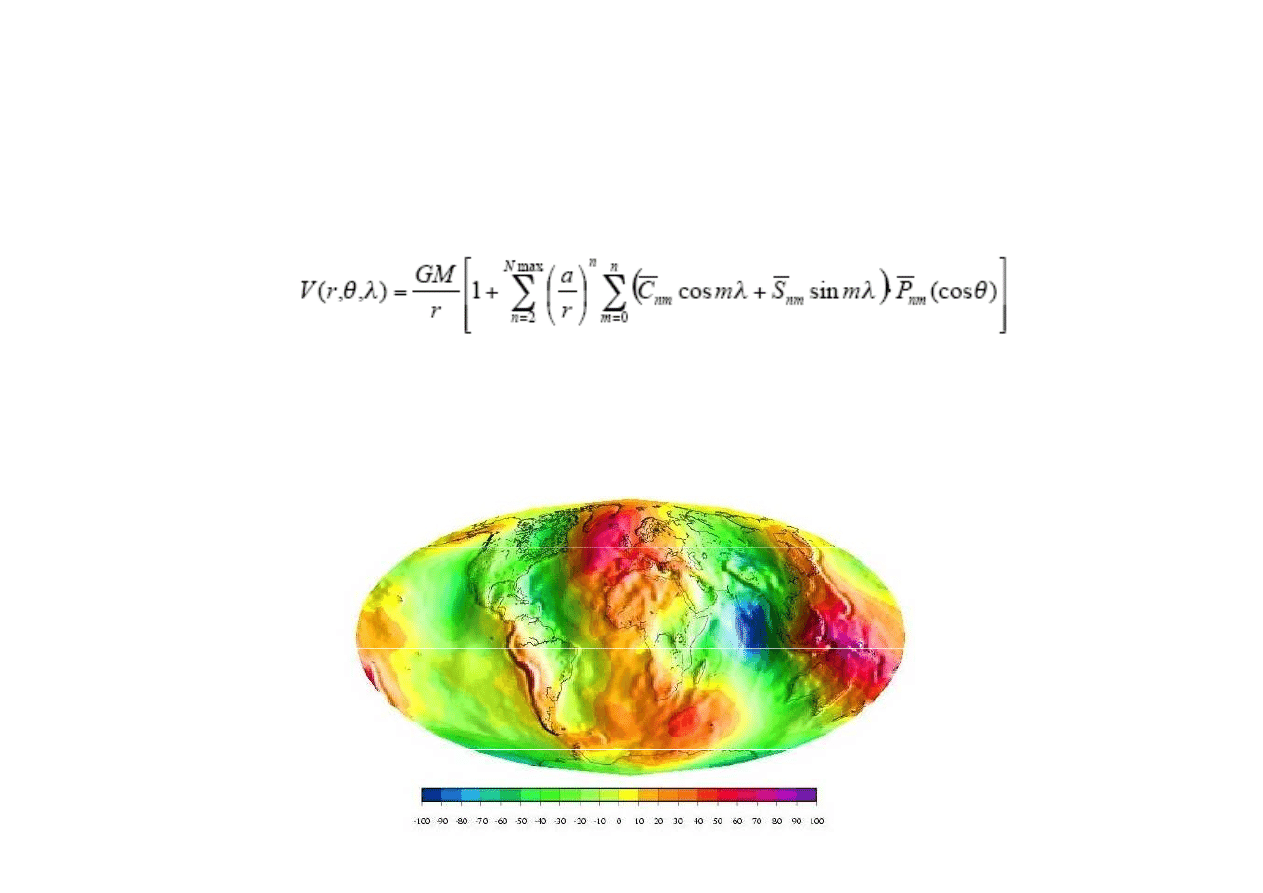
J.C/

1 ' 4 +

#

• =

'

5

′×5′

I

4

M

%

>

M

<

2HH

A ,

<

2HH

A ,

A HI4 @< HI4

@< A

-

-

-

*

1

1

•

1

'

&

#

N = H

– h

U

*

)

*

(

(

'

'

N

i

= H

i,elip

– h

i,Norm

•

'

'

1

2

?.

N

i

=a

0,0

+a

1,0

x

i

+ a

0,1

y

i

?.

N

i

=a

0,0

+a

1,0

x

i

+ a

0,1

y

i

?J

N

i

=a

0,0

+a

1,0

x

i

+ a

0,1

y

i

+ a

1,1

x

i

y

i

+ a

2,0

x

i

x

i

+ a

0,2

y

i

y

i

•

1 '

'

•

1 '

'

1

'

'

• V

*

#

"

.

.

/

/

-

#

.

0

-

#

.

0

< (&

A

(

Bx

A

y

+

=

2

O

:

%

(

Ax

l

=

2

O

:

%

(

Ax

l

=

x

y

1

1

1

=

=

=

B

A

x

x

x

A

y

y

l

,

1

1

,

2

1

2

1

=

=

=

B

x

x

A

y

l

N

N

,

1

,

x

y

N

N

1

1 /

2 "#$ /

1 /

2 "#$ /

l

Ax

v

−

=

9

E B

% 2

min

]

[

2

=

v

4

2

T

T

T

T

T

2

−

+

=

−

−

=

Ax

l

Ax

A

x

l

l

Ax

l

Ax

l

v

T

T

T

T

T

2

)

(

)

(

2

−

+

=

−

−

=

1

3

1

3

v

δ

0

2

2

=

−

=

l

A

Ax

A

x

v

T

T

δ

δ

0

2

2

=

−

=

l

A

Ax

A

x

δ

T

T

=

4

2

l

A

Ax

A

T

T

=

E

&

&

1 '(&

2

l

A

A

A

x

T

T

1

)

(

−

=

E

&

&

1 '(&

2

l

A

A

A

x

)

(

=

4 "

4 "

<

2

p

0

0

1

=

p

p

P

0

0

0

2

1

N

p

0

A2

2

1

m

p

=

Pl

A

PA

A

x

T

T

1

)

(

−

=

E

&

&

1 '(&

2

m

[ ]

T

PV

V

Pl

A

PA

A

x

T

T

1

)

(

−

=

[ ]

n

T

n

PV

V

m

=

0

-

2

-

2

PAx

l

Pl

l

PV

V

T

T

T

−

=

/

/

=

=

j

i

j

i

y

x

a

y

x

z

2

,

1

,

0

,

,

)

,

(

=

=

ij

j

i

ij

j

i

y

x

a

y

x

z

2

,

1

,

0

,

,

)

,

(

2

2

+

+

+

+

+

=

A

'

2

2

02

2

20

11

01

10

00

)

,

(

y

a

x

a

xy

a

y

a

x

a

a

y

x

z

+

+

+

+

+

=

=

2

h

y

a

x

a

xy

a

y

a

x

a

a

v

−

+

+

+

+

+

=

2

2

=

2

i

i

h

y

a

x

a

xy

a

y

a

x

a

a

v

−

+

+

+

+

+

=

2

02

2

20

11

01

10

00