
5.1 Zastosowanie równania Schrödingera
do rozwi
ą
zania zagadnienia Atomu
wodoru
5.2 Rozwi
ą
zanie równania Schrödingera
dla atomu wodoru
5.3 Liczby kwantowe
5.4 Efekt Zeemana
5.5 Spin
5.6 Uogólniona zasada nieokre
ś
lono
ś
ci
5.7 Prawdopodobie
ń
stwa przej
ść
. Reguły
wyboru
5.8 Superpozycja stanów
Rozdział 5
Atom Wodoru
Atom współczesnej fizyki jest reprezentowany jedynie poprzez równanie ró
ż
niczkowe
cz
ą
stkowe w abstrakcyjnej przestrzeni w wielu wymiarach, z równania mo
ż
na wyprowadzi
ć
wszystkie jego cechy. Atom nie ma bezpo
ś
rednio
ż
adnych materialnych cech a jego
zrozumienie, w tradycyjny, oparty na zmysłach sposób, jest niemo
ż
liwe.
- Werner Heisenberg
Werner Heisenberg
(1901-1976)
Przygotowanie Marek Szopa, na podstawie Rick Trebino, Georgia Tech, www.physics.gatech.edu/frog/lectures

Z elektrostatyki wiemy, jaka jest energia potencjalna układu elektron-
proton :
Wykorzystamy trójwymiarowe, bezczasowe równanie Schrodingera.
Dla atomów wodoropodobnych, takich jak (He
+
or Li
++
),
e
2
nale
ż
y
zast
ą
pi
ć
przez
Ze
2
(
Z
jest liczb
ą
atomow
ą
).
We wszystkich przypadkach, dla wi
ę
kszej dokładno
ś
ci,
m
nale
ż
y
zast
ą
pi
ć
mas
ą
zredukowan
ą
µ
.
( )
2
0
4
e
V r
r
πε
= −
5.1: Zastosowanie równania Schrödingera
do rozwi
ą
zania zagadnienia Atomu wodoru
(
)
(
)
(
)
(
)
( )
2
2
2
2
2
2
2
, ,
, ,
, ,
1
2
, ,
x y z
x y z
x y z
E V r
m
x y z
x
y
z
ψ
ψ
ψ
ψ
∂
∂
∂
−
+
+
= −
∂
∂
∂
ℏ
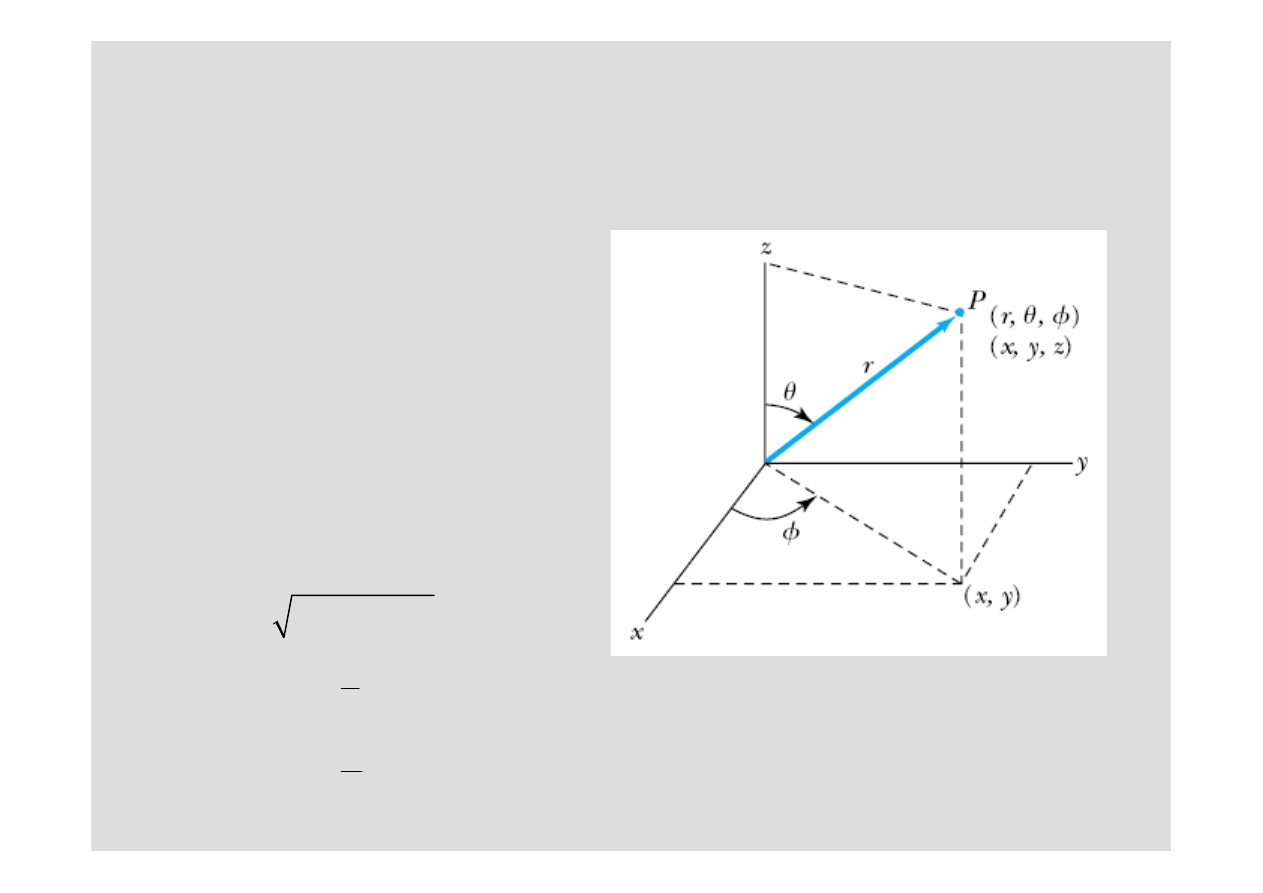
Współrz
ę
dne sferyczne
Potencjał siły centralnej
V(r)
zale
ż
y od odległo
ś
ci protonu
od elektronu.
Z powodu takiej (sferycznej)
symetrii zagadnienie nale
ż
y
przetransformowa
ć
do
współrz
ę
dnych sferycznych:
(
)
(
)
2
2
2
1
1
sin cos
sin sin
cos
cos
tan
x
r
y
r
z
r
r
x
y
z
z
r
y
x
θ
ϕ
θ
ϕ
θ
θ
ϕ
−
−
=
=
=
=
+
+
=
=
k
ą
t zenitalny
k
ą
t azymutalny
Równanie
Schrödingera we
współrz
ę
dnych
sferycznych
Równanie Schrödingera
przetransformowane do
współrz
ę
dnych
sferycznych ma
nast
ę
puj
ą
c
ą
posta
ć
:
(
)
2
2
2
2
2
2
2
2
1
1
1
2
sin
0
sin
sin
r
E V
r
r
r
r
r
ψ
ψ
ψ
µ
θ
ψ
θ θ
θ
θ ϕ
∂
∂
∂
∂
∂
+
+
+
−
=
∂
∂
∂
∂
∂
ℏ

Rozwi
ą
zanie w rozseparowanych
zmiennych
Funkcja falowa
ψ
zale
ż
y od 3 zmiennych
r,
θ
,
φ
. Jako taka mo
ż
e by
ć
potencjalnie bardzo skomplikowana.
B
ą
d
ź
my jednaj optymistami i załó
ż
my,
ż
e dla
ψ
mo
ż
liwe jest
rozdzielenie (separacja)
zmiennych, tzn.
ż
e jest ona iloczynem
trzech funkcji jednaj zmiennej:
Pochodne
ψ
ze wzgl
ę
du na poszczególne zmienne s
ą
wi
ę
c:
)
(
)
(
)
(
)
,
,
(
φ
θ
φ
θ
ψ
g
f
r
R
r
=
2
2
2
2
φ
φ
ψ
θ
θ
ψ
ψ
∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
g
Rf
f
Rg
r
R
fg
r
To zało
ż
enie znacznie upraszcza spraw
ę
, a co najwa
ż
niejsze działa!
5.2: Rozwi
ą
zanie równania
Schrödingera dla atomu wodoru
Rozwi
ąż
my wi
ę
c równanie Schrodingera zakładaj
ą
c separowalno
ść
ψ
:
Mno
żą
c obie strony przez
−
r
2
sin
2
θ
/ R f g:
Podstawmy:
(
)
2
2
2
2
2
2
2
2
1
1
1
2
sin
0
sin
sin
r
E V
r
r
r
r
r
ψ
ψ
ψ
µ
θ
ψ
θ θ
θ
θ ϕ
∂
∂
∂
∂
∂
+
+
+
−
=
∂
∂
∂
∂
∂
ℏ
2
2
2
2
φ
φ
ψ
θ
θ
ψ
ψ
∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
g
Rf
f
Rg
r
R
fg
r
(
)
0
2
sin
sin
sin
2
2
2
2
2
2
2
2
=
−
+
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
Rfg
V
E
g
r
Rf
f
r
Rg
r
R
r
r
r
fg
ℏ
µ
φ
θ
θ
θ
θ
θ
(
)
2
2
2
2
2
2
2
1
sin
sin
sin
2
sin
φ
θ
θ
θ
θ
θ
µ
θ
∂
∂
=
∂
∂
∂
∂
−
−
−
∂
∂
∂
∂
−
g
g
f
f
V
E
r
r
R
r
r
R
ℏ

Rozwi
ą
zanie równania Schrödingera
dla atomu wodoru
Lewa strona równania zale
ż
y tylko od
r
i
θ
a prawa tylko od
φ
.
Lewa strona nie mo
ż
e si
ę
zmieni
ć
jak zmieniamy
φ
.
Prawa strona nie mo
ż
e si
ę
zmieni
ć
jak zmieniamy
r
lub
θ
.
Ż
eby równanie było spełnione obie strony musz
ą
wi
ę
c by
ć
stał
ą
niezale
ż
n
ą
od
ż
adnej zmiennej.
Oznaczmy t
ą
stał
ą
przez
−m
ℓ
2
Jak wiemy rozwi
ą
zaniem tego równania s
ą
funkcje
ℓ
, cho
ć
równie
ż
sin i cos je spełniaj
ą
. Pami
ę
tamy jednak,
ż
e
ℓ
= cos
ℓ
+ sin
ℓ
równanie azymutalne
(
)
2
2
2
2
2
2
2
1
sin
sin
sin
2
sin
φ
θ
θ
θ
θ
θ
µ
θ
∂
∂
=
∂
∂
∂
∂
−
−
−
∂
∂
∂
∂
−
g
g
f
f
V
E
r
r
R
r
r
R
ℏ
g
m
d
g
d
2
2
2
ℓ
−
=
φ

Rozwi
ą
zanie równania Schrödingera
dla atomu wodoru
Równanie azymutalne
Jest spełnione przez
ℓ
dla dowolnej warto
ś
ci
m
ℓ
.
Jednak aby rozwi
ą
zanie miało sens musi by
ć
jednowarto
ś
ciow
ą
funkcj
ą
φ
:
Aby ten warunek był spełniony
m
ℓ
musi by
ć
liczb
ą
całkowit
ą
(dodatni
ą
, ujemn
ą
lub zerem).
Konkretnie:
Wi
ę
c:
g
m
d
g
d
2
2
2
ℓ
−
=
φ
( ) (
)
π
φ
φ
2
+
=
g
g
(
) (
)
π
φ
φ
2
0
=
=
=
g
g
ℓ
im
e
e
π
2
0
=
im
e
φ
ℓ
Rozwi
ą
zanie równania Schrödingera
dla atomu wodoru
Teraz przyrównajmy lew
ą
stron
ę
do
−m
ℓ
2
:
Teraz lewa strona zale
ż
y tylko od
r
, a prawa tylko od
θ
. Mo
ż
emy
zastosowa
ć
jeszcze raz t
ą
sam
ą
metod
ę
!
Po przekształceniu i podzieleniu przez
sin
2
(
θ
)
mamy:
(
)
2
2
2
2
2
2
2
1
sin
sin
sin
2
sin
φ
θ
θ
θ
θ
θ
µ
θ
∂
∂
=
∂
∂
∂
∂
−
−
−
∂
∂
∂
∂
−
g
g
f
f
V
E
r
r
R
r
r
R
ℏ
(
)
2
2
2
2
2
2
sin
sin
sin
2
sin
ℓ
ℏ
m
f
f
V
E
r
r
R
r
r
R
−
=
∂
∂
∂
∂
−
−
−
∂
∂
∂
∂
−
θ
θ
θ
θ
θ
µ
θ
(
)
∂
∂
∂
∂
−
=
−
+
∂
∂
∂
∂
θ
θ
θ
θ
θ
µ
f
f
m
V
E
r
r
R
r
r
R
sin
sin
1
sin
2
1
2
2
2
2
2
ℓ
ℏ
Rozwi
ą
zanie równania Schrödingera
dla atomu wodoru
Tym razem przyjmijmy,
ż
e obie strony s
ą
równe stałej:
ℓ
(ℓ + 1)
.
równanie radialne
równanie zenitalne
Tym sposobem rozseparowali
ś
my równanie Schrödingera na trzy
równania ró
ż
niczkowe zwyczajne drugiego rz
ę
du, jednej zmiennej.
(
)
∂
∂
∂
∂
−
=
−
+
∂
∂
∂
∂
θ
θ
θ
θ
θ
µ
f
f
m
V
E
r
r
R
r
r
R
sin
sin
1
sin
2
1
2
2
2
2
2
ℓ
ℏ
( )
0
1
2
2
1
2
2
2
2
2
=
+
−
−
+
∂
∂
∂
∂
R
r
V
E
r
R
r
r
r
ℓ
ℓ
ℏ
ℏ
µ
µ
( )
0
sin
1
sin
sin
1
2
2
=
−
+
+
∂
∂
f
m
f
d
d
θ
θ
θ
θ
θ
ℓ
ℓ
ℓ

Rozwi
ą
zanie równania radialnego
Równanie to nazywamy
równaniem stowarzyszonym Laguerre’a
a jego rozwi
ą
zania
R
funkcjami stowarzyszonymi Laguerre’a
.
Funkcji tych jest niesko
ń
czenie wiele dla
n = 1, 2, 3,
…
Załó
ż
my,
ż
e stan podstawowy ma
n = 1
i
ℓ
= 0
. Poszukajmy rozwi
ą
za
ń
.
Równanie radialne jest:
Pochodna
ma dwa składniki:
(
)
2
2
2
1
2
0
d
dR
r
E V R
r dr
dr
µ
+
−
=
ℏ
0
4
2
2
0
2
2
2
2
=
+
+
+
R
r
e
E
dr
dR
r
dr
R
d
πε
µ
ℏ

Rozwi
ą
zanie równania
radialnego dla
Podstawmy rozwi
ą
zanie
A
jest stał
ą
normalizacyjn
ą
a
0
jest stał
ą
o wymiarze długo
ś
ci.
Po zró
ż
niczkowaniu i podstawieniu do równania radialnego dostajemy.
Aby to równanie było spełnione dla dowolnego
r
, oba wyra
ż
enia w
nawiasach musz
ą
by
ć
równe zeru.
Po przyrównaniu do zera i rozwi
ą
zaniu
drugiego wyra
ż
enia wzgl
ę
dem
a
0
:
Po przyrównaniu do zera i rozwi
ą
zaniu
pierwszego wyra
ż
enia wzgl
ę
dem
E
:
Ale
a
0
znamy jako promie
ń
Bohra, a
E
jako
energie stanu podstawowego atomu Bohra!
⇒
0
4
2
2
0
2
2
2
2
=
+
+
+
R
r
e
E
dr
dR
r
dr
R
d
πε
µ
ℏ
0
1
2
4
2
2
1
0
2
0
2
2
2
0
=
−
+
+
r
a
e
E
a
ℏ
ℏ
πε
µ
µ
2
2
0
0
4
e
a
µ
πε
ℏ
=
2
2
0
2
0
0
0
2
8
e
E
E
a
e a
µ
π
= −
= −
= −
ℏ
0
/
( )
r a
R r
Ae
−
=
1,
0
n
l
=
=
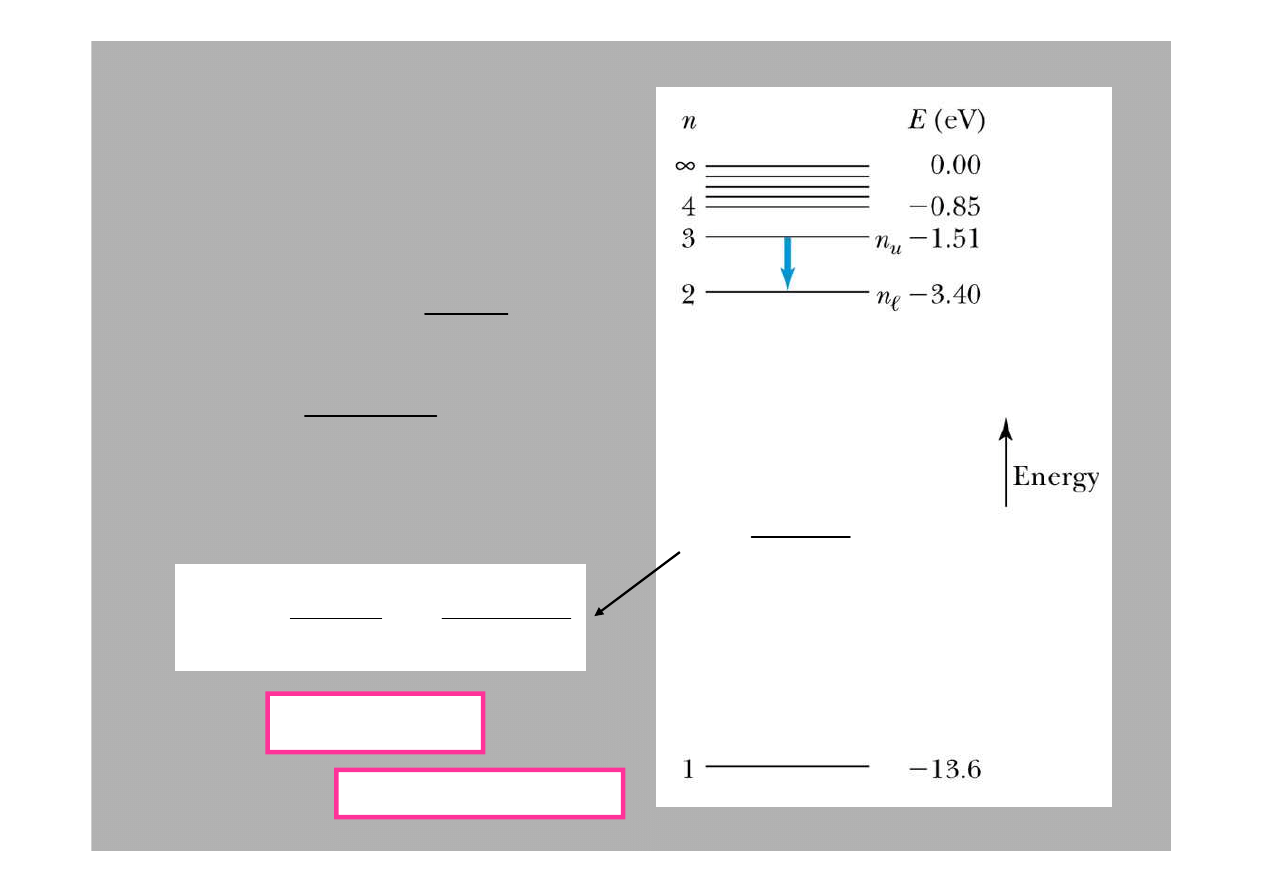
Energie Atomu
wodoru Bohra
(dla przypomnienia)
Tak wi
ę
c energie stanów
stacjonarnych s
ą
:
gdzie
E
0
= 13.6 eV
.
2
0
8
e
E
r
πε
= −
2
0
0
4
2
2
n
2
n
r
a n
me
πε
=
=
ℏ
Klasyczna
formuła dla
energii:
oraz:
E
n
=
−
E
0
/n
2
lub:
0
0
4
2
2
a
me
πε
≡
ℏ
2
0
0
2
0
2
8
8
n
a
e
r
e
E
n
n
πε
πε
−
=
−
=

Główna
liczba
kwantowa
n
Równanie radialne ma wiele rozwi
ą
za
ń
, po jednym dla ka
ż
dej
dodatniej całkowitej warto
ś
ci
n
.
Skwantowana energia wyra
ż
a si
ę
wzorem znanym z prac Bohra:
Energia ujemna oznacza,
ż
e elektron i proton s
ą
trwale zwi
ą
zane.
2
0
2
0
2
1
4
2
n
E
n
e
E
n
−
=
−
=
ℏ
πε
µ
( )
0
1
2
2
1
2
2
2
2
2
=
+
−
−
+
∂
∂
∂
∂
R
r
V
E
r
R
r
r
r
ℓ
ℓ
ℏ
ℏ
µ
µ

5.3: Liczby kwantowe
W wyniku rozwi
ą
zanie otrzymujemy 3 liczby kwantowe:
n
:
Główna liczba kwantowa
ℓ
: Liczba kwantowa p
ę
du orbitalnego
m
ℓ
: Magnetyczna liczba kwantowa
Liczby kwantowe spełniaj
ą
nast
ę
puj
ą
ce ograniczenia:
n = 1, 2, 3, 4, . . .
ℓ = 0, 1, 2, 3, . . . , n − 1
m
ℓ
= − ℓ, − ℓ + 1, . . . , 0, 1, . . . , ℓ − 1, ℓ
Równowa
ż
nie:
n > 0
ℓ < n
|m
ℓ
| ≤ ℓ
Poziomy energetyczne:
2
0
n
E
E
n
−
=

Radialne funkcje falowe atomu wodoru
Kilka
pierwszych
funkcji
radialnych
R
nℓ
Indeksy przy
R
oznaczaj
ą
warto
ś
ci
n
i
ℓ
.
wielomiany
stowarzyszone
Laguerre’a

Rozwi
ą
zania równa
ń
azymutalnego i
zenitalnego
Rozwi
ą
zania równania azymutalnego s
ą
postaci:
Rozwi
ą
zania równa
ń
azymutalnego i zenitalnego s
ą
zwi
ą
zane poniewa
ż
oba zawieraj
ą
t
ą
sam
ą
liczb
ę
m
ℓ
.
Zazwyczaj grupuje si
ę
te rozwi
ą
zania w funkcje znane jako
harmoniki sferyczne
:
harmoniki sferyczne
)
(
)
(
)
,
(
φ
θ
φ
θ
g
f
Y
=
φ
ℓ
im
e
(
)
∂
∂
∂
∂
−
=
−
+
∂
∂
∂
∂
θ
θ
θ
θ
θ
µ
f
f
m
V
E
r
r
R
r
r
R
sin
sin
1
sin
2
1
2
2
2
2
2
ℓ
ℏ
g
m
d
g
d
2
2
2
ℓ
−
=
φ

Znormalizowane
harmoniki
sferyczne
( , )

Rozwi
ą
zania równa
ń
azymutalnego i
zenitalnego
Radialna funkcja falowa
R
i harmonika sferyczna
Y
wyznaczaj
ą
g
ę
sto
ść
prawdopodobie
ń
stwa opisywanych stanów kwantowych.
Pełna funkcja falowa
( , , )
zale
ż
y od
n
,
ℓ
, i
m
ℓ
.
Funkcja falowa ma posta
ć
:
( , , )
( )
( , )
n m
n
n m
r
R
r Y
ψ
θ φ
θ φ
=
ℓ
ℓ
ℓ
ℓ
ℓ

G
ę
sto
ść
rozkładu prawdopodobie
ń
stwa
Funkcje falowe mog
ą
by
ć
wykorzystane do obliczania rozkładów
prawdopodobie
ń
stwa elektronów.
"Pozycja" elektronu jest rozproszona po całej przestrzeni i nie jest
dobrze zdefiniowana.
Radialn
ą
funkcj
ę
falow
ą R(r)
mo
ż
emy wykorzysta
ć
do obliczania
radialnego rozkładu prawdopodobie
ń
stwa elektronu.
Prawdopodobie
ń
stwa znalezienia elektronu w ró
ż
niczkowym
elemencie obj
ę
to
ś
ci
d
τ
jest:
Gdzie ten element obj
ę
to
ś
ci we współrz
ę
dnych sferycznych jest
dany wzorem:
* ( , , )
( , , )
dP
r
r
dx dy dz
ψ
θ φ ψ θ φ
=
2
sin
dx dy dz
r
dr d
d
θ
θ φ
=
G
ę
sto
ść
rozkładu prawdopodobie
ń
stwa
Na chwil
ę
we
ź
miemy pod uwag
ę
tylko zale
ż
no
ść
radialn
ą
Po scałkowaniu po wszystkich warto
ś
ciach
θ
i
φ
:
Całki po
θ
i
φ
s
ą
stałymi.
Zatem radialna g
ę
sto
ść
prawdopodobie
ń
stwa to
P(r) = r
2
|R(r)|
2
i
zale
ż
y tylko od
n
i
ℓ
.
2
2
2
2
0
0
( )
* ( ) ( )
( ) sin
( )
P r dr
r R r R r dr
f
d
g
d
π
π
θ
θ θ
φ
φ
=
∫
∫
dr
r
R
r
dr
r
P
)
(
)
(
2
2
=
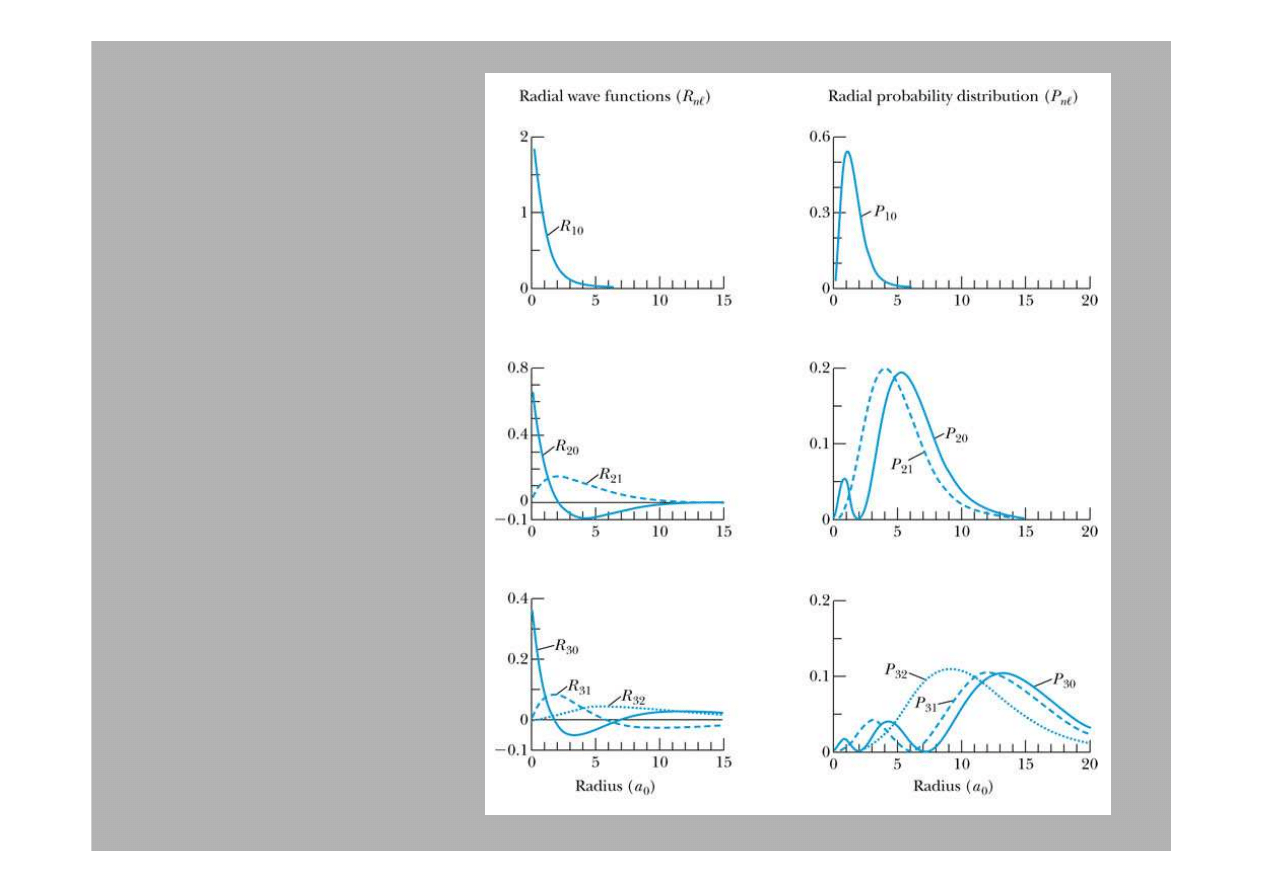
R(r)
i
P(r)
dla najni
ż
ej
le
żą
cych stanów w
atomie wodoru.
Zauwa
ż
my,
ż
e
R
n0
ma
w
r = 0
maksimum!
Jednak czynnik
r
2
redukuje w tym
miejscu prawd. do
zera Tym niemniej
jest niezerowe prawd.
ż
e elektron jest
wewn
ą
trz j
ą
dra.
Radialny
rozkład
prawdopodo-
bie
ń
stwa
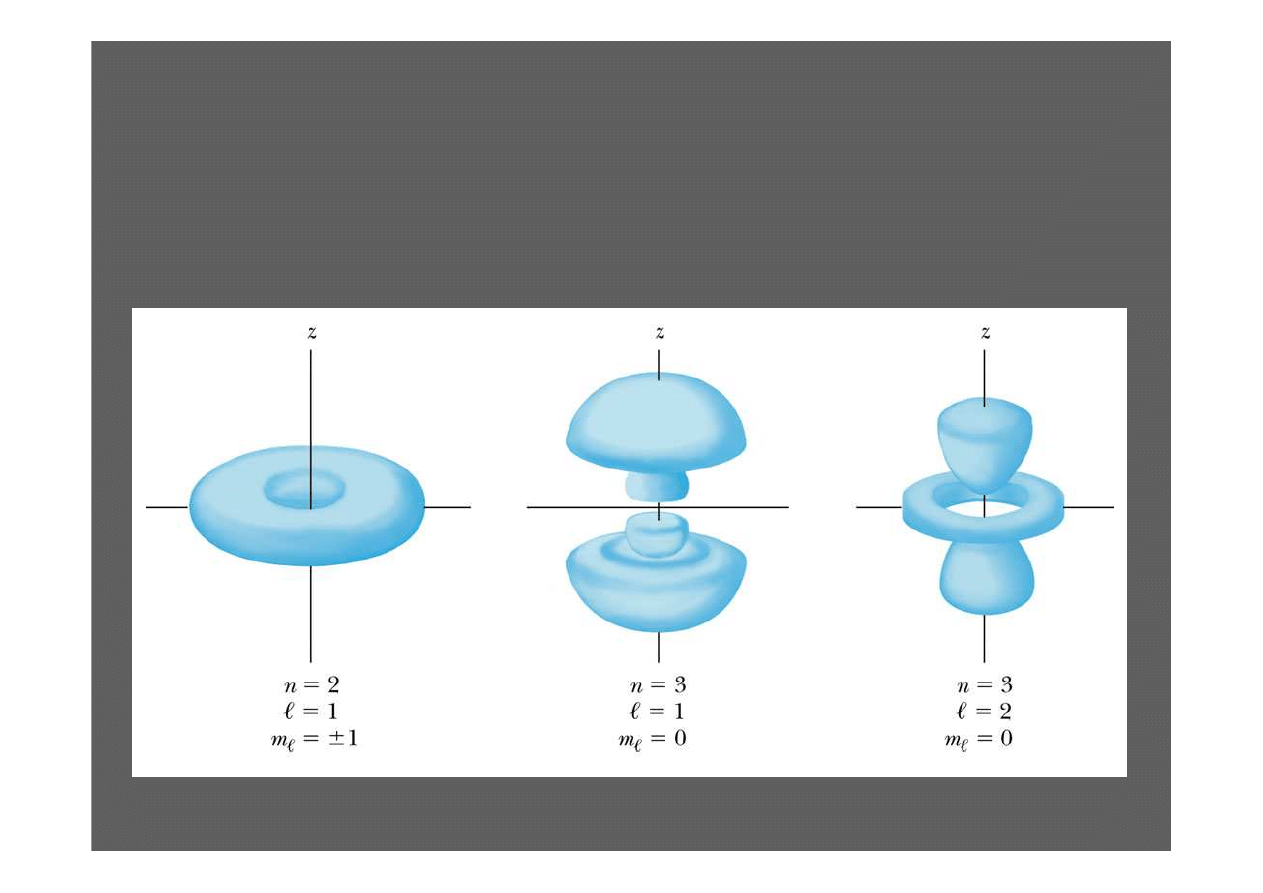
Funkcje rozkładu prawdopodobie
ń
stwa
G
ę
sto
ść
prawdopodobie
ń
stwa dla trzech ró
ż
nych stanów
elektronowych w atomie wodoru.

Liczba kwantowa
ℓ
orbitalnego momentu
p
ę
du.
Poziomy energetyczne s
ą
zdegenerowane
ze wzgl
ę
du na
ℓ
(energia
nie zale
ż
y od
ℓ
).
Dla oznaczenie ró
ż
nych warto
ś
ci liczby
ℓ
u
ż
ywamy liter:
ℓ
=
0
1
2
3
4
5 . . .
litera =
s
p
d
f
g
h . . .
Stany atomowe nazywamy zazwyczaj poprzez podanie dwu liczb
kwantowych
n
i
ℓ
.
Na przykład stan o
n
= 2 i
ℓ
= 1 nazywamy stanem 2p.
Wyst
ę
puje w cz
ęś
ciach
R(r)
i
f(
θ
)
funkcji falowej.
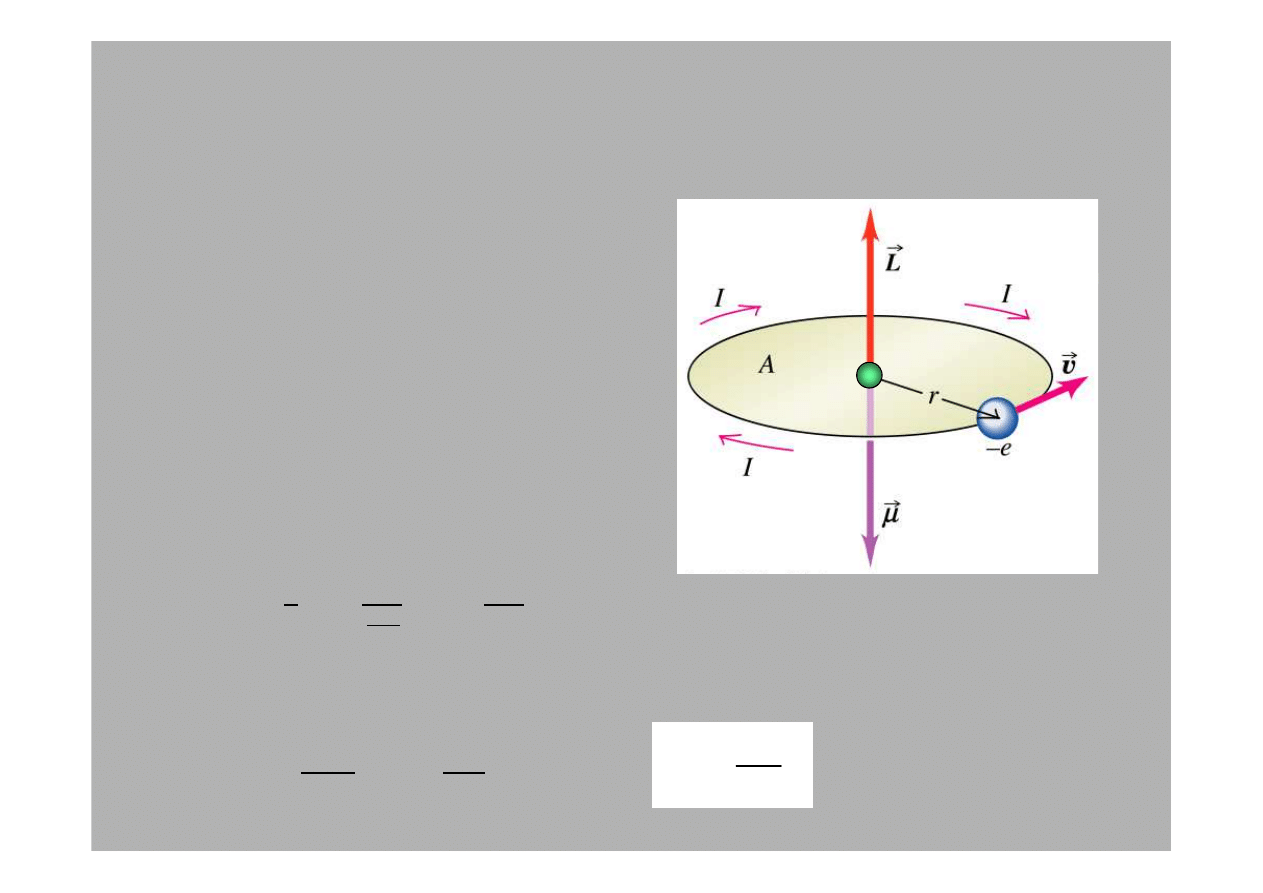
Klasycznie orbitalny moment p
ę
du jest równy
= × "
oraz
L = m v
orbital
r
.
Kwantowomechanicznie jednak,
L
wi
ąż
e si
ę
z
ℓ
poprzez:
A w stanie
ℓ
= 0,
=
0(1)ℏ = 0
Tan wynik jest niezgodny z
semiklasycznym „planetarnym”
modelem Bohra elektronów kr
ążą
cych
wokół j
ą
dra
L = nħ
, gdzie
n = 1, 2, …
Liczba kwantowa
ℓ
orbitalnego
momentu p
ę
du.
W mechanice kwantowej nie
istniej
ą
takie jak te orbity
klasyczne.
ℏ
ℓ
ℓ
)
1
(
+
=
L
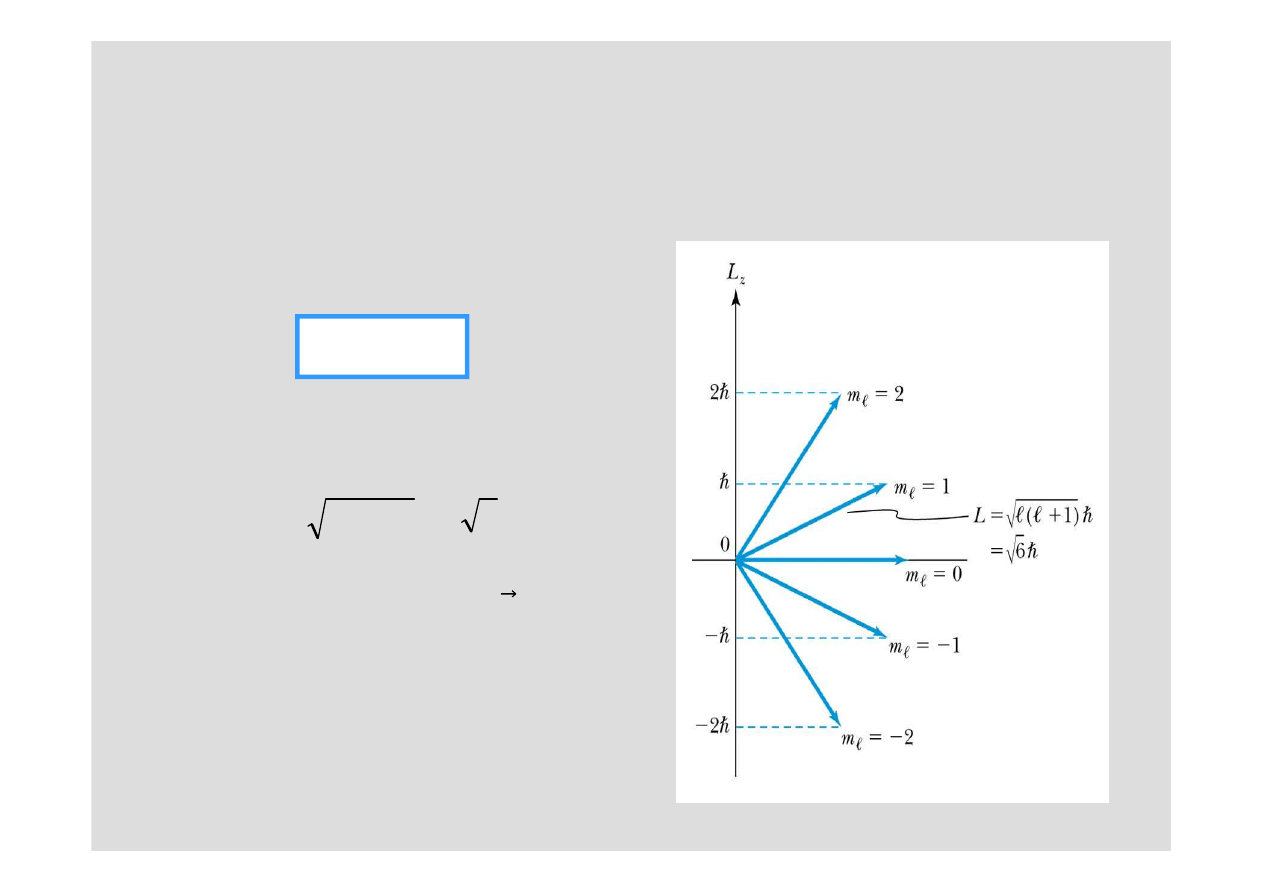
Na przykład dla
ℓ = 2
:
Tylko niektóre orientacje s
ą
dopuszczalne
Ponadto (za wyj
ą
tkiem kiedy
ℓ
= 0)
nie znamy
L
x
i
L
y
!
Magnetyczna liczba
kwantowa
m
ℓ
Z warunków brzegowych
równania azymutalnego na
g(
φ
)
wynika,
ż
e
m
ℓ
jest liczba całkowit
ą
zwi
ą
zan
ą
z
z-
t
ą
składow
ą L
:
ℏ
ℏ
ℓ
ℓ
6
)
1
(
=
+
=
L
ℏ
ℓ
m
L
z
=
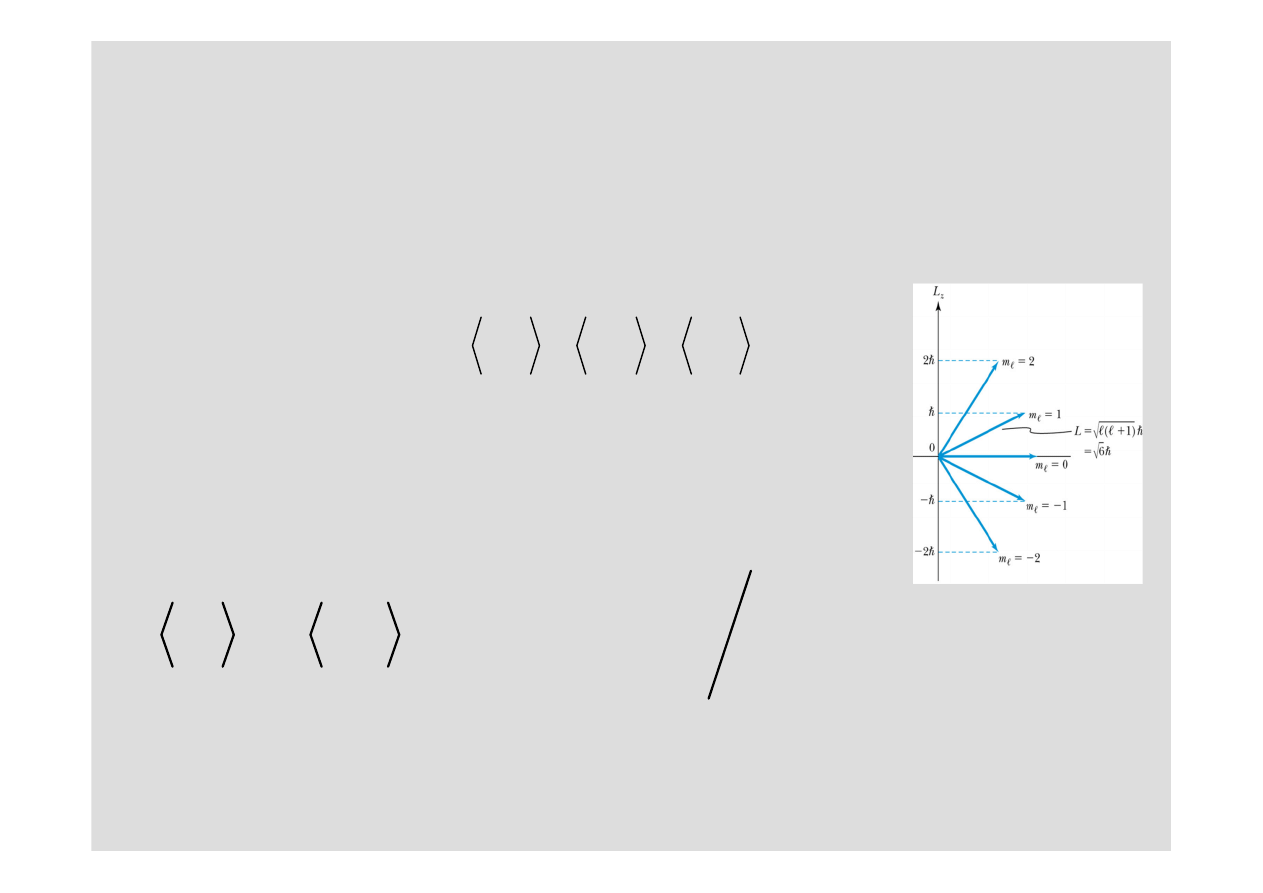
Szkic dowodu,
ż
e
‹
L
2
›
=
ℓ
(ℓ+1)ħ
2
W zwi
ą
zku, z symetri
ą
sferyczn
ą
atomu, mo
ż
emy zakłada
ć
,
ż
e
wszystkie składowe momentu p
ę
du maj
ą
takie same warto
ś
ci
ś
rednie:
Ale, jak wiemy
&
=
ℓ
%
Ś
redniuj
ą
c po wszystkich warto
ś
ciach
m
ℓ
(zakładamy,
ż
e s
ą
tak samo prawdopodobne) mamy:
2
(
1)(2
1) / 3
n
m
= −
=
+
+
∑
ℓ
ℓ
ℓ ℓ
ℓ
bo:
2
2
2
z
y
x
L
L
L
=
=
2
2
2
2
2
3
3
(2
1)
(
1)
z
m
L
L
m
=−
=
=
+ =
+
∑
ℓ
ℓ
ℓ
ℓ
ℏ
ℓ
ℓ ℓ
ℏ
Holender, Pieter Zeeman w 1896
zaobserwował,
ż
e linie spektralne
emitowane przez atomy w polu
magnetycznym rozszczepiaj
ą
si
ę
na szereg poziomów.
Gdyby elektron traktowa
ć
jako
ładunek kr
ążą
cy wokół j
ą
dra to
wytwarza on pr
ą
d
' = ()/(+
. Je
ś
li
okres tego ruchu jest dany przez
, = 2. //
, to:
' = −
1
2
= −
1
345
6
= −
7
8
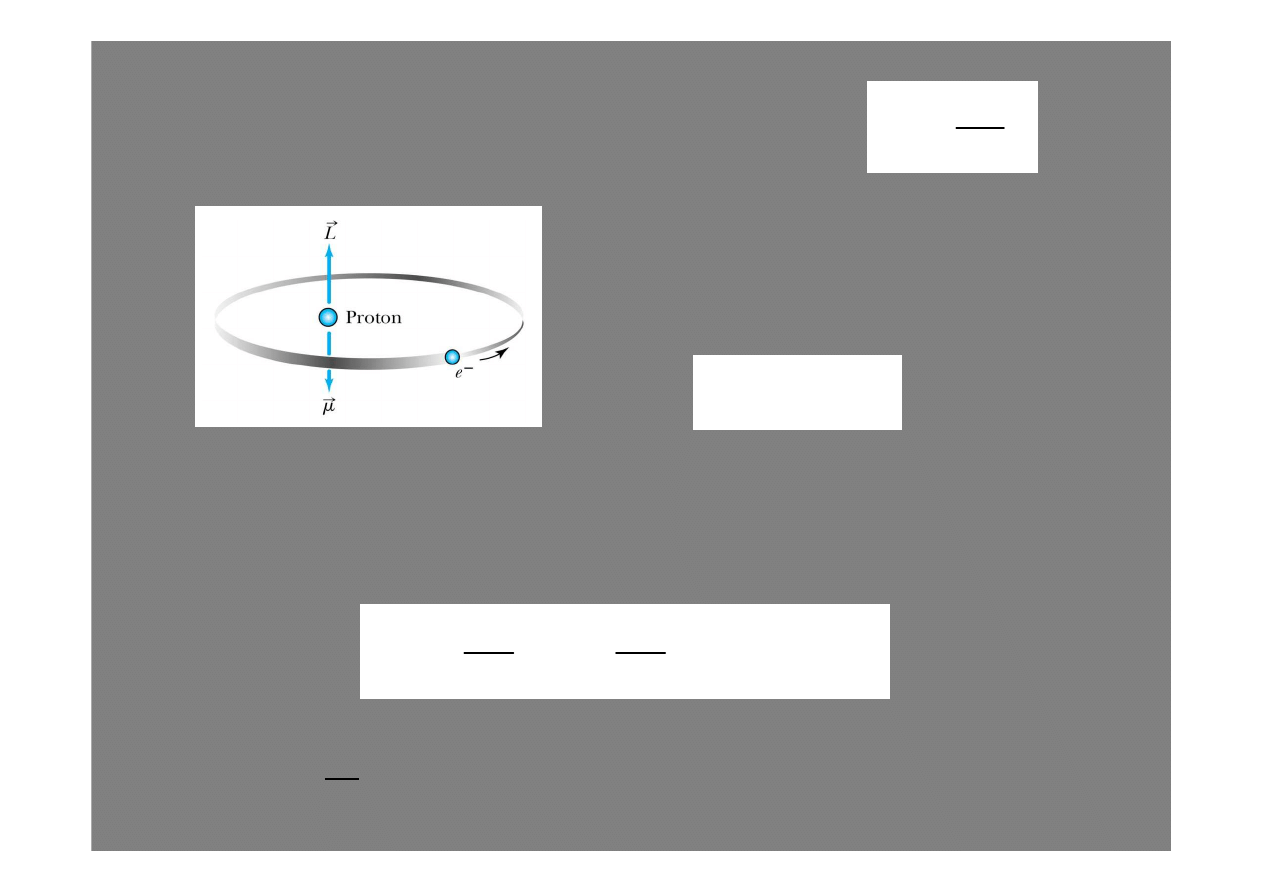
5.4: Efekt Zeemana
P
ę
tla z pr
ą
dem ma moment magnetyczny :
Nukleon
2
e
L
m
µ
= −
gdzie
L = mvr
jest
wielko
ś
ci
ą
orbitalnego
momentu p
ę
du
µ
= IA =
− /
2.
.
2
=
−
2
/
Je
ś
li pole magnetyczne ma tylko składow
ą
z
, to i moment
magnetyczny
µ
ma tylko składow
ą
z
:
gdzie
9
:
=
1ħ
inazywa si
ę
magnetonem Bohra
Energia potencjalna pola
magnetycznego jest równa:
Efekt Zeemana
(
)
2
2
z
z
B
e
e
L
m
m
m
m
µ
µ
= −
= −
= −
ℓ
ℓ
ℏ
2
e
L
m
µ
= −
B
V
B
⋅
−
=
µ
B
z
B
V
B
m B
µ
µ
= −
= −
ℓ
Efekt Zeemana
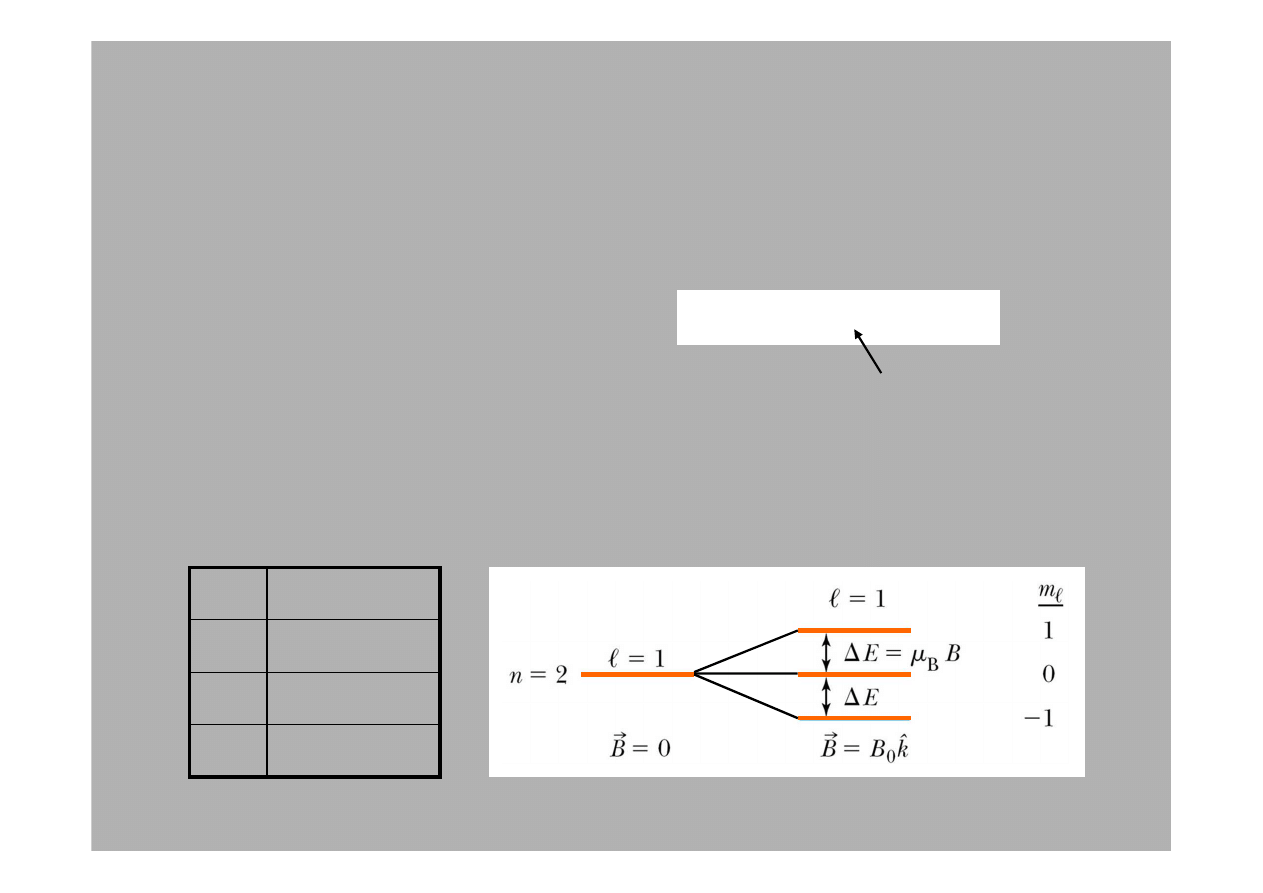
Widzimy,
ż
e pole magnetyczne
rozszczepia poziomy
m
ℓ
.
Energia potencjalna jest
skwantowana i równie
ż
zale
ż
y
od magnetycznej liczby
kwantowej
m
ℓ
.
m
ℓ
Energia
1
E
0
+
µ
B
B
0
E
0
−1
E
0
−
µ
B
B
Aby rozwi
ą
za
ć
równanie
Schrödingera z polem
magnetycznym trzeba wprowadzi
ć
nowy człon do energii:
Po przyło
ż
eniu pola magnetycznego, poziom 2p atomu wodoru
ulega rozszczepieniu na trzy poziomy o ró
ż
nej energii oddalone od
siebie o
∆
E =
µ
B
B
∆
m
ℓ
.
z
B
m
µ
µ
= −
ℓ
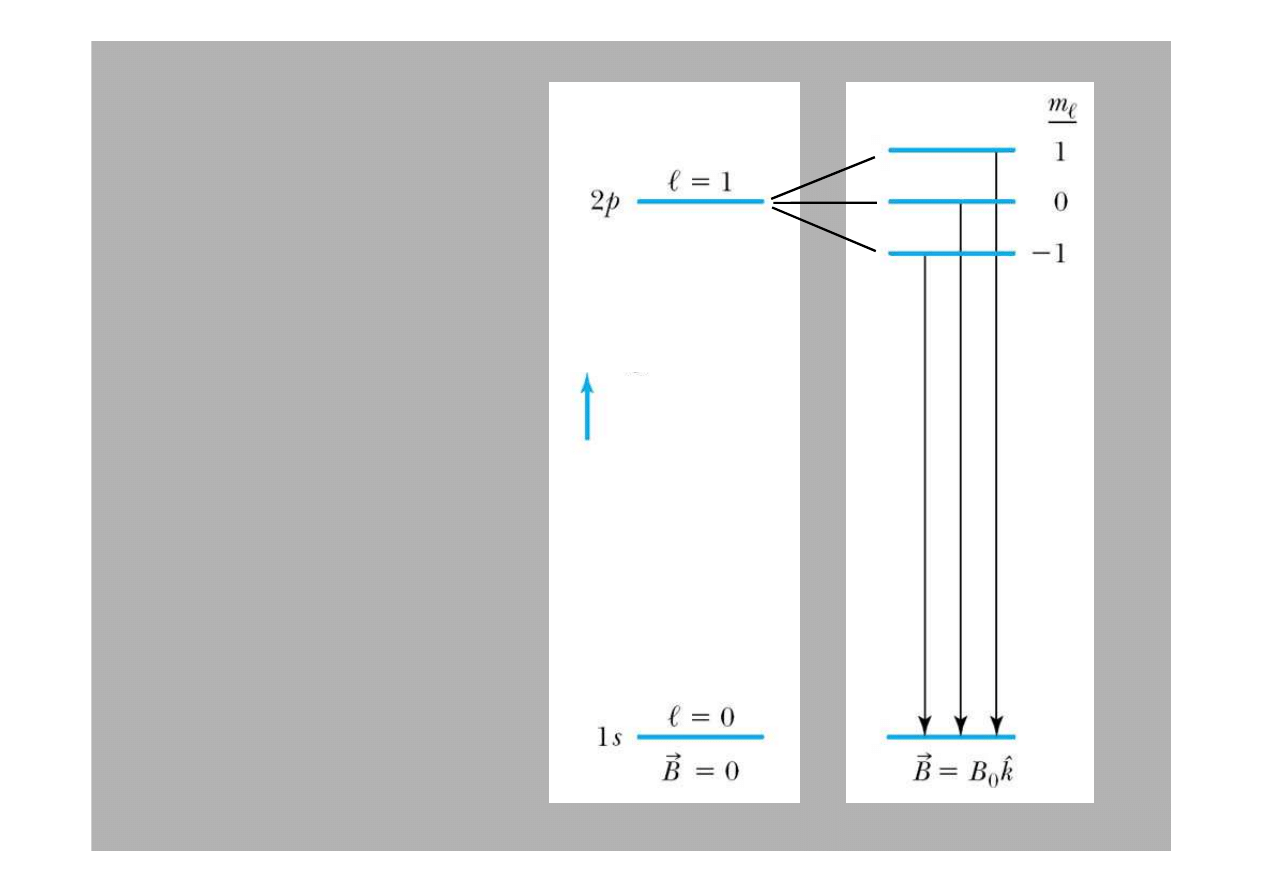
Efekt
Zeemana
Poziomy
przej
ś
cia z 2p
do 1s, równie
ż
ulegaj
ą
rozszczepieniu
przez pole
magnetyczne
Energia
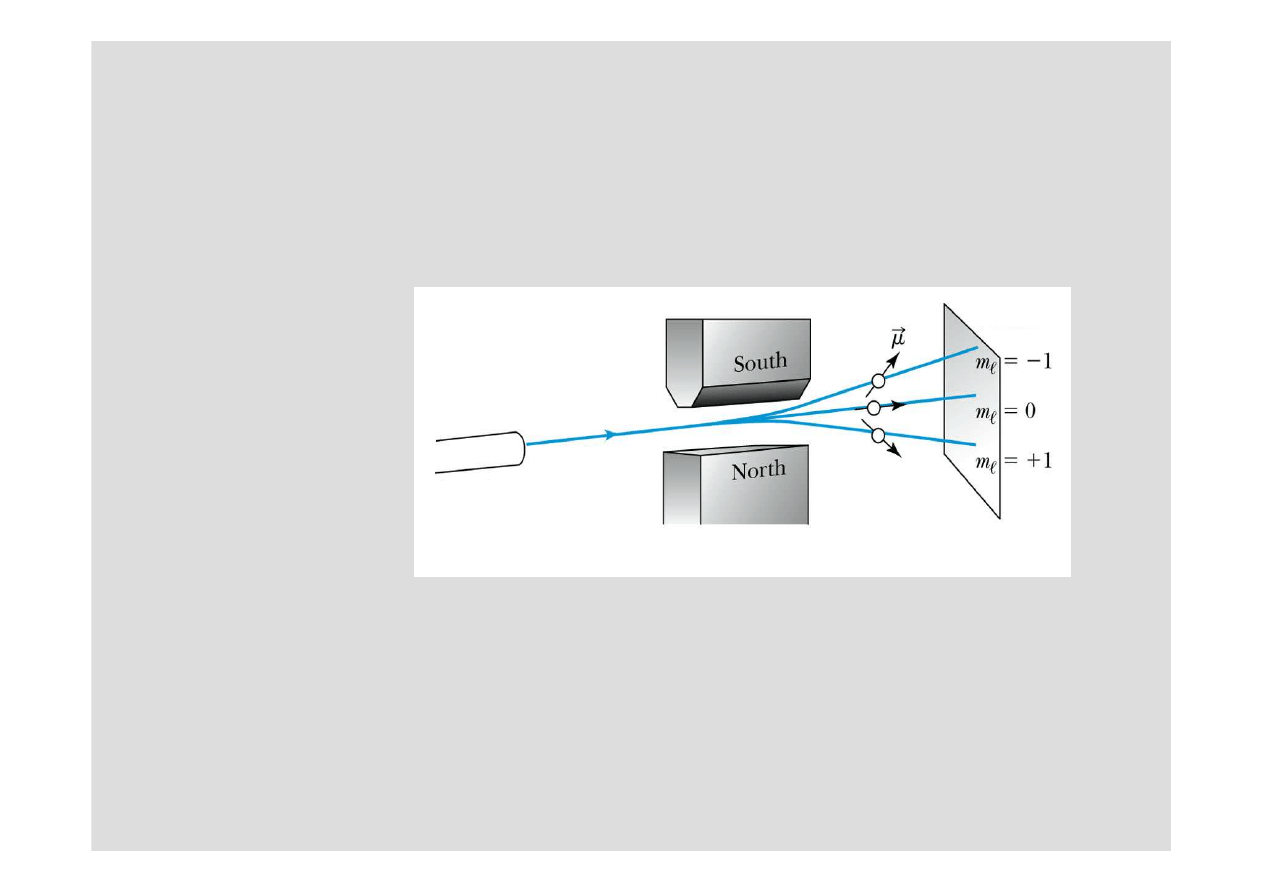
Wi
ą
zka atomów w stanie
ℓ
= 1 przechodzi przez
niejednorodne
pole
magnetyczne skierowane w kierunku osi
z
.
Eksperyment Sterna Gerlacha
Stan o
m
ℓ
= +1 b
ę
dzie odchylany w dół, stan
m
ℓ
= −1 w gór
ę
, a stan
m
ℓ
= 0 nie b
ę
dzie odchylany.
(
/
)
(
/
)
(
/
)
z
B
z
B
F
dV
dz
dB dz
m dB dz
µ
µ
= −
=
= −
ℓ
B
z
V
B
µ
= −
atomy p
ź
ródło
atomów
ekran
5.5: Spin
W 1925, holenderscy doktoranci
Samuel Goudsmit i George Uhlenbeck,
zapostulowali,
ż
e
elektrony musz
ą
mie
ć
wewn
ę
trzny moment p
ę
du
a, co za tym idzie i moment magnetyczny.
Nie byłoby z tym problemu gdyby nie obliczenia Paula
Ehrenfesta, który pokazał,
ż
e powierzchnia takiego elektronu
musiałaby wirowa
ć
z pr
ę
dko
ś
ci
ą
nad
ś
wietln
ą
!
Aby wyja
ś
ni
ć
obserwacje eksperymentalne, Goudsmit i
Uhlenbeck zaproponowali
ż
e
elektrony musz
ą
mie
ć
wewn
ę
trzn
ą
spinow
ą
liczb
ę
kwantow
ą
s = ½
.
S
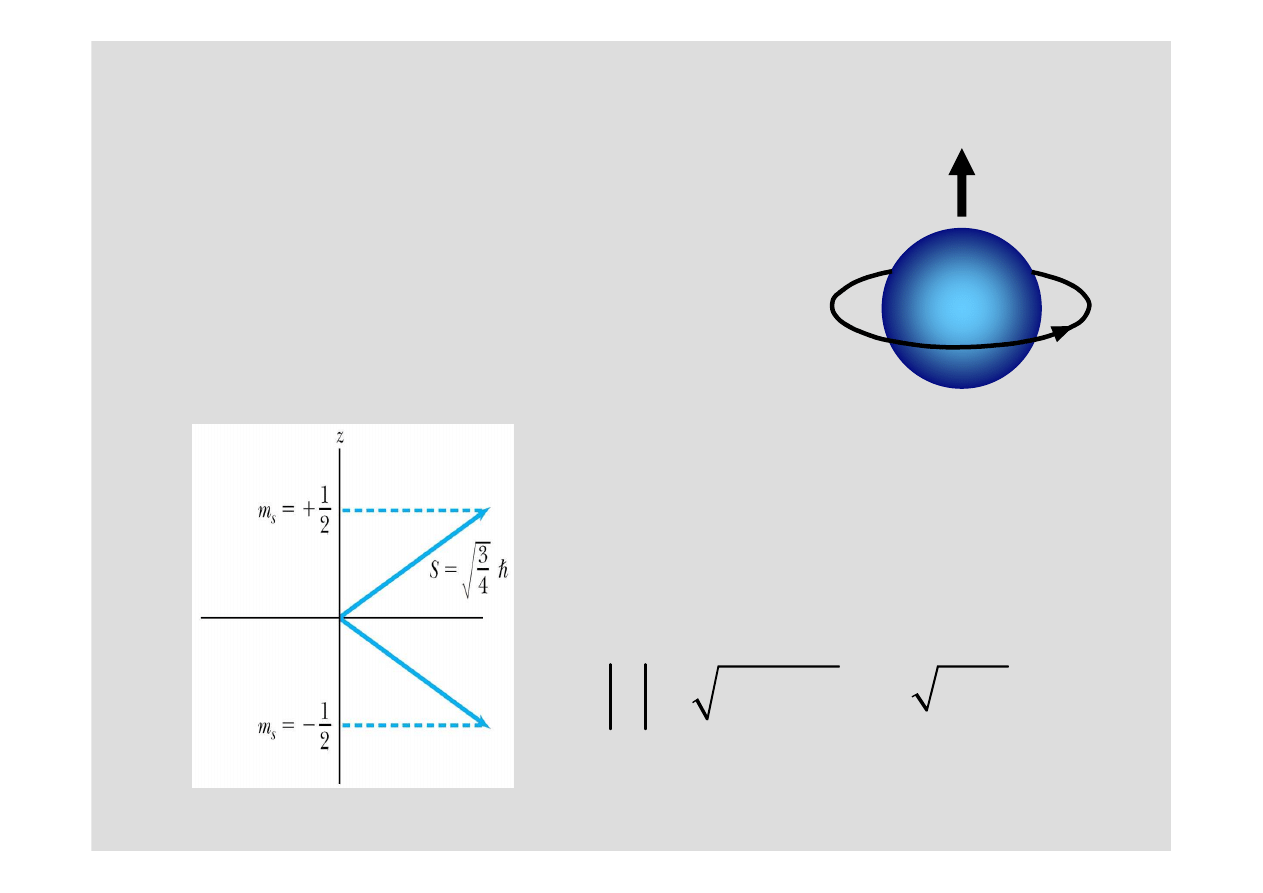
Spin
Elektron obdarzony spinem reaguje na pole
magnetyczne podobnie jak elektron orbitalny.
Magnetyczna spinowa liczba kwantowa
m
s
mo
ż
e przyjmowa
ć
tylko dwie warto
ś
ci,
m
s
=
±
½
.
Podobnie jak dla
&
, równie
ż S
z
= m
s
ħ.
Spin elektronu jest albo „do góry” (
m
s
= +½
)
albo „w dół” (
m
s
=
−
½
) lecz
nigdy
jego cały
moment magnetyczny
µ
S
nie jest
skierowany wzdłu
ż
osi
z
, gdy
ż
S
(
1)
3 / 4
S
s s
=
+
=
ℏ
ℏ
Notacja bra-ket dla atomu wodoru
Za pomoc
ą
notacji bra-ket mo
ż
emy łatwo i skrótowo zapisa
ć
dany
stan atomu wodoru. Jako,
ż
e liczby
n, ℓ, m
ℓ
,
i
m
s
całkowicie
determinuj
ą
stan kwantowy, mo
ż
emy zapisa
ć
stan atomu jako:
s
n m m
s
n m m
ψ
=
ℓ
ℓ
ℓ
ℓ
Nie ma potrzeby zapisywania wielko
ś
ci spinu
s
, gdy
ż
ona zawsze
jest dla elektronów równa ½.
Szczególna posta
ć
funkcji falowej okre
ś
lona przy pomocy funkcji w
wielu przypadkach nie jest istotna i mo
ż
na j
ą
pomin
ąć
.
W notacji bra-ket mo
ż
emy równie
ż
zapisa
ć
funkcj
ę
zespolenie
sprz
ęż
on
ą
:
*
s
n m m
s
n m m
ψ
=
ℓ
ℓ
ℓ
ℓ
Ile wynosz
ą S
x
i
S
y
?
Mechanika kwantowa mówi,
ż
e
niezale
ż
nie jak by
ś
my si
ę
starali to nie
mo
ż
emy ich jednoczesnie zmierzy
ć
!
Je
ś
li by si
ę
to nam udało,
uzyskaliby
ś
my ±
½ ħ
, tak jak dla
S
z
.
Ale wtedy ten pomiar zaburzyłby
pomiar
S
z
, która to wielko
ść
pozostałaby nieznana!
S
Całkowity spin jest
,
wi
ę
c byłoby kusz
ą
ce stwierdzenie,
ż
e ka
ż
da współrz
ę
dna
elektronu jest albo „do góry” (
+½ ħ
) albo „w dół” (
m
s
=
−
½ ħ
).
Ale tak nie jest! Te składowe s
ą
niemo
ż
liwe do wyznaczenia.
Jak dalej zobaczymy, nieokre
ś
lono
ść
ka
ż
dej z tych pozostałych
składowych jest równa ich maksymalnej mo
ż
liwej amplitudzie
(
½ ħ
)!
2
2
2
1
1
1
2
2
2
(
1)
3 / 4
( )
( )
( )
S
s s
=
+
=
=
+
+
ℏ
ℏ
ℏ
5.6: Uogólniona zasada nieokre
ś
lono
ś
ci
Zdefiniujmy komutator dwu operatorów
A
i
B
:
[
]
,
A B
AB
BA
≡
−
Je
ś
li
<, : = 0
to mówimy,
ż
e
<
i
:
komutuj
ą
z sob
ą
. Uogólniona
zasada nieokre
ś
lono
ś
ci pomi
ę
dzy obserwablami
<
i
:
ma posta
ć
:
[
]
*
1
2
,
A B
A B
∆ ∆ ≥
Ψ
Ψ
∫
Gdzie
∆<
i
∆:
s
ą
nieokre
ś
lono
ś
ciami tych obserwabli. Je
ś
li
<
i
:
komutuj
ą
z sob
ą
, to odpowiadaj
ą
ce im wielko
ś
ci fizyczne mo
ż
na
mierzy
ć
jednocze
ś
nie. W przeciwnym wypadku nie mo
ż
na.
Przykład:
ɵ
ɵ
ɵ
(
)
( )
,
p x
p x
x p
i
x
x
i
x
x
x
i
i x
x
i
i
x
x
x
∂
∂
Ψ ≡
−
Ψ = −
Ψ − −
Ψ
∂
∂
∂
∂Ψ
∂Ψ
= −
Ψ −
− −
= − Ψ
∂
∂
∂
ℏ
ℏ
ℏ
ℏ
ℏ
ℏ
ɵ
,
p x
i
= −
ℏ
czyli:
/ 2
p x
∆ ∆ ≥
ℏ
wi
ę
c:
Zasada
nieokre
ś
lono
ś
ci
Heisenberga

Nieokre
ś
lono
ść
momentu p
ę
du i spinu
Jak ju
ż
widzieli
ś
my, całkowity moment p
ę
du, jego
>
-ta składowa i spin
mog
ą
by
ć
mierzone jednocze
ś
nie. Z kolei
?
-owa i
@
-owa składowe nie
mog
ą
. Oto dlaczego. Okazuje si
ę
,
ż
e:
,
x
y
z
L L
i L
=
ℏ
[
]
*
1
2
,
A B
A B
∆ ∆ ≥
Ψ
Ψ
∫
Korzystaj
ą
c z:
Widzimy,
ż
e:
2
*
*
1
1
2
2
(
)
2
L
x
y
z
L
m
L
L
i L
i m
∆ ∆
≥
Ψ
Ψ =
Ψ
Ψ =
∫
∫
ℏ
ℏ
ℏ
ℏ
A zatem uzyskali
ś
my zasad
ę
nieokre
ś
lono
ś
ci pomi
ę
dzy
?
-ow
ą
i
@
-
ow
ą
składow
ą
momentu p
ę
du (o ile
≠ 0
). Taka sama zasada
obowi
ą
zuje dla pozostałych par składowych oraz dla spinu.
,
x
y
z
S S
i S
=
ℏ
i

Dwa rodzaje nieokre
ś
lono
ś
ci w
mechanice kwantowej
1. Niektóre wielko
ś
ci, mog
ą
by
ć
zmierzone z dowoln
ą
precyzj
ą
ale
ich pomiar zaburza pomiar innych, np.
B
i
+
,
"
i
?
,
L
x
i
L
y,
, S
x
i
S
y
.
Je
ś
li zmierzymy precyzyjnie jedn
ą
wielko
ść
to zasada
nieokre
ś
lono
ś
ci nie pozwoli nam zmierzy
ć
dokładnie drugiej,
która z ni
ą
nie komutuje. Na przykład, energi
ę
mo
ż
na zmierzy
ć
jedynie z dokładno
ś
ci
ą
ħ /2
∆
t
, gdzie
∆
t
jest czasem naszego
pomiaru, bo
CBC+ ≥
%
⁄
.
2. Jest jeszcze jeden rodzaj nieokre
ś
lono
ś
ci zwi
ą
zany z
nierozró
ż
nialno
ś
ci
ą
obiektów kwantowych o tych samych
zestawach liczb kwantowych. Według tej zasady, je
ś
li dwa
obiekty s
ą
w dokładnie tym samym stanie kwantowym – maj
ą
identyczne zestawy liczb kwantowych, np.:
|G
H
I
H
ℓH
JH
〉 =
|G I
ℓ
J
〉
to
ich rozró
ż
nienie jest niemo
ż
liwe
.
Wszystkie atomy w stanie podstawowym s
ą
nierozró
ż
nialne.
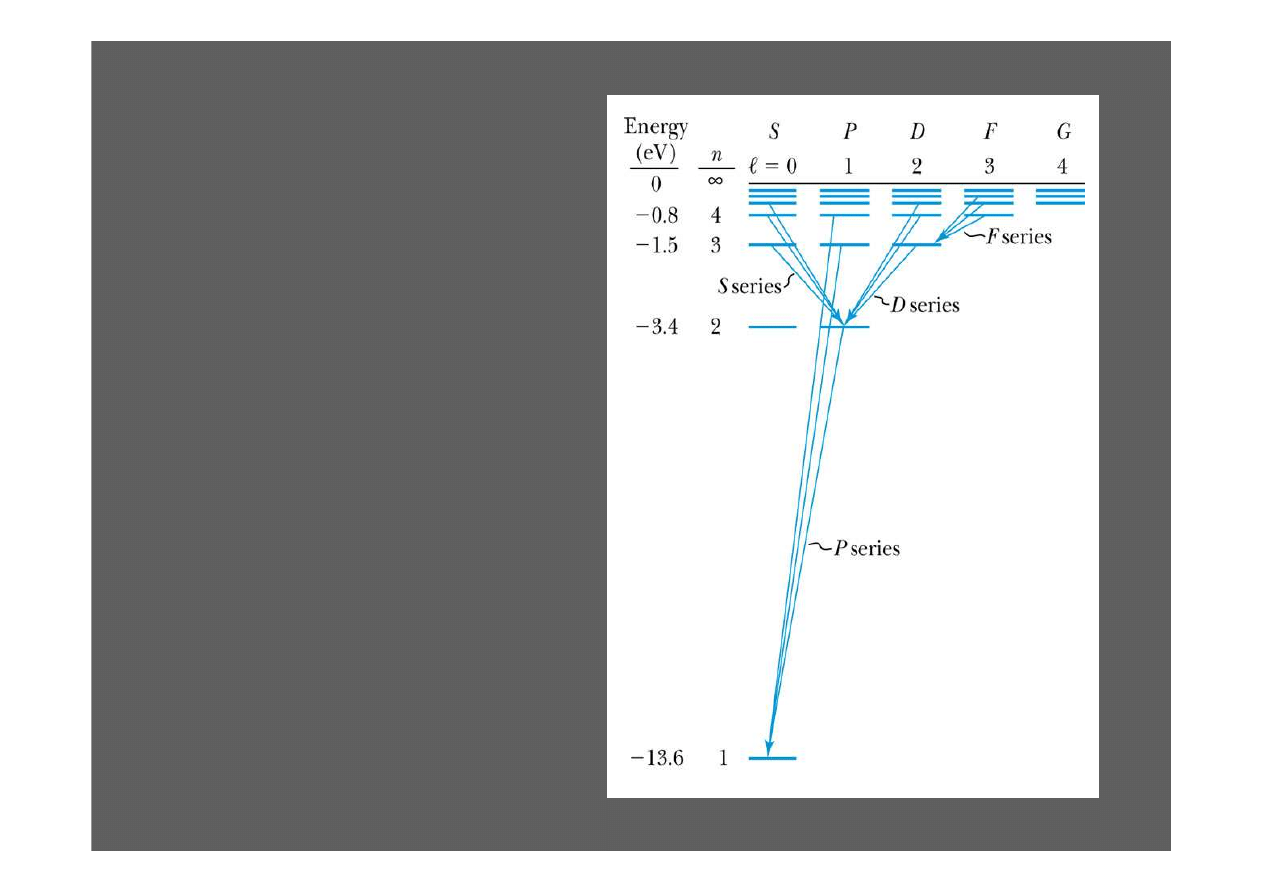
5.7: Prawdo-
podobie
ń
stwa
przej
ść
. Reguły
wyboru
Poziomy energetyczne
(bez pola magnetycznego)
zale
żą
od głównej liczby
kwantowej
n
.
Elektrony mog
ą
przechodzi
ć
z dowolnego stanu
n
na
dowolny inny.
Jakie znaczenie maj
ą
tu
pozostałe liczby kwantowe
ℓ
i
m
ℓ
?

Reguły wyboru
Prawdopodobie
ń
stwo jest
proporcjonalne do
ś
redniego
momentu dipolowego
Dopuszczalne przej
ś
cia:
Electrony absorbuj
ą
c lub emituj
ą
c fotony mog
ą
zmienia
ć
swój
stan tak aby
∆
ℓ =
±
1
oraz
∆
m
ℓ
= 0,
±
1
.
Przej
ś
cia zabronione:
Inne przej
ś
cia s
ą
mo
ż
liwe lecz
du
ż
o mniej prawdopodobne
∆G = dowolne
∆I = ±1
∆
Q
= 0, ±1
*
k
p
d
er
= Ψ
Ψ
∫
Aby obliczy
ć
prawdopodobie
ń
stwa
przej
ś
cia elektronu z jednego
stanu do innego mo
ż
na
wykorzysta
ć
funkcj
ę
falowe
gdzie
Ψ
p
oraz
Ψ
k
s
ą
pocz
ą
tkowym i
ko
ń
cowym stanem
elektronu
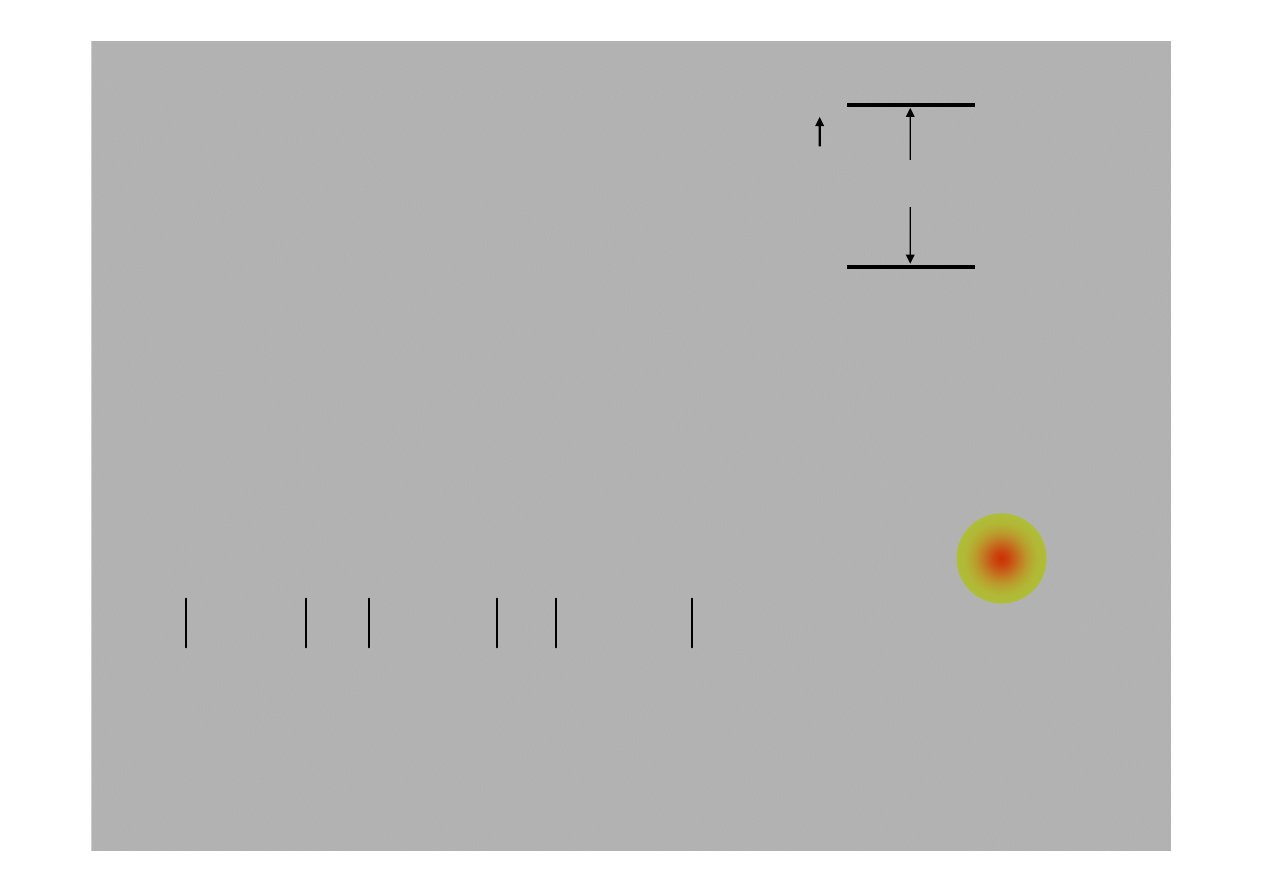
5.8: Superpozycja stanów
Atom mo
ż
e by
ć
w stanie stacjonarnym ale
mo
ż
e te
ż
by
ć
w stanie zwanym
superpozycj
ą
(sum
ą
) stanów stacjonarnych. B
ę
d
ą
c w stanie
superpozycji atom
porusza si
ę
…
1
1
1
2
2
2
( , )
( ) exp(
/ )
( ) exp(
/ )
r t
a
r
iE t
a
r
iE t
ψ
ψ
Ψ
=
−
+
−
ℏ
ℏ
2
2
2
1
1
2
2
*
*
1
1
2
2
2
1
( , )
( )
( )
2 Re[
( )
( )]cos[(
) / ]
r t
a
r
a
r
a
r a
r
E
E t
ψ
ψ
ψ
ψ
Ψ
=
+
+
−
ℏ
gdzie
|a
i
|
2
jest prawdopodobie
ń
stwem,
ż
e atom
znajduje si
ę
w stanie
i
.
Ciekawe jest,
ż
e prawdopodobie
ń
stwo znalezienia
atomu a takim stanie oscyluje w czasie:
E
n
e
rg
ia
E
1
stan
podstawowy
E
2
stan
wzbudzony
∆
E = h
ν
Oscylacje maj
ą
cz
ę
sto
ść
proporcjonaln
ą
do ró
ż
nicy energii stanów
stacjonarnych.
Wyszukiwarka
Podobne podstrony:
ATOM WODORU
9 atom wodoru
Atom Wodoru
06 Atom wodoruid 6249 Nieznany (2)
atom wodoru zadania
FIZA-2~1, Atom wodoru, Atom wodoru, f
atom wodoru II
Atom wodoru według Bohra
ATOM WODORU
Atom wodoru
ATOM WODORU
W 5 ATOM
W03 Orbitale wodoru
W Orbitale wodoru
atom Ih, chemia
więcej podobnych podstron