Budowa atomów
atom wodoru
atomy wieloelektronowe
zakaz Pauliego
układ okresowy pierwiastków
Budowa atomu wodoru
atom wodoru składa się z pojedynczego elektronu (-e)
związanego z jądrem – protonem (+e) przyciągającą siła
elektrostatyczną
rozmiary jądra – 10
-14
m
rozmiary atomu rzędu 10
-10
m
masa protonu = 1836 masy elektronu swobodnego
klasycznie energia elektronu przyjmuje dowolne wartości – w
rzeczywistości jest skwantowana
przy ruchu po orbicie elektron powinien tracić energię przez
promieniowanie i poruszając się po spirali spaść na jądro – w
rzeczywistości energia się nie zmienia
eksperyment Rutherforda
rok 1911
Równanie Schrodingera dla
atomu wodoru
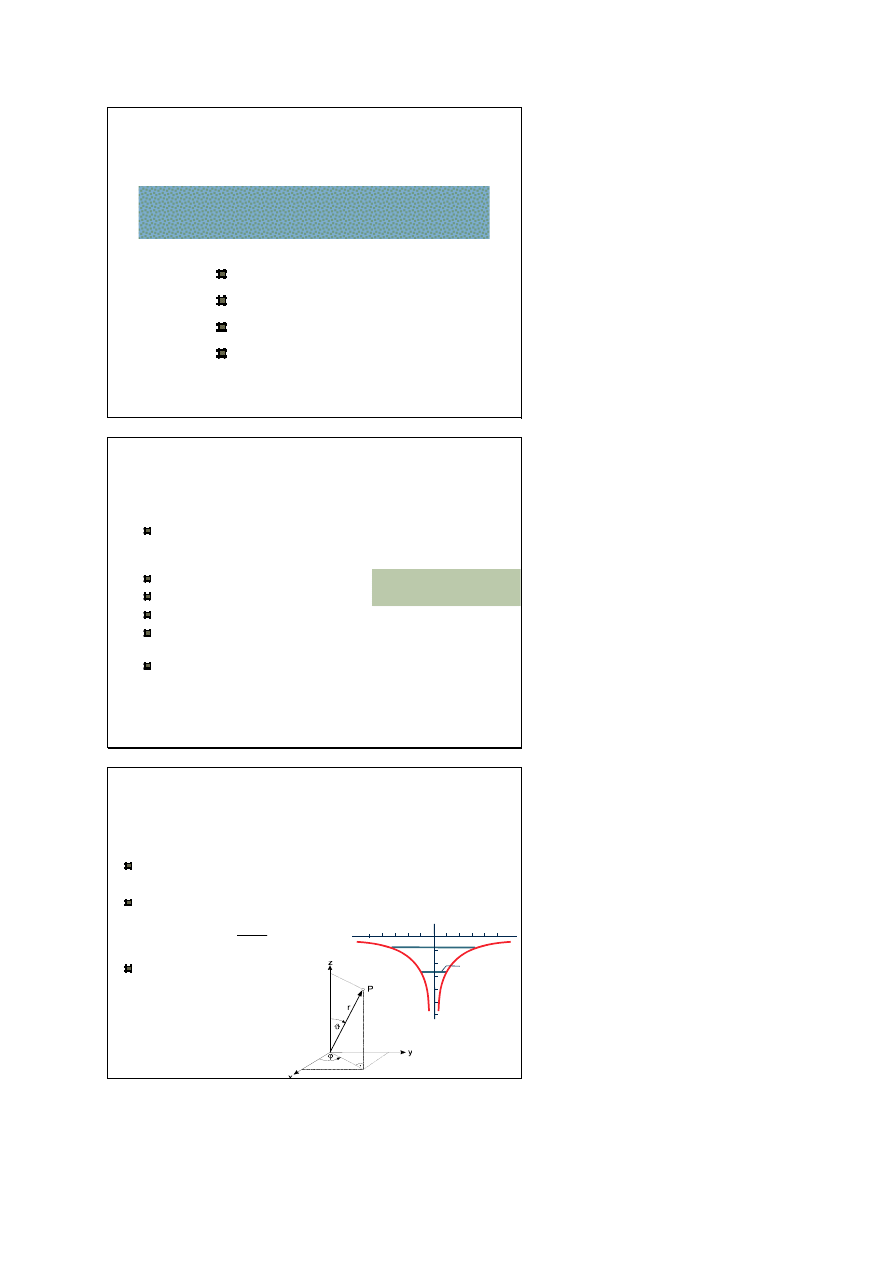
atom wodoru jest swego rodzaju studnią potencjału (naturalną
pułapką) dla elektronu
energia potencjalna oddziaływania elektron-jądro jest postaci
potencjał ma symetrię sferyczną
więc musimy wprowadzić
sferyczny układ współrzędnych
( )
r
e
r
U
o
πε
−
=
4
2
ϑ
=
ϕ
ϑ
=
ϕ
ϑ
=
cos
sin
sin
cos
sin
r
z
r
y
r
x
4
2
0
2
4
r[Å]
-10
-30
U[eV]
stan
podstawowy
r[Å]
(
)
Ψ
−
−
=
∂
Ψ
∂
+
∂
Ψ
∂
+
∂
Ψ
∂
U
E
m
z
y
x
2
2
2
2
2
2
2
2
h
Ψ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
πε
+
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂ϕ
Ψ
∂
ϑ
+
⎟
⎠
⎞
⎜
⎝
⎛
∂ϑ
Ψ
∂
ϑ
∂ϑ
∂
ϑ
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
∂
∂
r
e
E
m
r
r
r
r
r
o
4
2
1
1
1
1
2
2
2
2
2
2
2
2
h
sin
sin
sin
0
4
2
1
2
2
2
2
=
Ψ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
πε
+
+
⎟
⎠
⎞
⎜
⎝
⎛
Ψ
r
e
E
m
dr
d
r
dr
d
r
o
h
(
)
ϕ
ϑ
Ψ
,
,
r
(
)
( ) ( ) ( )
ϕ
Φ
ϑ
Θ
=
ϕ
ϑ
Ψ
r
R
r ,
,
podstawiając tą funkcję do równania Schrodingera otrzymujemy
trzy równania z których każde opisuje zachowanie się funkcji falowej
w zależności od r,
ϑ, ϕ - równanie radialne, biegunowe i azymutalne
Rozpatrzmy najprostszy przypadek, gdy
Ψ jest tylko funkcją r
tzn. żaden kierunek w przestrzeni nie jest wyróżniony – stan s
( )
o
r
r
o
e
r
/
−
Ψ
=
Ψ
Funkcja spełniająca to równanie to:
Równanie Schrodingera dla
przypadku trójwymiarowego i
we współrzędnych sferycznych
Prawdopodobieństwo znalezienia elektronu w
elemencie objętości
dr
r
dV
2
4
π
=
( )
dr
e
r
dr
r
r
dV
P
o
o
r
r
2
2
2
2
2
4
4
Ψ
π
=
π
Ψ
=
−
/
Fizyczna
interpretacja
wyrażenia na r
o
i E są identyczne jak w modelu Bohra
kwantyzacja wynikiem rozwiązania równania Schrodingera, a nie
postulatem jak u Bohra
r
o
to nie promień orbity, lecz odległość od jądra przy której
prawdopodobieństwo znalezienia się elektronu jest największe
przyjęcie klasycznej orbity traci sens
dla rozpatrywanego stanu s moment pędu jest równy zeru
w ogólności moment pędu nie jest równy lecz
osiąga maksimum dla r = r
o
h
n
(
)
h
1
+
=
l
l
L
Dokładne rozwiązanie równania
Schrodingera
rozwiązaniem równania biegunowego jest funkcja postaci
m
l
=0, 1, 2.., l
( )
ϕ
Φ
=
ϕ
Φ
l
im
o
e
rozwiązanie równania radialnego istnieje jeśli energia elektronu
przyjmuje ściśle określone wielkości
2
2
2
2
4
1
32
n
me
n
E
o
⋅
ε
π
−
=
h
( )
r
R
l
n,
n – całkowita liczba dodatnia
rozwiązaniem równania azymutalnego są tzw. wielomiany Legendre’a
( )
(
)
( )
ϑ
=
=
ϑ
=
ϑ
Θ
cos
;
.
cos
0
1
0
0
1 P
P
np
P
l
m
l
l – całkowita liczba dodatnia
Orbitalny moment pędu elektronu
z rozwiązania równania kątowego wynika, że wartość L
orbitalnego momentu pędu elektronu w atomie jest
skwantowana
liczba całkowita l to orbitalna liczba kwantowa
rzut momentu pędu na wyróżniony kierunek (z) jest
również skwantowany
liczba m
l
to magnetyczna liczba kwantowa
wektora L nie można w żaden sposób zmierzyć, możemy
jedynie zmierzyć składową tego wektora wzdłuż danej osi
np. określonej przez pole magnetyczne
(
)
h
1
+
=
l
l
L
l = 0, 1, 2
h
l
z
m
L =
l
m
l
≤
m
l
=0, 1, 2.., l
elektron porusza się po orbicie kołowej
droga przebyta przez elektron
więc jego funkcja falowa jest postaci
z jednoznaczności funkcji falowej
otrzymujemy warunek kwantyzacji L
z
długość orbity równa całkowitej wielokrotności
λ,
fale nie wygaszają się – orbita dozwolona
= 6
h
Falowa interpretacja kwantyzacji
momentu pędu elektronu
k
r
L
z
r
p
h
=
=
ϕ
r
s =
( )
ϕ
ϕ
ikr
o
iks
o
e
e
Ψ
=
Ψ
=
Ψ
( )
(
)
π
+
ϕ
Ψ
=
ϕ
Ψ
2
)
(
π
+
ϕ
ϕ
Ψ
=
Ψ
2
ikr
o
ikr
o
e
e
1
2
=
π
ikr
e
l
m
kr =
h
l
z
m
L =
r
p
r
r
r
L
z
(
)
h
1
+
=
l
l
L
l
m
l
≤
m
l
=0, 1, 2.., l
r
m
l
π
λ
2
=
z
Liczby kwantowe
główna liczba kwantowa
n = 1, 2, 3,...
określa możliwe wartości energii
orbitalna (poboczna) liczba kwantowa l = 0, 1, 2,....n-1
określa momentu pędu (kształt powłoki)
magnetyczna liczba kwantowa
m
l
= -l, -l+1,..,-1, 0, 1,....,l-1,l
określa składowe momentu pędu
dla danej wartości n liczba możliwych l i m
l
, czyli
liczba niezależnych rozwiązań równania Schrodingera
odpowiadająca jednej wartości energii wynosi
(
)
2
1
0
1
2
n
l
n
l
=
+
∑
−
=
stan jest n
2
-krotnie zwyrodniały
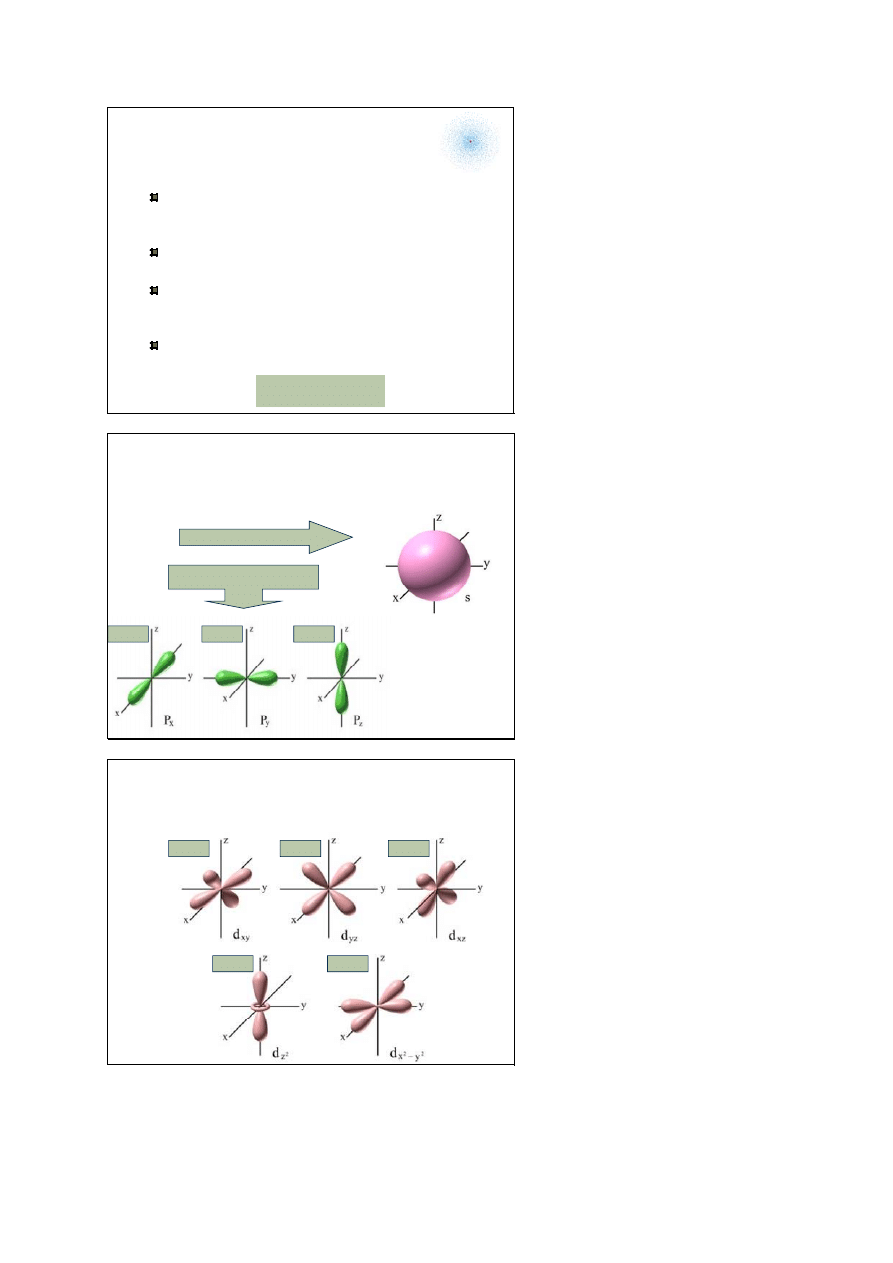
Orbital atomowy
orbital atomowy to funkcja falowa
Ψ opisująca
stan elektronu w atomie zależna od trzech liczb
kwantowych: n, l, m
|
Ψ|
2
dV – określa prawdopodobieństwo znalezienia
się elektronu w elemencie objętości dV
obszar w którym występuje duże
prawdopodobieństwo znalezienia się elektronu
nazywa się chmurą elektronową
każdy orbital atomowy jest związany z pewną
symetrią obszaru, w którym znajduje się elektron
orbitale: s, p, d, f, g, ....
l = 0, 1, 2, 3, 4,....
Orbitale s i p
orbital s (1,0,0)
orbitale p
(2,1,0)
(2,1,-1)
(2,1,1)
Orbitale d
(3,2,0)
(3,2,2)
(3,2,-2)
(3,2,-1)
(3,2,1)
Orbitalny moment magnetyczny
płaska ramka z prądem posiada moment magnetyczny
elektron krążący po orbicie kołowej też posiada tzw.
orbitalny moment pędu
elektron w atomie ma także moment pędu, zwany
orbitalnym (choć nie krąży), oraz towarzyszący mu
orbitalny moment magnetyczny
S
I
r
r
⋅
=
μ
L
m
e
p
r
m
e
l
r
r
r
r
2
2
−
=
×
−
=
μ
(
)
(
)
1
1
2
2
+
μ
−
=
+
−
=
−
=
μ
l
l
l
l
m
e
L
m
e
B
l
h
2
24
10
27
9
2
Am
m
e
B
−
×
=
=
μ
.
h
magneton Bohra – jednostka atomowego
momentu magnetycznego
Zjawisko Zeemana
B
m
Bm
m
e
B
U
l
B
l
l
μ
=
=
θ
μ
−
=
2
h
cos
Elektron w polu magnetycznym uzyskuje dodatkową energię
potencjalną, która jest skwantowana
pierwotny poziom energetyczny zostaje rozszczepiony na 2l+1
podpoziomów np. atom wodoru w stanie 2p (l=1) na 3 poziomy
⎪
⎩
⎪
⎨
⎧
−
=
×
−
=
=
×
=
−
−
1
10
27
9
0
0
1
10
27
9
24
24
l
l
l
m
J
m
m
J
U
,
,
Zjawisko Zeemana – rozszczepienie
linii widmowych w zewnętrznym
polu magnetycznym – potwierdza
skwantowanie orbitalnego momentu
pędu
2s
2p
m
l
1
0
-1
bez pola z polem
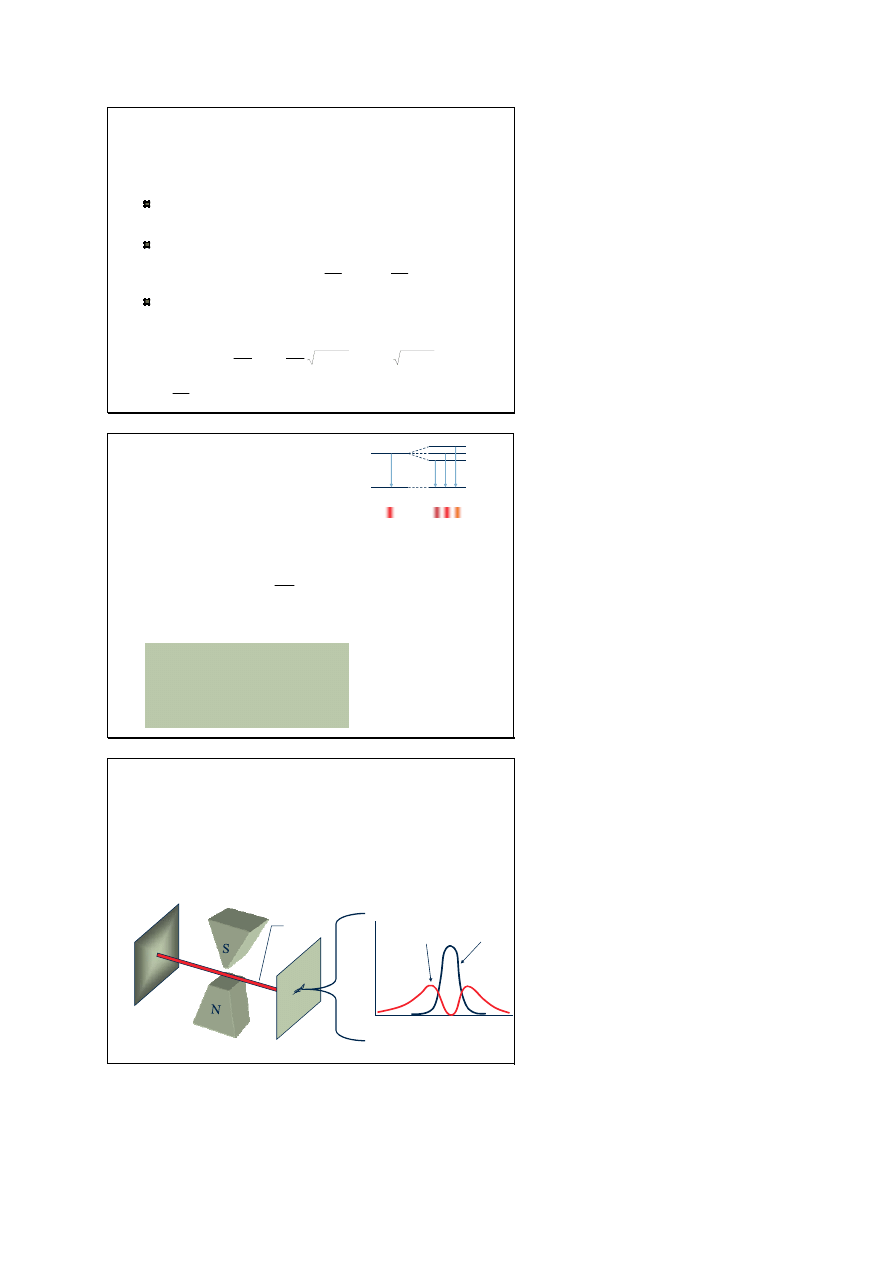
Doświadczenie Sterna-Gerlacha
W 1922 roku Stern i Gerlach badając wpływ niejednorodnego pola na
wiązkę atomów zaobserwowali jej rozszczepienie i parzystą liczbę
śladów na ekranie.
wiązka
elektromagnes
kolimator
detektor
położenie detektora
na
tęż
eni
e w
ią
zki
elektromagnes
włączony wyłączony
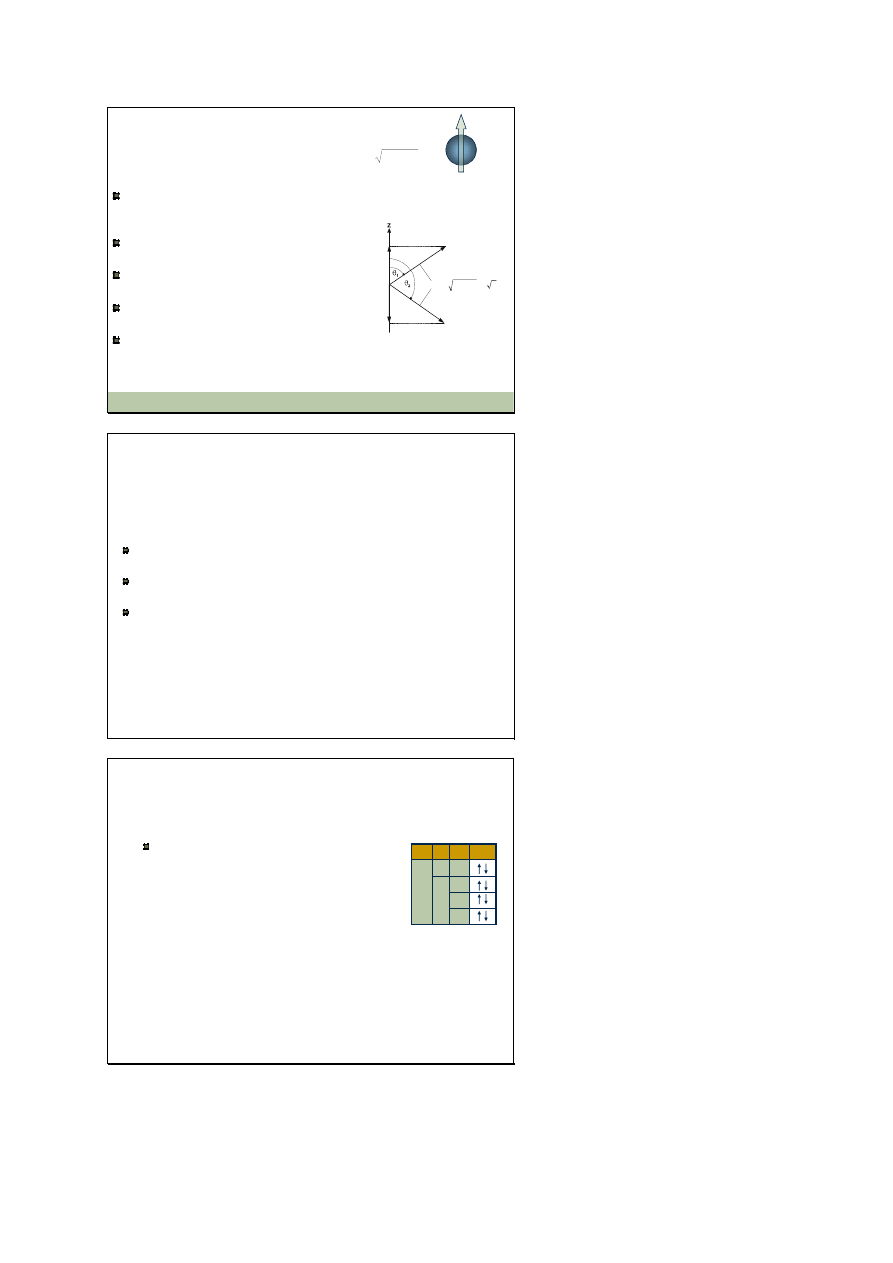
Spin elektronu
elektron charakteryzuje się własnym magnetycznym
momentem dipolowym, który związany jest z jego
spinowym momentem pędu (spinem)
choć słowo „spin” oznacza wirowanie
elektron w rzeczywistości nie wiruje
spin jest wewnętrzną własnością elektronu,
tak jak jego masa, czy ładunek elektryczny
wartość spinu jest skwantowana i zależy
od spinowej liczby kwantowej s = ½
rzut spinowego momentu pędu na wyróżniony
kierunek jest skwantowany
(
)
h
1
+
=
s
s
L
s
h
s
sz
m
L
=
m
s
= ½ lub m
s
= -½
Stan elektronu opisujemy za pomocą 4 liczb kwantowych n, l, m
l
, m
s
h/2
h/2
−
s s
=
+
=
1
3
h
h/2
( )
L
s
Atomy wieloelektronowe
Stan kwantowy n- elektronowego atomu zależy od
współrzędnych wszystkich n elektronów
Ścisłe rozwiązanie równania Schrodingera niemożliwe –
metoda przybliżona tzw. pola samouzgodnionego
Wyniki metody
opisanie stanu pojedynczego elektronu (orbital atomowy)
w atomie wieloelektronowym za pomocą jednoelektronowej
funkcji falowej
każdy orbital (funkcja jednoelektronowa ) jest określona za
pomocą zespołu liczb kwantowych n, l, m, s
elektrony obsadzające tą samą podpowłokę (stany o tej
samej liczbie n i l) mają tą sama energię
Zakaz Pauliego 1925 r
jeden orbital elektronowy (określony liczbami n,l,m)
mogą zajmować nie więcej niż dwa elektrony
n
l
m
2
0
0
1
1
0
-1
w danym stanie określonym czterema liczbami
kwantowymi (n, l, m, s
z
) może znajdować się nie więcej
niż jeden elektron
żadne dwa elektrony uwięzione w tej samej pułapce nie mogą
mieć jednakowych wszystkich liczb kwantowych
na n-tej powłoce może być N=2n
2
elektronów
rozmieszczenie elektronów odpowiada minimalnej energii
układu
liczbie kwantowej n=2 odpowiadają
cztery orbitale (2,0,0), (2,1,0), (2,1,-1),
(2,1,1) ⇒ 8 elektronów
Zasada Pauliego jest konsekwencją zasady nierozróznialności elektronów i
antysymetryczności funkcji falowej
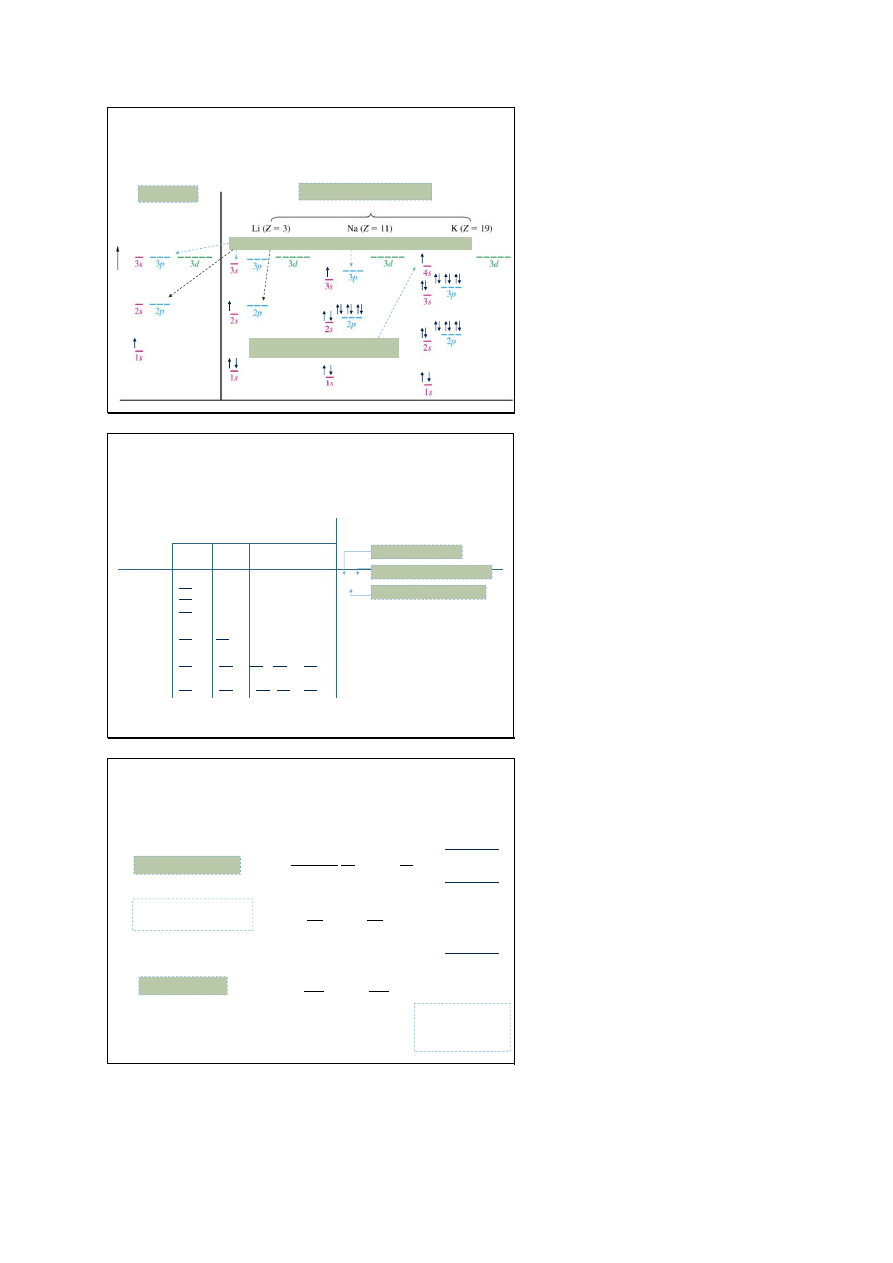
Atom wodoru,
a atomy wieloelektronowe
wodór
H (Z = 1)
atomy wieloelektronowe
dla atomów wieloelektronowych energia zależy od liczby kwantowej l
niektóre poziomy o większej liczbie n
mają mniejszą energię
En
er
g
ia
Konfiguracja elektronów
notacja orbitalna
1s
2s
2p
1
H
↑
1s
1
2
He
↑↓
1s
2
3
Li
↑↓
↑
1s
2
2s
1
[He] 2s
1
6
C
↑↓
↑↓ ↑ ↑
1s
2
2s
2
2p
2
[He] 2s
2
2p
2
8
O
↑↓
↑↓ ↑↓ ↑ ↑
1s
2
2s
2
2p
4
[He] 2s
2
2p
4
lub
orbitalna liczba kwantowa
liczba elektr. na podpowłoce
główna liczba kwant.
zapis uproszczony
Energia jonizacji atomów
energia oderwania najsłabiej związanego elektronu
eV
n
n
me
n
E
o
2
2
2
2
2
4
1
6
13
1
32
.
−
=
ε
π
−
=
h
w atomie wodoru
w atomie He
+
(wodoropodobnym)
eV
n
Z
n
Z
E
n
E
o
2
2
2
2
6
13.
−
=
−
=
E
jon
13,6 eV
54,4 eV
24,6 eV
eV
n
Z
n
Z
E
n
E
ef
ef
o
2
2
2
2
6
13.
−
=
−
=
w atomie helu
czynnik Z
2
jest związany z różnicą ładunku jądra
czynnik Z
ef
wynika z ekranowania jądra przez drugi
elektron i odpychania się elektronów
największa
energia jonizacji
wśród
pierwiastków
d
l=2
f
l=3
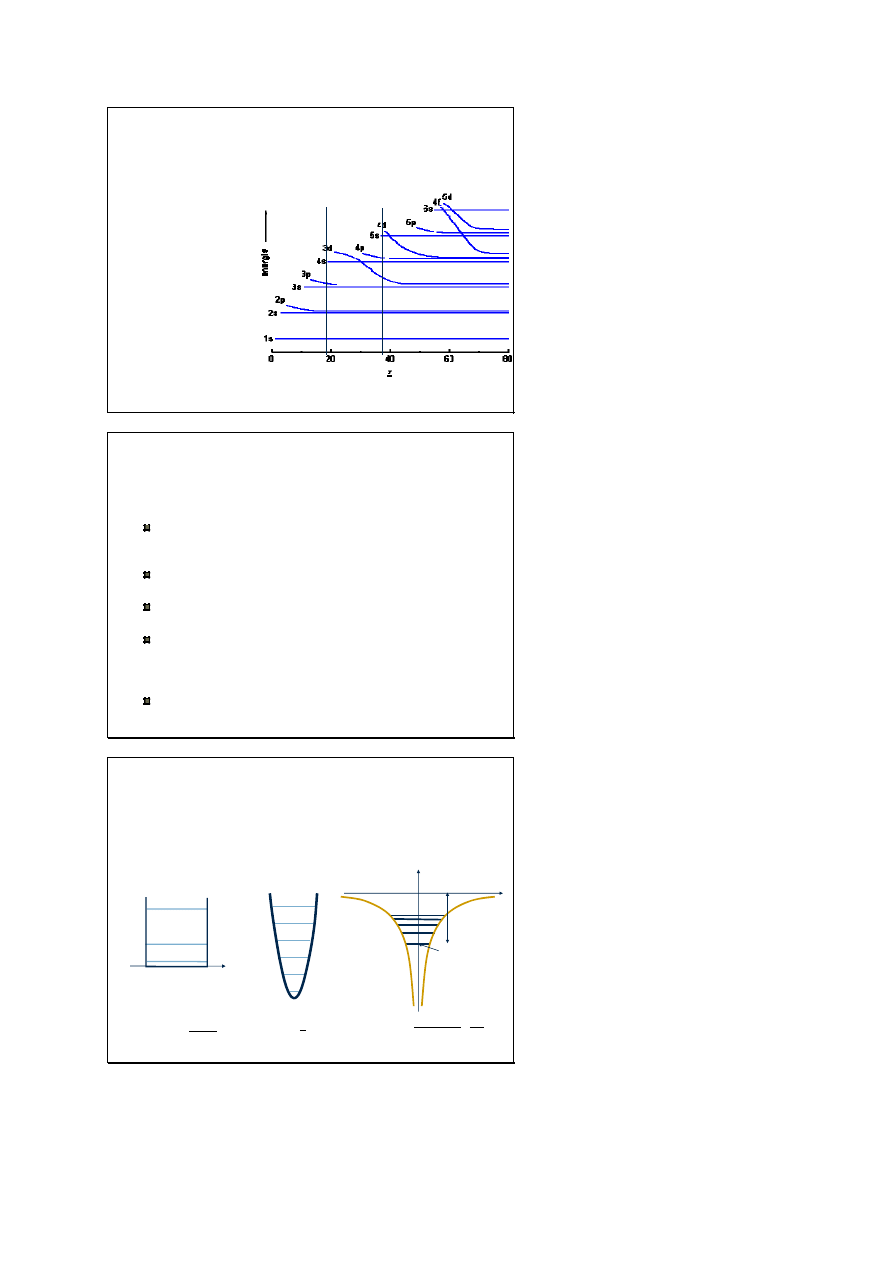
Kolejność zapełniania powłok
elektronowych
stan
n
2
3
4
5
6
10
10
10
14
14
1
p
l=1
s
l=0
6
2
2
2
2
2
6
6
6
6
2
właściwości fizyczne i chemiczne pierwiastków
zmieniają się zgodnie z kolejnością 2,8,8,18,18,32
10
liczba elektronów
Tablica Mendelejewa
Dmitrij Mendelejew ( 1871 r.) - ułożenie znanych wówczas
pierwiastków chemicznych w tablicy zwanej Układem Okresowym,
wg. wzrastających liczb atomowych
pierwiastki w pionowych kolumnach (grupach układu) miały podobne
właściwości chemiczne
fizyka kwantowa systematyzuje atomy poprzez podanie ich
konfiguracji elektronowej
numer porządkowy okresu odpowiada głównej liczbie kwantowej n
czy chemiczne właściwości pierwiastków wynikają z ich konfiguracji
elektronowej?
Konfiguracja elektronowa, a
właściwości fizyczne atomów
wodór
H: 1s
1
hel
He: 1s
2
obojętny chemicznie, gaz szlachetny
lit
Li:1s
2
2s
1
elektron 2s słabo związany, wartościowość +1
beryl
Be:1s
2
2s
2
podobny do litu, wartościowość +2
od boru (Z=5)
B: 1s
2
2s
2
2p
1
do neonu (Z=10)
Ne:
1s
2
2s
2
2p
6
elektrony zapełniają powłokę 2p,
w miarę jej wypełniania wzrasta energia jonizacji atomu,
jądro jest ekranowane przez 1s
2
neon
Ne: 1s
2
2s
2
2p
6
ma całkowicie zapełnioną drugą
powłokę, gaz szlachetny
sód
Na: 1s
2
2s
2
2p
6
3s
1
energia jonizacji 5,1 eV,
wartościowość +1, duża aktywność chemiczna
Poziomy energetyczne
a konfiguracja elektronowa
dla atomu potasu (19):
stan 3d leży wyżej niż 4s
K: 1s
2
2s
2
2p
6
3s
2
3p
6
4s
1
(zamiast 3d)
dla atomu rubinu (37):
stan 4d leży wyżej niż 5s
Rb: 1s
2
.... 3p
6
3d
10
4s
2
4p
6
5s
1
(zamiast 4d)
K
Rb
Zakaz Pauliego, a układ okresowy
gazy szlachetne – zamknięte powłoki, momenty pędu i
magnetyczne równe zero, orbitale o symetrii sferycznej,
nie aktywne chemicznie
metale alkaliczne – jeden elektron walencyjny określa
moment pędu i magnetyczny, aktywne chemicznie
fluorowce (halogeny) – brak elektronu na ostatniej
podpowłoce, aktywne chemicznie
metale przejściowe – zapełniona ostatnia podpowłoka
ekranuje niecałkowicie zapełnione niższe podpowłoki,
podobne właściwości chemiczne, zbliżone energie
jonizacji, istotne właściwości magnetyczne
pierwiastki ziem rzadkich – lantanowce, zbliżone
właściwości chemiczne, metale aktywne chemicznie
Pułapki elektronowe
2
2
2
2
2mL
n
E
n
h
π
=
0
L
∞
∞
E
1
E
2
E
3
studnia
potencjału
stan podstawowy
2
2
2
2
4
1
32
n
me
n
E
o
⋅
ε
π
−
=
h
atom wodoru
E
o
kl
n
n
E
ω
⎟
⎠
⎞
⎜
⎝
⎛ −
=
h
2
1
oscylator harmoniczny
E
1
E
2
E
3
E
4
E
5
E
6