7
NAGRZEWANIE POJEMNOŚCIOWE

7.1 Zasady nagrzewania pojemnościowego

Nagrzewanie pojemnościowe jest to nagrzewanie elektryczne związane z efektami pola-
ryzacji i przewodnictwa w ośrodkach dielektrycznych i półprzewodnikowych, do których
energia elektromagnetyczna wielkiej częstotliwości jest doprowadzana za pośrednictwem
elektrod.

Pierwszym badaczem, który dostrzegł i wyjaśnił nagrzewanie się dielektryka w

kondensatorze był W. Siemens (1864 r). Dopiero jednak w 1929 r. opracowane zostały przez
P. Debye'a pełne podstawy tej przemiany energii z wykorzystaniem pojęcia elektrycznego
momentu dipolowego dielektryka. Znaczne zasługi w tym zakresie ma także K.W. Wagner,
który doszedł do podobnych wniosków końcowych już w 1914 r., posługując się jednak
mniej przekonywającym sposobem dowodzenia. Pierwsze praktyczne wykorzystanie efektu
polaryzacji należy przypisać R. von Zeyneckowi. W roku 1899 zastosował on prąd o
częstotliwości 200 kHz w diatermii. Innym badaczem, który tworzył podstawy nagrzewania
pojemnościowego jest A. Esau - twórca lamp nadawczych dużej mocy (1925 r.). Zbudował
on zaawansowane technicznie pojemnościowe urządzenia terapeutyczne i pierwsze
urządzenia do zastosowań technologicznych (suszenie wyrobów tekstylnych i środków
spożywczych, klejenie drewna). Początkowy okres rozwoju tej metody zamyka M. Descarsin
(1946 r.), który wprowadza ją do nagrzewania materiałów ceramicznych.

Nagrzewanie pojemnościowe, nazywane niekiedy dielektrycznym (termin mniej

precyzyjny, wobec stosowania tej metody także do nagrzewania półprzewodników) jest
efektem różnych rodzajów polaryzacji. Efekt nagrzewania wzmacniają niekiedy zjawiska
przewodnictwa jonowego, elektronowego i dziurowego. Zasadne mogłoby się więc wydawać
oddzielne rozważenie „czystej" metody pojemnościowej, związanej wyłącznie z polaryzacją
oraz metod nagrzewania skojarzonego, wtedy gdy efektom tym towarzyszy zjawisko Joule'a,
np. w ośrodkach stałych bądź ciekłych. Tego rodzaju podejście nie przyjęło się, a
kompleksowość ujęcia użytkowych efektów cieplnych polaryzacji i Jou-

166

7. Zasady nagrzewania pojemnościowego
___________________________________________________________________________

le'a pod wspólną nazwę nagrzewania pojemnościowego znalazła swój wyraz w teorii tej
metody. Przejawia się ona w sposobie definiowania jednej z wielkości związanej ze stratami
w dielektryku, a mianowicie stratności elektrycznej [630].

2

2

P

S

P

δ

tg

−

=

(7.1)

przy czym: P - moc czynna wydzielana we wsadzie w wyniku efektów polaryzacji i prze-
wodnictwa, S - moc pozorna związana z tymi samymi efektami.

Polaryzacja - pierwszy z wymienionych efektów odpowiedzialnych za wydzielanie

ciepła - wynika z przesunięć ładunków związanych z atomami lub molekułami pod wpływem
zewnętrznego pola elektrycznego. Pole to jest wytwarzane za pośrednictwem układu elektrod
połączonych z generatorem wielkiej częstotliwości. Elektrody i nagrzewany wsad tworzą
układ zwany często kondensatorem grzejnym. Przesunięcia ładunków związanych są
możliwe dzięki występowaniu we wsadzie dipoli elektrycznych, czyli układów utworzonych
przez dwa różnoimienne ładunki elektryczne utrzymywane od siebie w pewnej odległości.
Dipole takie mogą powstać w wyniku działania sił zewnętrznych, powodując polaryzację
elektronową i atomową. Mogą też istnieć trwale we wsadzie, w przypadku gdy środki
ciężkości ładunków dodatnich i ujemnych w drobinie składającej się z różnych atomów nie
będą się pokrywać. Momenty te w izotropowych układach drobin, statystycznie rzecz biorąc,
będą się znosiły i na zewnątrz wsadu nie będzie pola elektrycznego. Przyłożenie
zewnętrznego pola elektrycznego powoduje pełne lub częściowe zorientowanie dipoli w
kierunku tego pola i w rezultacie tzw. polaryzację dipolową lub polaryzację orientacji.

Polaryzacja całkowita jest sumą efektów różnych rodzajów polaryzacji, a stopień

polaryzacji określa przenikalność elektryczna . Polaryzacja trwa tak długo, jak długo
istnieje zewnętrzne pole elektryczne, a gdy ono zanika - układ wraca do stanu poprzedniego.
Przy polaryzowaniu wsad pochłania energię, lecz z chwilą gdy pole ją wywołujące znika, pod
wpływem siły przeciwdziałającej ładunki wracają do zwykłych położeń, a część energii
pochłoniętej zostaje zwrócona do źródła zasilającego. Polaryzacja zmienia się w takt zmian
zewnętrznego pola elektrycznego, a wynikający z tego ruch ładunków związanych to prąd
przesunięcia o gęstości

. Ilość energii pobierana ze źródła i do niego oddawana nie jest

jednakowa. Pewna jej ilość zużywa się na tarcie i przemieszczanie się dipoli czyli na tzw.
straty dipolowe, wydzielające się we wsadzie pod postacią ciepła użytecznego.

ε

p

J

Przesunięcia dipoli wskutek strat dipolowych nie zawsze nadążają za zmianami pola

zewnętrznego, a więc polaryzacja się opóźnia. W polu sinusoidalnie zmiennym natężenie
pola osiąga wartość maksymalną z pewnym wyprzedzeniem maksymalnej wartości prądu
przesunięcia. Ze wzrostem częstotliwości opóźnienie to staje się coraz większe osiągając
wartość maksymalną przy częstotliwości zwanej relaksacyjną.

Najistotniejsze znaczenie w nagrzewaniu pojemnościowym ma polaryzacja dipolowa,

co ma bezpośredni związek z częstotliwością zmian pola elektrycznego i czasem

167

7. Nagrzewanie pojemnościowe
___________________________________________________________________________
ustalania się polaryzacji lub jej zaniku, czyli tzw. czasem relaksacji. Otóż przy niedopa-
sowaniu częstotliwości przeorientowywania pola zewnętrznego do „możliwości ruchowych"
ładunków związanych, stopień polaryzacji i efekt grzejny są znikome. Czasy relaksacji
elektronowej i atomowej są krótsze aniżeli czas relaksacji dipolowej. Oznacza to, że
wykorzystanie polaryzacji elektronowej i atomowej wymagałoby znacznie większych
częstotliwości przeorientowywania pól (odpowiadających zakresowi fal ultrafioletowych i
podczerwonych).

Czas relaksacji dipolowej wg Debye'a

kT

d

πη

4

τ

3

=

(7.2)

gdzie:

- lepkość dynamiczna nagrzewanego ośrodka (w modelu Debye'a przyjmuje się, że

jest to rozcieńczony roztwór substancji dipolowej w obojętnym rozpuszczalniku [395]);

d -

średnica drobiny dipolowej; k - stała Boltzmanna;

T - temperatura termodynamiczna.

η

Efekty polaryzacji są więc dwojakie. Pierwszy polega na ładowaniu i rozłado-

wywaniu kondensatora grzejnego, drugi - na wydzielaniu się ciepła. Stąd też operuje się
dwiema składowymi przenikalności elektrycznej, czyli

ε

j

ε

ε

′′

−

′

=

(7.3)

przy czym

p

δ

tg

ε

ε =

′

′′

(7.4)

Współczynnik

związany jest wyłącznie ze stratami wynikającymi z polaryzacji i jest

równy współczynnikowi stratności

tylko wtedy gdy polaryzacji nie towarzyszy efekt

Joule'a. Zatem

p

δ

tg

δ

tg

)

δ

tg

j

1

(

ε

ε

p

−

′

=

(7.5)

Składowe i określone są równaniami Debye’a [395]:

ε′ ε ′′

2

2

r

)

τ

ω

(

1

)

τ

ω

(

ε

ε

ε

′

+

′

+

=

′

∞

(7.6)

2

r

)

τ

ω

(

1

τ

ω

)

ε

ε

(

ε

′

+

′

+

=

′′

∞

(7.7)

2

r

r

P

)

τ

ω

(

ε

ε

τ

ω

)

ε

ε

(

δ

tg

′

+

′

+

=

∞

∞

(7.8)

168

7.1. Zasady nagrzewania pojemnościowego
__________________________________________________________________________
przy czym

2

ε

2

ε

τ

τ

r

+

+

=

′

∞

(7.9)

Dla

składowa przenikalności elektrycznej

0

ωτ

=

ε′

przyjmuje wartość

. Określa się ją

mianem przenikalności elektrycznej statycznej. Dla bardzo dużych

r

ε

ωτ

wartość ustala się

na poziomie tzw. przenikalności elektrycznej optycznej

. Przebieg

tg ma charakter

krzywej rezonansowej, której maksimum występuje przy

ε′

∞

ε

p

δ

∞

′

=

ε

ε

τ

1

ω

r

opt

(7.10)

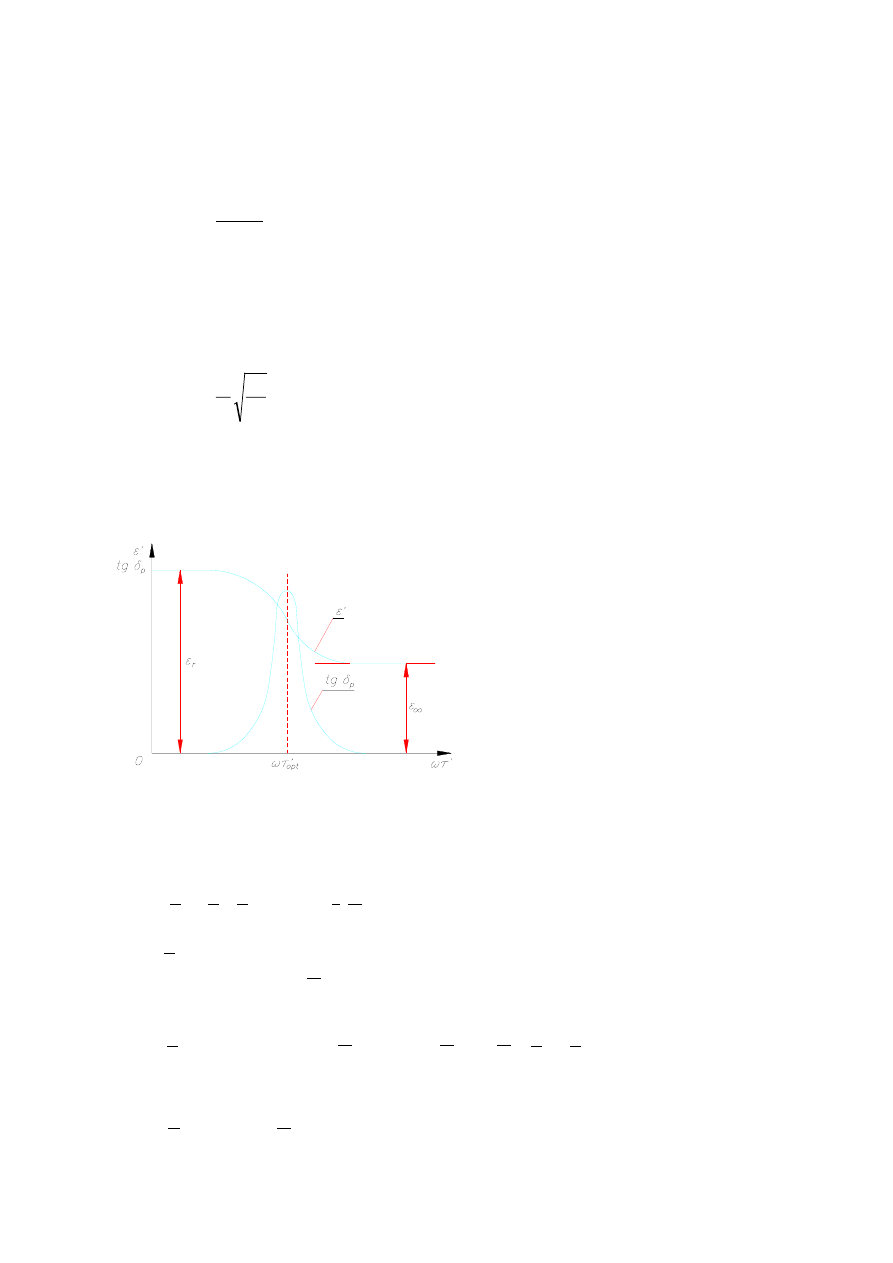
Obszar przejściowy, w którym maleje od do

zawiera się w przedziale od 10 MHz do

100 GHz i w tym obszarze mieści się

(rys. 7.1). We wsadzie niejednorodnym liczba

częstotliwości relaksacyjnych może być większa niż jedna.

ε′

r

ε

∞

ε

opt

ω

Rys.7.1. Charakterystyki częstotliwo-
ściowe składowej rzeczywistej przeni-
kalności elektrycznej i współczynnika
stratności związanego wyłącznie ze
zjawiskiem polaryzacji

τ

ω ′

- unormowana pulsacja

Mając powyższe na uwadze i zakładając, że nagrzewanie odbywa się w polach

sinusoidalnie zmiennych, gęstość prądu całkowitego we wsadzie możemy wyrazić w na-
stępujący sposób:

E

J

J

J

)

ε

ω

j

γ

(

p

c

+

=

+

=

(7.11)

gdzie

J

jest gęstością prądu przewodzenia, występującego tylko przy niezerowej

konduktywności wsadu

γ ,

E

jest natężeniem pola elektrycznego.

Po uwzględnieniu (7.3)

X

R

c

ω

j

)

ε

ω

γ

(

)]

ε

j

ε

(

ω

j

γ

[

J

J

E

E

E

J

+

=

′

+

′′

+

=

′′

−

′

+

=

(7.12)

Wektor gęstości prądu strat

E

J

)

ε

ω

γ

(

R

′′

+

=

(7.13)

169

7. Nagrzewanie pojemnościowe
___________________________________________________________________________
jest w fazie z wektorem natężenia pola elektrycznego

E

natomiast wektor gęstości prądu

pojemnościowego

E

J

ε

ω

j

X

′

=

(7.14)

jest przesunięty w fazie o

π

względem wektora natężenia pola elektrycznego (rys. 7.2).

2

/

Rys. 7.2. Składowe gęstości prądu całkowitego i

natężenia pola elektrycznego

Iloraz modułów gęstości prądu strat i gęstości prądu pojemnościowego jest współczynnikiem
stratności

p

δ

tg

ε

ω

γ

ε

ω

ε

ω

γ

δ

tg

+

′

=

′

′′

+

=

(7.15)

Niekiedy operuje się konduktywnością efektywną

(7.16)

ε

ω

γ

γ

e

′′

+

=

oraz efektywną zespoloną przenikalnością elektryczną wsadu [203]

e

e

ε

j

ε

ε

′′

−

′

=

′

(7.17)

przy czym

ω

γ

ε

ε

e

+

′′

=

′′

(7.18)

Moc czynną wydzielaną we wsadzie określa się przy wykorzystaniu wektora

Poyntinga (p. 6.1.2.2.). Po jej odniesieniu do jednostki objętości otrzymuje się

2

2

e

2

e

V

E

δ

tg

ε

ω

E

γ

J

γ

1

p

′

=

=

=

(7.19)

Tę samą zależność otrzymuje się wychodząc z iloczynu

2

R

R

R

R

E

δ

tg

ε

ω

E

J

)

,

cos(

E

J

′

=

=

=

E

J

E

J

(7.20)

170

7.1.

Zasady nagrzewania pojemnościowego

__________________________________________________________________________

Często moc grzejna w układzie pojemnościowym wyrażana w W/m

3

jest określona

zależnością

(7.21)

2

r

11

V

E

δ

tg

ε

f

10

56

.

5

p

′

⋅

=

−

przy czym:

f - częstotliwość w Hz,

0

r

ε

ε

ε

′

=

′

- przenikalność elektryczna względna wsadu

(ściśle rzecz biorąc jest to składowa rzeczywista zespolonej przenikalności elektrycznej
względnej wsadu),

tg - współczynnik stratności wsadu, E - wartość skuteczna natężenia pola

elektrycznego w V/m.

δ

Z przytoczonych wzorów wynika, że zwiększenie mocy grzejnej we wsadzie można

uzyskać poprzez zwiększenie natężenia pola elektrycznego bądź częstotliwości. Natężenie
pola elektrycznego

E nie może jednak przekroczyć wartości wywołującej przebicie

elektryczne materiału. Konieczność ograniczenia

E jest powodowana ponadto czynnikami

konstrukcyjnymi układów zasilających i względami bezpieczeństwa. Wówczas jedyną
możliwością zwiększenia

jest podwyższenie częstotliwości osiągającej w praktyce

wartości rzędu kilkudziesięciu megaherców. Wymaga to jednak spełnienia kilku warunków
gwarantujących eliminację szkodliwej interakcji z innymi urządzeniami eksploatowanymi w
tym samym przedziale częstotliwości oraz ograniczenia oddziaływania pól na organizmy
żywe, a zwłaszcza na człowieka [169]. Możliwości modyfikacji iloczynu

- nazywanego

niekiedy współczynnikiem pochłaniania

k - mają charakter incydentalny. Wartości tych

wielkości wyznacza się metodami falowodowymi i rezonatorowymi, rzadziej w wolnej
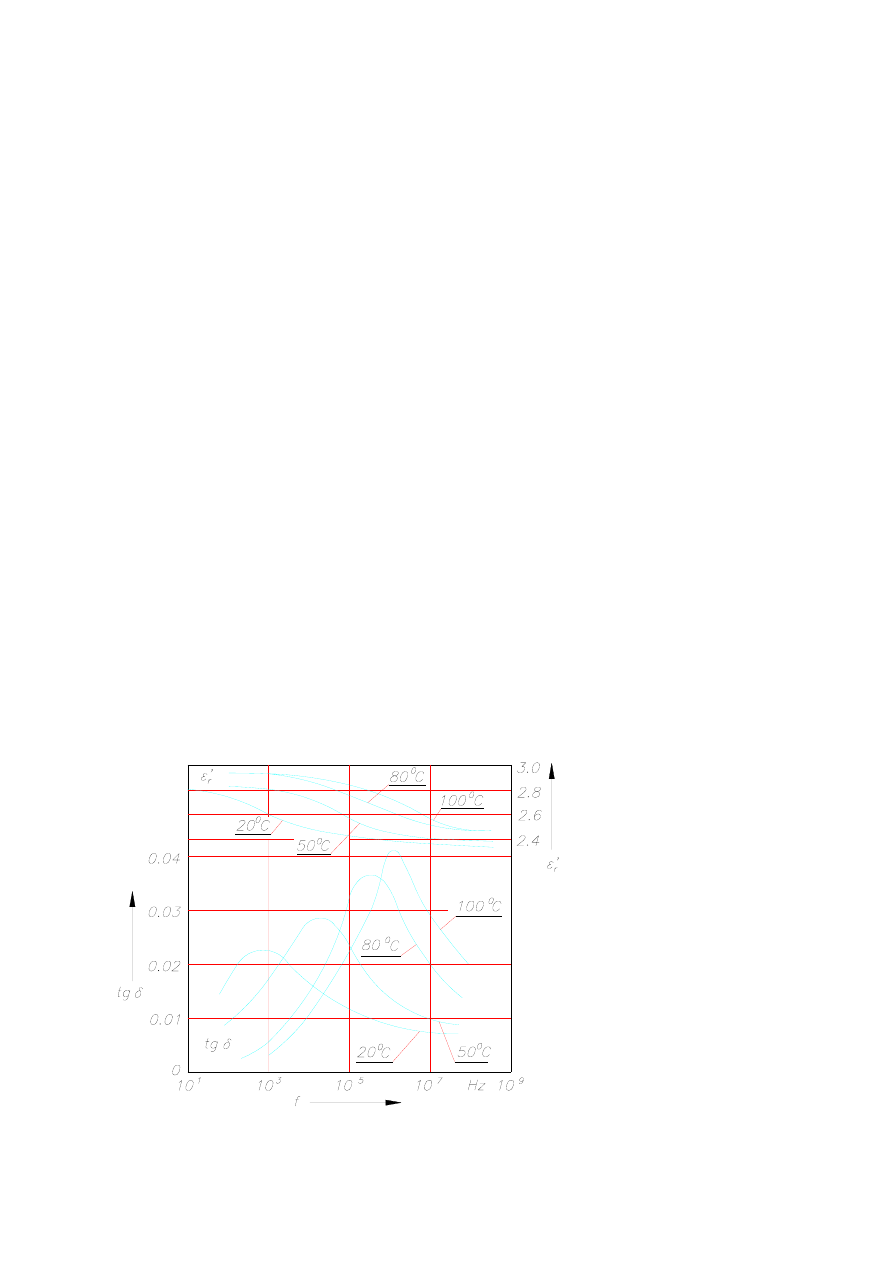
przestrzeni [395], [575]. Dane dielektryczne dotyczące niektórych materiałów zawarte są w
tabl. 7.1 i na rys. 7.3. Wynika z nich, że współczyn-

V

p

δ

tg

ε

r

′

Rys. 7.3. Przenikalność elektryczna względna ε

’

r

= ε

o

ε

’

i współczynnik stratności tg δ

polichrolotrójfluoroetylenu w funkcji częstotliwości dla kilku temperatur, wg [595]

171

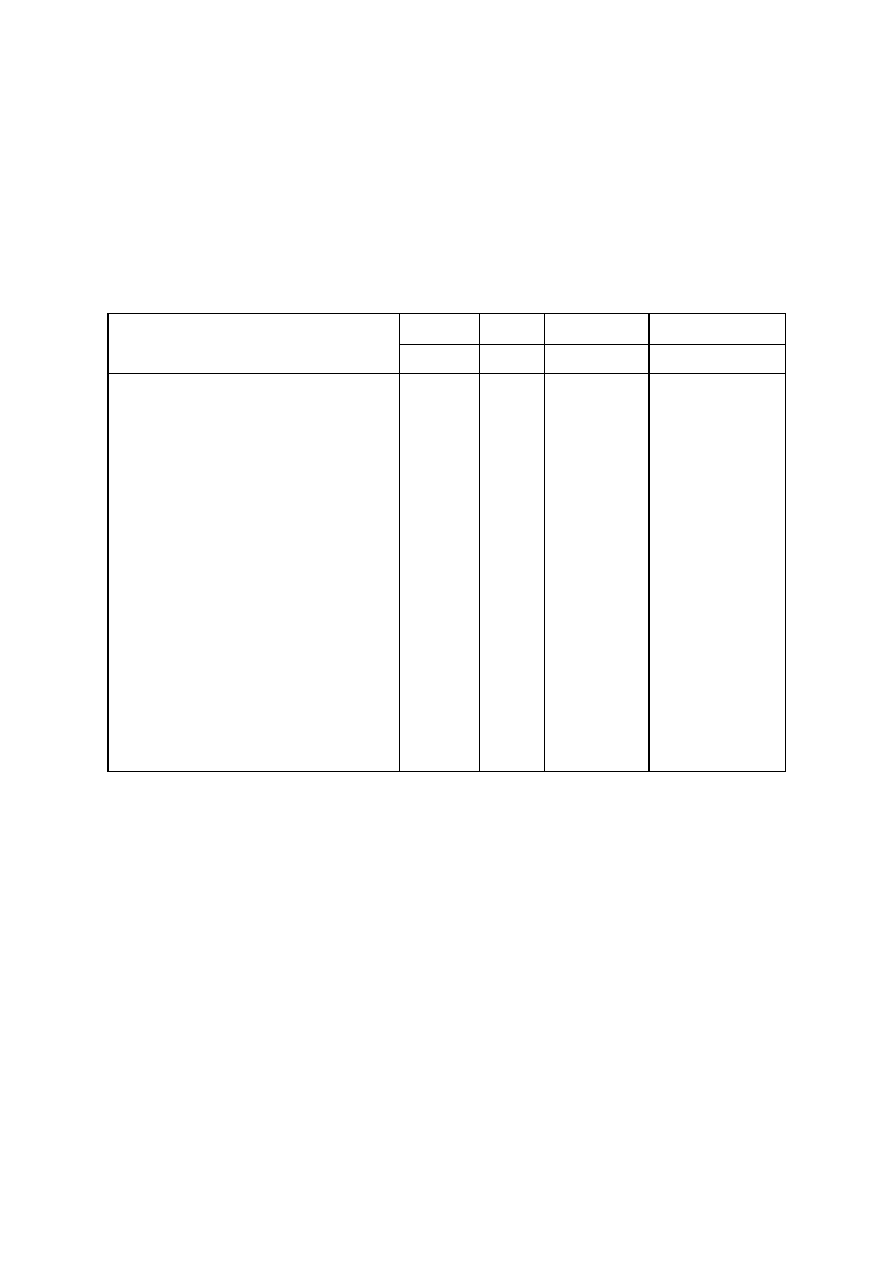
7. Nagrzewanie pojemnościowe
___________________________________________________________________________
nik pochłaniania jest zależny nie tylko od częstotliwości, lecz także od temperatury. Ponadto
niektóre materiały wykazują zależność

k od zawartości wody, inne od stopnia przemian

fazowych, a nawet od natężenia pola elektrycznego.

Tablica 7.1. Przenikalność elektryczna względna ε

’

r

i współczynnik stratności tgδ niektórych materiałów dla

wybranych temperatur t i częstotliwości zmian natężenia pola elektrycznego f, wg [92, 262, 314,
568, 355]

f t

r

ε′

δ

tg

Materiał

MHz

0

C

- -

Cukier mokry
Drewno jodłowe z zawartością 10% wody
Etyloceluloza
Folia PCV miękka
Folia PCV miękka
Guma silikonowa
Klej do drewna przed nagrzaniem
Mikaleks
Papier z zawartością 10% wody
PCV twardy
Polietylen
Porcelana
Polistyren
Steatyt specjalny
Szkło ołowiowe
Teflon
Żywica epoksydowa
Żywica fenolowo-formaldehydowa czysta
Żywica fenolowo-formaldehydowa czysta
Żywica fenolowa z mączką drewnianą

20.00
10.00

1.00

27.12
27.12

100.00

2÷15

1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0

20
20
20
20

140

25
20
20
20
20
20
20
20
20
20
20
20
20

140

20

1.73
3.20

2.80÷3.90

3.00
4.60

3.10÷3.27

20÷40

6÷8

3.20

2.80÷3.40
2.20÷2.40

4÷7

2.5

6÷8

7.0÷7.5
2.0÷2.1
3.5÷5.0

2.9
3.6

5÷7

0.0175

0.09

0.01÷0.06

0.05
0.29

0.0023÷0.0032

0.5÷0.8

0.012÷0.020

0.12

0.015÷0.040

0.0001÷0.0004

0.028÷0.055

< 0.0003

0.0003÷0.0008

0.007÷0.010

0.00016÷0.00030

0.002÷0.060

0.014
0.060

0.15÷0.50

Z zależności (7.19) - (7.21) wynika, że określenie mocy grzejnej w układzie

pojemnościowym wymaga znajomości rozkładu natężenia pola elektrycznego we wsadzie,
częstotliwości zmian tego pola oraz dwóch parametrów charakteryzujących wsad, a
mianowicie

i

tgδ. Układy grzejne (rys. 7.4) muszą mieć geometrię gwarantującą uzyskanie

pól elektrycznych, wynikających z nich rozkładów mocy grzejnej, a w końcowym efekcie pól
temperatur, wymaganych przez procesy technologiczne. Układy takie realizuje się dobierając
kształt, wielkość i liczbę elektrod, wzajemne ich usytuowanie, niekiedy wprowadzając w
otoczenie wsadu dodatkowe dielektryki stałe zmieniające rozkład mocy grzejnej. Często
kształtuje się rozkład natężenia pola poprzez dobór geometrii szczelin powietrznych między
elektrodami i wsadem, który może, lecz nie musi stykać się z elektrodami. Istniejące w tym
zakresie możliwości zilustrowane zostaną na przykładach czterech układów
płaskorównoległościennych: jednorodnego bez szczeliny, jednorodnego ze szczeliną,
niejednorodnego posobnego, niejednorodnego pobocznego oraz jednego układu przelotowego
z elektrodami prętowymi.

r

ε′

172

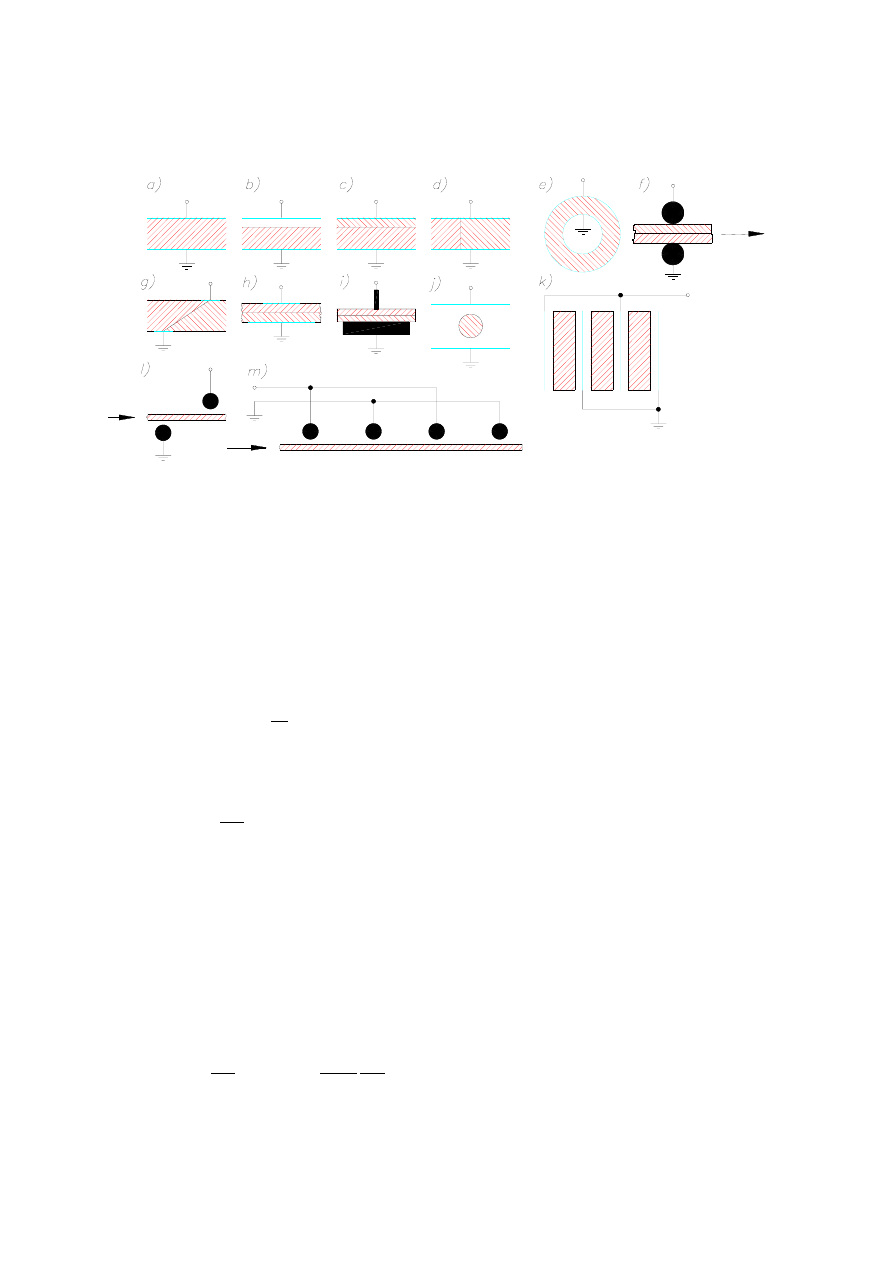
7.1.Zasady nagrzewania pojemnościowego
___________________________________________________________________________

Rys. 7.4. Przykłady pojemnościowych układów grzejnych: a) płaskorównoległościenny, b) płaskorównoległo-

ścienny ze szczeliną, c) płaskorównoległościenny posobny, d) płaskorównoległościenny poboczny,

e) cylindryczny, f) rolkowy przelotowy, g) płaskorównoległościenny z przesuniętymi elektrodami,
h) płaskorównoległościenny asymetryczny, i) płaskorównoległościenny z elektrodą ostrzową,
j) płaskorównoległościenny ze wsadem cylindrycznym, k) płaskorównoległościenny czteroelektro-

dowy, l) prętowy przelotowy dwustronny, m) prętowy przelotowy jednostronny

Układ płaskorównoległościenny jednorodny bez szczeliny przedstawia rys. 7.5a. Jeśli

założyć ekwipotencjalność obu elektrod, to przy napięciu między nimi

U i odległości d, z

(7.19) otrzymuje się

2

V

d

U

δ

tg

ε

ω

p













′

=

(7.22)

Ponieważ pojemność kondensatora płaskiego utworzonego przez dwie elektrody o po-
wierzchni

S jest równa

d

S

ε

C

r

′

=

(7.23)

to całkowita moc grzejna wydzielająca się we wsadzie

2

r

V

U

C

δ

tg

ω

Sd

p

P

=

=

(7.24)

Schemat zastępczy takiego układu grzejnego można przedstawić za pomocą dwóch

równoważnych dwójników (rys. 7.5b, c). Wielkości charakteryzujące dwójnik równoległy
określają zależności:

d

S

ε

C

r

′

=

,

δ

tg

1

S

ε

ω

d

R

r

′

=

(7.25)

173

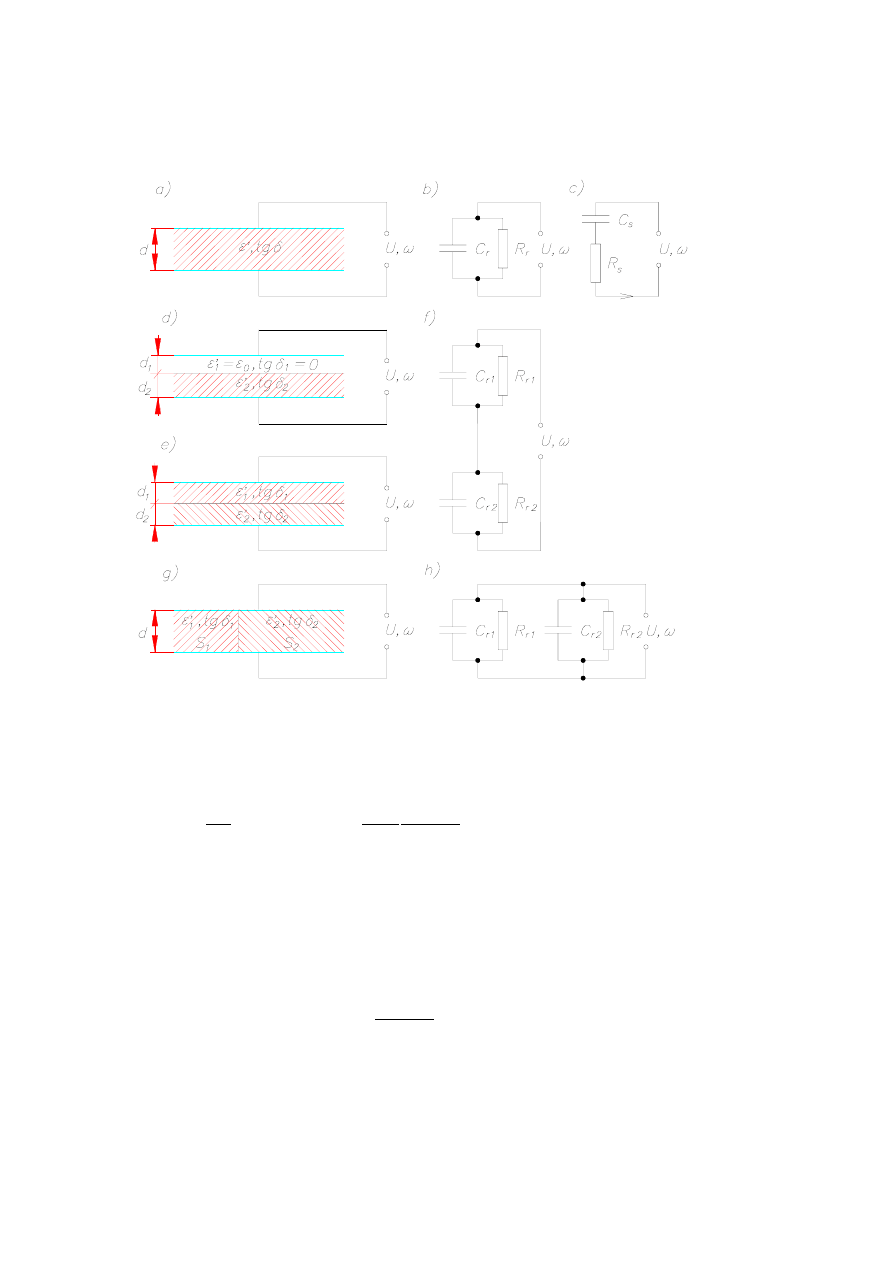
7. Nagrzewanie pojemnościowe
__________________________________________________________________________

Rys. 7.5. Wybrane pojemnościowe układy grzejne i ich schematy zastępcze

zaś dwójnik szeregowy

)

δ

tg

1

(

d

S

ε

C

2

s

+

′

=

,

δ

tg

1

δ

tg

S

ε

ω

d

R

2

s

+

′

=

(7.26)

Jak łatwo stwierdzić, moc grzejna

, w schemacie zastępczym równoległym

równa jest mocy grzejnej

w schemacie zastępczym szeregowym, ponieważ

. Zgodnie z (7.25) i (7.26) otrzymuje się

r

2

R

/

U

P

=

s

2

R

I

P

=

]

)

C

ω

/

1

(

R

/[

U

I

2

s

2

s

2

2

+

=

δ

tg

1

1

U

C

δ

tg

ω

U

C

δ

tg

ω

P

2

2

s

2

r

+

=

=

(7.27)

Układ płaskorównoległościenny jednorodny ze szczeliną (rys. 7.5d) oraz niejednorodny po-
sobny ze wsadem dwuelementowym (dwuwarstwowym) pokazany na rys. 7.5e są w istocie
rzeczy układami identycznymi. W tym pierwszym jedną z warstw stanowi

174

7.Zasady nagrzewania pojemnościowego
__________________________________________________________________________
powietrze, dla którego współczynnik stratności jest bardzo mały

i dlatego

uzasadnione jest założenie, że w warstwie tej nie wydziela się moc grzejna.

)

10

4

δ

tg

(

8

−

⋅

≈

Przy utrzymaniu założenia o ekwipotencjalności elektrod, jednostkowa moc grzejna

wydzielająca się w pierwszej warstwie wsadu o grubości

d

1

i współczynniku pochłaniania

1

δ

tg

ε′

2

1

1

1

1

2

1

1

1

1

V

d

U

δ

tg

ε

ω

E

δ

tg

ε

ω

p













′

=

′

=

(7.28)

W warstwie drugiej

2

2

2

2

2

2

2

2

2

2

V

d

U

δ

tg

ε

ω

E

δ

tg

ε

ω

p













′

=

′

=

(7.29)

O ile

2

1

1

2

1

r

2

r

2

1

d

ε

d

ε

C

ω

C

ω

U

U

′

′

=

≈

(7.30)

co jest do przyjęcia dla małych współczynników stratności, to zależności (7.28) i (7.29)
można wyrazić w funkcji napięcia zasilającego

U = U

1

+ U

2

2

2

1

1

2

1

1

1

V

d

ε

ε

d

U

δ

tg

ε

ω

p













′

′

+

′

=

(7.31)

2

1

1

2

2

2

2

2

2

V

d

ε

ε

d

U

δ

tg

ε

ω

p













′

′

+

′

=

(7.32)

Przy objętościach poszczególnych warstw

V

1

= Sd

1

V

2

=

Sd

2

moce grzejne

2

2

1

1

2

1

r

1

2

2

1

1

2

1

2

1

1

1

1

V

1

ε

d

ε

d

1

1

C

δ

tg

ω

ε

d

ε

d

1

d

SU

δ

tg

ε

ω

Sd

p

P













′

′

+

=













′

′

+

′

=

=

(7.33)

2

1

2

2

1

2

r

2

2

1

2

2

1

2

2

2

2

2

2

V

2

ε

d

ε

d

1

1

C

δ

tg

ω

ε

d

ε

d

1

d

SU

δ

tg

ε

ω

Sd

p

P













′

′

+

=













′

′

+

′

=

=

(7.34)

175

7. Nagrzewanie pojemnościowe
_________________________________________________________________________
Dla układu jednorodnego ze szczeliną powietrzną, gdy

tg

0

δ

1

≈

,

0

1

ε

ε

=

′

oraz przy ozna-

czeniu

r

0

2

r

0

2

ε

ε

ε

ε

ε

′

=

′

=

′

,

tg

, dla powierzchni elektrod

S

δ

tg

δ

2

=

2

2

1

r

2

2

r

0

2

d

d

ε

1

d

SU

δ

tg

ε

ωε

P

P













′

+

′

=

=

(7.35)

przy czym

d

1

jest grubością szczeliny powietrznej zaś

d

2

jest grubością wsadu.

Elektryczny schemat zastępczy układu płaskorównoległościennego dwuwarstwowego

przedstawia rys. 7.5f.

Dla układu płaskorównoległościennego niejednorodnego pobocznego ze wsadem

dwuelementowym (rys. 7.5g), przy zastąpieniu każdej warstwy dwójnikiem równoległym
(rys. 7.5h) i przy założeniu ekwipotencjalności elektrod, obowiązują następujące zależności:

2

1

1

2

1

1

1

V

d

U

δ

tg

ε

ω

E

δ

tg

ε

ω

p













′

=

′

=

(7.36)

2

2

2

2

2

2

2

V

d

U

δ

tg

ε

ω

E

δ

tg

ε

ω

p













′

=

′

=

(7.37)

oraz

2

1

r

1

2

1

1

1

1

1

V

1

U

C

δ

tg

ω

d

U

S

δ

tg

ε

ω

d

S

p

P

=

′

=

=

(7.38)

2

2

r

2

2

2

2

2

2

2

V

2

U

C

δ

tg

ω

d

U

S

δ

tg

ε

ω

d

S

p

P

=

′

=

=

(7.39)

Podane zależności na moce grzejne można akceptować, o ile rzeczywisty rozkład

natężenia pola elektrycznego odbiega w niewielkim stopniu od jednorodnego. Dla
rozważanych wyżej układów płaskorównoległościennych, przy zerowym potencjale jednej z
elektrod, na ogół przyjmuje się, że maksymalna różnica potencjałów na elektrodzie drugiej
nie powinna przekraczać 10%. Skutki takiej różnicy nie mają wówczas istotnego wpływu na
pole temperatury.

Rzeczywisty rozkład potencjałów jest wynikiem propagacji we wsadzie fal o

długościach porównywalnych w wielu przypadkach z maksymalnym wymiarem elektrody. W
celu wyjaśnienia tego zjawiska rozpatrzymy propagację fali elektromagnetycznej płaskiej
spolaryzowanej liniowo w układzie jak na rys. 7.6 (układ płaskorównoległościenny o długich
wąskich elektrodach), co oznacza, że w odniesieniu do wartości skutecznych

z

E

k

H

=

(7.40)

y

E

j

E

=

(7.41)

176

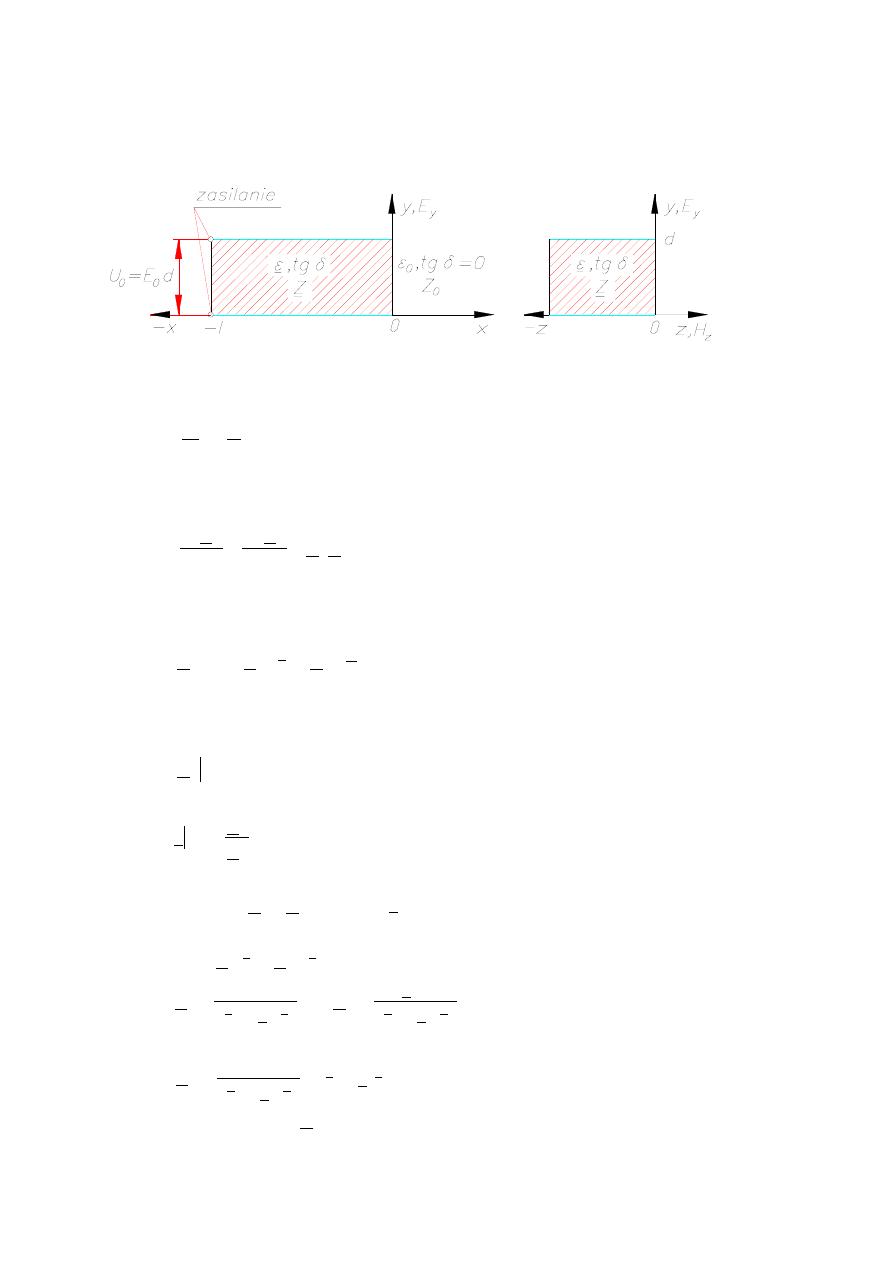
7.1. Zasady nagrzewania pojemnościowego
___________________________________________________________________________

Rys. 7.6. Układ z rozprzestrzeniającą się w nim falą płaską spolaryzowaną liniowo l - długość elektrody, d -

grubość wsadu, U

0

=E

0

d

- napięcie zasilające

Wektory

H

i

E

leżą w jednej płaszczyźnie i są ortogonalne. Fala elektromagnetyczna

rozchodzi się wzdłuż osi

x i ulega odbiciu od powierzchni granicznej wsad-powietrze (x = 0).

Z równania Helmholtza (6.15) po uwzględnieniu (7.41) wynika, że

y

2

2

y

2

2

y

2

E

Γ

dx

E

d

x

E

=

=

∂

∂

(7.42)

którego rozwiązaniem jest funkcja

x

Γ

2

x

Γ

1

y

e

C

e

C

)

x

(

E

+

−

+

=

(7.43)

Z następujących warunków brzegowych

0

1

x

y

E

E

=

−

=

(7.44)

1

2

0

x

C

C

n

=

=

(7.45)

wyznacza się stałe

1

C

i

2

C

przy czym

n jest współczynnikiem odbicia [206].

l

Γ

2

l

Γ

1

0

e

C

e

C

E

−

+

=

(7.46)

l

Γ

l

Γ

0

1

e

n

e

E

C

−

+

=

;

l

Γ

l

Γ

0

2

e

n

e

E

n

−

+

=

C

(7.47)

Rozwiązanie ma postać

)

e

n

e

(

e

n

e

E

E

x

Γ

x

Γ

l

Γ

l

Γ

0

y

+

+

=

−

−

(7.48)

Tamowność jednostkową

Γ

i jej dwie składowe, a mianowicie tłumienność jednostkową

α i

przesuwność jednostkową

β wyznacza się wychodząc z równania Hel-

177

7. Nagrzewanie pojemnościowe
_________________________________________________________________________
mholtza (6.15), w którym przenikalność elektryczna - tak jak to wynika z (7.3) - jest
wielkością urojoną. I tak

ε

ω

j

γ

(

ωµ

j

Γ

+

=

(7.49)

Uwzględniając (7.3) i (7.13), uzyskuje się zależność

β

j

α

)

ε

ω

j

γ

(

ωµ

j

Γ

e

+

=

′

+

=

(7.50)

Po podniesieniu do kwadratu obu stron tego równania i przyrównaniu jego części rzeczy-
wistych otrzymuje się różnicę

, a po przyrównaniu części urojonych

otrzymuje się iloczyn

. Jeśli wziąć pod uwagę (7.15) i (7.16), to

ε

µ

ω

β

α

2

2

2

′

−

=

−

2

/

ωµγ

αβ

e

=

(

)

1

δ

tg

1

2

ε

µ

ω

1

ε

ω

γ

1

2

ε

µ

ω

α

2

2

2

e

2

−

+

′

=















−













′

+

′

=

(7.51)

(

)

1

δ

tg

1

2

ε

µ

ω

1

ε

ω

γ

1

2

ε

µ

ω

β

2

2

2

e

2

+

+

′

=















+













′

+

′

=

(7.52)

Współczynnik odbicia n będący ilorazem natężeń pola elektrycznego fali odbitej i fali
padającej określa związek

Z

Z

Z

Z

n

0

0

+

−

=

(7.53)

w którym

Z

0

- impedancja falowa powietrza, czyli ośrodka do którego fala wnika po wyjściu

ze wsadu,

Z - impedancja falowa wsadu [579]. Impedancje te określone są zależnościami

0

0

0

ε

µ

Z

=

(7.54)

)

δ

jtg

1

(

ε

µ

ε

ω

ε

ω

γ

j

1

ε

µ

ε

ω

j

γ

ωµ

j

Z

0

−

′

=













′

′′

+

−

′

=

+

=

Ponieważ

oraz

0

r

0

µ

µ

µ

µ

=

=

r

0

ε

ε

ε

′

=

′

, to

1

δ

jtg

1

(

ε

1

δ

jtg

1

(

ε

n

r

r

+

−

′

−

−

′

=

(7.55)

Znajomość

Γ

i

n umożliwia na podstawie (7.48) określenie rozkładu natężenia pola

elektrycznego we wsadzie i w efekcie mocy grzejnej

178

7.1. Zasady nagrzewania pojemnościowego
___________________________________________________________________________

)

x

(

E

δ

tg

ε

ω

p

2

y

V

′

=

(7.56)

przy czym

)

x

(

E

)

x

(

E

y

y

=

czyli jest modułem natężenia pola elektrycznego. Rysunek 7.7

przedstawia przykładowe wyniki obliczeń pól elektrycznych dla trzech przypadków, a
mianowicie: gdy długość elektrody

l jest większa od długości fali

β

/

π

2

λ

=

, a zarazem nie

jest równa tzw. długości rezonansowej będącej krotnością

(rys. 7.7a) oraz gdy jest ona

dokładnie równa

(rys 7.7b oraz c). Jak wiadomo z teorii linii długich ma wówczas

miejsce rezonans szeregowy i bardzo znaczny wzrost napięcia [396]. Ze wzoru (7.47)
wynika, że w warunkach pełnego odbicia, tzn. gdy

n =1l, a ponadto gdy

4

/

λ

4

/

λ

0

δ

tg

=













=

2

π

k

cos

1

E

)

0

(

E

0

y

(7.57)

przy czym

k = l, 3, 5, 7.

Oznacza to wzrost napięcia w określonych miejscach układu grzejnego do wartości nie-
skończenie wielkiej (przypadek abstrakcyjny). Układy rzeczywiste charakteryzuje

n < l oraz

i taki właśnie układ pokazano na rys. 7.7 c. Celowe jest więc - przy zasilaniu jak na

rys. 7.6 - stosowanie elektrod o długości

0

δ

tg

>

4

/

λ

l

<

, a przy ich zasilaniu w połowie długości

powinien być spełniony warunek

2

/

λ

l

<

−

. O ile nierównomiemość natężenia pola

elektrycznego nadal przekracza granice dopuszczalne, zapobiega się temu w dwojaki sposób:
przez zasilanie kondensatora grzejnego w wielu miejscach lub przez włączenie indukcyjności
w dobrane miejsca między elektrody kondensatora grzejnego [921, [355], [568], [631].
Charakterystyczne jest też silne tłumienie

E

y

dla większych wartości

. Prowadzi ono przy

do przechodzenia rozkładu falowego

E

δ

tg

λ

l

>

y

(x) w rozkład wykładniczy.

Dla układu przelotowego z elektrodami prętowymi zlokalizowanymi po obu stronach

wsadu (rys 7.8), uzyskuje się korzystny rozkład natężenia pola elektrycznego. Wynika to z
bardzo dużej składowej wzdłużnej pola elektrycznego, co w przypadku wsadów cienkich o
dużych wartościach

ε′

(np. nagrzewany w przelocie papier, tkaniny) umożliwia uzyskanie

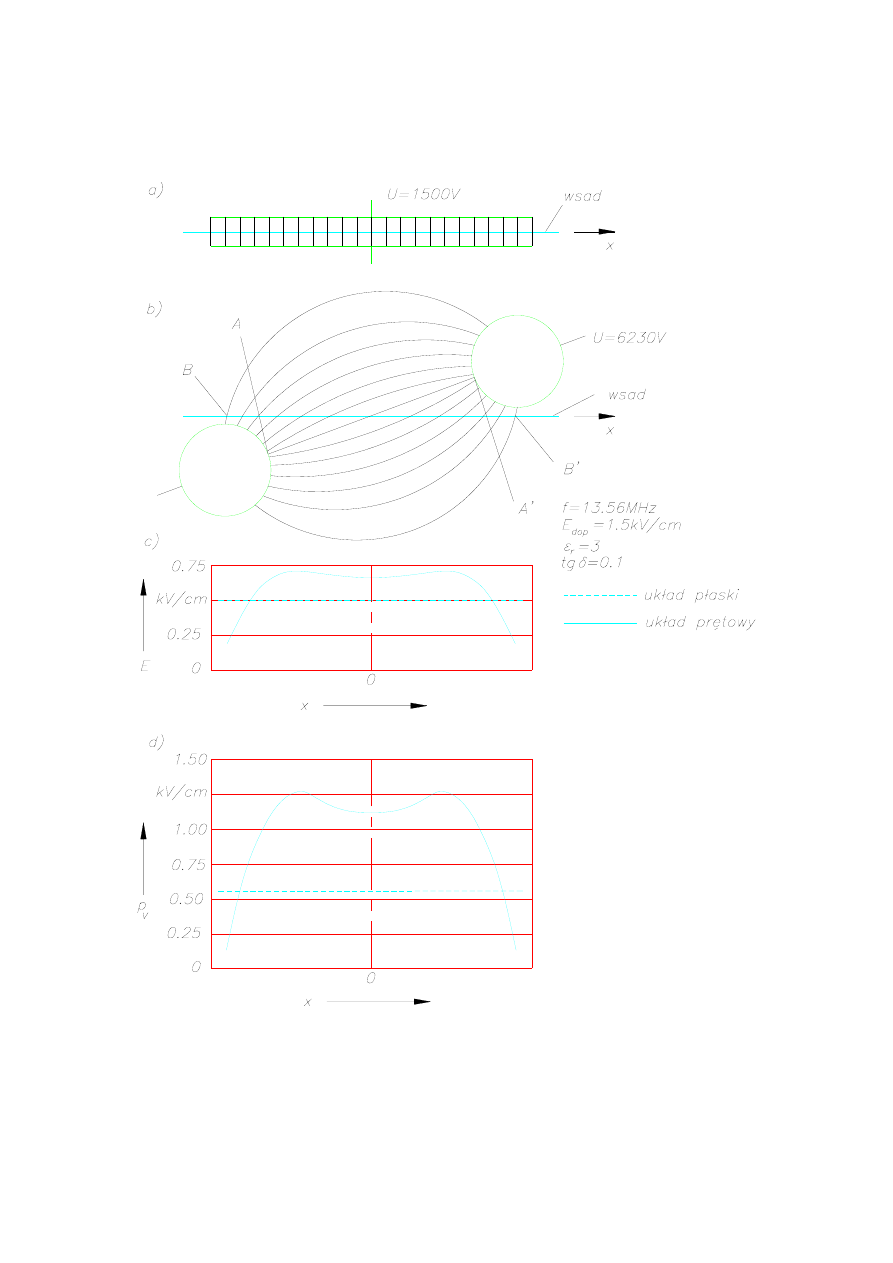
większych gęstości mocy bez przebić w układzie. W przypadku kondensatora
płaskorównoległościennego (rys. 7.8a) natężenie pola elektrycznego ma tylko składową
wzdłużną i w podanym przykładzie osiąga we wsadzie wartość 0,5 kV/m, co gwarantuje moc
jednostkową

p

V

= 0,56 W/cm

3

. W przypadku układu jak na rys 7.8b natężenie pola

elektrycznego jest nierównomierne. Największe wartości występują w punktach

A oraz A' na

powierzchniach elektrod prętowych. By wyeliminować niebezpieczeństwo wyładowań
koronowych, natężenie pola w tych punktach nie powinno przekroczyć wartości progowej,
którą określa się na podstawie ilorazu odległości środków elektrod i ich średnicy. Przy
wartości tego ilorazu równej 2,925 dopuszcza się największe wartości napięcia
międzyelektrodowego.

Elektrody prętowe powinny być zlokalizowane jak najbliżej wsadu, który nie

powinien jednak dotykać do nich w czasie przesuwania. W pobliżu punktów

B i B'

179

7. Nagrzewanie pojemnościowe
_________________________________________________________________________

natężenie pola we wsadzie ma wartość około 0,25 kV/cm, lecz między tymi punktami wzrasta
do wartości większej niż wartość charakterystyczna dla układu płaskorównoległościennego.
Wynika to z dominacji w tej przestrzeni składowej natężenia pola stycznej do wsadu. W
rezultacie uzyskuje się prawie dwukrotnie większą moc jednostkową

p

V

aniżeli w układzie

płaskorównoległościennym (rys. 7.8d). W obu przypadkach nie przekracza się przy tym
dopuszczalnego natężenia pola elektrycznego w powietrzu równego 1,5 kV/cm.

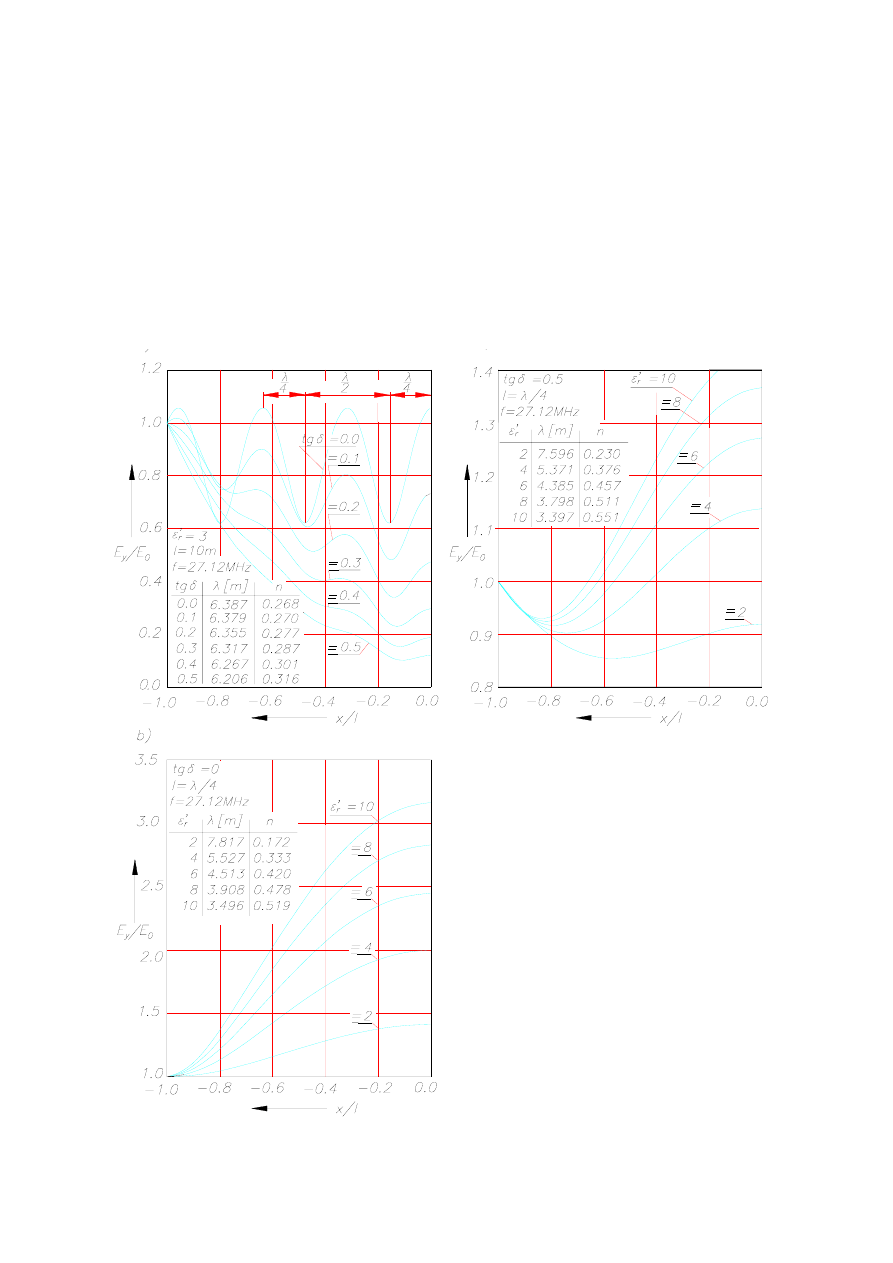
λ

l

>

4

/

λ

=

0

δ

tg

=

4

/

λ

l

=

5

.

0

δ

=

λ

Rys.7.7. Rozkład względnych natężeń pól
elektrycznych w układzie płaskorównoległo-
ściennym zasilanym w punkcie x = -l: a) przy

, b) przy

l

,

; c) przy

,

tg

l - długość elektrody, E

y

- moduł natężenia pola

elektrycznego w funkcji odległości x, E

0

- moduł

natężenia pola elektrycznego w płaszczyźnie
zasilania, - długość fali, n - moduł współczyn-
nika odbicia

180

7

.1.

Zasady nagrzewania pojemnościowego

__________________________________________________________________________

Rys. 7.8. Porównanie układów z elektrodami płaskimi i prętowymi, wg [274]: a) pole w układzie płaskim, b)

pole w układzie prętowym, c) natężenie pola elektrycznego we wsadzie w układzie płaskim i
prętowym, d) moc grzejna jednostkowa w obu układach

181

7. Nagrzewanie pojemnościowe
_________________________________________________________________________

Zwiększenie przelotności w układzie z elektrodami prętowymi uzyskuje się zwykle

przez zwiększenie liczby elektrod, przy czym w użyciu są zarówno układy z elektrodami
zlokalizowanymi po obu stronach wsadu, jak i z jednej jego strony (rys. 7.4m).

Znajomość rozkładu natężenia pola elektrycznego i wynikający z niej rozkład mocy

grzejnej (maksymalne wartości mogą sięgać 100 W/cm

3

[416]) pozwalają przy

wykorzystaniu równania Fouriera-Kirchhoffa określić pole temperatur we wsadzie [359]
Mimo wielkiej różnorodności geometrii układów grzejnych i warunków granicznych, wiele
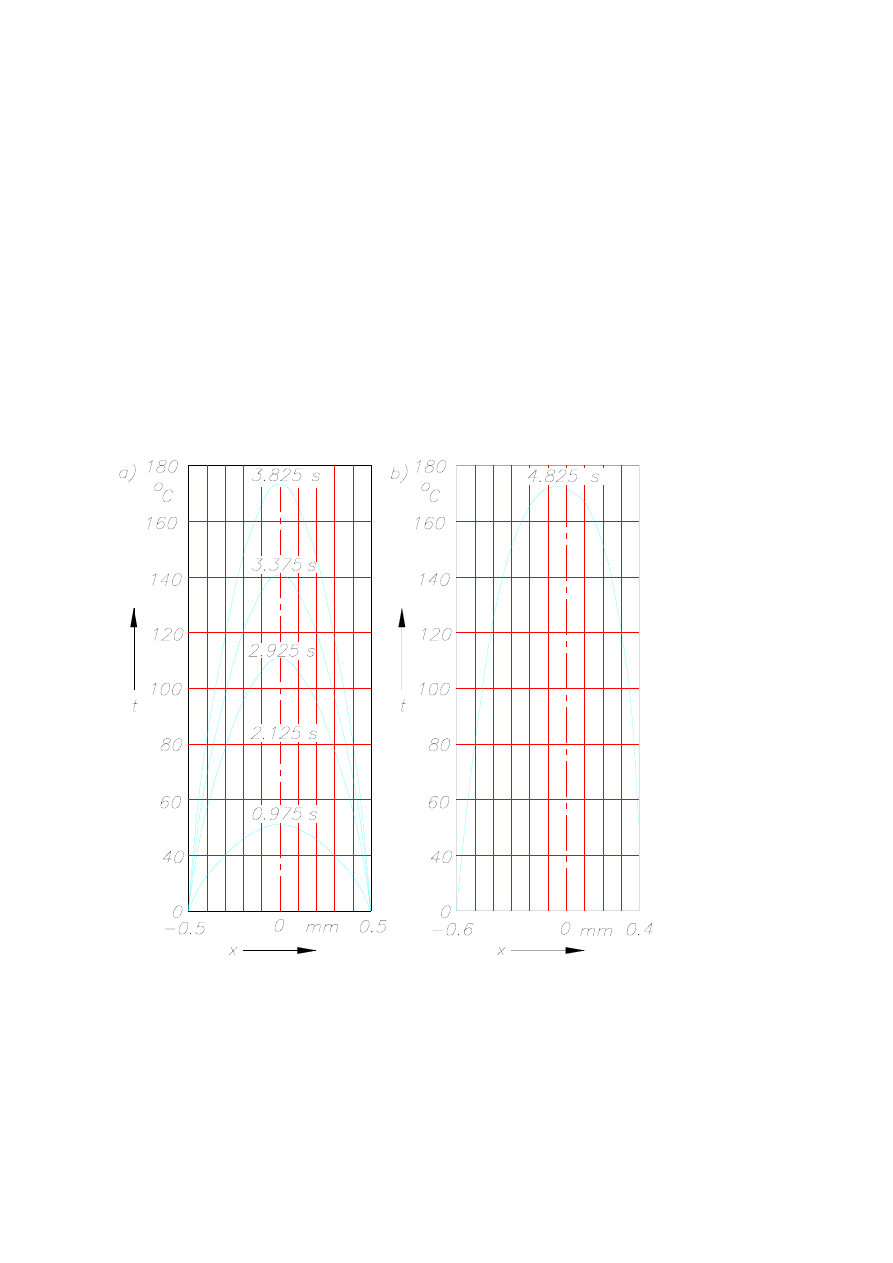
rozwiązań ma pewną cechę wspólną, co widać z rys. 7.9. Otóż przy nagrzewaniu wsadów
jednorodnych najwyższe temperatury występują w obszarach wewnętrznych'' wsadu. Ma to
bardzo duże znaczenie przy zgrzewaniu materiałów, ponieważ uzyskuje się rozkład
temperatur w strefie złącza gwarantujący uplastycznienie (stopienie) materiału, bez obawy o
jego przywarcie do elektrod.

Rys. 7.9. Rozkład temperatury w zgrzewanych foliach: a) o jednakowych grubościach, b) o niejednakowych

grubościach

Przy nagrzewaniu pojemnościowym istnieje znaczna łatwość kształtowania pola

temperatury. W przykładzie przedstawionym na rys. 7.9b uzyskano przesunięcie maksimum
temperatury do płaszczyzny złącza w warunkach zgrzewania dwóch folii o niejednakowych
grubościach. Uzyskuje się to m.in. przez ograniczenie odpływu ciepła do jednej z elektrod w
wyniku wprowadzenia między nią i wsad dodatkowego dielektryka.

182