1

Wydział Elektroniki Mikrosystemów i Fotoniki

Politechnika Wrocławska

Fizyka dla elektroników 2

Nr ćwiczenia:

Temat:

10

Sprawdzanie prawa Hooke’a i wyznaczanie modułu Younga

Termin zajęć

Prowadzący

Sprawozdanie wykonał

Ocena

Wt., 16 III 2010

Godz. 15.15-16.45

Dr inż. Ewa

Oleszkiewicz

Andrzej Głowacki 163968

I.

Cel ćwiczenia

Sprawdzenie prawa Hooke’a oraz wyznaczenie modułu Younga badanego drutu metodą

pomiaru wydłużenia.

II.

Spis przyrządów

•

Urządzenie do pomiaru wydłużenia

•

Przymiar metrowy

•

Ś

ruba mikrometryczna

•

Komplet metalowych walców

•

Waga

III.

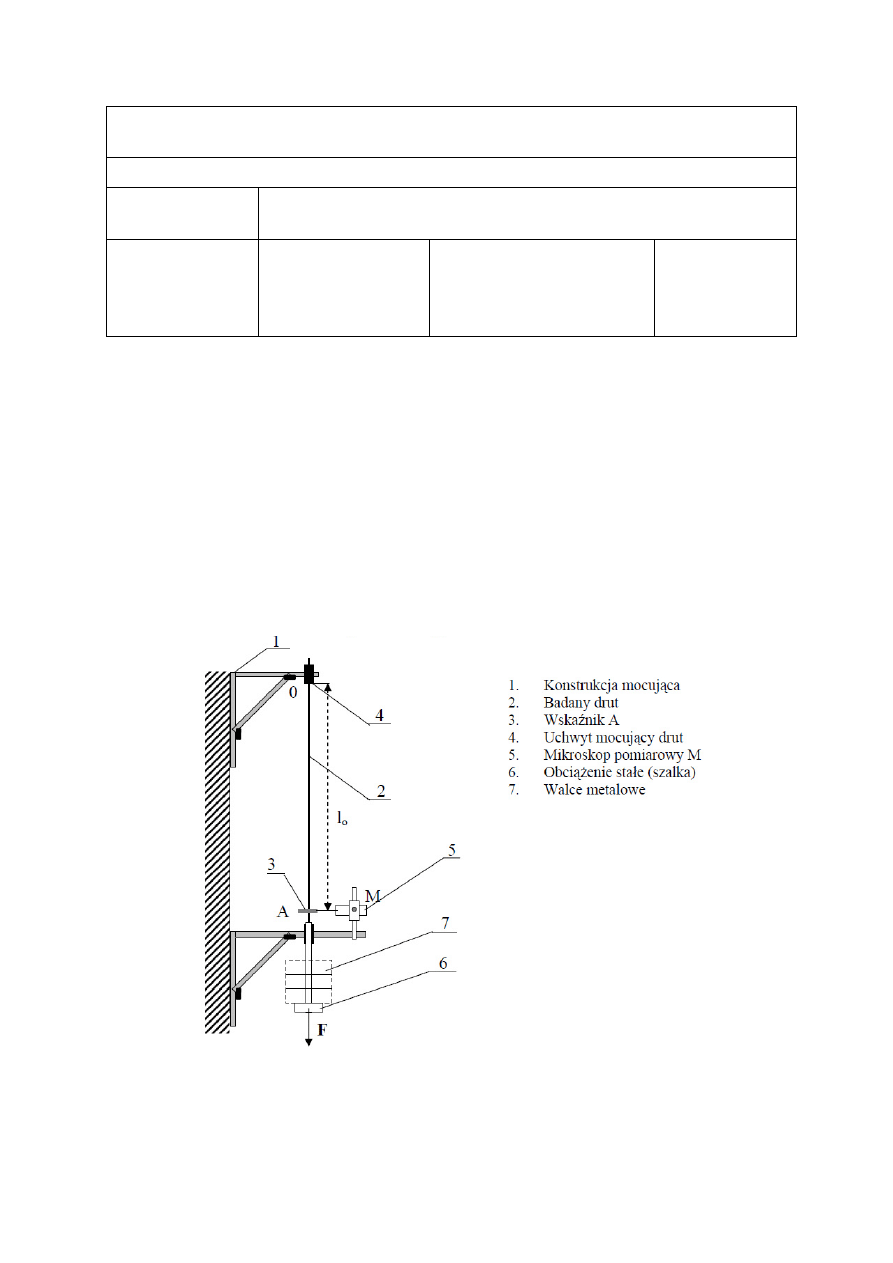
Układ pomiarowy

Po dokonaniu wstępnych pomiarów takich jak pomiar początkowej długości drutu, oraz

pomiarów koniecznych do wycechowania mikroskopu, mierzone było wydłużenie drutu pod
wpływem walców o zmierzonej wcześniej masie. Możliwe wówczas było wyznaczenie
zależności względnego wydłużenia drutu od naprężenia (sprawdzenia prawa Hooke’a). Na tej
podstawie metodą regresji liniowej wyznaczony został moduł Younga dla badanego drutu.

2

IV.

Wyniki i opracowanie pomiarów

(błędy bezwzględne były przybliżane do pierwszej cyfry znaczącej w górę, o ile wstępne przybliżenie nie
zmieniało ich wartości o więcej niż 10% - w przeciwnym wypadku do dwóch cyfr znaczących)

a)

Parametry stałe drutu oraz cechowanie mikroskopu

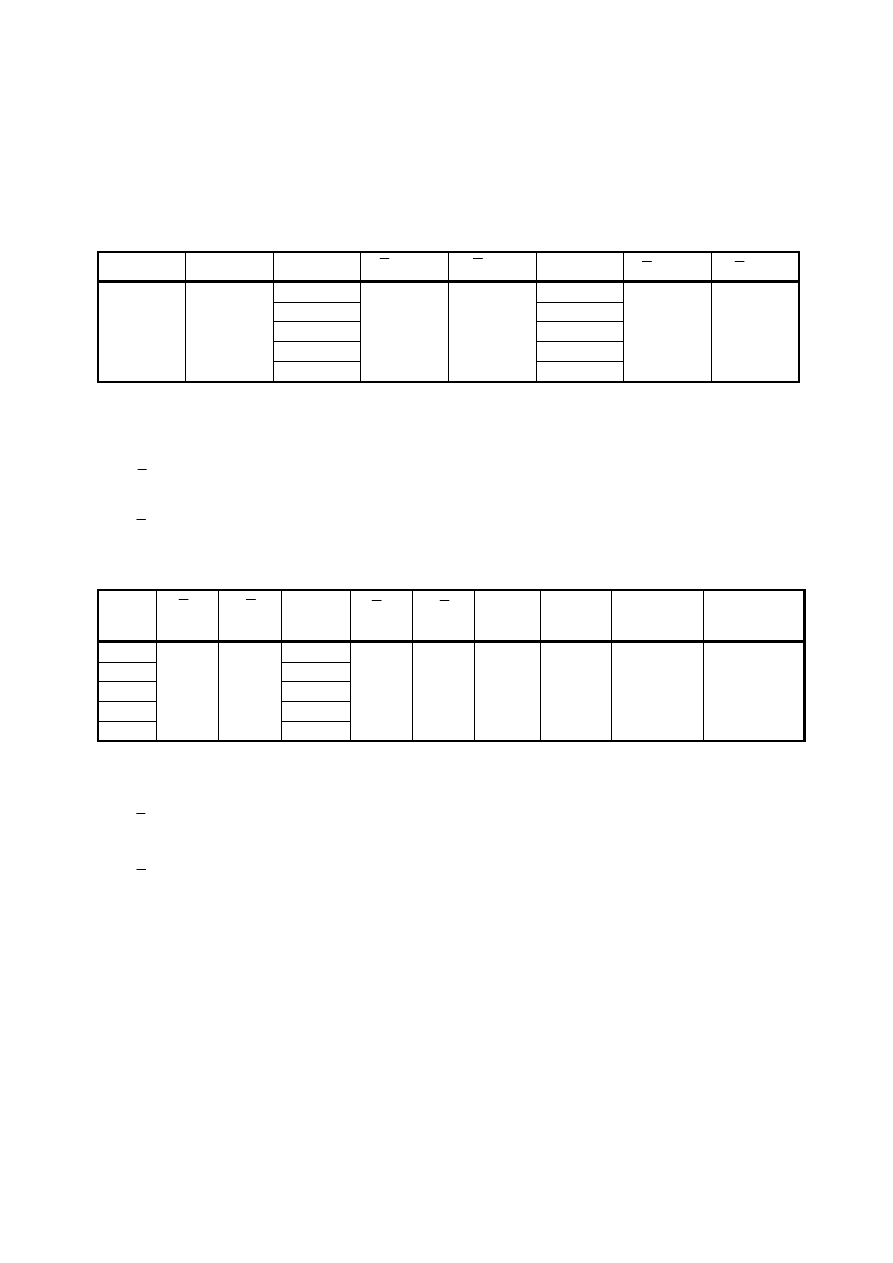
Tabela 1 – Wyniki wstępnych pomiarów i obliczeń

0

l

[mm]

0

l

∆

[mm]

i

d

[mm]

d

[mm]

d

∆

[mm]

i

a

[mm]

a

[mm]

∆

a

[mm]

1,19

0,77

1,18

0,78

1,20

0,79

1,17

0,77

613

±1

-

1,185

±0,010

0,78

0,778

±0,006

Oznaczenia:

0

l

- długość badanego drutu

i

d

- i-ty pomiar średnicy badanego drutu

d - statystycznie wyznaczona średnica badanego drutu (średnia arytmetyczna)

i

a

- i-ty pomiar średnicy wskaźnika za pomocą śruby mikrometrycznej

a - statystycznie wyznaczona średnica wskaźnika (średnia arytmetyczna)

Tabela 2 – Wyniki pomiarów i obliczeń dotyczących cechowania mikroskopu

'

ig

a

[dz]

'

ig

a

[dz]

'

ig

a

∆

[dz]

'

id

a

[dz]

'

id

a

[dz]

'

id

a

∆

[dz]

'

a

[dz]

'

a

∆

[dz]

w

[mm/dz]

w

∆

[mm/dz]

1,42

4,27

1,49

4,25

1,41

4,26

1,42

4,27

1,45

1,438

±0,022

4,30

4,270

±0,013

2,832

±0,035

0,275

±0,006

Oznaczenia:

'

ig

a - i-ty pomiar górnej krawędzi wskaźnika za pomocą mikroskopu

'

ig

a

- statystycznie wyznaczona górna krawędź wskaźnika (średnia arytmetyczna)

'

id

a

- i-ty pomiar dolnej krawędzi wskaźnika za pomocą mikroskopu

'

id

a

- statystycznie wyznaczona dolna krawędź wskaźnika (średnia arytmetyczna)

'

a

- wypadkowa średnica wskaźnika zmierzona za pomocą mikroskopu

w

- wartość działki skali mikroskopu

Wykorzystane wzory i przykładowe obliczenia:

Długość badanego drutu zmierzona została przymiarem metrowym o dokładności 1 mm

zatem za błąd bezwzględny tego pomiaru przyjęto ±1 mm. Pomiary średnicy badanego drutu,
ś

rednicy wskaźnika zmierzonej za pomocą śruby mikrometrycznej, oraz położenia dolnej i

górnej krawędzi wskaźnika w mikroskopie dokonane zostały kilkakrotnie, zatem pomiary te
poddane zostały analizie statystycznej. W charakterze najlepszej oceny wartości rzeczywistej
tych pomiarów przyjęto średnią arytmetyczną z serii. Natomiast za miarę niepewności pomiaru
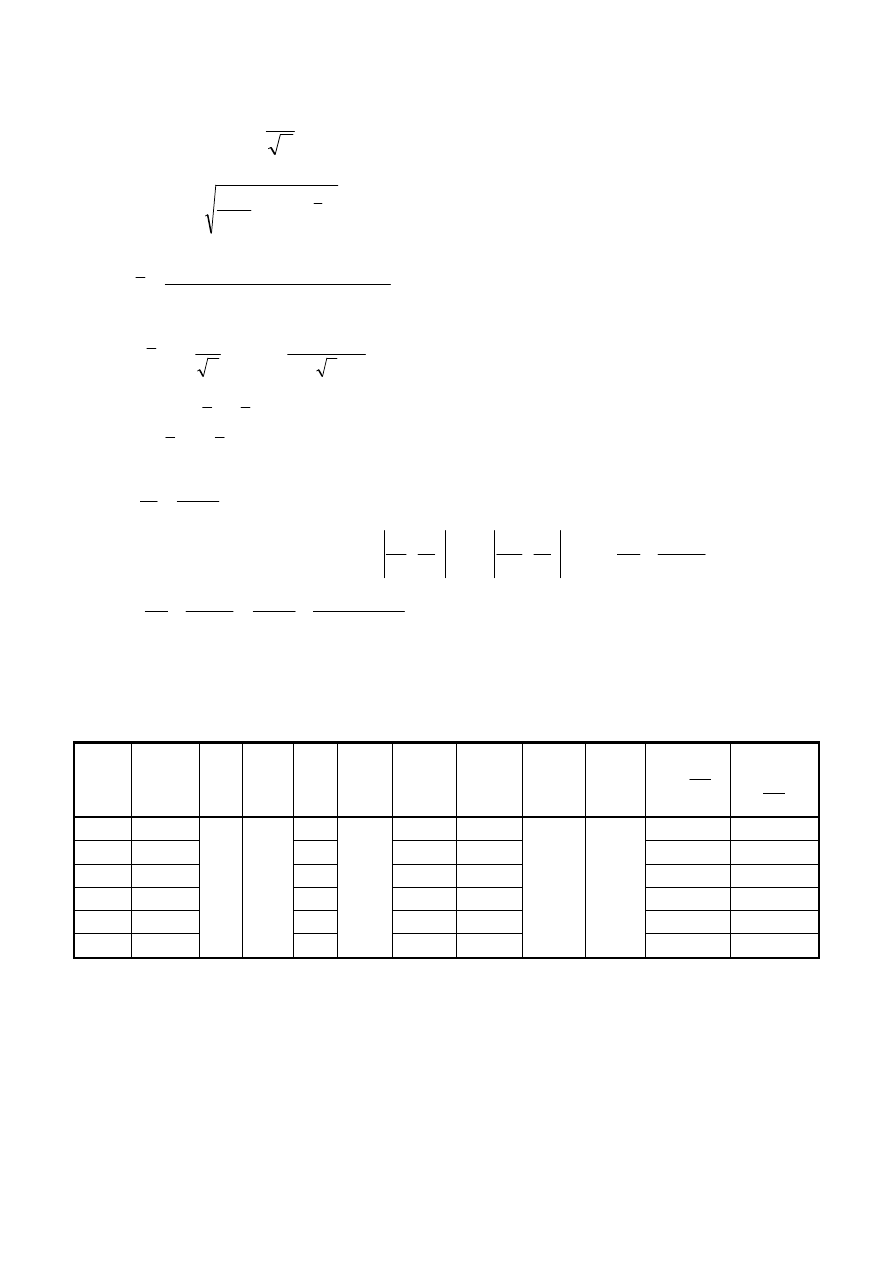
przyjęto wartość oszacowaną z wykorzystaniem rozkładu Studenta-Fishera, zgodnie z

3

zależnością:

n

k

x

σ

⋅

=

∆

, gdzie k jest współczynnikiem rozkładu t-Studenta (w obliczeniach

wykorzystano wartości dla poziomu ufności 0,75),

σ

-odchylenie standardowe pojedynczego

pomiaru

(

)

∑

=

−

−

=

n

i

i

x

x

n

1

2

1

1

σ

, n – liczba prób w serii pomiarów.

Przykładowo dla pomiaru średnicy wskaźnika:

]

[

778

,

0

5

78

,

0

77

,

0

79

,

0

78

,

0

77

,

0

mm

a

=

+

+

+

+

=

]

[

0,0083666 mm

=

σ

]

[

006

,

0

00552

,

0

5

0083666

,

0

476

,

1

mm

n

k

a

±

≈

=

⋅

=

⋅

=

∆

σ

Wypadkowa

ś

rednica wska

ź

nika zmierzona za pomoc

ą

mikroskopu została wyznaczona

jako:

]

[

832

,

2

438

,

1

270

,

4

'

'

'

dz

a

a

a

ig

id

=

−

=

−

=

,

natomiast

bł

ą

d

bezwzgl

ę

dny

jako:

]

[

035

,

0

013

,

0

022

,

0

'

'

'

dz

a

a

a

ig

id

=

+

=

∆

+

∆

=

∆

.

Wartość

działki

skali

mikroskopu

wyliczona

została

zgodnie

z

zależnością:

]

/

[

275

,

0

2747

,

0

832

,

2

778

,

0

'

dz

mm

a

a

w

≈

=

=

=

. Niepewność bezwzględna tego pomiaru wyznaczona

została metodą różniczki zupełnej:

( )

2

'

'

'

'

'

'

'

a

a

a

a

a

a

a

a

a

a

a

a

a

w

∆

⋅

+

∆

=

∆

⋅













∂

∂

+

∆

⋅













∂

∂

=

∆

.

( )

(

)

]

/

[

006

,

0

005514

,

0

003395

,

0

002119

,

0

832

,

2

035

,

0

778

,

0

832

,

2

006

,

0

2

2

'

'

'

dz

mm

a

a

a

a

a

w

±

≈

=

+

=

⋅

+

=

∆

⋅

+

∆

=

∆

b)

Pomiary wydłużenia drutu

Dokładanie walców:

Tabela 3 – Część pomiarów dotyczących wydłużenia drutu (dokładanie walców)

i

m

[kg]

i

m

∆

[kg]

0

a

[dz]

0

a

∆

[dz]

i

a

[dz]

i

a

∆

[dz]

i

F

[N]

i

F

∆

[N]

S

[

2

m

]

S

∆

[

2

m

]

i

σ









2

m

N

i

σ

∆









2

m

N

0,9986

±

0,0001

4,16

9,796

±

0,001

8,91

6

10

⋅

±

0,17

6

10

⋅

1,9970

±

0,0002

4,06

19,591

±

0,002

17,81

6

10

⋅

±

0,33

6

10

⋅

2,9950

±

0,0003

3,98

29,381

±

0,003

26,7

6

10

⋅

±

0,5

6

10

⋅

3,9937

±

0,0004

3,78

39,178

±

0,004

35,6

6

10

⋅

±

0,7

6

10

⋅

4,9918

±

0,0005

3,71

48,970

±

0,005

44,5

6

10

⋅

±

0,9

6

10

⋅

5,9900

±

0,0006

4,29

±

0,02

3,43

±

0,02

58,762

±

0,006

1,10

6

10

−

⋅

±

0,02

6

10

−

⋅

53,4

6

10

⋅

±

1,0

6

10

⋅

Oznaczenia:

i

m - sumaryczna masa dołożonych walców

0

a

- początkowe położenie wskaźnika

i

a

- położenie wskaźnika po wydłużeniu pod wpływem dołożonych walców

i

F

- siła z jaką walce działały na drut (siła ciężkości)

S

- powierzchnia przekroju drutu

i

σ

- naprężenie drutu

4

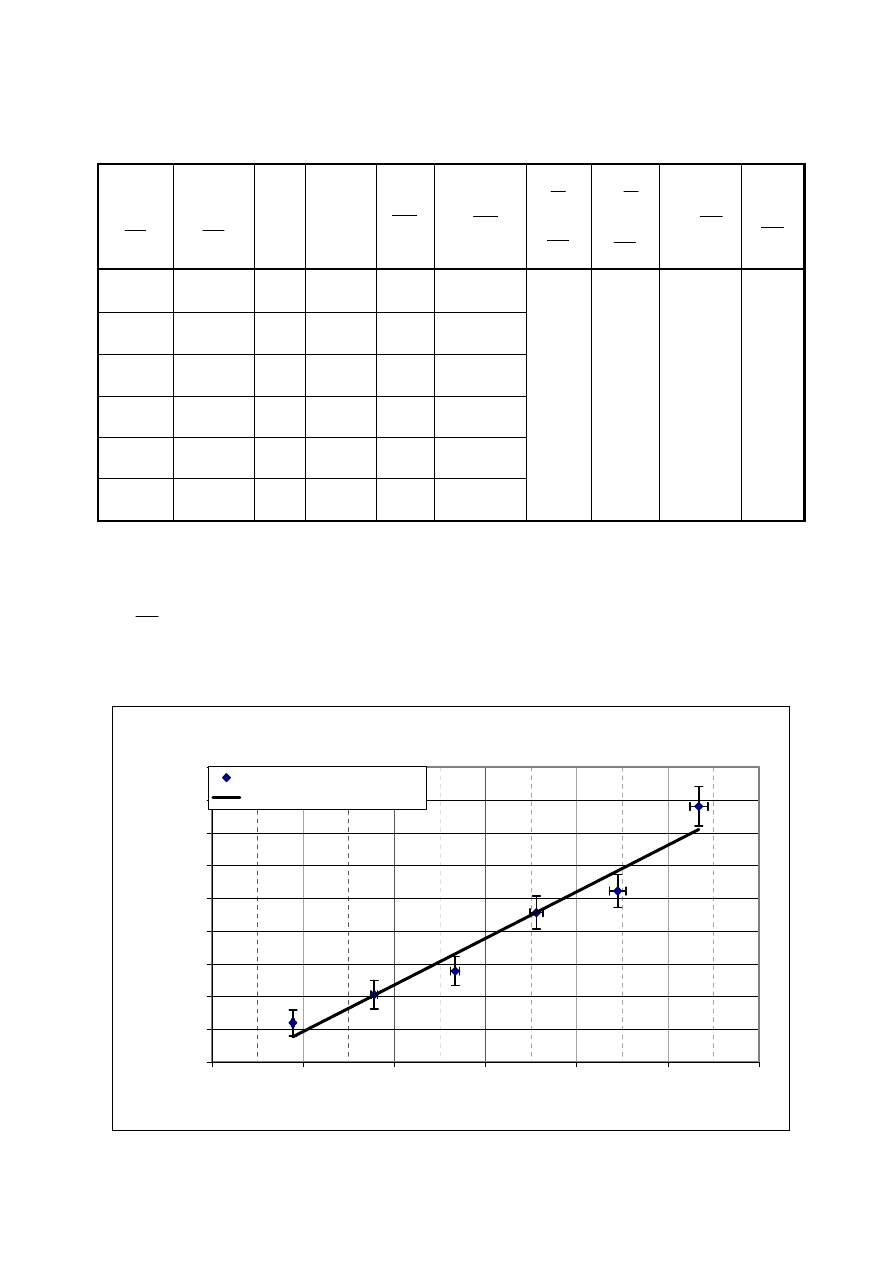
Tabela 4 – Ostateczne wyniki obliczeń (dokładanie walców)

i

σ









2

m

N

i

σ

∆









2

m

N

i

l

∆

[mm]

( )

i

l

∆

∆

[mm]

0

l

l

i

∆













∆

∆

0

l

l

i

E

1













N

m

2













∆

E

1













N

m

2

E









2

m

N

E

∆









2

m

N

8,91

6

10

⋅

±

0,17

6

10

⋅

0,036

±

0,012

0,6

4

10

−

⋅

±

0,2

4

10

−

⋅

17,81

6

10

⋅

±

0,33

6

10

⋅

0,063

±

0,013

1,03

4

10

−

⋅

±

0,22

4

10

−

⋅

26,7

6

10

⋅

±

0,5

6

10

⋅

0,085

±

0,013

1,39

4

10

−

⋅

±

0,22

4

10

−

⋅

35,6

6

10

⋅

±

0,7

6

10

⋅

0,140

±

0,015

2,28

4

10

−

⋅

±

0,25

4

10

−

⋅

44,5

6

10

⋅

±

0,9

6

10

⋅

0,160

±

0,015

2,61

4

10

−

⋅

±

0,25

4

10

−

⋅

53,4

6

10

⋅

±

1,0

6

10

⋅

0,237

±

0,017

3,9

4

10

−

⋅

±

0,3

4

10

−

⋅

7,1

12

10

−

⋅

±

0,8

12

10

−

⋅

1,41

11

10

⋅

±

0,16

11

10

⋅

Oznaczenia:

i

σ

- naprężenie drutu

i

l

∆

- wydłużenie drutu

0

l

l

i

∆

- względne wydłużenie drutu

E – moduł Younga

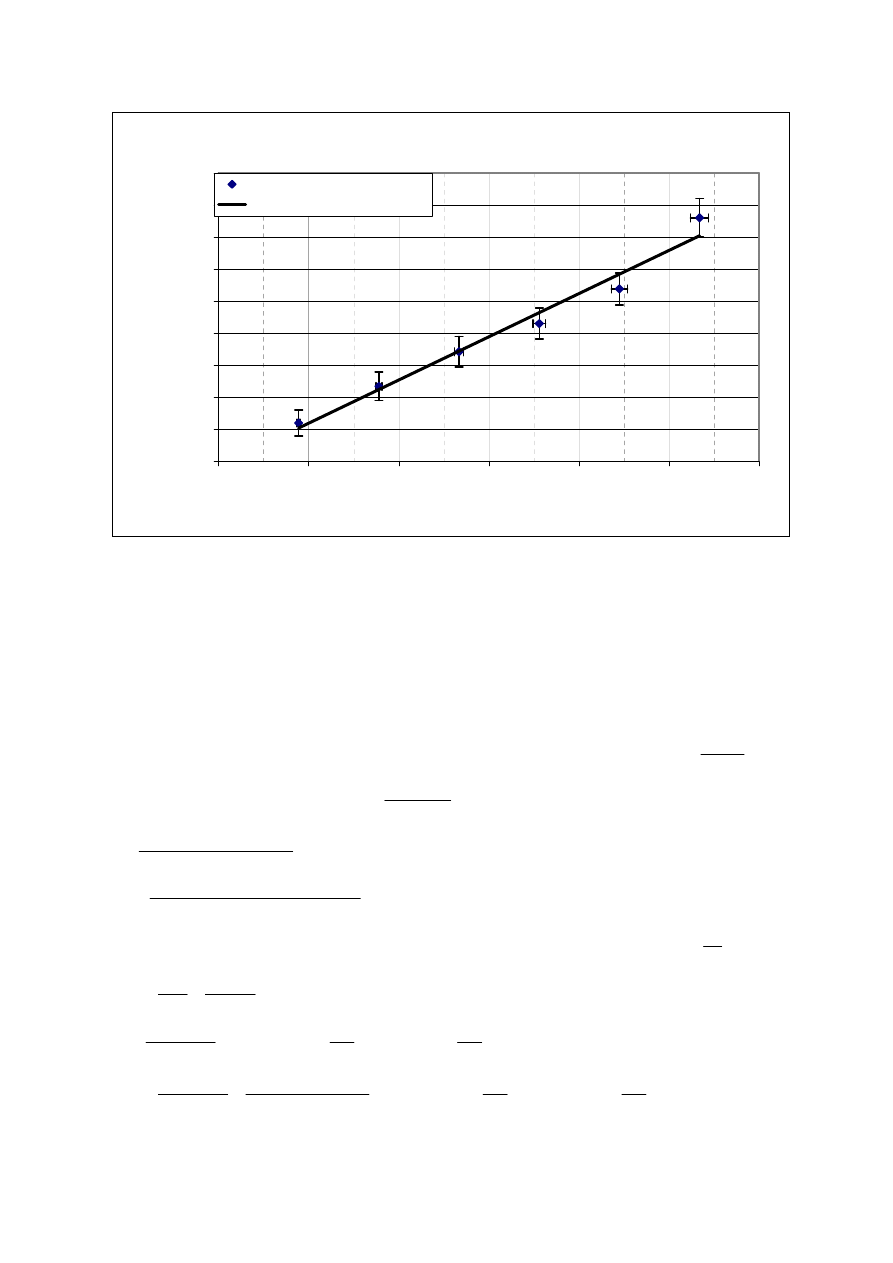
Zale

ż

no

ść

wzgl

ę

dnego wydłu

ż

enie drutu od napr

ęż

enia

(dokładanie walców)

0,00000

0,00005

0,00010

0,00015

0,00020

0,00025

0,00030

0,00035

0,00040

0,00045

0,0E+00

1,0E+07

2,0E+07

3,0E+07

4,0E+07

5,0E+07

6,0E+07

Napr

ęż

enie drutu [N/m

2

]

W

z

g

l

ę

d

n

e

w

y

d

łu

ż

e

n

ie

Punkty pomiarowe

Liniowy (Punkty pomiarowe)

5

Zdejmowanie walców:

Wyniki w tabelach zostały przedstawione w odwrotnej kolejności niż dokonywane były
pomiary w celu wygodniejszej korelacji z wynikami dla dokładania walców.

Tabela 5 – Część pomiarów dotyczących wydłużenia drutu (zdejmowanie walców)

i

m

[kg]

i

m

∆

[kg]

0

a

[dz]

0

a

∆

[dz]

i

a

[dz]

i

a

∆

[dz]

i

F

[N]

i

F

∆

[N]

S

[

2

m

]

S

∆

[

2

m

]

i

σ









2

m

N

i

σ

∆









2

m

N

0,9986

±

0,0001

4,15

9,796

±

0,001

8,91

6

10

⋅

±

0,17

6

10

⋅

1,9970

±

0,0002

4,02

19,591

±

0,002

17,81

6

10

⋅

±

0,33

6

10

⋅

2,9950

±

0,0003

3,9

29,381

±

0,003

26,7

6

10

⋅

±

0,5

6

10

⋅

3,9937

±

0,0004

3,8

39,178

±

0,004

35,6

6

10

⋅

±

0,7

6

10

⋅

4,9918

±

0,0005

3,68

48,970

±

0,005

44,5

6

10

⋅

±

0,9

6

10

⋅

5,9900

±

0,0006

4,28

±

0,02

3,43

±

0,02

58,762

±

0,006

1,10

6

10

−

⋅

±

0,02

6

10

−

⋅

53,4

6

10

⋅

±

1,0

6

10

⋅

Tabela 6 – Ostateczne wyniki obliczeń (zdejmowanie walców)

i

σ









2

m

N

i

σ

∆









2

m

N

i

l

∆

[mm]

( )

i

l

∆

∆

[mm]

0

l

l

i

∆













∆

∆

0

l

l

i

E

1













N

m

2













∆

E

1













N

m

2

E









2

m

N

E

∆









2

m

N

8,91

6

10

⋅

±

0,17

6

10

⋅

0,036

±

0,012

0,6

4

10

−

⋅

0,2

4

10

−

⋅

17,81

6

10

⋅

±

0,33

6

10

⋅

0,072

±

0,013

1,17

4

10

−

⋅

0,22

4

10

−

⋅

26,7

6

10

⋅

±

0,5

6

10

⋅

0,105

±

0,014

1,71

4

10

−

⋅

0,24

4

10

−

⋅

35,6

6

10

⋅

±

0,7

6

10

⋅

0,132

±

0,014

2,15

4

10

−

⋅

0,24

4

10

−

⋅

44,5

6

10

⋅

±

0,9

6

10

⋅

0,165

±

0,015

2,69

4

10

−

⋅

0,25

4

10

−

⋅

53,4

6

10

⋅

±

1,0

6

10

⋅

0,234

±

0,017

3,8

4

10

−

⋅

0,3

4

10

−

⋅

6,7

12

10

−

⋅

±

0,8

12

10

−

⋅

1,49

11

10

⋅

±

0,18

11

10

⋅

6

Zale

ż

no

ść

wzgl

ę

dnego wydłu

ż

enie drutu od napr

ęż

enia

(zdejmowanie walców)

0,00000

0,00005

0,00010

0,00015

0,00020

0,00025

0,00030

0,00035

0,00040

0,00045

0,0E+00

1,0E+07

2,0E+07

3,0E+07

4,0E+07

5,0E+07

6,0E+07

Napr

ęż

enie drutu [N/m

2

]

W

z

g

l

ę

d

n

e

w

y

d

łu

ż

e

n

ie

Punkty pomiarowe

Liniowy (Punkty pomiarowe)

Wykorzystane wzory i przykładowe obliczenia:

Każdy z walców ważony był osobno z dokładnością 0,1 g, zatem błąd bezwzględny

sumarycznej masy dołożonych walców, jest sumą niepewności masy pojedynczych walców.

Jako błąd pomiaru odczytów z mikroskopu, ze względu na nieostry obraz, przyjęto

±0,02 [dz]. Siłę działającą na drut wyznaczono jako:

g

m

F

i

i

⋅

=

, gdzie

i

m

oznacza sumaryczną masę

dołożonych

walców,

zatem

g

m

F

i

i

⋅

∆

=

∆

.

Przykładowo

dla

jednego

walca:

]

[

796

,

9

]

[

79627

,

9

81

,

9

9986

,

0

N

N

F

i

≈

=

⋅

=

,

]

[

001

,

0

]

[

000981

,

0

81

,

9

0001

,

0

N

N

F

i

±

≈

=

⋅

=

∆

.

Powierzchnia przekroju drutu wyznaczona została zgodnie z zależnością:

4

2

d

S

⋅

=

π

, gdzie

d oznacza średnicę drutu, zatem

2

d

d

S

∆

⋅

⋅

=

∆

π

. Obliczenia:

(

)

]

[

10

10

,

1

]

[

10

1028

,

1

4

001185

,

0

14159

,

3

2

6

2

6

2

m

m

S

−

−

⋅

≈

⋅

=

⋅

=

,

]

[

10

02

,

0

]

[

10

01861

,

0

2

000010

,

0

001185

,

0

14159

,

3

2

6

2

6

m

m

S

−

−

⋅

±

≈

⋅

=

⋅

⋅

=

∆

.

Warto

ść

napr

ęż

enia

drutu

wyznaczy

ć

mo

ż

na

ze

wzoru:

S

F

i

i

=

σ

,

zatem

2

S

F

S

S

F

i

i

i

⋅

∆

+

∆

=

∆

σ

(wyznaczone metod

ą

ró

ż

niczki zupełnej). Przykładowo:









⋅

≈









⋅

=

⋅

=

−

2

6

2

6

6

10

91

,

8

10

9055

,

8

10

10

,

1

796

,

9

m

N

m

N

i

σ

,

(

)









⋅

±

≈









⋅

=

⋅

⋅

⋅

+

⋅

=

∆

−

−

−

2

6

2

6

2

6

6

6

10

17

,

0

10

1628

,

0

10

10

,

1

796

,

9

10

02

,

0

10

10

,

1

001

,

0

m

N

m

N

i

σ

7

Wydłużenie drutu obliczone zostało jako:

(

)

i

i

a

a

w

l

−

⋅

=

∆

0

. Pomiary

0

a oraz

i

a obarczone

są niepewnością

±0,02 [dz], zatem

(

)

04

,

0

0

=

−

∆

i

a

a

[dz]. Niepewność bezwzględną pomiaru

wydłużenia drutu obliczyć więc można jako:

( )

(

)

(

)

(

)

04

,

0

0

0

0

⋅

+

−

⋅

∆

=

−

∆

⋅

+

−

⋅

∆

=

∆

∆

w

a

a

w

a

a

w

a

a

w

l

i

i

i

i

(wyznaczone metodą różniczki

zupełnej). Przykładowo (dla dokładania walców):

(

)

]

[

036

,

0

]

[

03575

,

0

16

,

4

29

,

4

275

,

0

mm

mm

l

i

≈

=

−

⋅

=

∆

,

(

)

]

[

012

,

0

]

[

01178

,

0

275

,

0

04

,

0

16

,

4

29

,

4

006

,

0

mm

mm

l

i

±

≈

=

⋅

+

−

⋅

=

∆

.

Względne

wydłużenie

drutu

wynosi:

0

l

l

i

∆

i

obarczone

jest

niepewnością:

( )

2

0

0

0

0

l

l

l

l

l

l

l

i

i

i

∆

⋅

∆

+

∆

∆

=













∆

∆

. Przykładowo:

4

5

0

10

6

,

0

10

873

,

5

613

036

,

0

−

−

⋅

≈

⋅

=

=

∆

l

l

i

,

4

4

2

0

10

2

,

0

10

1967

,

0

613

1

036

,

0

613

012

,

0

−

−

⋅

±

≈

⋅

=

⋅

+

=













∆

∆

l

l

i

.

Współczynnik sprężystości

E

1

(odwrotno

ść

modułu Younga) wyznaczony został metod

ą

regresji

liniowej

jako

nachylenie

prostej

postaci:

σ

⋅

=

∆

E

l

l

1

0

:

Γ

⋅





































−













=

∑

∑

∑

=

=

=

1

1

1

1

1

n

i

i

n

i

i

n

i

i

i

y

x

y

x

n

E

, gdzie

i

i

x

σ

=

,

0

l

l

y

i

i

∆

=

, n=6 (liczba punktów

pomiarowych) oraz

2

1

1

2













−













=

Γ

∑

∑

=

=

n

i

i

n

i

i

x

x

n

. Niepewno

ść

współczynnika spr

ęż

ysto

ś

ci

wyniosła:

Γ

=













∆

n

E

y

ς

1

, gdzie

(

)

2

1

2

−

−

=

∑

=

n

ax

y

n

i

i

i

y

ς

.

Moduł Younga wyznaczony został jako odwrotno

ść

współczynnika spr

ęż

ysto

ś

ci, a jego

niepewno

ść

wyniosła:

2

1

1

























∆

=

∆

E

E

E

.

V.

Wnioski

Otrzymane w wyniku analizy przeprowadzonych pomiarów warto

ś

ci modułu Younga

dla procesu dokładania i zdejmowania obci

ąż

enia s

ą

bardzo zbli

ż

one i bior

ą

c pod uwag

ę

przedziały niepewno

ś

ci, mo

ż

na stwierdzi

ć

,

ż

e s

ą

niesprzeczne (wyniki maj

ą

cz

ęść

wspóln

ą

).

Warto zauwa

ż

y

ć

,

ż

e ostatni z pomiarów (dla 6 walców) nieco bardziej odstaje od liniowego

rozło

ż

enia pozostałych punktów pomiarowych (nie jest to bł

ą

d gruby – po zako

ń

czeniu

pomiarów wła

ś

ciwych podczas laboratorium, został on niezale

ż

nie powtórzony w celu

weryfikacji), mo

ż

na wi

ę

c wnioskowa

ć

,

ż

e napr

ęż

enia działaj

ą

ce na drut przy obci

ąż

eniu

sze

ś

cioma walcami s

ą

blisko granic, w których stosowa

ć

mo

ż

na prawo Hooke’a dla badanego

drutu. Odst

ę

pstwo ostatniego punktu pomiarowego byłoby nieco lepiej widoczne, gdyby prost

ą

8

aproksymującą, wyliczoną metodą regresji liniowej, wyznaczyć nie biorąc go pod uwagę.
Pozostałe punkty pomiarowe cechują się dobrą liniowością, co jednoznacznie potwierdza
prawo Hooke’a.

Wyniki pomiarów modułu Younga obarczone są stosunkowo dużą niepewnością (w obu

przypadkach błąd względny wyniósłby ok. 11-12%) na co istotny wpływ miało rozproszenie
punktów pomiarowych względem prostej aproksymującej (szczególnie ostatni punkt
pomiarowy), jako że niepewność tego pomiaru wyznaczona została na podstawie metody
regresji liniowej.