Zarządzanie Finansami Przedsiębiorstw – Rozwiązania – Teoria – Egzamin.

1. Czynnikami kształtującymi poziom wymaganej stopy zwrotu szacowanej w oparciu o model CAPM są:

•

poziom stopy zwrotu z inwestycji wolnych od ryzyka,

•

poziom przeciętnej rynkowej stopy zwrotu z inwestycji w danej gospodarce,

•

poziom ryzyka inwestycyjnego związanego z danym przedsiębiorstwem.

2. Z punktu widzenia zakresu inwestowania inwestycje rzeczowe dzielimy na:

•

inwestycje odtworzeniowe,

•

inwestycje modernizacyjne,

•

inwestycje rozwojowe.

3. Do metod dynamicznej oceny efektywności inwestycji należą:

•

wartość zaktualizowana netto (NPV),

•

metoda wewnętrznej story zwrotu (IRR),

•

stopa zysku z inwestycji (wskaźnik rentowności).

4. Zyski wytransferowane w przedsiębiorstwie mogą być przeznaczane na:

•

tantiemy,

•

dywidendy,

•

cele charytatywne.

5. Z punktu widzenia postaci efektu inwestowania inwestycje dzielimy na:

•

rzeczowe,

•

niematerialne,

•

finansowe.

6. Realna stopa procentowa to:

•

stopa procentowa, pomniejszona o oczekiwaną stopę inflacji. Mówi o realnym poziomie pomnożenia

kapitału.

7. Okres zwrotu nakładów inwestycyjnych to:

•

czas, w jakim przewiduje się zrównanie nakładów inwestycyjnych z nadwyżkami finansowymi. Jest to

prosta metoda oceny projektów inwestycyjnych. Określa okres po upływie którego wpływy pokrywają

poniesione wydatki inwestycyjne.

8. Bezwzględna ocena efektywności inwestycji polega na:

•

ocenie z punktu widzenia zasadności jej realizacji przez inwestora, dane przedsiębiorstwo będzie

bezwzględnie efektywne, jeżeli zapewni inwestorowi akceptowalny przez niego poziom kosztów lub

poziom efektów.

9. Efektywna stopa procentowa to:

•

faktycznie uzyskiwana stopa procentowa, która uwzględnia kapitalizację odsetek w podokresach.

10. Wewnętrzna stopa zwrotu IRR to taka stopa przy której:

•

wartość zaktualizowana netto wynosi zero, czyli wartość wydatków na realizację projektu jest równa

wartości zaktualizowanych wpływów pieniężnych.

11. Informuje ona o:

•

rzeczywistej rentowności danej inwestycji.

12. Względna ocena efektywności inwestycji polega na:

•

porównaniu ze sobą efektywności różnych inwestycji i uszeregowanie ich od najbardziej do najmniej

efektywnych. Odnosi się do przedsięwzięć, które pozytywnie przeszły ocenę bezwzględną.

13. Obligacje kuponowe to:

•

obligacje sprzedawane po wartości nominalnej. Zobowiązują one emitenta do okresowego płacenia tzw.

kuponu (odsetek od wartości nominalnej). Terminy płatności kuponu ustalone są w obligacji.

14. Polityka stałej stopy wypłat dywidendy polega na:

•

wypłacaniu stałej, wyrażonej procentowo części zysku uzyskanego w danym roku obrotowym. Wielkość

dywidendy na akcję zmienia się wraz ze zmianą zysków przypadających na jedną akcję.

15. Niekompletny podział zysku netto w przedsiębiorstwie polega na:

•

część zysku zatrzymanego trafia wówczas do określonych kapitałów najczęściej kapitału zapasowego

część zaś powiększa pozycję bilansową “zyski nie rozdzielone z roku ubiegłego”.

16. Obligatariusz to:

•

posiadacz obligacji.

17. Niedobór kapitału obrotowego netto może zostać obniżony poprzez:

•

wydłużenie okresu płatności zobowiązań.

18. Ryzyko finansowe jest związane z:

•

doborem źródeł finansowania przedsiębiorstwa.

19. Mamy dwie inwestycje: A i B. Jeżeli: NPV(A)>NPV(B) oraz IRR(A)<IRR(B) to sytuacja podana oznacza, że:

•

obie inwestycje mogą być bezwzględnie efektywne, ale ryzyko przy inwestycji A jest większe niż przy

inwestycji B.

20. Instrumentami finansowania własnego – wewnętrznego mogą być:

•

amortyzacja, zyski refinansowane.

21. Instrumentami finansowania własnego – zewnętrznego mogą być:

•

emisja akcji, venture capital.

22. Zaciągnięcie przez inwestora kredytu na sfinalizowanie realizacji inwestycji powoduje:

•

wzrost przepływów pieniężnych przedsięwzięcia inwestycyjnego w okresie jego realizacji.

23. Stopa procentowa może wyrażać:

•

względne ujęcie ceny pieniądza.

24. Model Gordona jest wykorzystywany dla celów:

•

szacowania teraźniejszej wartości akcji zwykłej.

25. Ryzyko operacyjne jest związane z:

•

kształtowaniem się kosztów stałych i zmiennych.

26. Stopa dywidendy informuje bezpośrednio o:

•

opłacalności inwestowania w akcje.

27. Koszt kapitału przedsiębiorstwa wynika z:

•

konieczności wypłacenia odsetek właścicielom tego kapitału.

28. Polityka stałej stopy wypłat dywidendy polega na:

•

ciągłym przeznaczaniu takiej samej wartości procentowej zysku netto na wypłatę dywidend.

Zarządzanie Finansami Przedsiębiorstw – Rozwiązania – Zadania – Egzamin.

1. Inwestor lokujący jednorazowo kapitał w funduszu inwestycyjnym pragnie otrzymywać z tego tytułu wypłaty po

15000 zł na końcu kolejnych 20 lat. Jaką kwotę musi on ulokować na początku pierwszego roku, aby przy rocznej

stopie zwrotu w wysokości 10% oraz stopie podatku dochodowego 20% było to możliwe?

𝐴𝐴 = 15000

𝑛𝑛 = 20

Obliczenia prowadzimy z dołu, ponieważ na końcu każdego roku.

𝑘𝑘

1

= 10% = 0,1

𝑇𝑇 = 20% = 0,2

Uwzględniamy podatek dochodowy.

𝑘𝑘

2

= 𝑘𝑘

1

(1 − 𝑇𝑇) = 10 ∗ 0,8 = 8%

Obliczamy szukaną kwotę.
𝑃𝑃𝑃𝑃𝐴𝐴 = 15000 ∗ �

1

0,08 −

1

0,08 ∗ (1 + 0,08)

20

� = 15000 ∗ (12,5 − 2,68) = 15000 ∗ 9,82 = 147300

Odpowiedź: Inwestor powinien ulokować w funduszu 147 300 zł.

2. Nominalna stopa oprocentowania lokaty bankowej wynosi 5%. Odsetki są kapitalizowane kwartalnie, a stopa

inflacji wynosi 2%. Ile wynosi efektywna stopa oprocentowania tej lokaty w ujęciu realnym (stopa efektywna-

realna)?

𝑟𝑟

𝑛𝑛

= 5% = 0,05

𝑖𝑖 = 2% = 0,02

Obliczamy stopę realną.

𝑟𝑟

𝑟𝑟

=

(𝑟𝑟

𝑛𝑛

− 𝑖𝑖) ∗ 100

100 + 𝑖𝑖

=

(5% − 2%) ∗ 100

100 + 2

=

3% ∗ 100

102% =

300
102 = 2,94%

Odsetki są kapitalizowane kwartalnie więc obliczamy konkretną dla naszego przykładu stopę realną kwartalną.

𝑟𝑟

𝑟𝑟

= 2,94/4 = 0,735%

Obliczamy stopę efektywną.

𝑅𝑅 = (1 + 0,000735)

4

− 1 = 1,0297 − 1 = 0,297 ≈ 3%

Odpowiedź: Efektywna stopa zwrotu w ujęciu realnym wynosi 3%.

3. Zapotrzebowanie przedsiębiorstwa na kapitał obrotowy netto wynosi 3500 tyś. zł. Roczne koszty zakupu towarów

wynoszą 33 000 tyś. zł, a przeciętny okres płatności zobowiązań z tego tytułu wynosi 22 dni. Jak należałoby

zmienić ten okres, aby móc obniżyć zapotrzebowanie na kapitał obrotowy netto do 3300 tyś. zł?

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅1

= 3500

𝑡𝑡𝑡𝑡𝑡𝑡 = 33000

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅2

= 3300

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅

= 𝑍𝑍 + 𝑁𝑁 − 𝑍𝑍𝑂𝑂𝑂𝑂

𝑍𝑍𝑂𝑂𝑂𝑂

1

=

33000

360 ∗ 22 = 2016,67

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅1

= 𝑍𝑍 + 𝑁𝑁 − 𝑍𝑍𝑂𝑂𝑂𝑂

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅1

+ 𝑍𝑍𝑂𝑂𝑂𝑂

1

= 𝑍𝑍 + 𝑁𝑁

𝑍𝑍 + 𝑁𝑁 = 5516,67

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅2

= 𝑍𝑍 + 𝑁𝑁 − 𝑍𝑍𝑂𝑂𝑂𝑂

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅2

= 𝑍𝑍 + 𝑁𝑁 − ś𝑟𝑟. 𝑧𝑧𝑡𝑡𝑧𝑧.∗ 𝑋𝑋

−

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅2

− (𝑍𝑍 + 𝑁𝑁)

ś𝑟𝑟. 𝑧𝑧𝑡𝑡𝑧𝑧.

= 𝑋𝑋

𝑋𝑋 = −

3300 − 5516,67

91,67

= −

−2216,67

91,67 ≈ 24

Odpowiedź: Aby zapotrzebowanie na kapitał obrotowy zmalało do 3300 tyś. zł, okres płatności zobowiązań musi się

wydłużyć/zwiększyć do 24 dni zamiast 22 dni.

4. Przedsiębiorstwo XYZ posiada 600 akcji uprzywilejowanych w spółce ABC. Każda z tych akcji uprawnia do

otrzymywania dywidendy w wysokości 10% jej wartości nominalnej wynoszącej 100 zł. Przedsiębiorstwo

otrzymało od jednego z inwestorów ofertę zakupu tych akcji za kwotę 75000 zł. Wiedząc, że wymagana stopa

zwrotu wynosi 8%, określić, czy ta oferta byłaby dla przedsiębiorstwa opłacalna i dlaczego.

𝑘𝑘 = 8% = 0,08

𝐷𝐷 - oczekiwana kwota dywidendy.

𝐷𝐷 = (10% ∗ 100) ∗ 600 = 0,1 ∗ 100 ∗ 600 = 6000

Jako, że akcje są uprzywilejowane obliczamy ich wartość na zasadzie renty dożywotniej, gdyż wypłacanie dywidendy będzie

odbywać się niejako dożywotnio (w nieokreślonym okresie czasu i na stałym poziomie).
𝑃𝑃𝑃𝑃𝐴𝐴 = 𝐴𝐴 ∗

1
𝑘𝑘 ⇒ 𝑃𝑃

𝑎𝑎

= 𝐷𝐷 ∗

1
𝑘𝑘

𝑃𝑃

𝑎𝑎

= 6000 ∗

1

0,08 = 75000

Odpowiedź: Jako, że wartość akcji jest równa kwocie proponowanej przez inwestora oferta ta jest dla przedsiębiorstwa

neutralna. W tym momencie nie opłaca się jednak sprzedawać akcji, szczególnie biorąc pod uwagę postrzeganie

długoterminowe.

5. Wartość rynkowa spółki na koniec 2004 roku wynosiła 189 mln zł. Na koniec 2008 roku wartość ta wzrosła do

1436 mln zł. Ile wyniosła w rozpatrywanym okresie przeciętna roczna stopa zwrotu z kapitału zainwestowanego w

tę spółkę?

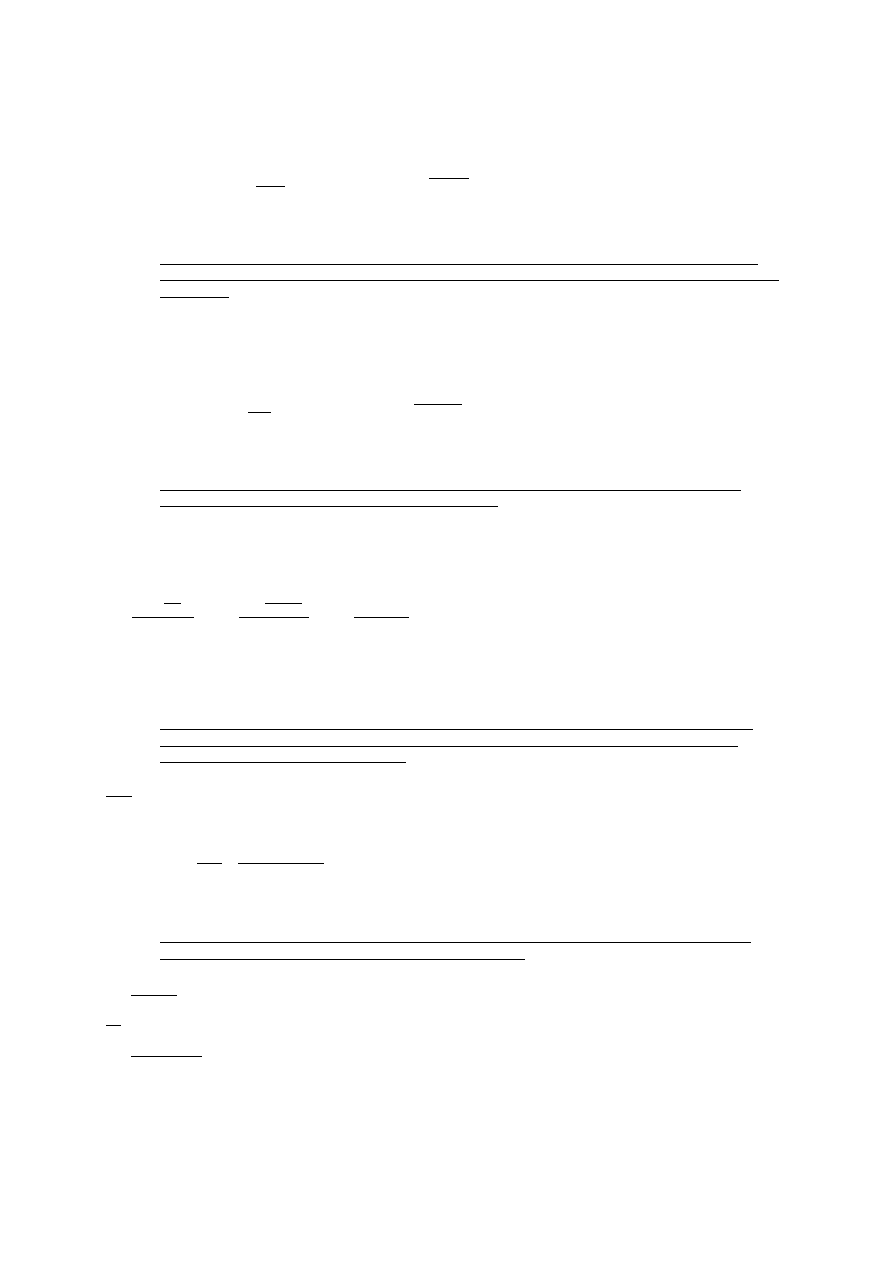
𝑃𝑃𝑃𝑃 = 189

𝐹𝐹𝑃𝑃 = 1436

𝑛𝑛 = 4

𝐹𝐹𝑃𝑃 = 𝑃𝑃𝑃𝑃 ∗ (1 + 𝑟𝑟)

𝑛𝑛

1436 = 189 ∗ (1 + 𝑟𝑟)

4

⇒

1436

189 = (1 + 𝑟𝑟)

4

⇒ 1 + 𝑟𝑟 = �7,5979

4

⇒ 𝑟𝑟 = 0,66 ≈ 66%

Odpowiedź: Roczna stopa zwrotu kapitału zainwestowanego w tą spółkę wynosi 66%.

6. Wartość rynkowa przedsiębiorstwa na koniec 2007 roku wynosiła 527 mln zł. Na koniec 2011 roku wartość ta

wzrosła do 875 mln zł. Ile wyniosła w rozpatrywanym okresie przeciętna stopa zwrotu kapitału zainwestowanego

w tę spółkę?

𝑃𝑃𝑃𝑃 = 527

𝐹𝐹𝑃𝑃 = 875

𝑛𝑛 = 4

𝐹𝐹𝑃𝑃 = 𝑃𝑃𝑃𝑃 ∗ (1 + 𝑟𝑟)

𝑛𝑛

875 = 527 ∗ (1 + 𝑟𝑟)

4

⇒

875
527 = (1 + 𝑟𝑟)

4

⇒ 1 + 𝑟𝑟 = �1,66034

4

⇒ 𝑟𝑟 = 0,14 ≈ 14%

Odpowiedź: Roczna stopa zwrotu kapitału zainwestowanego w tą spółkę wynosi 14%.

7. Inwestor ulokował 10000 zł przy przeciętnej stopie zwrotu wynoszącej 11%. Po jak długim okresie wartość

ulokowanego w ten sposób kapitału osiągnie kwotę 26000 zł?

𝑃𝑃𝑃𝑃 = 10000

𝐹𝐹𝑃𝑃 = 26000

𝑟𝑟 = 11% = 0,11

𝑛𝑛 =

log �𝐹𝐹𝑃𝑃

𝑃𝑃𝑃𝑃�

log⁡(1 + 𝑟𝑟) ⇒ 𝑛𝑛 =

log �26000

10000�

log(1,11) ⇒ 𝑛𝑛 =

0,41497

0,045322 = 9,156

0,156 ∗ 365 ≈ 57

Odpowiedź: Wartość ulokowanego kapitału osiągnie wielkość 26000 zł po 9 latach i 57 dniach.

8. Kredytobiorca zaciąga kredyt w kwocie 500000 zł na okres 8 lat. Stopa oprocentowania kredytu wynosi 12%.

Kredyt będzie spłacany metodą annuitetową w ratach płatnych na końcu kolejnych kwartałów bez okresu

karencji. Obliczyć wartość raty annuitetowej.

𝑃𝑃𝑃𝑃𝐴𝐴 = 500000

𝑛𝑛 = 8

𝑟𝑟 = 12% = 0,12

500000 = 𝐴𝐴 ∗ �

1

0,03 −

1

0,03 ∗ (1,03)

32

� ⇒ 500000 = 𝐴𝐴 ∗ (20,389) ⇒ 𝐴𝐴 = 24523,03

Odpowiedź: Wartość raty annuitetowej wynosi 24523 zł i 3 gr.

9. 4 letnia obligacja dyskontowa jest emitowana po kursie 87%. Jest ona również oprocentowana stopą 3%. Ile

wynosi przeciętna roczna stopa zwrotu z inwestycji w tą obligację?

𝑟𝑟 =

𝑑𝑑 ∗ 100

100 − 𝑑𝑑

87

4 = 21,75

𝑟𝑟 =

21,75 ∗ 100

100 − 21,75 = 27,79

𝑟𝑟 = 27,79 + 3 = 30,79%

Odpowiedź: Przeciętna stopa zwrotu z inwestycji w tą obligację wynosi 30,79%.

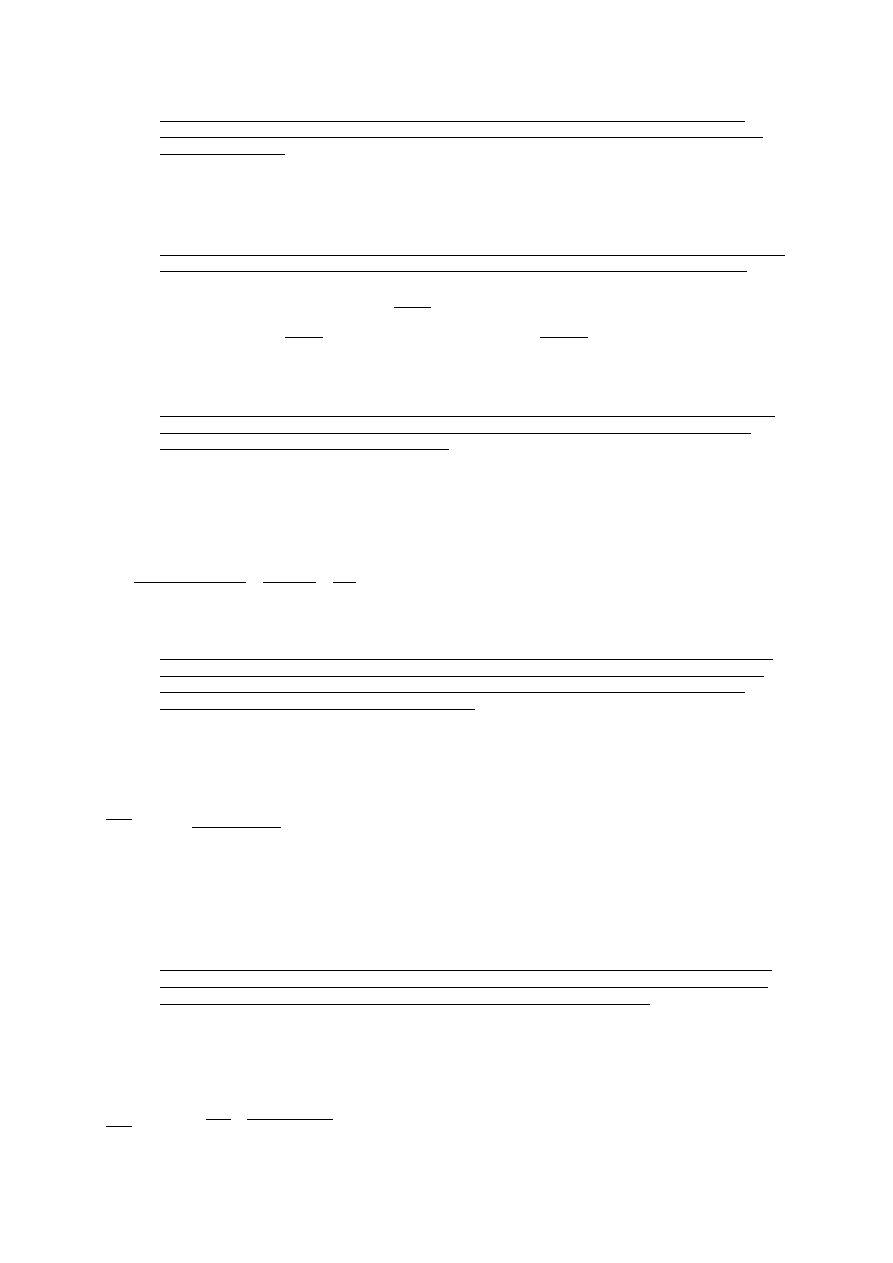
10. Stopa zwrotu z inwestycji wolnych od ryzyka wynosi 4,5% zaś przeciętna rynkowa stopa zwrotu wynosi 9%.

Współczynnik ryzyka beta dla przedsiębiorstwa X wynosi 1,25. Obliczyć ile wynosi wymagana stopa zwrotu dla

tego przedsiębiorstwa.

𝑟𝑟

𝑡𝑡

= 𝑟𝑟

𝑓𝑓

+ 𝛽𝛽 ∗ �𝑟𝑟

𝑚𝑚

− 𝑟𝑟

𝑓𝑓

� = 0,045 + 1,25 ∗ (0,09 − 0,045) = 0,045 + 0,05625 = 0,10125 ≈ 10%

Odpowiedź: Wymagana stopa zwrotu dla tego przedsiębiorstwa wynosi 10%.

11. Przedsiębiorstwo realizuje sprzedaż roczną na poziomie 10000 tyś zł. Przeciętny okres inkasa należności wynosi 32

dni. Jak należałoby zmienić ten okres, aby zapotrzebowanie na kapitał obrotowy netto obniżyć o 250 tyś zł?

𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅

= 𝑍𝑍 + 𝑁𝑁 − 𝑍𝑍𝑂𝑂𝑂𝑂 ⇒ 𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅

− 𝑍𝑍 + 𝑍𝑍𝑂𝑂𝑂𝑂 =

10000

360 ∗ 32 ⇒ 𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅

− 𝑍𝑍 + 𝑍𝑍𝑂𝑂𝑂𝑂 = 888,889

(𝑍𝑍𝑛𝑛𝑍𝑍

𝑂𝑂𝑂𝑂𝑅𝑅

− 𝑍𝑍 + 𝑍𝑍𝑂𝑂𝑂𝑂) − 250 =

10000

360 ∗ 𝑋𝑋 ⇒ 888,889 − 250 = 27,78 ∗ 𝑋𝑋 ⇒

638,889

27,78 = 𝑋𝑋 ⇒ 𝑋𝑋 = 22,99 ≈ 23

Odpowiedź: Okres ten należy zmniejszyć z 32 dni do 23 dni.

12. Kapitał jest lokowany w funduszu inwestycyjnym przy stopie rentowności wynoszącej 12%. Dochody z inwestycji

opodatkowane są 20-to% podatkiem dochodowym. Stopa inflacji wynosi 3%. Ile wyniesie roczna zmiana siły

nabywczej kapitału zainwestowanego w ten sposób?

𝑟𝑟

𝑛𝑛

= 12%

𝑖𝑖 = 3%

𝑇𝑇 = 20%

𝑟𝑟

𝑛𝑛𝑖𝑖

= 12% ∗ (1 − 20%) = 0,096 = 9,6%

𝑟𝑟

𝑟𝑟

=

(9,6% − 3%) ∗ 100

100 + 3

=

6,6 ∗ 100

103

=

660
103 = 6,41%

Odpowiedź: Roczna zmiana siły nabywczej kapitału w ten sposób zainwestowanego wyniesie 6,41%.

13. Inwestor lokuje kapitał w funduszu inwestycyjnym wnosząc na początku kolejnych lat po 3000 zł. Dodatkowo na

końcu 8-go roku inwestowania inwestor wniósł jednorazowo kwotę 12000 zł. Przyjmując, że przeciętna roczna

stopa zwrotu z inwestycji wynosi 10% a dochody z niej są opodatkowane stopą 20% obliczyć stan rachunku

posiadania inwestora na końcu 15-go roku inwestowania.

𝑘𝑘

1

= 10% = 0,1

𝑇𝑇 = 20% = 0,2

Uwzględniamy podatek dochodowy w obliczeniach.

𝑘𝑘

2

= 10% ∗ (1 − 20%) = 0,1 ∗ (1 − 0,2) = 0,08 = 8%

Obliczamy wartość przyszłą przepływów pieniężnych.

𝐹𝐹𝑃𝑃𝐴𝐴 = 3000 ∗

(1 + 0,08)

8

− 1

0,08

∗ (1 + 0,08) = 3000 ∗ 27,1521 ∗ 1,08 = 87972,80

I dokładamy ósmy rok.

𝐹𝐹𝑃𝑃 = 𝑃𝑃𝑃𝑃 ∗ (1 + 𝑟𝑟)

𝑛𝑛

= 12000 ∗ 1,7138 = 20565,60

Łącznie.

20565,60 + 87972,80 = 108538,40

Odpowiedź: Stan rachunku posiadacza (inwestora) na końcu 15-go roku inwestowania wyniesie 108 538 zł i 40 gr.

14. Inwestor lokujący jednorazowo kapitał w funduszu inwestycyjnym pragnie otrzymywać z tego tytułu wypłaty po

3500 zł na końcu kolejnych 20 lat. Jaką kwotę musi on ulokować na początku pierwszego roku, aby przy rocznej

stopie zwrotu w wysokości 10% oraz stopie podatku dochodowego 20% było to możliwe?

𝑘𝑘

1

= 10% = 0,1

𝑇𝑇 = 20% = 0,2

Uwzględniamy podatek dochodowy w obliczeniach.

𝑘𝑘

2

= 10% ∗ (1 − 20%) = 0,1 ∗ (1 − 0,2) = 0,08 = 8%

Obliczamy wartość teraźniejszą przepływów pieniężnych.
𝑃𝑃𝑃𝑃𝐴𝐴 = 15000 ∗ �

1

0,08 −

1

0,08 ∗ (1,08)

20

� = 15000 ∗ (12,5 − 2,68185) = 15000 ∗ 9,8181 = 147272,21

Odpowiedź: Musi ulokować w funduszu na początku 147 272 zł i 21 gr.

15. Inwestor pragnie ulokować kapitał w nabycie akcji spółki ABC. Jest zainteresowany nabyciem 1000 akcji zwykłych.

W minionym roku spółka wypłaciła posiadaczom akcji zwykłych dywidendę w wysokości 18 zł/akcję. W latach

następnych oczekuje się wzrostu dywidendy w tempie 3% rocznie. Inwestor otrzymał ofertę zakupu tych akcji za

kwotę 280000 zł. Jaką decyzję powinien on podjąć, jeżeli jego wymagana stopa zwrotu wynosi 10%?

𝑃𝑃𝑃𝑃 =

𝐷𝐷

𝑟𝑟 − 𝑞𝑞 =

18

0,1 − 0,03 ≈ 257

257 ∗ 1000 = 257000 < 280000

Odpowiedź: Inwestor powinien wstrzymać się z zakupem akcji, ponieważ przepłaci i będzie to dla niego niekorzystna

sytuacja.