1

W

YDZIAŁ

M

ECHATRONIKI

T

EMATY EGZAMINACYJNE Z FIZYKI

-

OPRACOWANIE

1.

Zasady dynamiki. Masa bezwładna i grawitacyjna.

a. Zasady dynamiki
I - ciało nie podlegające działaniu żadnej siły, lub będące pod wpływem sił
równoważących się, spoczywa lub porusza się ruchem jednostajnym prostoliniowym;
II - siłę działającą na ciało określamy jako pochodną pędu tego ciała po czasie

dt

V

m

d

F

)

(

r

r

=

III - każdemu działaniu towarzyszy równe co do wartości i przeciwne co do zwrotu
przeciwdziałanie

b. Masa

Wielkość określona dla danego ciała lub obiektu fizycznego, która wyznacza jego

zachowanie pod działaniem siły (m. inercjalna, czyli bezwładna, wywodząca się z II
zas. dyn. Newtona) lub pod działaniem pola grawitacyjnego (m. grawitacyjna, czyli
ważka, wywodząca się z prawa powszechnego ciążenia). Masy bezwładna i
grawitacyjna są doświadczalnie nierozróżnialne.

2.

Układy odniesienia inercjalne i nieinercjalne.

a. Układ odniesienia

Pewien wybrany układ ciał materialnych, względem którego, za pomocą jakiegoś

układu współrzędnych, określa się położenie dowolnego ciała w przestrzeni w
dowolnej chwili czasu.

b. U.o. inercjalny

Układ, w którym każde ciało nie podlegające zewnętrznemu oddziaływaniu

porusza się bez przyspieszenia (ruchem jedn. prost.) lub spoczywa. Każdy układ
poruszający się bez przyspieszenia lub spoczywający względem u.i. jest również
układem inercjalnym. Wszystkie u.i. (zgodnie z zasadą względności Galileusza) są
całkowicie równouprawnione i są w nich identyczne wszystkie prawa fizyki.

Przestrzeń u.i. jest jednorodna i izotropowa - tj. żadne miejsce ani żaden

kierunek nie jest wyróżniony przez właściwości samej przestrzeni.

c. U.o. nieinercjalny

Układ poruszający się z przyspieszeniem względem dowolnego układu

inercjalnego (np. obracający się względem niego). Występuje w nim działanie sił
pozornych (sił bezwładności), czyli wyrazów pojawiających się przy transformacji
równań ruchu z układu inercjalnego do nieinercjalnego i mających wymiar siły. Nie są
to jednak siły w sensie fizycznym, lecz matematyczne pozostałości przekształceń,
pochodzące właśnie od faktu istnienia przyspieszeń (np. siła Coriolisa, siła
odśrodkowa).

3.

Transformacja Galileusza.

a. Założenia

Jest to przekształcenie wiążące współrzędne punktu materialnego w dwóch

różnych układach współrzędnych związanych z inercjalnymi układami odniesienia. W
t.G. czas jest wielkością absolutną, jest niezmienniczy względem dowolnych u.o.

2

b. Równanie wektorowe transformacji

Gdy układ U’ porusza się względem układu U z prędkością

0

V

r

, to wtedy:

t

V

r

r

r

0

0

r

r

r

r

+

+

′

=

gdzie: r

r

- promień wodzący punktu materialnego w układzie U, r

r

′

- promień

wodzący punktu mat. w układzie U’,

0

r

r

- wektor łączący początki układów

współrzędnych w chwili t=0, od której liczymy czas, t -czas.

4.

Praca, energia kinetyczna i potencjalna, pęd i moment pędu.

a. Praca

Proces przekazywania energii oraz wielkość fizyczna charakteryzująca ten

proces. Definiowana jest jako całka z iloczynu skalarnego siły i elementarnego
przesunięcia na drodze od A do B.

s

d

F

W

r

r

∫

⋅

=

Jednostką pracy w układzie SI jest 1 dżul [J]:

[ ] [ ] [

]

m

N

J

W

1

1

1

⋅

=

=

Wykonanie pracy prowadzi do zmiany energii mechanicznej punktu

materialnego. Energia całkowita nie zmienia się tylko wtedy, gdy działają siły
zachowawcze (występuje wtedy równy wykonanej pracy ubytek energii kinetycznej i
taki sam przyrost energii potencjalnej, lub na odwrót).

b. Energia kinetyczna i potencjalna

* Jednostką energii jest 1 dżul.

I. E. kinetyczna - część energii ciała związana z jego ruchem względem określonego
układu odniesienia.

Wg. mechaniki klasycznej:

- dla p-tu materialnego lub ciała sztywnego poruszającego się ruchem
postępowym z prędkością V:

2

2

mV

E

k

=

- dla ciała sztywnego wirującego wokół pewnej osi z prędkością kątową

ω

ω

ω

ω

:

2

2

ω

ω

ω

ω

I

E

k

=

Wg. mechaniki relatywistycznej energia kinetyczna ciała to różnica jego energii w
ruchu i energii spoczynkowej:

2

0

2

2

2

0

0

1

c

m

c

V

c

m

E

E

E

E

k

k

−

−

=

⇒

−

=

II. E. potencjalna - część energii ciała związana z jego położeniem w polu
potencjalnym. E.p. punktu materialnego w punkcie przestrzeni P jest równa pracy
wykonanej przy przeniesieniu tego punktu materialnego z punktu przestrzeni, gdzie
e.p. określono jako 0, do punktu P.

3

c. Pęd i moment pędu

I. Pęd (

p

r

)- Wektorowa wielkość fizyczna zdefiniowana jako iloczyn masy i prędkości

punktu materialnego:

V

m

p

r

r

⋅

=

co dla mechaniki relatywistycznej przedstawia się jako:

2

2

0

1

c

V

V

m

p

−

=

r

r

jednostka pędu:

[ ] [

] [

]

s

m

kg

s

N

p

1

/

1

1

1

1

⋅

=

⋅

=

P. układu punktów nazywa się sumę pędów wszystkich punktów, równą iloczynowi
masy całego układu M i prędkości środka masy

s

V

r

:

s

V

M

V

m

P

r

r

r

∑

=

=

.

Do zmiany pędu konieczne jest działanie siły, jak to wynika z II zas. mech. Newt.

II. Moment pędu ( L

r

)

- Wektorowa wielkość fizyczna charakteryzująca ruch układu

mechanicznego względem pewnego wyróżnionego punktu przestrzeni. Moment pędu
punktu materialnego określony jest jako:

p

r

L

r

r

r

×

=

gdzie: r

r

-

wektor łączący punkt, względem którego moment jest określany, z punktem

materialnym;

p

r

- pęd rozpatrywanego punktu materialnego.

Zaś jednostka momentu pędu:

[ ] [

]

s

N

m

L

1

1

1

⋅

⋅

=

Dla ciała obracającego się:

ω

ω

ω

ω

r

r

r

×

=

I

L

gdzie: I

r

,

ω

ω

ω

ω

r

to odpowiednio moment bezwładności i prędkość kątowa ciała względem

określonej osi.

5.

Prawo zachowania energii, pędu i momentu pędu.

a. Prawo zachowania energii

W układzie izolowanym suma wszelkich form energii całości tego układu

pozostaje stała w czasie.

.

const

E

c

=

b. Prawo zachowania pędu

Jeżeli w układzie inercjalnym na ciało nie działa żadna siła, lub siły działające

równoważą się, to pęd całkowity układu nie ulega zmianie.

( )

.

0

0

0

const

p

dt

p

d

dt

p

d

F

=

⇒

=

⇒

=

⇒

=

∑

∑

∑

∑

r

r

r

r

4

c. Prawo zachowania momentu pędu

Jeżeli w układzie inercjalnym na ciało nie działają żadne momenty sił, lub

momenty te równoważą się, to całkowity moment pędu układu nie ulega zmianie.

( )

(

)

( )

M

p

r

dt

V

m

d

r

V

m

dt

r

d

V

dt

r

d

dt

V

d

m

r

V

m

dt

r

d

dt

V

m

r

d

dt

L

d

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

=

×

=

×

=













=

×

⇒

=

=

×

+

×

=

×

=

0

Z powyższego:

.

0

const

L

M

=

⇒

=

v

r

Dla układu ciał przedstawi się to w sposób następujący:

.

0

const

L

L

M

c

=

=

⇒

=

∑

∑

v

r

r

6.

Moment siły, moment bezwładności. Twierdzenie Steinera.

a. Moment siły

Jest to wielkość fizyczna zdefiniowana jako następujący iloczyn wektorowy:

F

r

M

r

r

r

×

=

gdzie: r

r

-

wektor łączący punkt, względem którego moment jest określany, z punktem

zaczepienia siły, F

r

- działająca siła.

Jednostka momentu siły:

[ ] [

]

m

N

M

1

1

⋅

=

b. Moment bezwładności

Wielkość fizyczna związana z geometrycznym rozkładem masy w ciele lub

układzie ciał. Zdefiniowana dla bryły sztywnej jako następująca całka po jej objętości:

∫

=

V

dV

r

I

2

ρρρρ

gdzie:

ρρρρ

- gęstość właściwa;

r

-

odległość elementarnej masy od wybranej

płaszczyzny, osi lub punktu obrotu, względem którego moment jest określany.

Dla układu n punktów materialnych równanie sprowadza się do sumy:

∑

=

=

n

i

i

i

r

m

I

1

2

c. Twierdzenie Steinera

Dotyczy znajdowania momentu bezwładności bryły względem wybranej osi, gdy

znany jest moment względem osi równoległej do wybranej i przechodzącej przez jej
środek masy.

2

0

md

I

I

+

=

gdzie:

0

I

- moment bezwładności względem osi przechodzącej przez środek masy; m

- masa bryły, d - odległość między osiami.

7.

Siły centralne. Siły proporcjonalne do l/r

2

a. Siła centralna

Jest to siła, której wektor jest zawsze skierowany do lub od pewnego punktu

określanego jako centrum siły (np. siła działająca między dwoma punktowymi
ładunkami elektrycznymi lub siła ciążenia między punktowymi masami). Jej wartość

5

zmienia się jedynie w zależności od odległości od centrum siły.

r

r

r

r

F

F

c

c

r

r

r

r

⋅

=

=

)

(

)

(

Φ

Φ

Φ

Φ

S.c. nie może zmienić momentu pędu ciała względem centrum siły.

0

)

(

)

(

=

×

=













×

=

×

=

r

r

r

r

r

r

r

r

F

r

M

c

c

r

r

r

r

r

r

r

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Gdy w danym układzie s.c. jest jedyną siłą działającą na swobodny punkt

materialny, to ruch tego punktu jest ruchem płaskim (cały tor leży w jednej
płaszczyźnie) wynika to z zerowego i niezmiennego momentu siły w takim układzie.

b. Siły proporcjonalne do l/r

2

Siły te skategoryzowane są jako następująca podgrupa:
Siły -> Siły potencjalne -> S. zachowawcze -> S. centralne -> S. proporcjonale do l/r

2

Rozróżniamy dwie ich klasy:

I.

2

r

F

αααα

−

=

, gdzie

0

>

αααα

- siły grawitacyjne

II.

2

r

F

αααα

−

=

, gdzie

0

<

αααα

- siły kulombowskie

Posiadają poniższe własności:
- jeżeli obiekt ma symetrię sferyczną (masy lub ładunku) to oddziałuje z otoczeniem
dokładnie jak punkt materialny.
- jeżeli obiekt jest sferą, to w jego wnętrzu siła wypadkowa pochodząca od niego
zeruje się.

8.

Prawa Keplera. Grawitacja. Energia pola grawitacyjnego.

a. Prawa Keplera
Są to empiryczne prawa ruchu planet Układu Słonecznego, oparte na obserwacjach
astronomicznych:
I - każda planeta porusza się po elipsie, której jednym z ognisk jest Słońce;
II - każda planeta ma stałą prędkość polową (tj. promień wodzący tej planety,
poprowadzony od Słońca, w jednakowych odcinkach czasu zakreśla takie same pola);
(to prawo wynika z zasady zachowania momentu pędu dla siły centralnej)
III - stosunek kwadratu okresu obiegu do sześcianu wielkiej półosi jest dla
wszystkich planet taki sam;

.

3

2

2

2

3

1

2

1

const

r

T

r

T

=

=

b. Grawitacja

Prawo powszechnego ciążenia:

Między dowolną parą ciał posiadających masy pojawia się siła przyciągająca,

która działa na linii łączącej ich środki, a jej wartość rośnie z iloczynem ich mas i
maleje z kwadratem odległości.

[ ]

N

r

r

r

m

m

G

F

g

r

r

⋅

−

=

2

2

1

gdzie: G- stała grawitacji; r

r

-

wektor łączący oddziałujące ciała;

2

1

m

m

- masy ciał.

6

Pole grawitacyjne jest polem potencjalnym, w związku z czym praca wykonywana w

nim nie zależy od drogi jaką przebywa ciało, lecz od jego przemieszczenia.

Natężenie pola grawitacyjnego:

2

r

M

G

m

F

g

−

=

=

r

r

γγγγ

gdzie: M - masa ciała będącego źródłem pola.

Potencjał pola grawitacyjnego w zadanym punkcie oblicza się przyjmując

nieskończoność jako punkt odniesienia o zerowym potencjale:

r

M

G

r

d

r

d

m

F

m

E

V

r

r

g

p

g

−

=

⋅

−

=

⋅

−

=

=

∫

∫

∞

∞

r

r

r

r

γγγγ

Natężenie pola wyraża się także jako gradient potencjału:

V

−∇

=

γγγγ

r

Praca w polu grawitacyjnym:













−

=

⋅

=

2

1

1

1

r

r

GMm

m

V

W

∆∆∆∆

gdzie:

2

1

r

r

- określają odpowiednio położenie początkowe i końcowe ciała względem

źródła pola.

Strumień pola grawitacyjnego przechodzący przez powierzchnię S:

∫∫

⋅

=

S

s

d

r

r

γγγγ

Φ

Φ

Φ

Φ

Twierdzenie Gaussa dla pola grawitacyjnego określa całkowity strumień

przechodzący przez powierzchnię zamkniętą zawierającą n mas:

∑

=

⋅

−

=

n

j

j

m

G

1

4

ππππ

Φ

Φ

Φ

Φ

c. Energia pola grawitacyjnego

Energia potencjalna w polu grawitacyjnym wyraża się jako:

r

Mm

G

m

V

E

p

−

=

⋅

=

Odpowiada ona pracy, jaką należy wykonać, aby przemieścić ciało o masie m z
nieskończoności do punktu leżącego w odległości r od źródła pola.

Ze względu na zachowawczy charakter pola grawitacyjnego, suma energii

kinetycznej i potencjalnej ciała, pozostającego pod jego działaniem, jest stała.

.

const

E

E

E

k

p

c

=

+

=

9.

„Własna" energia grawitacyjna.

a. Definicja

Własna energia grawitacyjna określa pracę, jaką należałoby włożyć, aby

utworzyć dane ciało „przenosząc je” w postaci elementarnych mas z nieskończoności
do zadanego punktu w przestrzeni.

Wynik otrzymuje się przez sumowanie prac całkowych.

∫

=

dW

W

7

b. Przykład

W wypadku kulistej masy m o promieniu R, obliczenia przedstawiają się

następująco:

r

mdm

G

dW

−

=

dr

r

dm

r

m

ρρρρ

ππππ

ρρρρ

ππππ

2

3

4

3

4

=

⇒

=

praca całkowa dW odpowiada w tym przypadku przeniesieniu z nieskończoności na
„budowaną” kulę powłoki o masie dm i grubości dr.

R

Gm

r

R

G

r

G

dr

r

G

R

r

dr

r

r

G

W

R

R

R

2

2

3

0

5

2

2

0

4

2

2

0

2

3

5

3

3

4

1

5

3

5

3

16

3

16

1

5

3

4

3

4

⋅

−

=













−

=

−

=

=

−

=

⋅

−

=

∫

∫

ρρρρ

ππππ

ρρρρ

ππππ

ρρρρ

ππππ

ρρρρ

ππππ

ρρρρ

ππππ

10.

Zasada względności. Transformacja Lorentza.

a. Zasada względności

Głosi ona, że każde prawo przyrody ma we wszystkich układach inercjalnych tą

samą postać. Oznacza to, że równania odnoszące się do tego prawa można zapisywać
w identyczny sposób - bez względu na obrany układ inercjalny. Są niezmiennicze
względem tych układów.

W mechanice nierelatywistycznej opis oddziaływań między ciałami opiera się

często na potencjałach: funkcjach niezależnych od czasu. Z tego wynika, że
oddziaływanie powinno być przekazywane w sposób natychmiastowy - jego prędkość
byłaby nieskończona.

Jednakże w rzeczywistości istnieje pewna graniczna prędkość C, która dotyczy

również oddziaływań. Ta skończona prędkość musi (jako stała uniwersalna) wobec
tego być jednakowa we wszystkich układach inercjalnych. Za tą stałą przyjęto
uznawać prędkość światła c, która do tej pory jest jej najlepszym osiągalnym dla nas
przybliżeniem.

Połączenie z.w. oraz postulatu skończonej prędkości rozchodzenia się sygnałów

zwane jest zasadą (teorią) względności Einsteina (w odróżnieniu od zasady
względności Galileusza, zakładającej nieskończoną prędkość rozchodzenia się tegoż
sygnału). Na niej opiera się mechanika relatywistyczna.

Z zastosowania z.w. wynika, że czas nie jest absolutem, zależy od wybranego

układu odniesienia. Również pomiar takich wielkości jak prędkość czy przyspieszenie
daje wyniki zależne od układu obserwatora.

b. Transformacja Lorentza

Jest to przekształcenie wielkości fizycznych pomiędzy układami, spełniające

warunek uwzględnienia prędkości granicznej. Dla zmiennych w układzie U, o osiach
równoległych do układu U

′

poruszającego się względem pierwszego z prędkością V,

t.L. przybiera postać:

2

2

2

2

2

1

;

;

;

1

c

V

c

x

V

t

t

z

z

y

y

c

V

t

V

x

x

−

′

+

′

=

′

=

′

=

−

′

+

′

=

8

11.

Doświadczenie Michelsona - Morleya. Postulaty Einsteina.

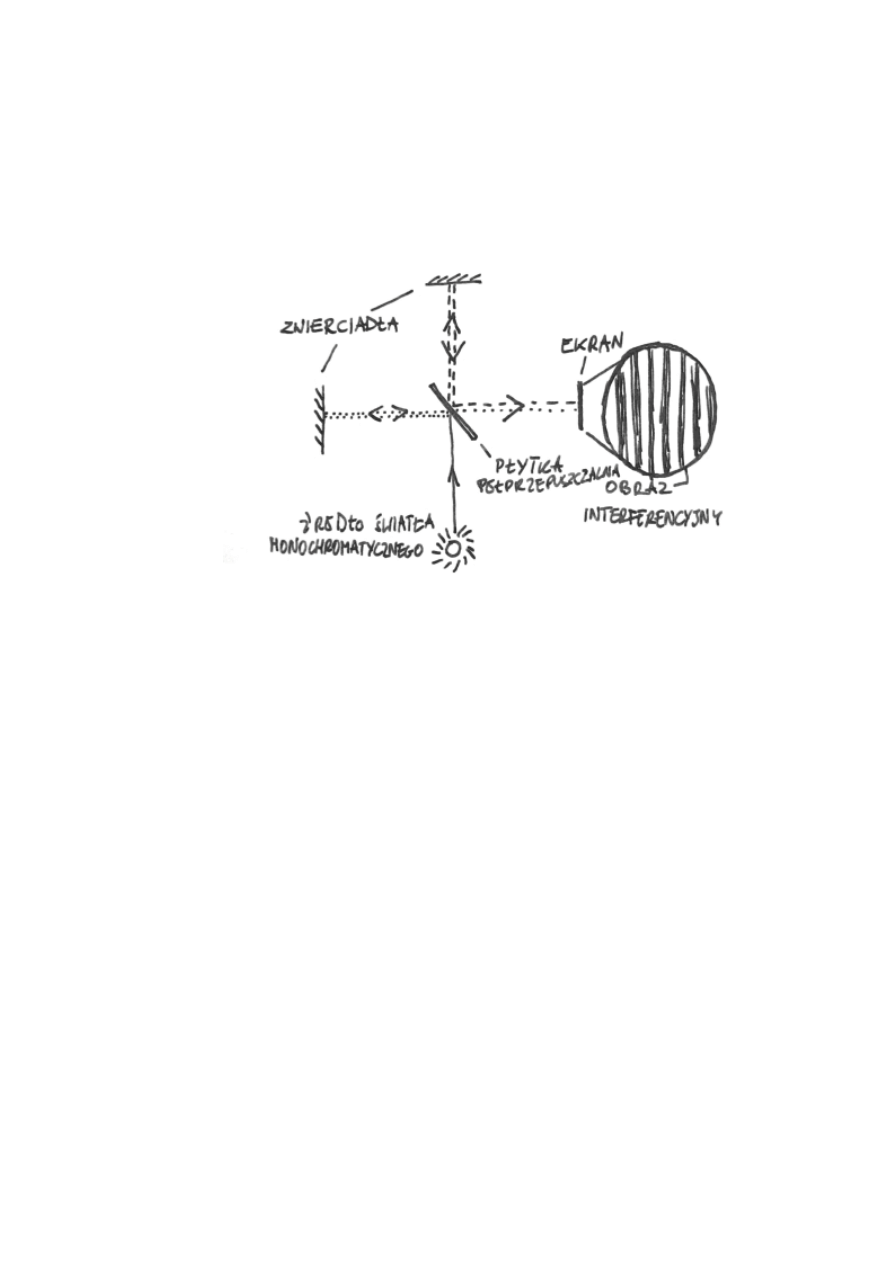
a. Doświadczenie Michelsona - Morleya

Zostało przeprowadzone, aby sprawdzić wpływ ruchu źródła światła na prędkość

światła, a przez to także zweryfikować hipotezę istnienia eteru jako ośrodka, w którym
światło (jako fala) miałoby się rozchodzić.

Urządzeniem wykorzystanym w doświadczeniu jest tzw. interferometr Michelsona.

Badano w nim prążki interferencyjne powstałe wskutek interferencji dwóch wiązek
światła monochromatycznego, część swej drogi przebiegających po kierunkach:
równoległym i prostopadłym do kierunku ruchu Ziemi. Przewidywano, że na kierunkach
tych prędkość rozchodzenia się światła będzie różna (Ziemia miałaby poruszać się
względem eteru). Dla wyeliminowania drgań interferometr pływał w basenie rtęciowym.

Aby doprowadzić do zmiany prędkości wiązek względem hipotetycznego eteru, a

zatem i zmiany obrazu, przyrząd obracano o 90˚. Nie zauważono jednak żadnego
przesunięcia. Dokładność interferometru czterokrotnie przewyższała wielkość
spodziewanego przesunięcia, toteż pomiar można uznać za wiarygodny.

Eksperyment ten stanowi istotną podstawę doświadczalną dla rozwoju teorii

względności.

b. Postulaty Einsteina

Swoją teorię względności Einstein oparł na następujących dwóch postulatach:

I - Zasadzie względności, mówiącej, że wszystkie podstawowe prawa fizyki

posiadają tą samą postać w każdym układzie inercjalnym.

II - Niezmienności prędkości światła, czyli stwierdzeniu, że prędkość światła w

próżni jest stała dla wszystkich obserwatorów, niezależnie od prędkości jego źródła czy
kierunku rozchodzenia się.

12.

Kontrakcja długości. Dylatacja czasu.

a. Kontrakcja długości

W mechanice relatywistycznej odległość między dwoma punktami zależy od układu

odniesienia obserwatora. Wszystkie poruszające się przedmioty obserwuje się jako
krótsze.

Schemat ideowy

interferometru Michelsona

9

Układ U’ porusza się ze stałą prędkością V względem układu U równolegle do osi x.

Długość pręta spoczywającego w układzie U wynosi l

0

= x

2

-x

1

, gdzie x

2

, x

1

- współrzędne

końców pręta. Zakładamy, że pomiar ma miejsce w tej samej chwili czasu t’. l - długość
pręta obserwowana w układzie U’.

2

2

0

1

2

2

2

2

2

2

2

1

1

1

1

1

c

V

l

x

x

l

c

V

t

V

x

x

c

V

t

V

x

x

−

=

′

−

′

=

−

′

+

′

=

−

′

+

′

=

;

;

b. Dylatacja czasu

Podobnie jak długość, od wyboru układu obserwatora zależy także odstęp czasu

między dwiema dowolnymi chwilami.

Przyjmijmy układy takie jak w punkcie a. Jeżeli w układzie U’ znajduje się zegar,

odmierzający odstęp czasu między dwoma zdarzeniami zachodzącymi w tym samym
punkcie x’,y’,z’, to różnica czasu między nimi wyniesie ∆t’ = t’

1

-t’

2

. Ze wzorów Lorentza

wynika:

2

2

1

2

2

2

2

2

2

2

2

2

1

1

1

1

1

c

V

t

t

t

t

c

V

c

x

V

t

t

c

V

c

x

V

t

t

−

′

=

−

=

−

′

+

′

=

−

′

+

′

=

∆∆∆∆

∆∆∆∆

;

;

gdzie ∆t - odstęp czasu mierzony w układzie U. Widać, że zegar będący w ruchu „późni
się” względem spoczywającego.

Występowanie d.c. potwierdzono w doświadczeniach z cząstkami nietrwałymi -

np. mezonami. Ich czas życia wydłuża się ze względu na wielkie prędkości jakie rozwijają.

13.

Transformacja prędkości. Masa relatywistyczna.

a. Transformacja prędkości

Prędkości w ujęciu relatywistycznym można łatwo otrzymać przez różniczkowanie

po czasie współrzędnych podanych w przekształceniu Lorentza.

Przyjmijmy takie układy U i U’ jak w punkcie 12, oraz punkt materialny

poruszający się w układzie U’, którego położenie opisują współrzędne x,y,z.

dt

z

d

v

dt

y

d

v

dt

x

d

v

U

dt

dz

v

dt

dy

v

dt

dx

v

U

z

y

x

z

y

x

′

=

′

′

=

′

′

=

′

′

=

=

=

:

:

Ze wzorów Lorentza…

z

d

dz

y

d

dy

c

V

t

Vd

x

d

dx

′

=

′

=

−

′

+

′

=

2

2

1

2

2

2

1

c

V

x

d

c

V

t

d

dt

−

′

+

′

=

Dzieląc stronami trzy pierwsze równania przez równanie czwarte…

2

2

2

2

2

2

2

1

1

1

1

1

c

v

V

c

V

v

v

c

v

V

c

V

v

v

c

v

V

V

v

v

x

z

z

x

y

y

x

x

x

′

+

−

′

=

′

+

−

′

=

′

+

+

′

=

10

b. Masa relatywistyczna

Jest to pojęcie wprowadzone dla łatwiejszego zaadaptowania niektórych wzorów

fizyki klasycznej do fizyki relatywistycznej. Jeżeli chodzi o symbolikę: m.r. oznaczana
jest literą m, podczas gdy masa spoczynkowa odróżniana jest za pomocą indeksu m

0

(masa spoczynkowa odpowiada masie relatywistycznej w chwili, gdy ciało pozostaje w
spoczynku). M.r. jest ściśle związana z prędkością ciała, rośnie wraz z nią, a gdy

c

V

→

, to

∞

→

m

. Określana jest następującym wzorem:

2

2

0

1

c

V

m

m

−

=

Z powyższego wynika możliwość zapisania pędu w następujący sposób:

mV

c

V

V

m

p

=

−

=

2

2

0

1

14.

Energia w teorii względności. Związek energii z pędem.

a. Energia w teorii względności

Konsekwencją teorii względności jest równoważność masy i energii: ciało o

masie relatywistycznej m posiada energię:

2

2

2

0

2

1

c

V

c

m

mc

E

−

=

=

Wyrażenie na energię całkowitą ciała można przedstawić także jako sumę

energii posiadanej przez nie w spoczynku i energii wynikającej z jego ruchu:

E=m

0

c

2

+E

k

b. Związek energii z pędem

Można znaleźć związek między energią ciała a jego pędem.

Dane są następujące zależności:

V

m

p

c

m

E

c

V

γγγγ

γγγγ

γγγγ

0

2

0

2

2

1

1

=

=

⇒

−

=

;

Stąd po pewnych zmianach:

4

2

0

2

2

4

2

2

0

2

2

2

1

c

m

c

V

c

m

c

p

E

=













−

=

−

γγγγ

I ostatecznie:

2

2

4

2

0

2

c

p

c

m

E

+

=

Zależność ta obowiązuje dla wszystkich cząstek, nawet tych pozbawionych

masy, jak foton czy neutrino.

15.

Zasada równoważności Einsteina. Doświadczenie Pounda - Rebki - Snidera.

a. Zasada równoważności Einsteina

Pozwoliła uogólnić szczególną teorię względności na wszystkie układy

odniesienia (także nieinercjalne).

11

Z.r.E. mówi, że przyspieszenie układu odniesienia jest lokalnie nieodróżnialne

od działania odpowiedniego pola grawitacyjnego. „Lokalnie” oznacza w tym wypadku
operowanie w obrębie danego układu odniesienia.

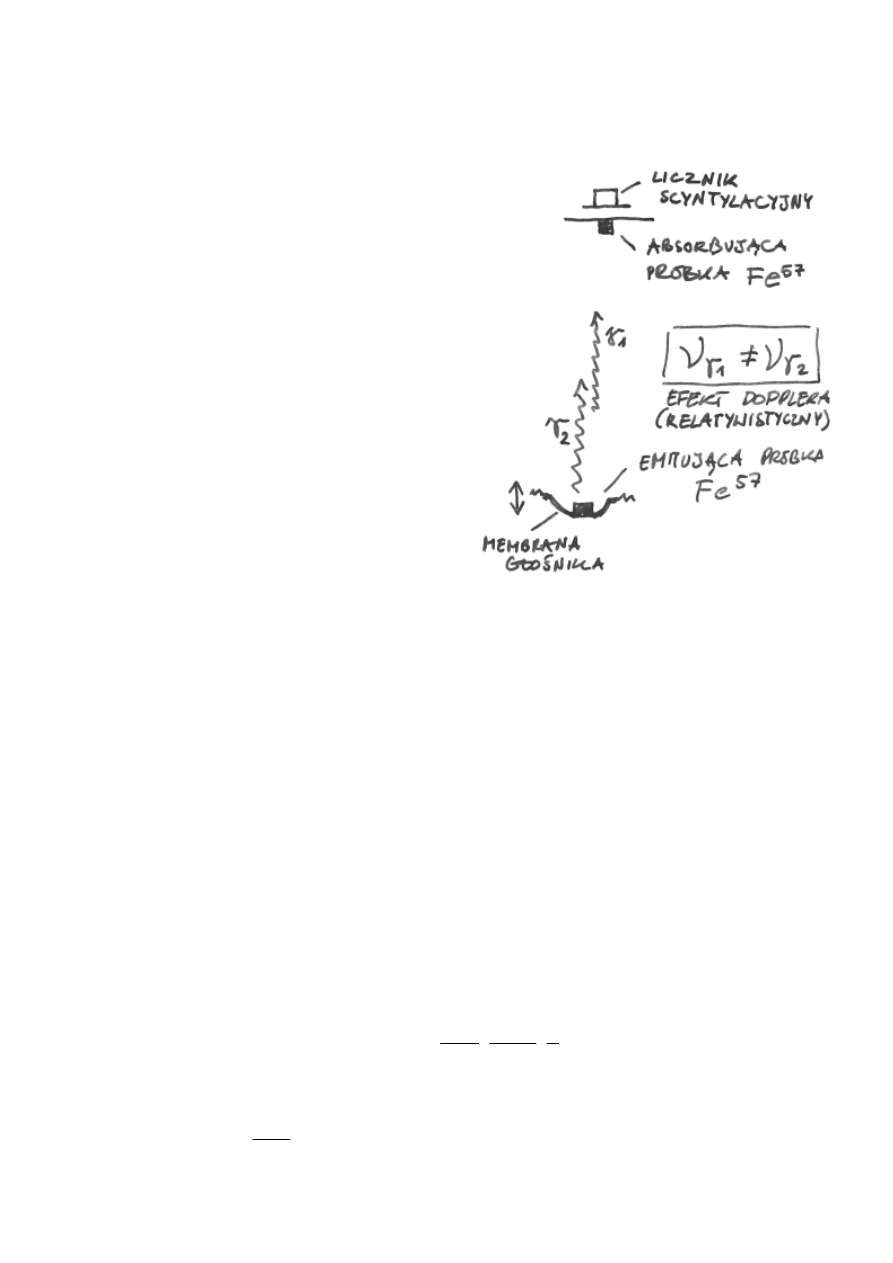
b. Doświadczenie Pounda - Rebki - Snidera

Miało na celu sprawdzić ogólną

teorię względności, która przewidywała,
że częstość fotonu

γγγγ

przemieszczającego

się w polu grawitacyjnym ulegnie
zmianie.

Eksperyment

opierał

się

na

następującym fakcie: atom przechodzący
ze

stanu

wzbudzenia

do

stanu

normalnego emituje foton o konkretnej
częstotliwości,

którego

energia

odpowiada różnicy pomiędzy poziomami
energetycznymi atomu. Gdy natomiast w
pobliżu atomu będącego w stanie
niewzbudzonym znajdzie się foton o
takiej

właśnie,

odpowiedniej

częstotliwości, to zostanie pochłonięty, a
atom ulegnie wzbudzeniu.

Jednak foton przebywając drogę w

polu

grawitacyjnym

zmienia

swoją

energię (a tym samym częstotliwość) co
powoduje tzw. przesunięcie ku czerwieni.
W związku z tym atom nie może go już zaabsorbować. Jednak jeżeli atom emitujący
foton będzie się przemieszczał względem atomu absorbującego z odpowiednią
prędkością, to deficyt energii zostanie pokryty (przesunięcie dopplerowskie). Względna
prędkość atomów jest zatem miarą przesunięcia ku czerwieni.

Doświadczenie przeprowadzono w wieży, w budynku Uniwersytetu Harvarda,

odległość między próbką izotopu żelaza 57 odbierającą foton a wysyłającą wyniosła 22.5
m. Próbkę „nadawczą” umieszczono na membranie głośnika, co pozwalało wprawiać ją
w drgania o regulowanej częstotliwości, wytwarzając różne wartości przesunięcia
dopplerowskiego. Za próbką „odbiorczą” znajdował się licznik fotonów, dający obraz
tego ile fotonów gamma nie zostało pochłoniętych. Zestrojenie drgań próbki emitującej
z absorbującą powodowało zmniejszenie ilości zliczanych fotonów.

Opracowanie wyników potwierdziło przewidywania OTW.

16.

Pole elektrostatyczne. Prawo Coulomba. Natężenie pola elektrostatycznego E.

a. Pole elektrostatyczne

Jest to stan przestrzeni, w której na ładunek elektryczny działa siła. Linie pola

elektrycznego biegną od ładunku dodatniego do ujemnego. Pole elektrostatyczne jest
źródłowe.

b. Prawo Coulomba:

r

r

r

Q

Q

F

r

r

⋅

⋅

−

=

2

2

1

0

4

1

πε

πε

πε

πε

gdzie: F

r

– siła z jaka działają na siebie dwa ładunki Q

1

i Q

2

, r

r

- wektor łączący te

ładunki.

Czynnik

0

4

1

πε

πε

πε

πε

zwykle wyraża się stosując zmienną k.

Schemat układu

doświadczalnego P-R-S

12

c. Natężenie pola elektrostatycznego E

Wektorowa wielkość fizyczna opisującą pole elektryczne, równa stosunkowi

wektora siły oddziaływania elektrostatycznego F, działającej na umieszczony w
danym punkcie pola dodatni ładunek próbny q, do wartości tego ładunku.

q

F

E

r

v

=

17.

Strumień wektora natężenia pola elektrycznego. Prawo Gaussa.

a. Strumień wektora natężenia pola elektrycznego

Wektorowa wielkość fizyczna opisująca liczbę linii pola elektrycznego

przechodzącą przez daną powierzchnię:













⋅

∠

=

⋅

=

∫∫

∫∫

C

m

N

s

d

E

Eds

s

d

E

S

S

2

)

,

cos(

r

r

r

r

Φ

Φ

Φ

Φ

gdzie: Φ - strumień pola, E - natężenie pola, S - pole powierzchni.

b. Prawo Gaussa

Strumień pola elektrycznego obejmowany przez dowolną powierzchnię

zamkniętą jest proporcjonalny do sumy ładunków zawartych wewnątrz powierzchni.

Najczęściej korzystamy ze wzoru:

0

εεεε

∑

∫∫

=

⋅

Q

s

d

E

S

r

r

18.

Praca sił pola elektrostatycznego.

Praca wykonana w centralnym polu elektrycznym zależy od położenia

początkowego i końcowego, a nie zależy od drogi, ponieważ pole elektryczne jest
polem centralnym (czyli zachowawczym).

∫

⋅

=

2

1

r

r

r

d

F

W

r

r

gdzie r

1

i r

2

to położenia: początkowe i końcowe ładunku.

Możemy zastąpić siłę F przez wzór na natężenie elektrostatyczne.

Pracę wykonaną przy przenoszeniu ładunku q można też wyrazić za pomocą

różnicy potencjałów ∆V w punkcie początkowym i końcowym:

V

q

W

∆∆∆∆

=

19.

Potencjał elektrostatyczny. Związek między potencjałem i natężeniem pola.

a. Potencjałem elektrycznym

nazywamy iloraz energii potencjalnej punktowego

ciała naelektryzowanego ładunkiem Q i wartości tego ładunku.

r

Q

k

Q

E

V

p

=

=

13

P.e. w punkcie P jest także określany jako praca, potrzebna na przeniesienie

jednostkowego ładunku z nieskończoności (w której przyjęto zerowy potencjał) do
tego punktu.

b. Energia pola elektrycznego.

r

Qq

k

E

p

=

jeżeli q to wartość ładunku wprowadzonego w odległości r od ładunku Q.

c. Związek między potencjałem a natężeniem pola.

gradV

E

−

=

r

20.

Dipol elektryczny. Moment dipolowy. Potencjał i natężenie pola od dipola.

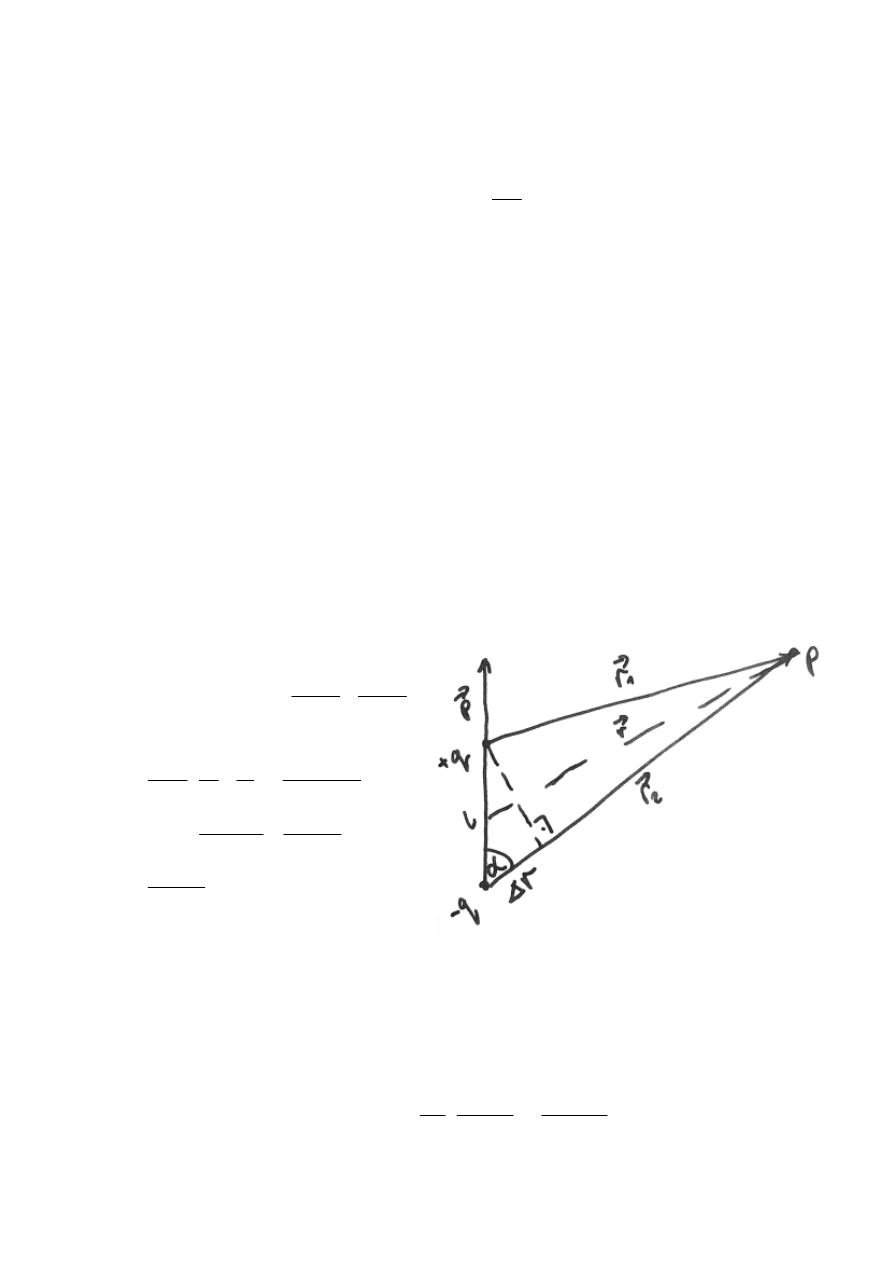
Dipol elektryczny

- układ dwóch różnoimiennych (jednakowych) ładunków

elektrycznych q, umieszczonych w pewnej odległości r od siebie

Elektryczny moment dipolowy

jest to wektorowa wielkość fizyczna

charakteryzująca dipol elektryczny. Elektryczny moment dipolowy

p

r

dwóch

punktowych ładunków q jest równy iloczynowi wektora r

r

(skierowanego od ładunku

ujemnego do dodatniego) i wartości ładunku dodatniego:

r

q

p

r

r

⋅

=

Potencjał pola od dipola:

gdzie:

p

r

- moment dipolowy, r

r

– wektor położenia punktu P, w którym liczymy

potencjał pola, skierowany od środka symetrii dipola do punktu P.

Natężenie pola od dipola:

V

P

E

⋅

−∇

=

)

(

r

3

0

2

0

4

2

4

r

p

r

p

r

V

P

E

πε

πε

πε

πε

αααα

πε

πε

πε

πε

αααα

cos

cos

)

(

=















∂

∂

−

=

r

{

}

3

0

2

0

2

0

2

1

2

1

2

0

1

2

1

2

0

1

2

0

0

4

4

4

4

1

1

4

4

4

r

r

p

P

V

r

p

r

ql

r

r

r

r

r

r

r

q

r

r

q

P

V

l

r

r

r

r

q

r

q

q

V

q

V

P

V

πε

πε

πε

πε

πε

πε

πε

πε

αααα

πε

πε

πε

πε

αααα

πε

πε

πε

πε

πε

πε

πε

πε

αααα

∆∆∆∆

πε

πε

πε

πε

πε

πε

πε

πε

r

r

⋅

=

=

=

≈

=

=

−

=













−

=

=

−

=

−

=

−

+

+

=

)

(

cos

cos

)

(

)

(

cos

)

(

)

(

)

(

14

21.

Dipol w zewnętrznym polu elektrycznym. Moment siły i energia dipola.

Na dipol elektryczny umieszczony w polu elektrycznym działa moment siły:

E

p

M

r

r

r

×

=

Energia potencjalna dipola wyraża się wzorem:

E

p

E

p

r

r

⋅

−

=

Najmniejszą energię potencjalną (równowaga trwała) posiada on gdy jego elektryczny
moment dipolowy jest zgodny z przebiegiem linii pola, a największą, gdy jest mu
przeciwny (równowaga nietrwała).

22.

Metale w polu elektrycznym.

Ponieważ metal jest przewodnikiem, to charakteryzuje się dużą ilością

elektronów swobodnych. Wypadkowe pole elektryczne w metalach (suma pola
zewnętrznego i wewnętrznego) jest równe zero. Potencjał na powierzchni metali jest
stały. Ładunki nie gromadzą się na powierzchniach wewnętrznych metali. W
przypadku, gdy metal ma tak zwane „ostrza”, ładunek wykazuje tendencję do
gromadzenia się w nich.

23.

Kondensatory. Pojemność elektryczna kondensatora. Energia kondensatora.

Kondensatorem określamy układ zbudowany dwóch przewodników

(okładzin) rozdzielonych dielektrykiem. Doprowadzenie napięcia do okładzin
kondensatora powoduje zgromadzenie się na nich ładunku elektrycznego. Jeżeli
kondensator jako całość nie jest naelektryzowany, to cały ładunek zgromadzony na
jego okładkach jest jednakowy, ale przeciwnego znaku.

Kondensator charakteryzuje pojemność określająca zdolność kondensatora do

gromadzenia ładunku:

U

Q

C

=

gdzie: C - pojemność (w faradach), Q - ładunek zgromadzony na jednej okładce (w
kulombach), U - napięcie elektryczne między okładkami (w woltach)

Energia kondensatora jest to praca, jaką trzeba wykonać aby przenieść

ładunek z jednej okładki na drugą:

2

2

CU

W

=

gdzie: C - pojemność (w faradach), U – napięcie elektryczne (różnica potencjałów)
między okładkami (w woltach).

24.

Energia pola elektrycznego.

Energia niejednorodnego pola elektrycznego w pewnej objętości (wyprowadzona

dzięki porównaniu do energii między okładkami kondensatora próżniowego o
powierchni S odległych o d):

15

∫∫∫

=

⇒

=













=

=

=

V

el

el

dV

E

E

V

E

Sd

d

U

d

S

U

C

U

E

2

0

2

0

0

2

0

2

2

2

1

2

1

2

1

2

2

εεεε

εεεε

εεεε

εεεε

Energia jednorodnego pola elektrycznego – przypadek szczególny (E

wyciągnięte przed całkę jako stała).

V

E

E

el

2

0

2

1

εεεε

=

25.

Pole elektryczne w dielektrykach.

Napięcie i natężenie pola elektrycznego w

materialnym dielektryku jest mniejsze ε

r

razy niż

w próżni:

r

E

E

U

U

εεεε

=

=

0

0

Co

w

przypadku

kondensatora

jest

równoznaczne ze zwiększeniem jego pojemności:

d

S

C

C

C

r

r

εεεε

εεεε

εεεε

0

0

=

⇒

=

Dzieje się tak, ponieważ w dielektryku

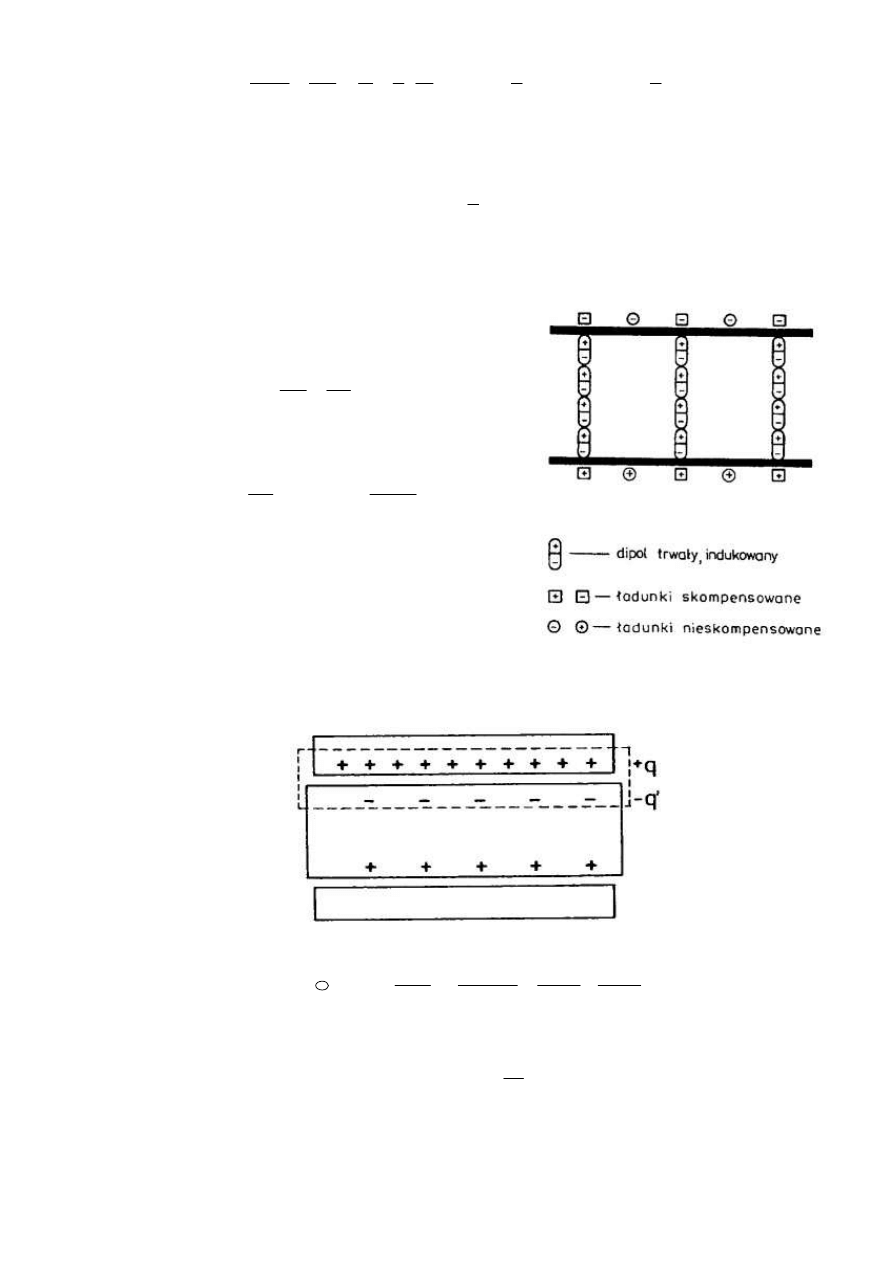
następuje zjawisko polaryzacji. Pod wpływem
pola powstają mikrodipole elektryczne lub
następuje uporządkowanie tych już istniejących.
Wówczas na powierzchni dielektryka pojawia się
warstwa

nieskompensowanych

ładunków

(rysunek z prawej).

Pole elektryczne (zmniejszone) wytwarzają w tym momencie ładunki na

elektrodzie nie będące skompensowane przez ładunek polaryzacyjny.

Po przekształceniach na podst. prawa Gaussa mamy:

)

(

)

(

)

(

S

q

S

q

S

q

q

s

d

E

r

S

r

0

0

0

0

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

′

−

=

⇒

=

⋅

∫∫

r

r

Idąc jeszcze dalej, nie zważając na krytyczne głosy reakcjonistów:













−

=

′

r

q

q

εεεε

1

1

Widzimy teraz, że w próżni (ε

r

=1) q'=0, natomiast dla ε

r

dążącego do

nieskończoności q' dąży do q i ładunki kompensują się całkowicie – pola nie ma.

16

26.

Wektor polaryzacji P. Polaryzowalnośc.

a. Wektor polaryzacji P

Jego wartość jest równa gęstości związanego ładunku polaryzacyjnego. Zwrot od

ładunku polaryzacyjnego ujemnego do dodatniego.

Sd

d

q

P

′

=

Można przyjąć, że P jest równe dipolowemu momentowi elektrycznemu

przypadającemu na jednostkę objętości dielektryka.

b. Polaryzowalność

Wielkość charakteryzująca zdolność powłok elektronowych do ulegania

deformacji pod wpływem zewnętrznego pola elektrycznego, czyli ulegania polaryzacji.

E

⋅

= αααα

µµµµ

αααα

- polaryzowlaność, µ- indukowany moment dipolowy

27.

Podatność dielektryczna χ

i względna przenikalność dielektryczna ε.

1

−

=

r

εεεε

χχχχ

28.

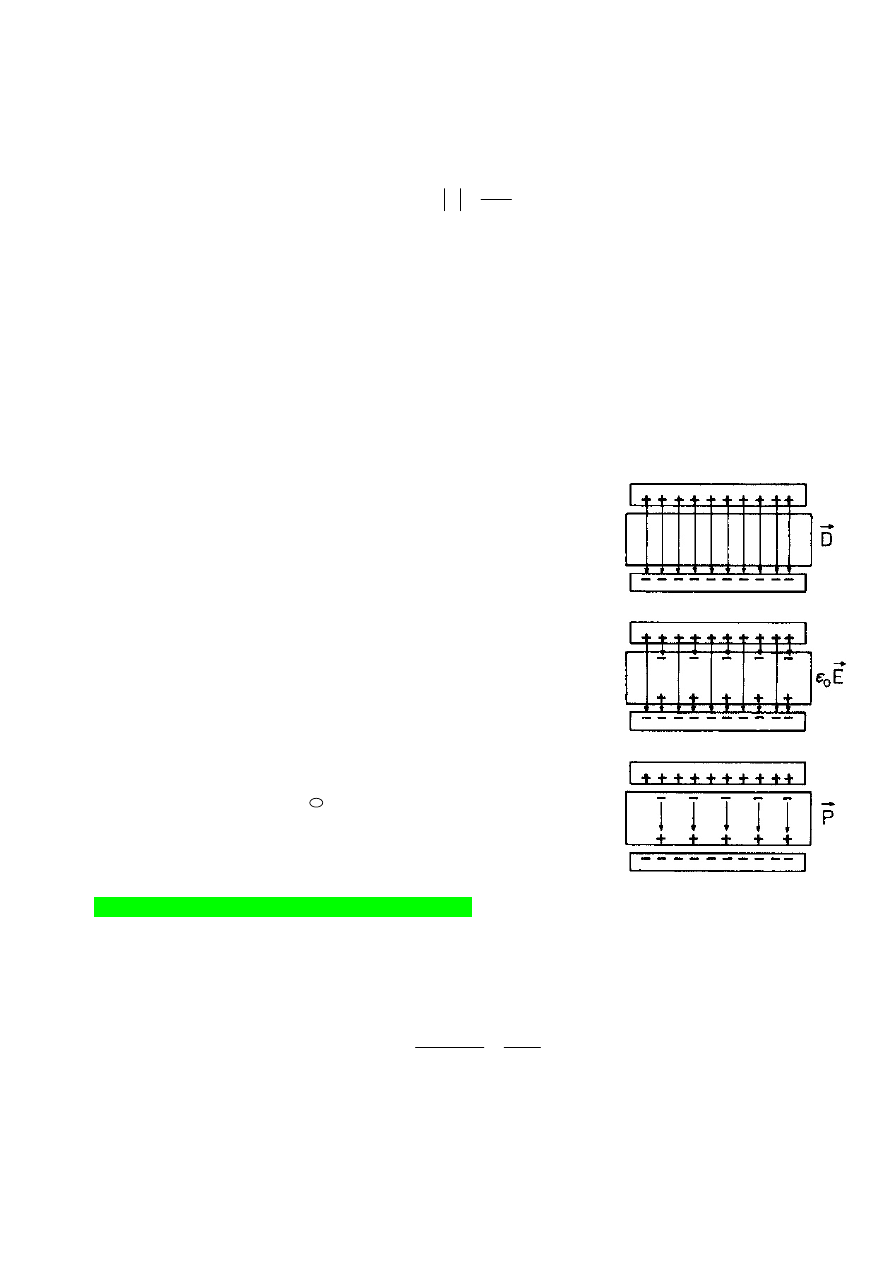
Związek pomiędzy natężeniem pola, wektorem polaryzacji i

wektorem indukcji (E,P i D)

Mówimy związek, bo na razie nie zalegalizowano małżeństw

wektorowych:

E

P

P

E

E

E

D

P

E

D

r

r

r

v

r

r

v

r

r

r

r

v

r

)

(

1

0

0

0

0

0

−

=

⇒

+

=







⇒

=

+

=

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

E

P

r

r

0

χε

χε

χε

χε

=

Postać prawa Gaussa słuszna dla ośrodków materialnych:

Q

s

d

D

S

=

∫∫

r

r

gdzie Q - sumaryczny ładunek zawarty wewnątrz powierzchni S

29.

Pole elektryczne we wnękach dielektryka. Wzór Claussiusa - Massottiego.

Wzór Claussiusa – Massottiego wiąże względną przenikalność dielektryka z

polaryzowalnością jego cząstek.

µµµµ

εεεε

αααα

ρρρρ

εεεε

εεεε

0

3

2

1

N

r

r

=

+

−

)

(

gdzie:

ρρρρ

- gęstość substancji,

µµµµ

– masa cząsteczkowa, N – liczba molekuł w jednostce

objętości – koncentracja molekuł,

αααα

– polaryzowalność.

17

30.

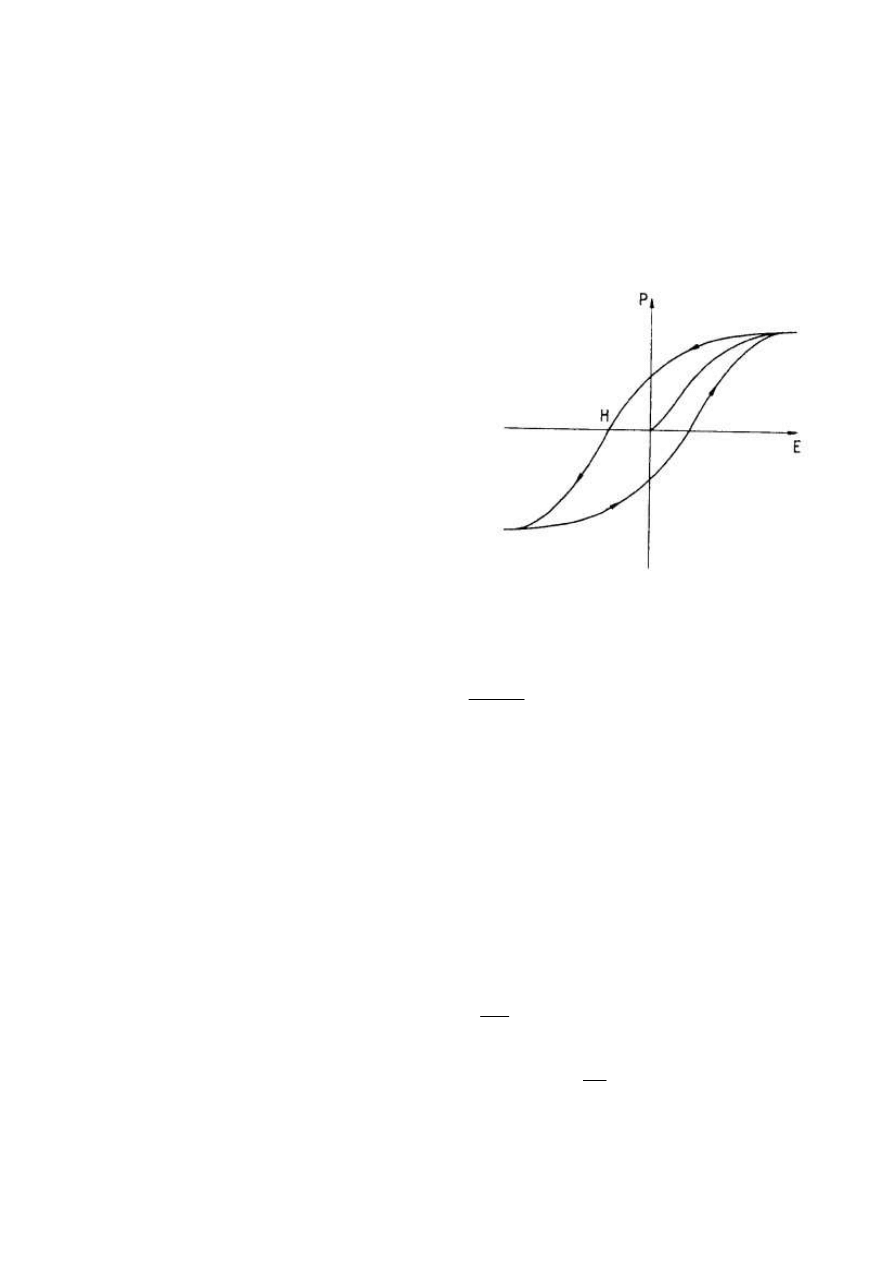
Ferroelektryki. Prawo Curie - Weissa

Ferroelektryki, to dielektryki zachowujące się w polu elektrycznym podobnie

do ferromagnetyków w polu magnetycznym.

W ferroelektrykach może występować polaryzacja nawet bez obecności pola

elektrycznego – wystarczają jedynie jego minimalne zmiany wywoływane przez ruch
termiczny jonów lub atomów. Taką polaryzację nazywamy spontaniczną. W
ferroelektryku pojawiają się wtedy domeny – fragmenty materii o pełnym
uporządkowaniu polaryzacyjnym. Zewnętrzny wektor polaryzacji można zwiększać
nieliniowo umieszczając ferroelektryk w polu elektrycznym. Osiąga on nasycenie
(nieprzekraczalną wartość całkowitego wektora polaryzacji) gdy wektory polaryzacji
domen osiągają orientację zgodną z
kierunkiem

pola.

Zależność

między

polaryzacją a natężeniem pola nazywamy
pętlą histerezy widoczną na wykresie
P(E).

Jak widać zmiana wektora polaryzacji

od

położenia

antyrównoległego

do

zgodnego z natężeniem pola ma inny
przebieg

niż

zmiana

w

kierunku

przeciwnym. Ważnym punktem wykresu
jest punkt H - pole koercji - wartość
natężenia pola E o kierunku przeciwnym
do polaryzacji pozwalającego zmniejszyć
polaryzację do zera, czyli zlikwidować
pozostałość elektryczną w materiale.

Prawo Curie – Weissa opisuje zależność podatności elektrycznej od temperatury
dielektryka T.

C

C

T

T

C

−

=

χχχχ

gdzie: C

c

– stała Curie-Weissa, T

c

– temperatura Curie, powyżej której maleje

koncentracja cząstek – N.

Prawo Curie-Weissa jest słuszne dla temperatur nieco przewyższających T

c

. Ze

wzoru tego wynika, że wykres podatności elektrycznej od temperatury dla T>T

c

jest

linią prostą.

31.

Prąd elektryczny. Gęstość prądu. Różniczkowe prawo Ohma.

a.

Prądem nazywamy uporządkowany ruch ładunków elektrycznych (zwanych

nośnikami prądu). Za kierunek przepływu prądu przyjęto kierunek ruchu dodatnich
nośników. Miarą prądu jest natężenie (z definicji: ładunek elektryczny, który
przepływa przez przekrój przewodnika w jednostce czasu):

dt

dQ

I

=

b.

Równanie definiujące wektor gęstości prądu:

s

d

dI

j

r

r

=

Stąd możemy zapisać:

∫∫

⋅

=

S

ds

n

j

I

r

r

18

c.

Mikroskopowa def. gęstości:

j=neV=neµE

gdzie: n - koncentracja nośników, V - prędkość ruchu uporządkowanego, µ=V/E -
ruchliwość nośników, E - natężenie pola elektrycznego.

d.

Różniczkowe prawo Ohma:

dI

dU

R

=

ρρρρ

ρρρρ

ρρρρ

E

j

l

ElS

jS

El

U

jS

I

R

U

I

S

l

R

=

⇒

=

⇒

=

=

=

=

jeśli podstawimy σ=1/ρ (konduktywność)

…

E

neV

E

neV

E

j

=

⇒

=

⇒

=

σσσσ

σσσσ

σσσσ

podstawiamy µ=V/E (ruchliwość ładunku)…

µµµµ

σσσσ

ne

=

32.

Pole magnetyczne w próżni. Siła Lorentza. Wektor indukcji magnetycznej B.

a.

Pole magnetyczne

w fizyce jest przestrzenią, w której siły działają na

poruszające się ładunki elektryczne, a także na ciała mające moment magnetyczny
(niezależnie od ich ruchu). W próżni pole magnetyczne może być scharakteryzowane
przez wektor indukcji magnetycznej B.

B

- wektor indukcji pola magnetycznego

H

- wektor natężenia p.m.

W próżni B=µ

0

H

, gdzie µ

0

=1/ε

0

c

2

b.

Siła Lorentza.

Dana jest następującym wzorem:

)

(

B

V

q

F

r

v

r

×

=

gdzie V to prędkość ładunku.

c.

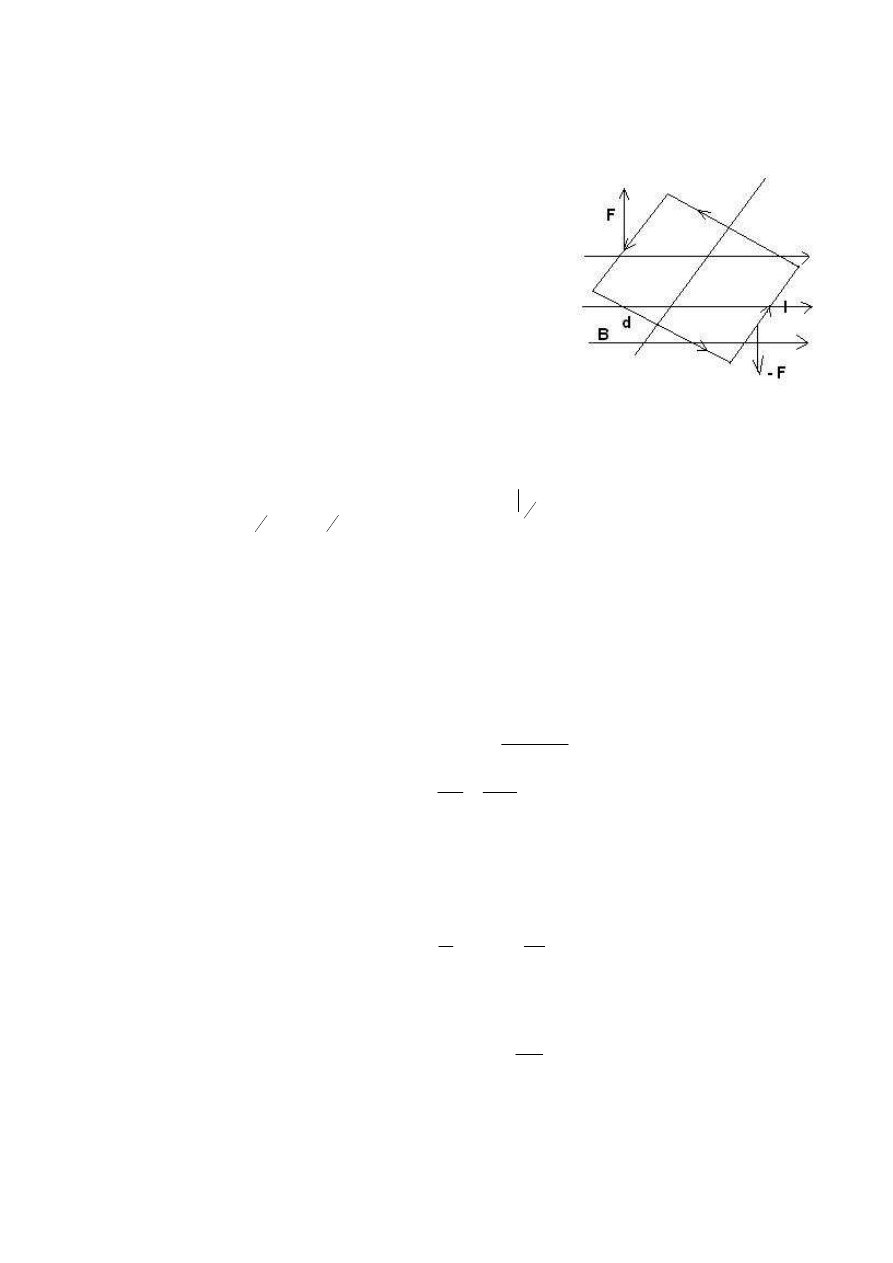
Siła elektrodynamiczna.

Siła działająca na N jednakowych ładunków poruszających się z prędkością V:

)

(

)

(

)

(

)

(

B

L

I

F

B

j

L

S

F

j

V

nq

B

V

Lnq

S

F

N

F

B

V

q

F

F

F

i

i

N

i

i

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

×

=

×

=

=

×

=

=

×

=

=

∑

=

∆∆∆∆

∆∆∆∆

∆∆∆∆

1

gdzie n - koncentracja ładunku, S - przekrój przewodnika,

L

∆∆∆∆

- element długości

przewodnika, L

r

∆∆∆∆

- wektor o wartości równej elementowi długości przewodnika oraz

zwrocie zgodnym z kierunkiem przepływu prądu I.

19

33.

Prawo Biota - Savarta - Laplace'a. Pole magnetyczne przewodnika kołowego.

a. Prawo Biota - Savarta - Laplace'a

Dane jest wzorem:

(

)

2

0

3

0

4

4

r

r

l

d

dl

I

B

d

r

r

l

d

I

B

d

r

r

r

r

r

r

,

sin

∠

=

×

=

ππππ

µµµµ

ππππ

µµµµ

gdzie element długości l

d

r

przewodnika skierowany zgodnie z kierunkiem prądu.

b. Pole magnetyczne przewodnika kołowego

Aby obliczyć pole magnetyczne w środku przewodnika kołowego o promieniu R, w

którym płynie prąd o natężeniu I, należy policzyć następującą całkę:

(

)

(

)

(

)

R

I

dl

R

I

B

r

l

d

R

r

l

d

dl

I

B

d

R

R

B

2

1

4

1

2

4

0

2

0

2

0

2

0

2

0

0

µµµµ

ππππ

µµµµ

ππππ

ππππ

µµµµ

Π

Π

Π

Π

Π

Π

Π

Π

=

=

⇒

=

=

∠

⇒

∠

=

∫

∫

∫

sin

,

sin

,

sin

r

r

r

r

r

34.

Prawo Ampere'a. Pole magnetyczne przewodnika prostoliniowego i solenoidu.

a. Prawo Ampere’a

Pozwala przyrównać tzw. krążenie wektora indukcji magnetycznej po

zamkniętym konturze

ΓΓΓΓ

do całkowitego prądu płynącego przez ten kontur

pomnożonego przez przenikalność magnetyczną ośrodka.

I

l

d

B

0

µµµµ

ΓΓΓΓ

=

∫

r

r

zaś gdy dana jest gęstość prądu j…

∫∫

∫

∫∫

⋅

=

⇒

⋅

=

S

S

ds

n

j

B

ds

n

j

I

r

r

r

r

r

0

µµµµ

ΓΓΓΓ

S jest rozpięte na

ΓΓΓΓ

.

Postać różniczkowa równania:

j

B

r

r

0

µµµµ

=

×

∇

b. Pole magnetyczne przewodnika prostoliniowego:

(w odległości r od przewodnika, w którym płynie prąd I)

r

I

B

ππππ

µµµµ

2

0

=

c.

P.m. solenoidu:

nI

l

NI

B

0

0

µµµµ

µµµµ

=

=

gdzie N - liczba zwojów solenoidu, l - długość
solenoidu, n - zagęszczenie zwojów solenoidu, I - prąd
płynący w solenoidzie.

20

35.

Moment magnetyczny. Moment siły i energia momentu magnetycznego.

a.

Moment magnetyczny

n

IS

r

=

µµµµ

gdzie n

r

- wektor normalny do powierzchni S

b.

Moment siły:

Moment siły działającej w polu magnetycznym

o indukcji B

r

na ciało o momencie magnetycznym

µµµµ

r

wynosi:

B

M

r

r

r

×

= µµµµ

c.

Energia potencjalna:

Energia potencjalna takiego ciała, gdy

αααα

to kąt między wektorem momentu

magnetycznego a wektorem indukcji…

B

E

B

B

d

B

Md

E

p

p

r

r

⋅

−

=

⇒

−

=

−

=

=

=

∫

∫

µµµµ

αααα

µµµµ

αααα

µµµµ

αααα

αααα

αααα

µµµµ

αααα

αααα

α

αα

α
Π

Π

Π

Π

Π

Π

Π

Π

Π

Π

Π

Π

cos

cos

sin

2

2

2

36.

Oddziaływanie prądów elektrycznych.

a. Siła działająca między przewodnikami

Dane są dwa nieskończenie długie przewodniki z prądem o natężeniach prądów

w nich płynących I

1

i I

2

, oddalone od siebie o d. Siła działająca na długość l

2

przewodnika 2 w polu magnetycznym B

1

wytworzonym przez przewodnik 1 wynosi:

d

l

I

I

l

I

B

F

ππππ

µµµµ

2

2

2

1

0

2

2

1

12

=

=

2

1

0

2

12

2

I

I

d

l

F

f

ππππ

µµµµ

=

=

Jeden amper - (

definicja) natężenie takiego prądu, który płynąc w dwóch

bardzo długich przewodnikach prostych odległych od siebie o 1m, powoduje
powstanie siły oddziaływania magnetycznego między nimi równej

m

N

l

F

f

7

10

2

−

⋅

=

=

Stąd wyznaczyć można przenikalność magnetyczną próżni:

2

7

0

10

4

A

N

−

⋅

= ππππ

µµµµ

21

37.

Prawo Gaussa dla wektora indukcji magnetycznej B.

a. Definicja

Całkowity strumień wektora indukcji magnetycznej B, przechodzący przez

dowolną powierzchnię zamkniętą, jest proporcjonalny do źródła pola magnetycznego
zamkniętego wewnątrz tej wybranej powierzchni.

b. Postać całkowa

∫∫

=

⋅

=

S

B

s

d

B

0

r

r

Φ

Φ

Φ

Φ

c. Postać różniczkowa

0

=

⋅

∇

B

r

38.

Względność pola elektrycznego

i magnetycznego.

Pole magnetyczne powstaje wtedy,

gdy mamy do czynienia z ruchem
ładunków. Ponieważ ruch jest pojęciem
względnym, w zależności od układu
odniesienia,

tym

samym

pole

magnetyczne jest względne.

Z punktu widzenia układu K

związanego z przewodnikiem, prąd
przepływający w przewodniku wytwarza
pole

magnetyczne

i

na

ładunek

poruszający się w tym układzie działa
siła Lorentza.

Jeśli natomiast układ odniesienia

K’ związany jest z nośnikiem prądu,
mającym

względem

przewodnika

prędkość równą prędkości unoszenia
przez pole elektryczne, to w układzie K’
nośniki będą nieruchome i pole nie
wystąpi.

Można

wykazać

za

pomocą

transformacji Lorentza, że na ładunek
spoczywający w tym układzie działa siła
elektrostatyczna

pochodząca

od

nadmiaru ładunku nośników. Siła ta jest
taka sama co do wartości i kierunku jak
siła Lorentza występująca w układzie K.

39.

Zjawisko indukcji elektromagnetycznej Faraday'a. Siła elektromotoryczna indukcji.

Prawo indukcji Faraday’a głosi, że indukowana w obwodzie siła

elektromotoryczna równa jest (wyłączając znak minus) szybkości z jaką zmienia się
strumień przechodzący przez obwód. Jeżeli szybkość zmian strumienia mierzona jest
w Wb/s to SEM otrzymamy w woltach.

dt

d

Φ

Φ

Φ

Φ

εεεε −

=

22

Jeżeli równanie zastosować do zwojnicy o N zwojach to w każdym z nich pojawi

się SEM i te SEM dodadzą się. Jeżeli zwojnica utworzona jest z cienkiego drutu i
nawinięta tak ciasno, że o każdym zwoju można powiedzieć że zajmuje to samo
miejsce w przestrzeni, to strumień przechodzący przez zwój będzie taki sam. Dlatego:

dt

Nd

Φ

Φ

Φ

Φ

εεεε −

=

40.

Samoindukcja i indukcja wzajemna. Współczynnik indukcji własnej L.

a. Samoindukcja

Kiedy w pojedynczej cewce zmienia się prąd pojawia się w niej SEM. Zjawisko to

nazywamy samoindukcją, a SEM wytwarzane w ten sposób nazywamy siłą
elektromotoryczną samoindukcji. Współczynnik samoindukcji L jest wielkością
charakterystyczną dla danej cewki i zależy od jej geometrii.

I

N

L

Φ

Φ

Φ

Φ

=

Jednostką indukcyjności jest 1 henr [H] = 1 V * s /A

b. Indukcja wzajemna

Dwa obwody elektryczne, znajdujące się obok siebie, nawzajem oddziałują na

siebie magnetycznie – strumień wytwarzany przez jeden obwód przenika drugi i w
przypadku zmiany tego strumienia od obwodu pierwszego, w drugim obwodzie
wyindukowana zostanie SEM.

2

21

1

11

1

I

L

I

L

+

=

Φ

Φ

Φ

Φ

gdzie L

11

– wsp. samoindukcji 1 obwodu, L

21

– wsp. indukcji wzajemnej, I1 i I2

prądy płynące w obwodach.

Ogólnie wsp. indukcji wzajemnej, gdy obwód 1 wytwarza pole przenikające

obwód 2, wyznaczamy jako:

1

12

12

I

L

Φ

Φ

Φ

Φ

=

i analogicznie w odwrotnej sytuacji:

2

21

21

I

L

Φ

Φ

Φ

Φ

=

41.

Pole magnetyczne materii. Wektor namagnesowania (magnetyzacja) M.

Namagnesowanie - wielkość wektorowa określająca magnetyczną odpowiedź

materiału na zewnętrzne pole magnetyczne oraz - w przypadku materiałów
namagnesowanych trwale - pole magnetyczne materiału.

∑

=

i

m

V

M

r

r

1

gdzie: V - objętość substancji,

i

m

r

- moment magnetyczny jednostki objętości tej

substancji (sumowany po całej jej objętości).

42.

Częstość Larmora. Podatność magnetyczna. Względna przenikalność magnetyczna µ.

Podatność magnetyczna jest współczynnikiem proporcjonalności w

równaniu określającym wielkość namagnesowania jako funkcję natężenia pola
magnetycznego:

H

M

χχχχ

=

gdzie: M - namagnesowanie (moment magnetyczny jednostki objętości substancji),
χ - objętościowa podatność magnetyczna, H - natężenie pola magnetycznego

23

W zależności od właściwości substancji jej podatność magnetyczna zmienia się

dość zasadniczo. Gdy:

χ < 0 - substancja jest diamagnetykiem, co oznacza że pole magnetyczne jest

"wypychane" z takiego ciała (maleje gęstość strumienia pola magnetycznego w
porównaniu z próżnią);

χ = 0 - brak podatności, np. dla próżni;

χ > 0 - substancja jest paramagnetykiem, co oznacza że pole magnetyczne jest

"wciągane" do takiego ciała (rośnie gęstość strumienia pola magnetycznego w
porównaniu z próżnią);

χ >> 0 - substancja jest ferromagnetykiem;

Względna przenikalność magnetyczna:

µµµµ

= 1 + χ

43.

Diamagnetyzm. Podatność magnetyczna diamagnetyków.

Diamagnetyzm - zjawisko polegające na indukcji w ciele znajdującym się w

zewnętrznym polu magnetycznym pola przeciwnego, osłabiającego działanie
zewnętrznego pola. Diamagnetyzm wykazują wszystkie materiały, lecz jest on bardzo
słabym efektem, więc w para- i ferromagnetykach jest niezauważalny. Diamagnetyki
mają podatność magnetyczną χ < 0 rzędu 10

-5

÷÷÷÷

10

-6

.

44.

Paramagnetyzm.

Jest to zjawisko magnesowania się makroskopowego ciała w zewnętrznym polu

magnetycznym, w kierunku zgodnym z kierunkiem pola zewnętrznego. Substancja
wykazująca takie własności to paramagnetyk - jest on przyciągany przez magnes,
jednak znacznie słabiej niż ferromagnetyk. Przyczyną paramagnetyzmu jest
porządkowanie się spinów elektronów ciała zgodnie z liniami zewnętrznego pola
magnetycznego, uporządkowaniu przeciwdziałają drgania cieplne cząsteczek. W
niskich temperaturach lub w silnych polach magnetycznych dochodzi do
uporządkowania niemal wszystkich dipoli magnetycznych elektronów w wyniku czego
dochodzi do nasycenia. Właściwości paramagnetyczne posiadają substancje o
niesparowanych elektronach.

45.

Ferromagnetyki. Pętla histerezy. Domeny ferromagnetyczne.

Właściwości

ferromagnetyczne

posiadają

wyłącznie ciała stałe. Występują one w substancjach,
których atomy w stanie gazowym są paramagnetyczne.
Wtedy, gdy atomy te są regularnie ułożone w sieci
krystalicznej, dochodzi do sprzężenia indywidualnych
atomowych

momentów

magnetycznych.

Poniżej

pewnej temperatury zwanej temperaturą Curie
sprzężenie to powoduje równoległe ułożenie się
wszystkich momentów atomowych w pewnych
obszarach zwanych domenami.

W stanie równowagi makroskopowe ciała mają wiele domen o kierunkach

namagnesowania

rozłożonych

chaotycznie,

co

sprawie,

że

wypadkowe

namagnesowanie

całej

próbki

jest

bliskie

zeru.

Jeżeli

ferromagnetyk

namagnetyzujemy polem zewnętrznym, to nastąpi w nim rozrost domen o momencie
magnetycznym zgodnym z kierunkiem zewnętrznego pola kosztem innych domen. W
rezultacie tego wypadkowe namagnesowanie próbki wzrośnie i będzie zgodne z zew.
polem.

Ułożenie domen w

ferromagnetyku będącym

w stanie równowagi

24

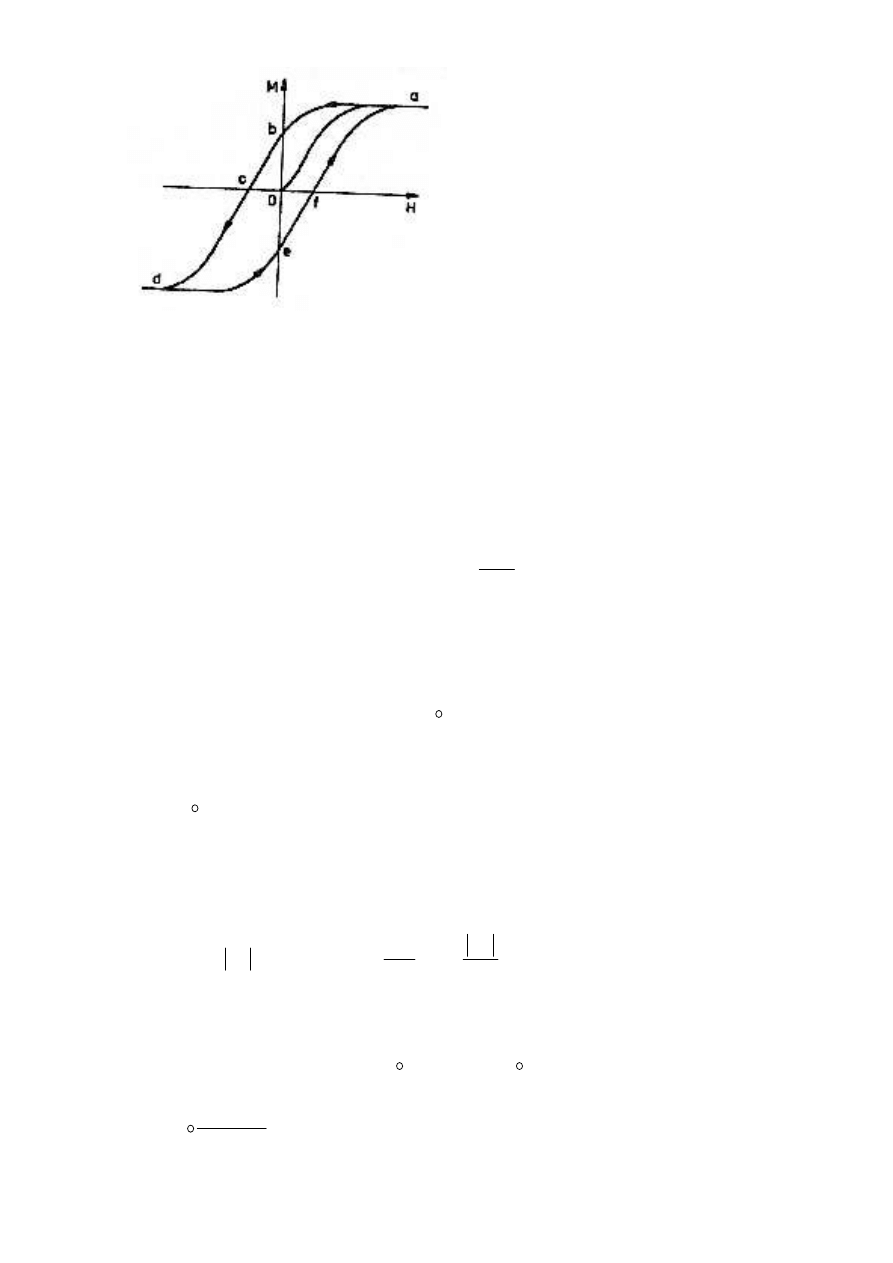
Proces ten przedstawia wykres obok. Próbka
ma na początku magnetyzacje zero. Pod
wpływem zew. pola rośnie aż do nasycenia w
pkt.

a

(wszystkie

domeny

są

już

namagnesowane w tym samym kierunku).
Gdy

pole

zew.

maleje

wypadkowa

magnetyzacja nie wraca do poprzedniego
stanu, gdyż swobodnemu rozrostowi domen
przeszkadzają defekty sieci krystalicznej. W
materiale

wciąż

obecna

jest

tzw.

pozostałość magnetyczna (b). Aby ją
zniwelować, należy umieścić próbkę w polu o

odpowiednim natężeniu, zwanym koercją magnetyczną (c). Duża wartość koercji
odpowiada materiałom ferromagnetycznie twardym, mała zaś - miękkim.

Zjawisko przedstawione na wykresie nosi nazwę pętli histerezy. Pole tej pętli

odpowiada pracy potrzebnej do przemagnesowania materiału.

46.

Związek między wektorami B, H i M.

Aby wyrazić związek między trzema wektorami magnetycznymi weźmy dla

przykładu cewkę toroidalną o N

0

zwojach, wypełnioną materiałem (cewkę z

rdzeniem). Przez wektor namagnesowania M będziemy rozumieli moment
magnetyczny jednostki objętości rdzenia

Adl

d

M

µµµµ

=

gdzie

µµµµ

d jest momentem magnetycznym wycinka rdzenia o długości dl i polu

przekroju A.

Prawo Ampere’a dla przestrzeni bez magnetyków ma postać

∫

=

I

Bdl

0

µµµµ

jednak w obecności magnetyka pole jest silniejsze, dlatego by zrównoważyć ten efekt
wprowadzamy fikcyjny prąd I

m.

Więc:

∫

+

=

)

(

m

I

I

Bdl

0

µµµµ

, czyli dla toroidu:

m

I

N

I

N

rB

0

0

0

0

2

µµµµ

µµµµ

ππππ

+

=

ze wzoru na moment magnetyczny mamy

MAdl

d

=

µµµµ

zastępujący go moment namagnesowania w zwojach nawiniętych na odcinku dl:

m

m

m

m

I

N

rM

I

N

r

Adl

d

dl

r

N

A

I

A

NI

d

0

0

0

2

2

2

=

⇒

=

⇒

=

=

ππππ

ππππ

µµµµ

ππππ

µµµµ

przyrównując oba wyrażenia mamy:

M

r

I

N

rB

0

0

0

2

2

µµµµ

ππππ

µµµµ

ππππ

+

=

w ogólnej postaci oznacza to, że

∫

∫

+

=

Mdl

I

Bdl

0

0

µµµµ

µµµµ

czyli:

∫

=

−

I

dl

M

B

0

0

µµµµ

µµµµ

Pętla histerezy

25

Wprowadźmy nową wielkość wektorową

0

0

µµµµ

µµµµ

M

B

H

−

=

(*)

jest to natężenie pola magnetycznego, którego cyrkulacja (krążenie) po zamkniętym
konturze równa jest rzeczywistemu prądowi obejmowanemu przez kontur

I

dl

H

=

∫

znaleźliśmy w ten sposób (*) zależność między trzema wektorami

M

H

B

0

0

µµµµ

µµµµ

+

=

Dla magnetyków liniowych (para i diamagnetyków)

H

B

r

µµµµ

µµµµ

0

=

a stąd wynika

H

H

M

r

χχχχ

µµµµ

=

−

=

)

(

1

47.

Zjawiska magnetomechaniczne. Doświadczenie Einsteina - de Haasa.

a. Zjawiska magnetomechaniczne

Są to

zjawiska które polegają na pojawieniu się momentu pędu elementu

wykonanego z ferromagnetyka przy jego namagnesowaniu.

b. Doświadczenie Einsteina - de Haasa

Dotyczy istnienia sprzężenia orbitalnego

momentu elektronów w atomie i momentu
magnetycznego.

Fizycy

umieścili

pręt

wykonany

z

ferromagnetyka w pionowym solenoidzie, po czym
włączyli zmienny prąd elektryczny, którego
częstotliwość

odpowiadała

rezonansowym

drganiom skrętnym pręta. W skutek przepływu
prądu pręt został namagnesowany. Zaobserwowali
oni obrót pręta wokół osi pionowej o określony kąt.

Na podstawie efektu magnetomechanicznego można wyznaczyć wartość

stosunku momentu magnetycznego atomów do ich momentu pędu J. Jest to tzw.
stosunek giromagnetyczny

γγγγ

.

Dla ruchu orbitalnego elektronu związanego w atomie:

0

2m

ge

e

=

γγγγ

gdzie: g - stały czynnik, zwany czynnikiem Landégo, e i m

0

- ładunek i masa

elektronu.

48.

Energia pola magnetycznego.

Pole

magnetyczne

wytwarzane

jest

poprzez

przepływające ładunki, zatem źródłami pola magnetycznego
są magnesy stałe albo przewodniki, przez które płynie prąd.
Aby wyliczyć energię pola magnetycznego rozważmy dwa
układy R-C, R-L i zastosujmy do nich prawo Kirchoffa.

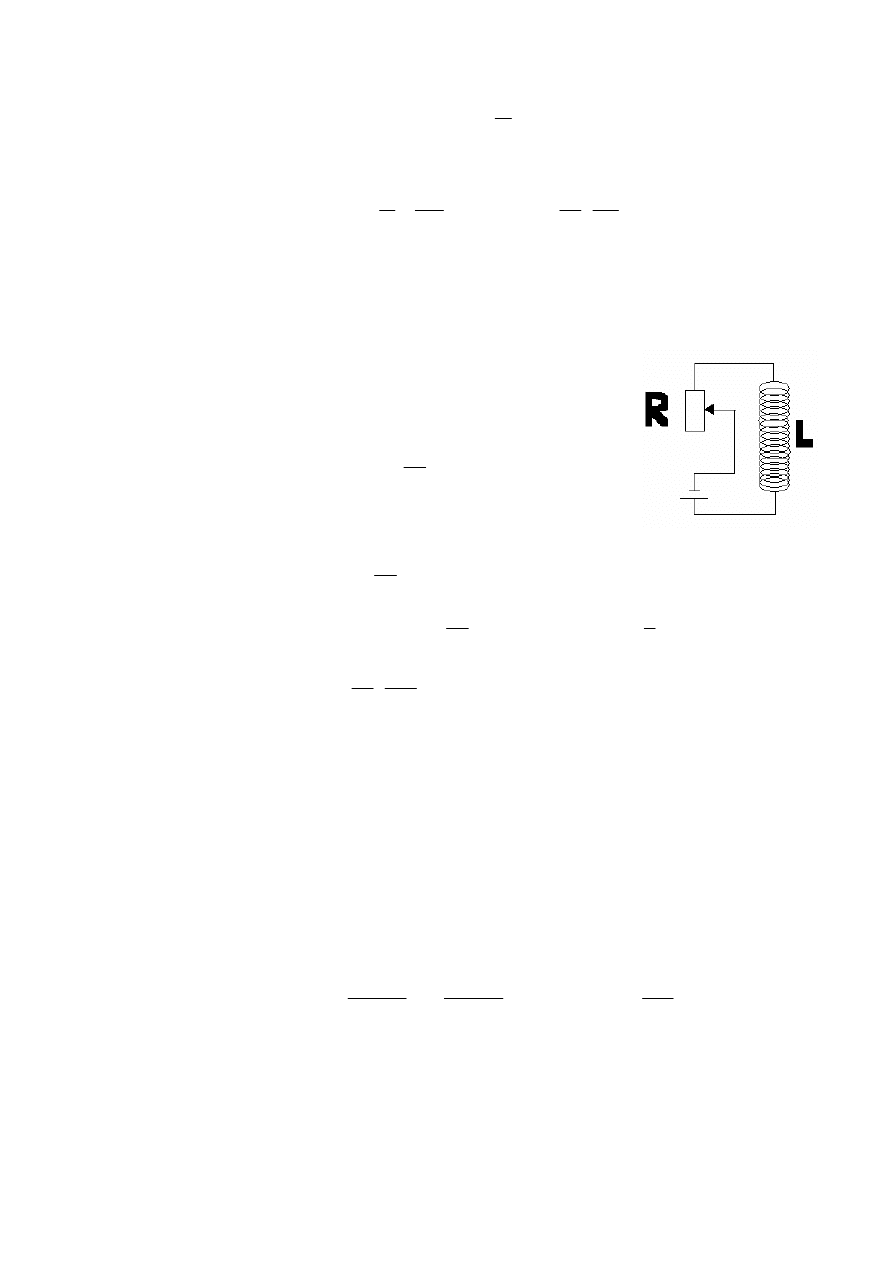
26

I. Obwód R-C:

E

C

Q

RI

=

+

Mnożymy obustronnie przez I…

EI

C

Q

dt

d

RI

EI

dt

dQ

Q

C

RI

=













+

⇒

=

+

2

1

2

2

2

Pierwszy człon przedstawia ciepło wydzielone w oporniku na jednostkę czasu,

drugi to szybkość zmiany energii naładowanego kondensatora o pojemności C,
natomiast prawa strona to moc dostarczona przez zewnętrzną siłę elektromotoryczną.
Zauważamy jednocześnie, że prawo Kirchoffa przedstawia bilans obwodu i opiera się
na zasadzie zachowania energii.

II. Analogicznie w obwodzie R-L:

Z prawa Kirchoffa:

E

dt

dI

L

RI

=

+

Mnożymy obustronnie przez I…

EI

LI

dt

d

RI

LI

I

d

I

L

W

dt

dt

dI

LI

Pdt

dW

EI

dt

dI

LI

RI

I

=













+













=

′

′

=

⇒













=

=

=

+

∫

2

2

1

2

2

2

0

2

Pierwszy człon to ponownie ilość energii cieplnej wytworzonej w oporniku, drugi

to energia magnetyczna zmagazynowana w polu magnetycznym cewki o
indukcyjności L.

Np. dla jednorodnego pola magnetycznego solenoidu, o zagęszczeniu zwojów na

jednostkę długości równym n i objętości V:

V

n

L

2

0

µµµµ

=

Po podstawieniu L otrzymamy wzór na energię magnetyczną:

{

}

V

B

nI

B

V

I

n

V

I

n

W

0

2

0

0

2

2

2
0

2

2

0

2

2

2

µµµµ

µµµµ

µµµµ

µµµµ

µµµµ

=

=

=

=

=

…z którego wynika, że energia pola magnetycznego związana jest z: objętością

zajmowaną przez pole i jego gęstością przestrzenną.

UWAGA: wzór ten jest również poprawny dla niejednorodnego pola

magnetycznego.

27

49.

Prąd przewodzenia i przesunięcia. Pole elektromagnetyczne.

a. Prąd przewodzenia

Wewnątrz

krążka wirującego

w

polu

magnetycznym istnieje naturalnie zamknięty
obwód prądu, w którym, podczas obrotów krążka,
oddziaływanie styczne działając na swobodne
elektrony przewodzenia wywołuje ich obwodowy
przepływ.

Wewnątrz

krążka

powstaje

prąd

przewodzenia płynący w zamkniętej pętli, zgodnie
z kierunkiem działania oddziaływania stycznego.

Przy dodatnim zwrocie linii sił pola

magnetycznego, elektrony przewodzenia wewnątrz wirującego krążka płyną w
kierunku zgodnym z ruchem wskazówek zegara, natomiast przy ujemnym zwrocie
linii sił pola magnetycznego - w kierunku przeciwnym do kierunku ruchu wskazówek
zegara. Widać, że indukowany oddziaływaniem stycznym wewnątrz krążka obwodowy
prąd przewodzenia płynie w takim kierunku, przy którym następuje wzmocnienie
pola magnetycznego przenikającego krążek.

b. Prąd przesunięcia

Prąd elektryczny wywołany zmianą natężenia pola elektrycznego w dielektryku.

W przeciwieństwie do prądu przewodnictwa, nie polega on na przepływie ładunków,
jednak pomimo tego również wywołuje wirowe pole magnetyczne.

50.

Równania Maxwella w postaci całkowej i różniczkowej.

Lp.

Postać

różniczkowa

Postać całkowa

Nazwa

Zjawisko fizyczne

opisywane przez

równanie

1.

ρρρρ

=

⋅

∇

D

r

∫∫∫

∫∫

⋅

=

⋅

V

S

dv

s

d

D

ρρρρ

r

r

prawo Gaussa dla

elektryczności

Źródłem pola
elektrycznego są
ładunki.

2.

t

B

E

∂

∂

−

=

×

∇

r

r

t

l

d

E

B

L

∂

∂

−

=

⋅

∫

Φ

Φ

Φ

Φ

r

r

prawo Faradaya

Zmienne w czasie
pole magnetyczne
wytwarza wirowe
pole elektryczne

3.

0

=

⋅

∇

B

r

0

=

⋅

∫∫

S

s

d

B

r

r

prawo Gaussa dla

magnetyzmu

Pole magnetyczne jest
bezźródłowe, jego
linie są zamknięte.

4.

t

D

j

H

∂

∂

+

=

×

∇

v

r

r

t

I

l

d

H

D

L

∂

∂

+

=

⋅

∫

Φ

Φ

Φ

Φ

r

r

prawo Ampère’a

rozszerzone przez

Maxwella

Przepływający prąd
oraz zmienne pole
elektryczne
wytwarzają wirowe
pole magnetyczne

gdzie: D - indukcja elektryczna [ C / m

2

], B - indukcja magnetyczna [ T ], E -

natężenie pola elektrycznego [ V / m ], H - natężenie pola magnetycznego [ A / m ],
Φ

D

- strumień indukcji elektrycznej [ C = A—s], Φ

B

- strumień indukcji magnetycznej [

Wb ], j - gęstość prądu [A/m

2

], ρ - gęstość ładunku [ C / m

3

]

28

51.

Fala elektromagnetyczna. Wektor Poyntinga.

a. Fala elektromagnetyczna

Maxwell wywnioskował z równań, że zmienne pole elektryczne w próżni

wywołuje zmienne pole magnetyczne, a zmienne pole magnetyczne wywołuje
zmienne pole elektryczne. Zmiany te, zwane falą elektromagnetyczną, rozchodzą się z
prędkością światła.

Fala elektromagnetyczna jest więc rozchodzącymi się w przestrzeni, sprzężonymi

polami: elektrycznym (opisuje je wektor natężenia elektrycznego E) i magnetycznym
(opisuje je wektor indukcji magnetycznej B), prostopadłymi do siebie i do kierunku
rozchodzenia się, o natężeniach zmieniających się sinusoidalnie.

W celu uzasadnienia tego stwierdzenia zajmijmy się rozwiązaniem równań

Maxwella w próżni, szukając funkcji E(r,t) oraz B(r,t). Wychodząc z tożsamości
operatorowej:

E

E

div

grad

E

r

r

r

2

∇

−

=

×

∇

×

∇

)

(

)

(

ponieważ brak jest ładunków objętościowych

0

=

E

div

r

i możemy zapisać:

(*)

)

(

E

B

t

E

t

B

r

r

r

r

2

2

−∇

=

×

∇

∂

∂

−

−∇

=















∂

∂

−

×

∇

Z czwartego równania Maxwella dla próżni:

t

E

B

∂

∂

=

×

∇

r

r

εεεε

µµµµ

0

Po podstawieniu do wzoru (*) otrzymujemy:

2

2

0

2

t

E

E

∂

∂

=

∇

r

r

εεεε

µµµµ

- funkcja falowa

Analogicznie dla pola magnetycznego:

2

2

0

2

t

B

B

∂

∂

=

∇

r

r

εεεε

µµµµ

b. Wektor Poyntinga

Rozważmy falę płaską elektro-

magnetyczną harmoniczną:

Równania opisujące tę falę mają

postać następującą:

)

sin(

)

,

(

)

sin(

)

,

(

t

kx

B

t

x

B

t

kx

E

t

x

E

ω

ω

ω

ω

ω

ω

ω

ω

−

=

−

=

0

0

gdzie

ω

ω

ω

ω

to częstotliwość fali.

Z równań Maxwella wynika że iloczyn wektorowy E i H wyznacza kierunek

rozchodzenia się fali oraz określa strumień energii elektromagnetycznej, czyli ilość
energii przesyłanej przez jednostkę powierzchni w jednostce czasu.

H

E

S

r

r

r

×

=

gdzie:

S

r

- wektor Poyntinga, E

r

- natężenie pola elektrycznego, H

r

- natężenie pola

magnetycznego

29

lub

B

E

H

E

S

r

r

r

r

r

×

=

×

=

µµµµ

1

Stosunek amplitud pola magnetycznego i elektrycznego zależy jedynie od

właściwości ośrodka i definiuje oporność (impedancję) falową ośrodka.

52.

Drgania harmoniczne: swobodne, tłumione i wymuszone (mechaniczne i elektryczne).

53.

Składanie drgań. Dudnienia.

54.

Fale. Równanie falowe i funkcja falowa.

55.

Zasada Fermata. Prawa optyki geometrycznej.

56.

Współczynnik załamania. Związki dyspersyjne.

57.

Doświadczenie Younga. Interferencja.

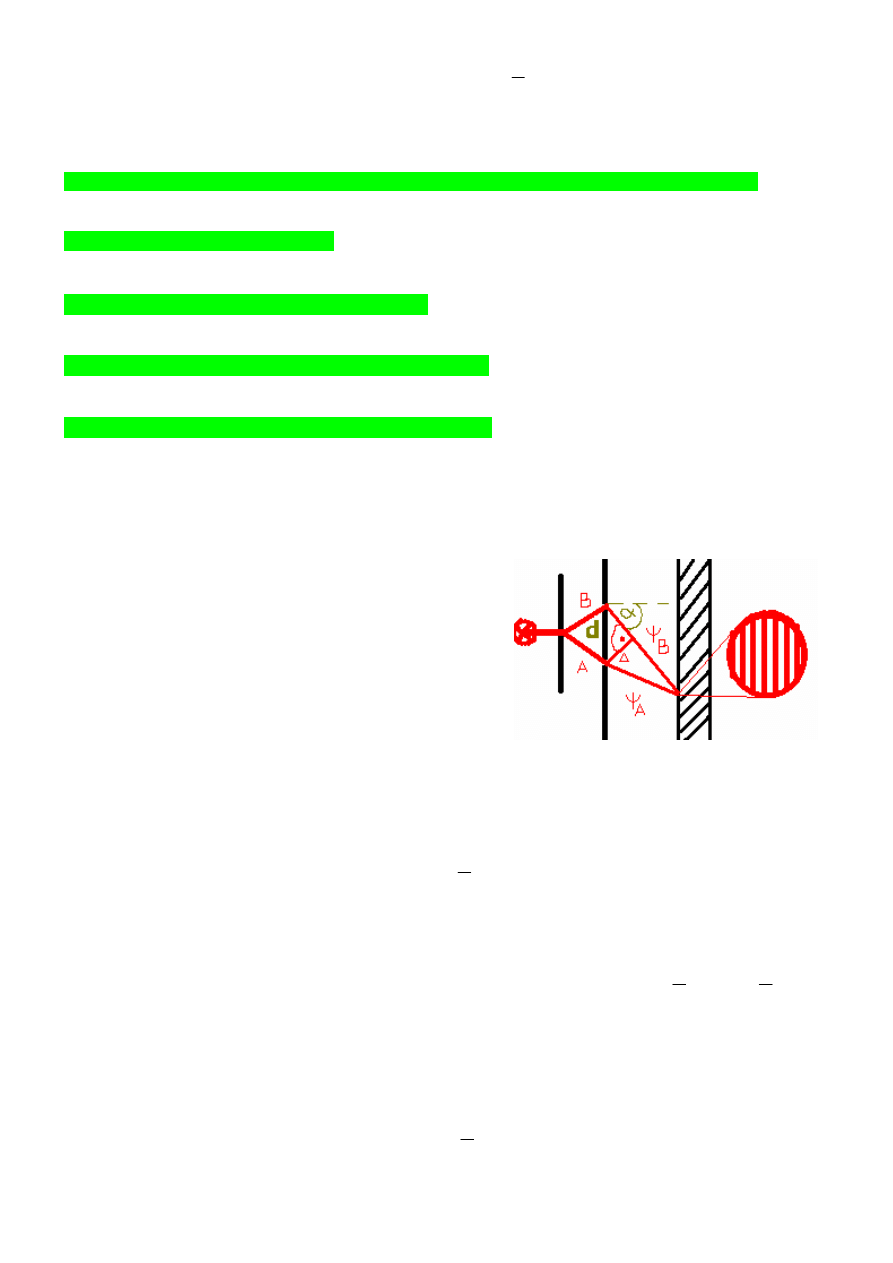
a. Doświadczenie Younga

Dzięki temu, że użyte zostało jedno

źródło światła to, fazy falowe w punktach A i
B są jednakowe. W efekcie czego na ekranie
w dowolnym punkcie ukazują się prążki
interferencyjne wynikające jedynie z różnicy
dróg optycznych przebytych przez promień A
i B. Tę różnicę dróg optycznych można
obliczyć prowadząc z punktu A odcinek
prostopadły do promienia B, a następnie
wykorzystując funkcję kosinus, do obliczenia
delty:

αααα

∆∆∆∆

sin

d

=

Warunek wzmocnienia:

λλλλ

∆∆∆∆

k

=

, gdzie k=1,2,3,4…

Warunek wygaszenia:

2

1

2

λλλλ

∆∆∆∆

)

(

+

=

k

, gdzie k=1,2,3,4….

Natężenie światła w doświadczeniu Younga:













+

=

+

=

⇒







+

=

=

2

2

2

ϕϕϕϕ

ω

ω

ω

ω

ϕϕϕϕ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

Ψ

ϕϕϕϕ

ω

ω

ω

ω

Ψ

Ψ

Ψ

Ψ

ω

ω

ω

ω

Ψ

Ψ

Ψ

Ψ

t

A

P

P

P

t

A

P

t

A

P

B

A

B

A

sin

cos

)

(

)

(

)

(

)

sin(

)

(

)

sin(

)

(

gdzie: Ψ - funkcja falowa (pochodząca od p-tu A lub B - patrz indeks), φ -
przesunięcie fazowe, P - dowolny punkt na ekranie

można zauważyć pojawienie się „nowej amplitudy”:

const

A

A

=

′

=

2

2

ϕϕϕϕ

cos

30

a stąd wynika…

2

2

A

I

A

I

Wypadkowe

′

⇒

~

~

2

4

2

2

ϕϕϕϕ

cos

A

I

W

′

=

Obok: wykres przedstawiający

natężenie światła w zależności od
kąta alfa

Warunek wzmocnienia

natężenia światła:

ππππ

δδδδ

ϕϕϕϕ

k

=

=

2

, gdzie k=1,2,3,4…

b. Interferencja światła w cienkich warstwach, np. w warstwie oleju na wodzie

d - grubość warstwy, n - współczynnik załamania światła w warstwie

Różnica dróg optycznych, czyli odcinek |12|, wynosi:

(

)

|

|

|

|

|

|

23

43

14

−

+

=

n

∆∆∆∆

- nierównoważność odbicia

A

n

d

2

2

2

sin

−

=

∆∆∆∆

Jeżeli promień światła odbija się od powierzchni, za którą jest ośrodek gęstszy

optycznie, to faza falowa zmienia się na przeciwną (jak w przypadku odbić w
punktach 1 oraz 3):

2

λλλλ

∆∆∆∆

∆∆∆∆

±

=

′

Warunek wygaszenia - wyprowadzenie:

λλλλ

λλλλ

λλλλ

λλλλ

λλλλ

∆∆∆∆

k

A

n

d

k

A

n

d

k

=

−

+

=

+

−

+

=

′

2

2

2

2

2

2

2

2

2

1

2

sin

sin

)

(

31

58.

Siatka dyfrakcyjna. Zdolność rozdzielcza siatki dyfrakcyjnej.

a. Siatka dyfrakcyjna

Jeden z najprostszych przyrządów do przeprowadzania analizy widmowej.

Tworzy ją układ równych, równoległych i jednakowo rozmieszczonych szczelin.

Jest to przezroczysta lub półprzezroczysta płytka – kryształowa, szklana lub z

tworzywa sztucznego. Na jedną ze stron płytki zostaje naniesiona seria równoległych
nieprzezroczystych linii, o stałym i odpowiednio małym rozstawie - od kilkunastu linii
na milimetr aż do tysiąca w przypadku dobrych siatek. Działanie siatki dyfrakcyjnej
polega na wykorzystaniu zjawiska dyfrakcji i interferencji światła do uzyskania jego
widma. W tym celu pomiędzy źródłem światła a białym ekranem umieszcza się siatkę
dyfrakcyjną. Na ekranie uzyskuje się w ten sposób widmo światła Była pierwszym
instrumentem pozwalającym wyznaczyć długość fal świetlnych.

Prążki jasne powstają dla kątów α

n

spełniających warunek:

λλλλ

αααα

n

d

n

=

)

sin(

gdzie: λ - długość fali, d - stała siatki, n - rząd ugięcia.

b. Zdolność rozdzielcza

Wiąże się ze zjawiskiem dyfrakcji (załamania fali). Pierwszy ułamek w niżej

podanym wzorze jest wartością kąta pod jakim obserwujemy dany obiekt.

Dla siatki dyfrakcyjnej otrzymujemy wzór:

d

s

m

mN

R

=

=

=

λλλλ

∆∆∆∆

λλλλ

gdzie: λ - długość fali, m - rząd dyfrakcji (numer prążka/plamki), N - liczba

szczelin siatki dyfrakcyjnej, d - stała siatki dyfrakcyjnej, s - szerokość czynna siatki.

Czynnikiem ograniczającym zdolność rozdzielczą nawet doskonałych przyrządów

optycznych są głównie efekty dyfrakcyjne, które powodują rozmycie obrazu punktu.

59.

Zjawisko dyfrakcji. Dyfrakcja na pojedynczej szczelinie.

a. Zasada Huygensa-Fresnela

Każdy punkt, do którego dociera fala, staje się

źródłem nowej fali kulistej. Powierzchnia falowa fali
wypadkowej powstałej z interferencji tej fali jest
obwiednią falową fal elementarnych.

Natężenie fali maleje wraz z odległością:

r

I

1

~

b. Opis zjawiska dyfrakcji

I - wg. Fresnela - wiązka światła padająca na szczelinę
pochodzi od źródła punktowego (rozchodzi się
koncentrycznie)

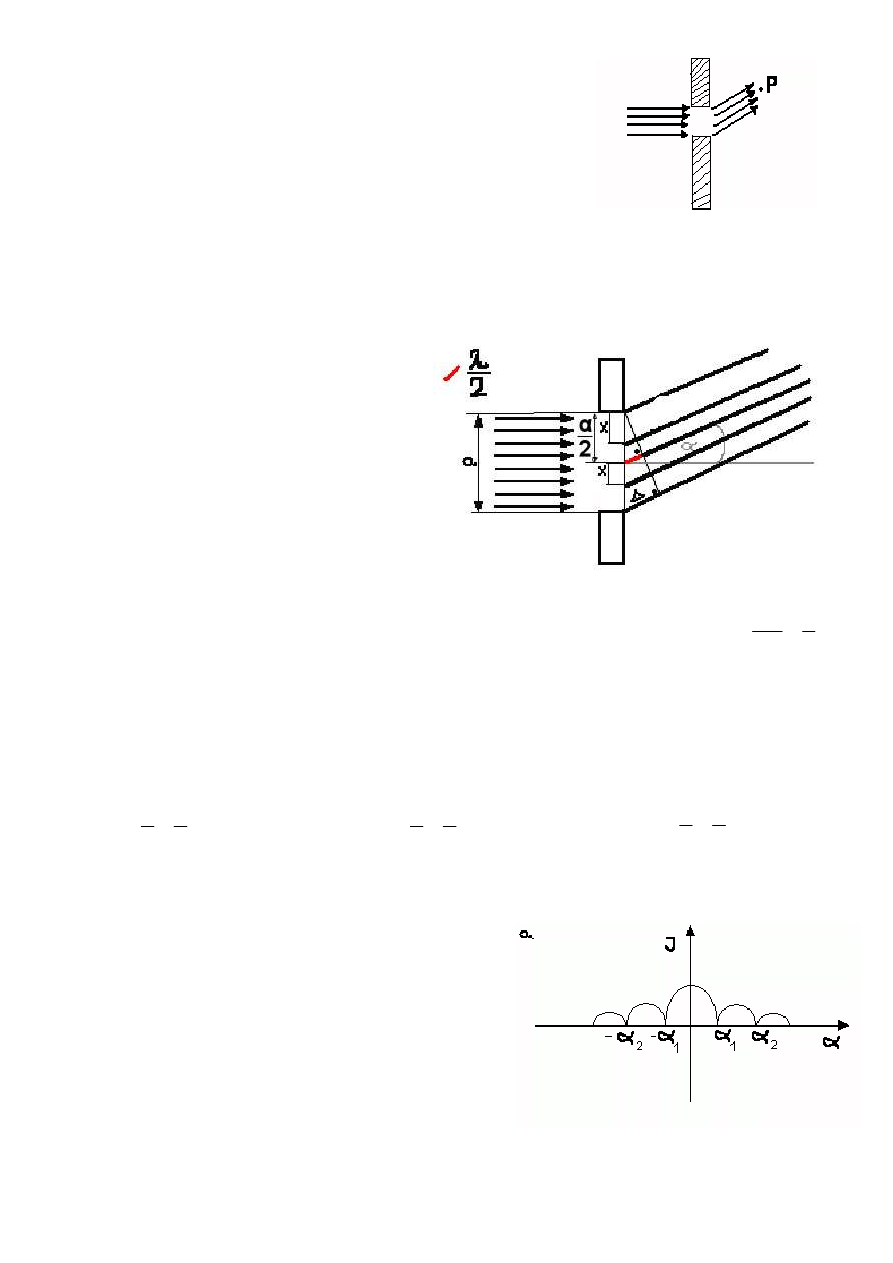
32

II - wg. Fraunhofera - wiązka światła padająca na
szczelinę jest równoległa

Dyfrakcja

jest

najlepiej

widoczna,

gdy

szczelina/przeszkoda ma wielkość porównywalna z długością fali.

Obraz dyfrakcyjny składa się z naprzemiennych stref wzmocnienia i wygaszenia

fali, powstałych w wyniku interferencji ugiętych fal elementarnych, o których mówi
zasada H-F.

c. Dyfrakcja światła na
pojedynczej szczelinie

I. Dla

0

=

αααα

natężenie światła jest

maksymalne i wynosi I

0

II. Dla

0

≠

αααα

:

αααα

∆∆∆∆

sin

a

=

Minima dyfrakcji (miejsca spełniające warunek wygaszenia fali

2

2

λλλλ

∆∆∆∆ =

m

wynikający z proporcji geometrycznej w trójkącie tworzonym na rysunku przez

∆∆∆∆

,

szczelinę a oraz odcinek prostopadły do wiązki ugiętej, gdzie

∆∆∆∆

- różnica dróg

optycznych dwóch promieni wybranych przy myślowym podziale szczeliny na m+1
części):

1 minimum dla

1

1

2

2

αααα

λλλλ

αααα

λλλλ

λλλλ

∆∆∆∆

sin

sin

a

a

=

=

=

2 minimum dla

2

2

2

4

2

2

αααα

λλλλ

αααα

λλλλ

λλλλ

∆∆∆∆

sin

sin

a

a

=

=

=

3 minimum dla

3

3

3

6

2

3

αααα

λλλλ

αααα

λλλλ

λλλλ

∆∆∆∆

sin

sin

a

a

=

=

=

Ogólny wzór na minima:

m

a

m

αααα

λλλλ

sin

=

gdzie m= 1,2,3,4…

Obok

znajduje

się

wykres

przedstawiający natężenie światła I w
zależności od kąta α - kąta minimum.

33

60.

Dyfrakcja promieni X na kryształach.

Promieniowanie rentgenowskie ulega

dyfrakcji

przez

odbicie

od

powierzchniowych

warstw

atomów

kryształu (na rysunku został schematycznie
przedstawiony

ich

regularny

rozkład).

Powstały obraz można oglądać kierując
odbitą wiązkę na odpowiedni ekran.

θ - kąt poślizgu, a - stała sieci krystalicznej
różnica drogi optycznej wynosi:

∆∆∆∆

2

θθθθ

∆∆∆∆

sin

a

=

Warunek wzmocnienia:

λλλλ

θθθθ

λλλλ

∆∆∆∆

k

a

k

=

⇒

=

sin

2

2

gdzie k=1,2,3,4…

61.

Polaryzacja światła.

Jest to zespół zjawisk w którym uwidaczniają się poprzeczne (względem

kierunku rozchodzenia się światła) cechy wiązek świetlnych. Podczas gdy
interferencja i dyfrakcja świadczą o falowej naturze światła, to p.ś. pozwala
stwierdzić, że jest ono falą poprzeczną.

Elektromagnetyczna teoria światła tłumaczy, że światło to fale e-m, czyli

rozchodzące się drgania elektryczne i magnetyczne wzajemnie sprzężone i
prostopadłe względem siebie oraz kierunku rozchodzenia się fali. Światło naturalne
nie jest spolaryzowane (drgania e-m zachodzą w nim we wszystkich płaszczyznach, w
których leży prosta określająca bieg wiązki).

Polaryzacja polega na przepuszczeniu wiązki światła przez układ tłumiący

wszystkie drgania elektryczne (i sprzężone z nimi magnetyczne) z wyjątkiem drgań
zachodzących w jednej płaszczyźnie. Wiązka po przejściu przez taki układ nazwana
będzie światłem spolaryzowanym liniowo względem wyróżnionej płaszczyzny
polaryzacji.

Do polaryzacji światła służą polaryzatory optyczne, takie jak polaroid czy

pryzmaty polaryzujące. Możliwe jest uzyskanie polaryzacji kołowej lub eliptycznej.
Polaryzacja częściowa lub całkowita występuje też zawsze przy odbiciu i załamaniu
światła (prawo Brewstera), przy przechodzeniu światła przez ośrodki optyczne
anizotropowe oraz przy jego rozpraszaniu.

Przykładem polaryzatora jest pryzmat Nicola (nikol), wykorzystujący zjawisko

dwójłomności światła (materiał posiada różny wsp. załamania dla promieni o różnej
polaryzacji). Zbudowany jest z kryształu szpatu islandzkiego, odpowiednio
obrobionego, rozciętego na dwie części i sklejonego balsamem kanadyjskim.

62.

Promieniowanie temperaturowe. Prawa: Kirchhoffa i Stefana-Boltzmana.

a. Promieniowanie temperaturowe (cieplne, termiczne)

Promieniowanie ciał o temperaturze wyższej od zera bezwzględnego. Wiąże się

ze wzbudzeniem cząsteczek lub atomów, wywołanym przez ich ruch cieplny. Polega
na emisji fali e-m o określonym widmie częstotliwości.

P.t. wysyłane przez ciało charakteryzuje wielkość określana jako zdolność

emisyjna ciała. Jest to ta część mocy (czyli całkowitej energii wysyłanej w jednostce
czasu przez element powierzchni ciała o polu jednostkowym), która przypada na

34

promieniowanie o częstościach zawartych w przedziale jednostkowym

νννν

∆∆∆∆

od

νννν

do

νννν

∆∆∆∆

νννν +

. Gdy ciało wysyła w jednostce czasu tyle samo energii, co pochłania, p.t. nosi

nazwę zrównoważonego.

W teorii p.t. występują następujące pojęcia:

I - ciało doskonale czarne - pochłaniające całkowicie promieniowanie e-m

padające na jego powierzchnię, bez względu na temp. tego ciała, kąt padania promieni
i widmo promieniowania. Jego zdolność absorpcyjna równa się jedności.

II - ciało doskonale szare - pochłaniające określoną przez zdolność absorpcyjną

część promieniowania padającego na jego powierzchnię, bez względu na temp. tego
ciała, kąt padania promieni i widmo promieniowania.

b. Prawo promieniowania Kirchhoffa

Stosunek zdolności emisyjnej ciała

( )

T

E ,

νννν

, gdzie

νννν

- częstość drgań

promieniowania, T - temperatura ciała, do jego zdolności absorpcyjnej

( )

T

A ,

νννν

jest

dla wszystkich ciał jednakowy,
tzn. jest niezależną od rodzaju
ciała

funkcją

temperatury

i

częstości promieniowania

( )

T

,

νννν

εεεε

zwaną funkcją Kirchhoffa:

( )

( ) ( )

T

T

A

T

E

,

,

,

νννν

εεεε

νννν

νννν

=

Z definicji ciała doskonale

czarnego wynika, że

( )

T

,

νννν

εεεε

jest po

prostu jego zdolnością emisyjną.

Popularnie p.p.K. można

sformułować następująco: ciało
promieniuje tym intensywniej, im
intensywniej pochłania.

c. Prawo Stefana-Boltzmanna

Całkowita energia

( )

T

ξξξξ

emitowana w jednostce czasu w postaci energii

promieniowania temperaturowego przez element powierzchni ciała doskonale
czarnego o polu jednostkowym (tj. całkowita zdolność emisyjna ciała dosk. czarnego)
wyraża się następująco:

( )

4

T

T

σσσσ

ξξξξ

=

gdzie:

σσσσ

- stała Stefana-Boltzmanna, T - temperatura ciała.

Prawo stosuje się także do ciał szarych, poprzez podstawienie do równania

zamiast stałej S-B iloczynu A

σσσσ

, gdzie A - zdolność absorpcyjna ciała szarego.

d. Prawo przesunięć Wiena

Długość fali

m

λλλλ

promieniowania odpowiadająca maksimum zdolności emisyjnej

ciała doskonale czarnego jest odwrotnie proporcjonalna do temperatury bezwzględnej
ciała T.

T

b

m

=

λλλλ

gdzie b - stała Wiena.

Ogólny przebieg funkcji ε (λ,T)

przy ustalonej temperaturze T

0

35

63.

Widmo promieniowania temperaturowego.

Widmem nazywamy przestrzenne rozdzielenie światła niemonochromatycznego

na wiązki monochromatyczne, albo też obraz, który tworzą te wiązki.

Natężenie i częstotliwość światła wchodzącego w skład p.t. są ściśle związane z

własnościami ciała promieniującego oraz jego temperaturą.

Dla gazów atomowych - widmo przybiera postać serii rozseparowanych

prążków, o wąskich zakresach częstotliwości.

Dla gazów cząsteczkowych - widmo składa się z pasów (widmo pasmowe).

Dla cieczy i ciał stałych - widmo p.t. ma formę ciągłą.

Promieniowanie temperaturowe ciała zaczyna być widoczne, gdy wartość jego

temperatury przekracza ok. 500˚C. W tej temp. ciała świecące mają barwę
ciemnoczerwoną. Przy wzroście temperatury ich barwa staje się czerwona,
czerwonożółta, żółta, biała, wreszcie - białoniebieska.

64.

Rozkłady promieniowania: Rayleigha-Jeansa, Wiena i Plancka.

a. Rozkład Rayleigha-Jeansa

Określa rozkład promieniowania ciała doskonale czarnego. Zgodnie z prawem

Rayleigha-Jeansa zdolność emisyjna ciała o temperaturze T do wysyłania fali e-m o
częstotliwości

νννν

wynosi:

( )

kT

c

T

2

2

2

,

νννν

ππππ

νννν

εεεε

νννν

=

lub w zależności od długości

λλλλ

fali:

( )

kT

c

T

4

2

,

λλλλ

ππππ

λλλλ

εεεε

λλλλ

=

gdzie: c - prędkość światła, k - stała Boltzmanna.

Tak opisany rozkład w zakresie dużych częstotliwości prowadzi do wniosku

sprzecznego z doświadczeniem i zasadą zachowania energii: całkowita zdolność
emisyjna ciała doskonale czarnego powinna rosnąć w nieskończoność. Problem ten
jest znany pod nazwą katastrofy w nadfiolecie.

Ilustracja prawa Wiena

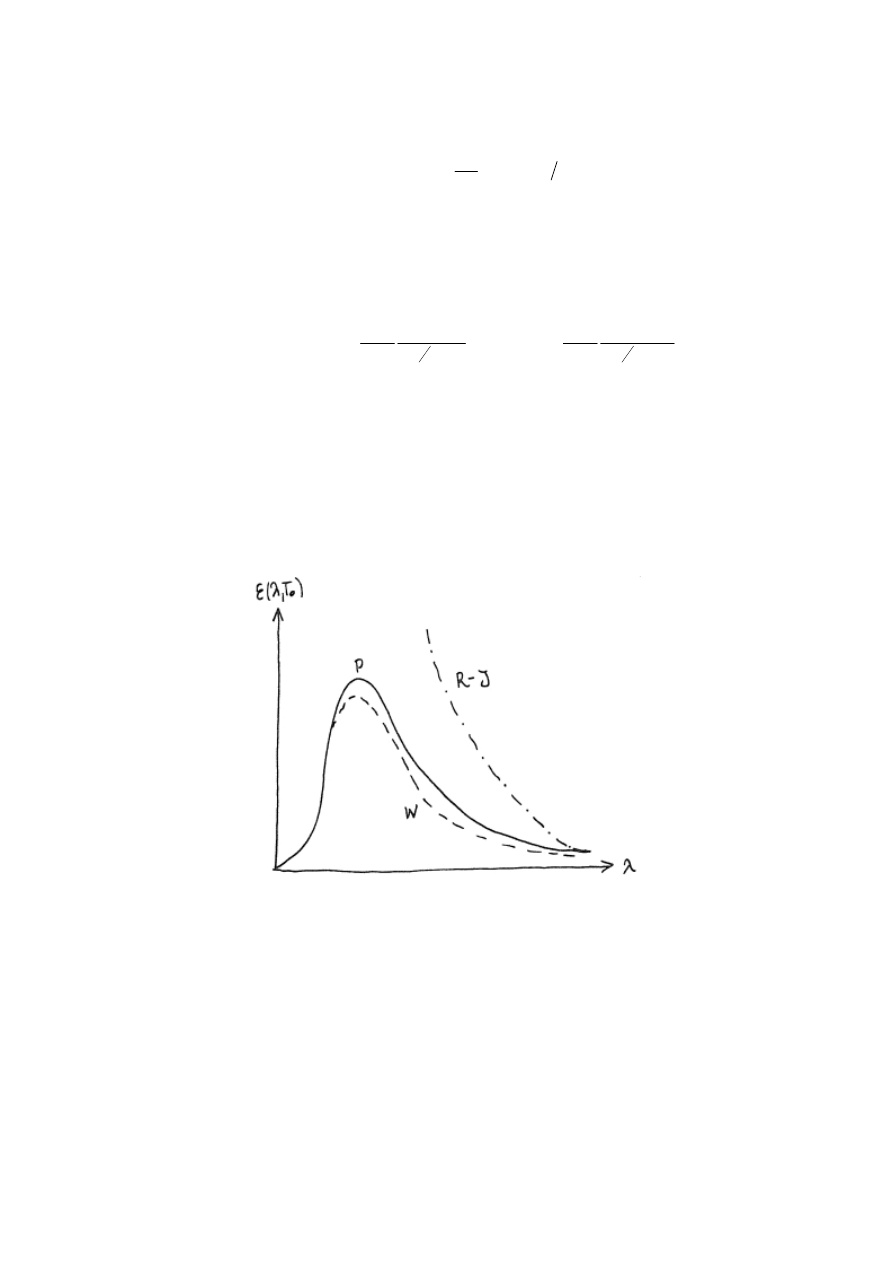
36

b. Rozkład Wiena

Przedstawiony przez Wiena, empirycznie określony charakter zależności między

zdolnością emisyjną ciała doskonale czarnego oraz jego temperaturą i częstotliwością
promieniowania temperaturowego:

( )

(

)

T

C

C

T

W

λλλλ

λλλλ

λλλλ

εεεε

2

5

1

−

=

exp

,

gdzie: C

1

,C

2

- stałe wyznaczone doświadczalnie.

Ten rozkład, choć sprawdzający się w zakresie wysokich częstotliwości, nie jest

zgodny z doświadczeniem dla częstotliwości niskich.

c. Rozkład Plancka

Prawidłową zależność zaproponował Planck:

( )

( )

1

2

,

1

2

,

2

5

3

2

−

=

−

=

kT

hc

P

kT

h

P

e

c

h

T

e

c

h

T

λλλλ

νννν

λλλλ

ππππ

λλλλ

εεεε

νννν

ππππ

νννν

εεεε

gdzie: h - stała Plancka, k - stała Boltzmanna, c - prędkość światła w próżni.

Jest to prawo niemożliwe do wyprowadzenia przy wykorzystaniu zasad fizyki

klasycznej. Planck wyszedł z założenia, że emisja i absorpcja może odbywać się tylko
za pośrednictwem ściśle określonych „porcji” energii - kwantów. Prawo to, zwane
prawem promieniowania Plancka, stanowiło podstawę i zarazem początek fizyki
kwantowej. Poprawnie opisuje ono rozkład natężenia w widmie promieniowania
temperaturowego ciała doskonale czarnego w całym zakresie częstotliwości i
temperatur ciała.

65.

Zjawisko fotoelektryczne.

Są to zjawiska elektryczne zachodzące pod działaniem światła. Fotony

pochłaniane przez ciało przekazują swoją energię elektronom. Gdy jest ona większa
od pracy wyjścia elektronów (pracy potrzebnej do uwolnienia e

-

z powierzchni ciała),

może nastąpić emisja elektronów, czyli tzw. zjawisko fotoelektryczne zewnętrzne (w
ciałach stałych i cieczach). Kiedy jednak dostarczona energia jest zbyt mała, dochodzi
tylko do zmiany stanu energetycznego elektronów, co nazywamy zjawiskiem
fotoelektrycznym wewnętrznym. W półprzewodnikach i dielektrykach prowadzi ono
do wzrostu przewodnictwa (fotoprzewodnictwo) lub, w przypadku półprzewodnika,
do powstania siły elektromotorycznej (zjaw. fotowoltaiczne). W gazach z.f. polega na
jonizacji ich atomów lub cząsteczek (fotojonizacja).

Zależność ε (λ,T)

według wzorów: Plancka (P),

Wiena (W) i Rayleigha-Jeansa (R-J)

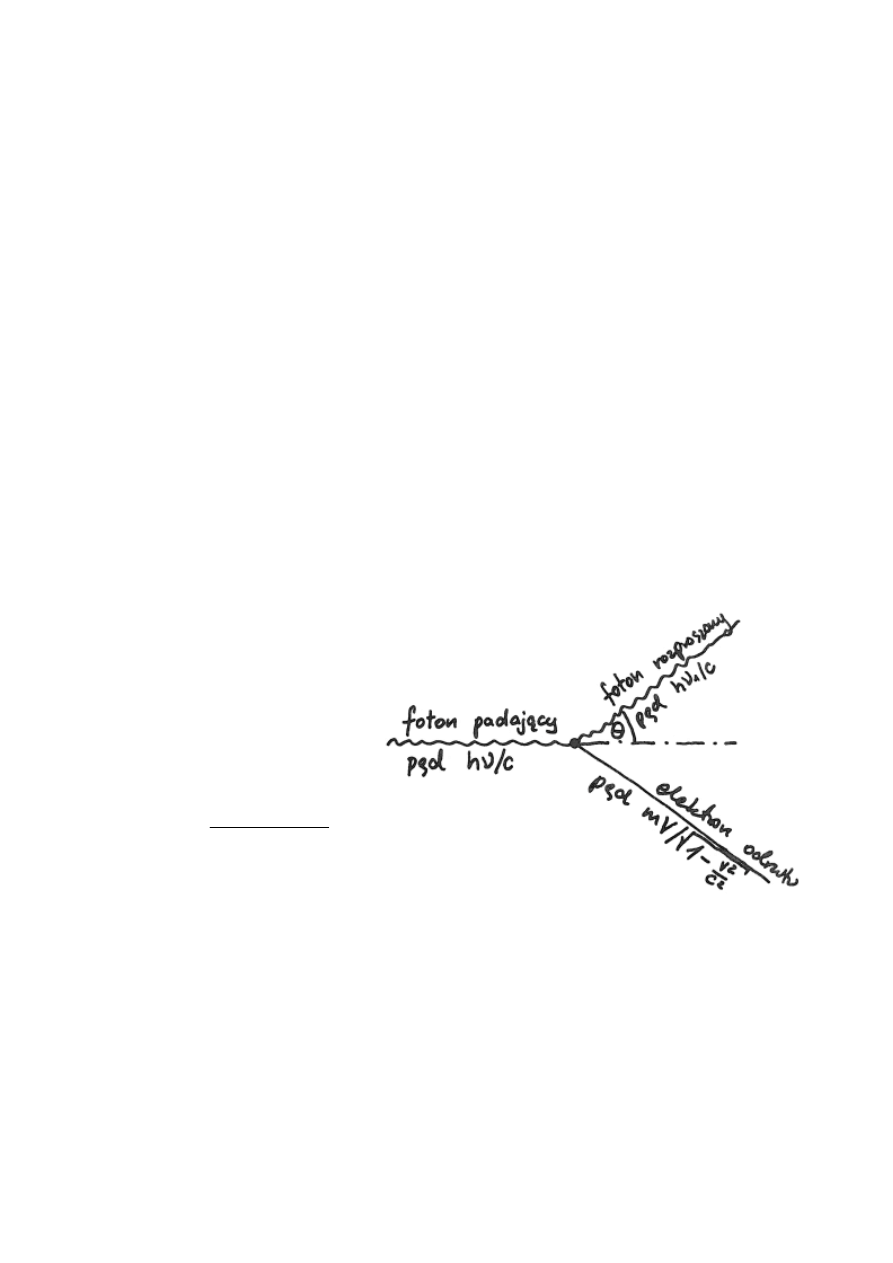
37

Równanie energii w z.f. zewnętrznym:

k

E

W

h

+

=

νννν

gdzie: h - stała Plancka,

νννν

- częstotliwość padającego światła, W - praca wyjścia z

materiału, E

k

- energia kinetyczna elektronu.

Zjawisko to było niemożliwe do wyjaśnienia w oparciu o założenie, że światło

jest falą. W takim wypadku natężenie światła powinno również mieć znaczenie dla
zaistnienia emisji elektronów. Energia byłaby gromadzona przez nie, aż do
przekroczenia wartości pracy wyjścia. Jednak jedynym czynnikiem wpływającym na
powstanie ww. zjawiska jest częstotliwość promieniowania oświetlającego.

Rozwiązanie zaproponował Einstein. W swojej teorii zinterpretował

promieniowanie jako strumień cząstek (fotonów), z których każda niesie niepodzielną
porcję energii, czyli kwant, równą

νννν

h . Przekazanie zaś przez foton energii

elektronowi jest pojedynczym aktem, wobec czego nie ma mowy o jej akumulacji.

66.

Efekt Comptona. Efekt tworzenia par.

a. Efekt Comptona

Zwany również rozpraszaniem comptonowskim. Podczas rozpraszania

krótkofalowego promieniowania e-m (rentgenowskie lub

γγγγ

) na swobodnych

elektronach dochodzi do zwiększenia długości fali promieniowania rozproszonego
(zmniejszeniu energii fotonów) w wyniku zderzeń z elektronami, analogicznych do
zderzeń sprężystych dwóch kul. Stosując zasady zachowania energii i pędu w postaci
obowiązującej w mechanice relatywistycznej można obliczyć tę zmianę długości fali,
zwaną przesunięciem Comptona:

)

cos

(

θθθθ

λλλλ

λλλλ

∆∆∆∆

−

=

1

e

gdzie:

e

λλλλ

- stała, zwana

comptonowską

długością

fali dla elektronu;

θθθθ

- kąt

między kierunkiem biegu
fotonu

rozproszonego

a

kierunkiem

pierwotnym

fotonu padającego.

Energia rozproszonego

fotonu:

)

cos

(

θθθθ

λλλλ

νννν

−

+

=

′

1

1

e

h

E

gdzie

νννν

to częstotliwość

fotonu przed rozproszeniem.


b. Efekt tworzenia par (

kreacji par)

Proces polegający na tworzeniu par cząstka-antycząstka z energii. Przykładem

jest wyprodukowanie elektronu e

-

i pozytonu e

+

przez kwant promieniowania

γγγγ

.

+

−

+

→

e

e

γγγγ

Jest to możliwe tylko dla kwantów gamma o energii większej niż energia

spoczynkowa dwóch elektronów (tj. 1,02 MeV). Efekt zachodzi w ośrodkach
materialnych, bowiem ze względu na zasadę zachowania energii i pędu może mieć
miejsce tylko w obecności innej cząstki (zwykle jądra atomowe ośrodka).

Prawdopodobieństwo kreacji jest związane z energią kwantu oraz rodzajem

ośrodka (silnie zależy od liczby atomowej Z).

E.t.p. odgrywa poważną rolę w tworzeniu kaskad fotonowo-elektronowych.

38

Efektem odwrotnym do e.t.p. jest anihilacja par. Para pozyton-elektron

anihilując wytwarza dwa fotony

γγγγ

.

γγγγ

2

→

+

+

−

e

e

67.

Widma emisyjne wodoru. Doświadczenie Rutherforda.

a. Widma emisyjne wodoru

Wodór posiada widmo liniowe. Kolejne serie powstają podczas przechodzenia

elektronów z wyższych poziomów energetycznych na poziomy (orbitale) niższe: K, L,
M etc. Długości fal emitowanego promieniowania opisuje wzór Rydberga:













−

=

2
2

2

1

2

1

1

1

n

n

Z

R

H

λλλλ

gdzie:

λλλλ

- długość emitowanej fali, R

H

- stała Rydberga dla wodoru; Z - liczba atomowa

(dla wodoru równa 1), n

1

- liczba całkowita określająca orbital docelowy (a zarazem

numer kolejny serii widmowej), n

2

- liczba całkowita określająca orbital, z którego

następuje przejście elektronu (z tym, że n

2

>n

1

).

Serie (odpowiadający orbital docelowy - nazwa):

1 -

seria Lymana (daleki nadfiolet)

2 - seria Balmera (bliski nadfiolet i światło widzialne)
3 -

seria Paschena (podczerwień - wszystkie kolejne serie także)

4 -

seria Bracketta

5 -

seria Pfunda

6 -

seria Humpreysa

b. Doświadczenie Rutherforda

Doświadczenie to doprowadziło do stworzenia modelu budowy atomu z

wyróżnionym jądrem, jako skupiskiem masy i ładunku dodatniego, oraz ujemnie
naładowanymi, krążącymi wokół jądra, elektronami.

Polegało ono na bombardowaniu cienkiej złotej folii szybkimi cząstkami alfa

(jądrami helu) i obserwowaniu ich odchyleń. Dawały one obraz rozmieszczenia
ładunku w atomie. Panująca wówczas teoria budowy atomu Tompsona zakładała
równomierny rozkład ładunku w całej objętości materiału (tzw. model ciasta z
rodzynkami, gdzie ładunek ujemny „porozrzucany” jest w rozległej strukturze
ładunku dodatniego), co powinno skutkować niezaburzonym przejściem cząstek przez
folię. Obserwacja wykazała jednak, że nie tylko ulegały one odchyleniu, ale z rzadka
nawet odbijały się od folii.

Można było wytłumaczyć to jedynie uznając, że atom w znacznym stopniu jest

„pusty”: rozmiary elektronu są dużo mniejsze od rozmiarów jądra, a to z kolei
niewielkie w porównaniu z promieniem orbity elektronowej.

68.

Teoria Bohra budowy atomu.

Model ten powstał w wyniku uzupełnienia przez Bohra warunkami kwantowymi

planetarnego modelu atomu Rutherforda. Warunki te zwane są postulatami Bohra.

a. Opis

Atom zbudowany jest z bardzo małego, w porównaniu do jego rozmiarów, jądra

obdarzonego ładunkiem dodatnim i skupiającego praktycznie całą masę atomu. Ujemnie
naładowane elektrony krążą wokół jądra w bardzo dużych (w stosunku do rozmiarów
jądra) odległościach. Ładunek całkowity elektronów równoważy ładunek jądra.

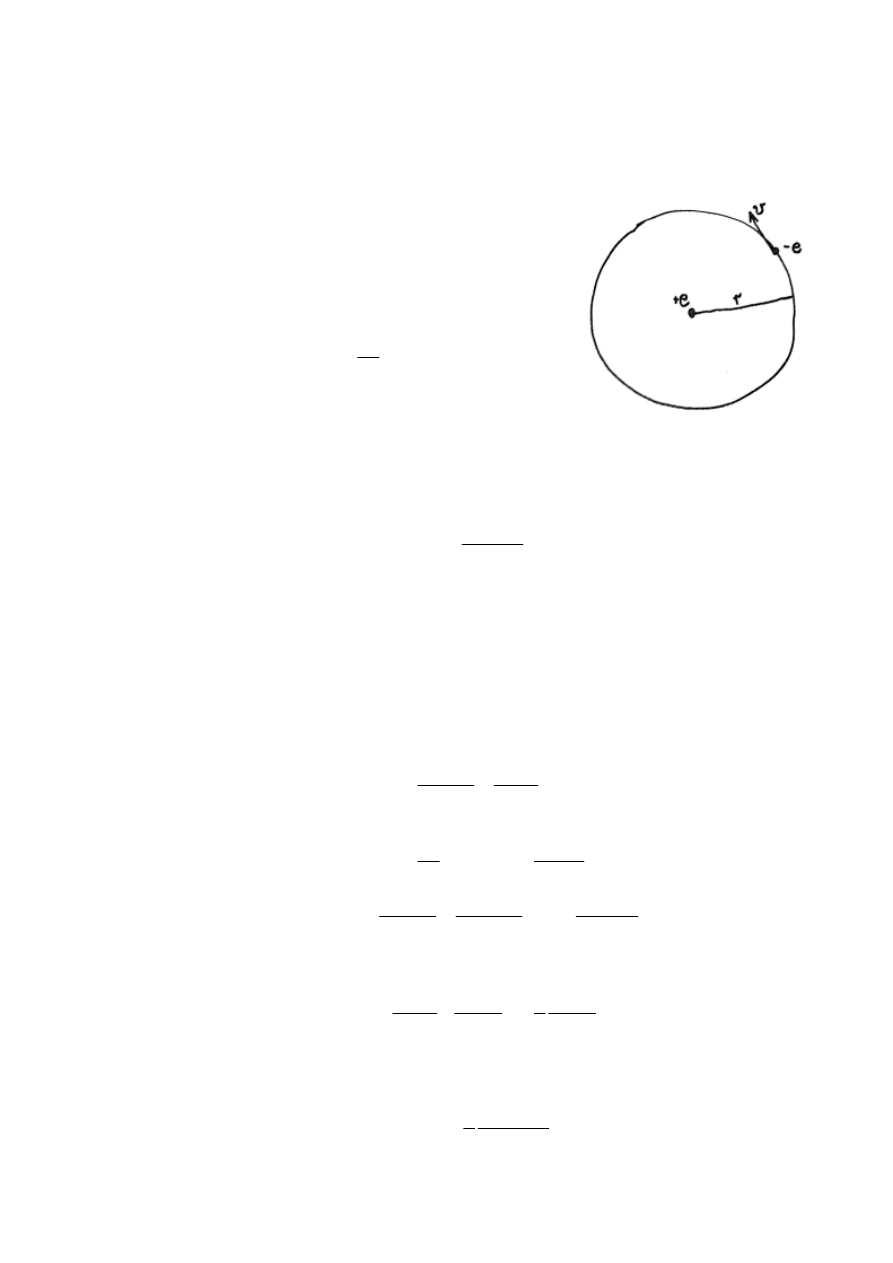
39

Bohra model atomu wodoru

Według elektrodynamiki klasycznej, ciągłe krążenie e

-

prowadziłoby do emisji

promieniowania e-m i skutkowało jego „spadnięciem” na jądro. Wobec tego atom
powinien być nietrwały, a widmo promieniowania ciągłe - co jest niezgodne z wynikami
doświadczeń. Trudności te Bohr przezwyciężył przyjmując następujące postulaty.

b. Postulaty Bohra

I - Istnieją stany podstawowe atomu z jednym

elektronem, będące stanami stacjonarnymi, tzn. w
nich nie zachodzi emisja promieniowania przez
elektron. Stany te, zależne od momentu pędu
elektronu, opisuje równanie (1):

n

h

mVr

ππππ

2

=

gdzie: n - liczba całkowita, nosząca nazwę głównej

liczby kwantowej, h - stała Plancka, mVr - moment
pędu elektronu na orbicie o promieniu r.

II - Wskutek oddziaływania z czynnikiem zewnętrznym może dojść do przejścia

elektronu pomiędzy dwoma stanami stacjonarnymi. Takim przejściom towarzyszy
emisja lub absorpcja promieniowania o częstotliwości:

h

E

E

2

1

−

=

νννν

gdzie: E

1

E

2

to energie całkowite atomu odpowiednio w stanie początkowym i końcowym.

Ponadto Bohr założył, że w atomie obowiązują prawa mechaniki klasycznej oraz

prawo Coulomba, a orbity elektronów są orbitami kołowymi.

c. Równania

Opis wartości: e - ładunek elektronu, r - promień jego orbity,

0

εεεε

- przenikalność

dielektryczna próżni, m - masa elektronu, V - jego prędkość orbitalna.

Siła przyciągania elektrostatycznego elektronu jest równa sile odśrodkowej (2):

r

mV

r

e

2

2

0

2

4

=

πε

πε

πε

πε

Z równań (1) i (2) można otrzymać tzw. promień orbity bohrowskiej:

2

2

2

0

3

2

2

2

2

0

2

2

2

4

4

2

1

2

2

2

me

n

h

r

mr

n

h

r

e

mr

hn

V

n

h

mVr

ππππ

εεεε

ππππ

πε

πε

πε

πε

ππππ

ππππ

=

⇒

=

+













=

⇒

=

)

(

)

(

Całkowita energia elektronu E jest równa sumie jego energii kinetycznej i

potencjalnej:

r

e

r

e

mV

E

0

2

0

2

2

4

2

1

4

2

πε

πε

πε

πε

πε

πε

πε

πε

−

=

−

=

Korzystając ze wzoru na promień orbity możemy wyprowadzić wzór na całkowitą

energię atomu wodoru w stanie kwantowym n.

2
0

2

2

4

4

2

1

εεεε

n

h

me

E

n

−

=

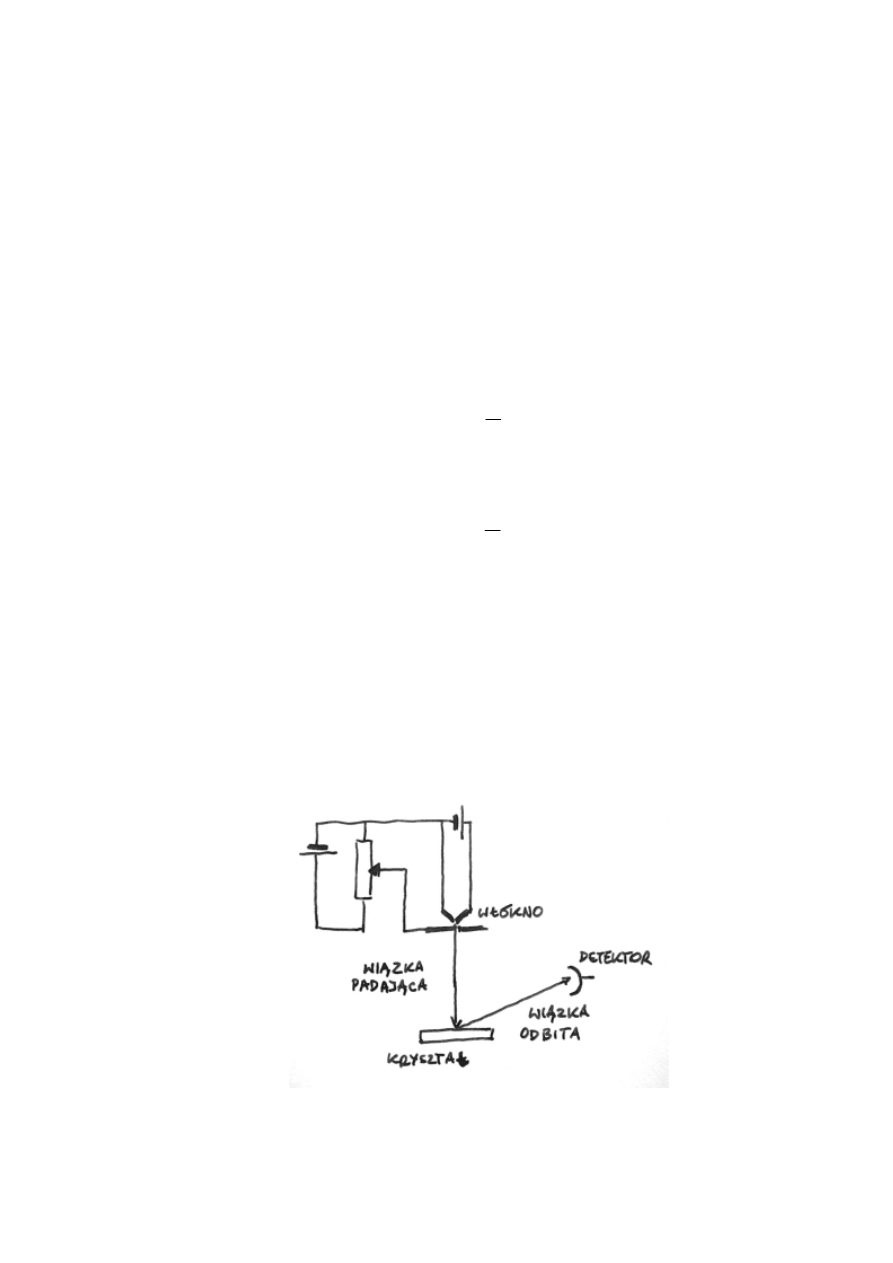
40

d. Wnioski

Otrzymane na podstawie równań częstotliwości linii widmowych wodoru zgadzają

się bardzo dobrze z obserwacjami doświadczalnymi. Teoria Bohra dała podwaliny dla
dalszego rozwoju fizyki kwantowej. Z modelu tego zrezygnowano jednak: przyjęto
uznawać, że elektronowi nie można przypisywać w atomie ściśle określonej lokalizacji na
ściśle określonych orbitach (patrz: zasada nieoznaczoności Heisenberga).

69.

Hipoteza de Broglie'a. Doświadczenie Davissona-Germera.

a. Hipoteza de Broglie’a

Francuski fizyk de Broglie wysunął hipotezę, że dualizm falowo-korpuskularny

odnosi się nie tylko do światła, ale każdego ciała posiadającego niezerowy pęd.
Zaproponował on, by takiemu ciału przypisywać falę prawdopodobieństwa (falę
materii, falę de Broglie’a) o długości:

p

h

=

λλλλ

gdzie: h - stała Plancka, p - pęd ciała.

Obiektowi o energii E odpowiada w sposób analogiczny częstotliwość:

h

E

=

νννν

Natężenie fali de Broglie’a w danym punkcie przestrzeni jest wprost

proporcjonalne do gęstości prawdopodobieństwa znalezienia cząstki w tym punkcie.

b. Doświadczenie Davissona-Germera

W doświadczeniu tym znalazła bezpośrednie potwierdzenie hipoteza de

Broglie’a. Skoro obiekt materialny może przejawiać falową naturę, to powinien ulegać
zjawiskom dyfrakcji i interferencji. Zgodnie z tym przewidywaniem Davisson i
Germer zaobserwowali ugięcie wiązki elektronów (emitowanych przez rozgrzane
włókno i przyspieszanych regulowanym napięciem) na monokrysztale niklu.
Otrzymany obraz był zgodny z wynikającym z równań falowych dyfrakcji, gdy za
długość fali podlegającej ugięciu przyjąć właśnie długość fali materii dla elektronu.

Schemat układu doświadczalnego

Davissona i Germera

41

70.

Dualizm korpuskularno-falowy.

Układy fizyczne można opisywać na dwa sposoby:

1. Jako zespoły cząstek o określonych położeniach i pędach, ogólnie zależnych od

czasu - jest to opis korpuskularny.

2. Jako pola, to znaczy obszary, w których określona jest pewna wielkość

polowa zależna od położenia i czasu. Wielkość polowa może być skalarem lub
wektorem, stąd analogicznie pola skalarne i pola wektorowe. Szczególnym typem pola
jest pole falowe, w którym wartość wielkości polowej nie zmienia się w czasie, a
jedynie przemieszcza w przestrzeni z prędkością zwaną prędkością grupową
rozchodzenia się fali - jest to opis polowy lub falowy.

W mechanice kwantowej stosuje się oba te opisy do przedstawiania tych samych

obiektów. Interpretacja zasady nieoznaczoności zabrania posługiwania się wszystkimi
informacjami zawartymi w tych opisach równocześnie. Przedstawienia te -
korpuskularne i falowe - uznaje się za wzajemnie komplementarne. Poznanie funkcji
falowej (funkcji stanu) umożliwia, w drodze operacji matematycznych właściwych dla
mechaniki kwantowej, wyznaczenie prawdopodobieństwa uzyskania określonych
wyników pomiaru wartości wielkości dynamicznych odnoszących się do aspektu
korpuskularnego, takich jak energia, pęd, moment pędu etc.

Przykład promieniowania e-m

Falowa natura światła może być łatwo zaobserwowana w zjawiskach dyfrakcji i

interferencji, kiedy zasada Huygensa-Fresnela pozwala prawidłowo przewidywać
powstające obrazy. Aspekt ten ujawnia się również w polaryzacji fali e-m.

O tym, że wiązkę światła tworzą paczki energii - fotony - świadczy z kolei

zjawisko fotoelektryczne zewnętrzne, absorpcja i emisja widm liniowych przez atomy,
czy wreszcie efekt Comptona.