www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´

N Z

M

ATEMATYKI

N

IERÓWNO ´SCI I DZIAŁANIA NA LICZBACH

Z

ESTAW ZADA ´

N OTWARTYCH NR

45288

WYGENEROWANY AUTOMATYCZNIE W SERWISIE

WWW

.

ZADANIA

.

INFO

POZIOM ROZSZERZONY

C

ZAS PRACY

: 60

MINUT

Z

ADANIE

1

(4

PKT

.)

Udowodnij, ˙ze je´sli liczby dodatnie a i b spełniaj ˛

a warunek a

2

+

b

2

=

23ab, to log

5

(

a

+

b

) =

log

5

√

ab

+

1.

R

OZWI ˛

AZANIE

Podany warunek mo ˙zemy zapisa´c w postaci

(

a

+

b

)

2

−

2ab

=

23ab

(

a

+

b

)

2

=

25ab.

Teraz logarytmujemy t˛e równo´s´c logarytmem przy podstawie 5.

log

5

(

a

+

b

)

2

=

log

5

(

25ab

)

2 log

5

(

a

+

b

) =

log

5

25

+

log

5

ab

2 log

5

(

a

+

b

) =

2

+

2 log

5

√

ab

log

5

(

a

+

b

) =

1

+

log

5

√

ab.

Z

ADANIE

2

(5

PKT

.)

Wyznacz przedziały, w których funkcja przyjmuje warto´sci dodatnie f

(

x

) =

|

x

−

2

|+

x

2

x

2

−|

x

−

2

|

.

R

OZWI ˛

AZANIE

Licznik podanej funkcji jest zawsze dodatni, bo

|

x

−

2

|

i x

2

zeruj ˛

a si˛e w innych punktach.

Pytanie wi˛ec brzmi, gdzie mianownik jest dodatni. Liczymy

x

2

− |

x

−

2

| >

0

x

2

> |

x

−

2

|

.

Nierówno´s´c t˛e mo ˙zna rozwi ˛

aza´c rozwa ˙zaj ˛

ac dwa przypadki lub patrz ˛

ac na wykresy. My

wybierzemy t˛e drug ˛

a metod˛e.

Materiał pobrany z serwisu

www.zadania.info

1

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´

N Z

M

ATEMATYKI

-5

-1

+1

+5

x

-5

-1

+1

+5

y

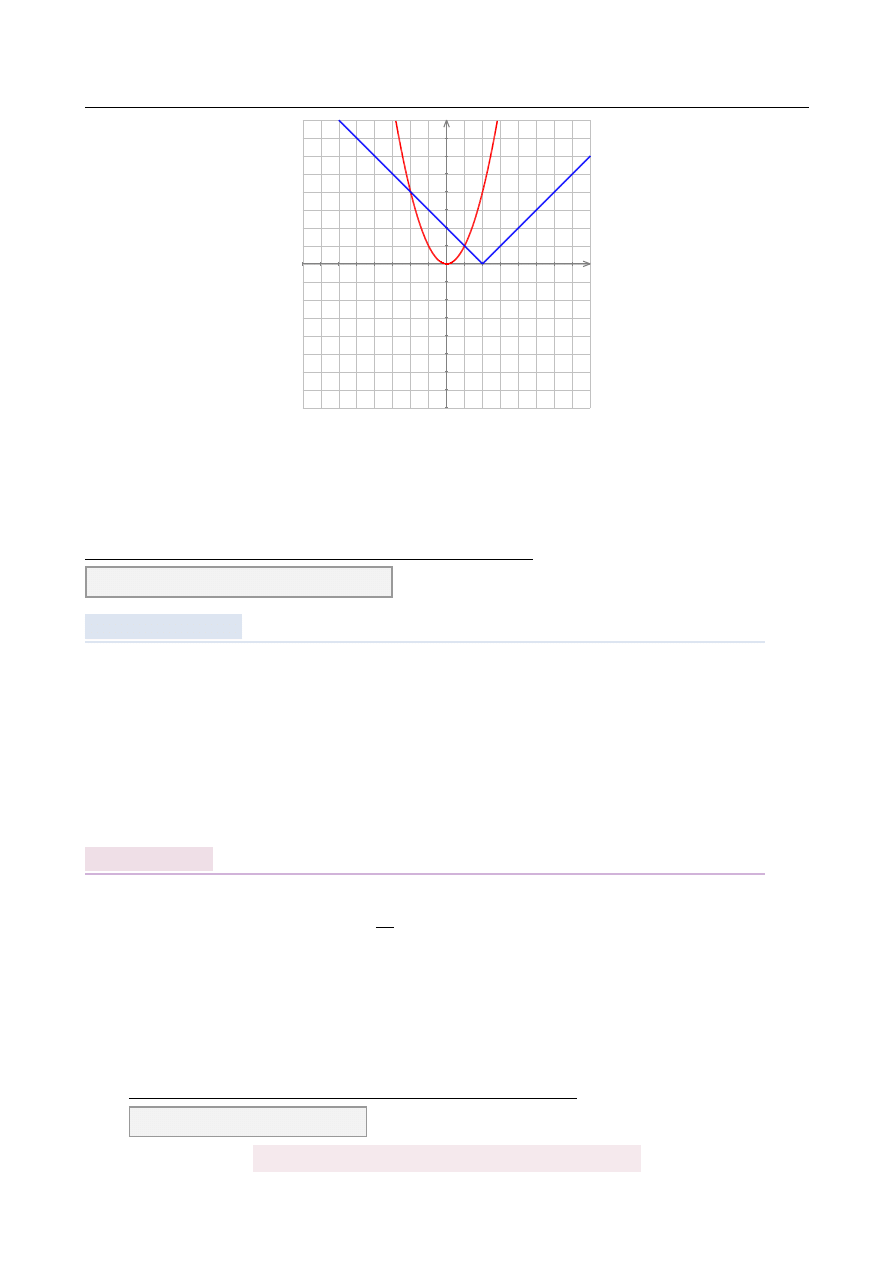
Z obrazka wida´c, ˙ze wykresy przecinaj ˛

a si˛e w dwóch punktach x

=

1 i x

= −

2. Spraw-

dzamy algebraicznie czy rzeczywi´scie tak jest i mamy rozwi ˛

azanie

x

∈ (−

∞,

−

2

) ∪ (

1,

+

∞

)

.

Odpowied´z: x

∈ (−

∞,

−

2

) ∪ (

1,

+

∞

)

Z

ADANIE

3

(5

PKT

.)

Dana jest nierówno´s´c kwadratowa z parametrem m:

x

2

+

8x

−

7

+

m

<

0.

a) Wyznacz wszystkie warto´sci parametru m, dla których przedział

(

3, 4

)

zawiera si˛e w

zbiorze rozwi ˛

aza ´n tej nierówno´sci.

b) Uzasadnij, ˙ze je ˙zeli dla pewnej warto´sci parametru m nierówno´s´c ta ma rozwi ˛

azanie

w przedziale

(

3, 4

)

, to ma ona w tym przedziale niesko ´nczenie wiele rozwi ˛

aza ´n.

R

OZWI ˛

AZANIE

a) Zacznijmy od zauwa ˙zenia, ˙ze wierzchołek paraboli f

(

x

) =

x

2

+

8x

−

7

+

m ma pierw-

sz ˛

a współrz˛edna równ ˛

a x

w

=

−

8

2

= −

4. Zatem wykres lewej strony nierówno´sci jest

parabol ˛

a o ramionach skierowanych w gór˛e i osi symetrii x

= −

4. W szczególno´sci

parabola ta jest funkcj ˛

a rosn ˛

ac ˛

a na przedziale

(

3, 4

)

. Zatem jej ujemno´s´c na tym prze-

dziale sprowadza si˛e do warunku f

(

4

) 6

0 (tu jest wa ˙zne, ˙ze przedział jest otwarty).

Daje to nam nierówno´s´c

16

+

32

−

7

+

m

6

0

m

6 −

41.

Odpowied´z: m

∈ (−

∞

−

41

i

Materiał pobrany z serwisu

www.zadania.info

2

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´

N Z

M

ATEMATYKI

b) Jak ju ˙z zauwa ˙zyli´smy w poprzednim podpunkcie, lewa strona nierówno´sci ro´snie na

przedziale

(

3, 4

)

. To oznacza, ˙ze je ˙zeli f

(

x

0

) <

0 dla pewnego x

0

∈ (

3, 4

)

to f

(

x

) <

0

dla x

∈ (

3, x

0

)

, co oznacza, ˙ze nierówno´s´c ma niesko ´nczenie wiele rozwi ˛

aza ´n.

Zadania

.info

Podobają Ci się nasze rozwiązania?

Pokaż je koleżankom i kolegom ze szkoły!

Z

ADANIE

4

(6

PKT

.)

Dla jakich warto´sci parametru m nierówno´s´c

mx

2

−(

m

−

1

)

x

+

1

x

2

−(

m

+

1

)

x

+

1

>

0 jest prawdziwa dla ka ˙zdej

liczby x

∈

R?

R

OZWI ˛

AZANIE

Zauwa ˙zmy, ˙ze w mianowniku mamy funkcj˛e kwadratow ˛

a z dodatnim współczynnikiem

przy x

2

. Musimy najpierw sprawdzi´c kiedy ta funkcja nie ma miejsc zerowych (aby dziedzi-

n ˛

a danej funkcji był zbiór

R).

0

>

∆

= (

m

+

1

)

2

−

4

= (

m

−

1

)(

m

+

3

)

⇒

m

∈ (−

3, 1

)

.

Zauwa ˙zmy, ˙ze ten warunek gwarantuje nam, ˙ze mianownik jest dodatni, pozostaje nam
wi˛ec nierówno´s´c

mx

2

− (

m

−

1

)

x

+

1

>

0.

Aby była ona zawsze prawdziwa musi by´c m

>

0 (trzeba te ˙z sprawdzi´c przypadek m

=

0!)

oraz

∆

<

0.

0

>

∆

= (

m

−

1

)

2

−

4m

=

m

2

−

2m

+

1

−

4m

=

m

2

−

6m

+

1

∆

=

36

−

4

=

32

m

1

=

3

−

2

√

2,

m

2

=

3

+

2

√

2

m

∈ (

3

−

2

√

2, 3

+

2

√

2

)

.

Ł ˛

acz ˛

ac otrzymane warunki mamy

m

∈ (

3

−

2

√

2, 1

)

.

Odpowied´z: m

∈ (

3

−

2

√

2, 1

)

Materiał pobrany z serwisu

www.zadania.info

3