INSTRUKCJA

ĆWICZENIA LABORATORYJNEGO NR 205

OBLICZANIE WIELOŚCI ZWARCIOWYCH

W SIECI ZE SKUTECZNIE I NIESKUTECZNIE

UZIEMIONYM PUNKTEM NEUTRALNYM

Łódź, wrzesień 2003 roku

- 2 -

- 3 -

1.

WSTĘP

Celem ćwiczenia jest wykonanie obliczeń wielkości zwarciowych początkowych dla zwarć

symetrycznych i niesymetrycznych w wielonapięciowej sieci elektroenergetycznej za pomocą
maszyny cyfrowej. Obliczenia te będą wykonywane w sieci ze skutecznie i nieskutecznie
uziemionym punktem neutralnym. W ramach ćwiczenia będą wykonywane następujące zadania:
1.

Budowa schematów zastępczych sieci dla składowej zgodnej i zerowej.

2.

Obliczanie impedancji elementów sieci dla składowej zgodnej i zerowej w jednostkach
względnych.

3.

Zapoznanie się ze sposobem wprowadzania danych w programie komputerowym
obliczającym wielkości zwarciowe.

4.

Przeprowadzenie obliczeń dla zwarcia trójfazowego za pomocą maszyny cyfrowej oraz
analiza wyników obliczeń.

5.

Dobór dławików ograniczających prądy zwarciowe.

6.

Wykonanie obliczeń dla zwarć niesymetrycznych w sieci ze skutecznie uziemionym punktem
neutralnym.

7.

Analiza wyników obliczeń z uwzględnieniem transformacji składowych symetrycznych.

8.

Analiza warunków skuteczności uziemienia sieci elektroenergetycznej.

9.

Wykonanie obliczeń i analizy wyników dla zwarć niesymetrycznych w sieci zawierającej
linie magnetyczne sprzężone.

10. Wykonanie obliczeń dla zwarć doziemnych w sieci z nieskutecznie uziemionym punktem

neutralnym, a więc:



w sieci z izolowanym punktem neutralnym,



w sieci z kompensacją prądu zwarcia doziemnego,



w sieci z kompensacją prądu zwarcia doziemnego i z automatyką wymuszania dodatkowej
składowej czynnej tego prądu,



w sieci z punktem neutralnym uziemionym przez rezystor.

W ramach obliczeń dla zwarć doziemnych w sieci z nieskutecznie uziemionym punktem
neutralnym zostanie przeanalizowany wpływ prądów odbiorów na prądy i napięcia
zakłóceniowe.

Obliczenia będą wykonywane przy wykorzystaniu programu ZWAK31.

2.

MODEL

MATEMATYCZNY

SYSTEMU

ELEKTROENERGETYCZNE-

GO

DLA

OBLICZEŃ

WIELKOŚCI

ZWARCIOWYCH

2.1 Zastosowanie metody potencjałów węzłowych do obliczania zwarć przy założeniu

jednakowych sił elektromotorycznych generatorów

2.1.1 Obliczanie prądów i napięć przy zwarciach symetrycznych

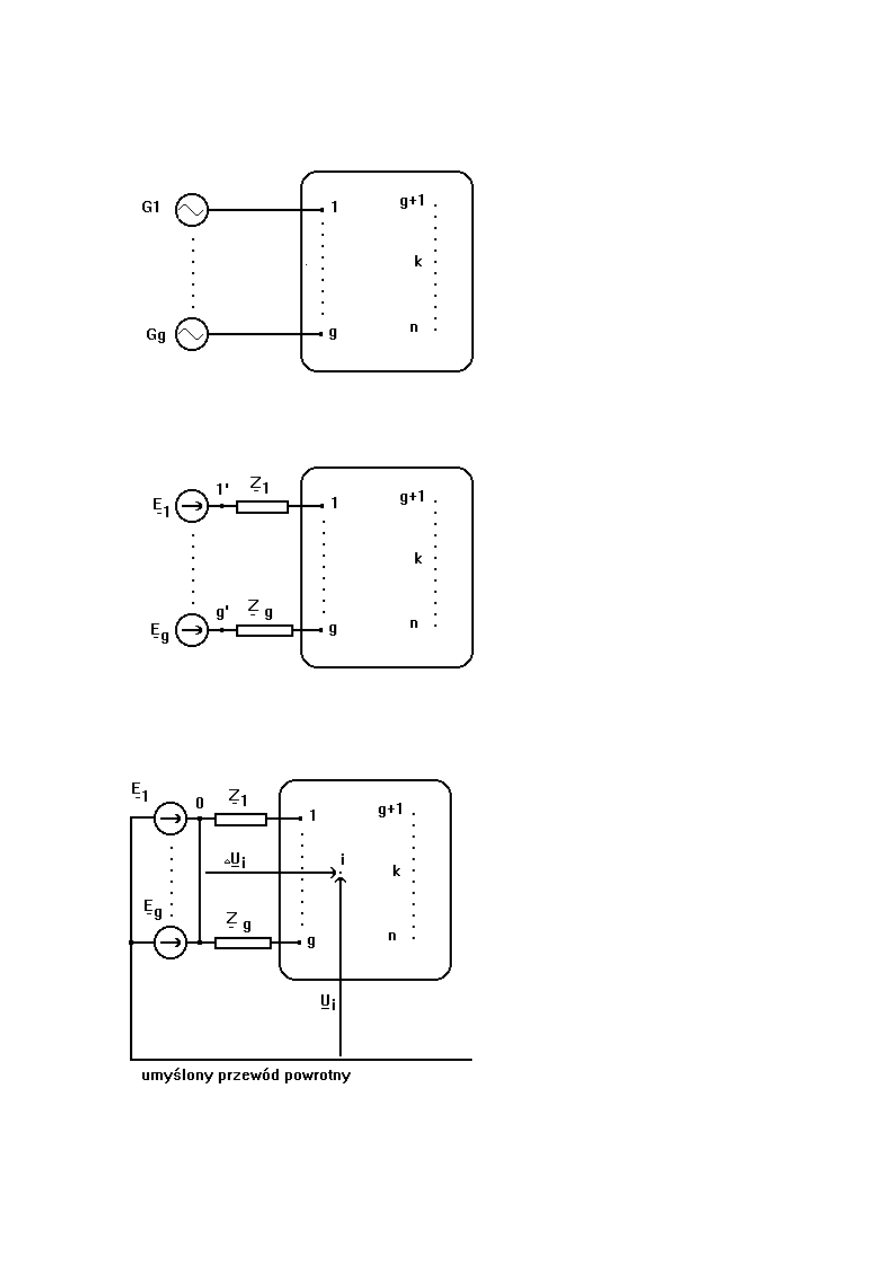
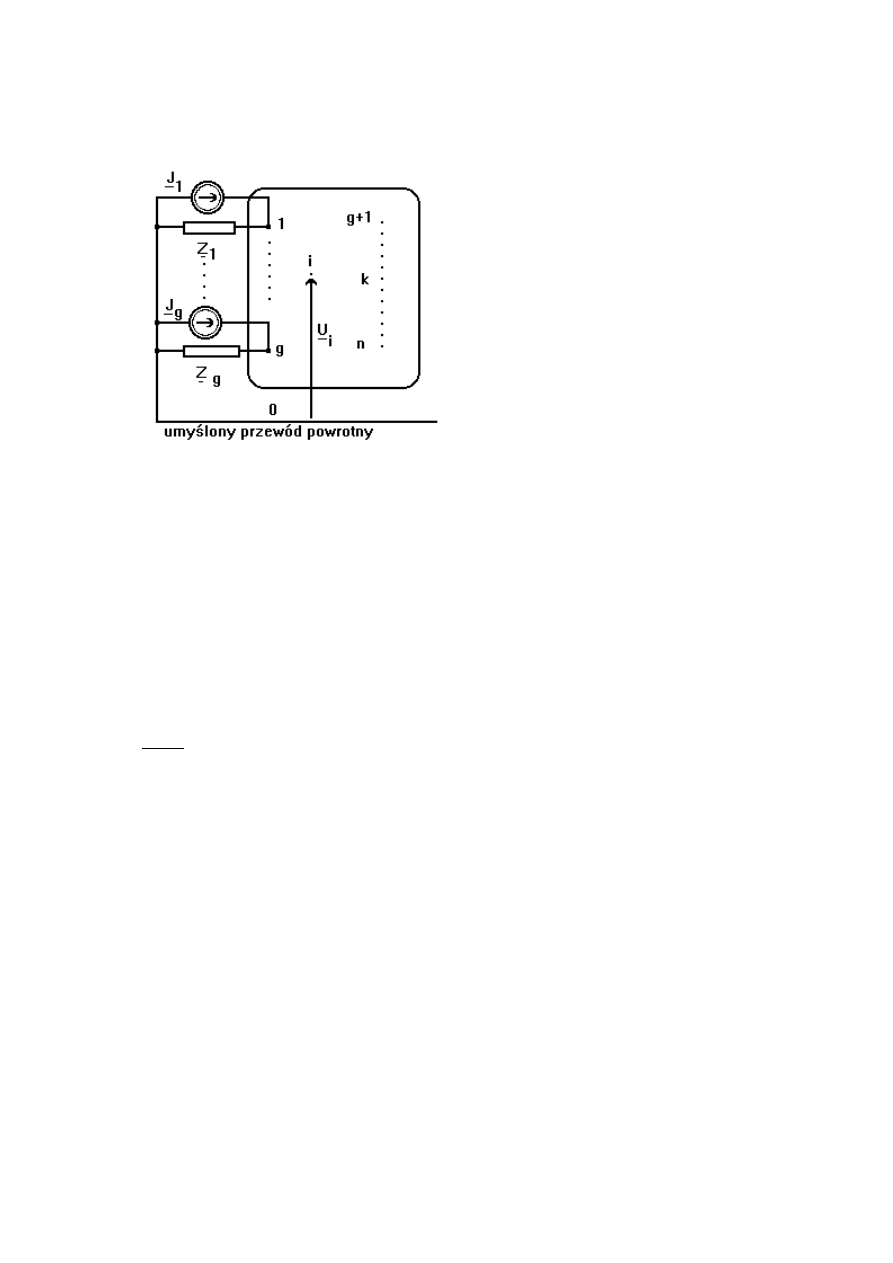
Rozpatrzmy sieć elektroenergetyczną, n-węzłową, w której w węzłach od 1 do g są

przyłączone generatory (rys.2.1). Dla obliczeń zwarciowych wszystkie generatory odwzorowujemy
za pomocą źródła napięciowego o jednakowej sile elektromotorycznej E

E

d

"



(siła

elektromotoryczna nadprzejściowa generatora) i impedancji nadprzejściowej Z

"

- różnej dla

każdego

generatora.

Rozpoczynając

tworzenie

modelu

matematycznego

systemu

elektroenergetycznego dla stanu zakłóceniowego założono, że:



rozpatrywana siec jest siecią symetryczną,



zostanie zastosowana metoda potencjałów węzłowych wraz z metodą składowych

symetrycznych.

- 4 -

Zakładając ponadto, że tworzymy schemat dla zwarcia symetrycznego w węźle k-tym można
narysować schemat zastępczy sieci do wyznaczania zwarć (rys. 2.2).

Rys. 2.1. Schemat ogólny sieci elektroenergetycznej.

Rys.2.2. Schemat sieci dla obliczeń zwarciowych.

Rys.2.3. Schemat zastępczy sieci dla obliczeń zwarciowych.

- 5 -

Węzły 1', 2'...g' są punktami ekwipotencjalnymi i można je połączyć. Przyjmiemy, że węzeł

ten jest węzłem odniesienia rozpatrywanej sieci i nadajemy mu numer zero. Posiada on zerowy
potencjał (rys.2.3). Równanie potencjałów węzłowych będzie postaci:











































































































n

k

1

n

,

n

k

,

n

1

,

n

n

,

k

k

,

k

1

,

k

n

,

1

k

,

1

1

,

1

n

k

1

U

U

U

Y

Y

Y

Y

Y

Y

Y

Y

Y

I

I

I





































(2.1)

gdzie:



k

1

I

I 

- prądy węzłowe;



n

1

U

U







- napięcia węzłów od 1 do n względem węzła odniesienia (napięcia węzłowe);



n

,

n

1

,

1

Y

Y



- elementy macierzy admitancyjnej węzłowej sieci.

Równanie (2.1) można zapisać w postaci:

I

Y

U

 

(2.2)

gdzie:



I - macierz prądów węzłowych;



Y - macierz admitancyjna węzłowa sieci;



U



- wektor napięć węzłowych.

Przy zwarciu w k-tym węźle mamy:

0

I

oraz

0

I

I

I

I

k

n

1

k

1

k

1























(2.3)



U

E

E

k

d

 

 

"

(2.4)

Wektory prądów i napięć węzłowych są, więc następujące:





T

k

0

0

I

0

0







I

(2.5)





T

n

1

k

1

k

1

U

U

E

U

U























U

(2.6)

Równanie (2.2) to układ n równań węzłowych, w których wielkościami nieznanymi są:



napięcia węzłowe oprócz

E

E

U

"

d

k











,



prąd węzłowy w węźle k-tym.

Aby rozwiązać powyższy układ równań można go przekształcić do postaci:



U

Y

I

Z I



  



1

(2.7)

gdzie:



Z - macierz impedancyjna węzłowa sieci.

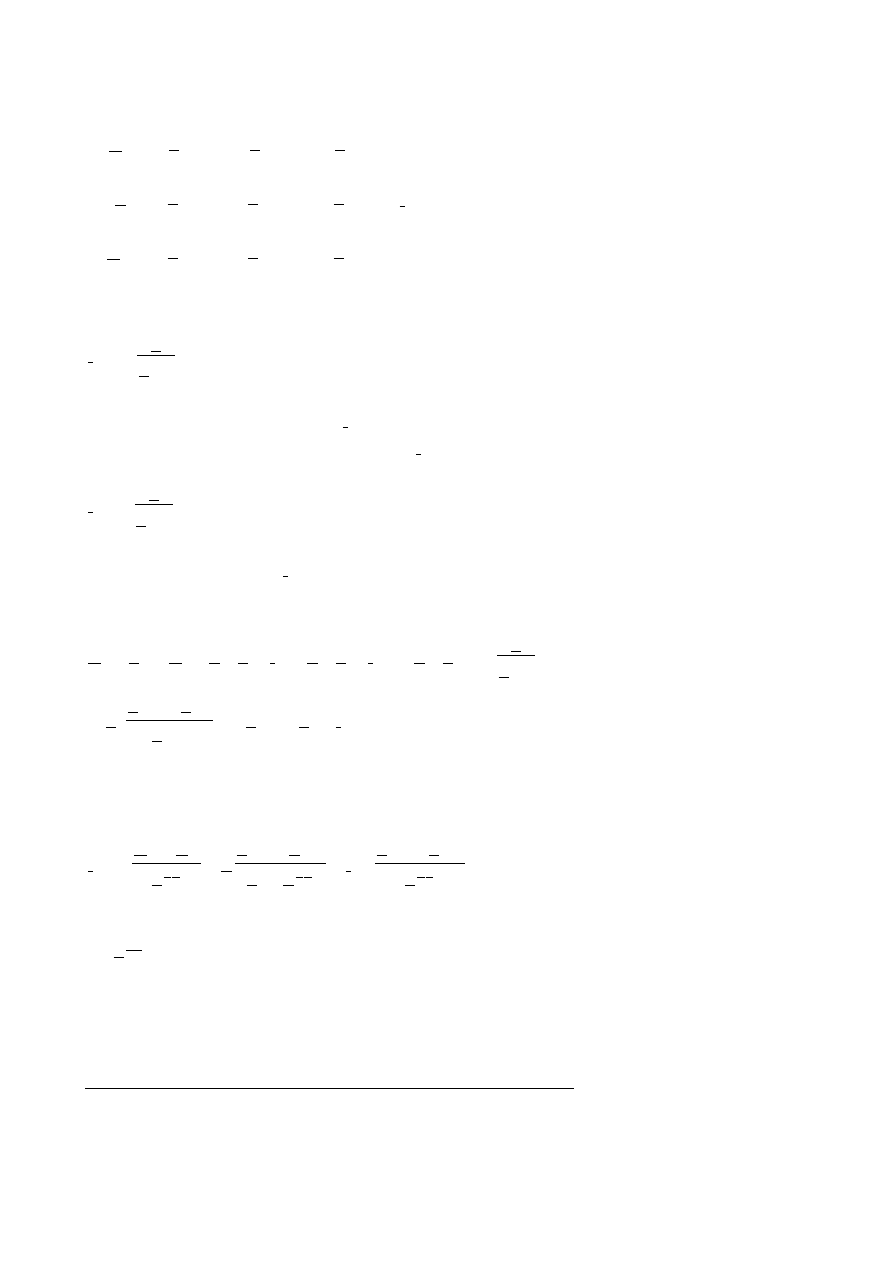
- 6 -

Równanie (2.7) jest postaci:











































































































0

I

0

Z

Z

Z

Z

Z

Z

Z

Z

Z

U

E

U

k

n

,

n

k

,

n

1

,

n

n

,

k

k

,

k

1

,

k

n

,

1

k

,

1

1

,

1

n

1





































(2.8)

Z równania (2.8) prąd węzłowy w węźle k-tym wynosi :

k

,

k

k

Z

E

I





(2.9)

W rzeczywistości prąd zwarciowy

Zk

I

przy zwarciu w węźle k-tym odpływa od tego węzła, a więc

ma kierunek przeciwny do prądu węzłowego

k

I , który dopływa do węzła, czyli:

k

,

k

Zk

Z

E

I



(2.10)

Należy zauważyć, że prąd

Zk

I

to prąd zwarciowy początkowy. Napięcie w dowolnym i-tym węźle

możemy obliczyć ze wzoru:





Zk

k

,

i

k

,

k

k

,

k

k

,

i

k

,

k

k

,

k

k

,

i

Zk

k

,

i

k

k

,

i

i

i

I

Z

Z

Z

Z

Z

E

Z

E

Z

E

I

Z

E

I

Z

E

U

E

U



























































(2.11)

Znając napięcia w węzłach można obliczyć rozpływ prądów, i tak prąd w gałęzi łączącej węzły
p oraz q wynosi:

q

p

k

,

p

k

,

q

Zk

q

p

k

,

k

k

,

p

k

,

q

q

p

q

p

pq

Z

Z

Z

I

Z

Z

Z

Z

E

Z

U

U

I













(2.12)

gdzie:



q

p

Z

- impedancja gałęzi łączącej węzły p oraz q.

Z powyższych rozważań wynika, że znając macierz impedancyjną węzłową sieci otrzymaną

poprzez odwrócenie macierzy admitancyjnej węzłowej możemy obliczać wielkości zwarciowe przy
zwarciu w dowolnym węźle sieci.

2.1.2 Obliczanie prądów i napięć przy zwarciach niesymetrycznych

Obliczanie wielkości zwarciowych przy zwarciach niesymetrycznych najlepiej wykonywać

przy zastosowaniu metody składowych symetrycznych. Załóżmy dodatkowo, że obliczenia te

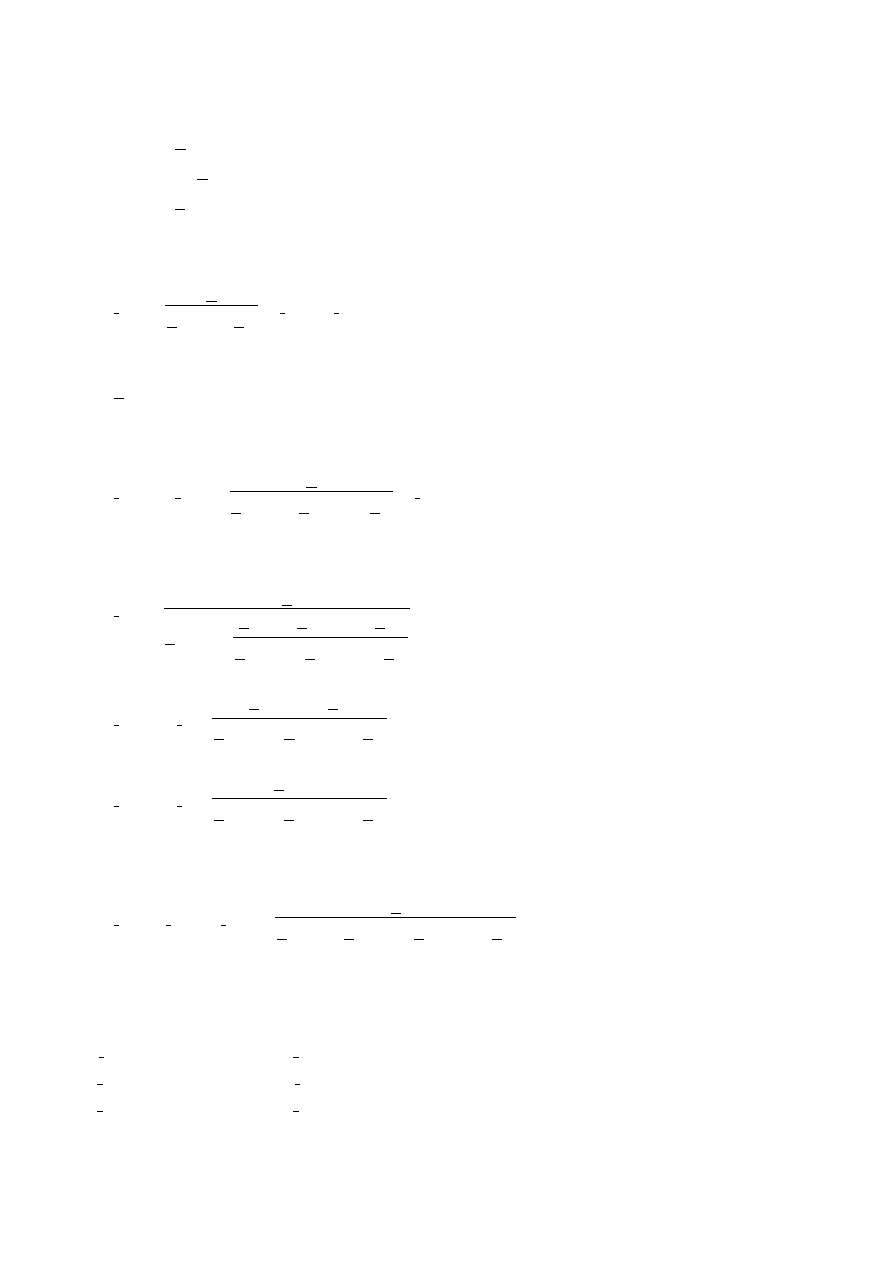
- 7 -

będziemy wykonywać w oparciu o otrzymane macierze impedancyjne węzłowe sieci dla
składowych symetrycznych:



zgodnej

 

1

Z

,



przeciwnej

 

2

Z

,



zerowej

 

0

Z

.

Składowe symetryczne prądu zwarciowego przy zwarciu w węźle k-tym wynoszą:



trójfazowym

 

 

 

 

0

I

I

Z

Z

E

I

k

0

k

2

P

k

,

k

1

k

1









(2.13)

gdzie:

P

Z

- impedancja przejścia w miejscu zwarcia.



dwufazowym

 

 

 

 

 

0

I

Z

Z

Z

E

I

I

k

0

P

k

,

k

2

k

,

k

1

k

2

k

1













(2.14)



dwufazowym doziemny

 

 

 

 





 

 

P

k

,

k

0

k

,

k

2

P

k

,

k

0

k

,

k

2

k

,

k

1

k

1

Z

3

Z

Z

Z

3

Z

Z

Z

E

I











(2.15)

 

 

 

 

 

P

k

,

k

0

k

,

k

2

P

k

,

k

0

k

1

k

2

Z

3

Z

Z

Z

3

Z

I

I











(2.16)

 

 

 

 

 

P

k

,

k

0

k

,

k

2

k

,

k

2

k

1

k

0

Z

3

Z

Z

Z

I

I









(2.17)



jednofazowym

 

 

 

 

 

 

P

k

,

k

0

k

,

k

2

k

,

k

1

k

0

k

2

k

1

Z

3

Z

Z

Z

E

I

I

I













(2.18)

Prądy fazowe w miejscu zwarcia obliczamy transformując prądy składowych symetrycznych do
układu współrzędnych fazowych wg zależności:

 

 

 

































































k

2

k

1

k

0

2

2

k

3

L

k

2

L

k

1

L

I

I

I

a

a

1

a

a

1

1

1

1

I

I

I

(2.19)

lub zapisując krócej:

- 8 -

s

1

f

I

S

I





(2.20)

Napięcia w dowolnym i-tym węźle, w tym i w węźle zwartym, obliczamy z wzoru:

 

 

 

k

1

k

,

i

1

i

1

I

Z

E

U





(2.21)

 

 

 

k

2

k

,

i

2

i

2

I

Z

U





(2.22)

 

 

 

k

0

k

,

i

0

i

0

I

Z

U





(2.23)

Następnie wyznaczamy wielkości fazowe:

s

1

f

U

S

U





(2.24)

Prądy w dowolnej gałęzi łączącej węzły p oraz q wyznaczyć można z wzoru:

 

 

 

 

 

 

 

 

0

,

2

,

1

dla

Z

Z

Z

I

Z

U

U

I

q

p

k

,

p

k

,

q

k

q

p

q

p

pq





























(2.25)

Przed określeniem wielkości fazowych prądu w gałęzi lub napięcia w węźle, w obliczeniach

wartości składowych symetrycznych, program uwzględnia transformacje składowych
symetrycznych na skutek stosowania w sieci transformatorów o układach połączeń Yd, Dy, Dz oraz
Zy. Program podczas wczytywania danych wejściowych, dla każdego węzła, określa kąt
przesunięcia napięcia w tym węźle, w stanie jałowym względem węzła sieci, który przyjmujemy
jako węzeł odniesienia. Powyższej transformacji możemy dokonać według zależności:

 

 





q

p

j

pq

1

pq

1

e

I

I











(2.26)

 

 





q

p

j

pq

2

pq

2

e

I

I













(2.27)

 

 





k

i

j

i

1

i

1

e

U

U











(2.28)

 

 





k

i

j

i

1

i

1

e

U

U













(2.29)

gdzie:



k

,

i

,

q

,

p

oraz









- kąty przesunięcia napięcia w tym węźle, w stanie jałowym względem

węzła odniesienia.

W oparciu o zaprezentowaną teorię możemy obliczać wielkości zwarciowe dla zwarć
symetrycznych i niesymetrycznych w sieci ze skutecznie uziemionym punktem neutralnym. Jest to
klasyczny algorytm obliczania tych stanów.

- 9 -

2.2 Zastosowanie metody potencjałów węzłowych do obliczania zwarć w sieci ze skutecznie

i nieskutecznie uziemionym punktem neutralnym

Rys.2.4. Schemat zastępczy sieci dla obliczeń zwarciowych.

Możliwość obliczania wielkości zwarciowych w sieci ze skutecznie i nieskutecznie

uziemionym punktem neutralnym jest dużym udogodnieniem. Model matematyczny dla obliczania
zwarć w sieci elektroenergetycznej ze skutecznie i nieskutecznie uziemionym punktem neutralnym
można otrzymać zamieniając modele matematyczne generatora, ze źródła napięciowego (rys.2.3) na
źródło prądowe (rys.2.4). Prąd ten jest prądem węzłowym dołączonym w węźle dołączenia
generatora do sieci. Węzłem odniesienia jest w tym przypadku umyślony przewód powrotny. Prąd
węzłowy źródła, dołączonego do j-tego węzła dla



-tej składowej I

j

n
( )



, otrzymujemy zamieniając

to źródło z modelu napięciowego na model prądowy, a prąd ten można obliczyć ze wzoru:

 
 

j

j

n

j

)

(

Z

E

I









dla

0

,

2

,

1





(2.30)

gdzie:



 

j

E



- siła elektromotoryczna źródła dołączonego do j-tego węzła dla



-tej składowej,



 

j

Z



- impedancja źródła dołączonego do j-tego węzła dla



-tej składowej.

W węzłach, do których nie jest dołączone żadne źródło prąd węzłowy źródła wynosi zero.
Równania dla każdej składowej możemy zapisać w postaci:

 

   











I

Z

U

dla

0

,

2

,

1





(2.31)

gdzie:



 



U

- napięcie węzłowe



-tej składowej, równe napięciu w danym węźle dla danej składowej,



 





I

- prąd węzłowy



-tej składowej,



 



Z

- macierz impedancyjna węzłowa sieci dla



-tej składowej.

Przy założeniu, że zakłócenia modelujemy za pomocą prądu węzłowego, prąd

)

(





I

ma dwa

składniki:

- 10 -



składnik prądu źródłowego

n

)

(



I

,



składnik prądu zakłóceniowego

)

(



I

,

przy czym:

)

(

n

)

(

)

(













I

I

I

(2.32)

W przypadku symetrii źródeł mamy, że:

0

i

0

n

)

1

(

n

)

0

(

n

)

2

(







I

I

I

(2.33)

Równanie (2.31) wygodnie jest przekształcić do postaci:

 

     





   

   

 

   



































I

Z

U

I

Z

I

Z

I

I

Z

U

n

n

n

(2.34)

Wektor

 

n



U

są to napięcia w poszczególnych węzłach w stanie normalnym. Taki sposób

postępowania umożliwia uwzględnianie:



różnych sił elektromotorycznych (co do modułu i fazy) w poszczególnych źródłach,



gałęzi przyłączonych między węzłem a węzłem odniesienia np. gałęzi odbiorczych czy gałęzi
poprzecznych w schematach zastępczych elementów.

Te możliwości modelu matematycznego sieci elektroenergetycznej pozwalają za pomocą

jednego modelu - równania (2.34) - obliczać:



prądy i napięcia podczas zwarć wielkoprądowych, tzn. zwarć symetrycznych
i niesymetrycznych w sieci ze skutecznie uziemionym punktem neutralnym,



prądy i napięcia podczas zwarć małoprądowych, tzn. zwarć jednofazowych w sieci
z nieskutecznie uziemionym punktem neutralnym,



stany ustalone normalne gdyby odbiory zamodelować stałymi impedancjami a wektor prądu

zakłóceniowego przyjąć równy zero,



stany ustalone normalne gdyby odbiory zamodelować stałymi prądami zapisanymi w wektorze
prądu zakłóceniowego,



stany ustalone normalne niesymetryczne, gdyby odbiory zamodelować stałymi prądami różnymi

w każdej fazie, zapisanymi w wektorze prądu zakłóceniowego,



prądy i napięcia podczas zakłóceń z uwzględnieniem prądów obciążeniowych przy
modelowaniu odbiorów za pomocą jednego z podanych sposobów.

W przypadku zwarcia w węźle k-tym wektor prądu zakłóceniowego jest następujący:





0

...

0

I

0

...

0

)k

(

T

)

(









I

(2.35)

a układ równań odwzorowujący zwarcie będzie postaci:

 

 

 

 

k

k

,

k

n

k

k

I

Z

U

U













(2.36)

gdzie:



 

k

,

k

Z



- impedancja własna węzła k-tego dla



-tej składowej.

- 11 -

W powyższym układzie trzech równań mamy sześć niewiadomych, trzy napięcia

 

k

U



oraz trzy

prądy

 

k

I



. Układ ten można rozwiązać dopisując trzy równania zależne od rodzaju zwarcia, tzn.

równania brzegowe zwarcia.

W przypadku gdyby stany ustalone, normalne, symetryczne obliczać poprzez modelowanie

odbiorów stałymi impedancjami to wektor prądu zakłóceniowego należy przyjąć równy zero.
Wtedy:

 

   

 

n

1

n

1

1

1

U

I

Z

U





(2.37)

W oparciu o zaprezentowaną teorię opracowano program ZWAK31. Za pomocą tego programu
możemy obliczać wielkości zwarciowe dla zwarć symetrycznych i niesymetrycznych w sieci ze
skutecznie i nieskutecznie uziemionym punktem neutralnym. W przypadku wykonywania obliczeń
zwarć doziemnych w sieci z nieskutecznie uziemionym punktem neutralnym należy w schematach
zastępczych gałęzi uwzględnić ich elementy poprzeczne (pojemności).

2.3 Impedancje elementów sieci elektroenergetycznej w układzie składowych symetrycznych

2.3.1 Wstęp

W programie ZWAK31 przyjęto następujące założenia odnośnie impedancji elementów sieci

elektroenergetycznej:



impedancje dla składowej przeciwnej mogą być równe impedancji składowej zgodnej dla
wszystkich elementów sieci,



schemat zastępczej sieci dla składowej zgodnej i zerowej musi być taki sam.

Założenie 2) można zrealizować poprzez wprowadzenie w schematach zastępczych elementów sieci
dla składowej zgodnej i zerowej dodatkowych, sztucznych gałęzi o bardzo dużych lub małych
impedancjach doprowadzających te schematy do jednakowej postaci. Dla typowych elementów
sieci elektroenergetycznej, które posiadają różne schematy zastępcze, w tabl. 2.1. zestawiono
wspólne schematy zastępcze tych elementów dla składowej zgodnej i zerowej.

- 12 -

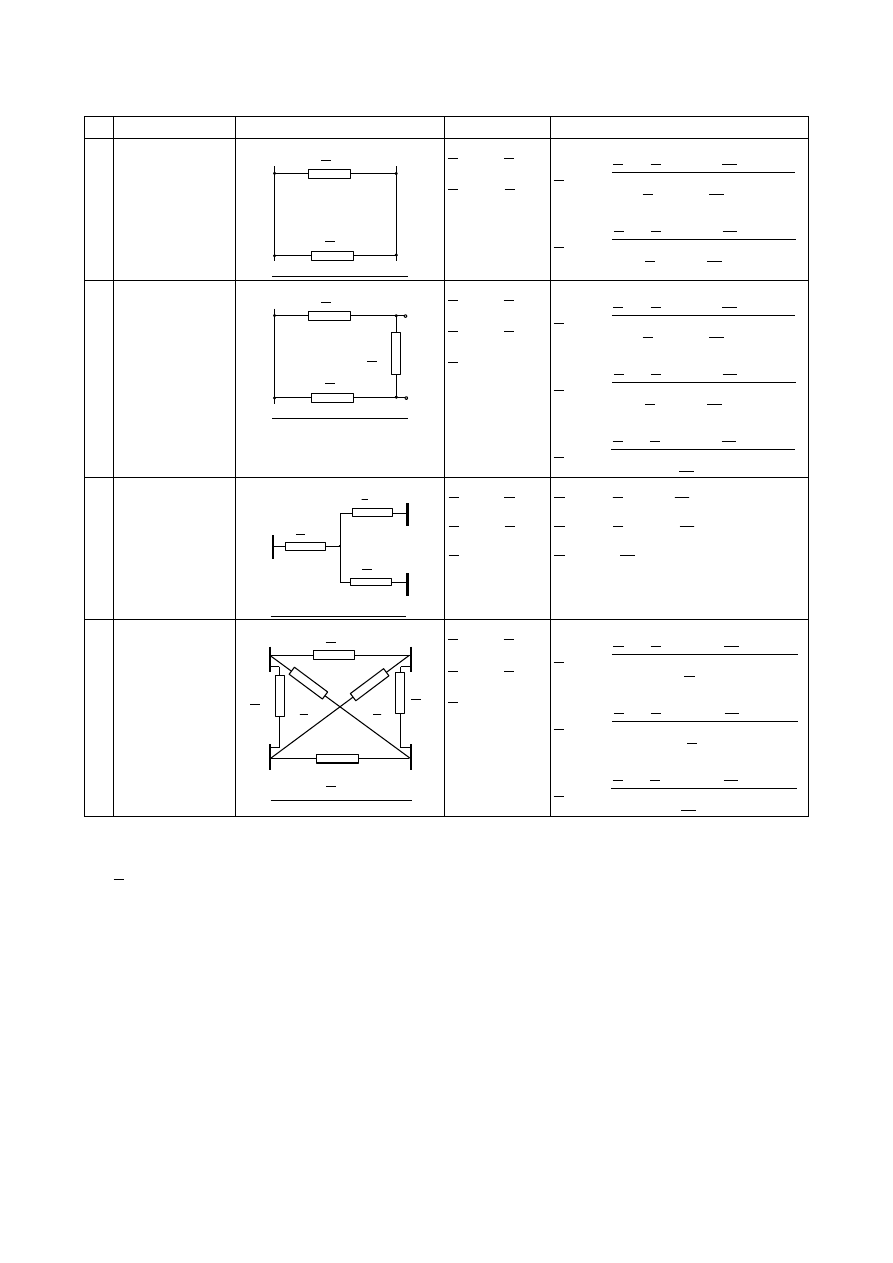
Tabl.2.1. Schematy zastępcze i impedancje elementów systemu elektroenergetycznego

Lp Nazwa elementu Schemat zastępczy Impedancje dla

składowej
zgodnej

Impedancje dla składowej zerowej

1

2

3

4

5

1

Transformator
YNd

a

Z

b

Z

c

Z

YN

d

 

 

 

 

 









c

1

T

1

b

1

T

1

a

1

Z

Z

2

1

Z

Z

2

1

Z

Rdzeń pięciokolumnowy:

 

 

 
 

0

Z

Z

Z

3

Z

Z

c

0

b

0

u

T

1

a

0











Rdzeń trójkolumnowy:

 

 

 
 

0

Z

Z

Z

3

Z

9

.

0

Z

c

0

b

0

u

T

1

a

0











2

Transformator
YNyn

a

Z

YN

yN

 

 

T

1

a

1

Z

Z



 

 

2

uy

uY

T

1

a

0

Z

3

Z

3

Z

Z









3

Transformator
YNy

a

Z

YN

y

 

 

T

1

a

1

Z

Z



Rdzeń pięciokolumnowy:

 





a

0

Z

Rdzeń trójkolumnowy:

 





 

uY

T

1

a

0

Z

3

Z

6

4

Z







4

Transformator
YNyn ze wspól-
nym
uziemieniem

a

Z

YN

yN

 

 

T

1

a

1

Z

Z



 

 





2

u

T

1

a

0

1

Z

3

Z

Z









5

Transformator
Zyn
(uziemiający)

a

Z

b

Z

c

Z

Z

yN

 

 

 

 

 









c

1

T

1

b

1

T

1

a

1

Z

Z

2

1

Z

Z

2

1

Z

 

 

 

 





 

 

0

Z

Z

3

Z

4

3

Z

Z

3

X

15

.

0

j

R

4

.

0

Z

c

0

uy

T

1

b

0

uZ

T

1

T

1

a

0















6

Transformator
Zyn lub Yzn

a

Z

b

Z

c

Z

ZN

Y

 

 

 

 

 









c

1

T

1

b

1

T

1

a

1

Z

Z

2

1

Z

Z

2

1

Z

 

 

 

 

 

0

Z

Z

3

X

15

.

0

j

R

4

.

0

Z

Z

c

0

2

uZ

T

1

T

1

b

0

a

0















7

Transformator
trójuzwojenio-
wy

YNyd

gdzie:
g - górne
s - średnie

d - dolne

a

Z

b

Z

c

Z

e

Z

d

g

s

 

 

 

 

 

 

 











e

1

T s

1

c

1

T g

1

b

1

T d

1

a

1

Z

Z

Z

Z

Z

Z

Z

Rdzeń pięciokolumnowy:

 

 

 

 

 

0

Z

Z

3

Z

Z

Z

Z

e

0

u

Tgd

1

b

0

c

0

a

0













Rdzeń trójkolumnowy:

 

 

 

 

 

0

Z

Z

3

Z

8

.

0

Z

Z

Z

e

0

u

Tgd

1

b

0

c

0

a

0













- 13 -

cd. tabl. 2.1.

1

2

3

4

5

8

Transformator
trójuzwojeniowy
YNdd gdzie:
g - górne
s - średnie
d - dolne

a

Z

b

Z

c

Z

e

Z

d

g

s

 

 

 

 

 

 

 











e

1

T s

1

c

1

T g

1

b

1

T d

1

a

1

Z

Z

Z

Z

Z

Z

Z

Rdzeń pięciokolumnowy:

 

 

 

 

 

 

 

 
 

0

Z

Z

Z

3

Z

Z

Z

Z

Z

Z

Z

e

0

c

0

u

Td

1

Ts

1

Td

1

Ts

1

Tg

1

b

0

a

0





















Rdzeń trójkolumnowy:

 

 

 

 

 

 

 

 
 

0

Z

Z

Z

3

Z

Z

Z

Z

Z

9

.

0

Z

Z

e

0

c

0

u

Td

1

Ts

1

Td

1

Ts

1

Tg

1

b

0

a

0



































9

Autotransformator
YautoNd

lub

transformator
YNynd

g gorne
s srednie
d do e







ln

a

Z

b

Z

d

Z

c

Z

e

Z

Y

y

d

 

 

 

 

 

 

 
 













e

1

d

1

Td

1

c

1

Ts

1

b

1

Tg

1

a

1

Z

0

Z

Z

Z

Z

Z

Z

Z

Rdzeń pięciokolumnowy:

 

 





 

 





 
 

 

 

0

Z

Z

3

Z

Z

Z

1

Z

3

Z

Z

1

Z

3

Z

Z

e

0

u

Td

1

d

0

c

0

u

Ts

1

b

0

u

Tg

1

a

0































Rdzeń trójkolumnowy:

 

 





 

 





 

 

 





 

 

 

 

0

Z

Z

6

Z

3

Z

85

.

0

Z

6

Z

3

Z

85

.

0

Z

Z

1

Z

3

Z

85

.

0

Z

1

Z

3

Z

85

.

0

Z

e

0

Tgs

1

u

Td

1

Tgs

1

u

Td

1

d

0

c

0

u

Ts

1

b

0

u

Tg

1

a

0







































10 Autotransformator

YautoN

a

Z

YN

yN

 

 

T

1

a

1

Z

Z



Rdzeń pięciokolumnowy:

 

 





2

u

T

1

a

0

1

Z

3

Z

Z









Rdzeń trójkolumnowy:

 

 





2

u

AT

1

a

0

1

Z

3

Z

85

.

0

Z









- 14 -

cd. tabl. 2.1.

1

2

3

4

5

11 Linia

dwutorowa
pracująca

z

połączonymi
torami na obu
końcach

a

Z

b

Z

I

II

 

 

 

 

II

1

b

1

I

1

a

1

Z

Z

Z

Z





 

   





 

 

   





 

II

mI

I

0

2

II

mI

II

0

I

0

b

0

II

mI

II

0

2

II

mI

II

0

I

0

a

0

Z

3

Z

Z

3

Z

Z

Z

Z

3

Z

Z

3

Z

Z

Z





























12 Linia

dwutorowa
pracująca

z

połączonymi
torami

na

jednym końcu

a

Z

b

Z

c

Z

I

II

 

 

 

 

 









c

1

II

1

b

1

I

1

a

1

Z

Z

Z

Z

Z

 

   





 

 

   





 

 

   





II

mI

2

II

mI

II

0

I

0

c

0

II

mI

I

0

2

II

mI

II

0

I

0

b

0

II

mI

II

0

2

II

mI

II

0

I

0

a

0

Z

3

Z

3

Z

Z

Z

Z

3

Z

Z

3

Z

Z

Z

Z

3

Z

Z

3

Z

Z

Z









































13 Linia

dwutorowa
pracująca

z

połączonymi
torami

na

jednym końcu

a

Z

b

Z

c

Z

I

II

 

 

 

 

 

0

Z

Z

Z

Z

Z

c

1

II

1

b

1

I

1

a

1







 

 

 

 

 

II

mI

c

0

II

mI

II

0

b

0

II

mI

I

0

a

0

Z

3

Z

Z

3

Z

Z

Z

3

Z

Z























14 Linia

dwutorowa
pracująca z nie
połączonymi
torami na obu
końcach

a

Z

b

Z

b

Z

c

Z

I

II

c

Z

c

Z



c

Z



 

 

 

 

 









c

1

II

1

b

1

I

1

a

1

Z

Z

Z

Z

Z

 

   





 

 

   





 

 

   





II

mI

2

II

mI

II

0

I

0

c

0

I

0

2

II

mI

II

0

I

0

b

0

II

0

2

II

mI

II

0

I

0

a

0

Z

3

Z

3

Z

Z

Z

Z

Z

3

Z

Z

Z

Z

Z

3

Z

Z

Z





























Wyjaśnienia do tabl. 2.1.:



u

Z

-impedancja uziemienia punktu gwiazdowego transformatora.





-przekładnia transformatora.



Impedancje transformatorów i autotransformatorów są sprowadzone na stronę górnego napięcia,



W niektórych punktach pominięto gałęzie odwzorowujące impedancje magnesowania

transformatora dla składowej zerowej.



Należy pamiętać, że prądy płynące w gałęziach schematu zastępczego nie mają odpowiedników
fizycznych. Prąd w torze należy, więc wyznaczać jako sumę prądów płynących w odpowiednich
gałęziach schematu zastępczego. Dotyczy to także linii dwutorowej pracującej z połączonymi
torami na jednym końcu - wiersz 12. W tym przypadku schemat zastępczy w postaci trójkąta
najlepiej jest przekształcić do postaci gwiazdy - wiersz 13.



Wyznaczanie prądów płynących w gałęziach sieci jako sumy geometrycznej prądów płynących
w odpowiednich gałęziach schematu zastępczego jest sposobem niewygodnym i może być
uproszczone poprzez dodanie gałęzi o małych impedancjach realizujących ten sam cel.

- 15 -

W tabl. 2.1. występują impedancje, które można uzyskać na podstawie pomiarów lub

w wyniku obliczeń w oparciu o dane znamionowe urządzenia lub w przypadku linii w oparciu
o schemat i odległości rozmieszczenia przewodów fazowych i odgromowych na słupie.

Poniżej zostaną zaprezentowane wzory umożliwiające obliczenie impedancji linii w oparciu

o rozmieszczenie przewodów na słupie. W obliczeniach tych będzie zakładane, że:



linia jest w pełni symetryczna geometrycznie oraz elektrycznie tzn. że linią jest
z przepleceniami,



przewody odgromowe są uziemione,



uziomy słupów nie uczestniczą w odprowadzaniu prądów płynących w przewodach
odgromowych.

2.3.2 Linia jednotorowa z jednym przewodem odgromowym

Impedancja własna i wzajemna kilometryczna przewodów fazowych:





 

km

r

D

lg

145

.

0

j

R

R

Z

o

z

zk

pk

wk









(2.38)

 

km

b

D

lg

145

.

0

j

R

Z

m

z

zk

mk







(2.39)

gdzie:



pk

R

- rezystancja kilometryczna przewodu fazowego obliczana z przekroju tego przewodu;



zk

R

- rezystancja kilometryczna ziemi (zwykle przyjmuje się, że

km

05

.

0

R

zk





);



z

D - odległość miedzy przewodem fazowym a umyślonym przewodem powrotnym

znajdującym się w ziemi, zwykle przyjmuje się, że

m

1000

D

z



;



o

r - zastępczy promień przewodu;



m

b

- średni odstęp przewodów od siebie.

Zastępczy promień przewodu dla pojedynczego przewodu typu AFl wynosi 0,8 promienia
rzeczywistego, a w przypadku przewodów wiązkowych, jeśli przewody w wiązce są ułożone na
wierzchołkach wieloboku foremnego wyraża się wzorem;

n

1

n

rz

o

D

r

8

.

0

r





(2.40)

gdzie:



rz

r - rzeczywisty promień przewodu;



D - odległość przewodu w wiązce;



n - liczba przewodów w wiązce.

Średni odstęp przewodów fazowych wynosi:

3

1

L

3

L

3

L

2

L

2

L

1

L

m

b

b

b

b



(2.41)

gdzie:



1

L

3

L

3

L

2

L

2

L

1

L

b

,

b

,

b

- rzeczywiste odstępy między przewodami fazowymi.

- 16 -

Impedancja własna kilometryczna

k

Z



przewodu odgromowego



i wzajemna kilometryczna

Z

m k



pętli przewód odgromowy - przewód fazowy wynosi:





 

km

r

D

lg

145

.

0

j

R

R

Z

z

zk

k

k















(2.42)

 

km

b

D

lg

145

.

0

j

R

Z

m

z

zk

k

m











(2.43)

gdzie:



k

R



- rezystancja kilometryczna przewodu odgromowego;





r

- zastępczy promień przewodu odgromowego;





m

b

- średnia odległość miedzy przewodem odgromowym a przewodami fazowymi.

Wielkość



m

b

obliczamy z wzoru:

3

3

L

2

L

1

L

m

b

b

b

b











(2.44)

Kilometryczna impedancja linii dla składowej zgodnej i zerowej wynosi:

 

 

km

r

b

lg

145

.

0

j

R

Z

Z

Z

o

m

pk

mk

wk

k

1











(2.45)

 

k

2

k

m

mk

wk

k

0

Z

Z

3

Z

2

Z

Z











(2.46)

Prąd w przewodzie odgromowym obliczamy z wzoru:

 

 





r

0

m

0

k

1

I

3

Z

Z

I

3

I

















(2.47)

gdzie:



r

k - współczynnik redukcyjny przewodów odgromowych, w skrócie współczynnik redukcyjny

linii.

Pozostała część prądu

 

0

I

3

płynącego daną linią wraca poprzez ziemię.

2.3.3 Linia jednotorowa z dwoma przewodami odgromowymi

Impedancja tej linii dla składowej zgodnej można obliczyć z wzoru (2.45) a dla składowej

zerowej z zależności:

 

k

k

2

k

m

mk

wk

k

0

Z

Z

Z

6

Z

2

Z

Z















(2.48)

- 17 -

gdzie:



k

Z



- impedancja wzajemna przewód odgromowy



- przewód odgromowy



.

W tym przypadku średnią odległość między przewodami odgromowymi i fazowymi



m

b

obliczamy z wzoru:

6

3

L

2

L

1

L

3

L

2

L

1

L

m

b

b

b

b

b

b

b

















(2.49)

Impedancję

k

Z



obliczamy z zależności:

 

km

b

D

lg

145

.

0

j

R

Z

z

zk

k











(2.50)

gdzie:





b

- odległość miedzy przewodami odgromowymi.

Prąd w przewodzie odgromowym teraz wynosi:

 



















Z

Z

Z

I

3

I

I

m

0

(2.51)

2.3.4 Linia dwutorowa z dwoma przewodami odgromowymi

Impedancję dla składowej zgodnej każdego z torów obliczamy z wzoru (2.45) podstawiając

parametry danego toru. Impedancję dla składowej zerowej toru obliczamy ze wzoru:

 















Z

Z

Z

2

3

Z

2

Z

Z

2
m

mI

wI

I

0

(2.52)

 















Z

Z

Z

2

3

Z

2

Z

Z

2
m

mII

wII

II

0

(2.53)

W przypadku linii dwutorowej występuje dodatkowa impedancja wzajemna przewody fazowe toru
I - przewody fazowe toru II, która bez uwzględnienia wpływu przewodów odgromowych określamy
z zależności:

 

km

b

D

lg

145

.

0

j

R

Z

II

mI

z

zk

IIk

mI











(2.54)

9

II

3

L

I

3

L

II

2

L

I

3

L

II

1

L

I

3

L

II

3

L

I

2

L

II

2

L

I

2

L

II

1

L

I

2

L

II

3

L

I

1

L

II

2

L

I

1

L

II

1

L

I

1

L

II

mI

b

b

b

b

b

b

b

b

b

b





(2.55)

gdzie:



II

1

L

I

1

L

b



- odległość miedzy faza L1 toru I a faza L1 toru II.

- 18 -

Całkowita impedancja wzajemna tor I - tor II z uwzględnieniem przewodów odgromowych wynosi:



















Z

Z

Z

2

3

Z

3

Z

3

2

m

II

I

m

II

I

m

(2.56)

Wzory (2.52), (2.53) i (2.56) uproszczono zakładając pełną symetrię obu torów oraz że:











m

mII

mI

Z

Z

Z

(2.57)

przy czym



m

b

obliczamy wtedy z wzoru:

6

II

3

L

II

2

L

II

1

L

I

3

L

I

2

L

I

1

L

m

b

b

b

b

b

b

b

















(2.58)

Prądy w przewodach odgromowych obliczamy z wzoru (2.51).

2.3.5 Wyznaczenie schematu zastępczego linii

W celu określenia schematów zastępczych omawianych linii, w oparciu o podane powyżej

wzory na impedancję dla składowej zerowej każdego z torów oraz impedancję wzajemną przewody
fazowe toru I - przewody fazowe toru II, należy zbudować macierz impedancyjną linii zwartej na
jej jednym końcu (przy takim założeniu wyprowadzano wzory na impedancje torów i impedancję
wzajemną w oparciu o wymiary geometryczne linii). Dla linii dwutorowej nie połączonej z obu
końców (przypadek najbardziej ogólny) macierz taka ma postać:

 

 

 























II

II

I

m

II

I

m

I

Lz

Z

Z

Z

Z

0

0

0

3

3

Z

(2.59)

Macierz tą należy odwrócić w celu otrzymania macierzy admitancyjnej linii zwartej:

 

 

 

 





 

 





 

 





 

 

 











































































2

0

0

0

2

0

0

2

0

0

2

0

0

0

0

3

3

3

3

3

3

II

I

m

II

I

I

II

I

m

II

I

II

I

m

II

I

m

II

I

II

I

m

II

I

m

II

I

II

Lz

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Y

(2.60)

Macierz admitancyjną linii zwartej zapiszemy w prostszej postaci:

 

 

 

 

 















II

I

Lz

Y

Y

Y

Y

0

0

0

0

0

Y

(2.61)

W celu otrzymania macierzy admitancyjnej linii nie zwartej należy każdy element powyższej
macierzy pomnożyć przez macierz jedynkową postaci:

















1

1

1

1

(2.62)

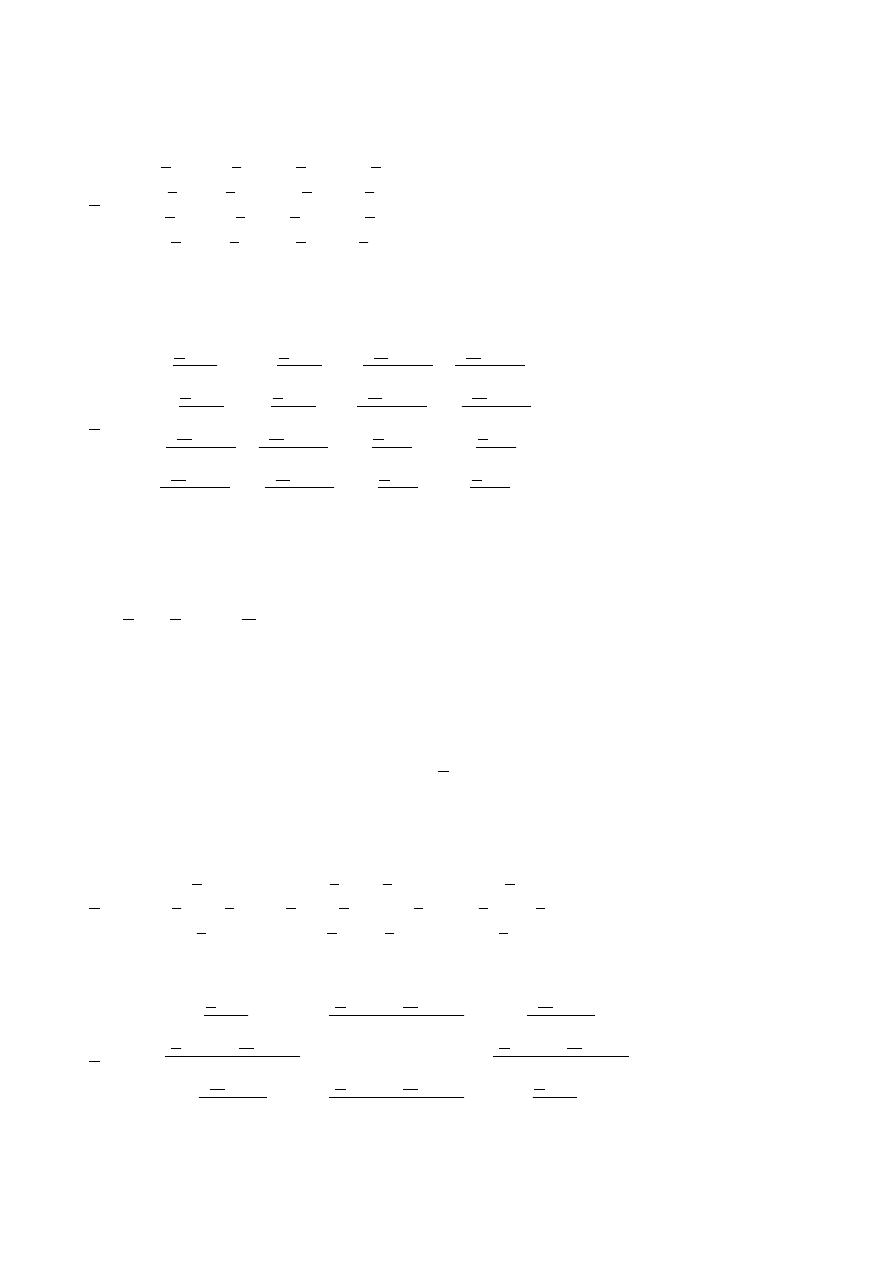
- 19 -

W wyniku otrzymujemy macierz admitancyjną linii włączonej pomiędzy węzłami I-I

'

dla toru 1-go

oraz II-II' dla toru 2-go:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

I

II

I

I

I

I

II

I

I

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

I

I

I

I

I

I

I

I

I

I

I

I

L























































0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

Y

(2.63)

czyli:

 

 

 

 

 

 

 

 

 

'

'

'

3

3

3

3

3

3

3

3

0

0

0

0

0

0

0

0

0

II

II

I

I

II

II

I

I

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

M

Z

I

I

II

I

m

II

I

m

I

I

II

I

m

II

I

m

II

I

m

II

I

m

II

II

II

I

m

II

I

m

II

II

L

































































































Y

(2.64)

gdzie:

 

 





2

0

0

3

II

I

m

II

I

Z

Z

Z

M











(2.65)

Elementy wzajemne macierzy z równania (2.64) wzięte ze znakiem minus to admitancje gałęzi
schematu zastępczego podane w tabl. 2.1 w wierszu 14 (podane tam impedancje są równe
odwrotności admitancji). Ponieważ w macierzy admitancyjnej brak zer tzn., że schemat zastępczy
będzie wielobokiem zupełnym o czterech wierzchołkach - mamy wtedy tzw. schemat kopertowy.
Suma elementów danego wiersza to admitancja gałęzi pomiędzy danym węzłem a węzłem
odniesienia jednak przy tak tworzonej macierzy

 

L

0

Y

wielkości te zawsze będą równe zeru.

W przypadku, gdy linia dwutorowa pracuje z połączonymi torami na jednym końcu np. węzły

I' oraz II' tworzą jeden węzeł I' to macierz admitancyjną tej linii otrzymujemy dodając do siebie
wiersz I' i II' a następnie kolumnę I' z II' w macierzy (2.63). W wyniku tej operacji otrzymamy:

 

 

 

 





 

 

 





 

 

 





 

 





 

 

 





 

II

I

I

II

I

I

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

I

I

I

I

I

I

I

I

I

I

I

I

I

I

L

















































0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

2

Y

(2.66)

 

 

 





 





 





 





 

II

I

I

II

I

I

M

Z

M

Z

Z

M

Z

M

Z

Z

M

Z

Z

M

Z

M

Z

Z

M

Z

II

II

I

m

II

II

I

m

II

I

m

II

II

I

m

II

II

I

m

II

I

m

II

II

L

'

'

3

3

3

3

3

3

0

0

0

0

0

0

0



















































































Y

(2.64)

- 20 -

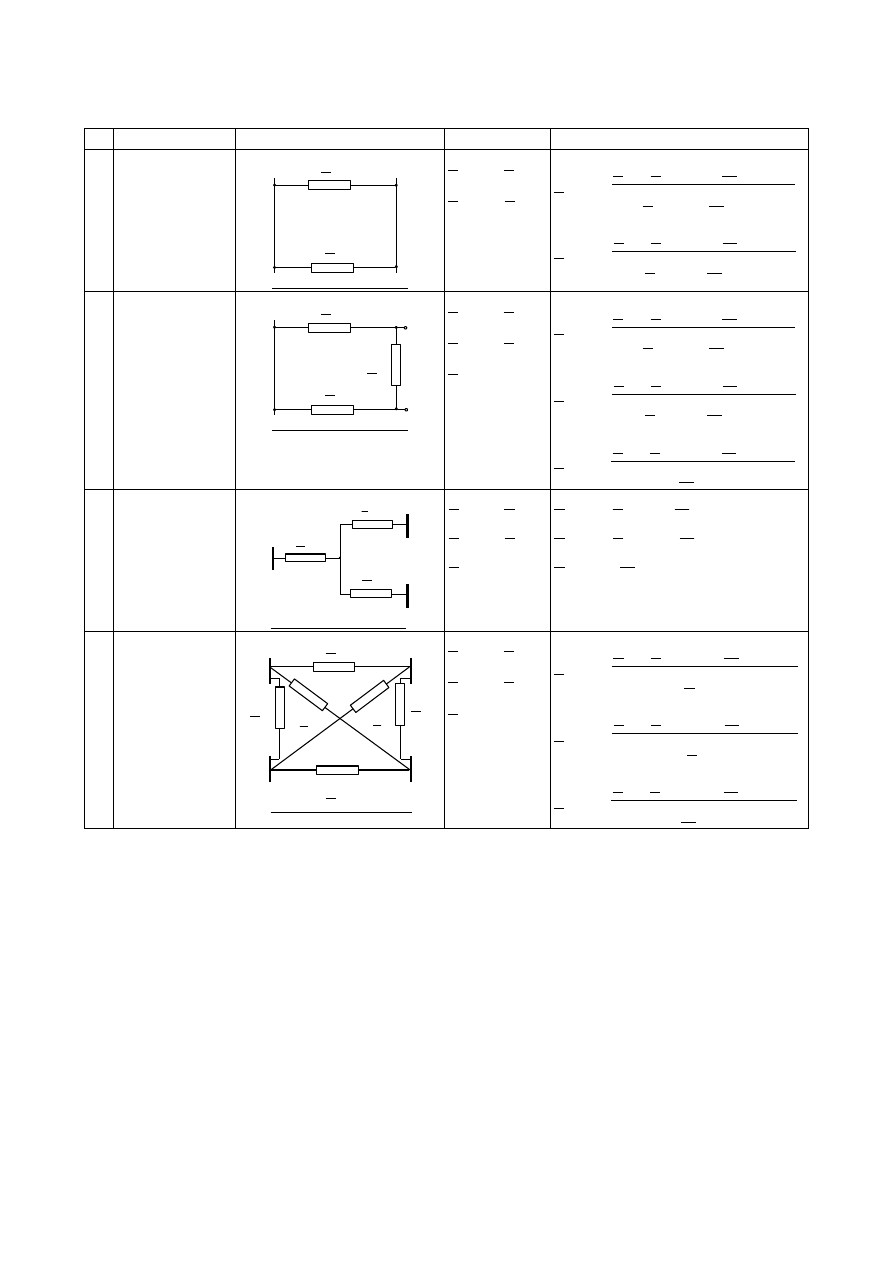
Schemat zastępczy tej linii będzie trójkątem.

1

2

3

4

5

11 Linia

dwutorowa
pracująca

z

połączonymi
torami na obu
końcach

a

Z

b

Z

I

II

 

 

 

 

II

1

b

1

I

1

a

1

Z

Z

Z

Z





 

   





 

 

   





 

II

mI

I

0

2

II

mI

II

0

I

0

b

0

II

mI

II

0

2

II

mI

II

0

I

0

a

0

Z

3

Z

Z

3

Z

Z

Z

Z

3

Z

Z

3

Z

Z

Z





























12 Linia

dwutorowa
pracująca

z

połączonymi
torami

na

jednym końcu

a

Z

b

Z

c

Z

I

II

 

 

 

 

 









c

1

II

1

b

1

I

1

a

1

Z

Z

Z

Z

Z

 

   





 

 

   





 

 

   





II

mI

2

II

mI

II

0

I

0

c

0

II

mI

I

0

2

II

mI

II

0

I

0

b

0

II

mI

II

0

2

II

mI

II

0

I

0

a

0

Z

3

Z

3

Z

Z

Z

Z

3

Z

Z

3

Z

Z

Z

Z

3

Z

Z

3

Z

Z

Z









































13 Linia

dwutorowa
pracująca

z

połączonymi
torami

na

jednym końcu

a

Z

b

Z

c

Z

I

II

 

 

 

 

 

0

Z

Z

Z

Z

Z

c

1

II

1

b

1

I

1

a

1







 

 

 

 

 

II

mI

c

0

II

mI

II

0

b

0

II

mI

I

0

a

0

Z

3

Z

Z

3

Z

Z

Z

3

Z

Z























14 Linia

dwutorowa
pracująca z nie
połączonymi
torami na obu
końcach

a

Z

b

Z

b

Z

c

Z

I

II

c

Z

c

Z



c

Z



 

 

 

 

 









c

1

II

1

b

1

I

1

a

1

Z

Z

Z

Z

Z

 

   





 

 

   





 

 

   





II

mI

2

II

mI

II

0

I

0

c

0

I

0

2

II

mI

II

0

I

0

b

0

II

0

2

II

mI

II

0

I

0

a

0

Z

3

Z

3

Z

Z

Z

Z

Z

3

Z

Z

Z

Z

Z

3

Z

Z

Z





























Powyższa metodologia ma charakter ogólny i może być stosowana dla linii wielotorowych

np. do aktualnie projektowanej linii czterotorowej (dwa tory na napięciu 400 kV i dwa tory na
napięciu 220 kV). Brakuje tutaj jedynie omówienia przypadku, gdy linie równoległe są różnych
napięć i występuje pomiędzy nimi przesunięcie fazowe. Obecnie buduje się wiele linii
napowietrznych z przewodami izolowanymi o napięciu znamionowym 15 kV (lub 20 kV) i 0,4 kV
na wspólnym słupie. Przesunięcie fazowe pomiędzy takimi liniami wynosi 150

o

, co wynika

z obecności pomiędzy tymi liniami transformatora Dy5 lub Yz5. Metodologia tworzenia schematu
zastępczego takich linii nie będzie tutaj omówiona a można ją znaleźć w [2].

- 21 -

3.

OPIS

UŻYTKOWANIA

PROGRAMU

ZWAK31

3.1. Ogólna charakterystyka programu

Programem ZWAK31 można obliczać wielkości zwarciowe początkowe przy pojedynczym

zwarciu symetrycznym lub niesymetrycznym, w miejscu zwarcia i w dowolnym miejscu sieci. Sieć
może być dowolną, wielonapięciową siecią. Rozpatrywana sieć może być ze skutecznie lub
nieskutecznie uziemionym punktem neutralnym lub być siecią gdzie znajdują się oba typy sieci.
Możliwość jednoczesnego modelowania sieci ze skutecznie lub nieskutecznie uziemionym punktem
neutralnym lub sieci gdzie znajdują się oba typy ww. sieci jest dużym udogodnieniem.

Wyniki obliczeń program podaje we współrzędnych fazowych i w składowych

symetrycznych, w jednostkach mianowanych i w jednostkach względnych. W wynikach obliczeń
uwzględniona jest transformacja prądów i napięć przez transformatory istniejące w sieci, co do
modułu i fazy względem miejsca zwarcia tzn. uwzględniona jest różna transformacja wielkości dla
składowej zgodnej i przeciwnej w transformatorze o grupie połączeń Yd. W programie parametry
sieci wczytywane są z klawiatury komputera lub z dysku. W programie przewidziano możliwość
wprowadzenia dowolnej zmiany we wczytanych danych wejściowych praktycznie w dowolnym
momencie wykonywania obliczeń np. po pomyłce w trakcie wczytywania danych lub, gdy chcemy
w trakcie obliczeń zmienić jedną z wczytanych danych. W wielu miejscach programu przewidziano
procedury kontrolujące odczytywane dane wejściowe i uniemożliwiające wczytywanie danych
niezgodnych z przyjętymi założeniami np. nie można podać dwukrotnie tego samego numeru
gałęzi.

Podstawową wielkością potrzebną dla tych obliczeń są impedancje własne i wzajemne będące

elementami macierzy impedancyjnej węzłowej sieci

Z

dla poszczególnych składowych. Macierz

impedancyjną węzłową sieci obliczamy z wykorzystaniem techniki macierzy rzadkich w oparciu
o macierz admitancyjną węzłową

Y

. W programie:



macierz Y rozkładamy za pomocą metody bifaktoryzacji,



impedancje własną lub wzajemne obliczamy za pomocą metody wektorów rzadkich.

W przypadku wykonywania obliczeń zwarć doziemnych w sieci z nieskutecznie uziemionym

punktem neutralnym należy w schematach zastępczych gałęzi uwzględnić ich elementy poprzeczne
(pojemności). W tym celu program ZWAK31 został wyposażony w procedurę, która dla linii
napowietrznych i kablowych średnich napięć oblicza ich impedancje podłużna i poprzeczne.

3.2. Wczytywanie danych wejściowych

Mając za zadanie wykonanie obliczeń zwarciowych za pomocą programu ZWAK31

w konkretnej sieci należy:
1.

Narysować schemat zastępczy tej sieci dla składowej zgodnej i zerowej.

2.

Przyjmując odpowiednią moc podstawową obliczyć impedancje (rezystancje i reaktancje) dla
składowej zgodnej, przeciwnej i zerowej każdej gałęzi rozpatrywanej sieci.

3.

Zbudować jeden wspólny schemat sieci dla obu składowych wprowadzając w obu tych
schematach dodatkowe gałęzie o bardzo dużych lub bardzo małych impedancjach
odwzorowujące przerwy lub połączenia w schematach dla składowej zgodnej i zerowej.
W praktyce impedancje te powinny mieć wartość największą (najmniejszą), jaką można
wprowadzić za pomocą programu. W praktyce przerwę (



) modelujemy za pomocą liczby

999999. Dla różnych elementów sieci elektroenergetycznej w tab. 2.1 podano praktyczny
sposób postępowania w tych przypadkach.

4.

W powyższym schemacie ponumerować wszystkie węzły i gałęzie dowolnymi liczbami
naturalnymi, przy czym węzeł odniesienia musi mieć numer zero. Zgodnie z rozdziałem 2
węzeł odniesienia przyjmujemy w umyślonym przewodzie powrotnym.

- 22 -

5.

Dla każdego węzła podać napięcie znamionowe oraz określić kąt przesunięcia napięcia w tym
węźle w stanie jałowym względem węzła, w którym przyjęliśmy że ma fazę zero (może to
być dowolny węzeł).

6.

Wczytać dane o topologii sieci i impedancjach gałęzi (w jednostkach względnych) do
komputera, przy czym dla gałęzi mamy do wyboru dwa sposoby postępowania:



wczytujemy impedancje gałęzi,



wczytujemy długość linii oraz rodzaj linii.

W tym drugim przypadku program sam oblicza impedancje wzdłużną oraz poprzeczną gałęzi.
Z tych impedancji tworzy czwórnik typu



. Powoduje to, że w przypadku zwarcia w sieci

z nieskutecznie uziemionym punktem neutralnym prąd w takiej gałęzi nie odpowiada prądowi
rzeczywistemu. Można temu zapobiec wprowadzając przed daną gałąź dodatkową gałąź
o bardzo małej impedancji i obliczając prąd w tej gałęzi zamiast w następnej.

7.

Wczytać napięcia znamionowe i fazę napięcia w każdym węźle.

8.

Wczytać następujące dane o źródłach prądu zwarciowego:



numery gałęzi z generatorem, podane w punkcie 6;



część rzeczywistą i urojoną siły elektromotorycznej każdego generatora.

9.

Wczytać dane sterujące obliczeniami, do których należą:



miejsce zwarcia ,



rodzaj zwarcia,



wartość rezystancji i reaktancji przejścia w miejscu zwarcia,



rodzaj obliczeń.

Dane wejściowe do programu ZWAK31 wczytywane są do komputera w trybie konwersacyjnym.
W programie przewidziano możliwość wprowadzenia dowolnej zmiany we wczytywanych danych
wejściowych po wykonaniu wczytywania tych danych lub po wykonaniu części obliczeń.

W ramach przygotowywania się do wykonania ćwiczenia, w domu dla zadanej przez

prowadzącego sieci należy wykonać punkty od 1) do 5).

3.3. Wyniki obliczeń

Wyniki obliczeń za pomocą programu ZWAK31 składają się z kilku typów wydruków,

a mianowicie:
1.

Wydruk aktualnej bazy danych do obliczeń.

2.

Wydruk wartości prądu w gałęziach, w stanie normalnym, we współrzędnych fazowych.

3.

Wydruk wartości napięć w węzłach, w stanie normalnym, we współrzędnych fazowych.

4.

Wydruk wartości prądu w miejscu zwarcia we współrzędnych fazowych i składowych
symetrycznych, przy czym fazy wszystkich wielkości obliczanych za pomocą programu są
liczone przy założeniu, że napięcie wymuszające jest położone w osi rzeczywistych.

5.

Wydruk wartości napięcia w miejscu zwarcia we współrzędnych fazowych i składowych
symetrycznych.

6.

Wydruk wartości napięcia w dowolnym węźle we współrzędnych fazowych i składowych
symetrycznych oraz wartości napięć międzyprzewodowych.

7.

Wydruk wartości prądu w dowolnej gałęzi sieci we współrzędnych fazowych i składowych
symetrycznych. Fazy prądu są tu określane przy założeniu, że prąd w gałęzi płynie od węzła
początkowego do końcowego. W przypadku, gdy jest odwrotnie należy fazę prądu zmienić
o 180

o

.

W wydrukach uwzględniona jest transformacja prądu i napięcia przez istniejące w sieci
transformatory. Transformacja ta jest wykonana, co do modułu i fazy, a określana jest względem
miejsca zwarcia. W przypadku, gdy wektory prądu lub napięcia tworzą układy niesymetryczne,
uwzględniona jest różna transformacja dla składowej zgodnej i przeciwnej.

- 23 -

4.

LITERATURA

[1]

Anderson P. M.: Analysis of Faulted Power Systems. The Iowa State University Press, Ames
1973.

[2]

Bernas S., Ciok Z.: Modele matematyczne elementów systemu elektroenergetycznego. WNT,
Warszawa 1977.

[3]

Kacejko P., Machowski J.: Zwarcia w sieciach elektroenergetycznych. W.N.T. Warszawa
1993.

[4]

Kobosko S.: Obliczanie zwarć w systemach elektroenergetycznych. W.P.W. Warszawa 1984.

[5]

Kończykowski S., Bursztyński J.: Zwarcia w układach elektroenergetycznych. W.N.T.,
Warszawa 1965.

[6]

Kowalski Z.: Teoria zwarć w układach elektroenergetycznych. W.P.Ł. Łódź 1988.

[7]

Stagg G.W., El-Abiad A.H.: Computer Methods in Power System Analysis. Mc Graw-Hill,
New York, 1968.

- 24 -

ZAŁĄCZNIK

NR

1:

O

BLICZANIE ZWARĆ SYMETRYCZNYCH

1.

Sieć do obliczania zwarć

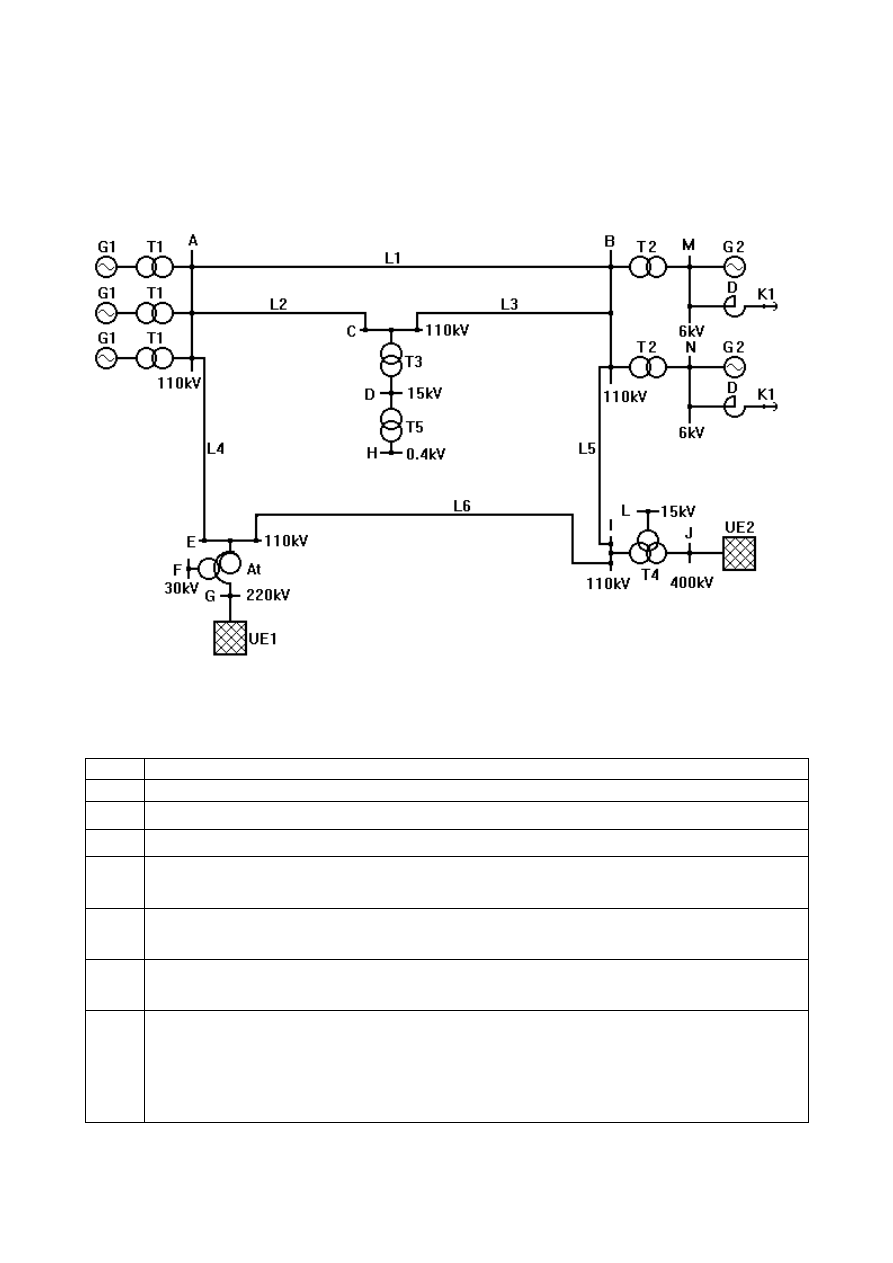
Dana jest wielonapięciowa sieć elektroenergetyczna przedstawiona na rys. 1 oraz 2.

Rys. 1

Schemat sieci dla obliczania zwarć.

Tabl. 1

Dane znamionowe elementów z rys. 1.

Symbol Dane znamionowe elementu

1

2

G1

%

15

X

kV

75

.

15

U

MVA

250

S

d

n

n









G2

%

12

X

kV

3

.

6

U

MVA

25

S

d

n

n









T1

kW

750

P

%

14

U

kV

75

.

15

U

kV

121

U

MVA

250

S

cu

z

nd

ng

n















YNd11; rdzeń trójkolumnowy

T2

11

YNd

kW

128

P

%

11

U

kV

3

.

6

U

kV

121

U

MVA

25

S

cu

z

nd

ng

n















rdzeń trójkolumnowy

T3

kW

128

P

%

11

U

kV

75

.

15

U

kV

121

U

MVA

25

S

cu

z

nd

ng

n















YNd11; rdzeń trójkolumnowy

T4

11

YNynd

kW

700

P

kW

900

P

kW

950

P

%

0

.

9

U

%

5

.

12

U

%

5

.

15

U

kV

15

U

kV

115

U

kV

400

U

M VA

50

/

M VA

250

/

M VA

250

S

w

d

cu

w

g

cu

d

g

cu

w

d

z

w

g

z

d

g

z

nw

nd

ng

n













































rdzeń pięciokolumnowy

- 25 -

cd. tabl.

1.

1

2

T5

5

Dyn

kW

6

.

6

P

%

6

U

kV

4

.

0

U

kV

75

.

15

U

kVA

630

S

cu

z

nd

ng

n















rdzeń trójkolumnowy

At

11

Nd

Y

kW

520

P

kW

540

P

kW

850

P

%

20

U

%

34

U

%

10

U

kV

30

U

kV

115

U

kV

220

U

M VA

50

/

M VA

160

/

M VA

160

S

auto

w

d

cu

w

g

cu

d

g

cu

w

d

z

w

g

z

d

g

z

nw

nd

ng

n













































rdzeń pięciokolumnowy

UE1

 

 

2

.

1

X

X

M VA

10000

S

kV

220

U

1

0

z

n







UE2

 

 

8

.

1

X

X

M VA

25000

S

kV

400

U

1

0

z

n







L1

 

 

 

km

50

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L2

 

 

 

km

20

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L3

 

 

 

km

30

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L4

 

 

 

km

30

L

km

07

.

1

X

km

41

.

0

X

km

125

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L5

 

 

 

km

30

L

km

07

.

1

X

km

41

.

0

X

km

125

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L6

 

 

 

km

40

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















Tabl. 2

Dane znamionowe dławików przeciwzwarciowych U

n

= 6kV.

n

I

A

250

250

400

400

630

630

630

1000 1000 1000 2000

U



%

4

6

4

6

5

6

8

6

8

10

10

- 26 -

L1

L5

L2

L3

L4

C

A

B

D

T4

15 kV

T4

UE2

110 kV

UE1

AT

L6

15 kV

400 kV

6 kV

15 kV

15 kV

0,4 kV

6 kV

220 kV

15 kV

T2

T2

T2

G2

G2

G2

T3

T3

T5

T1

T1

G1

G1

D1

D1

D2

E

F

G

H

I

J

K

L

M

N

K1

K1

R

P

L7

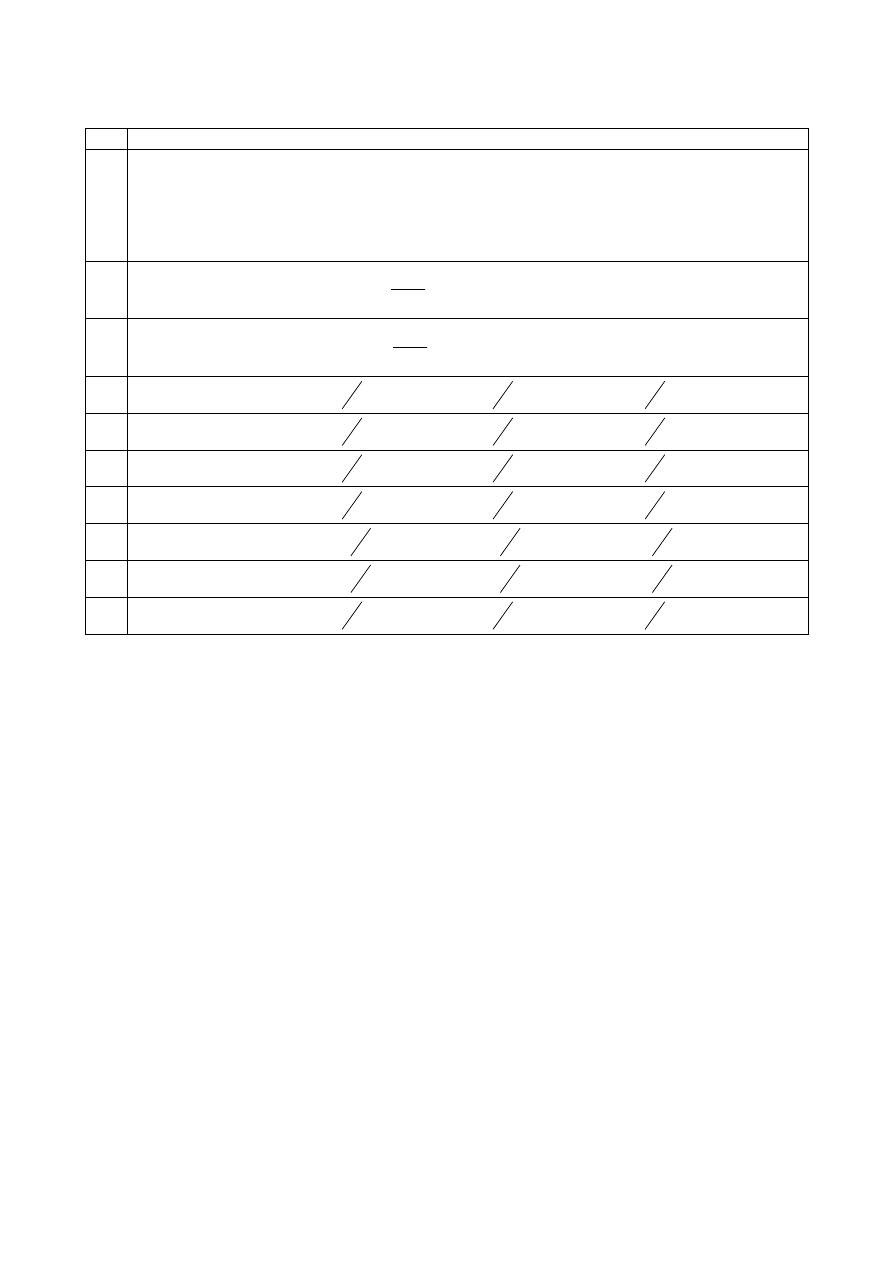
Rys. 2

Schemat sieci dla obliczania zwarć.

Tabl. 3

Dane znamionowe elementów z rys. 2.

Symbol Dane znamionowe elementu

1

2

G1

%

12

X

kV

3

.

6

U

MVA

15

S

d

n

n









G2

%

15

X

kV

5

.

10

U

MVA

150

S

d

n

n









T1

11

YNd

kW

128

P

%

11

U

kV

3

.

6

U

kV

121

U

MVA

25

S

cu

z

nd

ng

n















;

rdzeń trójkolumnowy

T2

kW

550

P

%

14

U

kV

75

.

15

U

kV

121

U

MVA

150

S

cu

z

nd

ng

n















rdzeń trójkolumnowy

T3

kW

128

P

%

11

U

kV

75

.

15

U

kV

121

U

MVA

25

S

cu

z

nd

ng

n















YNd11; rdzeń trójkolumnowy

T4

11

YNynd

kW

700

P

kW

900

P

kW

950

P

%

0

.

9

U

%

5

.

12

U

%

5

.

15

U

kV

15

U

kV

115

U

kV

400

U

M VA

50

/

M VA

250

/

M VA

250

S

w

d

cu

w

g

cu

d

g

cu

w

d

z

w

g

z

d

g

z

nw

nd

ng

n













































rdzeń pięciokolumnowy

T5

5

Dyn

kW

6

.

6

P

%

6

U

kV

4

.

0

U

kV

75

.

15

U

kVA

630

S

cu

z

nd

ng

n















rdzeń trójkolumnowy

- 27 -

cd. tabl.

3.

1

2

At

11

Nd

Y

kW

520

P

kW

540

P

kW

850

P

%

20

U

%

34

U

%

10

U

kV

15

U

kV

115

U

kV

220

U

M VA

50

/

M VA

160

/

M VA

160

S

auto

w

d

cu

w

g

cu

d

g

cu

w

d

z

w

g

z

d

g

z

nw

nd

ng

n













































rdzeń pięciokolumnowy

UE1

 

 

1

.

1

X

X

M VA

12000

S

kV

220

U

1

0

z

n







UE2

 

 

8

.

1

X

X

M VA

22000

S

kV

400

U

1

0

z

n







L1

 

 

 

km

50

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L2

 

 

 

km

50

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L3

 

 

 

km

20

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L4

 

 

 

km

30

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L5

 

 

 

km

30

L

km

07

.

1

X

km

41

.

0

X

km

125

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L6

 

 

 

km

30

L

km

07

.

1

X

km

41

.

0

X

km

125

.

0

R

kV

110

U

k

0

k

1

k

1

n

















L7

 

 

 

km

40

L

km

07

.

1

X

km

42

.

0

X

km

24

.

0

R

kV

110

U

k

0

k

1

k

1

n

















2.

Wykonanie ćwiczenia

1.

Wczytać przygotowane dane wejściowe do programu ZWAK31 opisujące sieć rys. 1 lub 2.

2.

Sprawdzić czy dla stanu przed zwarciem wszystkie napięci w węzłach wynoszą 1,05 jw.

3.

Dla zwarcia trójfazowego w wybranym węźle wykonać obliczenia:



prądów i napięć w miejscu zwarcia,



prądów w wybranych gałęziach,



napięć w wybranych węzłach.

4.

Sprawdzić czy suma prądów zwarciowych płynących w gałęziach jest równa zeru dla
wybranego węzła.

5.

Wykonać obliczenia wielkości zwarciowych koniecznych dla wyznaczenia impedancji
widzianej z jednego końca wybranego elementu.

6.

Określić parametry dławika D1, aby moc zwarciowa przy zwarciu w punkcie K1 była
mniejsza od 100 MVA. Prąd obciążenia przyjąć równy 350 A (200A, 500 A).

7.

Pomiędzy szyny M i N sieci włączyć dławik szynowy D2 o prądzie 1000 A, 10%. Określić
wpływ tego dławika szynowego na wielkości zwarciowe w tym na napięcie w sąsiednim
węźle.

8.

Wykonać poprzedni punkt z wyłączonym jednym z transformatorów T2.

3.

Wykonanie sprawozdania

W sprawozdaniu należy zamieścić:



Obliczenia impedancji elementów sieci z rys. 1 lub 2.

- 28 -



Schemat zastępczy tej sieci z ponumerowanymi węzłami i gałęziami.



Opisane wydruki wszystkich obliczeń.



Wnioski wynikające z zakresu wykonanego ćwiczenia.

- 29 -

ZAŁĄCZNIK

NR

2:

O

BLICZANIE ZWARĆ NIESYMETRYCZNYCH

1.

Sieć do obliczania zwarć

Do obliczeń wykorzystać wielonapięciową sieć elektroenergetyczną, przedstawioną na rys. 1 lub 2.

2.

Wykonanie ćwiczenia

1.

Wczytać przygotowane w domu dane wejściowe do programu ZWAK31 opisujące siec
z rys. 1 lub 2.

2.

Dla wybranego zwarcia niesymetrycznego z udziałem ziemi w wybranym węźle wykonać
obliczenia:



prądów i napięć w miejscu zwarcia,



prądów w wybranych gałęziach,



napięć w wybranych węzłach.

3.

Sprawdzić czy suma prądów zwarciowych płynących w gałęziach jest równa zeru dla
wybranego węzła i zwarcia niesymetrycznego.

4.

Wykonać obliczenia wielkości zwarciowych podczas zwarcia niesymetrycznego koniecznych
dla wyznaczenia impedancji widzianej z jednego końca wybranego elementu.

5.

Znaleźć element, w którym pojawia się prąd wyrównawczy.

6.

Dla zwarcia niesymetrycznego w wybranym węźle wykonać obliczenia obrazujące
transformacje prądów i napięć przez transformator o grupie połączeń Yd w układzie
składowych symetrycznych i współrzędnych fazowych.

3.

Wykonanie sprawozdania

W sprawozdaniu należy zamieścić:



Obliczenia impedancji elementów sieci z rys. 1. dla składowej zgodnej i zerowej.



Schemat zastępczy tej sieci z ponumerowanymi węzłami i gałęziami.



Opisane wydruki wszystkich obliczeń.



W oparciu o wydruki obliczeń z punktu 2 programu, narysować rozpływ prądów we fragmencie
sieci w układzie współrzędnych fazowych i składowych symetrycznych



W oparciu o wyniki obliczeń z punktu 2 programu ćwiczenia, narysować wykres wskazowy
napięć w miejscu zwarcia i w wybranym węźle, położonym bez pośrednictwa transformatora
w stosunku do miejsca zwarcia.



Punkt 5 powtórzyć, lecz dla zwarcia dwufazowego.



Omówić transformację prądu przez transformator Yd przy zwarciu dwufazowym w układzie
składowych symetrycznych i fazowych w oparciu o wyniki obliczeń.



W oparciu o wyniki obliczeń z punktu 2 określić prąd płynący w uzwojeniu wyrównawczym
autotransformatora oraz w uzwojeniu połączonym w trójkąt transformatora T3.

- 30 -

ZAŁĄCZNIK

NR

3:

A

NALIZA WARUNKÓW SKUTECZNOŚCI UZIEMIENIA SIECI

1.

Sieć dla przeprowadzenia analizy

Analiza warunków skuteczności uziemienia będzie przeprowadzona w sieci przedstawionej na
rys. 1 lub 2.

2.

Wykonanie ćwiczenia

1.

Wczytać przygotowane w domu dane wejściowe do programu ZWAK31 opisujące sieć
z rys. 1 lub 2.

2.

Dla zwarcia jednofazowego, kolejno we wszystkich węzłach sieci o skutecznie uziemionym
punkcie zerowym (sieci 110, 220 i 400 kV) sprawdzić czy napięcia faz zdrowych są mniejsze
od dopuszczalnego we wszystkich węzłach sieci o skutecznie uziemionym punkcie zerowym.

3.

Punkt 2 powtórzyć w przypadku, gdy wprowadzimy prace z izolowanym punktem zerowym
następujących transformatorów:



jednego T1,



dwóch T1,



wszystkich T1,



wszystkich T1 i T3,



jednego T2,



wszystkich T2,



jednego T1 i jednego T2,



wszystkich T1, T2 oraz T3,



wszystkich T1, T2, T3 i T4 po obu stronach,



po uziemieniu punktu gwiazdowego autotransformatora przez dławik o reaktancji 1



.

3.

Wykonanie sprawozdania

W sprawozdaniu należy zamieścić:



Opisane wydruki wszystkich obliczeń.



Zebrane w tablicy napięcia faz zdrowych we wszystkich węzłach sieci o skutecznie uziemionym
punkcie zerowym przy zwarciach w tych węzłach dla poszczególnych wariantów wg punktu 2
i 3 wykonywania ćwiczenia. W oparciu o te wyniki należy stwierdzić czy dla danego wariantu
siec jest w dalszym ciągu siecią o skutecznie uziemionym punkcie zerowym.



W oparciu o wyniki obliczeń podać napięcia panujące na punktach gwiazdowych względem
ziemi, odziemionych transformatorów.

- 31 -

ZAŁĄCZNIK

NR

4:

O

BLICZANIE ZWARĆ NIESYMETRYCZNYCH W UKŁADACH Z

LINIAMI MAGNETYCZNIE SPRZĘŻONYMI

1.

Sieć do obliczania zwarć

Dana jest sieć elektroenergetyczna zawierająca linie magnetycznie sprzężone a przedstawiona

na rys. 3.

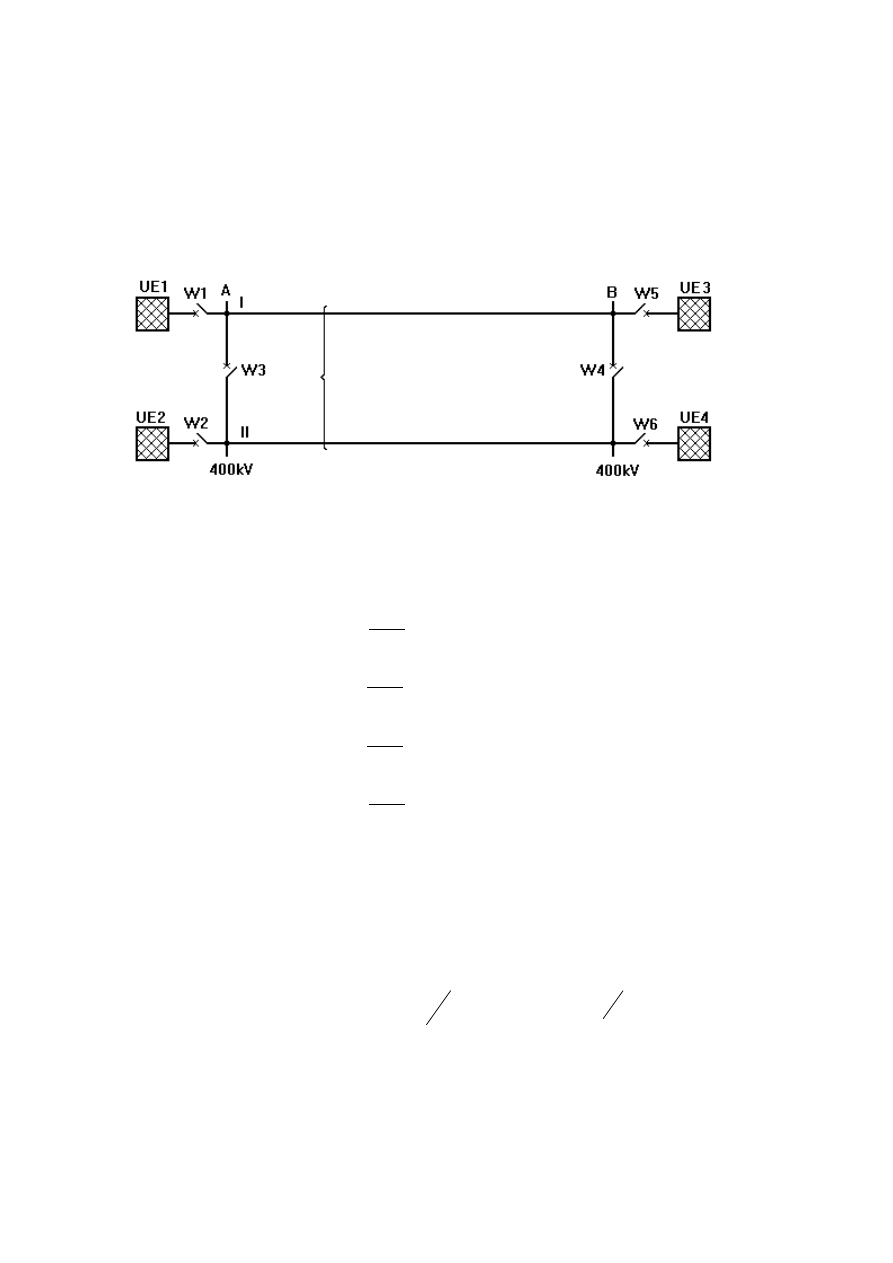
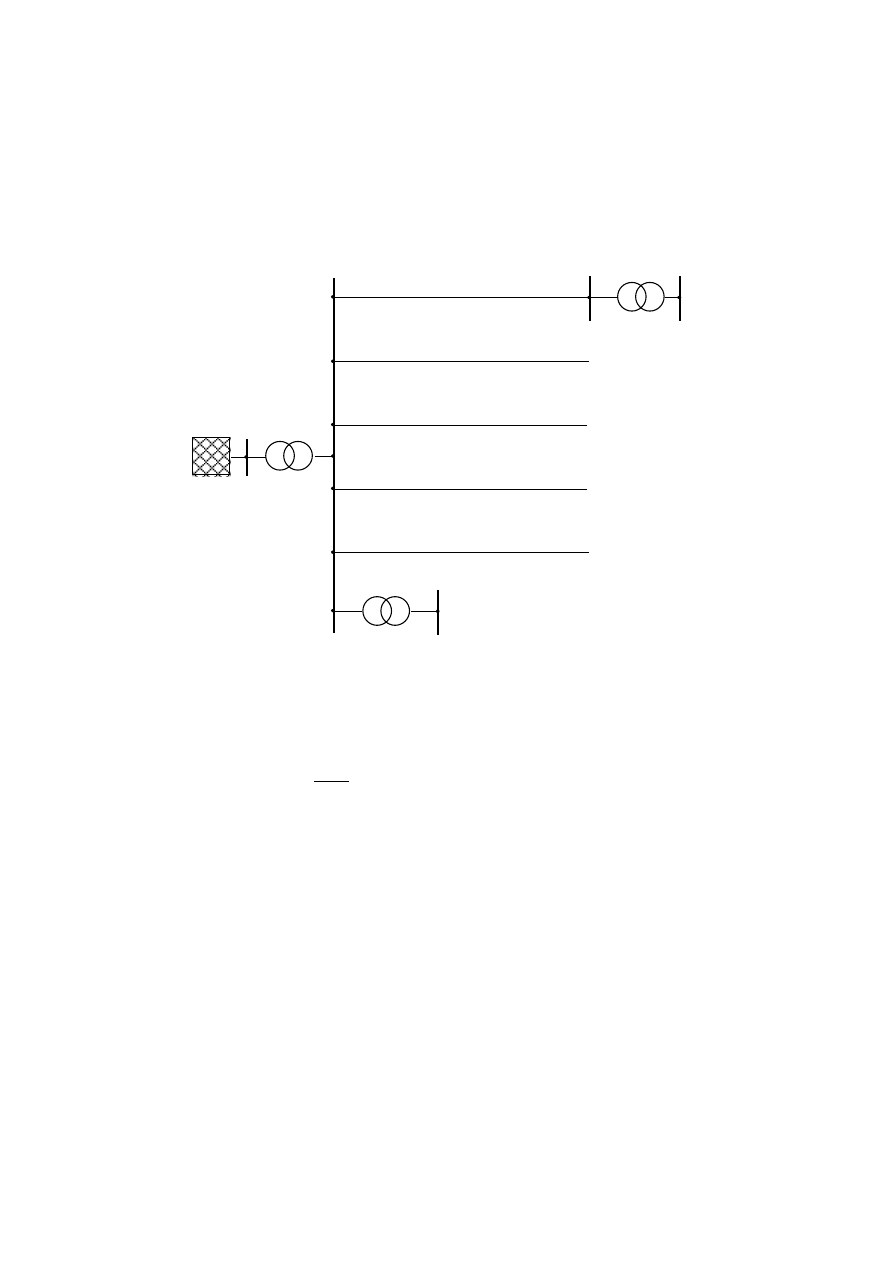
Rys. 3. Schemat sieci z linią magnetycznie sprzężoną.

Dane znamionowe elementów sieci z rys. 3. są następujące:

UE1:

 

 

8

.

1

X

X

M VA

25000

S

kV

400

U

1

0

z

n







UE2:

 

 

2

.

1

X

X

M VA

15000

S

kV

400

U

1

0

z

n







UE3:

 

 

85

.

0

X

X

M VA

12000

S

kV

400

U

1

0

z

n







UE4:

 

 

5

.

1

X

X

M VA

20000

S

kV

400

U

1

0

z

n







Linia 400 kV:



U

kV

n



400

;



dwutorowa,



przewody fazowe wiązkowe z dwoma przewodami w wiązce AFL 8/525 r=15,75 mm;



odstęp przewodów w wiązce 400 mm;



przewody odgromowe dwa AFL 1,7/70, r=7 mm;



odstępy przewodów fazowych i odgromowych od siebie pokazano na rys. 3;



do obliczeń przyjąć: D

m

m

mm

R

km

z

zk







1000

34

0 05

2

,

,

.







,



linia jest przepleciona



posiada długość 100 km.

- 32 -

Rys. 4. Rozmieszczenie przewodów fazowych i odgromowych na słupie (odległości w mm).

W ramach przygotowań do ćwiczenia w domu należy policzyć impedancje schematu zastępczego
linii dla następujących przypadków:



oba tory pracują na te same szyny;



oba tory są połączone na szynach A a rozdzielone na B,



oba tory nie są połączone z sobą,



tor II jest wyłączony,



tor II jest wyłączony i uziemiony dwustronnie (tor II potraktować, jako dodatkowe 3 przewody
odgromowe).

2.

Wykonanie ćwiczenia

W ramach ćwiczenia będą wykonywane obliczenia tylko dla zwarcia jednofazowego. Należy

policzyć prądy we wszystkich gałęziach sieci i napięcie we wszystkich węzłach.



Wczytać przygotowane w domu dane wejściowe do programu ZWAK31 opisujące sieć z rys. 3.



Wykonać obliczenia przy otwartych wyłącznikach W2, W5 i W6 dla zwarcia na szynach B.



Wykonać obliczenia przy otwartych wyłącznikach W2 i W6 dla zwarcia na szynach B.



Wykonać obliczenia przy otwartych wyłącznikach W2 i W6 oraz wyłączonym torze II linii dla
zwarcia na szynach B.



Wykonać obliczenia przy otwartych wyłącznikach W2 i W6 oraz wyłączonym torze II linii
i uziemionym na obu jego końcach dla zwarcia na szynach B.



Wykonać obliczenia przy otwartych wyłącznikach W2, W4, W5 i W6 dla zwarcia na dolnej
części szyn B.



Wykonać obliczenia przy otwartych wyłącznikach W2, W4, i W6 dla zwarcia na dolnej części
szyn B



Wykonać obliczenia przy otwartych wyłącznikach W3, W4, W5 i W6 dla zwarcia na dolnej
części szyn B.



Wykonać obliczenia przy otwartych wyłącznikach W3, W4 i W5 dla zwarcia na dolnej części
szyn B.



Wykonać obliczenia przy otwartych wyłącznikach W3 i W4 dla zwarcia na dolnej części szyn
B.



Wykonać obliczenia przy otwartych wyłącznikach W2 i W6 dla zwarcia w połowie toru II linii.



Wykonać obliczenia przy otwartych wyłącznikach W2 i W4 dla zwarcia w połowie toru II linii.

- 33 -

3.

Wykonanie sprawozdania

W sprawozdaniu należy zamieścić:
1.

Obliczenia impedancji elementów sieci z rys 3 dla składowej zgodnej i zerowej dla
wszystkich pięciu wariantów pracy linii.

2.

Schematy zastępcze tej sieci z ponumerowanymi węzłami i gałęziami dla wykonywanych
w czasie ćwiczenia wariantów pracy tej sieci.

3.

Opisane wydruki wszystkich obliczeń.

4.

W oparciu o wyniki obliczeń dla wykonywanych w czasie ćwiczenia wariantów pracy tej
sieci należy:



przedstawić i porównać prądy fazowe w poszczególnych torach linii,



podać napięcia na szynach A i B oraz wyjaśnić przyczyny zmian tych napięć,



obliczyć prądy płynące w przewodach odgromowych i w ziemi.

- 34 -

ZAŁĄCZNIK

NR

5:

O

BLICZANIE ZWARĆ DOZIEMNYCH W SIECI Z NIESKUTECZNIE

UZIEMIONYM PUNKTEM NEUTRALNYM

1.

Sieć do obliczania zwarć

Dana jest sieć elektroenergetyczna z nieskutecznie uziemionym punktem neutralnym,

przedstawiona na rys. 5.

L1

L5

L2

L3

L4

D

D1

D2

D3

TO

TU

0,4 kV

15 kV

0,4 kV

TZ

UE

110 kV

Rys. 5. Schemat sieci z nieskutecznie uziemionym punktem neutralnym.

Układ zasilający UE:

 

 

1

.

1

X

X

M VA

2500

S

kV

110

U

1

0

z

n







Transformator zasilający TZ:

11

YNd

kW

128

P

%

11

U

kV

75

.

15

U

kV

121

U

MVA

25

S

cu

z

nd

ng

n















rdzeń trójkolumnowy

Transformator uziemiający TU:

5

ZNyn

kW

32

.

1

P

%

5

.

5

U

kV

4

.

0

U

kV

75

.

15

U

kVA

160

S

cu

z

nd

ng

n















rdzeń trójkolumnowy

Transformator odbiorczy TO:

S

kVA U

kV U

kV

U

P

kW Dyn

n

ng

nd

z

cu











630

15 75

0 4

6

6 6

5

.

.

%

.





rdzeń trójkolumnowy

L1: U

kV kabel typuYHKXs s

mm

L

km

n







15

95

5

2

L2:

U

kV linia napowietrzna s

mm

L

km

n







15

120

10

2

L3:

U

kV kabel typuYHAKXs s

mm

L

km

n







15

95

8

2

L4: U

kV kabel typuYHAKXs s

mm

L

km

n







15

95

2

2

L5:

U

kV linia napowietrzna s

mm

L

km

n







15

120

20

2

- 35 -

Uwaga:



Linie kablowe i napowietrzne należy modelować za pomocą opcji "Podawanie typu i długości
dla linii 15 i 6 kV".



Pozostałe elementy modelujemy za pomocą opcji "Podawanie impedancji".



Linie kablowe modelować za pomocą odcinków po jednym kilometrze.



Linie napowietrzne modelować za pomocą odcinków po pięć kilometrów.



Na początku każdego odcinka program wprowadza dodatkowy odcinek o bardzo małej
impedancji w celu wykonywania pomiarów prądów w linii.

2.

Wykonanie ćwiczenia

1.

Wczytać dane wejściowe do programu ZWAK31 opisujące sieć z rys. 5.

2.

Dla tej sieci wydrukować dane o prądach i napięciach panujących w sieci przed zwarciem.

3.

Dla zwarcia doziemnego w sieci z izolowanym punktem neutralnym, w wybranym węźle
wykonać obliczenia umożliwiające zaprezentowanie rozpływu prądu w całej sieci w układzie
współrzędnych fazowych i składowych symetrycznych. Dokonać też obliczeń napięć
w wybranych węzłach.

4.

Obliczenia z punktu 2 i 3 powtórzyć po włączeniu na końcu jednej z linii oraz transformatora
TO symetrycznego obciążenia zamodelowanego poprzez impedancję.

5.

Obliczenia z punktu 3 powtórzyć po włączeniu cewki Petersena nastrojonej na k

K



1 1

.

6.

Obliczenia z punktu 5 powtórzyć po włączeniu równolegle do cewki Petersena rezystora
wymuszającego dodatkowy prąd czynny o wartości 40A.

7.

Obliczenia z punktu 3 powtórzyć po włączeniu rezystora uziemiającego o rezystancji 17



.

3.

Wykonanie sprawozdania

W sprawozdaniu należy zamieścić:
1.

Obliczenia impedancji elementów sieci z rys. 5. dla składowej zgodnej i zerowej.

2.

Schemat zastępczy tej sieci z ponumerowanymi węzłami i gałęziami.

3.

Opisane wydruki wszystkich obliczeń.

4.

W oparciu o wydruki obliczeń z punktu 2 programu, narysować rozpływ prądów i napięcia
w całej sieci w układzie współrzędnych fazowych panujących w sieci przed zwarciem.

5.

W oparciu o wydruki obliczeń z punktu 3 programu, narysować rozpływ prądów w całej sieci
w układzie współrzędnych fazowych i składowych symetrycznych.

6.

W oparciu o wydruki obliczeń z punktu 4 programu, narysować rozpływ prądów w całej sieci
w stanie przed i podczas zwarcia..

7.

W oparciu o wyniki obliczeń z punktu 3 programu ćwiczenia, narysować wykres wskazowy
napięć w miejscu zwarcia i w wybranym węźle.

8.

Punkt 5 sprawozdania powtórzyć, lecz dla punktów 5, 6 i 7.

9.

Omówić transformację prądu i napięcia przez transformator YNd (Dyn) przy zwarciu
doziemnym w układzie składowych symetrycznych i fazowych w oparciu o wyniki obliczeń.