Energia i moc sygnałów

Energia i moc sygnałów

Wartość skuteczna i współczynnik kształtu

Wartość skuteczna i współczynnik kształtu

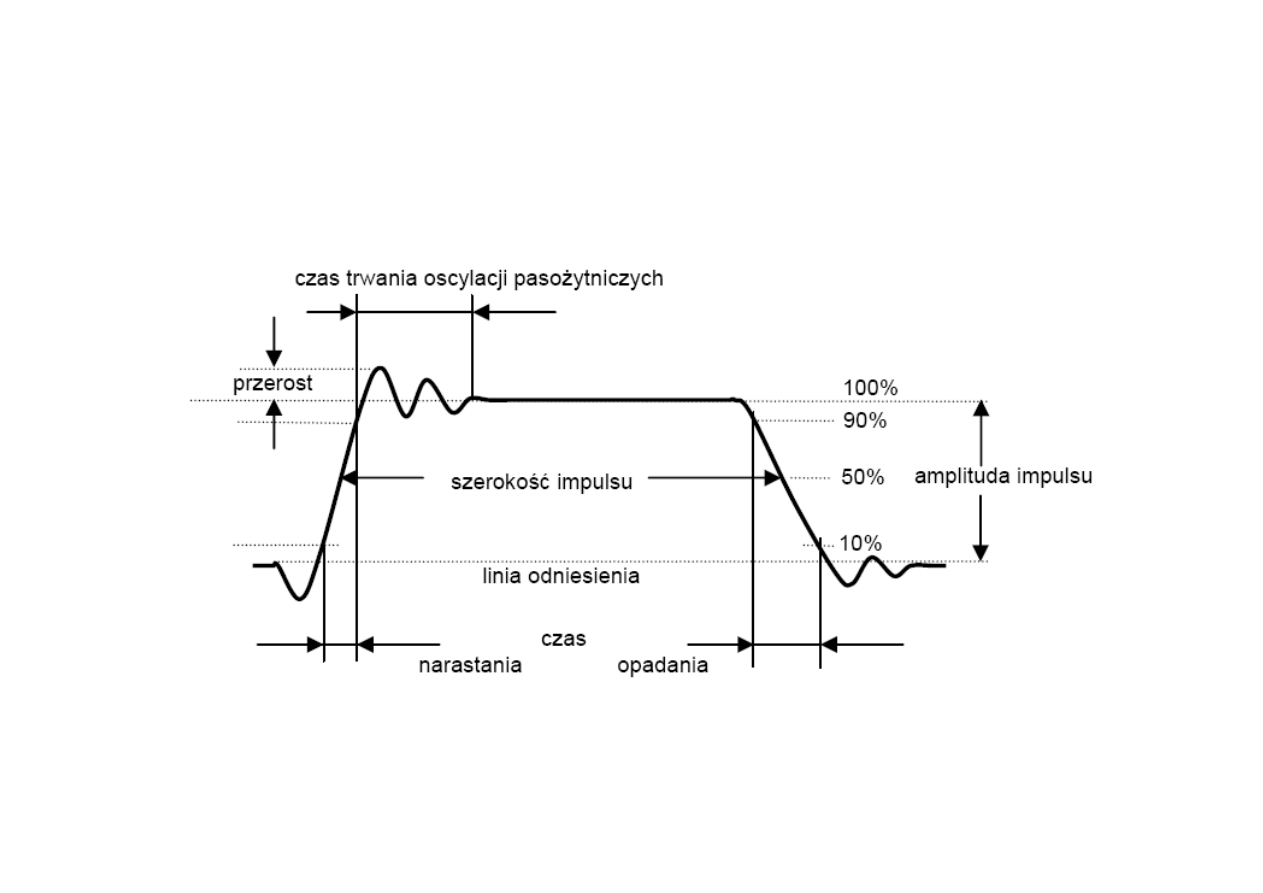
Parametry sygnału impulsowego

Definicje

Definicje cd.

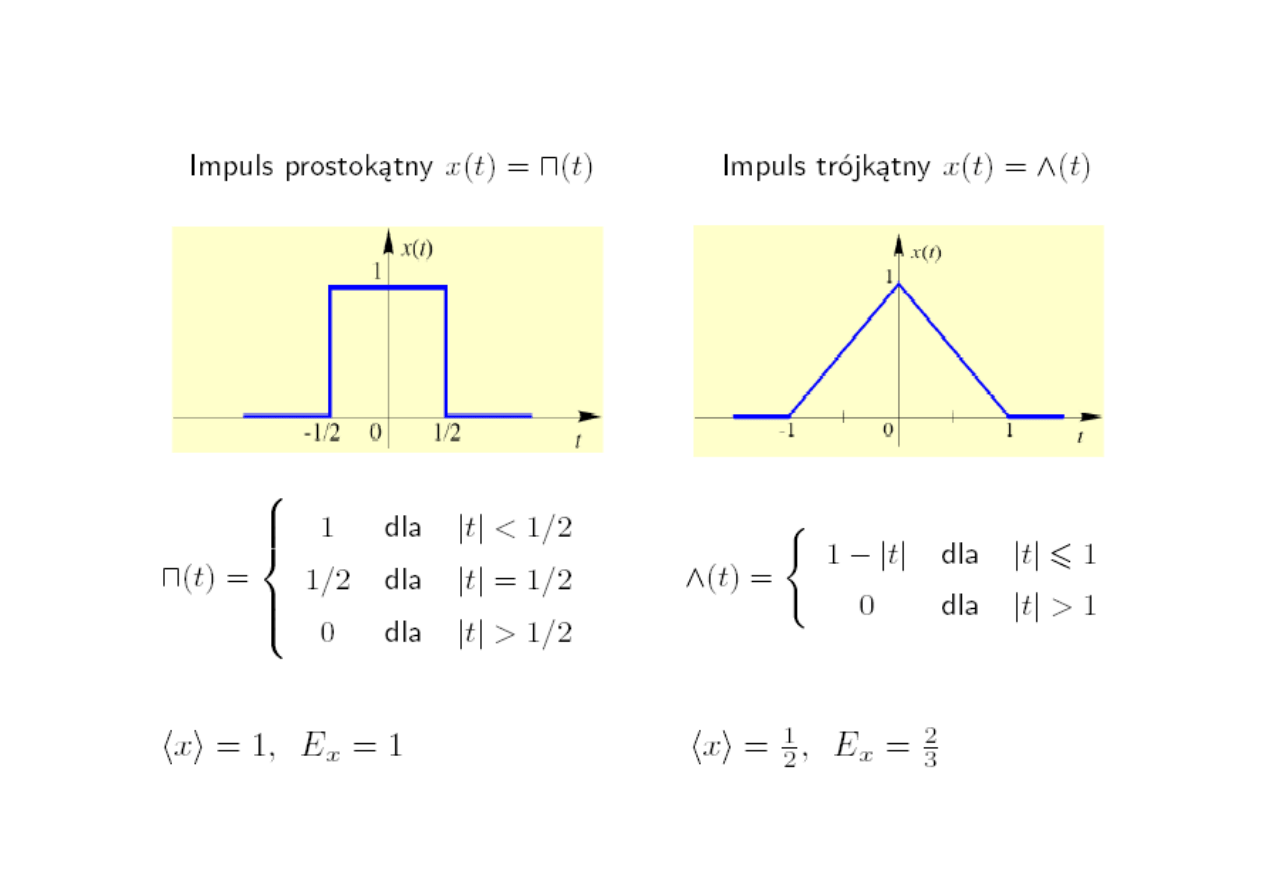
Przykłady sygnałów o skończonej energii

Obliczenie energii impulsu trójkątnego

E =  

∫

x

2

(t)dt = 2 

∫

(1 - t)

2 

dt = 2

∫

(1 - 2t – t

2 

)dt  =

_

0

0

1

1

=

2 

(t – t

2

+ t

3

/3



= 2/3

1

0

Umieć obliczyć dla dowolnej amplitudy A , dowolnego położenia na 

Umieć obliczyć dla dowolnej amplitudy A , dowolnego położenia na 
osi czasu i czasu trwania 2

osi czasu i czasu trwania 2

ττ

⇒

⇒

2/3 A

2/3 A

2

2

ττ

Sygnały o skończonej (ograniczonej) energii, 
a tym samym o zerowej mocy średniej,
nazywamy 

sygnałami energii

.

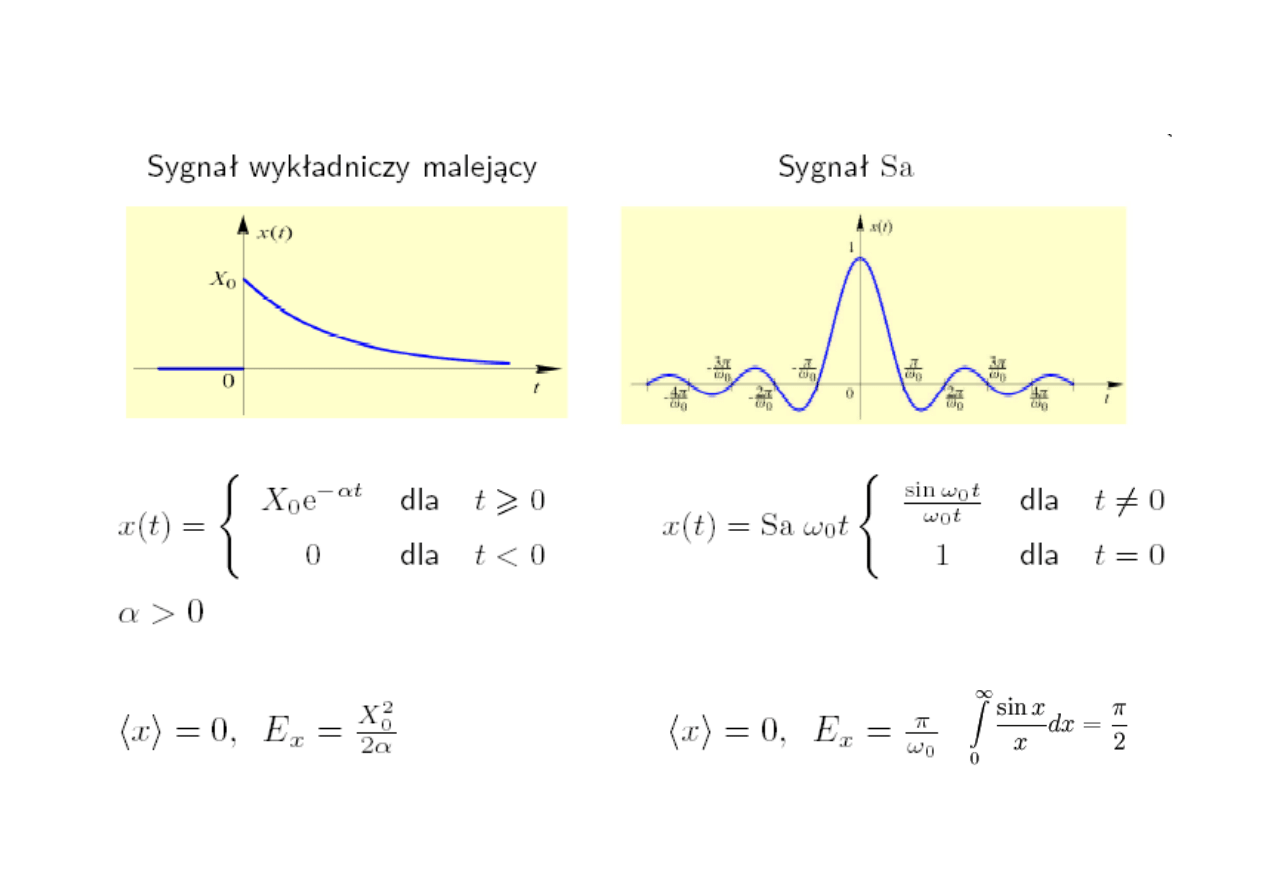
Przykłady sygnałów o skończonej energii cd.

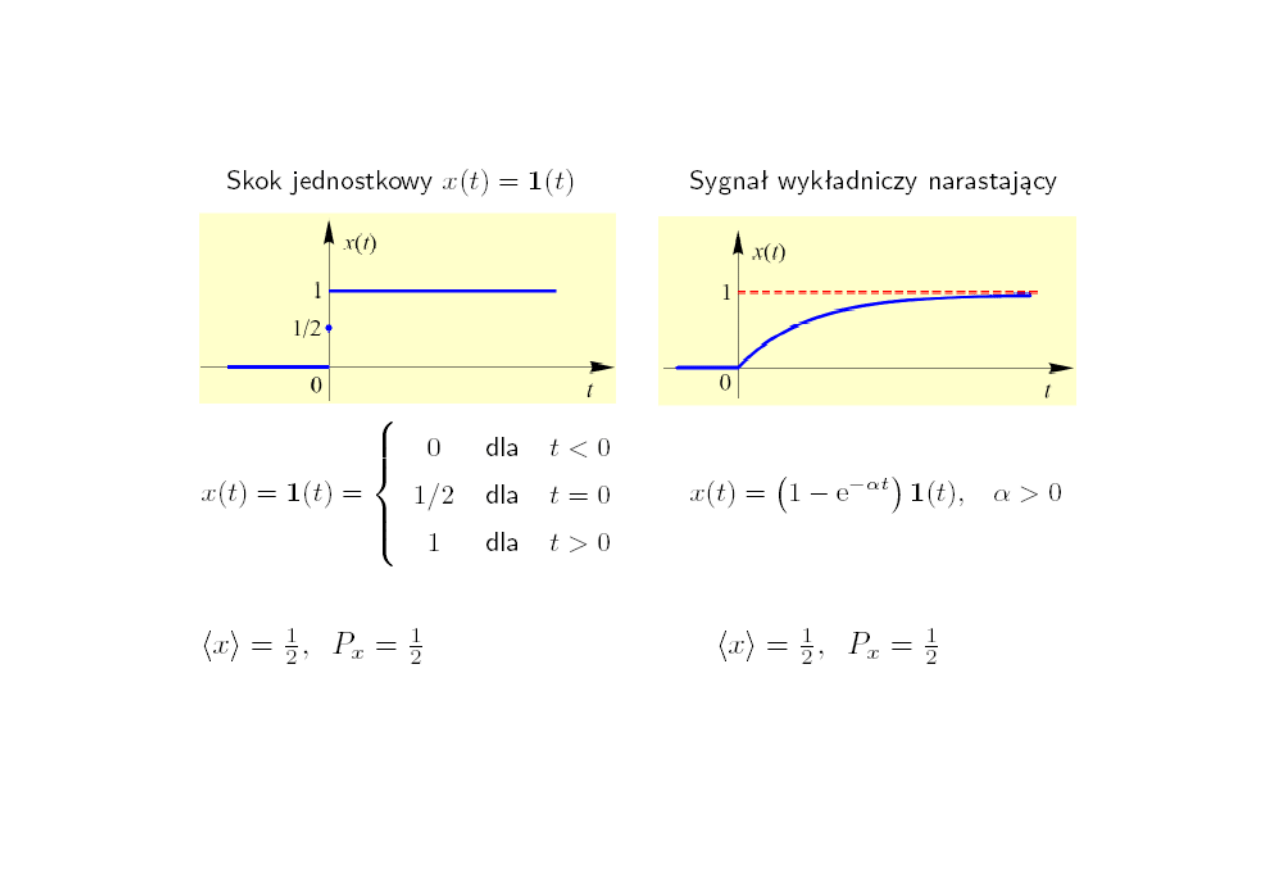
Przykłady sygnałów o skończonej mocy

Sygnały o nieskończonej energii, ale niezerowej 
lecz ograniczonej mocy średniej,
nazywamy 

sygnałami mocy

.

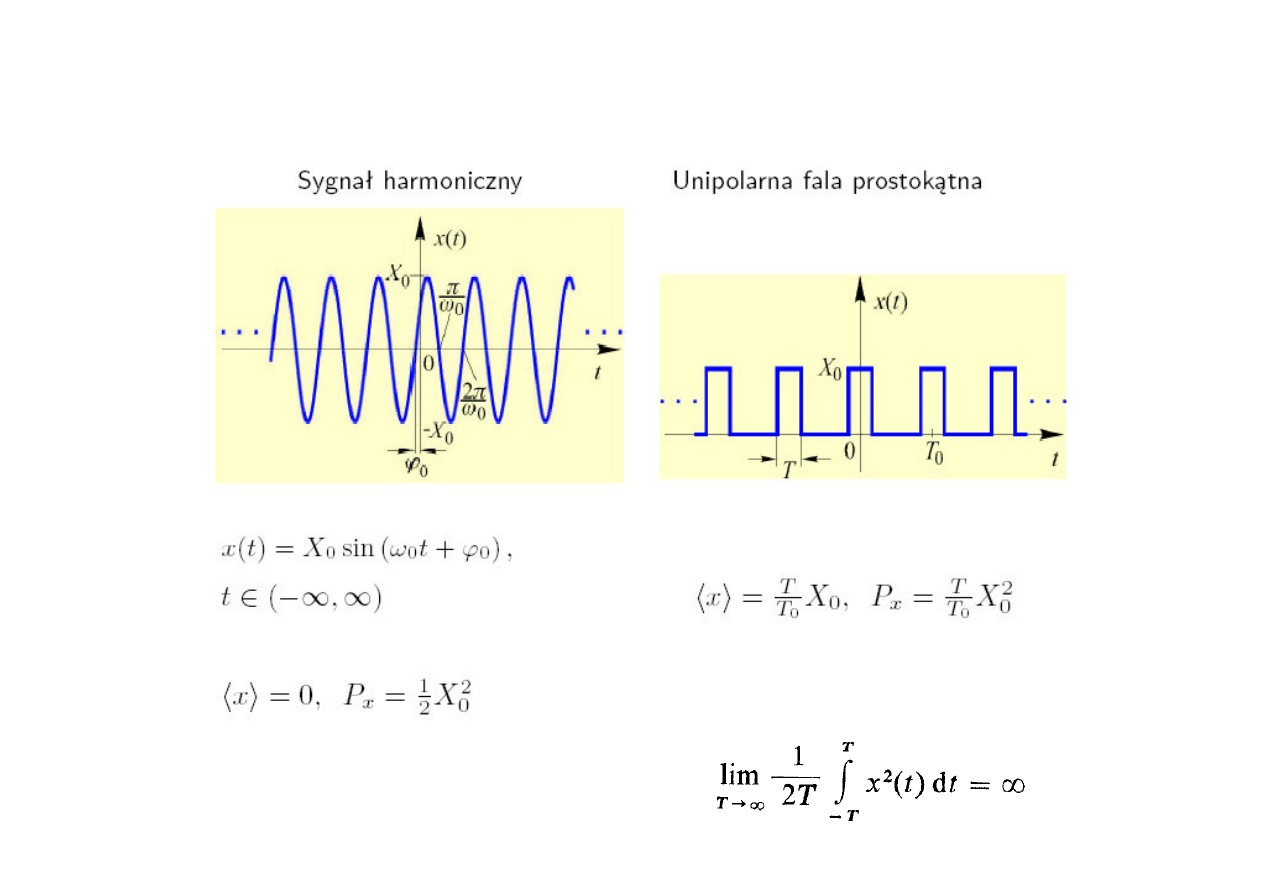
Przykłady sygnałów o skończonej mocy cd.

Sygnał

δ

(t) jest sygnałem

o nieograniczonej mocy, gdyż

Wartości skuteczna

Dla sygnału harmonicznego o amplitudzie X

m 

wartość 

X

sk  

= X

m 

/ 

2

(dla U

sk

= 230 V amplituda U

m

= 324 V )

RMS – ang. Root Mean Square Value

Współczynnik kształtu 

(definiowany dla okresowego sygnału przemiennego)

Wspólczynnik kształtu (

ang. form factor, FF

) 

definiowany jest jako 

stosunek wartości skutecznej do półokresowej wartości średniej przebiegu 
okresowego (lub średniej sygnału „wyprostowanego” czyli z

x).

Dla sygnału harmonicznego

X

ś

rp

= 2X

max

/ 

π ≅

0,64 X

max

k

k  

= X

sk

/ X

ś

rp

= 

π

/ 2  2 ≅ 1,111 

Dla fali trójkątnej

X

sk

= X

m

/ 

3

, X

ś

rp 

= 0,5 X

m 

, k

k 

≅ 1,15 

(Dla okresowej fali impulsowej o współczynniku wypełnienia 

γγγγ

= 

ττττ

/ T

k

k 

jest proporcjonalny do pierwiastka z 

1/ 

γγγγ

.)

Dopuszczalne zmiany
w sieci energetycznej
to +/- 1%.

(też ang.waveform factor)

Parametry sygnałów okresowych (przemiennych)

(antysymetrycznych wzglądem punktu t=T/2, czyli                      )

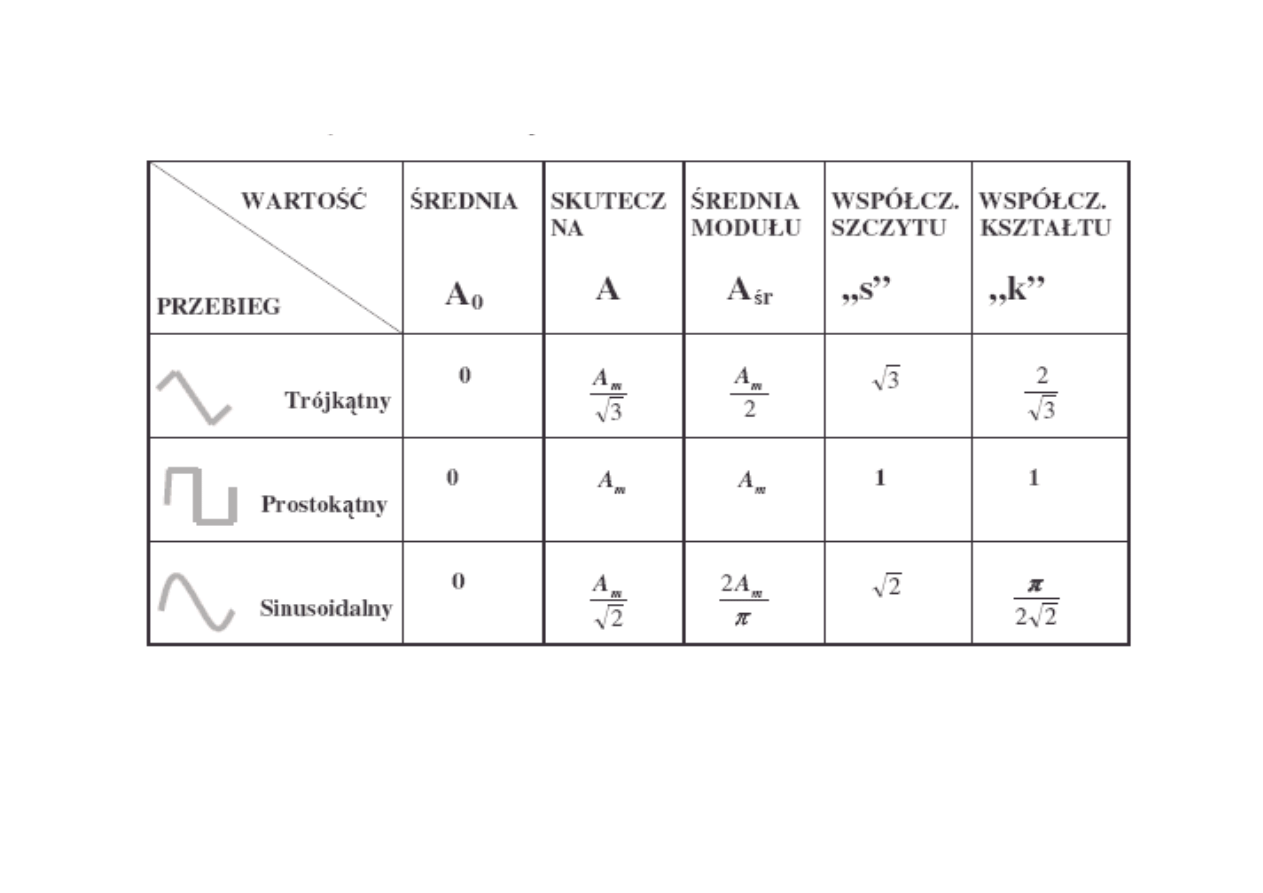
Tabela

A

m 

–

amplituda sygnału okresowego, przemiennego

=1,11

=1,15

Współczynnik kształtu dla figur geometrycznych

(jak kwadrat)