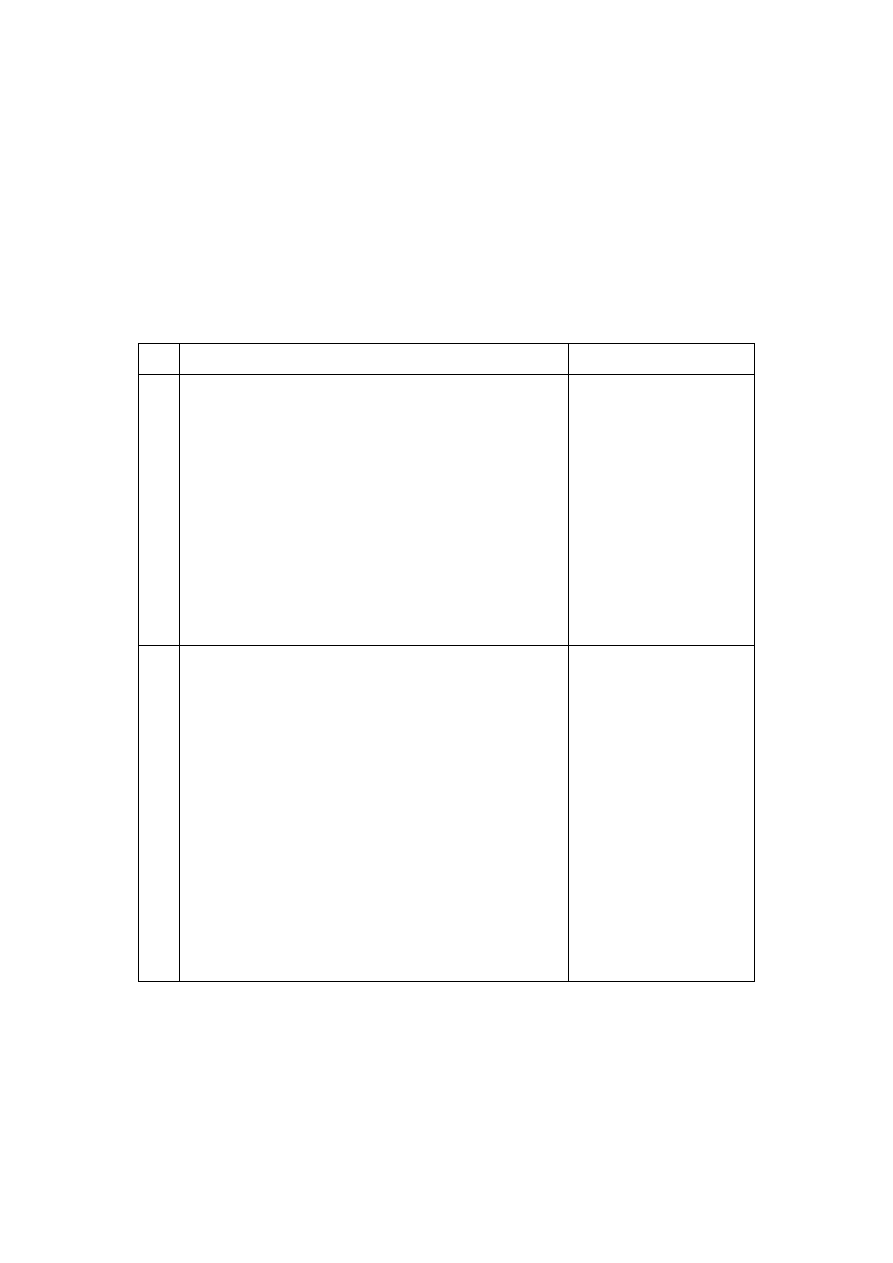
1
Data wykonania ćwiczenia: 12.12.2014r.
Prowadzący: dr inż. Tomasz Kapłon
LOGIKA UKŁADÓW CYFROWYCH
Temat: Automaty asynchroniczne
I.
Cel ćwiczenia
Nabycie praktycznej umiejętności projektowania automatów asynchronicznych
statycznych z uwzględnieniem metod eliminacji wyścigów oraz realizacji technicznej tych
układów.
II.
Program ćwiczenia
L.p.
Zadanie
Wykonanie
1.
Zrealizować statyczny automat asynchroniczny A
1
Wejścia: x
1
, x
2
Wyjścia: y
1
, y
2
Stan początkowy q
0
: x
1
= x
2
= 0, y
1
= y
2
= 0
Podanie x
1
= 1 na stan q
0
ustawia wyjścia y
1
= 0,
y
2
=1
Podanie x
1
= 1 na stan różny od q
0
ustawia
wyjścia y
1
= 1, y
2
= 0
Każdorazowe x
2
= 1 skutkuje y
1
= y
2
= 0
Zakładamy, że nie jest możliwe x
1
= x
2
= 1
automat wykonać za pomocą sprzężeń
zwrotnych oraz z przerzutnikami RS
Zaprojektowano, montaż
nie powiódł się
2.
Zaprojektować statyczny automat asynchroniczny A
2
–
licznik modulo 7
Wejścia: x
1
, x
2
Wyjścia: y
0
, y
1
, y
2
Stan początkowy q
0
: x
1
= x
2
= 0, y
0
= y
1
= y
2
= 0
Podanie x
1
= 1 na stan q
0
ustawia wyjścia y
0
= 1,
y
1
= y
2
=0 – stan q
1
Podanie x
1
= 1 na stan q
1
ustawia wyjścia y
0
= 0,
y
1
= 1, y
2
=0
i tak dalej, podawanie kolejnych „1” na x
1
skutkuje zliczaniem do 6 (gdzie y
0
to
najmłodszy bit)
niedopuszczalna sytuacja y
0
=
y
1
= y
2
=1
nie określamy wejść x
1
= x
2
= 1
każdorazowe x
2
= 1 oznacza y
0
=
y
1
= y
2
=0
Zaprojektowano
Tabela 1
III.
Wstęp teoretyczny
Automat asynchroniczny to automat, którego praca nie jest uzależniona od taktowania
zegara. Moment zmian stanu nie jest ograniczony do dyskretnych chwil czasowych, ale odbywa
się w sposób ciągły bezpośrednio po wprowadzeniu sygnałów wejściowych.
2
Wyróżniamy dwa typy automatów asynchronicznych – statyczne i dynamiczne. Statyczne są
sterowane zmianą poziomu sygnału, a dynamiczne – zboczem.
Asynchroniczne automaty są prostsze i tańsze w budowie niż synchroniczne, występują w
nich jednak niekorzystne zjawiska wyścigów i hazardu. Zjawisko wyścigów w automatach
asynchronicznych wynika z braku synchronizacji momentu zmiany stanu dla poszczególnych
sygnałów kodujących stan. Bity zmieniają się w sposób nieskoordynowany co prowadzi czasami
do losowości następnego stanu.
IV.
Realizacja ćwiczenia
1. Automat A
1
Możliwe kombinacje sygnałów wejściowych i wyjściowych oraz przypisane im stany:
x
1
x
2
y
1
y
2
q
i
0 0
0
0 q
0
1
0
0
1 q
1
0
0
0
1 q
2
1
0
1
0 q
3
0
0
1
0 q
4
0
1
0
0 q
5
Tabela 2
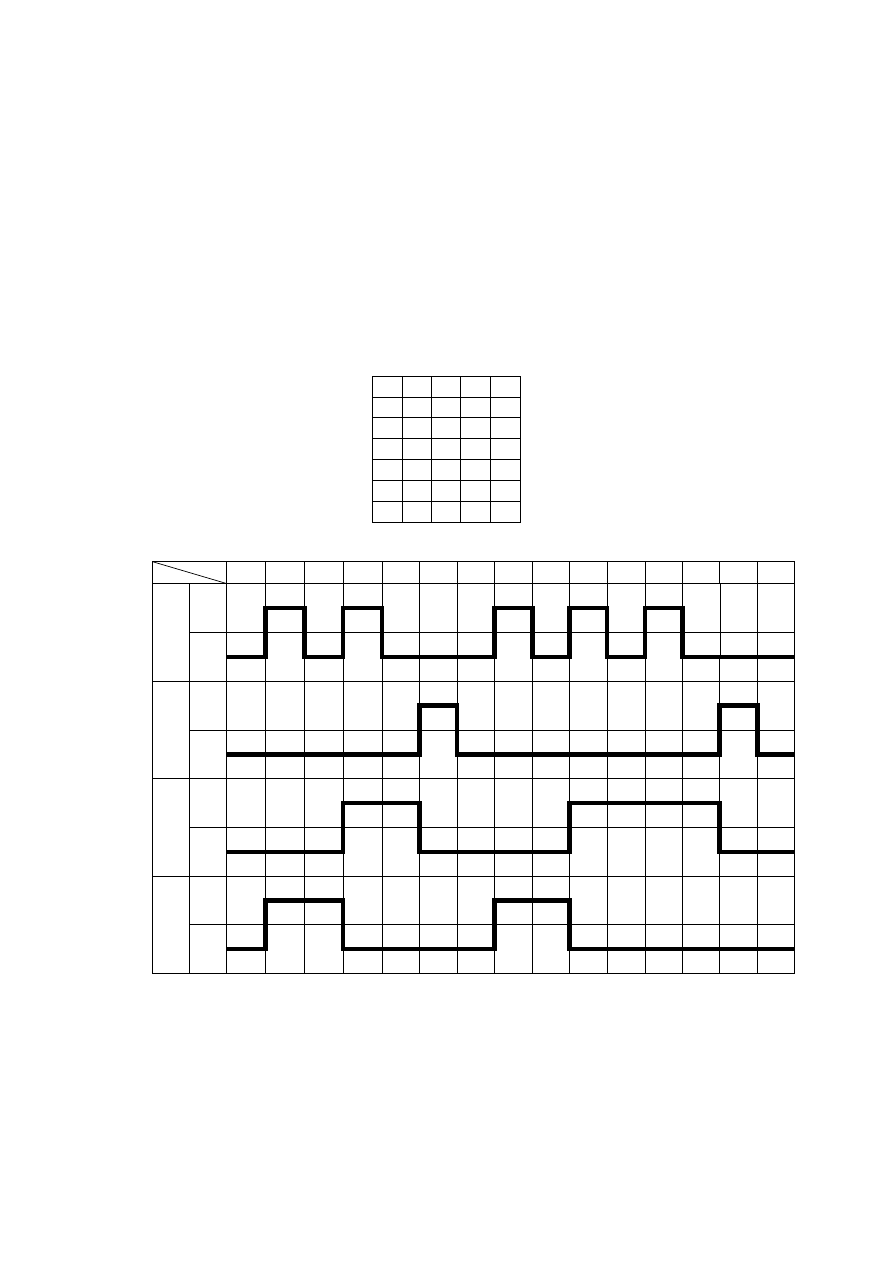
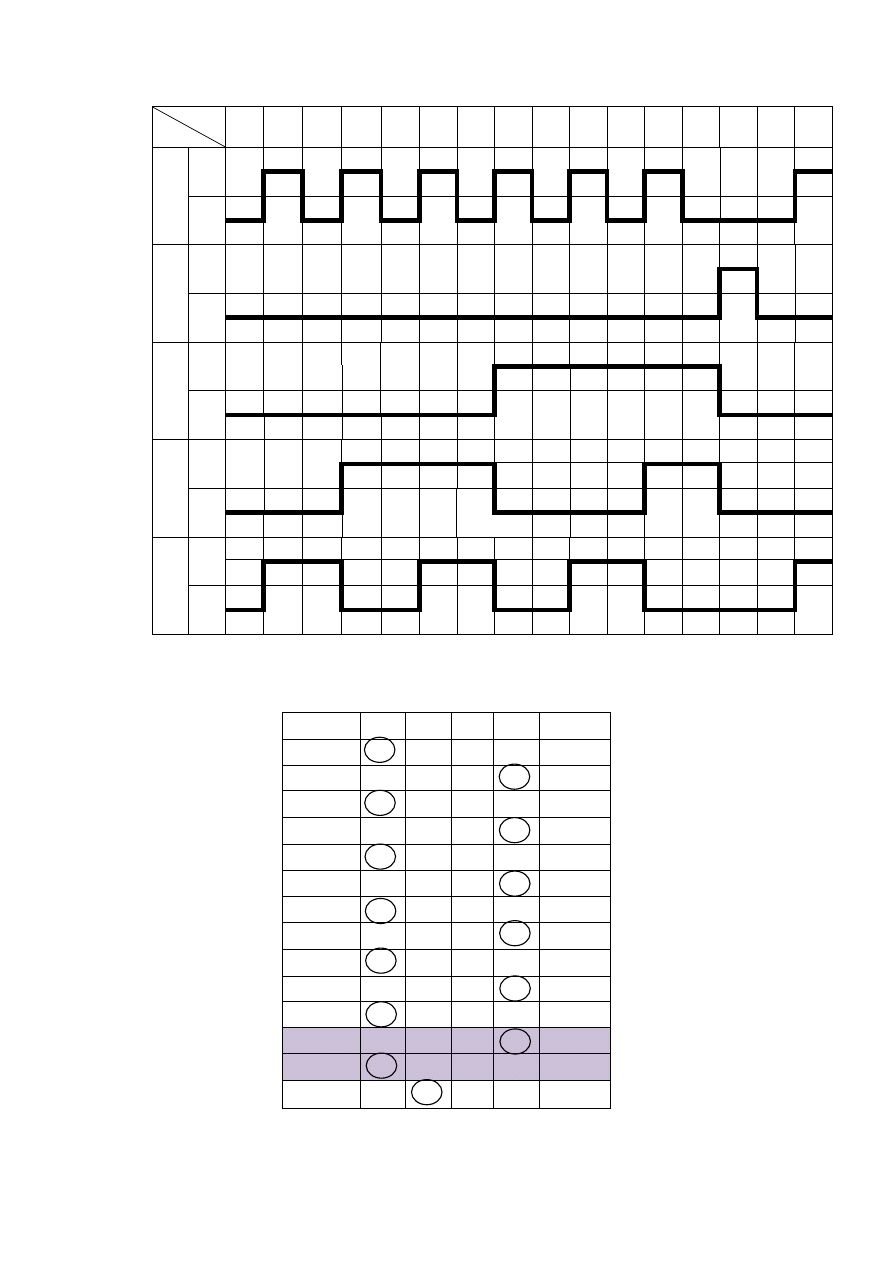
a) Wykres czasowy
q
0
q
1
q
2
q
3
q
4
q
5
q
0
q
1
q
2
q
3
q
4
q
3
q
4
q
5
q
0
x
1
1
0
x
2
1
0
y
1
1
0
y
2
1
0
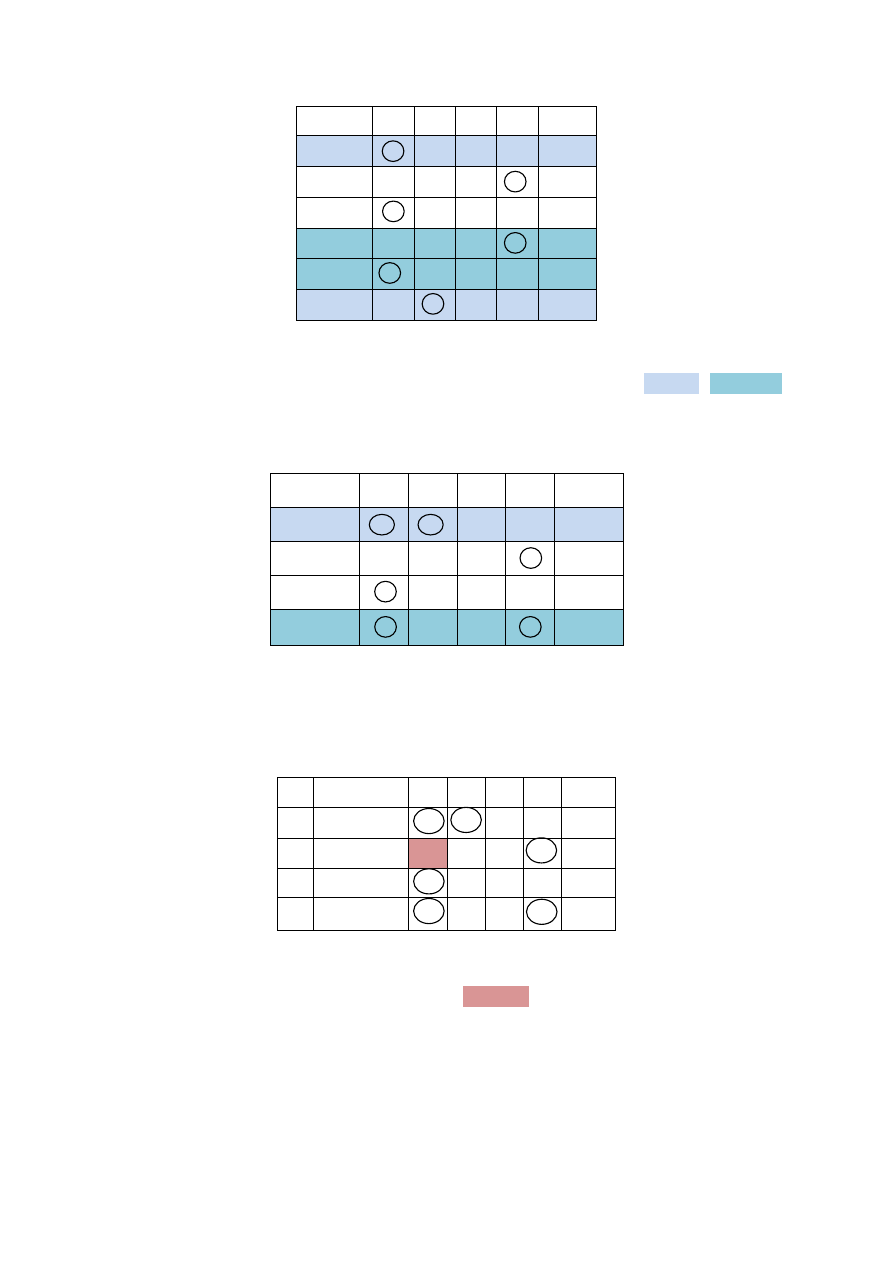
b) Tabela przejść/wyjść
Kolumna dla kombinacji x
1
= x
2
= 1 jest oznaczona kreskami, ponieważ nie taka kombinacja
nie jest określona dla tego automatu. Nie jest określone również przejście z q
1
za pomocą
sygnałów x
1
= 0 x
2
= 1, ponieważ do stanu q
1
przechodzimy kombinacją x
1
= 1 x
2
= 0 – w takiej
sytuacji nie możemy od razu podać x
1
= 0 x
2
= 1. Podobne zjawisko zachodzi dla pól q
3
01 oraz
q
5
10. Kółkiem oznaczono stany stabilne - czyli trwające cały czas, gdy sygnał wejściowy się nie
zmienia.
3
q
i
/x
1
x
2
00
01
11
10
y
1
y
2
q
0
q
0
q
5
-
q
1
00
q
1
q
2
-
-
q
1
01
q
2
q
2
q
5
-
q
3
01
q
3
q
4
-
-
q
3
10
q
4
q
4
q
5
-
q
3
10
q
5
q
0
q
5
-
-
00
Tabela 3
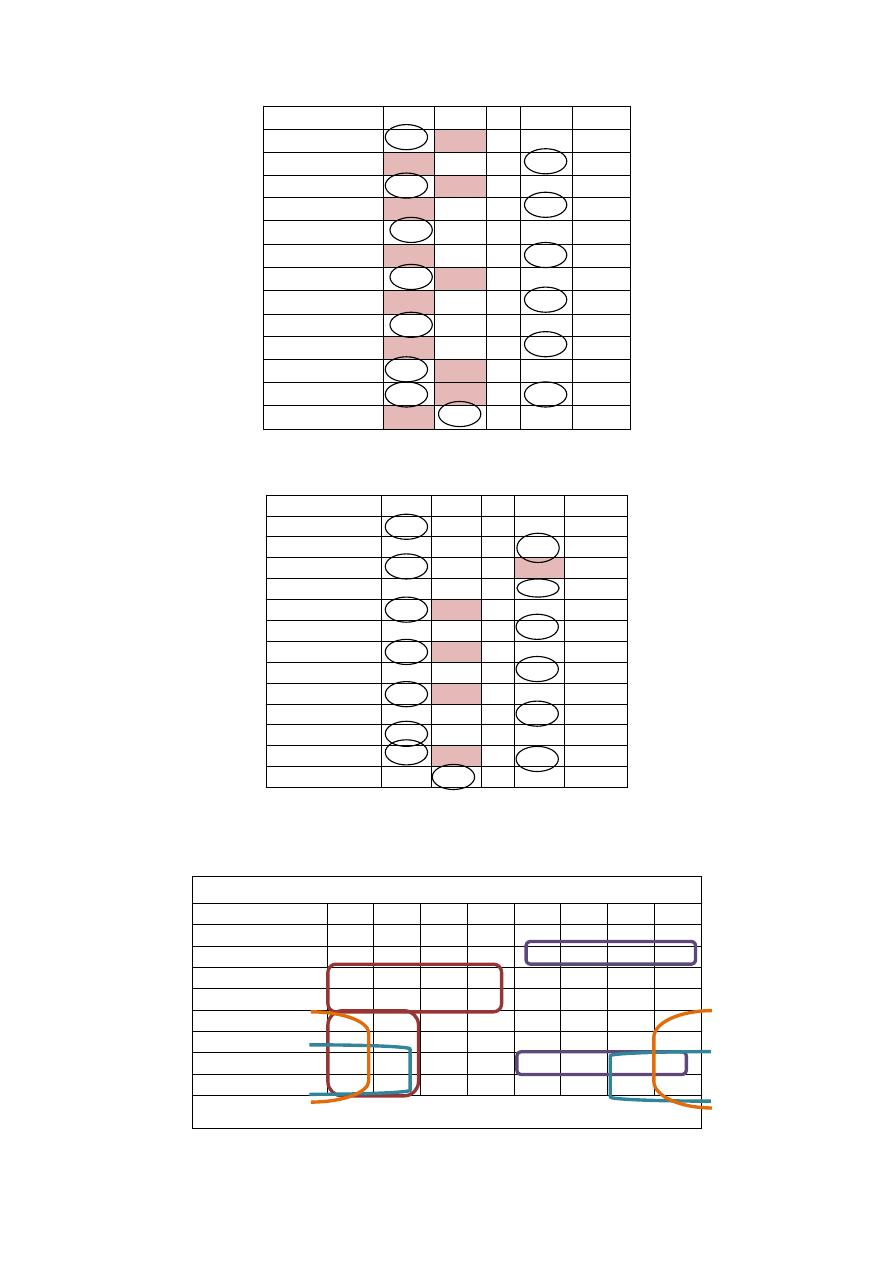
c) Zminimalizowana tabela przejść
Tabelę 3 można zminimalizować, „sklejając” stany oznaczone parami na błękitno i turkusowo,
tzw. stany pseudorównoważne – wyjścia odpowiadające obu stanom są jednakowe i z obu
stanów pod wpływem tych samych sygnałów automat przechodzi do tych samych stanów lub
stanów nieokreślonych (kreska).
q
i
/x
1
x
2
00
01
11
10
y
1
y
2
q
0
q
0
q
0
-
q
1
00
q
1
q
2
-
-
q
1
01
q
2
q
2
q
0
-
q
3
01
q
3
q
3
q
0
-
q
3
10
Tabela 4
d) Zakodowana tabela przejść
Aby wykonać syntezę automatu, musimy jakoś zakodować stany. Dla czterech stanów
potrzebujemy dwóch bitów – oznacza to również dwa sprzężenia zwrotne lub dwa
przerzutniki przy realizacji.
q
i
Q
1
Q
2
/x
1
x
2
00
01
11
10
y
1
y
2
q
0
00
00
00
-
01
00
q
1
01
10
-
-
01
01
q
2
10
10
00
-
11
01
q
3
11
11
00
-
11
10
Tabela 5
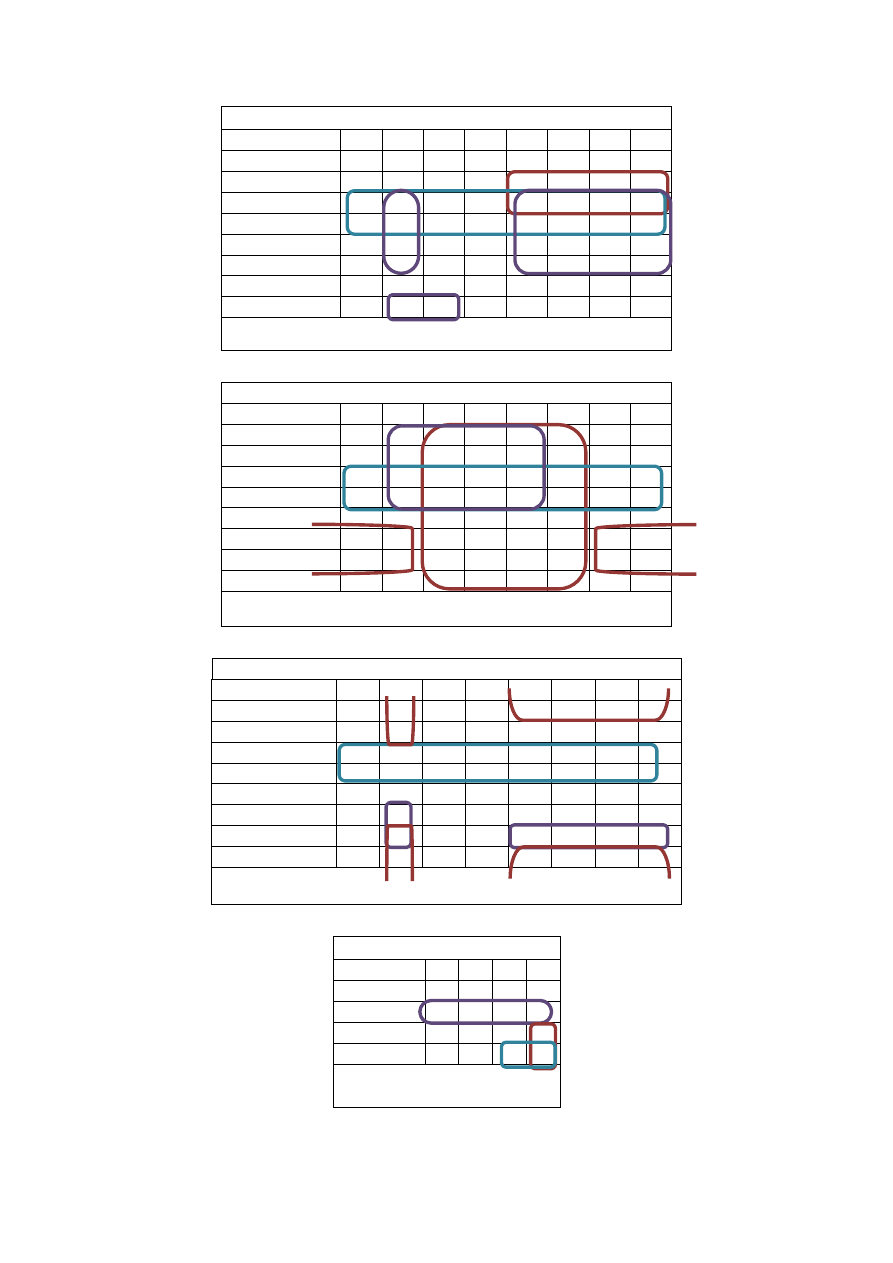
e) Eliminacja wyścigów
W tabeli 5 podczas przejścia oznaczonego na czerwono występuje wyścig krytyczny. Automat
może zachować się na dwa sposoby:
01 -> 00 -> 10
01 -> 11 -> 10
Taka sytuacja może doprowadzić do przejścia w losowy stan. Aby temu zapobiec wystarczy
inaczej zakodować stany. W tym przypadku stan q
3
zakodowaliśmy jako 10 zamiast 11, a stan
q
2
jako 11 zamiast 10. Wyeliminowaliśmy wyścig i nie pojawił się żaden nowy.
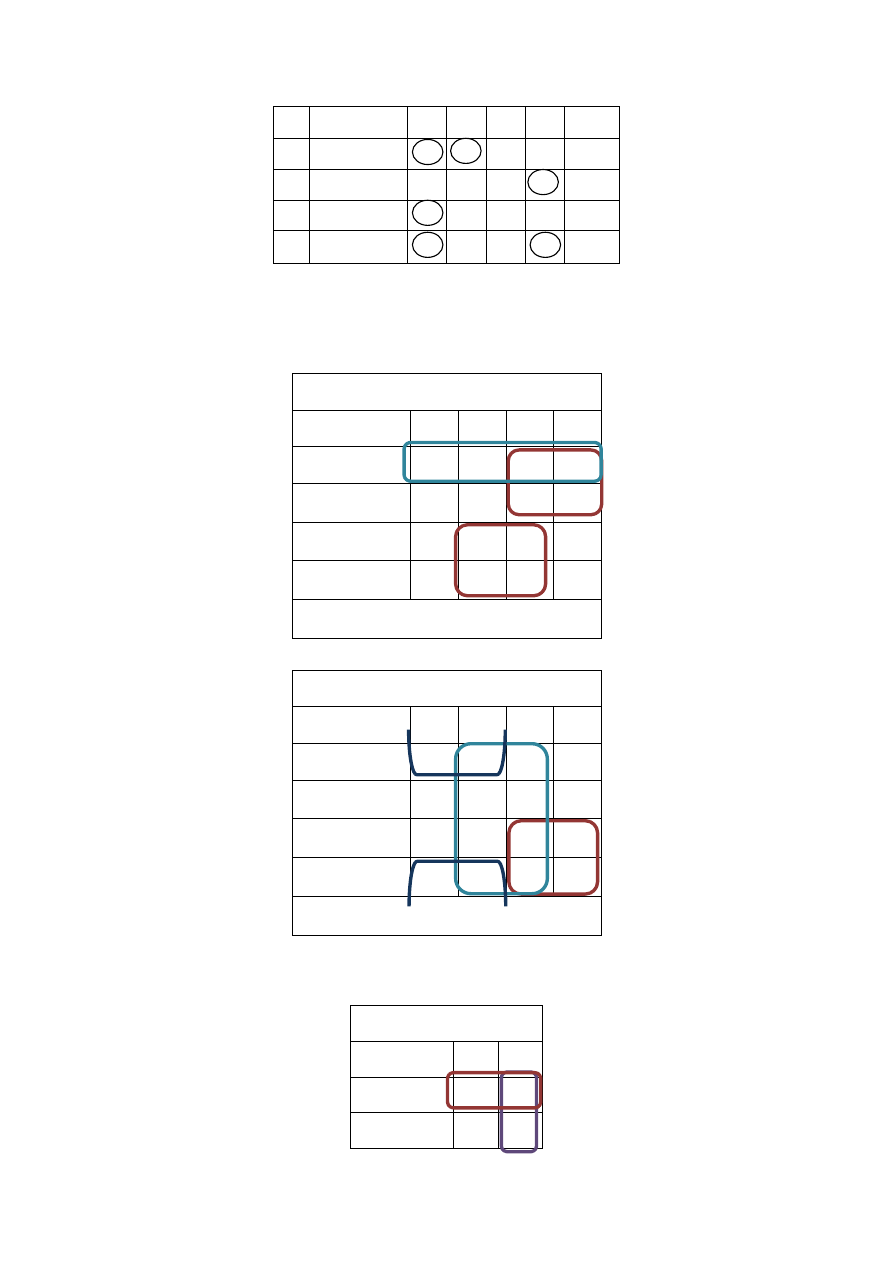
4
q
i
Q
1
Q
2
/x
1
x
2
00
01
11
10
y
1
y
2
q
0
00
00
00
-
01
00
q
1
01
11
-
-
01
01
q
2
11
11
00
-
10
01
q
3
10
10
00
-
10
10
Tabela 6
f) Układ ze sprzężeniami zwrotnymi
Siatki Karnaugh
(ukośnik przed zmienną oznacza negację tej zmiennej)
Q’
1
Q
1
Q
2
/x
1
x
2
00
01
11
10
00
0
0
-
0
01
1
-
-
0
11
1
0
-
1
10
1
0
-
1
Q’
1
= (Q
1
+ Q
2
)/x
2
(Q
1
+ /x
1
)
Tabela 7
Q’
2
Q
1
Q
2
/x
1
x
2
00
01
11
10
00
0
0
-
1
01
1
-
-
1
11
1
0
-
0
10
0
0
-
0
Q’
2
= (x
1
+ Q
2
)(/x
2
)(/Q
1
+ /x
1
)
Tabela 8
y
1
Q
1
/Q
2
0
1
0
0
0
1
1
0
5
y
1
= (Q
1
)(/Q
2
)
Tabela 9
y
2
Q
1
/Q
2
0
1
0
0
1
1
0
1
y
2
= Q
2
Tabela 10
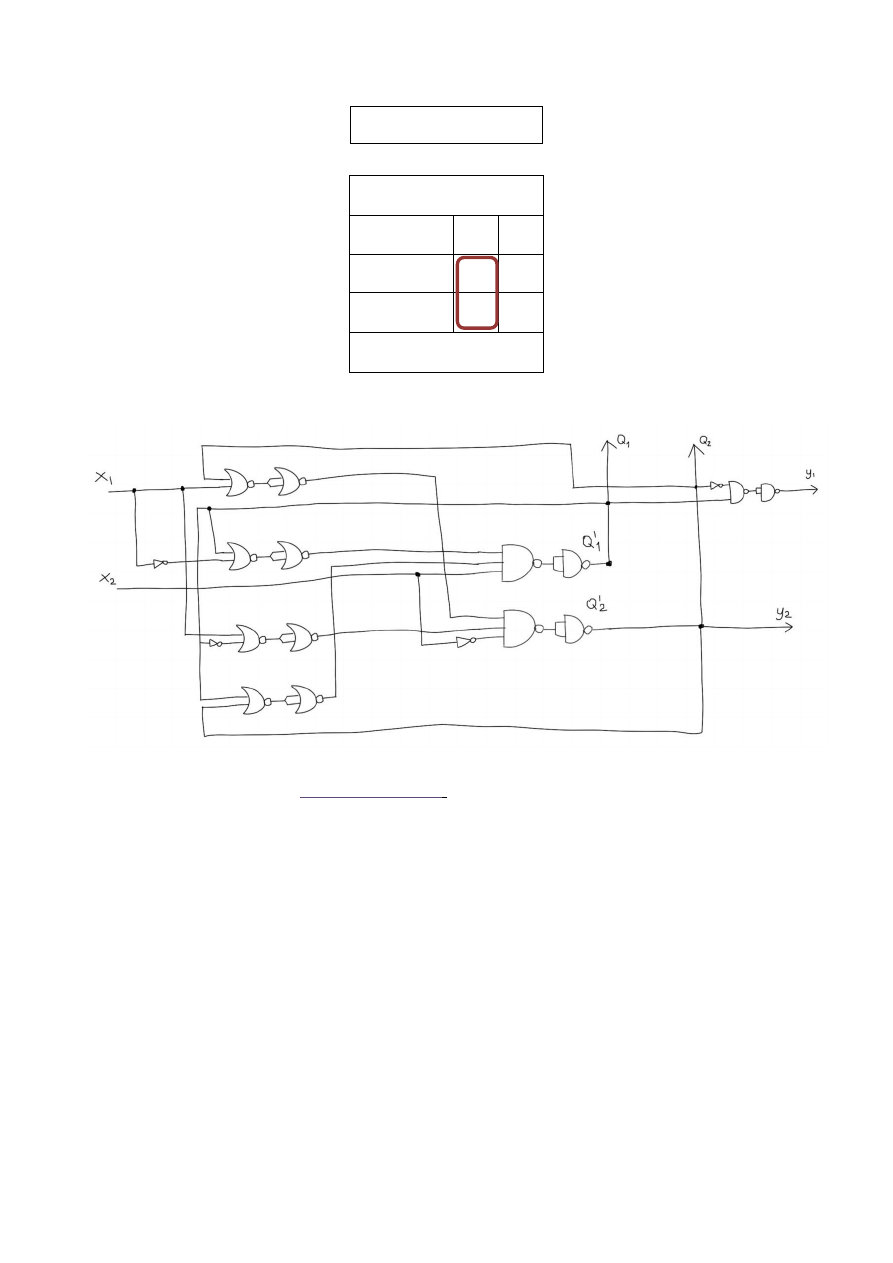
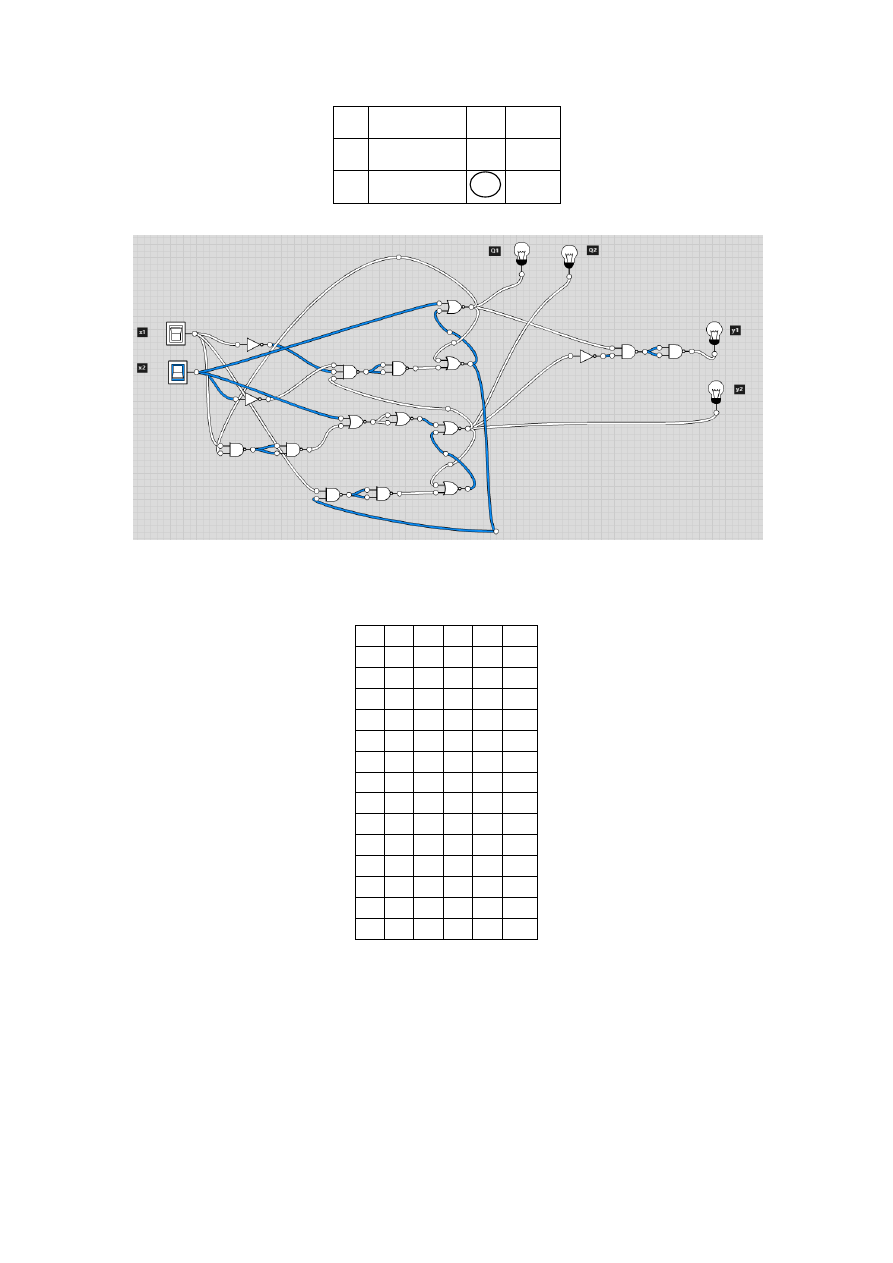
Schemat układu
Rysunek 1
Symulacja działania (
http://logic.ly/demo
)
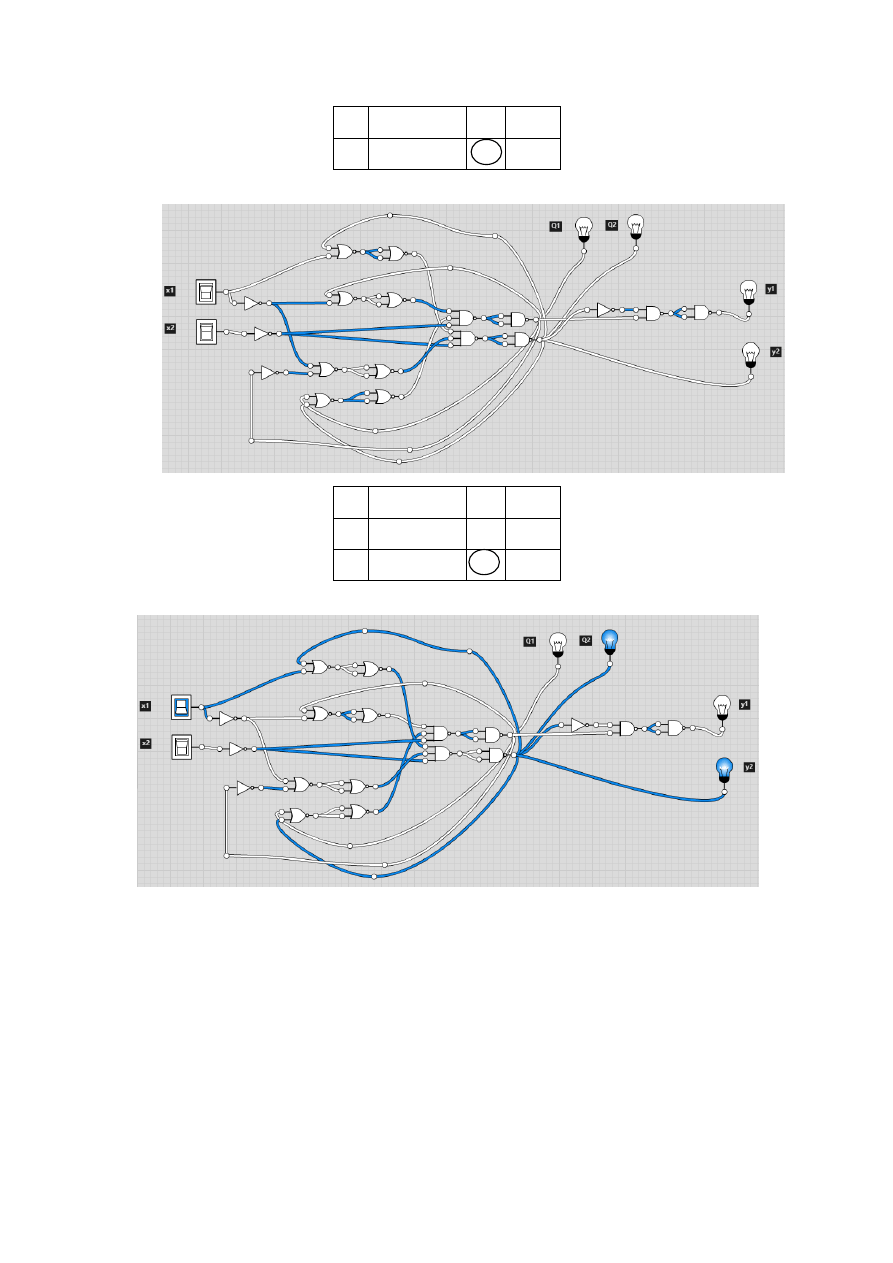
6
q
i
Q
1
Q
2
/x
1
x
2
00
y
1
y
2
q
0
00
00
00
Tabela 11
q
i
Q
1
Q
2
/x
1
x
2
10
y
1
y
2
q
0
00
01
00
q
1
01
01
01
Tabela 12
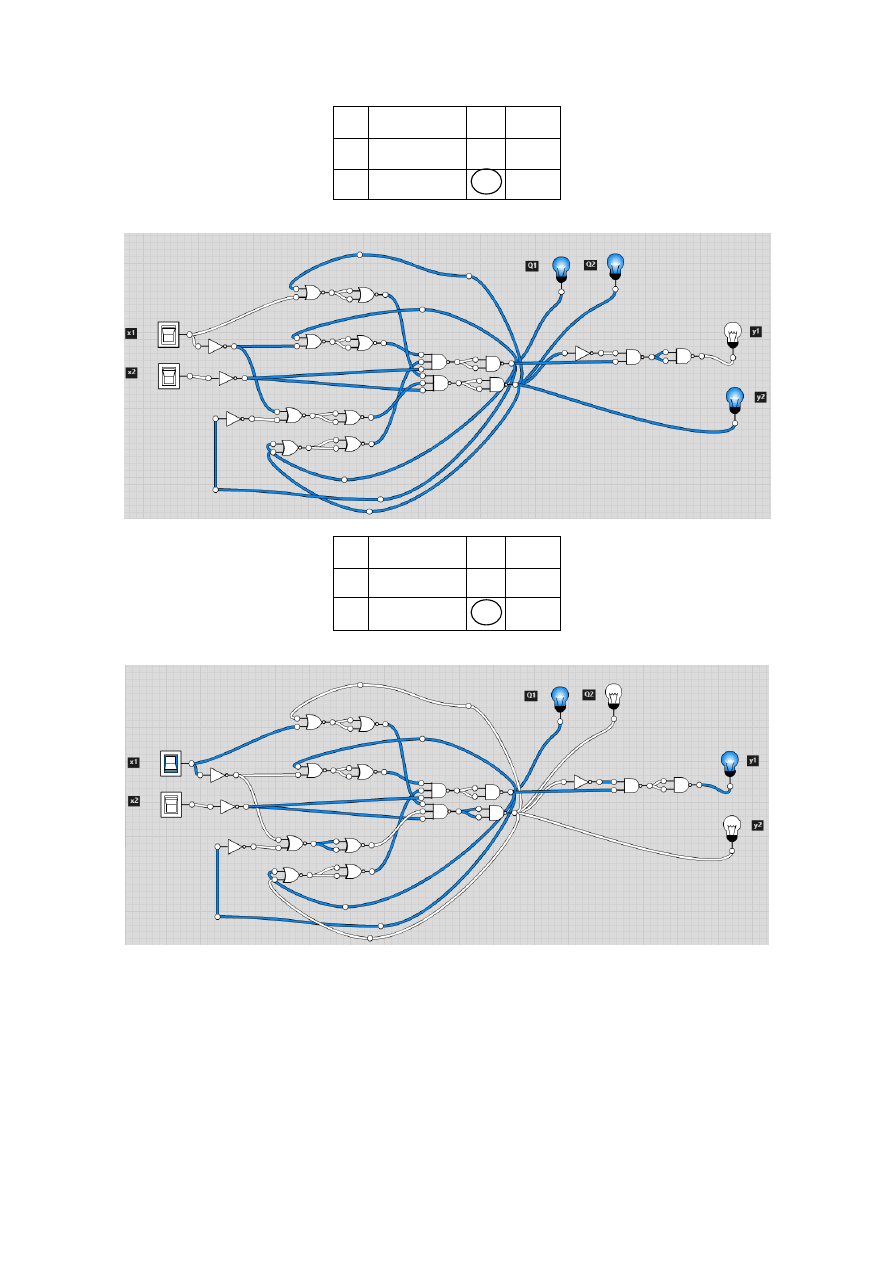
7
q
i
Q
1
Q
2
/x
1
x
2
00
y
1
y
2
q
1
01
11
01
q
2
11
11
01
Tabela 13
q
i
Q
1
Q
2
/x
1
x
2
10
y
1
y
2
q
2
11
10
01
q
3
10
10
10
Tabela 14
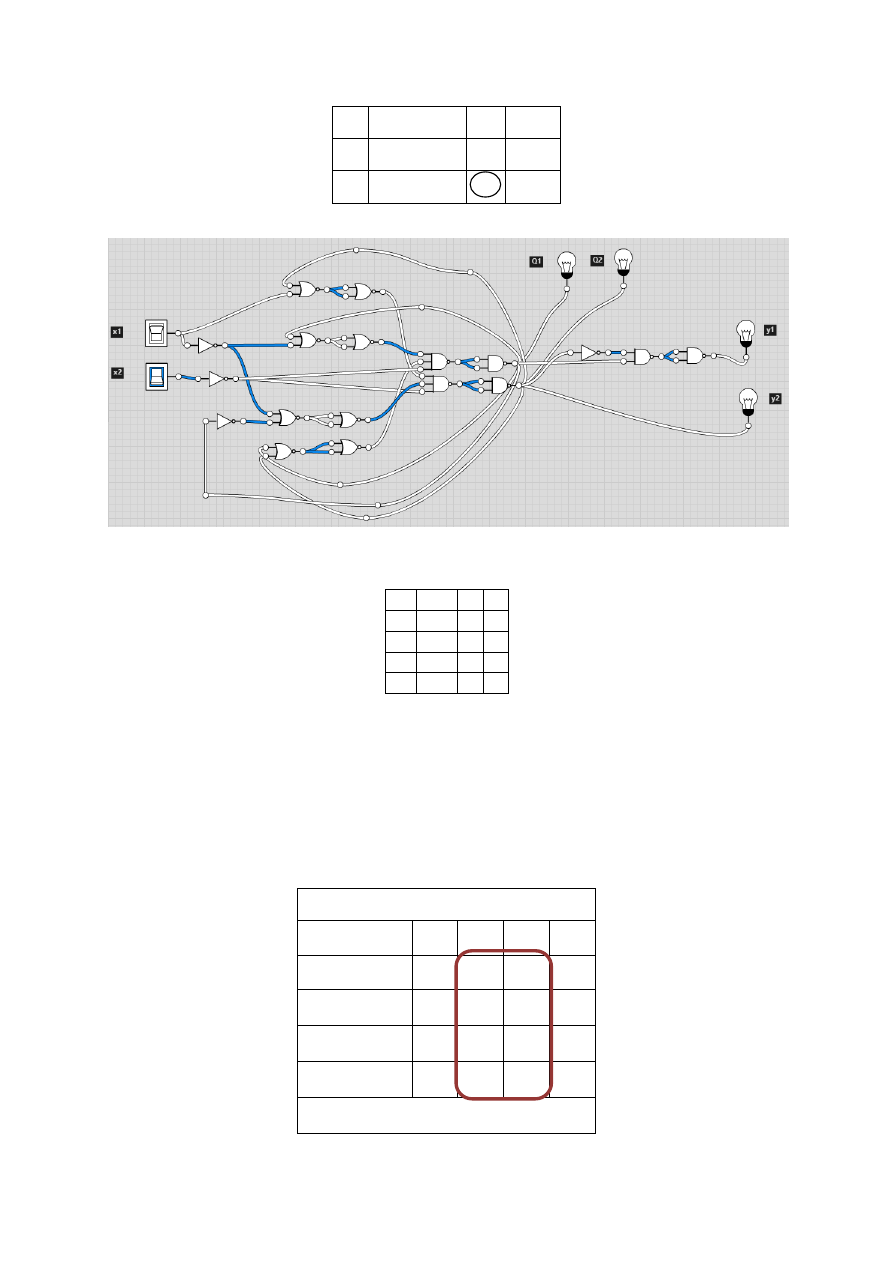
8
q
i
Q
1
Q
2
/x
1
x
2
01
y
1
y
2
q
3
10
00
10
q
0
00
00
00
Tabela 15
g) Układ z asynchronicznymi przerzutnikami RS
Tabela wzbudzeń przerzutnika RS
Q
t
Q
t+1
R S
0
0
- 0
0
1
0 1
1
0
1 0
1
1
0 -
Tabela 16
Układ będzie się składać z n przerzutników
k – liczba stanów
2
n-1
< k <= 2
n
2
n-1
< 4 <= 2
n
2
1
< 4 <= 2
2
n = 2
Siatki Karnaugh
Funkcje wyjść wyglądają tak samo, jak w układzie ze sprzężeniami zwrotnymi.
R
1
– rozpatrujemy Q
1
(t) i Q
1
(t+1)
Q
1
Q
2
/x
1
x
2
00
01
11
10
00
-
-
-
-
01
0
-
-
-
11
0
1
-
0
10
0
1
-
0
R
1
= x
2
Tabela 17
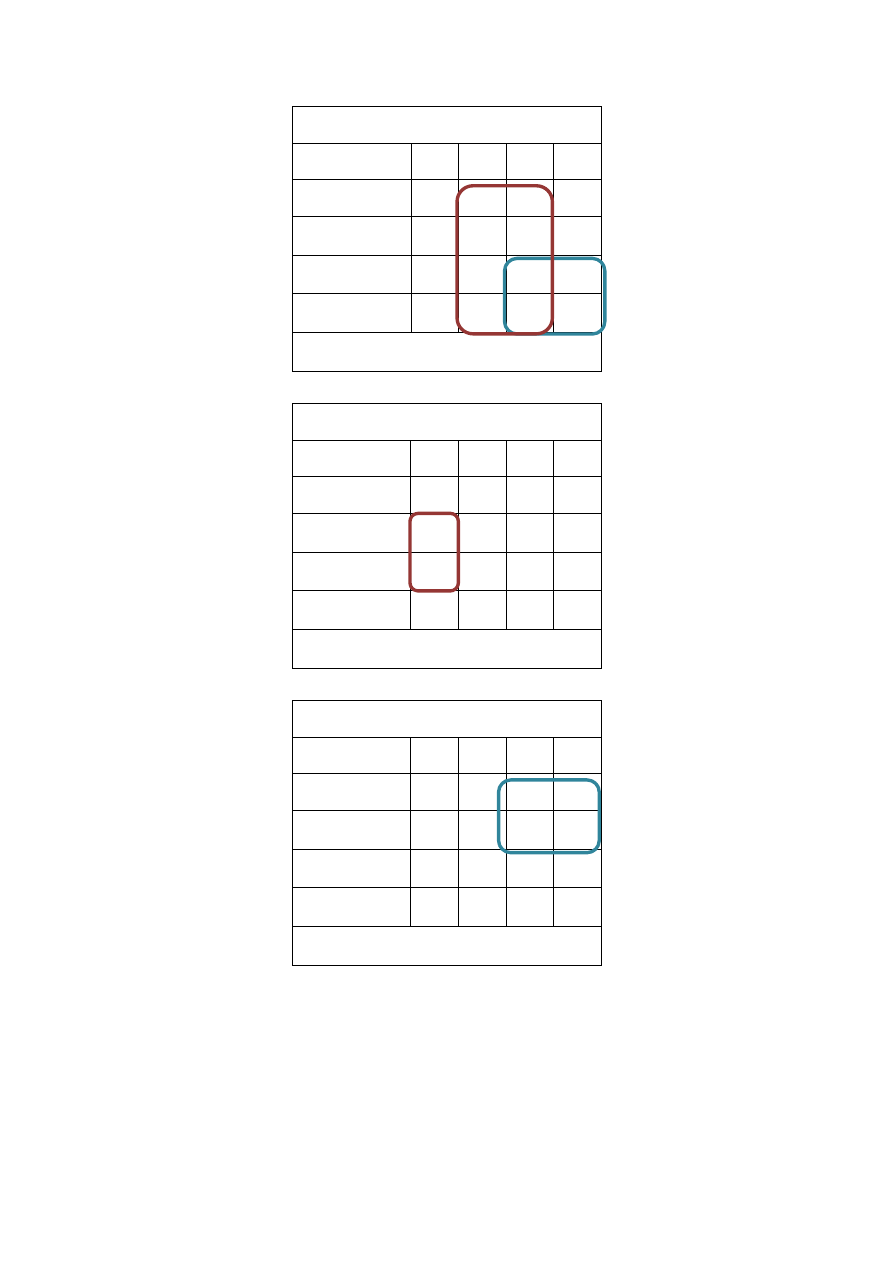
9
R
2
– rozpatrujemy Q
2
(t) i Q
2
(t+1)
Q
1
Q
2
/x
1
x
2
00
01
11
10
00
-
-
-
0
01
0
-
-
0
11
0
1
-
1
10
-
-
-
-
R
2
= x
2
+ Q
1
x
1
Tabela 18
S
1
– rozpatrujemy Q
1
(t) i Q
1
(t+1)
Q
1
Q
2
/x
1
x
2
00
01
11
10
00
0
0
-
0
01
1
-
-
0
11
-
0
-
-
10
-
0
-
-
S
1
= /x
1
/x
2
/Q
2
Tabela 19
S
2
– rozpatrujemy Q
2
(t) i Q
2
(t+1)
Q
1
Q
2
/x
1
x
2
00
01
11
10
00
0
0
-
1
01
-
-
-
-
11
-
0
-
0
10
0
0
-
0
S
2
= x
1
/Q
1
Tabela 20
10
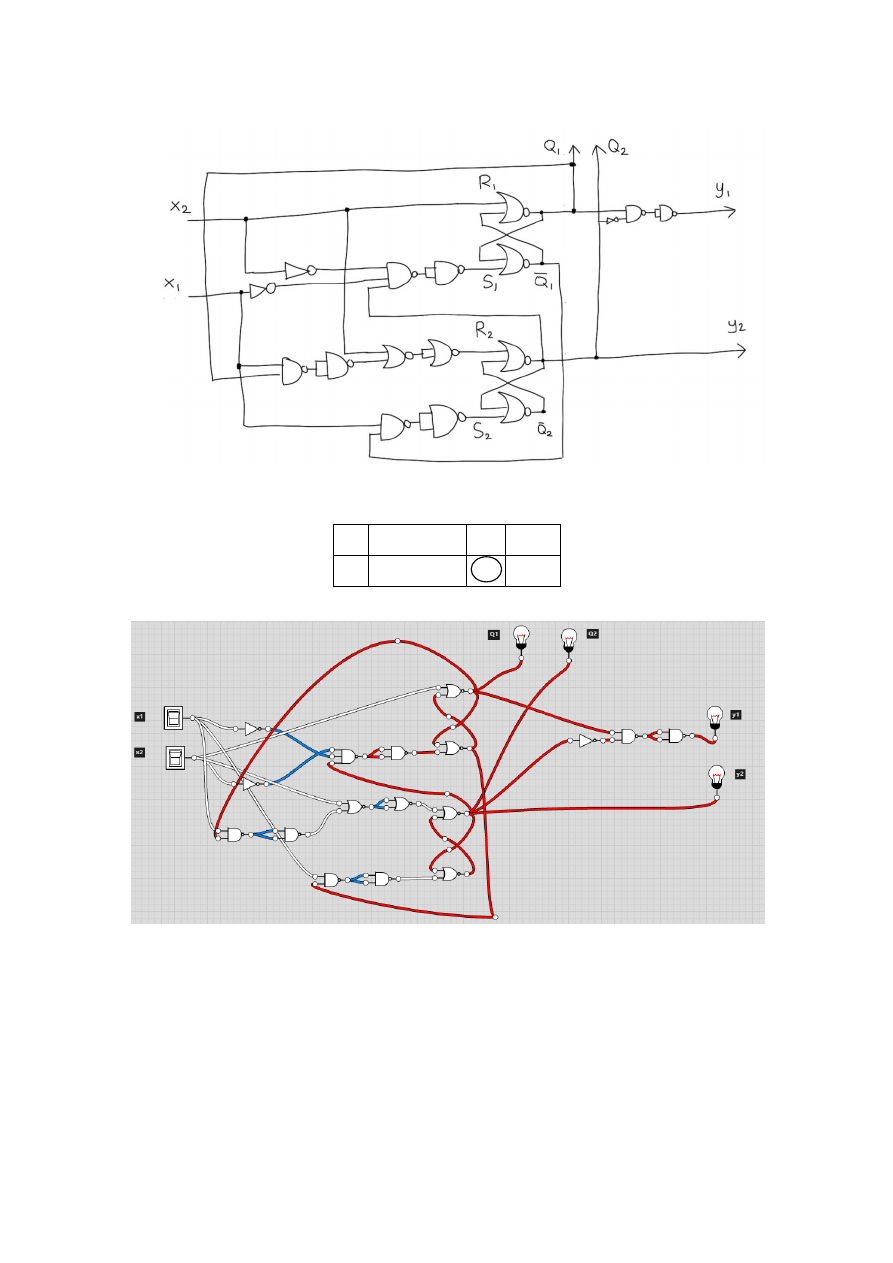
Schemat układu
Rysunek 2
Symulacja działania
q
i
Q
1
Q
2
/x
1
x
2
00
y
1
y
2
q
0
00
00
00
Tabela 21
11
q
i
Q
1
Q
2
/x
1
x
2
01
y
1
y
2
q
0
00
00
00
Tabela 22
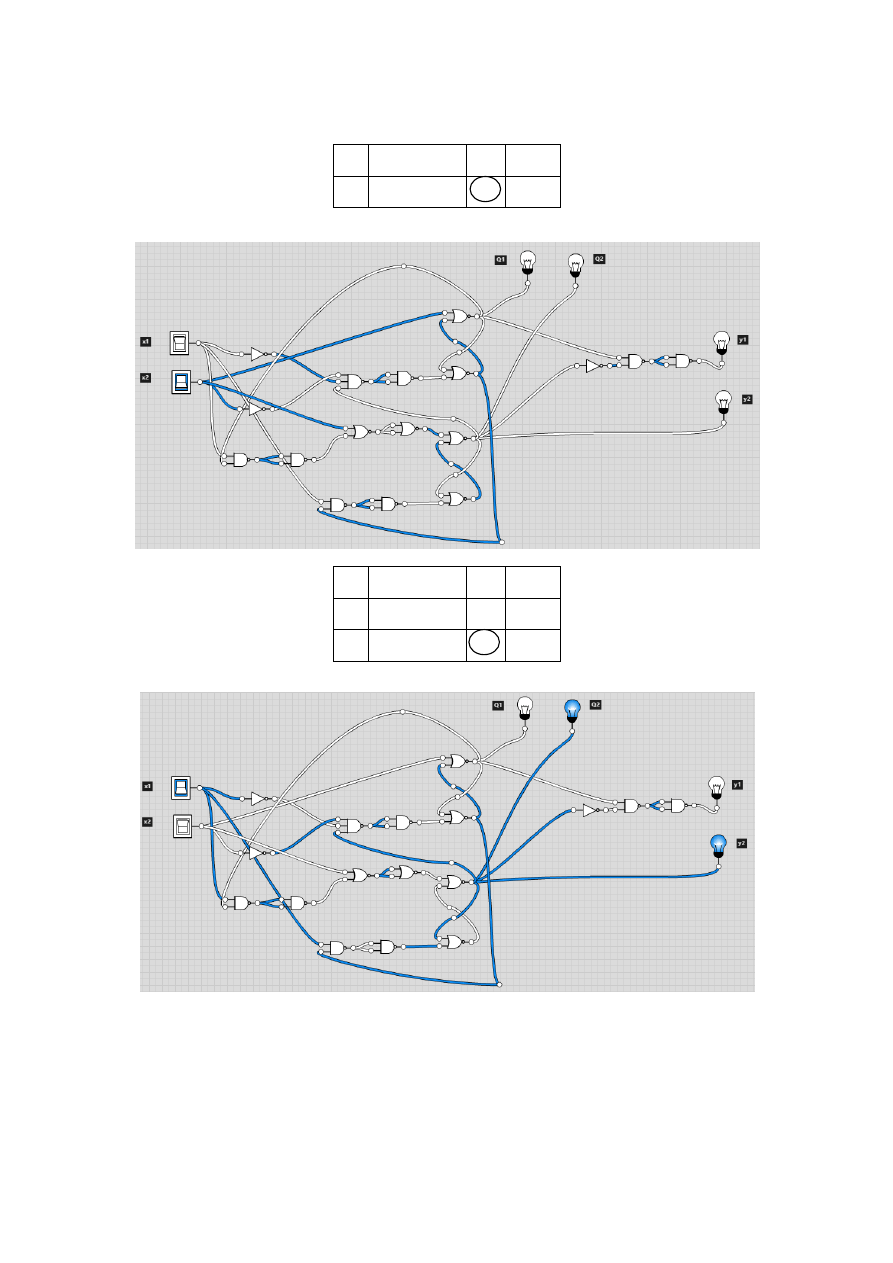
q
i
Q
1
Q
2
/x
1
x
2
10
y
1
y
2
q
0
00
01
00
q
1
01
01
01
Tabela 23
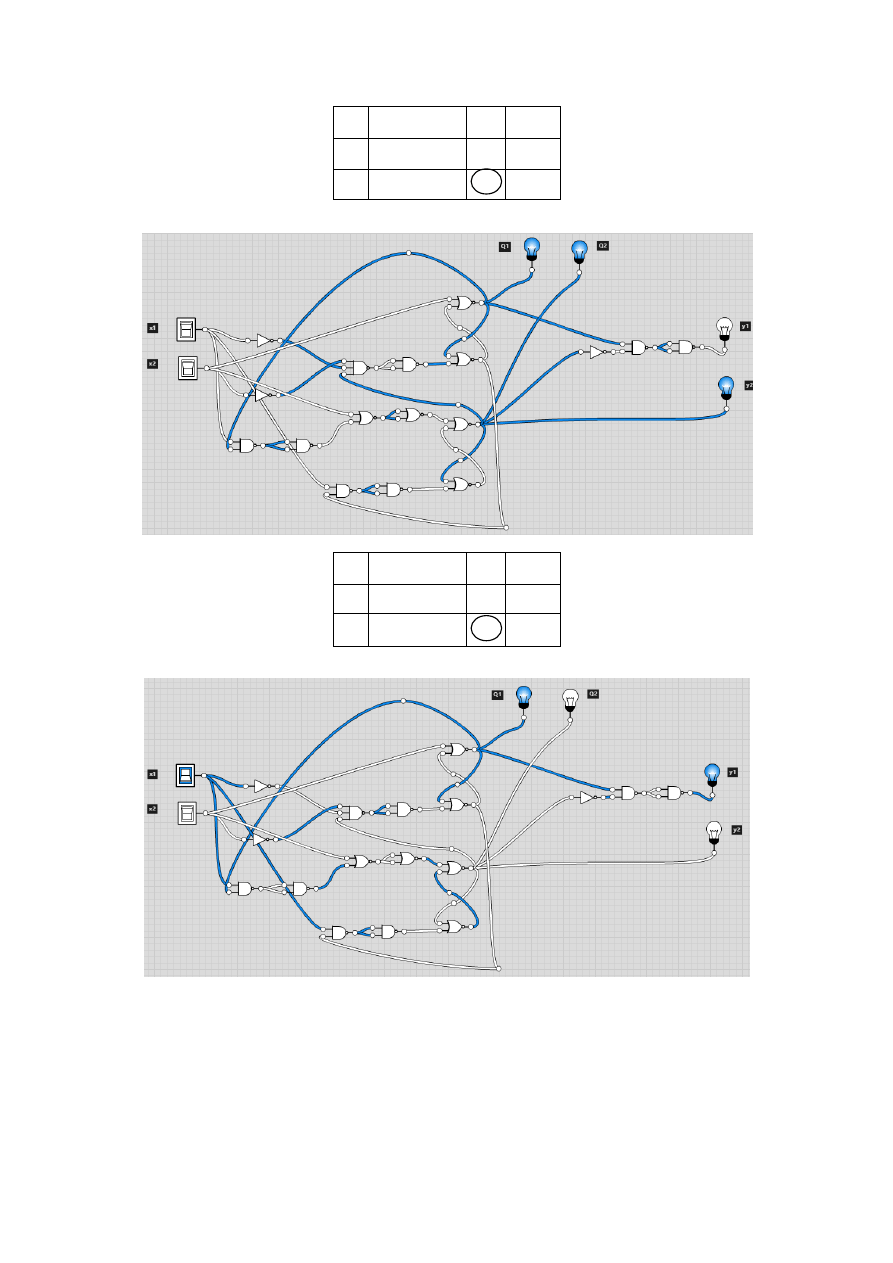
12
q
i
Q
1
Q
2
/x
1
x
2
00
y
1
y
2
q
1
01
11
01
q
2
11
11
01
Tabela 24
q
i
Q
1
Q
2
/x
1
x
2
10
y
1
y
2
q
2
11
10
01
q
3
10
10
10
Tabela 25
13
q
i
Q
1
Q
2
/x
1
x
2
01
y
1
y
2
q
3
10
00
10
q
0
00
00
00
Tabela 26
2. Automat A
2
Możliwe kombinacje sygnałów wejściowych i wyjściowych i przypisane im stany:
x
1
x
2
y
2
y
1
y
0
q
i
0
0
0
0
0
q
0
1
0
0
0
1
q
1
0
0
0
0
1
q
2
1
0
0
1
0
q
3
0
0
0
1
0
q
4
1
0
0
1
1
q
5
0
0
0
1
1
q
6
1
0
1
0
0
q
7
0
0
1
0
0
q
8
1
0
1
0
1
q
9
0
0
1
0
1 q
10
1
0
1
1
0 q
11
0
0
1
1
0 q
12
0
1
0
0
0 q
13
Tabela 27
a) Wykres czasowy
14
q
0
q
1
q
2
q
3
q
4
q
5
q
6
q
7
q
8
q
9
q
10
q
11
q
12
q
13
q
0
q
1
x
1
1
0
x
2
1
0
y
2
1
0
y
1
1
0
y
0
1
0
b) Tabela przejść/wyjść
Lawendowym kolorem oznaczono stany pseudorównoważne.
q
i
/x
1
x
2
00
01
11
10
y
2
y
1
y
0
q
0
q
0
q
13
-
q
1
000
q
1
q
2
-
-
q
1
001
q
2
q
2
q
13
-
q
3
001
q
3
q
4
-
-
q
3
010
q
4
q
4
q
13
-
q
5
010
q
5
q
6
-
-
q
5
011
q
6
q
6
q
13
-
q
7
011
q
7
q
8
-
-
q
7
100
q
8
q
8
q
13
-
q
9
100
q
9
q
10
-
-
q
9
101
q
10
q
10
q
13
-
q
11
101
q
11
q
12
-
-
q
11
110
q
12
q
12
q
13
-
-
110
q
13
q
0
q
13
-
-
000
Tabela 28
c) Zminimalizowana i zakodowana tabela przejść
15
Q
1
Q
2
Q
3
Q
4
/x
1
x
2
00
01
11
10
y
2
y
1
y
0
0000
0000 1100
-
0001
000
0001
0010
-
-
0001
001
0010
0010 1100
-
0011
001
0011
0100
-
-
0011
010
0100
0100 1100
-
0101
010
0101
0110
-
-
0101
011
0110
0110 1100
-
0111
011
0111
1000
-
-
0111
100
1000
1000 1100
-
1001
100
1001
1010
-
-
1001
101
1010
1010 1100
-
1011
101
1011
1011 1100
-
1011
110
1100
0000 1100
-
-
000
Tabela 29
d) Eliminacja wyścigów – nie udało się wyeliminować wszystkich wyścigów
Q
1
Q
2
Q
3
Q
4
/x
1
x
2
00
01
11
10
y
2
y
1
y
0
0000
0000 0010
-
0001
000
0001
0011
-
-
0001
001
0011
0011 0010
-
1100
001
1100
1000
-
-
1100
010
1000
1000 0010
-
1001
010
1001
1101
-
-
1001
011
1101
1101 0010
-
0111
011
0111
1111
-
-
0111
100
1111
1111 0010
-
1110
100
1110
1010
-
-
1110
101
1010
1010 0010
-
1011
101
1011
1011 0010
-
1011
110
0010
0000 0010
-
-
000
Tabela 30
e) Układ ze sprzężeniami zwrotnymi
Siatki Karnaugh
Q’
1
Q
1
Q
2
Q
3
/x
1
x
2
Q
4
000
001
011
010
110
111
101
100
000
0
0
-
0
-
-
0
0
001
0
0
0
0
-
-
1
-
011
-
1
-
-
-
-
0
-
010
-
-
-
-
-
-
-
-
110
1
1
0
-
-
-
0
1
111
1
1
0
-
-
-
1
1
101
1
1
0
0
-
-
1
1
100
1
1
-
0
-
-
1
1
Q’
1
= /Q
1
Q
2
/x
1
+ x
1
/Q
1
/Q
2
Q
3
+ x
1
Q
1
Q
2
Q
3
+ /x
1
/x
2
Q
1
+ Q
1
/x
2
/Q
4
+ Q
1
/Q
2
/x
2
Tabela 31
16
Q’
2
Q
1
Q
2
Q
3
/x
1
x
2
Q
4
000 001 011 010 110 111 101 100
000
0
0
-
0
-
-
0
0
001
0
0
0
0
-
-
1
-
011
-
1
-
-
-
-
1
-
010
-
-
-
-
-
-
-
-
110
0
1
0
-
-
-
1
1
111
0
1
0
-
-
-
1
1
101
0
0
0
0
-
-
0
0
100
0
1
-
0
-
-
0
0
Q’
2
= /Q
1
Q
2
+ x
2
Q
2
+ x
1
/Q
1
Q
3
+ /x
1
/x
2
Q
4
Q
2
+ /x
1
Q
4
Q
1
/Q
2
Q
3
Tabela 32
Q’
3
Q
1
Q
2
Q
3
/x
1
x
2
Q
4
000 001 011 010 110 111 101 100
000
0
1
-
1
-
-
0
0
001
0
1
1
1
-
-
0
-
011
-
1
-
-
-
-
1
-
010
-
-
-
-
-
-
-
-
110
0
0
1
-
-
-
0
0
111
1
1
1
-
-
-
1
1
101
1
1
1
1
-
-
1
1
100
0
0
-
1
-
-
0
0
Q’
3
= x
2
+ /Q
1
+ /Q
1
Q
2
+ /x
2
Q
1
Q
3
Tabela 33
Q’
4
Q
1
Q
2
Q
3
/x
1
x
2
Q
4
000 001 011 010 110 111 101 100
000
0
1
-
0
-
-
-
1
001
0
1
0
0
-
-
0
-
011
-
1
-
-
-
-
1
-
010
-
-
-
-
-
-
-
-
110
0
0
0
-
-
-
0
0
111
0
1
0
-
-
-
0
0
101
0
1
0
0
-
-
1
1
100
0
1
-
0
-
-
1
1
Q’
4
= x
1
/Q
2
/Q
3
+ x
1
Q
1
/Q
2
Q
3
+ /x
1
/x
2
Q
4
/Q
2
+ /x
1
/x
2
Q
4
Q
1
Q
2
Q
3
+ /Q
1
Q
2
Tabela 34
y
2
Q
1
Q
2
/Q
3
Q
4
00 01 11 10
00
0
0
0
0
01
-
-
1
-
11
0
0
0
1
10
0
0
1
1
y
2
= /Q
1
Q
2
+ Q
3
/Q
4
Q
1
+ Q
3
Q
1
/Q
2
Tabela 35
17
y
1
Q
1
Q
2
/Q
3
Q
4
00 01 11 10
00
0
0
0
0
01
-
-
0
-
11
1
1
0
0
10
1
1
1
0
y
1
= /Q
3
Q
1
+ Q
1
/Q
2
Q
4
Tabela 36
y
0
Q
1
Q
2
/Q
3
Q
4
00 01 11 10
00
0
1
1
0
01
-
-
0
-
11
0
1
0
1
10
0
1
0
1
y
0
= /Q
3
Q
4
+ /Q
1
/Q
2
Q
4
+ Q
3
/Q
4
Q
1
Tabela 37
18
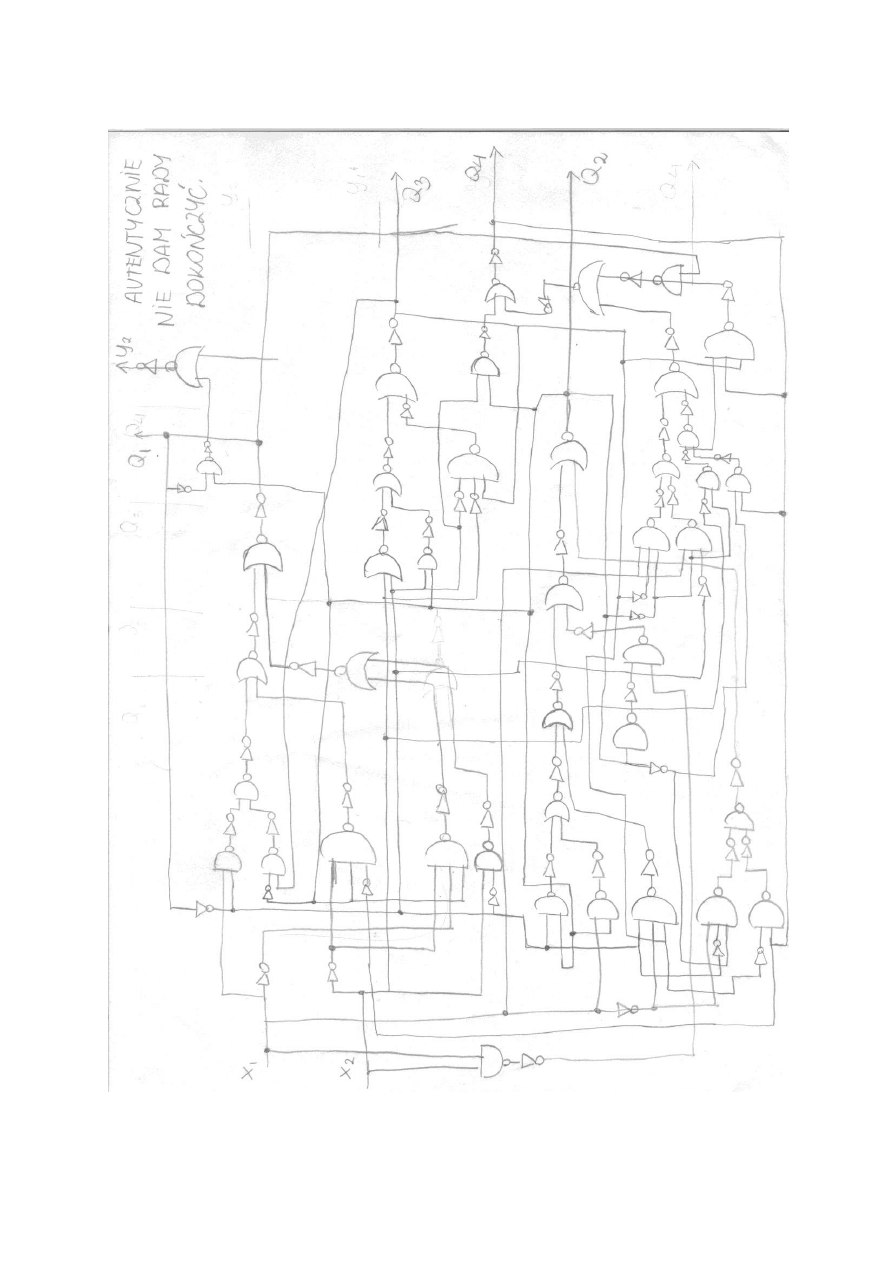
Schemat układu
Wyszukiwarka
Podobne podstrony:
Wykład VIII Przykłady kodowania automatów asynchronicznycvh II
211 automat asynchroniczny 2, Politechnika Wrocławska - Materiały, logika ukladow cyfrowych, sprawoz
Wykład VII Przykłady kodowania automatów asynchronicznycvh
Wykład VI Kodowanie automatów asynchronicznych
Wykład VIII Przykłady kodowania automatów asynchronicznycvh II
212 asynchroniczny
FESTO Podstawy automatyzacji
Automatyka (wyk 3i4) Przel zawory reg
Automatyzacja w KiC (w 2) Obiekty reg
AutomatykaII 18
Automatyka wykład 8
Wybrane elementy automatyki instalacyjnej
PA2 5 przerzutniki asynchr
12 Podstawy automatyki Układy sterowania logicznego
Automatyka dynamiakPAOo 2
Automatyka okrętowa – praca kontrolna 2
automatyczne swiatla
podstawy automatyki ćwiczenia lista nr 4b
więcej podobnych podstron