Częstotliwościowe metody analizy UR

Celem ćwiczenia jest komputerowa analiza własności układów regulacj na podstawie charakterystyk

częstotliwościowych:

- amplitudowo-fazowej (Nyquista),
- wskaźników jakości: regulacji oraz nadążania.

1. Przebieg ćwiczenia
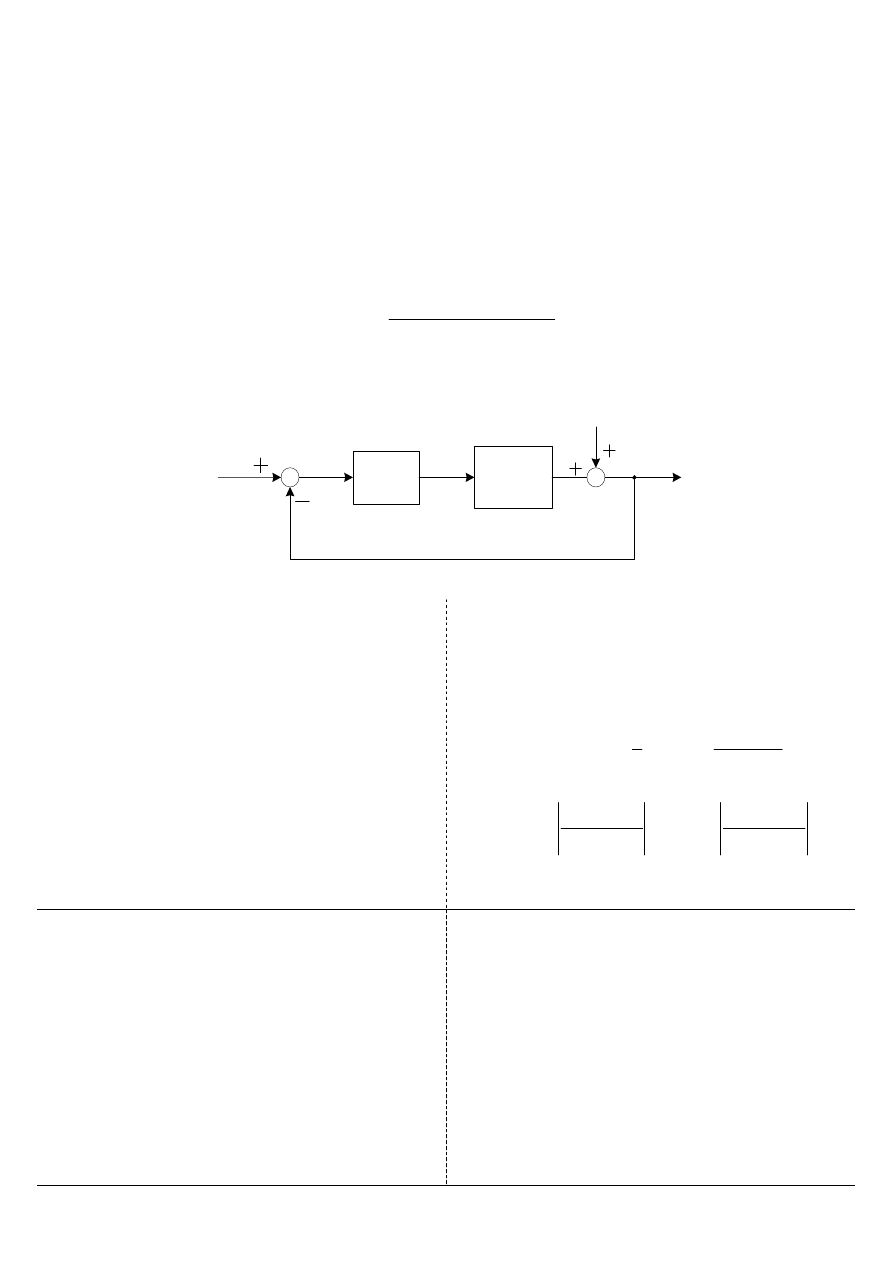
Przeprowadź analizę zamkniętego układu regulacji przedstawionego na rys.1 z obiektem o transmitancji:

( ) ( )(

)(

)

1

2

.

1

1

1

k

K s

s

sT

sT

=

+

+

+

Dobierz parametry k, T

1

oraz T

2

(k>1; T

1

, T

2

>0) tak aby zamknięty układ (dla

( )

1

r

K s

=

) b

Ry 1

1.1.Zbadaj własności zamkniętego układu regulacji

z obiektem o transmitancji

ył stabilny.

( )

w t

( )

y t

( )

r

K s

( )

K s

( )

z t

( )

u t

s.

•

( )

K s

oraz

( )

1

K s

r

=

otwartego, zaznacz
oraz fazy układu zamkniętego,
przebieg y(t) odpowiedzi układu zamkniętego
na wymuszenie skokowe w(t):

( )

( )

1

Y s

G s

s

=

;

( )

( )

( )

1

o

K s

G s

=

+

o

K s

,

c) przebieg wskaźników częstotliwościowych:

( )

( )

( )

( )

( )

1

o

o

K

j

ω

, q

1

1

o

M

K

j

K

j

ω

ω

ω

ω

=

=

( )

( ) ( )

.

o

r

K

j

K

j

K j

ω

ω

ω

=

( )

K s

k

=

r

r

r

k

a) charakterystykę amplitudowo-fazową układu

otwart
oraz fazy układu zamkniętego,
odpowiedź skokową układu zamkniętego,
przebieg wskaźników częstotliw

Wykreśl wszystkie odpowiednie przebiegi na jedn

nku

.

• Wskaż „optymalną” nastawę regulatora P i

uzasa
zapas modułu, czas regulacji, przeregulowanie,
błąd w stanie ustalonym).

.

W tym celu sporządź:

a) charakterystykę amplitudowo-fazową układu

i odczytaj zapas amplitudy

b)

+

+

1.2. Zbadaj wpływ nastaw regulatora P:

na własności układu.

• Dla trzech wybranych wartości wzmocnienia

wykreśl:

ego, zaznacz i odczytaj zapas amplitudy

b)
c)

ościowych.

ym

rysu

dnij swój wybór (uwzględnij: zapas fazy,

1.3. Zbadaj wpływ nastaw regulatora PI:

( )

1

c

K









1

r

r

s

k

sT

=

+

Prz

i T

c

.

obierz tak aby zapas amplitudy wynosił

∆k = 2.

.a, b i c).





na własności układu..

yjmij trzy dowolne wartośc

D

r

k

Wykreśl komplet charakterystyk (1.2
Wskaż „najlepsze” nastawy regulatora.

( )

1

c

K









1

r

r

d

s

k

T s

sT





na własności układu.

Wykreśl komplet charakterystyk (1.2.a,
je

r

c

d

„akceptowalne” własności zamkniętego układu
regulacji.

k T T

Dla wybra
o
nadążania oraz wskaźnik tłumienia zakłóceń.
Skomentuj uzyskane wyniki.

muszenie

( )

sin

w t

t

ω

=

.

Z charakterystyki nadążania

( )

M

ω

wybierz trzy

wartości częstotliwości z pasm:

1

ω

- nadążania,

2

ω

-

3

rezonansowego i

ω

- nadrezonansowego. W

O

y

l

kreś

ad

odpowiedzi (W STANIE USTAL NYM !) ukł u
zamkniętego na wymuszenie sinusoidalne:

( )

1

2

3

,

,

sin

w t

t

ω ω ω ω

ω

=

=

(

2

rez

ω

ω

=

). Porównaj stosunek

am it d sy nału wyjściowego y(t) do wejściowego

aź

ążania

pl u , g

w(t), z wartością wsk nika nad

( )

i

M

ω

.

ulacji powinny być stabilne.

1.4. Zbadaj wpływ nastawy regulatora PID:

=

+

+

b i c) dla

dnego zestawu nastaw , , zapewniającego

1.5. Zbadaj wpływ regulatorów P, PI, PID.

nych „najlepszych” nastaw regulatora P, PI

raz PID wykreśl (na jednych rysunkach) wskaźnik

1.6. Dokonaj analizy odpowiedzi układu

zamkniętego, z regulatorem PI (lub PID), na
wy

Uwaga: Wszystkie układy reg

2. Sprawozdanie

• Opracuj i przedstaw wszystkie charakterystyki u yskane podczas realizacji ćwiczenia

aną „optymalną” nastawę regulatora P

ów i odnieś je do

Po

e

ltiview(K), step(K), nyquist(K), bode(K),

zależność moduł transmitancji G od częstotliwości

ω

resu

usoidalne sin(

ω t):

,T] =gensig(’sin’,tau,czas_koncowy)

- wygenerowanie pobudzenia u(t) = sin(

ωt); tau – okres [s]

ia

z

• Omów wskaz

• Porównaj przebiegi wskaźników oraz zapasy stabilności dla różnych nastaw regulator

możliwości kształtowania własności układów

• Wyciągnij wnioski

lec nia Matlab’a:

bodemag(G) – rysuje
title(‘Text’) – dodaje tytuł do bieżącego wyk
legend(‘K1’,’ K2’,’ K3’, ...) – dodaje legendę do bieżącego wykresu

Konstrukcja odpowiedzi układu o transmitancji G na wymuszenie sin

[U
lsim(G,U,T)

-

symulacja

Zadania kontrolne przed przystąpieniem do ćwiczen :

obliczyć zapas fazy i zapas amplitudy dla zadanego

kładu dynamicznego lub parametry układu zapewniające daną wielkość zapasu fazy i amplitudy.

1)

u
Przykładowe transmitancje obiektu:

(

)

( )

1

K s

sT

+

(

)

2

( )

1

k

K s

s

sT

=

+

3)

(

)

( )

,

1

n

k

K s

n N

sT

=

∈

+

k

=

2)