Politechnika Śląska
Gliwice, 2006/2007
Wydział: Automatyki, Elektroniki i Informatyki
Semestr: 6 (letni)
Kierunek: Automatyka i robotyka
Podstawy Automatyki
– laboratorium
Ćw 5. Częstotliwościowe metody analizy UR.
Data ćwiczeń laboratoryjnych:
21.03.2007
Grupa: 1
Sekcja: 3
Skład osobowy sekcji:
Zięba Andrzej
Bojko Marcin
Pawliczek Krystian
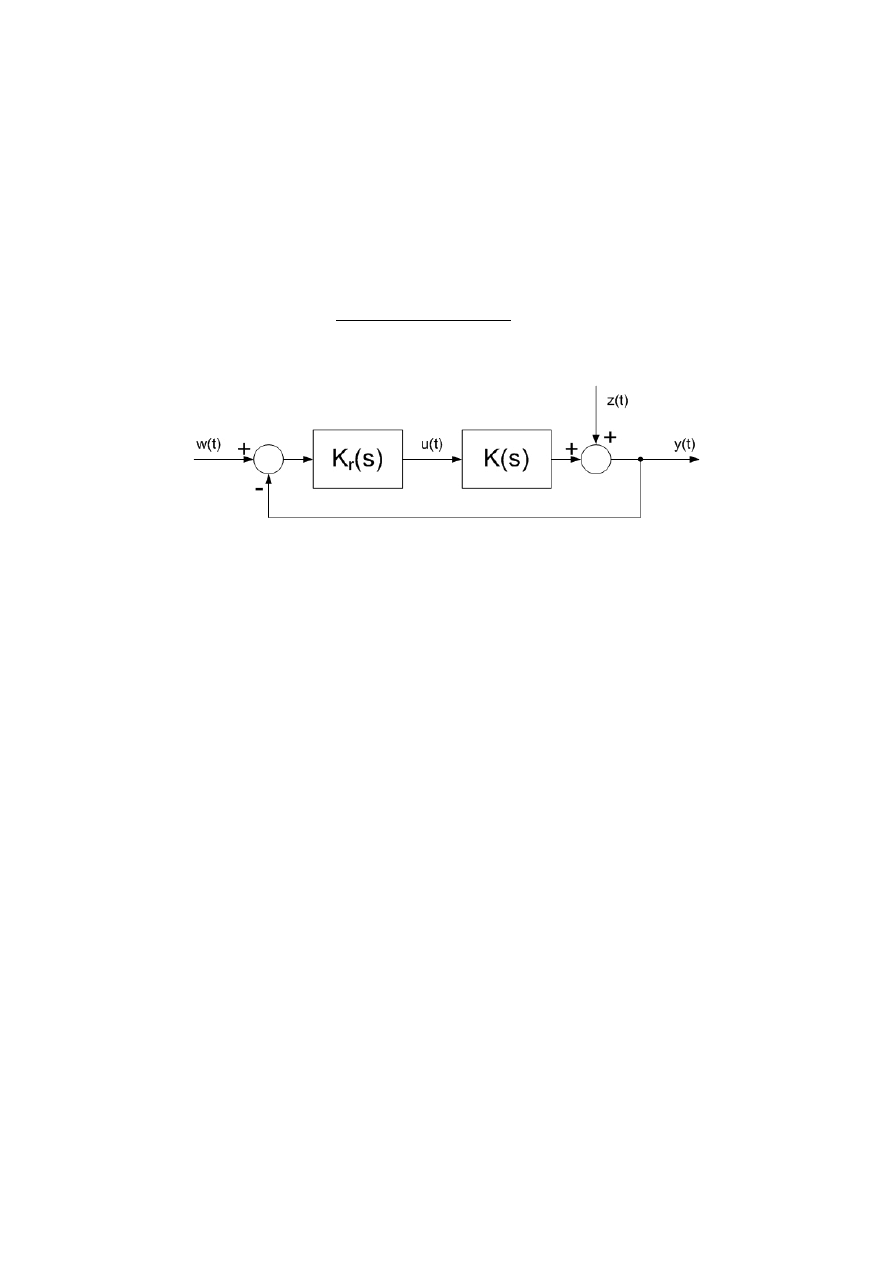
1. Cel ćwiczenia:
Celem ćwiczenia była komputerowa analiza własności układów regulacji na podstawie
charakterystyk częstotliwościowych: amplitudowo-fazowej (Nyquista) oraz wskaźników jakości
(regulacji oraz nadążania).
2. Program ćwiczenia:
Przeprowadź analizę zamkniętego układu regulacji przedstawionego na rysunku 1. z
obiektem o transmitancji: K s=
k
1s 1sT
1
1sT
2
; gdzie : k =3, T
1
=
4, T
2
=
6.
Rysunek 1. Schemat blokowy UR.
1. Zbadaj własności zamkniętego układu regulacji z obiektem o transmitancji K(s) i K
r
(s) = 1:
a) Sporządź charakterystykę amplitudowo-fazową układu otwartego, zaznacz i odczytaj
zapas amplitudy oraz fazy układu zamkniętego.
b) Sporządź przebieg y(t) odpowiedzi układu zamkniętego na wymuszenie skokowe w(t).
c) Sporządź przebiegi wskaźników regulacji oraz nadążania.
2. Zbadaj wpływ nastaw regulatora P { K
r
(s) = k
r
} na własności układu – dla trzech
wybranych wzmocnień k
r
wykreśl:
a) charakterystyki amplitudowo-fazowe układu otwartego, zaznaczyć zapasy amplitud i faz
układów zamkniętych;
b) odpowiedzi skokowe układu zamkniętych;
c) przebiegi wskaźników częstotliwościowych.
d) Wskaż „optymalną” nastawę regulatora P i uzasadnij swój wybór (uwzględnij: zapas
fazy, zapas modułu, czas regulacji, przeregulowanie, błąd w stanie ustalonym).
3. Zbadaj wpływ nastaw regulatora PI { K
r
(s) = k
r
(1+1/sT
c
) }na własności układu – dla trzech
dowolnych nastaw T
c
dobierz k
r
tak aby zapas amplitudy wynosił Δk = 2; wykreśl komplet
charakterystyk (jak w punkcie 2); wskaż „najlepsze” nastawy regulatora.
4. Zbadaj wpływ nastawy regulatora PID { K
r
(s) = k
r
(1+1/sT
c
+sT
d
) } na własności układu –
wykreśl komplet charakterystyk (jak w punkcie 2) dla jednego zestawu nastaw k
r
, T
c
, T
d
zapewniającego „akceptowalne” własności zamkniętego układu regulacji.
5. Zbadaj wpływ regulatorów P, PI, PID – dla wybranych „najlepszych” nastaw regulatora P,
PI oraz PID wykreśl wskaźnik nadążania oraz wskaźnik tłumienia zakłóceń; skomentuj
wyniki.
6. Dokonaj analizy odpowiedzi układu zamkniętego, z regulatorem PI (lub PID) na
wymuszenie w(t) = sin(ωt):
Z charakterystyki nadążania M(ω) wybierz trzy wartości częstotliwości z pasm: ω
1
–
nadążania, ω
2
– rezonansowego (ω
2
= w
rez
) i ω
3
– nadrezonansowego. Wykreśl
odpowiedzi (w stanie ustalonym) układu zamkniętego na wymuszenie sinusoidalne
w(t) = sin(ωt) dla ω = ω
1
, ω
2
, ω
3
. Porównaj stosunek amplitud, sygnału wyjściowego
y(t) do wejściowego w(t), z wartością wskaźnika nadążania dla odpowiednich ω.
3. Realizacja zadań:
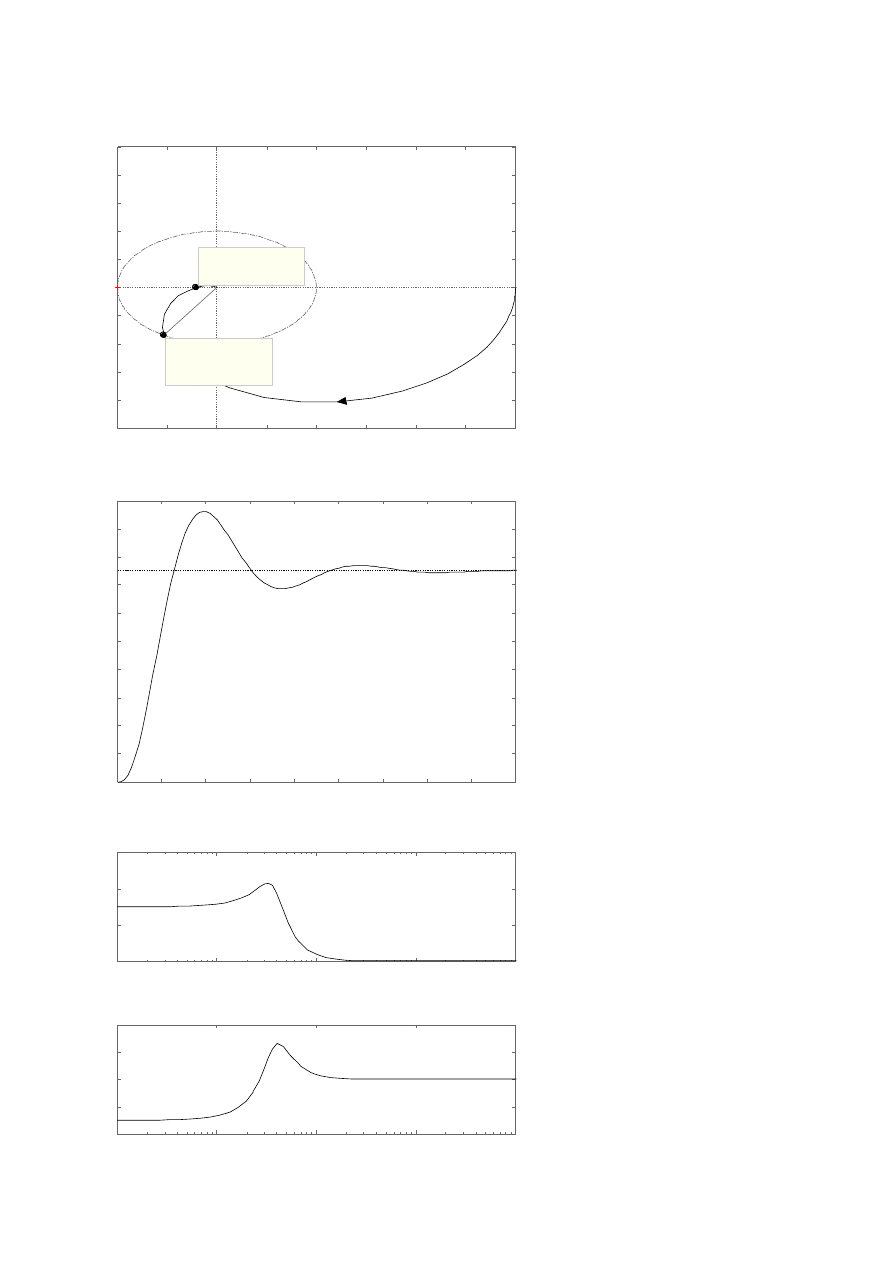
Ad 1.a)
L=13,7 dB
k ≈4,84
=
57,7
o
Ad 1.b)
Ad 1.c)
0
5
1 0
1 5
2 0
2 5
3 0
3 5
4 0
4 5
0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 7
0 . 8
0 . 9
1
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e
- 1
- 0 . 5
0
0 . 5
1
1 . 5
2
2 . 5
3
- 2 . 5
- 2
- 1 . 5
- 1
- 0 . 5
0
0 . 5
1
1 . 5
2
2 . 5
S y s t e m : K
G a in M a r g i n ( d B ) : 1 3 . 7
A t f r e q u e n c y ( r a d / s e c ) : 0 . 6 7 7
C lo s e d L o o p S t a b le ? Y e s
S y s t e m : K
P h a s e M a r g in ( d e g ) : 5 7 . 7
D e la y M a r g in ( s e c ) : 3 . 6 4
A t f r e q u e n c y ( r a d / s e c ) : 0 . 2 7 7
C l o s e d L o o p S t a b le ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
M
a
g
n
it
u
d
e
(
a
b
s
)
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
M
a
g
n
it
u
d
e
(
a
b
s
)
W s k a z n i k n a d a z a n i a
F r e q u e n c y ( r a d / s e c )
W s k a z n i k r e g u l a c j i
F r e q u e n c y ( r a d / s e c )
Ad 2.a)
Legenda:
– dla k
r
= 0,6
-- dla k
r
= 1,24
-·- dla k
r
= 2
Dla k
r
= 0,6: L=18,2 dB
k ≈8,13
=
88,6
o
Dla k
r
= 1,24: L=11,9 dB
k ≈3,94
=
47,4
o
Dla k
r
= 2: L=7,71 dB
k ≈2,43
=
28,0
o
Ad 2.b)
Legenda:
– dla k
r
= 0,6
-- dla k
r
= 1,24
-·- dla k
r
= 2
Ad 2.c)
Legenda:
– dla k
r
= 0,6
-- dla k
r
= 1,24
-·- dla k
r
= 2
- 1
- 0 . 5
0
0 . 5
1
1 . 5
- 2
- 1 . 5
- 1
- 0 . 5
0
0 . 5
1
S y s t e m : K 1
G a i n M a r g in ( d B ) : 1 8 . 2
A t f r e q u e n c y ( r a d / s e c ) : 0 . 6 7 7
C l o s e d L o o p S t a b le ? Y e s
S y s t e m : K 1
P h a s e M a r g in ( d e g ) : 8 8 . 6
D e la y M a r g in ( s e c ) : 8 . 8 2
A t f r e q u e n c y ( r a d / s e c ) : 0 . 1 7 5
C lo s e d L o o p S t a b l e ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : G 2
F r e q u e n c y ( r a d / s e c ) : 0 . 3 7 1
M a g n it u d e ( a b s ) : 1 . 3
W s k a z n i k n a d a z a n i a
F r e q u e n c y ( r a d / s e c )
W s k a z n i k r e g u l a c j i
F r e q u e n c y ( r a d / s e c )
Ad 2.d)
Ze wzrostem wzmocnienia regulatora k
r
:
●
zmniejsza się zapas fazy Δφ;
●
zmniejsza się zapas amplitudy Δk;
●
zwiększa się czas regulacji;
●
rośnie przeregulowanie;
●
zmniejsza się uchyb regulacji w stanie ustalonym ze względu na wymuszenie w;
●
rośnie szerokość pasma nadążania;
●
wzrasta wartość częstotliwości (pulsacji) rezonansowej ω
rez
;
●
wzrasta wartość piku rezonansowego;
●
wzrasta zdolność tłumienia zakłócenia z w pasmie niskich częstotliwości;
Układ regulacji uważamy za dobrej jakości jeżeli spełnione są jednocześnie dwa warunki:
●
zapas modułu jest większy niż 6 do 8 dB;
●
zapas fazy jest większy niż 30
o
.
Często przy określeniu jakości regulacji stosuje się kryterium maksymalnego modułu –
najkorzystniej jeśli charakterystyka nadążania posiada pik rezonansowy o wartości 1,2 do 1,3.
Aby działanie układu regulacji było optymalne sugerowano się kryterium maksymalnego modułu.
Na charakterystyce nadążania zaznaczono wartość maksymalnego modułu (równą 1,3) i w ten
sposób określono optymalną nastawę k
r
. Dla tej nastawy spełnione są warunki dotyczące zapasu
modułu i zapasu fazy.
Wybrana optymalna nastawa regulatora:
k
r
= 1,24
Ad 3.a)
Legenda:
– dla k
r
= 1,25, T
c
= 6
-- dla k
r
= 1,939, T
c
= 15
-·- dla k
r
= 2,182, T
c
= 30
Dla k
r
=1,25 T
c
=6: L=6,02 dB
k =2
=
16,8
o
Dla k
r
=1,939 T
c
=15: L=6,02 dB
k =2
=
19,8
o
Dla k
r
=2,182 T
c
=30: L=6,02 dB
k =2
=
20,6
o
- 2
- 1
0
1
2
3
4
- 1 0
- 8
- 6
- 4
- 2
0
S y s t e m : K 3
G a in M a r g in ( d B ) : 6 . 0 2
A t f r e q u e n c y ( r a d / s e c ) : 0 . 6 4 4
C lo s e d L o o p S t a b le ? Y e s
S y s t e m : K 3
P h a s e M a r g in ( d e g ) : 2 0 . 6
D e la y M a r g in ( s e c ) : 0 . 7 9 5
A t f r e q u e n c y ( r a d / s e c ) : 0 . 4 5 2
C lo s e d L o o p S t a b l e ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
Ad 3.b)
Legenda:
– dla k
r
= 1,25, T
c
= 6
-- dla k
r
= 1,939, T
c
= 15
-·- dla k
r
= 2,182, T
c
= 30
Ad 3.c)
Legenda:
– dla k
r
= 1,25, T
c
= 6
-- dla k
r
= 1,939, T
c
= 15
-·- dla k
r
= 2,182, T
c
= 30
Ad 3.d)
Ze wzrostem wartości nastaw regulatora w taki sposób, że zapas modułu jest stały Δk = 2 zachodzi:
●
zwiększa się zapas fazy Δφ;
●
maleje czas regulacji;
●
maleje wartość przeregulowania;
●
stały zerowy uchyb regulacji w stanie ustalonym ze względu na skokowe wymuszenie w;
●
rośnie szerokość pasma nadążania;
●
wzrasta wartość częstotliwości (pulsacji) rezonansowej ω
rez
;
●
zmniejsza się wartość piku rezonansowego;
●
wzrasta zdolność tłumienia zakłócenia z w pasmie niskich częstotliwości;
Należy zauważyć, że układ regulacji nie spełnia w żadnym z pokazanych przypadków warunku by
zapas fazy był większy od 30
o
. Zapewnienie aby ten warunek był spełniony wymaga zmiany
wartości żądanego zapasu modułu. Parametrów nie można zwiększać w nieskończoność z tego
względu, że dla bardzo wysokich wartości T
c
wpływ całkującego składnika będzie znikomy
(pomijalny) i regulacja będzie bardzo bliska tej jak gdyby zastosować regulator P.
Wybrana optymalna nastawa regulatora:
k
r
= 2,182, T
c
= 30
0
2 0
4 0
6 0
8 0
1 0 0
1 2 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 . 6
1 . 8
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
1
2
3
4
M
a
g
n
it
u
d
e
(
a
b
s
)
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
1
2
3
4
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : G 3
F r e q u e n c y ( r a d / s e c ) : 0 . 4 8 2
M a g n it u d e ( a b s ) : 3
W s k a z n i k n a d a z a n i a
F r e q u e n c y ( r a d / s e c )
W s k a z n i k r e g u l a c j i
F r e q u e n c y ( r a d / s e c )
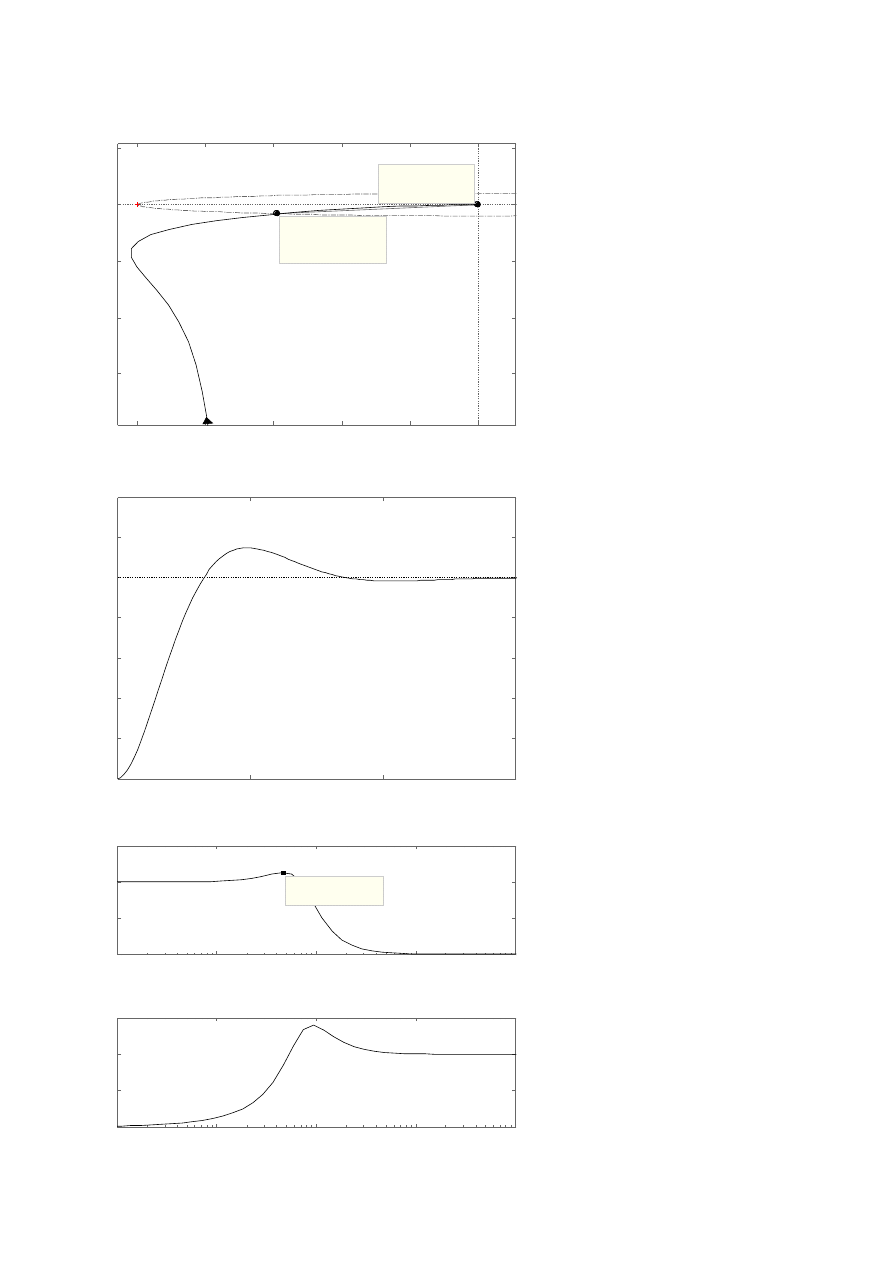
Ad 4.
Nastawy regulatora:
k
r
= 2.5,
T
c
= 10,
T
d
= 2
Ad 4.a)
L=∞
k =∞
=
53,9
o
Ad 4.b)
Ad 4.c)
- 1
- 0 . 8
- 0 . 6
- 0 . 4
- 0 . 2
0
- 1 5
- 1 0
- 5
0
5
S y s t e m : K o
P h a s e M a r g in ( d e g ) : 5 3 . 9
D e la y M a r g in ( s e c ) : 1 . 6 3
A t f r e q u e n c y ( r a d / s e c ) : 0 . 5 7 9
C lo s e d L o o p S t a b le ? Y e s
S y s t e m : K o
G a in M a r g in ( d B ) : In f
A t f r e q u e n c y ( r a d / s e c ) : In f
C lo s e d L o o p S t a b le ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
5
1 0
1 5
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
M
a
g
n
it
u
d
e
(
a
b
s
)
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 0 . 4 6 8
M a g n it u d e ( a b s ) : 1 . 1 3
W s k a z n i k n a d a z a n i a
F r e q u e n c y ( r a d / s e c )
W s k a z n i k r e g u l a c j i
F r e q u e n c y ( r a d / s e c )
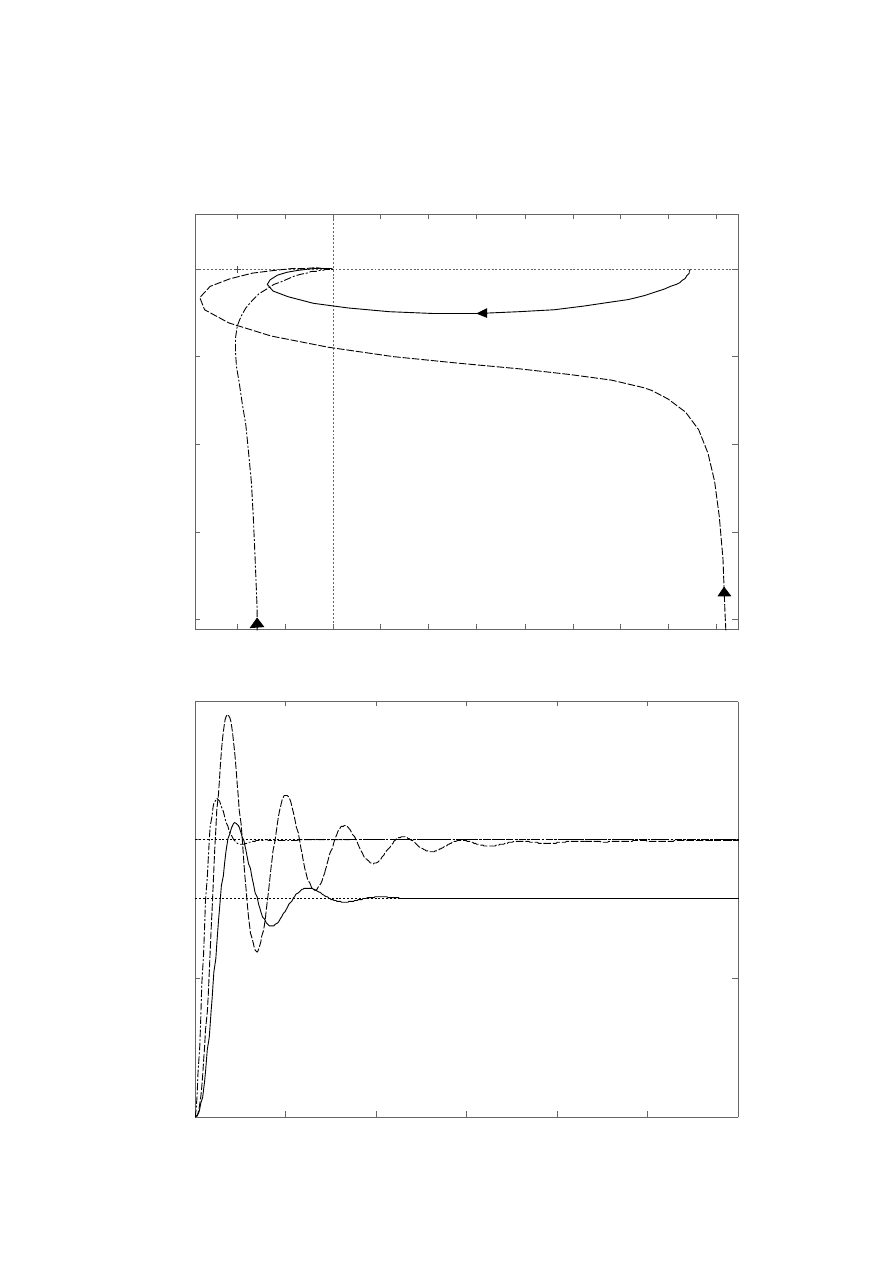
Ad 5.
Legenda:
Nastawy dla regulatorów:
P:
k
r
= 1,24
–
PI:
k
r
= 2,182 T
c
= 30
--
PID:
k
r
= 2,5
T
c
= 10
T
d
= 2
-·-
- 1
- 0 . 5
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
4
- 2 0
- 1 5
- 1 0
- 5
0
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
2 0
4 0
6 0
8 0
1 0 0
1 2 0
0
0 . 5
1
1 . 5
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
li
tu
d
e
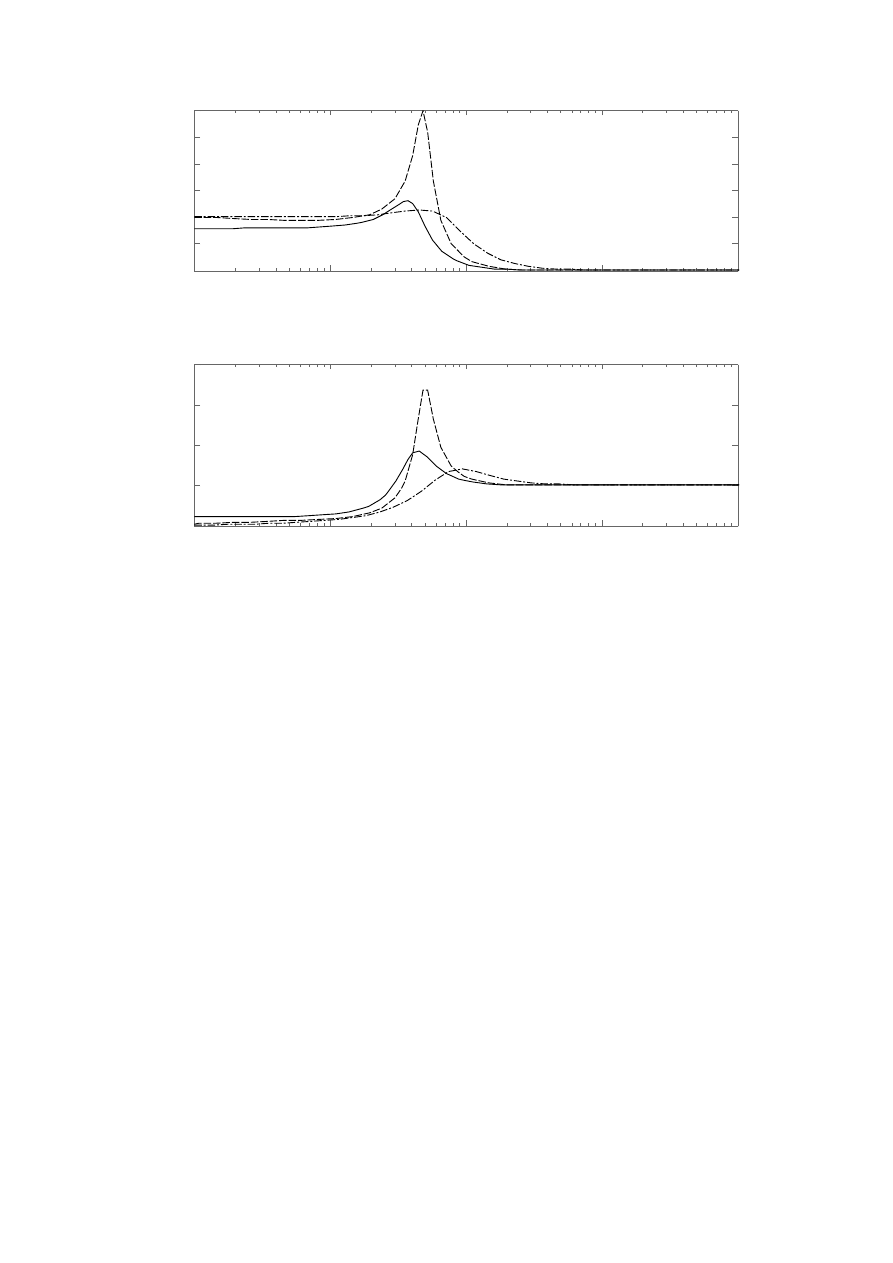
Komentarze:
●
Najszerszym pasmem tłumienia zakłócenia z charakteryzuje sie układ z regulatorem PID
natomiast najwęższym układ z regulatorem P.
●
Wartość piku rezonansowego charakterystyki nadążania jest najwyższa dla układu z
regulatorem PI. Świadczy to o tym że przy użyciu tego regulatora (te same nastawy) w
odpowiedzi skokowej będą występować stosunkowo duże oscylacje i przeregulowanie.
Natomiast dla regulatora PID pik ten ma najmniejszą wartość co jest równoznaczne z
niedużym przeregulowaniem odpowiedzi na wymuszenie skokowe w oraz krótkotrwałymi
oscylacjami.
●
Z faktu że wartość modułu dla niskich częstotliwości regulatorów PI i PID jest bliska jeden
można wnioskować o zerowej wartości uchybu regulacji w stanie ustalonym na wymuszenie
skokowe w. Dla regulatora P uchyb ten nie jest zerowy.
●
Układy regulacji z regulatorami PI i PID całkowicie tłumią zakłócenia nie zmieniające się w
czasie w odróżnienia do układu z regulatorem P.
●
Z faktu narzucenia wartości zapasu modułu na stałym poziomie dla układu z regulatorem PI
nie udało się uzyskać wymaganej wartości zapasu fazy ani maksymalnego modułu. Gdyby
zignorować ten warunek, wówczas można by dobrać nastawy regulatora tak, aby pasmo
nadążania było szersze niż dla regulatora P.
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
1
2
3
4
M
a
g
n
it
u
d
e
(
a
b
s
)
W s k a z n i k n a d a z a n i a
F r e q u e n c y ( r a d / s e c )
W s k a z n i k r e g u l a c j i
F r e q u e n c y ( r a d / s e c )
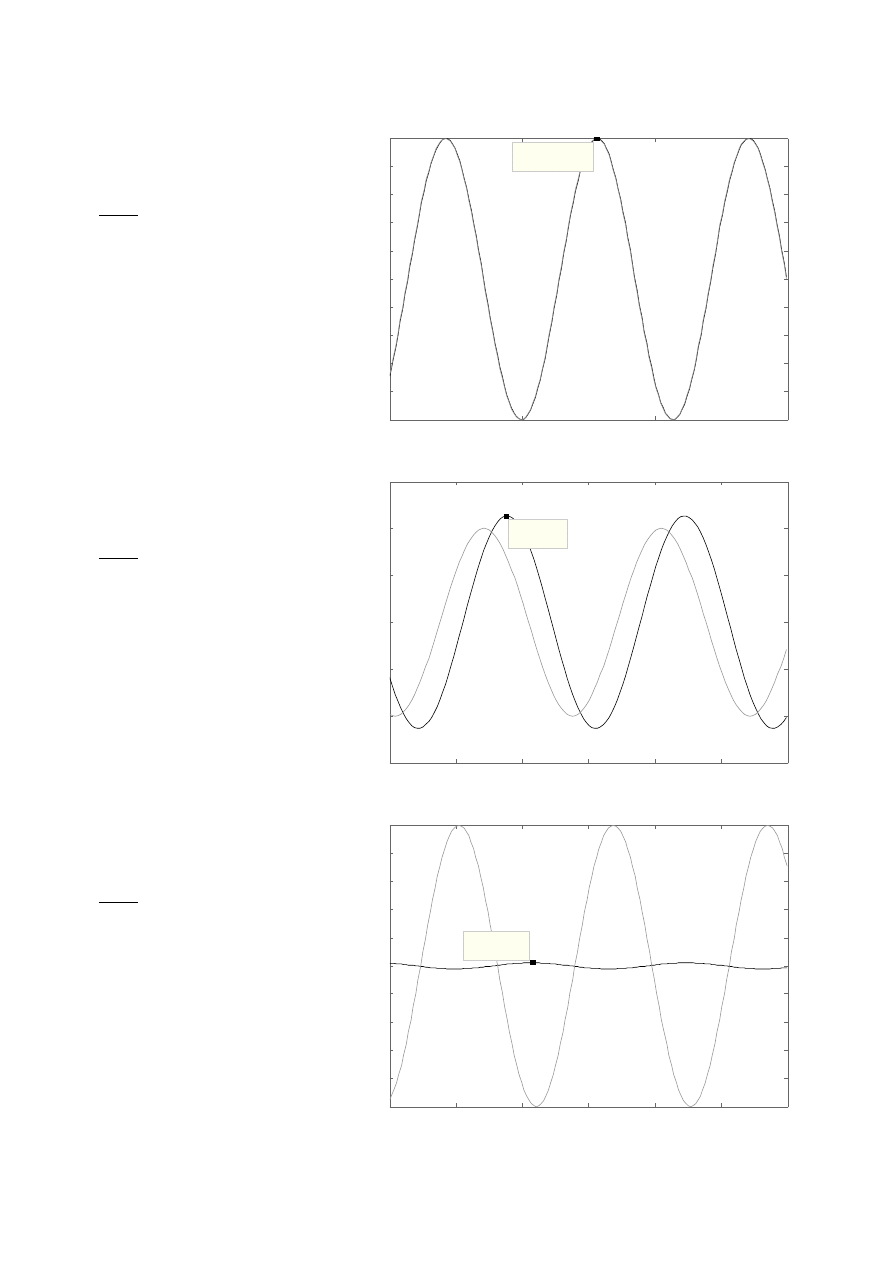
Ad 5.
Układ z regulatorem PID o nastawach:
k
r
= 2,5
T
c
= 10
T
d
= 2
Dla : w
1
=
0,011 rad /sec
W
max
=
1
Y
max
≈
1
Y
max
W
max
=
1
M w
1
=
1
Dla : w
2
=
w
rez
=
0,47 rad / sec
W
max
=
1
Y
max
≈
1,13
Y
max
W
max
=
1,13
M w
1
=
1,13
Dla : w
3
=
5,4 rad / sec
W
max
=
1
Y
max
≈
0,022
Y
max
W
max
=
0,022
M w
1
=
0,022
Stosunki amplitud sygnału wyjściowego do wejściowego dla odpowiednich wartości ω
są równe z dużą dokładnością wartością odpowiednich wskaźników nadążania M(ω).
8 5 0 0
9 0 0 0
9 5 0 0
1 0 0 0 0
- 1
- 0 . 8
- 0 . 6
- 0 . 4
- 0 . 2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
S y s t e m : G
T im e ( s e c ) : 9 . 2 8 e + 0 0 3
A m p l it u d e : 0 . 9 9 9
L i n e a r S i m u l a t i o n R e s u l t s
T i m e ( s e c )
A
m
p
li
tu
d
e
1 7 0
1 7 5
1 8 0
1 8 5
1 9 0
1 9 5
2 0 0
- 1 . 5
- 1
- 0 . 5
0
0 . 5
1
1 . 5
S y s t e m : G
T im e ( s e c ) : 1 7 9
A m p li t u d e : 1 . 1 3
L i n e a r S i m u l a t i o n R e s u l t s
T i m e ( s e c )
A
m
p
li
tu
d
e
3 7
3 7 . 5
3 8
3 8 . 5
3 9
3 9 . 5
4 0
- 1
- 0 . 8
- 0 . 6
- 0 . 4
- 0 . 2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
S y s t e m : G
T im e ( s e c ) : 3 8 . 1
A m p lit u d e : 0 . 0 2 1 5
L i n e a r S i m u l a t i o n R e s u l t s
T i m e ( s e c )
A
m
p
li
tu
d
e
4. Kody źródłowe programów:
Kod źródłowy do punktu 5 (kody źródłowe do punktów 1 do 4 są analogiczne):
close all;
clear all;
clc;
% Definicja transmitancji:
k=3;
T1=4;
T2=6;
s=tf('s');
K=k/(1+s)/(1+s*T1)/(1+s*T2);
Kr1=1.24;
Kr2=2.182*(1+1/(s*30));
Kr3=2.5*(1+1/(s*10)+(s*2));
K1=minreal(K*Kr1);
K2=minreal(K*Kr2);
K3=minreal(K*Kr3);
G1=minreal(K1/(1+K1));
G2=minreal(K2/(1+K2));
G3=minreal(K3/(1+K3));
G1z=minreal(1/(1+K1));
G2z=minreal(1/(1+K2));
G3z=minreal(1/(1+K3));
% Charakterystyki amplitudowo-fazowa:
figure;
hold on;
nyquist(K1,'-k');
nyquist(K2,'--k');
nyquist(K3,'-.k');
title('Nyquist Diagram','FontSize',14);
xlabel('Real Axis','FontSize',12);
ylabel('Imaginary Axis','FontSize',12);
% Odpowiedz skokowa ukladu zamknietego:
figure;
hold on;
step(G1,'-k');
step(G2,'--k');
step(G3,'-.k');
title('Step Response','FontSize',14);
xlabel('Time','FontSize',12);
ylabel('Amplitude','FontSize',12);
% Wskazniki czestotliwosciowe:
figure;
subplot(2,1,1);
hold on;
bodemag(G1,'-k');
bodemag(G2,'--k');
bodemag(G3,'-.k');
title('Wskaznik nadazania','FontSize',14);
xlabel('Frequency','FontSize',12);
ylabel('Magnitude','FontSize',12);
xlim([10^(-2) 10^(2)]);
subplot(2,1,2);
hold on;
bodemag(G1z,'-k');
bodemag(G2z,'--k');
bodemag(G3z,'-.k');
title('Wskaznik regulacji','FontSize',14);
xlabel('Frequency','FontSize',12);
ylabel('Magnitude','FontSize',12);
xlim([10^(-2) 10^(2)]);
Kod źródłowy do punktu 6:
close all;
clear all;
clc;
% Definicja transmitancji:
k=3;
T1=4;
T2=6;
s=tf('s');
K=k/(1+s)/(1+s*T1)/(1+s*T2);
Kr=2.5*(1+1/(s*10)+(s*2));
Ko=minreal(K*Kr);
G=minreal(Ko/(1+Ko));
% Definicja pulsacji:
w1=0.011; % pasmo nadazania Mag=1
w2=0.47; % pasmo rezonansowe (w2=w_rez) Mag=1,13
w3=5.4; % pasmo nadrezonansowe Mag=0,022
% Wygenerowania pobudzenia w(t)=sin(wT):
[W1,T1]=gensig('sin',2*pi/w1,10000);
[W2,T2]=gensig('sin',2*pi/w2,200);
[W3,T3]=gensig('sin',2*pi/w3,40);
% przebiegi w stanie ustalonym:
figure;
lsim(G,W1,T1);
xlim([8500 10000]);
title('Linear Simulation Results','FontSize',14);
xlabel('Time','FontSize',12);
ylabel('Amplitude','FontSize',12);
figure;
lsim(G,W2,T2);
xlim([170 200]);
title('Linear Simulation Results','FontSize',14);
xlabel('Time','FontSize',12);
ylabel('Amplitude','FontSize',12);
figure;
lsim(G,W3,T3);
xlim([37 40]);
title('Linear Simulation Results','FontSize',14);
xlabel('Time','FontSize',12);
ylabel('Amplitude','FontSize',12);
5. Wnioski końcowe:
●
Dla obiektów w których nie występuje czynnik całkujący i nie można dobrać zbyt dużego
wzmocnienia regulatora P ze względu na utratę stabilności układu, najkorzystniej urzyć
regulatora PI lub PID zapewniających zerowy uchyb regulacji w stanie ustalonym dla
skokowych zmian wymuszenia w. Regulator P zmniejsza wartość uchybu ze wzrostem jego
wzmocnienia.
●
Najlepszą jakość regulacji zapewnia regulator PID nawet przy zdroworozsądkowych jego
nastawach.
●
W przypadku układów śledzących najkorzystniej dobrać w taki sposób nastawy regulatora
aby maksymalna częstotliwość wymuszenia (bądź najwyższa znacząca harmoniczna)
znajdowała się w paśmie nadążania układu regulacji.
●
Aby uniknąć oscylacji sygnału wyjściowego dla wymuszeń skokowych należy zadbać aby
charakterystyka M(ω) nie posiadała piku rezonansowego.
●
Częstotliwości rezonansowe wskaźnika nadążania i wskaźnika tłumienia zakłócenia są
różne.