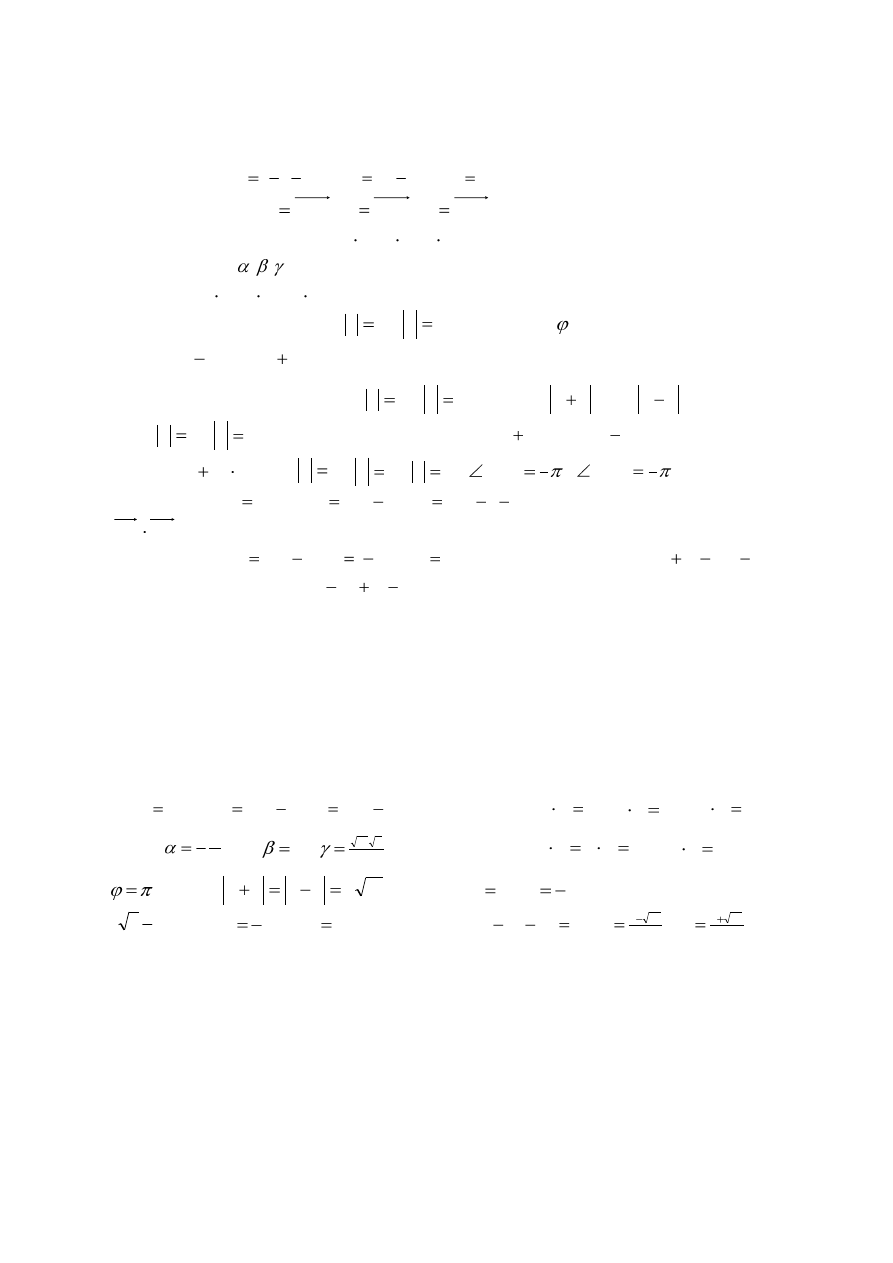
ILOCZYN SKALARNY.
1. Dane są punkty
).
1
,
1
,
3
(
),
4
,
1
,
2
(
),
2
,
2
,
1
(
3
2
1
A
A
A
(a) Znaleźć wektory
2
1
A
A
a
,
3
2
A
A
b
,
3
1
A
A
c
(b) Obliczyć iloczyny skalarne
a b b c a c
,
,
(c) Znaleźć kąty
,
,
pomiędzy wektorami, odpowiednio,
c
a
c
b
b
a
i
,
i
,
i
(d) Znaleźć
a a b b c c
,
,
2. Dane są wektory a
,
b
takie, że
4
a
,
2
b
. Obliczyć kąt pomiędzy tymi wektorami, jeśli
wektory
b
a
3
oraz
b
a
2
są prostopadłe.
3. Wektory a
,
b
są prostopadłe oraz
2
a
,
6
b
. Obliczyć
b
a
oraz
b
a
.
4. Dane:
6
a
,
2
b
. Wyznaczyć m tak, by wektory
b
m
a
oraz
b
m
a
były prostopadłe.
5. Obliczyć
c
b
a
)
(
, jeśli
5
a
,
3
b
,
2
c
,
6
1
)
,
( c
a
,
3
2
)
,
(
c
b
.
6. Dane są punkty
)
,
2
,
1
(
),
,
1
,
(
a
B
a
a
A
,
)
1
,
3
,
2
( a
C
. Znaleźć
a
takie, by wektory
AC
,
AB
były prostopadłe
7. Dane są wektory
]
1
,
2
,
1
[
a
,
]
3
,
1
,
2
[
b
]
1
,
2
,
0
[
c
. Dla jakiego t wektor
c
b
t
a
t
)
1
(
jest prostopadły do wektora
c
t
b
t
a
)
1
(
?
Odpowiedzi.
1. (a)
]
1
,
3
,
4
[
],
,
3
,
2
,
1
[
],
2
,
1
,
3
[
c
b
a
(b)
-1
b
a
,
13
c
a
.
13
c
b
(c)
14
1
cos
,
14
7
13
cos
cos
(d)
14
b
b
a
a
,
26
c
c
2.
3.
10
2
b
a
b
a
4.
3
m
,
3
m
5.
3
3
5
6.
4
a
lub
1
a
7.
0
10
4
3
2
t
t
,
3
34
2
1
t
,
3
34
2
2
t